Произведение векторов онлайн: Онлайн калькулятор. Векторное произведение векторов

Содержание

Векторная алгебра. Скалярное произведение векторов

Похожие презентации:

Векторная алгебра

Скалярное произведение векторов

Координаты вектора в пространстве. Скалярное и векторное произведения векторов

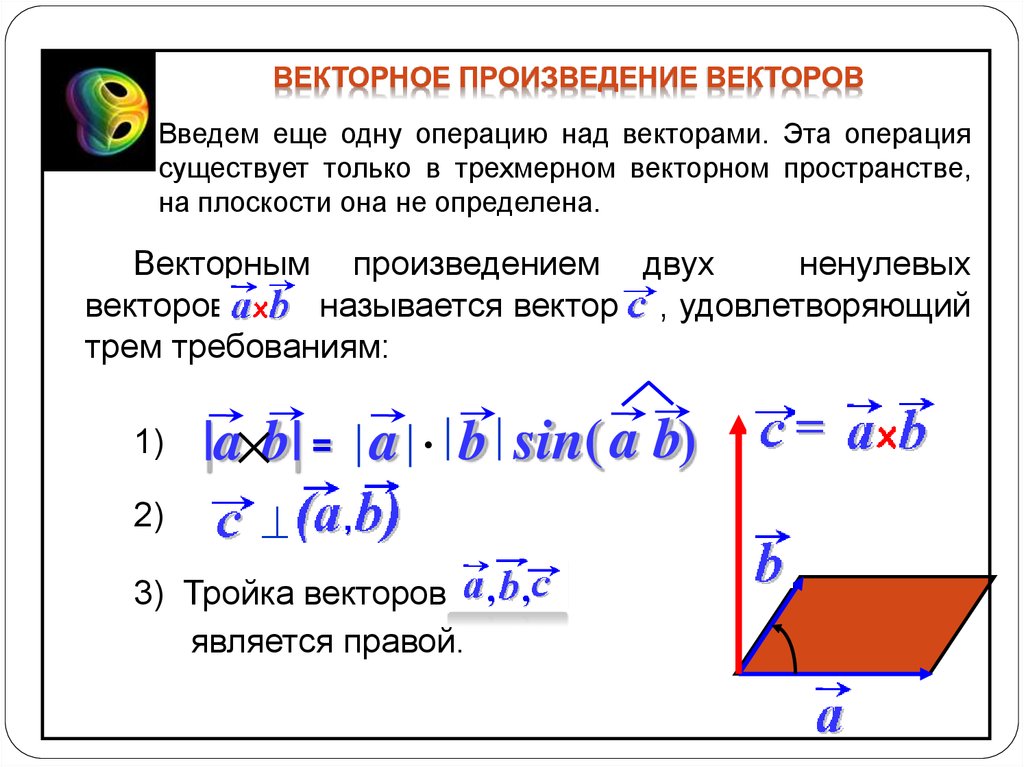
Векторное произведение векторов

Вектора. Пространства. Скалярное, векторное и смешанное произведение векторов

Векторная алгебра. Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов

Векторная алгебра

Векторы. Основные понятия

Векторы. Смешанное произведение векторов

Элементы векторной алгебры и аналитической геометрии

2. ВЕКТОРНАЯ АЛГЕБРА
2.1 Векторы, общие понятия
2.2 Скалярное произведение векторов
2.3 Векторное произведение векторов
2.4 Смешанное произведение векторов
2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ОПР. Скалярным произведением двух векторов a и b
называется число (скалярная величина), равная
произведению модулей этих векторов на косинус угла
между ними:

a b a b cos
Обозначение:
a b или
a,b
Свойства скалярного произведения
1)
a b b a
2)
(a b ) c a c b c
3)
( a ) b (a b ) a ( b )
2.

2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства скалярного произведения (продолжение)
4) Связь скалярного произведения с проекцией одного вектора на
ось, задаваемую другим:
a b a b cos a ПРa b
a b a cos b ПРb a b
ПРa b
a b
ПРb a
b
5) Связь скалярного произведения с длиной вектора:
a a a a cos0 a
2
длина вектора равна квадратному
корню из скалярного квадрата:
a b
a
a a
2
2
a a2
2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства скалярного произведения (продолжение)
6) Нахождение угла между векторами:
cos cos a , b
a b
cos
a b
m
а) если — острый угол, то
cos 0 a b 0
arccos m
б) если — тупой угол, то
cos 0
a b 0
arccos m
2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Свойства скалярного произведения (продолжение)
7) КРИТЕРИЙ ПЕРПЕНДИКУЛЯРНОСТИ ВЕКТОРОВ
a b a b 0
!
2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление скалярного произведения векторов,
заданных координатами
i 1;0;0 , j 0;1;0 , k 0;0;1
» » i
j
k
По определению скалярного произведения:
i
1
0
0
i i i i cos 00 1
j
0
1
0
j j j j cos 00 1
k
0
0
1
k k k k cos 00 1
i j j i i j cos900 0
j k k j j k cos900 0
k i i k k i cos900 0
2.

2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление скалярного произведения векторов,
заданных координатами
Пусть заданы векторы:
a ax ; a y ; az ax i a y j az k
b bx ; by ; bz bx i by j bz k
Найдем их скалярное произведение (выведем формулу):
a b ax i a y j az k bx i by j bz k
axbx i 1 i axby i 0 j axbz i 0 k
a ybx j0 i a yby j1 j a ybz j0 k
azbx k 0 i azby k 0 j azbz k 1 k ax bx a y by az bz
a b ax bx ay by az bz
2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
Даны векторы:
a 0;1; 3 , b 1;1;2
1) Найти их скалярное произведение.
2) Найти косинус угла между ними.
3) Найти проекцию вектора
a на вектор b .
1) a b 0 1 1 1 3 2 5
5
5
5
a b
2) cos
2
10 6
2 15
a b
02 12 3 12 12 22
a b
3) ПРb a
b
5
5
2
2
2
6
1 1 2
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ОПР. Векторным произведением вектора a на вектор b
называется вектор c , такой что:
1) (длина вектора)
c a b sin
2) (направление вектора)
c a; c b
3) (направление вектора)
a , b , c правая тройка
Обозначение:
a b или
a , b
Свойства векторного произведения
1)
a b b a
2)
(a b ) c a c b c
3)
( a ) b (a b ) a ( b )
2.

3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства векторного произведения (продолжение)
4) КРИТЕРИЙ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ
a b a b 0
!!
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление векторного произведения векторов,
заданных координатами
i 1;0;0 , j 0;1;0 , k 0;0;1
По определению векторного произведения:
2
» » i
1
j
k
i
0
k
j
i i i i sin 00 0
i i 0
j
k
0
i
j j j j sin 00 0
j j 0
j
i
0
k k k k sin 00 0
k k 0
k
i j i j sin 900 1
i j k
j k j k sin 900 1
j k i k j i
k i k i sin 900 1
k i j
j i k
i k j
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление векторного произведения векторов,
заданных координатами
Пусть заданы векторы:
a ax ; a y ; az ax i a y j az k
b bx ; by ; bz bx i by j bz k
Найдем их векторное произведение (выведем формулу):
a b ax i a y j az k bx i by j bz k
axbx i 0 i axby i k j axbz i kj
a ybx j
ki a yby j0 j a ybz ji k
azbx k j i azby k
ij azbz k 0 k
2.

3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление векторного произведения векторов,
заданных координатами
Сгруппируем по векторам:
i a ybz azby j axbz azbx k axby a ybx
Получили разложение определителя по 1 строке:
i
j
k
ax
ay
az
bx
by
bz
i
j
k
a b ax
ay
az
bx
by
bz
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Геометрический смысл векторного произведения
Sпараллелограмма a b sin
c
c
b
a
S пар. a b
Модуль векторного произведения двух векторов равен площади
параллелограмма, построенного на этих векторах.
1
S a b
2

Площадь треугольника, построенного на векторах a и b , равна
половине длины векторного произведения этих векторов.
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
1) Даны векторы:
a 3;0;2 , b 1;2; 1 .
Найти их векторное произведение.
i
j
a b 3 0
1
2
k
2 i 0 4 j 3 2 k 6 0
1
4 i j 6k 4; 1; 6
2.

3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
B
2) Найти высоту BD треугольника ABC, если
A 1;3;0 , B 0; 2;2 , C 5; 3;0 .
A
1
S AB AC
2
1
S AC BD
2
AC AC
D
1
1
AB AC AC BD
2
2
BD
AB AC
AC
C
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
AB AC
BD
AC
A 1;3;0 , B 0; 2;2 , C 5; 3;0
AB 0 1; 2 3;2 0 1; 5;2
AC 5 1; 3 3;0 0 6; 6;0
i
j
k
AB AC 1 5 2 i 0 12 j 0 12 k 6 30
6 6

12 i 12 j 24k 12; 12; 24
0
AB AC 122 12 24 12 6
2
AC
6 6
2
2
02 6 2
2
12 6
BD
2 3
6 2
2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ОПР. Cмешанным произведением трех векторов
называется число (скалярная величина): a b c
Обозначение:
a b c,
или
a, b, c ,
или abc
Свойства смешанного произведения
1)
2)
3)
a b c a b c
a a bc a bc a bc
1
2
1
2
c
b
Закон круговой переместительности:
abc bca cab bac cba acb
a
2.

4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
3) Тройка векторов определяет знак смешанного произведения:
abc 0
a, b, c правая тройка,
abc 0
a, b, c левая тройка.
4) КРИТЕРИЙ КОМПЛАНАРНОСТИ ВЕКТОРОВ
!!!
a, b,c — компланарны abc 0
В частности, смешанное произведение равно нулю, если в нем
два множителя одинаковы:

aac 0
2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление смешанного произведения векторов,
заданных координатами
Пусть заданы векторы:
a ax ; a y ; az ax i a y j az k
b bx ; by ; bz bx i by j bz k
c cx ; c y ; cz cx i c y j cz k
Найдем их смешанное произведение (выведем формулу):
abc a b c
a b i a ybz azby j axbz azbx k axby a ybx
a b a b ; a b a b ; a b
y z
z y
x z
z x
x y
a ybx
2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление смешанного произведения векторов,
заданных координатами
Используем формулу для нахождения скалярного произведения
векторов, заданных координатами:
abc a b c cx a ybz azby c y axbz azbx cz axby a ybx
Получили разложение определителя по 1 строке:
cx
cy
cz
ax
ay
az
bx
by
bz
Поменяем два раза
местами строки: 1 и 2,
2и3
ax
ay
az
abc bx
by
bz
cx
cy
cz
ax
ay
az
bx
by
bz
cx
cy
cz
2.

4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Геометрический смысл смешанного произведения
c b
Объем параллелепипеда,
построенного на трех векторах,
равен абсолютной величине (модулю)
их смешанного произведения:
a
Объём треугольной призмы:
Объём треугольной пирамиды:
Vпараллелепипеда abc
Vпризмы
1
abc
2
Vпирамиды
1
abc
6
2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Пример
Найти объём треугольной пирамиды с вершинами
A 2; 2; 2 , B 4; 3; 3 , C 4; 5; 4 , D 5; 5; 6 .
А
D
В
С
2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Пример
Vпирамиды
A 2; 2; 2 , B 4; 3; 3 , C 4; 5; 4 , D 5; 5; 6 .
1
AB, AC , AD
6
AB 4 2;3 2;3 2 2;1;1
AC 4 2;5 2;4 2 2;3;2
AD 5 2;5 2;6 2 3;3;4
AB, AC , AD
2 1 1
2 3 2 2 3 4 1 2 3 2 3 1

3 3 4 1 3 3 1 2 4 2 3 2
24 6 6 9 8 12 7
Vпирамиды
1
7
1
7 1
6
6
6
Лекция выложена впервые.
Если Вы заметили ошибку, то сообщите мне на эл.

почту.

English Русский Правила

Калькулятор перекрестного произведения — векторный расчет

Перекрестное произведение, онлайн-исчисление

Резюме :

Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.

cross_product online

Описание :

Калькулятор перекрестного произведения может выполнять вычисления, указывая шагов расчета 9vec(v)` образуют прямую ортогональную ссылку.

Расчет векторного произведения онлайн

Расчет векторного произведения двух векторов онлайн выполняется очень быстро с помощью калькулятора векторного произведения , просто введите координаты двух векторов, а затем нажмите кнопку, позволяющую выполнить расчет векторного произведения. Чтобы

вычислить векторное произведение следующих векторов `vec(u)` [1;1;1] и `vec(v)` [5;5;6] , введите выражение cross_product(`[1;1;1];[5;5;6]`) после вычисления возвращаются результаты [1;-1;0].
Синтаксис:
cross_product(vector;vector)
Примеры:
В этом примере показано, как использовать калькулятор перекрестного произведения:
cross_product(`[1;1;1];[5;5;6]`), возвращает [1;-1;0]
Расчет онлайн с помощью cross_product (калькулятор перекрестного произведения)
См. также
Список связанных калькуляторов:
Векторный калькулятор : vector_calculator. Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
Вычисление разности двух векторов: vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.
Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
Вычисление суммы двух векторов: vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Прочие ресурсы
Исправленные упражнения на векторах
Игры векторного расчета
Научитесь считать с векторами

Калькулятор перекрестного произведения — векторные решения с пошаговыми инструкциями
Введение в калькулятор векторного произведения
Калькулятор векторного произведения — это онлайн-инструмент для вычисления векторного произведения двух векторов с целью их умножения. Он использует метод расширения для нахождения векторного произведения двух векторов и строит трехмерную диаграмму относительно заданных векторов. Перекрестное произведение иногда также называют векторным произведением.
В векторном исчислении основными понятиями являются скаляр и вектор. Вам часто нужно найти равнодействующую двух векторов, перемножив их вместе. Процесс нахождения равнодействующей двух векторов будет проще с помощью инструмента. Вот почему мы представляем инструмент, который может легко оценить векторное произведение двух векторов.
Формула, используемая Калькулятором векторов перекрестного произведения
Калькулятор векторов использует следующие формулы для оценки двух данных векторов:
Векторное произведение двух векторов A и B в трех измерениях может быть записано как:
$$ \vec A \;X\; \vec В \;=\; |А||В|sinθ $$
Где
$$ \vec A \;=\; (а_1,\; а_2,\; а_3) $$ $$ \vec B \;=\; (b_1,\; b_2,\; b_3) $$
A×B — вектор, перпендикулярный к обоим векторам A и B и перпендикулярный плоскости, содержащей их.
$$\; нормированный\; вектор\; из\; \; продукт\; \vec С \;=\; \vec А \vec В \; может\; быть\; найденный\; к\; с использованием\; \; следующий\; формула: $$ $$ \шляпа C \;=\; ( \frac{c_1}{|C|} \;,\; \frac{c_2}{|C|} \;,\; \frac{c_3}{|C|}) $$ 92} $$ Пример
Рассмотрим два вектора A и B, которые можно записать как:
A = 2i + 3j — k
B = i — 3j — 2k
Нам нужно найти векторное произведение этих векторов.
Сейчас,
A × B = |i j k 2 3 -11 -3 -2|
А × В = |3 -1 -3 -2|i — |2 -11 -2|j + |2 3 1 -3 |k
А × В = (-6 -3)i-(- 4+1)j+(-6-3)k
A × B = -9i + 3j — 9k = C
Теперь найдем вектор нормали к C.
$$ \шляпа C \;=\; \frac{C}{|C|} $$ $$ |С| «=» \sqrt{(-92} $$ $$ |С| «=» \sqrt{171} \;=\; 3 \sqrt{19} $$
Теперь вектор нормали будет
$$ \шляпа C \;=\; (\frac{-3}{\sqrt{19}} \;,\; \frac{1}{\sqrt{19}} \;,\; \frac{-3}{\sqrt{19}}) $$
Как найти векторное произведение двух векторов
Есть несколько шагов для использования этого инструмента. Вот эти номера:
. Найдите сайт calculatees.com в нужном браузере. И выберите калькулятор векторного векторного произведения из списка доступных инструментов.
На первом этапе введите значения вектора A в поля X, Y и Z.
Теперь введите значения вектора B в поля X, Y и Z.
Нажмите кнопку «Рассчитать».
После нескольких секунд нажатия на кнопку расчета вы получите результаты.
Зачем использовать Калькулятор векторов перекрестного произведения 2?
В математике и физике векторы и скаляры важны для описания величины и направления различных величин. Обычно мы делаем это для 2 векторов. Таким образом, калькулятор произведения можно использовать для нахождения перекрестного произведения и нормализованного вектора для него.
При вычислении векторного произведения иногда забываешь формулу или пропускаешь член, чтобы расширить его. Или иногда вам может потребоваться много времени для вычисления продукта, потому что ручные вычисления могут быть сложными. Вот почему вам нужен этот инструмент, чтобы найти векторное произведение двух векторов.
Преимущества использования Калькулятора перекрестного произведения 2×2
Перекрестное произведение называется векторным произведением. Он представляет собой площадь параллелограмма, стороны которого определяются двумя векторами. Он также имеет множество применений в реальной жизни. Таким образом, векторный калькулятор упрощает поиск результата.
Есть несколько полезных применений этого инструмента. Это:
Это экономит ваше время от ручных вычислений, которые являются сложными и трудоемкими.
Вы можете использовать этот инструмент в образовательных целях и решать многие другие проблемы из реальной жизни.
Этот инструмент можно использовать для вычисления угла между двумя векторами.
Вам не нужно платить за его использование, потому что это бесплатно.
Калькулятор перекрестного произведения
прост в использовании, потому что он содержит простые и легкие шаги.
No related posts.