Вектор а равен минус вектору б если: Найдите координаты и длину вектора а если а =-b+1/2c B{3;-2} c{-6;2}

Свойства векторного произведения

1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).

 Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , bxa противоположной ориентации). Стало быть axb = -(bxa ).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l(а хb ) = (lа ) х b = а х (lb ).

Пусть l>0. Вектор l(ахb ) перпендикулярен векторам а и b . Вектор ( lа)хb также перпендикулярен векторам а и b (векторы а, lа лежат в одной плоскости). Значит, векторы l(ахb ) и ( lа)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

Поэтому l(a хb )= lахb . Аналогично доказывается при l<0.

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.

е. а||b <=>ахb =0.

В частности, i *i =j *j =k *k =0.

4. Векторное произведение обладает распределительным свойством:

(a+b) хс= ахс+b хс.

Механический смысл векторного произведения: Пусть у некоторой точки А приложена сила F под углом фи. Рассмотрим некоторую фиксированую точку О. Моментом F относительно О называется вектором , величина которого равна произведения модуля силы на плече

Момент силы приложеной к т. А относительно О равен векторному произведению радиусу вектора ОА на .

Геометрический смысл векторного произведения:

А) и — колинеарны

Б) построенного на этих векторах приведеных к общему началу. Отсюда

В) Если — единичные орты, то , , , .

8, Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов i , j и k :

если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».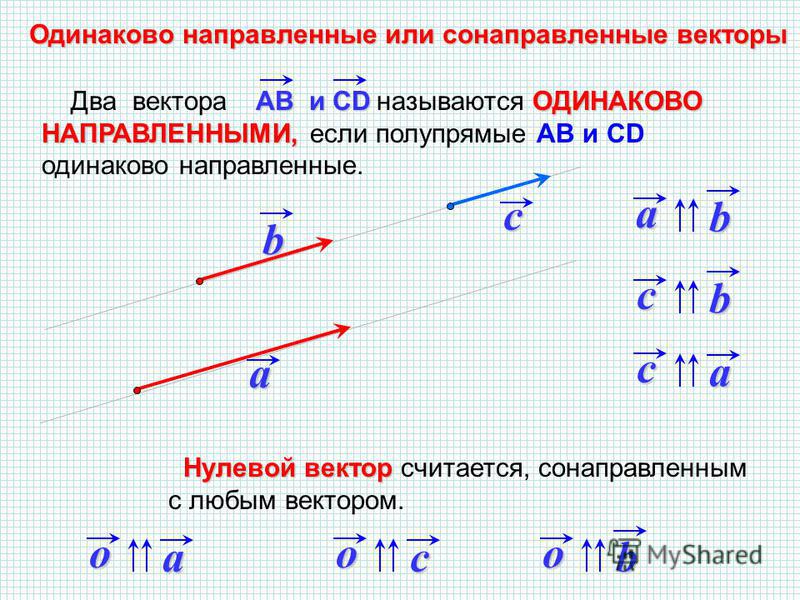

Пусть заданы два вектора а=а_хi +a_yj +a_zk и b =b_xi +b_yj +b_zk . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

Полученную формулу можно записать еще короче:

так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки.Равенство (7.2) легко запоминается.

Необхідна і достатня умова колінеарності двох векторів.

9, Мішаний добуток векторів, його обчислення і властивості. Геометричний зміст мішаного добутку. Необхідні і достатні умови компланарності трьох векторів.

Определения смешанного произведения, его геометрический смысл

Рассмотрим произведение векторов а, b и с, составленное следующим образом: (ахb )•с. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Выясним геометрический смысл выражения (ахb )*с. Построим параллелепипед, ребрами которого являются векторы а, b , с и вектор d =ахb (см. рис. 22).

 

Имеем: (а х b) • с = d • с = |d| • пр_dс, |d|=|а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, пр

dс = Н Для правой тройки векторов и пр_dс = — Н для левой, где Н— высота параллелепипеда. Получаем: (axb )*c =S *(±H ), т. е. (axb )*c =±V , где V — объем параллелепипеда, образованного векторами а, b и с.

Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

Как найти проекцию вектора на вектор? Формула, примеры решений



Рассмотрим ненулевые векторы  и :

Спроецируем вектор  на вектор , для этого из начала и конца вектора  опустим перпендикуляры на вектор  (зелёные пунктирные линии).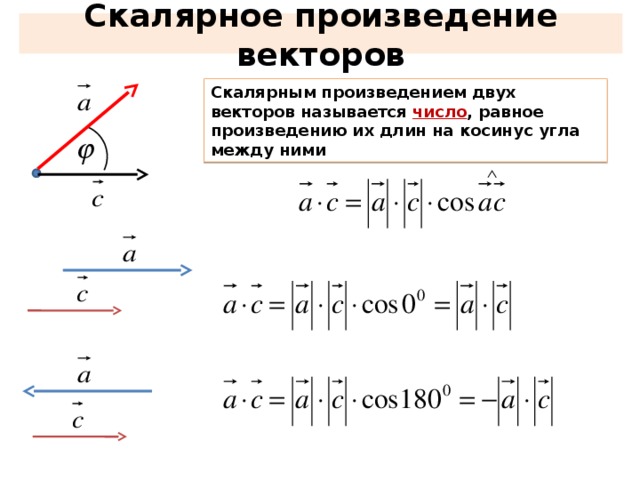

Представьте, что на вектор  перпендикулярно сверху падают лучи света. Тогда отрезок  будет «тенью» вектора . Проекцией вектора

 на вектор  является ДЛИНА отрезка . То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.

Это ЧИСЛО обозначается следующим образом: , «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НА который проецируют.

Сама запись  читается так: «проекция вектора «а» на вектор «бэ»».

Если угол между векторами  острый (как на рисунке выше), то

Если векторы  ортогональны, то  (проекцией является точка, размеры которой считаются нулевыми).

Если угол между векторами  тупой (на рисунке мысленно переставьте стрелочку вектора ), то  (та же длина с добавленным знаком «минус»).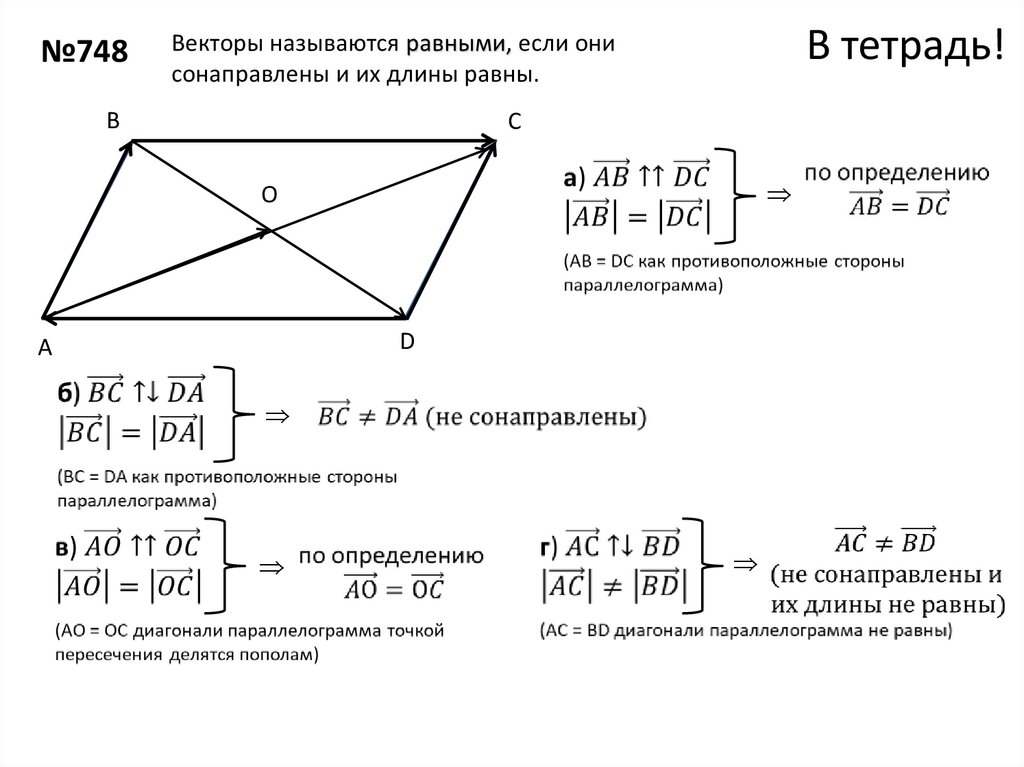

Отвечу на назревший вопрос: что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «бэ».

Из вышесказанного следует, что проекция вектора  на любой ненулевой сонаправленный вектор  будет точно такой же:
 – фактически это проекция вектора  на прямую , которая содержит сонаправленные векторы  (и поскольку векторы свободны, то таких прямых будет бесконечно много, все они будут параллельны друг другу);
а если векторы направлены противоположно , то добавится знак «минус»:

Отложим наши подопытные векторы от одной точки:

и рассмотрим прямоугольный треугольник. Косинус угла  – есть отношение прилежащего катета к гипотенузе:
, но с другой стороны, у нас уже получена формула косинуса угла между векторами:

…все ли догадались, что будет дальше?

Приравниваем формулы:

и сокращаем знаменатели обеих частей на , получая формулу для вычисления проекции:

Распишем её в координатах:

Если векторы плоскости  и  заданы в ортонормированном базисе , то проекция вектора  на вектор  выражается формулой:

Если векторы пространства  заданы в ортонормированном базисе , то проекция вектора  на вектор  

выражается формулой:

Легко убедиться, что проекция вектора  на коллинеарный вектор  может отличаться лишь знАком, приведу выкладки для «плоского» случая :

, если , и , если

Задача 34

Найти проекцию вектора  на вектор

Решение в одну строчку:
, на завершающем шаге я умножил числитель и знаменатель на , избавившись тем самым от иррациональности в знаменателе.

Ответ:

Проекция – это ДЛИНА, поэтому обязательно указываем размерность, правда, если получится знак «минус», то смотреться это будет своеобразно.

Задача 35

Треугольник задан своими вершинами . Найти:

а) проекцию стороны  на сторону ;
б) проекцию стороны  на сторону .

Это задача для самостоятельного решения.

Итак, как найти проекцию вектора  на отрезок с известными концами ? (как вариант, на продолжение этого отрезка). Находим вектор  и используем формулу . Либо вектор  и формулу . В одном из случаев получится отрицательное значение, и если оно вас напрягает, выберите другой вариант 🙂

О проекции же вектора на прямую поговорим в следующей главе, а пока выясним геометрический смысл координат векторов в ортонормированном базисе:

1.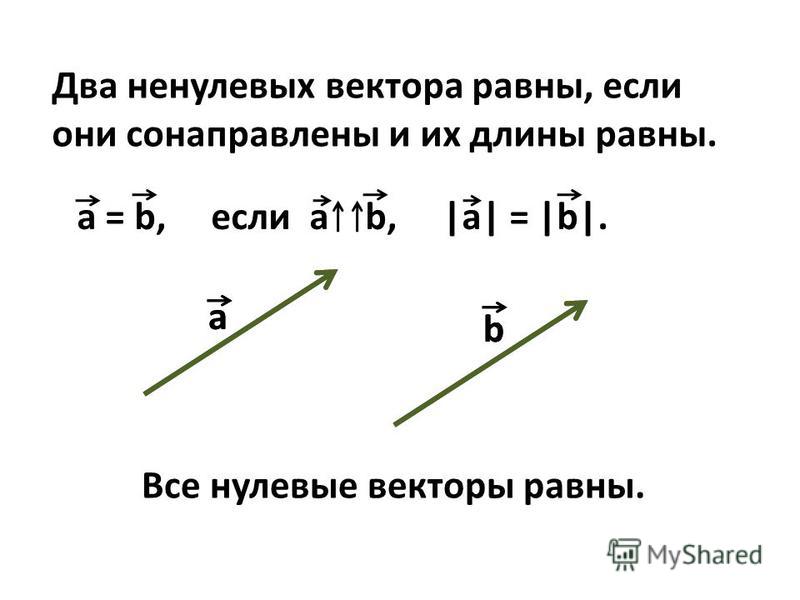 7.2. Проекции вектора на координатные оси. Направляющие косинусы

1.6.9. Как найти угол между векторами в координатах?

| Оглавление |



Автор: Aлeксaндр Eмeлин

Если a и b два вектора, то значение (a+b)xx(a-b) равно

DC PANDEY ENGLISH-BASIC MATHEMATICS-Exercise

14 видео Про и дехо сари видео бина киси объявление ки rukaavat ке!

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.

Стенограмма

привет всем в этом вопросе, если вектор a и вектор B являются двумя векторами, то значение вектора A + вектора B пересекает вектор a минус вектор P теперь есть варианты, данные здесь, мы должны найти векторное произведение, поэтому мы говорим, что дано, что это равно вектору A + вектору B и сумме вектора a минус вектор b вектор B теперь это можно записать, так как это равно нам нужно найти векторное произведение так, чтобы это был вектор перекрестный вектор a минус b вектор A + вектор b + векторная карта, чтобы найти путь, который является вектором B, пересекающим вектор a, и это минус, который является вектором B, пересекающим вектор a вектором b

теперь мы видим, что это вектор перекрестный вектор v, а это — вектор A + вектор B, а это вектор B Cross — factory, и мы знаем, что перекрестное произведение двух векторов, которое похоже на это, равно нулю, поэтому это ноль, и здесь мы видим, что это минус вектор A + вектор B, если мы перекрестное произведение этого смысла минус плюс показать на этой неделе g + вектор B пересечь вектор a и это вектор + вектор B пересечь вектор, и это просто просто то, что активный перекрестный вектор B с этим равен минус нулю, так что это в два раза больше, чем это в два раза больше, чем вектор перекрестного вектора B, это наш ответ, и этот вариант соответствует этому варианту, сначала покажите правильный вариант стул, который является вариантом сначала спасибо

---

Связанные видео

→band→c являются единичными векторами. Тогда для любого произвольного вектора →a,(((→a×→b)+(→a×→c))×(→b×→c)).→b−→c всегда равно а.|→а| б. 12|→а| в. 13|→а| д. ни один из этих

Если a и b — два вектора, то значение (a+b)×(a−b) равно

10955285

A и B — два числа. 6 умножить на квадрат B в 540 раз больше, чем квадрат A. Если соответствующее соотношение между A и B составляет 3:2, какова ценность B?

54785516

सिद्ध कीजिए कि F: a × b → b × a, इस प्रका возможности

54830070

दो धानात्मक पूर्णाकों, a और B के लिए H.C.F (A, B) × L.C.M (A, B) AB का मान लिखें |

109888945

Если vec(a) и vec(b) два вектора, то значение (vec(a) + vec(b)) xx (vec(a) — vec(b)) равно

141174204

যদি a এবং B দুটি 3 × 3 ক্রমের ম্যাট্রিক্স এমনভাবে সম্বন্ধ যুক্ত থাকে যাতে ab = a এবং ba = b হয় তবে- (a+b) 7 এর মান হবে-

352281743

Если A, B- идеальные квадратные цифры и ab представляет собой двузначное число в форме идеального квадрата, такое что (a×b)+(a+b)=ab, тогда значение [ba−(b+a)] равно:

446655914

দুটি সেট a ও b- এর 4 টি সাধারণ পদ আছে, যদি n (a) = 6 ও n (b) = 7 হয় n (a × b) এবং n [(a × b) ∩ (b ×A)]-এর মান নির্ণয় করো।

470820421

Если a и b любые два положительных целых числа, то HCF (a,b) × LCM (a,b) равно

599038995

Значение (b×c)⋅(a×d) +(c×a)⋅(b×d)+(a×b)⋅(c×d) равно

621730044

Text Solution

Если vec(a) и vec(b) — два вектора, то значение из (vec(a) + vec(b)) xx (vec(a) — vec(b)) равно

642978038

Если a и b два вектора, то значение (a+b)xx(a-b) равно

643180808

Если 6 A × B = A 8 B, то значение A — B равно

645588840

Если →a и →b два вектора такие, что ∣∣→a×→b∣∣=2, то найдите значение [→a→b→a×→b].

645602246

Два вектора одинаковой величины имеют равнодействующую, равную любому из них по величине. Угол между ними: А. 60°Б. 90°С. 105°Д. 120°

Дата последнего обновления: 01 марта 2023 г.

•

Всего просмотров: 260,4K

•

Просмотры сегодня: 2,44K

Ответ

Проверенные

260,4K+ виды

Ст. и B — два вектора, то $\mid A \mid = \mid B \mid$. Также упоминается, что величина равнодействующей равна величине любой из них, т.е. $\mid A \mid= \mid B \mid=\mid A+B \mid$. Найдите равнодействующую обоих векторов, а затем приравняйте ее к величине равнодействующей любого из векторов. Приравняв уравнение, решите его и найдите угол между ними. 9{ 2 }+2|\overrightarrow { A } ||\overrightarrow { B } |\cos { \theta } }$

Полный ответ:
Пусть два вектора равны $|\overrightarrow { A } |$ и $|\overrightarrow { B } |$.
$\theta$ — угол между обоими векторами.

No related posts.