Производная 3 cos 2x: Найти производное 3cos2x — ответ на Uchi.ru

2

Урок разноуровневого обобщающего повторения по теме «Производная .Геометрический и физический смысл производной.» – Документ 1 – УчМет

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 17 село Краснопартизанское

Урок разноуровневого обобщающего повторения

по теме «Производная .Геометрический и физический

смысл производной.»

по алгебре

для учащихся 11 класса

Автор разработки Титенко Ольга Григорьевна

С.Краснопартизанское

2012 год

Цели урока: — обобщить теоретические знания по теме производная, геометрический и физический смысл производной

— закрепить умение находить производные функций,

— решать задачи на геометрический и физический смысл производной,

— готовиться к ЕГЭ: повторить умение решать задачи на вычисления и преобразования тригонометрических, логарифмических, иррациональных и степенных выражений.

Оборудование: карточки трех цветов, компьютер.

Ход урока.

1. 1 этап – Организационный ( 1 мин).

Учитель сообщает тему урока, цель и поясняет, что во время урока будет использоваться раздаточный материал, который лежит на партах и проведена разноуровневая самостоятельная работа.

2. 2 этап- Повторение теоретического материала по теме производная. ( 10 мин).

Учитель приглашает к доске ученика написать таблицу производных элементарных функций.

Функция y=f (x)	Производная y′= f′(x)
C	0
xЄR	x-1
ax	ax lnx
ex	ex
log x
lnx
sinx	cosx
cosx	— sinx
tg x
ctgx	—

( Все теоретические и практические вопросы урока демонстрируются на экране).

Учитель: Сформулируйте определение производной функции в точке.

Ученик: Производной функции f в точке x0 называется число, к которому стремится разностное отношение при

Учитель: Сформулируйте и запишите правила вычисления производных.

Ученики. 1. Если функция y=f(x) y=g(x) имеют производную в точке x, то и их сумма имеет производную в точке x ,причем производная суммы равна сумме производных.

(f(x)+g(x))′= f′(x)+g′(x)

2. Если функция y=f(x) имеет производную в точке x, то и функция y=k f(x) имеет производную в точке x, причем (k (f(x))′=k f′(x)

Постоянный множитель можно выносить за знак производной.

3.Если функция y=f(x) и y=g(x) имеют производную в точке x, то и их произведение имеет производную в точке x

( f(x) g(x))′= f′(x) g(x)+f(x)g′(x)

Производная произведения двух функций равна сумме двух слагаемых; первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.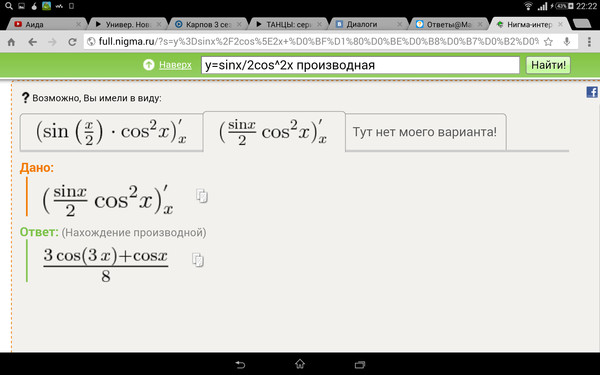

4. Если функция y=f(x) и y= g(x) имеют производную в точке x и в этой точкеg(x)≠0 , то и частное имеет производную в точке x , причем

Учитель. Что называется касательной к графику функции?

Ученик. Касательной к графику дифференцируемой в точке x

0 функции f- называется прямая, проходящая через точку (x₀ ;f(x₀) ) и имеющая угловой коэффициент f′(x₀).

Учитель: В чем состоит геометрический смысл производной?

Ученик. Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

Учитель. Назовите уравнение касательной к графику функции y=f(x) в точке с абсциссой x_0.

Ученик.y= f(x₀)+ f′(x₀) ( x-x₀)

Учитель. В чем состоит физический смысл производной?

Ученик. Если материальная точка движется прямолинейно по закону S(t) , то производная функции y= S(t)выражает мгновенную скорость материальной точки в момент времени t

0 , т.е. v= S′(t).Производная от координаты по времени есть скорость .Производная от скорости по времени есть ускорение.

Учитель. Решим у доски несколько задач на применение этих правил.

Задача№1. Найти угловой коэффициент касательной, проведенной к графику функции f(x)= 2-x²+3x⁴ в его точке с абсциссой x₀=-1.

Задача №2. Через точку графика функции y(x)= -0,5x²+4x+7 с абсциссой x₀=2 проведена касательная . Найдите тангенс угла наклона этой касательной к оси абсцисс.

Задача № 3. Составьте уравнение касательной к графику функции y= x²-2x в точке x₀=-1/

Задача №4.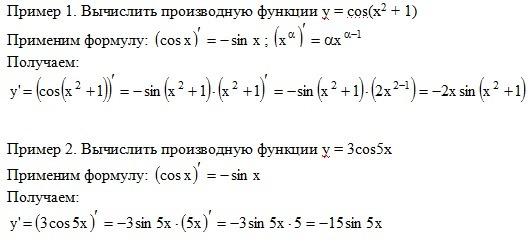

При движении тела по прямой расстояние S( в метрах) от начальной точки изменяется по закону S(t)=t³-t²+5t+1( t- время движения в секундах). Найти скорость в (м/с) тела через 3 секунды после начала движения.( Вопросы устного счета на экране).

3 этап – Устный счет ( на экране ) – 5 минут.

Найти производные функции.

5-4x 2e^x 2^x

x⁴

x⁸

x⁶

2x³

2x⁵-3x²+2

7x⁶+3x³+5x²

2x^-4

( 3x-6)²

(8+7x)²

log₂x sin 2x cos(3x+4)

ln x sin²x sin ( 3-2x)

cos 2x cos 3x

4 этап урока- Разноуровневая самостоятельная работа. ( 20 минут).

Дети получают карточки трех цветов, трех уровней: желтые – содержат задание базового уровня сложности, голубые – повышенного уровня сложности, розовые- высокого уровня сложности. Они так же содержат задания на вычисления и преобразования логарифмических, тригонометрических, иррациональных и степенных выражений. На самостоятельную работу отводится 20 минут. Дети выполняют работу в тетрадях для самостоятельных работ. Учитель вызывает к доске одного или двух учеников работающих с голубыми карточками, а во время работы оказывает помощь ученикам , работающим по желтым карточкам. После окончания работы ученики, работающие у доски, объясняют решение своих задач, а остальные внимательно слушают и задают вопросы по решению или поправляют, если есть ошибки.

Примерные варианты разноуровневых карточек.

Желтая карточка № 1.

1. Найти значение выражения. 3^{-4,5 а} 3 ^{2,5 а} при а= —

1) 2) 3 3) 1 4)

2. Вычислить log ₅^{15+ log ₅}

1) 5 2) 1 3) 4) -1

3. Найти значение производной функции y = x⁴ – 2x³ -x²-5 в точке с абсциссой x ₀ = 1

1) -3 2) 2 3) 0 4)1

4. Найдите производную функции y = e^3x+x2

1) y ′(x)= e^3x+2x 3) y′(x)= 3e^3x+2x

2) y ′(x)= 3 e^x+2x 4) y ′(x)= 3e^2x +2x

5. Материальная точка движется по закону x(t) = t³-4t²+3t-17 (x –перемещение в м,t-время в с ). Через сколько секунд после начала движения ускорение точки будет равно 10м ∕ с².

1) 6 2) 2 3) 3 4) 4

6. Определите абсциссу точки, в которой касательная к графику функции y= 4x² – 8x +4 параллельна оси абсцисс.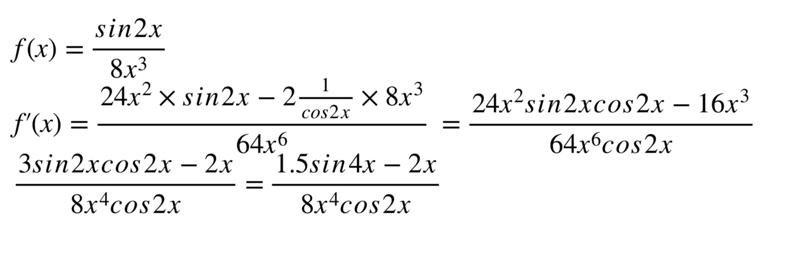

1) -8 2) 1 3) 0 4) 4

Желтая карточка № 2

1. Упростить 2,2а 5а^1,5

1) 7.2 a ^2,5 2) 11 а ^2,5 3) 7,2 а ^1,5 4) 11 а^1,5

2. Вычислить 12 – log₃ 16log ₁₆ 3

1) 0 2) -4 3) 12 4) 11

3. Найдите значение производной функции y(x) = ln ( x-3) в точке с абсциссой x₀=4

1) -1 2) -3 3) 1 4) 3

4. Найдите угловой коэффициент касательной, проведенной к графику функции

y= 3x³-2x² +5 в его точке с абсциссой x₀ = -3

1) 98 2) 69 3) 33 4) 93

5. Тело движется по прямой так, что расстояние S ( в м) от него до точки М этой прямой изменяется по закону S ( t ) = t⁴-t³ + 3t² -21. Чему будет равна мгновенная скорость ( (м/с) через 3 секунды после начала движения?

1) 70 2) 78 3) 81 4) 76

6. Найдите производную функции y ( x) = sin 4x – x⁴

1) y′ ( x) = 4 cos 3x – 4x³ 3) y′ (x) = -4 sin 4x – 4x³

2) y′ ( x) = 4 sin 4x – 3x³ 4) y′(x) = 4 cos 4x – 4x³

________________________________________________________________

Желтая карточка 3.

1. Вычислить 3 — 20

1) 250 2) 70 3) 10 4) 430

2. Найдите значение выражения log ₆ ( 36 m²), если log₆m= 3.

1) 8 2) 18 3) 12 4) 24

3. Найти производную функции y= 3x⁴-2x²+x-1 в точке с абсциссой x₀ = 1

1) 9 2) 5 3) 4 4) 6

4. Найдите угловой коэффициент касательной, проведенной к графику функции

y = -2x⁴+3x +5 в его точке с абсциссой x₀=-2

1) 67 2) -61 3) 19 4) 72

5. Материальная точка движется по закону x(t) = t³-5t²+6t+7 ( x – перемещение в м, t- время в с). Через сколько секунд после начала движения ускорение точки будет равно 8м/ с²

1) 1 2) 2 3) 3 4) 4

6. Найти производную функции y= 2^x+sinx

1) y(x)= 2^xln2 +cos x 3) y= x 2 ^x-1 +cosx

2)y(x) = + cosx 4)y= 2^x ln2 –cosx

Голубая карточка №1

1. Вычислить ( —

2. Вычислить ( , если tg =

3. Найдите значение производной функции y= sin ( 4x — ) в точке x₀=

4. Найдите угол наклона касательной, проведенной к графику функции f(x) = tgx+ в точке с абсциссой x₀=

5. Составьте уравнение касательной к графику функции y = 2+x, параллельной прямой y= 2x

6. Найти значение производной функции f (x)= в точке x₀= -1

Голубая карточка 2.

1. Вычислить

2. Найти значение выражения , если cos=Є

3. Найдите значение производной функции y= в точке x₀=2

4. Составьте уравнение касательной к графику функции y=2x- ln x, параллельной прямой y=x

5. Найти угловой коэффициент касательной к графику функции g(x)=, проведенной в точке с абсциссой x₀=-0,5

6. Закон движения тела задан формулой S(t)=0,5t² +3t +2( s-в метрах, t- время в с). Какой путь пройден телом за 4с? Какова скорость движения в этот момент времени?

Голубая карточка 3.

1. Вычислить log 36-2log 9+1

2. Вычислить (11⁰⁾² +

3. Найдите значение производной функции y=e^2x-1 в точке x₀=

4. Составьте уравнение касательной к графику функции y= в точке графика с ординатой 2.

5. Материальная точка движется по закону x(t)= (x –перемещение, t-время в с).

   No related posts.