Сложение двух векторов правило треугольника: Какие правила сложения векторов вы знаете?

Что такое сложение векторов?

Что такое сложение векторов?

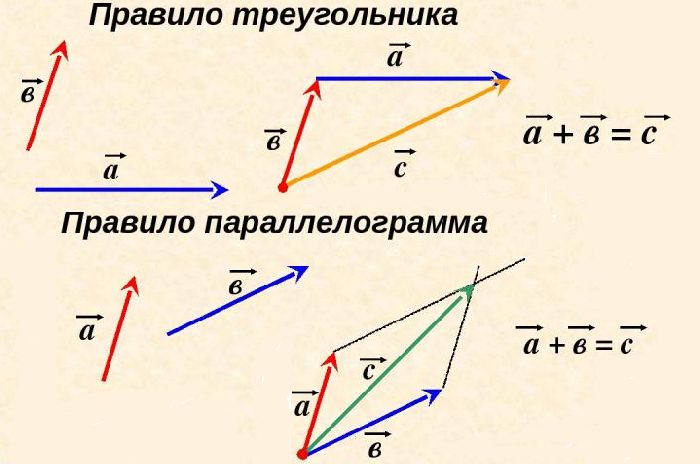
Суммой двух векторов u и v называется третий вектор w, проведенный из начала u к концу v, если начало вектора v совпадает с концом вектора u. Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Какой из векторов является суммой векторов?

Соединяем начало первого вектора и конец второго. Получившийся вектор, начало которого совпадает с началом вектора a → , а конец — с концом вектора b → , называется суммой этих векторов.

Как складывать и вычитать векторы?

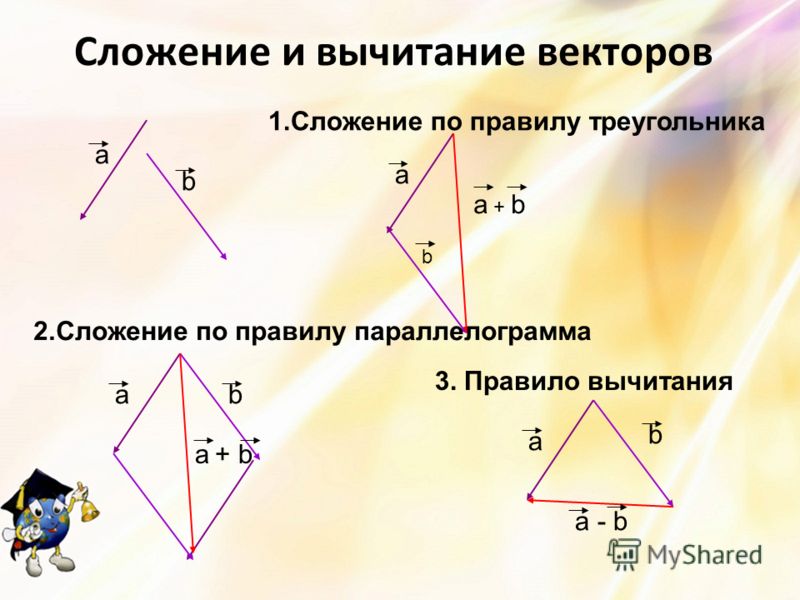
Если складываются два противоположно направленных вектора, то их значения вычитаются, а не складываются. Векторы, которые представлены в виде xi + yj + zk можно сложить или вычесть, просто сложив или вычтя соответствующие коэффициенты.

Какое равенство выражает правило треугольника для нахождения суммы векторов?

Правило треугольника (рис. 3). Нужно от конца вектора отложить вектор . Тогда сумма a → + b → – это вектор, начало которого совпадает с началом вектора , а конец – с концом вектора

Как выполнить вычитание векторов?

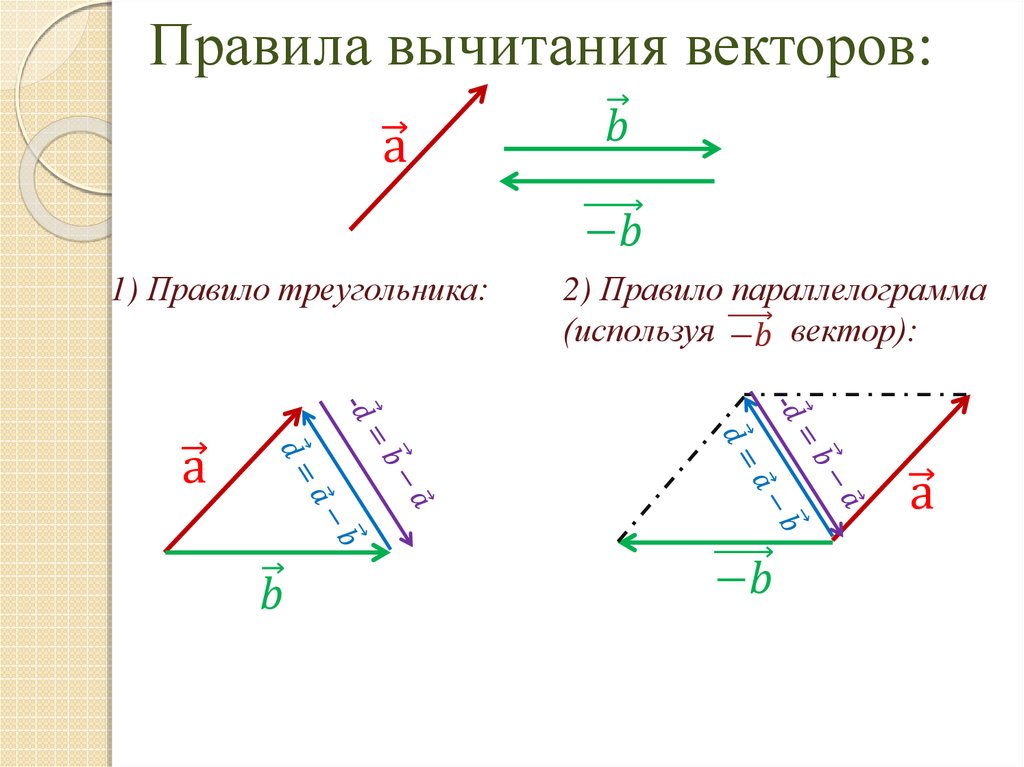
Легче запомнить, как найти разность векторов a → и b → , следующим образом:

1. векторы нужно привести к общему началу A;
2. соединить конечные точки B и C;
3. отметить направление вектора разности от конечной точки уменьшителя к конечной точке уменьшаемого вектора.

Как сложить два вектора с координатами?

При сложении первая координата первого вектора складывается с первой координатой второго вектора, вторая координата первого вектора складывается со второй координатой второго вектора и так далее в зависимости от размерности векторов.

Как сложить два вектора по правилу параллелограмма?

Такой приём сложения векторов называется правилом параллелограмма.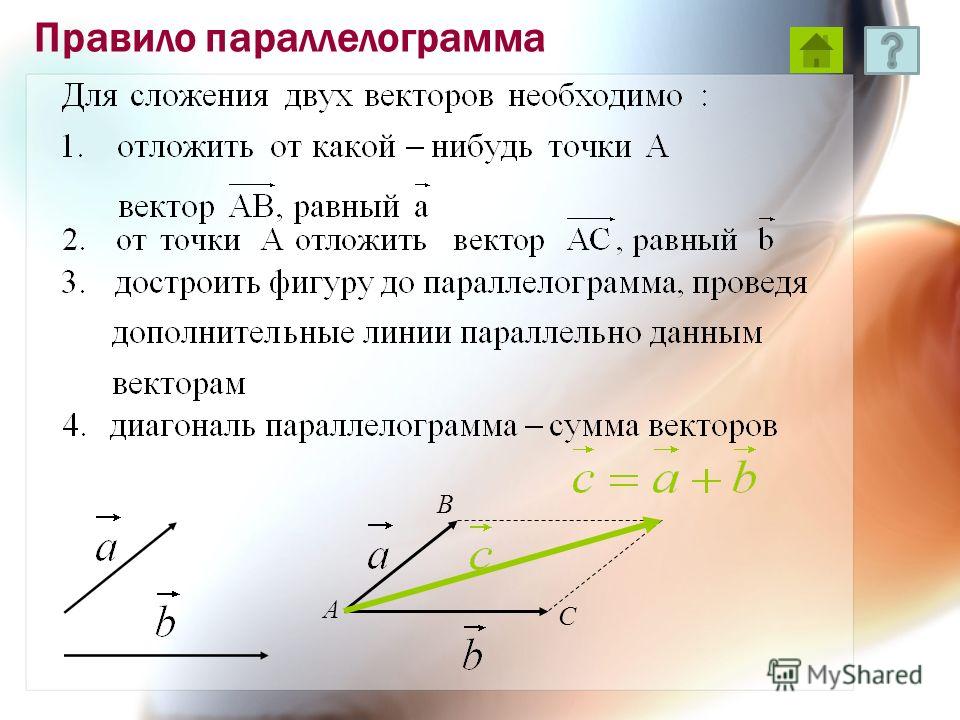 Так как DC → = AB → = b → , то a → + b → = AD → + DC → = AC → = c → ; выполняя сложение по правилу треугольника, убедимся, что суммой остаётся тот же вектор c → .

Как сложить 3 вектора по правилу параллелограмма?

Правило треугольника и правило параллелограмма находят сумму двух векторов, но как сложить несколько векторов? Чтобы сложить несколько векторов, необходимо сложить первый вектор со вторым, затем сложить их сумму с третьим вектором и так далее.

Как определяется сумма векторов по правилу треугольника по правилу параллелограмма?

Такой приём сложения векторов называется правилом параллелограмма. Так как DC → = AB → = b → , то a → + b → = AD → + DC → = AC → = c → ; выполняя сложение по правилу треугольника, убедимся, что суммой остаётся тот же вектор c → .

Как сложить четыре вектора по правилу многоугольника?

Сумму нескольких векторов получаем так: складываем первый и второй вектор, затем к их сумме прибавляем третий вектор и т.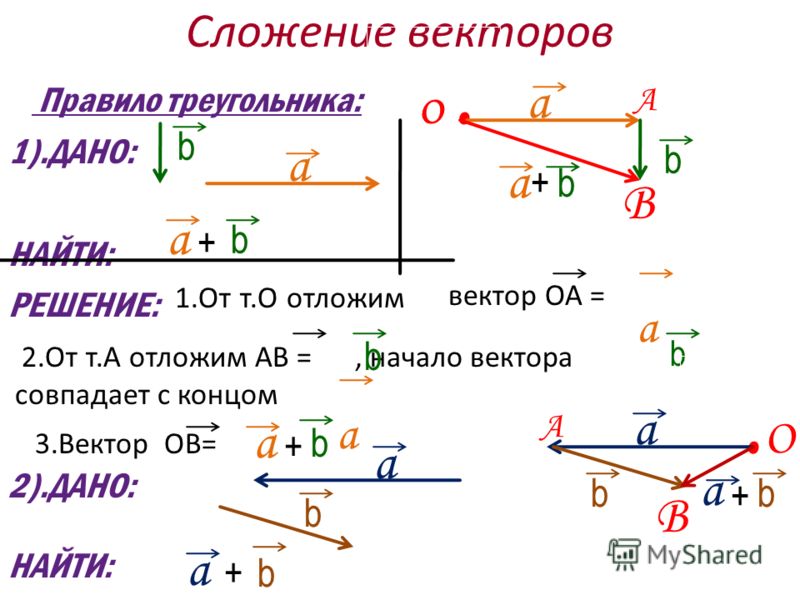 д. Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.

Чему равна сумма нескольких векторов Если при сложении их по правилу многоугольника начало первого вектора совпадает с концом последнего?

Его суть заключается в том, что векторы-слагаемые последовательно откладывают друг от друга, суммой является вектор, начало которого совпадает с началом первого вектора-слагаемого, а конец совпадает с концом последнего вектора-слагаемого. Если эти точки совпадают, то сумма данных векторов равна нулевому вектору.

Что такое координаты вектора чему равны?

Координатами вектора являются координаты конечной точки этого вектора, если вектор расположен так, что его начало находится в начале координат. Если вектор находится на координатной плоскости, то каждая координата вектора равна разности соответствующих координат его конца и начала.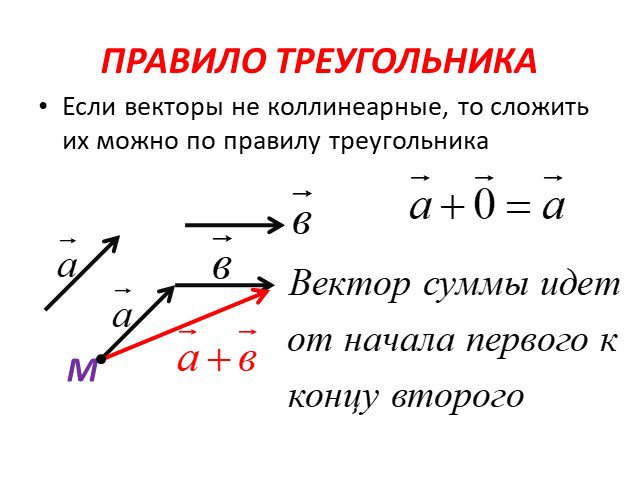

Как находить координаты векторов?

Чтобы найти координаты вектора AB, зная координаты его начальной точки А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. Смотрите также справочник: координаты вектора по двум точкам.

Как определяется положение точки на плоскости?

На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. … Географические координаты.

Как найти уравнение медианы в треугольнике?

Медиана — отрезок, соединяющий вершину с серединой противоположной стороны. Уравнение прямой по двум точкам (x−x1)/(x2−x1)=(y−y1)/(y2−y1), координаты середины отрезка x=(x1+x2)/2;y=(y1+y2)/2. Например для медианы AM,M — середина BC, имеем M:x=(−2−6)/2=−4,y=(−8+2)/2=−3.

Как найти Ортоцентр треугольника?

Ортоцентр — точка пересечения высот треугольника или их продолжений.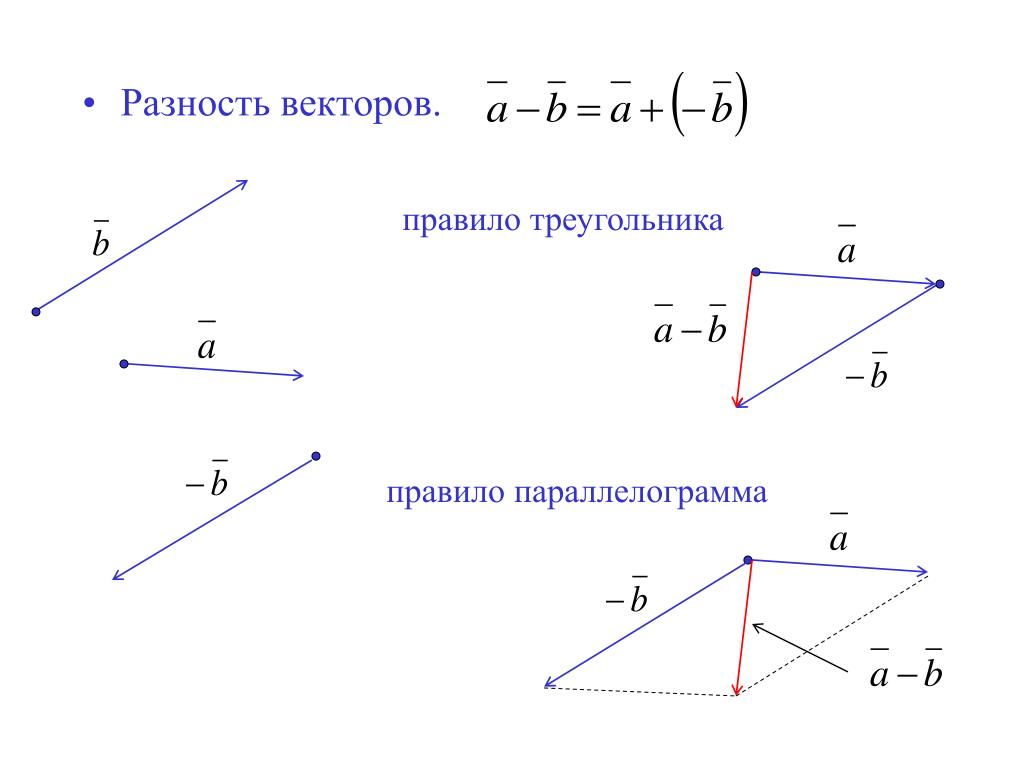 Традиционно обозначается латинской буквой H….Метод расчета ортоцентра треугольника

1. Наклон AB (m) = 5-3/0-4 = -1/2.
2. Наклон BC (m) = -6-5/3-0 = -11/3.
3. Наклон CA (m) = 3+6/4-3 = 9.

Как найти сторону треугольника если известна только одна сторона?

Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов. Если известны одна сторона и два прилежащих угла, то с помощью теоремы синусов можно вычислить остальные две стороны треугольника.

Векторы на плоскости и в пространстве. Основные понятия

1. Векторы на плоскости и в пространстве. Основные понятия.

2. Понятие вектора в пространстве

Вектор(направленный отрезок) –
отрезок, для которого указано какой из его
концов считается началом, а какой – концом.
В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0
Нулевым вектором называется вектор, начало и конец
которого совпадают.
Единичным вектором называется вектор, длина которого
равна единице.
Векторы называются коллинеарными, если они лежат на
одной прямой или параллельных прямых.
Векторы называются компланарными, если они лежат в одной
плоскости или в параллельных плоскостях.

4. Коллинеарные векторы

Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы

5. Равные векторы

Равные векторы — сонаправленные векторы,
длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.

6. Противоположные векторы

Противоположные векторы – противоположно
направленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.

7. Признак коллинеарности

Если существует такое число k при котором
выполняется равенство a k b и при том
вектор b 0 , то векторы a и b коллинеарн ы.
вектор k a b, если k 0
вектор k a b, если k 0

8. Действия с векторами

• Сложение
• Вычитание
• Умножение вектора на число

9. Сложение векторов

Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда

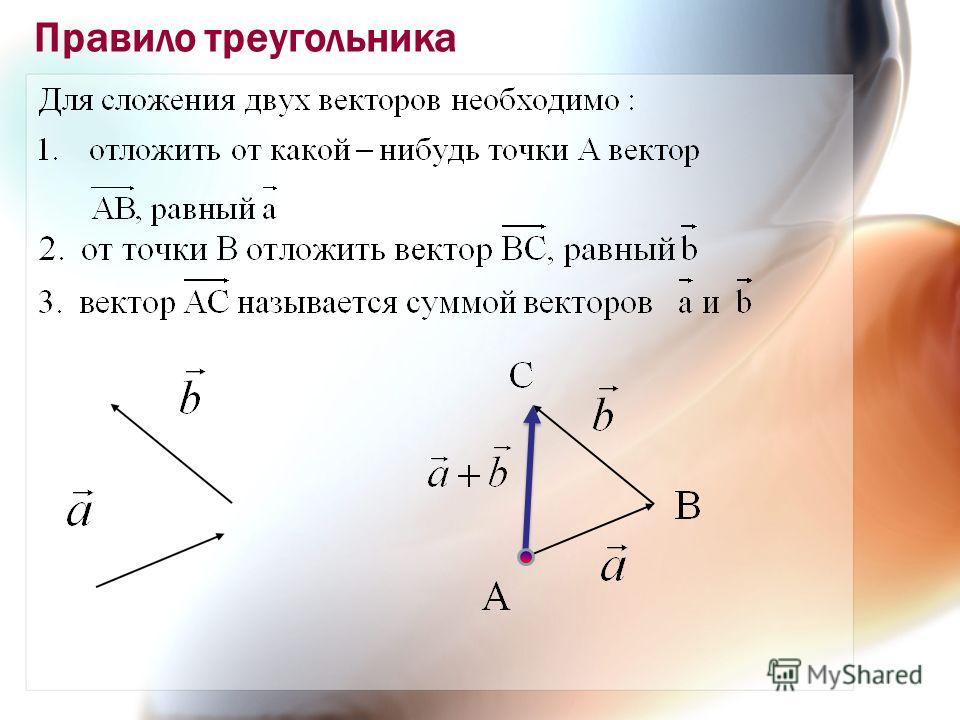
10. Правило треугольника

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
А
b
a b
b
C

11. Правило треугольника

B
a
А
a b
b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC

12. Правило параллелограмма

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b
с a b
C

13. Правило многоугольника

Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE

14. Пример

B1
A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0

15. Правило параллелепипеда

Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1
C1
1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d

16. Свойства

B1
A1
C1
d
D1
с aB
А
C
b
D
d a b c для любого параллелепипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда

17. Вычитание

Разностью векторов a и b называется такой
вектор, сумма которого с вектором b равна
вектору a .

18. Вычитание

Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C

19. Умножение вектора на число

Произведением ненулевог о вектора a на число k
называется такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

20. Свойства

Для любыхвект оровa и b и любых
чисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
1 ый распределит ельный
закон
(k l)a k a l a
2 ой распределит ельный
закон

21. Определение компланарных векторов

Компланарные векторы – векторы, при
откладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)

22. О компланарных векторах

Любые два вектора всегда компланарны.
α
a
b
a
b
a
b
a и b компланарн ы
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарн ы
если
a, b, c
a kb

23. Признак компланарности

Если вектор c можно разложить по векторам
а и b, т.е. представить в виде
с xa yb
где х и у некоторые числа, то векторы a, b
и c компланарн ы.

24. Разложение вектора

• По двум неколлинеарным векторам
• По трем некомпланарным векторам

25. Разложение вектора по двум неколлинеарным векторам

Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.

26. Разложение вектора по трем некомпланарным векторам

Если вектор p представлен в виде
p xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.

27. Доказательство теоремы

С
с
P
p
b
O
B
P2
P1
aA
Доказательство :
О произвольн ая точка
Дано :
abc
некомпланр ные
векторы
p x a yb z c
OA a OB b OC c OP p
AP OC AP (AOB) P1 P2 P1 OB
OP OP2 P2 P1 P1 P
OP2 , и OA , PP1 и OB , P1 P , OC коллинеарны
OP2 x OA , P2 P1 y OB , P1 P z OC
OP x OA y OB z OC
p x a yb z c ч.т.д.
Скалярное произведение векторов
Скалярным произведением двух векторов называется число
ab a b cos
Замечание. Если два вектора являются перпендикулярными, то
их скалярное произведение равно нулю, и наоборот.
Теорема. Скалярное произведение двух векторов
a X1 , Y1 , Z1 , b X 2 , Y2 , Z 2
вычисляется по формуле
ab X1 X 2 YY
1 2 Z1Z 2
Следствие 1. Косинус угла между векторами
a X1 , Y1 , Z1 , b X 2 , Y2 , Z 2
вычисляется по формуле
cos
ab
a b
X 1 X 2 Y1Y2 Z1Z 2
X 12 Y12 Z12 X 2 2 Y2 2 Z 2 2
Следствие 2. Необходимое и достаточное условие
перпендикулярности двух векторов выражается равенством
ab X1 X 2 YY
1 2 Z1Z 2 0

30. Базисные задачи

31. Вектор, проведенный в середину отрезка,

равен полусумме векторов, проведенных из той же
точки в его концы.
С
A
B
O
1
1
1
OC ( OA OB ) OA OB
2
2
2
Доказательство

32. Доказательство

С
A
B
O
Доказательство :
OC OA AC
OC OB BC
Дано :
AB отрезок
AC CB
Доказать :
1
OC ( OA OB )
2
2OC OA AC OB BC OA OB (
AC
BC
)
o
2OC OA OB 2
1
OC ( OA OB ) ч.т.д.
2

33. Вектор, соединяющий середины двух отрезков,

равен полусумме векторов, соединяющих их концы.
С
N
D
B
С
N
D
B
M
M
A
A
1
1
MN ( AD BC ) ( AC BD )
2
2
Доказательство

34.

ДоказательствоС
N
D
B
M
A
Доказатель ство :
MN MA AC CN
MN MB BD DN
2 MN AC BD
1
MN ( AC BD ) ч.т.д.
2
Дано :
AB; CD
BM AM
CN ND
Доказать :
1
MN ( AC BD )
2

35. Вектор, проведенный в точку пересечения диагоналей параллелограмма,

равен одной четверти суммы векторов, проведенных
из этой точки в вершины параллелограмма.
O
C
B
M
A
D
1
OM ( OA OB OC OD )
4
Доказательство

36. Доказательство

O
B
C
M
Дано :
ABCD пар м
BD AC M
Доказать :
1
OM ( OA OB OC OD )
4
A
D
1
OM ( OA OC )
2
1
OM ( OB OD )
2
1
1
1
1
2OM OA OB OC OD
2
2
2
2
1
1
1
1
OM OA OB OC OD
4
4
4
4
1
( OA OB OC OD ) ÷.ò.ä.
4

37. Задача 1. Разложение векторов

Разложите вектор по a, b и c :
D
N точка пересечения
медиан ABC
a
A
а) DB
б) CB
в) DC
г) DN
Решение
b
B
N
c
C

38.

Решениеа) DB b a
б) CB b c
в) DC c a
г) DN a 1 AN a 1 ( 1 ( b c ))
3
1
1
a b c
6
6
3 2

39. Задача 2. Сложение и вычитание

Упростите выражения:
а)
б)
в)
г)
д)
е)
CM MK
DM MA
SD ST
PL PK
AC BC PM AP BM
AD MP EK EP MD
Решение

40. Решение

а) CM MK CK
б) DM MA DA
в) SD ST TD
г) PL PK KL
д) AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK

Объяснение урока: Графические операции над векторами

В этом объяснении мы научимся выполнять операции над векторами графически используя правила треугольника и параллелограмма.

Векторы — это объекты, полностью определяемые своей величиной и направлением. Мы помним, что мы можем представлять векторы в виде направленного отрезка в подходящем виде. пространство, где длина отрезка говорит нам величину вектора а направление указывается начальной и конечной точками направленного отрезок. В этом пространстве мы можем думать о векторах как о представлениях смещения, от начальной точки до конечной точки.

Например, вектор от 𝐴 до 𝐵 можно представить в виде направленного отрезка от 𝐴 до 𝐵.

Длина этого отрезка равна величине 𝐴𝐵, написано ‖‖𝐴𝐵‖‖, и направление показано стрелкой. Стоит повторить, что вектор полностью определяется его величина и направление, поэтому любые два вектора с одинаковыми величинами и направление будет равно. В частности, мы можем нарисовать вектор в любом месте 𝑥𝑦-плоскость; это не изменит его величины или направления, и, следовательно, это будет все тот же вектор.

Мы также можем представить этот вектор изменением по горизонтали и по вертикали. Если 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦), то из диаграммы (или координаты) мы можем найти горизонтальные и вертикальные изменения при движении от 𝐴 до 𝐵.

Изменение горизонтальной координаты равно 𝑥−𝑥 а изменение вертикальной координаты равно 𝑦−𝑦. Мы пишем это как 𝐴𝐵=(𝑥−𝑥,𝑦−𝑦). Первая компонента говорит нам о горизонтальном смещении вектора, а вторая Компонент сообщает нам вертикальное смещение вектора.

Это позволяет нам складывать векторы вместе. С точки зрения смещения, сумма два вектора будут суммарным смещением обоих векторов. С точки зрения компонентов, напомним, что это означает, что если мы имеем ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦); мы добавляем горизонтальные и вертикальные компоненты отдельно. Затем это позволяет нам добавлять векторы вместе графически.

Например, если у нас есть вектор 𝐴𝐵, то в этом пространстве это смещение от точки 𝐴 указать 𝐵. Сходным образом, 𝐵𝐶 — смещение от точки 𝐵 указать 𝐶. Их сумма, 𝐴𝐵+𝐵𝐶, должно быть общее смещение обоих векторов, то есть смещение от 𝐴 до 𝐵 и затем от 𝐵 до 𝐶. Это вектор 𝐴𝐶, и мы можем показать это графически.

Мы видим, что смещение от 𝐴 к 𝐶 совпадает со смещением от 𝐴 в 𝐵 и затем из 𝐵 до 𝐶, так как их начальная и конечная точки подобные.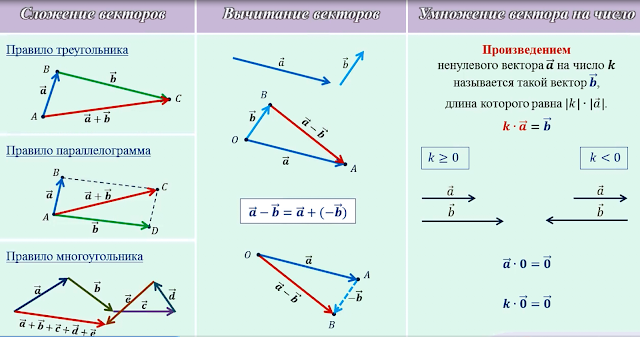

Это часто называют правилом треугольника для векторов. Мы можем констатировать это следующим образом.

Правило: Правило треугольника для векторов

Для любых трех точек 𝐴, 𝐵 и 𝐶, у нас есть 𝐴𝐵+𝐵𝐶=𝐴𝐶 как показано на диаграмме.

В результате правила треугольника, если у нас есть два вектора ⃑𝑢 и ⃑𝑣 представлены графически, то мы можем сложить эти векторы вместе, зарисовав конечная точка ⃑𝑢 должна быть начальной точкой ⃑𝑣, как показано.

Прежде чем мы увидим, как применить это к задачам, связанным с векторами, есть еще один правило мы можем показать. Рассмотрим параллелограмм 𝐴𝐵𝐶𝐷.

В параллелограмме противоположные стороны параллельны и имеют одинаковую длину; следовательно, 𝐴𝐷=𝐵𝐶𝐴𝐵=𝐷𝐶.and

Мы можем применить правило треугольника для векторов к этой диаграмме, учитывая стороны как векторы и добавление вектора 𝐴𝐶 к диаграмме, как показано.

Применение правила треугольника для векторов к точкам 𝐴, 𝐵 и 𝐶 имеем 𝐴𝐵+𝐵𝐶=𝐴𝐶.

Мы знаем, что 𝐴𝐷=𝐵𝐶 так как они имеют одинаковую величину и направление. Мы можем увидеть это графически как мы можем перевести векторы друг на друга. Подставив это в уравнение дает 𝐴𝐵+𝐴𝐷=𝐴𝐶.

Это известно как правило параллелограмма для векторов. следующим образом.

Правило: Правило параллелограмма для векторов

Для векторов 𝐴𝐵 и 𝐴𝐷 с той же начальной точкой, 𝐴, 𝐴𝐵+𝐴𝐷=𝐴𝐶, где 𝐶 — точка, из которой 𝐴𝐵𝐶𝐷 параллелограмм, как показано на следующем рисунке.

Поскольку векторы имеют ряд применений, например, в качестве инструмента для оценки равнодействующая сил или для решения геометрических задач треугольник и параллелограмм правила можно рассматривать исключительно с точки зрения области, в которой мы работаем. Однако обычно проще преобразовать проблему в векторы.

Давайте начнем с нескольких примеров сложения векторов. графически.

Пример 1.

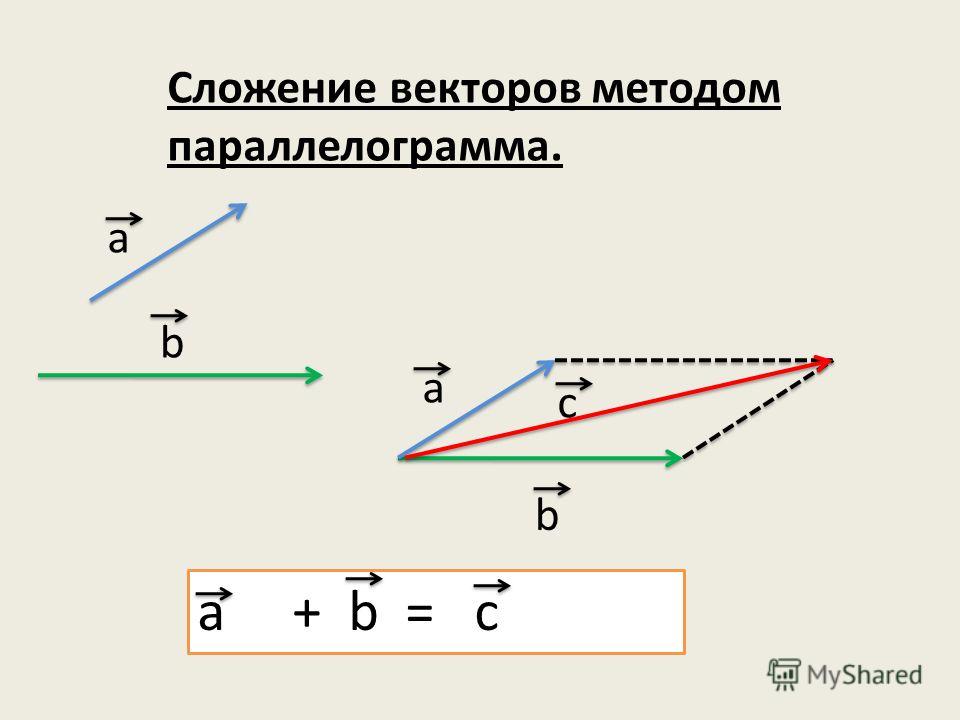Нахождение компонентов суммы сквозных векторов на Диаграмма

На сетке единичных квадратов показаны векторы ⃑𝑢 и ⃑𝑣.

1. Из каких компонентов состоит ⃑𝑢?
2. Из каких компонентов состоит ⃑𝑣?
3. Из каких компонентов состоит ⃑𝑢+⃑𝑣?

Ответ

Часть 1

Напомним, что компоненты вектора, представленного графически, это горизонтальные и вертикальные смещения вектора в этом пространстве. Особенно, для вектора из 𝐴(𝑥,𝑦) к 𝐵(𝑥,𝑦), его компонентами будут разница в координатах: 𝐴𝐵=(𝑥−𝑥,𝑦−𝑦).

Есть несколько способов использовать это для определения компонентов вектора ⃑𝑢. Например, мы могли бы ввести координату систему на сетку единичных квадратов. Однако в этом нет необходимости. Вместо, нам нужно знать только горизонтальные и вертикальные перемещения при движении от начальной точки ⃑𝑢 до конечной точки из ⃑𝑢. Начнем с горизонтального смещение.

Переход от хвоста к вершине вектора ⃑𝑢, мы путешествуем по трем квадратам. Так как это единичные квадраты и мы двигаться вправо, мы можем записать это как смещение +3 единицы.

То же самое можно сделать и по вертикали.

Мы перемещаемся на две единицы вверх, поэтому смещение равно +2 единицам. Это дает нам обе компоненты нашего вектора. Помните, нам не нужно включить положительный символ; это дает нам ⃑𝑢=(3,2).

Часть 2

Мы можем выполнить ту же процедуру для вектора ⃑𝑣.

Во-первых, мы видим, что сдвинулись на две единицы вправо, поэтому первый компонент вектор будет равен 2. Мы должны быть осторожны при проверке вертикального смещения вектор; так как мы движемся вниз, значение будет отрицательным.

Путешествие от хвоста к вершине вектора ⃑𝑣, мы перемещаемся на три единицы вниз. Поэтому вертикальная составляющая ⃑𝑣 будет −3. Следовательно, ⃑𝑣=(2,−3).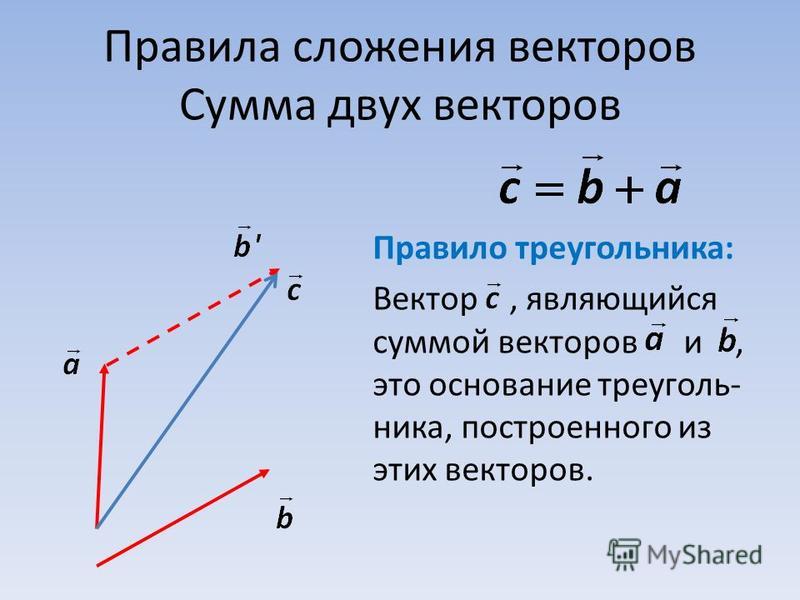

Часть 3

Есть два метода, которые мы можем использовать для сложения векторов.

Во-первых, мы можем вспомнить, что мы складываем векторы вместе по компонентам, а затем используем наши ответы в первых двух частях вопроса; это дает ⃑𝑢+⃑𝑣=(3,2)+(2,−3)=(3+2,2+(−3))=(5,−1).

Однако этот результат зависит от того, найдем ли мы компоненты обоих векторов правильно, а затем не допуская ошибок в расчетах. Это становится более проблема, чем больше векторов нас просят сложить вместе. Вместо этого мы также можем добавить два вектора вместе графически.

Поскольку мы складываем компоненты каждого вектора по отдельности, мы можем складывать векторы вместе методом «кончик к хвосту». Нарисуем векторы так, чтобы вершина одного вектора совмещена с хвостом следующего, поэтому сумма векторов — это вектор из начальной точки первого вектора в конечная точка конечного вектора. Так как векторы уже нарисованы в этом образом, мы имеем следующее.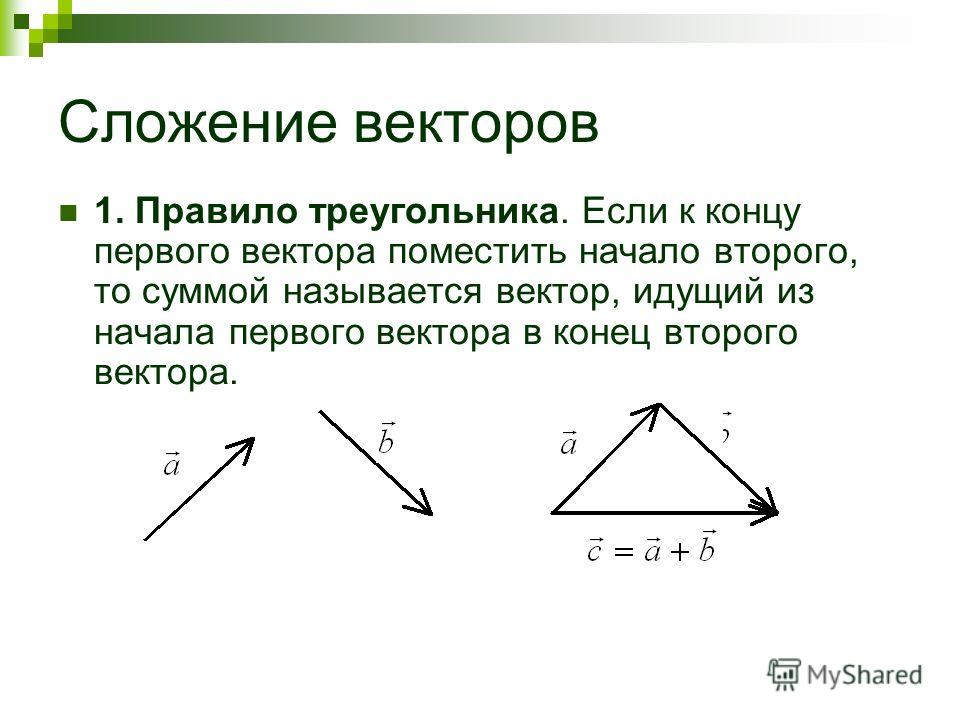

Вектор ⃑𝑢+⃑𝑣 представлена ​​третьей стороной в треугольнике, так как направления ⃑𝑢 и ⃑𝑣 совпадают. Затем мы можем найти компоненты ⃑𝑢+⃑𝑣 используя схему.

По вектору ⃑𝑢+⃑𝑣, мы перемещаемся на 5 единиц вправо и на 1 единицу вниз, поэтому горизонтальная составляющая равна 5, а вертикальная составляющая равна −1, что дает нам ⃑𝑢+⃑𝑣=(5,−1).

Мы видим, что это согласуется с прямым вычислением, которое мы сделали выше.

Пример 2. Нахождение суммы двух векторов, заданных графически

Какой график представляет ⃑𝐴+⃑𝐵, где ⃑𝐴=(3,4) и ⃑𝐵=(4,1)?

Ответ

Так как нам даны компоненты ⃑𝐴 и ⃑𝐵, мы можем складывать векторы покомпонентно получить ⃑𝐴+⃑𝐵=(3,4)+(4,1)=(3+4,4+1)=(7,5).

Глядя на варианты, мы видим, что единственный вариант A имеет ⃑𝐴=(3,4), ⃑𝐵=(4,1), и ⃑𝐴+⃑𝐵=(7,5), так что это правильный ответ. Проблема с таким ответом на вопрос состоит в том, что мы часто просят сложить векторы вместе графически, не давая вариантов, поэтому схему тоже построим сами.

Мы можем начать с рисования векторов ⃑𝐴=(3,4) и ⃑𝐵=(4,1) на диаграмму, где мы помним, что первая компонента сообщает нам горизонтальное смещение, а второй компонент говорит нам о вертикальном смещение. Также стоит отметить, что мы можем зарисовывать векторы в любом месте. на самолете. Однако для простоты мы начнем оба вектора с источник. Во-первых, ⃑𝐴=(3,4) переместится на 3 единицы вправо и на 4 единицы вверх, чтобы дать нам следующее.

То же самое можно сделать с вектором ⃑𝐵=(4,1), который переместится на 4 единицы вправо и на 1 единицу вверх, как показано на рисунке.

Стоит отметить, что поскольку мы начали наши векторы с начала координат, координаты конечных точек будут равны соответствующим компоненты вектора; их часто называют векторами положения.

Чтобы сложить эти два вектора вместе графически, мы начнем с их эскиза. так что конечная точка одного вектора является начальной точкой другого. Мы переместим ⃑𝐵 так, чтобы его начальная точка находилась в (3,4); он все равно переместится на 4 единицы вправо и 1 единицу вверх, что дает нам следующее.

Наконец, правило треугольника для векторов говорит нам, что сумма этих двух векторами будет вектор, имеющий начальную точку ⃑𝐴 и конечная точка ⃑𝐵 так как эти векторы нарисованы хвост, что дает нам следующее.

На диаграмме видно, что ⃑𝐴+⃑𝐵 перемещается на 7 единиц вправо и на 5 единиц вверх, поэтому ⃑𝐴+⃑𝐵=(7,5), и это показано в варианте A.

В наших предыдущих примерах мы использовали графические представления наряду с их компоненты для решения проблем. В нашем следующем примере мы будем использовать только графический представление векторов для решения геометрической задачи.

Пример 3. Определение правильной диагонали в законе параллелограмма

Какой вектор эквивалентен ⃑𝑢+⃑𝑣?

Ответ

Четырехугольник 𝐴𝐶𝐷𝐵 имеет противоположные стороны как равные векторы. Поскольку равные векторы имеют одинаковую величину и направление, мы можем сделать вывод что 𝐴𝐶𝐷𝐵 является параллелограммом. Мы хотим применить правило параллелограмма для векторов, чтобы сложить эти векторы. Для этого замечаем что ⃑𝑣 — это вектор из 𝐴 в 𝐶, поэтому ⃑𝑣=𝐴𝐶.

Аналогично, ⃑𝑢=𝐴𝐵.

Правило параллелограмма для сложения векторов говорит нам, что если 𝐴𝐶 и 𝐴𝐵 имеют одинаковую начальную точку, 𝐴, тогда 𝐴𝐶+𝐴𝐵=𝐴𝐷, где 𝐷 — точка, которая делает 𝐴𝐶𝐷𝐵 параллелограмм. Вектор 𝐴𝐷 — диагональ параллелограмма показано.

Следовательно, ⃑𝑢+⃑𝑣=𝐴𝐷.

Используя приведенный выше пример, мы можем показать полезный результат для параллелограмма, который мы построен.

Применяя правило треугольника для векторов в точках 𝐴, 𝐶 и 𝐷 имеем 𝐴𝐶+𝐶𝐷=𝐴𝐷.

В пересчете на ⃑𝑢 и ⃑𝑣, это говорит о том, что ⃑𝑣+⃑𝑢=⃑𝑢+⃑𝑣.

Другими словами, это геометрическая демонстрация коммутативности вектора добавление.

До сих пор мы рассматривали только совместное сложение векторов. Мы сейчас рассмотрим пример, где нас просят найти разность двух векторов.

Пример 4. Определение правильного графического представления разности двух Векторы

Какой из следующих параллелограммов показывает допустимый способ получения ⃑𝐴−⃑𝐵?

Ответ

Чтобы вычесть два вектора графически, мы будем использовать два результата. Во-первых, мы можем перепишем выражение в виде суммы двух векторов: ⃑𝐴−⃑𝐵=⃑𝐴+−⃑𝐵.

Это говорит нам о разнице между ⃑𝐴 и ⃑𝐵 равно сумме ⃑𝐴 и −⃑𝐵, и мы знаем, как графически складывать векторы, используя оба треугольника и правила паралл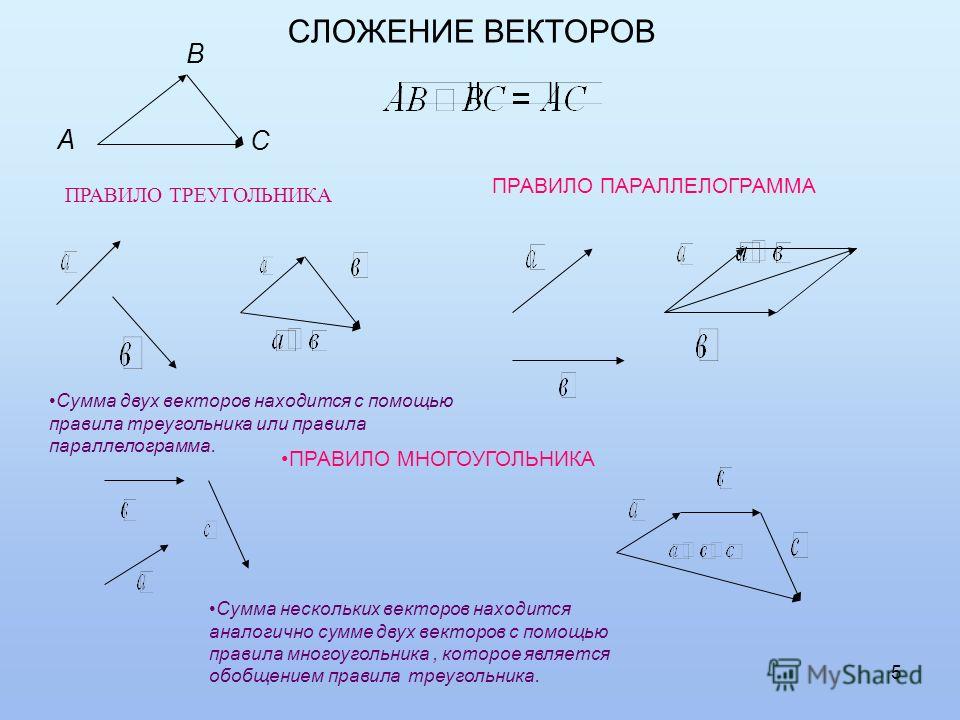елограмма. Поскольку в опции включены параллелограммы, мы будем использовать правило параллелограмма.

Правило параллелограмма для сложения векторов говорит нам, что если 𝑃𝑄 и 𝑃𝑆 — векторы с одинаковой начальной точкой, 𝑃, тогда 𝑃𝑄+𝑃𝑆=𝑃𝑅, где 𝑅 — точка, из которой 𝑃𝑄𝑅𝑆 параллелограмм, как показано на следующем рисунке.

Если обозначить векторы, являющиеся сторонами параллелограмма, ⃑𝐴 и −⃑𝐵 имеем следующее.

Тогда, поскольку ⃑𝐴−⃑𝐵=⃑𝐴+−⃑𝐵, мы можем заменить вектор на диагонали с ⃑𝐴−⃑𝐵, то же, что вариант C.

Тогда мы можем задать следующий вопрос: даны два вектора ⃑𝐴 и ⃑𝐵, графически, как мы можем найти ⃑𝐴−⃑𝐵? Сделать это, мы начнем с наброска ⃑𝐴 и ⃑𝐵 иметь одну и ту же начальную точку, скажем 𝑃; мы также пометим конечные точки векторов 𝑄 и 𝑅, как показано.

Мы хотим определить ⃑𝐴−⃑𝐵=𝑃𝑅−𝑃𝑄. Напомним, что ⃑𝐴−⃑𝐵=⃑𝐴+−⃑𝐵 и что умножение вектора на -1 меняет его направление и делает не изменить свою величину.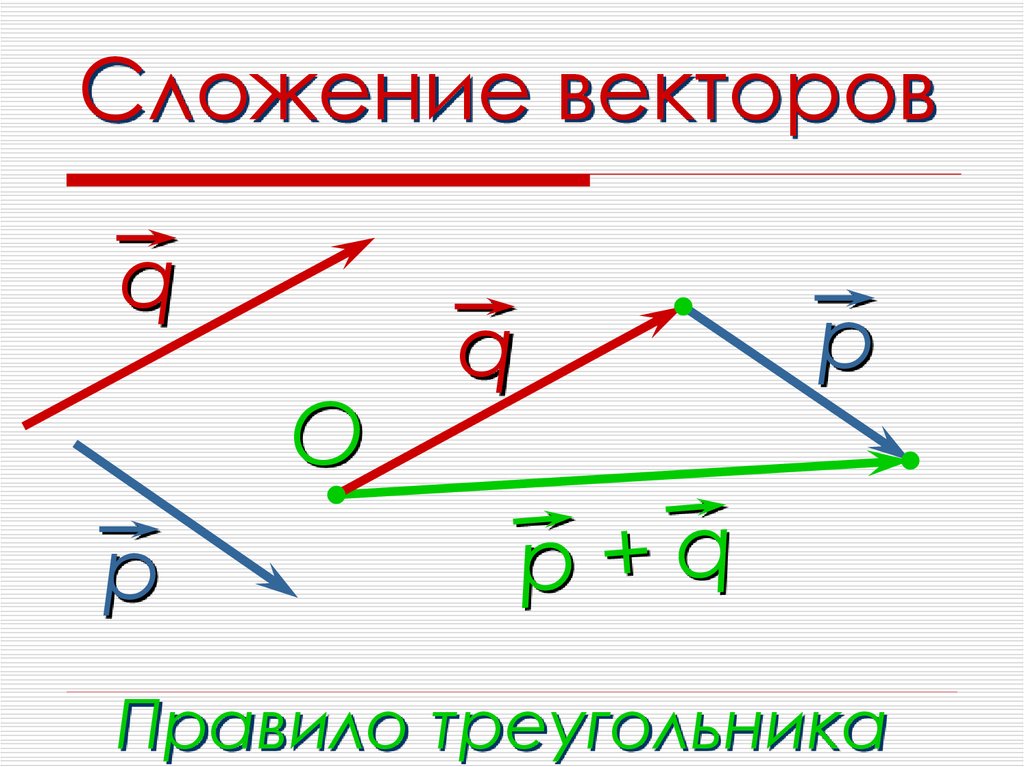 На нашей диаграмме это означает −⃑𝐵 это вектор от 𝑄 до 𝑃, как показано.

Тогда мы можем видеть, что конечная точка −⃑𝐵 является начальной точкой ⃑𝐴, поэтому мы можем добавить эти векторов с использованием правила треугольника для сложения векторов; имеем следующее.

Затем мы можем использовать коммутативность сложения векторов для записи −⃑𝐵+⃑𝐴=⃑𝐴−⃑𝐵. Это означает 𝑃𝑅−𝑃𝑄=𝑄𝑅.

Затем мы можем представить это графически, как показано на рисунке.

Давайте теперь посмотрим на несколько примеров применения этого рассуждения для вычитания двух вектора заданы графически.

Пример 5. Нахождение разности двух векторов, представленных графически

Что из следующего эквивалентно 𝐴𝐵−𝐷𝐵?

1.  40052
2.  𝐷𝐶
3.  40052
4.  40052
5. 𝐵𝐶

Ответ

. Мы просят найти разницу двух векторов. Для этого начнем с отметив, что умножение вектора на -1 меняет его направление но оставляет величину неизменной, поэтому −𝐷𝐵=𝐵𝐷.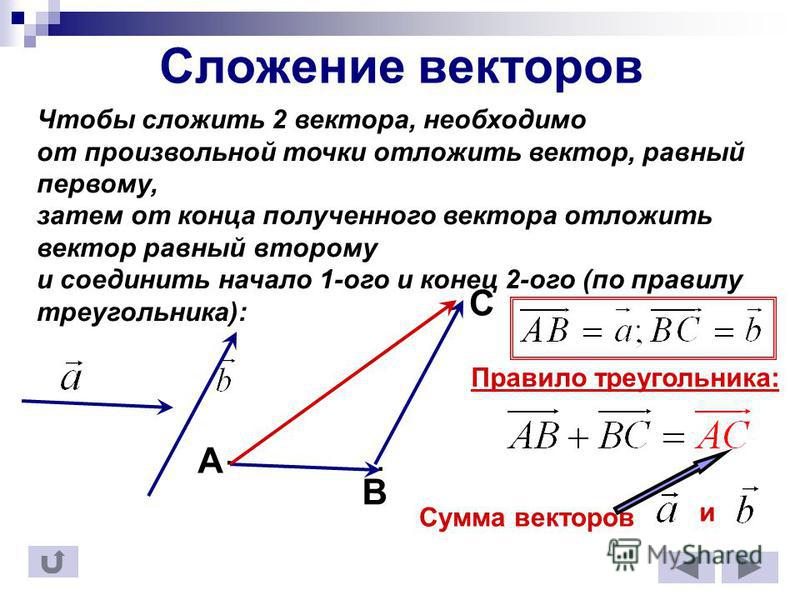

Следовательно, 𝐴𝐵−𝐷𝐵=𝐴𝐵+𝐵𝐷.

Мы можем нарисовать оба этих вектора на диаграмме.

Поскольку конечная точка 𝐴𝐵 является начальной точки 𝐵𝐷, мы можем сложить эти векторы, используя правило треугольника для сложения векторов, которое говорит нам 𝐴𝐵+𝐵𝐷=𝐴𝐷, что мы можем показать на схеме.

Однако это не один из предложенных вариантов. Нам также необходимо использовать факт что 𝐴𝐵𝐶𝐷 — параллелограмм, у которого противоположные стороны одинакового размера и параллельны. Следовательно, 𝐴𝐷=𝐵𝐶.

Следовательно, ответ — вариант E, 𝐵𝐶.

Пример 6. Решение геометрической задачи с использованием векторов в качестве сторон параллелограмма

Что из следующего эквивалентно 12𝐶𝐵−𝐷𝐶?

1.  40052
2. 𝐶𝐸
3. 𝐵𝐸
4.  40052
5. 𝐸𝐶

Ответ

Мы хотим определить вектор эквивалент к данному выражению с помощью использования с использованием с помощью диаграмма. Для этого сначала заметим, что для вектора ⃑𝑢, 12⃑𝑢 будет иметь то же направление, но вдвое меньше. Итак, мы начнем с нахождение вектора, эквивалентного 𝐶𝐵−𝐷𝐶. Мы можем сделать это, сначала вспомнив, что −𝐷𝐶=𝐶𝐷, поэтому 𝐶𝐵−𝐷𝐶=𝐶𝐵+𝐶𝐷.

Мы можем добавить эти векторы на диаграмму.

Чтобы сложить векторы вместе графически, мы можем использовать правило параллелограмма для векторы. Поскольку начальные точки обоих векторов одинаковы, их сумма будет диагональю параллелограмма.

Следовательно, 𝐶𝐵−𝐷𝐶=𝐶𝐵+𝐶𝐷=𝐶𝐴.

Мы хотим найти 12 таких векторов, поэтому нам нужен вектор в том же направлении, что и 𝐶𝐴 но с половинной величиной. Так как 𝐸 является серединой 𝐶𝐴, для этого есть два варианта; как 𝐶𝐸, так и 𝐸𝐴 будет иметь то же направление, что и 𝐶𝐴, но вдвое меньше.

Следовательно, 12𝐶𝐵−𝐷𝐶=12𝐶𝐵+𝐶𝐷=12𝐶𝐴=𝐶𝐸.

Итак, ответ вариант Б, 𝐶𝐸.

Стоит отметить, что мы можем применить эти правила для кратного сложения векторов раз. Например, рассмотрим следующую схему.

Если мы хотим найти 𝐴𝐵+𝐵𝐶+𝐶𝐷, мы можем сделать это, применив треугольник правило сложения векторов дважды. Во-первых, у нас есть 𝐴𝐵+𝐵𝐶=𝐴𝐶, как показано на следующей диаграмме.

Затем мы можем добавить 𝐴𝐶 и 𝐶𝐷 с правилом треугольника для сложения векторов. У нас есть 𝐴𝐶+𝐶𝐷=𝐴𝐷, как показано.

Следовательно, 𝐴𝐵+𝐵𝐶+𝐶𝐷=𝐴𝐷.

Графически мы можем представить это как три вектора 𝐴𝐵, 𝐵𝐶, и 𝐶𝐷 все нарисованы от кончика к хвосту, поэтому их сумма равна вектор, который имеет начальную точку 𝐴 и конечную точку 𝐷. Мы можем применить те же рассуждения к еще более сложным формы, как мы увидим в нашем последнем примере.

Пример 7. Упрощение суммы векторов, являющихся сторонами многоугольника

Завершено: На следующем рисунке 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=.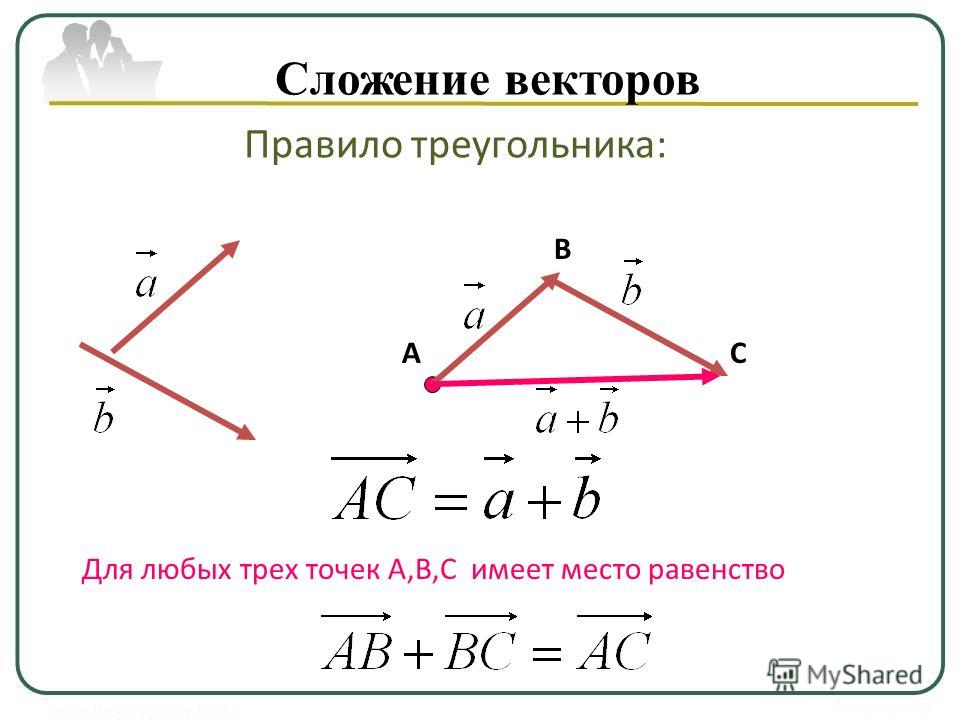

1.  40052
2.  40052
3.  40052
4. 2 40052
5. 2𝐵𝐸

Ответ

Мы начнем с добавления всех векторов в сумму на диаграмму.

Есть два способа определить эту сумму: мы можем сделать это непосредственно с помощью напоминая, что сумма любого количества векторов, проведенных от кончика к хвосту, будет иметь начальная точка первого вектора и конечная точка конечного вектор. На нашей диаграмме это будет вектор 𝐴𝐸 как показано.

Легче думать об этом как о следовании векторам из 𝐴 вплоть до 𝐸. У нас есть 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐸, который является вариантом B.

Чтобы понять, почему это так, нам нужно применить правило треугольника, которое гласит что для любых точек 𝑃, 𝑄, и 𝑅, 𝑃𝑄+𝑄𝑅=𝑃𝑅.

Мы можем применить это к первым двум векторам в сумме, чтобы получить 𝐴𝐵+𝐵𝐶=𝐴𝐶, так 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐶+𝐶𝐷+𝐷𝐸.

Затем мы можем снова применить правило треугольника и увидеть, что 𝐴𝐶+𝐶𝐷=𝐴𝐷, так 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐷+𝐷𝐸.

Наконец, мы применяем правило треугольника еще раз, чтобы получить 𝐴𝐷+𝐷𝐸=𝐴𝐸, и, следовательно 𝐴𝐵+𝐵𝐶+𝐶𝐷+𝐷𝐸=𝐴𝐸.

Следовательно, ответ — вариант Б, 𝐴𝐸.

Давайте закончим, повторив некоторые важные моменты этого объяснитель.

Ключевые точки

• Правило треугольника для векторов говорит нам, что для любых трех точек 𝐴, 𝐵 и 𝐶, 𝐴𝐵+𝐵𝐶=𝐴𝐶.
• Правило треугольника для векторов позволяет нам складывать два вектора графически, рисуя их так, что начальная точка одного вектора является конечной точкой другого.
• Правило параллелограмма для векторов говорит нам, что 𝐴𝐵+𝐴𝐷=𝐴𝐶, где 𝐶 — точка, из которой 𝐴𝐵𝐶𝐷 параллелограмм.
• Правило параллелограмма для векторов позволяет нам складывать векторы графически, рисуя их так, чтобы они имели одну и ту же начальную точку. Тогда их результирующая будет задается диагональю параллелограмма, натянутого на векторы.
• Мы можем вычесть два вектора, используя тот факт, что для любых трех точек 𝑃, 𝑄 и 𝑅, 𝑃𝑅−𝑃𝑄=𝑄𝑅.

Почему мы не можем применить правило параллелограмма сложения векторов для двух параллельных векторов?

спросил 2 года, 2 месяца назад

Изменено 2 года, 2 месяца назад

Просмотрено 468 раз

$\begingroup$

Мой учебник говорит, что мы не можем применить правило параллелограмма сложения векторов для двух параллельных векторов. Почему мы не можем применить правило?

• векторов

$\endgroup$

1

$\begingroup$

Сложение векторов параллелограмма говорит о том, что если два вектора имеют одну и ту же точку в качестве хвоста или начала координат, то они рассматриваются как два смежных сторон параллелограмма и построить параллелограмм. И тогда диагональ этого параллелограмма (через хвост этих векторов) даст вам направление результирующего вектора, а для величины вы знаете правила.

Если вам даны два параллельных вектора, совершенно очевидно, что вы не можете рассматривать их как смежных сторон параллелограмма и, следовательно, они перекрываются, и у вас остается только один вектор, величина которого равна алгебраически добавили величину двух векторов и указывали в одном направлении.

Вы не можете построить параллелограмм (я не говорю о вырожденном параллелограмме), взяв две параллельные стороны за смежных сторон, поскольку в этом случае они больше не будут параллельны друг другу.

Надеюсь поможет ☺️.

$\endgroup$

5

$\begingroup$

Потому что нельзя построить правильный параллелограмм из двух коллинеарных отрезков.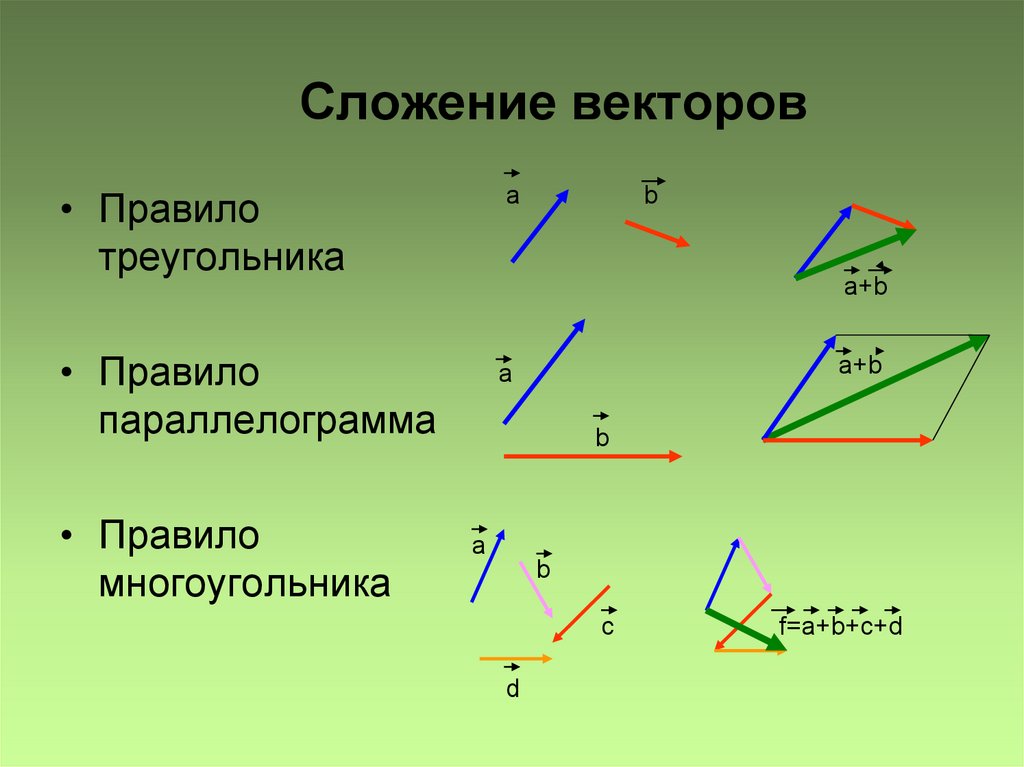

$\endgroup$

2

$\begingroup$

Если вы называете параллелограмм с углами 0 параллелограммом, вы все равно можете его использовать, но большинство людей просто добавляют два параллельных вектора, как в одну линию.

$\endgroup$

0

$\begingroup$

Если вы называете вырожденный параллелограмм, все четыре вершины которого лежат на одной прямой, а четыре внутренних угла равны 0, 180, 0 и 180 градусов, все еще «параллелограммом», то вы может использовать правило параллелограмма для параллельных (и антипараллельных) векторов. Точно так же, если вы позволяете стороне параллелограмма иметь нулевую длину, то вы можете использовать правило параллелограмма, если один или оба вектора являются нулевыми векторами.