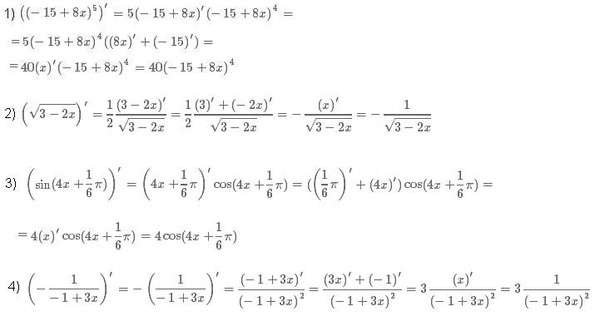Производная 5 в степени: Найти производную y’ = f'(x) = (5^x) ((5 в степени х))

Содержание

7. Дифференцирующие степени функции

М. Борна

Функция функции

Если y является функцией u , а u является функция x , тогда мы говорим

« y является функцией функции u «.

Пример 1

Не пропустите…

В этом разделе:
Цепное правило
Силовое правило

Рассмотрим функцию

y = (5 х + 7) ¹² .

Если мы допустим u = 5 x + 7 (самое внутреннее выражение), то мы могли бы записать нашу исходную функцию как

у = у ¹²

Мы записали х как функцию х , и, в свою очередь, х является функцией х .

Это жизненно важное понятие в дифференциации, так как многие из функций, с которыми мы столкнемся с этого момента, будут функциями функций, и нам нужно распознать их, чтобы правильно их дифференцировать.

Цепное правило

Чтобы найти производную функции от функции, нам нужно использовать цепное правило:

`(dy)/(dx) = (dy)/(du) (du)/(dx)`

Значит нам нужно

Распознайте `u` (всегда выбирайте самое внутреннее выражение, обычно часть в квадратных скобках или под знаком квадратного корня).
Затем нам нужно повторно выразить `y` через `u`.
Затем мы дифференцируем `y` (относительно `u`), затем мы заново выражаем все через `x`. 9(-1//2)=1/кв.м`? См.:
- Отрицательные индексы
- Дробные индексы
Вы можете поиграть с этим примером на странице интерактивного апплета «Дифференциация».
Производная степени функции (степенное правило)
Расширением цепного правила является степенное правило для дифференцирования. Находим производную
от от u ⁿ (степень функции):
94` у нас есть мощность функции.
Ответить
Если положить у = 2 х ³ — 1, то у = и ⁴ .
Итак, теперь
- y записывается как степень u ; и
- u является функцией x [ u = f ( x ) ].
Чтобы найти производную от такого выражения, мы можем использовать наш новое правило: 92
Исчисление
Саманта В.
спросил 06.03.20
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старый
Автор: Лучшие новыеСамые старые
Исидро Л. ответил 06.03.20
Репетитор
5,0 (456)
AP Исчисление AB Преподаватель 20 лет стажа.
Об этом репетиторе ›
Об этом репетиторе ›

Голосовать за 1 Понизить
Подробнее
Отчет
Аманда Б. ответил 07.03.20

Репетитор
5 (182)
Эксперт по алгебре 1 преподаватель с более чем 10-летним опытом преподавания
Об этом репетиторе ›
Об этом репетиторе ›
Чтобы получить производную от f(x) = 2 / (2t — 5) ² , у вас есть несколько вариантов. Вы можете:
1. Использовать правило отношения или
2. Переместите биномиальное выражение из знаменателя в числитель, а затем примените степенное правило и цепное правило .
В этом примере я покажу вам как использовать метод #2 .

Шаг 1: Во-первых, нам нужно изменить нашу функцию, чтобы избавиться от дроби. Мы можем сделать это, используя правила показателей, которые позволяют нам переместить весь бином из знаменателя в числитель, пока мы отрицаем его показатель. Вот как это будет выглядеть:
f(x) = 2 (2t — 5) ^-2 Теперь у нас больше нет дроби, но показатель степени (2t — 5) теперь равен -2.
Шаг 2: Теперь мы готовы взять производную. Во-первых, чтобы применить к правило степени, мы сделаем три вещи: :
1. Умножим показатель степени бинома (-2) на коэффициент бинома (который равен 2) и запишем их произведение перед скобки в качестве нового коэффициента.
2. Оставьте все, что находится внутри круглых скобок (пока), полностью нетронутым.
3. Уменьшите исходный показатель степени, вычитая из него 1 (таким образом, -2 -1).
Это дает нам: -4 (2t — 5) ^-3 **Мы еще не закончили!
Шаг 3 : Теперь нам понадобится , чтобы применить цепное правило, взяв производную бинома в скобках:
Производная бинома в скобках = 2 905 5 Шаг
3
4 : Умножая производную из шага 3 на выражение, полученное из шага 2, мы получаем окончательный ответ:
f'(x) = -4 (2t — 5) ^-3 (2) , которое можно упростить, умножив -4 на 2:
f'(x) = -8 (2t — 5) ^-3 Окончательный ответ

Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.

No related posts.