Что такое парабола в алгебре: Квадратичная функция — урок. Алгебра, 8 класс.

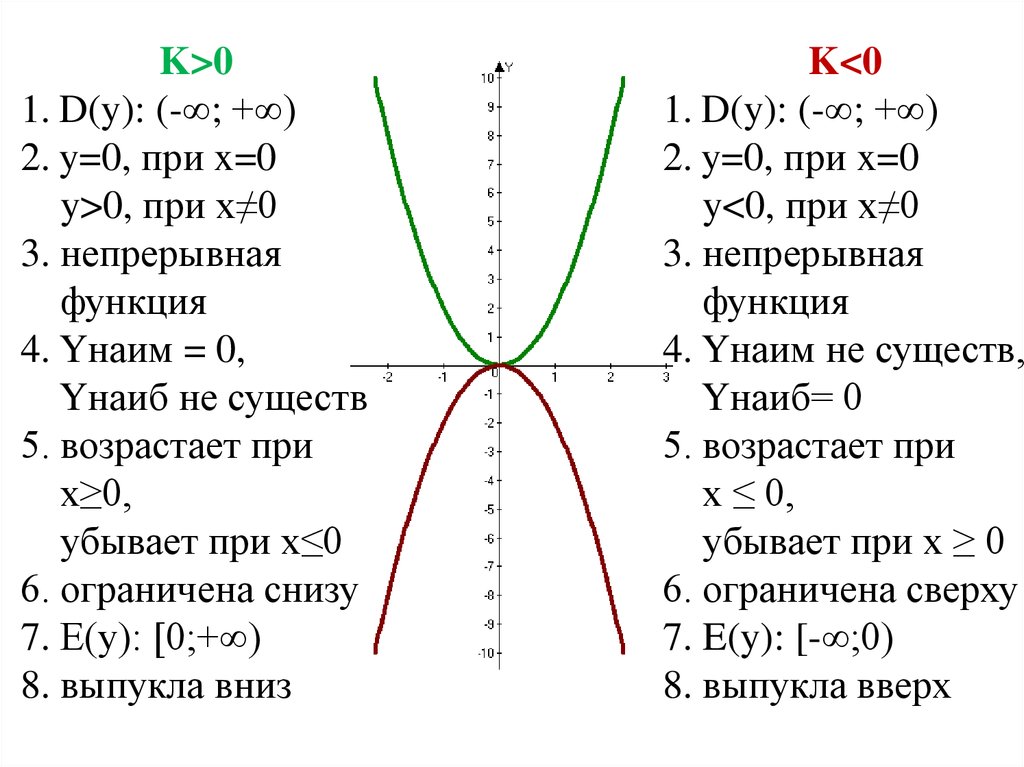
как выглядит, свойства, как определить направление ветвей

Содержание:

• Что такое парабола в математике
• Алгоритм построения параболы
  • Примеры решения задач на построение параболы
• Смещение параболы

Содержание

• Что такое парабола в математике
• Алгоритм построения параболы
  • Примеры решения задач на построение параболы
• Смещение параболы

Что такое парабола в математике

Парабола — график квадратичной функции вида \(f(x)=ax^2+bx+c\). 2\) на 3 единичных отрезка вправо.

 

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

«Зачем мне что-то знать о параболе в обычной жизни?» — Яндекс Кью

Популярное

Сообщества

Детский вопрос

Математика

Анонимный вопрос

19 августа 2019  ·

10,4 K

Ответить1Уточнить

Надежда Шихова

Математика

8,5 K

Редактор, автор и переводчик книг по математике  · 19 авг 2019  ·

problemaday

Парабола — график самой простой нелинейной функции, которая только бывает — квадратичной функции. Ее в школе потому так подробно и изучают, что это очень простой, почти игрушечный пример, на котором можно показать разные подходы и методы, в том числе и графический. Парабола — это не столько цель обучения, сколько средство. Умение легко и быстро переходить от функции к ее графику и обратно; умение легко и быстро переходить от одной модели данных к другой пригодится любому человеку, который будет заниматься математикой или применять математические методы.

В быту мы не решаем серьезных задач, а потому и не применяем математические методы. Но профессиональная жизнь — это самая обычная жизнь, если только вы не собираетесь существовать за чужой счет. Иметь представление о функциях нужно не во всех профессиях, но во многих. Например, в 2019 году школу профильный ЕГЭ по математике писали 60% выпускников — они планируют получать специальность, в которой нужна математическая подготовка. Кто-то не поступит, кто-то бросит. Во всяком случае, есть 30-40 процентов выпускников, которым потребуются математические умения, которыми они овладели, изучая параболу.

Может быть, Вы и не входите в эти проценты.

Комментировать ответ…Комментировать…

Maxim Vyalkov

Математика

1,3 K

Интересующие темы: история математики, история христианства, библеистика.   · 18 нояб

Тут всё зависит от того, какой будет ваша «обычная жизнь». Если в обычной жизни вы не будете заниматься оптикой, архитектурой, разрезанием конусов (парабола — это одно из конических сечений), метанием каких-либо снарядов (например, камней), дизайном интерьеров, живописью, анализом рынка ценных бумаг и валют (где может встречаться рост или падение стоимости тех или иных… Читать далее

Комментировать ответ…Комментировать…

Владимир Шитов

Биология

166

Молодой учёный, занимающийся биоинформатикой и анализом данных. В свободное время изучаю п…  · 18 сент 2019  ·

manoscience

Парабола — это не просто математическая функция, которую полезно знать для общего развития. У неё есть очень интересные и полезные свойства, которые с успехом применяются и в реальной жизни. Вот пример. У параболы есть особая точка, называемая фокусом параболы. Крутость этой точки заключается в том, что если на параболу направить пучок параллельных лучей, то… Читать далее

Андрей Подчуфаров

19 декабря 2019

Парабола испульзуют в военных силах, для расчёта дальности полёта снаряда. Траектория движения мяча, снаряда, пули… Читать дальше

Комментировать ответ…Комментировать…

Skysmart. Онлайн-школа для детей и подростков 

263

Skysmart – онлайн-школа для учеников 1–11 классов и тех, кто только готовится к учебе   · 18 дек 2019  · skysmart. ru

Отвечает

Yanchauskayte

Парабола — одна из универсальных траекторий движения, будь то движение космических тел во Вселенной или движение нарисованных противников в онлайн-шутере. Свойства параболических прямых используются при изготовлении различных линз — очков, стекол фонариков, фар, телескопов, при создании антенн и проектировании зданий. Поведение такой прямой на плоскости или в… Читать далее

Комментировать ответ…Комментировать…

American Пенсионер

234

Пенсионер, Ph.D. Работал в советских НИИ, ящиках и академиях, и в американских университет…  · 26 июл 2021

А математику уже затем учить следует, что она ум в порядок приводит. Ломоносов так сказал, и я в этом случае с ним согласен. Слишком много существует людей туповатых, математику ни разу не учивших, и от этого как-то грустно становится.

Комментировать ответ…Комментировать…

Вы знаете ответ на этот вопрос?

Поделитесь своим опытом и знаниями

Войти и ответить на вопрос

2 ответа скрыто(Почему?)

Фокус и Директриса Параболы — Концепция

Итак, есть пара дополнительных элементов
, которые может дать нам парабола.
Итак, мы привыкли знать, как изобразить их на графике,
с заданной вершиной и вроде того, как мы
с заданной формой, крутой или узкой, и все такое прочее.

Пара других вещей, которые вступают в игру
, это то, что называется focus и
directex. То, что они есть, в основном
две разные вещи.
Одна точка, одна линия.

Фокус — это в основном точка, равная
прямо над вершиной направленной вверх параболы
. Будет прямо под
вершиной параболы, обращенной вниз.
Что это такое, если вы думаете о том, что
идет на футбольный матч или что-то в этом роде
, вы видите парней на боковой линии
с этими большими полукругами, в основном похожими на вещи.
На самом деле это параболы, и
это то, что когда звук приходит
, на самом деле в этом фокусе есть маленький
микрофон.
Итак, все звуковые волны приходят, и они
все отражаются в одном месте.
Итак, куда бы что ни падало,
оно отражается в этом фокусе.

И тогда то, что такое директекс, не совсем применимо к
, потому что это
не совсем в этой маленькой параболической
звуковой сборке, а то, что это
, это линия, так что любая точка
на параболе будет экви
дальний от фокуса и
тот директекс.

Если бы вы провели линию прямо вниз
до прямых маршрутов, эта линия идет
будет точно на таком же расстоянии, если вы
въедете прямо в фокус.
Итак, у нас есть эти
два разных элемента.
Мой рисунок, как видите, немного неправильный.
Эта строка должна быть точно такой же длины.
Надеюсь, вы понимаете, что происходит.

Итак, эта парабола, которую я имею здесь, представляет собой просто
базовую параболу, A, X в квадрате, где
A положительно, потому что у нас есть
парабола, обращенная вверх.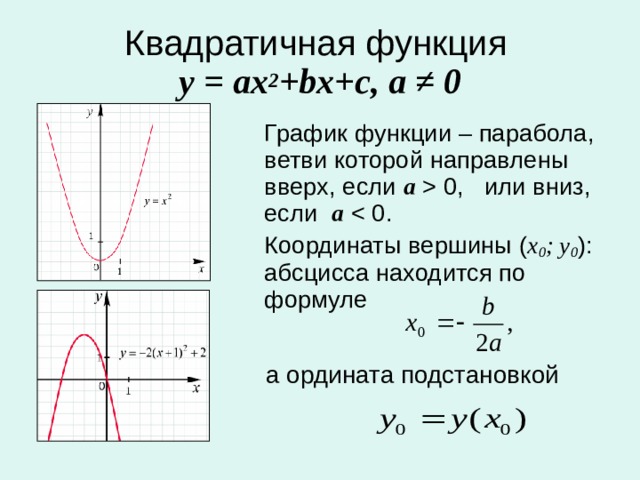
Мы привыкли видеть, что А диктует
крутизна эта.
Если число A больше
1, оно, вероятно, становится более крутым.
А меньше 1, становится шире.
Но на самом деле А является прямым отношением
к этому фокусу.

И на самом деле то, что мы называем… мы привыкли говорить, что
параболы — это уравнение,
для квадратичных уравнений — это AX в квадрате плюс
B плюс C, я хочу указать, что C
в квадратном уравнении отличается от
, чем C Сейчас я расскажу о
.

C, о котором мы здесь говорим, на самом деле
разница или, простите, расстояние
между вашим фокусом и вашей вершиной.
И абсолютное значение A собирается
быть равным 1 больше 4C. Это расстояние.
Так что на самом деле это один из способов
вычислить, насколько крута или широка эта
парабола, зная расстояние
между фокусом и вершиной.

Еще одна вещь, о которой я хочу поговорить о
, это то, что мы знаем это расстояние C между
фокусом и вершиной C. Мы также знаем, что
будет
одинаковое расстояние от точки
до директекса. Таким образом, по умолчанию прямо в этой точке вершины
будет такое же расстояние
C от директекса до вершины.

Итак, главное из этого небольшого разговора —
фокус — это точка, в которой все
линии, которые вы создаете,
идущие прямо, будут
отклоняться в этот фокус.
И связь между фокусом
и директексом такова, что любая точка на кривой
будет равноудалена
между ними.

И, наконец, этот А, этот коэффициент на
X в квадрате, может быть определен абсолютным
значением А, равным 1 больше 4С.
И причина, по которой у них есть это абсолютное значение
, заключается в том, что оно просто будет диктовать
величину A. На самом деле
не говорит нам знак.

Итак, парабола, обращенная вверх, A
будет положительной.
Парабола, направленная вниз, мы
знаем, что A должна быть отрицательной.
Чтобы потом мы могли добавить эти знаки
, но это говорит нам о
, по крайней мере, в числовом значении
этого коэффициента.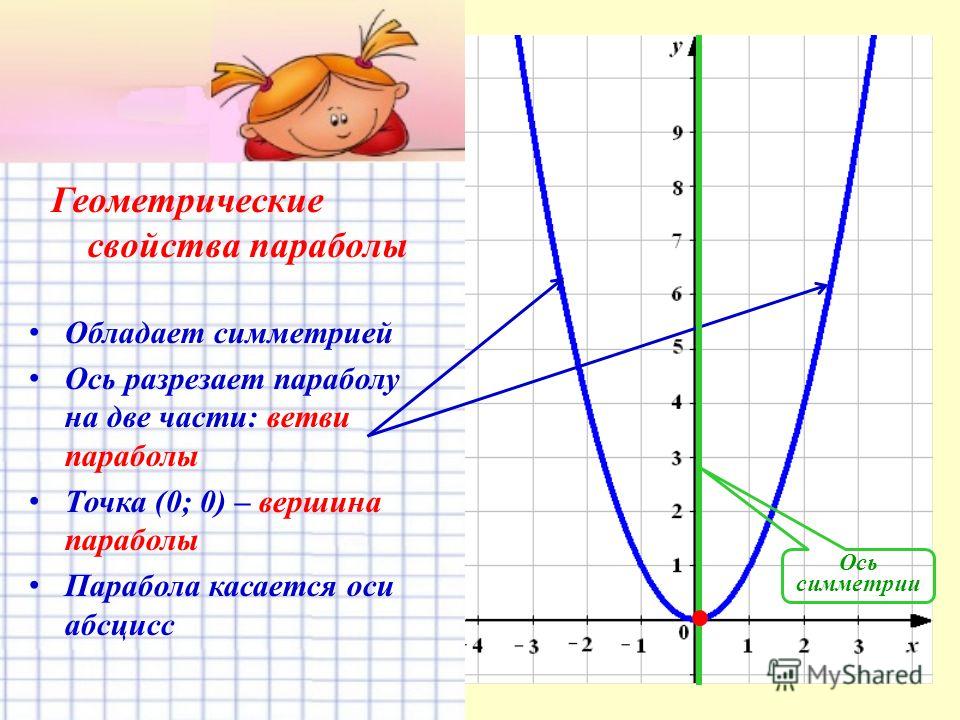

Математический обзор параболы

Математический обзор параболы https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=мм&r=г 3 апреля 2014 г. 2 декабря 2014 г.

Обзор:

Парабола — это коническое сечение, образующее незамкнутую кривую. Графики квадратичных функций имеют форму параболы.

Что такое парабола?

Парабола — это кривая, образованная по обе стороны от оси симметрии. Если парабола вертикальна, то линия с одной стороны параболы (называемая директрисой) вертикальна. Если он горизонтальный, то и директриса будет горизонтальной. Ось симметрии содержит две именованные точки: фокус параболы, который обычно находится внутри параболы, и вершину, являющуюся точкой на вершине параболы, где она меняет направление.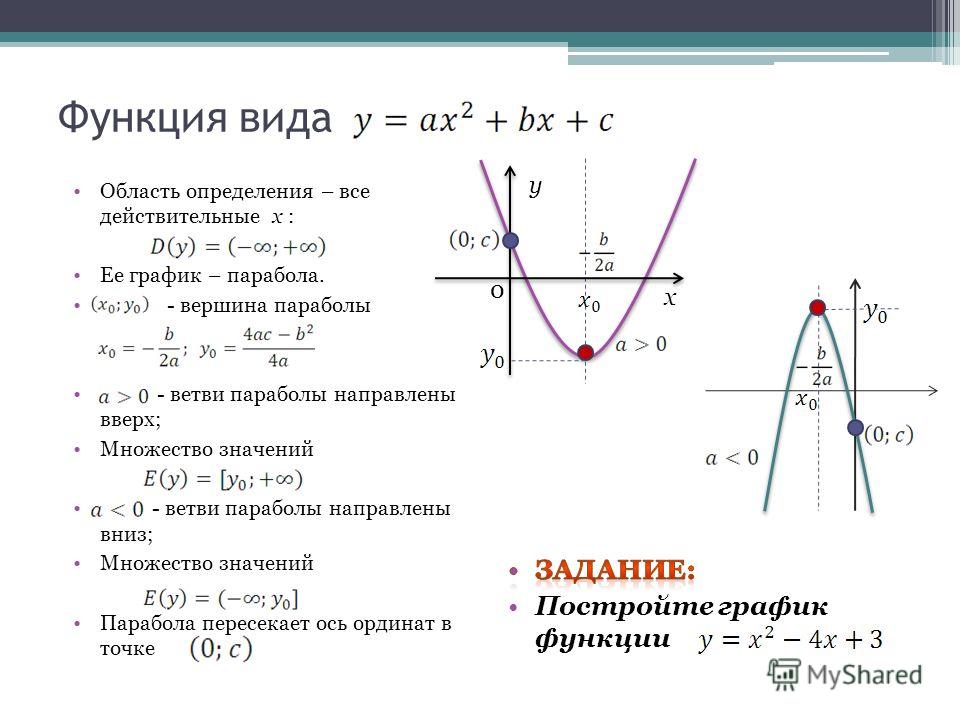

Почему квадратичная функция имеет параболическую форму?

Уравнение параболической функции является квадратичной функцией. В общих чертах уравнение выглядит так: ax ² + bx + c. Если вершина находится в (h,k), можно использовать формулу расстояния и вывести общее уравнение, так что y = a(x-h) ² + k. Предположим, что фокус параболы находится в точке (3, 5), а направляющая y = 1. Ось симметрии находится в точке x = 3. Используя уравнение для вершины, парабола изменит направление в точке (3, 3). Его уравнение (x-3) ² + 24 = 8y или x ² – 6x + 9 + 24 = 8y или (x ² – 6x + 33)/8 = y.

Какие параболические формы встречаются в природе?

Некоторые из параболических форм, встречающихся в природе, включают траекторию движения тела в однородном гравитационном поле. Например, бейсбольный мяч, подбрасываемый в воздух с малой скоростью, или центр тяжести ныряльщика, прыгающего с трамплина, без сопротивления воздуха образуют параболическую форму.