Производная сложной функции
Пусть переменная у есть функция от переменной U: y=y(U), а переменная U, в свою очередь есть функция от переменной V: U=U(V), а переменная V – функция независимой переменной х: V=V(x) (эту цепочку можно было бы и продолжить).
— Тогда переменная у является сложной функцией (суперпозиции функций) независимой переменной х: y=y(U(V(x))) («сложена» из различных функций).
— Если все функции в цепочке дифференцируемы, то производная сложной функции по независимой переменной (аргументу) равна произведению производных по промежуточным аргументам:
.
Аналогичную формулу
для дифференцирования сложной функции
можно получить при любом уровне
вложенности и любых обозначениях, если
заметить закономерность: производные
в произведении вычисляются «по
порядку», так, как записаны в выражении
для сложной функции.
Схема:
Еще один пример (попробуйте построить формулу сами и сравните):
здесь аргумент – это t.
Таблица производных основных элементарных функций
— Обратите внимание! При вычислении производных сложных функций в роли аргументахиз таблицы производных может выступать любая функция!
Функция | Производная | ||
1 | Степенная | = | |
Частные случаи | |||
2 | Показательная | = | |
Экспонента | = | ||
3 | Логарифмическая | = | |
Натуральный логарифм | = | ||
4 | Тригонометрические: | ||
синус | |||
косинус | |||
тангенс | |||
котангенс | |||
5 | Обратные тригонометрические | ||
арксинус | |||
арккосинус | |||
арктангенс | |||
арккотангенс | |||

На практике наиболее трудным оказывается дифференцирование сложной функции, когда необходимо правильно оценить порядок вложения функций. Поэтому здесь приведено несколько примеров. Напомним, чтонижний индекс в записи показывает, по какой переменной вычисляется производная.
Примеры
; | В этом примере функция «сложена» из показательной (3х), роль х играет sinx, и тригонометрической (sinx) функций. |
Здесь нижний индекс производной показывает, по какой переменной она вычисляется. | |
По таблице производных находим производные соответствующих функций и перемножаем их. |
| Функция
«сложена» из арктангенса (arctg
x), квадратного
корня
и линейной функции (2х-1). | ||
По таблице находим производные, учитывая, что в | |||
роли х выступают различные функции (показаны нижним индексом). Перемножаем табличные производные выделенных функций. | |||
После вычисления производных не следует делать никаких алгебраических преобразований.
Производная неявно заданной функции
— Если функция задается общим выражением относительно переменных x и y, то она называется заданной неявно:
F(x,y)=0,
(Сравните с явно заданной функцией: y=y(x)).
— Чтобы
найти производную
,
функции, заданной неявно, надо найти
производную по переменнойх обеих частей выражения, задающего
функцию.
— При этом следует учитывать, что переменная y зависит от x (y=y(x)), и вычислять производную, как от сложной функции. Затем полученное уравнение разрешают относительно .
ПРИМЕР
Найти производную неявно заданной функции:
.
Найдем производные по х от левой и правой частей равенства, неявно задающего функцию y=y(x).
Здесь использованы правила дифференцирования суммы и вынесения постоянной за знак производной (правила 3 и 5). | |
Первое слагаемое является произведением функций:и Используем правило дифференцирования произведения (правило 4). Второе и третье слагаемые дифференцируются как сложные функции. | |
Из
полученного уравнения с помощью
алгебраических преобразований
выделяется производная. | |
. | |
Производная сложной функции
- Понятие производной сложной функции
- Таблица производных некоторых сложных функций
- Найти производную сложной функции самостоятельно, а затем посмотреть решение
Пусть y – сложная функция x, т.е. y = f(u), u = g(x), или
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные — машинальное перенесение правил
дифференцирования простых функций на сложные функции.
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению — промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии — приготовлении запечёных яблок, фаршированных ягодами.
Итак, «яблоко» — это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x,
в свою очередь, является «фаршем» (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1.
При таком режиме духовка воздействует только на «яблоко», поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме.
Пример 1.Найти производную функции
Сначала определим, где здесь «яблоко», то есть функция по промежуточному аргументу
Тогда
Далее по правилам дифференцирования (производная суммы или разности) и таблице производных (производные синуса и косинуса) находим:
Требуемая в условии задачи производная (готовое «фаршированое яблоко»):
Нахождение производной сложной логарифмической функции имеет свои
особенности, поэтому у нас есть и урок «Производная логарифмической функции».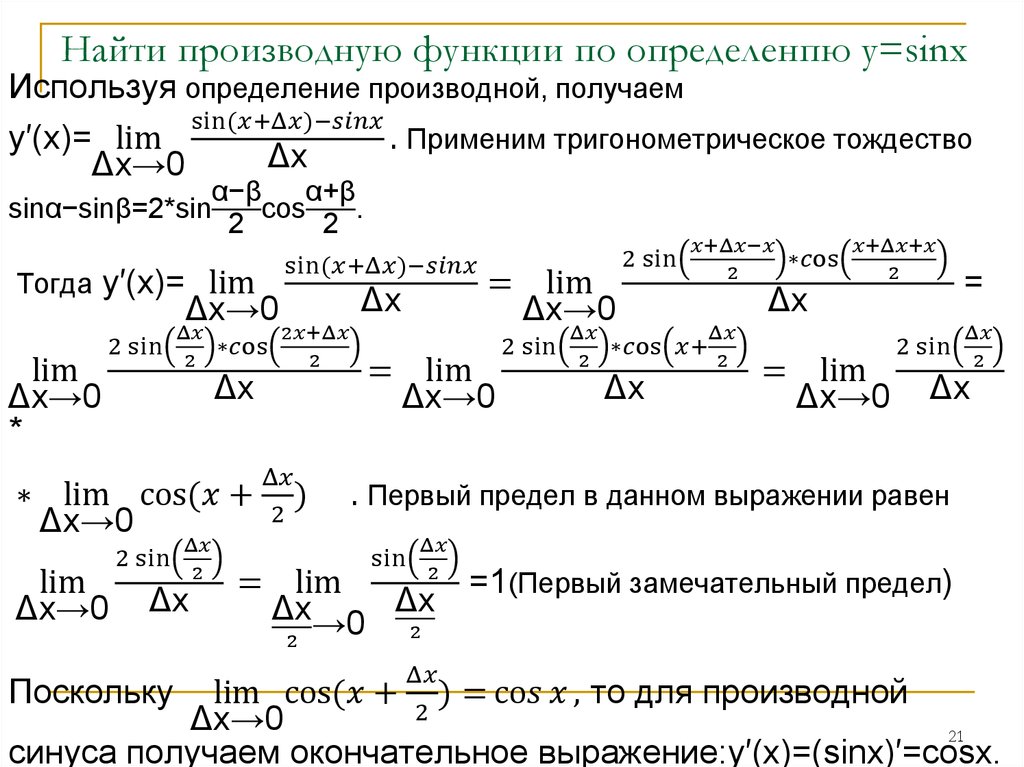
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Пример 2.Найти производную функции
Неправильное решение: вычислять натуральный логарифм каждого слагаемого в скобках и искать сумму производных:
Правильное решение: опять определяем, где «яблоко», а где «фарш». Здесь натуральный логарифм от выражения в скобках — это «яблоко», то есть функция по промежуточному аргументу u, а выражение в скобках — «фарш», то есть промежуточный аргумент u по независимой переменной x.
Тогда (применяя формулу 14 из таблицы производных)
Во многих реальных задачах выражение с логарифмом бывает несколько сложнее, поэтому и есть урок «Производная логарифмической функции».
Пример 3.Найти производную функции
Неправильное решение:
Правильное решение. В очередной раз определяем, где «яблоко», а где «фарш». Здесь
косинус от выражения в скобках (формула 7 в таблице производных)- это «яблоко», оно готовится в режиме 1, воздействующем только на него,
а выражение в скобках (производная степени — номер 3 в таблице производных) — это «фарш», он готовится при режиме 2, воздействующей только на него. И как всегда соединяем две производные знаком произведения. Результат:
В очередной раз определяем, где «яблоко», а где «фарш». Здесь
косинус от выражения в скобках (формула 7 в таблице производных)- это «яблоко», оно готовится в режиме 1, воздействующем только на него,
а выражение в скобках (производная степени — номер 3 в таблице производных) — это «фарш», он готовится при режиме 2, воздействующей только на него. И как всегда соединяем две производные знаком произведения. Результат:
Производная сложной логарифмической функции — частое задание на контрольных работах, поэтому настоятельно рекомендуем посетить урок «Производная логарифмической функции».
А проверить решение задачи на производную можно на калькуляторе производных онлайн.
Первые примеры были на сложные функции, в которых промежуточный аргумент по независимой переменной был простой функцией. Но в практических заданиях нередко требуется найти производную сложной функции, где промежуточный аргумент или сам является сложной функцией или содержит такую функцию. Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования.
Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы.
Ниже – два примера, как это делается.
Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования.
Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы.
Ниже – два примера, как это делается.
Кроме того, полезно знать следующее. Если сложная функция может быть представлена в виде цепочки из трёх функций
,
то её производную следует находить как произведение производных каждой из этих функций:
.
Для решения многих ваших домашних заданий может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Пример 4.Найти производную функции
Применяем правило дифференцирования сложной функции, не забывая, что в полученном произведении производных промежуточный аргумент по независимой переменной x не меняется:
Готовим второй сомножитель произведения и применяем правило дифференцирования суммы:
Второе слагаемое — корень, поэтому
Таким образом получили, что промежуточный аргумент, являющийся суммой, в качестве одного
из слагаемых содержит сложную функцию: возведение в степень — сложная функция, а то, что возводится
в степень — промежуточный аргумент по независимой переменной x.
Поэтому вновь применим правило дифференцирования сложной функции:
Степень первого сомножителя преобразуем в корень, а дифференцируя второй сомножитель, не забываем, что производная константы равна нулю:
Теперь можем найти производную промежуточного аргумента, нужного для вычисления требуемой в условии задачи производной сложной функции y:
Тогда
Пример 5.Найти производную функции
Сначала воспользуемся правилом дифференцирования суммы:
Получили сумму производных двух сложных функций. Находим первую из них:
Здесь возведение синуса в степень — сложная функция, а сам синус — промежуточный аргумент по независимой переменной x. Поэтому воспользуемся правилом дифференцирования сложной функции, попутно вынося множитель за скобки:
Теперь находим второе слагаемое из образующих производную функции y:
Здесь возведение косинуса в степень — сложная функция f[g(x)],
а сам косинус — промежуточный аргумент по независимой переменной x. Снова воспользуемся правилом дифференцирования сложной функции:
Снова воспользуемся правилом дифференцирования сложной функции:
Результат — требуемая производная:
Проверить решение задачи на производную можно на калькуляторе производных онлайн.
Для сложных функций на основании правила дифференцирования сложной функции формула производной простой функции принимает другой вид.
| 1. Производная сложной степенной функции, где u – дифференцируемая функция аргумента x | |
| 2. Производная корня от выражения | |
| 3. Производная показательной функции | |
| 4. Частный случай показательной функции | |
| 5. Производная логарифмической функции с произвольным положительным основанием а | |
| 6. Производная сложной логарифмической функции, где u – дифференцируемая функция аргумента x | |
7. Производная синуса Производная синуса | |
| 8. Производная косинуса | |
| 9. Производная тангенса | |
| 10. Производная котангенса | |
| 11. Производная арксинуса | |
| 12. Производная арккосинуса | |
| 13. Производная арктангенса | |
| 14. Производная арккотангенса |
Пример 6.Найти производную функции
Правильное решение и ответ.
Пример 7. Найти производную функции
.
Правильное решение и ответ.
Пример 8. Найти производную функции
.
Правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Производная, дифференциал и их применение
Поделиться с друзьями
Весь блок «Производная»
- Что такое производная
- Найти производную: алгоритм и примеры решений
- Производные произведения и частного функций
- Производная суммы дробей со степенями и корнями
- Производные простых тригонометрических функций
- Производная сложной функции
- Производная логарифмической функции
- Дифференциал функции
- Дифференциал сложной функции, инвариантность формы дифференциала
- Уравнение касательной и уравнение нормали к графику функции
- Правило Лопиталя
- Частные производные
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Производная сложной функции.
 — Студопедия
— СтудопедияПоделись
Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру, смотрится очень внушительно, но сложной эта функция не является, в отличие от .
В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров.
При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами.
Сложная функция – это функция, аргументом которой также является функция.
С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).
К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а — целая рациональная функция (смотритеклассификацию элементарных функций
Еще пример: f – функция возведения в четвертую степень, а — целая рациональная функция (смотритеклассификацию элементарных функций
), тогда .
В свою очередь, g(x) также может быть сложной функцией. Например, . Условно такое выражение можно обозначить как . Здесь f – функция синуса, — функция извлечения квадратного корня, — дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом .
Часто можно слышать, что сложную функцию называют композицией функций.
Формула нахождения производной сложной функции.
Пример.
Найти производную сложной функции .
Решение.
В данном примере f – функция возведения в квадрат, а g(x) = 2x+1 – линейная функция.
Вот подробное решение с использованием формулы производной сложной функции:
Давайте найдем эту производную, предварительно упростив вид исходной функции.
Следовательно,
Как видите, результаты совпадают.
Постарайтесь не путать, какая функция есть f, а какая g(x).
Поясним это примером на внимательность.
Пример.
Найти производные сложных функций и .
Решение.
В первом случае f – это функция возведения в квадрат, а g(x) – функция синуса, поэтому
.
Во втором случае f – это функция синуса, а — степенная функция. Следовательно, по формуле произведения сложной функции имеем
Формула производной для функции имеет вид
Пример.
Продифференцировать функцию .
Решение.
В этом примере сложную функцию можно условно записать как , где — функция синуса, функция возведения в третью степень, функция логарифмирования по основанию e, функция взятия арктангенса и линейная функция соответственно.
По формуле производной сложной функции
Теперь находим
1. как производную синуса из таблицы производных:
как производную синуса из таблицы производных:
2. — как производную степенной функции:
3. — как производную логарифмической функции:
4. — как производную арктангенса:
5. При дифференцировании выносим двойку за знак производной и применяем формулу производной степенной функции с показателем равным единице:
Собираем воедино полученные промежуточные результаты:
Страшного ничего нет, разбирайте сложные функции как матрешки.
На этом можно было бы и закончить статью, если бы ни одно но…
Желательно отчетливо понимать, когда применять правила дифференцирования и таблицу производных, а когда формулу производной сложной функции.
СЕЙЧАС БУДЬТЕ ОСОБЕННО ВНИМАТЕЛЬНЫ. Мы поговорим об отличии функций сложного вида от сложных функций. От того, насколько Вы видите это различие, и будет зависеть успех при нахождении производных.
Начнем с простых примеров. Функцию можно рассматривать как сложную:g(x) = tgx, . Следовательно, можно сразу применять формулу производной сложной функции
Следовательно, можно сразу применять формулу производной сложной функции
А вот функцию сложной уже назвать нельзя.
Эта функция представляет собой сумму трех функций , 3tgx и 1. Хотя — представляет собой сложную функцию: — степенная функция (квадратичная парабола), а f – функция тангенса. Поэтому, сначала применяем формулу дифференцирования суммы:
Осталось найти производную сложной функции :
Поэтому .
Надеемся, что суть Вы уловили.
Если смотреть более широко, то можно утверждать, что функции сложного вида могут входить в состав сложных функций и сложные функции могут быть составными частями функций сложного вида.
В качестве примера разберем по составным частям функцию .
Во-первых, это сложная функция, которую можно представить в виде , где f – функция логарифмирования по основанию 3, а g(x) есть сумма двух функций и . То есть, .
Во-вторых, займемся функцией h(x). Она представляет собой отношение к .
Она представляет собой отношение к .
— это сумма двух функций и , где — сложная функция с числовым коэффициентом 3. — функция возведения в куб, — функция косинуса, — линейная функция.
— это сумма двух функций и , где — сложная функция, — функция экспоненцирования, — степенная функция.
Таким образом, .
В-третьих, переходим к , которая представляет собой произведение сложной функции и целой рациональной функции
— функция возведения в квадрат, — функция логарифмирования по основанию e.
Следовательно, .
Подытожим:
Теперь структура функции понятна и стало видно, какие формулы и в какой последовательности применять при ее дифференцировании.
В разделе дифференцирование функции (нахождение производной) Вы можете ознакомиться с решением подобных задач.
Производная числа x.
 Производная первого порядка онлайн
Производная первого порядка онлайнФункции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y = sin x — (2 — 3) · a r c t g x x 5 7 x 10 — 17 x 3 + x — 11 , то ее нельзя считать сложной в отличие от y = sin 2 x .
Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.
Yandex.RTB R-A-339285-1
Основные определения
Определение 1
Сложной функцией считается такая функция, у которой аргумент также является функцией.
Обозначается это таким образом: f (g (x)) . Имеем, что функция g (x) считается аргументом f (g (x)) .
Определение 2
Если есть функция f и является функцией котангенса, тогда g (x) = ln x – это функция натурального логарифма. Получаем, что сложная функция f (g (x)) запишется как arctg(lnx). Или функция f , являющаяся функцией возведенной в 4 степень, где g (x) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f (g (x)) = (x 2 + 2 x — 3) 4 .
Или функция f , являющаяся функцией возведенной в 4 степень, где g (x) = x 2 + 2 x — 3 считается целой рациональной функцией, получаем, что f (g (x)) = (x 2 + 2 x — 3) 4 .
Очевидно, что g (x) может быть сложной. Из примера y = sin 2 x + 1 x 3 — 5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y = f (f 1 (f 2 (x))) . Откуда имеем, что f – это функция синуса, а f 1 — функция, располагаемая под квадратным корнем, f 2 (x) = 2 x + 1 x 3 — 5 — дробная рациональная функция.
Определение 3
Степень вложенности определено любым натуральным числом и записывается как y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) .
Определение 4
Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида
(f (g (x))) » = f » (g (x)) · g » (x)
Примеры
Пример 1
Найти производную сложной функции вида y = (2 x + 1) 2 .
Решение
По условию видно, что f является функцией возведения в квадрат, а g (x) = 2 x + 1 считается линейной функцией.
Применим формулу производной для сложной функции и запишем:
f » (g (x)) = ((g (x)) 2) » = 2 · (g (x)) 2 — 1 = 2 · g (x) = 2 · (2 x + 1) ; g » (x) = (2 x + 1) » = (2 x) » + 1 » = 2 · x » + 0 = 2 · 1 · x 1 — 1 = 2 ⇒ (f (g (x))) » = f » (g (x)) · g » (x) = 2 · (2 x + 1) · 2 = 8 x + 4
Необходимо найти производную с упрощенным исходным видом функции. Получаем:
y = (2 x + 1) 2 = 4 x 2 + 4 x + 1
Отсюда имеем, что
y » = (4 x 2 + 4 x + 1) » = (4 x 2) » + (4 x) » + 1 » = 4 · (x 2) » + 4 · (x) » + 0 = = 4 · 2 · x 2 — 1 + 4 · 1 · x 1 — 1 = 8 x + 4
Результаты совпали.
При решении задач такого вида важно понимать, где будет располагаться функция вида f и g (x) .
Пример 2
Следует найти производные сложных функций вида y = sin 2 x и y = sin x 2 .
Решение
Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g (x) – функцией синуса. Тогда получим, что
Тогда получим, что
y » = (sin 2 x) » = 2 · sin 2 — 1 x · (sin x) » = 2 · sin x · cos x
Вторая запись показывает, что f является функцией синуса, а g (x) = x 2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как
y » = (sin x 2) » = cos (x 2) · (x 2) » = cos (x 2) · 2 · x 2 — 1 = 2 · x · cos (x 2)
Формула для производной y = f (f 1 (f 2 (f 3 (. . . (f n (x)))))) запишется как y » = f » (f 1 (f 2 (f 3 (. . . (f n (x)))))) · f 1 » (f 2 (f 3 (. . . (f n (x))))) · · f 2 » (f 3 (. . . (f n (x)))) · . . . · f n » (x)
Пример 3
Найти производную функции y = sin (ln 3 a r c t g (2 x)) .
Решение
Данный пример показывает сложность записи и определения расположения функций. Тогда y = f (f 1 (f 2 (f 3 (f 4 (x))))) обозначим, где f , f 1 , f 2 , f 3 , f 4 (x) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е, функцией арктангенса и линейной.
Из формулы определения сложной функции имеем, что
y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x)
Получаем, что следует найти
- f » (f 1 (f 2 (f 3 (f 4 (x))))) в качестве производной синуса по таблице производных, тогда f » (f 1 (f 2 (f 3 (f 4 (x))))) = cos (ln 3 a r c t g (2 x)) .

- f 1 » (f 2 (f 3 (f 4 (x)))) в качестве производной степенной функции, тогда f 1 » (f 2 (f 3 (f 4 (x)))) = 3 · ln 3 — 1 a r c t g (2 x) = 3 · ln 2 a r c t g (2 x) .
- f 2 » (f 3 (f 4 (x))) в качестве производной логарифмической, тогда f 2 » (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
- f 3 » (f 4 (x)) в качестве производной арктангенса, тогда f 3 » (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2 .
- При нахождении производной f 4 (x) = 2 x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1 , тогда f 4 » (x) = (2 x) » = 2 · x » = 2 · 1 · x 1 — 1 = 2 .
Производим объединение промежуточных результатов и получаем, что
y » = f » (f 1 (f 2 (f 3 (f 4 (x))))) · f 1 » (f 2 (f 3 (f 4 (x)))) · · f 2 » (f 3 (f 4 (x))) · f 3 » (f 4 (x)) · f 4 » (x) = = cos (ln 3 a r c t g (2 x)) · 3 · ln 2 a r c t g (2 x) · 1 a r c t g (2 x) · 1 1 + 4 x 2 · 2 = = 6 · cos (ln 3 a r c t g (2 x)) · ln 2 a r c t g (2 x) a r c t g (2 x) · (1 + 4 x 2)
Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.
Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.
Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.
Пример 4
Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y = t g 2 x + 3 t g x + 1 , тогда ее можно рассмотреть в качестве сложной вида g (x) = t g x , f (g) = g 2 + 3 g + 1 . Очевидно, что необходимо применение формулы для сложной производной:
f » (g (x)) = (g 2 (x) + 3 g (x) + 1) » = (g 2 (x)) » + (3 g (x)) » + 1 » = = 2 · g 2 — 1 (x) + 3 · g » (x) + 0 = 2 g (x) + 3 · 1 · g 1 — 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g » (x) = (t g x) » = 1 cos 2 x ⇒ y » = (f (g (x))) » = f » (g (x)) · g » (x) = (2 t g x + 3) · 1 cos 2 x = 2 t g x + 3 cos 2 x
Функция вида y = t g x 2 + 3 t g x + 1 не считается сложной, так как имеет сумму t g x 2 , 3 t g x и 1 . Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g (x) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
Однако, t g x 2 считается сложной функцией, то получаем степенную функцию вида g (x) = x 2 и f , являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + (3 t g x) » + 1 » = = (t g x 2) » + 3 · (t g x) » + 0 = (t g x 2) » + 3 cos 2 x
Переходим к нахождению производной сложной функции (t g x 2) » :
f » (g (x)) = (t g (g (x))) » = 1 cos 2 g (x) = 1 cos 2 (x 2) g » (x) = (x 2) » = 2 · x 2 — 1 = 2 x ⇒ (t g x 2) » = f » (g (x)) · g » (x) = 2 x cos 2 (x 2)
Получаем, что y » = (t g x 2 + 3 t g x + 1) » = (t g x 2) » + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x
Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.
Пример 5
Для примера рассмотрим сложную функцию вида y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x · (x 2 + 1)
Данная функция может быть представлена в виде y = f (g (x)) , где значение f является функцией логарифма по основанию 3 , а g (x) считается суммой двух функций вида h (x) = x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 и k (x) = ln 2 x · (x 2 + 1) . Очевидно, что y = f (h (x) + k (x)) .
Очевидно, что y = f (h (x) + k (x)) .
Рассмотрим функцию h (x) . Это отношение l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 к m (x) = e x 2 + 3 3
Имеем, что l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) является суммой двух функций n (x) = x 2 + 7 и p (x) = 3 cos 3 (2 x + 1) , где p (x) = 3 · p 1 (p 2 (p 3 (x))) является сложной функцией с числовым коэффициентом 3 , а p 1 — функцией возведения в куб, p 2 функцией косинуса, p 3 (x) = 2 x + 1 — линейной функцией.
Получили, что m (x) = e x 2 + 3 3 = q (x) + r (x) является суммой двух функций q (x) = e x 2 и r (x) = 3 3 , где q (x) = q 1 (q 2 (x)) — сложная функция, q 1 — функция с экспонентой, q 2 (x) = x 2 — степенная функция.
Отсюда видно, что h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 · p 1 (p 2 (p 3 (x))) q 1 (q 2 (x)) + r (x)
При переходе к выражению вида k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x) видно, что функция представлена в виде сложной s (x) = ln 2 x = s 1 (s 2 (x)) с целой рациональной t (x) = x 2 + 1 , где s 1 является функцией возведения в квадрат, а s 2 (x) = ln x — логарифмической с основанием е. nx. Формулы производных высших порядков.
nx. Формулы производных высших порядков.
Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1) (e x )′
= e x
.
Производная показательной функции с основанием степени a
равна самой функции, умноженной на натуральный логарифм от a
:
(2) .
Вывод формулы производной экспоненты, e в степени x
Экспонента — это показательная функция, у которой основание степени равно числу e
,
которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.
Вывод формулы производной экспоненты
Рассмотрим экспоненту, e
в степени x
:
y = e x
.
Эта функция определена для всех .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
Для этого нам понадобятся следующие факты:
А) Свойство экспоненты :
(4) ;
Б) Свойство логарифма :
(5) ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7) .
Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.
Сделаем подстановку .
Тогда ;
.
В силу непрерывности экспоненты,
.
Поэтому при ,
.
В результате получаем:
.
Сделаем подстановку .
Тогда .
При ,
.
И мы имеем:
.
Применим свойство логарифма (5):
.
Тогда
.
Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.
Тем самым мы получили формулу (1) производной экспоненты.
Вывод формулы производной показательной функции
Теперь выведем формулу (2) производной показательной функции с основанием степени a
.
Мы считаем, что и .
Тогда показательная функция
(8)
Определена для всех .
Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции
и логарифма
.
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.
Производные высших порядков от e в степени x
Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14) .
(1) .
Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.
Отсюда видно, что производная n-го порядка также равна исходной функции:
.
Производные высших порядков показательной функции
Теперь рассмотрим показательную функцию с основанием степени a
:
.
Мы нашли ее производную первого порядка:
(15) .
Дифференцируя (15), получаем производные второго и третьего порядка:
;
.
Мы видим, что каждое дифференцирование приводит к умножению исходной функции на .
Поэтому производная n-го порядка имеет следующий вид:
.
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.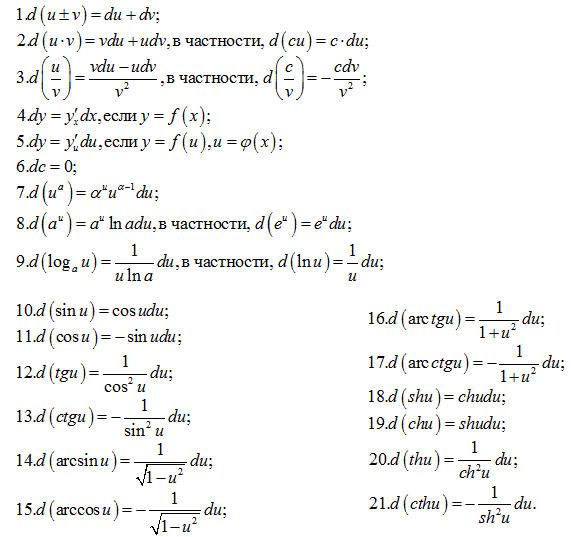
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Пример 2
Найти производную функции
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильно РАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например, и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
1) Сначала нам нужно вычислить выражение , значит, сумма — самое глубокое вложение.
2) Затем необходимо вычислить логарифм:
4) Потом косинус возвести в куб:
5) На пятом шагу разность:
6) И, наконец, самая внешняя функция — это квадратный корень:
Формула дифференцирования сложной функции применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:
Вроде без ошибок:
1) Берем производную от квадратного корня.
2) Берем производную от разности, используя правило
3) Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба).
4) Берем производную от косинуса.
6) И, наконец, берем производную от самого глубокого вложения .
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Пример 3
Найти производную функции
Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, а трёх функций. Как найти производную от произведения трёх множителей?
Пример 4
Найти производную функции
Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки. Но в рассматриваемом примере все функции разные: степень, экспонента и логарифм.
Но в рассматриваемом примере все функции разные: степень, экспонента и логарифм.
В таких случаях необходимо последовательно применить правило дифференцирования произведения два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций: , а за «вэ» — логарифм: . Почему так можно сделать? А разве — это не произведение двух множителей и правило не работает?! Ничего сложного нет:
Теперь осталось второй раз применить правило к скобке :
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде — легче будет проверять.
Рассмотренный пример можно решить вторым способом:
Оба способа решения абсолютно равноценны.
Пример 5
Найти производную функции
Это пример для самостоятельного решения, в образце он решен первым способом.
Рассмотрим аналогичные примеры с дробями.
Пример 6
Найти производную функции
Здесь можно пойти несколькими путями:
Или так:
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного , приняв за весь числитель:
В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить?
Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить?
Приведём выражение числителя к общему знаменателю и избавимся от трёхэтажности дроби :
Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:
Пример 7
Найти производную функции
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
И теорему о производной сложной функции, формулировка которой такова:
Пусть 1) функция $u=\varphi (x)$ имеет в некоторой точке $x_0$ производную $u_{x}»=\varphi»(x_0)$, 2) функция $y=f(u)$ имеет в соответствующей точке $u_0=\varphi (x_0)$ производную $y_{u}»=f»(u)$. Тогда сложная функция $y=f\left(\varphi (x) \right)$ в упомянутой точке также будет иметь производную, равную произведению производных функций $f(u)$ и $\varphi (x)$:
Тогда сложная функция $y=f\left(\varphi (x) \right)$ в упомянутой точке также будет иметь производную, равную произведению производных функций $f(u)$ и $\varphi (x)$:
$$ \left(f(\varphi (x))\right)»=f_{u}»\left(\varphi (x_0) \right)\cdot \varphi»(x_0) $$
или, в более короткой записи: $y_{x}»=y_{u}»\cdot u_{x}»$.
В примерах этого раздела все функции имеют вид $y=f(x)$ (т.е. рассматриваем лишь функции одной переменной $x$). Соответственно, во всех примерах производная $y»$ берётся по переменной $x$. Чтобы подчеркнуть то, что производная берётся по переменной $x$, часто вместо $y»$ пишут $y»_x$.
В примерах №1, №2 и №3 изложен подробный процесс нахождения производной сложных функций. Пример №4 предназначен для более полного понимания таблицы производных и с ним имеет смысл ознакомиться.
Желательно после изучения материала в примерах №1-3 перейти к самостоятельному решению примеров №5, №6 и №7. Примеры №5, №6 и №7 содержат краткое решение, чтобы читатель мог проверить правильность своего результата.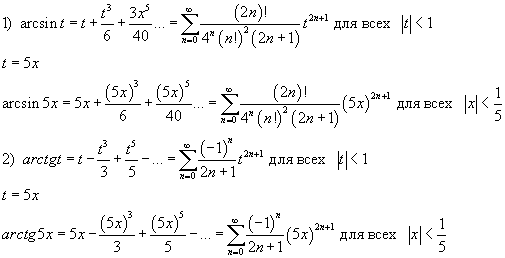 {\frac{1}{2}}}=\frac{1}{\sqrt{u}}$, то равенство (4.2) можно переписать в таком виде:
{\frac{1}{2}}}=\frac{1}{\sqrt{u}}$, то равенство (4.2) можно переписать в таком виде:
$$ (\sqrt{u})»=\frac{1}{2}\cdot \frac{1}{\sqrt{u}}\cdot u»=\frac{1}{2\sqrt{u}}\cdot u» $$
Полученное равенство $(\sqrt{u})»=\frac{1}{2\sqrt{u}}\cdot u»$ и есть формула №4 таблицы производных. Как видите, формулы №3 и №4 таблицы производных получаются из формулы №2 подстановкой соответствующего значения $\alpha$.
Производная сложной функции: как найти, примеры
Функции сложного вида не всегда подходят под определение сложной функции. Если имеется функция вида y=sin x-(2-3)·arctgxx57x10-17×3+x-11, то ее нельзя считать сложной в отличие от y=sin2 x.
Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.
Основные определения
Определение 1Сложной функцией считается такая функция, у которой аргумент также является функцией.
Обозначается это таким образом: f(g(x)). Имеем, что функция g(x) считается аргументом f(g(x)).
Определение 2Если есть функция f и является функцией котангенса, тогда g(x) = lnx – это функция натурального логарифма. Получаем, что сложная функция f(g(x)) запишется как arctg(lnx). Или функция f, являющаяся функцией возведенной в 4 степень, где g(x)=x2+2x-3 считается целой рациональной функцией, получаем, что f(g(x))=(x2+2x-3)4.
Очевидно, что g(x) может быть сложной. Из примера y=sin2x+1×3-5 видно, что значение g имеет кубический корень с дробью. Данное выражение разрешено обозначать как y=f(f1(f2(x))). Откуда имеем, что f – это функция синуса, а f1 — функция, располагаемая под квадратным корнем, f2(x)=2x+1×3-5 — дробная рациональная функция.
Определение 3Степень вложенности определено любым натуральным числом и записывается как y=f(f1(f2(f3(…(fn(x)))))).
Определение 4Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида
(f(g(x)))’=f'(g(x))·g'(x)
Примеры
Пример 1Найти производную сложной функции вида y=(2x+1)2.
Решение
По условию видно, что f является функцией возведения в квадрат, а g(x)=2x+1 считается линейной функцией.
Применим формулу производной для сложной функции и запишем:
f'(g(x))=((g(x))2)’=2·(g(x))2-1=2·g(x)=2·(2x+1);g'(x)=(2x+1)’=(2x)’+1’=2·x’+0=2·1·x1-1=2⇒(f(g(x)))’=f'(g(x))·g'(x)=2·(2x+1)·2=8x+4
Необходимо найти производную с упрощенным исходным видом функции. Получаем:
y=(2x+1)2=4×2+4x+1
Отсюда имеем, что
y’=(4×2+4x+1)’=(4×2)’+(4x)’+1’=4·(x2)’+4·(x)’+0==4·2·x2-1+4·1·x1-1=8x+4
Результаты совпали.
При решении задач такого вида важно понимать, где будет располагаться функция вида f и g(x).
Пример 2Следует найти производные сложных функций вида y=sin2x и y=sin x2.
Решение
Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g(x) – функцией синуса. Тогда получим, что
y’=(sin2x)’=2·sin2-1x·(sin x)’=2·sin x·cos x
Вторая запись показывает, что f является функцией синуса, а g(x)=x2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как
Отсюда следует, что произведение сложной функции запишем как
y’=(sin x2)’=cos(x2)·(x2)’=cos(x2)·2·x2-1=2·x·cos(x2)
Формула для производной y=f(f1(f2(f3(…(fn(x)))))) запишется как y’=f'(f1(f2(f3(…(fn(x))))))·f1′(f2(f3(…(fn(x)))))··f2′(f3(…(fn(x))))·…·fn'(x)
Пример 3Найти производную функции y=sin(ln3 arctg(2x)).
Решение
Данный пример показывает сложность записи и определения расположения функций. Тогда y=f(f1(f2(f3(f4(x))))) обозначим, где f, f1, f2, f3, f4(x) является функцией синуса, функцией возведения в 3 степень, функцией с логарифмом и основанием е, функцией арктангенса и линейной.
Из формулы определения сложной функции имеем, что
y’=f'(f1(f2(f3(f4(x)))))·f1′(f2(f3(f4(x))))··f2′(f3(f4(x)))·f3′(f4(x))·f4′(x)
Получаем, что следует найти
- f'(f1(f2(f3(f4(x))))) в качестве производной синуса по таблице производных, тогда f'(f1(f2(f3(f4(x)))))=cos(ln3 arctg(2x)).
- f1′(f2(f3(f4(x)))) в качестве производной степенной функции, тогда f1′(f2(f3(f4(x))))=3·ln3-1arctg(2x)=3·ln2arctg(2x).

- f2′(f3(f4(x))) в качестве производной логарифмической, тогда f2′(f3(f4(x)))=1arctg(2x).
- f3′(f4(x)) в качестве производной арктангенса, тогда f3′(f4(x))=11+(2x)2=11+4×2.
- При нахождении производной f4(x)=2x произвести вынесение 2 за знак производной с применением формулы производной степенной функции с показателем, который равняется 1, тогда f4′(x)=(2x)’=2·x’=2·1·x1-1=2.
Производим объединение промежуточных результатов и получаем, что
y’=f'(f1(f2(f3(f4(x)))))·f1′(f2(f3(f4(x))))··f2′(f3(f4(x)))·f3′(f4(x))·f4′(x)==cos(ln3 arctg(2x))·3·ln2 arctg(2x)·1arctg(2x)·11+4×2·2==6·cos(ln3 arctg(2x))·ln2 arctg(2x)arctg(2x)·(1+4×2)
Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.
Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.
Необходимо рассмотреть на приведении подобного примера. Если имеется функция вида y=tg2x+3tgx+1, тогда ее можно рассмотреть в качестве сложной вида g(x)=tgx, f(g)=g2+3g+1. Очевидно, что необходимо применение формулы для сложной производной:
f'(g(x))=(g2(x)+3g(x)+1)’=(g2(x))’+(3g(x))’+1’==2·g2-1(x)+3·g'(x)+0=2g(x)+3·1·g1-1(x)==2g(x)+3=2tgx+3;g'(x)=(tgx)’=1cos2x⇒y’=(f(g(x)))’=f'(g(x))·g'(x)=(2tgx+3)·1cos2x=2tgx+3cos2x
Функция вида y=tgx2+3tgx+1 не считается сложной, так как имеет сумму tgx2, 3tgx и 1. Однако, tgx2 считается сложной функцией, то получаем степенную функцию вида g(x)=x2 и f, являющуюся функцией тангенса. Для этого следует продифференцировать по сумме. Получаем, что
y’=(tgx2+3tgx+1)’=(tgx2)’+(3tgx)’+1’==(tgx2)’+3·(tgx)’+0=(tgx2)’+3cos2x
Переходим к нахождению производной сложной функции (tgx2)’:
f'(g(x))=(tg(g(x)))’=1cos2g(x)=1cos2(x2)g'(x)=(x2)’=2·x2-1=2x⇒(tgx2)’=f'(g(x))·g'(x)=2xcos2(x2)
Получаем, что y’=(tgx2+3tgx+1)’=(tgx2)’+3cos2x=2xcos2(x2)+3cos2x
Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.
Для примера рассмотрим сложную функцию вида y=log3x2+3cos3(2x+1)+7ex2+33+ln2x·(x2+1)
Данная функция может быть представлена в виде y=f(g(x)), где значение f является функцией логарифма по основанию 3, а g(x) считается суммой двух функций вида h(x)=x2+3cos3(2x+1)+7ex2+33 и k(x)=ln2x·(x2+1). Очевидно, что y=f(h(x)+k(x)).
Рассмотрим функцию h(x). Это отношение l(x)=x2+3cos3(2x+1)+7 к m(x)=ex2+33
Имеем, что l(x)=x2+3cos2(2x+1)+7=n(x)+p(x) является суммой двух функций n(x)=x2+7 и p(x)=3cos3(2x+1), где p(x)=3·p1(p2(p3(x))) является сложной функцией с числовым коэффициентом 3, а p1 — функцией возведения в куб, p2 функцией косинуса, p3(x)=2x+1 — линейной функцией.
Получили, что m(x)=ex2+33=q(x)+r(x) является суммой двух функций q(x)=ex2 и r(x)=33, где q(x)=q1(q2(x)) — сложная функция, q1 — функция с экспонентой, q2(x)=x2 — степенная функция.
Отсюда видно, что h(x)=l(x)m(x)=n(x)+p(x)q(x)+r(x)=n(x)+3·p1(p2(p3(x)))q1(q2(x))+r(x)
При переходе к выражению вида k(x)=ln2x·(x2+1)=s(x)·t(x) видно, что функция представлена в виде сложной s(x)=ln2x=s1(s2(x)) с целой рациональной t(x)=x2+1, где s1 является функцией возведения в квадрат, а s2(x)=ln x — логарифмической с основанием е.
Отсюда следует, что выражение примет вид k(x)=s(x)·t(x)=s1(s2(x))·t(x).
Тогда получим, что
y=log3x2+3cos3(2x+1)+7ex2+33+ln2 x·(x2+1)==fn(x)+3·p1(p2(p3(x)))q1(q2(x))=r(x)+s1(s2(x))·t(x)
По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Производная от арктана — Формула, доказательство, примеры
Перед тем, как узнать, что является производной от арктан, давайте рассмотрим некоторые факты об арктане. Arctan (или) tan -1 является функцией, обратной функции тангенса. т. е. если y = tan -1 x, то tan y = x. Кроме того, мы знаем, что если f и f -1 являются обратными функциями друг друга, то f(f -1 (x)) = f -1 (f(x)) = x. Отсюда tan(arctan x) = arctan(tan x) = x в соответствующих областях. Мы используем эти факты, чтобы найти производную от arctan x.
Arctan (или) tan -1 является функцией, обратной функции тангенса. т. е. если y = tan -1 x, то tan y = x. Кроме того, мы знаем, что если f и f -1 являются обратными функциями друг друга, то f(f -1 (x)) = f -1 (f(x)) = x. Отсюда tan(arctan x) = arctan(tan x) = x в соответствующих областях. Мы используем эти факты, чтобы найти производную от arctan x.
Давайте посмотрим формулу производной арктангенса вместе с доказательством и несколькими решенными примерами.
| 1. | Что является производным арктана? |
| 2. | Производное доказательство арктангенса по цепному правилу |
| 3. | Производная арктанга Доказательство по первому принципу |
| 4. | Часто задаваемые вопросы о производном Arctan |
Что является производным арктана?
Производная арктангенса х представлена как d/dx(арктан х) (или) d/dx(тангенс -1 х) (или) (арктан х)’ (или) (тангенс -1 х) ‘. Его значение равно 1/(1+x 2 ). Мы собираемся доказать это двумя методами в следующих разделах. Два метода:
Его значение равно 1/(1+x 2 ). Мы собираемся доказать это двумя методами в следующих разделах. Два метода:
- Использование цепного правила
- Использование первого принципа
Производное Arctan x Formula
Производная функции арктангенса:
-
- d/dx(tan -1 x) = 1/(1+x 2 )
Мы собираемся доказать эту формулу в следующих разделах.
Производное доказательство арктангенса по цепному правилу
Находим производную арктангенса по цепному правилу. Для этого предположим, что y = arctan x. Загар с обеих сторон,
tan y = tan (arctan x)
По определению обратной функции tan (arctan x) = x. Таким образом, приведенное выше уравнение принимает следующий вид:
tan y = x … (1)
Дифференцируя обе части по x,
d/dx (tan y) = d/dx(x)
Имеем d/ dx (тангенс х) = сек 2 х. Кроме того, по цепному правилу
Кроме того, по цепному правилу
сек 2 y · dy/dx = 1
dy/dx = 1/сек 2 y
Используя одно из тригонометрических тождеств, sec 2 y = 1 + tan 2 г.
dy/dx = 1/(1 + tan 2 y)
dy/dx = 1/(1 + x 2 ) (из (1))
Подставляя y = arctan x здесь,
d/dx (arctan x) = 1/(1 + x 2 )
Отсюда доказано.
Производное доказательство арктана по первому принципу
Производная функции f(x) по первому принципу определяется пределом f'(x) = limₕ→₀ [f(x + h) — f(x)] / h. Чтобы найти производную arctan x, предположим, что f(x) = arctan x. Тогда f(x + h) = arctg (x + h). Подставляя эти значения в указанный выше предел,
f'(x) = limₕ→₀ [arctan (x + h) — arctg x] / h
По обратным тригонометрическим формулам имеем arctg x — arctg y = arctg [(x — y)/(1 + ху)]. Применим это, получим
f'(x) = limₕ→₀ [arctan[(x + h — x)/(1 + (x + h) x)]] / h
= limₕ→₀ (1/ h) [arctan [ h / (1 + x 2 + hx) ] ]
У нас есть arctan x = x — x 3 /3 + x 5 /5 — . .. Используя это, мы получаем
.. Используя это, мы получаем
f'(x) = limₕ→₀ (1/h) [ h / (1 + x 2 + hx) — [h / (1 + x 2 + hx)] 3 / 3 + [h / (1 + x 2 + hx)] 5 / 5 — ….]
= limₕ→₀ (1/h) [ h / (1 + x 2 + hx) — [h 3 / [3(1 + x 2 + hx) 3 ] + [h 5 / [5(1 + x 2) + hx) 5 ] — ….]
Распределение (1/ч),
f'(x) = limₕ→₀ [ 1 / (1 + x 2 + hx) — [ h 2 / [3(1 + x 2 + hx) 3 ] + [h 4 / [5(1 + x 2 + hx) 5 ] — ….]
Применение ограничения h→0,
f'(x) = 1 / (1 + x 2 + 0) — 0 + 0 — …
f'(x) = 1/(1 + x 2 )
Отсюда доказано.
Статьи по теме:
Вот некоторые темы, связанные с производной от arctan x.
- Производная от ln x
- Производное от log x
- Производная от Sec x
- Производные формулы
- Калькулятор производных
Часто задаваемые вопросы о производном Arctan
Что такое производное арктана?
Производная арктангенса x равна 1/(1+x 2 ). т. е. d/dx(arctan x) = 1/(1+x 2 ). Это также можно записать как d/dx(tan -1 x) = 1/(1+x 2 ).
т. е. d/dx(arctan x) = 1/(1+x 2 ). Это также можно записать как d/dx(tan -1 x) = 1/(1+x 2 ).
Как доказать производную формулы арктана?
Чтобы получить производную arctan, предположим, что y = arctan x, тогда tan y = x. Дифференцируя обе части по y, затем сек 2 у = dx/dy. Принимая обратное значение с обеих сторон, dy/dx = 1/(sec 2 y) = 1/(1+tan 2 y) = 1/(1+x 2 ).
Что такое производная арктана x/2?
У нас есть производная от арктангенса x, равная 1/(1 + x 2 ). Используя это и цепное правило, d/dx(arctan x/2) = 1/(1+(x/2) 2 ) d/dx (x/2) = 1/(1 + (x 2 /4)) · (1/2) = [4/(4 + х 2 )] · (1/2) = 2/(4 + х 2 ).
Какая производная от Arctan √x?
Мы знаем, что производная от arctan x равна 1/(1 + x 2 ). Используя эту формулу и цепное правило, d/dx(arctan √x) = 1/(1+(√x) 2 ) d/dx (√x) = 1/(1 + x) · (1/ 2√х) = 1/(2√х(1+х)).
Является ли арктан производным от тан?
Нет, производное от arctan НЕ является tan. Производная арктангенса x равна 1/(1 + x 2 ).
В чем разница между производными Tan x и Arctan x?
Производная тангенса х равна сек 2 x, тогда как производная от arctan x равна 1/(1+x 2 ).
Что такое производное от Arctan x/a?
Производная арктангенса х должна быть 1/(1 + х 2 ). Используя это и цепное правило, d/dx(arctan x/a) = 1/(1+(x/a) 2 ) d/dx (x/a) = 1/(1 + (x 2 /а 2 )) · (1/а) = [а 2 /(а 2 + х 2 )] · (1/а) = а/(а 2 + х 2 ).
Исчисление I. Производные обратных триггерных функций
Онлайн-заметки Пола
Главная
/
Исчисление I
/
Производные
/ Производные обратных триггерных функций
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-7: Производные обратных триггерных функций
В этом разделе мы рассмотрим производные обратных триггерных функций. Чтобы вывести производные обратных тригонометрических функций, нам понадобится формула из последнего раздела, связывающая производные обратных функций. Если \(f\left( x \right)\) и \(g\left( x \right)\) являются обратными функциями, то
\[g’\left( x \right) = \frac{1}{{f’\left( {g\left( x \right)} \right)}}\]
Напомним также, что две функции являются обратными, если \(f\left( {g\left( x \right)} \right) = x\) и \(g\left( {f\left( x \right) } \справа) = х\). 9{ — 1}}x\hspace{0,5 дюйма} \Leftrightarrow \hspace{0,5 дюйма}\sin y = x\hspace{0,25 дюйма}{\mbox{for}}\,\,\,\,\,\, \,\,\, — \frac{\pi }{2} \le y \le \frac{\pi }{2}\]
9{ — 1}}x\hspace{0,5 дюйма} \Leftrightarrow \hspace{0,5 дюйма}\sin y = x\hspace{0,25 дюйма}{\mbox{for}}\,\,\,\,\,\, \,\,\, — \frac{\pi }{2} \le y \le \frac{\pi }{2}\]
Таким образом, оценка обратной триггерной функции аналогична вопросу, какой угол ( т. е. \(y\)) мы подставили в функцию синуса, чтобы получить \(x\). Ограничения на \(y\), данные выше, нужны для того, чтобы убедиться, что мы получаем непротиворечивый ответ из обратного синуса. Мы знаем, что на самом деле существует бесконечное количество углов, которые будут работать, и нам нужно постоянное значение, когда мы работаем с обратным синусом. Использование указанного выше диапазона углов дает все возможные значения функции синуса ровно один раз. Если вы не уверены в этом, нарисуйте единичный круг, и вы увидите, что этот диапазон углов (\(y\)) будет охватывать все возможные значения синуса. 9{ — 1}} \ влево ( {\ гидроразрыва {1} {2}} \ вправо) \)
Показать решение
Итак, мы действительно спрашиваем, какой угол \(y\) решает следующее уравнение.
\[\sin\left(y\right) = \frac{1}{2}\]
и мы ограничены значениями \(y\) выше.
Из единичного круга мы можем быстро увидеть, что \(y = \frac{\pi }{6}\).
У нас есть следующая связь между функцией обратного синуса и функцией синуса. 9{ — 1}}x\hspace{0,5 дюйма} \Leftrightarrow \hspace{0,5 дюйма}\cos y = x\hspace{0,25 дюйма}{\mbox{for}}\,\,\,\,\,\, \,\,\,0 \le y \le \pi \]
Как и в случае с арксинусом, у нас есть ограничение на углы \(y\), которые мы получаем из функции арккосинуса. Опять же, если вы хотите проверить это, быстрый набросок единичного круга должен убедить вас в том, что этот диапазон будет охватывать все возможные значения косинуса ровно один раз. Кроме того, у нас также есть \( — 1 \le x \le 1\), потому что \( — 1 \le \cos \left( y \right) \le 1\). 9{ — 1}}\left( { — \frac{{\sqrt 2}}{2}} \right)\).
Показать решение
Как и в случае с обратным синусом, мы просто спрашиваем следующее. { — 1}}\left({\cos x} \ справа) = х\]
9{ — 1}}x\hspace{0,5 дюйма} \Leftrightarrow \hspace{0,5 дюйма}\tan y = x\hspace{0,25 дюйма}{\mbox{for}}\,\,\,\,\,\, \,\,\, — \frac{\pi }{2} < y < \frac{\pi }{2}\]
{ — 1}}\left({\cos x} \ справа) = х\]
9{ — 1}}x\hspace{0,5 дюйма} \Leftrightarrow \hspace{0,5 дюйма}\tan y = x\hspace{0,25 дюйма}{\mbox{for}}\,\,\,\,\,\, \,\,\, — \frac{\pi }{2} < y < \frac{\pi }{2}\]
Опять же, у нас есть ограничение на \(y\), но обратите внимание, что мы не можем позволить \(y\) быть любой из двух конечных точек в приведенном выше ограничении, поскольку касательная даже не определена в этих двух точках. Чтобы убедиться, что этот диапазон охватывает все возможные значения тангенса, сделайте быстрый набросок функции тангенса, и мы увидим, что в этом диапазоне мы действительно покрываем все возможные значения тангенса. Также в этом случае нет ограничений на \(x\), так как тангенс может принимать все возможные значения. 9{- 1}}1\).
Показать решение
Здесь мы просим,
\[\тангенс у = 1\]
где \(y\) удовлетворяет указанным выше ограничениям. Из единичного круга видно, что \(y = \frac{\pi} }{4}\).
Из единичного круга видно, что \(y = \frac{\pi} }{4}\).
Поскольку ограничений на \(x\) нет, мы можем запросить пределы функции арктангенса, когда \(x\) стремится к плюс-минус бесконечности. Для этого нам понадобится график функции арктангенса. Это показано ниже. 9{ — 1}} х = {\ mathop {\ rm arccsc} \ nolimits} \, х \ конец {массив} \]
Производная арктангенса – вывод, объяснение и пример
В этой статье мы сосредоточимся на понимании процесса определения производной арктангенса и используем его для упрощения производной других функций. Знание того, как найти выражение производной арктангенса, также поможет нам интегрировать выражения, когда мы будем брать уроки интегрального исчисления. 92 +1}$
Изображения/математические чертежи создаются с помощью GeoGebra.
Производные обратной функции: методы
Существует множество электронных устройств, которые можно использовать для сбора информации о природных явлениях. Давайте подумаем, например, об электрокардиограмме, которая представляет собой устройство, которое собирает информацию о наших сердечных сокращениях и отображает ее на экране.
Давайте подумаем, например, об электрокардиограмме, которая представляет собой устройство, которое собирает информацию о наших сердечных сокращениях и отображает ее на экране.
Экран электрокардиограммы
Информация, полученная от устройства, сначала преобразуется с помощью функции, чтобы ее можно было обрабатывать. После этого необходимо отменить преобразование с помощью обратной функции. Этой обработкой может быть нахождение производной, а иногда даже возможно работать с производной самой обратной функции! В этой статье мы рассмотрим, как это делается. 9{-1}(х) \справа). \)
Это лучше понять, взглянув на несколько примеров.
Примеры производных обратных функций
Существует широкий спектр обратимых функций, которые мы можем дифференцировать, поэтому давайте рассмотрим несколько примеров.
Производные иррациональных функций
Функции квадратного корня и квадратичные функции обратны друг другу. Вы можете найти производную квадратичной функции, используя правило степени, а затем использовать этот результат, чтобы найти производную функции квадратного корня. 9{-1} \right)'(x)=\frac{1}{x}.$$
9{-1} \right)'(x)=\frac{1}{x}.$$
Эта процедура является прекрасной альтернативой нахождению производной натурального логарифма с использованием определения производной!
Распространенные ошибки при нахождении производной обратной функции
Существуют две распространенные ошибки при нахождении производной обратной функции.
Давайте рассмотрим каждый.
Составление композиции в неправильном порядке
Одна из частых ошибок — составление композиции в неправильном порядке. Помните, что в целом 92 \)
You can используйте приведенную выше таблицу, чтобы найти наклон секущей прямой к функции, взяв две точки и применив формулу наклона
\[ m=\frac{y_2-y_1}{x_2-x_1}\]
, как показано на следующее изображение.
График секущей прямой к функции в двух точках. 9{-1}(1)}{4-1} \\ &= \frac{2-1}{3} \\ &= \frac{1}{3}. \end{align} \]
Обратите внимание, что наклон секущей обратной функции равен обратной величине наклона секущей прямой к исходной функции. Кроме того, вам нужно составить функцию и обратную, чтобы найти вышеуказанный наклон. Эти шаги кажутся знакомыми?
Наклон секущих связаны с производными через предел. Приведенное выше рассуждение продолжает работать, когда вы берете меньшие интервалы, подключаясь к формуле производной обратной функции. 9{-1}(x) \right).\)
- Выполнение композиции в неправильном порядке.
- Забыв взять ответную часть композиции.
DLMF: 4.23 Обратные тригонометрические функции
Содержимое
- §4.23(i) Общие определения
- §4.23(ii) Основные ценности
- §4.
 23(iii) Формулы отражения
23(iii) Формулы отражения - §4.23(iv) Логарифмические формы
- §4.23(v) Основная собственность
- §4.23(vi) Действительные и мнимые части
- §4.23(vii) Особые ценности и взаимосвязи
- §4.23(viii) Функция Гудермана
§4.23(i) Общие определения
Общие значения обратных тригонометрических функций определяются по
| 4.23.1 | Arcsinz | =∫0zdt(1-t2)1/2, | ||
| 4.23.2 | Arccosz | =∫z1dt(1-t2)1/2, | ||
| 4.23.3 | Арктанz | =∫0zdt1+t2, | ||
| z≠±i, | ||||
| 4.23.4 | Arccscz | = арксинус(1/z), | ||
4. 23.5 23.5 | Arcsecz | = Arccos(1/z), | ||
| 4.23.6 | Арккотz | =Арктан(1/z). | ||
В (4.23.1) и (4.23.2) пути интегрирования могут не проходят ни через одну из точек t=±1. Функция (1-t2)1/2 принимает свое главное значение, когда t∈(-1,1); в другом месте на Интеграция путей ветви определяется преемственностью. В (4.23.3) путь интегрирования не может пересекаться с ±i. Каждый из шесть функций является многозначной функцией z. Арктанz и Arccotz имеют точки ветвления в точках z=±i; остальные четыре функции имеют точки ветвления при z=±1.
§4.23(ii) Основные ценности
главных значения (или главных ветвей ) обратного синуса,
косинус и тангенс получаются путем введения разрезов в плоскости z как
показанные на рисунках 4.23.1(i) и 4.23.1(ii), и требующие
пути интегрирования в (4. 23.1)–(4.23.3) не пересекаются
эти сокращения. Сравните главное значение логарифма
(§4.2(i)). Главные ветви обозначены arcsinz,
arccosz, arctanz соответственно.
Каждая двузначна на соответствующих разрезах,
и каждый реален со стороны настоящего
ось, оставшаяся после удаления пересечений с соответствующими разрезами.
23.1)–(4.23.3) не пересекаются
эти сокращения. Сравните главное значение логарифма
(§4.2(i)). Главные ветви обозначены arcsinz,
arccosz, arctanz соответственно.
Каждая двузначна на соответствующих разрезах,
и каждый реален со стороны настоящего
ось, оставшаяся после удаления пересечений с соответствующими разрезами.
Заданы главные значения арккосеканса, секанса и котангенса по
| 4.23.7 | arccscz | =угловой синус(1/z), | ||
| 4.23.8 | угловых секундz | = arccos(1/z). | ||
| 4.23.9 | арккотz | =арктан(1/z), | ||
| z≠±i. | ||||
Эти функции являются аналитическими в секущей плоскости, изображенной на рисунках. 4.23.1(iii) и 4.23.1(iv).
4.23.1(iii) и 4.23.1(iv).
Если не указано иное , во всем DLMF что обратные тригонометрические функции принимают свои главные значения.
| (i) arcsinz и arccosz | (ii) арктанz | (iii) arccscz и arcsecz | (iv) арккотz |
Графики главных значений действительных аргументов приведены в §4.15. Этот раздел также включает конформные отображения и поверхностные графики для сложных аргументов.
§4.23(iii) Формулы отражения
| 4.23.10 | угловой синус(-z) | =-угловой синусz, | ||
| 4.23.11 | arccos(-z) | = π-arccosz. | ||
4. 23.12 23.12 | арктан(-z) | =-arctanz, | ||
| z≠±i. | ||||
| 4.23.13 | arccsc(-z) | =-arccscz, | ||
| 4.23.14 | угловых секунд(-z) | =π-угл.секz. | ||
| 4.23.15 | арккот(-z) | =-arccotz, | ||
| z≠±i. | ||||
| 4.23.16 | арккосz | = 12π-угловой синусz, | ||
| 4.23.17 | угловых секундz | =12π-arccscz. | ||
4. 23.18 23.18 | арккотz | = ± 12π-арктанz, | ||
| ℜz≷0. | ||||
§4.23(iv) Логарифмические формы
В этом подразделе все величины принимают свои основные значения.
Обратный синус
| 4.23.19 | arcsinz=-iln((1-z2)1/2+iz), | ||
| z∈ℂ∖(-∞,-1)∪(1,∞); | |||
сравните рисунок 4.23.1(i). На разрезах
| 4.23.20 | угловой синусx | =12π±iln((x2-1)1/2+x), | ||
| x∈[1,∞), | ||||
| 4.23.21 | угловой синусx | =-12π±iln((x2-1)1/2-x), | ||
| x∈(-∞,-1], | ||||
верхние знаки берутся с верхних сторон, а нижние знаки с нижних сторон.
Обратный косинус
| 4.23.22 | arccosz=12π+iln((1-z2)1/2+iz), | ||
| z∈ℂ∖(-∞,-1)∪(1,∞); | |||
сравните рисунок 4.23.1(i). Эквивалентное определение
| 4.23.23 | arccosz=-2iln((1+z2)1/2+i(1-z2)1/2), | ||
| z∈ℂ∖(-∞,-1)∪(1,∞); | |||
см. Кахан (1987) .
На разрезы
| 4.23.24 | arccosx | =∓iln((x2-1)1/2+x), | ||
| x∈[1,∞), | ||||
| 4.23.25 | arccosx | =π∓iln((x2-1)1/2-x), | ||
| x∈(-∞,-1], | ||||
верхний/нижний знаки, соответствующие верхней/нижней сторонам.
Арктангенс
| 4.23.26 | арктанz=i2ln(i+zi-z), | ||
| z/i∈ℂ∖(-∞,-1]∪[1,∞); | |||
сравните рисунок 4.23.1(ii). На разрезах
| 4.23.27 | арктан(iy)=±12π+i2ln(y+1y-1), | ||
| y∈(-∞,-1)∪(1,∞), | |||
верхний/нижний знак, соответствующий правой/левой стороне.
Другие обратные функции
Для соответствующих результатов для arccscz, arcsecz и arccotz:
используйте (4.23.7)–(4.23.9). Необходимо соблюдать осторожность
разрезы, например, если 0 При k∈ℤ общие решения уравнений соответственно где z=x+iy и ±z∉(1,∞) в (4.23.34) и
(4.23.35) и |z|<1 в (4.23.36). Также Взаимосвязи см. в таблице 4.16.3. Например, из заголовка
и последняя запись в предпоследнем столбце: arcseca=arccot((a2-1)-1/2). Гудерманиан gd(x) определяется формулой Эквивалентно Обратная функция Гудермана определяется выражением Эквивалентно, и снова, когда -12π Функция арктангенса позволяет вычислить арктангенс числа.
Функция арктангенса является обратной функцией функции тангенса. arctan онлайн Функция arctan является обратной функцией
касательная функция,
это вычисляет арктангенс числа онлайн . Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция. Например, чтобы вычислить арктангенс следующего числа 10, введите
arctan(`10`), или сразу 10, если
кнопка arctan уже появляется, возвращается результат 1. §4.23(v) Основное свойство
4.23.28 г = sinw, 4.  23.29
23.29 г = cosw, 4.23.30 г = tanw, 4.23.31 с =Arcsinz=(-1)karcsinz+kπ, 4.23.32 с =Arccosz=±arccosz+2kπ, 4.23.33 с =Арктанz=арктанz+kπ, z≠±i. §4.23(vi) Действительные и мнимые части
4.23.34 угловой синусz = arcsinβ+iзнак(y)ln(α+(α2-1)1/2), 4. 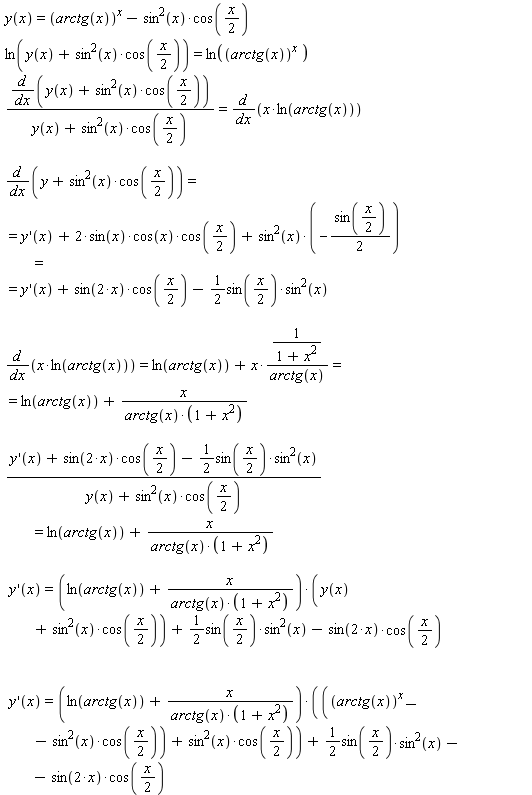 23.35
23.35 арккосz = arccosβ-iзнак(y)ln(α+(α2-1)1/2), 4.23.36 арктанz =12arctan(2x1-x2-y2)+14iln(x2+(y+1)2×2+(y-1)2), 4.23.37 α =12((х+1)2+у2)1/2+12((х-1)2+у2)1/2, 4.23.38 β =12((х+1)2+у2)1/2-12((х-1)2+у2)1/2. §4.23(vii) Особые значения и взаимосвязи
Таблица 4.23.1: Обратные тригонометрические функции: главные значения при 0, ±1, ±∞.
§4.23(viii) Функция Гудермана
4.23.39 гд(х)=∫0xsechtdt, -∞ 4.23.40 gd(x)=2arctan(ex)-12π=arcsin(tanhx)=arccsc(cothx)=arccos(sechx)=arcsec(coshx) =arctan(sinhx)=arccot(cschx). 4.23.41 gd-1(x)=∫0xsectdt, -12π 4,23,42 gd-1(x)=lntan(12x+14π)=ln(secx+tanx)=arcsinh(tanx)=arccsch(cotx) =arccosh(secx)=arcsech(cosx)=arctanh(sinx)=arccoth(cscx). 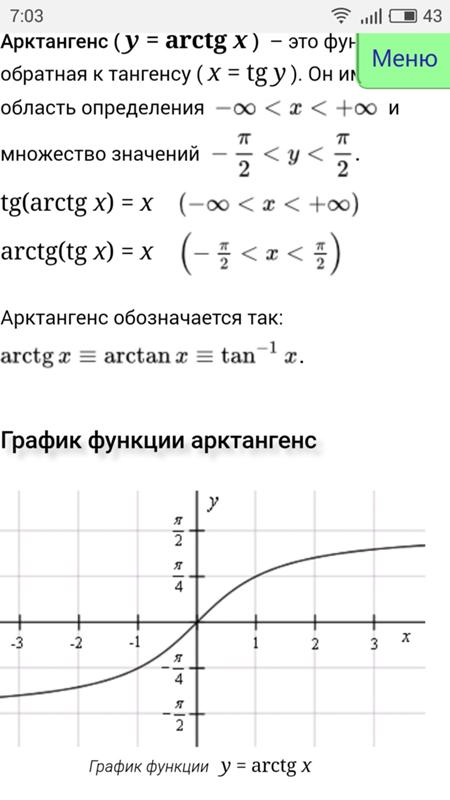
Калькулятор arctan онлайн — Расчет arctan — производная — первообразная — предел
Арктан, онлайн расчет
Сводка:
Описание:
 4711276743.
92)`.
4711276743.
92)`. `lim_(x->-oo)arctan(x)=pi/2`
`lim_(x->+oo)arctan(x)=-pi/2`
5. arctan(x) , x — число. 92)` arctan(`-1`) `3*pi/4` arctan(`-sqrt(3)/3`) `5*pi/6` `2*pi/3` arctan(`0`) `0` arctan(`sqrt(3)`) ` /3` Arctan (`1`) ` pi/4` Arctan (`sqrt (3)/3`) ` pi/6`
Предельный арктангенс :
Калькулятор пределов позволяет вычислять пределы функции арктангенса.
предел арктангенса(x) is limit(`»arctan»(x)`)
Обратная функция арктангенса :
обратная функция арктангенса представляет собой функцию тангенса, отмеченную как тангенс.
Графический арктангенс :
Графический калькулятор может отображать функцию арктангенса в интервале ее определения.
Свойство функции арктангенс:
Функция арктангенса является нечетной функцией.
Расчет онлайн с арктангенсом (арктангенсом)
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.






 23(iii) Формулы отражения
23(iii) Формулы отражения Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.