Длина Окружности Калькулятор — Расчет Длины Окружности
Онлайн-длина окружности калькулятор, который позволяет вам найти длину окружности, радиус, диаметр, площадь, площадь поверхности сферы и объем сферы круга. Этот расчет длины окружности на 100% бесплатный и предоставляет вам точные измерения. Что ж, в этом материале команда Calculator-Online решила предоставить вам лучшее понимание того, как найти площадь и окружность круга, и многое другое, что вам нужно знать! Но, прежде чем вы узнаете все эти термины, вам следует остерегаться некоторых ключевых моментов, касающихся этого длина окружности калькулятор, и сразу после этого мы начнем с некоторых основ!
Ключевой момент калькулятора окружности:Этот калькулятор лучше всего подходит для вычислений между:
- Окружность к диаметру
- диаметр до окружности
- длина окружности в радиус
- радиус по длине окружности
- окружность к площади
- площадь до окружности
- радиус к диаметру
- диаметр к радиусу
- радиус к площади
- площадь в радиус
- диаметр к площади
- площадь к диаметру
Что ж, совершенно не имеет значения, хотите ли вы преобразовать длину окружности в диаметр или радиус в диаметр, этот инструмент поможет вам найти все вышеперечисленные параметры для окружности.
Теперь пора начать с некоторых основных определений, поэтому прежде всего мы собираемся разработать определение окружности круга, проведите пальцем вниз!
Кроме того, этот онлайн-калькулятор геометрии от Calculator-Online лучше всего подходит для определения координат средней точки с координатами x и y.
Что такое окружность круга?Окружность – важное свойство круга; это относится к расстоянию по внешней стороне круга. Проще говоря, это линейное расстояние края круга. Окружность похожа на периметр геометрической фигуры, но следует помнить, что термин «периметр» используется только для многоугольников.
Формула окружности:- С = 2πr
В этом уравнении окружности:
- C представляет собой «окружность круга»
- r называется «радиусом круга.
- π – это отношение длины окружности к ее диаметру, это математическая константа, которая приблизительно равна «3,14159».

Если вы не любите математику, просто добавьте значения в приведенный выше калькулятор формулы окружности, чтобы вычислить длину окружности напрямую, поскольку он также использует то же уравнение для окружности.
О калькуляторе окружности:Простой, но очень точный длина окружности калькулятор круга, который поможет вам найти длину окружности, радиус, диаметр, площадь, площадь поверхности сферы и объем сферы круга. Этот калькулятор довольно прост в использовании и предоставляет вам точные измерения в течение нескольких секунд. расчет длины окружности вычисляет не только длину окружности, но и другие параметры, упомянутые выше.
Как пользоваться калькулятором окружности:Этот калькулятор для определения окружности окружности имеет простой и удобный интерфейс, с помощью которого вы можете легко найти окружность, площадь и другие параметры окружности.
Входы:
Калькулятор предоставляет 6 различных полей ввода:
- Радиус (R)
- Диаметр (D)
- Окружность (C)
- Площадь (А)
- Площадь поверхности сферы
- Объем сферы
Все, что вам нужно – ввести один из этих известных параметров, чтобы найти оставшиеся пять значений. Просто введите любое значение и нажмите кнопку «Рассчитать».
Просто введите любое значение и нажмите кнопку «Рассчитать».
Выходы:
После этого расчет длины окружности сгенерирует:
- Радиус (R)
- Диаметр (D)
- Окружность (C)
- Площадь (А)
- Площадь поверхности сферы
- Объем сферы
- Кроме того, этот калькулятор показывает вам формулу для каждого параметра, который использует наш калькулятор, чтобы предоставить вам точные измерения.
Значения для каждого параметра разные, так как они зависят от заданного значения.
Как найти площадь круга?Площадь любого круга можно рассчитать с помощью формулы или калькулятора площади круга. В разных условиях будут применяться разные формулы. Ситуация может быть такой:
- Площадь круга можно рассчитать как квадрат π r.
- Если вы знаете диаметр круга, то формула будет иметь следующий вид: (π / 4) × D квадрат.
- Если длина окружности известна, то формула будет иметь вид: A = C квадрат / 4π.

Пример:
Какой будет возможная площадь круга, если его радиус равен 3?
- Поскольку диаметр присутствует, формула будет иметь вид: π r квадрат.
Значение π (pi) фиксировано, то есть: 3,14 - Тогда как r = 3
- Радиус будет равен 9 после взятия его квадрата, поэтому новое значение r = 9
- Радиус умножим на значение пи = 28,27 м кв.
- Площадь круга = 28,27 м кв.
Окружность – это расстояние вокруг круга, которое можно рассчитать, применив простую формулу: π (умноженное на) d или 2πr.
- В приведенной выше формуле d представляет радиус круга.
Пример:
Если диаметр любого круга равен 18, то какой будет его длина?
- Мы применим формулу для окружности и просто поместим в нее значения следующим образом:
- Значение пи 3,14 и значение d равно 18. Следовательно, при
- умножении мы получим длину окружности = 56,5 дюймов.

Измеряем окружность в дюймах.
Кроме того, наш расчет длины окружности следует тому же самому способу определения длины окружности.
Как рассчитать окружность Земли?Хотите знать, насколько велика Земля? Вы в нужном месте! Что ж, все, что вам нужно, чтобы найти длину окружности Земли с помощью числа пи (π)! Поскольку ученые уже изобразили, что диаметр Земли составляет 12742 км. Итак, возьмите бумагу и карандаш, чтобы определить окружность земли.
Так,
- C = πd
- Диаметр земли 12,742 км.
- Итак, все, что вам нужно, добавить значения в приведенное выше уравнение для окружности, чтобы вычислить окружность Земли.
- C = π x 12,742 км = 40,030 км
- Итак, окружность Земли составляет 40 030 км.
Кроме того, онлайн-длина окружности калькулятор поможет вам рассчитать длину окружности Земли напрямую.
Часто задаваемые вопросы:Каков диаметр окружности 14 дюймов?Диаметр окружности 14 дюймов равен 4,45634 дюйма.
Вы можете легко найти длину окружности 15-футового круга по следующей формуле:
- C = πd
- Добавьте значения
- C = 3,14159 (15 футов)
- C = 47,12 футов
Окружность 30-сантиметрового круга равна 94,2478 см.
Диаметр составляет половину окружности?Расстояние по краю круга называется длиной окружности. В то время как расстояние от одной стороны круга до другого, которое проходит через центр круга, называется диаметром.
Какова окружность 14 футов?Окружность 14 футов круга равна 43,9823 фута.
Каков диаметр окружности 4 дюйма?
Диаметр окружности 4 дюйма составляет 1,27324 дюйма.
Каков радиус 20-футового круга?Радиус 20-футового круга равен 10 футам.
Насколько окружность больше диаметра?Окружность круга приблизительно равна его диаметру в три раза.
К счастью, вы узнали, как найти окружность и другие параметры круга. Имейте в виду, что окружность, диаметр и радиус – это то, что можно измерить в линейных единицах, включая дюймы и сантиметры. Однако у круга есть много разных диаметров и много разных радиусов, каждый из которых проходит через центр. Итак, используйте этот простой длина окружности калькулятор с помощью онлайн-калькулятора, чтобы решить параметры окружности!
Other Languages: Circumference Calculator, Calculadora Circunferência, Obwód Koła Kalkulator, Kalkulator Keliling Lingkaran, Kreisumfang Rechner, 円周 計算, Výpočet Obvodu, Calcul Circonférence Cercle, Calcolo Circonferenza Cerchio.
Длина окружности (периметр круга) и формула длины окружности (периметра круга), бесплатный онлайн сервис
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное ненулевое.
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая. Также круг можно определить как часть плоскости, ограниченную окружностью.
Также круг можно определить как часть плоскости, ограниченную окружностью.
Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π = 3.14159…
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина. Наш онлайн калькулятор вычисляет периметр круга по значению длины его радиуса.
Формула для вычисления длины окружности
$S = 2 \pi r$, где:
r — радиус окружности
Здесь вы найдете ответы.
Периметр круга – что это такое?
Периметр круга, также называемый длиной окружности, представляет собой число, получаемое в результате умножения его радиуса на два Пи, либо путем перемножения между собой его диаметра и числа Пи. Формула, используемая для расчета периметра круга, представлена в следующем виде:
L = d*π = 2*r*π.
Расшифровка обозначений:
d — диаметр круга,
r — его радиус,
π — это величина, которая является константой, выражающей отношение длины окружности к ее диаметру. Ее значение постоянно равно 3,14.
Каким способом производится вычисление периметра круга?
Под определением «расчет периметра круга» подразумевается процедура, направленная на установление длины окружности, ограничивающей его. В случае, когда длина радиуса круга является известной величиной, длина окружности может быть вычислена с применением приведенной ниже формулы:
l=2*π*r,
в ней радиус круга обозначен как r.
Под радиусом окружности подразумевается отрезок, который соединяет центр окружности с любой из множества точек, находящихся на ней.
Значение длины окружности также может быть вычислено, если диаметр круга
известен. С этой целью нужно произвести умножение ее диаметра (d) на число
Пи (π). В этом случае следует пользоваться формулой:
С этой целью нужно произвести умножение ее диаметра (d) на число
Пи (π). В этом случае следует пользоваться формулой:
l=πd.
Если раскрывать такое понятие, как «диаметр окружности», то стоит отметить, что им является отрезок, проходящий через ее центр и соединяющий две любые точки этой окружности.
Число Пи (π) является математической постоянной, рассчитываемой как отношение длины окружности к величине ее диаметра. Оно равно 3,14.
В квадрат, длина стороны которого равна 20 см, вписан круг. Как вычислить периметр данного круга?
Периметр круга представлен величиной, равной длине окружности, которая ограничивает его. Это значит, что данная величина может быть рассчитана по формуле:
P = L = d*π.
В описанном в задании случае сторона квадрата, в который вписан круг,
выступает в роли его диаметра. Это дает основания для расчета периметра
круга следующим образом:
Это дает основания для расчета периметра
круга следующим образом:
P = 20 * 3,14 = 62,8 см.
Ответ: Периметр круга, который вписан в квадрат, имеющий сторону 20 см, равен 62,8 см.
Периметр круга равен 30 π. Как можно вычислить длину его окружности?
Длина окружности представляет собой произведение, полученное в результате умножения ее диаметра (D) на число Пи (π): L = π*D = 30*π. В данном случае длина окружности – это ее периметр. Из этого следует, что диаметр окружности D равен 30.
Известно, что длина одного круга равна 3,6 дм. Каким образом можно определить длину второго круга, если известно то, что диаметр первого круга в три раза меньше диаметра второго?
Решение поставленной задачи следует начинать с расчета длины первого
круга. Для этого число Пи, равное 3,14, нужно умножить на два, а затем
полученное значение также умножить на длину радиуса круга. Формула,
используемая при этом, выглядит так:
Формула,
используемая при этом, выглядит так:
L=2пR.
Принимая во внимание тот факт, что диаметр второго круга в три раза превышает диаметр первого из них, то можно с уверенностью говорить о том, что его радиус также будет троекратно превышать радиус первого круга. Это означает, что формула, применяемая для расчета длины второго круга, будет выглядеть так:
L=2п*3R
2п*3R/2пR=3.
Подставив в формулу величины, приведенные в задании, можно получить следующий результат:
3,6*3=10,8 дм.
Ответ: Длина второго круга равна 10,8 дм.
Каким образом можно высчитать длину круга, если известно, что его площадь составляет 25 дм.кв?
В задании указано, что площадь круга составляет 25 дм.кв. Это значит, что
произведение числа Пи и радиуса круга, возведенного в квадрат, равно 25
дм. кв. Из этого следует, что радиус данного круга равен величине,
полученной в результате деления 5 на квадратный корень из числа Пи (r =
5/√π). На основании этого можно сделать вывод о том, что длина круга может
быть высчитана по следующей формуле:
кв. Из этого следует, что радиус данного круга равен величине,
полученной в результате деления 5 на квадратный корень из числа Пи (r =
5/√π). На основании этого можно сделать вывод о том, что длина круга может
быть высчитана по следующей формуле:
L = 2πr = 10√π дм.
В результате получается число, приблизительно равное 17,72 дм.
Ответ: Длина круга равна примерно 17,72 дм.
Как высчитать диаметр круга, длина которого равна 40 Пи см?
Формула, которая предназначена для расчета длины круга выглядит так:
L = πD.
По сути, это произведение числа Пи и диаметра круга.
В случае, который описан в задании, длина круга равна 40 Пи см, а это значит следующее:
πD = 40π.
Число Пи сокращается в обеих частях получившегося уравнения, и в итоге получается, что диаметр круга равен 40 см:
D = 40 cм.
Каким образом следует рассчитывать площадь круга, если известно, что его длина составляет 19,1 м?
Располагая информацией о длине круга, можно вычислить его радиус. Это
можно сделать на основании приведенной ниже формулы:
Это
можно сделать на основании приведенной ниже формулы:
r = L/(2*π) = 19,1:(2*3,14)=3 м.
Таким образом удалось установить, что радиус круга равен 3 м.
Теперь, зная длину радиуса круга, можно произвести расчет его площади по формуле:
π*r2 = 3,14*3*3 = 28,26 м².
Ответ: Площадь круга равна 28,26 м. кв.
Величина длины круга известна. Она составляет 26 см. Как можно рассчитать его площадь и диаметр?
При расчете таких показателей, как площадь и диаметр круга, следует использовать его длину. Она обозначается как с и равна 26 см. Согласно формуле вычисления длины круга, она равна произведению 2 Пи и радиуса круга, либо Пи и его диаметра (с=2πr или c=πd). Исходя из этого, диаметр круга можно найти путем деления длины круга на число Пи:
d=c/π
В данном случае d=26/3,14=8,28 см.
Теперь, когда все необходимые для вычисления площади круга параметры известны, можно перейти непосредственно к ее расчету:
S=2πr²=2*3,14*8,28*8,28=53,7 см².
Как выглядит формула, используемая для расчета длины окружности по радиусу?
В целях выполнения вычисления длины окружности по радиусу (r) следует произвести умножение величины, выражающей его значение, на два Пи. При этом используется следующая формула:
P=2πr.
Чему равна длина окружности, диаметр которой 4 м?
При расчете длины окружности используется формула, которая имеет следующий вид:
L = π*D.
Согласно данной формуле, для того чтобы вычислить, чему равна длина окружности, необходимо произвести умножение ее диаметра на число Пи, равное 3,14.
Подставляя в приведенную выше формулу числа, указанные в задании, можно произвести расчет длины окружности, которая будет равна:
3,14*4 = 12,56 м.
Ответ: Длина окружности диаметром в 4 м равна 12,56 м.
Какому числу будет равна длина окружности круга при условии, что его площадь
равна Пи м.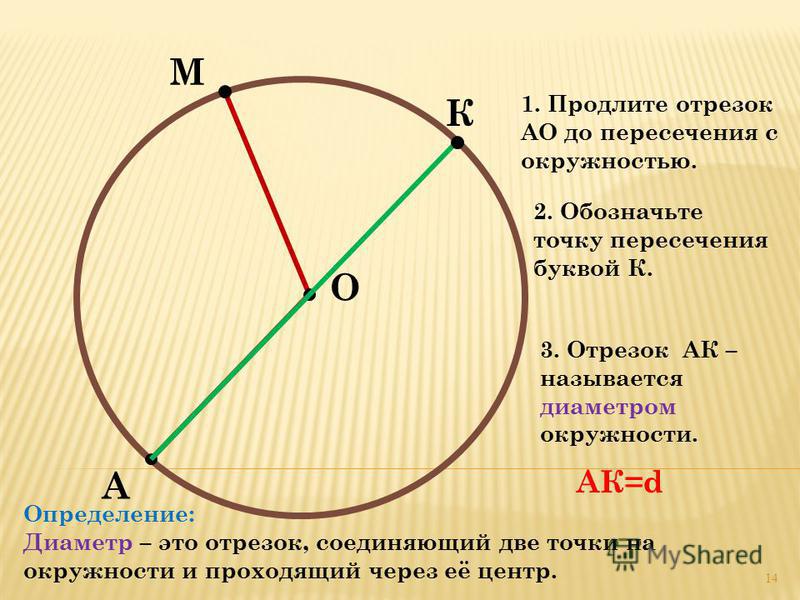 кв?
кв?
Площадь круга высчитывается при помощи формулы:
S=πR².
В данном конкретном случае указано, что площадь равна Пи м. кв. (S=π).
Исходя из вышеизложенного, можно произвести расчет величины радиуса, которая будет равна отношению корня квадратного из числа Пи и числа Пи:
R=√π/π=1.
Теперь можно приступить к вычислению непосредственно длины окружности, используя следующую формулу:
C = 2πR = 2π⋅1 = 2π.
Ответ: Длина окружности круга площадью Пи кв. м равна 2 Пи.
Чему будет равна длина круга диаметром 16 см?
При расчете длины круга следует брать за основу формулу, которая предполагает умножения числа Пи, равного 3,14, на диаметр окружности круга. Если говорить о конкретном случае, упомянутом в задании, то расчет длины окружности будет выглядеть следующим образом:
L=16 см*3,14=50,24 см.
Ответ: Длина круга, диаметр которого равен 16 см, составляет 50,24 см.
Диаметр круга составляет 5,8 дм. Какому числу будет равна длина этого круга?
Длина окружности рассчитывается с применением формулы, составными элементами которой являются диаметр (d) и число ПИ, равное 3,14. Для вычисления длины окружности упомянутые величины следует перемножить:
L=π*d=3,14*5,8=18,212 дм.
Ответ: Круг диаметром 5,8 дм имеет длину окружности, равную 18,212 дм.
Известно, что круг имеет диаметр 18 м. Как вычислить длину этого круга по диаметру?
Если диаметр круга является известной величиной, то ее вполне достаточно, для того чтобы произвести расчет длины данного круга. С этой целью следует использовать формулу, приведенную ниже:
l = 2πr = πd.
Если подставить в данную формулу величины, заданные в вопросе, то можно получить следующий результат:
l = 3,14*18 = 56,52 м.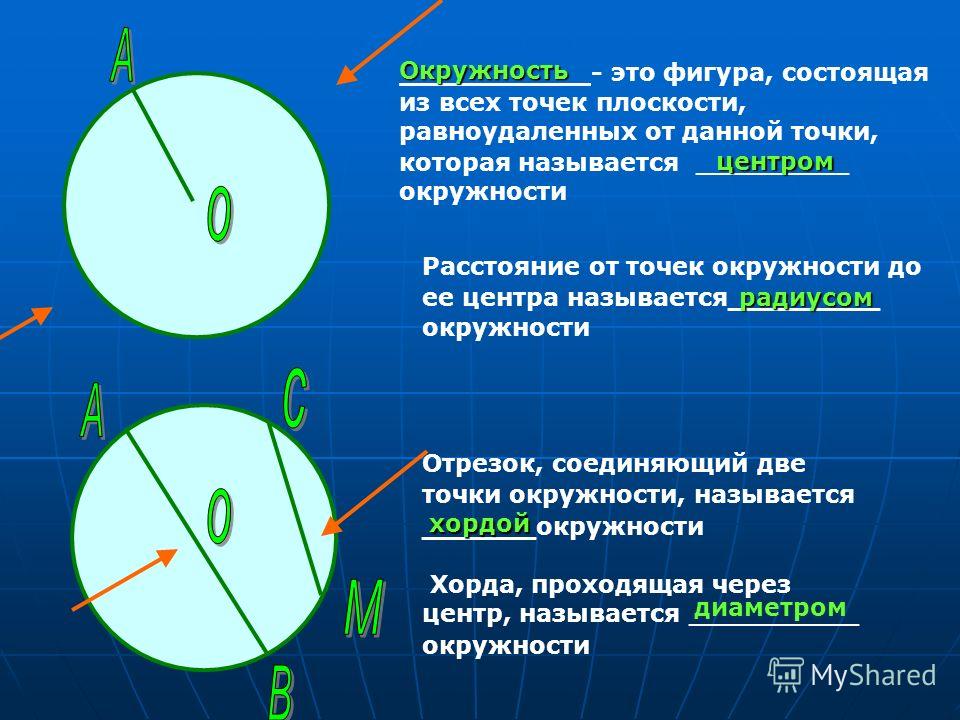
Ответ: Длина круга, диаметр которого равен 18 м, составляет 56,52 м.
Длина окружности круга через диаметр — онлайн калькулятор
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
На нашем сайте собраны программы, которые помогают сделать расчеты по алгебре, геометрии. Сервис содержит расчеты по всем основным темам. Вы сможете найти длину окружности, периметры, объемы фигур, а также получить решение более сложных задач. Для этого достаточно только ввести данные. Сразу после этого будут доступны действия и ответ.
Использование автоматических подсчетов избавляет от промежуточных ошибок, неточностей при переводе из одних величин в другие. Чтобы получить точный ответ, воспользуйтесь нашим сервисом.
- Введите диаметр окружности.
- Установите необходимые единицы измерения для диаметра и площади. Отправьте задание на расчет кнопкой «Найти».
- Получите решение и ответ.
Ответ:
Решение
Ответ:
Похожие калькуляторы:
- Длина окружности круга (По радиусу)
- Периметр квадрата
- Периметр треугольника
- Периметр трапеции
- Периметр прямоугольника
- Периметр ромба
- Периметр параллелограмма
- Периметр квадрата по диагонали
Программа позволяет рассчитать длину окружности по формуле:
Любой пользователь может производить расчеты на сайте без регистрации и платежей.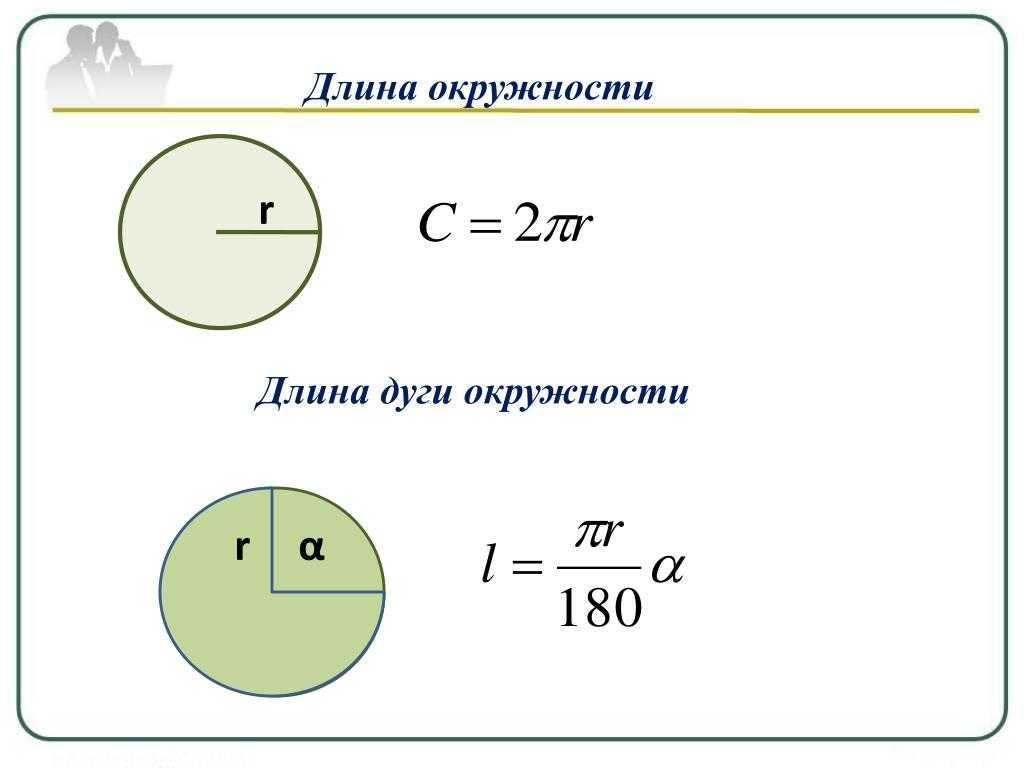 Это создано для повышения уровня образования, возможности повысить успеваемость по математике, самостоятельно разобраться в непонятной теме.
Это создано для повышения уровня образования, возможности повысить успеваемость по математике, самостоятельно разобраться в непонятной теме.
Кто чаще всего пользуется нашим сервисом:
- Школьники. Новую или непонятную тему можно быстро усвоить с помощью калькуляторов. Чертеж и последовательные действия помогут запомнить алгоритм подсчетов. Набор основных программ позволяет быстро переключаться между темами, готовиться к поступлению в ВУЗ.
- Родители. Для помощи детям в освоении учебного материала и во время проверки домашнего задания уже не придется вникать в тему, искать нужную формулу. Достаточно ввести цифры и получить готовое решение.
- Учителя. Планирование уроков теперь выполняется быстрее. При этом меньше времени понадобится, чтобы составить ученикам несколько вариантов задач и проверить автоматически.
- Студенты. В процессе зачета или экзамена будет возможность мгновенно получить верное решение.
Понравился калькулятор? Поделись с друзьями!
Разделы калькуляторов
- Решение матриц
- Точка, прямая, плоскость
- Конвертеры
- Объем фигур
- Калькуляторы площади фигур
- Решение уравнений
- Операции над векторами
- Периметр фигур
Поможем с любой работой
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Решение задач
- Отчеты по практике
Все наши услуги
Узнай бесплатно стоимость работыНе получается написать работу самому?
Доверь это кандидату наук!
как найти длину окружности зная диаметр.
 Онлайн калькулятор длины окружности
Онлайн калькулятор длины окружностиОкружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда.
 Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.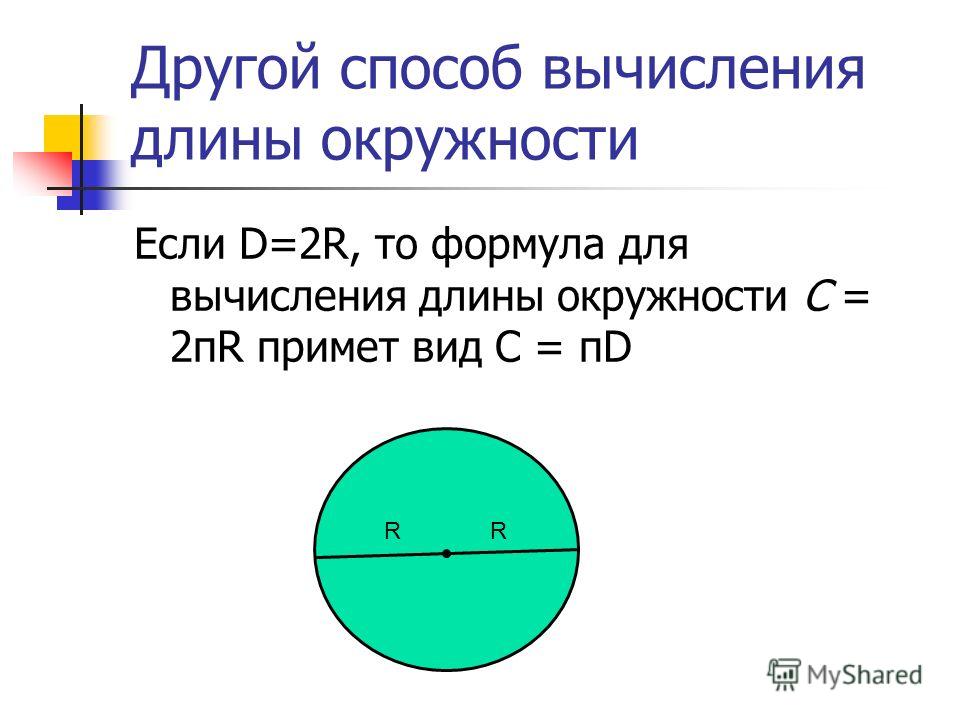
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка.
 Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным.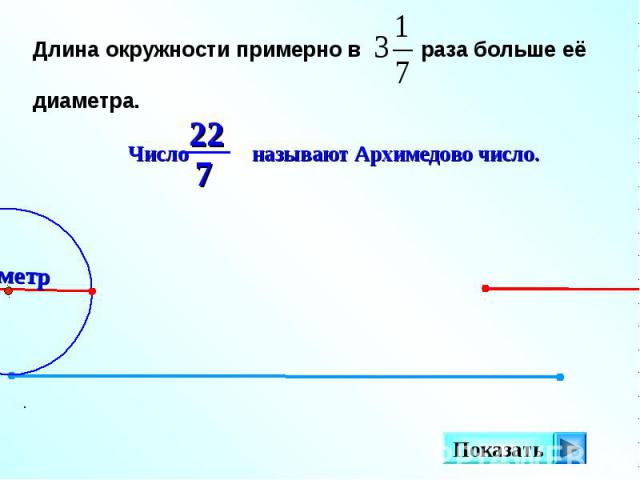 Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Вконтакте
§ 117. Длина окружности и площадь круга.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.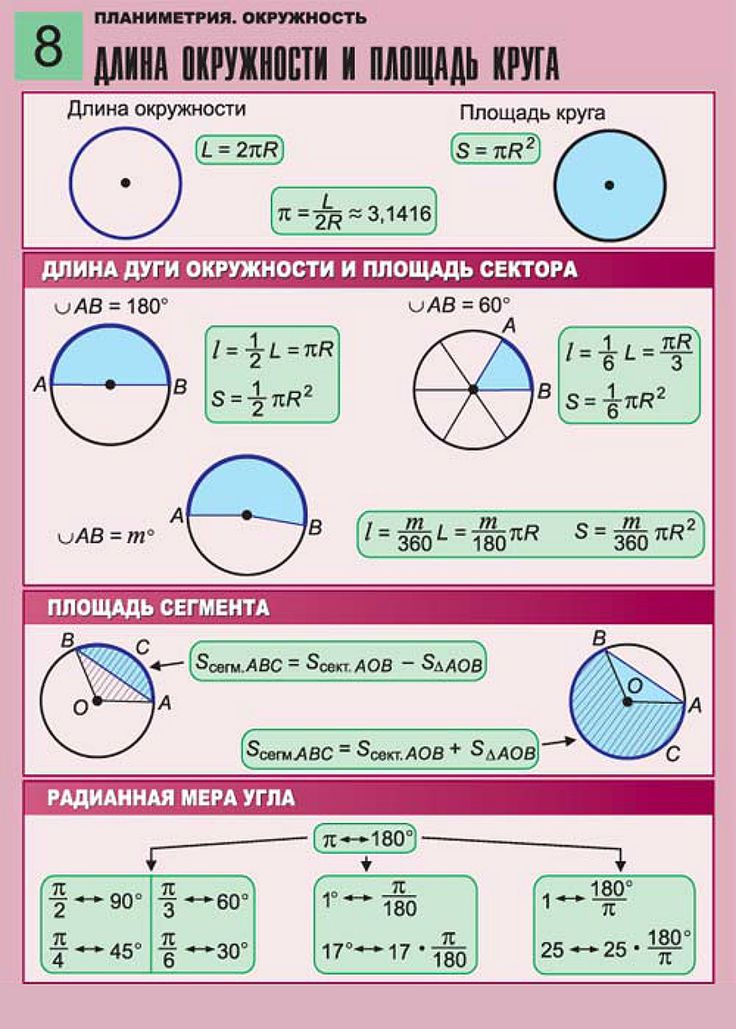
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.
Как узнать длину окружности зная диаметр онлайн. Как рассчитать длину окружности, если не указан диаметр и радиус круга
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.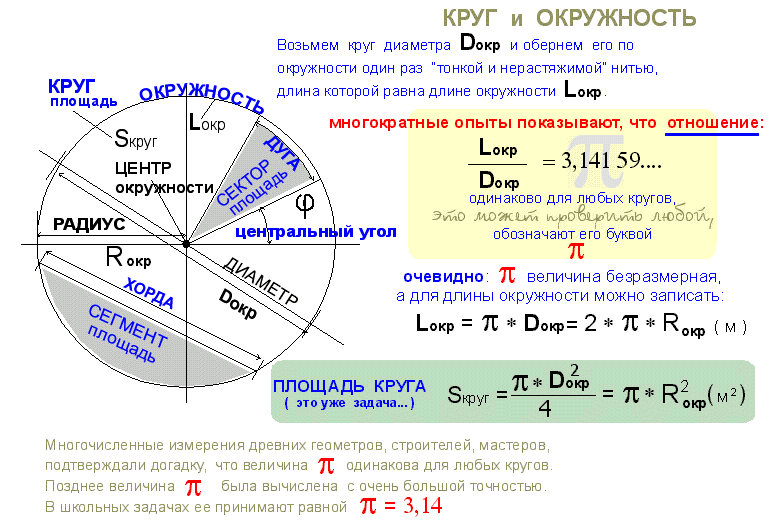
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1.
 Предположим, получилось 5 см.
Предположим, получилось 5 см. - Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице.
 Если это условие не соблюдается, то это не окружность.
Если это условие не соблюдается, то это не окружность. - Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра.
 Формулу обычно записывают следующим образом: C = π*D.
Формулу обычно записывают следующим образом: C = π*D. - Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство.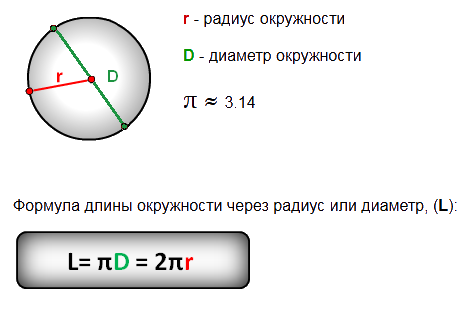 Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14.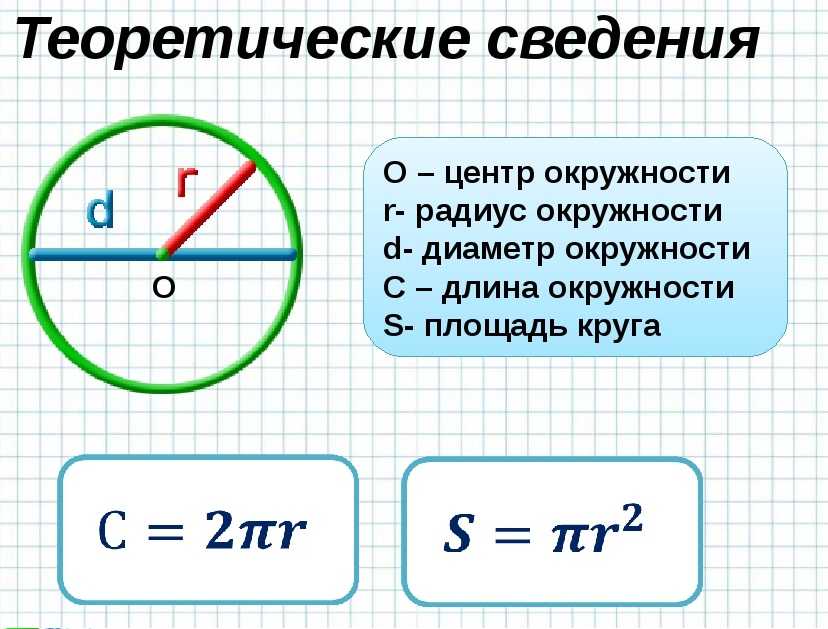 Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.
Для любой точки L , лежащей на окружности, действует равенство OL=R . (Длина отрезка OL равняется радиусу окружности).
Отрезок, который соединяет две точки окружности, является ее хордой .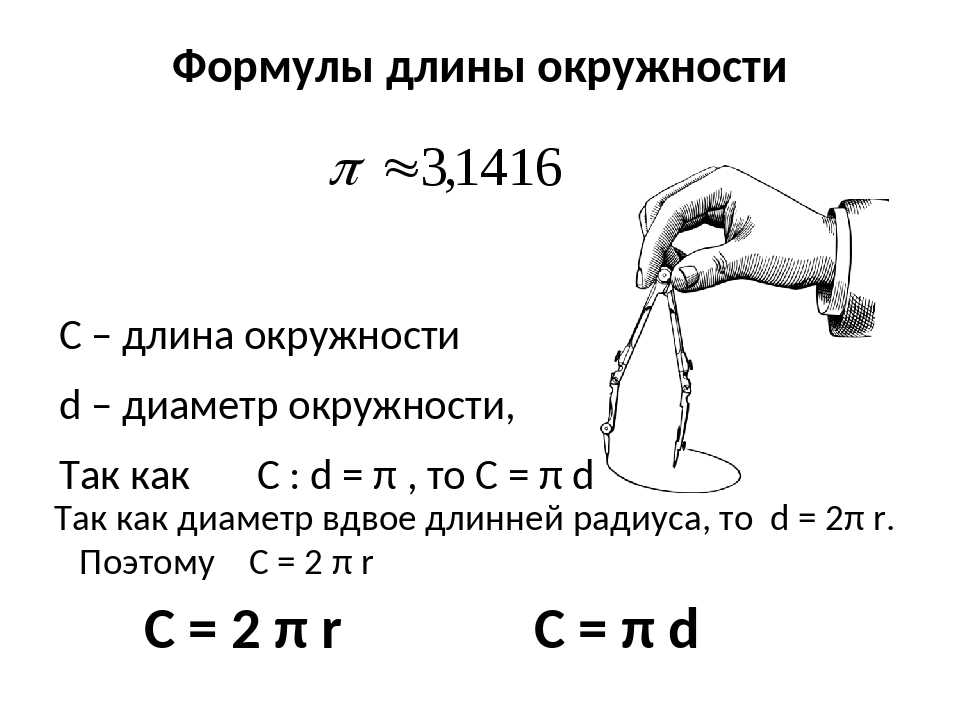 {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть.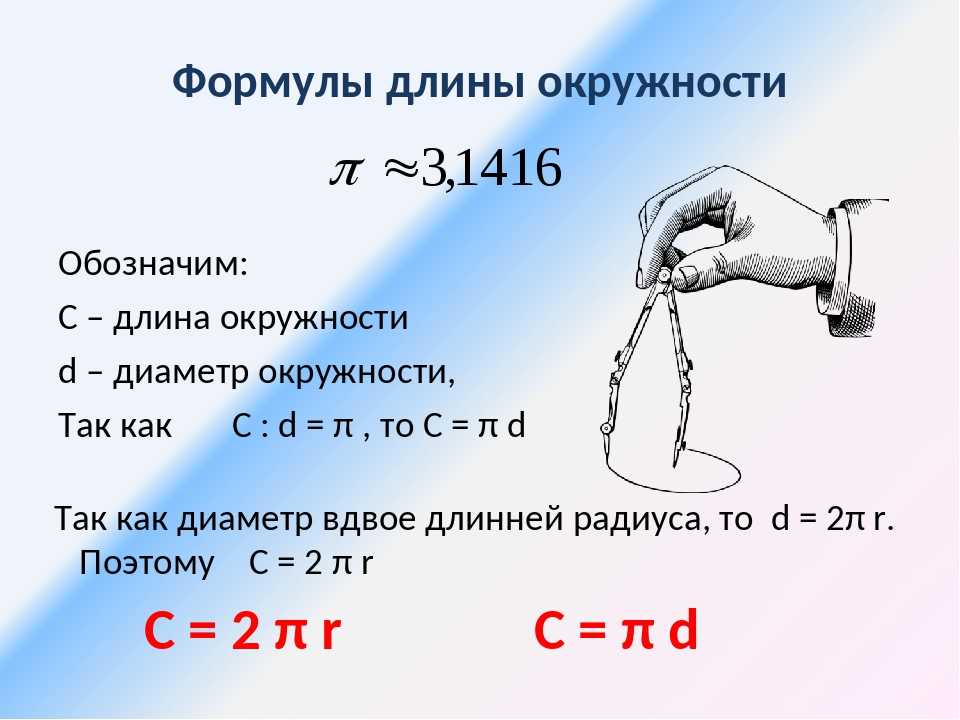 {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Если в задаче известны такие величины, как длина окружности, ее радиус или площадь круга, который ограничен данной окружностью, то вычисление диаметра будет несложным. Существует несколько способов, которыми можно высчитать диаметр окружности. Они довольно просты и вовсе не вызывают никаких трудностей, как многим кажется на первый взгляд.
Как найти диаметр окружности – 1 способ
Когда дано значение радиуса окружности, то можно считать задачу наполовину решенной, поскольку радиус представляет собой расстояние от точки, которая лежит в любом месте на окружности, до центра этой самой окружности. Все, что нужно сделать для нахождения диаметра в этом случае, это умножить данную величину радиуса на 2. Такой способ вычисления объясняется тем, что радиус является половиной диаметра. Поэтому, если известно, чему равен радиус, то и значение половины искомой величины диаметра уже фактически найдено.
Как найти диаметр окружности – 2 способ
Если в задаче дано только значение длины окружности, то для нахождения величины диаметра нужно просто поделить ее на число, известное как π, приблизительное значение которого равно 3,14. То есть, если значение длины равняется 31,4, то разделив его на 3,14, получаем значение диаметра, которое равняется 10.
Как найти диаметр окружности – 3 способ
Если в исходных данных приведено значение площади круга, то диаметр найти тоже просто.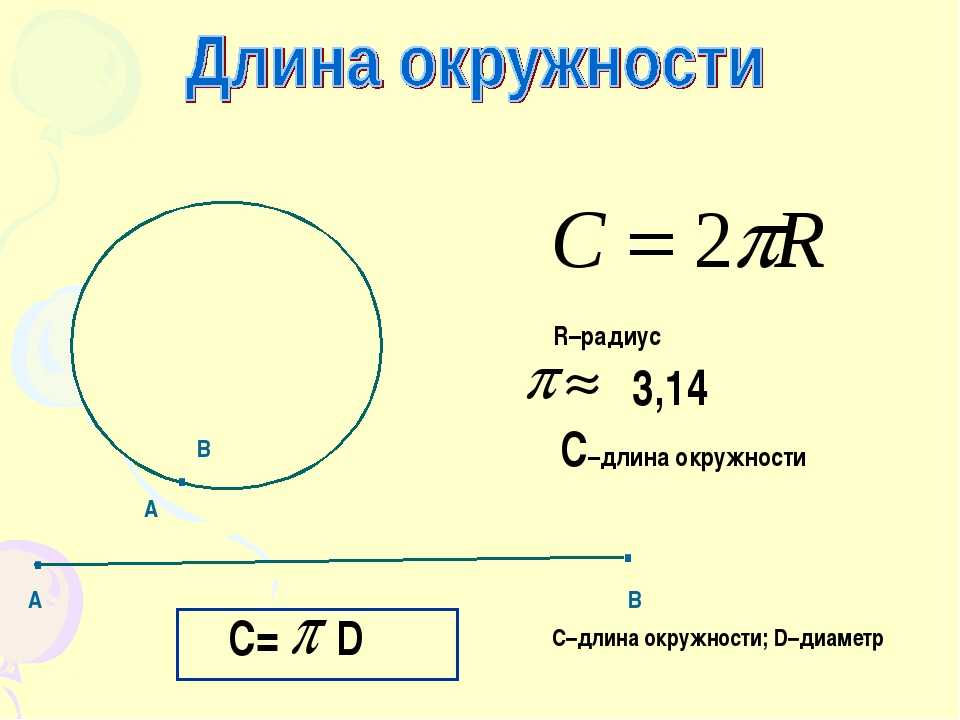 Все, что нужно сделать, это извлечь квадратный корень из данной величины и поделить полученный результат на число π. Это значит, что если значение площади равно 64, то при извлечении корня остается число 8. Если разделить полученную 8 на 3,14, то получим величину диаметра, которая равна примерно 2,5.
Все, что нужно сделать, это извлечь квадратный корень из данной величины и поделить полученный результат на число π. Это значит, что если значение площади равно 64, то при извлечении корня остается число 8. Если разделить полученную 8 на 3,14, то получим величину диаметра, которая равна примерно 2,5.
Как найти диаметр окружности – 4 способ
Внутри окружности нужно начертить при помощи линейки или угольника прямую горизонтальную линию от одной точки до другой. Пересечения этой прямой с линией окружностью пометьте буквами, например, А и В. Не имеет никакого значения, в какой из частей круга будет расположена эта прямая.
После этого нужно начертить еще две окружности. Но таким образом, чтобы точки А и В стали их центрами. Вновь образованные фигуры будут пересекаться в двух точках. Через них нужно провести еще одну прямую линию. После этого измеряем ее длину с помощью линейки. Значение измерения и будет равно длине диаметра, потому что последняя начерченная линия и есть сам диаметр.
Интересно, что еще очень далеко в прошлом для плетения корзин определенного размера прутики брали примерно в 3 раза длиннее. Ученые объяснили и доказали экспериментальным путем, что если длину любой окружности разделить на диаметр, то в результате получается почти одно и то же число.
Площадь круга — онлайн калькулятор CALC.WS
Площадь круга — онлайн калькулятор CALC.WSКалькулятор на данной странице поможет быстро вычислить площадь круга на основе имеющихся у вас данных: это может быть радиус, диаметр или длина окружности
Найти площадь круга через:
Через радиус Через диаметр Через длину окружности
Знаков после запятой:
Результат
Вычисляем площадь круга через = :
Формула
S = π × r2
Решение
S = × 2
S = ×
S =
Формула
S = π × d2 / 4
Решение
S = × 2 / 4
S = × / 4
S = / 4
S =
Формула
S = L2 / (4 × π)
Решение
S = 2 / (4 × )
S = /
S =
Формула площади круга
S = π × r2
Площадь круга — это мера заполненности области внутри окружности, являющейся границей круга, выраженная в квадратных единицах.
В геометрии площадь окруженная окружностью с радиусом R определяется как π × R2. Чтобы запомнить, подумайте: «Пирог в квадрате». Здесь греческая буква π представляет постоянное отношение длины окружности любого круга к его диаметру, примерно равное 3,1416.
Часто понятия круг и окружность путают, хотя это разные вещи. Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.
Видео
Подробно про площадь круга можно узнать из видео:
Примеры
-
Задание: Рассчитать площадь круга, если известен радиус круга R = 3
Решение: 28.
 2743
2743S = 3.141592653589793 × 32 = 3.141592653589793 × 9 = 28.2743
-
Задание: Найти площадь круга диаметром 1 метр
Решение: S = π × d2 / 4 = 3.141592653589793 × 12 / 4 = 3.141592653589793 × 1 / 4 = 3.141592653589793 / 4 = 0.7854
-
Задание: Определить площадь круга, если известна длина окружности, равная 30 см
Решение: S = L2 / (4 × π) = 302 / (4 × 3.141592653589793) = 900 / 12.566370614359172 = 71.6197
Как найти окружность — Базовая геометрия
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 Следующая →
Справка по основам геометрии » Плоская геометрия » Круги » Радиус » Как найти окружность
Если этот круг имеет диаметр 12 дюймов, какова его окружность?
Возможные ответы:
Ни один из этих
Правильный ответ:
Объяснение:
Знайте, что формула длины окружности такова, где C – длина окружности, а D – диаметр.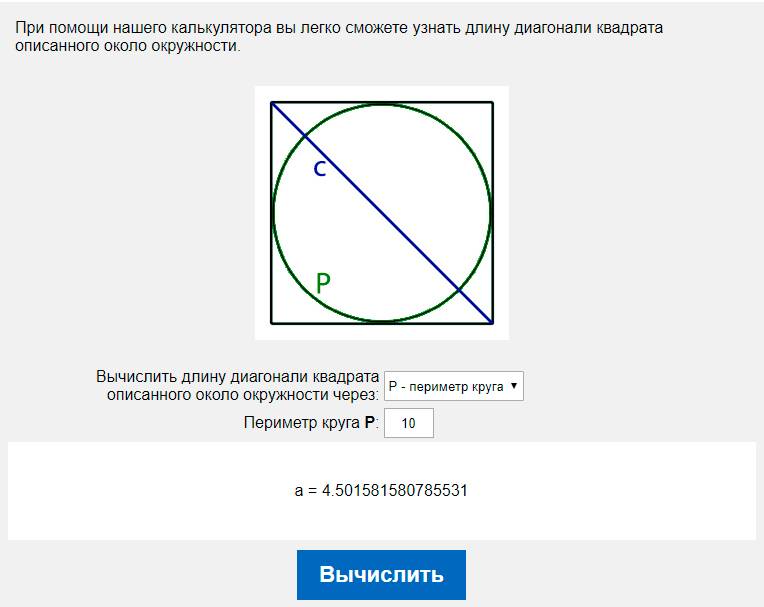 Дано, что диаметр 12 дюймов. Следовательно, длина окружности
Дано, что диаметр 12 дюймов. Следовательно, длина окружности
Сообщить об ошибке
Вокруг квадрата со стороной 5 см описана окружность. Чему равен периметр круга?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку круг описан вокруг квадрата, диагональ квадрата равна диаметру круга. Таким образом, чтобы найти диагональ, мы используем теорему Пифагора:
Таким образом, уравнение для решения становится or
Периметр, или длина окружности, задается or
Сообщить об ошибке
Найдите периметр катка, образованного прямоугольником и полукругами с указанными размерами.
Возможные ответы:
Правильный ответ:
Пояснение:
Периметр катка проходит по внешней стороне объединенных фигур.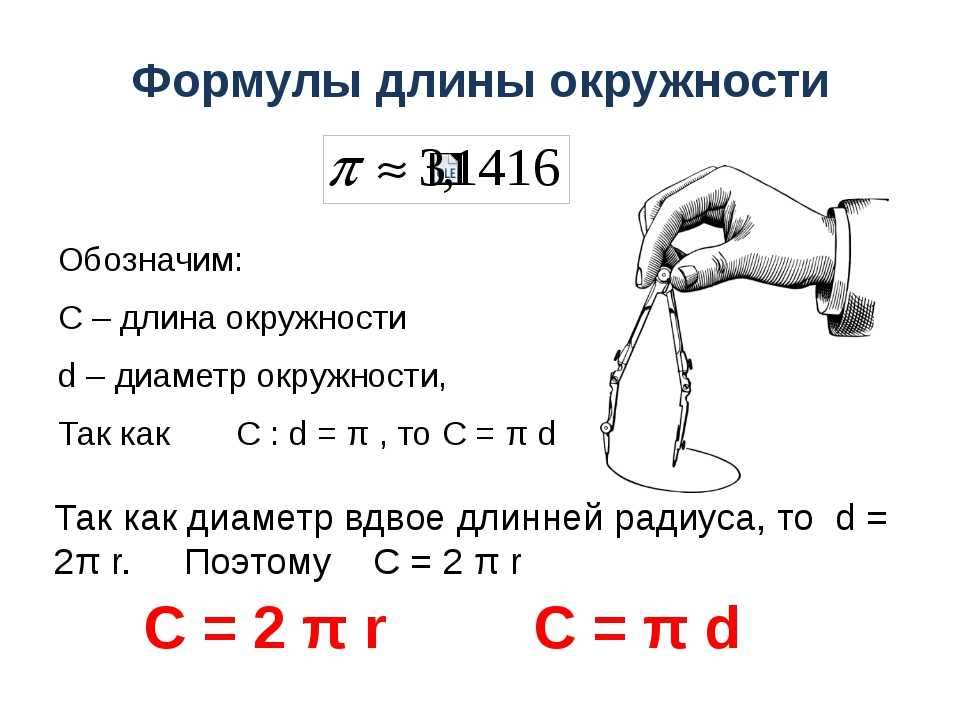 Два внешних края прямоугольника равны друг другу, поэтому периметр состоит из этих двух сторон.
Два внешних края прямоугольника равны друг другу, поэтому периметр состоит из этих двух сторон.
Два полукруга, образующие оставшуюся часть периметра, можно считать двумя половинами одного круга. Диаметр круга будет . Окружность круга будет составлять внешние края двух полукругов на катке. Найдите длину окружности по формуле следующим образом.
Наконец, добавьте эту длину окружности, которая составляет полукруги, к длине двух сторон, образованных прямоугольником, чтобы найти общий периметр катка.
Сообщить об ошибке
Если площадь круга равна , какова длина окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула площади круга: πr 2 . Площадь этого конкретного круга равна 81π, поэтому 81π = πr 2 .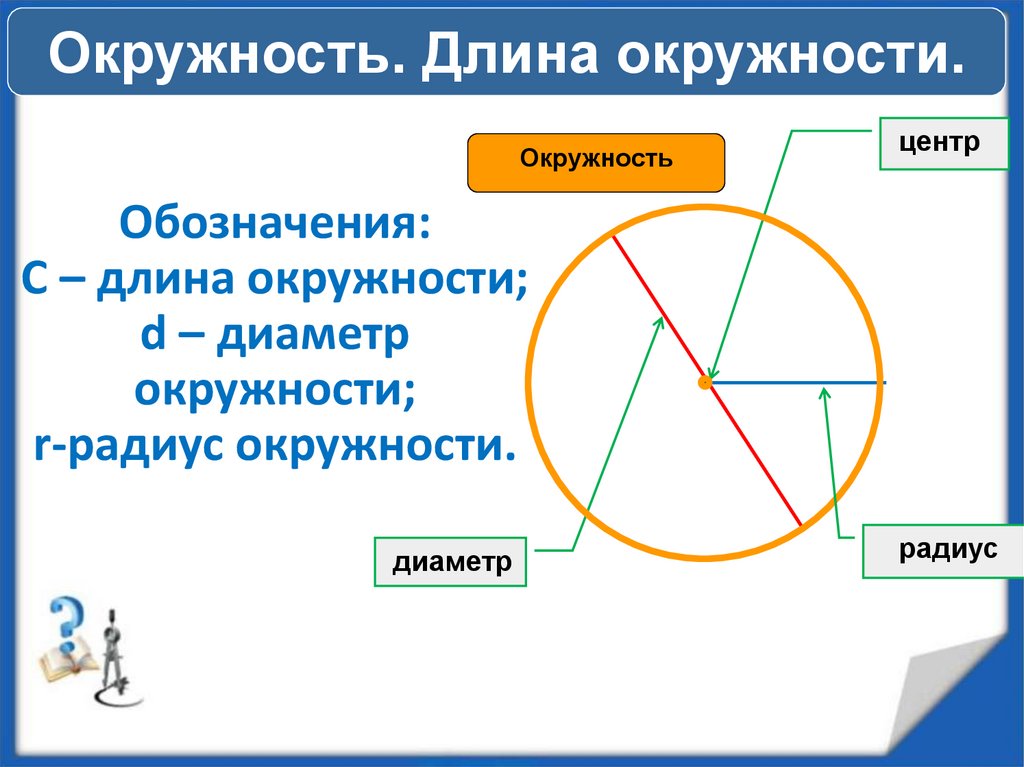 Разделите обе части на π, и у нас останется r 2 = 81. Извлеките квадратный корень из обеих сторон, чтобы найти r = 9.. Формула длины окружности: 2πr = 2π(9) = 18π. Правильный ответ 18π.
Разделите обе части на π, и у нас останется r 2 = 81. Извлеките квадратный корень из обеих сторон, чтобы найти r = 9.. Формула длины окружности: 2πr = 2π(9) = 18π. Правильный ответ 18π.
Сообщить об ошибке
Окружность площадью 13 π в 2 с центром в точке C . Чему равна окружность этого круга?
Possible Answers:
2√13 π
√26 π
13 π
√13 π
26 π
Правильный ответ:
2√13 π
Объяснение:
Формула площади круга: A = πr 2 .
Нам дана площадь, и подстановкой мы знаем, что 13 π = πr 2 .
Разделим π и получим 13 = r 2 .
Возьмем квадратный корень из из , чтобы найти, что г = √13.
Найдем длину окружности по формуле C = 2 πr .
Затем мы подставляем наши значения, чтобы найти C = 2√13 π .
Сообщить об ошибке
Прямоугольник 6 на 8 вписан в окружность. Какова окружность круга?
Возможные ответы:
12 π
25 π
10 π 7
0008
8 π
Правильный ответ:
10 π
Пояснение:
Сначала вы должны нарисовать схему. Диагональ прямоугольника также является диаметром круга. Диагональ является гипотенузой, кратной 2 треугольника 3,4,5, и поэтому равна 10.
Окружность = π * диаметр = 10 π .
Сообщить об ошибке
Садовник хочет построить забор вокруг своего сада, показанного ниже. Сколько метров ограждения им понадобится, если длина стороны прямоугольника 12, а ширина 8?
Сколько метров ограждения им понадобится, если длина стороны прямоугольника 12, а ширина 8?
Возможные ответы:
40 фут. Пояснение:
Форма сада состоит из прямоугольника и двух полукругов. Поскольку они строят забор, нам нужно найти периметр. Периметр длины прямоугольника равен 24. Периметр или длину окружности можно найти с помощью уравнения C=2π(r), где r= радиус окружности. Поскольку у нас есть две полуокружности, мы можем найти длину окружности одной полной окружности с радиусом 4, что будет равно 8π.
Сообщить об ошибке
Диаметр круга определяется двумя точками (2,5) и (4,6). Чему равна окружность этого круга?
Возможные ответы:
2,5π
5π
π√2.5
Ни один из других ответов
π√5
Правильный ответ:
π√5
. Объяснение:
Объяснение:
Сначала мы должны вычислить расстояние между этими двумя точками. Напомним, что формула расстояния: √((x 2 — х 1 ) 2 + (у 2 — у 1 ) 2 )
Следовательно, для нас: — 5) 2 ) = √((2) 2 + (1) 2 ) = √(4 + 1) = √5
Если d = √5, длина окружности равна πd, или π√5.
Сообщить об ошибке
Диаметр круга 16 сантиметров. Какова окружность круга?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти длину окружности, умножьте диаметр окружности на число пи (3.14).
Сообщить об ошибке
Автомобильная шина имеет радиус 18 дюймов. Когда шина сделала 200 оборотов, какое расстояние проехала машина в футах?
Возможные ответы:
500π
600π
300π
3600π
Правильный ответ:
600π
Объяснение:
Если радиус равен 18 дюймам, диаметр равен 3 футам. Таким образом, длина окружности шины равна 3π на C=d(π). После 200 оборотов шина и автомобиль прошли 3π x 200 = 600π футов.
Таким образом, длина окружности шины равна 3π на C=d(π). После 200 оборотов шина и автомобиль прошли 3π x 200 = 600π футов.
Сообщить об ошибке
← Назад 1 2 3 4 5 6 7 8 9 10 11 12 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции
Калькулятор окружности | Калькулятор формулы окружности
Введение в калькулятор окружности
Окружность — это расстояние по внешней стороне круга, обозначенное (C). Его также называют периметром круга. Калькулятор окружности позволяет рассчитать диаметр, площадь и окружность онлайн.
Если известно значение (r), формула для вычисления длины окружности будет:
$$C\;=\;2πr$$
Как мы знаем, число Пи фиксировано для всех кругов.
Если известно значение (d), формула для длины окружности будет следующей . Калькулятор длины окружности использует эту формулу длины окружности
Калькулятор длины окружности использует эту формулу длины окружности
$$C\;=\;2πr$$
Что такое радиус?
Радиус равен половине расстояния диаметра, обозначенного (r).
$$r\;=\;\frac{d}{2}$$
Калькулятор окружности и вращения также вычисляет площадь окружности. Он использует ту же формулу для нахождения этих результатов.
$$r\;=\;\frac{C}{(*2)}$$
Предположим, что длина окружности равна 20 см, вы хотите найти радиус. Подставьте значение в уравнение.
$$r\;=\;\frac{C}{(*2)}$$ $$r=\frac{20}{(3,14*2)}=3,18 см$$
Следуя этому пути калькулятор формулы окружности работает, чтобы узнать радиус круга.
Окружность в основном относится к длине дуги. Найдите решатель длины дуги для расчета запросов, сделав несколько кликов.
Что такое диаметр?
Диаметр – это расстояние через центр окружности, обозначенное (d). Если вы знаете радиус окружности, вы можете рассчитать диаметр, умножив радиус на 2.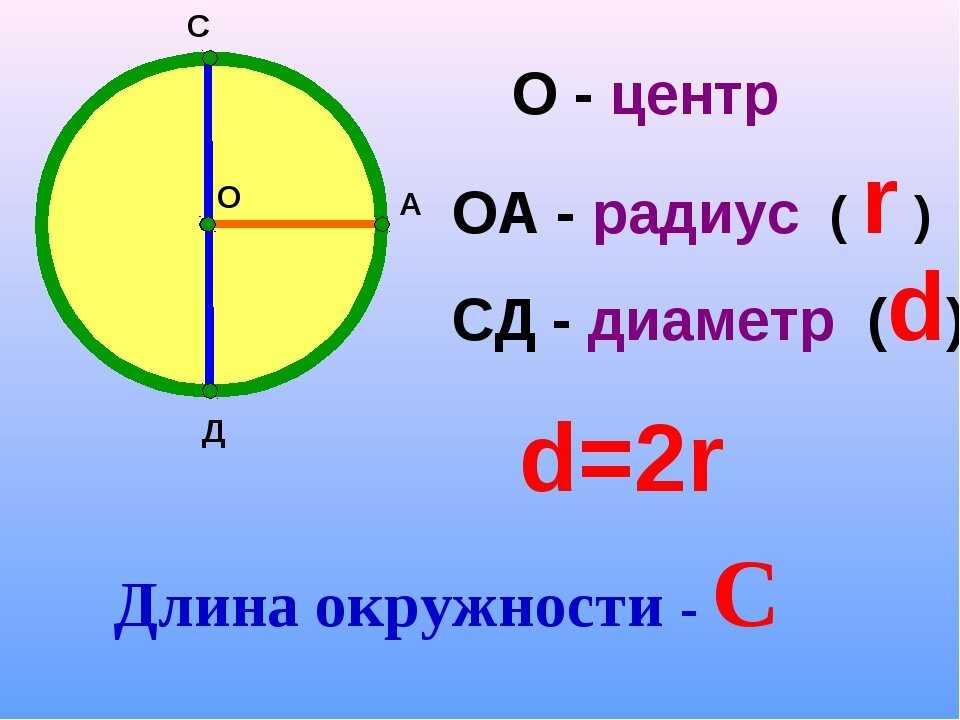 Калькулятор длины окружности позволяет без проблем рассчитать диаметр в цифровом виде.
Калькулятор длины окружности позволяет без проблем рассчитать диаметр в цифровом виде.
$$d = 2 * r$$
Если вы не знаете радиус, вы можете рассчитать диаметр, разделив длину окружности на число Пи.
$$d\;=\;\frac{c}{π}$$
Если вы не знаете длину окружности или радиус окружности, вы можете найти диаметр, разделив площадь на число пи, а затем найти квадратный корень из этого числа, чтобы получить радиус.
Что такое Пи?
Пи — отношение длины окружности к диаметру окружности. Значение этого отношения равно 3,14156. Это значение верно для всех кругов.
$$π=\frac{C}{d}$$
Как рассчитать длину окружности?
Вы можете использовать калькулятор формулы окружности, чтобы решить окружность онлайн . Для ручных расчетов предположим, что мы рисуем круг радиусом 3,5 сантиметра. Это будет выглядеть примерно так. Как мы знаем, эта синяя граница круга будет его периметром. Периметр круга также называют окружностью.
Но как мы можем измерить длину окружности ? Окружность круглая, и шкала используется для измерения любой прямой длины. Это очень просто. Взгляните на приведенный ниже метод или посетите учебник по окружности. Найдите длину окружности данного круга, радиус которого равен 3,5 см.
Как рассчитать окружность по формуле окружности?
Чтобы избежать ручных вычислений, можно использовать калькулятор формулы окружности, чтобы быстро решить уравнение для окружности . Для ручных вычислений процесс описан ниже.
Длина окружности = 2πr
Пока π = 3,14
Положив значения C = 2 * 3,14 * 3,5
$$C\;=\;22cm$$
Таким образом, в этом случае дан радиус, мы можем вычислить длину окружности по приведенной выше формуле длины окружности. Но если задан диаметр, то формула длины окружности будет:
$$Окружность\;=\;πd\;\;$$ $$d\;=\;диаметр$$
Положив значение C = 3,14 * 7
$$C\;=\;22см$$
Как мы можем найти длину окружности по диаметру , так и мы можем найти диаметр, если нам известна длина окружности.
Пример
Задача об окружности
Диаметр колеса 40 см. Сколько полных оборотов составит расстояние в 1 км?
Как
$$C\;=\;d$$
В то время как
$$π\;=\;3.14$$
Подставляя значения в формулу
$$C\;=\; 3.14 * 40$$ $$C\;=\;126 см$$
При этом 1км = 100000
Число полных оборотов = 100 000 / 126
$$=\;794km$$
Также найдите калькулятор теоремы Пифагора для подсчета длин сторон прямоугольного треугольника.
Калькулятор отношения окружности к диаметру
Как вы могли заметить, диаметр в 2 раза больше радиуса, а окружность и диаметр зависят друг от друга в окружности. Итак,
$$C/D=2πr/2r=π$$
$$\frac{C}{D}\;=\;\frac{2πr}{2r}\;=\;π$$
Это уравнение диаметра к окружности также является определением константы. Он также используется для нахождения объема конуса.
Как пользоваться калькулятором окружности?
Калькулятор формулы длины окружности прост и удобен в использовании. Чтобы рассчитать длину окружности , просто укажите радиус в нашем калькуляторе длины окружности и получите ответ. Наш калькулятор отношения окружности к диаметру покажет вам диаметр, окружность и площадь в качестве результатов.
Чтобы рассчитать длину окружности , просто укажите радиус в нашем калькуляторе длины окружности и получите ответ. Наш калькулятор отношения окружности к диаметру покажет вам диаметр, окружность и площадь в качестве результатов.
Надеемся, вам понравился наш калькулятор длины окружности и его теория . Вы также можете найти другие полезные калькуляторы на нашем портале, но не забудьте оставить нам свой ценный отзыв. Ваше здоровье!
Внешние ресурсы:
- Окружность круга.
- Как рассчитать длину окружности?
Калькулятор длины окружности | Бесплатный онлайн-калькулятор длины окружности с шагами
Онлайн-калькулятор длины окружности
Как использовать калькулятор длины окружности?
1.
Введите известный ввод только в одно поле ввода, остальные будут рассчитаны.
Если вы введете радиус в качестве входных данных, то будут рассчитаны диаметр и длина окружности.
Если вы введете диаметр в качестве входных данных, то будут рассчитаны радиус и длина окружности.
Если вы введете окружность в качестве входных данных, то будут рассчитаны радиус и диаметр.
2.
Выберите соответствующую единицу измерения для ввода и вывода.
3.
Вы также можете выбрать нужное значение числа пи из раскрывающегося списка: 3,14, \(\pi\) или \(\frac{22}{7}\).
4.
Теперь нажмите «Решить», чтобы получить результат.
5.
Вы можете установить флажок «Показать шаги», щелкнув в поле, чтобы понять пошаговый метод получения ответа.
6.
Вы можете нажать кнопку сброса, чтобы сбросить входные и выходные значения. Вы можете повторить описанные выше шаги для некоторых других входных значений.
7.
Нажмите кнопку «Пример», чтобы поиграть с различными случайными входными значениями.
8.
Нажмите кнопку «Исследовать», чтобы увидеть, как диаметр связан с длиной окружности.
9.
Находясь на странице «Исследовать», нажмите кнопку «Рассчитать», если хотите вернуться к калькулятору.
Что такое круг?
Окружность — двумерная круглая фигура. Все точки на границе окружности равноудалены от центра окружности.
Какова длина окружности?
Окружность или периметр круга является измерением границы круга.
Представьте, что границу круга нужно разрезать и положить на плоскую поверхность. Теперь измерьте границу круга, как если бы это была струна; измеренная таким образом длина будет окружностью круга. Следовательно, окружность будет выражаться в таких единицах длины, как сантиметры, метры, километры, футы и т. д.
Окружность, C = 2πr, где r — радиус
Окружность, C = πd, где d — диаметр.
Решенные примеры на калькуляторе длины окружности:
Пример 1:
Радиус окружности равен 14 см. Сможете ли вы найти его окружность? Используйте \(\frac{22}{7}\) для π . C = 2πr0004 = \(2\times\frac{22}{7}\times 14\) Подставьте \(\frac{22}{7}\) вместо π и 14 для r
Сможете ли вы найти его окружность? Используйте \(\frac{22}{7}\) для π . C = 2πr0004 = \(2\times\frac{22}{7}\times 14\) Подставьте \(\frac{22}{7}\) вместо π и 14 для r
= 88 сантиметров
составляет 88 сантиметров.
Пример 2:
Диаметр круглого парка составляет 70 метров. Найдите длину окружности парка. Используйте \(\frac{22}{7}\) вместо π .
Решение:
C = πd Запишите подходящую формулу для длины окружности
= \(\frac{22}{7}\times 70\) Подставьте \(\frac{22}{7}\) вместо π и 70 вместо d
= 220 метров
, метров.
Пример 3:
Окружность круглого стола составляет 110 сантиметров. Найдите радиус круглого стола. Используйте \(\frac{22}{7}\) вместо 𝛑.
Решение:
C = 2𝛑r Запишите подходящую формулу для длины окружности
110 = 2 × \(\frac{22}{7}\) × r Подставьте \(\frac{22}{7}\) вместо 𝛑 и 110 вместо C 110}{44}\) Крест умножьте на 7 и разделите обе стороны на 44
= 17,5 см
Следовательно, радиус круглого стола равен 17,5 см.
Пример 4:
Длина окружности 220 метров. Найдите диаметр круга. Используйте \(\frac{22}{7}\) вместо 𝛑.
Решение:
C = 𝛑d Напишите подходящую формулу для окружности
220 = \ (\ frac {22} {7} \) × D Заместитель \ (\ frac {22} {7} \) для 𝛑 и 220 для C
d = \(\frac{7×220}{22}\) Перекрестите умножьте на 7 и разделите обе стороны на 22
= 70 метров
, отсюда 70 метров.Часто задаваемые вопросы о калькуляторе длины окружности
Какие единицы измерения периметра?
Периметр определяется как сумма длин сторон объекта. Периметр различных плоских форм измеряется в любых единицах, которые используются для измерения длины; включая метры, сантиметры, мили, футы, дюймы и т. д.
Что такое число Пи?
Пи — математическая константа, которую можно использовать для вычисления площади и длины окружности круга или других круглых фигур. Мы можем получить значение числа пи, разделив длину окружности на ее диаметр. Пи имеет символ \(\pi\), а его числовое значение примерно равно \(\frac{22}{7}\) = 3,142857…, это иррациональное число, которое не заканчивается и не повторяется. Кроме того, эти числовые значения используются в зависимости от контекста уравнения.
Мы можем получить значение числа пи, разделив длину окружности на ее диаметр. Пи имеет символ \(\pi\), а его числовое значение примерно равно \(\frac{22}{7}\) = 3,142857…, это иррациональное число, которое не заканчивается и не повторяется. Кроме того, эти числовые значения используются в зависимости от контекста уравнения.
Как мы можем отличить диаметр круга от его длины окружности или периметра?
Диаметр окружности — это самая длинная хорда окружности, проходящая через центр этой окружности. Длина окружности равна длине внешней границы окружности. Диаметр и длина окружности — это длины, которые измеряются в линейных единицах. Длина окружности равна его диаметру, умноженному на константу (пи).
Как радиус связан с диаметром круга?
Радиус круга равен половине диаметра или, другими словами, диаметр равен удвоенному радиусу круга, \(r=\frac{d}{2}\) или d = 2r.
Сможете ли вы сосчитать все диаметры, которые можно изобразить в окружности?
Мы знаем, что через одну точку можно провести бесконечное количество линий. Диаметр — это отрезок, проведенный через центр окружности. Следовательно, мы можем сказать, что для окружности можно нарисовать бесконечные диаметры. Так что всех пересчитать невозможно!
Диаметр — это отрезок, проведенный через центр окружности. Следовательно, мы можем сказать, что для окружности можно нарисовать бесконечные диаметры. Так что всех пересчитать невозможно!
Ознакомьтесь с другими нашими курсами
Калькулятор окружности и формула — [100% бесплатно]
Используйте этот калькулятор окружности, когда вам нужно решать различные виды геометрических упражнений. Этот калькулятор отношения длины окружности к диаметру специально создан, чтобы помочь вам найти длину окружности, диаметр и площадь круга. В этой статье вы узнаете, как пользоваться калькулятором, как рассчитать длину окружности вручную, используя формулу длины окружности, и многое другое.
Загрузка калькулятора…
Содержание
Как пользоваться калькулятором длины окружности?
Этот калькулятор длины окружности прост и чрезвычайно удобен в использовании. Вы можете использовать его, чтобы найти отношение диаметра к окружности, когда сталкиваетесь с геометрическими задачами. Самое замечательное в этом онлайн-инструменте то, что его очень легко понять, и он дает вам мгновенные ответы. Вот шаги, которые нужно выполнить для этого калькулятора длины окружности в диаметр:
Самое замечательное в этом онлайн-инструменте то, что его очень легко понять, и он дает вам мгновенные ответы. Вот шаги, которые нужно выполнить для этого калькулятора длины окружности в диаметр:
- Сначала введите значение Радиуса и выберите единицу измерения в раскрывающемся меню.
- Затем введите значение диаметра и выберите единицу измерения в раскрывающемся меню.
- После ввода обоих значений калькулятор окружности автоматически сгенерирует для вас значения окружности и площади.
Как рассчитать длину окружности?
Вы можете использовать этот калькулятор, чтобы найти отношение диаметра к окружности для различных применений. Планируете ли вы заняться рукоделием, планируете ли вы поставить забор вокруг джакузи, вам нужно решить математическую задачу для школы или по какой-либо другой причине, знание того, как решить окружность круга, пригодится.
Пока вы сталкиваетесь с проблемами, связанными с окружностью, этот калькулятор длины окружности и формула длины окружности помогут вам. If you want to solve for circumference by hand, here are some steps for you:
If you want to solve for circumference by hand, here are some steps for you:
C = 2πr
C = 2π x 5
C = 10π
C = 31.4 inches
Как видите, найти длину окружности очень просто. Давайте поработаем с другим примером. На этот раз давайте попробуем найти длину окружности, когда значение радиуса равно 9.0017 14 см . Поскольку у вас уже есть значение радиуса, вы можете подставить его в формулу:
C = 2*π*R
4 Следовательно, длина окружности для этого примера равна 87,9646 см . Помимо длины окружности, имея значение радиуса, вы также можете найти площадь круга. На этот раз вы используете другую формулу:
C = 2*π*14
C = 87,9646 см92
A = 615,752 см2Следовательно, площадь для этого примера равна 615,752 см2 .
Наконец, вы также можете использовать те же значения, чтобы найти диаметр круга. Это значение проще всего найти, так как оно удваивает значение радиуса:
D = 2*R
2, следовательно, диаметр этого примера 28 см. Независимо от того, какую формулу вы используете или какое значение вы вычисляете, вы можете использовать калькулятор длины окружности, чтобы проверить свой ответ и посмотреть, правильно ли вы выполнили вычисления.
D = 2*14
D = 28 смЧто такое формула длины окружности?
Окружность круга относится к линейному расстоянию от его края. Длина окружности равна периметру любой данной геометрической фигуры. Однако слово «периметр» обычно используется только для полигонов. В предыдущем разделе мы выполнили шаги для вычисления окружности.
Чтобы найти это значение, вам нужно использовать формулу длины окружности. Эта формула описывала отношение между радиусом круга и его длиной окружности.
The formula is:
C = 2πR
where:
π refers to a constant value that’s approximately equal to 3.1416
R refers to the radius of the circleКак из диаметра определить длину окружности?
В некоторых случаях у вас нет значения радиуса. Вместо этого вы должны работать со значением диаметра. Следовательно, вы также должны научиться находить длину окружности, зная только это значение. Формула для длины окружности с использованием диаметра на самом деле намного проще:
C = πd
В этой формуле C относится к длине окружности, а d относится к диаметру круг. Проще говоря, вы можете найти длину окружности, умножив значение диаметра на постоянное значение числа Пи.
Как упоминалось выше, вставив число π в калькулятор, вы получите числовое значение константы, равное приблизительно 22/7 или 3.
1416 . Давайте рассмотрим еще один пример, который поможет вам понять эту формулу и как ее лучше использовать.
Предположим, например, что у вас есть круглая ванна диаметром 8 футов. Вы хотели бы построить забор вокруг этой ванны шириной 6 футов. Чтобы найти окружность этого забора, вы должны сначала решить диаметр ванны вместе с забором:
8 футов + 6 футов + 6 футов = 20 футов
Это значение учитывает общий диаметр ванны и ограждения. Теперь используйте это значение в формуле окружности:
C = πd
C = π x 20
C = 62,8 футаОкружение круга — Обзор и примеры как найти периметр многоугольника. Мы знаем, что круг не является многоугольником. Поэтому у него не должно быть периметра. Мы используем эквивалентную форму для круга, называемую окружностью.
В этой статье мы обсудим, как найти длину окружности , формулу длины окружности, примеры и примеры задач на длину окружности.
Какова длина окружности?
Расстояние вокруг многоугольника, такого как квадрат или прямоугольник, называется периметром (P) . С другой стороны, расстояние по окружности называется окружностью (C) . Следовательно, длина окружности — это линейное расстояние от края окружности.
Зачем нам нужно вычислять длину окружности?
Нахождение окружности объекта важно в следующих случаях:
Если вы хотите купить бюстгальтер, брюки или свитер, вам необходимо знать расстояние вокруг талии или груди. Хотя ваше тело не является идеальным кругом, вам придется измерить его окружность с помощью рулетки. Портные в основном используют эту технику для определения обхвата платья.
Вам также необходимо знать окружность круга, занимаясь рукоделием, ограждая джакузи или просто решая математическую задачку в школе.
Как найти длину окружности?
Как указывалось ранее, периметр или длина окружности — это расстояние вокруг окружности или любой круглой формы.
Длина окружности равна длине прямой линии, сложенной или согнутой, чтобы получился круг. Длина окружности измеряется в метрах, километрах, ярдах, дюймах и т. д.
Существует два способа нахождения периметра или длины окружности . первая формула предполагает использование радиуса, а второй предполагает использование диаметра круга. Важно отметить, что оба метода дают одинаковый результат.
Давайте посмотрим.
Длина окружности определяется выражением;
C = 2 * π* R = 2πR
где,
C = окружность или периметр,
R = радиус окружности,
π = математическая константа, известная как Pi0005
Или
C = π* D = π D
где D = 2R = диаметр круга
Для любого круга отношение длины его окружности к диаметру равно константе, известной как пи .
Длина окружности/диаметр = Пи
C/D = Пи или С/2R = Пи
Приблизительное значение Пи (π) = 22/7 = 3,1415926535897….
(значение без конца)
Для упрощения вычисления длины окружности число пи принимается равным 3,14 (π = 3,14).
Давайте рассмотрим несколько примеров ниже, чтобы уточнить концепцию окружности.
Пример 1
Найдите длину окружности радиусом 8 см.
Решение
Окружность = 2 * π* R = 2πR
= 2 * 3,14 * 8
= 50,24 см.
Пример 2
Вычислите длину окружности диаметром 70 мм
Решение
Окружность = π* D = π D
= 3,14 * 70
= 219,8 мм
Решение
Окружность = 2 * π* R = 2πR
= 2 * 3,14 * 10
= 62,8 м.
Пример 4
Длина окружности 440 ярдов. Найдите диаметр и радиус окружности.
Решение
Окружность = 2 * π * r = 2πr
440 = 2 * 3,14 * R
440 = 6,28R
Разделите обе стороны на 6,28,
R = 70,06
, поэтому на 6,28 радиус окружности 70,06 ярда.
Но, поскольку диаметр в два раза больше радиуса круга, диаметр равен 140,12 ярда.
Пример 5
Диаметр колес велосипеда 100 см. Сколько оборотов совершит каждое колесо, чтобы проехать 157 м?
Решение
Рассчитайте длину окружности велосипедного колеса.
Окружность = π D
= 3,14 * 100
= 314 см
Чтобы получить количество оборотов колеса, разделите пройденное расстояние на длину окружности колеса.
Нам нужно преобразовать 157 метров в см перед делением, поэтому мы умножаем 157 на 100, чтобы получить 15700 см. Следовательно,
Количество оборотов = 15700 см/314 см
= 50 оборотов.
Пример 6
Кусок проволоки в форме прямоугольника длиной 100 см и шириной 50 см отрезают и сгибают, чтобы получился круг. Вычислите длину окружности и радиус образовавшейся окружности.
Решение
Длина окружности сформированного круга = периметру прямоугольного провода.
Периметр прямоугольника = 2(Д + Ш)
= 2(100 + 50) см
= 2 * 150 см
= 300 см.
Следовательно, длина окружности будет 300 см.
Теперь вычислите его радиус.
Окружность = 2 π R
300 см = 2 * π * R
300 см = 2 * 3,14 * R
300 см = 6,28R
Разделите обе стороны на 6,28.
R = 47,77 см
Значит, радиус окружности будет 47,77 см.
Пример 7
Радиус каждого колеса мотоцикла равен 0,85 м. Какое расстояние проедет мотоцикл, если каждое колесо совершит 1000 оборотов? Предположим, мотоцикл движется прямолинейно.
Решение
Сначала найдите длину окружности колеса.
Окружность = 2 π R
= 2 * 3,14 * 0,85
= 5,338 м.
Чтобы найти пройденное расстояние, умножьте длину окружности колеса на количество сделанных оборотов.
Расстояние = 5,338 * 1000
= 5338 м
Следовательно, пройденное расстояние равно 5,338 километра.


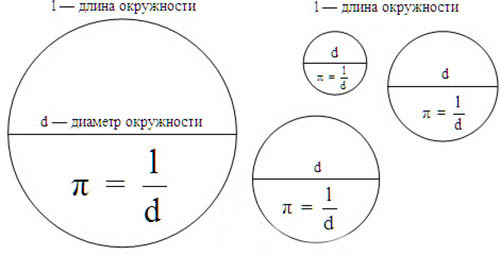

 Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром. Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора. Предположим, получилось 5 см.
Предположим, получилось 5 см. Если это условие не соблюдается, то это не окружность.
Если это условие не соблюдается, то это не окружность. Формулу обычно записывают следующим образом: C = π*D.
Формулу обычно записывают следующим образом: C = π*D. 2743
2743