Производная и первообразная таблица: Тема 8. Производная и первообразная функции

Первообразная функции. Формула Ньютона-Лейбница — подготовка к ЕГЭ по Математике

Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x). Функции вида у = F(x) + C образуют множество первообразных функции у = f(x).

Сейчас объясним, что это значит.

Вспомним таблицу производных. В левой колонке — функции, в правой — их производные. Например, — производная от функции , — производная функции . А чем будет являться для функции ? Или — для функции ? Вы уже догадались. Первообразной.

Заметим, кстати, что — производная не только функции , но и функций , — в общем, всех функций вида Здесь C — константа, то есть постоянная величина, и ее производная равна нулю.

Аналогично, функция — производная для всех функций вида , где — константа.

Посмотрим на таблицу первообразных. Каждая функция в левом столбце таблицы является производной для функции в правом столбце.

Таблица первообразных

Первообразная суммы функций равна сумме их первообразных.

Первообразная разности функций — разности первообразных.

Первообразная от функции , где — постоянный множитель, равна произведению на первообразную функции , то есть .

Множество всех первообразных функции называется неопределенным интегралом данной функции. Записывается это так:

Нахождение первообразной называется также интегрированием функции. А нахождение производной — дифференцированием функции. Интегрирование (то есть нахождение первообразной) и дифференцирование (взятие производной) — взаимно-обратные действия.

Но интегралы — отдельная тема. В задачах ЕГЭ по математике неопределенные интегралы не встречаются, а теме «Первообразная» посвящено всего несколько задач в первой части ЕГЭ. Для их решения надо знать только таблицу первообразных и еще одну важную формулу.

Формула для вычисления площади под графиком функции (Формула Ньютона-Лейбница) 

Пусть в прямоугольной системе координат задана фигура, ограниченная графиком непрерывной функции , осью и прямыми и .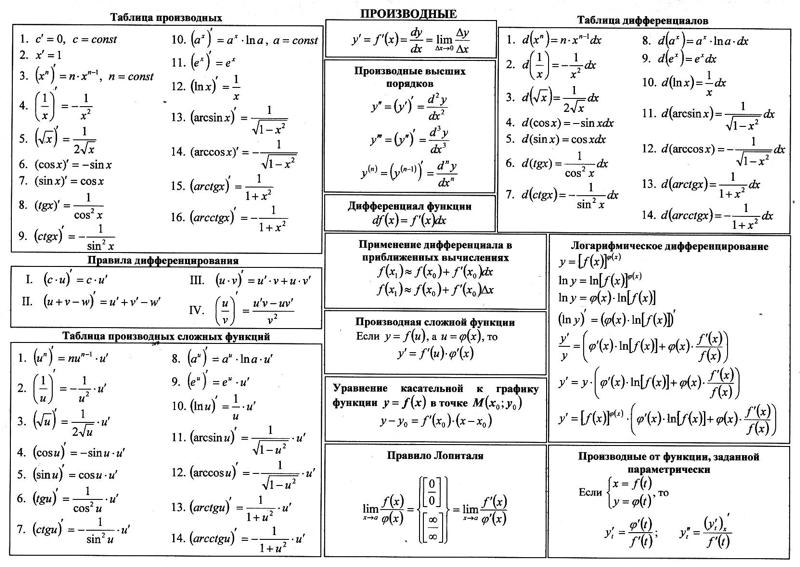

Пусть функция неотрицательна на отрезке [a; b].

Тогда площадь этой фигуры вычисляется по формуле:

Такую фигуру называют еще криволинейной трапецией. А сама формула носит название «Формула Ньютона-Лейбница».

1. Значение первообразной функции в точке 0 равно 6. Найдите . 

Найдем первообразную функции с помощью таблицы первообразных. Получим:

При получим:

Значит, и

Ответ: 40,5

2. Значение первообразной функции в точке 0 равно -13. Найдите

Найдем первообразную функции с помощью таблицы первообразных. Получим:

При x = 0 получим: Значит, и

Ответ: -14

3. На рисунке изображен график функции . Найдите значение выражения , где — одна из первообразных функции .

По формуле Ньютона-Лейбница, разность первообразных — это площадь, ограниченная графиком функции, осью X и прямыми y=a и y=b.

В этой задаче нужная фигура ограничена графиком функции, осью и прямыми и . Это квадратик, и площадь его равна 4.

Ответ: 4.

4. На рисунке изображён график некоторой функции . Функция  — одна из первообразных функции . Найдите площадь закрашенной фигуры.

Решение. По формуле Ньютона-Лейбница, площадь под графиком функции на отрезке [a,b] равна разности значений первообразной в концах отрезка, то есть

В нашей задаче имеем:

Дальше — просто арифметика.

Ответ: 13,5.

Одновременное изучение производной и первообразной функции

Одновременное изучение производной и первообразной функции

Л. Саютина,
школа № 104 “ЮНЕСКО”,
г. Челябинск

производной и первообразной функции

Взаимообратные действия, к которым относятся вычисление производной и первообразной, должны изучаться по возможности одновременно и совместно, на одном уроке и на одной странице тетради.

Психологическая полнота ассоциации достигается в системе упражнений общностью приемов вычислений, формул, таблиц.

Первое задание – вычисление производной – дается, а второе – вычисление первообразной – проверяет решение первой задачи, так как известное в первой задаче становится неизвестным, искомым во второй задаче. За счет всего этого идет саморазвитие мысли ученика, творчество, меньше делается ошибок при вычислении первообразной, что часто бывает при раздельном изучении этих тем; кроме того, экономится время.

До одновременного изучения производной и первообразной обязательно нужно дать историческую справку о дифференциальном и интегральном исчислениях; объяснить смысл предела функции, понятия приращения функции, аргумента, понятия средней скорости изменения функции, мгновенной скорости изменения функции.

Производная

1. Определение. Производной функции f(x) в точке x₀ называется предел (если он существует) отношения приращения функции Df(x) в этой точке к приращению Dx аргумента, когда Dx стремится к нулю

2. Вычисление производной из определения.

• Находим приращение функции в точке x₀  D 
  f = f(x₀ + Dx) – f(x₀)

или в точке x  D f = f(x + Dx) – f(x).

• находим разностное отношение
• Вычисляем предел этого отношения при  Dx ® 0 (если он существует)

Пример. f(x) = . Найти f  ‘(x)

Решение.

.

3. Правила вычисления производных.

• Производная суммы двух или нескольких функций равна сумме производных этих функций, если производные всех слагаемых существуют.

 

Пример 1.

f  ‘(x) = (x² + x + 2) ‘ = (x²) ‘ + (x) ‘ + 2 ‘ = 2x + 1 + 0 = 2x + 1.

Пример 2. –

или можно

• Производная степенной функции f(x) = xⁿ, где n О Z, равна произведению показателя n на степень xⁿ–1, т. е.

(xn) ‘ = nxⁿ–1.

(Доказательство методом математической индукции.)

Пример 1.  

 

• Производная произведения вычисляется по формуле (fg) ‘ = f ‘g + g ‘f, если каждая из производных f  ‘ и g ‘ существует.

Пример 1. f  ‘(x

) = (x²(x³ + 1)) ‘ = x²(x³ + 1) ‘ + (x³ + 1)(x²) ‘ = x²*3x² + (x³ + 1)*2x = 3x⁴ + 2x⁴ + 2x = 5x⁴ + 2x.

Пример 2. F ‘(x) = (2x² – 3x + C) ‘ = (2x²) ‘ – (3x) ‘ + C ‘ = 2(x²) ‘ – 3(x) ‘ + 0 = 2*2x – 3 = 4x – 3 = f(x).

• Производная сложной функции.

Если функция f имеет производную в точке x₀, а функция g имеет производную в точке y₀ = f(x₀), то сложная функция h(x) =

g(f(x)) имеет производную в точке x₀, при этом   h ‘(x₀) = g ‘(f(x₀))*f  ‘(x₀).

Пример 1. h(x) = (3x – 1)⁵, Обозначим 3x – 1 = y, тогда h(x) = y⁵.

y ‘(x) = (3x – 1) ‘ = 3, h_y ‘ = 5y⁴.

Тогда  h ‘(x) = 5(3x – 1)⁴*3 = 15(3x – 1)⁴  или проще h ‘(x) = ((3x – 1)⁵) ‘ = 5(3x – 1)⁴(3x – 1)’ = 3*5(3x – 1)⁴ = 15(3x – 1)⁴.

Пример 2.

Решение.

Пример 3. h(x) = (2x + 3)¹⁰⁰,

h ‘(x) = ((2x + 3)¹⁰⁰) ‘ = 100(2x + 3)⁹⁹(2x + 3)’ = 100(2x + 3)⁹⁹*2 = 200(2x + 3)⁹⁹.

Первообразная

1. Определение. Функция F(x) называется первообразной для функции f(x) на заданном промежутке J, если для всех x из этого промежутка выполняется равенство F ‘(x) = f(x).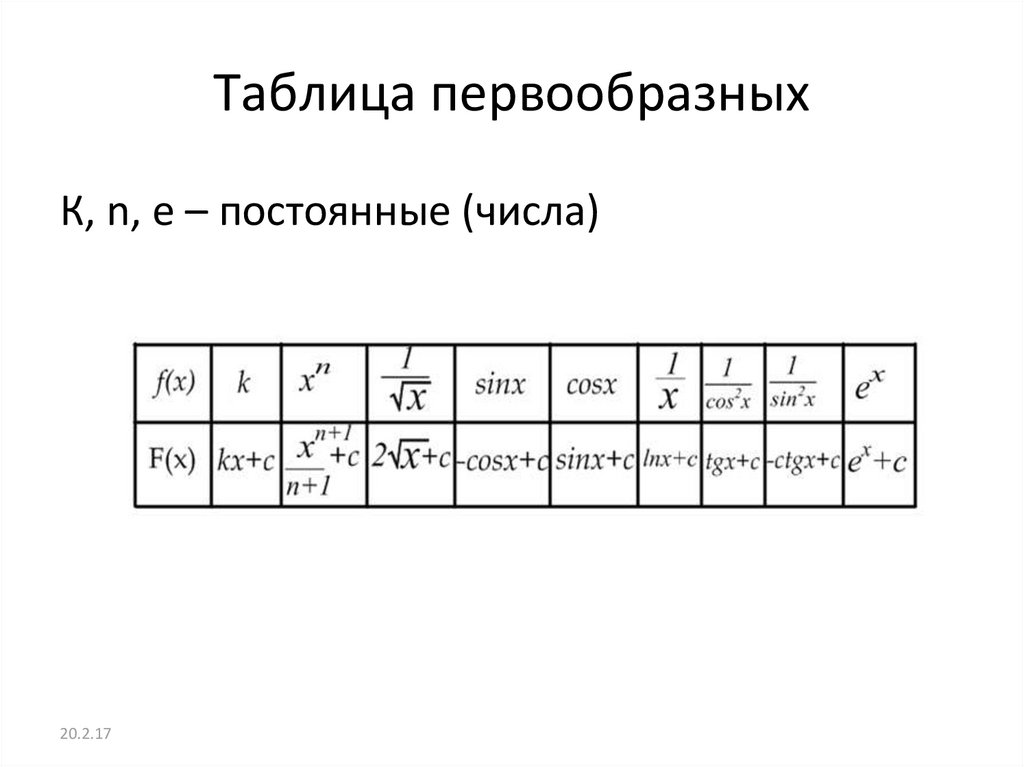

Нахождение первообразной – интегрирование – операция, обратная операции дифференцирования.

2. Алгоритм вычисления первообразной. Любая первообразная для функции

f(x) на промежутке J может быть записана в виде F(x) + C, где F(x) – одна из первообразных для функции f(x) на промежутке J, а C – постоянная.

• F(x) – первообразная для f(x), следовательно, по определению F ‘(x) = f(x) для » x О J.

Тогда (F(x) + C) ‘ = F ‘(x) + C ‘ = f(x) + 0 = f(x), т. е. F(x) + C – тоже первообразная для f(x).

Пример 1. Для функции на интервале (0; + Ґ) найти первообразную.

Решение. Первообразной для является функция

так как

Пример 2. Известны значения производных, найти сами функции:

(   ) ‘ = 2; (   ) ‘ = x²; (   ) ‘ = 2x;

(   ) ‘ = 1; (   ) ‘ = x³;

(   ) ‘ = x³ + x² + 1; (   ) ‘ = x + 3,5.

3. Правила нахождения первообразных.

• Первообразная суммы двух или нескольких функций равна сумме первообразных этих функций на данном промежутке.

Пример 1. f(x) = 2x + 1. F(x) – ?

Решение. где C может быть равно 2.

Пример 2.

Решение.

• Первообразная степенной функции f(x) = xⁿ, где n О Z, равна

так как

Пример 1.

Решение.

Пример 2.

Решение.

Постоянный множитель можно выносить за знак производной/первообразной. Пусть k – постоянное число.

(kf) ‘ = k ‘f + f ‘k = 0*f + kf ‘ = kf ‘, т. е. (kf) ‘ = kf ‘.

F ‘(x) = f(x), то kF – первообразная для kf, так как (kF) ‘ = kF ‘ = kf.

Пример 1. f(x) = 5x⁴ + 2x. F(x) – ?

Решение.

x²(x³ + 1) + C, так как F ‘(x) = f(x).

Пример 2. f(x) = 4x – 3. F(x) – ?

Решение.

• Первообразная сложной функции.

Если F(x) есть первообразная для f(x), а k и b – постоянные, причем

есть одна из первообразных для f(kx + b).

Если F ‘(x) = f(x), то по правилу нахождения производной сложной функции:

f(kx + b).

Пример 1. f(x) = 15(3x – 1)⁴. F(x) – ?

Решение.

(3x – 1)⁵ + C, так как F ‘(x) = f(x).

Пример 2.

Решение.

Для первообразной является а функция f(x) –

Пример 3. f(x) = 200(2x + 3)⁹⁹. F(x) – ?

Исходя из рассмотренных правил и аналогично разобранным примерам составим таблицу нахождения производных и первообразных элементарных функций:

Затем изучается применение производной в физике, геометрии, для исследования функций, а также применение первообразной в вычислении площади криволинейной трапеции.

Таблица интегралов

Таблица интегралов

(Математика)

Степень x.

x n dx = x n+1 (n+1) -1 + C (н -1) Доказательство

x -1 dx = ln|x| + С

Экспоненциальный/логарифмический

е х dx = е х + С Доказательство	b x dx = b x / ln(b) + C Доказательство, Кончик!
пер(х) дх = х ln(х) — х + С Доказательство

Тригонометрический

sin x dx = -cos x + C Доказательство	csc x dx = — ln|csc x + кроватка x| + С Доказательство
cos x dx = sin x + C Доказательство	сек x dx = ln|sec x + tan x| + С Доказательство
tan x dx = -ln|cos x| + С Доказательство	раскладушка x dx = ln|sin x| + С Доказательство

Тригонометрический результат

cos x dx = sin x + C Доказательство	csc x кроватка x dx = — csc x + C Доказательство
sin x dx = -cos x + C Доказательство	сек x тангенс x dx = сек x + C Доказательство
сек 2 x dx = tan x + C Доказательство	csc 2 x dx = — детская кроватка x + C Доказательство

Обратный тригонометрический

arcsin x dx = x arcsin x + (1-x 2 ) + С

arccsc x dx = x arccos x — (1-x 2 ) + С

arctan x dx = x arctan x — (1/2) ln(1+x 2 ) + С

Обратный тригонометрический результат

дх (1 — х 2 )  = угловой синус x + C     дх х (х 2 — 1)  = угловая секунда|x| + С     дх 1 ​​+ х 2  = арктангенс x + C

Полезные идентификаторы arccos x = /2 — arcsin x (-1 <= х <= 1) arccsc x = /2 — угловая секунда x (|х| >= 1) arccot ​​x = /2 — arctan x (для всех х)

Гиперболический

sin x dx = ch x + C Доказательство	csch x dx = ln |tanh(x/2)| + С Доказательство
ш х дх = ш х + С Доказательство	sech x dx = арктангенс (sinh x) + C
танх х dx = ln (ш х) + C Доказательство	coth x dx = ln |sinx x| + С Доказательство

---

Нажмите на доказательство для доказательства/обсуждения теоремы.

Чтобы решить более сложный интеграл, см. Интегратор на http://integrals.com.

Примитивные и производные силы | Лейбниц: детерминист, теист, идеалист

Фильтр поиска панели навигации Oxford AcademicЛейбниц: детерминист, теист, идеалист Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicЛейбниц: детерминист, теист, идеалист Термин поиска на микросайте

Расширенный поиск

• Иконка Цитировать Цитировать

• Разрешения

• Делиться
  • Твиттер
  • Еще

Cite

Меррихью Адамс, Роберт,

‘Primitive and Derivative Forces’

,

Leibniz: Determinist, Theist, Idealist

(

New York,

1999;

online edn,

Oxford Academic

, 1 Nov. 2003

), https://doi.org/10.1093/0195126491.003.0014,

, по состоянию на 25 октября 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Фильтр поиска панели навигации Oxford AcademicЛейбниц: детерминист, теист, идеалист Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicЛейбниц: детерминист, теист, идеалист Термин поиска на микросайте

Advanced Search

Abstract

Отношение между первобытными и производными силами может быть самой сложной проблемой в связи между физикой Лейбница и его метафизикой. Он считает, что производные силы являются модификациями первобытных сил, но также и то, что физические силы, которые он классифицирует как производные силы, принадлежат телам, являющимся совокупностями, тогда как первобытные силы принадлежат непротяженным воспринимающим субстанциям (монадам) и составляют их сущность. В этой главе рассматривается эта проблема, утверждая, что большую ее часть можно решить, исходя из предположения, что физические события являются лишь феноменами и, следовательно, в конечном счете определяются модификациями первобытных сил воспринимающих субстанций (монад).

Ключевые слова: агрегаты, производные силы, Лейбниц, метафизика, модификации, монады, воспринимающие субстанции, явления, физические силы, физика, примитивные силы

Предмет

Философия 17-18 вековИстория западной философии

В настоящее время у вас нет доступа к этой главе.

Войти

Получить помощь с доступом

Получить помощь с доступом

Доступ для учреждений

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок.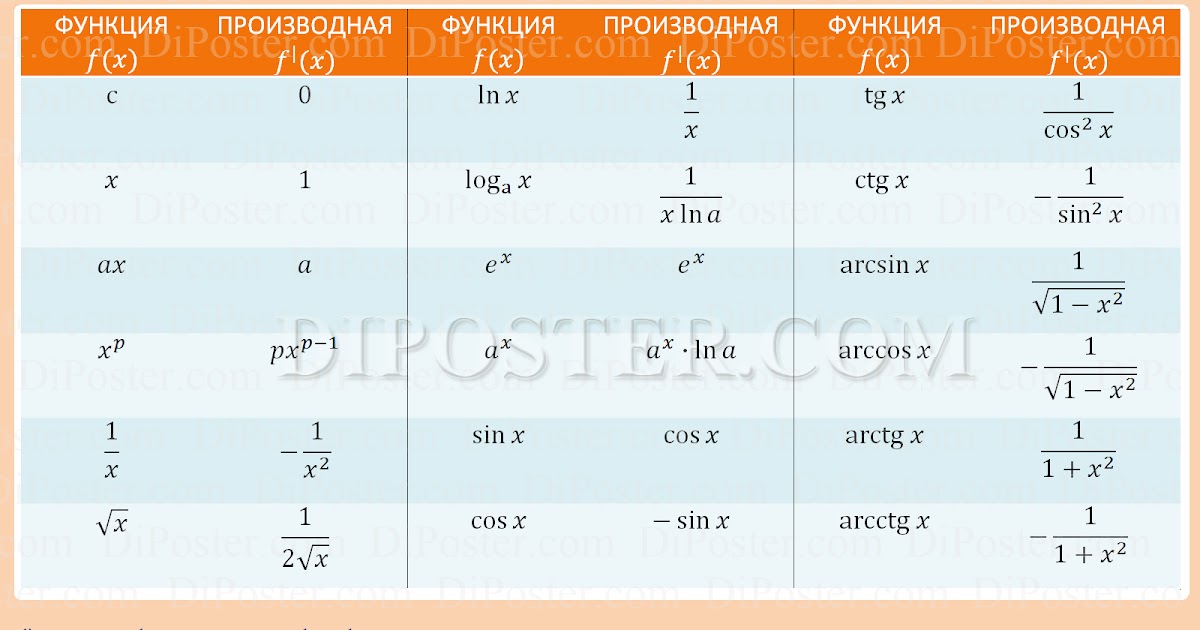 Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

1. Нажмите Войти через свое учреждение.
2. Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа в систему.
3. При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
4. После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

1. Щелкните Войти через сайт сообщества.
2. При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
3. После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

• Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

  No related posts.