Производная корня (√x)’ · Как пользоваться Контрольная Работа РУ
Для нахождения производных от сложный функций, содержащих корень, используйте калькулятор производных на этом сайте (тем более он даёт ещё ПОДРОБНОЕ РЕШЕНИЕ). Этот калькулятор находится по ссылке:
https://www.kontrolnaya-rabota.ru/s/proizvodnaya-funktsii/one/
Например, если надо найти производную от корня из x, умноженного на e в степени x.
Вводим в форму эту функцию sqrt(x)*exp(x) как изображено на рисунке выше.
Получим результат, когда нажмём на кнопку «Найти производную«.
Результат вычисления производной от функции f(x) = sqrt(x)*exp(x):
x
___ x ℯ
╲╱ x ⋅ℯ + ───────
___
2⋅╲╱ x
|
| = |
sqrt(x)*exp(x) + exp(x)/(2*sqrt(x)) |
Общее правило
Производную от корня очень просто посчитать.
-
Применим правило производной частного:
и .
Чтобы найти :
-
Заменим .
-
В силу правила, применим: получим
-
-
Затем примените цепочку правил. Умножим на :
-
дифференцируем почленно:
-
Производная постоянной равна нулю.
-
В силу правила, применим: получим
В результате:
-
В результате последовательности правил:
-
Чтобы найти :
-
дифференцируем почленно:
-
Производная постоянной равна нулю.
 2-1)/x
2-1)/x-
Применим правило производной частного:
и .
Чтобы найти :
-
Заменим .
-
В силу правила, применим: получим
-
-
Затем примените цепочку правил. Умножим на :
-
дифференцируем почленно:
-
Производная постоянной равна нулю.
-
В силу правила, применим: получим
В результате:
-
В результате последовательности правил:
-
Чтобы найти :
-
В силу правила, применим: получим
Теперь применим правило производной деления:
-
-
Теперь упростим:
- 0
- +0
- Авторизоваться Зарегистрироваться
- 0
- +0
- Авторизоваться Зарегистрироваться
- Общие шаги по использованию цепного правила.

- Экспоненциальные функции
- Функции синуса, косинуса или касания.
- «e» Функции
- Умноженные константы
- Число в возведенном в степень
- Функции квадратного корня
- Общее правило мощности для функций мощности
- Правило многопараметрической цепочки (открывается в новом окне)
- f (x) = x 2–3
- г (х) = х 2 ,
Ответ:
Mathway | Популярные задачи
1 Trovare la Derivata — d/dx натуральный логарифм x 2 Вычислим интеграл интеграл натурального логарифма x по x 3 Trovare la Derivata — d/dx e^x 4 Вычислим интеграл интеграл e^(2x) относительно x 5 Trovare la Derivata — d/dx 1/x 6 Trovare la Derivata — d/dx x^2 7 Trovare la Derivata — d/dx 1/(x^2) 8 Trovare la Derivata — d/dx sin(x)^2 9 Trovare la Derivata — d/dx sec(x) 10 Вычислим интеграл интеграл e^x относительно x 11 Вычислим интеграл интеграл x^2 относительно x 12 Вычислим интеграл интеграл квадратного корня x по x 13 Trovare la Derivata — d/dx cos(x)^2 14 Вычислим интеграл интеграл 1/x относительно x 15 Вычислим интеграл интеграл sin(x)^2 относительно x 16 Trovare la Derivata — d/dx x^3 17 Trovare la Derivata — d/dx sec(x)^2 18 Вычислим интеграл интеграл cos(x)^2 относительно x 19 Вычислим интеграл интеграл sec(x)^2 относительно x 20 Trovare la Derivata — d/dx e^(x^2) 21 Вычислим интеграл интеграл в пределах от 0 до 1 кубического корня 1+7x по x 22 Trovare la Derivata — d/dx sin(2x) 23 Trovare la Derivata — d/dx tan(x)^2 24 Вычислим интеграл интеграл 1/(x^2) относительно x 25 Trovare la Derivata — d/dx 2^x 26 График натуральный логарифм a 27 Trovare la Derivata — d/dx cos(2x) 28 Trovare la Derivata — d/dx xe^x 29 Вычислим интеграл интеграл 2x относительно x 30 Trovare la Derivata — d/dx ( натуральный логарифм x)^2 31 Trovare la Derivata — d/dx натуральный логарифм (x)^2 32 Trovare la Derivata — d/dx 3x^2 33 Вычислим интеграл интеграл xe^(2x) относительно x 34 Trovare la Derivata — d/dx 2e^x 35 Trovare la Derivata — d/dx натуральный логарифм 2x 36 Trovare la Derivata — d/dx -sin(x) 37 Trovare la Derivata — d/dx 4x^2-x+5 38 Trovare la Derivata — d/dx y=16 корень четвертой степени 4x^4+4 39 Trovare la Derivata — d/dx 2x^2 40 Вычислим интеграл интеграл e^(3x) относительно x 41 Вычислим интеграл интеграл cos(2x) относительно x 42 Trovare la Derivata — d/dx 1/( квадратный корень x) 43 Вычислим интеграл интеграл e^(x^2) относительно x 44 Вычислить e^infinity 45 Trovare la Derivata — d/dx x/2 46 Trovare la Derivata — d/dx -cos(x) 47 Trovare la Derivata — d/dx sin(3x) 48 Trovare la Derivata — d/dx 1/(x^3) 49 Вычислим интеграл интеграл tan(x)^2 относительно x 50 Вычислим интеграл интеграл 1 относительно x 51 Trovare la Derivata — d/dx x^x 52 Trovare la Derivata — d/dx x натуральный логарифм x 53 Trovare la Derivata — d/dx x^4 54 Оценить предел предел (3x-5)/(x-3), если x стремится к 3 55 Вычислим интеграл интеграл от x^2 натуральный логарифм x по x 56 Trovare la Derivata — d/dx f(x) = square root of x 57 Trovare la Derivata — d/dx x^2sin(x) 58 Вычислим интеграл интеграл sin(2x) относительно x 59 Trovare la Derivata — d/dx 3e^x 60 Вычислим интеграл интеграл xe^x относительно x 61 Trovare la Derivata — d/dx y=x^2 62 Trovare la Derivata — d/dx квадратный корень x^2+1 63 Trovare la Derivata — d/dx sin(x^2) 64 Вычислим интеграл интеграл e^(-2x) относительно x 65 Вычислим интеграл интеграл натурального логарифма квадратного корня x по x 66 Trovare la Derivata — d/dx e^2 67 Trovare la Derivata — d/dx x^2+1 68 Вычислим интеграл интеграл sin(x) относительно x 69 Trovare la Derivata — d/dx arcsin(x) 70 Оценить предел предел (sin(x))/x, если x стремится к 0 71 Вычислим интеграл интеграл e^(-x) относительно x 72 Trovare la Derivata — d/dx x^5 73 Trovare la Derivata — d/dx 2/x 74 Trovare la Derivata — d/dx натуральный логарифм 3x 75 Trovare la Derivata — d/dx x^(1/2) 76 Trovare la Derivata — d/d@VAR f(x) = square root of x 77 Trovare la Derivata — d/dx cos(x^2) 78 Trovare la Derivata — d/dx 1/(x^5) 79 Trovare la Derivata — d/dx кубический корень x^2 80 Вычислим интеграл интеграл cos(x) относительно x 81 Вычислим интеграл интеграл e^(-x^2) относительно x 82 Trovare la Derivata — d/d@VAR f(x)=x^3 83 Вычислим интеграл интеграл 4x^2+7 от 0 до 10 относительно x 84 Вычислим интеграл интеграл от ( натуральный логарифм x)^2 по x 85 Trovare la Derivata — d/dx логарифм x 86 Trovare la Derivata — d/dx arctan(x) 87 Trovare la Derivata — d/dx натуральный логарифм 5x 88 Trovare la Derivata — d/dx 5e^x 89 Trovare la Derivata — d/dx cos(3x) 90 Вычислим интеграл интеграл x^3 относительно x 91 Вычислим интеграл интеграл x^2e^x относительно x 92 Trovare la Derivata — d/dx 16 корень четвертой степени 4x^4+4 93 Trovare la Derivata — d/dx x/(e^x) 94 Оценить предел предел arctan(e^x), если x стремится к 3 95 Вычислим интеграл интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x 96 Trovare la Derivata — d/dx 3^x 97 Вычислим интеграл интеграл xe^(x^2) относительно x 98 Trovare la Derivata — d/dx 2sin(x) 99 Вычислить sec(0)^2 100 Trovare la Derivata — d/dx натуральный логарифм x^2 Производная от корня из x.
 Производная степенной функции (степени и корни)
Производная степенной функции (степени и корни)На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 .
 Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01.
 Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .

3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.

8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
На котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком.
 Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.
Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции – и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию я буду называть внешней функцией , а функцию – внутренней (или вложенной) функцией .
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим:
Пример 1
Найти производную функции
Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится.
 Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочлен является внутренней функцией (вложением), а – внешней функцией.
Первый шаг , который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней .
В случае простых примеров вроде понятно, что под синус вложен многочлен . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения при (вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому многочлен и будет внутренней функцией :
Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции .
Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:
Сначала находим производную внешней функции (синуса), смотрим на таблицу производных элементарных функций и замечаем, что . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением
Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем .
Ну и совершенно очевидно, что
Результат применения формулы в чистовом оформлении выглядит так:
Постоянный множитель обычно выносят в начало выражения:
Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 2
Найти производную функции
Пример 3
Найти производную функции
Как всегда записываем:
Разбираемся, где у нас внешняя функция, а где внутренняя.
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция: Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения . Таким образом, результат применения правила дифференцирования сложной функции следующий:Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция у нас не меняется:
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:Пример 4
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).

Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?
Пример 5
а) Найти производную функции
б) Найти производную функции
Пример 6
Найти производную функции
Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :
Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:
Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью.
 Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).Пример 7
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного , но такое решение будет выглядеть как извращение необычно. Вот характерный пример:
Пример 8
Найти производную функции
Здесь можно использовать правило дифференцирования частного , но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :Находим производную внутренней функции, косинус сбрасываем обратно вниз:
Готово.
 В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.Пример 9
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5 функций.
Пример 10
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения . Как бы мы считали на калькуляторе?
Сначала нужно найти , значит, арксинус – самое глубокое вложение:
Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.

Начинаем решать
Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: Единственное отличие – вместо «икс» у нас сложное выражение , что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функции следующий.
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования.
 Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.
 К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.Таблица производных простых функций
Правила дифференцирования
1. Производная суммы или разности 2. Производная произведения 2a. Производная выражения, умноженного на постоянный множитель 3. Производная частного 4. Производная сложной функции Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.
 е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой. Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .

Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число, например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений.
 Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение, а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
 В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного: производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2.
 Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Решение.
 В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:
В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция.
 Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной.
 Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Здравствуйте, уважаемые читатели.
 После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант . Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.

На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение ) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями.
 {k_n-1}(x).$
{k_n-1}(x).$Замечание. Для нахождения корней $f(x)$ можно использовать соображение:
$\frac{f(x)}{НОД(f,f’)}=p_1(x)…p_n(x)$
Производная степени | Математика
Производная степени встречается в большинстве примеров на дифференцирование. Само правило нахождения производной степени простое. При дифференцировании степени с натуральным показателем проблем, как правило, не возникает. А вот найти производную степени с отрицательным или дробным показателями несколько сложнее. Легче всего понять, как найти производную степени, на примерах.
Открываем таблицу производных и правила дифференцирования.
Основная формула, по которой может быть найдена производная любой степени —
Примеры. Найти производную степени:
Поскольку при дифференцировании число выносится за знак производной, то множитель, стоящий перед степенью, при нахождении производной просто переписываем:
Нахождение производной степени, стоящей в знаменателе дроби, немного сложнее.
 Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.
Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.Производная степени используется и для дифференцирования корней. Предварительно корень приводится к степени, а в найденной производной снова возвращаемся к корню.
Например,
Если корень в знаменателе, сначала преобразовываем его в степень, затем — поднимаем наверх с отрицательным показателем, а далее — как обычно, производная степени.
Например,
Примеры для самопроверки. Найти производную степени:
Показать решение
«Решаем с помощью производной»
Производная широко применяется при решении ряда задач элементарной математики.
 Из
всего круга таких задач выделим те, при решении
которых используется теорема Лагранжа и ее
следствия. К ним относятся задачи на
доказательство тождеств, неравенств, вывод
формул тригонометрии, разложение алгебраических
выражений на множители, решение уравнений,
неравенств, систем уравнений, уравнений с
параметрами. При этом можно указать общие методы
решения и некоторые частные приемы.
Из
всего круга таких задач выделим те, при решении
которых используется теорема Лагранжа и ее
следствия. К ним относятся задачи на
доказательство тождеств, неравенств, вывод
формул тригонометрии, разложение алгебраических
выражений на множители, решение уравнений,
неравенств, систем уравнений, уравнений с
параметрами. При этом можно указать общие методы
решения и некоторые частные приемы.Теорема Лагранжа. Пусть функция f непрерывна на отрезке [a;b] и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что <Рисунок1>.
Следствие 1 (условие постоянства). Если функция f непрерывна на отрезке [a;b], а ее производная равна нулю внутри этого отрезка, то функция f постоянна на [a;b].
Следствие 2. Если функции и непрерывны на отрезке [a;b] и имеют одинаковые производные внутри этого отрезка, то они отличаются лишь постоянным слагаемым.

Условие монотонности функции также является следствием теоремы Лагранжа. В школьном учебнике оно устанавливается отдельно в виде теоремы.
Следствие 3 (условие монотонности). Если функция f непрерывна на промежутке I и ее производная положительна (соответственно отрицательна) во внутренних точках этого промежутка, то функция f возрастает (соответственно убывает) на I.
Теорему Лагранжа можно применять:
— при доказательстве неравенств, в частности – числовых неравенств;
— при исследовании вопроса о корнях многочлена или уравнения;
— при решении уравнений.
В процессе решения таких задач вводится в рассмотрение функция f(x) на отрезке [a;b], удовлетворяющая условиям теоремы Лагранжа, для нее записывается формула Лагранжа <Рисунок1>, c (a;b) и оценивается f’(c), а, следовательно, и выражение <Рисунок2>, что позволяет доказать рассматриваемое неравенство или решить вопрос о корнях многочлена, уравнения.

Пример 1. Доказать, что <Рисунок3>.
Решение. Функция f(x)=arccosx на отрезке [0,6;0,8] непрерывна и дифференцируема на интервале (0,6;0,8), <Рисунок4>. Следовательно, для функции f(x) на данном отрезке выполняются условия теоремы Лагранжа и <Рисунок5>, где 0,6<c<0,8. Имеем <Рисунок6>, т.е. <Рисунок7>. Оценим число<Рисунок8>. Так как 0,6<c<0,8, то 0,36<1-c2<0,64 и 0,6<<Рисунок9><0,8, следовательно <Рисунок10>. Тогда <Рисунок11> и окончательно <Рисунок3>.
Пример 2. Доказать, что ex>=ex.
Решение. Неравенство справедливо при х=1. Рассмотрим функцию f(x)=ex-ex. Тогда для любого числа b (b>1) для данной функции выполняются условия теоремы Лагранжа на отрезке [1;b], а для b<1 – выполняется условие теоремы на отрезке [b;1] и, следовательно, существует внутренняя точка соответствующего отрезка, такая, что <Рисунок12>, т.
 е. <Рисунок13>. Так
как c>1 при b>1, то ec>e и, следовательно, ec-e>0.
Тогда <Рисунок14>, а значит eb-eb>0, т.е. eb>eb
для любого b>1. Таким образом доказано, что ex>=ex
при x>=1.
е. <Рисунок13>. Так
как c>1 при b>1, то ec>e и, следовательно, ec-e>0.
Тогда <Рисунок14>, а значит eb-eb>0, т.е. eb>eb
для любого b>1. Таким образом доказано, что ex>=ex
при x>=1.Если b<1, то <Рисунок15>, т.е. с<1, тогда ec<e и ec-e<0. Учитывая, что b-1<0, из равенства <Рисунок13>, следует, что eb-eb>0, т.е. eb>eb.
Итак, доказано, что неравенство ex>=ex верно при любом действительном х. В частности, при x=c+1 получим ec+1>=e(c+1), т.е. ec>=c+1, где с – любое действительное число.
Пример 3. Доказать, что уравнение <Рисунок16> не имеет действительных положительных корней.
Решение.
 Пусть b – любое
положительное число. Рассмотрим функцию f(x)=
<Рисунок17>, непрерывную на отрезке [a;b] и
имеющую производную <Рисунок18> на интервале
(0;b). По теореме Лагранжа имеем <Рисунок19>,
0<c<b, т.е. <Рисунок20>. А так как при любом с>0 ec>c+1
(доказано в примере 2), то ec-c>1 и,
следовательно, <Рисунок21>. Отсюда получим
<Рисунок22>, а значит <Рисунок23> для любого
b>0. Таким образом, <Рисунок24> при x>0, т.е.
<Рисунок25>, следовательно, равенство
<Рисунок16> не выполняется ни при каком x>0. А,
значит, уравнение <Рисунок16> не имеет
действительных положительных корней.
Пусть b – любое
положительное число. Рассмотрим функцию f(x)=
<Рисунок17>, непрерывную на отрезке [a;b] и
имеющую производную <Рисунок18> на интервале
(0;b). По теореме Лагранжа имеем <Рисунок19>,
0<c<b, т.е. <Рисунок20>. А так как при любом с>0 ec>c+1
(доказано в примере 2), то ec-c>1 и,
следовательно, <Рисунок21>. Отсюда получим
<Рисунок22>, а значит <Рисунок23> для любого
b>0. Таким образом, <Рисунок24> при x>0, т.е.
<Рисунок25>, следовательно, равенство
<Рисунок16> не выполняется ни при каком x>0. А,
значит, уравнение <Рисунок16> не имеет
действительных положительных корней.Пример 4. Доказать, что на промежутке (0, 2) имеется не более двух различных действительных корней уравнения <Рисунок26>.
Решение.
 Предположим, что
уравнение имеет не менее трех различных
действительных корней х1, х2, х3,
принадлежащих промежутку (0,2), и пусть x1<x2<x3.
Тогда они являются нулями функции <Рисунок27>,
т.е. f(x1)=f(x2)=f(x3)=0. На каждом из
отрезков [x1;x2], [x2;x3] для
функции f(x) выполняются условия теоремы Лагранжа,
следовательно, существуют числа c1 и с2
из интервалов (х1;х2), (х2;х3)
соответственно, такие, что <Рисунок28> и
<Рисунок29>. А так как f(x1)=f(x2)=f(x3)=0,
то f’(c1)=0 и f’(c2)=0, причем с1с2.
Предположим, что
уравнение имеет не менее трех различных
действительных корней х1, х2, х3,
принадлежащих промежутку (0,2), и пусть x1<x2<x3.
Тогда они являются нулями функции <Рисунок27>,
т.е. f(x1)=f(x2)=f(x3)=0. На каждом из
отрезков [x1;x2], [x2;x3] для
функции f(x) выполняются условия теоремы Лагранжа,
следовательно, существуют числа c1 и с2
из интервалов (х1;х2), (х2;х3)
соответственно, такие, что <Рисунок28> и
<Рисунок29>. А так как f(x1)=f(x2)=f(x3)=0,
то f’(c1)=0 и f’(c2)=0, причем с1с2.Найдем производную f’(x):
<Рисунок30>. Так как <Рисунок31> для любых х, то уравнение f’(x)=0 имеет единственный корень x=, принадлежащий промежутку (0, 2).
 Пришли к противоречию, так как с1 и с2
(с1с2)
являются корнями уравнения f’(x)=0, тем самым
доказано, что уравнение <Рисунок26> имеет на
промежутке (0,2) не более двух различных
действительных корней.
Пришли к противоречию, так как с1 и с2
(с1с2)
являются корнями уравнения f’(x)=0, тем самым
доказано, что уравнение <Рисунок26> имеет на
промежутке (0,2) не более двух различных
действительных корней.Пример 5. Решить уравнение x9-9x5+63x-55=0.
Решение. Легко заметить, что число х1=1 является корнем данного уравнения. Предположим, что существует еще хотя бы один действительный корень х2, отличный от х1. Числа х1 и х2 являются нулями функции f(x)=x9-9x5+63x-55 и, следовательно, f(x1)=f(x2)=0. Применим терему Лагранжа к функции f(x) на отрезке [x1;x2], если x1<x2 или на отрезке [x2;x1], если x1>x2.
 Следовательно, найдется такая внутренняя точка с
этого отрезка, что будет выполняться
<Рисунок32>. Учитывая, что f(x1)=f(x2)=0,
получим f’(с)=0, т.е. число с – корень уравнения
f’(x)=0. Но производная f’(x)=9x8-45x4+63, т.е.
f’(x)=9(x4-2,5)2+6,75 положительна для любых
х, а значит уравнение f’(x)=0 не имеет корней.
Полученное противоречие доказывает, что
найденный корень х1=1 является единственным
корнем уравнения x9-9x5+63x-55=0.
Следовательно, найдется такая внутренняя точка с
этого отрезка, что будет выполняться
<Рисунок32>. Учитывая, что f(x1)=f(x2)=0,
получим f’(с)=0, т.е. число с – корень уравнения
f’(x)=0. Но производная f’(x)=9x8-45x4+63, т.е.
f’(x)=9(x4-2,5)2+6,75 положительна для любых
х, а значит уравнение f’(x)=0 не имеет корней.
Полученное противоречие доказывает, что
найденный корень х1=1 является единственным
корнем уравнения x9-9x5+63x-55=0.Пример 6.
Определить число критических точек функции y=(x2-1)(x2-8х)(x-9).
Решение. Так как степень многочлена f(x)= (x2-1)(x2-8х)(x-9) равна 5, то его производная f’(x) является многочленом четвертой степени и имеет не более четырех действительных корней.
 Применим теорему
Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках
[-1;0], [0;1], [1;8], [8;9] и при этом учтем, что
f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся
внутренние точки х1, х2, х3, х4
соответственно, такие, что <Рисунок33>,
<Рисунок34>, <Рисунок35>, <Рисунок36>,
т.е. f’(x1)=0, f’(x2)=0, f’(x3)=0, f’(x4)=0.
А учитывая, что x1, х2, х3, х4
– различные корни многочлена f’(x) четвертой
степени, делаем вывод, что других корней,
отличных от полученных, нет и, следовательно,
функция y=(x2-1)(x2-8х)(x-9) имеет четыре
критические точки.
Применим теорему
Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках
[-1;0], [0;1], [1;8], [8;9] и при этом учтем, что
f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся
внутренние точки х1, х2, х3, х4
соответственно, такие, что <Рисунок33>,
<Рисунок34>, <Рисунок35>, <Рисунок36>,
т.е. f’(x1)=0, f’(x2)=0, f’(x3)=0, f’(x4)=0.
А учитывая, что x1, х2, х3, х4
– различные корни многочлена f’(x) четвертой
степени, делаем вывод, что других корней,
отличных от полученных, нет и, следовательно,
функция y=(x2-1)(x2-8х)(x-9) имеет четыре
критические точки.Условие монотонности функции можно применять:
— при решении неравенств;
— при доказательстве неравенств с переменной;
— при доказательстве числовых неравенств;
— при исследовании вопроса о количестве корней уравнения;
— в некоторых случаях при решении уравнений, уравнений с параметрами, систем уравнений.

Решение задач с использованием условия монотонности основано на связи между возрастанием или убыванием функции и знаком ее производной на некотором промежутке. При этом, сравнивая различные значения аргумента из этого промежутка рассматриваемой монотонной функции, делается вывод о соответствующих значениях данной функции.
Пример 7. Доказать, что 3xcosx<sinx+sin2x, если 0<x<<Рисунок37>.
Решение. Докажем, что, если 0<x<<Рисунок37>, то sinx+sin2x-3xcosx>0, т.е. cosx(tgx+2sinx-3x)>0. Рассмотрим непрерывную на промежутке <Рисунок38>функцию f(x)=tgx-3x+2sinx. Ее производная <Рисунок39> при <Рисунок40> принимает положительные значения, следовательно, функция f(x) возрастает на промежутке <Рисунок38>и на нем f(x)>f(0).
Учитывая, что f(0)=0, будем иметь tgx-3x+2sinx>0.
 А так как на промежутке <Рисунок38>
cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано,
что sinx+sin2x-3xcosx>0, то есть, что 3xcosx<sinx+sin2x, если
0<x<<Рисунок37>.
А так как на промежутке <Рисунок38>
cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано,
что sinx+sin2x-3xcosx>0, то есть, что 3xcosx<sinx+sin2x, если
0<x<<Рисунок37>.Пример 8. Доказать, что
1) <Рисунок41> и <Рисунок42>, если 0<x1<x2<=e;
2) <Рисунок43>и <Рисунок44>, если e<=x1<x2.
Решение. Рассмотрим непрерывную на промежутке (0;+) функцию <Рисунок45>. Так как ее производная <Рисунок46> равна нулю при х=е, а при 0<x<e f’(x)>0 и f’(x)<0 при x>e, то на промежутке (0;e] функция f(x) возрастает, а на промежутке [e;+) - убывает. Тогда для любых значений х1 и х2 таких, что 0<x1<x2<=e, будет выполняться неравенство f(x1)<f(x2), то есть <Рисунок47>.
 Запишем его в виде
<Рисунок48>, <Рисунок49>. Учитывая, что
функция ln t возрастающая, получим <Рисунок50>. А
если обе части неравенства <Рисунок47>
умножить на произведение x1x2>0, то
получим x2lnx1<x1lnx2, далее
<Рисунок51>, откуда и будем иметь <Рисунок52>.
Запишем его в виде
<Рисунок48>, <Рисунок49>. Учитывая, что
функция ln t возрастающая, получим <Рисунок50>. А
если обе части неравенства <Рисунок47>
умножить на произведение x1x2>0, то
получим x2lnx1<x1lnx2, далее
<Рисунок51>, откуда и будем иметь <Рисунок52>.Если же e<=x1<x2, то f(x1)>f(x2), то есть <Рисунок47>, откуда и получим <Рисунок53>и <Рисунок54>.
Доказанными в примере 8 неравенствами можно воспользоваться при сравнении чисел и при доказательстве числовых неравенств.
Пример 9. Сравнить (сtg48°)tg48° и (сtg50°)tg50°.
Решение. Заметим, что сtg48°=сtg<Рисунок55>, tg48°=tg<Рисунок55>, ctg50°=ctg<Рисунок55>, tg50°=tg<Рисунок55>, а также, что <Рисунок57>.
 Взяв <Рисунок58>,
<Рисунок59> и учитывая, что <Рисунок53>, если
0<x1<x2<=e, получим <Рисунок60>, т.е.
(сtg48°)tg48° > (сtg50°)tg50°.
Взяв <Рисунок58>,
<Рисунок59> и учитывая, что <Рисунок53>, если
0<x1<x2<=e, получим <Рисунок60>, т.е.
(сtg48°)tg48° > (сtg50°)tg50°.Пример 10. Доказать, что 2006 2007>2007 2006.
Решение. Воспользуемся неравенством x1x2>x2x1, если e<=x1<x2. Положив х1=2006 и х2=2007, имеем e<2006<2007, следовательно, 2006 2007>2007 2006.
Пример 11.
Определить число действительных корней уравнения 2х3-24х-19=0.
Решение. Функция f(x)= 2х3-24х-19 непрерывна на всей числовой прямой и имеет производную f’(x)=6x2-24=6(x-2)(x+2).

При x<-2 и x>2 f’(x)>0, а при –2<x<2 f’(x)<0. Следовательно, на промежутках (-:-2],[2;+) функция возрастает, а на промежутке [-2;2] – убывает. Вычислим значения функции в точках х=-3, х=-2, х=2, х=5. Имеем f(-3)=-1<0, f(-2)=13>0, f(2)=-51<0, f(5)=111>0. Так как функция f(x) на концах отрезков [-3;-2], [-2;2], [2;5] принимает значения разных знаков, то на каждом из них имеется только один корень уравнения. Таким образом, уравнение 2х3-24х-19=0 имеет три действительных корня, которые находятся на промежутках (-3;-2), (-2;2), (2;5).
Остальные следствия теоремы Лагранжа можно применять:
— при доказательстве тождеств, в частности при выводе формул элементарной математики;
— при упрощении выражений;
— при разложении алгебраических выражений на множители.
При решении ряда таких задач на некотором промежутке рассматривается либо одна функция f(x), такая, что ее производная f’(x)=0 и, следовательно, функция постоянна, т.
 е. имеет вид
f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x),
и делается вывод, что f(x)=g(x)+c (c — постоянная). Эту
постоянную находят, положив х равным некоторому
значению х1.
е. имеет вид
f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x),
и делается вывод, что f(x)=g(x)+c (c — постоянная). Эту
постоянную находят, положив х равным некоторому
значению х1.Пример 12. Вывести формулу <Рисунок61>.
Решение. Функция f(x)= <Рисунок62> непрерывна на всей числовой прямой. Найдем производную этой функции f’(x)=2sinxcosx-sin2x=sin2x-sin2x. f’(x)=0 для любого действительного значения х, следовательно, на основании условия постоянства функции можно сделать вывод, что функция f(x) постоянна, т.е. f(x)=c. Для определения постоянной c положим х=0 и получим f(0)=c, т.е. sin20-0,5+0,5cos0=c. Таким образом, с=0 и значит f(x)=0, откуда и получим <Рисунок62>=0, или <Рисунок61>.
Пример 13. Доказать, что arctgx=arcsin<Рисунок63> при x<0.

Решение. Рассмотрим две непрерывные на промежутке (-;0] функции f(x)=arctgx и g(x)=arcsin<Рисунок64>, тогда они непрерывны на любом отрезке [b;0]. Найдем производные этих функций.
<Рисунок65>, <Рисунок66>. Так как при x<0 |x|=-x, то <Рисунок67> и тогда f’(x)=g’(x) внутри отрезка [b;0]. На основании следствия 2 имеем f(x)=g(x)+c, где с – постоянная. Для определения с положим, например, х=-1, что дает arctg(-1)=arcsin<Рисунок69>, то есть <Рисунок68> Итак, получим arctgx=arcsin<Рисунок63> при x<0.
Пример 14. Доказать тождество
<Рисунок70>
Решение. Заметим, что <Рисунок71>, <Рисунок72> для любого действительного х и функции <Рисунок73>, <Рисунок74> непрерывны на всей числовой прямой.
 Имеем <Рисунок75>,
Имеем <Рисунок75>,<Рисунок76>.
1) Рассмотрим функцию F(x)=f(x)+g(x), x (-;-1) (0;1).
F(x)= <Рисунок77>, а F’(x)=f’(x)+g’(x)= <Рисунок78>. Если x (-;-1), то |х2-1|=х2-1, |х|=-х и F’(x)=0. Если x (0;1), то |х2-1|=-(х2-1), |х|=х и F’(x)=0. На основании условия постоянства функции F(x)=c, то есть <Рисунок79>. На каждом из рассматриваемых промежутков определим с, положив, например, х=<Рисунок80> и x=<Рисунок81>.
<Рисунок82>, cледовательно, с=.
<Рисунок83>, следовательно, с=0. Имеем: <Рисунок84> при x (-;-1), <Рисунок85> при x (0;1).
2) Рассмотрим функцию G(x)=f(x)-g(x), x (-1;0) (1; +).
<Рисунок86>, <Рисунок87>.
Если x (-1;0), то |х2-1|=-(х2-1), |x|=-x и G’(x)=0.

Если x (1; +), то |х2-1|=х2-1, |x|=x и G’(x)=0. Тогда на указанных промежутках функция G(x) постоянна, т.е. <Рисунок88>. Положим x=<Рисунок80> и x=<Рисунок81>, получим <Рисунок89>, следовательно, с=; <Рисунок90>, тогда с=0.
Имеем: <Рисунок91> при x (-1;0), <Рисунок92> при x (1;+ ).
3) Вычислим значения f(x) и g(x) при х=± 1 и х=0.
f(-1)=arccos(-1)=, g(-1)=arcsin0=0; следовательно, при х=-1 f(x)=+g(x), то есть <Рисунок93>. <Рисунок94>, <Рисунок95>, следовательно, при х=0 f(x)=-g(x), то есть <Рисунок96>. f(1)=arccos1=0, g(1)=arcsin0=0, следовательно, при х= 1 f(x)=g(x), то есть <Рисунок97>.
Таким образом, данное тождество доказано для всех действительных х.
Пример 15. Разложить на множители выражение
y2(x-z)+x2(z-y)+z2(y-x).

Решение. На данное выражение будем смотреть как на функцию от переменной х: f(x)=y2(x-z)+x2(z-y)+z2(y-x).
Найдем f’(x).
f’(x)=y2+2x(z-y)-z2=y2-z2-2x(y-z)=(y-z)(y+z)-2x(y-z)=(y-z)(y+z-2x).
Будем считать, что (y-z)(y+z-2x) есть производная некоторой другой функции g(x), при этом множитель (y-z) будем рассматривать как постоянную, вынесенную при дифференцировании за знак производной, т.е.
g’(x)=(y-z)((y+z)-2x). В качестве функции g(x) можно взять g(x)=(y-z)((y-z)x-x2).
Так как функции f(x) и g(x) непрерывны и дифференцируемы на всей числовой прямой и f’(x)=g’(x), то по следствию 2 f(x)=g(x)+c, где с не зависит от х, но, возможно, зависит от y и z. Имеем y2(x-z)+x2(z-y)+z2(y-x)=(y-z)((y+z)x-x2)+c.
 Найдем с, полагая в этом равенстве, например, х=0.
Имеем yz2-zy2=c. Тогда f(x)=g(x)+yz2-zy2,
то есть
Найдем с, полагая в этом равенстве, например, х=0.
Имеем yz2-zy2=c. Тогда f(x)=g(x)+yz2-zy2,
то естьf(x)=(y-z)((y+z)x-x2)+yz2-zy2=(y-z)(xy+xz-x2)-yz(y-z)=(y-z)(xy-x2+xz-yz)=(y-z)(x(y-x)-z(y-x))=(y-z)(y-x)(x-z).
Итак, y2(x-z)+x2(z-y)+z2(y-x)=(y-z)(y-x)(x-z).
Рисунки
Исчисление— Производная квадратного корня от X
исчисление — Производная квадратного корня от X — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 11к раз
$ \ begingroup $Хотите улучшить этот вопрос? Добавьте подробности и проясните проблему, отредактировав этот пост.

Закрыт 5 лет назад.
Учитывая $ y = \ sqrt x $ и ничего более, используя формулу предела $$ f ‘(x) = \ lim_ {h \ to0} \ frac {f (x + h) -f (x)} { h} $$ (то есть, f, простое число x, равно пределу стремления h к нулю с уравнением ((f суммы x и h) минус (функция x)) по h)
как нам преобразовать (не оценивать) в нотацию Лейбница, $ \ frac {dy} {dx} $?
У меня здесь много проблем, и я ненавижу исключать радикалы из знаменателей.Кто-нибудь проведет меня через это?
(Также, что такое MathJaX?)
Вопрос 22 на странице 107 книги из этой задачи здесь
Создан 11 сен.
Нефер00711 золотой знак11 серебряный знак55 бронзовых знаков
$ \ endgroup $ 3 $ \ begingroup $Вот как оценить лимит, если вы об этом спрашиваете: $$ \ begin {align} \ lim_ {h \ to 0} \ dfrac {f (x + h) -f (x)} {h} & = \ lim_ {h \ to 0} \ dfrac {\ sqrt {x + h} — \ sqrt {x}} {h} \\ & = \ lim_ {h \ to 0} \ dfrac {\ sqrt {x + h} — \ sqrt {x}} {h} \ dfrac {\ sqrt {x + h} + \ sqrt {x}} {\ sqrt {x + h} + \ sqrt {x}} \\ & = \ lim_ {h \ to 0} \ dfrac {h} {h (\ sqrt { x + h} + \ sqrt {x})} \\ & = \ lim_ {h \ to 0} \ dfrac {1} {(\ sqrt {x + h} + \ sqrt {x})} \\ & = \ dfrac {1} {2 \ sqrt {x}} \ end {align} $$
Полезно помнить, что два величайших математических трюка — это умножение на 1 доллар и сложение на 0 долларов.
 Выше я просто умножил на особенно полезную версию числа 1 $.
Выше я просто умножил на особенно полезную версию числа 1 $.Создан 11 сен.
пользователь 26935122911 серебряных знаков33 бронзовых знака
$ \ endgroup $ $ \ begingroup $Мы хотим оценить
$$ \ lim_ {h \ rightarrow 0} \ frac {\ sqrt {x + h} — \ sqrt {x}} {h}
$Умножьте верхнюю и нижнюю на $ \ sqrt {x + h} + \ sqrt {x} $, чтобы найти, что это равно
.$ \ lim_ {h \ rightarrow 0} \ frac {x + hx} {h (\ sqrt {x + h} + \ sqrt {x})} = \ lim_ {h \ rightarrow 0} \ frac {h} {h ( \ sqrt {x + h} + \ sqrt {x})}
$Отмена $ h $ сверху и снизу, это
$$ \ lim_ {h \ rightarrow 0} \ frac {1} {\ sqrt {x + h} + \ sqrt {x}} = \ frac {1} {2 \ sqrt {x}}
$Создан 11 сен.
$ \ endgroup $ $ \ begingroup $
$$ f ‘(x) = \ frac {dy} {dx} $$ for $$ y = f (x) $$ Это два разных способа написать одно и то же.Преобразование не требуется, равно как и «5 долларов» нужно преобразовать в римскую цифру « V ».
Просто выберите свое оружие.
Создан 12 сен.
Математика Адам3,09911 золотых знаков1414 серебряных знаков3636 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Почему бы нам не найти общую форму правила власти, а затем решить вашу проблему? позволять $$ f (x) = x ^ n $$ где $ n $ — любое действительное число, давайте найдем $ \ frac {dy} {dx} $ или аналогично $ f ‘$, используя уравнение: $$ f ‘(x) = \ frac {dy} {dx} = \ lim \ limits_ {h \ to 0} \ left (\ frac {f (x + h) -f (x)} {h} \ right ) $$ $$ = \ lim \ limits_ {h \ to 0} \ left (\ frac {(x + h) ^ n — x ^ n} {h} \ right) $$ $$ = \ lim \ limits_ {h \ to 0} \ left (\ frac {\ sum_ {r = 0} ^ {n} \ left ({{n} \ choose {r}} x ^ {nr} h ^ r \ right) — x ^ n} {h} \ right) $$ $$ = \ lim \ limits_ {h \ to 0} \ left (\ frac {(x ^ n + nx ^ {n-1} h.
 {\ frac {1} {2}}} = \ frac {1} {2 \ sqrt {x}} $$
{\ frac {1} {2}}} = \ frac {1} {2 \ sqrt {x}} $$Создан 12 сен.
ChaoSXDemonChaoSXDemon23711 серебряный знак77 бронзовых знаков
$ \ endgroup $ 4 Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

Принимать все файлы cookie Настроить параметры
исчисление — производная с квадратным корнем
исчисление — производная с квадратным корнем — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack ExchangeMathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу Регистрация займет всего минуту.
Регистрация займет всего минуту.Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 378 раз
$ \ begingroup $Я пытался составить это уравнение в течение некоторого времени, но ничего не вышло.
$ {1/2} $.\ frac {3} {2}}
{1/2} $.\ frac {3} {2}}Создан 05 июн.
M47145M471453,93333 золотых знака1414 серебряных знаков3333 бронзовых знака
$ \ endgroup $ $ \ begingroup $Есть еще один способ, который облегчает жизнь, когда вы сталкиваетесь с продуктом и / или факторами: это логарифмическая дифференциация.2 + 8x-3} {2x \ sqrt x} $$
Создан 05 июня ’16 в 5: 492016-06-05 05:49
Клод ЛейбовичиКлод Лейбовичи173 11 золотой знак 22 серебряных знака 22 бронзовых знака
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

Принимать все файлы cookie Настроить параметры
Доказательство производной квадратного корня
$ x $ — переменная, и ее квадратный корень записывается как $ \ sqrt {x} $.Производная квадратного корня из $ x $ по $ x $ записывается в дифференциальном исчислении следующим образом.
$ \ dfrac {d} {dx} {(\ sqrt {x})}
долл. СШАБыстрая производная функции в режиме ограничения
Согласно определению производной, дифференцирование $ \ sqrt {x} $ по $ x $ может быть записано в форме предельной операции.
$ \ dfrac {d} {dx} {\ sqrt {x}} $ $ \, = \, $ $ \ displaystyle \ large \ lim _ {\ Delta x \, \ to \, 0} {\ normalsize \ dfrac { \ sqrt {x + \ Delta x} — \ sqrt {x}} {\ Delta x}}
долларовТеперь возьмите $ \ Delta x = h $ и преобразуйте уравнение через $ h $ из $ \ Delta x $.

$ \ подразумевает $ $ \ dfrac {d} {dx} {\ sqrt {x}} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ sqrt {x + h} — \ sqrt {x}} {h}}
долларов СШАТеперь давайте вычислим дифференцирование квадратного корня из $ x $ относительно $ x $ по первому принципу.
Оценить предел методом прямой замены
Предел алгебраической функции в радикальной форме может быть вычислен методом прямой подстановки.
$ \ подразумевает $ $ \ dfrac {d} {dx} {\ sqrt {x}} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ sqrt {x + h} — \ sqrt {x}} {h}}
долларов$ = \, \, \, $ \ dfrac {\ sqrt {x + 0} — \ sqrt {x}} {0} $
.$ = \, \, \, $ \ dfrac {\ sqrt {x} — \ sqrt {x}} {0} $
$ = \, \, \, $ \ dfrac {0} {0} $
Вычислено, что предел алгебраической функции неопределен.Таким образом, невозможно найти производную квадратного корня из $ x $ прямым методом пределов подстанции.
долларов 2} {h \ times (\ sqrt {x + h} + \ sqrt {x})}}
2} {h \ times (\ sqrt {x + h} + \ sqrt {x})}}$ = \, \, \, $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {x + hx} {h \ times (\ sqrt {x + h} + \ sqrt {x})}}
долларов США$ = \, \, \, $ $ \ require {cancel} \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cancel {x} + h- \ cancel {x }} {h \ times (\ sqrt {x + h} + \ sqrt {x})}}
долларов$ = \, \, \, $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {h} {h \ times (\ sqrt {x + h} + \ sqrt {x})}}
долларов США$ = \, \, \, $ $ \ require {cancel} \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {\ cancel {h}} {\ cancel {h} \ times (\ sqrt {x + h} + \ sqrt {x})}}
долларов$ \ подразумевает $ $ \ dfrac {d} {dx} {\ sqrt {x}} $ $ \, = \, $ $ \ displaystyle \ large \ lim_ {h \, \ to \, 0} {\ normalsize \ dfrac {1} {\ sqrt {x + h} + \ sqrt {x}}}
долл. СШАОценить предел методом прямой замены
Теперь оцените предел алгебраической функции при приближении $ h $ к $ 0 $ методом прямой подстановки.

$ \ подразумевает $ $ \ dfrac {d} {dx} {\ sqrt {x}} $ $ \, = \, $ $ \ dfrac {1} {\ sqrt {x + 0} + \ sqrt {x}} $
$ \ подразумевает $ $ \ dfrac {d} {dx} {\ sqrt {x}} $ $ \, = \, $ $ \ dfrac {1} {\ sqrt {x} + \ sqrt {x}} $
$ \, \, \, \ следовательно \, \, \, \, \, \, $ $ \ dfrac {d} {dx} {\ sqrt {x}} $ $ \, = \, $ $ \ dfrac {1} {2 \ sqrt {x}}
долларов СШАСледовательно, из первого принципа доказано, что производная квадратного корня из $ x $ равна частному из $ 1 $, умноженному на двукратный квадратный корень из $ x $.
Видео с вопросом: Нахождение производной корневой функции с использованием предельного определения производных
Стенограмма видео
Определите производную функции от 𝑥, равной квадратному корню из двух 𝑥 минус 16, используя определение производной.
Прежде всего напомним определение производной: простое число равно пределу, когда ℎ стремится к нулю of из 𝑥, добавить минус из 𝑓 над ℎ.
 Помните, что чтобы получить 𝑓 из 𝑥 add ℎ, мы просто заменяем 𝑥 на 𝑥 add ℎ в 𝑓 из 𝑥. Это дает нам 𝑓 из сложить ℎ равно квадратному корню из двух, умноженному на 𝑥 добавить ℎ минус 16. Затем мы можем расширить эти скобки, чтобы получить, что 𝑓 из плюс ℎ равно квадратному корню из двух 𝑥 плюс два ℎ минус 16.
Помните, что чтобы получить 𝑓 из 𝑥 add ℎ, мы просто заменяем 𝑥 на 𝑥 add ℎ в 𝑓 из 𝑥. Это дает нам 𝑓 из сложить ℎ равно квадратному корню из двух, умноженному на 𝑥 добавить ℎ минус 16. Затем мы можем расширить эти скобки, чтобы получить, что 𝑓 из плюс ℎ равно квадратному корню из двух 𝑥 плюс два ℎ минус 16.Давайте теперь сделаем эту замену в определении производной.Теперь, отсюда, на самом деле есть небольшой трюк, который мы используем, когда пытаемся найти производную корневой функции по определению. Это то, что мы часто делаем, когда имеем дело с корнями, — умножение на сопряжение. Помните, что сопряжение — это то место, где мы меняем знак в середине двух членов. Но мы также должны умножить знаменатель на то же самое. Таким образом, мы просто умножаем то, что имеем, на единицу и, следовательно, технически ничего не меняем.
Начнем с умножения числителей.Мы можем думать об этом так же, как если бы мы умножили две скобки, содержащие алгебраические термины. Мы можем начать с умножения квадратного корня из двух 𝑥 добавить два ℎ минус 16 на квадратный корень из двух 𝑥 добавить два ℎ минус 16.
 Для этого напомним, что квадратный корень из, умноженный на квадратный корень из, дает нас 𝑎. Таким образом, умножение этих двух членов вместе дает нам то, что у нас есть внутри квадратного корня: два 𝑥 добавить два ℎ минус 16. То же самое применяется, когда мы умножаем квадратный корень из двух минус 16 на квадратный корень из двух минус 16.Но на этот раз перед одним из условий стоит отрицание. Так что нам нужно помнить об этом. Используя те же правила, что и раньше, это дает нам отрицательные два минус 16.
Для этого напомним, что квадратный корень из, умноженный на квадратный корень из, дает нас 𝑎. Таким образом, умножение этих двух членов вместе дает нам то, что у нас есть внутри квадратного корня: два 𝑥 добавить два ℎ минус 16. То же самое применяется, когда мы умножаем квадратный корень из двух минус 16 на квадратный корень из двух минус 16.Но на этот раз перед одним из условий стоит отрицание. Так что нам нужно помнить об этом. Используя те же правила, что и раньше, это дает нам отрицательные два минус 16.Теперь мы также можем умножить отрицательный квадратный корень из двух 𝑥 минус 16 на квадратный корень из двух 𝑥 добавить два ℎ минус 16. Мы можем просто написать это рядом, чтобы показать, что мы умножили их вместе. На самом деле это не упрощает ничего, кроме этого. И наконец, нам нужно умножить квадратный корень из двух 𝑥 добавить два ℎ минус 16 на квадратный корень из двух 𝑥 минус 16.Когда мы это делаем, мы видим, что эти два термина фактически сокращаются. Итак, наш числитель — это просто два 𝑥 сложить два ℎ минус 16 минус два 𝑥 минус 16.

Теперь давайте умножим знаменатели вместе. Мы можем просто записать это как, умноженное на квадратный корень из двух, добавить два минус 16, добавить квадратный корень из двух 𝑥 минус 16. Давайте упростим числитель, расширив эту скобку, умножив ее на отрицательную единицу. Обратите внимание, что минус 16 превращается в плюс 16. Отсюда давайте упростим числитель.Два 𝑥 отменяются двумя отрицательными 𝑥, а отрицательные 16 отменяются добавлением 16. Итак, у нас осталось только два.
И теперь мы замечаем, что мы действительно можем что-то отменить здесь в числителе и знаменателе. У нас есть в числителе и знаменателе. И поскольку приближается к нулю, а не равно нулю, это нормально. И поскольку ℎ в знаменателе умножается на все в знаменателе, мы можем отменить это. Итак, теперь давайте применим предел, когда ℎ приближается к нулю.Единственное ℎ, которое у нас есть, стоит в знаменателе. Итак, мы думаем, что произойдет, когда ℎ приблизится к нулю.
Мы можем сделать это прямой заменой ℎ равным нулю, потому что это непрерывная функция.
 Это оставляет нам два вместо квадратного корня из двух 𝑥 минус 16, прибавляем квадратный корень из двух 𝑥 минус 16. И поскольку в знаменателе у нас есть квадратный корень из двух минус 16, прибавляем квадратный корень из двух 𝑥 минус 16, мы можно записать это как два, умноженные на квадратный корень из двух 𝑥 минус 16.Затем мы замечаем, что два в числителе и два в знаменателе компенсируют друг друга. Итак, у нас остается единица больше квадратного корня из двух 𝑥 минус 16. И это наш окончательный ответ.
Это оставляет нам два вместо квадратного корня из двух 𝑥 минус 16, прибавляем квадратный корень из двух 𝑥 минус 16. И поскольку в знаменателе у нас есть квадратный корень из двух минус 16, прибавляем квадратный корень из двух 𝑥 минус 16, мы можно записать это как два, умноженные на квадратный корень из двух 𝑥 минус 16.Затем мы замечаем, что два в числителе и два в знаменателе компенсируют друг друга. Итак, у нас остается единица больше квадратного корня из двух 𝑥 минус 16. И это наш окончательный ответ.Одна из важных вещей, которую следует отметить из этого видео, заключается в том, что когда мы находим производную корневой функции, используя определение производной, нам часто придется умножать ее на сопряжение. А дальше это был просто случай некоторых манипуляций с алгеброй и применения предела.
Производная квадратного корня из синуса x на основе первых принципов
Недавно я получил несколько писем от читателей, спрашивающих, как найти производную различных тригонометрических функций, используя первые принципы.
 Один из них чуть не попросил в ответ статью. Барун написал:
Один из них чуть не попросил в ответ статью. Барун написал:Как вы оцениваете использование 1-го принципа дифференциации?
Обычно в большинстве учебников перечисляются производные триггерных функций и говорится что-то вроде «они были найдены путем дифференцирования по первым принципам», но на самом деле не объясняется, как.Давай выясним.
Во-первых, немного предыстории.
Производная от Первых принципов
Многие концепции дифференциации и интеграции были известны и понятны древнегреческим математикам, но нам пришлось ждать до времен Исаака Ньютона и Готфрида Лейбница для мышления (и алгебры), которое мы используем сегодня.
Чтобы найти производную («скорость изменения») функции f ( x ), нам нужно найти следующий предел:
Используя это, мы можем найти производные от полиномиальных выражений, таких как:
(См. Несколько примеров на этой странице: Производная от Первых Принципов)
Я использую h вместо Δ x или δ x для облегчения чтения и соответствия моим обозначениям в производной от первых принципов.

Если мы просто подставим h = 0, мы всегда получим, что, конечно, не определено. Нам нужно сделать некоторую алгебру, чтобы привести дробь в форму, в которой мы можем вычислить предел, поскольку h приближается к 0.
Давайте сначала рассмотрим более простой пример тригонометрии, прежде чем пытаться вычислить производную от √ (sin x ).
A. Производная греха (
x ) по Первым принципамНам нужно несколько результатов, прежде чем мы сможем найти эту производную.
(A1) Предел греха θ / θ как x → 0
Во-первых, нам нужен этот общеизвестный предел.
Сначала мы рисуем график y = sin θ / θ и видим, что предел функции, когда θ приближается к 0, равен 1. (Конечно, на графике есть «дыра» при θ = 0. )
Итак имеем:
Вы можете увидеть результат здесь.
(A2) Разница двух синусов
Нам также понадобится следующее тригонометрическое тождество.
 (Вы можете доказать это, развернув синус и косинус справа.)
(Вы можете доказать это, развернув синус и косинус справа.)(А3) Фракция по фракции
Это всегда сбивает студентов с толку. Разделить пополам — 2.
Это правда, потому что:
Включено с производной синуса x
Теперь мы готовы найти производную греха ( x ) из первых принципов.
Если оставить в стороне предел, наш первый шаг — оценить дробь с f ( x ) = sin x .
С правой стороны у нас разница в 2 синуса, поэтому мы применяем формулу в (A2) выше:
Упрощение правой части дает:
Теперь, чтобы собрать все вместе и рассмотреть предел:
Мы используем (3), дробь на дробь, чтобы вывести эти 2 вперед вниз:
Теперь предел продукта — это произведение пределов, поэтому мы можем записать это как:
Итак, первый предел имеет вид Предел греха θ / θ , который мы встретили в (A1) выше.

Мы знаем, что он имеет значение 1.
Для правого предела мы просто получаем cos x .
Таким образом, можно сделать вывод, что
B. Производная квадратного корня из греха
x из первых принциповПрежде чем мы начнем, нам нужно установить некоторые важные алгебраические тождества.
(B1) Рационализация знаменателя
Мы стремимся удалить любые квадратные корни из знаменателя. Умножаем верхнюю и нижнюю часть дроби на , сопряженное с знаменателя.Напомним, что сопряжение (3 + √2) равно (3 — √2).
Пример: Мы стремимся рационализировать знаменатель числа
.Умножение верха и низа на (3 — √2) дает:
(B2) Рационализация числителя
Это то же самое, что и B1 , но мы пытаемся удалить квадратные корни из верхних дроби. Мы делаем это, умножая верх и низ на конъюгат верха.

(B3) Разлагающий синус суммы
Это одна из первых тригонометрических идентичностей, которые мы узнали:
sin (A + B) = sin A cos B + cos A sin B.
(B4) Предел (cos θ — 1) / θ как x → 0
Вот график
Из графика видно, что предел равен 0.
Итак, мы можем написать:
Теперь о производной от √ (sin x ) из первых принципов
Имеем f ( x ) = √ (sin x )
Итак, применив формулу первой производной к этой функции, наша производная будет:
Далее нам нужно рационализировать числитель .(Почему? Получить выражение, предел которого x приближается к 1, возможно.)
Оставляя на данный момент предел, правая часть эквивалентна:
Умножение дает:
Раскладывая этот грех ( x + h ) сверху, получаем:
Мы можем разложить верхнюю часть на множители и записать это как:
Теперь мы готовы рассмотреть предел, поскольку x приближается к 0.

Внизу имеем:
Учитывая то, что осталось, первый член в числителе:
Ранее в B4 мы нашли
Итак, мы можем сделать вывод
Остается второй член:
Ранее в A1 мы обнаружили, что
Итак, мы можем сделать вывод
Собирая все вместе, получаем:
Я надеюсь, вы понимаете, почему Ньютон и Лейбниц стремились найти набор непротиворечивых правил, чтобы им не приходилось проходить через все это каждый раз, когда они хотели найти производную!
График
y = √sin θЧтобы закончить, давайте посмотрим, как выглядит график y = √ (sin θ), показанный здесь синим цветом (с y = sin θ, показанным зеленым для сравнения).Примечание y = √ (sin θ) не определено для n π <θ <2 n π.
См. 14 комментариев ниже.
Более простой способ вычисления производной сложных логарифмических функций
Математика часто может показаться сложной.
 Иногда выглядит просто ошеломляющим, даже если вы действительно знаете, как это сделать. Этот фактор визуального запугивания порождает беспокойство, вызывает першение в мозгах на тестах и, в конечном итоге, отвлекает многих людей от математики.2-x}} \ вправо) \)
Иногда выглядит просто ошеломляющим, даже если вы действительно знаете, как это сделать. Этот фактор визуального запугивания порождает беспокойство, вызывает першение в мозгах на тестах и, в конечном итоге, отвлекает многих людей от математики.2-x}} \ вправо) \)Подсказка: есть простой и сложный способ решения этой проблемы. Используйте простой способ.
Эта функция, честно говоря, выглядит устрашающе. Он полон экспонатов, натуральных бревен и квадратных корней, прижатых друг к другу в каком-то ночном тревожном сне. Подсказка дает проблеск комфорта, если только мы сможем найти «легкий путь». Если нет, мы всю ночь будем выполнять правила цепочки внутри правил продукта внутри правил отношения частных внутри правил цепочки, время истечет и, возможно, провалит экзамен.В принципе, если вы видите такую проблему и не знаете, в чем суть трюка, вам лучше полностью ее пропустить.
Но не будем этого делать! Уловка состоит в том, чтобы использовать правила логарифмов для расширения или переписать функцию до того, как мы даже упомянем слово «производная».
 Я сказал это. Чтобы кратко рассмотреть правила логарифмов (и \ (ln \), который является особым типом логарифма), важными из них являются:
Я сказал это. Чтобы кратко рассмотреть правила логарифмов (и \ (ln \), который является особым типом логарифма), важными из них являются:Первое правило говорит нам, как расширить журнал продукта, второе — журнал частного, а третье — журнал степени.Как это помогает? Обратите внимание, что наша задача состоит из логарифма произведения множителей в числителе, деленного на произведение некоторых других множителей в знаменателе. Мы можем определить правило составного логарифма , которое говорит нам, как подходить к подобным ситуациям с умножением и делением нескольких факторов:
Обратите внимание, что множители в числителе становятся логарифмами, которые складываются, а множители в знаменателе становятся логарифмами, которые вычитаются.Теперь давайте посмотрим на факторы в нашей проблеме:
Как видите, у нас есть три множителя в числителе и два в знаменателе. Раскладывая сразу весь этот логарифм, получаем:
Обратите внимание, что последние два члена отрицательны, потому что их множители взяты из знаменателя.
 Мы могли бы остановиться на этом, но мы также можем еще больше упростить, переписав квадратный корень в последнем члене как рациональную экспоненту, используя правило логарифма степеней (третье в нашем списке правил) для первого, второго и последний член и с учетом того факта, что \ (ln \) и \ (e \) инвертируют друг друга в третьем члене:
Мы могли бы остановиться на этом, но мы также можем еще больше упростить, переписав квадратный корень в последнем члене как рациональную экспоненту, используя правило логарифма степеней (третье в нашем списке правил) для первого, второго и последний член и с учетом того факта, что \ (ln \) и \ (e \) инвертируют друг друга в третьем члене:Хорошо.Мы сделали все, что могли (обратите внимание, что четвертый член, имеющий журнал внутри журнала, не может быть еще более упрощен). Теперь пора заняться производными. Это будет намного легче различить, потому что у нас есть набор терминов, которые добавляются и вычитаются вместо умножения и деления. Это означает: до свидания, неприятный продукт и частные правила. Тем не менее, цепное правило нам все еще понадобится для первых двух и последних двух членов. Цепное правило для логарифмов — это просто частный случай цепного правила, которое вы выучили в начале семестра.Но если это не сразу очевидно, вот он:
Применяя это правило к каждому члену, получаем:
Собирая все вместе, получаем окончательный ответ:
Понял? Это всего лишь еще один пример того, как изучение математики помогает нам разбивать большие, пугающие проблемы на несколько более мелких и решаемых.
Примеры правил цепочки Что может облегчить жизнь, чем это?
Что может облегчить жизнь, чем это?— Calculus How To
Посмотрите видео с парой примеров цепных правил или прочтите ниже:
Не можете посмотреть видео? Кликните сюда.Следующие примеры правил цепочки показывают вам, как различать (находить производную) многие функции, которые имеют «внутреннюю функцию» и «внешнюю функцию». В качестве примера возьмем функцию y = √ (x 2 — 3). Внутренняя функция — это в круглых скобках : x 2 -3. Внешняя функция — √ (x).
Проблема заключается в распознавании тех функций, которые можно различить с помощью правила. Решение? Взгляните на следующие примеры правила цепочки, которые иллюстрируют различные способы внешнего вида внутренних и внешних функций. Если ваша производная имеет внутреннюю и внешнюю функции, вы можете использовать цепное правило.
Примеры правил цепочки: содержание
Формальное определение цепного правила:
Это не очень поможет, если вы еще не очень хорошо с ним знакомы.
Что нужно, так это более простой и интуитивно понятный подход!
Когда вы применяете одну функцию к результатам другой функции, вы создаете композицию функций. Например, предположим, что у вас есть функции:
Состав g (f (x)), который также записывается как (g ∘ f) (x), будет (x 2-3 ) 2 . Это указывает на то, что функция f (x), внутренняя функция, должна быть вычислена до того, как будет найдено значение g (x), внешней функции.

Чтобы дифференцировать состав функций, цепное правило разбивает вычисление производной на серию простых шагов.
Примеры правил цепочки: общие шаги
Шаг 1: Определите внутренние и внешние функции .
Например, пусть составная функция имеет вид y = √ (x 4 — 37). Внутренняя функция — это в круглых скобках : x 4 -37. Внешняя функция — это √, которая также совпадает с рациональным показателем ½.Шаг 2: Сначала выделите внешнюю функцию .
√ (x 4 — 37) равно (x 4 — 37) 1/2 , что при дифференцировании (только внешняя функция!) Равно ½ (x 4 — 37) (1 — ½) или ½ (x 4 — 37) (-½).Шаг 3: Определите внутреннюю функцию .
Производная x 4 -37 равна 4x (4-1) -0, что также равно 4x 3 .Шаг 4.
 Умножьте шаг 3 на производную внешней функции.
Умножьте шаг 3 на производную внешней функции.
Умножение 4x 3 на ½ (x 4 — 37) (-½) дает 2x 3 (x 4 — 37) (-½) , что при вычислении составляет 2x 3 / (x 4 — 37) (-½) или 2x 3 / √ (x 4 — 37).Вот и все!
Дифференциация с использованием цепного правила обычно требует некоторой интуиции. Чем чаще вы применяете цепное правило к разным задачам, тем легче становится распознать, как применять правило.В этом разделе показано, как дифференцировать функцию y = 3x + 1 2 с помощью правила цепочки. Однако этот метод может быть применен к широкому спектру функций с любой внешней экспоненциальной функцией (например, x 32 или x 99 .
Шаг 1: Определите внешнюю функцию . В данном случае внешняя функция равна x 2 . Примечание: оставьте в уравнении 3x + 1. Просто пока игнорируйте это.
 Обратите внимание, что я использую букву D для обозначения производной.
Обратите внимание, что я использую букву D для обозначения производной.
D (3x + 1) 2 = 2 (3x + 1) 2-1 = 2 (3x + 1)Шаг 2: Определите внутреннюю функцию .В этом примере внутренняя функция равна 3x + 1.
D (3x + 1) = 3.Шаг 3: Объедините ваши результаты из Шага 1 2 (3x + 1) и Шага 2 (3).
= 2 (3x + 1) (3)Шаг 4: Упростите свою работу, если это возможно. В этом примере 2 (3x +1) (3) можно упростить до 6 (3x + 1).
Вот и все!
Совет: этот метод также можно применить к внешним функциям, которые являются квадратными корнями. Например, чтобы дифференцировать
√ X + 1
: (x + 1) ½ — внешняя функция, а x + 1 — внутренняя функция.На первый взгляд дифференцирование функции y = sin (4x) может показаться запутанным. Знать, с чего начать, — это половина дела. Цепное правило в исчислении — это один из способов упростить дифференцирование.
 В этом разделе объясняется, как дифференцировать функцию y = sin (4x) с помощью цепного правила. Однако этот метод может быть применен к любой аналогичной функции с синусом, косинусом или тангенсом.
В этом разделе объясняется, как дифференцировать функцию y = sin (4x) с помощью цепного правила. Однако этот метод может быть применен к любой аналогичной функции с синусом, косинусом или тангенсом.Шаг 1 Дифференцируйте внешнюю функцию , используя таблицу производных .В этом случае внешней функцией является синусоидальная функция. Примечание: оставьте в уравнении 4x, но пока не обращайте на него внимания. Производная sin равна cos, поэтому:
D (sin (4x)) = cos (4x).Шаг 2 Дифференцируйте внутреннюю функцию , используя таблицу производных . В этом примере внутренняя функция равна 4x.
D (4x) = 4Шаг 3. Объедините ваши результаты из Шага 1 (cos (4x)) и Шага 2 (4).
= соз (4х) (4)Step 4 Упростите свою работу, если это возможно.В этом примере cos (4x) (4) нельзя упростить, но более традиционный способ записи cos (4x) (4) — 4cos (4x).

Вот и все!
Число e (число Эйлера), эквивалентное примерно 2,71828, является математической константой и основанием многих натуральных логарифмов. Производная от e x равна e x , но вы редко встретите такую простую форму e в исчислении. Чаще вы увидите, что e возведено в полином или другую более сложную функцию. Дифференцирование функций, содержащих e, например e 5x 2 + 7x-19 , возможно с помощью цепного правила.Чтобы использовать правило цепочки, вы должны идентифицировать внешнюю функцию и внутреннюю функцию.
Шаг 1 Сначала выделите внешнюю функцию . В этом примере внешняя функция — e x . Примечание: оставьте в уравнении 5x 2 + 7x — 19. Просто пока игнорируйте это. Производная от e x равна e x , поэтому:
D (e 5x 2 + 7x — 19 ) = e 5x 2 + 7x — 19 .Шаг 2 Выделите внутреннюю функцию , которая равна
5x 2 + 7x — 19.
D (5x 2 + 7x — 19) = (10x + 7)Шаг 3. Объедините результаты из Шага 1 (e 5x 2 + 7x — 19 ) и Шага 2 (10x + 7).
= e 5x 2 + 7x — 13 (10x + 7)Шаг 4 Перепишите уравнение и, если возможно, упростите. В этом примере нет необходимости в упрощении, но более традиционно уравнение записывается следующим образом:
(10x + 7) e 5x 2 + 7x — 19Вот и все!
Совет. Это правило также можно использовать для различения логарифмов с натуральным и десятичным десятичным основанием (D (ln x) = (1 / x) и D (log x) = (1 / x) log e.
Перемноженные константы добавляют еще один уровень сложности к дифференциации с помощью правила цепочки . Функции, которые содержат перемноженные константы (например, y = 9 cos √x, где «9» — умноженная константа), не нуждаются в дифференцировании с использованием правила произведения.
 Фактически, чтобы дифференцировать перемноженные константы, вы можете игнорировать константу во время дифференцирования.
Фактически, чтобы дифференцировать перемноженные константы, вы можете игнорировать константу во время дифференцирования.Пример задачи: Продифференцируйте y = 7 tan √x, используя цепное правило.
Шаг 1
Выделите внешнюю функцию , игнорируя константу.Внешняя функция в этом примере — «загар». (Примечание: оставьте внутреннюю функцию в уравнении (√x), но пока проигнорируйте и это) Производная tan x равна sec 2 x, поэтому:
D (tan √x) = sec 2 √xШаг 2 Определите внутреннюю функцию , которая равна
√x.
D (√x) = (1/2) X -½Шаг 3. Объедините результаты из Шага 1 (сек. 2 √x) и Шага 2 ((½) X — ½ ).
= (сек 2 √x) ((½) X — ½ ).Шаг 4
Добавьте возвращенную константу в уравнение.
7 (сек 2 √x) ((1/2) X — ½ ).Шаг 5 Перепишите уравнение и, если возможно, упростите.

7 (сек 2 √x) ((½) X — ½ ) =
7 (сек 2 √x) ((½) 1 / X ½ ) =
7 (сек 2 √x) / 2√xВот и все!
Цепное правило можно использовать для различения многих функций, у которых число возведено в степень.Ключ в том, чтобы искать внутреннюю функцию и внешнюю функцию.
Пример задачи: дифференцировать y = 2 cot x , используя цепное правило.
Шаг 1 Определите внешнюю функцию . Внешняя функция в этом примере — 2 x . Примечание: оставьте кроватку x в уравнении, но пока просто игнорируйте внутреннюю функцию. Производная 2 x равна 2 x ln 2, поэтому:
D (2 cot x ) = 2 cot x (ln 2)Шаг 2 Выделите внутреннюю функцию , которая равна
.
cot x.Производная от cot x равна -csc 2 , поэтому:
D (cot 2) = (-csc 2 )Шаг 3.
 Объедините результаты из Шага 1 (2 cot x ) (ln 2) и Step 2 ((-csc 2 )).
Объедините результаты из Шага 1 (2 cot x ) (ln 2) и Step 2 ((-csc 2 )).
= (2 кроватка x (ln 2) (-csc 2 ) x).Шаг 4 Перепишите уравнение и, если возможно, упростите. В этом примере отрицательный знак заключен во второй набор круглых скобок. Более традиционно его можно переписать как:
-2 cot x (ln 2) (csc 2 x)Вот и все!
Другой способ записать квадратный корень — это показатель степени 1/2.Этот показатель ведет себя так же, как целочисленный показатель при дифференцировании — он уменьшается с 1 до –½, а член умножается на 1/2. Следовательно, sqrt (x) различается следующим образом:
d / dx sqrt (x) = d / dx x (1/2) = (1/2) x (-½)Чтобы дифференцировать более сложную функцию извлечения квадратного корня в исчислении, используйте правило цепочки . Это способ разбить сложную функцию на более простые части, чтобы дифференцировать ее по частям.
 Затем результаты объединяются для получения окончательного результата:
Затем результаты объединяются для получения окончательного результата:
dF / dx = dF / dy * dy / dx
, где y — это просто метка, которую вы используете для представления части функции, например, внутри квадратного корня.Пример задачи : дифференцировать функцию квадратного корня sqrt (x 2 + 1).
Шаг 1. Запишите функцию как (x 2 +1) (½) . Обозначьте функцию внутри квадратного корня как y, то есть y = x 2 +1.
Шаг 2: дифференцировать и (1/2) от и .
d / dy y (½) = (½) y (-½)Шаг 3: дифференцируйте y по отношению к x .
dy / dx = d / dx (x 2 + 1 ) = 2xШаг 4: Умножьте результаты Шага 2 и Шага 3 в соответствии с правилом цепочки и замените y на x.
2x * (½) y (-½) = x (x 2 + 1 ) (-½)Шаг 5: Упростите ответ, записав его в виде квадратных корней.
 Помните, что функция, возведенная в степень -1, эквивалентна 1 по функции, а показатель степени ½ такой же, как функция квадратного корня.
Помните, что функция, возведенная в степень -1, эквивалентна 1 по функции, а показатель степени ½ такой же, как функция квадратного корня.
x (x 2 + 1) (-½) = x / sqrt (x 2 + 1 )Совет: Независимо от того, насколько сложна функция внутри квадратного корня, вы можете дифференцировать ее, повторяя применение правила цепочки.
Общее правило мощности — это частный случай цепного правила, используемое для работы степенных функций вида y = [u (x)] n . Общее правило мощности гласит, что если y = [u (x)] n ], то dy / dx = n [u (x)] n — 1 u ‘(x). Более простая форма правила гласит, что если y — u n , то y = nu n — 1 * u ’.Может показаться подавляющим, что существует множество правил дифференциации, но вы можете думать об этом так: на самом деле существует только одно правило дифференциации — использование определения предела. Технически вы можете вычислить производную для любой функции, используя это определение.
 Однако в действительности определение иногда бывает длинным и обременительным для работы (не говоря уже о том, что легко допустить ошибку). Вот почему математики разработали серию сокращений или правил для производных, таких как общее правило мощности.
Однако в действительности определение иногда бывает длинным и обременительным для работы (не говоря уже о том, что легко допустить ошибку). Вот почему математики разработали серию сокращений или правил для производных, таких как общее правило мощности.Пример вопроса: Какая производная y = √ (x 2 — 4x + 2)?
Шаг 1: Перепишите квадратный корень в степень ½:
y = (x 2 — 4x + 2) ½Шаг 2: Вычислите производную для «внутренней» части функции , которая равна (x 2 — 4x + 2). Вы можете найти производную этой функции, используя правило мощности:
f ‘(x 2 — 4x + 2) = 2x — 4)Шаг 3: Перепишите уравнение в виде общего правила мощности (другими словами, выпишите общее правило мощности, подставив свою функцию в нужные места).Включите производную, которую вы вычислили на шаге 1:
f ‘= ½ (x 2 — 4x + 2) ½ — 1 (2x — 4)
= f’ = ½ (x 2 -4x + 2 ) — ½ (2x — 4)Шаг 4: (Необязательно) Перепишите с использованием алгебры:
(2x — 4) / 2√ (x 2 — 4x + 2)Вот и все!
Совет: Самая сложная часть использования общего правила мощности — это распознать, когда вы по существу пропускаете средние этапы работы над определением предела и сразу переходите к решению.

-

 2-1)/x
2-1)/x Производная степенной функции (степени и корни)
Производная степенной функции (степени и корни) Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.
Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.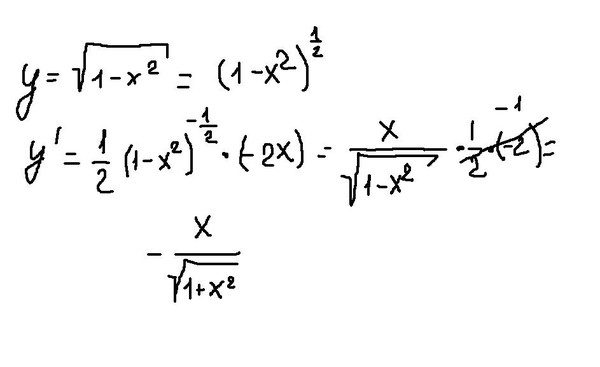 Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =
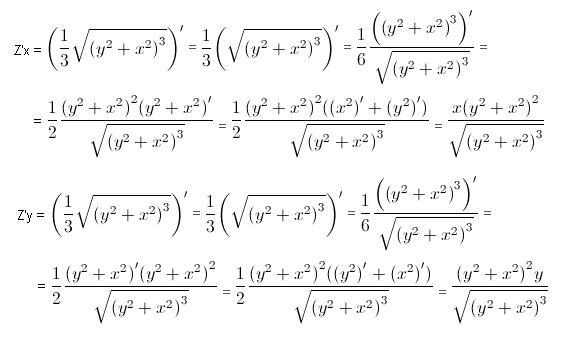
 Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.
Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.

 Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
Для этого пробуем (мысленно или на черновике) вычислить значение выражения при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, многочлен – и есть внутренняя функция:
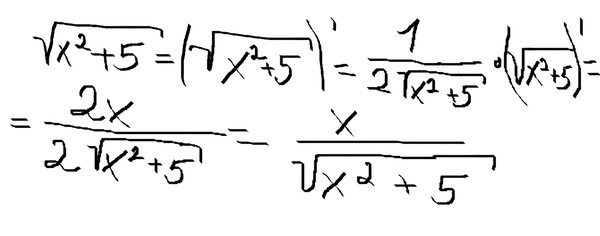 Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).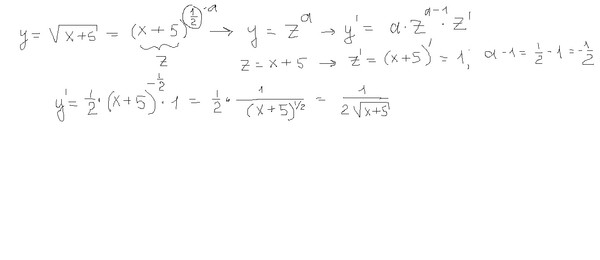 В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
 Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм. К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас. е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой. 
 Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями . В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных:
В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим
и независимую переменную, производная которой равна единице, и константу (число), производная
которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль.
Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как
производную «икса». Получаем следующие значения производных: Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Не забудем также,
что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус: В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем:
В данной функции видим частное, делимое которого — квадратный корень
из независимой переменной. По правилу дифференцирования частного, которое мы повторили
и применили в примере 4, и табличному значению производной квадратного корня получаем: Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной: Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .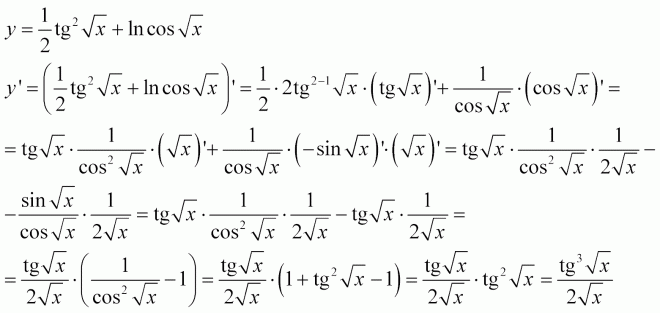
 После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.

 {k_n-1}(x).$
{k_n-1}(x).$ Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем.
Прежде чем воспользоваться основной формулой, степень поднимаем из числителя в знаменатель. Получившуюся в результате вычислений степень с отрицательным показателем снова преобразовываем. Из
всего круга таких задач выделим те, при решении
которых используется теорема Лагранжа и ее
следствия. К ним относятся задачи на
доказательство тождеств, неравенств, вывод
формул тригонометрии, разложение алгебраических
выражений на множители, решение уравнений,
неравенств, систем уравнений, уравнений с
параметрами. При этом можно указать общие методы
решения и некоторые частные приемы.
Из
всего круга таких задач выделим те, при решении
которых используется теорема Лагранжа и ее
следствия. К ним относятся задачи на
доказательство тождеств, неравенств, вывод
формул тригонометрии, разложение алгебраических
выражений на множители, решение уравнений,
неравенств, систем уравнений, уравнений с
параметрами. При этом можно указать общие методы
решения и некоторые частные приемы.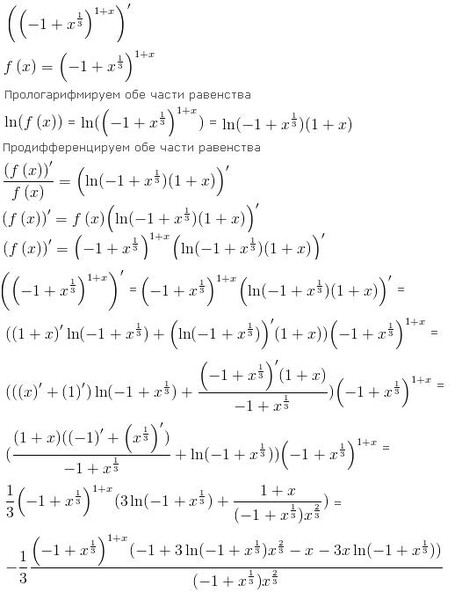
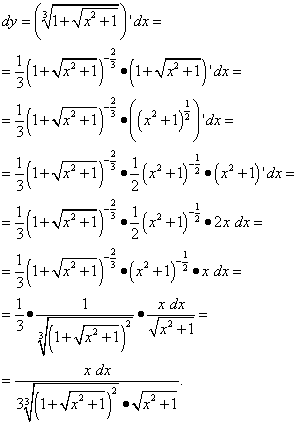
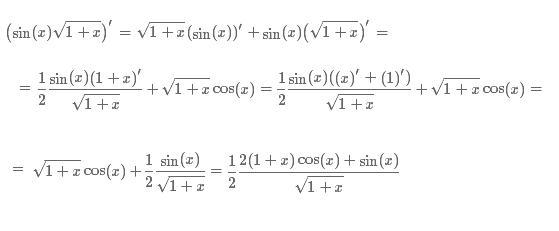 е. <Рисунок13>. Так
как c>1 при b>1, то ec>e и, следовательно, ec-e>0.
Тогда <Рисунок14>, а значит eb-eb>0, т.е. eb>eb
для любого b>1. Таким образом доказано, что ex>=ex
при x>=1.
е. <Рисунок13>. Так
как c>1 при b>1, то ec>e и, следовательно, ec-e>0.
Тогда <Рисунок14>, а значит eb-eb>0, т.е. eb>eb
для любого b>1. Таким образом доказано, что ex>=ex
при x>=1.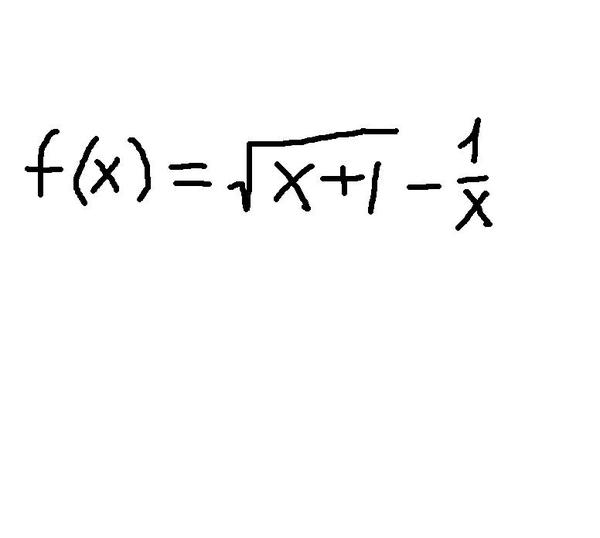 Пусть b – любое
положительное число. Рассмотрим функцию f(x)=
<Рисунок17>, непрерывную на отрезке [a;b] и
имеющую производную <Рисунок18> на интервале
(0;b). По теореме Лагранжа имеем <Рисунок19>,
0<c<b, т.е. <Рисунок20>. А так как при любом с>0 ec>c+1
(доказано в примере 2), то ec-c>1 и,
следовательно, <Рисунок21>. Отсюда получим
<Рисунок22>, а значит <Рисунок23> для любого
b>0. Таким образом, <Рисунок24> при x>0, т.е.
<Рисунок25>, следовательно, равенство
<Рисунок16> не выполняется ни при каком x>0. А,
значит, уравнение <Рисунок16> не имеет
действительных положительных корней.
Пусть b – любое
положительное число. Рассмотрим функцию f(x)=
<Рисунок17>, непрерывную на отрезке [a;b] и
имеющую производную <Рисунок18> на интервале
(0;b). По теореме Лагранжа имеем <Рисунок19>,
0<c<b, т.е. <Рисунок20>. А так как при любом с>0 ec>c+1
(доказано в примере 2), то ec-c>1 и,
следовательно, <Рисунок21>. Отсюда получим
<Рисунок22>, а значит <Рисунок23> для любого
b>0. Таким образом, <Рисунок24> при x>0, т.е.
<Рисунок25>, следовательно, равенство
<Рисунок16> не выполняется ни при каком x>0. А,
значит, уравнение <Рисунок16> не имеет
действительных положительных корней.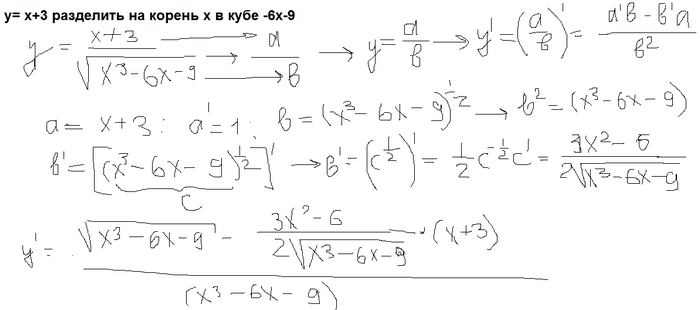 Предположим, что
уравнение имеет не менее трех различных
действительных корней х1, х2, х3,
принадлежащих промежутку (0,2), и пусть x1<x2<x3.
Тогда они являются нулями функции <Рисунок27>,
т.е. f(x1)=f(x2)=f(x3)=0. На каждом из
отрезков [x1;x2], [x2;x3] для
функции f(x) выполняются условия теоремы Лагранжа,
следовательно, существуют числа c1 и с2
из интервалов (х1;х2), (х2;х3)
соответственно, такие, что <Рисунок28> и
<Рисунок29>. А так как f(x1)=f(x2)=f(x3)=0,
то f’(c1)=0 и f’(c2)=0, причем с1с2.
Предположим, что
уравнение имеет не менее трех различных
действительных корней х1, х2, х3,
принадлежащих промежутку (0,2), и пусть x1<x2<x3.
Тогда они являются нулями функции <Рисунок27>,
т.е. f(x1)=f(x2)=f(x3)=0. На каждом из
отрезков [x1;x2], [x2;x3] для
функции f(x) выполняются условия теоремы Лагранжа,
следовательно, существуют числа c1 и с2
из интервалов (х1;х2), (х2;х3)
соответственно, такие, что <Рисунок28> и
<Рисунок29>. А так как f(x1)=f(x2)=f(x3)=0,
то f’(c1)=0 и f’(c2)=0, причем с1с2. Пришли к противоречию, так как с1 и с2
(с1с2)
являются корнями уравнения f’(x)=0, тем самым
доказано, что уравнение <Рисунок26> имеет на
промежутке (0,2) не более двух различных
действительных корней.
Пришли к противоречию, так как с1 и с2
(с1с2)
являются корнями уравнения f’(x)=0, тем самым
доказано, что уравнение <Рисунок26> имеет на
промежутке (0,2) не более двух различных
действительных корней. Следовательно, найдется такая внутренняя точка с
этого отрезка, что будет выполняться
<Рисунок32>. Учитывая, что f(x1)=f(x2)=0,
получим f’(с)=0, т.е. число с – корень уравнения
f’(x)=0. Но производная f’(x)=9x8-45x4+63, т.е.
f’(x)=9(x4-2,5)2+6,75 положительна для любых
х, а значит уравнение f’(x)=0 не имеет корней.
Полученное противоречие доказывает, что
найденный корень х1=1 является единственным
корнем уравнения x9-9x5+63x-55=0.
Следовательно, найдется такая внутренняя точка с
этого отрезка, что будет выполняться
<Рисунок32>. Учитывая, что f(x1)=f(x2)=0,
получим f’(с)=0, т.е. число с – корень уравнения
f’(x)=0. Но производная f’(x)=9x8-45x4+63, т.е.
f’(x)=9(x4-2,5)2+6,75 положительна для любых
х, а значит уравнение f’(x)=0 не имеет корней.
Полученное противоречие доказывает, что
найденный корень х1=1 является единственным
корнем уравнения x9-9x5+63x-55=0.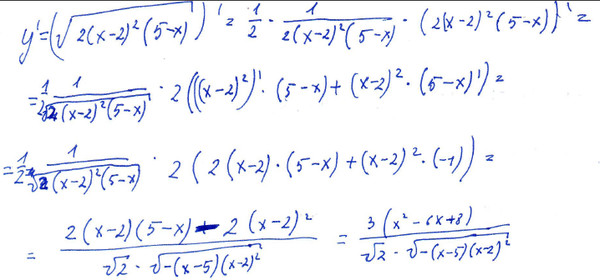 Применим теорему
Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках
[-1;0], [0;1], [1;8], [8;9] и при этом учтем, что
f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся
внутренние точки х1, х2, х3, х4
соответственно, такие, что <Рисунок33>,
<Рисунок34>, <Рисунок35>, <Рисунок36>,
т.е. f’(x1)=0, f’(x2)=0, f’(x3)=0, f’(x4)=0.
А учитывая, что x1, х2, х3, х4
– различные корни многочлена f’(x) четвертой
степени, делаем вывод, что других корней,
отличных от полученных, нет и, следовательно,
функция y=(x2-1)(x2-8х)(x-9) имеет четыре
критические точки.
Применим теорему
Лагранжа к функции f(x)=(x+1)(x-1)х(x-8)(x-9) на отрезках
[-1;0], [0;1], [1;8], [8;9] и при этом учтем, что
f(-1)=f(0)=f(1)=f(8)=f(9)=0. На каждом таком отрезке найдутся
внутренние точки х1, х2, х3, х4
соответственно, такие, что <Рисунок33>,
<Рисунок34>, <Рисунок35>, <Рисунок36>,
т.е. f’(x1)=0, f’(x2)=0, f’(x3)=0, f’(x4)=0.
А учитывая, что x1, х2, х3, х4
– различные корни многочлена f’(x) четвертой
степени, делаем вывод, что других корней,
отличных от полученных, нет и, следовательно,
функция y=(x2-1)(x2-8х)(x-9) имеет четыре
критические точки.
 А так как на промежутке <Рисунок38>
cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано,
что sinx+sin2x-3xcosx>0, то есть, что 3xcosx<sinx+sin2x, если
0<x<<Рисунок37>.
А так как на промежутке <Рисунок38>
cosx>0, то и cosx(tgx+2sinx-3x)>0. Таким образом доказано,
что sinx+sin2x-3xcosx>0, то есть, что 3xcosx<sinx+sin2x, если
0<x<<Рисунок37>. Запишем его в виде
<Рисунок48>, <Рисунок49>. Учитывая, что
функция ln t возрастающая, получим <Рисунок50>. А
если обе части неравенства <Рисунок47>
умножить на произведение x1x2>0, то
получим x2lnx1<x1lnx2, далее
<Рисунок51>, откуда и будем иметь <Рисунок52>.
Запишем его в виде
<Рисунок48>, <Рисунок49>. Учитывая, что
функция ln t возрастающая, получим <Рисунок50>. А
если обе части неравенства <Рисунок47>
умножить на произведение x1x2>0, то
получим x2lnx1<x1lnx2, далее
<Рисунок51>, откуда и будем иметь <Рисунок52>. Взяв <Рисунок58>,
<Рисунок59> и учитывая, что <Рисунок53>, если
0<x1<x2<=e, получим <Рисунок60>, т.е.
(сtg48°)tg48° > (сtg50°)tg50°.
Взяв <Рисунок58>,
<Рисунок59> и учитывая, что <Рисунок53>, если
0<x1<x2<=e, получим <Рисунок60>, т.е.
(сtg48°)tg48° > (сtg50°)tg50°.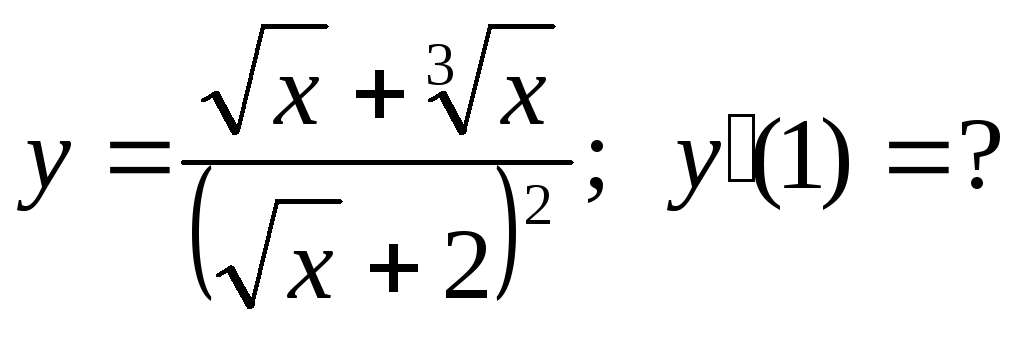
 е. имеет вид
f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x),
и делается вывод, что f(x)=g(x)+c (c — постоянная). Эту
постоянную находят, положив х равным некоторому
значению х1.
е. имеет вид
f(x)=c, либо две функции f(x) и g(x), такие, что f’(x)=g’(x),
и делается вывод, что f(x)=g(x)+c (c — постоянная). Эту
постоянную находят, положив х равным некоторому
значению х1.
 Имеем <Рисунок75>,
Имеем <Рисунок75>,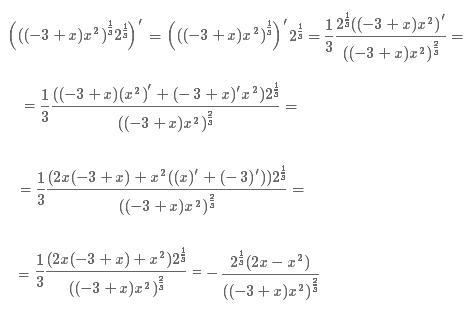

 Найдем с, полагая в этом равенстве, например, х=0.
Имеем yz2-zy2=c. Тогда f(x)=g(x)+yz2-zy2,
то есть
Найдем с, полагая в этом равенстве, например, х=0.
Имеем yz2-zy2=c. Тогда f(x)=g(x)+yz2-zy2,
то есть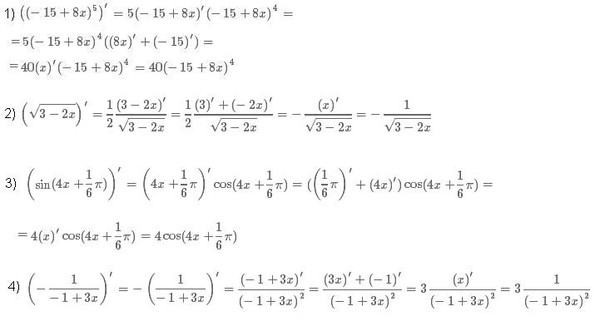

 Выше я просто умножил на особенно полезную версию числа 1 $.
Выше я просто умножил на особенно полезную версию числа 1 $.
 {\ frac {1} {2}}} = \ frac {1} {2 \ sqrt {x}} $$
{\ frac {1} {2}}} = \ frac {1} {2 \ sqrt {x}} $$
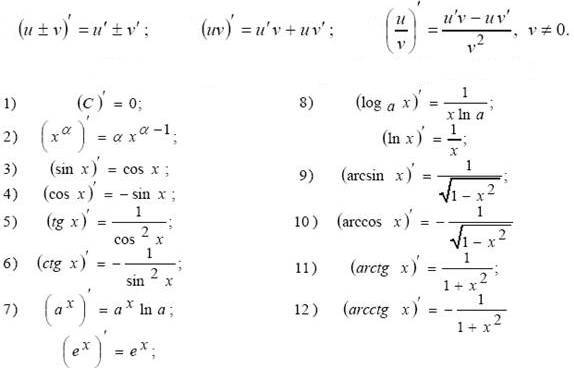 Регистрация займет всего минуту.
Регистрация займет всего минуту. {1/2} $.\ frac {3} {2}}
{1/2} $.\ frac {3} {2}}
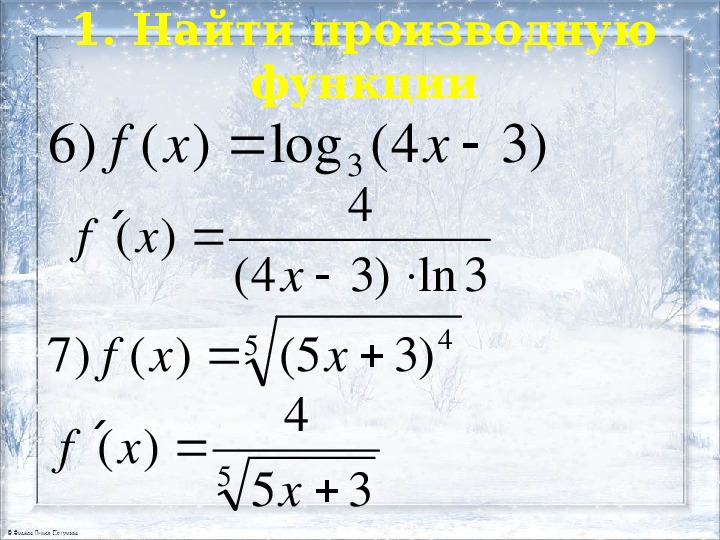
 2} {h \ times (\ sqrt {x + h} + \ sqrt {x})}}
2} {h \ times (\ sqrt {x + h} + \ sqrt {x})}}
 Помните, что чтобы получить 𝑓 из 𝑥 add ℎ, мы просто заменяем 𝑥 на 𝑥 add ℎ в 𝑓 из 𝑥. Это дает нам 𝑓 из сложить ℎ равно квадратному корню из двух, умноженному на 𝑥 добавить ℎ минус 16. Затем мы можем расширить эти скобки, чтобы получить, что 𝑓 из плюс ℎ равно квадратному корню из двух 𝑥 плюс два ℎ минус 16.
Помните, что чтобы получить 𝑓 из 𝑥 add ℎ, мы просто заменяем 𝑥 на 𝑥 add ℎ в 𝑓 из 𝑥. Это дает нам 𝑓 из сложить ℎ равно квадратному корню из двух, умноженному на 𝑥 добавить ℎ минус 16. Затем мы можем расширить эти скобки, чтобы получить, что 𝑓 из плюс ℎ равно квадратному корню из двух 𝑥 плюс два ℎ минус 16.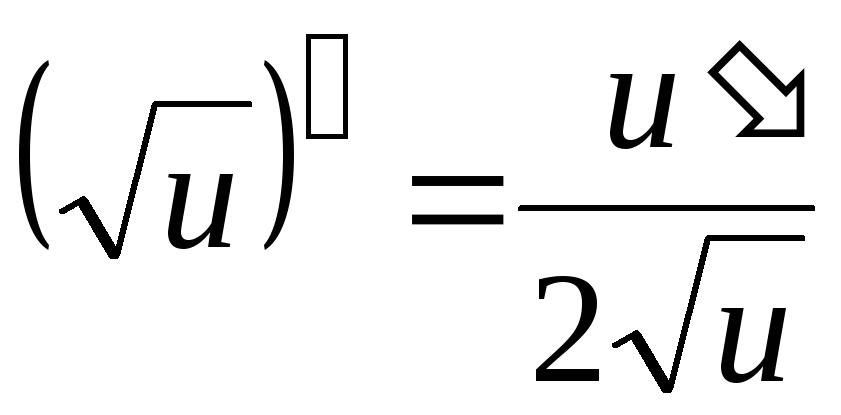 Для этого напомним, что квадратный корень из, умноженный на квадратный корень из, дает нас 𝑎. Таким образом, умножение этих двух членов вместе дает нам то, что у нас есть внутри квадратного корня: два 𝑥 добавить два ℎ минус 16. То же самое применяется, когда мы умножаем квадратный корень из двух минус 16 на квадратный корень из двух минус 16.Но на этот раз перед одним из условий стоит отрицание. Так что нам нужно помнить об этом. Используя те же правила, что и раньше, это дает нам отрицательные два минус 16.
Для этого напомним, что квадратный корень из, умноженный на квадратный корень из, дает нас 𝑎. Таким образом, умножение этих двух членов вместе дает нам то, что у нас есть внутри квадратного корня: два 𝑥 добавить два ℎ минус 16. То же самое применяется, когда мы умножаем квадратный корень из двух минус 16 на квадратный корень из двух минус 16.Но на этот раз перед одним из условий стоит отрицание. Так что нам нужно помнить об этом. Используя те же правила, что и раньше, это дает нам отрицательные два минус 16.
 Это оставляет нам два вместо квадратного корня из двух 𝑥 минус 16, прибавляем квадратный корень из двух 𝑥 минус 16. И поскольку в знаменателе у нас есть квадратный корень из двух минус 16, прибавляем квадратный корень из двух 𝑥 минус 16, мы можно записать это как два, умноженные на квадратный корень из двух 𝑥 минус 16.Затем мы замечаем, что два в числителе и два в знаменателе компенсируют друг друга. Итак, у нас остается единица больше квадратного корня из двух 𝑥 минус 16. И это наш окончательный ответ.
Это оставляет нам два вместо квадратного корня из двух 𝑥 минус 16, прибавляем квадратный корень из двух 𝑥 минус 16. И поскольку в знаменателе у нас есть квадратный корень из двух минус 16, прибавляем квадратный корень из двух 𝑥 минус 16, мы можно записать это как два, умноженные на квадратный корень из двух 𝑥 минус 16.Затем мы замечаем, что два в числителе и два в знаменателе компенсируют друг друга. Итак, у нас остается единица больше квадратного корня из двух 𝑥 минус 16. И это наш окончательный ответ. Один из них чуть не попросил в ответ статью. Барун написал:
Один из них чуть не попросил в ответ статью. Барун написал: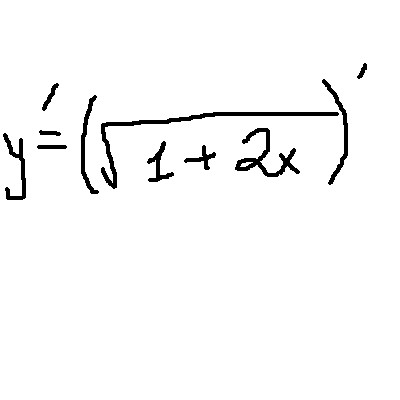
 (Вы можете доказать это, развернув синус и косинус справа.)
(Вы можете доказать это, развернув синус и косинус справа.)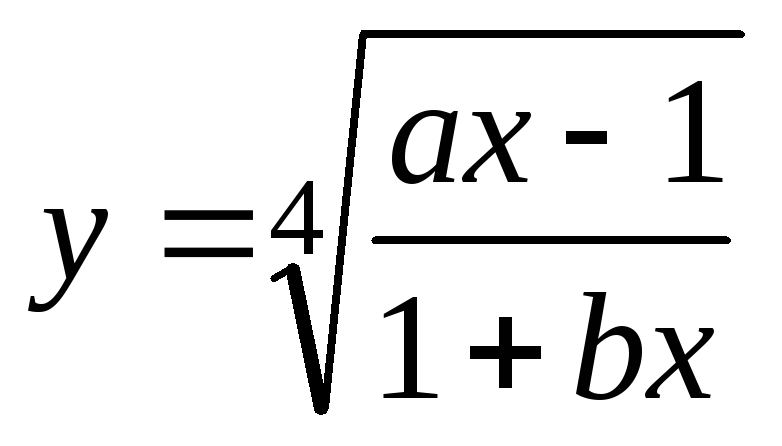

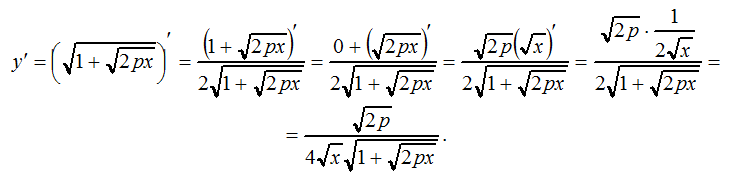
 Иногда выглядит просто ошеломляющим, даже если вы действительно знаете, как это сделать. Этот фактор визуального запугивания порождает беспокойство, вызывает першение в мозгах на тестах и, в конечном итоге, отвлекает многих людей от математики.2-x}} \ вправо) \)
Иногда выглядит просто ошеломляющим, даже если вы действительно знаете, как это сделать. Этот фактор визуального запугивания порождает беспокойство, вызывает першение в мозгах на тестах и, в конечном итоге, отвлекает многих людей от математики.2-x}} \ вправо) \)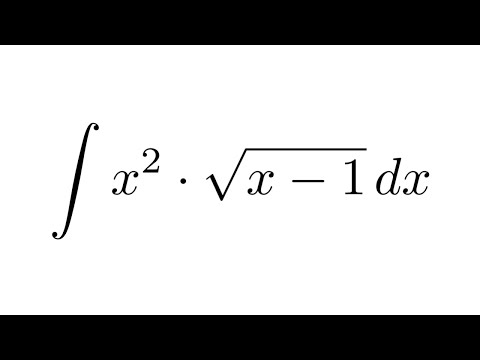 Я сказал это. Чтобы кратко рассмотреть правила логарифмов (и \ (ln \), который является особым типом логарифма), важными из них являются:
Я сказал это. Чтобы кратко рассмотреть правила логарифмов (и \ (ln \), который является особым типом логарифма), важными из них являются: Мы могли бы остановиться на этом, но мы также можем еще больше упростить, переписав квадратный корень в последнем члене как рациональную экспоненту, используя правило логарифма степеней (третье в нашем списке правил) для первого, второго и последний член и с учетом того факта, что \ (ln \) и \ (e \) инвертируют друг друга в третьем члене:
Мы могли бы остановиться на этом, но мы также можем еще больше упростить, переписав квадратный корень в последнем члене как рациональную экспоненту, используя правило логарифма степеней (третье в нашем списке правил) для первого, второго и последний член и с учетом того факта, что \ (ln \) и \ (e \) инвертируют друг друга в третьем члене: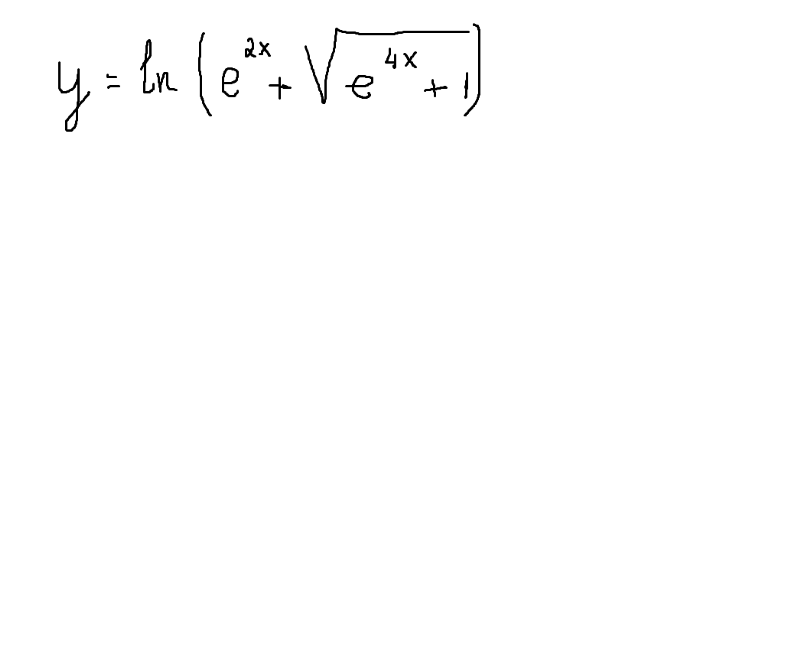 Что может облегчить жизнь, чем это?
Что может облегчить жизнь, чем это?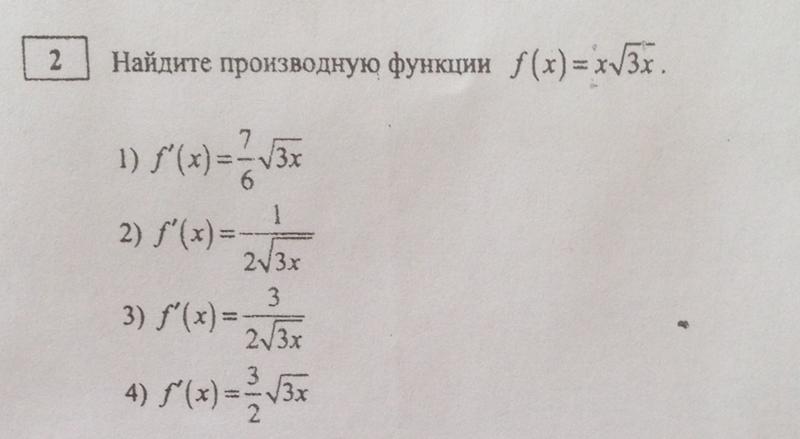

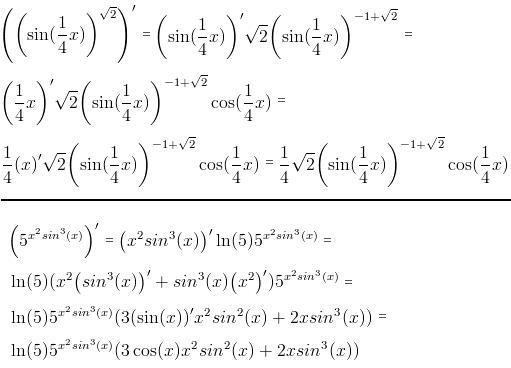 Умножьте шаг 3 на производную внешней функции.
Умножьте шаг 3 на производную внешней функции. Обратите внимание, что я использую букву D для обозначения производной.
Обратите внимание, что я использую букву D для обозначения производной.  В этом разделе объясняется, как дифференцировать функцию y = sin (4x) с помощью цепного правила. Однако этот метод может быть применен к любой аналогичной функции с синусом, косинусом или тангенсом.
В этом разделе объясняется, как дифференцировать функцию y = sin (4x) с помощью цепного правила. Однако этот метод может быть применен к любой аналогичной функции с синусом, косинусом или тангенсом.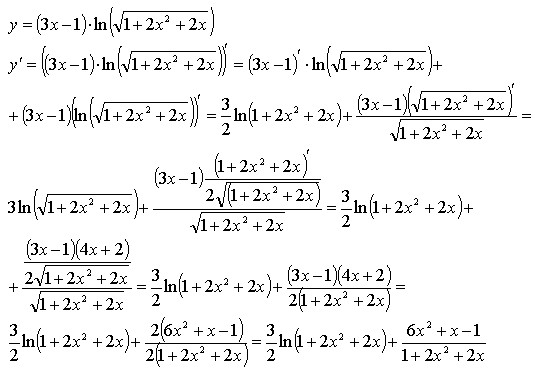
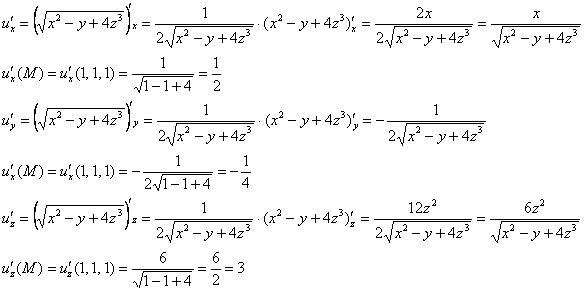
 Фактически, чтобы дифференцировать перемноженные константы, вы можете игнорировать константу во время дифференцирования.
Фактически, чтобы дифференцировать перемноженные константы, вы можете игнорировать константу во время дифференцирования.
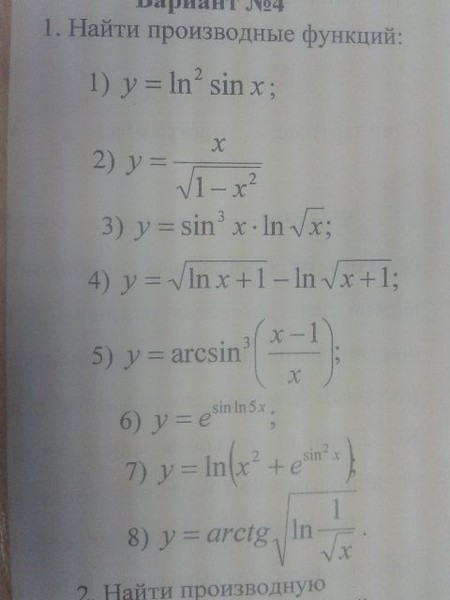 Объедините результаты из Шага 1 (2 cot x ) (ln 2) и Step 2 ((-csc 2 )).
Объедините результаты из Шага 1 (2 cot x ) (ln 2) и Step 2 ((-csc 2 )).  Затем результаты объединяются для получения окончательного результата:
Затем результаты объединяются для получения окончательного результата:  Помните, что функция, возведенная в степень -1, эквивалентна 1 по функции, а показатель степени ½ такой же, как функция квадратного корня.
Помните, что функция, возведенная в степень -1, эквивалентна 1 по функции, а показатель степени ½ такой же, как функция квадратного корня. Однако в действительности определение иногда бывает длинным и обременительным для работы (не говоря уже о том, что легко допустить ошибку). Вот почему математики разработали серию сокращений или правил для производных, таких как общее правило мощности.
Однако в действительности определение иногда бывает длинным и обременительным для работы (не говоря уже о том, что легко допустить ошибку). Вот почему математики разработали серию сокращений или правил для производных, таких как общее правило мощности.