Производная кубического корня: Как найти производную корня 🚩 Производная корня 🚩 Математика

2-3ac=1-3\lt 0 \)
Один корень

Содержание

п.2. Количество корней произвольного уравнения

Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.

Пример 2. а) Найдите число корней уравнения $\frac 1x+\frac{1}{x-1}+\frac{1}{x-3}$
б) Найдите число корней уравнения $\frac 1x+\frac{1}{x-1}+\frac{1}{x-3}=k$

Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью $y=1$. Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=\frac1x+\frac{1}{x-1}+\frac{1}{x-3} $$ Алгоритм исследования и построения графика – см. §49 данного справочника.
1) ОДЗ: $x\ne\left\{0;1;3\right\}$
Все три точки – точки разрыва 2-го рода. \begin{gather*} \lim_{x\rightarrow -0}\left(\frac1x+\frac{1}{x-1}+\frac{1}{x-3}\right)=-\infty-1-\frac13=-\infty\\ \lim_{x\rightarrow +0}\left(\frac1x+\frac{1}{x-1}+\frac{1}{x-3}\right)=+\infty-1-\frac13=+\infty\\ \lim_{x\rightarrow 1-0}\left(\frac1x+\frac{1}{x-1}+\frac{1}{x-3}\right)=1-\infty-\frac12=-\infty\\ \lim_{x\rightarrow 1+0}\left(\frac1x+\frac{1}{x-1}+\frac{1}{x-3}\right)=1+\infty-\frac12=+\infty\\ \lim_{x\rightarrow 3-0}\left(\frac1x+\frac{1}{x-1}+\frac{1}{x-3}\right)=\frac13+\frac12-\infty=-\infty\\ \lim_{x\rightarrow 3+0}\left(\frac1x+\frac{1}{x-1}+\frac{1}{x-3}\right)=\frac13+\frac12+\infty=+\infty \end{gather*} 2) Функция ни четная, ни нечетная.

2}\lt 0 $$ Производная отрицательная на всей ОДЗ.
Функция убывает.

5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.

6) Точки пересечения с OY – нет, т.к. $x=0$ – асимптота
Точки пересечения с OX – две, $0\lt x_1\lt 1,1\lt x_2\lt 3$

7) График

Получаем ответ для задачи (а) 3 корня.

Решаем более общую задачу (б). Передвигаем горизонталь $y=k$ снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:

При $k\lt 0$ — три корня
При $k=0$ — два корня
При $k\gt 0$ — три корня

Ответ: а) 3 корня; б) при $k=0$ два корня, при $k\ne 0$ три корня.

Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ \sqrt{x-1}+\sqrt{10-2x}=a $$ имеет по крайней мере одно решение.

Исследуем функцию $f(x)=\sqrt{x-1}+\sqrt{10-2x}$
ОДЗ: $ \begin{cases} x-1\geq 0\\ 10-2x\geq 0 \end{cases} \Rightarrow \begin{cases} x\geq 1\\ x\leq 5 \end{cases} \Rightarrow 1\leq x\leq 5 $
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: $f(1)=0+\sqrt{8}=2\sqrt{2},\ f(5)=\sqrt{4}+0=2$
Первая производная: \begin{gather*} f'(x)=\frac{1}{2\sqrt{x-1}}+\frac{-2}{2\sqrt{10-2x}}=\frac{1}{2\sqrt{x-1}}-\frac{1}{\sqrt{10-2x}}\\ f'(x)=0\ \text{при}\ 2\sqrt{x-1}=\sqrt{10-2x}\Rightarrow 4(x-1)=10-2x\Rightarrow 6x=14\Rightarrow x=\frac73\\ f\left(\frac73\right)=\sqrt{\frac73-1}+\sqrt{10-2\cdot \frac73}=\sqrt{\frac43}+\sqrt{\frac{16}{3}}=\frac{6}{\sqrt{3}}=2\sqrt{3} \end{gather*} Промежутки монотонности:

$x$	1	(1; 7/3)	7/3	(7/3; 5)	5
$f'(x)$	∅	+	0	—	∅
$f(x)$	$2\sqrt{2}$	$\nearrow $	max $2\sqrt{3}$	$\searrow $	2

Можем строить график:

$y=a$ — горизонтальная прямая.
Количество точек пересечения $f(x)$ и $y$ равно количеству решений.
Получаем:

$$ a\lt 2 $$	нет решений
$$ 2\leq a\lt 2\sqrt{2} $$	1 решение
$$ 2\sqrt{2}\leq a\lt 2\sqrt{3} $$	2 решения
$$ a=2\sqrt{3} $$	1 решение
$$ a\gt 2\sqrt{3} $$	нет решений

По крайней мере одно решение будет в интервале $2\leq a\leq 2\sqrt{3}$.

Ответ: $a\in\left[2;2\sqrt{3}\right]$

п.3. Решение неравенств с построением графиков

Пример 4. Решите неравенство $\frac{2+\log_3 x}{x-1}\gt \frac{6}{2x-1}$

Разобьем неравенство на совокупность двух систем.
Если $x\gt 1$, то $x-1\gt 0$, на него можно умножить слева и справа и не менять знак.
Если $x\lt 1$, то $x-1\lt 0$, умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: $x\gt 0$

Получаем совокупность: \begin{gather*} \left[ \begin{array}{l} \begin{cases} x\gt 1\\ 2+\log_3 x\gt\frac{6(x-1)}{2x-1} \end{cases} \\ \begin{cases} 0\lt x\lt 1\\ 2+\log_3 x\lt\frac{6(x-1)}{2x-1} \end{cases} \end{array} \right. \\ 2+\log_3 x\gt \frac{6(x-1)}{2x-1}\Rightarrow \log_3 x\gt \frac{6(x-1)-2(2x-1)}{2x-1}\Rightarrow \log_3 x\gt \frac{2x-4}{2x-1}\\ \left[ \begin{array}{l} \begin{cases} x\gt 1\\ \log_3 x\gt\frac{2x-4}{2x-1} \end{cases} \\ \begin{cases} 0\lt x\lt 1\\ \log_3 x\lt\frac{2x-4}{2x-1} \end{cases} \end{array} \right. \end{gather*} Исследуем функцию $f(x)=\frac{2x-4}{2x-1}=\frac{2x-1-3}{2x-1}=1-\frac{3}{2x-1}$
Точка разрыва: $x=\frac12$ – вертикальная асимптота
Односторонние пределы: \begin{gather*} \lim_{x\rightarrow \frac12 -0}\left(1-\frac{3}{2x-1}\right)=1-\frac{3}{-0}=+\infty\\ \lim_{x\rightarrow \frac12 +0}\left(1-\frac{3}{2x-1}\right)=1-\frac{3}{+0}=-\infty \end{gather*} Второе слагаемое стремится к 0 на бесконечности, и это дает горизонтальную асимптоту: $y=1$ \begin{gather*} \lim_{x\rightarrow -\infty}\left(1-\frac{3}{2x-1}\right)=1-\frac{3}{-\infty}=1+0\\ \lim_{x\rightarrow +\infty}\left(1-\frac{3}{2x-1}\right)=1-\frac{3}{+\infty}=1-0 \end{gather*} На минус бесконечности кривая стремится к $y=1$ сверху, а на плюс бесконечности – снизу.

3} $$ Одна критическая точка 2-го порядка $x=\frac12$

$x$	$\left(0;\frac12\right)$	$\frac12$	$\left(\frac12;+\infty\right)$
$f»(x)$	>0	∅	<0
$f(x)$	$\cup$	∅	$\cap$

Пересечения с осью OY: $f(0)=1-\frac{3}{0-1}=4$, точка (0;4)
Пересечение с осью OX: $1-\frac{3}{2x-1}=0\Rightarrow 2x-1=3 \Rightarrow x=2$, точка (2;0)

Строим графики $f(x)=\frac{2x-4}{2x-1}$ и $g(x)=\log_3 x$

Первая система из совокупности $ \begin{cases} x\gt 1\\ \log_3 x\gt \frac{2x-4}{2x-1} \end{cases} $
Логарифм при $x\gt 1$ все время выше, чем правая ветка гиперболы, т.е. система справедлива для всех $x\gt 1$.
Вторая система из совокупности $ \begin{cases} 0\lt x\lt 1\\ \log_3 x\lt \frac{2x-4}{2x-1} \end{cases} $
Логарифм попадает под левую ветку гиперболы на интервале $0\lt x\lt\frac12$, т.

е. $$ \begin{cases} 0\lt x\lt 1\\ 0\lt x\lt\frac12 \end{cases} \Rightarrow 0\lt x\lt\frac12 $$ Решение совокупности – это объединение полученных решений систем: $$ 0\lt x\lt\frac12\cup x\gt 1 $$ Ответ: $x\in\left(0;\frac12\right)\cup (1;+\infty)$

§25 Решение кубических уравнений

Пусть дано

уравнение 3 степени. нормируя получим (1) применим подстановку:

Пусть :

Если система имеет решение то сумма эти чисел равно которое будет решением уравнения (2) а потом и данного уравнения. Перепишем систему (3):

Считая некоторыми корнями квадратного уровнения составим его с помощи теоремы Виета.

Так как кубическое уравнение имеет 3 решения то для u и v найдется по 3 решения, а их сумма дает 9 вариантов корней в действительности они должны быть выбраны, что бы выполнялись условия системы (3`) то есть .

Докажем что корней 3. Воспользуемся теоремой из комплексных чисел:

Т1: Что бы извлечь корень энной степени из комплексного числа z достаточно какое-нибудь 1 значение корня

умножить последовательно на корни энной степени из 1 тоесть

также являются корнями.

Извлекаем корень из 1

Пусть какой-то значения кубических корней:

Тогда другими значения первого кубического корня будут

Заметим, что значению отвечает значение

Значению отвечает значение

Корнями уравнения (2) будут:

■

Решения приведенного кубического уравнения (2) находят по формулам:

Где выражения дискриминант.

Пример 1:

Т2: Если дискриминант кубического уравнения равен 0 то уравнение имеет 2 равных корня.

Доказательство:

Пусть одно из значений получается при тогда найдем соответствующее значение из условия:

■

Т3: Пусть кубическое уравнение имеет действительные коэффициенты:

Если D>0 то уравнение имеет 3 различных корня причем 1 действительный и 2 комплексных сопряжённых.
Если дискриминант меньше 0 то уравнение имеет три различных действительных корня.
Если декремента равен 0 то три действительных корня 2 из которых равны между собой.

Доказательство:

Пусть D>0 тогда два действительных числа, тогда получаем 1 корня действительных, а 2 мнимых, обозначим:

тогда получим тогда мнимые. И все корни кубические из этих чисел также будут мнимыми. Все корни мнимые причем все эти корни имеют один и тот же модуль. . Покажем, что мнимые: ,u—0.,v—0.=-,p—3.>0(т.к дескрименант меньше 0). Таким образом, равенство модулей и положительное действительное число произведение, возможно только для комплексных сопряжённых

В Т1 было показано, что ,u—0.=,3q—2p. ,v—0.=,3q—2p. и корни ,z—0.=,3q—p. ,z—1,2.=-,3q—2p.

■

Пусть дано нормированное уравнение 4 степени ,x—4.+a,x—3.+b,x—2.+cx+d=0

Все слагаемые начиная с 2 переносим в право ,x—4.+a,x—3.=-b,x—2.-cx-d

,,,x—2.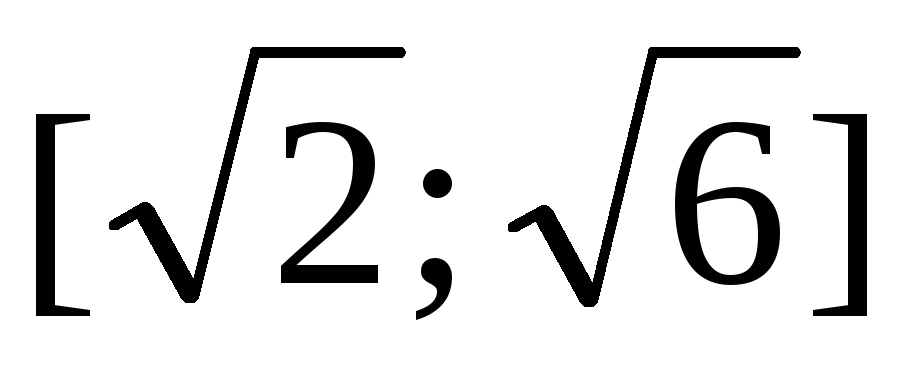 .-2.+,2a—2.,x—2.x+,,a—2.-4.,x—2.=,,a—2.-4.,x—2.-b,x—2.-cx-d

,,,x—2.+,a—2.x.-2.=,,,x—2.-4.-b.,x—2.-cx-d

Введём вспомогательную переменную t что бы левая и правая имели полные квадраты

,,,,x—2.+,a—2.x.+,t—2..-2.=,,,a—2.-4.-b.,x—2.-cx-d+,2t—2.,,x—2.+,a—2.x.+,,t—2.-4.

,,,,x—2.+,a—2.x.+,t—2..-2.=,,,a—2.-4.-b+t.,x—2.+,,at—2.-c. x+,,,t—2.-4.-d.

Чтобы правая часть была полным квадратом необходимо чтобы дискрименат был равен 0

D=,,,at—2.-c.-2.-4,,,a—2.-4.-b+t.,,,t—2.-4.-d.=,,a—2.,t—2.-4.—,2at—2.c+,c—2.—,,a—2.,t—2.-4.+b,t—2.—,t—3.+,a—2.d—abd+4td

,t—3.-b,t—2.+,ac-4d.t+4bd-,c—2.—,a—2.d=0-кубическая резальента уровнения 4 степени

Находим 1 из корней кубической резольвенты и подставляем его:

,,,x—2.+,a—2.x+,,t—0.-2..-2.=,,Ax+B.-2.

Существуют и другие например способ Эйлера Декарта.

Пример1:

,x—4.-2,x—3.+2,x—2.+4x-8=0

,,,x—2..-2.-2,x—2.x+,x—2.=-,x—2.-4x+8

,,,x—2.-x.-2.=-,x—2.-4x+8

,,,x—2.-x+,t—2..-2.=-,x—2.-4x+8+,2t—2.,,x—2.-x.+,,t—2.-4.

,,,x—2.-x+,t—2..-2.=,t-1.,x—2.—,t+4.x+,8,t—2.-4.

D=,,t+4.-2.-4,t-1.,8+,,t—2.-4..=,t—2.+8t+16-32t+32-,t—3.+,t—2.=-,t—3. 2-6x+9

,,,x—2.-x+1.-2.=,,x-3.-2.

,,,x—2.-x+1=x-3,-,x—2.-x+1=3-x..

Замечание: Начиная с 16 века почти 3 лет продолжались попытки ученых разрешить уравнения 5 степени и выше в радикалах (выразить корни уравнений в виде выражений содержащих коэффициенты). В 19 веке была доказана теорема Руфини Абеля о том, что алгебраическое уравнение n степени с произвольными буквенными коэффициентам при n>=5 нельзя решить в радикалах.

Производная квадратного корня (3 ключевых понятия, которые вы должны знать) – JDM Educational

Нам часто приходится находить производную квадратного корня на курсах математического анализа. Мы можем вычислить производную квадратного корня, используя определение предела или используя ярлык, описанный ниже.

Итак, как извлечь производную из квадратного корня? Чтобы получить производную функции квадратного корня f(x) = √x, сначала преобразуйте ее в форму f(x) = x ^1/2 . Затем используйте правило степени для производных, чтобы найти f’(x) = (1/2)*x ^-1/2 . Затем упростите до вида 1/2√ x. Мы также можем использовать цепное правило, чтобы найти производную функции композиции квадратного корня.

Конечно, аналогичное правило применяется для извлечения производной кубического корня, корня четвертой степени и других радикальных функций.

В этой статье мы поговорим о том, как извлечь производную из функции квадратного корня и когда использовать цепное правило. Мы также рассмотрим несколько примеров, чтобы прояснить концепцию.

Начнем.

Производная квадратного корня

Производная функции квадратного корня f(x) = √x определяется как:

f'(x) = 1/2√x

Мы можем доказать это формулу путем преобразования радикальной формы квадратного корня в выражение с рациональным показателем степени. Помните, что для f(x) = √x. у нас есть радикал с индексом 2.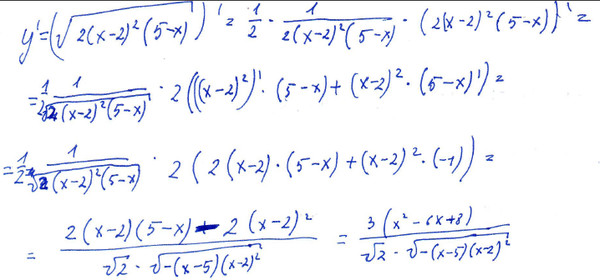

Вот график квадратного корня из x, f(x) = √x.
Это дает нам рациональный показатель степени 1/2. Итак, у нас есть:
Использование квадратных корней
Пожалуйста, включите JavaScript что степенное правило для производных говорит нам, что для g(x) = x ^N производная определяется как:
g'(x) = Nx ^N-1
Используя правило степени (с N = ½] если взять производную от f(x), получим:
f'(x) = (1/2)*x ^{(1/2) – 1} [здесь, N = 1/2]
f'(x) = (1/2)*x ^-1/2
f'(x) = 1/2x ^1/2 [так как x ^-1/2 = 1/x ^1/2 ]
f'(x) = 1/2√x
9002 9
Вот график f'(x) = 1/2√x, производной f(x) = √x:
Это график производной квадратного корня из x, f'(x) = 1/2√ Икс.
Аналогичным образом мы можем найти производную от кубических корней, корней четвертой степени и т. д.:
Функция Производная
Кубический корень
f(x) = x ^1/3 f'( х) = 1/(3x ^2/3 )
Корень четвертой степени
f(x) = x ^1/4 f'(x) = 1/(4x ^3/4 )
Корень пятой степени
f(x) = x ^1/5 f'(x) = 1/(5x ^4/5 )
N-й корень
f(x) = x ^1/N f'(x) = 1/(Nx ^(N-1)/N )
В этой таблице показаны различные радикальные функции
и их производные.
Производная квадратного корня с помощью цепного правила
Чтобы найти производную квадратного корня с функциональной композицией, нам нужно будет использовать цепное правило.
Помните, что цепное правило говорит нам: для функциональной композиции f(g(x)) производная есть f'(g(x))*g'(x):
Если h(x) = f(g(x)), то h'(x) = f'(g(x))*g'(x)
Предполагается, что функции дифференцируемы.
Применение цепного правила, когда f(x) является функцией квадратного корня, даст нам:
Если h(x) = √g(x), то h'(x) = (1/2)*g (x) ^-1/2 *g'(x)
После упрощения получаем h'(x) = g'(x)/2√g(x)
Как найти производную Квадратный корень с использованием определения
Мы также можем использовать определение предела, чтобы найти производную квадратного корня.
Помните, что предельное определение производной говорит нам, что:
f'(x) = lim _h–>0 [f(x + h) – f(x)] / h
Используя f(x) = √x в приведенном выше уравнении получаем:
f'(x) = lim _h–>0 [√(x + h) – √x] / h
Мы умножит верх и низ на √(x + h) + √x, сопряженное с числителем.
Новый числитель:
[√(x + h) – √x]*[ √(x + h) + √x] = (x + h) – x [средние члены отменяются, когда мы используем FOIL]
Поскольку (x + h) – x = h, наш новый числитель равен h.
Новый знаменатель равен h*[√(x + h) + √x].
Итак, новый предел:
f'(x) = lim _h–>0 [h] / h*[√(x + h) + √x]
f'( x) = lim _h–>0 [1] / 1*[√(x + h) + √x] [отменить h вверху и внизу]
f'(x) = [1] / 1*[√(x + 0) + √x] [подставить h = 0]
f'(x) = [1] / 1*[√(x) + √x]
f'(x) = [1] / [2√(x)] [объединить подобные термины внизу]
f'(x) = 1/2√x
Это то же самое, что (1/2)*x ^-1/2 , что мы получаем из правила степени для производных.
Как извлечь производную квадратного корня
Чтобы извлечь производную квадратного корня, лучше всего начать с преобразования радикала в выражение с рациональным показателем степени. Затем вы можете использовать правило степени для производных (и, если необходимо, цепное правило), чтобы найти производную.
Давайте рассмотрим несколько примеров.
Пример 1. Чему равна производная квадратного корня из 2x?
Допустим, мы хотим взять производную функции f(x) = √(2x). Его график показан ниже.
Это график функции f(x) = √(2x).
Сначала преобразуем радикал в выражение с рациональным показателем:
f(x) = √(2x)
f(x) = (2x) ^1/2
90 029
Сейчас , мы используем степенное правило и цепное правило, чтобы взять производную:
f'(x) = (1/2)(2x) ^-1/2 *(2) [1/2 соответствует степенному правилу, а 2 — цепному правилу]
f'(x) = (2x) ^-1/2    [(1/2)*2 = 1]
f'(x) = 1/(2x) ^1/2
f'(x) = 1/√(2x)
Вы можете увидеть график f'(x) = 1/√(2x) ниже.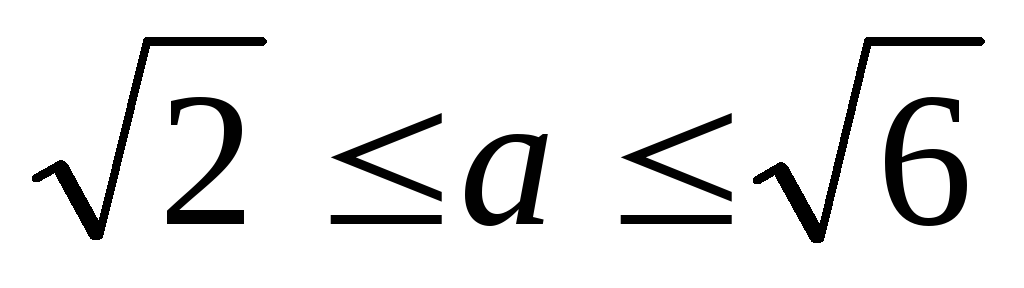
Это график функции f'(x) = 1/√(2x).
Пример 2. Чему равна производная квадратного корня из 3x?
Допустим, мы хотим взять производную функции f(x) = √(3x). Его график показан ниже.
Это график функции f(x) = √(3x).
Сначала преобразуем радикал в выражение с рациональным показателем:
f(x) = √(3x)
f(x) = (3x) ^1/2
90 029
Сейчас , мы используем степенное правило и цепное правило для получения производной:
f'(x) = (1/2)(3x) ^-1/2 *(3) [½ из правила степени, а 3 из правила цепочки]
f'(x) = (3/2)(3x) ^-1/2    [(1/2)* 3 = 3/2]
f'(x) = 1,5/(3x) ^1/2
f'(x) = 1,5/√(3x)
9000 2 Вы можете увидеть график f'(x) = 1,5/√(3x) ниже.
Это график функции f'(x) = 1,5/√(3x).
Пример 3. Чему равна производная квадратного корня из x + 1?
Допустим, мы хотим взять производную функции f(x) = √(x+1). Его график показан ниже.
Это график функции f(x) = √(x+1).
Сначала преобразуем радикал в выражение с рациональным показателем:
f(x) = √(x+1)
f(x) = (x+1) ^1/2
Теперь воспользуемся степенным правилом и цепным правилом для получения производной:
f'(x) = (1/2)(x+1) ^-1/2 *(1) [½ из правила степени, а 1 из правила цепочки]
f'(x) = 0,5*(x+1) ^-1/2
f'(x) = 0,5/(x+1) ^1/2
f'(x) = 0,5/√(x+1) 9 0028
Вы можете увидеть график f'(x) = 0,5/√(x+1) ниже.
Это график функции f'(x) = 0,5/√(x+1).
Пример 4: Чему равна производная квадратного корня из 1 – x
² ?
Допустим, мы хотим взять производную функции f(x) = √(1 – x ² ). Его график показан ниже.
Это график функции f(x) = √(1 – x ² ).
Сначала преобразуем радикал в выражение с рациональным показателем:
f(x) = √(1 – x ² )
f(x) = (1 – x ² ) ^1/2
Теперь воспользуемся степенным правилом и цепным правилом, чтобы найти производную: 1/2 *(-2x) [½ соответствует степенному правилу, а -2x соответствует цепному правилу]
f'(x) = -x*(1 – x ² ) ^-1/2    [(1/2)*(-2x) = -x]
f'(x) = — x/(1 – x ²) ^1/2
f'(x) = -x/√(1 – x ²)
график f'( x) = -x/√(1 – x ² ) ниже.
Это график функции f'(x) = -x/√(1 – x ² ).
Пример 5: Чему равна производная квадратного корня из x
³ ?
Допустим, мы хотим взять производную функции f(x) = √(x ³). Его график показан ниже.
Это график функции f(x) = √(x ³ ).
Сначала преобразуем радикал в выражение с рациональным показателем:
f(x) = √(x ³ )
f(x) = (x ³ ) 90 006 1/2
f(x) = x ^3*1/2
f(x) = x ^3/2
900 02 Теперь воспользуемся степенным правилом, чтобы найти производную:
f'(x) = (3/2)x ^1/2
f'(x) = 1,5√x
Вы можете увидеть график f'( х) = 1,5√x ниже.
Это график функции f'(x) = 1,5√x.
Пример 6. Чему равна производная квадратного корня из 1/квадратный корень из x?
Допустим, мы хотим взять производную функции f(x) = √(1/√x). Его график показан ниже.
Это график функции f(x) = √(1/√x).
Сначала преобразуем радикал в выражение с рациональным показателем:
f(x) = √(1/√x)
f(x) = √(1/x ^1/2 ) [√x = x ^{1/2 9 0007 ]}
f(x) = √(x ^-1/2 ) [1/x ^1/2 = x ^-1/2 ]
f(x) = (x ^-1/2 ) ^1/2
f(x) = x ^(-1/2)*(1/2)
f(x) = x ^{-1/4 900 07}
Теперь воспользуемся степенным правилом для получения производной:
f'(x) = (-1/4)x ^-5/4
f'(x) = -0,25/x ^5/4
9000 2 Вы можете увидеть график f'(x) = -0,25/x ^5/4 ниже.
Это график функции f'(x) = -0,25/x ^5/4 .
Как найти вторую производную квадратного корня
Чтобы найти вторую производную квадратного корня, мы используем правило степени, чтобы найти производную первой производной.
Если f(x) = √x, то f’(x) = (1/2)x ^-1/2 , как мы видели ранее.
Если снова взять производную, то получим:
f»(x) = (-1/2)*(1/2)*x ^{-1/2 – 1}
f »(x) = (-1/4)*x ^-3/2
f»(x) = -1/4x ^3/2
Эта вторая производная говорит нам вогнутость функции квадратного корня f(x) = √x. Поскольку f’’(x) < 0 (оно всегда отрицательное), мы знаем, что график f(x) = √x вогнут вниз (вогнут).
Заключение
Теперь вы знаете, как найти производную функции квадратного корня. Вы также знаете, как найти производные для некоторых его распространенных вариаций, используя цепное правило.
Здесь вы можете узнать, как построить график функции от ее производной.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
~Джонатон
Видео с вопросами: Нахождение первой частной производной корневой функции нескольких переменных двух переменных 𝑦 минус четыре относительно 𝑥.
В этом вопросе нам дана многомерная функция, функция от двух переменных: 𝑥 и 𝑦. Нас просят найти первую частную производную этой функции по 𝑥. Так что это значит? Что ж, в данном случае это означает, что мы рассматриваем любую другую переменную, кроме 𝑥, как константу. Итак, мы рассматриваем 𝑦 здесь как константу. Мы представляем эту частную производную, как показано. Итак, чтобы найти частную производную нашей функции по 𝑥, мы собираемся продифференцировать ее и рассматривать 𝑦 как константу. Мы собираемся немного переписать его как 𝑥 в квадрате плюс 𝑦 минус четыре в степени одной трети.
И тогда мы видим, что относительно 𝑥 у нас есть функция от функции или составная функция. Итак, мы могли бы использовать цепное правило или общее правило мощности, чтобы различать его. Воспользуемся цепным правилом. Цепное правило гласит, что если 𝑦 — некоторая дифференцируемая функция от 𝑢, а сама 𝑢 — некоторая дифференцируемая функция от 𝑥, то производная от 𝑦 по 𝑥 равна произведению производных каждой из наших функций, d𝑦 на d𝑢 раз д𝑢 от д𝑥.
Теперь нам нужно быть немного осторожными, так как наша функция выражена в терминах 𝑥 и 𝑦. Итак, пусть 𝑢 будет равно внутренней части нашей функции, 𝑥 в квадрате плюс 𝑦 минус четыре. Тогда 𝑓 из 𝑢 равно 𝑢 в степени одной трети. Первая частная производная нашей функции по 𝑥 — это произведение производных каждой из этих функций. Когда мы находим частную производную от 𝑢, мы получаем два 𝑥. Помните, мы рассматриваем 𝑦 как константу, а производная константы равна нулю. Затем мы дифференцируем нашу функцию в 𝑢 по 𝑢. Итак, мы получаем третье умножение на 𝑢 в степени отрицательных двух третей.
Помните, мы умножаем весь член на показатель степени, а затем уменьшаем эту степень на единицу. Но, конечно, наша частная производная относится к 𝑥. Итак, мы возвращаемся к нашей первоначальной замене. Мы заменяем 𝑢 на 𝑥 в квадрате плюс 𝑦 минус четыре. И наша первая частная производная равна двум 𝑥, умноженным на треть, умноженным на 𝑥 в квадрате плюс 𝑦 минус четыре в степени отрицательных двух третей. Теперь отрицательный показатель говорит нам найти обратную величину. Итак, мы можем записать это как два 𝑥 на три, умноженные на 𝑥 в квадрате плюс 𝑦 минус четыре в степени две трети.
Используя один из наших законов показателей, который гласит, что 𝑥 в степени 𝑎 в степени 𝑏 равно 𝑥 в степени 𝑎, умноженной на 𝑏, мы можем разделить наш показатель степени. И мы можем записать 𝑥 в квадрате плюс 𝑦 минус четыре в степени двух третей как 𝑥 в квадрате плюс 𝑦 минус четыре в квадрате в степени одной трети. Но, конечно, мы уже видели, что степень одной трети равна нахождению кубического корня из этого числа.
No related posts.