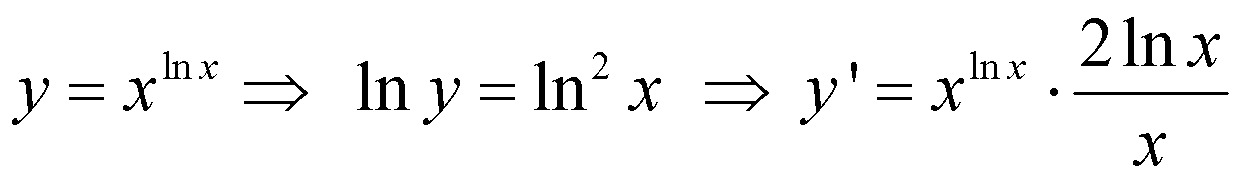Производная от логарифма натурального: Производная натурального логарифма (lnx)’

2

Натуральные логарифмы

Очень важным в математике и физике является предел функции при стремлении х к нулю. Это иррациональное число обозначается буквой е и вычислено с очень большой степенью точности:

(6)

Как известно, логарифмом числа по основанию называется показатель степени х, в которую надо возвести основание, чтобы получить число: . Логарифм записывают в виде

Если в качестве основания логарифмов выбрано число 10, получаются десятичные логарифмы: Примем теперь в качестве основания логарифмов число е. Получим натуральные логарифмы, которые обозначаются Общее правило перехода к логарифму по другому основанию

Для перехода от натуральных логарифмов к десятичным логарифмам положим . Тогда

Модулем этого перехода является натуральный логарифм десяти:

Поэтому для нахождения натурального логарифма числа можно использовать десятичный логарифм:

(с точностью, достаточной для решения задач).

Суммирование

Часто результаты измерений или вычислений представляют собой сумму определенного числа слагаемых. Обозначим все слагаемые суммы какой-нибудь буквой с индексом, который будет изменяться при переходе от одного слагаемого к другому. Например: .

Сложение (суммирование, нахождение разного рода сумм – арифметической, геометрической, алгебраической) обозначают греческой заглавной буквой сигма . Результат суммирования тогда можно записать в виде

Элементы дифференциального исчисления

Производная. Пусть в некоторой непрерывной области значений х существует функция , удовлетворяющая условию дифференцирования, которые мы здесь не рассматриваем. В большинстве интересующих нас физических вопросов эти условия выполняются автоматически. Пример такой функции изображен на рисунке 8.

Введем обозначения: и . Достаточно малый участок кривой между близкими точками 1 и 3 можно представить как отрезок прямой и тем точнее, чем меньше приращение аргумента . Мы получили элементарный треугольник 1 2 3, в котором катетами являются приращение функции и приращение аргумента .

Их отношение характеризует скорость возрастания функции при увеличении аргумента х, зависит от х и интервала .

Устремим это отношение к пределу при , т.е. «стянем» интервал в точку х. При этом и приращение функции (2 3) и приращение аргумента (1 2) устремятся к нулю, т.е. станут бесконечно малыми величинами. Имеем

Этот предел называется

первой производной функции .

Пусть, например, задана функция . Ее производная

а приращение функции

, т.е. почти равно произведению производной функции и приращения ее аргумента. Следовательно, отношение приращения функции к приращению ее аргумента приблизительно равно производной этой функции и тем точнее, чем меньше приращение аргумента.

Обозначим бесконечно малое приращение d (в отличие от обозначения конечного приращения ). Тогда сколь угодно малое (но не равное нулю!) приращение аргумента будет обозначено dx, соответствующее приращение функции df(x) и .

Аналогичное приближенное равенство справедливо и для других функций. Таким образом, производная

(7)

(с точностью до бесконечно малого слагаемого). При вычислении производных мы часто будем пользоваться последним приближенным равенством.

Как видно из рисунка 8, производная характеризует скорость возрастания функции в точке х. Геометрический смысл производной понятен из рисунка: она равна тангенсу угла наклона касательной к кривой в точке х по отношению к оси абсцисс. Выражение означает, что при возрастании аргумента х функция увеличивается; наоборот, если , то функция уменьшается при возрастании х. Условие

(8)

(касательная параллельна оси абсцисс) есть условие минимума, максимума или точки перегиба, в которой касательная к графику горизонтальна.

Производная представляет собой новую функцию своего аргумента, обычно имеющую конечное значение, хотя пределы числителя и знаменателя в выражении (7) – нули (задав определенное значение аргумента, получим конкретное числовое значение производной).

От нее снова можно взять производную, это будет вторая производная первоначальной функции и т.д. математическое действие, состоящее в нахождении производной от заданной функции, называется дифференцированием⁴.

Свойства производной.

1. Постоянный сомножитель. Если C=const⁵ и , то

(9)

Постоянный сомножитель можно вынести за знак производной.

2. Производная суммы функций. Пусть . тогда

(10)

Такое же соотношение справедливо при любом числе слагаемых:

(11)

Производная суммы функций равна сумме производных от этих функций.

3. производная произведений от двух функций. Пусть . Производная

В этом выражении опущено бесконечно малое первое слагаемое (в пределе оно равно нулю). Мы получили

(12)

Производная произведения двух функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй.

4. Производная отношения двух функций. Пусть . Тогда и

Отсюда . Следовательно,

. (13)

Производная отношения двух функций равна деленной на квадрат знаменателя разности произведений производной числителя на знаменатель и числителя на производную знаменателя (естественно, предполагается, что знаменатель не обращается в нуль).

Производные логарифмических функций — Концепция

Производная натуральной логарифмической функции (ln[x]) просто делится на 1 на x. Эту производную можно найти, используя как определение производной, так и калькулятор.

Производные логарифмических функций проще, чем могут показаться, хотя сами функции исходят из важного предела исчисления.

производная формула пределы производная число е численное приближение производной натуральный логарифм

Говоря о производных функций и одной специальной функции, это натуральная логарифмическая функция. Теперь вспомним определение натурального логарифма y=lnx, означающего, что от e до y равно x. И помните, что e — это специальное число 2,71828, это иррациональное число и имеет бесконечное неповторяющееся десятичное представление, как и число пи. Хотя считается, что это очень важное число, потому что когда вы создаете экспоненциальную функцию от e к x, ее производная также равна e к x.

Так что это одна из важных вещей в этом числе.
Теперь, я изобразил y равным e относительно x, и я изобразил y равным lnx, и помните, что это обратные функции друг друга, и поэтому они имеют симметрию относительно диагональной линии y, равной x. Теперь я хочу поговорить о производной натурального логарифма, поэтому я начну с определения предела производной, когда h приближается к нулю f от x плюс h минус f от x по h. Затем я подставляю f в натуральный лог и вот что получаю. Итак, наша цель здесь — попытаться выяснить, что такое производная, и мы не сможем сделать это с помощью алгебры. Поэтому вместо этого я собираюсь сыграть в небольшую игру, угадывая функцию, теперь я собираюсь это сделать так, что мне нужно получить это в форме, которую я могу на самом деле построить на своем калькуляторе. Итак, что я собираюсь сделать, так это аппроксимировать этот предел, взяв значение h, которое действительно очень мало, например, 0,001, и я собираюсь аппроксимировать этот предел с помощью натурального логарифма x плюс 0,001 минус lnx всего 0,001, и это будет красиво. близко, достаточно близко для наших целей, чтобы сказать, какой функцией на самом деле является производная от lnx. Итак, моя цель на этом уроке — построить график f от x, равного lnx, и его производной на ti84, и определить функцию производной.
Давайте сделаем это сейчас, поэтому мы смотрим на ti84. Первое, что я хочу сделать, это перейти в режим графика, так что нажмите кнопку y равно, и я собираюсь ввести свою функцию natural log x. Теперь для y2 мне нужно ввести производную или мое приближение для производной, которая представляет собой натуральный логарифм x + 0,001 минус натуральный логарифм x. Закройте скобки и разделите полученное значение на 0,001. Итак, это коэффициент разности с h, равным 0,001, он будет довольно близок к пределу, когда h приближается к нулю коэффициента разности.
Давайте посмотрим, что дает нам график. Итак, вы смотрите сюда, прежде всего, на эту возрастающую кривую, которая является естественной логарифмической кривой. Эта убывающая кривая здесь является его производной, и есть смысл в том, что производная должна уменьшаться, потому что помните, что это дает мне наклон натурального логарифма в любой точке. Здесь очень близко к тому, когда x близок к нулю, наклон круче, и поэтому производная должна быть больше. А здесь, где этот склон менее крутой, производная должна быть меньше, и именно это и происходит здесь внизу. Давайте попробуем выяснить, что это за функция как производная функция, поэтому я нажму кнопку трассировки. Теперь прямо сейчас он начинается с x равно нулю, и, конечно, обе эти функции не определены x равно нулю, позвольте мне немного переместить курсор вправо.
Хорошо, теперь мы находимся на одной из кривых, на самом деле мы на естественной логарифмической кривой, поэтому вам нужно нажать кнопку вверх и вниз, чтобы переключиться на другую кривую, и теперь я занимаюсь аппроксимацией производной. Теперь x равно 0,1063, это мне не очень поможет, давайте на самом деле перейдем к x, равному 0,5, и я смогу ввести 0,5 дюйма. Теперь обратите внимание, какое значение у, оно действительно очень близко к 2, давайте попробуем x равно 1, и я могу просто ввести 1 очень близко к 1. Позвольте мне ввести 2 и заметить, что это значение очень близко к половине. И поэтому я начинаю замечать, что значение y близко к обратному значению x. Давайте попробуем 3, 0,333, определенно близкое к одной трети, а затем я попробую еще одно 4, очень близкое к четверти, что равно 0,25, поэтому я предполагаю, что производная этой функции y равна 1 по x. Вернемся к доске.
Итак, мы только что выяснили, что производная натурального логарифма на самом деле является функцией 1 от x. Это еще одна особенность числа e, потому что это логарифм основания, у него есть очень хорошая алгебраическая производная, и поэтому очень важный результат, который мы будем часто использовать в следующих задачах, заключается в том, что производная lnx равна 1 больше x. .

Репетиторы College Park — Блог — Исчисление

Математика часто может показаться непосильной. Иногда просто 92-x}} \справа )\)

Подсказка: есть простой и сложный пути решения этой проблемы. Воспользуйтесь простым способом.

Эта функция, честно говоря, выглядит устрашающе. Он полон экспонентов, натуральных бревен и квадратных корней, прижатых друг к другу в каком-то тревожном сне перед экзаменом. Намек дает проблеск комфорта, если только мы сможем найти «легкий путь». Если нет, мы всю ночь будем выполнять цепные правила внутри правил продукта внутри частных правил внутри цепных правил, у нас не хватит времени и, возможно, мы провалим экзамен. По сути, если вы видите подобную проблему и не знаете, как это сделать, вам лучше вообще ее пропустить.

Но не будем этого делать! Хитрость заключается в том, чтобы использовать правила логарифмирования для расширения или переписать функцию еще до того, как мы упомянем слово «производная». Вот, я сказал это. Кратко рассмотрим правила логарифмирования (и \(ln\), который является особым типом логарифма), наиболее важными из них являются:

журнал частного, а третий журнал мощности. Как это помогает? Обратите внимание, что наша задача состоит из логарифма произведения факторов в числителе, деленного на произведение некоторых других факторов в знаменателе. Мы можем определить Правило сложного логарифма , которое говорит нам, как действовать в таких ситуациях, когда несколько факторов умножаются и делятся:

Обратите внимание, что множители в числителе становятся логарифмами, которые складываются, а множители в знаменателе становятся логарифмами, которые получают вычитано. Теперь давайте посмотрим на множители в нашей задаче:

Как видите, у нас три множителя в числителе и два в знаменателе. Разлагая сразу весь этот логарифм, получаем:

Обратите внимание, что два последних члена отрицательны, потому что их множители взяты из знаменателя. Мы могли бы остановиться на этом, но мы также можем еще больше упростить, переписав квадратный корень в последнем члене как рациональную экспоненту, используя правило логарифмирования степеней (третье в нашем списке правил) для первого, второго и в последнем члене и используя тот факт, что \(ln\) и \(e\) обратны друг другу в третьем члене:

Хорошо.