Производная от натурального логарифма в степени: Производная натурального логарифма (lnx)’

Traduzione di %d0%bd%d0%b0%d1%82%d1%83%d1%80%d0%b0%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9%20%d0%bb%d0%be%d0%b3%d0%b0%d1%80%d0%b8%d1%84%d0%bc in italiano

Esempio di frase tradotta: Еще 10 минут на 20 подъемов. ↔ Ancora dieci minuti per arrivare a venti.

• Glosbe Translate

• Google Translate

+ Aggiungi una traduzione Aggiungi

Al momento non abbiamo traduzioni per %d0%bd%d0%b0%d1%82%d1%83%d1%80%d0%b0%d0%bb%d1%8c%d0%bd%d1%8b%d0%b9%20%d0%bb%d0%be%d0%b3%d0%b0%d1%80%d0%b8%d1%84%d0%bc nel dizionario, forse puoi aggiungerne una? Assicurati di controllare la traduzione automatica, la memoria di traduzione o le traduzioni indirette.

Aggiungi un esempio Aggiungi

Declinazione Tema

Насколько же это было уместно, ведь выпускники назначались служить в 20 стран мира!

(Matteo 28:19, 20) Com’erano appropriate, visto che i diplomati sono stati mandati a servire in 20 paesi!

jw2019

Еще 10 минут на

20 подъемов.

Ancora dieci minuti per arrivare a venti.

OpenSubtitles2018.v3

Я знала, как высоко Бог ценит человека и его тело, но даже это не останавливало меня. Дженнифер, 20 лет

So che per Dio il corpo umano è prezioso, ma ciò non mi ha impedito di farlo”. — Jennifer, 20 anni.

jw2019

Впоследствии Бог прописал этот порядок в соглашении Закона, которое заключил с народом Израиль при посредстве Моисея (Исх 20:8—11; Вт 5:12—15).

Poi nel patto della Legge stipulato da Dio tramite Mosè con la nazione d’Israele questo diventò uno statuto legale. — Eso 20:8-11; De 5:12-15.

jw2019

Спорим на 20 баксов, что ты не сможешь провести целый день одна.

Scommetto venti dollari che non riuscirai a stare tutto il giorno da sola.

OpenSubtitles2018.v3

Когда мы помогаем другим, мы и сами в какой-то мере испытываем счастье и удовлетворение, и наше собственное бремя становится легче (Деяния

20:35).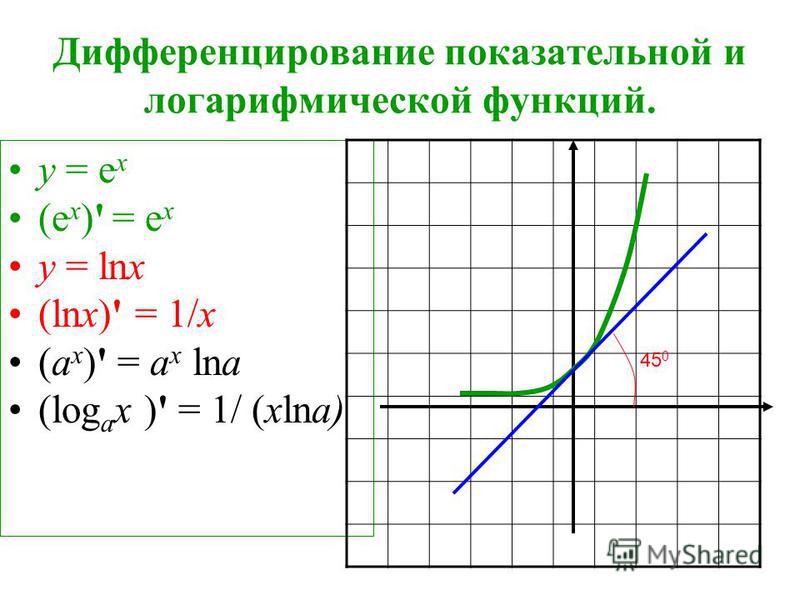

Quando ci prodighiamo per i nostri simili non solo aiutiamo loro, ma noi stessi proviamo una certa felicità e soddisfazione, e questo rende più sopportabili i nostri pesi. — Atti 20:35.

jw2019

20 Слова Иисуса из Матфея 28:19, 20 показывают, что креститься следует тем, кто сделался Его учеником.

20 Le parole di Gesù in Matteo 28:19, 20 indicano che si dovrebbero battezzare coloro che sono diventati suoi discepoli.

jw2019

Речь и обсуждение со слушателями, основанные на «Сторожевой башне» от 15 июля 2003 года, с. 20.

Discorso con partecipazione dell’uditorio basato sulla Torre di Guardia del 15 luglio 2003, pagina 20.

jw2019

Длина самолета составляла около 25 метров, размах крыльев –

20 метров.

L’aereo era lungo in tutto poco meno di venti metri, con un’apertura alare di diciannove metri e ventitre centimetri.

Literature

Спустя почти 40 лет, ко времени проведения второй переписи, число мужчин в племени Манассии возросло до 52 700, что было на 20 200 больше, чем в племени Ефрема (Чс 26:28—34, 37).

(Nu 13:1, 2, 11, 25-33) Quando circa quarant’anni più tardi si fece un secondo censimento, gli uomini della tribù erano saliti a 52.700, 20.200 più di Efraim.

jw2019

Ну, в то время, мы говорим о 80-х, в то время это было модно.

Beh, all’epoca, parliamo degli anni’80, erano molto di moda.

OpenSubtitles2018.v3

Мы входим в мир “Я исповедуюсь”[83].

Stiamo entrando nel mondo di Io confesso.

Literature

Он уехал 20 минут назад.

Se ne e’andato 20 minuti fa.

OpenSubtitles2018.v3

В 1996 году Ланге вступился за противоречивую работу исследователя ВИЧ/СПИДА Дэвида Хо, который лечил инфицированных пациентов, прописывая им по 20 таблеток в день, как одну из процедур режима по приему «коктейля» из множества лекарств.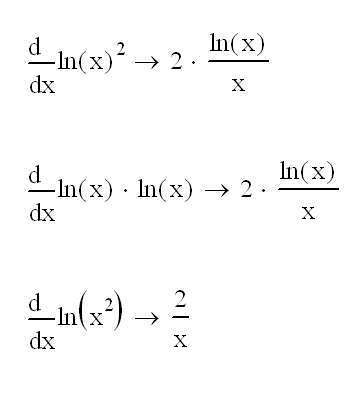

Nel 1996, Lange ha difeso il lavoro di David Ho, controverso ricercatore sull’HIV e l’AIDS, che trattava i pazienti infetti facendogli assumere 20 pillole al giorno all’interno di un regime terapeutico costituito da un «cocktail» di molti farmaci.

WikiMatrix

Предполагая, что такие вкладчики находят держателей FE желающих приобрести их BE, то вырисовывается значительный курс BE к FE, который зависит от размера сделки, относительного нетерпения держателей

BE и ожидаемой продолжительности контроля над движением капитала.

Supponendo che tali depositanti trovano dei possessori di euro liberi disposti ad acquistare i loro euro bancari, emerge un sostanziale tasso di cambio euro libero-euro bancario, che varia con le dimensioni dell’operazione, l’impazienza dei titolari di euro bancari e la durata prevista dei controlli sui capitali.

ProjectSyndicate

Я был женат 20 лет.

Sono stato sposato per vent’anni.

OpenSubtitles2018.v3

Их высота варьирует от 2 до 20 м. Листья перистые, длиной 2—12 м. По информации базы данных The Plant List, род включает 25 видов: Arenga australasica (H.Wendl. & Drude) S.T.Blake ex H.E.Moore Arenga brevipes Becc.

Comprende palme generalmente di dimensioni piccole o medie, alte da 2 a

20 m e con foglie lunghe da 2 a 12 m. Comprende le seguenti specie: Arenga australasica (H.Wendl. & Drude) S.T.Blake ex H.E.Moore Arenga brevipes Becc.

WikiMatrix

20 Оставлена родителями, но любима Богом

20 Abbandonata dai genitori, amata da Dio

jw2019

(Смех) А теперь, встаньте те, кто сел, когда я сказал 20.

(Risate) Vediamo gli altri, chiunque si sia seduto durante i 20, di nuovo in piedi.

ted2019

Она ушла минут 20 назад.

Se n’e’andata 20 minuti fa.

OpenSubtitles2018. v3

Ты сейчас рванул с 20 до 150 километров за 2 секунды!

Sei appena passato da 10 a tipo 110 in 2 secondi netti.

OpenSubtitles2018.v3

Когда в 80-х годах люди якудзы увидели, как легко брать ссуды и «делать» деньги, они создали компании и занялись операциями с недвижимым имуществом и куплей-продажей акций.

Quando la Yakuza vide quanto era facile ottenere prestiti e far soldi negli anni ’80, costituì delle società e si tuffò nelle operazioni immobiliari e nelle speculazioni in borsa.

jw2019

Вот что пророчествовал Алма жителям Гидеона около 83 года до Р. Х.:

Attorno all’83 a.C.Alma profetizzò quanto segue al popolo di Gedeone:

Обычно проводят связь между этим древним городом и современной Газой (Газза, Азза), расположенной примерно в 80 км к З.-Ю.-З. от Иерусалима.

In genere l’antica città viene identificata con l’odierna Gaza (Ghazzeh; ʽAzza), circa 80 km a OSO di Gerusalemme.

jw2019

Искренне беспокоясь о Павле, который находился в заключении в Риме, они помогали ему справляться с трудностями, поддерживая его материально (Фп 4:15—

20).

(Flp 4:14) Poiché si interessavano sinceramente di Paolo, prigioniero a Roma, lo incoraggiarono a sopportare la tribolazione aiutandolo materialmente. — Flp 4:15-20.

jw2019 Elenco delle richieste più frequenti: 1K, ~2K, ~3K, ~4K, ~5K, ~5-10K, ~10-20K, ~20-50K, ~50-100K, ~100k-200K, ~200-500K, ~1M

Запишите основание натурального логарифма

Определение

Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x )′ = 1/ x .

Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045. ;
.

График натурального логарифма ln x

График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .

Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.

Область определения	0
Область значений	– ∞
Монотонность	монотонно возрастает
Нули, y = 0	x = 1
Точки пересечения с осью ординат, x = 0	нет
+ ∞
– ∞

Значения ln x

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе «Логарифм».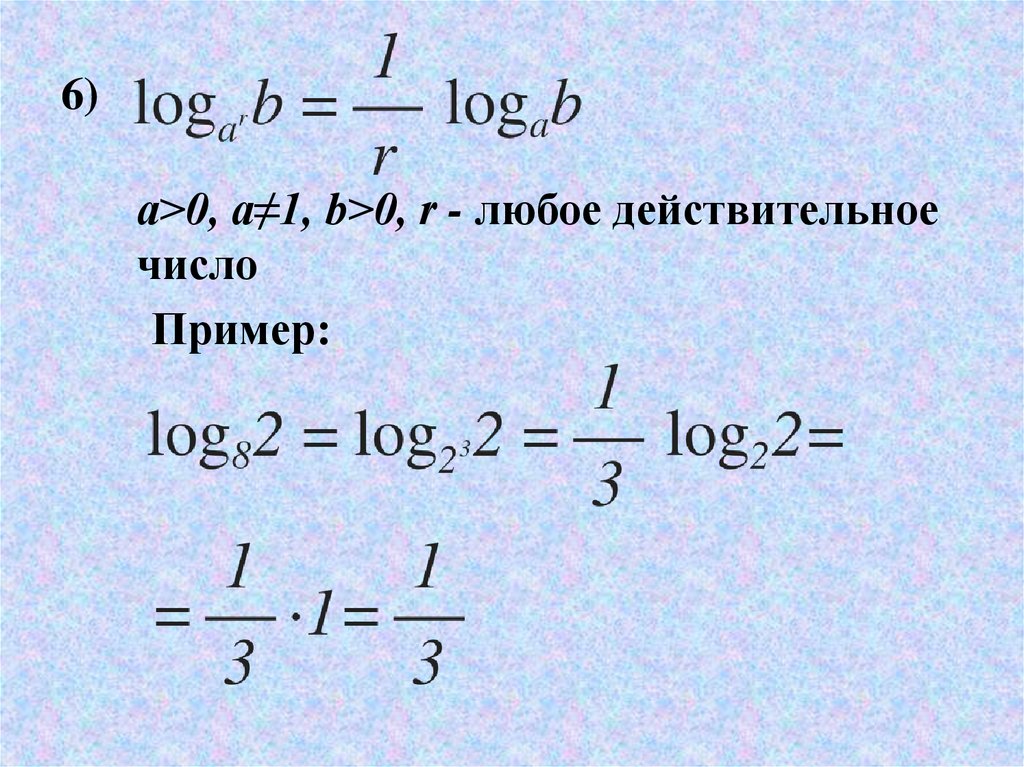

Обратная функция

Обратной для натурального логарифма является экспонента.

Если 0)»> , то

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Выражения через комплексные числа

Рассмотрим функцию комплексной переменной z :
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n .

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов . Опубликовано: 05-04-2014 Изменено: 20-03-2017

Число e может быть определено несколькими способами.

• Через предел: (второй замечательный предел).
• Как сумма ряда: или .
• Как единственное число a, для которого выполняется
• Как единственное положительное число a, для которого верно

Свойства

• 
  Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения является функция , где c — произвольная константа.
• Число eиррационально и даже трансцендентно. Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 годуШарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
• , см. формула Эйлера, в частности

Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса»

Для любого комплексного числаz верны следующие равенства:

Число e разлагается в бесконечную цепную дробь следующим образом: , то есть

Представление Каталана:

История

Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен

.

Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).

Предполагается, что автором таблицы был английский математик Отред.

Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:

Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.

Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.

Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler ).

Способы запоминания

• Для получения приблизительного значения нужно выписать подряд цифры, выражающие число букв в словах следующего стишка, и поставить запятую после первого знака: «Мы порхали и блистали, но застряли в перевале; не признали наши крали авторалли».
• Стишок:

Два и семь, восемнадцать, Двадцать восемь, восемнадцать, Двадцать восемь, сорок пять, Девяносто, сорок пять.

• Легко запомнить как 2, далее запоминаем 71, потом повторяющиеся 82, 81, 82
• Число e можно запомнить по следующему мнемоническому правилу: два и семь, далее два раза год рождения Льва Толстого (1828), затем углы равнобедренного прямоугольного треугольника (45, 90 и 45 градусов). Стихотворная мнемофраза, иллюстрирующая часть этого правила: «Экспоненту помнить способ есть простой: две и семь десятых, дважды Лев Толстой»
• Цифры 45, 90 и 45 можно запоминать как «год победы над фашистской Германией, затем дважды этот год и снова он»
• В другом варианте правила e связывается с президентом СШАЭндрю Джексоном: 2 — столько раз избирался, 7 — он был седьмым президентом США, 1828 — год его избрания, повторяется дважды, поскольку Джексон дважды избирался. Затем — опять-таки равнобедренный прямоугольный треугольник.

Доказательство иррациональности

Пускай

рационально. Тогда , где и целые положительные, откуда

Умножая обе части уравнения на

, получаем

Переносим

в левую часть:

Все слагаемые правой части целые, следовательно:

— целое

Но с другой стороны

Интересные факты

• В IPO компании 2004 году было объявлено о намерении компании увеличить свою прибыль на 2 718 281 828 долларов. Заявленная цифра представляет собой первые 10 цифр известной математической константы.
• В языках программирования символу e в экспоненциальных записях числовых литералов соответствует число 10, а не Эйлерово число. Это связано с историей создания и использования языка для математических вычислений FORTRAN[2] :

Я начал программировать в 1960 году на FORTRAN II, используя компьютер IBM 1620. В то время, в 60-е и 70-е годы, FORTRAN использовал только заглавные буквы. Возможно, это произошло потому, что большинство старых устройств ввода были телетайпами, работавшими с 5-битовым кодом Бодо, который не поддерживал строчные буквы. Буква E в экспоненциальной записи тоже была заглавной и не смешивалась с основанием натурального логарифма e , которое всегда записывается маленькой буквой. Символ E просто выражал экспоненциальный характер, то есть обозначал основание системы — обычно таким было 10. В те годы программисты широко использовали восьмеричную систему. И хотя я не замечал такого, но если бы я увидел восьмеричное число в экспоненциальной форме, я бы предположил, что имеется в виду основание 8. Первый раз я встретился с использованием маленькой e в экспоненциальной записи в конце 70-х годов, и это было очень неудобно. Проблемы появились потом, когда строчные буквы по инерции перешли в FORTRAN. У нас существовали все нужные функции для действий с натуральными логарифмами, но все они записывались прописными буквами.

Примечания

1. ↑2 миллиона цифр после запятой
2. ↑Эккель Б. Философия Java = Thinking in Java. — 4-е изд. — СПб.: Питер, 2009. — С. 84. — (Библиотека программиста). — ISBN 978-5-388-00003-3

См. также

Ссылки

• История числа e (англ.)
• e for 2.71828… (история и правило Джексона, англ.)
• последовательность A001113 в OEIS

Числа с собственными именами
Вещественные	Золотое сечение | e (число Эйлера) | Пи | Число Скьюза
Натуральные	Чёртова дюжина | Число зверя | Число Рамануджана — Харди
Степени десяти	Мириада | Гугол | Асанкхейя | Гуголплекс
Степени тысячи	Тысяча | Миллион | Миллиард | Биллион | Триллион … | … Центиллион | Зиллион
Степени двенадцати	Дюжина | Гросс | Масса
Литературные меры счёта	Доцанд | Мириад

Wikimedia Foundation .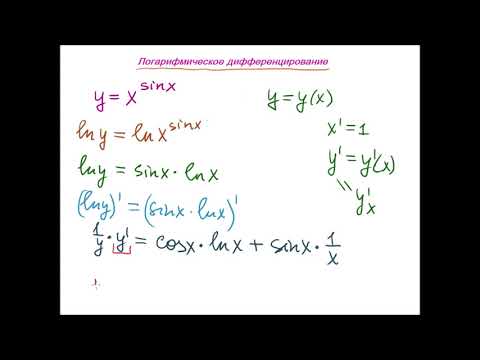 2010 .

Смотреть что такое «Основание натуральных логарифмов» в других словарях:

ОСНОВАНИЕ (ЛОГАРИФМОВ) — (base, logarithms) Число, степени которого являются значениями логарифма (logarithms). Наиболее распространенными основаниями являются число 10, когда при у=log(x), х=10y; и число е, для натуральных логарифмов (natural logarithms), часто… … Экономический словарь

Стирлинга формула — формула где π = 3,14159. е = 2,71828. (основание натуральных логарифмов), дающая приближённое выражение произведения n первых натуральных чисел (факториала): 1∙2∙. ∙n = n!, когда число n сомножителей велико. Формула Стирлинга получена… … Энциклопедический словарь

Знаки математические — условные обозначения, предназначенные для записи математических понятий, предложений и выкладок. Например, √2 (квадратный корень из двух), 3 > 2 (три больше двух) и т.п. Развитие математической символики было тесно… … Большая советская энциклопедия

ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения, предназначенные для записи математич. понятий и выкладок. Напр., понятие квадратный корень из числа, равного отношению длины окружности к ее диаметру обозначается кратко а предложение отношение длины окружности к ее диаметру … Математическая энциклопедия

ЯДЕРНЫЙ СИНТЕЗ — термоядерный синтез, реакция слияния легких атомных ядер в более тяжелые ядра, происходящая при сверхвысокой температуре и сопровождающаяся выделением огромных количеств энергии. Ядерный синтез это реакция, обратная делению атомов: в последней… … Энциклопедия Кольера

Непер — I Непер Нейпир (Napier) Джон (1550, Мерчистон Касл, близ Эдинбурга, 4.4.1617, там же), шотландский математик, изобретатель Логарифмов. Учился в Эдинбургском университете. Основными идеями учения о логарифмах Н. овладел не позднее 1594,… … Большая советская энциклопедия

КОНЕЧНЫЕ РАЗНОСТИ — Исчисление конечных разностей связано с изучением свойств и применений разностей между соседними членами какой нибудь последовательности или между значениями функции в точках, расположенных с постоянным интервалом в некотором пространстве. Слово… … Энциклопедия Кольера

Единицы измерения информации — служат для измерения объёма информации величины, исчисляемой логарифмически.[1] Это означает, что когда несколько объектов рассматриваются как один, количество возможных состояний перемножается, а количество информации складывается. Не важно,… … Википедия

Единицы количества информации — Единицы измерения информации служат для измерения объёма информации величины, исчисляемой логарифмически.[1] Это означает, что когда несколько объектов рассматриваются как один, количество возможных состояний перемножается, а количество… … Википедия

Единицы измерения ёмкости носителей и объёма информации — Единицы измерения информации служат для измерения различных характеристик связанных с информацией. Чаще всего измерение информации касается измерения ёмкости компьютерной памяти (запоминающих устройств) и измерения объёма данных, передаваемых по… … Википедия

Определение. Логарифмом числа b по основанию a , где a > 0 , a ≠ 1 , b > 0 , называется показатель степени, в которую нужно возвести основание a , чтоб получить число b .

Определение. Натуральный логарифм — логарифм основанием, которого является число e .

Другими словами, натуральный логарифм числа b является решением уравнения e x = b .

Обозначение. Натуральный логарифм обозначается ln x .

Калькулятор натуральных логарифмов

Свойства натуральных логарифмов

ln x = log _e x — так как основание натурального логарифма равно числу e .

ln( x · y ) = ln x + ln y

ln x y = ln x — ln y

ln x y , 0 x y (ln x — возрастающая функция)

x 1 + x ≤ ln (1 + x ) ≤ x , если x > -1

∫	ln x dx = x ln x — x + C

lim	ln x = -∞
x → +0

lim	ln (1 — x ) x = 1
x → +0

ln (1 + x ) = ∑ n = 1 ∞ (-1) n + 1 n x n , для | x | x ) = x — x 2 2 + x 3 3 — x 4 4 + . + (-1) n + 1 x n n , (| x | a может быть определен как площадь, заключённая под кривой графика 1 x на участке от 1 до a ,

ln a = ∫ 1 a d x x

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Мэтуэй | Популярные задачи

92) 9(3x) по отношению к x 92+1

1	Найти производную — d/dx	бревно натуральное х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найти производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найти производную — d/dx	грех(2x)
23	Найти производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) относительно x
42	Найти производную — d/dx	1/(корень квадратный из х)
43	Оценка интеграла 9бесконечность
45	Найти производную — d/dx	х/2
46	Найти производную — d/dx	-cos(x)
47	Найти производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найти производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найти производную — d/dx	лог х
86	Найти производную — d/dx	арктан(х)
87	Найти производную — d/dx	бревно натуральное 5х92

Видео с вопросами: Использование логарифмического дифференцирования для дифференцирования логарифмической функции в степени X

Стенограмма видео

Учитывая, что 𝑦 равно натуральному логарифму 𝑥, возведенному в степень 𝑥, найдите d𝑦 по d𝑥.

Нам дана функция 𝑦, представляющая собой натуральный логарифм, то есть логарифм по основанию 𝑒 всех 𝑥, возведенных в степень 𝑥. И нам нужно найти производную d𝑦 по d𝑥. Для этого мы будем использовать технику логарифмического дифференцирования и иногда будем называть натуральные логарифмы ln.

Мы используем логарифмическое дифференцирование, чтобы дифференцировать функции, которые нелегко дифференцировать с помощью наших обычных методов, например, когда наш показатель степени является переменной, как в этом случае. Если у нас есть функция 𝑦 есть 𝑓 от 𝑥, наш первый шаг в логарифмическом дифференцировании — применить натуральный логарифм к обеим частям. Это дает нам ln 𝑦 равно ln 𝑓 из 𝑥. И это справедливо для 𝑦 больше нуля. Нам нужно указать это условие, поскольку журнал не существует для отрицательных значений, а журнал нулей не определен.

В нашем случае наша функция 𝑦 есть число 𝑥, возведенное в степень 𝑥. Итак, взяв натуральные логарифмы, мы имеем, что ln 𝑦 равно натуральному логарифму числа ln 𝑥, возведенному в степень 𝑥. И это для 𝑦 больше нуля.

Наш второй шаг — использовать законы логарифмов для упрощения или расширения. В нашем случае справа стоит показатель степени 𝑥. И мы можем использовать правило степени для логарифмов. Это говорит нам о том, что логарифм по основанию 𝑎 числа 𝑏, возведенный в степень 𝑐, равен 𝑐, умноженному на логарифм по основанию 𝑎 числа 𝑏. То есть мы можем вывести наш показатель степени 𝑐 вперед и умножить на него. Тогда в нашей правой части мы можем вывести наш показатель степени 𝑥 вперед и умножить на него. Итак, мы имеем, что ln 𝑦 равно 𝑥, умноженному на натуральный логарифм ln 𝑥.

Наш третий шаг в логарифмическом дифференцировании — дифференцировать обе части по 𝑥. С левой стороны мы можем использовать известный результат, что d на d𝑥 от ln 𝑢, где 𝑢 — функция от 𝑥, которая больше нуля, равно единице на 𝑢, умноженной на d𝑢 на d𝑥. В нашем случае это означает, что в левой части получается один более чем 𝑦, умноженный на d𝑦 на d𝑥.

Теперь, чтобы продифференцировать правую часть, заметим, что у нас есть произведение функций от 𝑥. Таким образом, мы можем положить 𝑢 of 𝑥 равным 𝑥, а 𝑣 of 𝑥 равным натуральному логарифму ln 𝑥. И чтобы дифференцировать наш продукт, мы можем использовать правило продукта для дифференциации. Это говорит нам о том, что для произведения 𝑢𝑣 d на d𝑥 из 𝑢𝑣 равно 𝑢, умноженному на d𝑣 на d𝑥, плюс 𝑣, умноженному на d𝑢 на d𝑥.

Теперь, поскольку наша функция 𝑢 равна 𝑥, d𝑢 на d𝑥 равно единице. И теперь для нашей функции 𝑣, которая равна натуральному логарифму ln 𝑥, мы можем снова использовать известный результат. Это говорит нам, что для 𝑔, функции от 𝑥, которая больше нуля, d на d𝑥 от ln 𝑔 равно единице над 𝑔, умноженной на d𝑔 на d𝑥. В нашем случае 𝑔 равно ln 𝑥. Итак, мы имеем d𝑣 на d𝑥 на единицу над ln 𝑥, умноженное на d на d𝑥 из ln 𝑥.

Теперь мы также знаем, что d на d𝑥 числа ln 𝑥 равно единице на 𝑥. Это для 𝑥 больше нуля. Итак, наконец, мы имеем d𝑣 на d𝑥 равно единице на ln 𝑥, умноженной на единицу на 𝑥. И мы можем переписать это как единицу над 𝑥, умноженную на ln 𝑥.

И, сделав немного места и заметив это, теперь у нас есть все, что нам нужно, чтобы применить правило произведения для дифференциации. Это дает нам 𝑥, то есть 𝑢, умноженное на единицу на 𝑥 ln 𝑥, что является 𝑣 простым, это d𝑣 на d𝑥, плюс натуральный логарифм ln 𝑥, который равен 𝑣, умноженный на единицу, что является 𝑢 простым числом. Это d𝑢 от d𝑥.

Разделив числитель и знаменатель на 𝑥 в нашем первом члене, они сокращаются. А поскольку все, что умножается на единицу, равно самому себе, в правой части у нас есть единица над ln 𝑥 плюс натуральный логарифм от ln 𝑥.

И это подводит нас к четвертому шагу логарифмического дифференцирования, который заключается в том, чтобы найти d𝑦 с помощью d𝑥. Мы можем сделать это, умножив обе части на 𝑦, которые затем сокращаются в левой части. Таким образом, d𝑦 на d𝑥 равно 𝑦, умноженному на единицу над ln 𝑥 плюс натуральный логарифм от ln 𝑥.

А теперь, вспомнив, что 𝑦 равно ln 𝑥, возведенному в степень 𝑥, подставив это вместо 𝑦, мы получим ln 𝑥, возведенное в степень 𝑥, умноженное на единицу над ln 𝑥 плюс натуральный логарифм числа ln 𝑥. Преобразуя это для нашего окончательного ответа, тогда, если 𝑦 равно ln 𝑥, возведенному в степень 𝑥, то d𝑦 на d𝑥 равно ln 𝑥, возведенному в степень 𝑥, умноженному на натуральный логарифм числа ln 𝑥 плюс один поверх ln 𝑥.