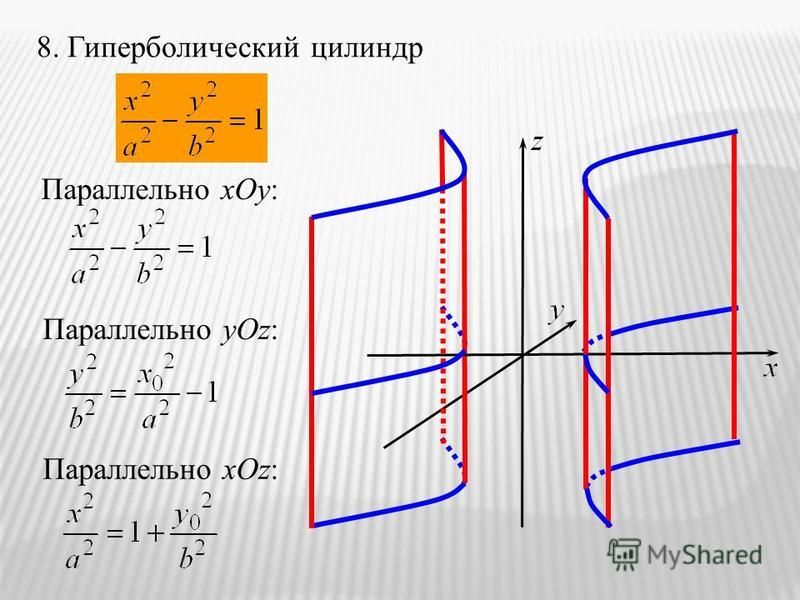
Косинус гиперболический 0: Онлайн калькулятор: Гиперболические функции

Гиперболические функции, и обратные им.

Следующая сервисная программа «Hyp» (КС 33671/101, mkp) позволяет использовать в расчётах на МК-152 гиперболические и обратные гиперболические функции, превращая С/П в префиксную клавишу Hyp:

 00.БП    01.82   02.БП   03.27   04.БП   05.34   06.БП   07.41   08.БП   09.50
 10.БП    11.57   12.БП   13.65   14.БП   15.71   16.В↑   17.1    18.-    19.2
 20.XY    21.%    22.1    23.+    24.F√   25.Fln  26.В/О  27.Fe^x  28.В↑   29.F1/x
 30.-     31.2    32.%    33.В/О  34.Fe^x  35.В↑   36.F1/x 37.+    38.2    39.%
 40.В/О   41.Fe^x  42.В↑   43.В↑   44.ПП   45.36   46.-    47.FВx  48.%    49.В/О
 50.Fe^x   51.В↑   52.В↑   53.ПП   54.29   55.БП   56.46   57.В↑   58.Fx²  59.1
 60.+     61.F√   62.+    63.Fln  64.В/О  65.В↑   66.Fx²  67.1    68.-    69.БП
 70.61    71.В↑   72.1    73.XY   74.+    75.1    76.FВx  77.-    78.%    79.F√
 80.Fln   81.В/О  82.ПП   83.87   84.С/П  85. БП   86.82   87.PП   88.94   89.PП
 90.90    91.Fo   92.PП   93.91   94.Fo   95.PП   96.92   97.XY   98.PП   99.93
100.PPИП  01.90   02.29   03.KNOT 04.Fx≠0 05.00   06.PPИП 07.90   08.41   09.6
110.2     11.+    12.PП   13.96   14.PPП  15.90   16.42   17.XY   18.В↑   19.PPИП
120.90    21.44   22.Fx≠0 23.59   24.-    25.Fx=0 26.17   27.PPИП 28.90   29.42
130.В↑    31.PИП  32.96   33.-    34.PП   35.97   36.+    37.1    38.7    39.1
140.-     41.PП   42.95   43.PИП  44.97   45.ПП   46.88   47.1    48.0    49.4
150.PPП   51.90   52.25   53.PИП  54.94   55.PKПП 56.95   57.PП   58.90   59.PИП
160.94    61.XY   62.PИП  63.93   64.PИП  65.92   66.PИП  67.91   68.PИП  69.90
170.В/О   71.F8   72.F7   73.F6   74.EF   75.FB   76.FA   77.F9   78.F0   79.00
180.50    81.20   82.00   83.50   84.20   85.61   86.72   87.00   88.5    89.-
190.Fx<0  91.97   92.4    93.+    94.9    95.БП   96.99   97.1    98.2    99.PИП
200.96    01.+    02.PPП  03.90   04.26   05.XY   06.2    07.-    08.Fx≠0 09.14
210. 
  Fx≥0  11.19   12.ПП   13.23   14.1    15.1    16.6    17.БП   18.25   19.1
220.+     21.Fx=0 22.29   23.9    24.9    25.PPП  26.90   27.25   28.В/О  29.1
230.1     31.5    32.БП   33.25

Программа работает с действительными числами (если приходится извлекать корень из отрицательного числа, выдаётся сообщение об ошибке, которое сбрасывается клавишей В/О) и развивает идею «Программы 4.8» (Дьяконов-89, стр. 175). С математической точки зрения добавлено вычисление гиперболического котангенса (cth x) и обратного гиперболического котангенса (arcth x). Сервис программы улучшен, т.к. использует новые возможности МК-152 по опросу клавиатуры и выводу видеосообщений.

Изменения в стеке — обычные для вычисления унарных функций, аргумент можно восстановить по F Вx. Программа использует только десятичные регистры 90-96, то есть регистры R0…RE доступны для использования при вычислениях, как обычно. Переключатель размерности угловых величин Р-ГРД-Г может стоять в любом положении, на вычисление гиперболических функций он не влияет.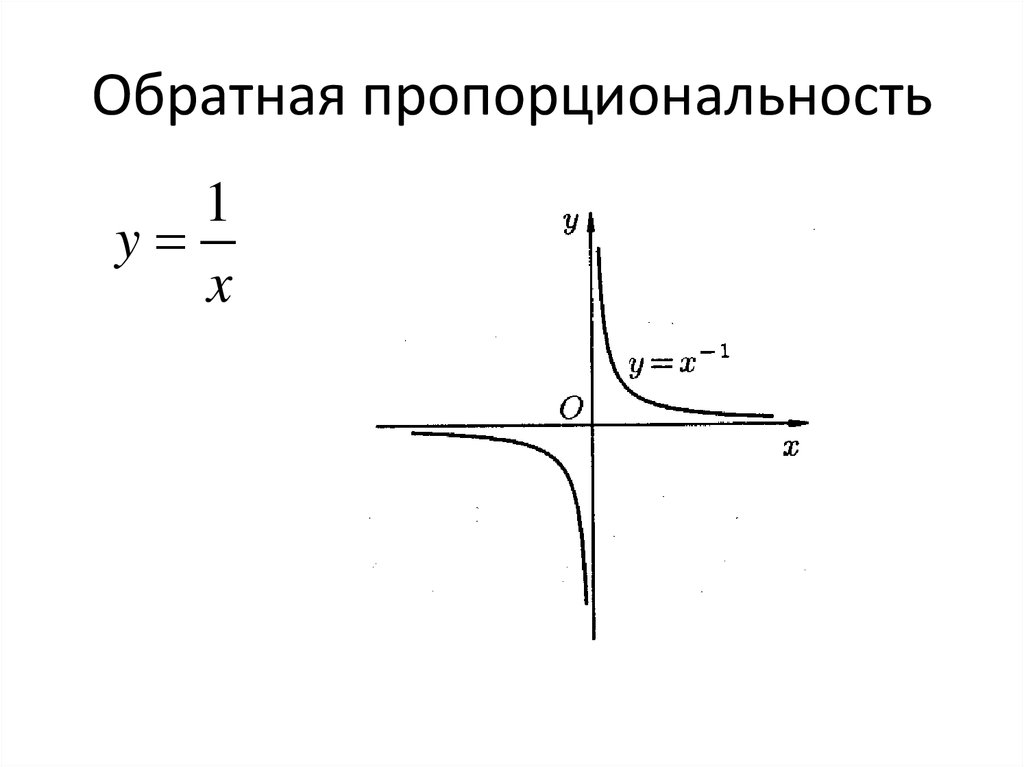

Третий тест Фролова (1 – arsh arch arth arcth cth th ch sh 1) даёт 1e-11, что довольно неплохо.

Инструкция: ввести аргумент, последовательно нажать «префиксную» клавишу С/П и клавишу соответствующей тригонометрической функции (например 7 для sin, 5 для arccos; для котангенса и арккотангенса используются клавиши «минус» и «плюс»). Перед первым запуском (и в случае появления сообщения об ошибке) следует нажать В/О или перейти на начало программы с помощью P БП, если «Hyp» загружена не с нулевой страницы.

Пример: В/О 1 С/П 7. На экране sh (1) = 1,1752012.

Расчётная часть программы (шаги 02-81) почти не изменилась за прошедшие 18 лет и может использоваться отдельно, как библиотека. В этом случае для вычисления гиперболических функций используются следующие точки входа (сохранность стека не гарантируется, зато регистры не используются вообще):

ПП 02 — sh x = (e^x–e^–x)/2 — гиперболический синус

ПП 04 — ch x = (e^x+e^–x)/2 — гиперболический косинус

ПП 06 — th x = sh x / ch x — гиперболический тангенс

ПП 08 — cth x = ch x / sh x — гиперболический котангенс

ПП 10 — arsh x = ln (x+ sqr(x²+1)) — обратный гиперболический синус

ПП 12 — arch x = ln (x+ sqr(x²–1)) — обратный гиперболический косинус

ПП 14 — arth x = ln sqr ((1+x)(1–x)) — обратный гиперболический тангенс

ПП 16 — arcth x = ln sqr ((x+1)/(x–1)) — обратный гиперболический котангенс

Трюк с главным циклом (82-86), позволяющий зациклить многостраничную программу, нам уже знаком по программе «Календарь-2».

Блоки сохранения (87-99) и восстановления (159-170) стека в R90-R94 тоже тривиальны. Отмечу лишь, что регистр X1 сохранить не удаётся, а из-за пропускания чисел через регистры стек в новой прошивке «усекается» с 14 разрядов до 12-ти. Вызов подпрограмм 02…16 напрямую не сильно повысит точность, т.к. используемая функция Fe^x не даёт точный 14-й знак (можете сверить результат 1 Fe^x с точным значением e).

В тексте программы есть два небольших блока данных, набираемых в режиме HEX (P ПРГ). Первый (171-179) содержит инвертированные (KNOT) коды восьми задействованных клавиш и завершается нулём, а второй (180-187) — два видеосообщения, для гиперболических и обратных функций. Шаги 100-105 ожидают нажатие клавиши, а блок 106-126 находит её в первом блоке данных. Адрес этого блока высчитывается относительно счётчика адреса и записывается в R96. Значение регистра 96 позже используется в блоке вывода (194-204), что делает программу перемещаемой.

Блок 127-142 вычисляет адрес подпрограммы, которая соответствует нажатой клавише и записывает его в R95.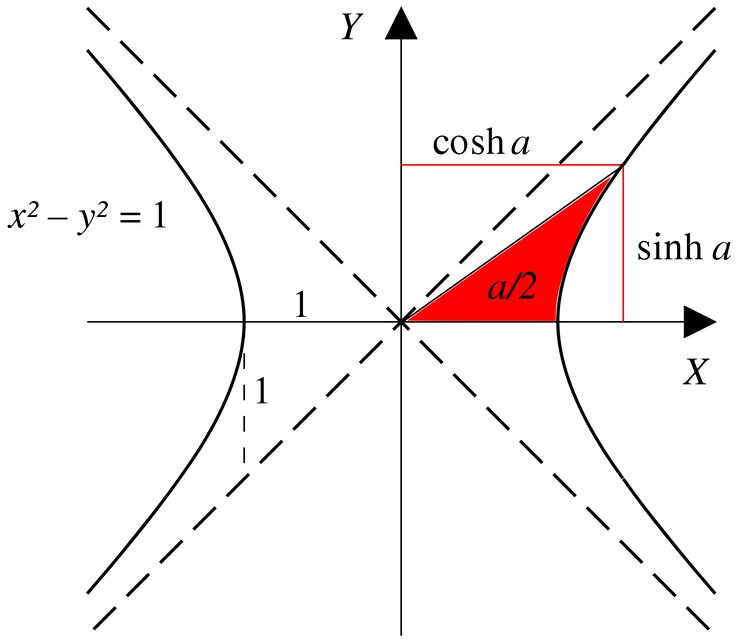 Блок 143-152 с помощью забавной подпрограммы 188-233 выводит в строку комментария название вычисляемой функции. Ну и, наконец, блок 153-158 организует вызов требуемой функции.

2=1$, и рассмотрим площадь, ограниченную дугой этой гиперболы, начинающейся в точке $(1,0)$, если оба конца этой дуги соединены с началом координат $(0,0)$. Дважды эта площадь соответствует углу круговой тригонометрической функции, а синус и шиш этого аргумента будут координатами $y$ и $x$ точки, где заканчивается ваша дуга на гиперболе.

Используя изображение из Википедии, чтобы проиллюстрировать это:

Как они вообще связаны с числом Эйлера? 94}{4!} &&&&{}+ \;\cdots \\ \end{alignat*}

Как видите, все тригонометрических функций тесно связаны с экспоненциальной функцией и, следовательно, с $e$. Круговые тригонометрические функции имеют эти чередующиеся знаки, которые лучше всего объясняются чисто воображаемым аргументом экспоненциальной функции. У гиперболических функций этого нет, поэтому выражение их через $e$ довольно интуитивно понятно даже по сравнению с вещественными числами. Если вы хотите выразить все через экспоненциальную функцию, вы можете сделать это так:
\begin{выравнивание*} \sin(x) &= \frac{\exp(ix)-\exp(-ix)}{2i} & \sinh(x) &= \frac{\exp(x)-\exp(-x)}{2} \\ \cos(x) &= \frac{\exp(ix)+\exp(-ix)}{2} & \ сп (х) & = \ гидроразрыва {\ ехр (х) + \ ехр (- х)} {2} \end{выравнивание*}
Как были получены/открыты гиперболические функции?
Обратите внимание, что приведенное выше является объяснением того, как вы можете интерпретировать эти функции и как вы можете увидеть связь с экспоненциальной функцией. Это ни в коем случае не историческое объяснение того, как эти вещи были впервые обнаружены.
Я недостаточно знаю математику, чтобы ответить на этот вопрос. В этом смысле приведенный выше ответ неполный.
Если бы мне пришлось гадать, то я бы предположил, что эти ряды или члены, использующие экспоненциальные функции, появлялись в некоторых уравнениях, и после того, как они появлялись достаточно часто, кто-то решил дать им имя. Выбранное название указывало на то, что к тому времени было понятно как отношение к круговой тригонометрической функции, так и к гиперболе, но это не обязательно означает, что гиперболы были предметом изучения, когда они впервые появились. Хотя может быть.
Википедия говорит об этом:
Гиперболические функции были введены в 1760-х годах независимо друг от друга Винченцо Риккати и Иоганном Генрихом Ламбертом.
[3]
Может быть, эта книга даст больше информации.
мягкий вопрос — Использование гиперболических тригонометрических функций в реальном мире
спросил 12 лет, 8 месяцев назад
Изменено 3 года, 6 месяцев назад
Просмотрено 61к раз
$\begingroup$
Я изучал гиперболические тригонометрические функции на недавнем курсе математики. Однако мне никогда не приводили никаких причин относительно , почему (или даже если) они полезны.
Есть ли хорошие примеры их использования вне научных кругов?
мягкий вопрос
большой список
приложения
гиперболические функции
$\endgroup$
1
$\begingroup$
Если вы возьмете веревку, закрепите два конца и позволите ей висеть под действием силы тяжести, она естественным образом образует гиперболическую косинусную кривую.
$\endgroup$
3
$\begingroup$
Контактная сеть упоминалась несколько раз, но, по-видимому, не соответствующая поверхность вращения, катеноид. Она и плоскость — единственные поверхности вращения, имеющие нулевую среднюю кривизну (т. е. они равны минимальные поверхности ). Эта поверхность представляет собой форму мыльного пузыря (приблизительно), когда он растягивается на два кольца:

(изображение отсюда)
$\endgroup$
$\begingroup$
На карте, использующей проекцию Меркатора, отношение между широтой L точки и ее координатой y на карте определяется выражением $y = \operatorname{arctanh}(\sin(L))$, где $\operatorname{arctanh}$ — функция, обратная гиперболическому тангенсу.
$\endgroup$
$\begingroup$
Сложение скоростей в (специальной) теории относительности не является линейным, но становится линейным, если выражается в терминах функций гиперболического тангенса.
Точнее, если добавить два движения в одном направлении, например, человека, идущего со скоростью $v_1$ в поезде, который движется со скоростью $v_2$ относительно земли, скорость человека относительно земли $v$ не $v_1 + v_2$; скорости не складываются (в противном случае, добавив достаточное количество из них, вы могли бы превысить скорость света). Что добавляет, так это 9{-x}}=\frac{1+\tanh(\frac{x}{2})}{2}$
Среди многих применений и применений логистической функции/гиперболического тангенса есть:
Будучи функция активации для нейронных сетей. Это универсальные аппроксиматоры функций, которые в значительной степени становятся центральными в современном ИИ.
Распределение Ферми-Дирака и модель Изинга в статистической механике
Быть сигмовидной функцией («S-образной») означает, что она может быть кандидатом в кумулятивную функцию распределения, предполагая, что ее производная может использоваться для моделирования некоторой случайной величины
Моделирование прироста/убыли населения. Хотя это больше относится к области биологии, с точки зрения динамической системы она, безусловно, весьма привлекательна.
Рассматривая $\tanh(kx)$, можно аппроксимировать ступенчатую функцию Хевисайда (задав $k$ достаточно большим числом) так, чтобы она оставалась непрерывной и бесконечно дифференцируемой. Это можно использовать при решении ДУ в физике для анализа действия, например, включения выключателя.
Переходя к $\cosh (x)$, у него также есть несколько интересных вариантов использования:
Висячая неэластичная цепь принимает форму $\cosh (x)$. Эта форма называется контактной сетью .
Мыльная пленка, соединяющая две параллельные непересекающиеся каркасные окружности, является поверхностью вращения $\cosh (x)$. Обычно это часто всплывает при изучении минимальных поверхностей.
В каноническом формализме статистической механики статистическая сумма двухуровневой системы с энергиями состояний системы $\pm\varepsilon$ определяется выражением $Z\propto\cosh(\varepsilon/k_B T)$. Это дает нам, что средняя энергия системы определяется выражением $\langle E\rangle \propto \varepsilon \tanh(\varepsilon/k_B T)$, что возвращает нас к $\tanh (x)$
В архитектуре, если у вас есть отдельно стоящая (то есть ненагруженная и неподдерживаемая) арка, оптимальная форма для обработки линий тяги, создаваемых собственным весом, равна $\cosh(x)$. Купол собора Святого Павла в Англии имеет поперечное сечение $\cosh(x)$. Этот тип арки также предпочитал в своей работе архитектор Антонио Гауди.
$\endgroup$
2
$\begingroup$
Я не знаю, считаете ли вы общую теорию относительности «вне академических кругов» (и я не хочу спорить об этом!), но если да, то
группу симметрий по отношению к лоренцевской метрике можно записать как Матрицы, содержащие в качестве элементов гиперболические триггерные функции.
Обратите внимание на комментарий Кенни.
$\endgroup$
2
$\begingroup$
Многие виды нелинейных УЧП имеют волновые решения, явно выраженные с помощью гиперболических тангенсов и секущих: профили ударных волн, солитоны, фронты реакции-диффузии и фронты фазового перехода, для начала.
No related posts.