Почему цифры так называются? Цифры во фразеологизмах.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Смирнова А.С. 1
1МБОУ СОШ №15 г.Красногорск
Пашкова О.М. 1
1МБОУ СОШ №15 г.Красногорск
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Цель:
Узнать, как появилось понятие «цифра».
Задачи:
Познакомиться с литературой по этой теме.
Подобрать иллюстрации.
Подобрать примеры из русского языка, в которых используются цифры.
Подготовить презентацию для выступления перед одноклассниками.
Введение
Мне нравится математика. Мы на уроке учимся считать, решать интересные задачи. Знакома с цифрами я давно. Когда была маленькой, то на пальчиках показывала, сколько конфеток хочу взять. Сейчас уже знаю все цифры, умею их писать и могу сосчитать даже до 100, а если меня не остановить, то и до 1000. Я всегда задаю много вопросов «Почему?». И вот мне в голову пришёл очередной вопрос: «А почему у нас в стране цифры называются именно так: один, два, три, четыре, пять…?». И всегда ли так было? Надо бы провести расследование.
Числа и цифры
Перед собой поставила цель: узнать, как появилось понятие «цифра». Мы уже выучили, что цифр всего 10. Это такие цифры: 1 — один, 2 — два, 3 – три, 4 – четыре, 5 – пять, 6 – шесть, 7 – семь, 8 – восемь, 9 – девять и 0 — ноль.
Возраст первой письменной системы цифр почти 5000 лет. Она появилась у шумеров в Месопотамии. Но и раньше люди пытались посчитать, например, количество зверей или собранных грибов. Сначала считала на пальцах одной руки, затем количество пальцев фиксировали. Часто говорят: «Знаю, как свои пять пальцев» (рис.1). Не с этого ли далекого времени пошло это выражение, когда знать, что пальцев пять, значило то же, что уметь считать?
Рис.1 Счёт на пальцах (10)
Известно, что в каменном веке люди делали насечки на костях (рис.2). Похожие палки с насечками использовались в Англии вплоть до 19 века. С их помощью запоминались чьи-либо долги.
Рис.2 Насечки на костях.
Славянские цифры
Старинная русская нумерация (возникшая около 10 в. и встречавшаяся до 16 в.) была алфавитной с применением славянской азбуки (рис.3).
Рис.3Старинная русская нумерация.
Славянские цифры — цифры древнерусского счёта, в котором каждое из целых чисел от 1 до 9, а также десятки и сотни обозначались буквами славянского алфавита с надписанным над ними знаком — (титло). Целые числа до 999 составлялись с помощью рядом стоящих славянских цифр. Например, = 324. Здесь = 300, = 20, = 4. Тысячи обозначались с помощью приставки к цифре, выражающей число тысяч некоторого знака.
В России славянская нумерация сохранилась до конца 17 века, а при Петре I перешли к “арабской нумерации”, которой мы пользуемся и сейчас.Арабские цифры
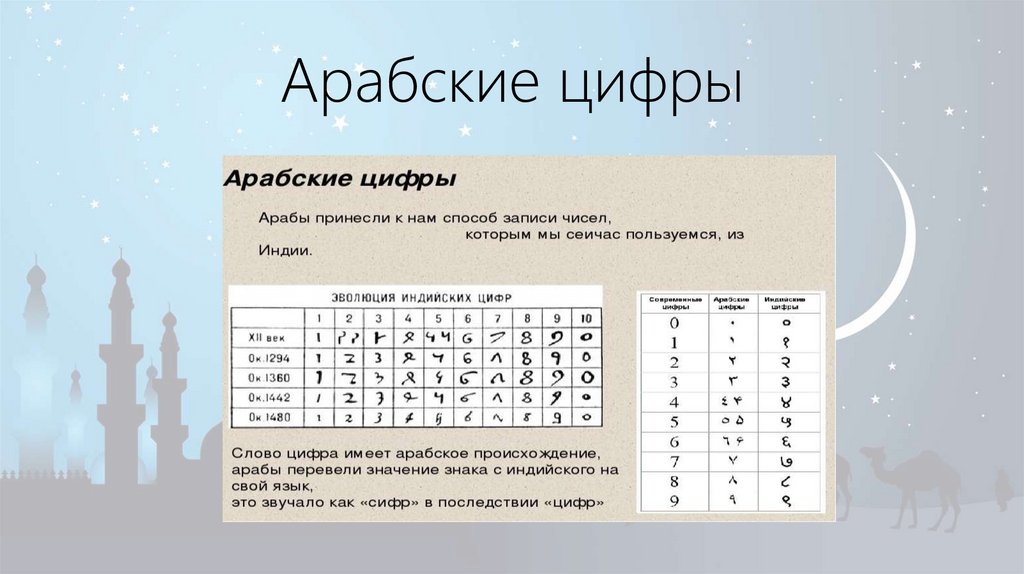
Цифры от 0 до 9 мы называем арабскими, потому что европейцы заимствовали их у арабов, а к нам они пришли уже из Европы.
Но вот сами арабы именуют эти цифры индийскими, а арифметику, основанную на счёте десятками – индийским счётом. Большинство древних индийских книг написано на санскрите – языке науки, который объединял учёных. Индийские цифры возникли в Индии не позднее V века. Как арабские цифры они стали известны европейцам в X веке. Индийскую систему записи широко популяризировал учёный Аль-Хорезми. В XII веке книга Аль-Хорезми «Об индийском счёте» была переведена на латинский язык и сыграла очень большую роль в развитии европейской арифметики и внедрении арабских цифр.
С середины ХVIII века слово цифра приобрело новое значение — знак числа. Совокупность цифр в русском языке называлась «цифирь». Дети, изучавшие счёт, говорили: «учу цифирь, пишу цифирь».
Современное слово “нуль” появилось гораздо позже, чем “цифра”.
Оно происходит от латинского слово “нулла” – “никакая”. Изобретение нуля считается одним из важнейших математических открытий. При новом способе записи чисел значение каждой написанной цифры стало прямо зависеть от позиции, места в числе. При помощи десяти цифр можно записать любое, даже самое большое число, и сразу ясно, какая цифра что обозначает.
Помимо знаков у чисел есть и собственные названия. Так нуль обозначали словами «пустой», «небо» или «дыра»; единицу – названиями одиночных предметов: «Луна», «Земля»; двойку — названиями парных предметов: «близнецы», «глаза», «губы»; четверка – словами “океаны”, “стороны света».
Например, число 1021 записывалось словами «Луна – дыра – крылья – Луна».
Есть несколько версий происхождения арабских цифр, но ни одна из них не объясняет, каким образом появились названия цифр и каким образом эти названия связаны с формой цифр (рис.4).
Рис.
4 Форма цифр.
Названия чисел тоже менялись. Так, до 15 века число “двадцать” обозначалось как “два десяти” (два десятка), а потом сократилось для более быстрого произношения. Число 40 до 15 века называлось “четыредесяте”, затем было вытеснено словом “сорок”, обозначающим первоначально мешок, вмещающий 40 беличьих или соболиных шкурок.
Цифры во фразеологизмах и их значение
Интересно было сделать небольшую подборку о том, как встречаются числа во фразеологизмах – устойчивых выражениях, которыми мы часто пользуемся, и что они значат.
Фразеологизмы с цифрой 0:
Ноль без палочки – так говорят про человека, которого не уважают и считают, что он без помощи другого ничего не значит и не может.
Ноль внимания – это полное равнодушие и безразличие к чему-либо.
Нулевая видимость – это в условиях плохой видимости ничего не видно впереди.
Фразеологизмы с цифрой 1:
Первый парень на деревне — это всеобщий любимец.
Одна нога здесь, другая там – очень быстро.
Играть первую скрипку – задавать тон, направление, которому следуют другие.
Фразеологизмы с цифрой 2:
Сидеть между двух стульев — так говорят о человеке, который либо не может решить, что ему важнее, либо хочет получить выгоду сразу с двух сторон.
Палка о двух концах — значит, что данная ситуация имеет несколько значений.
Как две капли воды – говорят о чем-то очень похожем.
Фразеологизмы с цифрой 3:
В трёх соснах заблудиться — запутаться в очень простой ситуации.
Слёзы в три ручья – это значит заплакать, зарыдать.
Катись на все четыре стороны – это выражение злобы; уходи.
Как дважды два четыре – очень легко решается.
Играть в четыре руки — играть вдвоём, например, на рояле.
Фразеологизмы с цифрой 5:
Как телеге пятое колесо – лишний, не нужный.
Как собаке пятая нога – это о совершенно ненужной вещи.
Искать пятый угол — искать спасения там, где его нет; угроза создать невыносимые условия, наказать.
Фразеологизмы с цифрой 6:
Шестое чувство — это значит обладать интуицией.
Ходить в шестерках — быть в подчинении, на побегушках.
Фразеологизмы с цифрой 7:
На седьмом небе – это когда очень счастливы, всё у нас прекрасно.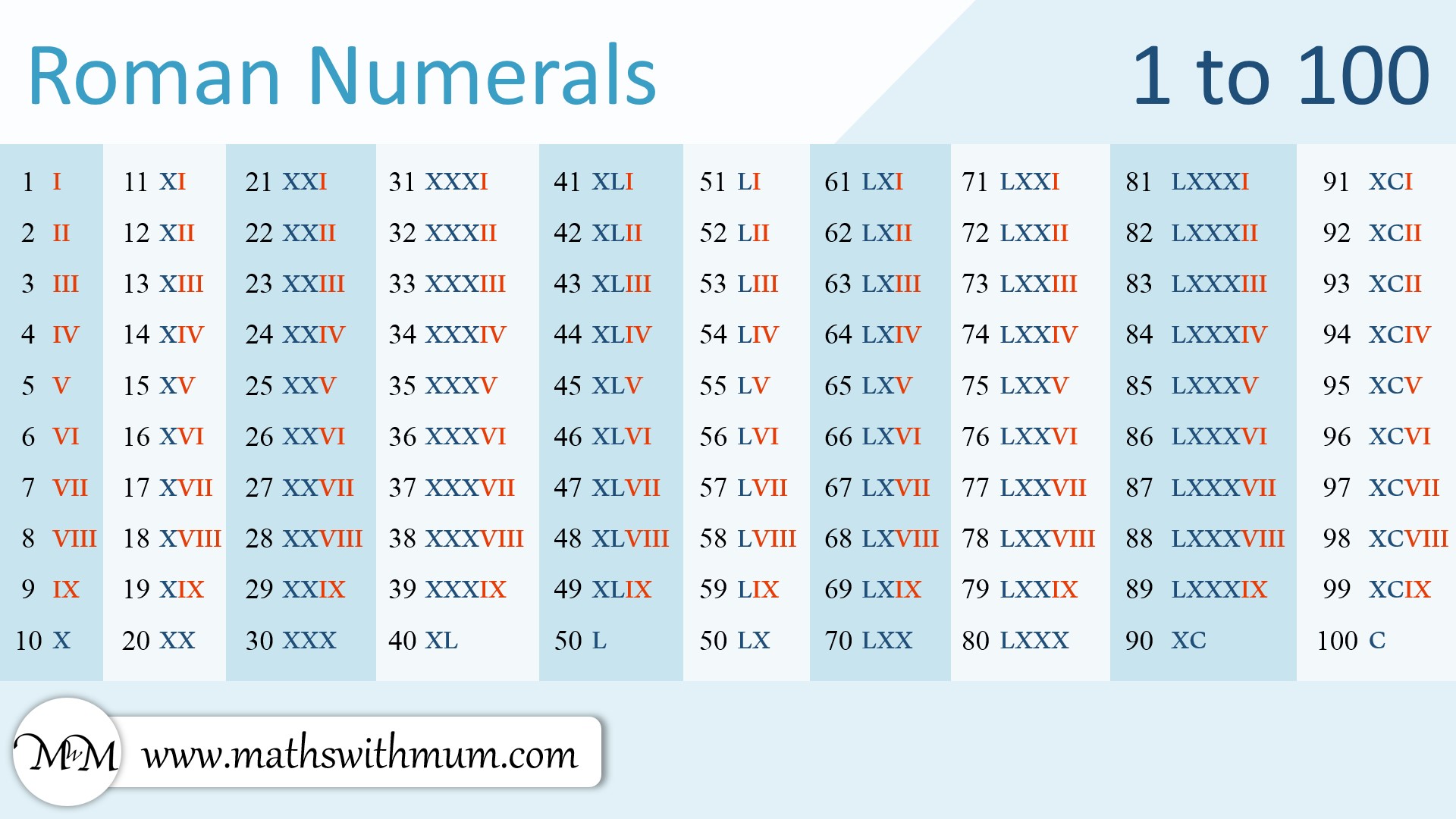
За семь вёрст киселя хлебать — ехать далеко и попусту, напрасно.
Семь пятниц на неделе – так говорят о человеке, кто часто меняет свои решения.
Фразеологизмы с цифрой 8:
Восьмое чудо света – это означает нечто выдающееся, исключительное создание, изобретение, открытие.
На будущую осень, годов через восемь – так говорят скупом человеке.
Фразеологизмы с цифрой 9:
Девятый вал -– грозная, несокрушимая сила.
За тридевять земель, в тридевятом (тридесятом) царстве – очень далеко.
Работать над темой мне понравилось. Особенно понравилось изучить значение некоторых фразеологизмов с цифрами.
Арабская запись цифр 0, 1, 2, 3,4, 5, 6, 7, 8, 9 наиболее удобна и проста, в отличие, например, от древнекитайской или римской.
Продолжим и дальше изучать мир чисел и цифр, их коды, различные шифры и способы передачи чисел на расстояние, способы чтения чисел людьми с плохим зрением или слухом. Мир чисел очень интересен и увлекателен.
«Числа не управляются миром, но показывают, как управляется мир.» — сказал Иоганн Вольфганг Гёге.
Список используемой литературы.
1. Усачёв А.А. «Считарь», «РООСА»,
2. Энциклопедия для детей. Том 11. Математика. «Аванта», 2003г.
3. Этимологический онлайн-словарь русского языка.
4. Большая энциклопедия знаний. «Издательство «Эксмо», 2015г.
5. Иллюстрированный энциклопедический словарь. Москва. Научное издательство «Большая Российская энциклопедия», 1998год.
6. Интернет –ресурсы.
Просмотров работы: 354
Проект «Цифры разных народов» | Образовательная социальная сеть
Слайд 1
Цифры разных народов Работу выполнила ученица 6 «Д» класса Луценко Алина
Слайд 2
План: Арабская нумерация Древнеегипетская нумерация Римская нумерация Нумерация Племени Майя Нумерация Древней Греции Нумерация Древнего Китая Славянская кириллическая нумерация Древнеармянская и древнегрузинская нумерации Славянская глаголическая нумерация Древнеиндийская нумерация Вавилонская нумерация Нумерация Древней Руси История цифр от 1 до 9
Слайд 3
Арабская нумерация Арабские цифры в России стали применять в основном в XVIII в.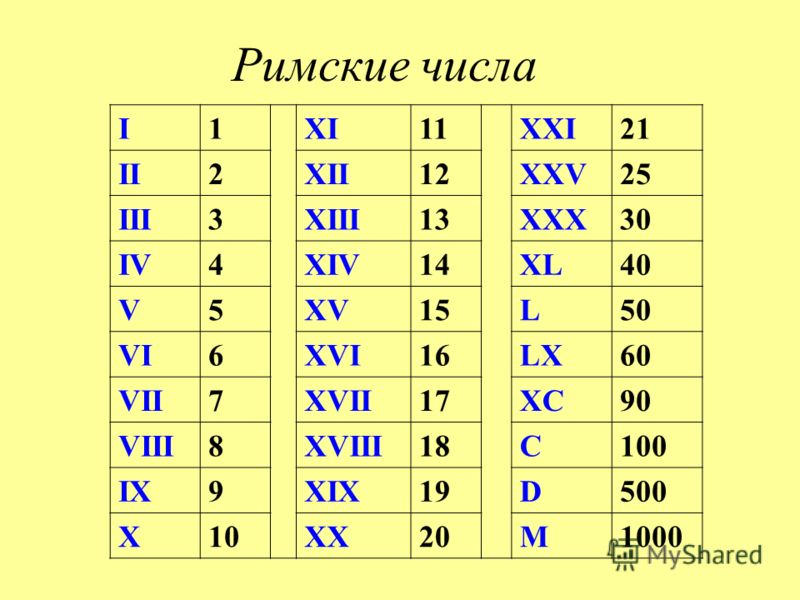
До этого наши предки пользовались славянской нумерацией. Над буквами ставили титлы (чёрточки), тогда эта буква обозначала число. Первые десять букв служили для обозначения первых десяти чисел, следующие буквы обозначали десятки, далее – сотни. Например:
Слайд 4
Древнеегипетская нумерация Первые написанные цифры, о которых мы имеем достоверные свидетельства, появились в Египте и Месопотамии около 5000 лет назад. Хотя эти две культуры находились очень далеко одна от другой, их числовые системы очень похожи: использование засечек на дереве или камне для записи прошедших дней. Египетские жрецы писали на папирусе, изготовленном из стеблей определенных сортов тростника, а в Месопотамии на мягкой глине. В египетской системе цифрами являлись иероглифические символы; они обозначали числа 1, 10, 100 и т. д. до миллиона. Изображение чисел: 1 черта, 10 пятка, 100 петля веревки, 1 000 кувшинка (или лотос), 10 000 палец, 100 000 жаба или личинка, 1 000 000 человек с поднятыми вверх руками, Числа , не кратные 10, записывались путем повторения этих цифр.
Каждая цифра могла повторяться от одного до 9 раз. Например, число 4622 обозначалось следующим образом: Фиксированного направления записи чисел не существовало: они могли записываться справа налево или слева направо и даже вертикально. Например: иероглифическая запись , и обратная запись тех же иероглифов, обозначали одно и то же число — «12».
Слайд 5
Римская нумерация Древние римляне изобрели систему исчисление, основанную на использовании букв для отображения цифр. Каждая буква имела различное значение, каждая цифра соответствовала номеру положения буквы. Для того чтобы прочесть римскую цифру, следует следовать пяти основным правилам: Буквы пишутся слева направо, начиная с самого большого значения. Например: X V (15), CCXLIII (243), ZCXV (2115). Буквы I , X, C и M могут повторяться до трёх раз подряд, например: III (3), XX (20), ССC (300), MCCXXX (1320). Буквы V, L, D не могут повторяться. Цифры 6, 8, 40, 80, 800 следует писать, комбинируя буквы: VII (6), VIII (8), XL (40), LXXX (80), CD (400), DCCC (800).
Например, 48 следует писать, комбинируя буквы XLVIII, 449 – CDXLIX _ Горизонтальная линия над буквой увеличивает её значение в 1000 раз.
Слайд 6
Нумерация Племени Майя Очень интересная система счета была у народа Майя, который жил в Центральной Америке там, где сейчас государство Мексика. Чванливая Европа еще считала по пальцам, когда математики древних майя ввели понятие нуля и оперировали бесконечно большими величинами. Древние майя самостоятельно пришли к использованию позиционного принципа. В отличие от нас, европейцев, им не у кого было заимствовать этот принцип, и они сами додумались до него, причем почти на целое тысячелетие (!) раньше Старого Света. Запись цифровых знаков, образующих число, майя вели вертикально, снизу вверх, как бы возводя некую этажерку из цифр. Майя считали двадцатками – у них была двадцатеричная система счёта. Числа от 1 до 20 обозначались точками и чёрточками. Цифры майя: Пример: 20+7 =27 Иногда для записи цифр от 1 до 19 также использовались изображения божеств.
Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах.
Слайд 7
Нумерация Древней Греции В Древней Греции имели хождение две основных системы счисления — аттическая (или геродианова ) и ионическая (она же александрийская или алфавитная). Аттическая система счисления использовалась греками, по-видимому, уже к 5 в. до н.э. По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Г, первую букву слова «пента» (пять) (буква Г употреблялась для обозначения звука «п», а не «г»). Дойдя до десяти, они ввели еще один новый символ D, первую букву слова «дека»(десять). Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ H означал 100 ( гекатон ), X — 1000 ( хилиои ), символ M — 10000 ( мириои или мириада ).
Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков: Вторая принятая в Древней Греции ионическая система счисления — алфавитная — получила широкое распространение в начале Александрийской эпохи, хотя возникнуть она могла несколькими столетиями раньше , по всей видимости, уже у пифагорейцев . Чтобы отличить числа от слов , греки над соответствующей буквой ставили горизонтальную черту. Сходство греческой буквы О с современным обозначением нуля может быть чем-то большим , чем случайное совпадение, но у нас нет точных данных, позволяющих утверждать это со всей определенностью. Запись алфавитными символами могла делаться в любом порядке, так как число получалось как сумма значений отдельных букв .
Слайд 8
Нумерация Древнего Китая Эта нумерация одна из старейших и самых прогрессивных. Возникла эта нумерация около 4 000 тысяч лет тому назад в Китае. Записывались цифры и числа начиная с больших значений и заканчивая меньшими . Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду.
(Во времена династии Мин был введен знак для пустого разряда — кружок — аналог нашего нуля ). Чтобы не перепутать разряды использовали несколько служебных иероглифов , писавшихся после основного иероглифа, и показывающих какое значение принимает иероглиф-цифра в данном разряде. 10 100 1 000 — 1 000; — 548 Такая запись числа мультипликативная, то есть в ней используется умножение.
Слайд 9
Славянская кириллическая нумерация Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. Если посмотреть внимательно , то увидим, что после «а» идет буква «в», а не «б» как следует по славянскому алфавиту, то есть используются только буквы, которые есть в греческом алфавите. Чтобы различать буквы и цифры, над числами ставился особый значок — титло ( ~ )
Слайд 10
Древнеармянская и древнегрузинская нумерации Армяне и грузины пользовались алфавитным принципом нумерации. Но в древнеармянском и древнегрузинском алфавитах было гораздо больше букв, чем в древнегреческом.
Это позволило ввести особые обозначения для чисел 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000.
Слайд 11
Славянская глаголическая нумерация Эта система была создана для обозначения чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в . 1 2 3 4 5 6 7 8 9 10 20 30 40 50 60 70 80 90 100 200 300 400 500 600 700 800 900 Числа записывали из цифр так же слева, направо, от больших к меньшим цифрам. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Такая запись числа аддитивная, то есть в ней используется только сложение : 800+60+3 = 863 Для того чтобы не перепутать буквы и цифры, использовались титла — горизонтальные черточки над числами, или точки.
Слайд 12
Древнеиндийская нумерация Система счисления кхарошти имела хождение в Индии между VI веком до нашей эры и III веком нашей эры. Эта была непозиционная аддитивная система счисления.
О ней мало что известно, так как сохранилось мало письменных документов той эпохи. Система кхарошти интересна тем, что в качестве промежуточного этапа между единицей и десятью выбирается число четыре. Числа записывались справа налево. Наряду с этой системой существовала в Индии еще одна система счисления брахми . Числа брахми записывались слева направо. Однако в обеих системах было не мало общего. В частности первые три цифры очень похожи. Общим было то, что до сотни применялся аддитивный способ, а после мультипликативный. Важным отличием цифр брахми , было то, что цифры от 4 до 90, были представлены только одним знаком. Эта особенность цифр брахми в дальнейшем была использована при создании в Индии позиционной десятичной системы. В древней Индии так же была словесная система счисления. Она была мультипликативная, позиционная. Знак нуля произносился как «пустое», или «небо», или «дыра». Единица как «луна», или «земля». Двойка как «близнецы», или «глаза», или «ноздри», или «губы». Четыре как «океаны», «стороны света».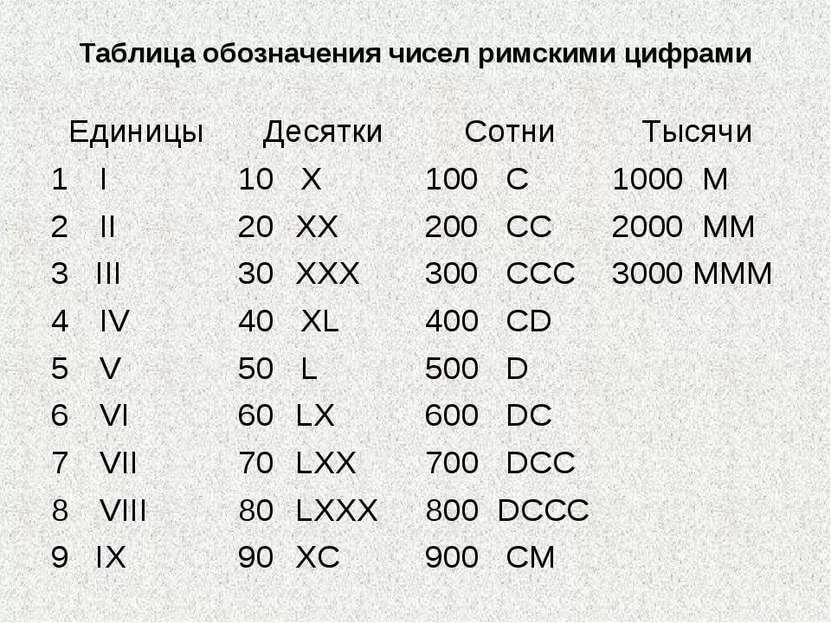
Например, число 2441 произносилось так: глаза океанов стороны света луны.
Слайд 13
Вавилонская нумерация В Древнем Вавилоне примерно за 40 веков до нашего времени создалась по-местная (позиционная) нумерация, т.е. такой способ изображения чисел, при котором одна и та же цифра может обозначать разные числа в зависимости от места, занимаемого этой цифрой. Наша современная нумерация тоже поместная: в числе 52 цифра 5 обозначает пятьдесят, т.е.5х10, а в числе 576 эта же цифра обозначаёт пятьсот, т.е. 5х10х10. В вавилонской поместной нумерации ту роль, которую играет у нас число 10, играло число 60, и потому эту нумерацию называют шестидеситеричной . Числа, меньшие 60, обозначались с помощью двух знаков. Они имели клинообразный вид, так как вавилоняне писали на глиняных дощечках палочками треугольной формы. Эти знаки повторялись нужное число раз . Шестидесятеричная система возникла позднее десятичной, ибо числа до 60 записываются в ней по десятичному принципу. Но до сих пор неизвестно, когда и как возникла у вавилонян шестидесятеричная система.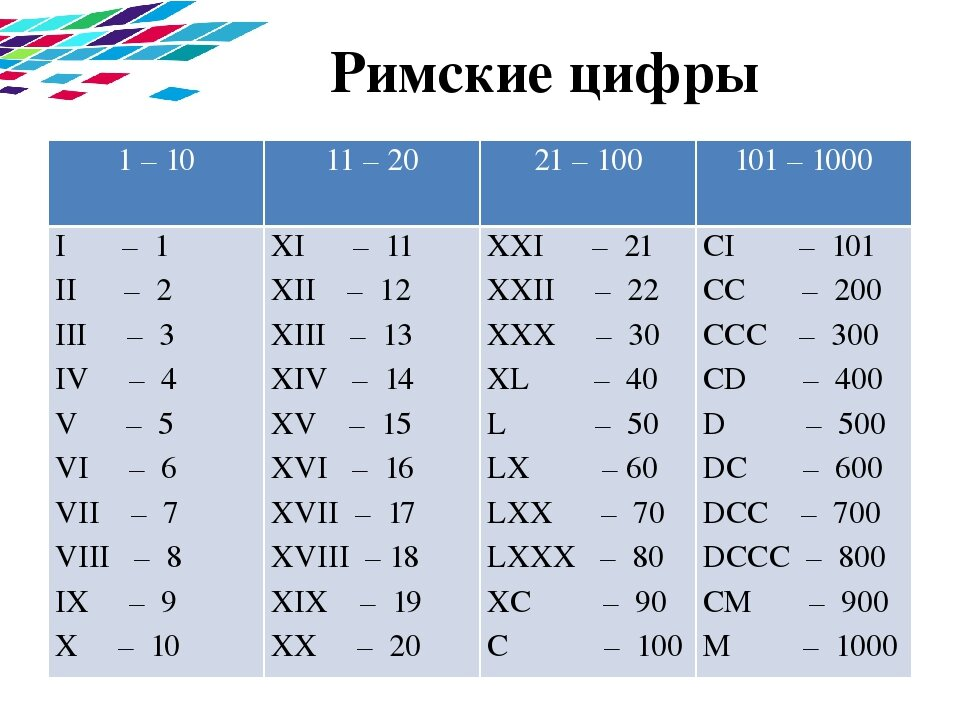
На этот счет строилось много гипотез, но ни одна пока не доказана. Мнения историков по поводу того, как именно возникла эта система счисления, расходятся. Существуют две гипотезы. Первая исходит из того, что произошло слияние двух племен, одно из которых пользовалось шестеричной, другое — десятичной. Шестидесятеричная система счисления в данном случае могла возникнуть в результате своеобразного политического компромисса. Суть второй гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60 . Шестидесятеричная запись целых чисел не получила распространения за пределами ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: в страны Ближнего Востока, Средней Азии, в Северную Африку и Западную Европу. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей, т.е. до начала XVII в.
Слайд 14
Нумерация Древней Руси Как ни странно, Русь повторила алфавитную систему счисления.
Каждая цифра была названа соответствующей ее рангу буквой алфавита. Цифра 1 выглядела как «А», 2 – «Б», 3 – «В» и т.д. Десятки и сотни также были подписаны соответствующими буквами славянского алфавита. Чтобы не путать в тексте слова с цифрами, над числовыми записями рисовали титло ( ~ )
Слайд 15
История цифры 1 Не только первая цифра в ряду, но и символ единства, совершенной целостности, как бог или космос. Смысл числительного «первый» семантически связано с именем Адама («первый человек»), а также с именами мифических персонажей Атум (созвучно со словом «атом», а мы знаем, что он неделимый), Один (от сканд. «первый», «верховный», «главенствующий»). Чувствуется фонетическое подобие слова «один» с « ЕДИНый », « жАДИНа ».
Слайд 16
История цифры 2 В названии цифры чувствуется парность, бинарное противопоставление, антонимичность , дуальность , четность. 2 – это защита от небытия и одиночества, противостояние единому. Вспомним, что Адам значит «первый», но после него не землю пришла Ева, она была «вторая».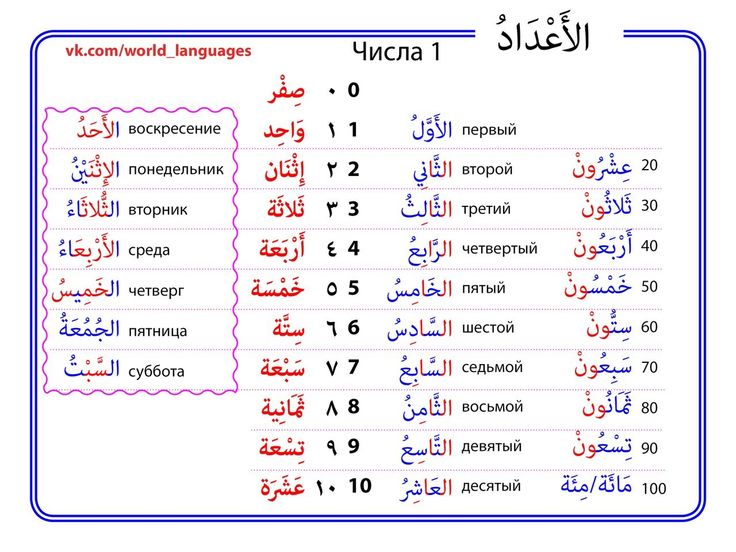
Ева значит «дева», а поскольку в древней Руси буквы «о» и «е» отсутствовали, то слово «дева» в письменном варианте выглядело как « дъва ». Учитывая глубокую религиозную приверженность наших предков, имя «два» могло произойти из христианской мифологии.
Слайд 17
История цифры 3 Недаром китайский цифровой ряд начинается с «тройки». Это совершенное число, за которым стоит ряд русских традиций – трижды постучать по дереву, трижды произнести «аминь» по окончанию молитвы, бог в православной вере существует в трех ипостасях. Цифра 3 обозначает крайнюю степень какой-либо характеристики. Например, «треклятый», « трисвятый ». «Тройка» пишется практически одинаково с буквой «з», с которой начинается слово «земля». Как одна из стихий (1 – огонь, 2 – вода), земля вполне может оказаться третьей.
Слайд 18
История цифры 4 Сравните русское слово «веер» с немецким словом « vier » («четыре»). Четвертая стихия – ветер — прячется под «четверкой». Кроме того, это четное число, « четыр ».
Оттуда и название.
Слайд 19
История цифры 5 Одна из важнейших характеристик микро- и макрокосма. Ничего загадочного в этом нет. Вспомните, сколько у нас чувств, сколько классов животных, сколько элементов в буддийских упанишадах? Их пять. Цифра 5 находится у истоков навыков счета. В древней Руси считали «на пятках», то есть на пальцах руки. Выражение «знать, как пять своих пальцев», родом из той эпохи.
Слайд 20
История цифры 6 На Руси цифру записывали под буквой «зело», пока не были введены арабские цифры. Сравните слова «зело» и «зло». Ведь 666 – три «зело» — обозначает абсолютное зло, треклятое (см. историю цифры 3).
Слайд 21
История цифры 7 Цифра 7 начертанием и произношением сходна с латинской буквой Z (« zet »). «Семь» созвучно с « земь », то есть «опора», «центр».
Слайд 22
История цифры 8 Сразу слышится « осемь », т.е. «ось». Цифра 8 напоминает букву «В», с которой начинается ее буквенная запись.
Слайд 23
История цифры 9 Мы слышим троекратное повторение триады.
«Девятка» — это обобщение всего цифрового ряда и ее превосходство одновременно.
Слайд 24
Древнеегипетские обозначения Вавилонская система счисления
Слайд 25
Числа Древней Руси Римские числа
Слайд 26
Вывод: Я узнала когда и где появились первые системы счисления, как записывались раньше цифры разных народов.
Слайд 27
Спасибо за внимание!
Арабские цифры от 1 до 20 — Плакаты
PDF | 21 страницы | Годы: 1–6
Плакаты с цифрами от 1 до 20 и переводом на арабский язык.
Этот учебный материал содержит плакаты, переводящие числа с английского языка на арабский с соответствующей цифрой.
Разместите эти плакаты в классе в качестве вспомогательного средства для учащихся, изучающих английский как второй язык, и при изучении новых языков. В игре «Счет» используйте фишки и десять рамок в нижней части каждого плаката, чтобы в увлекательной игровой форме научиться считать в классе.
учебный ресурс
Числа и слова до 20 — набор рабочих листов
Используйте этот набор рабочих листов, когда учащиеся тренируются связывать числа со словами и количествами.
1 страница Годы: Ф — 1учебное пособие
Десятки кадров, подсчет цветов, карточки с заданиями
Улучшите навыки распознавания чисел, счета и субитизации своих учеников с помощью набора карточек с заданиями Tens Frame, которые можно распечатать.
1 страница Год: Фучебный ресурс
Субитизирующая игра — Slap It!
Помогите учащимся укрепить навыки построения субтитров в этой многопользовательской математической карточной игре!
1 страница Годы: Ф — 1учебное пособие
Числовые линии — вырезать и вставить рабочий лист
Вырежьте и вставьте, чтобы завершить числовые строки с этим рабочим листом.
1 страница Год: 1
учебное пособие
Числовые линии — рабочий лист
Заполните пропущенные числа с помощью этого рабочего листа числовой строки.
1 страница Год: 1учебное пособие
Настольная игра «Подсчет предметов» — цифры 6–10
Потренируйтесь считать до 10 в увлекательной настольной игре.
1 страница Годы: Ф — 1учебное пособие
Настольная игра «Подсчет предметов» — цифры 1–5
Попрактикуйтесь в базовых математических навыках с помощью настольной игры со счетом предметов.
1 страница Годы: Ф — 1учебное пособие
Построение и сравнение целых чисел — Рабочий лист
Потренируйтесь выводить целые числа на числовую прямую и выполнять операторы сравнения с помощью этого рабочего листа.
1 страница Год: 6учебное пособие
Подсчет предметов Охота на медведя — цифры 6–10
Используйте индивидуальную переписку и базовые навыки счета в этом практическом упражнении.
1 страница Год: Фучебное пособие
Подсчет предметов Охота на медведя — цифры 1–5
В этой практической игре используйте переписку один на один и базовые навыки счета.
1 страница Год: Ф
номеров
номеровРаздел 9.5
Если вы не следуете руководству по стилю, которое указывает иное, соблюдайте следующие рекомендации при использовании числа.
- Как правило, используйте арабские цифры вместо слов в научно-техническое письмо как для кардинальных, так и для порядковые номера:
- Однако в некоторых научных и технических стилях напишите числа от одного до десяти и дроби из двух слов которые не следуют целому числу:
- Если вам нужно начать предложение с цифры, напишите ее по буквам
вне. Однако лучше переформулировать предложение, если
возможный.
- Если одно число непосредственно следует за другим в предложение, укажите то, которое может быть выражено в меньше слов. Попробуйте, однако, выразить единицы измерения арабскими цифрами. Другим решением является переформулировка предложение.
- Всегда произносите местоимение по буквам один :
- Используйте цифры для дат, времени суток, страниц, рисунков, и примечания:
- Используйте арабские цифры, за которыми следует знак процента, ( % ), чтобы выразить проценты, за исключением случаев, когда число начинает предложение:
3 подпрограммы 6 скобы 61 аминокислоты 3-я подпрограмма 6-я скоба 61-я аминокислота
три подпрограммы шесть скобы 61 аминокислоты 1½ часа половина час
Однако лучше переформулировать предложение, если
возможный. Тридцать две рабочие станции были предоставлены
Университет. Университет предоставил 32 рабочие станции.
Затем мы подготовили восемь 20 мл
образцы. Затем мы подготовили 8 образцов 20 шт. по мл.
Защищая частную жизнь физических лиц, один надо всегда рассматривать все возможные пути
данные могут быть доступны и использованы. 
5 Август 1994 1 вечера
стр. 43
Ссылка 6
Рисунок 43
Только 3 % систем вышли из строя во время
тестовый период. Три процента систем вышли из строя во время
тестовый период.
Британское и американское формирование чисел
- Целые числа от двух до четырех цифр без знаков препинания и пробелов:
- Используйте точку ( . ) для
указать десятичную точку и использовать начальный ноль
( 0 ) для чисел меньше 1. 0:
31,31,41
0,414
- Сформируйте числа из пяти и более цифр, используя запятую (, ) для выделения группы из трех цифр, начиная с десятичного точка:
21 412
8024
0: 10 000 12 341
12 341,34
12 432 421
Европейские и международные стандарты формирования номеров
- Составлять целые числа от двух до четырех цифр без каких-либо пунктуация или пробел:
- Используйте запятую (, ) для обозначения десятичного числа. указать и использовать начальный ноль ( 0 ) для чисел менее 1,0:
- Числа из пяти и более цифр образуют с помощью точки ( . ), чтобы выделить группы из трех цифр, начиная с десятичной точки:
21 412
8024
31,3 1,41
0,414
10.