Дифференциал функции. Дифференциалы первого порядка.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Определение. Функция $y=f(x)$ называется дифференцируемой в точке $x_0,$ если ее приращение $\Delta y(x_0, \Delta x)$ может быть представлено в виде $$\Delta y(x_0, \Delta x)=A\Delta x+o(\Delta x).$$
Главная линейная часть $A\Delta x$ приращения $\Delta y$ называется дифференциалом этой функции в точке $x_0,$ соответствующим приращению $\Delta x,$ и обозначается символом $dy(x_0, \Delta x).$
Для того, чтобы функция $y=f(x)$ была дифференцируема в точке $x_0,$ необходимо и достаточно, чтобы существовала производная $f'(x_0),$ при этом справедливо равенство $A=f'(x_0).$
Выражение для дифференциала имеет вид $$dy(x_0, dx)=f'(x_0)dx,$$ где $dx=\Delta x.$
Свойства дифференциала:1. $d(C)=0,$ где $C -$ постоянная;
2. 2}.$
2}.$
Ответ: $\frac{x+y}{x-y}dx.$
Докажите что заданная функция возрастает y cosx 2x
Упр.44.10 ГДЗ Мордковича 10 класс профильный уровень
(Алгебра)©Reshak.ru — сборник решебников для учеников старших классов. Здесь можно найти решебники, ГДЗ, переводы текстов по школьной программе. Практически весь материал, собранный на сайте — авторский с подробными пояснениями профильными специалистами. Вы сможете скачать гдз, решебники, улучшить школьные оценки, повысить знания, получить намного больше свободного времени.
Главная задача сайта: помогать школьникам и родителям в решении домашнего задания. Кроме того, весь материал совершенствуется, добавляются новые сборники решений.
Докажите что заданная функция возрастает y cosx 2x
Вопрос по алгебре:
Докажите, что заданная функция возрастает на R y=cosx+2x
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Пробный урок — бесплатно!
- 25.08.2016 16:06
- Алгебра
- remove_red_eye 19717
- thumb_up 49
Ответы и объяснения 1
- 26.08.2016 17:50
- thumb_up 26
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Докажите, что заданная функция возрастает на R y = cosx + 2x?
Докажите, что заданная функция возрастает на R y = cosx + 2x.
Найдём производную y’y’ = (cos(x) + 2x)’ = 2 — sin(x) — 1 ≤ — sin(x) ≤ 1 | + 2 — 1 + 2 ≤ 2 — sin(x) ≤ 1 + 21 ≤ 2 — sin(x) ≤ 3 Из данного двойного неравенства следует, что производная будет всегда больше 0, следовательно функция будет постоянно возрастать.
Докажите что функция у 3х — 5 / 2 возрастает?
Докажите что функция у 3х — 5 / 2 возрастает.
Докажите, что функция у = (3х — 5) / 2 возрастает?
Докажите, что функция у = (3х — 5) / 2 возрастает.
Докажите, что функция y = 3x — 5 / 2 возрастает?
Докажите, что функция y = 3x — 5 / 2 возрастает.
Напишите какую — нибудь формулу, задающую возрастающую линейную функцию ; убывающую линейную функцию?
Напишите какую — нибудь формулу, задающую возрастающую линейную функцию ; убывающую линейную функцию. 3 + 7x + 4.
3 + 7x + 4.
Докажите что функция у = 3х — 5 / 2 возрастает?
Докажите что функция у = 3х — 5 / 2 возрастает.
Докажите что функция y = (6 / x) + 4 возрастает?
Докажите что функция y = (6 / x) + 4 возрастает.
Докажите , что функция возрастает?
Докажите , что функция возрастает.
Объясните, пожалуйста, задание?
Объясните, пожалуйста, задание.
Пробовала решать сама, а ответ неверным оказался.
Докажите, что заданная функция возрастает :
На странице вопроса Докажите, что заданная функция возрастает на R y = cosx + 2x? из категории Алгебра вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи. 2..
2..
Производные тригонометрических функций. — КиберПедия
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Интересное: Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего. Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
А. В случае сложной функции u = u(х) получим формулу . Б.Производная функции y = cosx выражается формулой . В случае сложной функции u = u(х) получим формулу .
В.Производная функции y = tgx выражается формулой , где . В случае сложной функции u = u(х) получим формулу . Г.Производная функции y = ctgx выражается формулой ,где . В случае сложной функции u = u(х) получим формулу . Производные обратных тригонометрических функций. А.Производная функции y = arcsinx, |x|£1, выражается формулой . В случае сложной функции u = u(х) получим формулу .
Б.Производная функции y = arccosx, |x|£1, выражается формулой . В случае сложной функции u = u(х) получим формулу .
В.Производная функции y = arctgx выражается формулой . В случае сложной функции u = u(х) получим формулу .
Г.Производная функции y = arcctgx выражается формулой . В случае сложной функции u = u(х) получим формулу .
Пример. Вычислить производные функций: 1) ; 2) . Решение 1) Производную сложной функции вычисляем по формуле . Получим .
2) Сначала используем формулу для производной степенной функции , где . Получим
Вопрос 4. Производные высших порядков
Производная у′ = f′(х) функции у = f(х) есть так же функция от х и называется производной первого порядкаили первой производной. Возможно, что эта функция сама имеет производную. О.4.1. Производная от первой производной функции у = f(х) называется производной второго порядка или второй производнойданной функции и обозначается одним из символов Таким образом О.4.2. Производная от второй производной функции у = f(х) называется производной третьего порядка или третьей производнойданной функции и обозначается одним из символов Таким образом Производные, начиная со второй, называются производными высших порядков. О.4.3. Производная от (n‒1)-й производной функции у = f(х) называется Таким образом Начиная с производной 4-го порядка, производные обозначают римскими цифрами или числами в скобках. Пример. уV или у(5) — производная 5-го порядка.
Для некоторых элементарных функций можно вывести формулы нахождения производных любого порядка.
Пример. Найти производную n-го порядка функции у = ах. Решение …..,
Механический (физический) смысл второй производной
Производные второго и вообще высших порядков оказываются необходимыми для определения важных понятий математики, механики, физики, а так же для более полного исследования функций. Пусть материальная точка движется прямолинейно по закону S = S(t). Можно показать, что вторая производная от пути по времени есть величина ускорения прямолинейного движения точки, т.е.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Производная функции y 2 корень x. Калькулятор онлайн. Найти (с решением) производную функции
 Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:
Ниже приводится таблица нахождения производных простых функций. Более сложные правила дифференцирования смотрите в других уроках:- Таблица производных экспоненциальных и логарифмических функций
Приведенные формулы используйте как справочные значения. Они помогут в решении дифференциальных уравнений и задач. На картинке, в таблице производных простых функций, приведена «шпаргалка» основных случаев нахождения производной в понятном для применения виде, рядом с ним даны пояснения для каждого случая.
Производные простых функций
1. Производная от числа равна нулю
с´ = 0
Пример:
5´ = 0
Пояснение :
Производная показывает скорость изменения значения функции при изменении аргумента. Поскольку число никак не меняется ни при каких условиях — скорость его изменения всегда равна нулю.
2. Производная переменной равна единице
x´ = 1
Пояснение :
При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение :
В данном случае, при каждом изменении аргумента функции (х ) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с .
Откуда следует, что
(cx + b)» = c
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|» = x / |x| при условии, что х ≠ 0
Пояснение :
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами. Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.
5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
(x c)»= cx c-1 , при условии, что x c и сx c-1 ,определены а с ≠ 0
Пример:
(x 2)» = 2x
(x 3)» = 3x 2
Для запоминания формулы :
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x 2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x 3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x 2 . Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)» = — 1 / x 2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)» = (x -1)» , тогда можно применить формулу из правила 5 таблицы производных
(x -1)» = -1x -2 = — 1 / х 2
7.
(1 / x c)» = — c / x c+1
Пример:
(1 / x 2)» = — 2 / x 3
8. Производная корня (производная переменной под квадратным корнем)
(√x)» = 1 / (2√x) или 1/2 х -1/2
Пример:
(√x)» = (х 1/2)» значит можно применить формулу из правила 5
(х 1/2)» = 1/2 х -1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
(n √x)» = 1 / (n n √x n-1)
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше
предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться
таблицей производных и правилами дифференцирования. Для нахождения производной подходит
следующий алгоритм.
Для нахождения производной подходит
следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице производных, а формулы производных произведения, суммы и частного — в правилах дифференцирования. Таблица производных и правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило,
проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования.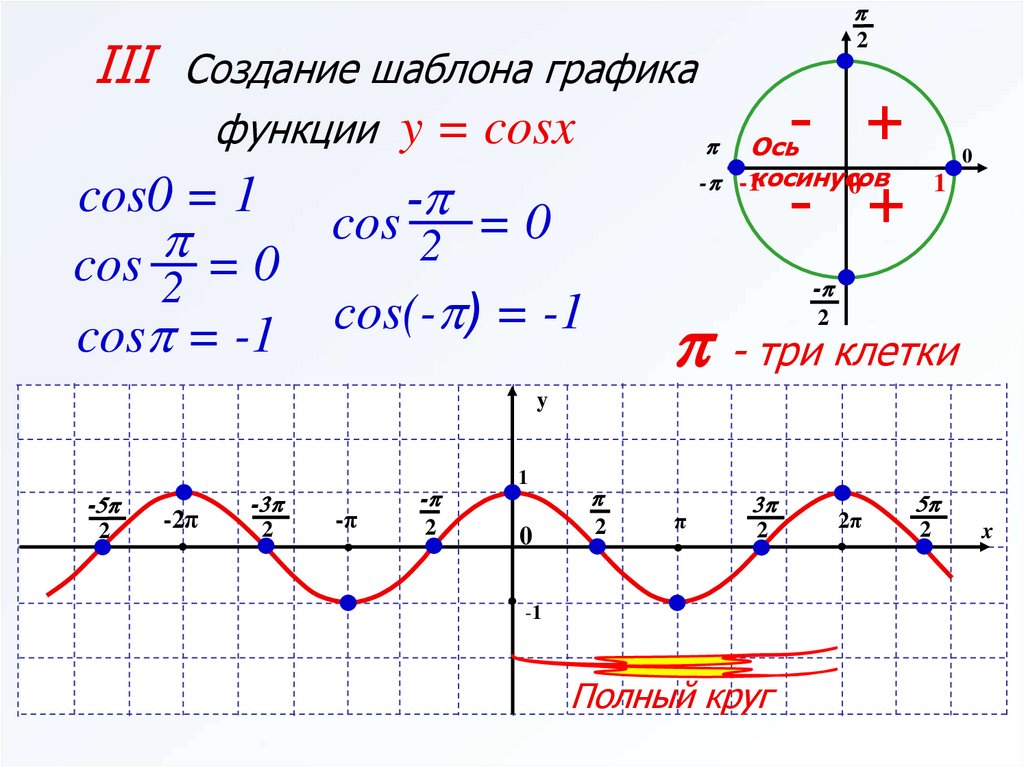 К ним мы и переходим прямо сейчас.
К ним мы и переходим прямо сейчас.
Таблица производных простых функций
| 1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
11. Производная арккосинуса Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
| 14. Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т. е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т.е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.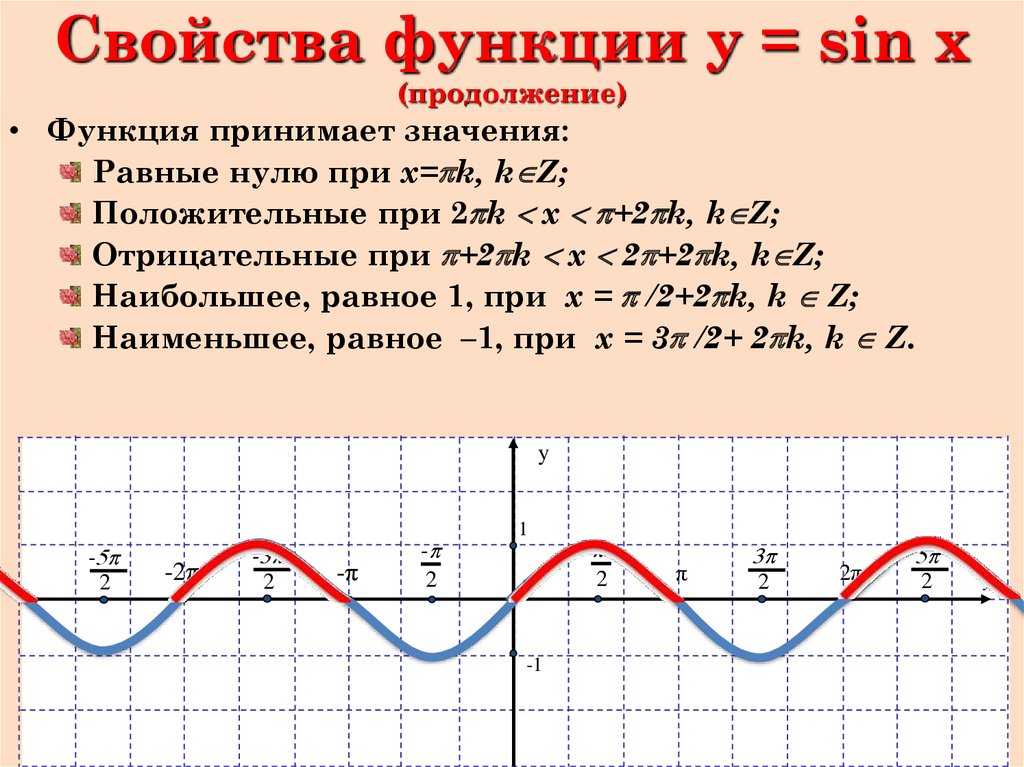 е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем.
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \). Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение \(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y».
Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых
существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) .
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция \(y = f(x) \) имеет
производную в конкретной точке \(x \):
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x) $$
Это означает, что около точки х выполняется приближенное равенство \(\frac{\Delta y}{\Delta x} \approx f»(x) \), т.е.
\(\Delta y \approx f»(x) \cdot \Delta x \).
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально»
приращению аргумента, причем коэффициентом пропорциональности является значение производной в заданной точке х. 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
2. Дать аргументу \(x \) приращение \(\Delta x \), перейти в новую точку \(x+ \Delta x \), найти \(f(x+ \Delta x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.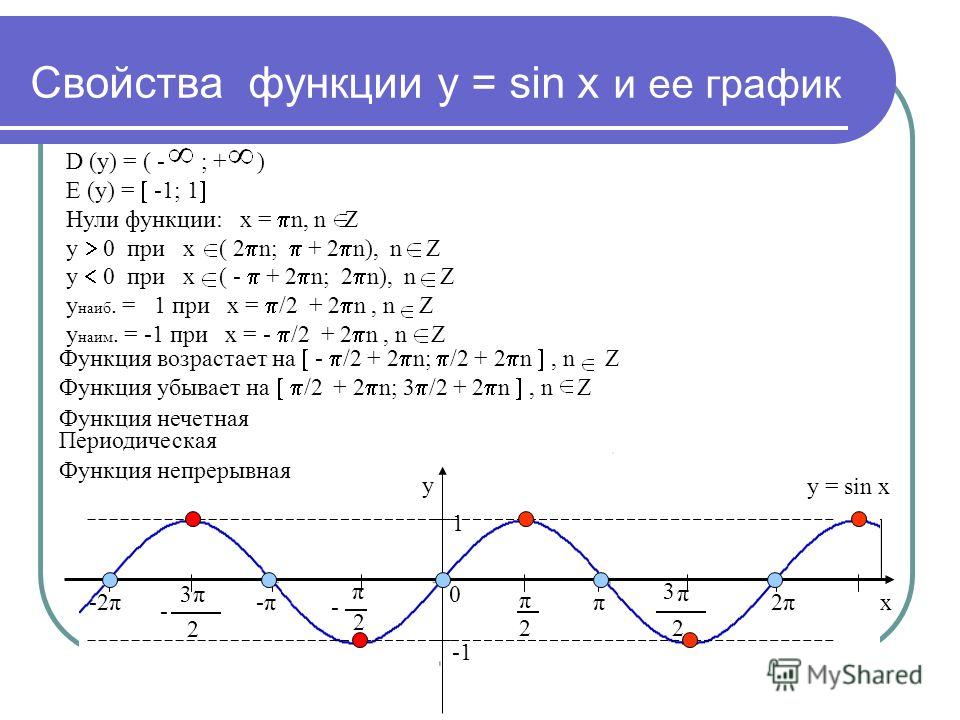
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями.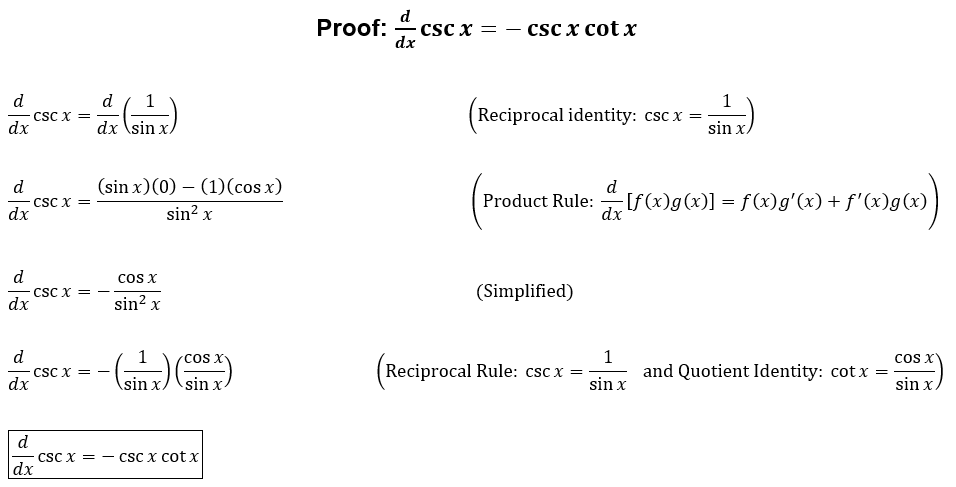 2} $$
2} $$
Дата: 10.05.2015
Правила дифференцирования.
Чтобы найти производную от любой функции, надо освоить всего три понятия:
2. Правила дифференцирования.
3. Производная сложной функции.
Именно в таком порядке. Это намёк.)
Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных — доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования.
Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения «найти производную функции» и «продифференцировать функцию» — это одно и то же.
Выражение «правила дифференцирования» относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове.
Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:
Вот они, правила дифференцирования:
В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 — это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу.
Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).
Рассмотрим несколько примеров. Сначала — самые простые.
Найти производную функции y=sinx — x 2
Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx — это функция U , а x 2 — функция V. Имеем полное право написать:
y» = (sinx — x 2)» = (sinx)»- (x 2)»
Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x 2 ), смотрим, какие у них производные и записываем ответ:
y» = (sinx)» — (x 2)» = cosx — 2x
Вот и все дела.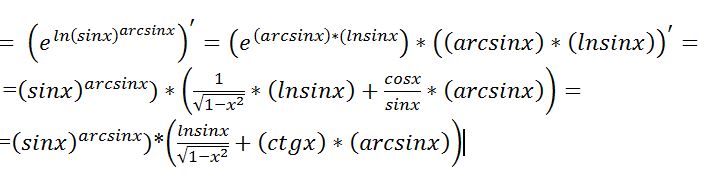 Правило 1 дифференцирования суммы работает точно так же.
Правило 1 дифференцирования суммы работает точно так же.
А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например:
Найти производную функции y=sinx — x 2 +cosx — x +3
Смело пишем:
y» = (sinx)» — (x 2)» + (cosx)» — (x)» + (3 )»
В конце урока дам советы по облегчению жизни при дифференцировании.)
Практические советы:
1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию.
2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами.
3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4.
Задача нахождения производной от заданной функции является одной из основных в курсе математики старшей школы и в высших учебных заведениях. Невозможно полноценно исследовать функцию, построить ее график без взятия ее производной. Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производную функции легко можно найти, зная основные правила дифференцирования, а также таблицу производных основных функций. Давайте разберемся, как найти производную функции.
Производной функции называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Понять это определение достаточно сложно, так как понятие предела в полной мере не изучается в школе. Но для того, чтобы находить производные различных функций, понимать определение не обязательно, оставим его специалистам математикам и перейдем сразу к нахождению производной.
Процесс нахождения производной называется дифференцированием. При дифференцировании функции мы будем получать новую функцию.
Для их обозначения будем использовать латинские буквы f, g и др.
Существует много всевозможных обозначений производных. Мы будем использовать штрих. Например запись g» означает, что мы будем находить производную функции g.
Таблица производных
Для того чтобы дать ответ на вопрос как найти производную, необходимо привести таблицу производных основных функций. Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
Для вычисления производных элементарных функций не обязательно производить сложные вычисления. Достаточно просто посмотреть ее значение в таблице производных.
- (sin x)»=cos x
- (cos x)»= –sin x
- (x n)»=n x n-1
- (e x)»=e x
- (ln x)»=1/x
- (a x)»=a x ln a
- (log a x)»=1/x ln a
- (tg x)»=1/cos 2 x
- (ctg x)»= – 1/sin 2 x
- (arcsin x)»= 1/√(1-x 2)
- (arccos x)»= — 1/√(1-x 2)
- (arctg x)»= 1/(1+x 2)
- (arcctg x)»= — 1/(1+x 2)
Пример 1. Найдите производную функции y=500.
Мы видим, что это константа. По таблице производных известно, что производная константы, равна нулю (формула 1).
Пример 2. Найдите производную функции y=x 100 .
Это степенная функция в показателе которой 100 и чтобы найти ее производную нужно умножить функцию на показатель и понизить на 1 (формула 3).
(x 100)»=100 x 99
Пример 3. Найдите производную функции y=5 x
Это показательная функция, вычислим ее производную по формуле 4.
Пример 4. Найдите производную функции y= log 4 x
Производную логарифма найдем по формуле 7.
(log 4 x)»=1/x ln 4
Правила дифференцирования
Давайте теперь разберемся, как находить производную функции, если ее нет в таблице. Большинство исследуемых функций, не являются элементарными, а представляют собой комбинации элементарных функций с помощью простейших операций (сложение, вычитание, умножение, деление, а также умножение на число). Для нахождения их производных необходимо знать правила дифференцирования. Далее буквами f и g обозначены функции, а С — константа.
1. Постоянный коэффициент можно выносить за знак производной
Пример 5. Найдите производную функции y= 6*x 8
Выносим постоянный коэффициент 6 и дифференцируем только x 4 . Это степенная функция, производную которой находим по формуле 3 таблицы производных.
(6*x 8)» = 6*(x 8)»=6*8*x 7 =48* x 7
2. Производная суммы равна сумме производных
(f + g)»=f» + g»
Пример 6.
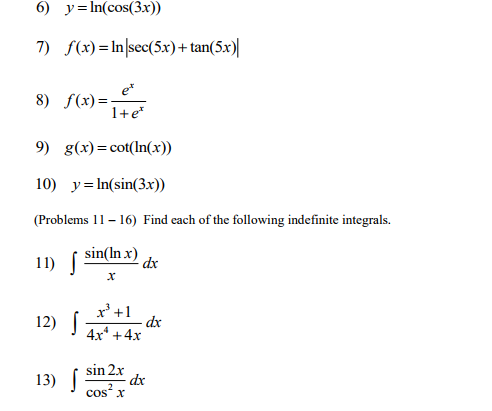 Найдите производную функции y= x 100 +sin x
Найдите производную функции y= x 100 +sin xФункция представляет собой сумму двух функций, производные которых мы можем найти по таблице. Так как (x 100)»=100 x 99 и (sin x)»=cos x. Производная суммы будет равна сумме данных производных:
(x 100 +sin x)»= 100 x 99 +cos x
3. Производная разности равна разности производных
(f – g)»=f» – g»
Пример 7. Найдите производную функции y= x 100 – cos x
Эта функция представляет собой разность двух функции, производные которых мы также можем найти по таблице. Тогда производная разности равна разности производных и не забудем поменять знак, так как (cos x)»= – sin x.
(x 100 – cos x)»= 100 x 99 + sin x
Пример 8. Найдите производную функции y=e x +tg x– x 2 .
В этой функции есть и сумма и разность, найдем производные от каждого слагаемого:
(e x)»=e x , (tg x)»=1/cos 2 x, (x 2)»=2 x. Тогда производная исходной функции равна:
(e x +tg x– x 2)»= e x +1/cos 2 x –2 x
4. Производная произведения
(f * g)»=f» * g + f * g»
Пример 9.
 Найдите производную функции y= cos x *e x
Найдите производную функции y= cos x *e xДля этого сначала найдем производного каждого множителя (cos x)»=–sin x и (e x)»=e x . Теперь подставим все в формулу произведения. Производную первой функции умножим на вторую и прибавим произведение первой функции на производную второй.
(cos x* e x)»= e x cos x – e x *sin x
5. Производная частного
(f / g)»= f» * g – f * g»/ g 2
Пример 10. Найдите производную функции y= x 50 /sin x
Чтобы найти производную частного, сначала найдем производную числителя и знаменателя отдельно: (x 50)»=50 x 49 и (sin x)»= cos x. Подставив в формулу производной частного получим:
(x 50 /sin x)»= 50x 49 *sin x – x 50 *cos x/sin 2 x
Производная сложной функции
Сложная функция — это функция, представленная композицией нескольких функций. Для нахождения производной сложной функции также существует правило:
(u (v))»=u»(v)*v»
Давайте разберемся как находить производную такой функции. Пусть y= u(v(x)) — сложная функция. 2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите , функции tg, ctg в любой степени периодичны П.
2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите , функции tg, ctg в любой степени периодичны П.
Если вам дано уравнение, содержащее или частное двух тригонометрических функций, сначала найдите период для каждой из них отдельно. Затем найдите минимальное число, которое умещало бы в себе целое количество обоих . Например, дана функция у=tgx*cos5x. Для тангенса период П, для косинуса 5х – период 2П/5. Минимальное число, в которое можно уместить оба этих периода, это 2П, таким образом, искомый период – 2П.
Если вы затрудняетесь действовать предложенным образом или сомневаетесь в ответе, попытайтесь действовать по определению. Возьмите в качестве периода функции Т, он больше нуля. Подставьте в уравнение вместо х выражение (х+Т) и решите полученное равенство, как если бы Т было параметром или числом. В результате вы найдете значение тригонометрической функции и сможете подобрать минимальный период. Например, в результате упрощения у вас получилось тождество sin (Т/2)=0. Минимальное значение Т, при котором оно выполняется, 2П, это и будет задачи.
Минимальное значение Т, при котором оно выполняется, 2П, это и будет задачи.
Источники:
- период sin
Периодической функцией называется функция, повторяющая свои значения через какой-то ненулевой период. Периодом функции называется число, при добавление которого к аргументу функции значение функции не меняется.
Вам понадобится
- Знания по элементарной математике и началам анализа.
Инструкция
Видео по теме
Обратите внимание
Все тригонометрические функции являются периодическими, а все полиномиальные со степенью больше 2 — апериодическими.
Полезный совет
Периодом функции, состоящей из двух периодический функций, является Наименьшее общее кратное периодов этих функций.
Тригонометрические уравнения — это уравнения, которые содержат в себе функции неизвестного аргумента (для примера: 5sinx-3cosx =7). Чтобы научиться решать их — нужно знать некоторые для этого методы.
Инструкция
Разложение уравнения на множители. Сначала переносим все члены влево и раскладываем на множители.
Сначала переносим все члены влево и раскладываем на множители.
Важно помнить, что о четности и нечетности функции имеет прямую с областью определения функции. Если, например, четная либо нечетная функция не при х=5, то она не существует и при х=-5, чего нельзя сказать про функцию общего вида. При установлении четности и нечетности обращайте внимание на область определения функции.
Исследование функции на четность и нечетность коррелирует с нахождением множества значений функции. Для нахождения множества значений четной функции достаточно рассмотреть половину функции, правее либо левее нуля. Если при x>0 четная функция y(x) принимает от А до В, то те же значения она будет и при xДля нахождения множества значений, принимаемых нечетной функцией, тоже достаточно рассмотреть только одну функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x
«Тригонометрическими» когда-то стали называть функции, которые определяются зависимостью острых углов в прямоугольном треугольнике от длин его сторон. К таким функциям относят в первую очередь синус и косинус, во вторую — обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Правильнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.
К таким функциям относят в первую очередь синус и косинус, во вторую — обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Правильнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.
Инструкция
Если аргумент тригонометрической неизвестен, то вычислить ее значение можно косвенным способом исходя из определений этих функций. Для этого требуется знать длины сторон треугольника, тригонометрическую для одного из углов которого требуется вычислить. Например, синус острого угла в прямоугольном треугольнике — это отношение длины противолежащего этому углу катета к длине гипотенузы. Из этого вытекает, что для угла достаточно знать длины этих двух сторон. Аналогичное гласит, что синусом острого угла является отношение длины прилежащего к этому углу катета к длине гипотенузы. Тангенс острого угла можно вычислить, разделив длину противолежащего ему катета на длину прилежащего, а требует деления длины прилежащего катета к длине противолежащего. Для вычисления секанса острого угла надо найти отношение длины гипотенузы к длине прилежащего к нужному углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета.
Для вычисления секанса острого угла надо найти отношение длины гипотенузы к длине прилежащего к нужному углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета.
Если же аргумент тригонометрической функции известен, то знать длины сторон треугольника не требуется — можно воспользоваться таблицами значений или калькуляторами тригонометрических функций. Такой есть среди стандартных программ операционной системы Windows. Для его запуска можно нажать сочетание клавиш Win + R, ввести команду calc и щелкнуть кнопку «OK». В интерфейсе программы следует раскрыть раздел «Вид» и пункт «Инженерный» или «Научный». После этого можно вводить аргумент тригонометрической функции. Для вычисления функций синус, косинус и достаточно после ввода значения щелкнуть по соответствующей кнопке интерфейса (sin, cos, tg), а для нахождения обратных им арксинуса, арккосинуса и следует предварительно поставить отметку в чекбоксе Inv.
Есть и альтернативные способы. Один из них — перейти на сайт поисковой системы Nigma или Google и ввести в качестве поискового запроса нужную функцию и ее аргумент (например, sin 0. 47). Эти поисковики имеют встроенные калькуляторы, поэтому после отправки такого запроса вы получите значение введенной вами тригонометрической функции.
47). Эти поисковики имеют встроенные калькуляторы, поэтому после отправки такого запроса вы получите значение введенной вами тригонометрической функции.
Видео по теме
Тригонометрические функции вначале возникли как инструменты абстрактных математических вычислений зависимостей величин острых углов в прямоугольном треугольнике от длин его сторон. Сейчас они очень широко применяются как в научных, так и в технических областях человеческой деятельности. Для практических вычислений тригонометрических функций от заданных аргументов можно использовать разные инструменты — ниже описано несколько наиболее доступных из них.
Инструкция
Воспользуйтесь, например, устанавливаемой по умолчанию вместе с операционной системой программой-калькулятором. Она открывается выбором пункта «Калькулятор» в папке «Служебные» из подраздела «Стандартные», помещенного в раздел «Все программы». Этот раздел можно , открыв щелчком по кнопке «Пуск» главное меню операционной . Если вы используете версию Windows 7, то имеете возможность просто ввести «Калькулятор» в поле «Найти программы и файлы» главного меню, а затем щелкнуть по соответствующей ссылке в результатах поиска.
Введите угла, для которого надо рассчитать тригонометрическую функцию, а потом кликните по соответствующей этой кнопке — sin, cos или tan. Если вас интересуют обратные тригонометрические функции (арксинус, арккосинус или ), то сначала кликните кнопку с надписью Inv — она меняет присвоенные управляющим кнопкам функции на противоположные.
В более ранних версиях ОС (например, Windows XP) для доступа к тригонометрическим функциям надо раскрыть в меню калькулятора раздел «Вид» и выбрать строку «Инженерный». Кроме того, вместо кнопки Inv в интерфейсе старых версий программы присутствует чекбокс с же надписью.
Можно и без калькулятора, если у вас есть доступ в интернет. В сети много сервисов, которые предлагают по-разному организованные вычислители тригонометрических функций. Один их наиболее удобных встроен в поисковую систему Nigma. Перейдя на ее главную страницу, просто введите в поле поискового запроса интересующее вас значение — например, «арктангенс 30 ». После нажатия кнопки «Найти!» поисковик рассчитает и покажет результат вычисления — 0,482347907101025.
Видео по теме
Тригонометрия – раздел математики для изучения , выражающих различные зависимости сторон прямоугольного треугольника от величин острых углов при гипотенузе. Такие функции получили называние тригонометрических, а для упрощения работы с ними были выведены тригонометрические тождества .
Понятие тождества в означает равенство, которое выполняется при любых значениях аргументов входящих в него функций. Тригонометрические тождества – это равенства тригонометрических функций, доказанные и принятые для облегчения работы с тригонометрическими формулами.Тригонометрическая функция – это элементарная функция зависимости одного из катетов прямоугольного треугольника от величины острого угла при гипотенузе. Чаще всего используются шесть основных тригонометрических функций: sin (синус), cos (косинус), tg (тангенс), ctg (котангенс), sec (секанс) и cosec (косеканс). Эти функции называются прямыми, существуют также
Число T, что для любого x F(x + T) = F(x). Это число T и называется периодом функции.
Это число T и называется периодом функции.
Периодов может быть и несколько. Например, функция F = const для любых значений аргумента принимает одно и то же значение, а потому любое число может считаться ее периодом.
Обычно интересует наименьший не равный нулю период функции. Его для краткости и называют просто периодом.
Классический пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период одинаков и равен 2π, то есть sin(x) = sin(x + 2π) = sin(x + 4π) и так далее. Однако, разумеется, тригонометрические функции — не единственные периодические.
Относительно простых, базовых функций единственный способ установить их периодичность или непериодичность — вычисления. Но для сложных функций уже есть несколько простых правил.
Если F(x) — с периодом T, и для нее определена производная, то эта производная f(x) = F′(x) — тоже периодическая функция с периодом T. Ведь значение производной в точке x равно тангенсу угла касательной графика ее первообразной в этой точке к оси абсцисс, а поскольку периодически повторяется, то должна повторяться . Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.
Например, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется неизменно.
Однако обратное не всегда верно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.
Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Например sin(2x) — периодическая функция, и ее период равен π. Наглядно это можно представить так: умножая x на какое-нибудь число, вы как бы сжимаете функции по горизонтали именно в столько раз
Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Однако ее период не будет простой суммой периодов T1 и T2. Если результат деления T1/T2 — рациональное число, то сумма функций периодична, и ее период равен наименьшему общему кратному (НОК) периодов T1 и T2. Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.
Например, если период первой функции равен 12, а период второй — 15, то период их суммы будет равен НОК (12, 15) = 60.
Наглядно это можно представить так: функции идут с разной «шириной шага», но если отношение их ширин рационально, то рано или (а точнее, именно через НОК шагов), они снова сравняются, и их сумма начнет новый период.
Однако если соотношение периодов , то суммарная функция не будет периодической вовсе. Например, пусть F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 здесь будет равен 2, а T2 равен 2π. Соотношение периодов равняется π — иррациональному числу. Следовательно, функция sin(x) + x mod 2 не является периодической.
Источники:
- Теоретические сведения о функциях
Многие математические функции имеют одну особенность, облегчающую их построение, — это периодичность , то есть повторяемость графика на координатной сетке через равные промежутки.
Инструкция
Самыми известными периодическими функциями математики синусоида и косинусоида. Эти функции имеют волнообразный и основной период, равный 2П. Также частным случаем периодической функции является f(x)=const. На позицию х подходит любое число, основного периода данная функция не имеет, так как представляет собой прямую.
Эти функции имеют волнообразный и основной период, равный 2П. Также частным случаем периодической функции является f(x)=const. На позицию х подходит любое число, основного периода данная функция не имеет, так как представляет собой прямую.
Вообще функция является периодической, если существует целое число N, которое от нуля и удовлетворяет правилу f(x)=f(x+N), таким образом обеспечивая повторяемость. Период функции — это и есть наименьшее число N, но не ноль. То есть, например, функция sin x равна функции sin (x+2ПN), где N=±1, ±2 и т.д.
Иногда при функции может множитель (например sin 2x), который увеличит или сократит период функции. Для того чтобы найти период по
С центром в точке A .
α — угол, выраженный в радианах.
Определение
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
>> Периодичность функций у = sin х, у = cos х
§ 11. Периодичность функций у = sin х, у = cos х
Периодичность функций у = sin х, у = cos х
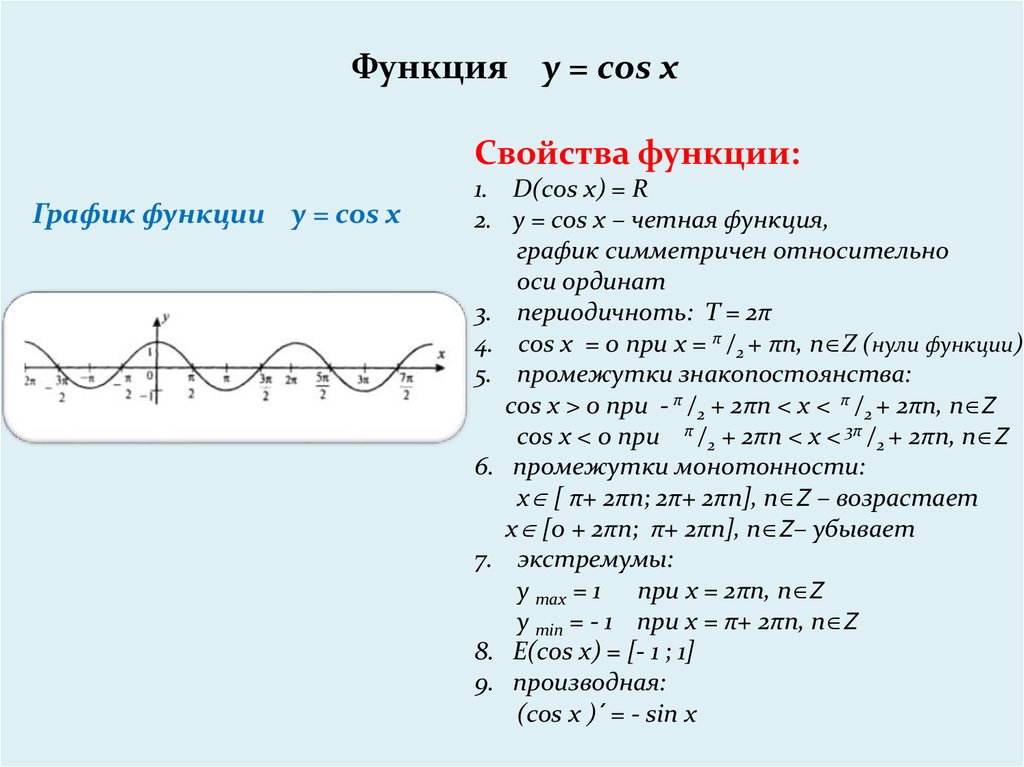
В предыдущих параграфах мы использовали семь свойств функций : область определения, четность или нечетность, монотонность, ограниченность, наибольшее и наименьшее значения, непрерывность, область значений функции. Использовали мы эти свойства либо для того, чтобы построить график функции (так было, например, в § 9), либо для того, чтобы прочитать построенный график (так было, например, в § 10). Теперь настал благоприятный момент для введения еще одного (восьмого) свойства функций, которое прекрасно просматривается на построенных выше графиках функций у = sin х(см. рис. 37), у=соs х(см. рис. 41).
Определение. Функцию называют периодической, если существует такое отличное от нуля число T, что для любого х из множествах выполняется двойное равенство :
Число Т, удовлетворяющее указанному условию, называют периодом функции у = f(х).
Отсюда следует, что, поскольку для любого х справедливы равенства:
то функции у = sin х, у=соs х являются периодическими и число 2п служит периодом и той, и другой функции.
Периодичность функции — это и есть обещанное восьмое свойство функций.
А теперь посмотрите на график функции у = sin х (рис. 37). Чтобы построить синусоиду, достаточно построить одну ее волну (на отрезке а затем сдвинуть эту волну по оси х на В итоге с помощью одной волны мы построим весь график.
Посмотрим с этой же точки зрения на график функции у =соs х (рис. 41). Видим, что и здесь для построения графика достаточно сначала построить одну волну (например, на отрезке
А затем сдвинуть ее по оси х на
Обобщая, делаем следующий вывoд.
Если функция у = f(х) имеет период Т, то для построения графика функции нужно сначала построить ветвь (волну, часть) графика на любом промежутке длины Т (чаще всего берут промежуток с концами в точках а затем сдвинуть эту ветвь по оси х вправо и влево на Т, 2Т, ЗТ и т.д.
У периодической функции бесконечно много периодов: если Т — период, то и 2Т — период, и ЗТ — период, и -Т — период; вообще периодом является любое число вида KТ, где к = ±1, ±2, ± 3. .. Обычно стараются, если это возможно, выделить наименьший положительный период, его называют основным периодом.
.. Обычно стараются, если это возможно, выделить наименьший положительный период, его называют основным периодом.
Итак, любое число вида 2пк, где к = ±1, ± 2, ± 3,является периодом функций у = sinп х, у=соs х; 2п- основной период и той, и другой функции.
Пример. Найти основной период функции:
а) Пусть Т — основной период функции у = sin х. Положим
Чтобы число Т было периодом функции, должно выполняться тождество Но, поскольку речь идет об отыскании основного периода, получаем
б) Пусть Т — основной период функции у =соs 0,5х. Положим f(х)=соs 0,5х. Тогда f(х + Т)=соs 0,5(х + Т)=соs (0,5х + 0,5Т).
Чтобы число Т было периодом функции, должно выполняться тождество соs (0,5х + 0,5Т)=соs 0,5х.
Значит, 0,5т = 2пп. Но, поскольку речь идет об отыскании основного периода, получаем 0.5Т = 2 л, Т =4л.
Обобщением результатов, полученных в примере, является следующее утверждение: основной период функции
А.Г. Мордкович Алгебра 10 класс
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие
Совершенствование учебников и уроковисправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
Мэтуэй | Популярные задачи
92) 9(3x) по отношению к x 92+1| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | ||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | ||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | |
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная cosx, формула, доказательство, правило произведения, первый принцип
Производная cosx является частью Дифференциации, которая является подтемой исчисления. В производной от cosx есть чистая тригонометрическая функция. cosx — это основная тригнометрическая функция, используемая в различных приложениях. Производные cosx позволяют учащимся решать различные задачи тригонометрии, комплексных чисел и т. д.
В производной от cosx есть чистая тригонометрическая функция. cosx — это основная тригнометрическая функция, используемая в различных приложениях. Производные cosx позволяют учащимся решать различные задачи тригонометрии, комплексных чисел и т. д.
В этой статье мы узнаем, как дифференцировать cosx, используя различные правила дифференцирования, такие как первый принцип производной, цепное правило и правило частных вместе с решенные примеры и часто задаваемые вопросы
Что такое cosx?
Производная функции — это математическое понятие вещественной переменной, которое измеряет чувствительность к изменению значения функции (выходного значения) по отношению к изменению ее аргумента (входного значения). Они являются частью дифференциального исчисления. Существуют различные методы дифференциации. Производная функции одной переменной при выбранном входном значении, если она существует, представляет собой наклон касательной к графику функции в этой точке. Производные используются для нахождения решений дифференциальных уравнений.
Косинус – это тригонометрическая функция угла. Мы можем легко найти производные тригнометрических функций. Косинус острого угла определяется в контексте прямоугольного треугольника: для указанного угла косинус представляет собой отношение длины прилежащего катета к длине гипотенузы. Косинус можно определить как бесконечный ряд или как решение некоторых дифференциальных уравнений, допуская их распространение на произвольные положительные и отрицательные значения и даже на комплексные числа. Закон косинусов используется для нахождения остальных частей косого (непрямоугольного) треугольника, когда известны либо длины двух сторон и мера прилежащего к ним угла (SAS), либо длины трех сторон (SSS). известен.
Доказательство производной cosx
Теперь мы узнаем, как дифференцировать cosx, используя различные методы дифференцирования, такие как первый принцип производной, дифференцировать cosx по цепному правилу и дифференцировать cosx по правилу частных.
Производная cosx по первому принципу
Производная по первому принципу относится к использованию алгебры для нахождения общего выражения для наклона кривой. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна:
Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна:
\(f'(x)={dy\over{dx}}=\lim _{h{\rightarrow}0}{f(x+h)–f(x)\over{h}}\)
Если f(x) = cosx , найдите f'(x)
\(\begin{matrix}\
f'(x)={dy\over{dx}}=\lim _{h{\rightarrow }0}{f(x+h)–f(x)\over{h}}
f(x)=cosx\\
f(x+h)=cos(x+h)\\
f(x +h)–f(x)= cos(x+h) – cos(x) = cosxcosh – sinxsinh – cosx\\
= cosx(cosh-1) – sinxsinh\\
{f(x+h) – f (x)\over{h}}={ cosx(cosh-1) – sinxsinh\over{h}}\\
\lim _{h{\rightarrow}0}{f(x+h) –f(x )\over{h}} = \lim _{h{\rightarrow}0} { cosx(cosh-1) – sinxsinh\over{h}}\\
\lim _{h{\rightarrow}0}{f(x+h) –f(x)\over{h}} = \lim _{h{\rightarrow}0} {cosx(cosh-1)\ over{h}} – \lim _{h{\rightarrow}0} {sinxsinh\over{h}}\\
= cosx \lim _{h{\rightarrow}0} {(cosh-1)\over{ h}} – sinx \lim _{h{\rightarrow}0} {sinh\over{h}}\\
\text{Положим h = 0 в первом пределе}\\
cosx \lim _{h{\rightarrow }0} {(cosh-1)\over{h}} = cosx\times0 = 0\\
\text{Использование правила Больниц L’ на втором пределе}\\
\lim _{h{\rightarrow}0} {f(x+h) –f(x)\over{h}} = -sinx \lim _{h{\rightarrow}0} {{d\over{dh}} sinh\over{{d\over{ дч}}ч}}\\
\lim _{h{\rightarrow}0}{f(x+h) –f(x)\over{h}} = -sinx \lim _{h{\rightarrow}0} {cosh\over{1 }}\\
\lim _{h{\rightarrow}0}{f(x+h) –f(x)\over{h}} = -sinx \times1 = -sinx\\
f'(x) ={dy\over{dx}} = {d(cosx)\over{dx}} = -sinx
\end{matrix}\)
Альтернативно,
\(\begin{matrix}\
f'( x) = {dy \ over {dx}} = \ lim _ {h {\ rightarrow} 0} {f (x + h) – f (x) \ over {h}}
f (x) = cosx \\
f(x+h)=cos(x+h)\\
f(x+h)–f(x)= cos(x+h) – cos(x) = {-2sin({x+h+ x\over{2}})sin({x+h-x\over{2}})\over{h}}\\
\lim _{h{\rightarrow}0}{f(x+h) –f(x)\over{h}} = \lim _{h{\rightarrow}0} {-2sin({2x+h \over{2}})sin({h\over{2}})\over{h}}\\
\lim _{h{\rightarrow}0}{f(x+h) –f(x) \ over {h}} = \ lim _ {h {\ rightarrow} 0} -2cos (x + {h \ over {2}}) {sin ({h \ over {2}}) \ over {h}} \ \
\ lim _ {h {\ rightarrow} 0} {f (x + h) -f (x) \ over {h}} = \ lim _ {h {\ rightarrow} 0} — 2sin (x + {h \ над {2}}) {sin ({h \ over {2}}) \ over {{h \ over {2}}}} \\
\ lim _ {h {\ rightarrow} 0} {f (x + h) –f(x)\over{h}} = \lim _{h{\rightarrow}0} -2sin(x+{h\over{2}})\times1\\
{\ потому что} \ lim _ {h {\ rightarrow} 0} {sin ({h \ over {2}}) \ over {{h \ over {2}}}} = 1 \\
\ lim _ { h{\rightarrow}0}{f(x+h) –f(x)\over{h}} = \lim _{h{\rightarrow}0} -2sin(x+{h\over{2}}) = -sinx\\
f'(x)={dy\over{dx}} = {d(sinx)\over{dx}} = -sinx
\end{matrix}\)
Производная cosx по формуле Цепное правило
Цепное правило помогает нам дифференцировать составные функции, количество функций, составляющих композицию, определяет, сколько шагов дифференцирования необходимо. Цепное правило гласит, что
Цепное правило гласит, что
\(\begin{matrix}
{d\over{dx}}f(g(x)) = f'(g(x))⋅g'(x).\\
{d\over{dx }}f[g(h(x))] = f'(g(h(x)))⋅g'(h(x))h'(x)
\end{matrix}\)
g и h, составляют составную функцию f, вы должны учитывать производные g′ и h′ при дифференцировании f(x).
Если f(x) = cosx , найти f'(x)
\(\begin{matrix}
f(x) = cosx = sin({\pi\over{2}} -x )\\
\text{ Используя цепное правило, }\\
f'(x) = cos({\pi\over{2}} -x) · {d\over{dx}} ({\pi\over{2}} -х)\\
= cos({\pi\over{2}} -x) · (-1)\\
= -cos({\pi\over{2}} -x)\\
= -sinx
\end{ matrix}\)
Производная cosx по правилу отношения
Существует специальное правило, правило отношения, для дифференцирования отношений двух функций. Функции часто приходят в виде частных, под которыми мы подразумеваем одну функцию, деленную на другую функцию. Есть формула, которую мы можем использовать, чтобы дифференцировать частное — она называется правилом частного.
Если f и g дифференцируемы, то:
\({d\over{dx}}({f(x)\over{g(x)}}) = {g(x){d\over{dx}}f(x) — f(x ){d\over{dx}}g(x)\over{g(x)}}\)
Чтобы решить производную по цепному правилу, нужно знать правило LIATE.
Правило LIATE
Правило LIATE выглядит следующим образом
Было предложено эмпирическое правило, состоящее в выборе в качестве u функции, которая стоит первой в следующем списке:
- L – логарифмические функции: \({ln( x),log _{b}(x) }\) и др.
- I – обратные тригонометрические функции (включая гиперболические аналоги): arctg(x), arcsec(x), arsinh(x) и др. 92x}}\\
= -{tanx\over{secx}}\\
= -{{sinx\over{cosx}}\over {{1\over{cosx}}}}\\
= -sinx
\end{matrix}\)Антипроизводная cos x
Антипроизводная cos x есть не что иное, как интегрирование cos x. Антипроизводная означает обратный процесс дифференцировки. Как мы теперь знаем, производная от cosx равна -sinx. Следовательно, первообразная производной cos x равна sin x + C.

Решенные примеры производной cosx
Давайте посмотрим на некоторые примеры производной cosx 92x\\
= 2cosx\times{d\over{dx}}(cosx)\\
= 2cosx\times(-sinx)\\
= -2sinxcosx\\
= -sin2x
\end{matrix}\)Надеюсь, эта статья о производной cosx была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Производная от Cos x Часто задаваемые вопросы
В.1 Что такое cosx?
Ответ 1 Косинус — это тригонометрическая функция угла. Косинус острого угла определяется в контексте прямоугольного треугольника: для указанного угла косинус представляет собой отношение длины прилежащего катета к длине гипотенузы. Косинус можно определить как бесконечный ряд или как решение некоторых дифференциальных уравнений, допуская их распространение на произвольные положительные и отрицательные значения и даже на комплексные числа. Закон косинусов используется для нахождения остальных частей косого (непрямоугольного) треугольника, когда известны либо длины двух сторон и мера прилежащего к ним угла (SAS), либо длины трех сторон (SSS).
 известен.
известен.Q.2 Что такое первообразная cosx?
Ответ 2 Антипроизводная cos x есть не что иное, как интегрирование cos x. Антипроизводная означает обратный процесс дифференцировки. Как мы теперь знаем, производная от cosx равна -sinx. Следовательно, первообразная cos x равна sin x + C.
Q.3 Как найти производную функции косинуса?
Ответ 3 Производная функции синуса записывается как cos′(a) = -sin(a), что означает, что скорость изменения cos(x) при конкретном угле x = a дается на косинус этого угла. Если f(x) = cosx, найти f’(x)
\(\begin{matrix}
f(x) = cosx = sin({\pi\over{2}} -x)\\
\text{Используя цепное правило,}\\
f'(x) = cos({\pi\over{2}} -x) · {d\over{dx}} ({\pi\over{2}} -x)\\
= cos({\pi\over{2} } -x) · (-1)\\
= -cos({\pi\over{2}} -x)\\
= -sinx
\end{matrix}\)Q.4 Что такое Производная от cos x.sin x?
Ответ 4 Если f(x) = cosx.
 sinx , найти f'(x)
sinx , найти f'(x)
\(\begin{matrix}
f(x) = cosx.sinx \\
\text{ Используя правило произведения, } {dy\over{dx}} = u{dv\over{dx}} + v{du\over{dx}}\\ 92x\\
= 1
\end{matrix}\)Q.5 Чему равна вторая производная cosx?
Ответ 5 Вторая производная или производная второго порядка функции f — это производная производной от f. Вторая производная — это скорость изменения скорости изменения точки на графике. Здесь функция cosx. Сначала вычислим производную от cosx. Это дает нам значение -sinx. Теперь, чтобы вычислить вторую производную, продифференцируем -sinx по x. 92x с использованием правила произведения
Правило произведения для дифференцирования утверждает, что производная от f(x).g(x) равна f'(x)g(x) + f(x).g'(x)
Правило произведения:
Для двух дифференцируемых функций f(x) и g(x)
Если F(x) = f(x). g(x) 6 11009 1
g(x) 6 11009 1
Тогда производная F(x) есть F'(x) = f'(x)g(x) + f(x)g'(x)Сначала пусть F(x) = cos 2 (x)
Тогда помните, что cos 2 (x) равно cos(x).cos(x)
Итак, F(x) = cos(x)cos(x)
Устанавливая f( x) и g(x), поскольку cos(x) означает, что F(x) = f(x).g(x), и мы можем применить правило произведения, чтобы найти F'(x)
92x с использованием цепного правилаЦепное правило полезно для нахождения производной функции, которую можно было бы дифференцировать, если бы она была по x, но она представлена в форме другого выражения, которое также можно было бы дифференцировать, если бы оно стояло само по себе .
В этом случае:
- Мы знаем, как дифференцировать cos(x) (ответ -sin(x))
- Мы знаем, как дифференцировать x 2 (ответ 2x)
Это означает цепное правило позволит нам выполнить дифференцирование выражения cos^2x.
 92x
92xХотя выражение cos 2 x не содержит скобок, мы все же можем рассматривать его как составную функцию (функцию функции).
Мы можем записать cos 2 x как (cos(x)) 2 .
Теперь функция имеет форму x 2 , за исключением того, что она не имеет x в качестве основания, вместо этого она имеет другую функцию x (cos(x)) в качестве основания.
Назовем функцию основания g(x), что означает:
g(x) = cos(x)
Отсюда следует, что:
cos(x) 2 = g(x) 2
Итак, если функция f(x) = x 2 и функция g(x) = cos(x ), то функция (cos(x)) 2 может быть записана как составная функция.
f(x) = x 2
f(g(x)) = g(x) 2 (но g(x) = cos(x))
f(g(x)) = (cos(x)) 2
Определим эту составную функцию как F(x):
F(x) = f(g(x)) = (cos(x)) 92x с использованием цепного правила:
92x is -2cos(2x)F'( x) = f'(x)g(x) + f(x)g'(x) Определение правила продукта = f'(x)cos(x) + cos(x) )g'(x) f(x) = g(x) = cos(x) 2.8: Производные тригонометрических функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 89720
- Джоэл Фельдман, Эндрю Рехницер и Элиз Йегер
- Университет Британской Колумбии
Теперь мы собираемся вычислить производные различных тригонометрических функций, \(\sin x\text{,}\) \(\cos x\) и так далее.
 Вычисления более сложны, чем другие, которые мы делали до сих пор, и будут состоять из нескольких шагов. К счастью, окончательные ответы будут очень простыми.
Вычисления более сложны, чем другие, которые мы делали до сих пор, и будут состоять из нескольких шагов. К счастью, окончательные ответы будут очень простыми.Обратите внимание, что нам нужно вычислить только производные от \(\sin x\) и \(\cos x\text{,}\), поскольку остальные тригонометрические функции на самом деле являются просто частными этих двух функций. Напомним:
\begin{align*} \tan x &= \frac{\sin x}{\cos x} & \cot x &= \frac{\cos x}{\sin x} & \csc x &= \frac {1}{\sin x} & \sec x &= \frac{1}{\cos x}. \конец{выравнивание*}
Первым шагом к вычислению производных \(\sin x, \cos x\) является нахождение их производных в \(x=0\text{.}\). Производные в общих точках \(x\) будут следовать быстро из них, используя триггерные тождества. Важно отметить, что в дальнейшем мы должны измерять углы в радианах 1 , а не в градусах. Действительно, если явно не указано иное, любое число, вводимое в тригонометрическую функцию, измеряется в радианах.
Эти доказательства необязательны, результаты — нет.

Хотя мы ожидаем, что вы прочтете эти корректуры и будете им следовать, мы не ожидаем, что вы сможете их воспроизвести. Вам потребуется знать результаты, в частности теорему 2.8.5 ниже.
Шаг 1: \(\mathbf{\dfrac{d}{dx} \{ \sin x \} \big|_{x=0}}\)
По определению, производная от \(\sin x \) оценивается при \(x=0\) равно
\begin{gather*} \dfrac{d}{dx} \{ \sin x \} \Big|_{x=0} =\lim_{h\ стрелка вправо 0}\frac{\sin h-\sin 0}{h} =\lim_{h\стрелка вправо 0}\frac{\sin h}{h} \end{gather*}
Мы докажем этот предел, используя теорему сжатия (теорема 1.4.18). Чтобы добраться туда, нам сначала нужно сделать некоторую геометрию. Но сначала мы построим некоторую интуицию.
На рисунке ниже изображена часть окружности радиусом 1. Напомним, что дуга длины \(h\) на такой окружности образует угол \(h\) радиан в центре окружности. Таким образом, затемненная дуга на рисунке имеет длину \(h\), а затемненная вертикальная линия на рисунке имеет длину \(\sin h\text{.
 }\). Мы должны определить, что происходит с отношением длин затемненных вертикальная линия и затемненная дуга при стремлении \(h\) к нулю.
}\). Мы должны определить, что происходит с отношением длин затемненных вертикальная линия и затемненная дуга при стремлении \(h\) к нулю.Вот увеличенная версия части рисунка выше, которая содержит затемненную дугу и вертикальную линию.
Эта конкретная фигура была нарисована в \(h=0,4\) радианах. Вот еще три таких взрыва. В каждой последующей фигуре значение \(h\) меньше. Чтобы сделать цифры более четкими, степень увеличения увеличивалась при каждом уменьшении \(h\).
По мере того, как мы уменьшаем \(h\) и смотрим на фигуру со все возрастающим увеличением, дуга длины \(h\) и вертикальная линия длины \(\sin h\) выглядят все больше и больше одинаковый Отсюда можно предположить, что
\[ \lim_{h\rightarrow 0}\frac{\sin h}{h}=1 \nonumber \]
Следующие таблицы значений
F'(x) = f'(g(x)).  g'(x)
g'(x)Определение цепного правила g(x))(-sin(x)) g(x) = cos(x) ⇒ g'(x) = sin(x) = (2cos(x)).( -sin(x)) f(g(x)) = (cos(x)) 2 ⇒ f'(g(x)) = 2cos(x) = -2cos(x)sin(x) \(\грех ч\) \(\tfrac{\sin ч}{ч}\) 0,4 .3894 .  9735
97350,2 .1987 .9934 0,1 .09983 .9983 0,05 .049979 .99958 0,01 .00999983 .999983 0,001 .0099999983 .9999983 ч \(\грех ч\) \(\tfrac{\sin ч}{ч}\) \(-0,4\) \(-.3894\) .9735 \(-0,2\) \(-.1987\) .9934 \(-0,1\) \(-.09983\) .9983 \(-0,05\) \(-.  049979\)
049979\).99958 \(-0,01\) \(-.00999983\) .999983 \(-0,001\) \(-.0099999983\) .9999983 предполагает ту же догадку. Вот аргумент, который показывает, что догадка действительно верна.
Доказательство того, что \(\mathbf{\lim\limits_{h\rightarrow 0}\tfrac{\sin h}{h}=1}\)
Круг на рисунке выше имеет радиус \(1\ text{.}\) Следовательно,
\begin{align*} |OP|=|OR|&=1 & |PS|&=\sin h\\ |OS|&= \cos h & |QR|&=\tan h \end{align *}
Теперь мы можем использовать несколько геометрических фактов об этой фигуре, чтобы установить как верхнюю, так и нижнюю границы для \(\frac{\sin h}{h}\), при этом как верхняя, так и нижняя границы стремятся к \ (1\) поскольку \(h\) стремится к \(0\text{.}\) Таким образом, теорема о сжатии говорит нам, что \(\frac{\sin h}{h}\) также стремится к \(1 \) при стремлении \(h\) к \(0\text{.
 }\)
}\)- Треугольник \(OPR\) имеет основание \(1\) и высоту \(\sin h\text{,}\ ) и, следовательно
\begin{align*} \text{площадь}\треугольника OPR &=\frac{1}{2}\times1\times\sin h=\frac{\sin h}{2}. \конец{выравнивание*}
- Треугольник \(OQR\) имеет основание \(1\) и высоту \(\tan h\text{,}\) и, следовательно,
\begin{align*} \text{площадь}\треугольника OQR &= \frac{1}{2}\times1\times\tan h=\frac{\tan h}{2}. \конец{выравнивание*}
- «Кусок пирога» \(OPR\), вырезанный из круга, представляет собой долю \(\frac{h}{2\pi}\) всего круга (поскольку угол в углу куска пирога равен \(h\) радианам, а угол для всей окружности равен \(2\pi\) радианам). Так как круг имеет радиус \(1\), мы имеем 92= \frac{h}{2} \end{align*}
Теперь треугольник \(OPR\) содержится внутри куска пирога \(OPR\text{.}\), поэтому площадь треугольника меньше площади куска пирога. Точно так же кусок пирога \(OPR\) содержится внутри треугольника \(OQR\text{.
 }\) Таким образом, мы имеем
}\) Таким образом, мы имеем\begin{gather*} \text{площадь треугольника } OPR \leq \text{ площадь круга } OPR \leq \text{ площадь треугольника } OQR \end{gather*}
Подстановка в области, которые мы вычислили, дает
\begin{align*} \frac{\sin h}{2} &\leq \frac{h}{2} \leq \frac{\tan h}{2}\\ \end{align*}
, которое очищается, чтобы дать
\begin{align*} \sin h &\leq h \leq \frac{\sin h}{\cos h} \end{align*}
Перепишем эти два неравенства так, чтобы \(\frac{\sin h}{h}\) появляется в обоих случаях.
- Так как \(\sin h \leq h\text{,}\) мы имеем, что \(\displaystyle \frac{\sin h}{h} \leq 1\text{.}\)
- Так как \(\displaystyle h \leq \frac{\sin h}{\cos h}\) мы имеем, что \(\displaystyle \cos h \leq \frac{\sin h}{h}\text{.} \)
Таким образом, мы приходим к «сжимаемому» неравенству
\begin{gather*} \cos h \leq \frac{\sin h}{h} \leq 1 \end{gather*}
Мы знаем 2 что
\begin{align*} \lim_{h \to 0} \cos h &=1.
 \end{align*}
\end{align*}Поскольку \(\tfrac{\sin h}{h}\) зажато между \(\cos h\) и 1, мы можем применить теорему сжатия для пределов (теорема 1.4.18) вывести следующую лемму:
Лемма 2.8.1.
\begin{align*} \lim_{h \to 0} \frac{\sin h}{h} &= 1. \end{align*}
Поскольку над этим аргументом пришлось немного потрудиться, возможно, нам следует напомнить себе, зачем он нам вообще понадобился. Мы вычисляли
\begin{align*} \dfrac{d}{dx} \{ \sin x\}\Big|_{x=0} &= \lim_{h \to 0} \frac{\sin h — \sin 0}{h}\\ &= \lim_{h \to 0} \frac{\sin h}{h} & \text{(Вот почему!)}\\ &= 1 \end{ align*}
Это завершает шаг 1. Теперь мы знаем, что \(\dfrac{d}{dx}\sin x\big|_{x=0}=1\text{.}\) Остальные шаги проще .
Шаг 2: \(\mathbf{\dfrac{d}{dx} \{ \cos x \} \big|_{x=0}}\)
По определению, производная от \(\cos x\), оцененная при \(x=0\), равна
\begin{align*} \lim_{h\rightarrow 0}\frac{\cos h-\cos 0}{h} &=\lim_{h\rightarrow 0}\frac{\cos h — 1}{h} \end{align*}
К счастью, нам не нужно пробираться через геометрию, как мы это делали для предыдущий шаг.
 2 h=1$)}\\ &= — \frac{\sin h}{h} \cdot \frac{\sin h}{1 + \cos h} \end{align*}
2 h=1$)}\\ &= — \frac{\sin h}{h} \cdot \frac{\sin h}{1 + \cos h} \end{align*}Теперь мы можем взять предел как \(h \to 0\) по лемме 2.8.1.
\begin{align*} \lim_{h \to 0} \frac{\cos h — 1}{h} &= \lim_{h \to 0} \left( \frac{-\sin h}{ h} \cdot \frac{\sin h}{1 + \cos h} \right)\\ &= -\lim_{h \to 0}\left( \frac{\sin h}{h} \right) \cdot \lim_{h \to0} \left( \frac{\sin h}{1 + \cos h} \right)\\ &= — 1 \cdot \frac{0}{2}\\ &= 0 \end{align*}
Метод 2 — с помощью формулы двойного угла
Другой способ использует формулу двойного угла 92}\\ &= — \theta \cdot \frac{\sin \theta}{\theta} \cdot \frac{\sin \theta}{\theta} \end{align*}
Когда мы берем предел как \(h \to 0\text{,}\), мы также берем предел как \(\theta=h/2 \to 0\text{,}\) и, таким образом,
\begin{align*} \lim_{h \to 0} \frac{\cos h — 1}{h} &= \lim_{\theta \to 0} \left[ — \theta \cdot \frac{\sin \theta}{\theta} \cdot \frac{\sin \theta}{\theta} \right]\\ &= \lim_{\theta \to 0} \left[- \theta \right] \cdot \lim_ {\ тета \ до 0} \ влево [\ гидроразрыва {\ грех \ тета} {\ тета} \ вправо] \ cdot \ lim _ {\ тета \ до 0} \ влево [\ гидроразрыва {\ грех \ тета} {\ тета }\right]\\ &= 0 \cdot 1 \cdot 1\\ &= 0 \end{align*}
, где мы использовали тот факт, что \(\displaystyle \lim_{h \to 0} \frac{\sin h}{h} = 1\) и что предел произведения есть произведение пределов (т.
 е. лемма 2.8.1 и теорема 1.4.3).
е. лемма 2.8.1 и теорема 1.4.3).Таким образом, мы получили два доказательства следующей леммы:
Лемма 2.8.2.
\begin{align*} \lim_{h \to 0} \frac{\cos h -1}{h} &= 0 \end{align*}
Опять же, нам пришлось немного потрудиться, так что мы должны напомнить себе, зачем нам это нужно. Мы вычисляли
\begin{align*} \dfrac{d}{dx} \{ \cos x \} \Big|_{x=0} &= \lim_{h \to 0} \frac{\cos h — \cos 0}{h}\\ &= \lim_{h \to 0} \frac{\cos h — 1}{h}\\ &= 0 \end{align*}
Вооружившись этими результатами, теперь мы можем построить производные синуса и косинуса.
Шаг 3: \(\dfrac{d}{dx} \{ \sin x \}\) и \(\dfrac{d}{dx} \{ \cos x\}\) для общего \(x\)
Чтобы перейти к общим производным \(\sin x\) и \(\cos x\), мы собираемся использовать два приведенных выше результата и пару тригонометрических тождеств. Помните формулы сложения 5
\begin{align*} \sin(a+b) &= \sin(a) \cos(b) + \cos(a) \sin(b)\\ \cos(a+b) &= \cos(a) \cos(b) — \sin(a) \sin(b) \end{align*}
Чтобы вычислить производную \(\sin(x)\), мы просто начинаем с определение производной:
\begin{align*} \dfrac{d}{dx}\sin x &=\lim_{h\rightarrow 0}\frac{\sin (x+h)-\sin x}{ h} \\ &=\lim_{h\стрелка вправо 0}\frac{\sin x\cos h +\cos x\sin h-\sin x}{h}\\ &=\lim_{h\стрелка вправо 0} \bigg[\sin x\frac{\cos h-1}{h} +\cos x\frac{\sin h-0}{h}\bigg]\\ &=\sin x\ \lim_{h\ стрелка вправо 0}\frac{\cos h-1}{h} \ +\ \cos x\ \lim_{h\стрелка вправо 0}\frac{\sin h-0}{h}\\ &=\sin x\ \ underbrace {\ bigg [\ dfrac {d} {dx} \ cos x \ bigg] _ {x = 0}} _ {= 0} \ +\ \ cos x \ \ underbrace {\ bigg [\ dfrac {d} {dx}\sin x\bigg]_{x=0}}_{=1}\\ &=\cos x \end{align*}
Вычисление производной \(\cos x\) очень похоже.

\begin{align*} \dfrac{d}{dx}\cos x &=\lim_{h\rightarrow 0}\frac{\cos (x+h)-\cos x}{h}\\ & =\lim_{h\стрелка вправо 0}\frac{\cos x\cos h -\sin x\sin h-\cos x}{h}\\ &=\lim_{h\стрелка вправо 0}\bigg[\cos x \ frac {\ cos h-1} {h} — \ sin x \ frac {\ sin h-0} {h} \ bigg] \\ & = \ cos x \ \ lim_ {h \ rightarrow 0} \ frac {\ cos h-1} {h} \ — \ \ sin x \ \ lim_ {h \ rightarrow 0} \ frac {\ sin h-0} {h} \\ & = \ cos x \ \ underbrace {\ bigg [\dfrac{d}{dx}\cos x\bigg]_{x=0}}_{=0} \ -\ \sin x\ \underbrace{\bigg[\dfrac{d}{dx}\sin x\bigg]_{x=0}}_{=1}\\ &=-\sin x \end{align*}
Теперь мы нашли производные от \(\sin x\) и \(\cos x\text{,}\) при условии, что \(x\) измеряется в радианах .
Лемма 2.8.3.
\begin{align*} \dfrac{d}{dx}\sin x &=\cos x & \dfrac{d}{dx}\cos x &=-\sin x \end{align*}
Приведенные выше формулы справедливы при условии, что \(x\) измеряется в радианах.
Эти формулы довольно легко запомнить — применение \(\dfrac{d}{dx}\) к \(\sin x\) и \(\cos x\) просто меняет местами \(\sin x\) и \ (\cos x\text{,}\), кроме знака минус 6 в производной от \(\cos x\text{.
 }\)
}\)Замечание 2.8.4 Необязательно. Другой вывод от \(\dfrac{d}{dx}\cos x =-\sin x\) .
Заметим, что, зная, что \(\dfrac{d}{dx}\sin x =\cos x\text{,}\), его легко использовать, а тождество триггера \(\cos(x ) = \sin\big(\frac{\pi}{2}-x\big)\) для получения \(\dfrac{d}{dx}\cos x =-\sin x\text{.}\) Вот как 7 .
\begin{align*} \dfrac{d}{dx}\cos x &=\lim_{h\rightarrow 0}\frac{\cos (x+h)-\cos x}{h} =\lim_ {h \ стрелка вправо 0} \ frac {\ sin \ big (\ frac {\ pi} {2} -xh) — \ sin \ big (\ frac {\ pi} {2} — x \ big)} {h} \\ &=-\lim_{h’\rightarrow 0}\frac{\sin\big(x’+h’)-\sin(x’)}{h’} \qquad\text{with}x’= \tfrac{\pi}{2}-x,\ h’=-h\\ &=-\dfrac{d}{dx’}\sin x’\Big|_{x’=\tfrac{\pi} {2}-x} =-\cos\big(\tfrac{\pi}{2}- x\big)\\ &=-\sin x \end{align*}
Заметим, что если \(х\) измерять в градусах, то формулы леммы 2.8.3 неверны. Есть похожие формулы, но для их построения нам понадобится цепное правило — это тема следующего раздела. Но сначала мы должны найти производные других тригонометрических функций.
 2 x\\ \dfrac{d}{dx} \csc x &= -\csc x \cot x & \ dfrac{d}{dx} \sec x &= \sec x \tan x \end{align*}
2 x\\ \dfrac{d}{dx} \csc x &= -\csc x \cot x & \ dfrac{d}{dx} \sec x &= \sec x \tan x \end{align*}Из этих 6 производных вам действительно следует запомнить производные синуса, косинуса и тангенса. Мы, конечно, ожидаем, что вы сможете вычислить котангенс, косеканс и секанс.
Упражнения
Этап 1
Упражнение \(\PageIndex{1}\)
График синуса и косинуса на одних и тех же осях, от \(x=-2\pi\) до \(x=2\pi\ text{.}\) Отметьте точки, в которых \(\sin x\) имеет горизонтальную касательную. Чему соответствуют эти точки на графике косинуса?
Упражнение \(\PageIndex{2}\)
График синуса и косинуса на одних и тех же осях, от \(x=-2\pi\) до \(x=2\pi\text{.}\) Отметьте точки, где \(\sin x\) имеет линия касания максимального (положительного) наклона. Чему соответствуют эти точки на графике косинуса?
Этап 2
Упражнение \(\PageIndex{3}\)
Дифференцировать \(f(x)=\sin x + \cos x +\tan x\text{.}\)
Упражнение \(\PageIndex {4}\)
При каких значениях \(x\) функция \(f(x)=\sin x + \cos x\) имеет горизонтальную касательную? 96-\csc x)\text{.
 }\)
}\)Упражнение \(\PageIndex{11}\)
Дифференцировать \(f(\theta)=\sin\left(\frac{\pi}{2} -\theta \right)\text{.}\)
Упражнение \(\PageIndex{12}\)
Дифференцировать \(f(x)=\sin(-x)+\cos(-x)\text {.}\)
Упражнение \(\PageIndex{13}\)
Дифференцировать \(s(\theta)=\dfrac{\cos \theta + \sin \theta}{\cos \theta — \sin\ theta}\text{.}\)
Упражнение \(\PageIndex{14}\)(✳)
Найдите значения констант \(a\) и \(b\), для которых
\[ f(x) = \left\{ \begin{array}{cc} \cos(x) & x\le 0\\ ax + b & x \gt 0\end{массив} \right. \nonumber \]
везде дифференцируемо.
Упражнение \(\PageIndex{15}\)(✳)
Найдите уравнение касательной к графику \(y=\cos(x)+2x\) в точке \(x=\dfrac{\ пи}{2}\текст{.}\)
Этап 3
Упражнение \(\PageIndex{16}\)(✳)
Вычислить \(\displaystyle \lim_{x\to \pi/3}\left( \dfrac{\cos(x)-1/ 2}{x-\pi/3}\right).\) Используйте любой метод.
Упражнение \(\PageIndex{17}\)
Покажите, как можно использовать правило частных для нахождения производной тангенса, если вы уже знаете производные синуса и косинуса.

Упражнение \(\PageIndex{18}\)(✳)
Производная функции
\[ f(x)=\left\{\begin{array}{ll} ax+b& \mbox{for }x \lt 0\\ \frac{6\cos x}{2+\sin x+\cos x}& \mbox{для }x\ge 0 \end{массив}\right. \nonumber \]
существует для всех \(x\text{.}\) Определите значения констант \(a\) и \(b\text{.}\) 9x\sin x\) имеют горизонтальную касательную?
Упражнение \(\PageIndex{25}\)
Пусть
\[ f(x)=\left\{\begin{array}{ccc} \frac{\sin x}{x}&,&x \ neq 0\\ 1&,&x=0 \end{массив}\right. \nonumber \]
Найти \(f'(0)\text{,}\) или показать, что его не существует.
Упражнение \(\PageIndex{26}\)(✳)
Дифференцируйте функцию
\[ h(x) = \sin(|x|) \nonumber \]
и укажите область, в которой существует производная .
Упражнение \(\PageIndex{27}\)(✳)
Для функции
\[ f(x) =\left\{\begin{array}{ll} 0 & x\le 0\\ \frac {\sin(x)}{\sqrt{x}} & x\gt 0\end{массив}\right. \номер\]
какое из следующих утверждений верно?
- \(f\) не определено в \(x = 0\text{.
 }\)
}\) - \(f\) не является ни непрерывным, ни дифференцируемым в \(x = 0\text{.}\)
- \(f\) непрерывна, но не дифференцируема в \(x = 0\text{.}\)
- \(f\) дифференцируема, но не непрерывна в \(x = 0\text{.}\) 95 х}\текст{.}\)
Эта страница под названием 2.8: Производные тригонометрических функций распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джоэлем Фельдманом, Эндрю Рехнитцером и Элиз Йегер посредством исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- CLP Учебники по математическому анализу
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://personal.
 math.ubc.ca/~CLP/CLP1
math.ubc.ca/~CLP/CLP1
- источник@https://personal.
Исчисление: дифференциальные карточки Кванеле Туакли
Чему равен дифференциал y = ax n ?
если y = ax n , то dy/dx = anx n-1
также
если f(x) = ax n , то f ‘(x) = anx n-1
Продифференцировать y = x 3 .sinx по x.
If y = x 3 ·sinx
dy/dx = x 3 (cos x) + sinx(3x 2 )
= x 3 cosx + 3x 2 sinx
= x 2 (xcosx + 3sinx)
Чему равен дифференциал y = ax?
Если y = ax, тогда dy/dx = a
также
, если f(x) = ax, то f ‘(x) = a
Каков дифференциал y = a?
Если y = a, , то dy/dx = 0
также
, если f(x) = a, то f ‘(x) = 0
Чему равна вторая производная от y = ax n
Если y = ax n , то dy/dx = anx n-1
и
d 2 y/dx 2 = (n-1)anx n-2
например.

, если y = 2x 3 , затем DY/DX = 6x 2
и
D 2 Y/DX 2 = 12x
Y/DX 2 = 12x Y/DX 2 = 12X 2 = 12x 2 = 12x 907 . dy/dx = f ‘(x)d 2 y/dx 2 = f »(x)
Учитывая уравнение y = f(x) и точку P на кривой с координатами (x 1 , y 1 ), найти уравнение касательной к кривой.
Можно показать, что уравнение линии выглядит следующим образом:
(y — y 1 ) = m(x — x 1 )
, где m = уклон линии.
Градиент находится с помощью дифференцирования.
м = dy/dx
Имея уравнение y = f(x) и точку P на кривой с координатами (x1, y1), найдите уравнение нормали к кривой.
Можно показать, что уравнение прямой, перпендикулярной касательной, имеет вид:
(y — y1) = (-1/m)(x — x1)
, где m = градиент линии, касательной к кривой.
 .
.Этот градиент находится с помощью дифференцирования.
м = dy/dx
Какая производная от Sin x?
Если y = Sin x, тогда dy/dx = cos x
Какая производная от Cos x?
если y = Cos x, тогда dy/dx = — Sin x
Какова производная e x по x?
Если y = e x , dy/dx = e x
Дифференцировать y = uv , где u и v являются функциями x .
Подсказка: правило произведения.
Если y = uv , то dy/dx = u(dv/dx) + v(du/dx)
т. е. чтобы продифференцировать произведение двух функций:
Проставить первую (дифференцировать вторую) + проставить вторую (дифференцировать первый)
Продифференцировать y = x 4 .
 cos x относительно x.
cos x относительно x.IF Y = x 4 COS X , затем DY/DX = X 4 (-SIN X) + COSX (4x 3 )
= 4x )
= 4x )1216 3 cosx — x 4 sinx
=x 3 (4cosx — xsinx)
Дифференцировать y = x 5 .e x относительно x.
IF Y = x 5 E x , затем DY/DX = x 5 (E x ) + E x (5x
) + 9116) + E x (5x
) + E x (5x
) + E x (5x
) + E x (5x
) + E x (5 x 916) + E x (5 x 916) + E x (5 x 916). 5 e x +5x 4 e x
=x 4 e x (x +5)
Дифференцировать y = e x .
 sinx относительно x
sinx относительно xIF Y = E x .SINX , затем DY/DX = E x (COSX) + SINX (E x )
= E )6 = E )
6 = x )
6 = x ). sinx
=e x (cosx + sinx)
Дифференцировать y = 4x 3 .sinx относительно x
IF Y = 4x 3 .SINX , затем DY/DX = 4x 3 (COSX) + SINX (12x 2 )
= 4x 11111111111111111111111111111111111111111111111111111111111111111111111111111111111 2). sinx
= 4x 2 (xcosx + 3sinx)
Дифференцировать y = e x .
 cosx относительно x
cosx относительно xIf y = e x .cosx , then dy/dx = e x (-sinx) + cosx(e x )
= e x cosx — e x sinx
= e x (cosx — sinx)
Дифференцировать y = cosx.sinx относительно x
Если y = cosx.sinx , то dy/dx = cosx(cosx) + sinx(-sinx)
= cos 2 x — sin 2 x
= cos(2x)
Дифференцировать y = 3x 3 .e x относительно x
If y = 3x 3 .e x , then dy/dx = 3x 3 (e x ) + e x (9x 2 )
= 3x 3 e x + 9x 2 e x
= 3x 2 д х (х + 3)
Дифференцировать y = 2x 5 .
 cosx относительно x
cosx относительно xIF Y = 2x 5 .COSX , затем DY/DX = 2x 5 (-SINX) + COSX (10x 4 )
9
411217)9 6 411117)
9 6 411117)
9 6. 5 sinx
=2x 4 (5cosx — xsinx)
Дифференцировать y = u/v , где u и v являются функциями x .
Подсказка: Правило частных.
Чтобы продифференцировать частное двух функций:
[Проставить низ (дифференцировать верх) — проставить верх (дифференцировать низ)] по всему низу в квадрате.
«низкий d высокий над высоким d низкий, по всему квадрату того, что ниже»
Что такое производное от желтовато-коричневый х ?
Подсказка: правило частных
TAN X = SIN X / COS X
IF Y = SINX / COSX ,
Тогда DY / DX = [Coss X.
 COS X — SIN X. )] / (cos x) 2
COS X — SIN X. )] / (cos x) 2 = (cos 2 x + sin 2 x) / cos 2 x
= 1 / cos 2 x
= сек 2 х
Продифференцируем y = sin x / x 2 по x.
If y = sin x / x 2 , then dy/dx = [x 2 (cosx) — sinx (2x)] / (x 2 ) 2
= [x(xcos x — 2sin x)] / x 4
= (xcos x — 2sin x) / x 3
Дифференцировать y = 5e x / cos x в отношении x.
Если y = 5e x / cos x ,
, то dy/dx = [cos x.(5e x ) — 5e x 9121x ) (-scos .s ) (-incos .x s ).



 Производная функции y = sinx выражается формулой .
Производная функции y = sinx выражается формулой .



 известен.
известен. sinx , найти f'(x)
sinx , найти f'(x) 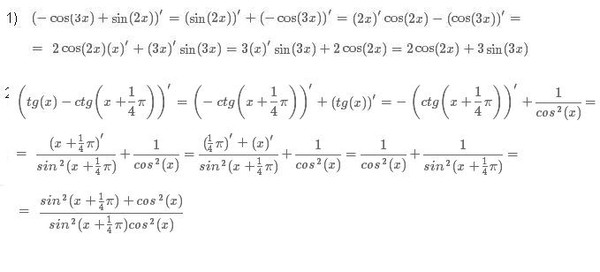 g(x) 6 11009 1
g(x) 6 11009 1