Примеры решения матриц с ответами
О чем статья
Алгоритм решения матрицТеорема
Матрица – это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими буквами.
Есть два отличия между матрицами:
- Комплексные матрицы. Это когда хотя бы одно число равно комплексному.
- Действительные матрицы. Это когда в матрице содержаться действительные числа.
С матрицей можно выполнять самые наипростейшие действия: умножение, деление, сложение, вычитание и трансформация.
Сложение и вычитание
Данные действия можно совершать тогда, когда матрицы равны между собой, чтобы в конце получилось выражение аналогичной размерности. Сложение и вычитание выполняются по аналогии друг друга.
Пример 1
Задание
Даны две матрицы, найдите их сумму.
Решение
Элемент первой строки складывается с элементом второй. Абсолютно также совершается вычитание, только вместо плюса, нужно поставить минус.
Абсолютно также совершается вычитание, только вместо плюса, нужно поставить минус.
Пример 2
Задание
Даны две матрицы, найдите их разность.
Решение
Пример 3
Задание
Найдите C=2A +3B, если :
Решение
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Заказать работу
Умножение
В математике умножать таблицу с числами можно абсолютно любую. В таком случае число умножается с показателем. Умножаем первое число на первой строке с числом второго столбца и так далее.
Пример
Задание
Даны две матрицы. Умножьте их друг на друга.
Умножьте их друг на друга.
Решение
=
Матрицы можно перемножать друг на друга, только если количество столбцов в первой матрице, равно количеству строк второй. Элемент матрицы будет равняться сумме произведений (Aji), где i – строки в таблице; j – строки чисел второй таблицы.
Возведение матрицы в степень
Данную формулу используют лишь в случаях, если матрица стоит в квадратном выражении. Важно знать, что степень должна быть у таких выражений натуральной!
Если число не будет натуральным, то это усложняет возведение матрицы в степень, так как степень n придётся умножить саму на себя n количество раз. Но если у Вас такой случай, то используется следующая формула.
Пример
Задание
Найдите
матрицы.
Решение
В первую очередь найдём, для этого нужно будет просто умножить её саму на себя.
После по формуле подставляем числовые значения.
Расчёт определителя
В математике линейной есть два понятия – определитель и детерминант. Определитель – это какое-либо число, которое ставится в соответствии с квадратной матрицей. Определитель используется при решении многих задач. Найти его можно с помощью формулы.
А детерминант находиться с помощью перемножения простых матриц, используются числа только с побочной и главной диагоналях.
Есть вероятность, что произведения матрицы будут значительно отличаться друг от друга. Если индекс чётный, то число будет со знаком плюс, если нечётный, то число будет со знаком минус. Обозначается определитель det А, а круглые скобки меняются на квадратные.
Пример 1
Дано
Решение
Пользуемся свойствам степеней – A^{3}=A^{2}*A
Возведём А в A^{2}
Далее используем свойство степеней
Ответ
Пример 2
Задание
Найдите определитель матрицы А.
Решение
Обратная матрица
Перед тем, как речь непосредственно пойдёт о самой обратной связи матрицы, давайте разберём алгоритм трансформирования матрицы. Во время трансформации столбцы и строки меняются местами.
Пример
Задание
Найти обратную матрицу А.
Решение
Приписываем к матрице А матрицу третьего ряда.
Переводим всё в единичную матрицу.
Ответ
Обратная матрица
Обратная матрица схожа с алгоритмом нахождения обратных чисел. К примеру, если умножить матричную таблицу на обратную матрицу, то в итоге мы получаем A*A(-1)=E. Но чтобы перейти уже к нахождению обратной матрицы, нам придётся найти её определитель. Мы рассмотрим самый простой способ – алгебраических дополнений.
Мы рассмотрим самый простой способ – алгебраических дополнений.
Пример 1
Задание
В пример возьмём квадратную матрицу, она находиться с помощью следующей формулы:
, где
-транспортированные матрицы;|А| – определитель.
Рассмотрим самый простейший пример, где размер таблицы 2*2.
Найти обратную матрицу
Решение
Для начала находим определитель матрицы.
Если ответ равен нулю, то обратной матрицы нет! Так как наш ответ равен -2, то всё в порядке. Следующим действием нам нужно будет рассчитать матрицу миронов. Таблица элементов при этом не изменяется. Где прописан нужным нам элемент, нужно вычеркнуть строчку или столбец, оставшееся число и будет являться мироном.
Подставляем числа, возвращаясь к матрица, которая указана выше.
Всегда начинаем с левого верхнего угла и делаем следующее:
← линиями показано, что нужно и как зачеркнуть.
Как итог, у нас остаётся число 4
Теперь мы переходим к нахождению алгебраических дополнений.
Первым делом нужно поменять знаки у двух чисел в мироне.
← подчёркнуты те числа, у которых мы будем менять знаки.
, вот что у нас получилось.
И наконец-то мы переходим к завершающему этапу, к нахождению транспортированной матрице.
, вспоминаем формулу нахождения, и подставляем числовые значения
В завершении желательно проверить правильно ли мы нашли числовую таблицу. Это делать не обязательно, но рекомендуется, чтобы удостовериться в том, то ответ верный.
Пример 2
Задание
Найдите матрицу А.
Начинаем с определения матрицы.
Дело осталось за малым – осталось начти алгебраическое дополнение матрицы А:
Не забываем записать союзную матрицу:
И уже из неё находим обратную матрицу:
Получаем ответ
Средняя оценка 2 / 5. Количество оценок: 39
Количество оценок: 39
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
65043
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Матрицы и детерминанты — задачи с решениями
Задача 1
Каков размер матрицы $A$?
5
$5 \times 4$
$4 \times 5$
20
Задача 2
$A=\left( \begin{array}{ccccc} 2 & -2 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 3 \\ 1 & -1 & 3 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1% \end{array}% \right) $
Чему равен элемент $A_{2,4}$?
Задача 3
$A=\left( \begin{array}{ccccc} 2 & -2 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 3 \\ 1 & -1 & 3 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1% \end{array}% \right) $
Чему равен элемент $A_{3,2}$?
Задача 4
Запишите данную систему уравнений в виде расширенной матрицы.
$\left\{ \begin{array}{c} 3x-2y=3 \\ 5x+y=0 \end{array} \right\} $
$\left( \begin{array}{ccc} 3 & -2 \\ 5 & 1 \end{array} \right)$
$\left( \begin{matrix} 3 & 5 \\ -2 & 1 \\ 3 & 0 \end{matrix} \right)$
$\left( \begin{array}{ccc} 3 & -2 & 3 \\ 5 & 1 & 0 \end{array} \right)$
$\left( \begin{array}{ccc} 3 & -2 & 3 \\ 5 & 1 & 3 \end{array} \right)$
Задача 5
Чему равна сумма матриц?
$\left(
\begin{array}{cc}
2 & -1 \\
1 & 3
\end{array}
\right) +\left(
\begin{array}{cc}
1 & 0 \\
2 & -1
\end{array}
\right) =$
$\left( \begin{array}{cc} 3 & 1 \\ 2 & 2 \end{array} \right)$
$\left( \begin{array}{cc} 3 & -1 \\ 3 & 2 \end{array} \right)$
$\left( \begin{array}{cc} 3 & -1 \\ 3 & 4 \end{array} \right)$
$\left( \begin{array}{cc} 3 & 3 \\ 2 & -1 \end{array} \right)$
Задача 6
Найдите матрицу $A$, чтобы выполнялось следующее равенство.
$A+\left( \begin{array}{cc} 2 & 3 \\ -4 & 1 \end{array} \right) =\left( \begin{array}{cc} 5 & -1 \\ 1 & 5 \end{array} \right) $
$A=\left( \begin{array}{cc} 5 & 4 \\ 3 & -4 \end{array} \right)$
$A=\left( \begin{array}{cc} 3 & -4 \\ 5 & 4 \end{array} \right)$
$A=\left( \begin{array}{cc} -3 & 4 \\ -5 & -2 \end{array} \right)$
$A=\left( \begin{array}{cc} 7 & 2 \\ -3 & 4 \end{array} \right)$
Задача 7
Каков результат умножения?
$5 \times \left(
\begin{array}{c}
-2 \\
3 \\
-4
\end{array}
\right) =$
$\left( \begin{array}{ccc} -20 & 15 & -10 \end{array} \right)$
$\left( \begin{array}{c} 10 \\ 15 \\ 20 \end{array} \right)$
$\left( \begin{array}{c} -20 \\ 15 \\ -10 \end{array} \right)$
$\left( \begin{array}{c} -10 \\ 15 \\ -20 \end{array} \right)$
Задача 8
Найдите матрицу $X$.
$\frac{3}{2}X+\left( \begin{array}{cc} -1 & 3 \\ 2 & -2 \end{array} \right) =\left( \begin{array}{cc} 3 & -4 \\ 5 & 4 \end{array} \right) $
$X=\left( \begin{array}{cc} 2 & 4 \\ \frac{8}{3} & -\frac{14}{3} \end{array} \right)$
$X=\left( \begin{array}{cc} 6 & -\frac{21}{2} \\ \frac{9}{2} & 9 \end{array} \right)$
$X=\left( \begin{array}{cc} \frac{8}{3} & -\frac{14}{3} \\ 2 & 4 \end{array} \right)$
$X=\left( \begin{array}{cc} 3 & -\frac{3}{2} \\ \frac{21}{2} & 3 \end{array} \right)$
Задача 9
Если $A=B\times C$, найдите матрицу $A$.
$B=\left( \begin{array}{ccc} 1 & -3 & -2 \\ 2 & 0 & 1 \end{array} \right)$ $C=\left( \begin{array}{cc} 2 & 1 \\ -2 & -1 \\ 3 & 0 \end{array} \right)$
$\left( \begin{array}{cc} 4 & 1 \\ 0 & 3 \\ 3 & 0 \end{array} \right)$
$\left( \begin{array}{ccc} 2 & 6 & -6 \\ 2 & 0 & 0 \end{array} \right)$
$\left( \begin{array}{cc} 7 & 2 \\ 2 & 4 \end{array} \right)$
$\left( \begin{array}{cc} 2 & 4 \\ 7 & 2 \end{array} \right)$
Задача 10
Найдите определитель матрицы.
$A=\left(
\begin{array}{cc}
2 & -3 \\
4 & 5
\end{array}
\right) $
Задача 11
Найдите определитель матрицы.
$A=\left(
\begin{array}{cc}
3 & 4 \\
0 & 0
\end{array}
\right) $
Задача 12
Найдите обратную матрицу матрицы $A=\left( \begin{array}{cc} 2 & -3 \\ 4 & 5 \end{array} \right) $
$\left(\begin{matrix}110 & 66\\-88 & 44\end{matrix} \right)$
$\frac{1}{22}$
$\left(\begin{matrix}\frac{5}{22} & \frac{3}{22}\\\frac{-2}{11} & \frac{1}{11}\end{matrix} \right)$
Задача 13
Найдите обратную матрицу матрицы $A=\left( \begin{array}{cc} 0 & \frac{-3}{4} \\ \frac{7}{3} & 0 \end{array} \right)$
$A^{-1}=\left(\begin{array}{cc} 0 & \frac{3}{7} \\ -\frac{4}{3} & 0 \end{array}\right)$
$A^{-1}=\left(\begin{array}{cc} \frac{3}{7} & 0 \\ 0 & -\frac{4}{3} \end{array}\right)$
$A^{-1}=\left(\begin{array}{cc} 0 & \frac{3}{4} \\ -\frac{7}{3} & 0 \end{array}\right)$
Обратная матрица матрицы A не существует. {-1}=\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right)$
{-1}=\left(\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right)$
Обратная матрица матрицы A не существует.
Задача 15
$A=\left(
\begin{array}{cc}
7 & -4 \\
4 & -3
\end{array}
\right)$ $B=\left(
\begin{array}{cc}
\frac{3}{5} & -\frac{4}{5} \\
\frac{4}{5} & -\frac{7}{5}
\end{array}
\right) $
Является ли $B$ мультипликативной инверсией $A$(можем ли мы сказать, что $A \cdot B = B \cdot A$)?
Задача 16
$A=\left(
\begin{array}{cc}
2 & -3 \\
1 & -2
\end{array}
\right)$ $B=\left(
\begin{array}{cc}
-2 & 1 \\
-3 & 2%
\end{array}
\right)$
Можем ли мы сказать, что $A \cdot B = B \cdot A$?
Задача 17
Какое значение должен принимать $x$, чтобы $B$ была бы обратной $A$?
$A=\left(
\begin{array}{cc}
1 & 3 \\
-1 & 2
\end{array}%
\right) \qquad B=\left(
\begin{array}{cc}
\frac{2}{5} & x \\
\frac{1}{5} & \frac{1}{5}
\end{array}
\right)$
Задача 18
Какое значение должен принимать $x$, чтобы у матрицы $A$ не было бы обратной матрицы?
$A=\left( \begin{array}{cc} 2 & 3 \\ x & -2 \end{array} \right)$
$\frac{4}{3}$
$-\frac{3}{4}$
$-\frac{4}{3}$
$\frac{3}{4}$
Задача 19
Какое значение должен принимать $x$, чтобы у матрицы $A$ не было бы обратной матрицы?
$A=\left( \begin{array}{cc} 1 & 2+x \\ x & -1 \end{array} \right)$
Прислать задачу
Правильный:
Неверный:
Неразрешенные задачи:
Матрицы и действия над ними.
 Решение задач и контрольных работ по высшей математике онлайн
Решение задач и контрольных работ по высшей математике онлайнЧто такое матрица
Таблица чисел вида
состоящая из строк и столбцов называется матрицей. Числа называются ее элементами.
Под решением матрицы обычно понимают проведение таких операций как нахождение обратной матрицы, нахождение определителя, умножение матрицы на число и другое. Кроме того действия могут проводиться сразу над несколькими матрицами. То есть матрицы могут между собой складываться, перемножаться. Все эти так называемые решения матриц проводятся по определенным схемам или алгоритмам. Обратите внимание что действия над матрицами выполняются по определенным правилам и дело тут не в сложности этих правил, а в старательности и внимательности при вычислениях.
Определитель матрицы и его вычисление
Рассмотрим квадратную матрицу:
порядка
. Из элементов этой матрицы составим всевозможные
произведения так, чтобы они содержали по одному и только по одному элементу из
каждой строки и каждого столбца. В каждом из этих произведений сомножители
(которых будет
) расположим таким образом, чтобы первые индексы
образовали перестановку
. В результате полученные произведения будут иметь
вид:
Из элементов этой матрицы составим всевозможные
произведения так, чтобы они содержали по одному и только по одному элементу из
каждой строки и каждого столбца. В каждом из этих произведений сомножители
(которых будет
) расположим таким образом, чтобы первые индексы
образовали перестановку
. В результате полученные произведения будут иметь
вид:
где
– некоторая
перестановка чисел 1,2,3…n. Очевидно, что число всевозможных
произведений составленных из элементов матрицы по приведенному выше правилу
будет равно числу всевозможных перестановок из множества вторых индексов
сомножителей произведений, то есть из чисел
, или то же самое, числу
перестановок из чисел
, а таких перестановок будет
. Каждая перестановка будет иметь
некоторое число инверсий, образованных вторыми индексами сомножителей
произведений. Условимся перед
произведением ставить плюс если число инверсий четное (то есть перестановка
вторых индексов четная), и минус, если число инверсий нечетное (то есть
перестановка вторых индексов нечетная).
Просуммировав все произведения вида (*) составленные из матрицы и взятые с указанными знаками, получим число, называемое определителем.
Для определителя, как и для матрицы, используются такие понятия, как строка, столбец, главная и побочная диагонали и т. п. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной, а матрица с определителем, равным нулю,— вырожденной.
Рассмотрим частные случаи определителей:
Определитель 2-го порядка:
Определитель третьего порядка:
Для его вычисления удобно пользоваться следующей схемой:
Для определителей порядка выше третьего неудобно запоминать какую-либо символическую схему, так как, например, определитель уже четвертого порядка есть алгебраическая сумма 24 слагаемых, каждое из которых является произведением четырех сомножителей.
Минором какого-либо элемента определителя
называется определитель, полученный из данного вычерчиванием той строки и того
столбца, которым принадлежит этот элемент.
Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком .
В общем случае определителем порядка, соответствующим квадратной матрице порядка можно назвать число, равное сумме парных произведении элементов какой-либо строки (столбца) на их алгебраические дополнения.
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля.
Обратная матрица
Пусть – квадратная невырожденная матрица n-го порядка. Обратной матрицей для матрицы называется матрица, для которой справедливо равенство:
где – единичная матрица
Обратная матрица определена только для квадратных невырожденных матриц и вычисляется по формуле:
где
– определитель
матрицы
, а матрица
(союзная
матрица) получается из матрицы
заменой всех ее
элементов соответствующими им алгебраическими дополнениями.
Транспонирование матрицы
Замена каждой строки матрицы ее столбцов называется транспонированием. Транспонированная по отношению к матрице матрица обозначается .
Если задана матрица
то ее транспонированная матрица имеет вид:
Сумма матриц и произведение матрицы на число
Суммой матриц и называется матрица , элементы которой вычисляются по формуле:
Для суммы матриц используют обозначение
Произведением матрицы на число называется матрица , элементы которой вычисляются по формуле:
Для произведения матрицы на число используют обозначение .
Произведение матриц
Произведением матрицы на матрицу называется матрица , элементы которой вычисляются по формуле:
Из определения умножения матриц
следует, что элемент
в матрице
является суммой
произведений соответствующих элементов i-й строки матрицы
и j-го столбца матрицы
. На рисунке схематично показано получение элемент
в произведении
матриц
На рисунке схематично показано получение элемент
в произведении
матриц
Для произведения матриц используют обозначение
Произведение матриц определено только в том случае, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведение матриц содержит столько строк, сколько имеет первая матрица, и столько столбцов, сколько имеет вторая матрица.
Error
Sorry, the requested file could not be found
More information about this error
Jump to…
Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции. Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2.
Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson. Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2.

 Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.
Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.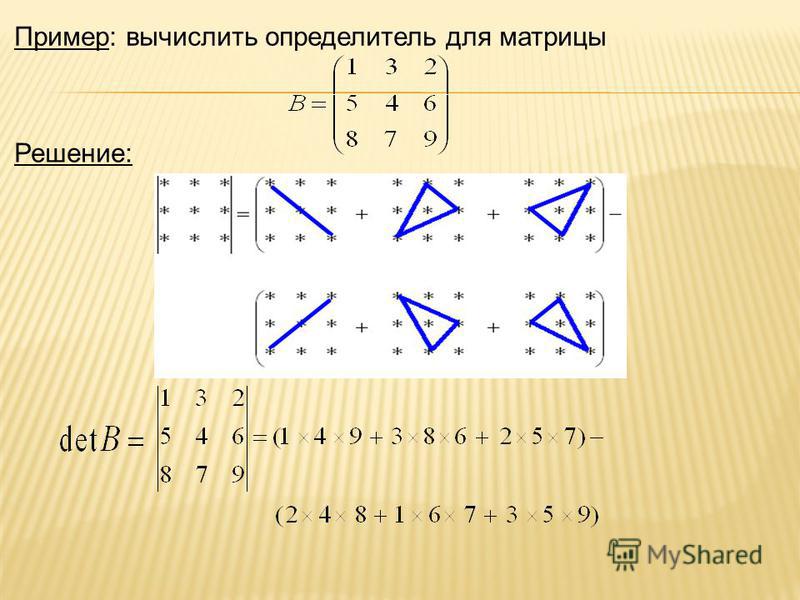 2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.
2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1. 2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1.
2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.
Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1. 3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1).
3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1.
Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.
Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2. 1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1.
1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1.
Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2.
Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1.
Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1.
2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.
Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3. 5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1).
5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1.
Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)python — Заполнить матрицу, зная сумму по строке и по столбцу
Вопрос задан
Изменён 7 месяцев назад
Просмотрен 117 раз
Всем привет!
Есть задача заполнить матрицу MxN рандомными целыми значениями от a до b. Затык в том, что по каждой строке и по каждому столбцу есть фиксированная сумма. И надо, чтобы эти вот рандомные значения в сумме давали эти числа.
Затык в том, что по каждой строке и по каждому столбцу есть фиксированная сумма. И надо, чтобы эти вот рандомные значения в сумме давали эти числа.
Пробовал выехать на рандоме (цикл выбрал с ограничением, чтобы не работал слишком долго):
from random import randint
import numpy as np
stolbcov = 3
strok = 3
massiv = np.zeros(shape=(strok,stolbcov), dtype=int) #создаю нулевой массив
summy_strok = np.array([10,12,6]) #Указываю суммы по каждой строке
summy_stolbcov = np.array([10,11,7]) #Указываю суммы по каждому столбцу
#беру функцию, которая дает мне строку данных с нужной суммой
def create_array(n, b):
for i in range(100):
a = np.random.randint(0,6,n)
sum = np.sum(a)
if sum == b:
return(a)
break
else:
return(np.random.randint(0,6,stolbcov)) #возвращаем рандомную строку, если не получилось
#в цикле построчно заполняю матрицу. В конце итерации проверяю совпадение по сумме стобцов
for i in range(1000):
for x in range(strok):
massiv[x] = create_array(stolbcov,summy_strok[x])
if np. array_equal(np.sum(massiv, axis=0), summy_stolbcov):
print(massiv)
break
array_equal(np.sum(massiv, axis=0), summy_stolbcov):
print(massiv)
break
Проблема в том, что он отрабатывает на небольших матрицах 4х4 ещё приемлемо решает. Дальше уже задумывается надолго.
Пробовал просто рандомно создавать массивы нужной размерности стандартной функцией numpy. Сравнивая суммы в итоге. Этот вариант оказался вообще провальным. Даже 3х3 решить не может.
Может быть, кто знает нормальный алгоритм решения такой задачи без такого вот наглого рандома? Тут больше матан, чем программирование, но буду признателен, если натолкнете на мысль.
- python
- массивы
- pandas
- numpy
- матрицы
1
Такие задачи обычно решаются методом поиска с возвратом. Но, по сути, это тоже перебор значений, хотя и оптимизированный. например, есть библиотека python-constraint, которая может решать такого типа задачи просто задав входные значения и наложив на них ограничения. Но её скорость тоже оставляет желать лучшего. Пример:
Пример:
from constraint import *
from random import shuffle
summy_strok = [14, 16, 12, 20, 15] #Указываю суммы по каждой строке
summy_stolbcov = [16, 15, 21, 25] #Указываю суммы по каждому столбцу
assert sum(summy_strok) == sum(summy_stolbcov)
stolbcov = len(summy_stolbcov)
strok = len(summy_strok)
a, b = 1, 9
values = list(range(a, b+1))
shuffle(values)
#print(values)
problem = Problem()
problem.addVariables(range(strok*stolbcov), values)
for col in range(stolbcov):
v = [col + stolbcov*row for row in range(strok)]
problem.addConstraint(ExactSumConstraint(summy_stolbcov[col]), v)
for row in range(strok):
v = [col + stolbcov*row for col in range(stolbcov)]
problem.addConstraint(ExactSumConstraint(summy_strok[row]), v)
solution = problem.getSolution()
result = [v for k,v in sorted(solution.items())]
print(*[result[i:i+stolbcov] for i in range(0, strok*stolbcov, stolbcov)], sep="\n")
Результат:
[8, 2, 2, 2] [2, 8, 2, 4] [3, 2, 6, 1] [2, 2, 7, 9] [1, 1, 4, 9]
В общем случае ваша задача не имеет решения, даже в вещественных, а не целых числах.
Задачу можно сформулировать так. Есть M*N неизвестных, M+N уравнений: M уравнений для строк и N уравнений для столбцов. Нужно найти решение такой недоопределённой системы уравнений.
Если переменные упорядочены слева направо сверху вниз, то элемент матрицы, стоящий в строке r и столбце c будет иметь номер r*N + c. Тогда матрица системы уравнений будет выглядеть как-то так
array([[1., 1., 1., 0., 0., 0.],
[0., 0., 0., 1., 1., 1.],
[1., 0., 0., 1., 0., 0.],
[0., 1., 0., 0., 1., 0.],
[0., 0., 1., 0., 0., 1.]])
(пример для случая 2 x 3).
Такие системы проще всего «решать» методом наименьших квадратов, который найдёт такое значение x, что |Ax - B| будет минимальным. Если у системы есть решение, то минимум достигается именно в нём. Слово «решать» взято в кавычки, так как в общем случае минимум совсем не обязательно равен нулю. Другими словами, решение задачи наименьших квадратов вовсе необязательно является решением исходной системы.
Другими словами, решение задачи наименьших квадратов вовсе необязательно является решением исходной системы.
Я попробовал решить вашу задачу для случая матрицы 2 x 3, переменные от 1 до 5, сумма по строкам 7, сумма по столбцам 5.
По ссылке лежит блокнот Jupyter с решением средствами numpy и scipy. Наименьшие квадраты глобальный минимум нашли, но он даже близко не является решением. То есть такая система решений не имеет. В вещественных числах не имеет, не говоря уже о целых.
2
Ваш ответ
Зарегистрируйтесь или войдите
Регистрация через Google
Регистрация через Facebook
Регистрация через почту
Отправить без регистрации
Почта
Необходима, но никому не показывается
Отправить без регистрации
Почта
Необходима, но никому не показывается
Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки
Задачи линейной алгебры.
 Понятие матрицы. Виды матриц. Операции с матрицами. Решение задач на преобразование матриц реферат по математике | Сочинения Математика
Понятие матрицы. Виды матриц. Операции с матрицами. Решение задач на преобразование матриц реферат по математике | Сочинения МатематикаСкачай Задачи линейной алгебры. Понятие матрицы. Виды матриц. Операции с матрицами. Решение задач на преобразование матриц реферат по математике и еще Сочинения в формате PDF Математика только на Docsity! Министерство науки и образования Украины ДГМА Реферат на тему: Задачи линейной алгебры. Понятие матрицы. Виды матриц. Операции с матрицами. Решение задач на преобразование матриц. Подготовил учащийся 1КД гр. Сергей Шрам Краматорск 2003 Задачи линейной алгебры. Понятие матрицы. Виды матриц. Операции с где d1 , d2 , …, dn—какие угодно числа. Легко видеть, что если все эти числа равны между собой, т. е. d1 = d2 = … = dn то для любой квадратной матрицы А порядка п справедливо равенство А D = D А. Среди всех диагональных матриц (1.5) с совпадающими элементами d1 = d2 = … = dn = = d особо важную роль играют две матрицы. Первая из этих матриц получается при d = 1, называется единичной матрицей n-го порядка и обозначается символом Е. Вторая матрица получается при d = 0, называется нулевой матрицей n-го порядка и обозначается символом O. Таким образом, E = O = В силу доказанного выше А Е = Е А и А О = О А. Более того, легко показать, что А Е = Е А = А, А О = О А = 0. (1.6) Первая из формул (1.6) характеризует особую роль единичной матрицы Е, аналогичную той роли, которую играет число 1 при перемножений вещественных чисел. Что же касается особой роли нулевой матрицы О, то ее выявляет не только вторая из формул (1.7), но и элементарно проверяемое равенство А + 0 = 0 + А = А. В заключение заметим, что понятие нулевой матрицы можно вводить и для неквадрат- ных матриц (нулевой называют любую матрицу, все элементы которой равныї нулю). Блочные матрицы Предположим, что некоторая матрица A = || a ij || при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых представляет собой матрицу меньших размеров и называется блоком исходной матрицы. В таком случае возникает возможность рассмотрения исходной матрицы А как некоторой новой (так называемой б л о ч н о й) матрицыі А = || A F 0 6 1F 0 6 2 ||, элементами которой служат указанные блоки.
Вторая матрица получается при d = 0, называется нулевой матрицей n-го порядка и обозначается символом O. Таким образом, E = O = В силу доказанного выше А Е = Е А и А О = О А. Более того, легко показать, что А Е = Е А = А, А О = О А = 0. (1.6) Первая из формул (1.6) характеризует особую роль единичной матрицы Е, аналогичную той роли, которую играет число 1 при перемножений вещественных чисел. Что же касается особой роли нулевой матрицы О, то ее выявляет не только вторая из формул (1.7), но и элементарно проверяемое равенство А + 0 = 0 + А = А. В заключение заметим, что понятие нулевой матрицы можно вводить и для неквадрат- ных матриц (нулевой называют любую матрицу, все элементы которой равныї нулю). Блочные матрицы Предположим, что некоторая матрица A = || a ij || при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых представляет собой матрицу меньших размеров и называется блоком исходной матрицы. В таком случае возникает возможность рассмотрения исходной матрицы А как некоторой новой (так называемой б л о ч н о й) матрицыі А = || A F 0 6 1F 0 6 2 ||, элементами которой служат указанные блоки. Указанные элементы мы обозначаем большой латинской буквой, чтобы подчеркнуть, что они являются, вообще говоря, матрицами, а не числами и (как обычные числовые элементы) снабжаем двумя индексами, первый из которых указывает номер «блочной» строки, а второй — номер «блочного» столбца. Например, матрицу можно рассматривать как блочную матрицу элементами которой служат следующие блоки: Замечательным является тот факт, что основные операции с блочными матрицами совершаются по тем же правилам, по которым они совершаются с обычными числовыми матрицами, только в роли элементов выступают блоки. Понятие определителя. 0 0 1 FРассмотрим произвольную квадрат ную матрицу любого порядка п: A = (1.7) 0 0 1 FС каждой такой матрицей свяжем вполне определенную числен ную характеристику, называемую определителем, соответствующим этой матрице. Если порядок n матрицы (1.7) равен единице, то эта матрица состоит из одного элемен- та аi j определителем первого порядка соответствующим такой матрице, мы назовем величину этого элемента.
Указанные элементы мы обозначаем большой латинской буквой, чтобы подчеркнуть, что они являются, вообще говоря, матрицами, а не числами и (как обычные числовые элементы) снабжаем двумя индексами, первый из которых указывает номер «блочной» строки, а второй — номер «блочного» столбца. Например, матрицу можно рассматривать как блочную матрицу элементами которой служат следующие блоки: Замечательным является тот факт, что основные операции с блочными матрицами совершаются по тем же правилам, по которым они совершаются с обычными числовыми матрицами, только в роли элементов выступают блоки. Понятие определителя. 0 0 1 FРассмотрим произвольную квадрат ную матрицу любого порядка п: A = (1.7) 0 0 1 FС каждой такой матрицей свяжем вполне определенную числен ную характеристику, называемую определителем, соответствующим этой матрице. Если порядок n матрицы (1.7) равен единице, то эта матрица состоит из одного элемен- та аi j определителем первого порядка соответствующим такой матрице, мы назовем величину этого элемента. Если далее порядок п матрицы (1.7) равен двум, т. е. если эта матрица имеет вид A = (1.8) 0 0 1 Fто определителем второго порядка, соответствующим такой мат рице, назовем число, равное а11 а22 — а12 а21 и обозначаемое одним из символов: Итак, по определению (1.9) Формула (1.9) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.8), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали. Определители второго и более высоких порядков находят широкое применение при решении систем линейных уравнений. Рассмотрим, как выполняются операции с матрицами в системе MathCad. Простейшие операции матричной алгебры реализованы в MathCad в виде операторов. Написание операторов по смыслу максимально приближено к их математическому действию. Каждый оператор выражается соответствующим символом.
Если далее порядок п матрицы (1.7) равен двум, т. е. если эта матрица имеет вид A = (1.8) 0 0 1 Fто определителем второго порядка, соответствующим такой мат рице, назовем число, равное а11 а22 — а12 а21 и обозначаемое одним из символов: Итак, по определению (1.9) Формула (1.9) представляет собой правило составления определителя второго порядка по элементам соответствующей ему матрицы. Словесная формулировка этого правила такова: определитель второго порядка, соответствующий матрице (1.8), равен разности произведения элементов, стоящих на главной диагонали этой матрицы, и произведения элементов, стоящих на побочной ее диагонали. Определители второго и более высоких порядков находят широкое применение при решении систем линейных уравнений. Рассмотрим, как выполняются операции с матрицами в системе MathCad. Простейшие операции матричной алгебры реализованы в MathCad в виде операторов. Написание операторов по смыслу максимально приближено к их математическому действию. Каждый оператор выражается соответствующим символом. Рассмотрим матричные и векторные операции MathCad 2001. Векторы являются частным случаем матриц размерности n x 1, поэтому для них 0 0 1 Fсправедливы все те операции, что и для матриц, если ограничения осо бо не оговорены (например, некоторые операции применимы только к квадратным матрицам n x n). Какие-то действия допустимы только для векторов (например, скалярное произведение), а какие-то, 0 0 1 Fнесмотря на одинако вое написание, по-разному действуют на векторы и матрицы. При работе с матрицами используется панель инструментов “Матрицы” Рис.1 Панель инструментов Матрицы Для ввода матрицы: • введите имя матрицы и знак присваивания (двоеточие) • щелкните по значку “создать матрицу” в панели “Матрицы”. • В появившемся диалоге задайте число строк и столбцов матрицы. • После нажатия кнопки OK открывается поле для ввода элементов матрицы. Для того, чтобы ввести элемент матрицы, установите курсор в отмеченной позиции и введите с клавиатуры число или выражение. Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно: • выделить матрицу и щелкнуть в панели по кнопке операции, • или щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы.
Рассмотрим матричные и векторные операции MathCad 2001. Векторы являются частным случаем матриц размерности n x 1, поэтому для них 0 0 1 Fсправедливы все те операции, что и для матриц, если ограничения осо бо не оговорены (например, некоторые операции применимы только к квадратным матрицам n x n). Какие-то действия допустимы только для векторов (например, скалярное произведение), а какие-то, 0 0 1 Fнесмотря на одинако вое написание, по-разному действуют на векторы и матрицы. При работе с матрицами используется панель инструментов “Матрицы” Рис.1 Панель инструментов Матрицы Для ввода матрицы: • введите имя матрицы и знак присваивания (двоеточие) • щелкните по значку “создать матрицу” в панели “Матрицы”. • В появившемся диалоге задайте число строк и столбцов матрицы. • После нажатия кнопки OK открывается поле для ввода элементов матрицы. Для того, чтобы ввести элемент матрицы, установите курсор в отмеченной позиции и введите с клавиатуры число или выражение. Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно: • выделить матрицу и щелкнуть в панели по кнопке операции, • или щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы. Меню “Символы” содержит три операции — транспонирование, инвертирование, определитель. Это означает, например, что вычислить определитель матрицы можно, выполнив команду Символы/Матрицы/Определитель. Номер первой строки (и первого столбца) матрицы MathCAD хранит в переменной ORIGIN. По умолчанию отсчет ведется от нуля. В математической записи чаще принято вести отсчет от 1. Для того, чтобы MathCAD вел отсчет номеров строк и столбцов от 1, нужно задать значение переменной ORIGIN:=1. Функции, предназначенные для работы с задачами линейной алгебры, собраны в разделе “Векторы и матрицы” диалога “вставить функцию” (напоминаем, что он вызывается кнопкой на панели “Стандартные”). Основные из этих функций будут описаны позже. Транспонирование Транспортированием 0 01 F называют операцию, переводящую матрицу размерно сти mxn в матрицу размерности n x m, 0 01 F делая столбцы исходной матрицы стро ками, а строки — столбцами. Пример приведен в листинге на рис.2. Ввод символа транспонирования (transpose) 0 0 1 Fосуществляется с помощью панели инстру ментов Matrix (Матрица) или нажатием клавиш <Ctrl>+<1>.
Меню “Символы” содержит три операции — транспонирование, инвертирование, определитель. Это означает, например, что вычислить определитель матрицы можно, выполнив команду Символы/Матрицы/Определитель. Номер первой строки (и первого столбца) матрицы MathCAD хранит в переменной ORIGIN. По умолчанию отсчет ведется от нуля. В математической записи чаще принято вести отсчет от 1. Для того, чтобы MathCAD вел отсчет номеров строк и столбцов от 1, нужно задать значение переменной ORIGIN:=1. Функции, предназначенные для работы с задачами линейной алгебры, собраны в разделе “Векторы и матрицы” диалога “вставить функцию” (напоминаем, что он вызывается кнопкой на панели “Стандартные”). Основные из этих функций будут описаны позже. Транспонирование Транспортированием 0 01 F называют операцию, переводящую матрицу размерно сти mxn в матрицу размерности n x m, 0 01 F делая столбцы исходной матрицы стро ками, а строки — столбцами. Пример приведен в листинге на рис.2. Ввод символа транспонирования (transpose) 0 0 1 Fосуществляется с помощью панели инстру ментов Matrix (Матрица) или нажатием клавиш <Ctrl>+<1>. He забывайте, что для вставки символа транспонирования матрица должна 0 0 1 Fнаходиться ме жду линиями ввода. Напоминание о линиях ввода по отношению к матрицам приведено ранее. Сложение В MathCAD можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются символы <+> или <-> 0 01 F соответст венно. Матрицы должны иметь 0 0 1 Fодинаковую размерность, иначе будет выда но сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых (пример на рис.3). Кроме сложения матриц, MathCAD поддерживает операцию сложения матрицы со скалярной величиной, т.е. числом (пример на рис.4). Каждый элемент результирующей матрицы равен сумме соответст-вующего элемента исходной матрицы и скалярной величины. Результат смены знака матрицы эквивалентен смене знака всех ее элементов. Для того чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом (пример на рис.4). Умножение При умножении следует помнить, что матрицу размерности m x n допустимо умножать только на матрицу-размерности n x p (р может быть любым).
He забывайте, что для вставки символа транспонирования матрица должна 0 0 1 Fнаходиться ме жду линиями ввода. Напоминание о линиях ввода по отношению к матрицам приведено ранее. Сложение В MathCAD можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются символы <+> или <-> 0 01 F соответст венно. Матрицы должны иметь 0 0 1 Fодинаковую размерность, иначе будет выда но сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых (пример на рис.3). Кроме сложения матриц, MathCAD поддерживает операцию сложения матрицы со скалярной величиной, т.е. числом (пример на рис.4). Каждый элемент результирующей матрицы равен сумме соответст-вующего элемента исходной матрицы и скалярной величины. Результат смены знака матрицы эквивалентен смене знака всех ее элементов. Для того чтобы изменить знак матрицы, достаточно ввести перед ней знак минуса, как перед обычным числом (пример на рис.4). Умножение При умножении следует помнить, что матрицу размерности m x n допустимо умножать только на матрицу-размерности n x p (р может быть любым). В результате получается матрица размерности m х р. Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение) (рис.1). Умножение матриц обозначается по умолчанию точкой, как показано в примере на рис 6. Символ умножения матриц можно выбирать точно так же, как и в скалярных выражениях. Обратите внимание, что попытка перемножить матрицы A и B несоответствующего (одинакового 2х3) размера оказалась безрезультатной: после введенного знака равенства находится пустой местозаполнитель, а само выражение в редакторе MathCad выделяется красным цветом. При установке курсора на это выражение, появляется сообщение о несовпадении числа строк первой матрицы числу столбцов второй матрицы. Еще один пример, относящийся к умножению вектора на матрицу- строку и, наоборот, строки на вектор, приведен на рис. 7. Во второй строке этого примера показано, как выглядит формула при выборе отображения оператора умножения No Space (Вместе).
В результате получается матрица размерности m х р. Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение) (рис.1). Умножение матриц обозначается по умолчанию точкой, как показано в примере на рис 6. Символ умножения матриц можно выбирать точно так же, как и в скалярных выражениях. Обратите внимание, что попытка перемножить матрицы A и B несоответствующего (одинакового 2х3) размера оказалась безрезультатной: после введенного знака равенства находится пустой местозаполнитель, а само выражение в редакторе MathCad выделяется красным цветом. При установке курсора на это выражение, появляется сообщение о несовпадении числа строк первой матрицы числу столбцов второй матрицы. Еще один пример, относящийся к умножению вектора на матрицу- строку и, наоборот, строки на вектор, приведен на рис. 7. Во второй строке этого примера показано, как выглядит формула при выборе отображения оператора умножения No Space (Вместе). Однако тот же самый оператор умножения действует на два вектора по-другому. Аналогично сложению матриц со скаляром определяется умножение и деление матрицы на 0 0 1 Fскалярную величину (пример на рис.8). Символ умножения вво дится так же, как и в случае 0 0 1 Fумножения двух матриц. На скаляр можно ум ножать любую матрицу размера m x n. Определитель квадратной матрицы Определитель (Determinant) матрицы обозначается стандартным математическим
Однако тот же самый оператор умножения действует на два вектора по-другому. Аналогично сложению матриц со скаляром определяется умножение и деление матрицы на 0 0 1 Fскалярную величину (пример на рис.8). Символ умножения вво дится так же, как и в случае 0 0 1 Fумножения двух матриц. На скаляр можно ум ножать любую матрицу размера m x n. Определитель квадратной матрицы Определитель (Determinant) матрицы обозначается стандартным математическим
Матрицы — Решение, Типы, Значение, Примеры
Матрицы — форма множественного числа матрицы, которая представляет собой прямоугольный массив или таблицу, в которой числа или элементы расположены в строках и столбцах. Они могут иметь любое количество столбцов и строк. С матрицами можно выполнять различные операции, такие как сложение, скалярное умножение, умножение, транспонирование и т. д.
Существуют определенные правила, которым необходимо следовать при выполнении этих матричных операций, например, их можно складывать или вычитать, если только они имеют одинаковое количество строк. и столбцы, тогда как они могут быть умножены, если только столбцы в первом и строки во втором точно такие же. Давайте разберемся в различных типах матриц и этих правилах в деталях.
и столбцы, тогда как они могут быть умножены, если только столбцы в первом и строки во втором точно такие же. Давайте разберемся в различных типах матриц и этих правилах в деталях.
| 1. | Что такое матрицы? |
| 2. | Определение матрицы |
| 3. | Обозначение матриц |
| 4. | Вычислить матрицы |
| 5. | След матрицы |
| 6. | Определитель матриц |
| 7. | Минор матрицы |
| 8. | Кофактор матрицы |
| 9. | Сопряжение матриц |
| 10. | Обратные матрицы |
| 11. | Типы матриц |
| 12. | Решение системы уравнений с использованием матриц |
| 13. | Ранг матрицы |
14. | Собственные значения и собственные векторы матриц |
| 15. | Матричные формулы |
| 16. | Часто задаваемые вопросы о матрицах |
Что такое матрицы?
Матрицы , множественная форма матрицы, представляют собой расположение чисел, переменных, символов или выражений в прямоугольной таблице, которая содержит различное количество строк и столбцов. Это массивы прямоугольной формы, для которых определены различные операции, такие как сложение, умножение и транспонирование. Числа или записи в матрице известны как ее элементы. Горизонтальные элементы матрицы называются строками, а вертикальные — столбцами.
Определение матрицы
Матрица — это прямоугольный массив чисел, переменных, символов или выражений, которые определены для таких операций, как вычитание, сложение и умножение. Размер матрицы (известный как порядок матрицы) определяется количеством строк и столбцов в матрице. Порядок матрицы с 6 строками и 4 столбцами представлен как 6 × 4 и читается как 6 на 4. Например, данная матрица B является матрицей 3 × 4 и записывается как \([{B}] _{3 \раз 4}\):
Порядок матрицы с 6 строками и 4 столбцами представлен как 6 × 4 и читается как 6 на 4. Например, данная матрица B является матрицей 3 × 4 и записывается как \([{B}] _{3 \раз 4}\):
\(B = \left[\begin{array}{ccc} 2 & -1 & 3 & 5 \\ 0 & 5 & 2 & 7\\ 1 & -1 & -2 & 9 \end{array} \справа]\)
Обозначение матриц
Если в матрице m строк и n столбцов, то в ней будет m × n элементов. Матрица представлена заглавной буквой, в данном случае «А», а элементы в матрице представлены строчной буквой и двумя нижними индексами, представляющими положение элемента в номере строки и столбца в том же порядке. , в данном случае ‘\(a_{ij}\)’, где i — количество строк, а j — количество столбцов. Например, в данной матрице A элемент в 3-й строке и 2-м столбце будет \(a_{32}\), что можно проверить в приведенной ниже матрице:
\(A = \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} .. .& a_{1n} \\ a_{21} & a_{22} & a_{23} … & a_{2n} \\ a_{31} & a_{32} & a_{33} . ..& a_{3n} \\ : & : & : & : \\ a_{ m1} & a_{m2} & a_{m3} …& a_{mn} \end{массив}\right] \)
..& a_{3n} \\ : & : & : & : \\ a_{ m1} & a_{m2} & a_{m3} …& a_{mn} \end{массив}\right] \)
Вычисление матриц
Мы можем решать матрицы, выполняя над ними такие операции, как сложение, вычитание, умножение и так далее. Вычисление матриц зависит от количества строк и столбцов. Для сложения и вычитания количество строк и столбцов должно быть одинаковым, тогда как для умножения количество столбцов в первой и количество строк во второй матрице должно быть равным. Основные операции, которые можно выполнять с матрицами:
- Сложение матриц
- Вычитание матриц
- Скалярное умножение
- Умножение матриц
- Транспонирование матриц
Добавление матриц
Добавление матриц возможно только в том случае, если количество строк и столбцов обеих матриц одинаково. Добавляя 2 матрицы, мы добавляем соответствующие элементы. т. е. (A + B) = [a\(_{ij}\)] + [b\(_{ij}\)] = [a\(_{ij}\) + b\(_{ij} \)], где i и j — количество строк и столбцов соответственно. Например: \(\begin{bmatrix} 2 & {-1}\\ \\ 0 & 5\end{bmatrix} + \begin{bmatrix} 0 & 2 \\ \\ 1 & -2 \end{bmatrix} \\ = \begin{bmatrix} 2+0 & {-1} +2 \\ \\ 0+1 & 5+(-2) \end{bmatrix}\\ = \begin{bmatrix} 2 & 1 \\ \\1 & 3 \end{bmatrix} \)
Например: \(\begin{bmatrix} 2 & {-1}\\ \\ 0 & 5\end{bmatrix} + \begin{bmatrix} 0 & 2 \\ \\ 1 & -2 \end{bmatrix} \\ = \begin{bmatrix} 2+0 & {-1} +2 \\ \\ 0+1 & 5+(-2) \end{bmatrix}\\ = \begin{bmatrix} 2 & 1 \\ \\1 & 3 \end{bmatrix} \)
Вычитание матриц
Вычитание матриц также возможно, только если количество строк и столбцов обеих матриц одинаково. Вычитая 2 матрицы, мы вычитаем соответствующие элементы. т. е. (A — B) = [a\(_{ij}\)] — [b\(_{ij}\)] = [a\(_{ij}\) — b\(_{ij} \)], где i и j — номер строки и номер столбца соответственно. Например: \( \begin{bmatrix} 2 & {-1}\\ \\ 0 & 5 \end{bmatrix} -\begin{bmatrix} 0 & 2 \\ \\1 & -2 \end{bmatrix} \\ = \begin{bmatrix} 2-0 & {-1} -2\\ \\ 0-1 & 5-(-2) \end{bmatrix} \\ = \begin{bmatrix} 2 & -3\ \ \\ -1 & 7 \end{bmatrix} \)
Скалярное умножение
Произведение матрицы A с любым числом «c», полученное путем умножения каждого элемента матрицы A на c, называется скалярным умножением. т. е. (cA)\(_{ij}\) = c(A\(_{ij}\))
Свойства скалярного умножения в матрицах
Различные свойства матриц для скалярного умножения любых скаляров K и l с матрицами A и B задаются как
- K(A + B) = KA + KB
- (К + 1)А = КА + 1А
- (Кл)А = К(1А) = 1(КА)
- (-К)А = -(КА) = К(-А)
- 1·А = А
- (-1)А = -А
Умножение матриц
Умножение матриц определяется только в том случае, если число столбцов в первой матрице и количество строк во второй матрице равны. Чтобы понять, как перемножаются матрицы, давайте сначала рассмотрим вектор-строку \(R=\left[ {{r}_{1}}\ {{r}_{2}}…{{r}_{n }} \right]\) и вектор-столбец \(C=\left[ \begin{align} \; \ {{c}_{1}} \;\\ \; \ {{c}_{2} } \; \\ \; \ \ \vdots \; \ \\ \; \ {{c}_{n}} \;\ \\ \end{align} \right]\). Тогда произведение R и C можно определить как
Чтобы понять, как перемножаются матрицы, давайте сначала рассмотрим вектор-строку \(R=\left[ {{r}_{1}}\ {{r}_{2}}…{{r}_{n }} \right]\) и вектор-столбец \(C=\left[ \begin{align} \; \ {{c}_{1}} \;\\ \; \ {{c}_{2} } \; \\ \; \ \ \vdots \; \ \\ \; \ {{c}_{n}} \;\ \\ \end{align} \right]\). Тогда произведение R и C можно определить как
\(RC=\left[ {{r}_{1}}\ \ {{r}_{2}}\ \ …\ {{r} _{n}} \right]\ \left[ \begin{align} & \ {{c}_{1}} \\ & \ {{c}_{2}} \\ & \ \ \\vdots \ \ \ & \ {{c}_{n}}\ \\ \end{align} \right]\ \\ =[{{r}_{1}}{{c}_{1}}+{{r }_{2}}{{c}_{2}}+…+{{r}_{n}}{{c}_{n}}]\). Например,
\(\left[ 1\ \ 3\ \ 2 \right]\ \ \left[ \begin{align} & \ \ 2 \\ & -1 \\ & \ \ 4 \\ \end{ align} \right]=[7]\)
Теперь мы обсудим умножение матриц. Вскоре станет очевидно, что для умножения 2 матриц на A и B и чтобы найти AB , количество столбцов в A должно равняться количеству строк в B .
Пусть A имеет порядок m × n и B имеет порядок n × p . Матрица AB будет иметь порядок m × p и будет получена путем последовательного умножения каждого вектора-строки A на вектор-столбец в B . Давайте разберемся в этом на конкретном примере: \(A=\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ {{c}_{1}} & {{c}_{2 }} & {{c}_{3}} \\\end{matrix} \right]B=\left[ \begin{matrix} {{\alpha }_{1}} & {{\beta}_{ 1}} \\ {{\alpha}_{1}} & {{\beta}_{2}} \\ {{\alpha}_{3}} & {{\beta}_{3}} \ \\конец{матрица} \право]\)
Матрица AB будет иметь порядок m × p и будет получена путем последовательного умножения каждого вектора-строки A на вектор-столбец в B . Давайте разберемся в этом на конкретном примере: \(A=\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} & {{a}_{3}} \\ {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ {{c}_{1}} & {{c}_{2 }} & {{c}_{3}} \\\end{matrix} \right]B=\left[ \begin{matrix} {{\alpha }_{1}} & {{\beta}_{ 1}} \\ {{\alpha}_{1}} & {{\beta}_{2}} \\ {{\alpha}_{3}} & {{\beta}_{3}} \ \\конец{матрица} \право]\)
Чтобы получить элемент \(a_{11}\) из AB, мы умножаем \(R_1\) из A на \(C_1\) из B :
Чтобы получить элемент \(a_{12}\ ) из AB, мы умножаем \(R_1\) из A на \(C_2\) из B:
Чтобы получить элемент \({{a}_{21}}\) из AB, мы умножаем \( R_2\) из A с \(C_1\) из B:
Продолжая таким образом, мы получаем все элементы AB.
Обобщим это: если A имеет порядок m × n и B порядка n × p, то для получения элемента \( a_{ij}\) в AB умножаем \(R_i\) в A на \(C_j\) в B:
Свойства умножения матриц
Существуют различные свойства, связанные с умножением матриц. Для любых трех матриц A, B и C:
Для любых трех матриц A, B и C:
- AB ≠ BA
- А(ВС) = (АВ)С
- А(В + С) = АВ + АС
- (А + В)С = АС + ВС
- A\(I_m\) = A = AI n , для единичных матриц I\(_m\) и I n .
- A\(_{m\times n}\)O\(_{n\times p}\) = O\(_{m\times p}\), где O — нулевая матрица.
Транспонирование матрицы
Транспонирование матрицы выполняется при замене строк матрицы столбцами и столбцов строками. Перестановка строк и столбцов называется транспонированием матриц. В приведенной ниже матрице у нас есть элементы строки: строка-1: 2, -3, -4 и строка-2: -1, 7, -7. При транспонировании мы получим элементы в столбце-1: 2, -3, -4 и столбце-2: -1, 7, -7, мы можем проверить это на изображении, приведенном ниже:
Свойства транспонирования в матрицах
Существуют различные свойства, связанные с транспозицией. Для матриц A и B, заданных как
- (A T ) T = A
- (A + B) T = A T + B T , A и B одного порядка.

- (KA) T = KA T , K — любой скаляр (действительный или комплексный).
- (AB) T = B T A T , A и B соответствуют продукту AB. (Этот закон также называют обратным законом.)
Помимо этих операций, у нас есть несколько других операций с матрицами, таких как нахождение следа, определителя, миноров и кофакторов, сопряженных, обратных и т. д. Давайте подробно изучим каждую из них в следующих разделах.
След матрицы
След любой матрицы A, Tr(A) определяется как сумма ее диагональных элементов. Некоторые свойства следа матриц:
- tr(AB) = tr(BA)
- tr(A) = tr(A Т )
- tr(cA) = c tr(A), для скаляра ‘c’
- тр(А + В) = тр(А) + тр(В)
Определитель матриц
Определитель матрицы — это число, определенное только для квадратных матриц. Он используется при анализе линейных уравнений и их решении. Формула определителя помогает вычислить определитель матрицы, используя элементы матрицы. Определитель матрицы равен сумме произведений элементов определенной строки или столбца с их соответствующими кофакторами. Определитель матрицы A обозначается как |A|. Допустим, мы хотим найти определитель матрицы \(A = \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22 } & a_{23} \\ a_{31} & a_{32} & a_{33} \end{массив}\right] \) 9{1 + 3} \!\!\left|\begin{matrix}a_{21}\!\!\!&a_{22}\\a_{31}\!\!\!&a_{32}\end{ матрица}\справа|\)
Формула определителя помогает вычислить определитель матрицы, используя элементы матрицы. Определитель матрицы равен сумме произведений элементов определенной строки или столбца с их соответствующими кофакторами. Определитель матрицы A обозначается как |A|. Допустим, мы хотим найти определитель матрицы \(A = \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22 } & a_{23} \\ a_{31} & a_{32} & a_{33} \end{массив}\right] \) 9{1 + 3} \!\!\left|\begin{matrix}a_{21}\!\!\!&a_{22}\\a_{31}\!\!\!&a_{32}\end{ матрица}\справа|\)
Минор матрицы
Минор для конкретного элемента в матрицах определяется как определитель матрицы, который получается при удалении строки и столбца матрицы, в которой находится этот конкретный элемент, и минор элемента \(a_{ij} \) обозначается как \(M_{ij}\). Например, для данной матрицы минор \( a_{12}\) матрицы \(A = \left[\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{массив}\right] \) равно:
\(M_{12} = \left|\begin{array}{ccc} a_{21} & a_{23} \\ \\ a_{31} & a_{33} \end{array}\right| \)
Аналогично, мы можем найти все миноры матрицы и получим минорную матрицу M данной матрицы A как:
\(M = \left[\begin{array}{ccc} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{массив}\right] \)
Кофактор матрицы
Кофактор элемента в матрице A получается, когда минор \(M_{ij}\) матрицы умножается на (-1) 9{i+j} M_{ij}\)
Найдя все сомножители матрицы, мы получим матрицу сомножителей C данной матрицы A:
\(C = \left[\begin{array}{ ccc} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end {array}\right] \)
Примечание. Будьте особенно осторожны с отрицательным знаком при вычислении кофактора матрицы.
Будьте особенно осторожны с отрицательным знаком при вычислении кофактора матрицы.
Сопряжение матриц
Сопряжение матриц вычисляется путем нахождения транспонирования сомножителей элементов данных матриц. Чтобы найти сопряжение матрицы, мы должны вычислить кофакторы элементов матрицы, а затем транспонировать матрицу кофакторов, чтобы получить сопряжение данной матрицы. Сопряженная матрица A обозначается через adj(A). Давайте разберем это на примере: у нас есть матрица \(A = \left[\begin{array}{ccc} 2 & -1 & 3 \\ 0 & 5 & 2 \\ 1 & -1 & -2 \ конец{массив}\справа] \)
Тогда минорная матрица M данной матрицы будет:
\(M = \left[\begin{array}{ccc} -8 & -2 & -5 \\ 5 & -7 & -1 \\ -17 & 4 & 10 \end{array}\right] \)
Мы получим матрицу кофакторов C данной матрицы A как:
\(C = \left[\begin{array}{ccc} — 8 & 2 & -5 \\ -5 & -7 & 1 \\ -17 & -4 & 10 \end{array}\right] \)
Тогда транспонирование матрицы кофакторов даст сопряжение заданного матрица:
прил(А) = C T = \(\left[\begin{array}{ccc} -8 & -5 & -17 \\ 2 & -7 & -4 \\ -5 & 1 & 10 \конец{массив}\справа] \)
Обратные матрицы
Обратная любая матрица обозначается как матрица, возведенная в степень (-1), т. е. для любой матрицы «А» обратная матрица обозначается как А -1 . Обратная квадратная матрица A равна A -1 только тогда, когда: A × A -1 = A -1 × A = I . Существует вероятность того, что иногда обратная матрица не существует, если определитель матрицы равен нулю (|A| = 0). Обратная матрица показана как A -1 . Обратные матрицы вычисляются по следующей формуле:
е. для любой матрицы «А» обратная матрица обозначается как А -1 . Обратная квадратная матрица A равна A -1 только тогда, когда: A × A -1 = A -1 × A = I . Существует вероятность того, что иногда обратная матрица не существует, если определитель матрицы равен нулю (|A| = 0). Обратная матрица показана как A -1 . Обратные матрицы вычисляются по следующей формуле:
A -1 = (1/|A|)(Adj A)
, где
- |A| является определителем матрицы A и |A| ≠ 0,
- Adj A является сопряженным к данной матрице A.
Обратная матрица 2 × 2 \(A = \left[\begin{array}{ccc} a_{11} & a_{12} \\ \\ a_{21} & a_{22} \end{ array}\right] \) вычисляется по формуле: A -1 = \(\dfrac{1}{a_{11}a_{22} — a_{12}a_{21}}\left(\begin{matrix}a_{22}&-a_{12}\ \ \\-a_{21}&a_{11}\end{matrix}\right)\)
Найдем обратную матрицу 3 × 3, которую мы использовали в предыдущем разделе: \(A = \left[ \begin{массив}{ccc}
2&-1&3\
0 и 5 и 2 \
1 и -1 и -2
\end{массив}\right] \)
Так как adj(A) = \(\left[\begin{array}{ccc}
-8&-5&-17\
2&-7&-4\
-5 и 1 и 10
\end{array}\right] \)
И вычислив определитель, получим |A| = -33
Следовательно, A -1 = (1/-33) × \(\left[\begin{array}{ccc}
-8&-5&-17\
2&-7&-4\
-5 и 1 и 10
\end{массив}\right] \)
Следовательно, A -1 = \(\left[\begin{array}{ccc}
0,24&0,15&0,51\
-0,06&0,21&0,12\
0,15 и -0,03 и -0,39
\конец{массив}\справа] \)
Типы матриц
Существуют различные типы матриц в зависимости от количества элементов и расположения элементов в них.
Матрица-строка: Матрица-строка — это матрица, имеющая одну строку, которая называется матрицей-строкой. Пример: [1, −2, 4].
Матрица-столбец: Матрица-столбец — это матрица, имеющая один столбец, которая называется матрицей-столбцом. Пример: [−1, 2, 5] Т .
Квадратная матрица: Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной матрицей. Например: \(B= \left[\begin{array}{ccc} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 0 &6& 1 \end{array}\right] \)
Прямоугольная матрица : Матрица, имеющая неравное количество строк и столбцов, называется прямоугольной матрицей. Например: \(B= \left[\begin{array}{ccc} 1 & 2 & 3 \\ \\ 0 & 1 & 4 \end{array}\right] \)
Диагональные матрицы: Матрица, в которой все недиагональные элементы равны нулю, называется диагональной матрицей.
Пример: \(A = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 &0 & 3 \end{array}\right] \)
Матрицы идентичности : Диагональная матрица, все диагональные элементы которой равны 1, называется единичной матрицей.
Пример: \(B= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 &0 & 1 \end{array}\right] \)
Симметричные и кососимметричные матрицы:
Симметричные матрицы: квадратная матрица D размера n×n считается симметричной тогда и только тогда, когда D T = D. Например, D = \(\left[\begin{array}{lll} 2 & 3 & 6 \\ 3 & 4 & 5 \\ 6 & 5 & 9 \end{array}\right] \) является симметричной матрицей, потому что
D T = \(\left[\begin{array}{lll} 2 & 3 & 6 \\ 3 & 4 & 5 \\ 6 & 5 & 9 \end{массив}\right]\) = D
Кососимметричные матрицы. Квадратная матрица F размера n×n считается кососимметричной тогда и только тогда, когда F T = — F.
\(F = \left[\begin{array}{ccc } 0 & 3 \\ \\ -3 & 0 \end{array}\right]\) является кососимметричной матрицей, поскольку
- F T = \(\left[\begin{array}{cc} 0 & -3\\ \\ 3 & 0 \end{массив}\right]\)
- -F = \(\left[\begin{array}{cc} 0 & -3\\ \\ 3 & 0 \end{array}\right]\)
Инвертируемая матрица: Любая квадратная матрица A называется обратимой матрицей, если существует другая матрица B, такая что AB = BA = \(I_n\), где \(I_n\) — единичная матрица размера n × n.
Ортогональная матрица: Любая квадратная матрица A является ортогональной, если ее транспонирование равно обратному. т. е. А Т = А -1
Решение системы уравнений с использованием матриц
При решении системы уравнений с использованием матриц у нас есть три матрицы A, B и X, где A известна как матрица коэффициентов, B известна как матрица констант, а X содержит все известные переменные уравнений как переменная матрица. Матрица A имеет порядок m × n, а B — матрица-столбец порядка m × 1. Произведение матрицы A и матрицы X дает матрицу B; следовательно, X также является матрицей-столбцом порядка n × 1,
Матрицы расположены следующим образом:
A • X = B
Давайте разберемся, как решить систему уравнений с помощью матриц на примере. У нас есть набор из двух уравнений, как показано ниже. Уравнения:
x + y = 8
2x + 3y = 10
Расположите все коэффициенты, переменные и константы в матрице таким образом, чтобы всякий раз, когда мы находим произведение матриц, полученный результат приводил к уравнению.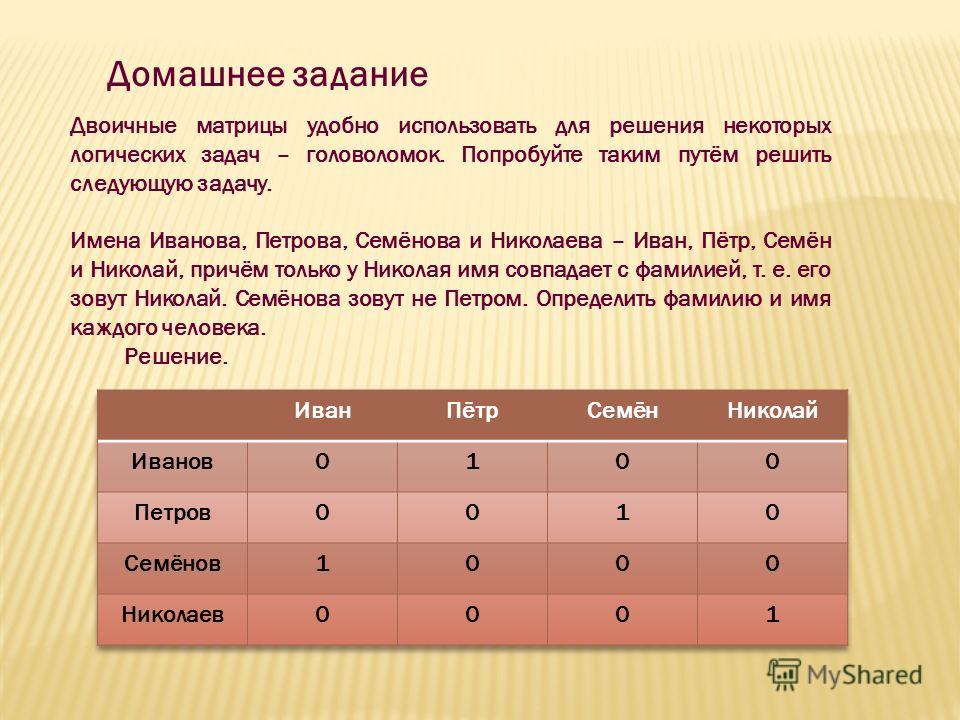 Тогда матричное уравнение будет таким: AX = B, где: 9{-1}\) и B. Получаем
Тогда матричное уравнение будет таким: AX = B, где: 9{-1}\) и B. Получаем
\(\begin{bmatrix}
3&-1\\
-2 и 1
\end{bmatrix}
%
\begin{bmatrix}
8\\
10
\end{bmatrix}
\
=
\begin{bmatrix}
14\\
-6
\end{bmatrix}
\)
Следовательно, значение матрицы X равно
\(X = \begin{bmatrix}
14\\\
-6\
\end{bmatrix}\)
Ранг матрицы
Ранг матрицы A определяется как максимальное количество линейно независимых векторов строк (или столбцов) матрицы. Это означает, что ранг матрицы всегда будет меньше или равен количеству ее строк или столбцов. Ранг нулевой матрицы равен нулю, поскольку она не имеет независимых векторов строк или столбцов.
Собственные значения и собственные векторы матриц
Если A — любая квадратная матрица порядка n, то можно составить матрицу A — λI, где I — единичная матрица порядка n, такая, что число λ, называемое собственным значением, и ненулевой вектор v , называемый собственным вектором, удовлетворяют уравнению Av = λv. λ является собственным значением n × n-матрицы A тогда и только тогда, когда A − λI n необратим, что эквивалентно Det(A — λI) = 0,
λ является собственным значением n × n-матрицы A тогда и только тогда, когда A − λI n необратим, что эквивалентно Det(A — λI) = 0,
Матричные формулы
Существуют различные формулы, связанные с матричными операциями, в зависимости от типа матрицы. Некоторые формулы матриц перечислены ниже:
- A(adj A) = (adj A) A = | А | я п
- | прил А | = | А | н-1
- прил (прил А) = | А | н-2 А
- | прил (прил А) | = | А | 92
- прил (АВ) = (прил Б) (прил А)
- прил (А м ) = (прил А) м ,
- прил (kA) = k n-1 (прил A) , k ∈ R
- прил(I n ) = I n
- прил 0 = 0
- А симметрично ⇒ (прил. А) также симметрично.
- А диагональное ⇒ (прил. А) также диагональное.
- A треугольный ⇒ прил. A также треугольный.
- A в единственном числе ⇒| прил А | = 0
- А -1 = (1/|А|) прил А
- (АВ) -1 = В -1 А -1
Важные примечания о матрицах:
- Кофактор матрицы A получается, когда минор \(M_{ij}\) матрицы умножается на (-1) i+j .

- Матрицы представляют собой массивы прямоугольной формы.
- Обратная матрица вычисляется по данной формуле: A -1 = (1/|A|)(прил. A).
- Обратная матрица существует тогда и только тогда, когда |A| ≠ 0,
☛ Связанные темы:
- Матричный калькулятор
- Калькулятор диагональной матрицы
- Калькулятор матрицы транспонирования
- Калькулятор сложения матриц
Решенные примеры на матрицах
Пример 1: Пусть \(A=\left[ \begin{matrix} 1 & 2\\ \\ 3 & 1 \\\end{matrix} \right],\ B=\left[ \begin{matrix } 1 & 4\\ \\ 3 & -1 \\\end{matrix} \right]\). Вычислите А + В.
Решение:
Здесь матрица A = \(\left[ \begin{matrix} 1 & 2\\ \\ 3 & 1 \\\end{matrix} \right]\)
матрица B = \(\left[ \begin{matrix} 1 & 4\\ \\ 3 & -1 \\\end{matrix} \right]\)Используя свойство сложения матриц, A + B = \( \left[ \begin{matrix} 1 & 2 \\ \\ 3 & 1 \\\end{matrix} \right]\) + \(\left[ \begin{matrix} 1 & 4\\ \\ 3 & -1 \\\end{matrix} \right]\) = \(\left[ \begin{matrix} 2 & 6\\ \\ 6 & 0 \end{matrix} \right]\)
Ответ: Сумма матриц A и B, A + B = \(\left[ \begin{matrix} 2 & 6\\ \\ 6 & 0 \end{matrix} \right]\)
Пример 2: Найдите обратную матрицу A =\(\left[\begin{matrix}1 & -2\\ \\2 & -3 \end{matrix}\right]\).

Решение:
Дана матрица A = \(\left[\begin{matrix}1 & -2\\ \\2 & -3 \end{matrix}\right]\).
Используя формулу обратной матрицы: A -1 = \(\dfrac{1}{a_{11}a_{22} — a_{12}a_{21}}\left[\begin{matrix}a_{22}&-a_{12}\ \ \\-a_{21}&a_{11}\end{matrix}\right]\)
Используя обратную матричную формулу, мы можем вычислить A -1 следующим образом.
A -1 = \(\dfrac{1}{(1 × -3) — (-2 × 2)}\left[\begin{matrix}-3&2\\ \\-2&1\end{matrix }\right]\)
= \(\dfrac{1}{-3 +4}\left[\begin{matrix}-3&2\\ \\-2&1\end{matrix}\right]\)
= \(\left[\begin{matrix}-3&2\\ \\-2&1\end{matrix}\right]\)
Ответ: Поэтому A -1 = \(\left[\begin{matrix}-3&2\\ \\-2&1\end{matrix}\right]\).
Пример 3: Докажите, что произведение матриц A = \(\left[\begin{array}{rr}1 & 2 & -1\\ 3 & 2 & 0\\ -4 & 0 & 2\ end{array}\right]\), а единичная матрица порядка 3×3 является самой матрицей.

Решение:
Единичная матрица порядка 3×3: I = \(\left[\begin{array}{rr}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{массив}\right]\).
Теперь AI = \(\left[\begin{array}{rr}1 & 2 & -1\\ 3 & 2 & 0\\ -4 & 0 & 2\end{array}\right]\) \(\left[\begin{array}{rr}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{массив}\right]\)
= \(\left[ \begin{массив}{rr}1+0+0 и 0+2+0 и 0+0-1
\\ 3+0+0 и 0+2+0 и 0+0+0
\\ -4+0+0& 0+0+0& 0+0+2\end{массив}\right]\)= \(\left[\begin{массив}{rr}1 & 2 & -1 \\ 3 & 2 & 0\\ -4 & 0 & 2\end{массив}\right]\)
= A
Ответ: Мы доказали, что AI = A.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по матрицам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о матрицах
Что такое матрица в математике?
Матрица в представляет собой расположение чисел, переменных, символов или выражений в прямоугольной таблице, которая содержит различное количество строк и столбцов, для которых определены такие операции, как сложение, умножение, транспонирование и т. д.
д.
Как решать матрицы?
Мы можем решать матрицы , выполняя над ними матричные операции, такие как сложение, вычитание, умножение и т. д. Мы должны заботиться о порядке при решении матриц.
- Для сложения/вычитания 2-х матриц их порядок должен быть одинаковым.
- Для умножения матриц количество столбцов левой матрицы должно быть равно количеству строк правой матрицы.
Как решать системы уравнений с матрицами?
Чтобы решить систему уравнений с матрицами, мы выполним шаги, указанные ниже.
- Расположите элементы уравнений в матрицах и найдите матрицу коэффициентов, матрицу переменных и матрицу констант.
- Запишите уравнения в форме AX = B.
- Возьмем обратную А, найдя сопряженную и определитель А.
- Умножить обратную матрицу A на матрицу B, тем самым найдя значение переменной матрицы X.
Что такое формула обратной матрицы 3×3?
Формула обратной матрицы для матрицы 3×3: A -1 = adj(A)/|A|; |А| ≠ 0, где A = квадратная матрица, adj(A) = сопряженная квадратная матрица и A -1 = обратная матрица A.
В чем особенность формулы определителя матриц?
Определитель матрицы определен только для квадратных матриц, и это свойство формулы определителя делает ее единственной. Кроме того, значение определителя можно вычислить, используя элементы любой строки или любого столбца.
Как вычислить определитель матрицы 2×2, используя формулу определителя?
Формула определителя для матрицы 2×2, \(A =\begin{pmatrix}a &b\\ \\c&d\end{pmatrix}\) определяется формулой |A| = объявление — до н.э.
При каком условии возможно умножение матриц?
Умножение матриц возможно только в том случае, если матрицы совместимы, т. е. умножение матриц допустимо только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы.
Каковы свойства перестановки матриц?
Для заданных 2 матриц, A и B, свойства перестановки матриц могут быть объяснены следующим образом:
- (A Т ) Т = А
- (А + В) Т = А Т + В Т
- (кА) T = кА T , k — любой скаляр
- (АВ) Т = В Т А Т
Что такое формула обратной матрицы?
Формула обратной матрицы используется для определения обратной матрицы для любой заданной матрицы. Обратная квадратная матрица A равна A -1 . Формула обратной матрицы может быть представлена как A -1 = прил(А)/|А|; |А| ≠ 0, где A — квадратная матрица. Также для матрицы и ее обратной мы имеем A × A -1 = A -1 × A = I.
Обратная квадратная матрица A равна A -1 . Формула обратной матрицы может быть представлена как A -1 = прил(А)/|А|; |А| ≠ 0, где A — квадратная матрица. Также для матрицы и ее обратной мы имеем A × A -1 = A -1 × A = I.
Как использовать обратную формулу матрицы?
Формулу обратной матрицы можно использовать, выполнив указанные шаги:
- Шаг 1: Найдите матрицу миноров для данной матрицы.
- Шаг 2: Преобразуйте полученную минорную матрицу в матрицу кофакторов.
- Шаг 3: Найдите сопряженную матрицу путем транспонирования матрицы кофакторов.
- Шаг 4: Наконец, разделите сопряженную матрицу на ее определитель.
Какие бывают типы матриц?
Существуют различные типы матриц в зависимости от свойств их свойств. Некоторые из них задаются как
- Матрица строк и матрица столбцов
- Квадратная матрица и прямоугольная матрица
- Диагональная матрица
- Скалярная матрица
- Идентификационная матрица
- Нулевая матрица
- Верхняя треугольная матрица и нижняя треугольная матрица
- Идемпотентная матрица
- Симметричная и кососимметричная матрица
Каковы свойства скалярного умножения в матрицах?
Имея матрицы A и B (обе одного порядка) и скаляры K и l, различные свойства, связанные с умножением матриц, можно представить как
- (K + l)A = KA + lA
- К(А + В) = КА + КБ
- (-К)А = -(КА) = К(-А)
- (Кл)А = К(1А) = 1(КА)
- (-1)А = -А
- 1·А = А
Что такое матричный многочлен?
Дан многочлен вида f(x) = a 0 x n + a 1 x n-1 + a 2 x n-1 + . . . + a n-1 x + a n и A как квадратная матрица порядка n. Тогда f(A) = a 0 A n + a 1 А н-1 + а 2 А н-2 + . . . + a n-1 A + a n A + a n называется матричным полиномом.
. . + a n-1 x + a n и A как квадратная матрица порядка n. Тогда f(A) = a 0 A n + a 1 А н-1 + а 2 А н-2 + . . . + a n-1 A + a n A + a n называется матричным полиномом.
Что такое эшелонированная форма матриц?
Матрица A = (a\(_{ij}\)\(_{m\times n}\) называется ступенчатой, если она находится либо в верхнетреугольной, либо в нижнетреугольной форме. Чтобы преобразовать матрицу
Как представить матрицу в виде суммы симметричной и несимметричной матриц?
Любая квадратная матрица A может быть записана как A = P + Q, где P и Q — симметричная и кососимметричная матрицы соответственно, такие, что P = (A + A T )/2 и Q = (A — А Т )/2.
Матрица решения проблем — Discover Your Solutions LLC
Расширенный решатель сложных проблем.
«Не то, чего ты не знаешь, приводит тебя в беду. Это то, что ты точно знаешь, что это не так.» — Марк Твен
Это то, что ты точно знаешь, что это не так.» — Марк Твен
Цель: Решить вашу проблему с помощью нашей уникальной 4-мерной матрицы.
Матричная диаграмма
Шаг 1. Изучите приведенную ниже диаграмму — это визуализация всей нашей Матрицы решения проблем.
Полезный совет:
Если вы смотрите на этот рисунок впервые, мы не ожидаем, что вы полностью поймете его с первого взгляда. Мы знаем, что это выглядит сложно, но каждый шаг довольно прост. Причина, по которой мы представили его здесь, заключается в том, что вы можете иметь обзор, на который можно ссылаться, когда вы проходите через этот процесс.
Word-версия Матрицы решения проблем.docx ( Щелкните ссылку для загрузки Word версии ).
Версия Excel для решения проблем Matrix.xlsx ( Щелкните ссылку, чтобы загрузить версию Excel ).
PDF-версия Матрицы решения проблем.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Основные категории
Шаг 2: Разбейте свою проблему на ее основные составные части. Мы называем эти основные категории. Ваша цель здесь состоит в том, чтобы определить все ваши основные категории. Для справки используйте наш инструмент «Основные категории» в наборе инструментов, чтобы разложить вашу проблему на ее основные факторы.
Мы называем эти основные категории. Ваша цель здесь состоит в том, чтобы определить все ваши основные категории. Для справки используйте наш инструмент «Основные категории» в наборе инструментов, чтобы разложить вашу проблему на ее основные факторы.
Основные категории должны быть:
- Четко определены,
- Взаимоисключающие и
- В совокупности исчерпывающий.
Полезный совет:
Это очень важный шаг! Ваши основные категории — это основа, на которой будет строиться остальная часть вашей структуры решения проблем. Не торопитесь здесь. Вы хотите получить это право в первый раз.
Объективные данные вашей проблемы
Шаг 3: Мы начнем с работы над 1-м квадрантом матрицы решения проблем. Это упражнение фокусирует ваш анализ на объективных данных вашей проблемы (обведены красным ниже).
Шаг 4. Теперь давайте увеличим масштаб. Вот
крупный план 1-го квадранта матрицы решения проблем. Эта матрица показывает ваши основные категории в столбцах по вопросительным параметрам в строках. Вы, возможно, заметили, что это очень похоже на List Solver, за исключением того, что основные категории отображаются в столбцах.
Вы, возможно, заметили, что это очень похоже на List Solver, за исключением того, что основные категории отображаются в столбцах.
Версия Word Матрицы решения проблем для объективных данных.docx ( Щелкните ссылку, чтобы загрузить версию Word ).
Excel-версия Матрицы решения проблем для объективных данных.xlsx ( Щелкните ссылку, чтобы загрузить версию Excel ).
PDF-версия Матрицы решения проблем для объективных данных.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 5: Загрузите или распечатайте нашу Форму решателя матриц для ваших объективных данных (см. версии Word, Excel и PDF ниже). Распечатайте по одной копии формы решателя матриц для каждой из ваших основных категорий.
Версия Word формы Matrix Solver для объективных данных.docx ( Щелкните ссылку, чтобы загрузить Word версии ).
Excel версия формы решателя матриц для объективных данных.xlsx ( Щелкните ссылку для загрузки Excel версии ). Предпочтительный вариант — для опытных пользователей Excel (см. вкладку «Все данные о задаче»).
Предпочтительный вариант — для опытных пользователей Excel (см. вкладку «Все данные о задаче»).
PDF-версия формы решателя матриц для объективных данных.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 6: Подготовьтесь записывать свои объективные данные в формы для решения матриц. Ваши объективные данные включают в себя: Ключевые вопросы, информацию (ответы), задачи и цели.
Вы будете группировать их по: Кто, Что, Когда, Где, Почему, Как, Откуда и Куда.
Шаг 7. Начните с формы решателя матриц для ответа «Кто». У вас должна быть форма «Кто» для каждой из ваших основных категорий. Впишите свои основные категории в отведенное место в верхней части каждой из ваших форм.
Запишите вопросы «Кто», которые, по вашему мнению, наиболее важны для понимания вашей проблемы.
Если вам нужна помощь в составлении хороших вопросов «Кто», перейдите в Инструментарий и ознакомьтесь с нашим Предварительным списком стандартных вопросов «Кто».
Полезный совет:
Не зацикливайтесь на ответах на каждый из ключевых вопросов по мере их возникновения; просто запишите их. После того, как вы составили список всех ключевых вопросов, вы можете вернуться и решить, на какие из них нужно ответить в первую очередь. При этом, если появится хороший быстрый ответ — обязательно запишите его.
Шаг 8: Запишите любую информацию, связанную с вашими вопросами «Кто» (т. е. вашими ответами). Помните, что вопросы «Кто» связаны с людьми, группами и человеческими аспектами, имеющими отношение к вашей проблеме. Кроме того, запишите задачи и цели, которые у вас есть для себя, для других людей и для групп, которые вы включили в свой анализ.
Шаг 9: После того, как вы закончите изучение аспектов проблемы «Кто», повторите процесс (этапы 7 и 8) для определения «Что», «Когда», «Где», «Почему», «Как», «Откуда» и «Куда».
Шаг 10. Просмотрите объективные данные о своей проблеме. Есть ли пробелы в ваших данных?
Полезный совет:
Сложные проблемы могут генерировать сотни и даже тысячи строк данных. Вот почему мы создали программное обеспечение базы данных MySolver™. Это для решения действительно больших проблем.
Вот почему мы создали программное обеспечение базы данных MySolver™. Это для решения действительно больших проблем.
Субъективные мысли о вашей проблеме
Шаг 11: Далее мы начнем работать над 2-м квадрантом матрицы решения проблем (обведен красным). Здесь вы анализируете свои субъективные мысли о своей проблеме.
Шаг 12. Вот крупный план 2-го квадранта матрицы решения проблем. Эта матрица показывает ваши основные категории в столбцах по предрасположенностям в строках.
Word-версия Матрицы решения проблем для субъективных мыслей.docx ( Щелкните ссылку для загрузки Word версии ).
Excel-версия Матрицы решения проблем для субъективных мыслей.xlsx ( Щелкните ссылку, чтобы загрузить Excel-версию ).
PDF-версия Матрицы решения проблем для субъективных мыслей.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 13: Загрузите или распечатайте нашу Форму решателя матриц для ваших субъективных мыслей (см. версии Word, Excel и PDF ниже):
версии Word, Excel и PDF ниже):
Версия Word формы решателя матриц для субъективных мыслей.docx ( Щелкните ссылку для загрузки Word версии ).
Excel-версия формы решателя матриц для субъективных мыслей.xlsx ( Щелкните ссылку, чтобы загрузить Excel-версию ). Предпочтительный вариант — для опытных пользователей Excel (см. вкладку «Все субъективные мысли о проблеме»).
PDF-версия формы Matrix Solver Form for Subjective Thoughts.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 14: Подготовьтесь записывать свои субъективные мысли в формах решателя матриц. Ваши субъективные мысли — это ваши личные мысли, тесно связанные с вашей проблемой.
Вы будете группировать их по: намерениям, ожиданиям, предположениям, интуиции, мнениям, заключениям, суждениям, убеждениям, надеждам и внутренним ощущениям.
Шаг 15: Начните с формы решателя матриц для «Намерений». Запишите свои Намерения, которые, по вашему мнению, наиболее важны в вашей ситуации. Не забудьте сгруппировать их в соответствии с вашими основными категориями. Если вам нужна помощь в определении ваших намерений, перейдите к нашему инструменту Intentions в нашем наборе инструментов.
Не забудьте сгруппировать их в соответствии с вашими основными категориями. Если вам нужна помощь в определении ваших намерений, перейдите к нашему инструменту Intentions в нашем наборе инструментов.
Полезный совет:
Если вы не можете быстро придумать свои Намерения, просто пропустите это и перейдите к следующей предрасположенности. Имейте в виду, что ваше внимание должно быть сосредоточено на личных мыслях, которые лежат в основе вашей проблемы. Другими словами, это упражнение больше касается качества, чем количества.
Шаг 16: Запишите любую другую информацию, связанную с вашими «Намерениями». Помните, что ваши «намерения» связаны с вашими стремлениями, целями и амбициями.
Шаг 17: После завершения изучения Намерений, связанных с вашей проблемой, повторите процессы, описанные в Шагах 11 и 12, для ваших ожиданий, предположений, интуиции, мнений, выводов, суждений, убеждений, надежд и внутренних ощущений.
Шаг 18: Распечатайте приведенную ниже форму субъективных мыслей. Если вы впервые используете эту форму, потратьте несколько минут, чтобы ознакомиться с ней.
Если вы впервые используете эту форму, потратьте несколько минут, чтобы ознакомиться с ней.
,
Word-версия формы субъективных мыслей.docx ( Щелкните ссылку, чтобы загрузить Word-версию ).
PDF-версия формы субъективных мыслей.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 19. Выберите одну из своих субъективных мыслей, которая лежит в основе вашей проблемы. Запишите это в поле 1 формы субъективных мыслей.
Шаг 20: Следуйте инструкциям в форме субъективных мыслей и заполните остальные поля формы.
Шаг 21: Просмотрите свои субъективные мысли, особенно любые неоспоримые ментальные модели, которые могут их поддерживать.
Создайте свои решения
Шаг 22: Теперь, когда у вас есть полное представление о вашей проблеме, пришло время обратить внимание на ваше решение. Вы можете начать процесс создания решений, взглянув на свои цели и задачи. Перейдите к своим формам решателя матриц для ваших объективных данных и выделите свои цели. В ваших формах «Куда» должны быть какие-то цели.
В ваших формах «Куда» должны быть какие-то цели.
Шаг 23. Используйте инструмент «Цели» в нашем наборе инструментов, чтобы найти и упорядочить свои цели.
Полезный совет:
Уточнение ваших целей поможет правильно сфокусировать вашу цель на пути к успешному решению.
Шаг 24: Если у вас еще нет идей для решений, найдите несколько минут, чтобы просмотреть раздел «Создание решений» в нашем наборе инструментов. Мы посвятили целый раздел в нашем Инструментарии, чтобы помочь вам создавать решения. Ниже мы перечислили несколько рекомендуемых нами инструментов.
Шаг 25. Перейдите к нашему инструменту «Аналогии», чтобы создавать новые идеи, проводя аналогии.
Шаг 26. Сравните свою проблему с аналогией, используя наш инструмент сходств и различий.
Шаг 27: Используйте наш инструмент «Матрица структурированных аналогий», чтобы сравнить свою проблему с несколькими аналогиями.
Шаг 28. Создавайте метафоры для создания новых идей.
Шаг 29. Создайте гипотетические решения с помощью нашего инструмента Генератор гипотез.
Шаг 30: Используйте наш Генератор множественных гипотез, чтобы создать несколько гипотез из одной гипотезы.
Полезный совет:
Ваше решение может быть не одним БОЛЬШИМ решением. Его можно разбить на множество более мелких решений. Разбейте свою проблему на более мелкие части. Посмотрите на решение каждой части отдельно. Атакуйте по одной проблеме за раз. Если проблем несколько, нужно решить, какую из них нужно решить в первую очередь.
Шаг 31. Составьте список альтернатив.
Шаг 32. Найдите точки доступа.
Шаг 33. Если у вас еще нет четкого понимания, почему вам нужно более одного решения, воспользуйтесь нашим инструментом Rival Hypotheses. Итог: Выбор одного – это не выбор.
Объективные данные ваших решений
Шаг 34: Далее мы начнем работать с вашими решениями. Третий квадрант матрицы решения проблем имеет дело с объективными данными ваших решений (обведены красным ниже).
Полезный совет:
Как видите, 3-й квадрант является зеркальным отражением 1-го квадранта (за исключением Решений, а не Проблем). отражайте аспекты вашей проблемы. Эти «зеркальные» аспекты могут быть чрезвычайно важны для решения вашей проблемы.
Шаг 35. Вот третий квадрант матрицы решения проблем. Ваши решения заполняют столбцы этого графика.
Word версия Матрица решения проблем для объективных данных.docx ( Щелкните ссылку, чтобы загрузить версию Word ).
Версия Excel Матрица решения проблем для объективных данных.xlsx ( Щелкните ссылку, чтобы загрузить версию Excel ).
PDF версия Матрица решения проблем для объективных данных.pdf ( Щелкните ссылку, чтобы скачать PDF версии ).
Шаг 36: Подготовьтесь записать объективные данные ваших решений. Вы соберете воедино свои ключевые вопросы, информацию (ответы), задачи и цели для каждого решения, а затем сгруппируете их в вопросительные параметры: кто, что, когда, где, почему, как, откуда и Куда.
Шаг 37: Загрузите или распечатайте наши формы решателя матриц для объективных данных (см. версии Word, Excel и PDF ниже):
Версия Word формы решателя матриц для объективных данных.docx ( Щелкните ссылку для загрузки Word версии ).
Excel версия формы решателя матриц для объективных данных.xlsx ( Щелкните ссылку для загрузки Excel версии ). Предпочтительный вариант — для опытных пользователей Excel (см. вкладку «Объективные данные всех решений».
PDF-версия формы решения матрицы для объективных данных.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 38. Начните с матрицы Формы решателя для «Кто». У вас должна быть форма «Кто» для каждого из ваших потенциальных Решений. Напишите свои Решения в верхней части каждой формы в отведенном месте. Затем начните вводить вопросы «Кто», которые вы считаете наиболее важными. важно. Если вам нужна помощь, чтобы придумать хорошие вопросы, перейдите к нашему списку стандартных вопросов Who в нашем наборе инструментов.
Полезный совет:
Пока не зацикливайтесь на ответах на каждый вопрос. После того, как вы составили список всех ключевых вопросов, вы можете расставить их по приоритетам.
Шаг 39. Запишите любую информацию, связанную с вашими вопросами «Кто». Помните, что вопросы «Кто» связаны с «Людями, группами и человеческими аспектами». Кроме того, перечислите свои задачи и цели для людей и групп в форме.
Шаг 40. После изучения аспектов проблемы «Кто» перейдите к разделам «Что», «Когда», «Где», «Почему», «Как», «Откуда» и «Куда».
Шаг 41. Просмотрите объективные данные.
Субъективные мысли о ваших решениях
Шаг 42: Далее мы начнем работать над 4-м квадрантом матрицы решения проблем (обведен красным). Здесь вы анализируете свои субъективные мысли о своих решениях.
Полезный совет:
Как видите, 4-й квадрант является зеркальным отражением 2-го квадранта (за исключением того, что вы анализируете свои решения). Мы использовали этот «зеркальный» дизайн, потому что некоторые аспекты вашего решения будут отражать аспекты. вашей проблемы. Эти аспекты могут быть чрезвычайно важны для решения вашей проблемы.
вашей проблемы. Эти аспекты могут быть чрезвычайно важны для решения вашей проблемы.
Шаг 43. Еще один способ просмотреть 4-й квадрант матрицы решения проблем.
Word версия Матрица решения проблем для субъективных мыслей.docx ( Щелкните ссылку, чтобы загрузить версию Word ).
Версия Excel Матрица решения проблем для субъективных мыслей.xlsx ( Щелкните ссылку, чтобы загрузить версию Excel ).
PDF версия Матрица решения проблем для субъективных мыслей.pdf ( Щелкните ссылку, чтобы скачать PDF версию ).
Шаг 44: Подготовьтесь записывать свои субъективные мысли. Соберите воедино свои личные мысли, которые тесно связаны с вашей проблемой. Вы будете сортировать их по своим решениям, а затем группировать их по предрасположенностям: намерения, ожидания, предположения, интуиция, мнения, выводы, суждения, убеждения, надежды и внутренние ощущения.
Шаг 45: Загрузите или распечатайте наши формы решателя матриц для субъективных мыслей (см. версии Word, Excel и PDF ниже):
версии Word, Excel и PDF ниже):
Версия Word формы Matrix Solver для субъективных мыслей.docx ( Щелкните ссылку, чтобы загрузить версию Word ).
Excel-версия формы решателя матриц для субъективных мыслей.xlsx ( Щелкните ссылку, чтобы загрузить Excel-версию ). Предпочтительный вариант — для опытных пользователей Excel (см. вкладку «Все решения, субъективные мысли»).
PDF-версия формы Matrix Solver Form for Subjective Thoughts.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 46: Начните с формы решателя матриц для «Намерений». Просто запишите свои Намерения, которые, по вашему мнению, важны в этой ситуации. Если вам нужна помощь в определении ваших намерений, перейдите к нашему инструменту Intentions в нашем наборе инструментов.
Полезный совет:
Если вы не можете быстро придумать свои Намерения, просто пропустите его и перейдите к следующей предрасположенности. Имейте в виду, что ваше внимание должно быть сосредоточено на личных мыслях, которые лежат в основе вашей проблемы. Другими словами, это больше о качестве, чем о количестве.
Другими словами, это больше о качестве, чем о количестве.
Шаг 47. После того, как вы изучили свои Намерения, перейдите к своим Ожиданиям, Предположениям, Интуиции, Мнениям, Выводам, Суждениям, Убеждениям, Надеждам и Внутренним Чувствам.
Шаг 48: Распечатайте приведенную ниже форму субъективных мыслей. Если вы впервые используете эту форму, потратьте несколько минут, чтобы ознакомиться с ней.
,
Word-версия формы субъективных мыслей.docx ( Щелкните ссылку, чтобы загрузить Word-версию ).
PDF-версия формы субъективных мыслей.pdf ( Щелкните ссылку, чтобы загрузить PDF-версию ).
Шаг 49: Возьмите одну из своих Предрасположенностей, лежащую в основе вашего Решения, и запишите ее в поле 1 формы субъективных мыслей.
Шаг 50: Следуйте инструкциям и заполните оставшуюся часть формы субъективных мыслей.
Шаг 51. Просмотрите свои субъективные мысли и бесспорные ментальные модели, которые их поддерживают.
Оценка Ваши решения
Шаг 52: Теперь, когда вы создали и проанализировали свои решения, вам может потребоваться определить, какое решение лучше всего подходит для вас. Чтобы оценить свои решения, перейдите в раздел «Оценка решений» нашего инструментария. Ниже мы перечислили несколько рекомендуемых нами инструментов.
Шаг 53. Перейдите к нашему инструменту негативного мозгового штурма, чтобы проверить свои решения на наличие потенциальных сбоев.
Шаг 54. Проанализируйте свои решения на наличие потенциальных проблем с помощью нашего инструмента анализа потенциальных проблем.
Шаг 55. Сыграйте в роль Адвоката дьявола, представив наилучшее из возможных доводов против предложенного плана.
Шаг 56. Ранжируйте альтернативы, сравнивая их в парных наборах с помощью нашего инструмента анализа парных сравнений.
Шаг 57: Используйте наш инструмент анализа сетки, чтобы создать оценку для каждой из ваших альтернатив, ранжируя свои решения для каждой основной категории, а затем взвешивая каждую из ваших основных категорий.
Шаг 58. Создайте матрицу для проверки гипотез с помощью нашего инструмента «Матрица проверки гипотез».
Шаг 59. У нас также есть много методов принятия решений, перечисленных в конце раздела «Оценка решений» нашего инструментария.
Полезный совет:
Сложные проблемы могут генерировать сотни и даже тысячи строк данных. Вот почему мы создали программное обеспечение базы данных MySolver™. MySolver поможет вам справиться с действительно большими проблемами. Он помещает всю вашу информацию на кончиках ваших пальцев.
Ключевые точки:
- Определите основные категории вашей проблемы.
- Упорядочивайте свои данные и мысли, используя наши формы для решения матриц.
- Найдите ответы на свои ключевые вопросы и соберите другую важную информацию.
- Определите свои задачи и цели.
- Изучите свои субъективные мысли (то есть мысли, к которым вы предрасположены).
- Открывайте, тестируйте и улучшайте бесспорные ментальные модели.

- Придумайте разумные решения своей проблемы.
- Оцените свои решения.
Решенные примеры задач на приложения матриц: Решение системы линейных уравнений
Главная | | Математика 12 Std | Решенные примеры задач по применению матриц: решение системы линейных уравнений
- Предыдущая страница
- Следующая страница
Глава:
12-я математика: РАЗДЕЛ 1: Применение матриц и определителейРешение системы линейных уравнений: (i) Метод матричной инверсии (ii) Правило Крамера (iii) Метод исключения Гаусса
Решение системы линейных уравнений
(i) Метод обращения матриц
Пример 1.22
Решите следующую систему линейных уравнений, используя метод обращения матриц:
5 x + 2 y = 3, 3 x + 2 y = 5 .
Решение
Матричная форма системы имеет вид AX = B , где
Находим |A| = = 10 — 6= 4 ≠ 0. Итак, A−1 существует и A−1 =
Тогда, применяя формулу X = A−1B , мы получаем
Таким образом, решение ( x = −1, y = 4).
Пример 1.23
Решите следующую систему уравнений, используя метод обращения матриц:
2 x 1+ 3 x 2+ 3 x 3 = 5,
x 1 -2 x 2+ x 3 = -4,
3 0 x 3 = -4,
3 0 x 3 = -4,
3 0 x 3 = -4,
3 0 x 3 = -4,
3 0 x 3 = -4, 3 0 x . – x2 – 2 x 3 = 3Решение
Матричная форма системы AX = B, где
Итак, решение ( x 1 = 40, 1 x 9144 2, x 3 = −1) .
Пример 1.24
Если , найти произведения AB и BA и, следовательно, решить систему уравнений x − y + z = 4, x – 2y – 2z = 9, 2x + y + 3z = 1.
Решение
Написание данной системы уравнений в форме матрицы, мы получаем
Следовательно, решение составляет ( x = 3, y = — 2, Z = −1 = −1 = −1 = −1 = −1 = −1 = −1 = −1 = −1 = y = -2, Z = Y ).
(ii) Правило Cramer
Пример 1.25
Решение, правилом Cramer, Система уравнений
x 1 — x 2 = 3, 2 x 1+3 0 2 = 3, 2 x 1+3 0 2 = 3, 2 x 1+3 0 29441441441441441441. x 3 = 17, x 2+2 x 3 = 7.
Решение
Сначала мы оцениваем детерминанты
Итак, решение составляет ( x1 = 2, x2 = -1, 0 = 2, x2 = -1, 0 = 41440. ).
Пример 1.26
В матче T20 команде Chennai Super Kings понадобилось всего 6 пробежек, чтобы выиграть, а до последнего броска оставался 1 мяч. Последний мяч был забит, и игрок с битой на складке ударил его высоко. Мяч прошел путь в вертикальной плоскости, и уравнение пути равно y = ax 2 + bx + c относительно xy -системы координат в вертикальной плоскости и шара, пройденного через точки (10,16), (20,16), ( 30,18) , можете ли вы сделать вывод, что Ченнаи Супер Кингз выиграли матч?
Мяч прошел путь в вертикальной плоскости, и уравнение пути равно y = ax 2 + bx + c относительно xy -системы координат в вертикальной плоскости и шара, пройденного через точки (10,16), (20,16), ( 30,18) , можете ли вы сделать вывод, что Ченнаи Супер Кингз выиграли матч?
Обоснуйте свой ответ. (Все расстояния измеряются в метрах, а точка пересечения плоскости пути с самой дальней линией границы равна (70, 0).)
Решение
Путь y = x 2 + bx + c проходит через точки (10,8), (20,16), (40, 22) . Таким образом, мы получаем систему уравнений 100 A +10 B + C = 8, 400 A +20 B + C = 161600 B + C = 161600 B + C = 161440 + C = 161440 B + C = 161440 B + C . + c = 22. Чтобы применить правило Крамера, находим
.0003
Итак, мяч пролетел на высоте 6 метров над ограничительной линией и полевой игрок, стоящий даже перед ограничительной линией, не может прыгнуть и поймать мяч.
Следовательно, мяч попал в супершестерку, и Chennai Super Kings выиграли матч.
(iii) Метод исключения Гаусса
Пример 1.27
Решите следующую систему линейных уравнений методом исключения Гаусса:1441 = 25, x +5 y +7 z = 13, 2 x + y + z = 1.
Решение
. get
Эквивалентная система записывается с использованием ступенчатой формы:
x + 5y + 7z = 13 , … (1)
17y + 22z = 27 , … (2)
399 z = 199 . … (3)
Подставляя z = 2, y = -1 в (1), получаем x = 13 — 5 × (−1 ) − 7 × 2 = 4 .
Итак, решение ( x =4, y = — 1, z = 2 ).
Примечание. Описанный выше метод перехода от последнего уравнения к первому называется методом обратной подстановки. Пример 1.28 с являются константами. Было обнаружено, что скорость в моменты времени t = 3, t = 6 и t = 9 секунд соответственно составляет 64, 133 и 208 миль в секунду. Найдите скорость в момент времени t = 15 секунд. (Используйте метод исключения Гаусса.)
Найдите скорость в момент времени t = 15 секунд. (Используйте метод исключения Гаусса.)
Решение
Так как v (3) =64, v (6) = 133 и v (9) = 208 , получаем следующую систему линейных уравнений + 9a3b +
3 9 c = 64 ,
36a + 6b + c = 133,
81a + 9b + c = 208 .
Приведенную выше систему линейных уравнений решаем методом исключения Гаусса.
Приведя расширенную матрицу к эквивалентной строчно-ступенчатой форме с помощью элементарных операций со строками, мы получим
Записав эквивалентные уравнения из ступенчато-строковой матрицы, получим
9a + 3b + c = 64, 2b + c = 41, c = 1.
Итак, получаем v (t) = 1/3 t2 + 20t + 1.
Отсюда v (15) = 1/3 (225) + 20(15) + 1 = 75 + 300 + 1 = 376
- Предыдущая страница
- Следующая страница
Теги : Определение, Формулы, Примеры решенных задач , 12th Математика : РАЗДЕЛ 1 : Применение матриц и определителей
Учебный материал, Лекционные заметки, Задание, Справочник, Вики-описание, пояснение, краткая информация
12-я математика: РАЗДЕЛ 1: Применение матриц и определителей: Решенные примеры задач по применению матриц: Решение системы линейных уравнений | Определение, формулы, решенные примеры задач
- Предыдущая страница
- Следующая страница
Связанные темы
Maths 12th Std — TN 12th Maths (английский средний) | Вопросы с ответами, решение
TN Государственная школа Совета — Все субъекты
12 -й стандарт — Все субъекты
12 -й математика: Блок 1: Применение Matrices и Detrinants
. s. 908.s. 908. Обратная невырожденная квадратная матрица — Применение матриц и определителей
s. 908.s. 908. Обратная невырожденная квадратная матрица — Применение матриц и определителей
Сопряженная квадратная матрица — Определение, теорема, формулы, решенные примеры задач | Обратная неособая квадратная матрица
Определение обратной матрицы квадратной матрицы — Определение, теорема, формулы, решенные примеры задач | Обратная неособая квадратная матрица
Свойства обратных матриц — Определение, теорема, формулы, решенные примеры задач | Обратная неособая квадратная матрица
Применение матриц к геометрии — Определение, теорема, формулы, решенные примеры задач | Обратная неособая квадратная матрица
Применение матриц в криптографии — Определение, теорема, решенные примеры задач |
Упражнение 1.1. Обратное невырожденной квадратной матрицы Преобразования матрицы — определение, теорема | Элементарные операции со строками и столбцами
Row Echelon form — Определение, теорема, формулы, решенные примеры задач | Элементарные преобразования матрицы
Ранг матрицы — определение, теорема, формулы, решенные примеры задач | Элементарные преобразования матрицы
Метод Гаусса-Жордана — определение, теорема, формулы, решенные примеры задач | Элементарные преобразования матрицы
Упражнение 1. 2. Элементарные преобразования матрицы — Проблемные вопросы с ответом, решение
2. Элементарные преобразования матрицы — Проблемные вопросы с ответом, решение
Элементарные преобразования матрицы: решенные примеры задач — с ответами, решение
Применение матриц: решение системы линейных уравнений
Формирование системы линейных уравнений — Применение системы матриц Линейные уравнения
Система линейных уравнений в матричной форме — Применение матриц: решение системы линейных уравнений
Решение системы линейных уравнений — Применение матриц: решение системы линейных уравнений
Метод обращения матриц — Определение, формулы, примеры решенных задач
Упражнение 1.3. Матричные линейные уравнения методом обращения матриц — Проблемные вопросы с ответом, решение
Матрицы: правило Крамерса — определение, формулы, решенные примеры задач
Упражнение 1.4: матрицы: правило Крамерса — задачи с ответом, решение
Матрица: метод исключения Гаусса — Определение, решенные примеры задач
Упражнение 1. 5: Матрица: метод исключения Гаусса — Проблемные вопросы с ответом, решение
5: Матрица: метод исключения Гаусса — Проблемные вопросы с ответом, решение
Пример решенных задач по применению матриц: решение системы линейных уравнений — Определение, формулы, примеры решенных задач
Матрица: неоднородные линейные уравнения — Определение, теоремы, формулы, примеры решенных задач | Приложения матриц: непротиворечивость системы линейных уравнений ранговым методом
Упражнение 1.6: Матрица: Неоднородные линейные уравнения — Проблемные вопросы с ответом и решением
Матрица: Однородная система линейных уравнений — Определение, теорема, формулы, решенные примеры задач | Применение матриц: непротиворечивость системы линейных уравнений ранговым методом
Упражнение 1.7. Матрица: однородная система линейных уравнений — Проблемные вопросы с ответом, решение
Выберите правильный ответ – Применение матриц и определителей
Резюме – Применение матриц и определителей
Решение систем уравнений матричным методом
Матричный метод решения систем уравнений также известен как метод строк-эшелонов.
Матричный метод аналогичен методу исключения as, но намного чище
, чем метод исключения.
Решение систем уравнений матричным методом предполагает выражение системы
уравнений в виде матрицы, а затем преобразование этой матрицы в то, что известно как
Row Echelon Form.
Ниже приведены два примера матриц в форме Row Echelon Form
.
Первая представляет собой матрицу 2 x 2 в форме Row Echelon, а вторая представляет собой матрицу 3 x 3
в форме Row Echelon.
Выражение систем уравнений в виде матриц
Учитывая следующую систему уравнений:
Приведенная выше система уравнений с двумя переменными может быть выражена в виде матричной системы, поскольку
следует за
.
Если мы решим приведенное выше, используя правила умножения матриц, мы должны получить
с системой уравнений, с которой мы начали. Мы можем дополнительно изменить приведенные выше матрицы
Мы можем дополнительно изменить приведенные выше матрицы
и скрыть матрицу, содержащую переменные. Мы не удаляем его, а просто прячем
, чтобы сделать наши вычисления чище.
Вышеупомянутое далее преобразуется в единую матрицу, как показано ниже
.
Часто вертикальная линия рисуется, чтобы указать, что самый правый столбец представляет
записей справа от знака равенства в системе уравнений.
То же самое можно сделать для системы уравнений с тремя переменными.
Вышеупомянутое может быть выражено как произведение матриц в виде:
Скрывая матрицу, содержащую переменные, мы можем выразить это как:
Затем складываем все это в одну матрицу:
или как
Вышеупомянутая форма называется расширенной матрицей . В расширенной матрице
В расширенной матрице
выше мы знаем, что элементы слева представляют коэффициенты к переменным
в системе уравнений.
Метод приведения к форме эшелонирования строк
Прежде чем читать этот раздел, вы должны взглянуть на раздел «Сокращение до формы эшелона
» в разделе «Матрицы».
Теперь, когда вы знаете, как преобразовать матрицу в форму эшелона строк, давайте посмотрим, как применить алгоритм
к расширенным матрицам, сформированным из систем уравнений.
Пример 1:
Найдите решение следующей системы уравнений
Решение:
Первый шаг состоит в том, чтобы выразить приведенную выше систему уравнений в виде расширенной матрицы.
Далее мы маркируем строки:
Теперь мы начнем фактически приводить матрицу к форме эшелона строк. Сначала мы меняем старший коэффициент
Сначала мы меняем старший коэффициент
первой строки на 1,9.0003
Мы достигаем этого, умножая R 1 на -1 ⁄ 3 :
Затем мы меняем коэффициент во второй строке, который находится ниже старшего коэффициента
в первой строке. Это достигается путем умножения R 2 на -1 ⁄ 5
и последующего прибавления результата к R 1 .
Добавление результата к Р’ 1 :
Итак, теперь наша новая матрица выглядит так:
.
На этом этапе мы повторно вводим переменные в строку 2, так как теперь у нас будет одно уравнение с
переменными:
Мы можем найти y из приведенного выше уравнения:
Теперь, когда у нас есть y , мы можем использовать обратную подстановку для решения x на
, заменив y в уравнении с двумя переменными, составленном из R’ 1 :
Следовательно, решение системы уравнений: {x,y} = {2,-2}
Пример 2:
Найдите x, y и z в системе уравнений ниже
Решение:
Первый шаг — превратить систему уравнений с тремя переменными в расширенную матрицу
3×4.
Далее помечаем строки матрицы:
Поскольку в приведенной выше расширенной матрице мы не можем найти ни одной строки с единицей в качестве ведущего коэффициента
, нам не нужно выполнять операцию переключения строк. Однако нам нужно изменить
строку 1 так, чтобы ее старший коэффициент был равен 1.
Мы можем добиться этого, умножив строку 1 на 1 ⁄ 3 :
Далее нам нужно изменить все записи ниже старшего коэффициента первой строки
на нули.
Для второй строки мы можем добиться этого, сначала умножив на -1 ⁄ 3
, а затем добавив результат к строке 1.
Добавление результата в строку 1:
Затем мы переходим к строке 3; здесь мы умножаем строку на -1 ⁄ 5
, а затем добавляем результат к строке 1, чтобы обнулить первый элемент.
Добавление результата в строку 1:
Нам нужно, чтобы ведущий элемент во второй строке тоже был единицей. Мы получаем этот результат
, умножая вторую строку на -3 ⁄ 2 :
Затем мы обнуляем элемент в третьей строке под старшим коэффициентом во второй строке
. Для этого умножаем третью строку на 5 ⁄ 4
Добавление результата в строку 2:
Наконец, мы умножаем строку 3 на -12, чтобы ведущий элемент третьей строки
был равен единице:
.
Из приведенной выше матрицы мы находим переменные, начинающиеся с z в последней строке
.
Затем мы находим y, заменяя z в уравнении, образованном второй строкой:
Наконец, мы находим x, подставляя значения y и z в уравнение, сформированное
первой строкой:
.
Следовательно, решение системы уравнений {x,y,z} = {1,-2,1}
Уступайте место матрице — Полное руководство по решению проблем кодирования 2D-массивов | by Mohima Chaudhuri
Photo by Josh Riemer on UnsplashБольшинство матричных проблем могут быть пугающими на первый взгляд. Однако решить их совсем не сложно! В этой статье я расскажу о шагах по решению этих проблем, начиная с обзора матрицы и того, как она используется.
Перво-наперво! Давайте рассмотрим, что такое матрица.
Что такое матрица?
Определение из Википедии: «В математике матрица (множественное число матриц ) представляет собой прямоугольный массив чисел, символов или выражений, расположенных в строках, и столбцах».
В большинстве случаев термины «матрица» и «двумерный массив» взаимозаменяемы. Двумерный массив может функционировать точно так же, как матрица. Двумерные массивы можно представить в виде таблицы, состоящей из строк и столбцов.
Двумерный массив может функционировать точно так же, как матрица. Двумерные массивы можно представить в виде таблицы, состоящей из строк и столбцов.
- Преимущественно в системах баз данных, где данные в таблицах хранятся на пересечении определенной строки и столбца.
- В графике, где матрицы представляют пиксели.
- В системе продажи билетов в кино (ряд-место-номер) или любой системе бронирования (автобус/поезд/авиалинии), которая использует строку и столбец для идентификации места.
Двумерные массивы представлены в виде списка списков. Каждый список обычно представляет собой строку, а каждый элемент списка представляет собой столбец. В этом примере мы создадим театральную рассадку из 5 рядов по 10 мест в каждом ряду.
Инициализировать 2D-массивВышеупомянутое также можно выполнить с помощью вложенного списка:
Инициализировать 2D-массив со списком Предположим, теперь нам нужно обновить, что последние 2 строки зарезервированы, установив значение 1. Вот как для этого:
Вот как для этого:
Теперь, когда мы рассмотрели основы, давайте начнем с простой задачи.
Транспонирование матрицы — это замена значений ее строк значениями столбцов.
Для каждой ячейки result[i][j] нам нужно заменить значение на input[j][i]
, где ввод — это транспонируемая матрица, а
результат — заполнитель для транспонированной матрицы.74. Поиск в двумерной матрице
В этой задаче нам нужно найти значение в отсортированной матрице. По сути, отсортированная матрица означает, что значение в ячейке A[i][j] всегда будет больше, чем значения во всех предшествующих ей ячейках.
Ввод и ожидаемый результатРешение1 : Подход грубой силы к решению этой проблемы заключается в переборе каждой строки и каждого столбца, пока не будет найден целевой элемент или не будет достигнут конец матрицы.
search Matrix — Brute ForceОднако это O(M*N) и не использует структурную информацию матрицы, представленную в описании задачи.
Как мы можем сделать это лучше? В матрице каждый элемент в строке сортируется, а все строки сортируются в порядке возрастания. Что мы используем для искать значение в отсортированных массивах ? Введите Двоичный поиск !
Solution2 : Инициализируйте начало до 0 и конец до M-1, где M = количество строк. Найдите среднюю строку, а затем примените двоичный поиск для поиска целевого элемента в строке. Если целевой элемент найден, верните True, в противном случае измените среднюю строку по мере необходимости и продолжите поиск до начала ≤ конца. Итак, внешний бинарный поиск ищет строку, а внутренний бинарный поиск ищет элемент внутри строки. Вот прохождение:
решение для бинарного поискаА вот код:
Матрица поиска — Бинарный поискРешение3 : Если мы внимательно посмотрим на матрицу, то увидим более простое решение. Обратите внимание, что элементы становятся меньше, когда мы двигаемся влево по строке, и больше, когда мы двигаемся вниз по столбцу .
Матрица поиска — используйте направлениеИспользуя эту информацию, мы можем перемещаться по матрице, меняя направление в зависимости от значения в ячейке. Вот пошаговое руководство:
Вот код:
поиск в матрице с использованием направленияПримечание : Мы начинаем не с верхнего левого угла матрицы , а с верхнего правого . Почему? Потому что, если мы проходим сверху слева, мы можем двигаться вправо или вниз, и в обоих случаях значения будут только увеличиваться.
240. Поиск в 2D Matrix II
Это очень похоже на предыдущую задачу. В отличие от предыдущей задачи, где все элементы были отсортированы, здесь предыдущая строка может иметь более высокие значения, чем строки, следующие за ней . Таким образом, мы не можем использовать бинарный поиск, чтобы определить конкретную строку для поиска цели.
Давайте сосредоточимся на направлении роста элементов. Значения увеличиваются вниз, а значения уменьшаются при движении влево.
searchMatrixII пошаговое руководствоИспользуя эту информацию, мы можем использовать тот же алгоритм, что и в приведенной выше задаче, чтобы решить эту проблему. Вот пошаговое руководство:
Вот код:
searchMatrixII73. Установка нулей матрицы
Моя первоначальная попытка решить эту проблему состояла в том, чтобы пройти по массиву и, если найден 0, обновить всю строку до 0. Плохая идея! Это приведет к потере информации о том, какие столбцы имели значение 0. Итак, перед тем, как мы на самом деле обновим массив, нам нужно что-то, чтобы сохранить запись о том, какие строки и столбцы содержат 0.
Вот пошаговое руководство:
setZeroMatrix пошаговое руководствоВот код:
setZeros.pyТеперь давайте посмотрим на обход матрицы по разному: по спирали и по диагонали .
54. Спиральная матрица
Проблема на входе и ожидаемый результатПримечание : Эту проблему можно решить несколькими способами.
Однако то, чем я здесь делюсь, кажется наиболее интуитивным решением. Итак, давайте рассмотрим это шаг за шагом.
Шаг 1 : Представьте, что мы решаем это вручную, и в этом случае мы можем двигаться только в 4 направлениях: мы начинаем с вправо , затем двигаем вниз , затем влево и, наконец, вверх (затем вправо опять таки).
куда мы можем переехать?Шаг 2 : Как долго мы будем это делать? Посмотрите на изображение ниже.
когда мы прекратим обходРассмотрим матрицу как сжимающееся пространство между границами, которые движутся в . Мы знаем, что прошли всю матрицу, когда эти границы встречаются.
Шаг 3 : Теперь мы уже обсудили направления движения. Давайте посмотрим, как меняются границы, когда мы перемещаемся в направлении.
граница изменяется при движении по спиралиШаг 4 : Наконец, как нам избежать пересечения элемента, через который мы уже прошли ранее? Для этого мы поддерживаем другую матрицу, в которой мы храним информацию о том, какие позиции уже пройдены с логическим значением.
Вот код
SpiralMatrix159. Spiral Matrix II
Эта задача очень похожа на первую. Вместо обхода матрицы здесь нам нужно построить квадрат матрицы «n». Для этого мы сначала строим матрицу из n*n логических значений, чтобы сохранить нашу результирующую матрицу, и продолжаем заполнять ее по мере продвижения по спирали — вправо → вниз → влево → вверх → вправо…, пока мы не заполним значения до n*n.
Вот пошаговое руководство:
Создать пошаговое руководство по матрицеВот код:
SpiralMatrix2498. Диагональный ход
Ввод и ожидаемый результатРешение1 : Решая это вручную, мы видим, что мы можем двигаться в 4 направлениях: по диагонали вверх ( DU ), по диагонали вниз ( DD ), Вправо( R ) на 1 шаг, Вниз( D ) на 1 шаг.
Теперь давайте посмотрим, как меняются идентификаторы строк и столбцов при движении в этих направлениях:
обход матрицы по диагоналиВот код:
диагональMatrix1Решение2 : Существует более простое решение, основанное на том факте, что сумма координат каждого элемента на диагонали будет одинаковой.
Вот реализация:
диагональMatrix.pyСпасибо за чтение, и я надеюсь, что это помогло. Заканчивая этой цитатой из Матрицы, помните об этом при решении матричных задач или любой другой задачи :).
Нео : Что такое Матрица?
Тринити : Ответ где-то рядом, Нео. Он ищет тебя, и он найдет тебя, если ты этого захочешь.
- https://www.ict.social/python/basics/многомерные-списки-в-питоне
- https://www.hackerearth.com/practice/data-structures/arrays/multi-diversity/tutorial /
- https://www.hackerearth.com/practice/data-structures/arrays/multi-diversity/tutorial/
- https://en.wikipedia.org/wiki/Matrix_(mathematics)
- https:/ /leetcode.com/
Полное руководство по решению уравнений с помощью матриц
Многие ученики испытывают трудности с математикой, особенно с решением уравнений с матрицами. Прежде чем углубиться в тему, очень важно знать, что такое матрица.
Матрица представляет собой прямоугольное расположение столбцов и чисел в строке. Это прямоугольное расположение чисел заключено в большие скобки [ ] или маленькие скобки ( ). Кроме того, матрицы обычно пишутся заглавными буквами, такими как A, B, C, D и т. д., а их множители — с мелкими элементами a, b, c, d и т. д.
Например: A= [1, 6, 8], В= (а, б, в)
Эти матричные уравнения несложно решить тем, кто знает хитрость. Но большинство учащихся сталкиваются с трудностями при быстром решении уравнений. Если вы один из них, то не расстраивайтесь. Вы находитесь в правильном месте, чтобы решить свои проблемы с математикой. Здесь вы можете получить подробное руководство по решению уравнений с матрицами.
Изучить теоремы о матрицах:
Если вы испытываете трудности при решении уравнений с матрицей, одной из причин может быть отсутствие базовых знаний теорем о матрицах. Теорема о матрицах проведет вас через умножение матриц, сложение матриц, правила транспонирования, обратные правила и многие другие.
Вам нужно понять и запомнить правила матричной алгебры, которые помогут вам решить матрицу.
Знаете ли вы? Если у вас есть понимание основ матрицы, вы можете решить любую матричную задачу простым способом. И ваши базовые знания улучшат ваше решение уравнений с матрицей.
Понимание типов матриц:
После понимания основных правил работы с матрицами важно понимать различные формы матриц. В главе о матрицах вам нужно пройти через такие типы, как матрица-строка, квадратная матрица, матрица-столбец, скалярная матрица, единичная матрица, одноэлементная матрица, сингулярная матрица, равная матрица, треугольная матрица, нулевые или нулевые матрицы и диагональная матрица.
При решении уравнений с матрицами можно встретить любые вопросы, связанные с типами этих матриц. Поэтому вам нужно различать эти типы при попытке задать вопрос. Даже вам нужно понять некоторые приемы, чтобы решить матричные уравнения. Кроме того, более простое матричное уравнение можно легко решить, используя скалярное умножение и сложение матриц.
Понять проблему или вопрос:
Многие студенты не пытаются глубоко понять вопросы из-за ограниченного времени экзамена или по другим причинам. По этой причине учащиеся не могут решить матричные вопросы. Отсутствует понимание матричного вопроса.
Поэтому, когда вы сидите за решением математической задачи, не пугайтесь, увидев сам вопрос. И не паникуйте
об ограничении времени. Вам нужно прочитать матричный вопрос дважды или трижды. Здесь вам нужно дать время и попытаться подумать, каким образом вы можете решить вопросы. Уверены, вы найдете ответ.Делайте больше практик:
Вы, должно быть, слышали, что практика делает человека совершенным. Да, больше практики поможет вам в решении матричных задач. Даже вы можете чувствовать себя уверенно при решении задач, связанных с матрицей. Иногда студенты не могут управлять своим временем и не выбирают матричные вопросы на экзаменах. Но здесь больше практики поможет вам лучше решать матричные уравнения, и это поможет вам управлять временем во время экзамена.
Если вы хотите решить матричное уравнение, вам нужно уделить больше времени этой главе. И вы должны увеличить практику матричного уравнения.
Примите участие в групповых занятиях:
Многие люди думают, что групповые занятия — пустая трата времени. Многие говорят, что студенты не читают и не практикуются в групповых занятиях. Но это не совсем так. Есть много студентов, которые хотят узнавать что-то новое каждый день. Они не хотят тратить свое время. Если вы один из них, то групповые занятия — лучший способ получить знания. И это улучшает критическое мышление учащихся и навыки решения проблем.
Если вы хотите повысить скорость решения матричных уравнений, вы можете пригласить своих друзей на групповые занятия. Здесь вы можете привлечь несколько способных студентов и некоторых средних студентов и сформировать группу, чтобы учиться друг у друга. Кроме того, вы можете узнать некоторые методы решения от своих друзей.
Самостоятельная или индивидуальная практика:
Даже если вы выполняете групповую практику по решению уравнения с матрицей, вам нужно уделять ей отдельное время для практики.
Часто учащиеся забывают методы и приемы решения уравнений, которые они узнали от своих друзей на групповых занятиях.
Эта проблема не возникнет, если вы запишете приемы и методы решения вопросов, а также будете практиковать их дома. Самостоятельная практика — отличный способ улучшить свои навыки решения проблем.Свяжитесь со своими факультетами/преподавателями:
Иногда студенты застревают в некоторых матричных задачах, где им нужна помощь эксперта. Ну не все же гении в решении уравнений матрицы. В какой-то момент вам понадобится помощь учителя или преподавателя.
Если вы потратили достаточно времени на решение уравнения, но так и не нашли никаких результатов, вы должны связаться со своим преподавателем. Они являются экспертами в этих главах, поскольку они учат тому же в течение длительного времени.МАКЕТ-тест:
МАКЕТ-тест означает проверку множественных вариантов. Этот тест помогает учащимся практиковать многие типы матричных вопросов. Даже многие эксперты говорят, что в настоящее время очень важно сдать пробный тест перед тем, как сдать выпускные экзамены.

 array_equal(np.sum(massiv, axis=0), summy_stolbcov):
print(massiv)
break
array_equal(np.sum(massiv, axis=0), summy_stolbcov):
print(massiv)
break



