Сумма двух векторов / Векторы / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Векторы
- Сумма двух векторов
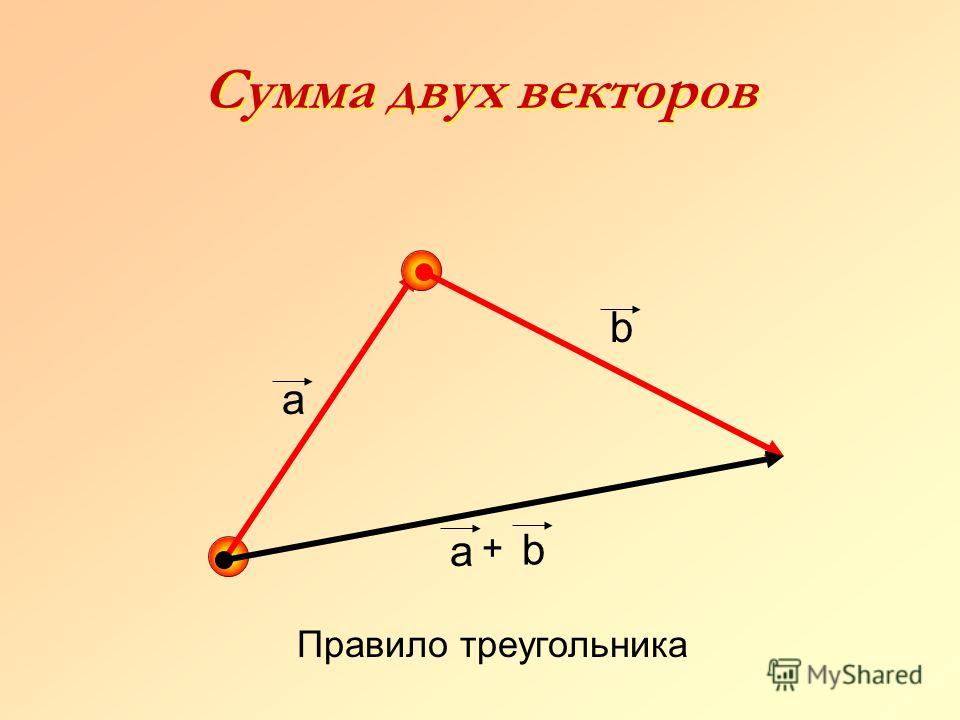
Рассмотрим два вектора и и найдем их сумму. Для этого отметим произвольную точку А и отложим от этой точки вектор , равный . Затем от точки В отложим вектор , равный . Вектор , равный вектору , называется суммой векторов и .
| Суммой двух векторов и называется третий вектор , проведенный из начала вектора к концу вектора , если начало вектора совпадает с концом вектора . |
Данное правило сложения векторов называется правилом треугольника (рисунок поясняет это название).
Сумма векторов и обозначается так: + .
| Результат сложения (сумма) векторов и не зависит от выбора точки, от которой откладывается вектор . |
Доказательство
Дано: = , = .
Доказать: = .
Доказательство:
Допустим, что точки А, В, А1, точки В, С, В1 и точки А, С, А1 не лежат на одной прямой. Из равенства = следует, что стороны АВ и А1В1 четырехугольника АВВ1А1 равны и параллельны, т. к. равные векторы сонаправлены и их длины равны, поэтому этот четырехугольник — параллелограмм. Поэтому АА1 = ВВ1, значит, и . Аналогично из равенства = следует, что четырехугольник ВСС1В1 — параллелограмм. Поэтому .
к. равные векторы сонаправлены и их длины равны, поэтому этот четырехугольник — параллелограмм. Поэтому АА1 = ВВ1, значит, и . Аналогично из равенства = следует, что четырехугольник ВСС1В1 — параллелограмм. Поэтому .
Итак, , , следовательно, . Поэтому АА1С1С — параллелограмм, и, значит, = . Что и требовалось доказать.
Складывая по правилу треугольника произвольный вектор с нулевым вектором, получаем, что для любого вектора справедливо равенство + = .
Правило треугольника можно сформулировать и так:
| Если А, В и С — произвольные точки, то + = . |
Данное правило справедливо для произвольных точек А, В и С, даже в том случае, когда две из них или даже все три совпадают.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие вектора
Равенство векторов
Откладывание вектора от данной точки
Законы сложения векторов. Правило параллелограмма
Сумма нескольких векторов
Вычитание векторов
Произведение вектора на число
Применение векторов к решению задач
Средняя линия трапеции
Векторы
Правило встречается в следующих упражнениях:
7 класс
Задание 758, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 762, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 765, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 767, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 774, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 782, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 904, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1074, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Законы сложения векторов.
 Правило параллелограмма
Правило параллелограммаУрок 5. Геометрия 9 класс ФГОС
На этом уроке продолжается изучение правил построения вектора суммы двух векторов, и, в частности, рассматривается правило параллелограмма. Также проводятся доказательства переместительного и сочетательного законов сложения векторов, которые находят своё применение при выполнении практических заданий.
Конспект урока «Законы сложения векторов. Правило параллелограмма»
С прошлых уроков вам уже известно, что векторы можно складывать и делать это вы уже умеете с помощью правила треугольника.
Для того, чтобы изобразить вектор суммы двух векторов и , от некоторой точки А откладывают вектор . Далее от точки B откладывают вектор . Тогда вектор .
Для дальнейшей работы с векторами нам понадобится знание следующих законов сложения векторов.
Сумма
векторов .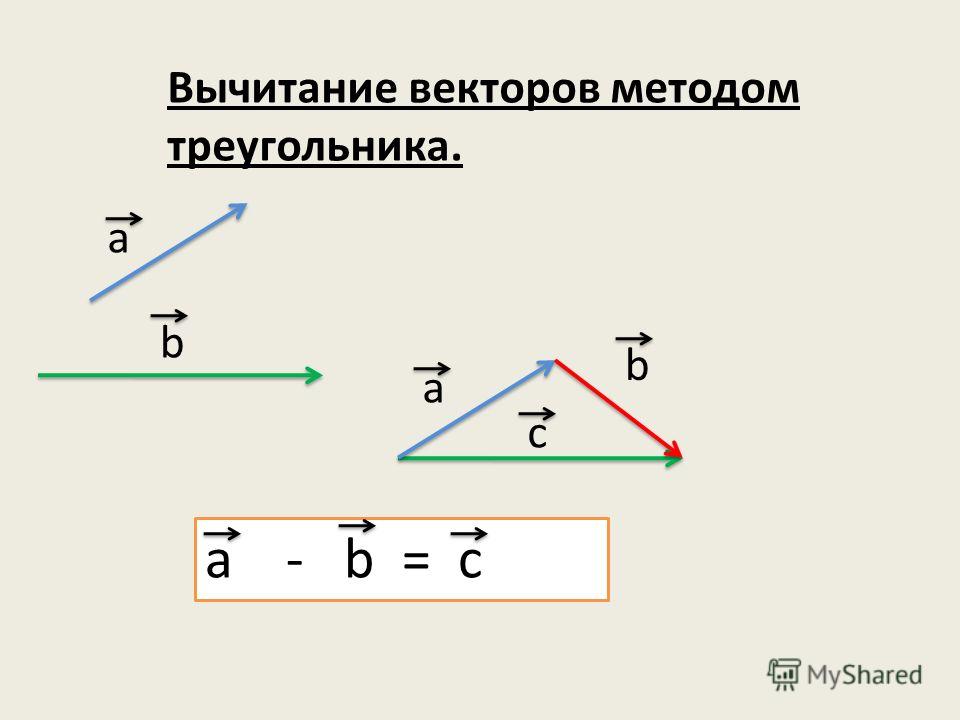 Этот закон называют переместительным законом: от перемены мест
слагаемых сумма не меняется.
Этот закон называют переместительным законом: от перемены мест
слагаемых сумма не меняется.
И ещё один закон. . Этот закон называют сочетательным законом.
По очереди докажем каждый из них.
Рассмотрим переместительный закон для неколлинеарных векторов и .
Доказательство.
Итак, от произвольной точки А отложим вектор , и вектор .
На этих векторах построим параллелограмм ABCD.
А теперь, пользуясь правилом треугольника сложения двух векторов, заметим, что , то есть равен сумме векторов .
,
С дугой стороны, ,
Отсюда можем сделать вывод, что сумма векторов равна сумме векторов .
Что и требовалось доказать.
Теперь перейдём к доказательству сочетательного закона для трёх неколлинеарных векторов , , .
От
произвольной точки А отложим Вектор ,
равный вектору . От точки B отложим вектор ,
равный вектору .
А от точки C отложим вектор ,
равный вектору .
От точки B отложим вектор ,
равный вектору .
А от точки C отложим вектор ,
равный вектору .
Рассмотрим левую часть равенства, выражающего сочетательный закон. Запишем вектора , , как .
В скобках записана сумма векторов . Пользуясь правилом треугольника, можем записать, что эта сумма равна вектору .
А сумма вектора и , в свою очередь, по правилу треугольника равна вектору .
Теперь аналогично поступим с правой частью равенства, задающего сочетательный закон.
По правилу треугольника .
Отсюда делаем вывод, .
Что и требовалось доказать.
Вернёмся к рисунку из доказательства переместительного закона.
Обратите внимание, если векторы , отложить от одной точки и построить на них параллелограмм, то диагональ этого параллелограмма задаёт вектор суммы векторов и .
Такое
правило сложения векторов называют правилом параллелограмма.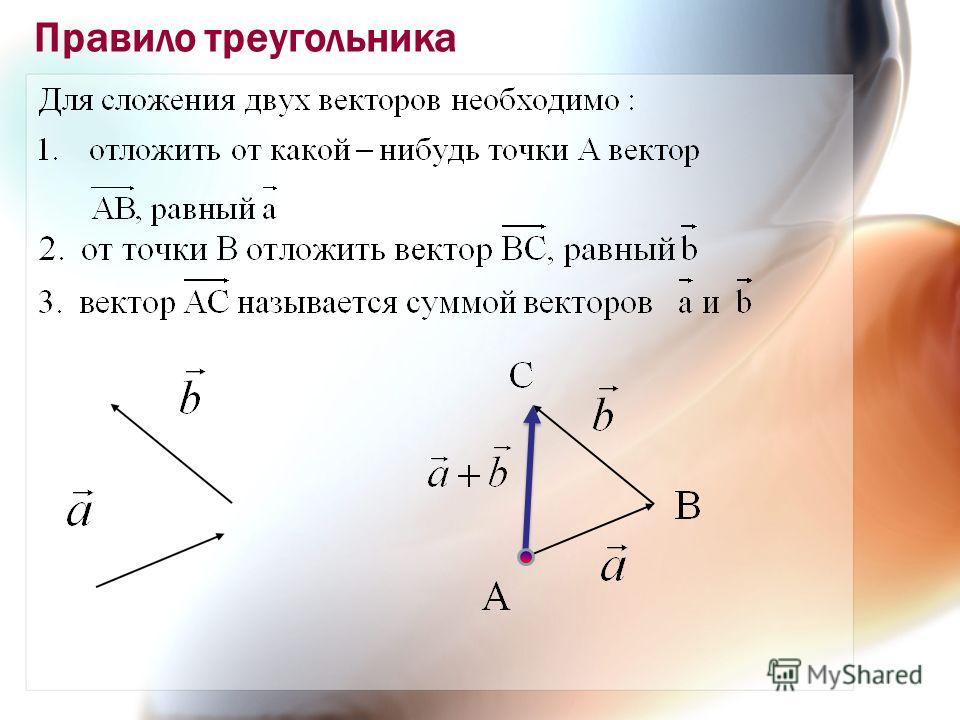
Изобразим вектор суммы для каждой пары векторов, пользуясь правилом параллелограмма.
Первым изобразим вектор суммы векторов и .
Отложим от произвольной точки А вектор , равный вектору .
Далее от точки А отложим вектор , равный вектору .
Теперь на этих векторах построим параллелограмм ABCD. Вектор является вектором суммы векторов и .
Далее изобразим вектор суммы векторов и .
Обратите внимание, что каждый раз вектор суммы берёт своё начала из точки начала обоих векторов-слагаемых.
Последним изобразим вектор суммы векторов и .
Задача. В треугольнике сторона равна , — , а .
Найти длину векторов и .
Решение.
Ответ: , .
Давайте
подведём итоги нашего урока.
Сегодня вы познакомились с законами сложения векторов. А именно с переместительным и сочетательным законами сложения векторов. А так же освоили правило параллелограмма для сложения двух векторов.
Оно заключается в следующем: чтобы сложить
неколлинеарные векторы и
,
нужно отложить от произвольной точки А векторы и
равные
векторам и
соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор
Предыдущий урок 4 Сумма двух векторов
Следующий урок 6 Сумма нескольких векторов
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Урок 2.
 сумма двух векторов. правило треугольника. законы сложения векторов. правило параллелограмма. сумма нескольких векторов — Геометрия — 9 класс
сумма двух векторов. правило треугольника. законы сложения векторов. правило параллелограмма. сумма нескольких векторов — Геометрия — 9 классВыберите правильный ответ.
Какой вектор является результатом суммы векторов ?
Выберите правильный ответ.
На каком изображении вектор , равен сумме векторов ?
Выберите правильный ответ.
Упростите: .
Выберите правильный ответ.
Равенство называется…
правилом параллелограмма | |
правилом треугольника | |
переместительным законом | |
сочетательным законом |
Впишите правильный ответ.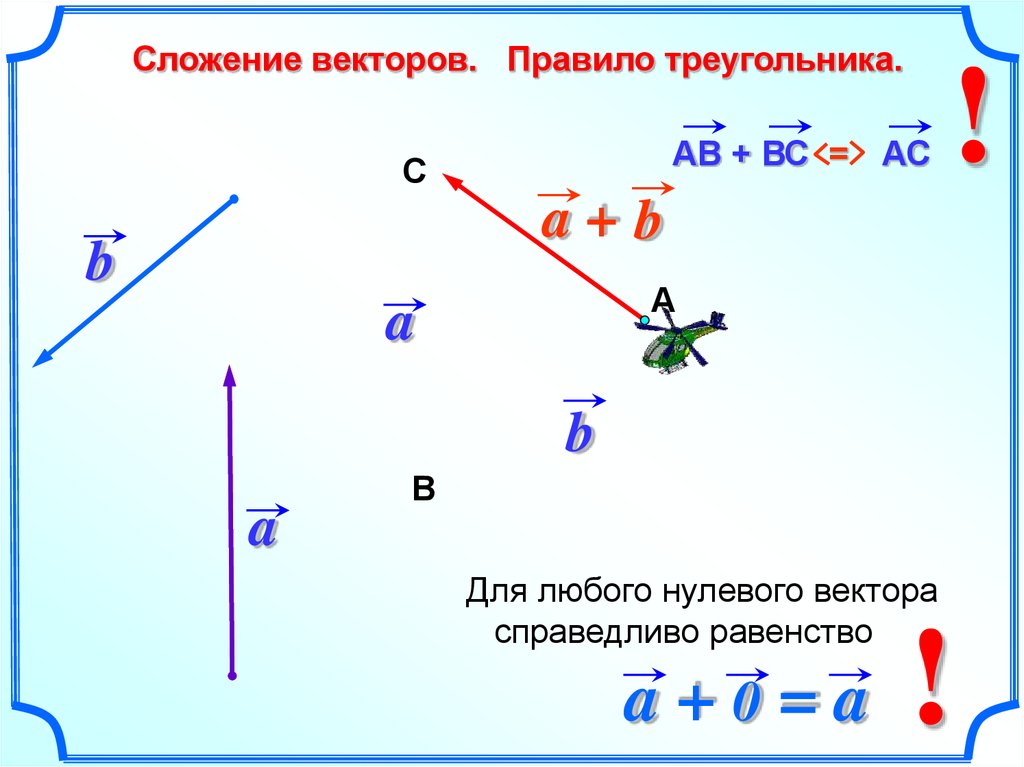
АВСD – равнобедренная трапеция, АВ = СD = 4, ∠D = 60°, АD = 11. Найдите .
Ответ: .
Выберите правильный ответ.
АВСD – ромб, АВ = 26, BD = 20. Найдите .
48 | |
12 | |
46 | |
24 |
Впишите правильный ответ.
В прямоугольном треугольнике АВС (∠C = 90°) проведена медиана CH, AB = 26. Найдите .
Ответ: .
Выберите правильный ответ.
Сколько различных целых значений может принимать длина вектора , если , ,
а ?
8 | |
4 | |
2 | |
5 |
Сбросить ответы Сохранить и перейти к следующему Проверить
Назад Вперёд
Сообщить об ошибке в уроке
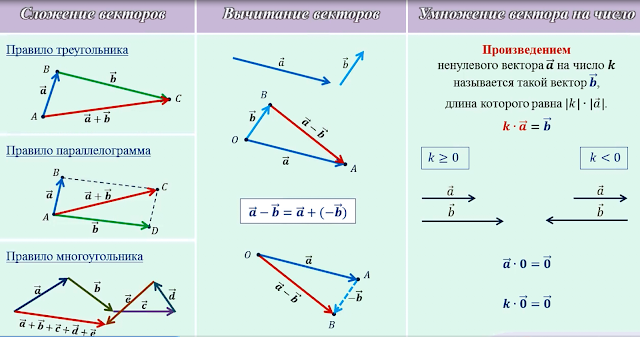
Сложение векторов.
 Как найти сумму векторов
Как найти сумму векторовОткладывание вектора от данной точки
Для того, чтобы ввести сумму векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Определение 1
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
Теорема 1
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
Вектор $\overrightarrow{a}$ — нулевой.
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow{KK}$.
Вектор $\overrightarrow{a}$ — ненулевой.
Обозначим точкой $A$ начало вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$.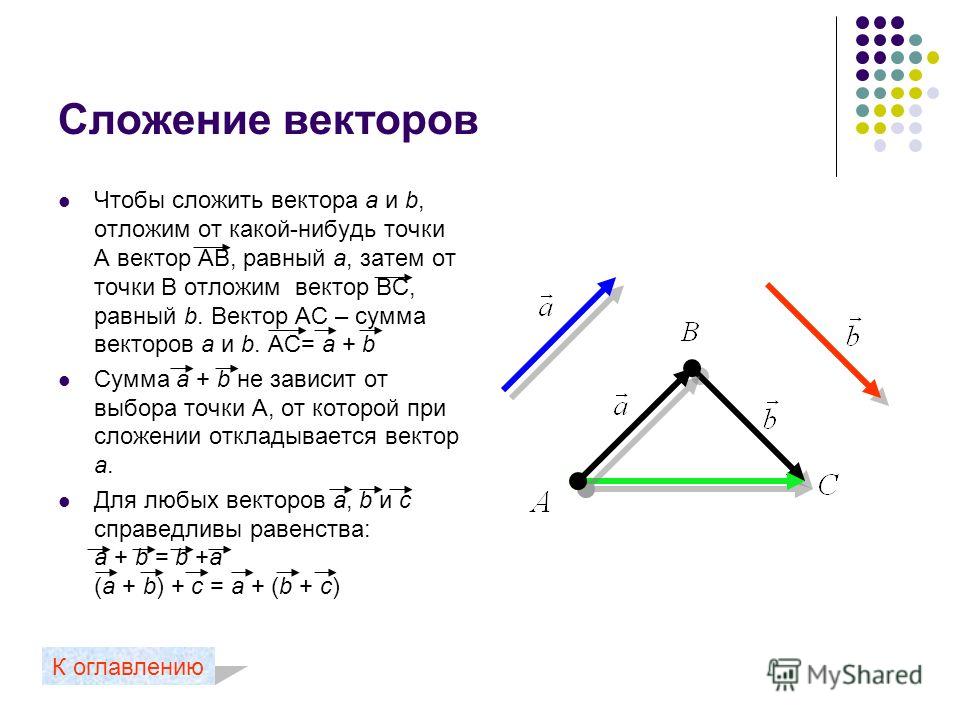 Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Сложение векторов. Правило треугольника
Пусть нам даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Определение 2
Суммой векторов $\overrightarrow{a}+\overrightarrow{b}$ называется вектор $\overrightarrow{c}=\overrightarrow{AC}$, построенный следующим образом: От произвольной точки $A$ отклабывается вектор $\overrightarrow{AB}=\overrightarrow{a}$, затем от полученной точки $B$ откладывается вектор $\overrightarrow{BC}=\overrightarrow{b}$ и соединяют точку $A$ c точкой $C$ (рис.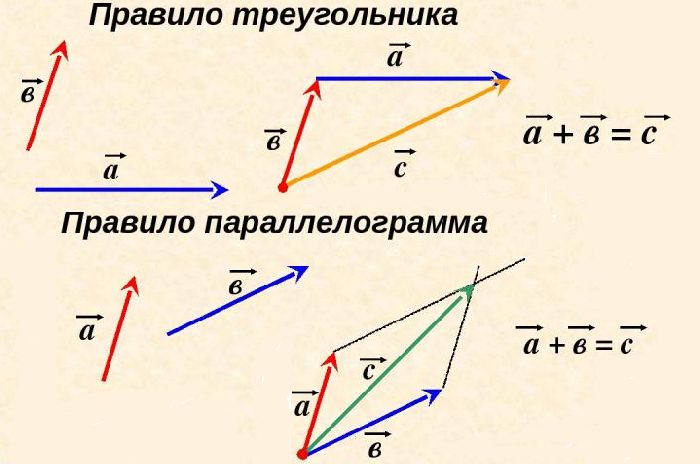 3).
3).
Рисунок 3. Сумма векторов
Замечание 1
Иначе, определение 2, еще называют правилом треугольника для сложения двух векторов.
Из этого правила следует несколько свойств сложения двух векторов:
Для любого вектора $\overrightarrow{a}$ выполняется равенство
\[\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\]Для любых произвольных точек $A,\ B\ и\ C$ выполняется равенство
\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]
Замечание 2
Аналогично правилу треугольника можно строить сумму любого количества векторов. Такое правило сложения называется правилом многоугольника.
Правило параллелограмма
Помимо правила треугольника для сложения двух векторов, есть еще правило параллелограмма для сложения двух векторов. Сформулируем и докажем для начала следующую теорему.
Теорема 2
Для любых треух векторов $\overrightarrow{a},\ \overrightarrow{b}\ и\ \overrightarrow{c}$ справедливы следующие два закона:
- Переместительный закон:
\[\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\]
- Сочетательный закон:
\[\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)\]
Доказательство.
Переместительный закон:
Пусть векторы $\overrightarrow{a}\ и\ \overrightarrow{b}$ не коллинеарны.
Возьмем произвольную точку $A$ и построим от нее (на одном рисунке) суммы $\overrightarrow{a}+\overrightarrow{b}\ и\ \overrightarrow{b}+\overrightarrow{a}$. Получим следующий рисунок (рис 4).
Рисунок 4. Иллюстрация переместительного закона
Очевидно, что $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, а $\overrightarrow{b}+\overrightarrow{a}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$
Следовательно, $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}$.
Пусть векторы $\overrightarrow{a}\ и\ \overrightarrow{b}$ коллинеарны.
Тогда выполнение переместительно закона будет очевидно вытекать из равенства длин $\left|\overrightarrow{a}+\overrightarrow{b}\right|и\ |\overrightarrow{b}+\overrightarrow{a}|$.

Сочетательный закон:
Построим следующий рисунок: Отложим от произвольной точки $A$ вектор $\overrightarrow{AB}=\overrightarrow{a}$, от полученной точки $B$ — вектор $\overrightarrow{BC}=\overrightarrow{b}$ и от точки $C$ — вектор $\overrightarrow{CD}=\overrightarrow{c}$ (Рис. 5).
Рисунок 5. Иллюстрация сочетательного закона
Из свойства правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
Следовательно, $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$.
Теорема доказана.
Из этой теоремы мы теперь можем выделить правило параллелограмма для суммы двух неколлинеарных векторов: чтобы сложить два неколлинеарных вектора $\overrightarrow{a}$ и $\overrightarrow{b}$, нужно отложить от произвольной точки $A$ векторы $\overrightarrow{AB}=\overrightarrow{a}$ и $\overrightarrow{AD}=\overrightarrow{b}$ и построить параллелограмм $ABCD$. Тогда $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AC}$.
Тогда $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AC}$.
Пример задачи на сложение векторов
Пример 1
Дан четырехугольник $ABCD$. Доказать, что $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AD}$
Рисунок 6.
Доказательство.
Воспользуемся свойством правила треугольника $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:
\[\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}\]
ч. т. д.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Линейная алгебра. Вектора, матрицы, определители, миноры, детерминанты… / / Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор. Поделиться:
 Введите свой запрос: Введите свой запрос: | |||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||
Сложение векторов — свойства, правила и примеры решения задач » Kupuk.net
Отрезок, который имеет направление, называется вектором. По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.
По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.
Общие сведения
Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.
Обозначают отрезок помощью заглавных латинских букв, сверху которых ставится чёрточка. Рисуют же его с помощью прямой ограниченной линии.
Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.
В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.
Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.
Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:
- коллинеарными — отрезки лежат на одной линии или ей параллельны;
- соноправленными — замкнутые линии направление которых одинаковое;
- противоположными — вектора направлены в разные стороны;
- ортогональными — перпендикулярными друг другу;
- компланарными — лежащими на одной плоскости или ей параллельные;
- равными — ограниченными прямыми, совпадающими как по направлению, так и по величине.
Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.
Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.
Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.
Сложение координат
Существует простое правило применимое для направленных отрезков и позволяющее найти их сумму. Заключается оно в следующем: если необходимо прибавить один вектор к другому описывающийся каждый своими координатами, достаточно сложить соответствующие их орты. Например, предположим есть два вектора a и b.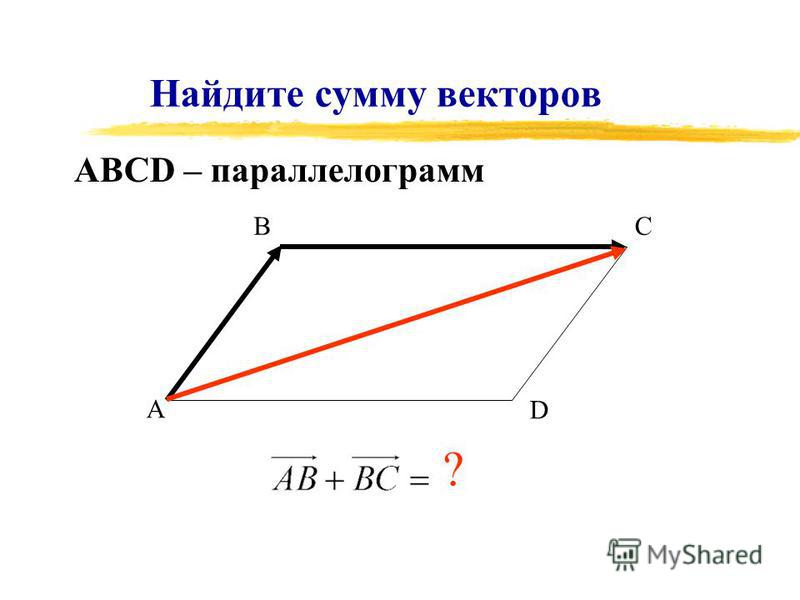 Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).
Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).
Это теорема доказывается просто. Пусть даны отрезки f (x 1; y 1) и g (x 2; y 2). В системе координат относительно рассматриваемых векторов получится: f = x 1 a + y 1 b; g = x 2 a + y 2 b. Тогда искомая сумма будет: f + g = x1a + y1b + x2a + y2b = a (x 1 + x 2) + b (y 1 + y 2). Что и нужно было доказать. Это правило применимо к векторам имеющим любые координаты. Например, пусть есть a (1; 2), b (-3; 1). Нужно найти их сумму. С помощью формулы сложения получится новый направленный отрезок с координатами a + b = (1 — 3; 2 + 1) = (-2; 3).
Как и при операциях с простыми числами при работе с векторными выражениями используют различные их свойства. Существует три правила сложения векторов:

Приведённые свойства соответственно называют переместительным, сочетательным, нулевым законом. Например, предположим есть два направленных отрезка a (2; 2) и b (-4; 1). Согласно первому свойству, очерёдность значения не имеет, поэтому что при прибавлении b к a, что при a к b результат будет одинаковый: a + b = (2 -4; 2 + 1) = (-2; 3), b + a = (-4 + 2; 1 +2) = (-2; 3). По аналогии можно проверить правильность утверждения и двух оставшихся свойств.
Следует отметить, что при сложении двух противоположных ограниченных прямых сумма будет равняться нуль-вектору: a + (-a) = 0. Это утверждение не требует доказательства, так как здесь используется фундаментальный закон алгебры — правило знаков.
Правило параллелограмма
По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.
Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.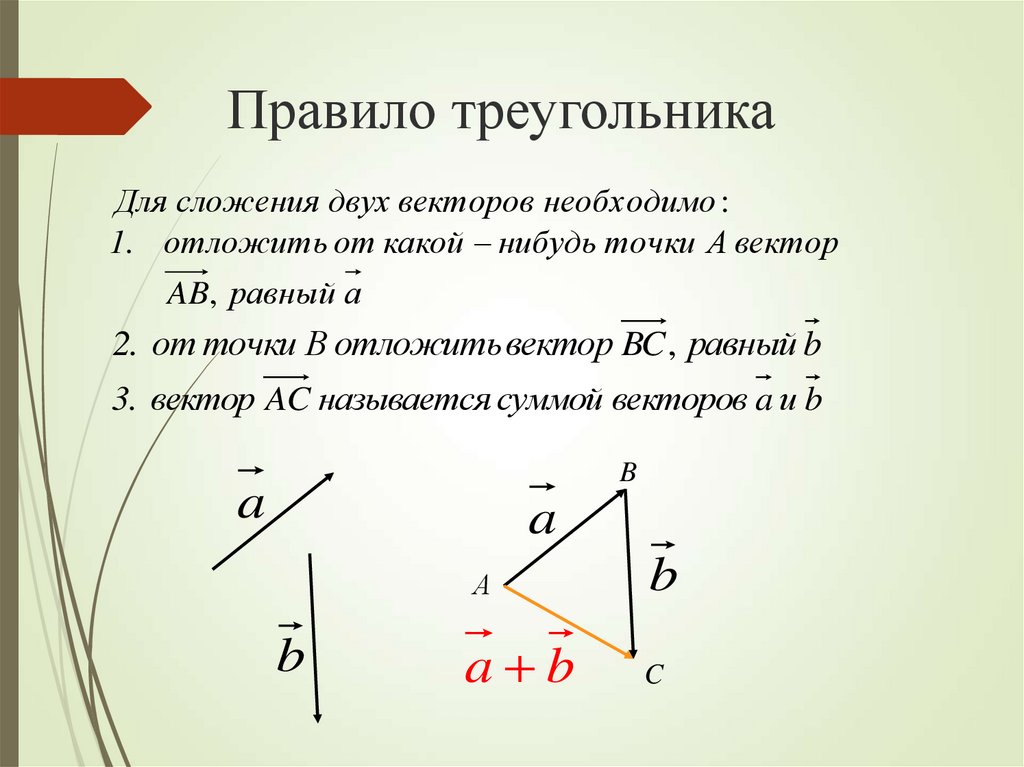
Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.
Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.
Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.
Простыми словами это правило можно рассказать так: сумма двух отрезков будет равняться диагонали параллелограмма, построенного на исходных векторах. Эта теорема чаще используется не в геометрии, а физике, например, при сложении сил.
Альтернативные методы
Операцию по сложению двух векторов можно выполнить и с помощью правила треугольника. Делается это так. Выбирается любая точка на плоскости, от которой откладываются два вектора. При этом необходимо соблюдать их размерность и наклон по отношению друг к другу. Затем две конечные точки соединяют прямой. Её длина и будет искомой величиной. То есть в итоге должна получиться равнобедренная фигура.
Применение метода сложения векторов по правилу треугольника позволяет довольно легко находить сумму для трёх и более отрезков. Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.
Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.
При сложении нескольких векторов удобно выполнять следующую последовательность построений:
- от выбранной точки пространства рисуется вектор, равняющийся первому слагаемому;
- от конечной точки откладывается вектор, совпадающий со вторым слагаемым;
- приведённая последовательность потеряется необходимое число раз;
- прямой линией соединяется точка, с которой началось построение с конечной последнего вектора;
- длина полученного отрезка и будет являться результатом сложения.
Этот способ получил название метод многоугольника. Он довольно часто применяется на практике, позволяя, довольно просто выполнить нахождение суммы. Из правила треугольника, а, следовательно, и многоугольника, вытекает следствие, которое подтверждает, что если складывается отрезок с нулевым векторным выражением, то в ответе получится длина, совпадающая со значимым слагаемым.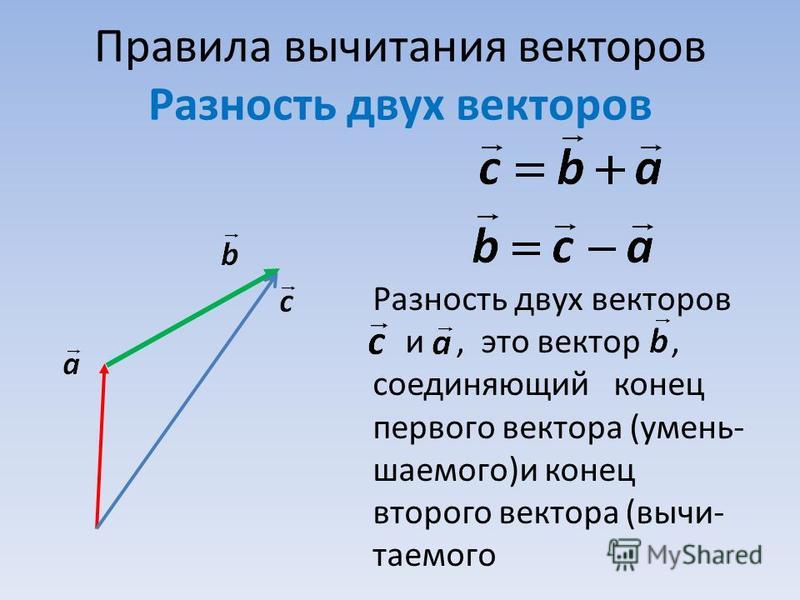
Следует отметить, что методы используются только, если направление отрезков является сонаправленным.
Если же отрезки неколлинеарные, то от конца одного откладывается другой. Тогда искомая сумма будет равняться длине линии, первой точкой которой будет начало одной векторной прямой, а конец совпадать с точкой, завершающей другую. То есть сумма — это отрезок, начало которого совпадает с началом обеих линий, а длина равна разности их длин, при этом направление его будет совпадать с тем что больше по длине.
Сложение векторов — Формула, Законы, Сумма
Сложение векторов означает объединение двух или более векторов. При добавлении векторов мы добавляем два или более векторов, используя операцию сложения, чтобы получить новый вектор, равный сумме векторов. Сложение векторов находит свое применение в физических величинах, где векторы используются для представления скорости, смещения и ускорения.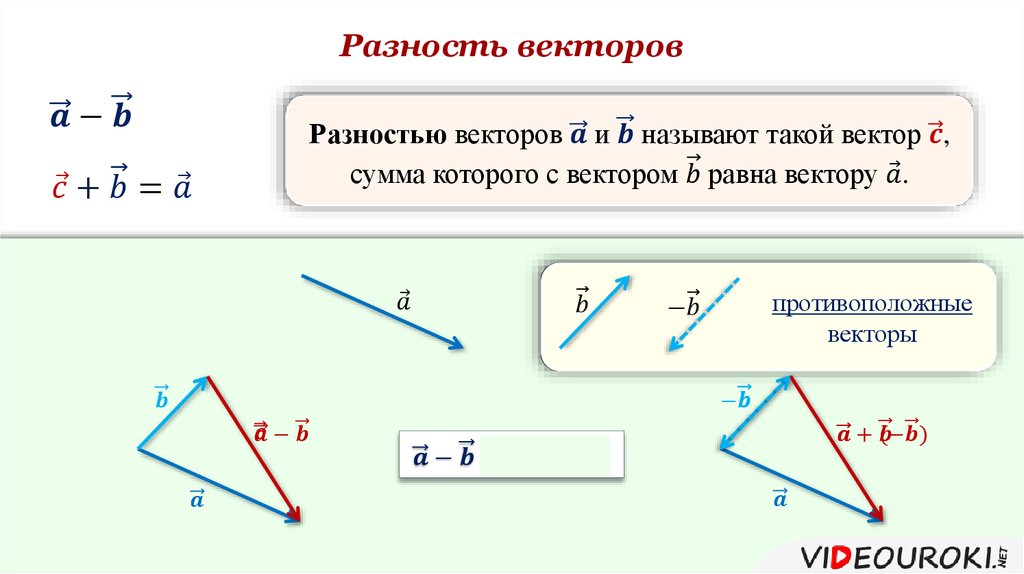
В этой статье давайте узнаем о сложении векторов, их свойствах и различных законах с решенными примерами.
| 1. | Что такое векторное сложение |
| 2. | Свойства векторного сложения |
| 3. | Добавление векторов графически |
| 4. | Законы сложения векторов |
| 5. | Треугольный закон сложения векторов |
| 6. | Параллелограммный закон сложения векторов |
| 7. | Формулы сложения векторов |
| 8. | Часто задаваемые вопросы о добавлении векторов |
Что такое сложение векторов?
Векторы представляются комбинацией направления и величины и записываются с помощью алфавита и стрелки над ними (или) с помощью алфавита, выделенного жирным шрифтом. Два вектора, a и b можно сложить вместе, используя векторное сложение , и результирующий вектор можно записать как: a + b .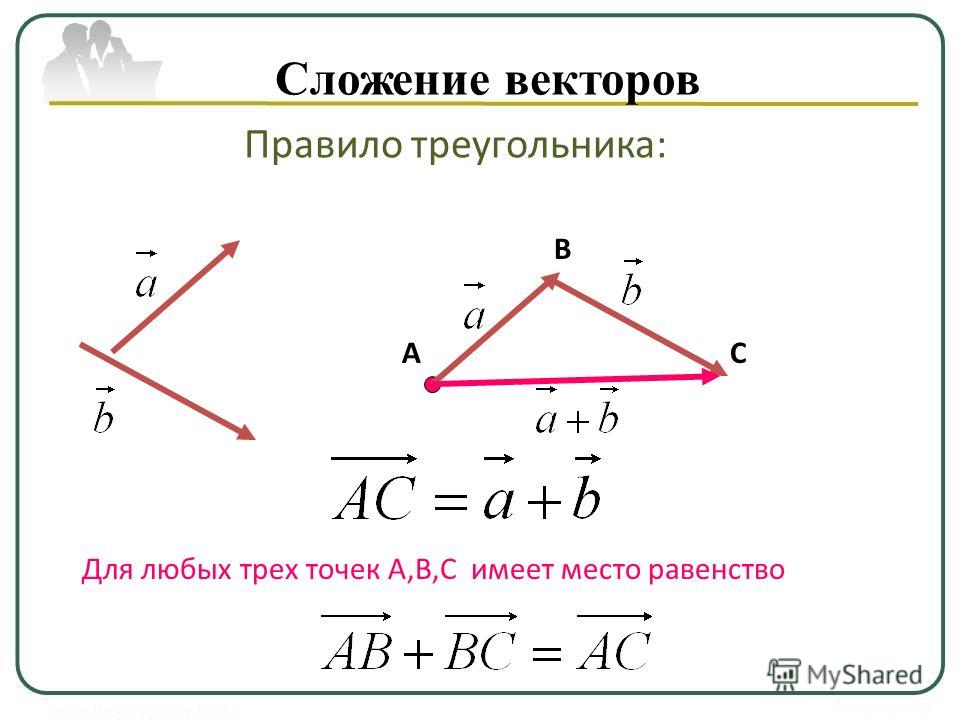 Прежде чем узнать о свойствах добавления векторов, нам нужно знать об условиях, которые необходимо соблюдать при добавлении векторов. Условия следующие:
Прежде чем узнать о свойствах добавления векторов, нам нужно знать об условиях, которые необходимо соблюдать при добавлении векторов. Условия следующие:
- Векторы можно добавлять, только если они имеют одинаковую природу. Например, к ускорению нужно добавить только ускорение, а не массу 9.0076
- Мы не можем складывать векторы и скаляры вместе
Рассмотрим два вектора C и D . Где, C = C x i + C y j + C z k и D = D x i + D y j + Dzk. Тогда результирующий вектор (или векторная сумма) R = C + D = (C x + D x )i + (C y + D y )j + (C z + С z ) к
Свойства векторного сложения
Векторное сложение отличается от алгебраического сложения. Вот некоторые из важных свойств, которые следует учитывать при сложении векторов:
| Свойство сложения векторов | Пояснение |
|---|---|
| Наличие личности | Для любого вектора v , v + 0 = v Здесь вектор 0 является аддитивной идентичностью. |
| Наличие обратного | Для любого вектора v , v + — v = 0 , и, таким образом, для каждого вектора существует аддитивный обратный. |
| Коммутативность | Сложение коммутативно; для любых двух произвольных векторов c и d , в + д = д + в |
| Ассоциативность | Сложение ассоциативно; для любых трех произвольных векторов i , j и k , i + j + k = i + j + k , т. е. порядок добавления не имеет значения. |
Добавление векторов графически
Добавление векторов возможно графическими и математическими методами. Эти методы следующие:
Эти методы следующие:
- Сложение векторов с использованием компонентов
- Треугольный закон сложения векторов
- Закон параллелограмма сложения векторов
Сложение векторов с использованием компонентов
Векторы, представленные в декартовых координатах, могут быть разложены на вертикальные и горизонтальные компоненты. Например, вектор A под углом Φ, как показано на изображении ниже, может быть разложен на его вертикальную и горизонтальную составляющие следующим образом:
, представляет компонент вектора A по горизонтальной оси (ось x) и
Мы можем заметить, что три вектора образуют прямоугольный треугольник и что вектор A может быть выражен как: величина и угол данного вектора, мы можем определить компоненты вектора.
A x = A cos Φ
A y = A sin Φ
Для двух векторов, если известны их горизонтальная и вертикальная составляющие, можно вычислить результирующий вектор. Например, если заданы значения A x и A y , то мы сможем вычислить угол и модуль вектора A следующим образом:
| А | = √ (( A x ) 2 +( A Y ) 2 )
, а угол можно найти в виде:
φ = TAN-1 ( A Y / A a Y / A x y / A x y / A a y / A a y / A a Y / A )
Отсюда можно сделать вывод, что:
- Если компоненты вектора заданы, то можно определить результирующий вектор
- Точно так же мы можем определить компоненты вектора, используя приведенные выше уравнения, если вектор предоставлен
Точно так же мы можем выполнять сложение векторов, используя их компоненты, если эти векторы выражены упорядоченными парами, т. е. векторами-столбцами. Например, рассмотрим два вектора P и Q .
е. векторами-столбцами. Например, рассмотрим два вектора P и Q .
P = (P 1 , P 2 )
Q = (Q 1 , Q 2 )
. два вектора P и Q , путем сложения соответствующих компонентов x и y этих двух векторов.
M = P + Q
M = (p 1 +q 1 , p 90 7 8 q 8098).
Это можно явно выразить как:
M x = p 1 + q 1
M y = p 2 0 2 90 88 + q 9.
Формула величины для нахождения величины результирующего вектора М это: | М | = √ ((M x ) 2 + (M y ) 2 )
Законы сложения векторов
Существует два закона сложения векторов (как упоминалось в предыдущем разделе).
- Закон треугольника
- Закон параллелограмма
Используя эти два закона, мы собираемся доказать, что сумма двух векторов получается путем присоединения их головы к хвосту, а сумма векторов определяется вектором, соединяющим свободный хвост и свободную голову. Давайте подробно изучим каждый из этих законов в следующих разделах.
Треугольный закон сложения векторов
Знаменитый закон треугольника можно использовать для сложения векторов, и этот метод также называется методом головы к хвосту. По этому закону два вектора можно сложить, поместив их вместе таким образом, чтобы голова первого вектора соединилась с хвостом второго вектора. Таким образом, соединяя хвост первого вектора с головой второго вектора, мы можем получить результирующую векторную сумму. Сложение векторов по закону треугольника может быть выполнено со следующими шагами:
- Сначала два вектора M и N размещаются вместе таким образом, что начало вектора M соединяется с хвостом вектора N .

- Затем, чтобы найти сумму, рисуется результирующий вектор S таким образом, чтобы он соединял хвост M с головой N .
- Таким образом, математически сумма или результирующий вектор S на приведенном ниже изображении может быть выражена как С = М + Н .
Таким образом, когда два вектора M и N складываются по закону треугольника, мы можем видеть, что треугольник образован двумя исходными векторами M и N и вектором суммы С .
Закон параллелограмма сложения векторов
Другим законом, который можно использовать для сложения векторов, является закон параллелограмма сложения векторов. Возьмем два вектора p и q , как показано ниже. Они образуют две смежные стороны параллелограмма по своей величине и направлению. Сумма p + q представлена по величине и направлению диагональю параллелограмма, проходящей через их общую точку. Это закон параллелограмма сложения векторов.
Сумма p + q представлена по величине и направлению диагональю параллелограмма, проходящей через их общую точку. Это закон параллелограмма сложения векторов.
На приведенном выше рисунке, используя закон Треугольника, мы можем заключить следующее:
OP + PR = ИЛИ
OP + OQ = ИЛИ , так как PR = OQ
Следовательно, мы можем заключить, что треугольные законы сложения векторов и параллелограммный закон сложения векторов эквивалентны друг другу.
Формулы сложения векторов
Мы используем одну из следующих формул для сложения двух векторов a = 1 , a 2 , a 3 > и b = 1 , б 2 , б 3 >.
- Если векторы в компонентной форме, то их сумма равна a + b = 1 + b 1 , a 2 + b 2 8 , a 2 + b 2 8 , a 3 >.

- Если два вектора расположены путем присоединения головы одного вектора к хвосту другого, то их сумма будет вектором, соединяющим свободную голову и свободный хвост (по закону треугольника).
- Если два вектора представляют две смежные стороны параллелограмма, то сумма представляет собой диагональный вектор, проведенный из точки пересечения обоих векторов (по закону параллелограмма).
Важные примечания по сложению векторов
Вот несколько моментов, которые следует помнить при изучении сложения векторов:
- Векторы представлены в виде комбинации направления и величины и нарисованы стрелкой. представление.
- Если компоненты вектора заданы, то мы можем определить результирующий вектор
- Знаменитый закон треугольника можно использовать для сложения векторов, и этот метод также называется методом «голова к хвосту»
☛ Статьи по теме:
Ознакомьтесь со следующими страницами, посвященными добавлению векторов:
- Калькулятор добавления векторов
- Калькулятор угла между двумя векторами
- Неравенство треугольников в векторах
- Вычитание двух векторов
Часто задаваемые вопросы о добавлении векторов
Что такое сложение векторов?
Добавление векторов означает объединение двух или более векторов. При добавлении векторов мы добавляем два или более векторов, используя операцию сложения, чтобы получить новый вектор, равный сумме двух или более векторов. Два вектора, , и 9.0063 b , можно сложить вместе, используя сложение векторов, и результирующий вектор можно записать как: a + b .
При добавлении векторов мы добавляем два или более векторов, используя операцию сложения, чтобы получить новый вектор, равный сумме двух или более векторов. Два вектора, , и 9.0063 b , можно сложить вместе, используя сложение векторов, и результирующий вектор можно записать как: a + b .
Пример: Даны два вектора, a = (2, 5) и b = (4, -2), сумма этих двух векторов равна (6,3)
Какова формула сложения векторов?
Это формула сложения векторов: Даны два вектора a = (a 1 , a 2 ) и b = (b 1 , b 2 ), тогда вектор сумма, M = (a 1 + b 1 , a 2 + b 2 ) = (M x , M y ). В этом случае
- величина результирующей векторной суммы M = | М | = √ ((M x ) 2 +(M y ) 2 ) и
- угол можно вычислить как θ = tan -1 (M y / M x )
Что такое правило сложения векторов?
Это правила, которым необходимо следовать при добавлении векторов. Условия правил следующие:
Условия правил следующие:
- Векторы можно добавлять, только если они имеют одинаковую природу. Например, к ускорению нужно добавлять только ускорение, а не массу .
- Мы не можем складывать векторы и скаляры вместе
Что такое формула параллелограмма закона сложения векторов?
Согласно закону параллелограмма сложения векторов, для двух заданных векторов u и v , заключающих в себе угол θ, модуль суммы, | и + v |, определяется как √( u 2 + v 2 +2 uv cos(θ)).
Является ли сложение векторов коммутативным?
Да, сложение векторов коммутативно; для любых двух произвольных векторов c и d , c + d = d + c .
В чем разница между законом сложения векторов треугольника и законом сложения векторов параллелограмма?
Для любых двух заданных векторов, согласно закону сложения векторов треугольника, третья сторона треугольника станет результирующим вектором суммы. Принимая во внимание, что согласно закону сложения векторов параллелограмма диагональ становится результирующим вектором суммы.
Принимая во внимание, что согласно закону сложения векторов параллелограмма диагональ становится результирующим вектором суммы.
Что такое ассоциативное свойство сложения векторов?
Сложение ассоциативное; для любых трех произвольных векторов a , b и c , a + b + c = a + b + c. , т. е. порядок добавления не имеет значения.
Что такое треугольный закон сложения векторов?
Закон треугольника сложения векторов гласит, что два вектора можно сложить, поместив их вместе таким образом, чтобы голова первого вектора соединилась с хвостом второго вектора. Таким образом, соединяя хвост первого вектора с головой второго вектора, мы можем получить результирующий вектор суммы.
Сложение векторов
С векторами и над ними можно выполнять различные математические операции. Одной из таких операций является сложение векторов. Два вектора могут быть сложены вместе, чтобы определить результат (или результирующую). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомним в нашем обсуждении законов движения Ньютона, что результирующая сила , воздействующая на объект, была определена путем вычисления векторной суммы всех отдельных сил, действующих на этот объект. То есть результирующая сила была результатом (или равнодействующей) сложения всех векторов сил. В течение этого модуля правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Два вектора могут быть сложены вместе, чтобы определить результат (или результирующую). Этот процесс добавления двух или более векторов уже обсуждался в предыдущем разделе. Вспомним в нашем обсуждении законов движения Ньютона, что результирующая сила , воздействующая на объект, была определена путем вычисления векторной суммы всех отдельных сил, действующих на этот объект. То есть результирующая сила была результатом (или равнодействующей) сложения всех векторов сил. В течение этого модуля правила суммирования векторов (например, векторов силы) оставались относительно простыми. Обратите внимание на следующие суммы двух векторов силы:
Эти правила суммирования векторов были применены к диаграммам свободного тела, чтобы определить результирующую силу (т. е. векторную сумму всех отдельных сил). Примеры приложений показаны на диаграмме ниже.
В этом разделе задача суммирования векторов будет распространена на более сложные случаи, когда векторы направлены в направлениях, отличных от чисто вертикального и горизонтального направлений. Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Например, вектор, направленный вверх и вправо, будет добавлен к вектору, направленному вверх и влево. векторная сумма будет определена для более сложных случаев, показанных на диаграммах ниже.
Существует множество методов определения величины и направления результата сложения двух или более векторов. Два метода, которые будут обсуждаться в этом уроке и использоваться на протяжении всего раздела:
- теорема Пифагора и тригонометрические методы
- метод «голова к хвосту» с использованием масштабированной векторной диаграммы
Теорема Пифагора
Теорема Пифагора — полезный метод для определения результата сложения двух (и только двух) векторов , образующих прямой угол друг с другом. Этот метод неприменим для добавления более двух векторов или для добавления векторов, которые равны , а не под углом 90 градусов друг к другу. Теорема Пифагора — это математическое уравнение, связывающее длину сторон прямоугольного треугольника с длиной гипотенузы прямоугольного треугольника.
Теорема Пифагора — это математическое уравнение, связывающее длину сторон прямоугольного треугольника с длиной гипотенузы прямоугольного треугольника.
Чтобы увидеть, как работает метод, рассмотрим следующую задачу:
Эрик покидает базовый лагерь и проходит 11 км на север, а затем 11 км на восток. Определите результирующее перемещение Эрика.
В этой задаче требуется определить результат сложения двух векторов смещения, расположенных под прямым углом друг к другу. Результатом (или равнодействующей) прохождения 11 км на север и 11 км на восток является вектор, направленный на северо-восток, как показано на диаграмме справа. Поскольку смещение на север и смещение на восток находятся под прямым углом друг к другу, теорему Пифагора можно использовать для определения равнодействующей (то есть гипотенузы прямоугольного треугольника).
Результат сложения 11 км, север плюс 11 км, восток — вектор с величиной 15,6 км. Позже будет рассмотрен метод определения направления вектора.
Позже будет рассмотрен метод определения направления вектора.
Давайте проверим ваше понимание с помощью следующих двух практических задач. В каждом случае используйте теорему Пифагора, чтобы определить величину векторной суммы . Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
Использование тригонометрии для определения направления вектора
Большинство студентов помнят значение полезной мнемоники SOH CAH TOA из курса тригонометрии. SOH CAH TOA — это мнемоника, которая помогает запомнить значение трех общих тригонометрических функций — функций синуса, косинуса и тангенса. Эти три функции связывают острый угол прямоугольного треугольника с отношением длин двух сторон прямоугольного треугольника. функция синуса связывает меру острого угла с отношением длины стороны, противоположной углу, к длине гипотенузы. Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Тангенс-функция связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, прилегающей к углу. Три приведенных ниже уравнения суммируют эти три функции в форме уравнения.
Функция косинуса связывает меру острого угла с отношением длины стороны, прилегающей к углу, к длине гипотенузы. Тангенс-функция связывает меру угла с отношением длины стороны, противоположной углу, к длине стороны, прилегающей к углу. Три приведенных ниже уравнения суммируют эти три функции в форме уравнения.
Эти три тригонометрические функции можно применить к задаче путешественника, чтобы определить направление общего перемещения путешественника. Процесс начинается с выбора одного из двух углов (кроме прямого угла) треугольника. После того, как угол выбран, можно использовать любую из трех функций для определения меры угла. Напишите функцию и выполните соответствующие алгебраические шаги, чтобы найти меру угла. Работа представлена ниже.
Как только мера угла определена, можно найти направление вектора. В этом случае вектор образует угол 45 градусов с востоком. Таким образом, направление этого вектора записывается как 45 градусов. (Напомним, что ранее в этом уроке направление вектора — это угол поворота против часовой стрелки, на который вектор поворачивается строго на восток.)
(Напомним, что ранее в этом уроке направление вектора — это угол поворота против часовой стрелки, на который вектор поворачивается строго на восток.)
Вычисленный угол не всегда является направлением
Мерой угла, определенной с помощью SOH CAH TOA, является , а не всегда направление вектора. Следующая диаграмма сложения векторов является примером такой ситуации. Обратите внимание, что угол внутри треугольника определяется как 26,6 градусов с помощью SOH CAH TOA. Этот угол представляет собой южный угол поворота, который вектор R делает по отношению к западу. Тем не менее, направление вектора, выраженное с помощью соглашения CCW (против часовой стрелки с востока), составляет 206,6 градуса.
Проверьте свое понимание двух векторов практики использования SOH CAH, пытаясь определить направление использования SOH CAH. В каждом случае используйте SOH CAH TOA, чтобы определить направление равнодействующей. Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
В каждом случае используйте SOH CAH TOA, чтобы определить направление равнодействующей. Когда закончите, нажмите кнопку, чтобы просмотреть ответ.
В приведенных выше задачах величина и направление суммы двух векторов определяется с помощью теоремы Пифагора и тригонометрических методов (SOH CAH TOA). Процедура ограничена добавлением двух векторов, образующих прямые углы друг к другу . Когда два вектора, которые должны быть сложены, не образуют прямых углов друг к другу или когда нужно сложить более двух векторов, мы будем использовать метод, известный как метод сложения векторов «голова к хвосту». Этот метод описан ниже.
Использование векторных диаграмм в масштабе для определения результата
Величина и направление суммы двух или более векторов также могут быть определены с помощью точно нарисованной векторной диаграммы в масштабе. Используя масштабированную диаграмму, метод головы к хвосту используется для определения векторной суммы или результирующей. Обычная лаборатория по физике включает обходов векторов . Либо используя сантиметровые смещения на карте, либо метровые смещения на большой открытой местности, учащийся делает несколько последовательных перемещений, начиная с обозначенной начальной позиции. Предположим, вам дали карту вашего района и набор из 18 направлений, которым нужно следовать. Начиная с исходная база , эти 18 векторов смещения могут быть последовательно сложены вместе для определения результата сложения набора из 18 направлений. Возможно, первый вектор измеряется в 5 см на восток. Там, где заканчивалось это измерение, начиналось следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда заканчивалось одно измерение, начиналось следующее измерение. По сути, вы будете использовать метод сложения векторов «голова к хвосту».
Обычная лаборатория по физике включает обходов векторов . Либо используя сантиметровые смещения на карте, либо метровые смещения на большой открытой местности, учащийся делает несколько последовательных перемещений, начиная с обозначенной начальной позиции. Предположим, вам дали карту вашего района и набор из 18 направлений, которым нужно следовать. Начиная с исходная база , эти 18 векторов смещения могут быть последовательно сложены вместе для определения результата сложения набора из 18 направлений. Возможно, первый вектор измеряется в 5 см на восток. Там, где заканчивалось это измерение, начиналось следующее измерение. Процесс будет повторяться для всех 18 направлений. Каждый раз, когда заканчивалось одно измерение, начиналось следующее измерение. По сути, вы будете использовать метод сложения векторов «голова к хвосту».
Метод «голова к хвосту» включает в себя рисование вектора в масштабе на листе бумаги, начиная с заданной начальной позиции. Там, где заканчивается голова этого первого вектора, начинается хвост второго вектора (таким образом, метод «голова к хвосту» ). Процесс повторяется для всех добавляемых векторов. После того, как все векторы были сложены «голова к хвосту», результирующий результат рисуется от хвоста первого вектора к началу последнего вектора; то есть от начала до конца. После того, как результирующая нарисована, ее длину можно измерить и преобразовать в реальных единиц при использовании данного масштаба. Направление равнодействующей можно определить с помощью транспортира и измерения его угла поворота против часовой стрелки с востока.
Там, где заканчивается голова этого первого вектора, начинается хвост второго вектора (таким образом, метод «голова к хвосту» ). Процесс повторяется для всех добавляемых векторов. После того, как все векторы были сложены «голова к хвосту», результирующий результат рисуется от хвоста первого вектора к началу последнего вектора; то есть от начала до конца. После того, как результирующая нарисована, ее длину можно измерить и преобразовать в реальных единиц при использовании данного масштаба. Направление равнодействующей можно определить с помощью транспортира и измерения его угла поворота против часовой стрелки с востока.
Ниже приведен пошаговый метод применения прямого метода для определения суммы двух или более векторов.
- Выберите масштаб и укажите его на листе бумаги. Наилучший выбор масштаба — тот, при котором диаграмма будет как можно большего размера, но при этом уместится на листе бумаги.
- Выберите начальную точку и нарисуйте первый вектор в масштабе в указанном направлении.
 Обозначьте величину и направление масштаба на диаграмме (например, МАСШТАБ: 1 см = 20 м).
Обозначьте величину и направление масштаба на диаграмме (например, МАСШТАБ: 1 см = 20 м). - Начиная с того места, где заканчивается голова первого вектора, нарисуйте второй вектор в масштабе в указанном направлении. Обозначьте на диаграмме величину и направление этого вектора.
- Повторите шаги 2 и 3 для всех векторов, которые нужно добавить
- Нарисуйте результат от конца первого вектора до начала последнего вектора. Пометьте этот вектор как Resultant или просто R .
- С помощью линейки измерьте длину равнодействующей и определите ее величину, переведя в действительные единицы по шкале (4,4 см x 20 м/1 см = 88 м).
- Измерьте направление равнодействующей, используя правило против часовой стрелки, рассмотренное ранее в этом уроке.
Пример использования прямого метода показан ниже. Задача состоит в сложении трех векторов:
 + 15 м, 210 град.
+ 15 м, 210 град.Метод «голова к хвосту» используется, как описано выше, и определяется результат (обозначен красным). Его величина и направление обозначены на диаграмме.
Интересно, что порядок, в котором складываются три вектора, не влияет ни на величину, ни на направление равнодействующей. Результирующая по-прежнему будет иметь ту же величину и направление. Например, рассмотрим сложение тех же трех векторов в другом порядке.
При суммировании в другом порядке эти три вектора по-прежнему дают результирующую с той же величиной и направлением, что и раньше (20 м, 312 градусов). ). Порядок, в котором векторы добавляются методом «голова к хвосту», не имеет значения.
Дополнительные примеры сложения векторов с использованием метода «голова к хвосту» приведены на отдельной веб-странице.
Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей интерактивной игры Name That Vector Interactive, нашей интерактивной игры с добавлением векторов или нашей интерактивной игры на угадывание вектора. Все три интерактива можно найти в разделе Physics Interactive на нашем веб-сайте, и они обеспечивают интерактивный опыт с возможностью добавления векторов.
Посетите: Назовите этот вектор | Добавление вектора | Игра «Угадай вектор»
Следующий раздел:
Перейти к следующему уроку:
Сложение векторов – объяснение и примеры
Как и скалярное сложение, сложение векторов включает в себя объединение двух или более векторов. В частности, когда вы добавляете векторы, вы:
В частности, когда вы добавляете векторы, вы:
«Сложение двух или более векторов с использованием операции сложения для получения нового вектора, равного сумме двух или более векторов».
В этом разделе мы обсудим сложение векторов со следующих аспектов:
- Что такое сложение векторов?
- Как складывать векторы графически
- Как складывать два вектора
Что такое сложение векторов?
Два вектора, A и B , могут быть сложены вместе с помощью сложения векторов, и результирующий вектор может быть записан как:
R = A + B
Как добавить векторы графически
При использовании сложения векторов мы должны учитывать оба компонента вектора, а именно направление и величину.
Имейте в виду, что два вектора с одинаковыми величиной и направлением могут быть сложены как скаляры.
В этом разделе мы рассмотрим графические и математические методы сложения векторов, в том числе:
- Сложение векторов с использованием правила «голова к хвосту»
- Сложение векторов с использованием метода параллелограмма
- Сложение векторов с использованием компонентов
Сложение векторов с использованием правила «голова к хвосту»
Сложение векторов может быть выполнено с использованием известного метода «голова к хвосту». Согласно этому правилу, два вектора можно сложить, поместив их вместе так, чтобы голова первого вектора соединилась с хвостом второго вектора. Результирующий вектор суммы может быть получен путем соединения хвоста первого вектора с головой второго вектора. Иногда его также называют треугольным методом сложения векторов.
Сложение векторов по правилу «голова к хвосту» показано на рисунке ниже. Два вектора P и Q складываются методом «голова к хвосту», и мы можем видеть треугольник, образованный двумя исходными векторами и вектором суммы.
Сначала два вектора P и Q размещаются вместе так, что начало вектора P соединяется с хвостом вектора Q . Далее, чтобы найти сумму, результирующий вектор R нарисован так, что он соединяет хвост P с головкой Q .
Математически сумма или результирующий вектор R, на изображении ниже может быть выражена как: сложение векторов методом параллелограмма мы рассмотрим и поясним на рисунке ниже.
Сначала нарисуйте заданные векторы, A и B, , чтобы иметь ту же начальную точку, как показано на изображении ниже. Затем нарисуйте параллелограмм, используя копии данных векторов.
Во-вторых, нарисуйте копию вектора B с именем B’, , и поместите ее параллельно вектору B, чтобы соединился с началом первого вектора, A . Точно так же нарисуйте копию вектора A с именем A’, и поместите ее параллельно A так, чтобы ее хвост соединился с головой вектора 9.0063 B.
Точно так же нарисуйте копию вектора A с именем A’, и поместите ее параллельно A так, чтобы ее хвост соединился с головой вектора 9.0063 B.
Наконец, равнодействующая двух векторов, равная сумме векторов A и B , будет диагональю параллелограмма. Его можно нарисовать, соединив начальную точку двух векторов A и B с головками векторов A’ и B’ .
Таким образом, для сложения векторов методом параллелограмма требуется три шага:
Шаг 1. Поместите два вектора так, чтобы они имели общую начальную точку
Шаг 2: Нарисуйте и завершите параллелограмм, используя копии двух исходных векторов
Шаг 3: Тогда диагональ параллелограмма будет равна сумме двух векторов
Сложение векторов с использованием компонентов
Как мы Известно, что векторы, заданные в декартовых координатах, можно разложить на горизонтальную и вертикальную составляющие. Например, вектор P под углом Φ, как показано на изображении ниже, можно разложить на составляющие как:
Например, вектор P под углом Φ, как показано на изображении ниже, можно разложить на составляющие как:
P x , который представляет компонент вектора P по горизонтальной оси (ось x), и
P y , который представляет компонент вектора P по вертикали. ось (ось Y).
Можно видеть, что три вектора образуют прямоугольный треугольник и что вектор P может быть выражен как:0088
Математически компоненты вектора можно также вычислить, используя величину и угол данного вектора.
P x = P cos Φ
P y = P sin Φ
Более того, мы можем также определить результирующий вектор, если известны его горизонтальная и вертикальная компоненты. Например, если даны значения P x и P y , то мы можем вычислить модуль и угол вектора P следующим образом: 92
А угол можно найти как:
Φ = tan -1 (P y / P x )
Таким образом, в итоге мы можем определить результирующий вектор, если его компоненты заданы. В качестве альтернативы, если задан сам вектор, мы можем определить компоненты, используя приведенные выше уравнения.
В качестве альтернативы, если задан сам вектор, мы можем определить компоненты, используя приведенные выше уравнения.
Аналогично, если векторы представлены упорядоченными парами (векторы-столбцы), мы можем выполнить операцию сложения векторов, используя их компоненты. Например, рассмотрим два вектора M и N задаются как:
M = (m1, m2)
N = (n1, n2)
компоненты x и y. Это дает результирующий вектор S :
S = M + N
S = (m1+n1, m2+ n2).
Можно явно записать так:
Sx = m1 + n1
Sy = m2 + n2. 92
И угол можно вычислить как:
Φ = tan -1 (S y / S x ).
Как сложить два вектора
В этом разделе обсуждаются примеры сложения векторов и их пошаговые решения, чтобы попрактиковаться в использовании различных методов, описанных выше.
Примеры
Пример 1
Учитывая, что два вектора, A и B, как показано на изображении ниже, графически определяют их сумму, используя метод «голова к хвосту».
Решение
Первый шаг прямого метода заключается в размещении заданных векторов A и B таким образом, чтобы хвост вектора B соединился с вектором 9063, головка 6 вектора . A, , как показано на изображении ниже. Далее, чтобы найти их сумму, рисуем результирующий вектор R так, чтобы он соединял хвост вектора A с головой вектора B . Математически результирующая может быть выражена как: 9Пример 2 правило «голова к хвосту».
Раствор
AB + до н.э. = (3, 2) + (2, 2)
AB + BC = (3 + 2, 2 + 2)
до н. э. АВ + ВС = (5, 4).
э. АВ + ВС = (5, 4).
Или, как показано на изображении ниже, результирующий вектор можно записать как: 92
| АС | = √ 25 + 16
| АС | = 6,403 единицы (приблизительно).
Угол результирующего вектора AC можно найти следующим образом: )
Φ = tan -1 (4/5)
Φ = 38,66 градуса
Пример 3
Даны два вектора, S = 3 м, 0 Φ = 10 м,0063 T = 20м, Φ = 60 градусов, определить их сумму. Затем вычислите величину и угол результирующего вектора с помощью метода компонентов.
Решение
Пусть R — результирующий вектор, равный сумме заданных векторов, который может быть выражен как: , мы сначала посмотрим на составные части данных векторов. Горизонтальная составляющая S IS:
SX = S COS φ
SX = 10 COS 30
SX = 8,660 м (приблизительно)
Аналогично, для вертикального компонента:
9002 SY SIN φ
SIN φSY = 10 SIN 30
SY = 5 м
Далее мы рассчитываем компоненты вектора T:
TX = T COS φ
TY = T COS φ
TY = T0064 = t sin φ
, где,
TX = 20 COS 60
TX = 10M
TY = 20 SIN 60
TY = 17.320 (приблизительно
9006 Вычислите вектор SUM, добавив индивидуальные компоненты X и Y вектор S и T . Rx = 16,660 м 92
|Р| = 23,292 м (приблизительно)
φ = TAN -1 (RY/RX)
φ = TAN -1 (22,32/16,66)
φ = 53,26 градусов (приблизительно)
Таким вектор суммы:
R = 23,292 м, Φ = 53,26 градуса.
Пример 4
Путешественник идет P = 20 м прямо на запад, а затем Q = 10 м прямо на север. Определить, как далеко путешественник находится от начальной точки. Также укажите величину и угол результирующего вектора.
Определить, как далеко путешественник находится от начальной точки. Также укажите величину и угол результирующего вектора.
Решение
Сначала мы графически представляем заданные векторы смещения P и Q, а затем рисуем их результирующий вектор, используя правило «голова к хвосту», как показано на рисунке ниже. Из изображения видно, что путешественник преодолел расстояние, равное величине вектора R от начальной точки.
Теперь, чтобы математически вычислить результирующий вектор, мы используем следующие формулы:
R = P + 92
|Р| = 22,36 м (Приблизительно)
И угол можно вычислить как: исходная точка под углом 26,57 градусов к северо-западу.
Пример 5
Определите результирующий вектор суммы для двух векторов A = (-5, -1) и B = (2, -1).
Решение
Данные векторы уже находятся в компонентной форме, поэтому сначала определим их углы.
Для вектора A:
Φ = tan -1 (Ay/Ax)
Φ = tan -1 (-1/-5)
Φ1 = 11,3 градуса
Для вектора B:
Φ = tan -1 (By/Bx)
Φ = tan -1 (-1/2)
Φ = -26,5 градусов
Далее находим результирующий вектор, складывая отдельные компоненты:
S = A + B
Sx = Ax + Bx
Sx = -5 + 2
Sx = -3
Sy = Ay + By
Sy = -1 -1
Sy = -2
Результирующий вектор S может быть выражен как вектор-столбец:
-3-6 S 90,003 9006 .Наконец, величина и угол результирующего вектора: 92
|С| = 3,605 единиц (приблизительно)
Φ = тангенс -1 (Sy/Sx)
Φ = тангенс -1 (-2/-3)
Φ2 = 33,69 градуса, сумма 9003 градусов 9003 вектор:
S = 3,605 единицы, Φ = 33,69 градуса. Пример 6
Пример 6
| PR | = √ 17
| PR | = 4,123 единиц (приблизительно)
Угол результирующего вектора PR можно найти следующим образом:
φ = TAN -1 (1/4)
- Имея два вектора, V = (2, 5) и C = (3, -2), определите их сумму, используя правило «голова к хвосту». Кроме того, определите модуль и угол результирующего вектора, Р .
- Имея два вектора G = (5, 5) и H = (4, -10), определите их сумму, используя правило «голова-лет-решка». Кроме того, определите модуль и угол результирующего вектора P .
- Даны векторы OA, , где O = (-1, 3) и A = (5,2), и вектор UV, , где U = (1, -2) и V = (-2,2), определить результирующий вектор суммы S.
 Затем найти его модуль и угол.
Затем найти его модуль и угол. - Учитывая четырехугольник ABCD, определите следующее:
- DC + CA = ?
- BD + DC = ?
- AD + DC = ?
- M = 10 м на восток и N = 15 м на север. Определите сумму двух векторов, затем найдите модуль и угол результирующего вектора.
Ответы
- Результирующий вектор R равно R = (5, 3), величина R равна | Р | = 5,830 единиц, а угол Φ = 30,96 градуса.
- Результирующий вектор P равен P = (9, 5), величина P равна | Р | = 10,30 ед., а угол Φ = 29,05 градуса.
- Векторы OA = (6, -1) и UV = (-3, 4), результирующий вектор суммы S задается как S = (3, 3), величина S есть | С | = 4,242 единицы, а угол Φ = 45 градусов.

- In the given quadrilateral, the sum is computed as:
DC + CA = DA
BD + DC = BC
AD + DC = AC
- Результат двух векторов:
R = M + N
|R| = 18,027 м,
И угол можно вычислить как:
Φ = tan -1 (15/10)
Φ = 56,30 градуса.
Таким образом, результирующий вектор равен R = 18,027 м , Φ = 56,30 градусов на северо-восток.
Предыдущий урок | Главная страница | Следующий урокЗаконы сложения векторов. Процедура, условия и пример
Векторы относятся к объектам, которые могут иметь как направление, так и величину. Если найдутся два любых вектора, имеющих одинаковую величину и направление, то эти два вектора считаются одинаковыми. Это геометрические объекты, представленные линией и стрелкой. Эта стрелка указывает направление вектора, тогда как длина линии представляет величину вектора. Следовательно, эти стрелки имеют начальную точку и конечную точку. Векторы представляют физические величины, такие как скорость, смещение и ускорение.
Если найдутся два любых вектора, имеющих одинаковую величину и направление, то эти два вектора считаются одинаковыми. Это геометрические объекты, представленные линией и стрелкой. Эта стрелка указывает направление вектора, тогда как длина линии представляет величину вектора. Следовательно, эти стрелки имеют начальную точку и конечную точку. Векторы представляют физические величины, такие как скорость, смещение и ускорение.
Давайте рассмотрим закон сложения векторов pdf.
Вектор имеет величину (то есть размер) и направление. Длина линии или стрелки, приведенной выше, показывает ее величину, а наконечник указывает направление. Теперь мы можем добавить два вектора, просто соединив их «голова к хвосту». Для лучшего понимания обратитесь к приведенной ниже диаграмме. Кроме того, не имеет значения, в каком порядке складываются два вектора, мы все равно получим один и тот же результат.
(Изображение будет добавлено в ближайшее время)
Обозначение
Вектор часто может быть написан жирным шрифтом, как a или b.

Вектор можно также записать в виде букв хвоста и головы со стрелкой над ними, как показано справа.
В этой статье мы обсудим сложение векторов, закон сложения векторов треугольника, закон сложения векторов параллелограмма и закон сложения векторов pdf.
Что такое сложение двух векторов?
В общих чертах говорится, что вы можете сложить два вектора, и в результате получится вектор. Например, давайте рассмотрим
V=R 2 = {(a,b)|a,b∈R}
Тогда для вектора (v 1 )=(x 1 , y 1 ), (v 2 ) = (x 2 , Y 2 ).
Каковы свойства сложения векторов?
Добавление векторов удовлетворяет двум важным свойствам.
1. Коммутативный закон гласит, что порядок сложения не имеет значения, то есть: А+В равно В+А.
2. Ассоциативный закон гласит, что сумма трех векторов не зависит от того, какая пара векторов добавлена первой, то есть (A+B)+C=A+(B+C).
Треугольный закон сложения векторов
Давайте обсудим треугольный закон сложения векторов в законе сложения векторов pdf. Предположим, у нас есть два вектора, а именно A и B, как показано.
(Изображение будет добавлено в ближайшее время)
Теперь метод сложения этих двух векторов очень прост. Нам нужно просто поместить голову одного вектора над хвостом другого вектора, как показано на рисунке ниже.
(Изображение будет добавлено в ближайшее время)
Теперь, после этого, нам нужно соединить другие конечные точки обоих векторов вместе, как показано ниже,
(Изображение будет добавлено в ближайшее время)
Результирующая заданных векторов (A и B) задается вектором C, который представляет собой сумму векторов A и B, то есть C = A+B
Из закона сложения векторов pdf сложение векторов является коммутативным по своей природе, т. е.
е.
Если C=A+ Б; тогда мы можем написать C = B+A
Точно так же, если нам нужно вычесть оба вектора, используя закон треугольника, мы просто меняем направление любого вектора, а затем добавляем его к другому, как показано ниже.
(Изображение будет добавлено в ближайшее время)
Теперь мы можем математически представить это как C = AB (поскольку они в противоположных направлениях). Это закон треугольника сложения векторов.
Закон сложения векторов в виде параллелограмма
Математический закон сложения векторов, называемый законом сложения векторов в виде параллелограмма, обычно утверждает, что сумма квадратов длин четырех сторон параллелограмма равна сумме квадратов длины двух диагоналей параллелограмма. В евклидовой геометрии необходимо, чтобы параллелограмм имел равные противоположные стороны.
(Изображение будет добавлено в ближайшее время)
Если ABCD параллелограмм, то AB равен DC, а AD равен BC. Тогда в соответствии с определением закона параллелограмма это формулируется как
Тогда в соответствии с определением закона параллелограмма это формулируется как
2(AB) 2 + 2 (BC) 2 = (AC) 2 + (BD) 2
В случае , параллелограмм является прямоугольником, то закон можно сформулировать так:
2(AB) 2 + 2 (BC) 2 = (AC) 2
Это потому, что в прямоугольнике два диагонали имеют одинаковую длину. т. е. (AC=BD)
Закон сложения векторов в виде параллелограмма Процедура
Шаги для закона сложения векторов в виде параллелограмма приведены ниже:
Шаг 1) Нарисуйте вектор в подходящем масштабе в направлении вектора.
Шаг 2) На этом шаге вам нужно нарисовать второй вектор в том же масштабе из хвоста первого заданного вектора.
Шаг 3) Теперь вам нужно рассматривать эти векторы как смежные стороны, а затем завершить параллелограмм.
Шаг 4) Теперь образованная диагональ в основном представляет результирующий вектор как по величине, так и по направлению.
Каковы основные условия сложения векторов?
Существенным условием сложения двух векторов является то, что они должны иметь одинаковые размеры и одинаковые единицы измерения. Например, можно добавить вектор силы к другому вектору силы, когда они выражены в одних и тех же единицах, но нельзя добавить силу и скорость, так как они имеют разные размерности.
Например: Если у нас есть скорости 30 м/с и 50 м/с в заданных направлениях, мы можем легко сложить их, но мы не можем напрямую сложить скорости, скажем, 3 км/с и 500 м/с, если только обе скорости не будут преобразованы в одни и те же единицы.
Если два вектора принадлежат одному и тому же векторному пространству, они имеют одинаковую размерность, но также можно добавить два вектора с разными размерностями. Например, у нас есть вектор A=3i+4j и вектор B=8i+5j+9k, тогда мы также можем найти сумму, хотя они имеют разные размерности. Здесь мы должны рассмотреть A=3i+4j+0k. Сумма векторов A+B = 11i+9дж+9к. Проще говоря, мы можем сказать, что два вектора можно сложить тогда и только тогда, когда они имеют одинаковую единицу измерения.
Сумма векторов A+B = 11i+9дж+9к. Проще говоря, мы можем сказать, что два вектора можно сложить тогда и только тогда, когда они имеют одинаковую единицу измерения.
Где мы можем использовать концепцию сложения векторов?
Существует множество областей, в которых может использоваться концепция сложения векторов, например, различные области техники, такие как силы, магнитные поля, электрические поля, импульс, положение, траектории, угловой момент, поляризация, намагниченность, кинетическая плотность, крутящий момент, и скорости. Так как законы сложения векторов являются фундаментальными математическими законами, то они справедливы и приняты для всех векторов, в том числе и для векторных величин из областей физики, используемых в технике.
Решенные вопросы
1) Даны векторы A = 2i + 6j — 3k и B = 3i — 3j + 2k. Найдите А+В.
Анс. Сложим данные векторы,
A = 2i + 6j — 3k + B = 3i — 3j + 2k
= (2+3)i + (6-3)j + (-3+2)k
Следовательно , A+B = 5i+ 3j-1k
2) Предсказать сложение векторов PQ и QR, если PQ = (3, 2) и QR = (2, 6).
Анс. Согласно вопросу, PQ + QR = (3, 4) + (2, 6), что будет равно (3 + 2, 4 + 6). Следовательно, значение PQ + QR будет (5, 10).
3) Вычислить a + 2b — 3c, если векторы положения a, b и c заданы как A (3, 4), B (5, -6) и C (4, -1)?
Анс. Поскольку A, B и C являются векторами положения точек A (3, 4), B (5, -6) и C (4, -1), поэтому соответствующие векторы будут равны
a = 3i + 4j
b = 5i — 6j
c = 4i — j
Теперь подставьте эти значения a, b и c в a + 2b — 3c, чтобы вычислить его значение. При расчете это значение выйдет как i — 5j.
4) Вершины A, B и C треугольника ABC имеют векторы положения как a, b и c. Найдите значения векторов AB + BC + CA.
Ответ. В соответствии с вопросом, a, b и c представляют векторы положения вершин A, B и C, поэтому в этом случае
Вектор AB = b — a
Вектор BC = c — b
Вектор CA = a — c
Теперь, чтобы вычислить значение AB + BC + CA, подставьте вышеуказанные значения в данную формулу. При расчете значение AB + BC + CA будет равно 0.
При расчете значение AB + BC + CA будет равно 0.
Вопросы для самооценки и практики
Вот несколько вопросов, которые даны вам для практики и оценки вашего изучения концепций соответственно.
1) Чему будет равна сумма перемещений 15 км и 25 км, если между ними образуется угол 60 градусов?
2) Вычислить модуль вектора, полученного из двух векторов, заданных как (2, 3) и (2, -2). Также найдите угол между двумя векторами.
3) Если сторона BC треугольника ABC имеет середину D такую, что сумма векторов AB + AC равна вектору AD, то вычислить значение a.
4) Докажите, что сумма трех векторов, определенных с помощью медианы треугольника и направленных из вершин, равна нулю.
Сложение векторов — определение, метод сложения, формула, закон и часто задаваемые вопросы
Мы не можем сложить два вектора напрямую, как числа, чтобы получить результат, поскольку они имеют не только направление, но и величину. Добавление скалярной величины очень просто, но в случае векторов требуется другой процесс.
Добавление скалярной величины очень просто, но в случае векторов требуется другой процесс.
Чтобы понять разницу и лучше изучить ситуацию, предположим, что автомобиль движется на 10 миль на север, а затем на 10 миль на юг. Мы можем легко оценить общее расстояние, пройденное автомобилем, сложив эти два числа, например, 20 миль. Но в случае векторного сложения результат нулевой.
Причина в том, что северное и южное направления противоположны друг другу, поэтому они сокращаются, поэтому сумма векторов будет равна нулю. В этой статье представлен четкий вывод о сложении двух векторов, или, можно сказать, «сумма векторов».
Сумма двух векторов
Рассмотрим два вектора \[\underset{u}{\rightarrow} + \underset{v}{\rightarrow}\]. Мы собираемся добавить соответствующие компоненты. Напишем о компонентах векторов:
\[\underset{u}{\rightarrow} = (u_{1}, u_{2}) и \underset{v}{\rightarrow} = (v_{1}, v_{2})\]
Когда мы суммируем вышеуказанные векторы, результат будет:
\[\underset{u}{\rightarrow} + \underset{v}{\rightarrow} = (u_{1} + v_{1} , u_{2} + v_{2})\]
Суммирование двух векторов можно назвать равнодействующим.
Формула сложения векторов
Существует два типа методов сложения векторов:
Закон векторов треугольника
Закон векторов параллелограмма
Как сложить два вектора?
Вам все еще интересно, как добавлять векторы?
Вот несколько советов по сложению векторов:
Сложение векторов выполняется геометрически, а не алгебраически.
Векторные величины должны вести себя как независимые друг от друга величины до сложения.
Из сложения векторов мы заключаем только равнодействующую числа векторов, распространяющихся на теле.

Из сложения векторов получаем результирующий вектор, который не зависит от порядка суммирования векторов как \[\underset{A}{\rightarrow} + \underset{B}{\rightarrow} = \underset {B}{\rightarrow} + \underset{A}{\rightarrow}\]
Треугольный закон сложения векторов
Сложение векторов зависит от треугольников. Теперь нам нужно выяснить, как это работает.
Предположим, что \[\underset{a}{\rightarrow}~и~\underset{b}{\rightarrow}\] являются двумя векторами.
Здесь нужно провести линию АВ, которая называется хвостом с А и В с головой. Давайте нарисуем линию BC, которая выделяет B в качестве конца и C в качестве начала.
Завершим треугольник, нарисовав линию AC с концом A и вершиной C. Сумма двух векторов \[\underset{a}{\rightarrow}~и~\underset{b}{\rightarrow}\] представлена линией AC. 9{2} + 2ab cos \theta}\]
9{2} + 2ab cos \theta}\]
Здесь
Величина вектора \[\underset{a}{\rightarrow} = a\]
Величина вектора \[ \underset{b }{\rightarrow} = b\]
θ — это угол, покрываемый вектором \[\underset{a}{\rightarrow} и ~Vector~\underset{b}{\rightarrow}\].
Предположим, что равнодействующая векторов составляет угол \[\Phi\] с \[\underset{a}{\rightarrow}\], тогда выражение будет таким:
\[tan \ phi = \ frac {b sin \ theta} {a + b cos \ theta} = tan \ frac {\ theta} {2} \] 9{2} + 2AAcos \theta} = 2A cos \frac{\theta}{2} \]
Считаем, что равнодействующая векторов составляет угол ф с а; тогда выражение будет таким:
\[tan \phi = \frac{A sin\theta}{A + A cos\theta} = tan\frac{\theta}{2} \]
Тогда , \[\phi = \frac{\theta}{2} \]
Параллелограмм Закон сложения векторов
Мы также можем понять концепцию сложения векторов, используя закон параллелограмма.
Закон параллелограмма гласит, что «когда два вектора действуют одновременно в одном месте (обозначается обеими сторонами параллелограмма, проведенными из точки), то результат определяется диагональю этого параллелограмма с величиной и направлением, проходящим через ту же точку».
Чтобы облегчить понимание закона, рассмотрим два вектора \[\underset{P}{\rightarrow} и \underset{Q}{\rightarrow}\]
Эти векторы обозначены двумя соседними сторонами параллелограмма. Они указаны вдали от точки согласно рисунку, приведенному ниже. 9{-1}\frac{Q sin\theta}{P + Q cos\theta} \]
Вычитание векторов
Вычитание двух векторов очень похоже на сложение. Нам нужно предположить, что вектор a будет вычтен из вектора b.
\[\underset{a}{\rightarrow} — \underset{b}{\rightarrow}\], мы можем написать выражение следующим образом.
Можно также сказать, что это сложение \[\underset{a}{\rightarrow} и \underset{-b}{\rightarrow}\]. Вот почему мы можем применить ту же формулу для вычисления результирующего вектора. 9{2} — 2abcos\theta}\]
Определение, формула, правила и примеры
Возможно, мы этого не осознаем, но каждый день добавляем немного. Мы делаем это, когда идем в продуктовый магазин, чтобы купить что-то, мы делаем это, когда добавляем ингредиенты в еду во время приготовления пищи и даже когда играем с друзьями. Это часть нашей повседневной жизни, и ее также можно применять к более сложным вещам, таким как векторы.
В этой статье мы узнаем о векторах и различных способах добавления векторов.
Определение сложения векторов
Сложение векторов можно определить как процедуру сложения двух или более векторов.
Вектор, образованный сложением векторов, называется результирующим вектором и обычно обозначается как . Способ добавления этих векторов может различаться в зависимости от того, заданы ли они в виде точек или в геометрическом представлении. Хотя сложение можно выполнить с помощью математики для точек, практично использовать закон параллелограмма, когда они представлены геометрически.
Способ добавления этих векторов может различаться в зависимости от того, заданы ли они в виде точек или в геометрическом представлении. Хотя сложение можно выполнить с помощью математики для точек, практично использовать закон параллелограмма, когда они представлены геометрически.
Формула сложения векторов
Предположим, что A и B являются точками на плоскости с их координатами, заданными как и соответственно. Тогда формула сложения векторов для может быть записана как:
Свойства сложения векторов
Коммутативность: Изменение порядка векторов не меняет сумму.
Ассоциативность: Изменение группировки сложений не меняет сумму.
Нулевой элемент: Добавление точки с нулем равно точке. Если нулевой элемент , то
Аддитивная обратная: Если точка A , то ее обратная . Когда эти векторы складываются, в результате получается ноль.

Графическое сложение векторов
Как можно графически выполнить сложение векторов? Ниже приведены различные методы.
Треугольный закон векторного сложения
Закон треугольника — это закон сложения векторов. Он также известен как метод «голова к хвосту» , потому что головы и хвосты задействованных векторов помещаются друг на друга при попытке найти их сумму. На рисунке ниже показано, как выглядят голова и хвост вектора.
Показ головы и хвоста вектора
Посмотрим, как используется этот закон. Рассмотрим векторы A и B ниже.
Отображение двух векторов A и B
Чтобы сложить два вектора, используя метод «голова к хвосту», выполните следующие процедуры.
- Поместите конец второго вектора на начало первого вектора.
- Чтобы найти сумму, нарисуйте результирующий вектор, чтобы соединить хвост первого вектора с головой второго вектора.
Сложение двух векторов
На рисунке выше .
Если есть третий вектор, вы продолжаете размещать хвост третьего вектора на голове второго вектора. Результирующий вектор будет нарисован так, чтобы соединить хвост первого вектора с головой второго вектора.
Вектор можно перемещать вдоль своей плоскости до тех пор, пока длина/направление не меняются.
Закон сложения векторов в виде параллелограмма
Согласно закону параллелограмма, если два вектора можно представить как две смежные стороны, исходящие из общей вершины, а затем дополнить их так, как если бы они образовывали параллелограмм, то результирующий вектор можно найти из диагонали этого параллелограмма.
Чтобы найти:
Сложите хвосты векторов вместе
Завершите параллелограмм, нарисовав две параллельные стороны.
После завершения параллелограмма нарисуйте диагональ, начинающуюся с вершины исходных векторов, как показано на рисунке ниже.
Демонстрация сложения двух векторов
Закон параллелограмма также можно использовать, когда вам заданы векторы, определенные как координаты.
Для точек и сумму можно найти по закону параллелограмма, показанному на рис. 2.
Отображение суммы двух точек вектора
Вычитание вектора
Чтобы понять вычитание, нужно сначала понять, что такое отрицательное значение вектора. Допустим, есть вектор A. Отрицательное значение этого вектора определяется как -A. Отрицательный вектор вектора А имеет ту же величину, что и вектор А, однако они направлены в противоположные стороны.
Разность между вектором А и отрицательным значением вектора А
Закон параллелограмма для векторного вычитания
Чтобы найти , его следует рассматривать как . Имея это в виду, мы получим следующий рисунок:
Закон параллелограмма для вычитания векторов
Примеры сложения векторов
Давайте рассмотрим несколько примеров.
Если и — две векторные точки, какова сумма векторов?
Ответ.
Формула сложения векторов:
Полученные точки равны и
Из заданных точек:
Если подставить в формулу сложения векторов, то получится:
Если и — две векторные точки, найти сумму векторов.
Ответ.
Полученные точки:
Формула сложения векторов:
Из точек, которые мы имеем:
Применение формулы сложения векторов:
Возьмем другой пример.
Игрушечная машинка перемещается на 10 см на восток и на 24 см на север. Используя закон треугольника, найдите результирующий вектор двух векторов.
Ответ.
У нас есть два вектора величиной 10 см и 24 см. Назовем их A и B.
Направление на восток и направление на север. Таким образом, мы имеем:
Обратите внимание, что хвост второго вектора помещается на голову первого вектора, как и говорит закон. Чтобы найти результирующий вектор, мы завершим треугольник, нарисовав линию, соединяющую хвост первого вектора с головой второго вектора, а затем добавим обе величины.
Назовем результирующий вектор C.
Результирующий вектор:
Возьмем другой пример.
Рассмотрим векторы в восточном направлении, в северном направлении и в восточном направлении. Используя правило треугольника, найдите результирующий вектор.
Ответы.
Во-первых, нам нужно нарисовать векторы в соответствии с их направлениями. При этом имейте в виду, что хвост одного вектора должен располагаться над головой другого вектора.
Как видно из рисунка выше, хвост второго вектора помещается на начало первого вектора, а хвост третьего вектора — на начало второго вектора.
Результирующий вектор будет суммой величин всех векторов.
Чтобы найти результирующий вектор, была проведена линия, соединяющая хвост первого вектора с головой третьего вектора. результирующий вектор:
Используя рисунок выше, найдите векторы по закону параллелограмма.
Решение
- Чтобы найти , можно применить закон параллелограмма, как показано на рисунке.
 Диагональ параллелограмма представляет собой сумму векторов, как на рисунке ниже.
Диагональ параллелограмма представляет собой сумму векторов, как на рисунке ниже.
- Чтобы найти , сначала нужно инвертировать вектор B, а затем применить закон параллелограмма, как показано на рисунке ниже.
- Чтобы найти , сложение векторов можно выполнить с помощью закона параллелограмма, как показано на рисунке ниже.
- Чтобы найти , сначала нужно обратить вектор C, а затем применить закон параллелограмма, как показано на рисунке ниже.
Сложение векторов – ключевые выводы
- Сложение векторов можно определить как процедуру сложения двух или более векторов.
- Формула сложения векторов для заданных точек:
- Согласно закону параллелограмма, если два вектора можно представить как две смежные стороны, исходящие из общей вершины, а затем дополнить их так, как если бы они образовывали параллелограмм, то сумму можно найти из диагонали этого параллелограмма.


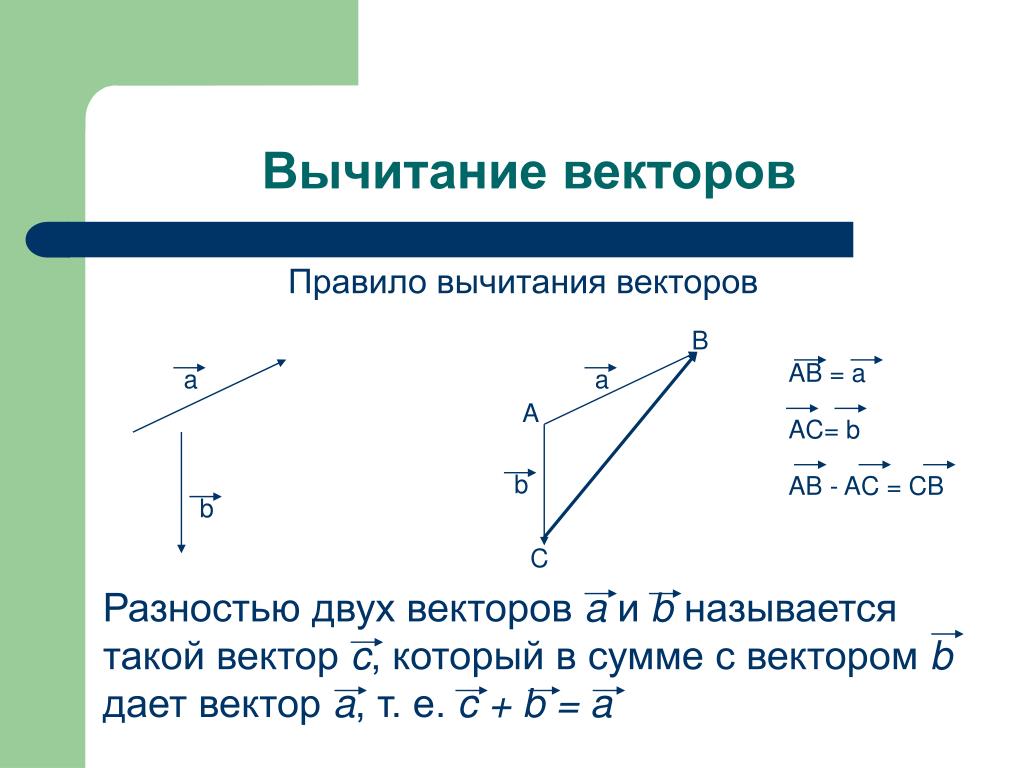

 д.
д.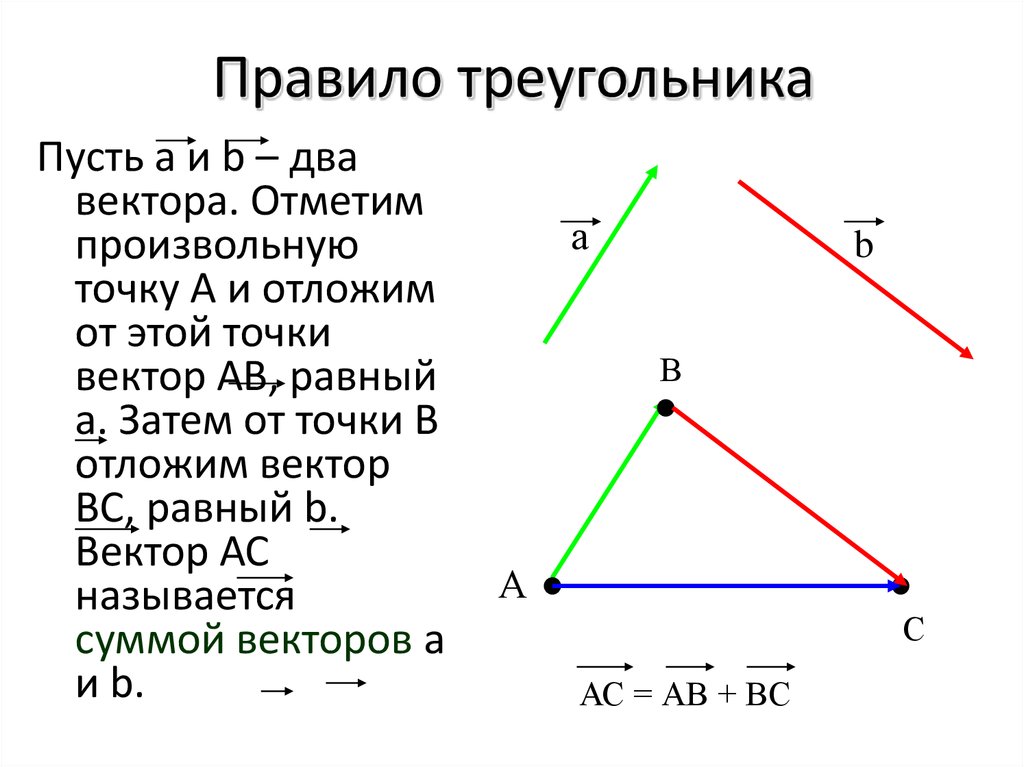 Сложение векторов по правилу параллелограмма.
Сложение векторов по правилу параллелограмма.