Решение матрицы 4 на 4: Как вычислить определитель матрицы 4х4

4 порядка матрицы

Вы искали 4 порядка матрицы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление определителей 4 порядка, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «4 порядка матрицы».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 4 порядка матрицы,вычисление определителей 4 порядка,вычисление определителя 4 порядка,вычисление определителя 4 порядка сведением его к определителю 2 порядка,вычисление определителя матрицы 4 порядка,вычисление определителя четвертого порядка,вычислите определитель 4 порядка,вычислите определитель четвертого порядка от треугольной матрицы,вычислить определитель 4 го порядка,вычислить определитель 4 порядка,вычислить определитель матрицы 4 на 4,вычислить определитель матрицы 4 порядка с решением,вычислить определитель матрицы четвертого порядка,вычислить определитель четвертого порядка,вычислить определитель четвертого порядка матрицы,как вычислить минор матрицы 4 порядка,как вычислить определитель 4 порядка,как вычислить определитель матрицы 4 на 4,как вычислить определитель матрицы 4 порядка,как вычислить определитель четвертого порядка,как вычислять определители 4 порядка,как искать определитель матрицы 4 порядка,как найти минор 4 порядка,как найти определитель 4 порядка,как найти определитель 4 порядка для чайников,как найти определитель матрицы 4 на 4,как найти определитель матрицы 4 порядка,как найти определитель матрицы четвертого порядка,как найти определитель четвертого порядка,как найти определитель четвертого порядка матрицы,как находить определитель 4 порядка,как находить определитель матрицы 4 порядка,как посчитать определитель 4 порядка,как посчитать определитель матрицы 4 на 4,как решать матрицу 4 порядка,как решать матрицы 4 на 4,как решать матрицы 4 порядка,как решать определители 4 порядка,как решать определители 4 порядка для чайников,как решать определитель 4 порядка,как решить матрицу 4 на 4,как решить определитель 4 порядка примеры,как решить определитель 4 порядка решить,как считать матрицу 4 на 4,как считать определители 4 порядка,как считать определитель 4 на 4,как считать определитель 4 порядка,как считать определитель матрицы 4 на 4,как считать определитель матрицы 4 порядка,матрица 4 порядка,матрица 4 порядка определитель,матрица 4 порядка примеры,матрица определитель 4 порядка,матрица четвертого порядка,матрицы 4 на 4 как решать,матрицы 4 порядка,матрицы 4 порядка как решать,матрицы 4 порядка решение,матрицы вычисление определителя 4 порядка,матрицы вычислить определитель четвертого порядка,матрицы определитель 4 на 4,матрицы определитель четвертого порядка,матрицы четвертого порядка,найти определитель 4 порядка,найти определитель матрицы 4 на 4,найти определитель матрицы 4 порядка,найти определитель четвертого порядка,нахождение определителя матрицы 4 порядка,определители 4 порядка,определители 4 порядка как вычислять,определители 4 порядка как решать,определители 4 порядка примеры,определители четвертого порядка,определители четвертого порядка примеры,определитель 4 го порядка примеры,определитель 4 на 4,определитель 4 на 4 как считать,определитель 4 порядка,определитель 4 порядка как найти,определитель 4 порядка как находить,определитель 4 порядка как решать,определитель 4 порядка как считать,определитель 4 порядка матрица,определитель 4 порядка найти,определитель 4 порядка примеры,определитель 4 порядка примеры решения,определитель матрица 4 порядка,определитель матрицы 4 порядка,определитель матрицы 4 порядка как считать,определитель матрицы четвертого порядка,определитель четвертого порядка,определитель четвертого порядка как вычислить,определитель четвертого порядка как найти,определитель четвертого порядка матрицы,определитель четвертого порядка найти,определитель четвертого порядка формула,решение матриц 4 порядка,решение матрица 4 на 4,решение матрицы 4 на 4,решение матрицы 4 порядка,решение определителей 4 порядка,решение определителя 4 порядка,треугольный определитель 4 порядка,формула определитель четвертого порядка.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 4 порядка матрицы. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычисление определителя 4 порядка).

Решить задачу 4 порядка матрицы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Вычисление определителей. Миноры, алгебраические дополнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

 

Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$

Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$

— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число

$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}.$$

Эту формулу называют «правило треугольника»: одно из трех слагаемых, входящих в правую часть со знаком «+», есть произведение элементов главной диагонали матрицы, каждое из двух других — произведение элементов лежащих на параллели к этой диагонали и элемента из противоположного угла матрицы, а слагаемые, входящие в со знаком минус, строятся таким же образом, но относительно второй (побочной) диагонали. 2+5x+4=0:$

$D=25-16=9$

$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$

Ответ: $x_1=-4;\,\,\, x_2=-1.$

 {jumi[*4]}

 

3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$

Решение.

$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$

$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$

Ответ: $0.$

 

3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$

 Решение.

 $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$

$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$

$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha).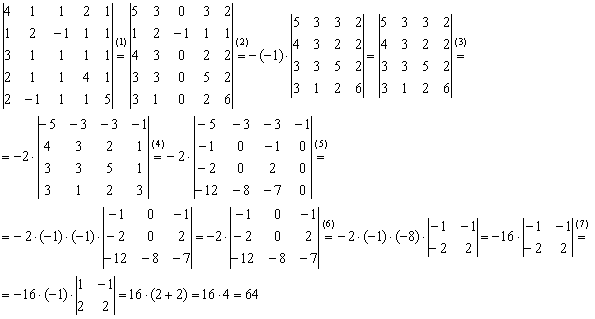 T=\det A.$

2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.

3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.

4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.

5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.

6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).

 

Примеры:

3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. $

Доказательство.

$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$

 $\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$ 

 

$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$ 

$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ 

$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. {3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$

$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$

$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$

$=8a+15b+12c-19d.$

Ответ: $8a+15b+12c-19d.$

   {jumi[*4]}

3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$

Решение.

 Вычислим этот определитель с помощью приведения определителя к треугольному виду:

$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два 

$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394. 2.$

 

Вычислить определители, используя подходящее разложение по строке или столбцу.

 

3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$

Ответ: $-14.$

 

3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$

Ответ: $4.$

 

3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$

Ответ: $2a-8b+c+5d.$

 

3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$

Ответ: $665.$

  {jumi[*4]}

Определитель матрицы: алгоритм, примеры вычисления, правила

Определение 1

Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.  

|А|, ∆, det A — символы, которыми обозначают определитель матрицы.

Способ вычисления определителя выбирают в зависимости от порядка матрицы.

Пример 1​​​​​

Определитель матрицы 2-го порядка вычисляют по формуле:

А=1-231.

Решение:

det A=1-231=1×1-3×(-2)=1+6=7

Определитель матрицы 3-го порядка: правило треугольника 

Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:

• правило треугольника;
• правило Саррюса.

Как найти определитель матрицы 3-го порядка по методу треугольника?

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 2

А=13402115-1

Решение:

det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

• дописать слева от определителя два первых столбца;
• перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
• перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32

Пример 3

А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:

• разложением по элементам строки;
• разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Пример 4

Разложение матрицы по элементам строки:

det A=ai1×Ai1+ai2×Ai2+…+аin×Аin

Разложение матрицы по элементам столбца:

det A=а1i×А1i+а2i×А2i+…+аni×Аni

Замечание

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

Пример 5

А=01-132100-24513210

Решение:

• раскладываем по 2-ой строке:

А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310

• раскладываем по 4-му столбцу:

А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321

Свойства определителя

Свойства определителя:

• если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
• если поменять местами строки и столбцы, то знак поменяется на противоположный;
• определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.

Пример 6

А=134021005

Решение:

det А=134021005=1×5×2=10

Замечание

Определитель матрицы, который содержит нулевой столбец, равняется нулю.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики.

Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Сложение и вычитание

Следующая статья

Ранг матрицы

• Равенство матриц
• Ранг матрицы
• Сложение и вычитание
• Умножение матриц
• Все темы по математике

• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе

Узнать подробнее

Компьютерная графика

Заказать такую же работу

Чертеж и D модель в компасе

• Вид работы:

  Чертёж

• Выполнена:

  26 мая 2022 г.

• Стоимость:

  5 200 руб

Заказать такую же работу

нужно сделать технологическую карту перекраски кузова синтетической эмалью

• Вид работы:

  Чертёж

• Выполнена:

  16 мая 2022 г.

• Стоимость:

  1 200 руб

Заказать такую же работу

Серверные технологии облачные вычисления и виртуализация

Заказать такую же работу

Процессы формообразования и инструменты

• Вид работы:

  Контрольная работа

• Выполнена:

  9 марта 2022 г.

• Стоимость:

  2 300 руб

Заказать такую же работу

по термодинамике

• Вид работы:

  Решение задач

• Выполнена:

  20 февраля 2022 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

Смотреть все работы по компьютерной графике

как считать по столбцу, как вычислить от треугольной матрицы

Определитель матрицы 4 порядка

Определение

Матрица представляет собой прямоугольную таблицу скаляров, то есть элементов некоторого поля, которая состоит из определенного числа столбцов и определенного числа строк.

Существует разные типы матриц. При рассмотрении данной темы важно уточнить понятия некоторых из них:

• в том случае, когда матрица обладает единственным элементом, она является совпадающей со своим единственным скаляром;
• квадратная матрица представляет собой такую матрицу, которая имеет равное число столбцов и строк.

Алгебраические действия с матрицами характеризуются определенным алгоритмом и порядком. Подобные операции отличаются от манипуляций с простыми числами. Кроме алгебраических действий, над матрицами выполняют и другие операции. К примеру, транспортирование матрицы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В задачах часто встречаются примеры нахождения определителя матриц разных порядков. Матрицы первого, второго, третьего, четвертого и других порядков относят к квадратным матрицам.

Определение

Определитель или детерминант матрицы является определенным числом, которое можно поставить в соответствие некой квадратной матрице.

В том случае, когда элементы матрицы имеют вид действительных чисел, то и определитель является действительным числом. Определитель обозначают detA или |A|. Определитель первого порядка соответствует скаляру рассматриваемой матрицы.

Определители второго и третьего порядка определяются в соответствии со стандартным алгоритмом, то есть с помощью известных формул. Для того чтобы вычислить определитель больше третьего порядка, требуется ознакомиться с понятием минора матрицы (М).

Определение

Минор матрицы третьего порядка является определителем второго порядка, который получен из заданной матрицы третьего порядка путем вычеркивания i-ой степени и j-го столбца.

Примечание

Изучая материалы по теме матричного определителя, можно встретить термин «детерминант». Фактически данные понятия идентичны. Однако детерминант обладает множеством значений в других научных областях, что объясняет использование его русского перевода в математике.

Свойства определителя:

• при перестановке местами двух строк или столбцов знак определителя меняется;
• при умножении строки или столбца на число, весь определить также умножится на число;
• в том случае, когда одну строку сколько угодно раз прибавляют или вычитают из другой, определитель не меняется;
• при наличии одинаковых, пропорциональных или заполненных нулями двух строк определителя весь определитель равен нулю;
• все перечисленные свойства справедливы в случае столбцов;
• транспортирование матрицы не сопровождается изменением определителя;
• определитель произведения матриц равен произведению определителей.

Геометрическое и алгебраическое определение и формула для нахождения

Формула для вычисления определителя четвертого порядка имеет вид:

\(\left| A\right|=a_{11}M_{11}-a_{12}M_{12}+a_{13}M_{13}-a_{14}M_{14}\)

Алгебраический смысл определителя заключается в том, что определитель матрицы А = (n*n) – является алгебраической суммой n слагаемых.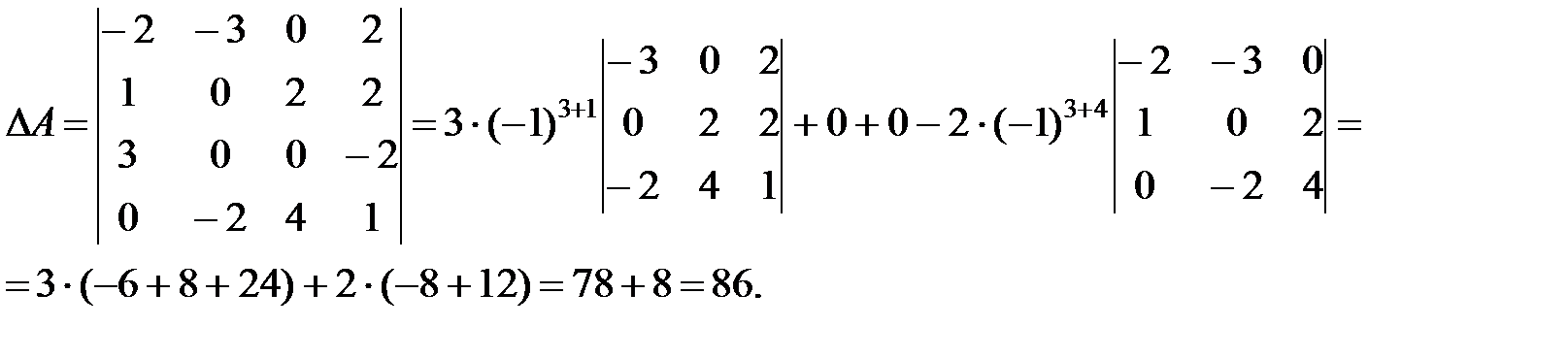 {N (a_{1},a_{2},…a_{n})}}*a_{1a_{1}}a_{2a_{2}}…a_{na_{n}}\)

Каждое слагаемое является произведением n-элементов, которые взяли по одному из каждой строки и каждого столбца, умноженное на (-1) в степени Np, определяемое, как количество инверсий.

Геометрический смысл понятия заключается в том, что определитель представляет собой объем параллелепипеда, получаемый в том случае, если рассмотреть строки, как вектора, образующие ребра геометрической фигуры.

При этом число строк или столбцов соответствует количеству векторов. Таким образом, в случае матрицы А = (2*2), получается двухмерный параллелограмм, а детерминант является площадью рассматриваемой фигуры. Если А = (3*3), то геометрическая фигура будет иметь вид трехмерного параллелепипеда, а определитель – являться его объемом.

Правильная расстановка индексов в матрице

Определение

Индексы являются координатами элемента в системе.

Каждый элемент обладает парой индексов:

• первый – определяет строку;
• второй – указывает столбец.

Так как порядок представляет собой число строк или столбцов в квадратной матрице, то он определяется с помощью m-индекса нижней строки или n-индекса крайнего правого столбца. Данный метод используют при очень больших таблицах, когда считать строки или столбы неудобно.

Матрица представляет собой таблицу, заполненную числами. Одной из ее ключевых характеристик является размерность, то есть число строк и столбцов, из которых она состоит. Как правило, говорят, что какая-то матрица A имеет размер \(\left[ m\times n \right]\), если в ней имеется m строк и n столбцов. Запись имеет следующий вид:

\(A=\left[ m\times n \right]\)

или  \(A=\left( {{a}_{ij}} \right),\quad 1\le i\le m;\quad 1\le j\le n.\)

Существуют и другие обозначения для матрицы. В любом случае, при разных \(\left[ m\times n \right]\) и \({{a}_{ij}}\) возникает вопрос расстановки индексов. В этом случае целесообразно обратиться к обычной системе координат:

Источник: berdov. com

Данная система имеет начало координат (точка \( O=\left( 0;0 \right)\)) оси x и y, а каждая точка на плоскости однозначно определяется по координатам:

\(A=\left( 1;2 \right)\)

\(B=\left( 3;1 \right)\) и так далее.

Следует поставить рассматриваемую систему рядом с матрицей, таким образом, чтобы начало координат совпадало с левым верхним углом, что существенно облегчит задачу определения индексов. Оси должны быть направлены так, чтобы охватить всю систему. При этом необходимо повернуть систему координат. Правильный вариант расположения представлен на рисунке:

Источник: berdov.com

Получается, что любая клетка матрицы обладает однозначными координатами х и у. К примеру, запись \({{a}_{24}}\) означает, что мы обращаемся к элементу с координатами x=2  и y=4. Размеры матрицы также однозначно заданы двумя числами:

Источник: berdov.com

Общая схема вычисления определителей

Определение

Теорема Лапласа о разложении определителя: пусть в матрице размера выбрано k строк или столбцов, причем . {i+j}}\cdot {{M}_{ij}}}\)

Таким образом удалось вывести формулу для разложения определителя по строке. Аналогичный метод можно использовать для того, чтобы разложить определитель по столбцам.

Данное следствие позволяет сделать несколько выводов:

• методика подходит для строк и столбцов;
• число слагаемых в разложении в любом случае составляет n;
• вместо одного определителя \(\left[ n\times n \right]\) необходимо вычислить несколько определителей размера на единицу меньше \(\left[ \left( n-1 \right)\times \left( n-1 \right) \right].\)

Практическое применение алгоритма можно продемонстрировать, решая задачу по нахождению определителя матрицы:

\(\left| \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\end{matrix} \right|\)

В первую очередь необходимо разложить данный определитель по первой строке:

\(\begin{align} \left| A \right|=1\cdot {{\left( -1 \right)}^{1+1}}\cdot \left| \begin{matrix} 5 & 6 \\ 8 & 9 \\\end{matrix} \right|+ & \\ 2\cdot {{\left( -1 \right)}^{1+2}}\cdot \left| \begin{matrix} 4 & 6 \\ 7 & 9 \\\end{matrix} \right|+ & \\ 3\cdot {{\left( -1 \right)}^{1+3}}\cdot \left| \begin{matrix} 4 & 5 \\ 7 & 8 \\\end{matrix} \right|= & \\\end{align}\)

Отсюда следует:

\(\begin{align} &=1\cdot \left( 45-48 \right)-2\cdot \left( 36-42 \right)+3\cdot \left( 32-35 \right)= \\ &=1\cdot \left( -3 \right)-2\cdot \left( -6 \right)+3\cdot \left( -3 \right)=0. {4+4}}\cdot \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end{matrix} \right| & \\\end{align}\)

От пары слагаемых можно избавиться. В результате останется пара определителей 3х3:

\(\begin{align} & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+0+1-1-1-0=-1; \\ & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+1+1-0-0-1=1. \\\end{align}\)

\(\left| \begin{matrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end{matrix} \right|=1\cdot \left( -1 \right)+\left( -1 \right)\cdot 1=-2\)

В результате вычислений получен ответ: -2

Метод понижения порядка

Упростить расчеты при вычислении определителей можно, используя их свойства. Например, требуется вычислить определитель:

\(\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}\)

Следует вынести из третьего столбца множитель 4:

\(\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}=4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}\)

Далее следует вынести из четвертого столбца множитель 2:

\(4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}=4\cdot2\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}\)

Затем можно прибавить к строке №1 строку №2, умноженную на (-2):

\(8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}\)

Следующим шагом будет сложение строки №3 и строки №2, умноженной на (-1):

\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}\)

Далее нужно прибавить к четвертой строке вторую, умноженную на 1:

\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}\)

Можно разложить определитель по третьему столбцу:

\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}=8\cdot1\cdot(-1)^{2+3}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=8\cdot(-1)^{5}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}\)

Если прибавить к первой строке третью, умноженную на 1, получим:

\(-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}\)

Затем необходимо разложить определитель по третьему столбцу и вычислить его:

\(-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}=-8\cdot4\cdot(-1)^{3+3}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\cdot(-1)^{6}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}\)

Далее следует прибавить к строке №2 строку №1, умноженную на 1:

\(-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}\)

При разложении определителя по столбцу №1 и замене определителя 1-го порядка единственным его элементом получим:

\(-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}=-32\cdot5\cdot(-1)^{1+1}\cdot(-5)=-32\cdot5\cdot1\cdot(-5)=800\)

Приведение к треугольному виду

Методика заключается в приведении определителя к треугольнику. После этого остается вычислить произведение элементов, расположенных на главной диагонали. С помощью данного способа вычислим определитель:

\(\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}\)

В первую очередь следует поменять местами первую и третью строки:

\(\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}\)

Далее первую строку, умноженную на 1, можно прибавить к четвертой:

\(-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}\)

Затем нужно к строке №3 прибавить строку №1, умноженную на 2:

\(-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)

Следующий шаг – умножение второй строки на 2:

\(\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)

Сложим вторую и первую строку, умноженную на 3:

\(-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)

После умножения строки №4 на 7 получим:

\(-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}\)

Затем следует прибавить к четвертой строке вторую строку, умноженную на (-4):

\(-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}\)

В результате смены мест столбцов №3 и №4 получим:

\(-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}\)

После того, как третья строка, умноженная на 8, будет прибавлена к четвертой строке, получится вычислить определитель:

\(\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&0&7\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\cdot(-2)\cdot7\cdot3\cdot7=-21\)

Матрицы

Матрицы

Определители

Вычисление определителей

Задачи:

Вычислить определители

1. \[ A=\left| \begin{array}{cc} 1 &4 \\ 7 & 5 \end{array} \right| \]

2. \[ A=\left| \begin{array}{cc} a+b & a-b \\ a-b & a+b \end{array} \right| \]

3. \[ A=\left| \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 3 \\ 1 & 3 & 6 \end{array} \right| \]

4. \[ A=\left| \begin{array}{ccc} 246 &427 & 327 \\ 1014 & 543 & 443 \\ -342 & 721 & 621 \end{array} \right| \]

5. \[ A=\left| \begin{array}{ccc} x &y & x+y \\ y & x+y & x \\ x+y & x & y \end{array} \right| \]

6. \[ A=\left| \begin{array}{cccc} 1 &2 & 3 & 4 \\ 2 & 3 & 4 &1 \\ 3 & 4 & 1 & 2 \\ 4 &1 &2 &3 \end{array} \right| \]

7. \[ A=\left| \begin{array}{cccc} 1 &2 & 3 & 4 \\ -2 & 1 & -4 & 3 \\ 3 & -4 & -1 & 2 \\ 4 & 3 & -2 & -1 \end{array} \right| \]

8.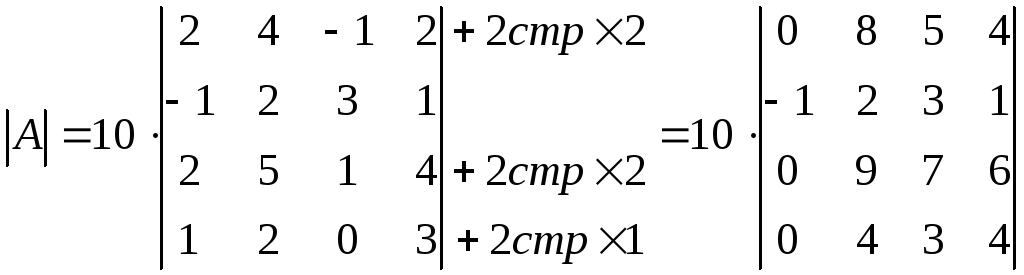 \[ A=\left| \begin{array}{cccc} 1 &1 & 1 & 1 \\ 1 & 2 & 3 &4 \\ 1 & 3 & 6 &10 \\ 1 &4 &10 &20 \end{array} \right| \]

9. \[ A=\left| \begin{array}{ccccc} 4 & 3 & 0 & 0 & 0 \\ 1 & 4 & 3 & 0 &0 \\ 0 &1 & 4 & 3 & 0 \\ 0 & 0 & 1 & 4 & 3 \\ 0 & 0 & 0 &1 & 4 \end{array} \right| \]

Действия с матрицами

Элементарные свойства операций с матрицами

Задачи:

1. Умножить матрицы:

а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]

б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). 2-(a+d)x+(ad-bc)=0. \]

Обратная матрица

Задачи:

Найти обратную матрицу для матрицы

1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]

2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]

3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]

Матричные уравнения

Задачи:

1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]

2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]

3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]

4. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) , G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) . \]

5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]

6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]

Ранг матрицы

Вычисление ранга матрицы и нахождение базисного минора

Задачи:

1. Вычислить ранг матрицы

а) \[ \left( \begin{array}{cccc} 1 &2 &1 & 1 \\ 2& 4 & 2 & 2\\ 3 & 6& 3& 5 \end{array} \right) . \]

б) \[ \left( \begin{array}{cccc} 1 &7 &7 & 9 \\ 7& 5 & 1 & -1\\ 4 & 2& -1& -3 \\ -1 & 1 & 3 &5 \end{array} \right) . \]

в) \[ \left( \begin{array}{cccc} 2 & 1 &11 & 2 \\ 1& 0 & 4 & -1\\ 11 & 4& 56& 5 \\ 2 & -1 & 5 &- 6 \end{array} \right) . T)\).

3. Пусть \(A\) и \(B\) — матрицы с одинаковым числом строк. Доказать, что \[ rang\left( \begin{array}{cc} A & B\\ 2A & 3B \end{array} \right)=rang(A)+rang(B). \]

Следующий раздел

Линейная алгебра на Python. [Урок 4]. Определитель матрицы

Четвертый урок из цикла “Линейная алгебра на Python“, посвящен понятию определителя матрицы и его свойствам.

Определитель матрицы

Определитель матрицы размера (n-го порядка) является одной из ее численных характеристик. Определитель матрицы A обозначается как |A| или det(A), его также называют детерминантом. Рассмотрим квадратную матрицу 2×2 в общем виде:

Определитель такой матрицы вычисляется следующим образом:

➣ Численный пример

Перед тем, как привести методику расчета определителя в общем виде, введем понятие минора элемента определителя. Минор элемента определителя – это определитель, полученный из данного, путем вычеркивания всех элементов строки и столбца, на пересечении которых стоит данный элемент. Для матрицы 3×3 следующего вида:

Минор M₂₃ будет выглядеть так:

Введем еще одно понятие – алгебраическое дополнение элемента определителя – это минор этого элемента, взятый со знаком плюс или минус:

В общем виде вычислить определитель матрицы можно через разложение определителя по элементам строки или столбца. Суть в том, что определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения. Для матрицы 3×3 это правило будет выполняться следующим образом:

Это правило распространяется на матрицы любой размерности.

➣ Численный пример

➤ Пример на Python

На Python определитель посчитать очень просто. Создадим матрицу A размера 3×3 из приведенного выше численного примера:

>>> A = np. matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

 

Для вычисления определителя этой матрицы воспользуемся функцией det() из пакета linalg.

>>> np.linalg.det(A)
-14.000000000000009

 

Мы уже говорили про особенность работы Python с числами с плавающей точкой, поэтому можете полученное значение округлить до -14.

Свойства определителя матрицы.

Свойство 1. Определитель матрицы остается неизменным при ее транспонировании:

➤Пример на Python

Для округления чисел будем использовать функцию round().

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(A.T)
[[-4 10 8]
[-1 4 3]
[ 2 -1 1]]

>>> det_A = round(np. linalg.det(A), 3)
>>> det_A_t = round(np.linalg.det(A.T), 3)
>>> print(det_A)
-14.0
>>> print(det_A_t)
-14.0

 

Свойство 2. Если у матрицы есть строка или столбец, состоящие из нулей, то определитель такой матрицы равен нулю:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 0 0 0; 8 3 1')
>>> print(A)
[[-4 -1 2]
[ 0 0 0]
[ 8 3 1]]
>>> np.linalg.det(A)
0.0

 

Свойство 3. При перестановке строк матрицы знак ее определителя меняется на противоположный:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

>>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1')
>>> print(B)
[[10 4 -1]
[-4 -1 2]
[ 8 3 1]]

>>> round(np. linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
14.0

 

Свойство 4. Если у матрицы есть две одинаковые строки, то ее определитель равен нулю:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> np.linalg.det(A)
0.0

 

Свойство 5. Если все элементы строки или столбца матрицы умножить на какое-то число, то и определитель будет умножен на это число:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

>>> k = 2
>>> B = A.copy()
>>> B[2, :] = k * B[2, :]
>>> print(B)
[[-4 -1 2]
[10 4 -1]
[16 6 2]]

>>> det_A = round(np. linalg.det(A), 3)
>>> det_B = round(np.linalg.det(B), 3)

>>> det_A * k
-28.0
>>> det_B
-28.0

 

Свойство 6. Если все элементы строки или столбца можно представить как сумму двух слагаемых, то определитель такой матрицы равен сумме определителей двух соответствующих матриц:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> B = np.matrix('-4 -1 2; 8 3 2; 8 3 1')
>>> C = A.copy()
>>> C[1, :] += B[1, :]
>>> print(C)
[[-4 -1 2]
[ 4 2 4]
[ 8 3 1]]
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 8 3 2]
[ 8 3 1]]
>>> round(np.linalg.det(C), 3)
4.0
>>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3)
4.0

 

Свойство 7. Если к элементам одной строки прибавить элементы другой строки, умноженные на одно и тоже число, то определитель матрицы не изменится:

 

➤ Пример на Python

>>> A = np. matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> k = 2
>>> B = A.copy()
>>> B[1, :] = B[1, :] + k * B[0, :]
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 2 2 3]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
-14.0

 

Свойство 8. Если строка или столбец матрицы является линейной комбинацией других строк (столбцов), то определитель такой матрицы равен нулю:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

>>> k = 2
>>> A[1, :] = A[0, :] + k * A[2, :]
>>> round(np.linalg.det(A), 3)
0.0

 

Свойство 9. Если матрица содержит пропорциональные строки, то ее определитель равен нулю:

➤ Пример на Python

>>> A = np. matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = k * A[0, :]
>>> print(A)
[[-4 -1 2]
[-8 -2 4]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
0.0

 

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.  Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

linear алгебра — Как показать, что матрица $3\times 4$ не имеет решения, единственное решение или бесконечно много решений?

Спросил 8 лет, 7 месяцев назад

Изменено 5 лет, 6 месяцев назад

Просмотрено 3к раз

$\begingroup$

Система:

$$ \begin{матрица} 1 и -4 и 6 и а и | & 0 \\ -2 и 5 и -4 и -1 и | & б \\ 1 и -10 и 22 и 8 и | и с \end{матрица} $$

После исключения Гаусса я обнаружил, что

$$ \begin{массив}{cccc|cc} 1&-4&6&а&&0\ 0 & 1 & -\tfrac{8}{3} & — \left( 2a- \tfrac{1}{3} \right) & & — \tfrac{1}{3}b \\ 0 и 0 и 0 и 10-5a и & c-2b \конец{массив} $$

Верно ли это, и я могу продолжать определять, существует ли решение, единственное решение или бесконечно много решений?

Вот операции:

$$ \begin{матрица} 1 и -4 и 6 и а и | & 0 \\ -2 и 5 и -4 и -1 и | & б \\ 1 и -10 и 22 и 8 и | и с \end{матрица} $$

$R_2+2R_1\стрелка вправо R_2$ $$ \begin{матрица} 1 и -4 и 6 и а и | & 0 \\ 0 и -3 и 8 и 2а-1 и | & б \\ 1 и -10 и 22 и 8 и | и с \end{матрица} $$

$R_3-R_1\стрелка вправо R_3$ $$ \begin{матрица} 1 и -4 и 6 и а и | & 0 \\ 0 и -3 и 8 и 2а-1 и | & б \\ 0 и -6 и 16 и 8-а и | и с \end{матрица} $$

$R_3-2R_2\стрелка вправо R_3$ $$ \begin{матрица} 1 и -4 и 6 и а и | & 0 \\ 0 и -3 и 8 и 2а-1 и | & б \\ 0 и 0 и 0 и 10-5а и | и с-2b \end{матрица} $$

$-\frac 13(R_2)\стрелка вправо R_2$ $$ \begin{матрица} 1 и -4 и 6 и а и | & 0 \\ 0 & 1 & -\frac 83 & -\tfrac{2a-1}{3} & | &-\фракция 13б\\ 0 и 0 и 0 и 10-5а и | и с-2b \end{матрица} $$

• линейная алгебра
• матрицы
• исключение Гаусса

$\endgroup$

5

$\begingroup$

Нет решения, если есть строка вида $0 0 0 0 | Q$, где $Q$ не равно нулю.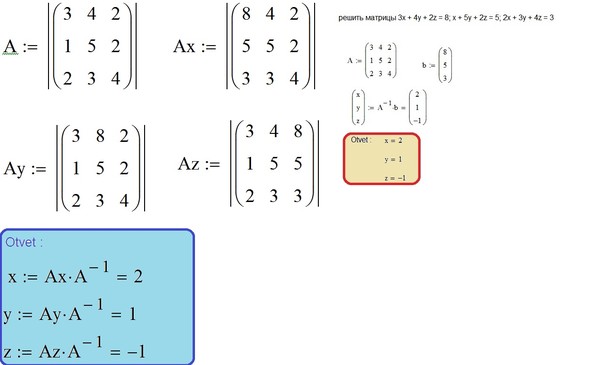 Какой ряд может выглядеть так? Что должно произойти (с $a$, $b$ и $c$), чтобы строка выглядела так?

Если есть решение, то переменная, представленная в 3-м столбце, произвольна, поэтому решений бесконечно много.

$\endgroup$

$\begingroup$

Ограничения на $a$

В общем, мы имеем существование решения, когда вектор данных находится в пространстве столбцов целевой матрицы $\mathbf{A}$. То есть, если вектор данных может быть записан как линейная комбинация основных столбцов $\mathbf{A}$. 9{*} \right)$ тривиально, то решение также уникально .

Найдите основные столбцы. Начните с сокращенной формы эшелона строк: $$ \начать{выравнивать} \mathbf{A} &\mapsto \mathbf{E} _{\mathbf{A}} \\ % \оставил[ \начать{массив}{рррр} 1 и -4 и 6 и а \\ -2&5&-4&-1\ 1 и -10 и 22 и 8 \\ \конец{массив} \Правильно] % &\mapsto % \оставил[ \начать{массив}{рррр} \color{blue}{1} & 0 & -\frac{14}{3} & 0 \\ 0 & \color{blue}{1} & -\frac{8}{3} & 0 \\ 0 & 0 & 0 & \цвет{синий}{1} \\ \конец{массив} \Правильно] % \end{выравнивание} $$ Основные столбцы отмечены синими опорными точками. Поскольку 3-й столбец линейно зависим, мы можем игнорировать его и изучить более простую эквивалентную форму: $$ \ шляпа {\ mathbf {А}} = % \оставил[ \начать{массив}{рррр} 1 и -4 и а \\ -2&5&-1\ 1&-10&8\ \конец{массив} \Правильно] $$ Две матрицы имеют одинаковое пространство диапазона: $$ \mathcal{R} \left( \mathbf{A} \right) = \mathcal{R} \left( \hat{ \mathbf{A} } \right) $$ Определитель определит, когда есть нулевое пространство. $$ \det \hat{\mathbf{A}} = 15 \left( a — 2 \right) $$ Когда $a=2$ больше нет трех линейно независимых столбцов. Если решение существует, оно не будет единственным. 9{3}$.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Определитель матрицы 4×4 – Как вычислить определитель матрицы 4×4?

Определитель матрицы 4×4 — это уникальное число, которое также рассчитывается по определенной формуле. Если порядок матрицы равен n x n, то это квадратная матрица. Итак, здесь 4×4 — это квадратная матрица, состоящая из четырех строк и четырех столбцов. Если A — квадратная матрица, то определитель матрицы A представлен как |A|.

 

Найдите определитель матрицы 4×4? мы будем использовать нормальный метод, есть формула определителя матрицы 4 × 4, которую мы обычно используем для нахождения определителя матрицы 3 × 3.

 

Определение определителя

Самым простым способом будет сформулировать определитель, учитывая верхний ряд элементов и соответствующие миноры. Возьмите первый элемент верхней строки и затем умножьте его на минор, а после этого вычтите произведение второго элемента на минор. Продолжайте поочередно складывать и вычитать произведение каждого элемента верхней строки с заданным минором, пока не будут учтены все элементы верхней строки.

 

Детерминанты также играют очень важную роль при нахождении обратной матрицы, а также при решении систем линейных уравнений. В следующей части мы также предполагаем, что у нас есть квадратная матрица (m равно n). Определитель матрицы A будет стоять через det(A) или |A|. Сначала вводится определитель матрицы 2×2 и 3×3, затем ставится случай n×n.

Что такое Матрица?

Прежде чем изучать операции с матрицей, давайте обсудим, что такое матрица. Матрица может быть определена как прямоугольный массив чисел или символов, которые обычно располагаются в строках и столбцах. Порядок матрицы также может быть определен как количество строк и количество. столбцов. Элементы также являются числами в матрице, и каждое из чисел называется элементом. Множественное число слова матрица известно как матрицы.

Размер матрицы называется матрицей «n на m» и записывается как m×n, где n — количество строк, а m — количество столбцов. Например, у нас есть матрица 3×2, потому что количество строк здесь равно 3, а количество столбцов здесь равно 2.

[Изображение скоро будет загружено]

Размеры матрицы также может быть определено как количество строк и столбцов матрицы в указанном порядке. Поскольку приведенная выше матрица А имеет 2 строки и 3 столбца, она известна как матрица 2 × 3.

 

Ярлык для определения ранга матрицы

Общее количество линейно независимых векторов в матрице равно общему количеству ненулевых строк в ее строке, присутствующей в ступенчатой ​​матрице. Итак, чтобы узнать ранг матрицы, мы должны в общем случае преобразовать матрицу в ее эшелонированную форму строк, а затем подсчитать общее количество ненулевых строк.

 

Символ определителя

Символ определителя представляет собой две вертикальные линии с обеих сторон.

Пример:

|А| обозначает определитель матрицы A

(тот же символ, что и абсолютное значение)

Для матрицы 2×2

Для матрицы 2×2 (2 строки, 2 столбца):

A = \[\begin {bmatrix} a & b \\ c & d \end{bmatrix}\]

Определитель записывается как:

|A| = ad − bc

Очень легко запомнить, когда вы думаете о кресте:

Определитель матрицы 2×2

Если A — произвольная матрица A 2×2, элементы задаются следующим образом:

A = \[\begin{bmatrix} a_{11} & a_{12} \ \ a_{21} & a_{22} \end{bmatrix}\]

, то определитель матрицы a и этой матрицы представляется следующим образом:

det(A) = lAl = \[\begin{vmatrix} a_ {11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}\] = a\[_{11}\]a\[_{22}\] — a\[_ {21}\]a\[_{12}\]

Для матрицы 3×3

Для матрицы 3×3 (3 строки, 3 столбца):

A = \[\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

Определитель записывается как:

|A| будет равно a(ei − fh) − b(di − fg)  + c(dh − eg)

Это может показаться сложным, но есть известная закономерность:

[Изображение скоро будет загружено]

вычислить определитель матрицы 3×3 вот точки:

• Умножить a на определитель матрицы 2×2, которая не находится ни в строке, ни в столбце a.

• Также для b, и для c тоже

• Сложите их, но также помните о минусе перед b

Что касается формулы (помните, что вертикальные черточки || определитель»):

lAl = a . \[\begin{vmatrix} e & f \\ h & i \end{vmatrix}\] — b . \[\begin{vmatrix} d & f \\ g & i \end{vmatrix}\] + c . \[\begin{vmatrix} d & e \\ g & h \end{vmatrix}\]

Как вычислить определитель матрицы 4×4?

Прежде чем мы попытаемся найти определитель матрицы 4×4, сначала давайте проверим несколько условий, приведенных ниже.

• Если имеется какое-либо условие, при котором определитель матрицы 4×4 может быть равен 0 (например, полная строка или полный столбец равны 0)

• возможный.

• Если элементы матрицы одинаковы, но затем переупорядочены в любом из столбцов или строк.

В любом из трех вышеприведенных случаев используются соответствующие методы вычисления определителей 3 x 3. Мы меняем строку или столбец, чтобы заполнить их 0, за исключением одного элемента. Определитель матрицы 4 × 4 будет эквивалентен произведению этого элемента и его кофактора. В этой ситуации кофактор представляет собой детерминант 3 × 3, который оценивается по своей конкретной формуле.

4×4 Определитель | Superprof

Что такое детерминанты?

Определитель представляет собой скалярную величину, полученную из элементов квадратной матрицы. Другими словами, мы можем сказать, что при вычислении определителя вход представляет собой квадратную матрицу, а выход — скалярное число. В квадратной матрице количество строк и столбцов равно. Определитель матрицы обозначается двумя вертикальными линиями ||. Например, определитель матрицы A будет обозначаться как |A|.

Определитель матрицы является важным понятием в линейной алгебре, так как он очень полезен при решении линейных уравнений, изменении переменных в интегралах, и говорит нам, как линейные преобразования изменяют площадь или объем. Они также полезны при вычислении обратной матрицы и имеют некоторые приложения в исчислении.

Определителем матрицы 1×1 является само число. Например, определитель матрицы .

Определитель матрицы 2×2 приведен ниже:

Поскольку нам даны матрицы более высокого порядка, вычисление определителей становится все более и более сложным. Например, просто взгляните на следующую формулу для вычисления определителя матрицы 3×3.

Для этой матрицы вам нужно разбить большую матрицу на меньшие матрицы 2×2. В следующем разделе мы увидим, как вычислить определитель матрицы 4×4.

 

Лучшие репетиторы по математике

Поехали

Вычисление определителя матрицы 4×4

Матрица 4×4 имеет 4 строки и 4 столбца. Было бы очень сложно найти определитель матрицы 4×4, используя элементы в первой строке и разбивая матрицу на более мелкие подматрицы 3×3.

В этом разделе мы увидим, как вычислить определитель матрицы 4×4, используя исключение Гаусса и свойства матрицы. Но прежде чем перейти к примерам, вы должны знать, что такое исключение Гаусса и разные виды треугольных матриц.

Исключение по Гауссу

Исключение по Гауссу также называется сокращением строки. В линейной алгебре алгоритм Гаусса используется для решения системы линейных уравнений. В основном это серия операций, применяемых к матричным элементам. Этот метод полезен при нахождении рангов, вычислении определителей и обратных матриц.

Для сокращения строк мы применяем ряд арифметических операций над матрицей, так что каждый элемент ниже главной диагонали матрицы становится равным нулю. Этот метод влечет за собой три вида операций со строками:

• Перестановка двух рядов местами. Значение определителя меняет свой знак, т. е. если оно было отрицательным, то становится положительным и наоборот.
• Умножение строки с ненулевой константой. Определитель остается неизменным.
• Добавление или вычитание одной строки из другой. На значение определителя это не влияет.

 

Треугольное свойство матрицы

Вспомните треугольное свойство определителя, которое гласит, что если каждый элемент в матрице выше или ниже главной диагонали равен нулю, определитель равен произведению элементов на диагонали . Существует три вида треугольных матриц:

Верхняя треугольная матрица

Матрицы, в которых все, что ниже диагонали, равно нулю. Все ненулевые элементы находятся выше главной диагонали. Например, рассмотрим следующую матрицу в форме верхнего треугольника:

Нижняя треугольная матрица

Матрицы, в которых все элементы выше главной диагонали равны нулю. Все ненулевые элементы присутствуют ниже главной диагонали. Например, рассмотрим следующую матрицу в форме нижнего треугольника:

Диагональная матрица

Все ненулевые элементы присутствуют на главной диагонали. Все, что выше или ниже главной диагонали, равно нулю. Например, рассмотрим следующую диагональную матрицу, в которой все элементы, кроме главной диагонали, равны нулю.

Определители таких матриц являются произведением элементов их диагоналей.

 

При нахождении определителя матрицы 4×4 целесообразно преобразовать матрицу в треугольную форму, применяя операции со строками в свете метода исключения Гаусса. После того, как мы преобразовали матрицу в треугольную форму, мы можем просто перемножить элементы по диагонали, чтобы получить определитель матрицы.

 

Пример 1

Найдите определитель следующей матрицы 4×4.

Решение

 

Находя определители матриц, мы можем добавлять строки и столбцы к другим строкам и столбцам. Это не повлияет на определитель матрицы. Применим эти операции к приведенной выше матрице, чтобы преобразовать ее в треугольную форму:

Результирующий определитель будет выглядеть следующим образом:

Как видите, все элементы ниже главной диагонали нулевые, поэтому эта матрица имеет верхнетреугольную форму. Перемножим элементы по диагонали, чтобы получить определитель.

 

Пример 2

Найдите определитель следующей матрицы 4×4.

Решение

Применим эти операции к приведенной выше матрице, чтобы преобразовать ее в треугольную форму:

Результирующий определитель будет выглядеть так:

Как видите, все элементы ниже главной диагонали равны нулям, поэтому эта матрица имеет верхнетреугольную форму. Чтобы получить определитель, перемножим элементы главной диагонали.

 

 

Пример 3

Найдите определитель следующей матрицы 4×4.

Решение

Применим эти операции к приведенной выше матрице, чтобы преобразовать ее в треугольную форму:

Результирующий определитель будет выглядеть так:

Как видите, все элементы ниже главной диагонали нулевые, поэтому эта матрица имеет верхнетреугольную форму. Вы можете видеть ниже, что мы перемножили все элементы главной диагонали друг с другом, чтобы получить определитель.

 

 

Mathway | Популярные задачи

Популярные задачи

Базовая математикаПредварительная алгебраАлгебраТригонометрияПредварительный исчислениеИсчислениеКонечная математикаЛинейная алгебраХимияФизика

94

Ранг	Тема	Проблема	Проблема с форматированием
1	Решение с использованием обратной матрицы	х+2у=1, 4х+5у=13	,
2	Умножение матриц	[[1/(квадратный корень из 17),-4/(квадратный корень из 17)]][[1/(квадратный корень из 17)],[-4/(квадратный корень из 17)]]
3	Найти домен	х+у=3
4	Найти домен	х-у=3
5	Найти домен 92+9х+3 , х=х+2	,
8	Найти домен	у=2х
9	Найти домен	у=-3x
10	Найти домен	у=3х-2
11	Найти домен	у=4х
12	Найти домен	3x+2y=6
13	Найдите матрицу идентичности 5×5	5
14	Найдите матрицу идентичности 6×6	6
15	Найдите матрицу идентичности 4×4	4
16	Решение с использованием обратной матрицы	2х+у=-2, х+2у=2	,
17	Решение с использованием обратной матрицы	4х+4=у, у=6х	,
18	Решение с использованием обратной матрицы	4х+2=5у-3, у=3х-1	,
19	Найдите силовой набор	(3,4)
20	Оценить	кубический корень из 216
21	Найдите силовой набор	(1,3)
22	Найти домен	3x-2y=12
23	Найти домен	у=5х+2
24	Найти домен	у=2х-3
25	Найти домен	у=2х-4
26	Найти домен	у=2х+5
27	Найти домен	у=1/2х
28	Найти домен	у=1/2x-3
29	Найти домен	у=2/3х-2
30	Найти домен	х=2у
31	Найти домен	х-2у=2
32	Найти домен	х-2у=6
33	Найти домен	2г+х
34	Найти домен	2х+у=0
35	Найти домен	у=5х+6
36	Найти домен	у=х+3
37	Решить с помощью матрицы методом исключения	у=4х+3х-2, у=6	,
38	Определить, является ли линейно зависимым	Б={[[-10,2],[5,-2,5]]}
39	Добавить	[[2,4],[6,-4]]+[[-3,-7],[20,10]]
40	Определить, является ли линейно зависимым	Б={[[-1,2],[0,-2,5]]}
41	Умножение матриц	[[0,0,1,1],[1,0,1,0],[0,0,0,1],[0,1,0,0]][[0,0,1, 1],[1,0,1,0],[0,0,0,1],[0,1,0,0]]
42	Найти домен	у=5х
43	Найти домен	у=7х
44	Найти домен	у=-х-2
45	Найти домен	у=х-2
46	Найти домен	у=х-3
47	Найти сокращенную форму эшелона строк	[[4,-3,1,0],[1,0,-2,0],[-2,1,1,0]]
48	Записать как векторное равенство	х+у+г=2, 4х+5у+г=12, 2х=-4	, ,
49	Найдите определитель	[[0,-1,а],[3,-а,1],[1,-2,3]]
50	Найти домен	у=-х+2
51	Найти определитель	[[2,5,0],[1,0,-3],[2,-1,2]]
52	Найдите определитель	[[7,5,0],[4,5,8],[0,-1,5]]
53	Найдите обратное	[[1,-3,0,-2],[3,-12,-2,-6],[-2,10,2,5],[-1,6,1,3]]
54	Найдите обратное	[[1,2,3],[2,5,7],[3,7,9]]
55	Найти сокращенную форму Echelon Row	[[0,1,5,-4],[1,4,3,-2],[2,7,1,-2]]
56	Найти сокращенную форму эшелона строк	[[1,1,0],[1,0,1],[1,0,1],[2,1,0],[2,1,0]]
57	Найти сокращенную форму эшелона строк	[[1,2,3],[4,5,6],[7,8,9]]
58	Найти сокращенную форму эшелона строк	[[7,8]]
59	Найти домен	2х+у=1
60	Записать как векторное равенство	2х+у=-2, х+2у=2	,
61	Найти домен	х-2у=4
62	Найти домен	х-у=-1
63	Найти домен	х+у=5
64	Найти домен	х=-3у-8
65	Найти домен	х=-2у-8
66	Найти домен	х+у=6
67	Найти домен	х+у=4
68	Найти домен	х+2у=4
69	Найти домен	х+у
70	Найти домен	у=7х+9
71	Найти домен	у=1/2x-5
72	Найти домен	у=1/2х+2
73	Найти домен	у=1/2х+3
74	Найти домен	х-у=-3
75	Найти домен	х-у=4
76	Найти домен	г=-2x
77	Найти домен	у=-2х+1	92
80	Найти домен	у=2х-6
81	Найти домен	у=-2x-3
82	Найти домен	у=3х-8
83	Найти домен	у=3х
84	Найти домен	у=-3х+1
85	Найти домен	у=4х+3
86	Найти домен	у=3х-4
87	Найти домен	у=4х-2
88	Найти домен	у=-6х
89	Найти домен	у=х-4
91	Найти домен	с=5/9*(ф-32)
92	Найти домен	ф=9/5с+32
93	Оценить	квадратный корень из 4
94	Найти сокращенную форму эшелона строк	[[-6,7],[2,6],[-4,1]]
95	Найдите собственные значения	[[2,1],[3,2]]
96	Найдите собственные значения	[[4,0,1],[2,3,2],[49,0,4]]
97	Найдите силовой набор	А=(2,3,4,5)
98	Найти мощность	(2,1)
99	Решение с использованием обратной матрицы	-3x-4y=2 , 8y=-6x-4	,
100	Решение с использованием обратной матрицы	2x-5y=4 , 3x-2y=-5	,

Наборы решений

Цели

1. Поймите взаимосвязь между набором решений Ax=0 и набором решений Ax=b.
2. Поймите разницу между набором решений и диапазоном столбцов.
3. Рецепты: параметрическая векторная форма, запишите множество решений однородной системы в виде промежутка.
4. Картинки: множество решений однородной системы, множество решений неоднородной системы, взаимосвязь между ними.
5. Словарь: однородный / неоднородный , тривиальное решение .

В этом разделе мы изучим геометрию множества решений любого матричного уравнения Ax=b.

Уравнение Ax=b легче решить, когда b=0, поэтому начнем с этого случая.

Определение

Система линейных уравнений вида Ах=0 называется однородной .

Система линейных уравнений вида Ax=b при bB=0 называется неоднородной .

Однородная система — это просто система линейных уравнений, в которой все константы справа от знака равенства равны нулю.

Однородная система всегда имеет решение x=0.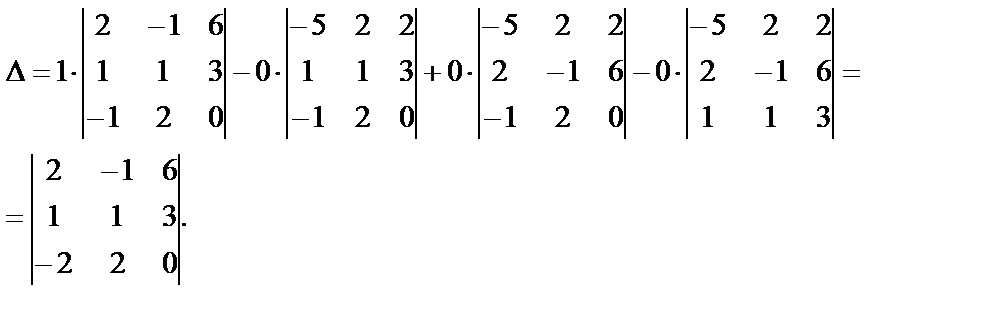 Это называется тривиальным решением . Любое ненулевое решение называется нетривиальным .

Пример (нет нетривиальных решений)

Когда однородное уравнение Ax=0 действительно имеет нетривиальные решения, оказывается, что множество решений удобно выразить в виде интервала.

Форма параметрического вектора (однородный случай)

Рассмотрим следующую матрицу в сокращенной ступенчатой ​​форме строк:

А=С10-8-701430000D.

Матричное уравнение Ax=0 соответствует системе уравнений

Tx1-8×3-7×4=0x2+4×3+3×4=0.

Мы можем записать параметрическую форму следующим образом:

GMKMIx1=8×3+7x4x2=-4×3-3x4x3=x3x4=x4.

Мы написали избыточные уравнения x3=x3 и x4=x4, чтобы превратить приведенную выше систему в векторное уравнение :

.

x=EPNx1x2x3x4FQO=x3EPN8-410FQO+x4EPN7-301FQO.

Это векторное уравнение называется параметрической векторной формой набора решений. Поскольку x3 и x4 могут быть любыми, это говорит о том, что набор решений представляет собой набор всех линейных комбинаций EPN8-410FQO и EPN7-301FQO. Другими словами, набор решений равен

SpanGMKMIEPN8-410FQO,EPN7-301FQOHMLMJ.

Вот общая процедура.

Рецепт: Параметрическая векторная форма (однородный случай)

Пусть A — матрица размера m × n. Предположим, что свободными переменными в однородном уравнении Ax=0 являются, например, x3,x6 и x8.

1. Найдите сокращенную ступенчатую форму строки A.
2. Напишите параметрическую форму набора решений, включая избыточные уравнения x3=x3,x6=x6,x8=x8. Поставьте уравнения для всех xi по порядку.
3. Составьте одно векторное уравнение из этих уравнений, превратив коэффициенты x3,x6 и x8 в векторы v3,v6 и v8 соответственно.

Решения для Ax=0 тогда будут выражены в форме

х=x3v3+x6v6+x8v8

для некоторых векторов v3,v6,v8 в Rn и любых скаляров x3,x6,x8. Это называется параметрической векторной формой решения.

В этом случае набор решений можно записать как Span{v3,v6,v8}.

Особо подчеркнем следующий факт.

Множество решений однородного уравнения Ax=0 является пролетом.

Пример (набор решений представляет собой строку)

Поскольку в приведенном выше примере было две переменные , набор решений является подмножеством R2. Поскольку одна переменная была свободна, набор решений представляет собой строку :

.

Для того, чтобы действительно найти нетривиальное решение Ax=0 в вышеприведенном примере, достаточно подставить любое ненулевое значение вместо свободной переменной x2. Например, взятие x2=1 дает нетривиальное решение x=1·A31B=A31B. Сравните с этим важным примечанием в Разделе 1.3.

Пример (множество решений представляет собой плоскость)

Поскольку в приведенном выше примере было три переменных, набор решений является подмножеством R3. Поскольку две переменных были свободны, множество решений представляет собой плоскость .

Здесь возникает естественный вопрос: можно ли написать решение однородного матричного уравнения, используя меньше векторов, чем указано в приведенном выше рецепте? В примере из раздела 2.5 мы увидим, что ответ равен 9.0061 no : векторы из рецепта всегда линейно независимы, что означает, что нет возможности записать решение с меньшим количеством векторов.

Другой естественный вопрос: являются ли множества решений неоднородных уравнений также остовными? Как мы вскоре увидим, они никогда не являются интервалами, но они тесно связаны с интервалами.

Существует естественная связь между количеством свободных переменных и «размером» набора решений, как показано ниже.

Размер набора растворов

Приведенные выше примеры показывают нам следующую закономерность: когда в согласованном матричном уравнении есть одна свободная переменная, множество решений представляет собой прямую, а когда есть две свободные переменные, множество решений представляет собой плоскость и т. д. Количество свободных переменных называется измерением множества решений.

Мы разработаем строгое определение размерности в разделе 2.7, но сейчас размерность будет означать просто количество свободных переменных. Сравните с этим важным примечанием в Разделе 2.5.

Интуитивно понятно, что размерность набора решений — это количество параметров, необходимых для описания точки в наборе решений. Для линии нужен только один параметр, а для плоскости нужны два параметра. Это похоже на то, как расположение здания на Пичтри-стрит, похожее на линию, определяется одним числом, а угол улицы на Манхэттене, похожее на плоскость, определяется двумя числами.

Напомним, что матричное уравнение Ax=b называется неоднородным , когда bB=0.

Пример (набор решений представляет собой строку)

В приведенном выше примере набором решений были все векторы вида

х=Rx1x2S=x2R31S+R-30S

, где x2 — любой скаляр. Вектор p=A−30B также является решением Ax=b: возьмем x2=0. Мы называем p частным раствором .

В наборе решений x2 может быть любым, поэтому набор решений получается следующим образом: мы берем все скалярные числа, кратные A31B, и затем добавляем конкретное решение p=A−30B к каждому из этих скалярных кратных. Геометрически это достигается тем, что сначала рисуется отрезок A31B, который представляет собой линию, проходящую через начало координат (и, что не случайно, решение Ax=0), и мы переведите или протолкните эту строку вдоль p=A−30B. Переведенная строка содержит p и параллельна Span{A31B}: это перевод строки .

Ах=0Ах=бп

Пример (множество решений представляет собой плоскость)

В приведенном выше примере набором решений были все векторы вида

х=Cx1x2x3D=x2C110D+x3C−201D+C100D.

, где x2 и x3 — любые скаляры. В этом случае частным решением является p=C100D.

В предыдущем примере и в предыдущем примере параметрическая векторная форма набора решений Ax=b была точно такой же, как параметрическая векторная форма набора решений Ax=0 (из этого примера и этого примера соответственно) , плюс конкретное решение.

Ключевое замечание

Если Ax=b непротиворечиво, множество решений получается путем взятия одного частного решения p задачи Ax=b и сложения всех решений задачи Ax=0.

В частности, если Ax=b непротиворечиво, набор решений представляет собой преобразование диапазона .

Параметрическая векторная форма решений Ax=b — это просто параметрическая векторная форма решений Ax=0 плюс конкретное решение p.

Нетрудно понять, почему ключевое наблюдение верно. Если p — частное решение, то Ap=b, а если x — решение однородного уравнения Ax=0, то

А(х+р)=Ах+Ар=0+b=b,

, так что x+p является еще одним решением Ax=b. С другой стороны, если мы начнем с любого решения x для Ax=b, то x−p будет решением для Ax=0, поскольку

А(х-р)=Ах-Ар=b-b=0.

Пример (множество решений — точка)

См. интерактивные рисунки в следующем подразделе для визуализации ключевого наблюдения.

Размер набора растворов

Как и в этом важном примечании, когда в согласованном матричном уравнении есть одна свободная переменная, множество решений представляет собой линию — эта линия не проходит через начало координат, когда система неоднородна — когда есть две свободные переменные, множество решений является плоскостью (опять же не через начало координат, когда система неоднородна) и т. д.

Еще раз сравните с этим важным примечанием в Разделе 2.5.

Каждой матрице A размера m×n мы теперь связали два совершенно разных геометрических объекта, оба описываемых с помощью интервалов.

Не путайте эти две геометрические конструкции! В первом случае вопрос заключается в том, какие х работают для данного b, а во втором вопрос заключается в том, какие b работают для некоторого х.

Интерактивный: набор решений и диапазон столбцов (1)

Интерактивный: набор решений и диапазон столбцов (2)

Interactive: Набор решений и диапазон столбцов (3)

Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)

Часть 5: Изображение строки и изображение столбца | Авниш | Линейная алгебра

Существует два способа представления системы линейных уравнений в виде матриц.

В представлении изображения строки мы делаем матрицу коэффициентов, переменную матрицу и постоянную матрицу. Мы обсуждали это ранее. Рекомендуется открыть часть 1 на другой вкладке, потому что нам приходится много раз ссылаться на нее в этой статье.

Предполагая следующую систему линейных уравнений:

3x-5y = 6 →(1)

x+y = 4 →(2)

3x+y = 0 →(3)

Представление этой системы на картинке строки будет:

После умножения этих матриц мы получим наши уравнения обратно из графика следует, что эта система не имеет единственного решения

Чтобы найти решение системы линейных уравнений из рисунка строки, мы смотрим на график и видим, есть ли какая-либо одна точка пересечения для всех линий, эта точка называется решением для система уравнений.

Если нет общей точки, то нет решения для системы уравнений (как видно из случая выше).

Изображение столбца представляет собой матрицу коэффициентов, сформированную отдельно для каждой переменной. После этого переменные перемножаются со своими матрицами коэффициентов (скалярное умножение) и складываются.

Затем приравнивается к постоянной матрице.

Принимая систему линейных уравнений (1), (2) и (3), картина столбца будет следующей:

«x» и «y» — скаляры, умноженные на соответствующие им матрицы коэффициентов

Изображение столбца на графике

Чтобы показать изображение столбца на графике, мы обрабатываем отдельные матрицы коэффициентов как векторы и наносим эти векторы на график.

Синий вектор — матрица коэффициентов X, Красный вектор — матрица коэффициентов Y, а Зеленый вектор — матрица констант вместе (сложение векторов аналогично сложению матриц). Если результат оказывается равным постоянной матрице, то такие значения x и y называются решением системы линейных уравнений.

Для этого примера, как мы видели на картинке ряда, решения нет. Следовательно, при отсутствии значений x и y в изображении столбца вектор суммы будет равен постоянной матрице (или вектору).

Одно уникальное решение

Рассмотрим систему линейных уравнений:

4x+y = 9→(4)

2x-y = 3→(5)

5x-3y = 7→(6)

График эти уравнения в виде изображения строки и изображения столбца на графике:

Изображение строки (4), (5) и (6) Изображение столбца (4), (5) и (6)

Чтобы проверить решение x= 2 и y=1, из картинки столбца подставляем их значения и вычисляем.

Итак, результат равен постоянной матрице. Следовательно, x=2 и y=1 — одно единственное решение системы уравнений (4), (5) и (6).

Бесконечное множество решений

Рассмотрим систему линейных уравнений:

x+2y = 4→(7)

2x+4y = 8→(8)

Нанесение этих уравнений на график в виде строки и столбца:

Обе линии перекрывают друг друга

Здесь у нас есть решения, но их бесконечно много (поскольку обе линии пересекаются почти в каждой точке).

Кажется, что красный вектор и зеленый вектор являются скалярным произведением синего вектора

Таким образом, может быть бесконечно много значений для x и y, так что изображение столбца возвращает постоянную матрицу.

Нет решения

Рассмотрим систему линейных уравнений:

x+y = 4→(9)

x+y = 8→(10)

x-y = 0→(11)

Отображение этих уравнений в виде изображения строки и изображения столбца на графике:

Нет точки пересечения для всех трех линий Мы видим, что нет возможных значений «x» и «y»

Умножение через изображение строки и столбца

Другое чем способ умножения матриц, рассмотренный ранее, мы можем выполнить умножение еще двумя способами:

Умножение строк на изображения

Когда отдельные столбцы одной матрицы умножаются на строки (скалярное умножение) другой матрицы, а результирующие матрицы складываются вместе.