Деление на: Онлайн калькулятор. Деление столбиком

Математика Письменное деление на двузначное число

Материалы к уроку

Конспект урока

49. Письменное деление на двузначное число

 

Организационный этап   Говорит Знайка (везде) Тут примеры и задачи, Игры, шутки, всё для вас! Пожелаем всем удачи – За работу, в добрый час!

Говорит  Знайка Решите примеры, заполните  таблицу, и узнаете, тему сегодняшнего урока. — Во сколько раз 721 день больше, чем неделя? 721:7=103, в 103 раза Сколько часов в 1/8 суток? Сутки=24часам; 24:8=3ч Сколько см в 1/5 дм? 1дм=10см; 10:5=2см Прошла 1/5 часть века. Сколько это лет? 1 век=100 лет; 100:5=20 Найдите 1\4 от числа 6400 Нужно 6400:4 получится 1600 Прочитайте тему урока? Деление.

Сегодня на уроке мы познакомимся с письменным приёмом деления на двузначное число, будем совершенствовать вычислительные навыки. К концу урока вы должны знать, как выполнить деление на двузначное число. Уметь решать соответствующие примеры.

Этап подготовки учащихся к активному сознательному усвоению знаний   Устный счёт   Задание 1 Решите примеры. 720:9=              80 186:2=              93 174:3=              58 526:2=              263 420:5=               84 540:5=              108 1760:4=            440 Что общего в этих примерах?              Правильно. Это примеры с делением на однозначное число.

Задание 2 Помогите доставить паромом груз на остров. Сравните вес вагонов, поставьте знаки: «>», « Выдержит ли паром вес груза, если допустимая норма груза 5 тонн? Сравните массу вагона №1=5 т 2 ц и №2=3200 кг. Ответ: первый тяжелее второго, паром выдержит вес второго вагона. Сравните массу вагона №3=234 кг и №4=8 ц 75 кг. Ответ: знак меньше, паром выдержит вес груза. Сравните массу вагона №5=60 ц 7 кг и №6=6007 кг. Ответ: знак равенства, но паром не выдержит вес груза.   Задание 3 Решите задачу. В древности люди считали железо драгоценным металлом. Археологи на острове Крит нашли серебряное кольцо, покрытое железом весом 40 граммов, 1/10 часть массы кольца составляло железо. Сколько граммов серебра содержало кольцо? Кольцо=40г Железо — 1/10 часть=?г Серебро — ?г Проверьте себя. Решение 1) 40:10=4г- масса железа. 2) 40-4=36г – масса серебра. Ответ: 36г. Молодцы, ребята! Вы хорошо умеете устно решать примеры, сравнивать величины веса, находить долю чисел, решать задачи. А теперь я научу вас делить на двузначное число.

Этап усвоения новых знаний   Рассмотрите числовое выражение. Вы уже можете делить многозначные числа на однозначное число. Давайте попробуем разделить на двузначное число. Сколько десятков в делимом?                В делимом 6 десятков. Сколько десятков в делителе?                В делителе 7 десятков. Делить на однозначное число вы умеете. Разделим 62 на 7. Получаем 8. Это пробная цифра. Ее нельзя сразу записывать в частном. Сначала надо проверить, подходит ли цифра 8. Умножим  78 на 8, получаем 624. Значит частное 8 подходит. Записываем число 8 в частном.       Составим алгоритм действий при делении на двузначное число. Делим на 10 делимое и делитель. Делим двузначное число на однозначное. Проверяем, умножаем частное на делитеть в уме.         а) Если совпало  с делимым, то записываем частное.         б) Если не совпало, то пробуем другое частное.

Первичное закрепление   Задание   Помогите парашютисту приземлиться на остров. Найдите значение числовых выражений, выполнив деление столбиком. Проверьте себя. 448:64=7 952:34=28 851:23=37 Задание Помогите почтальону разнести письма, решив уравнения. 252:х=63 504:х=84 365:х=73 Проверьте себя. 252:х=63 Х – это делитель, чтобы найти делитель, нужно делимое разделить на частное: 252:63 получим 4. Делаем проверку: 252: 4 будет 63. Уравнение решено верно, х=4 Следующий пример. 504:х=84 Х – это делитель, чтобы найти делитель, нужно делимое разделить на частное: 504:84 получим 6. Делаем проверку: 504: 6 будет 84. Уравнение решено верно, х=6 Следующий пример. 365:х=73 Х – это делитель, чтобы найти делитель, нужно делимое разделить на частное: 365:73 получим 5. Делаем проверку: 365: 5 будет 73. Уравнение решено верно, х=5   Решите задачу Поезд выехал из пункта А в пункт В, расстояние между которыми 600км. Первые 120 км поезд ехал со скоростью 60 км\ч, а оставшийся путь – со скоростью 80км\ч. Сколько времени понадобилось поезду, чтобы попасть из пункта А в пункт В? Выполним условный чертёж и подпишем известные данные задачи. Теперь отметим ?, что нам надо узнать,  и подчеркнём главный вопрос задачи. (появляется чертеж, выделяется главный вопрос задачи) Вспомним формулы взаимосвязи расстояния, скорости и времени. S=v·t   v=S:t    t=S:v Решите задачу самостоятельно. Проверьте себя. 1) Мы узнаем время первоначального движения поезда: 120:60=2 2) Узнаем оставшийся путь: 600-120=480(км) 3) Узнаем время, затраченное на второй отрезок пути: 480:80=6(ч) 4) Найдем, сколько времени понадобилось поезду, чтобы попасть из пункта А в пункт В: 2+4=6(ч) 6 часов понадобилось поезду, чтобы попасть из пункта А в пункт В

Подведение итогов урока   Вспомните алгоритм деления на двузначное число. 1. Делим на 10 делимое и делитель. 2. Делим двузначное число на однозначное. 3. Проверяем, умножаем частное на делитеть в уме. а) Если совпало  с делимым, то записываем частное. б) Если не совпало, то пробуем другое частное.

 

 

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

Почему деление на физиков и лириков уходит в прошлое

Неужели деление на «физиков и лириков» уходит в прошлое? Можно ли стать одновременно и программистом, и лингвистом? Нужно ли вводить в школе новые предметы на стыке гуманитарных и технических дисциплин? «РГ» опросила экспертов из ведущих российских вузов — участников Проекта 5-100.

Анастасия Таболина, доцент Высшей школы инженерной педагогики, психологии и прикладной лингвистики Санкт-Петербургского политехнического университета Петра Великого (СПбПУ)

Деление детей на технарей и гуманитариев всегда было достаточно условным. Как оно вообще формируется? Тех ребят, кто больше успевает по математике, автоматически причисляют к технарям. Тех, кто хорошо формулирует свои мысли, с ранних лет родители и даже учителя называют «гуманитариями». Вырваться из этих шаблонов бывает очень сложно. Поэтому нельзя вешать ярлыки на ребенка. Нужно с детства учить его находить общий язык с людьми, но и не забывать о техническом творчестве.

Факт: навык общения формируется у ребенка быстрее, а к успехам в математике нужно идти гораздо дольше — нужна способность долго работать над одной задачей, внимательность. Структуры мозга, отвечающие за техническое мышление, формируются гораздо дольше, чем речевые. Только к пяти-шести годам начинает формироваться образно-логическое мышление. Поэтому в массовом сознании и сложился стереотип, что гуманитариев больше.

На него работает и то, что дети-технари зачастую более усидчивы, среди них больше интровертов. Но учеными доказано, что успешный гуманитарий может быть и успешным технарем. Мы можем менять профиль подготовки, обучаться в течение всей жизни и переходить из одной специальности в другую. Это вопрос тренировки и желания.

Сейчас ученые сходятся на том, что необходимо междисциплинарное обучение гуманитариев и технарей. Например, одна из наиболее популярных профессий сейчас — программист, дизайнер виртуальной реальности. Такие специалисты хорошо сочетают и гуманитарные, и технические профили. Популярна тема развития soft-skills, digital skills, hard skills. Человек с многофункциональным набором навыков точно будет более востребован на рынке труда, чем просто гуманитарий или технарь.

Константин Воронцов, руководитель лаборатории машинного интеллекта МФТИ

Занятие программированием, как и изучение иностранных языков, требует педантичности, усидчивости и очень хорошей памяти. Поэтому неудивительно, что люди с такими способностями оказываются успешными и в том, и в другом. Однако на этом сходство заканчивается.

Суть работы программиста не в освоении языков программирования. Это инженерная деятельность, требующая системного мышления, конструкторского воображения, большого внимания к деталям, знания алгоритмов, постоянного освоения новых технологий, командной работы.

По мере развития программирования в нем все меньше остается места для математики и искусства, и все больше требуется инженерного ремесла. Современное программирование нацелено на быстрое коллективное создание сложных приложений из разнообразных готовых компонентов. Гуманитариям, за редким исключением, такая деятельность просто не нравится. Им это скучно.

С другой стороны, владение двумя профессиями всегда дает человеку огромное преимущество на рынке труда. Программист, который понимает многое и в лингвистике или, например, в социологии, сегодня будет крайне востребованным и высокооплачиваемым специалистом.  Работать на стыке дисциплин всегда увлекательно: ты легко понимаешь то, что другие просто не видят. Однако достижение этой цели требует большого труда. И еще увлеченности.

Роль школы я вижу не в том, чтобы вводить новые специализации и дисциплины. Дети и так перегружены. Нужно рассказывать и показывать, для чего на практике нужны знания. Нужно чаще приводить в школу успешных состоявшихся людей, хотя бы из числа ее выпускников. Рассказы профессионалов о своем деле гораздо больше мотивируют работать на стыке нескольких профессий.

Анна Плотникова, директор департамента «Филологический факультет» УГИ УрФУ, научный руководитель направления «Цифровая гуманитаристика»

Гуманитариям сложно адаптироваться к традиционным техническим профессиям. На должность инженера-авиаконструктора необходимо брать человека с соответствующим техническим дипломом. Ожидать, что выпускник философского факультета справится с этой работой лучше, не стоит. Но рынок труда постоянно меняется, каждый год появляются новые профессии, которым никто никогда не учил и про которые мы, строго говоря, плохо понимаем, технические они или гуманитарные. Скажем, профессия системного аналитика в IT-отрасли предполагает знание основ технологии производства продукта, но суть ее все же не в этом: задача в том, чтобы понять пользователя, а затем перевести его потребность на технический язык, понятный программисту-разработчику. Системный аналитик — это своего рода переводчик между участниками сложно организованной технологической цепочки, в которой задействованы специалисты с разным образованием. Как показывает опыт, на такую роль скорее подойдет человек с гуманитарным дипломом (например, в области прикладной лингвистики), нежели с техническим. Хотя определенное дополнительное обучение ему, несомненно, будет необходимо.

Но есть сферы, где гуманитарий с техническими навыками заведомо проиграет «чистому» технарю. Например, в разработке IT-продуктов: даже если исследования показывают, что среди успешных программистов велик процент людей, имеющих склонности к иностранным языкам, это совсем не значит, что в реальном рынке труда полиглот сможет конкурировать со специалистом, которого учили разбираться в языках программирования. В то же время в современных IT-компаниях есть огромное количество позиций, где именно гуманитарий с системным мышлением может иметь преимущество. Лингвист, знающий основы языка Python, или социолог, разбирающийся в SQL, без работы точно не останутся.

Разделение на технарей и гуманитариев в целом искусственно и создано самой системой образования: техническое или гуманитарное мышление студент приобретает в процессе обучения. Не бывает технарей и гуманитариев от рождения.

Да, если ребенку с детства интересна история, взрослые скорее всего будут поощрять его интерес. Математика при этом может даваться хуже и тяжелее, осваиваться по остаточному принципу. Так школьник, сам того не понимая, становится гуманитарием. Это не значит, что он не смог бы осилить математику, просто для этого нужно больше сил.

В высокотехнологичных областях экономики, кроме конкретных знаний и системного мышления, требуется гибкость и высокая степень адаптивности, готовность постоянно развиваться. Даже если человек всю жизнь собирается работать на одном месте, переобучаться ему точно придется. Именно с этим связан один из самых сложных вызовов для системы гуманитарного образования: перестать воспитывать в студентах консервативные установки, убежденность, что полученные знания самодостаточны в силу их фундаментального характера и по той же причине неизменны. К сожалению, именно консерватизм оказывается наиболее значимым фактором профессиональных неудач даже самых неглупых и потенциально успешных ребят.

Дмитрий Яковлев, руководитель ФабЛаб ТюмГУ

Мир невероятно быстро меняется, и человек за жизнь может сменить несколько десятков видов деятельности. Постоянно учиться и получать новые компетенции — норма в современном мире. Поэтому вопрос, нужно ли гуманитариев учить программированию, в принципе не стоит.

Однако как технарь с гуманитарными наклонностями я действительно могу сказать, что склонность к изучению естественных языков может помочь при изучении языка программирования, особенно его основ. Эти два процесса очень похожи. При углублении же в искусство программирования уже не обойтись без математики и способности думать как технарь, которая приобретается при многократном решении задач; и тут условным гуманитариям без подготовки может быть сложнее. Но дорогу осилит идущий.

Зоя Резанова, профессор Томского государственного университета, заведующая лабораторией когнитивных исследований языка

В системе современного высшего образования России уже существует направление подготовки, которое ориентировано на междисциплинарную интеграцию лингвистики, информатики и математики. Это направление «Фундаментальная и прикладная лингвистика». Потребности автоматической обработки текстовой информации лавинно возрастают, возрастает и потребность в специалистах с междисциплинарными компетенциями в сфере естественных языков, когнитивной науки и информатики.

Электронная библиотека: Административно-территориальное деление

Оглавление [с. 5]

Предисловие [с. 9]

I. Верхкамский округ [с. 11]

Географическое положение [с. 11]

Геологический очерк [с. 11]

Минеральные источники [с. 12]

Пути сообщения [с. 13]

Демография [с. 15]

Центры распределения [с. 18]

Общие условии сельского хозяйства [с. 19]

Животноводство [с. 24]

Кустарные промыслы [с. 27]

Мелкая и средняя промышленность [с. 28]

Торф [с. 30]

Каменно-угольная промышленность [с. 30]

Лесная промышленность [с. 32]

Перспективы бумажной промышленности [с. 36]

Золотопромышленность [с. 36]

Перспективы медной промышленности [с. 36]

Железные руды Верхкамского округа [с. 37]

Крупная железная промышленность [с. 38]

Прикамсний соленосный район [с. 42]

Драгоценные и поделочные камни [с. 44]

Доломиты (магнезит) [с. 44]

Строительные материалы [с. 44]

Электротехнические установки [с. 45]

Общая характеристика ресурсов промышленного развития Верхкамского округа [с. 47]

II. Пермский округ [с. 49]

Географическое положение [с. 49]

Геологический очерк [с. 49]

Пути сообщения [с. 50]

Демография [с. 52]

Центры распределения [с. 55]

Сельское хозяйство [с. 57]

Полеводство [с. 60]

Животноводство [с. 62]

Мукомольная промышленность [с. 66]

Винокуренная и пивоваренная промышленность [с. 66]

Кожевенная промышленность [с. 66]

Кустарная промышленность [с. 67]

Мелкая и средняя промышленность [с. 70]

Каменноугольная промышленность [с. 72]

Торф [с. 73]

Лесная промышленность [с. 73]

Писчебумажная промышленность [с. 76]

Золотопромышленность [с. 76]

Перспективы медной промышленности [с. 76]

Месторождения железных руд Пермского округа и их запасы [с. 78]

Железная промышленность [с. 80]

Хромистый железняк [с. 86]

Основная химическая промышленность [с. 86]

Месторождение каолина, боксита и алунит [с. 86]

Стекольная промышленность в округе [с. 87]

Поделочные камни [с. 87]

Строительные материалы [с. 87]

Работающие электрические установки округа [с. 87]

Ориентировочный приблизительный запас белого угля в Пермском округе [с. 89]

Заключение [с. 89]

III. Сарапульский округ [с. 91]

Географическое положение [с. 91]

Геологический очерк [с. 91]

Пути сообщения [с. 91]

Демография [с. 92]

Центры распределения [с. 95]

Сельское хозяйство [с. 96]

Полеводство [с. 98]

Животноводство [с. 100]

Мукомольная промышленность [с. 102]

Винокуренная промышленность [с. 102]

Кожевенная промышленность [с. 102]

Кустарные промыслы [с. 103]

Мелкая и средняя, промышленность [с. 105]

Торф [с. 107]

Лесная промышленность [с. 107]

Перспективы медной промышленности [с. 109]

Железная промышленность [с. 109]

Поделочные камни [с. 110]

Строительные материалы [с. 110]

Электрические установки [с. 110]

Ориентировочный приблизительный подсчет запасов белого угля по Сарапульскому округу [с. 111]

Заключение [с. 111]

IV. Кунгурский округ [с. 114]

Географическое положение. Границы [с. 114]

Геологический очерк [с. 114]

Минеральные источники [с. 115]

Пути сообщения [с. 116]

Демография [с. 117]

Центры распределения [с. 119]

Сельское хозяйство [с. 120]

Животноводство [с. 126]

Мукомольная промышленность [с. 128]

Винокуренная промышленность [с. 128]

Мыловаренная, свечная и салотопенная промышленность [с. 129]

Кожевенная промышленность [с. 129]

Кустарная промышленность [с. 129]

Мелкая и средняя промышленность [с. 132]

Торф [с. 134]

Лесная промышленность [с. 134]

Месторождения платины [с. 135]

Перспективы медной промышленности [с. 135]

Месторождения огнеупорных глин Кунгурского округа [с. 136]

Стекольная промышленность округа [с. 137]

Строительные материалы [с. 137]

Электрические установки [с. 138]

Белый уголь [с. 138]

Приблизительный ориентировочный подсчет запасов белого угля по Кунгурскому округу [с. 138]

Заключение [с. 140]

V. Верхотурский округ [с. 142]

Географическое положение [с. 142]

Геологический очерк [с. 142]

Минеральные воды [с. 144]

Пути сообщения [с. 144]

Демография [с. 146]

Сведения о городах, находящихся на территории Верхотурского округа [с. 148]

Центры распределения [с. 148]

Сельское хозяйство [с. 151]

Животноводство [с. 155]

Кустарная промышленность [с. 157]

Мелкая и средняя промышленность [с. 159]

Каменноугольная промышленность [с. 161]

Торф [с. 162]

Лесная промышленность [с. 162]

Писчебумажная промышленность [с. 167]

Золотопромышленность [с. 167]

Платинопромышленность [с. 168]

Медная промышленность [с. 171]

Медные заводы [с. 173]

Железные руды Верхотурского округа [с. 175]

Железная промышленность [с. 177]

Хромистые руды [с. 190]

Основная химическая промышленность [с. 190]

Драгоценные, цветные и поделочные камни [с. 190]

Месторождения огнеупорной глины [с. 191]

Асбестовая промышленность [с. 191]

Строительные материалы [с. 192]

Электрические установки [с. 193]

Ориентировочный приблизительный подсчет запасов белого угля в Верхотурском округе [с. 195]

Заключение [с. 196]

VI. Туринский округ [с. 198]

Географическое положение [с. 198]

Геологический очерк [с. 198]

Пути сообщения [с. 198]

Демография [с. 199]

Центры распределения [с. 202]

Сельское хозяйство [с. 203]

Животноводство [с. 208]

Мукомольная промышленность [с. 211]

Винокуренная промышленность [с. 211]

Мыловаренная промышленность [с. 211]

Кожевенная промышленность [с. 212]

Кустарная промышленность [с. 212]

Мелкая и средняя промышленность [с. 213]

Торф [с. 215]

Лесная промышленность [с. 215]

Перспективы писчебумажной промышленности [с. 218]

Строительные материалы [с. 218]

Электрические установки [с. 218]

Заключение [с. 218]

VII. Тюменский округ [с. 220]

Географическое положение [с. 220]

Геологический очерк [с. 220]

Пути сообщения [с. 220]

Демография [с. 221]

Сведения о городах на территории Тюменского округа [с. 224]

Центры распределения [с. 224]

Сельское хозяйство [с. 227]

Животноводство [с. 233]

Выводы [с. 235]

Мукомольная промышленность [с. 236]

Винокуренная, пивоваренная и дрожжевая промышленность [с. 237]

Мыловаренная и салотопенная промышленность [с. 237]

Кожевенная промышленность [с. 237]

Кустарные промыслы [с. 238]

Мелкая и средняя промышленность [с. 240]

Стекольная промышленность [с. 242]

Торф [с. 243]

Лесная промышленность [с. 243]

Писчебумажная промышленность [с. 244]

Строительные материалы [с. 245]

Электрические установки [с. 245]

Заключение [с. 245]

VIII. Екатеринбургский округ [с. 246]

Географическое положение [с. 246]

Геологический очерк [с. 246]

Минеральные воды [с. 247]

Пути сообщения [с. 249]

Железные дороги Екатеринбургского округа [с. 249]

Демография [с. 250]

Центры распределения [с. 254]

Сельское хозяйство [с. 255]

Мукомольная промышленность [с. 264]

Важнейшие вальцовые мельницы округа [с. 266]

Винокуренная, пивоваренная и дрожжевая промышленность [с. 266]

Мыловаренная, свечная и клеевая промышленность [с. 267]

Кожевенная промышленность [с. 268]

Кустарная промышленность [с. 268]

Мелкая и средняя промышленность [с. 273]

Каменноугольная промышленность [с. 278]

Графит [с. 280]

Торф [с. 280]

Лесная промышленность [с. 281]

Писчебумажная промышленность [с. 283]

Золотопромышленность [с. 284]

Платиновая промышленность [с. 285]

Медная промышленность [с. 286]

Медные заводы [с. 289]

Месторождения железных руд [с. 291]

Железная промышленность [с. 294]

Марганцевые руды [с. 303]

Хромовые руды [с. 303]

Нинкелевые руды [с. 303]

Вольфрамовые руды [с. 304]

Основная химическая промышленность [с. 305]

Драгоценные и подлоченые камни [с. 307]

Месторождения магнезита [с. 308]

Асбестовая промышленность [с. 309]

Тальк [с. 310]

Фосфориты [с. 310]

Корунд и наждак [с. 311]

Месторождения огнеупорных глин Екатеринбургского округа [с. 313]

Стекольная промышленность округа [с. 314]

Месторождения полевых шпатов [с. 315]

Цементная промышленность [с. 315]

Строительные материалы [с. 315]

Электрические установки [с. 316]

Ориентировочный приблизительный подсчет запасов белого угля Екатеринбургского округа [с. 318]

Заключение [с. 320]

IX. Шадринский округ [с. 322]

Географическое положение [с. 322]

Геологический очерк [с. 322]

Минеральные источники [с. 322]

Пути сообщения [с. 323]

Демография [с. 323]

Сведения о городах, находящихся на территории Шадринского округа [с. 325]

Центры распределения [с. 326]

Сельское хозяйство [с. 326]

Животноводство [с. 330]

Винокуренная и пивоваренная промышленность [с. 332]

Крахмально-паточная промышленность [с. 332]

Мыловаренная и салотопенная промышленность [с. 332]

Мукомольная промышленность Шадринского округа [с. 332]

Кустарная промышленность [с. 333]

Мелкая и средняя промышленность [с. 334]

Торф [с. 336]

Лесная промышленность [с. 336]

Строительные материалы [с. 336]

Электрические установки [с. 337]

Заключение [с. 337]

X. Курганский округ [с. 338]

Географическое положение [с. 338]

Геологическое строение [с. 338]

Пути сообщения [с. 338]

Демография [с. 339]

Центры распределения [с. 342]

Сельское хозяйство [с. 343]

Животноводство [с. 347]

Винокуренная и пивоваренная промышленность [с. 351]

Крахмально-паточная промышленность [с. 351]

Кожевенная промышленность [с. 351]

Мелкая и средняя промышленность [с. 353]

Торф [с. 356]

Лесная промышленность [с. 356]

Стеклянная промышленность [с. 356]

Строительные материалы [с. 357]

Электрические установки [с. 357]

Заключение [с. 357]

XI. Челябинский округ [с. 358]

Географическое положение [с. 358]

Геологический очерк [с. 358]

Минеральные воды [с. 359]

Пути сообщения [с. 360]

Демография [с. 361]

Центры распределения [с. 363]

Сельское хозяйство [с. 364]

Кожевенная промышленность [с. 370]

Мукомольная промышленность [с. 371]

Кустарная промышленность [с. 372]

Мелкая и средняя промышленности [с. 373]

Буроугольная промышленность [с. 375]

Торф [с. 376]

Лесная промышленность [с. 376]

Золотопромышленность [с. 377]

Месторождения огнеупорных и фарфоровых глин [с. 378]

Месторождение кварца [с. 378]

Перспективы фарфоро-фаянсовой промышленности [с. 379]

Строительные материал [с. 379]

Электрические установки [с. 379]

Ориентировочный приблизительный подсчет запасов белого угля в Челябинском округе [с. 380]

Заключение [с. 381]

XII. Троицкий округ [с. 382]

Географическое положение [с. 382]

Геологический очерк [с. 382]

Пути сообщения [с. 383]

Демография [с. 384]

Центры распределения [с. 386]

Сельское хозяйство [с. 387]

Животноводство [с. 391]

Винокуренная и пивоваренная промышленность [с. 394]

Мыловаренная и салотопенная промышленность [с. 394]

Кожевенная промышленность [с. 394]

Мукомольная промышленность [с. 395]

Кустарная промышленность [с. 396]

Мелкая и средняя промышленность [с. 396]

Каменноугольная промышленность [с. 398]

Графит [с. 399]

Торф [с. 399]

Лесная промышленность [с. 399]

Золотопромышленность [с. 400]

Медные полиметаллические руды [с. 400]

Железные руды [с. 401]

Драгоценные и поделочные камни [с. 401]

Строительные материалы [с. 402]

Ориентировочный приблизительный подсчет запасов белого угля Троицкого округа [с. 403]

Заключение [с. 403]

XIII. Златоустовский округ [с. 404]

Общие замечания [с. 404]

Географическое положение [с. 404]

Геологический очерк [с. 405]

Пути сообщения [с. 406]

Демография [с. 407]

Центры распределения [с. 409]

Сельское хозяйство [с. 410]

Винокуренная промышленность [с. 414]

Кожевенная промышленность [с. 414]

Мукомольная промышленность [с. 414]

Наиболее крупные мельницы Златоустовского округ [с. 415]

Кустарная промышленность [с. 415]

Средняя и мелкая промышленность [с. 416]

Месторождения графита [с. 419]

Торф [с. 419]

Лесная промышленность [с. 420]

Золотопромышленность [с. 422]

Платинопромышленность [с. 422]

Перспективы медной промышленности [с. 422]

Месторождения железных руд [с. 423]

Крупная железная промышленность [с. 425]

Месторождения хромистого железняка [с. 435]

Месторождения марганцевых руд [с. 435]

Драгоценные и поделочные камни [с. 435]

Корундовая промышленность [с. 436]

Магнезитовая промышленность [с. 436]

Тальк [с. 437]

Месторождения асбеста [с. 438]

Цементная промышленность [с. 438]

Месторождения полевого шпата [с. 438]

Стекольная промышленность [с. 438]

Строительные материалы [с. 439]

Электрические установки [с. 439]

Ориентировочный приблизительный подсчет запасов белого угл [с. 441]

Заключение [с. 442]

XIV. Тобольский округ [с. 444]

Географическое положение [с. 444]

Геология Тобольского Севера [с. 444]

Пути сообщения [с. 445]

Демография [с. 446]

Центры распределения [с. 450]

Сельское хозяйство [с. 453]

Кустарные промыслы [с. 456]

Мелкая и средняя промышленность [с. 457]

Рыболовство [с. 459]

Звероловство [с. 460]

Сбор кедровых орехов [с. 461]

Лесная промышленность. [с. 461]

Полезные ископаемые и перспективы горной промышленности [с. 463]

Заключение [с. 463]

XV. Ишимский округ [с. 466]

Геологическая характеристика [с. 466]

Соленые озера [с. 466]

Пути сообщения [с. 466]

Демография [с. 467]

Центры распределения [с. 470]

Сельское хозяйство [с. 470]

Кустарные промыслы [с. 474]

Мелкая и средняя промышленность [с. 474]

Лесная промышленность [с. 476]

Торф [с. 476]

Строительные материалы [с. 477]

Заключение [с. 477]

Послесловие [с. 478]

Дополнения и поправки [с. 480]

I. Верхкамский округ [с. 480]

II. Пермский округ [с. 481]

III. Сарапульский округ [с. 482]

IV. Куигурский округ [с. 482]

V. Верхотурский округ [с. 482]

VII. Тюменский округ [с. 484]

IX. Шадринский округ [с. 484]

XI. Челябинский округ [с. 484]

XII. Троицкий округ [с. 485]

XIII. Златоустовский округ [с. 486]

Замеченные опечатки [с. 488]

Пояснение к картам [с. 492]

I. Перечень уездов Уральской области [с. 492]

II. Перечень Намечаемых округов Уральской области [с. 492]

Деление / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Деление

В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.

Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.

В математике существует знак для умножения — это точка ( • ) посередине строки между числами, которые нужно перемножить, а для деления существует особый знак — это две точки ( : ) между числами, которые нужно поделить между собой.

Как ёжикам поделить между собой яблоки поровну?

Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.

1) 6 : 3 = 2 (яб.) — мы узнали, сколько яблок получит каждый ёжик.

2) 6 : 2 = 3 (ёж.) — мы узнали, сколько ёжиков получат по 2 яблока.

3) 2 • 3 = 6 (яб.) — мы узнали, сколько яблок нужно, чтобы у каждого из трёх ёжиков было по 2 яблока.

---

Любой пример на умножение можно представить двумя примерами на деление.

Например, для выражения 6 • 4 = 24 есть два обратных выражения:

24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.

24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.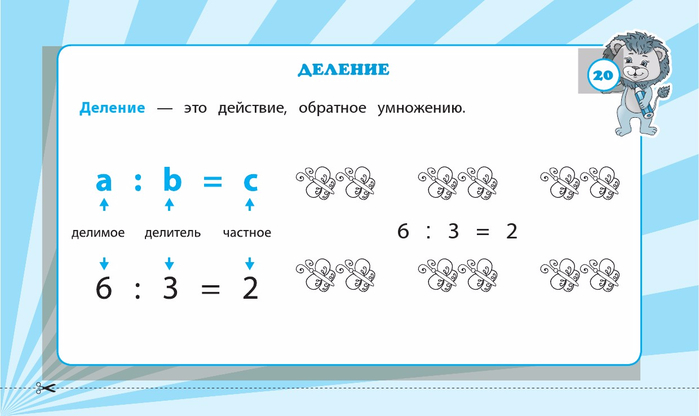

---

Числа при делении

При делении, как и при другом математическом действии, каждое число имеет свое название.

Число, которое делят, называется делимое.

Число, на которое делят, называется делитель.

Результат деления называется частное.

---

Чтение числовых выражений

24 : 6 = 4

Этот пример можно прочитать по-разному.

• 24 разделить на 6 равняется 4.
• 24 уменьшить в 6 раз – получится 4.
• Делимое – 24, делитель – 6, частное – 4.
• Частное от деления числа 24 на 6 равно 4.

---

Деление на 1

4 : 1 = 4

23 : 1 = 23

---

Деление на 0

---

Деление числа само на себя

---

Связь деления и умножения

---

Чётные и нечётные числа

Числа, которые делятся на 2 без остатка, назы­ваются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.

Чётные: 6, 22 44, 60, 74, 82, 96

Нечётные: 7, 13, 21, 37, 45, 97

---

В несколько раз меньше

Для примера решим задачу:

В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?

составим схему:

Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)

Вывод: Если в задаче есть слова «в … раз меньше», то задача решается делением.

---

Во сколько раз больше? Во сколько раз меньше?

Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?

Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?

8 : 2 = 4 (раза)

Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.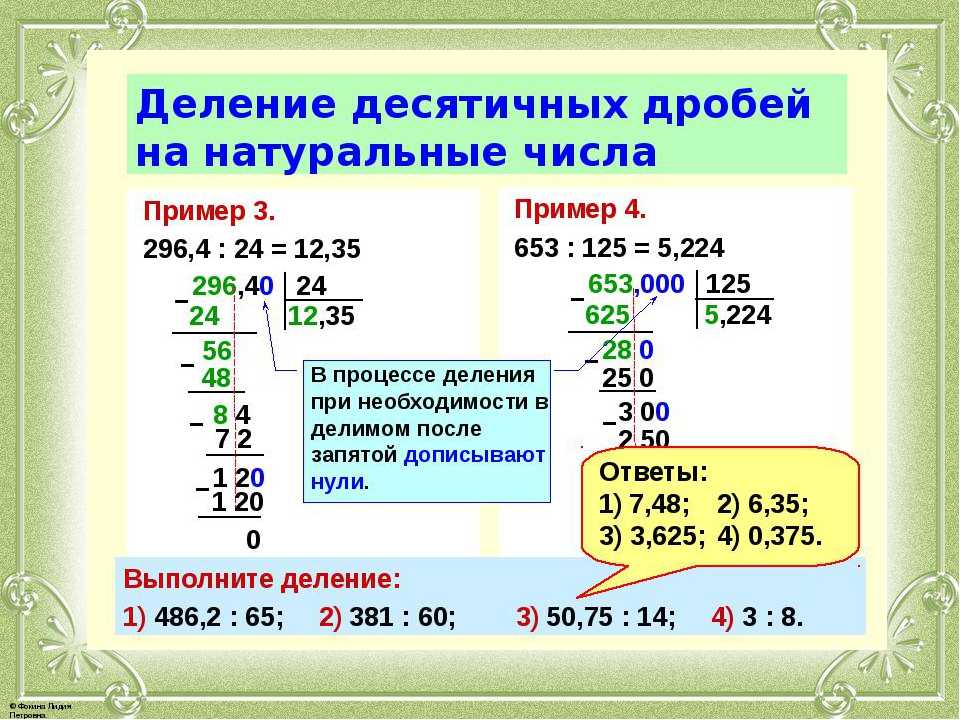

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Табличное деление

Внетабличное деление

Деление с остатком

Деление суммы на число

Деление на однозначное число

Деление чисел, оканчивающихся нулями

Свойства деления

Правило встречается в следующих упражнениях:

2 класс

Страница 59. Вариант 2. № 1, Моро, Волкова, Проверочные работы

Страница 65. Вариант 2. Тест 1, Моро, Волкова, Проверочные работы

Страница 67. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы

Страница 66, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 75, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 103, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 65, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 66, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 108. Урок 44, Петерсон, Учебник, часть 2

3 класс

Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 54, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 81, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 13, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 29, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 56, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 40. Вариант 1. № 6, Моро, Волкова, Проверочные работы

Страница 55. Вариант 2. Тест 2, Моро, Волкова, Проверочные работы

Страница 30, Моро, Волкова, Рабочая тетрадь, часть 2

Страница 48, Моро, Волкова, Рабочая тетрадь, часть 2

4 класс

Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 82, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 90, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 26, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 40. Вариант 1. Тест 1, Моро, Волкова, Проверочные работы

Страница 54, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 55, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 64, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 89, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 16, Моро, Волкова, Рабочая тетрадь, часть 2

5 класс

Задание 441, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 673, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 818, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Номер 36, Мерзляк, Полонский, Якир, Учебник

Номер 1, Мерзляк, Полонский, Якир, Учебник

Номер 520, Мерзляк, Полонский, Якир, Учебник

Номер 656, Мерзляк, Полонский, Якир, Учебник

Номер 657, Мерзляк, Полонский, Якир, Учебник

Номер 673, Мерзляк, Полонский, Якир, Учебник

Номер 1050, Мерзляк, Полонский, Якир, Учебник

6 класс

Задание 1211, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1222, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1262, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1266, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1473, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

---

Маркетинг и деление на ноль — Маркетинг на vc.

ru

Почему нельзя делить на ноль? Вообще то можно, но не позволяет табу. Да да, именно табу. Его наложили математики не случайно. Открытие истины в этой запретной области станет открытием ящика пандоры. Никто этого не хочет. Последствия будут глобальны и затронут не только математику и физику, но и маркетинг с продажами. Дело в том, что само понимание того, что такое ноль, тесно связано с вопросами социальных законов, а через них и с принципами работы бизнеса, с такими вещами как ошибки, ведущими к успеху.

858 просмотров

Согласитесь, что информация о том, что успех является не следствием правильных действий, а именно сделанных ошибок…как то напрягает и выглядит феерично… Тем не менее вся цивилизация и вообще эволюция развивается за счет ошибок, именно они являются драйвером. И к понятию нуля это имеет прямое отношение, потому что алгоритмы, использующие ошибки как движущую силу, используют операции с нулем…корректные операции с нулем.

Начнем с того, что в двоичной логике, к которой приводятся вообще все виды логик включая нечеткую и логику марковскую, не бывает запрещенных операций. ..не бывает неопределенностей, бесконечностей, сингулярностей и прочих математических бредней.Двоичная логика хороша тем, что она очень проста и если на ней что то вычислять, в том числе умножать и делить на ноль, получатся всегда корректные ответы в виде нулей и единиц.

Нельзя взять и запретить чипам двоичных сумматоров, на которых физически в компьютерах и калькуляторах реализуется жесткая схема сложения или вычитания, стоящие в основе вывода функции умножения и деления, выдавать нечто невнятное. На выходе двоичного вентиля может быть либо 0 либо 1 и третьего не дано.

Извините, закон исключенного третьего работает жестко и ему плевать на табу математиков.Разложите функцию умножения на сложение и попробуйте умножить таким образом любое число N на ноль и…вы никогда не получите ноль!Просто потому что вы не сможете сложить N с самим собой НИСКОЛЬКО раз…а именно это следует делать согласно правилу вывода функции умножения из сложения.

Также и с делением N на ноль, при котором также придется вычитать N само из себя нисколько раз. Также и с возведением в нулевую степень, где основание степени следует помножать само себя нисколько раз.Как же калькулятор и компьютер решает такие задачи, если реальным логическим вентилям нельзя поставить эту задачу?С какой стати вообще сложение N неважно с чем и неважно сколько раз может в буквальном смысле слова АННИГИЛИРОВАТЬ N до нуля?

Может кто то сомневается, что под числами все таки подразумевается нечто реально существующее, что не может просто так взять и исчезнуть при операции сближения (сложения) одного с другим! Закон сохранения энергии никто не отменял.На самом деле математики отрицают какую либо взаимосвязь математики с физикой, да и вообще с любой реальностью, поэтому такое требование на счет согласованности результатов их вычислений с реальностью, ставит математиков в безвыходное положение и уводит почву из под их ног.Но вернемся к калькуляторам и компьютерам. Как же они умножают на ноль, делят на ноль и возводят в нулевую степень?А никак 🙂

Они просто при любой операции делают проверку аргументов на ноль и если он есть, тупо ПОДСТАВЛЯЮТ «правильный ответ»: В случае с умножением подставляют ноль, в случае деления включают ошибку переполнения, а в случае возведения в степень подставляют в ответ 1. 0=1 это математическая аксиома.

Ну, так принято в математике считать. Это называется у них невыводимой истиной, потому что по правилу вывода степенной функции из умножения, ну никак 1 не получается, если ему следовать.В общем, математикам очень не хочется признавать связь реальности с их математическими конструкциями, хотя только тем и занимаются, что пытаются описывать физику через формулы (это кстати их прямая обязанность между прочим).

А тут такая подстава…двойные стандарты. Всю ньютоновскую механику описали, за квантовый мир принялись, а там кроме математики вообще ничего нет…верьте нам. А как на ноль помножить, так наша хата с краю, на закон сохранения нам плевать, и вообще мы тут рыбу заворачиваем. Вы как говориться либо трусы наденьте, либо крестик снимите.

Где же истина на самом деле и что такое ноль в математике и в двоичной логике, самое интересное.На самом деле, ноль, это не математическое понятие, а скорее геометрическое. Под нулем правильно понимать точку, разделяющую границы систем координат. 0=N/N Потому и получается 1…корректно заметьте получается, потому что операция с нулем это операция с системой, а не с пустым множеством. Это операция с ИЗМЕНЕНИЕМ критериев истинности системы на противоположные по знаку.

И ноль это не НИСКОЛЬКО, а 1 раз по дефолту, если функция задана а число повторений нет. Значит ее нужно сделать минимум 1 раз. Это логика! Тут нельзя назначить сложение и не сказать сколько раз. Сказал сложение-складывай. Все предельно однозначно, как и должно быть в двоичной логике.

Только такое ТЗ на вычисление может корректно интерпретироваться компьютерным железом. Но…этого не делают, хотя функцию инверсии широко применяют для вычитания…ведь в булевской логике нет функции вычитания, есть только сложение. Примерно по той же причине что и фарш невозможно провернуть назад…из за вектора течения времени…связь математики и логики с физикой опять…что поделать.

Поэтому чтобы вычесть применяя для этого сумматоры, прибегают к хитрости с подменой критериев истинности системы на зеркальные. ..обратные и при помощи инверсии делают т.н. допкод.А по сути, используют свойства нуля переворачивать всю логику в обратную сторону.Т.е. чтобы превратить прямую функцию сложения в обратную, нужно просто отзеркалить двоичное слагаемое побитной инверсией, потом сложить с другим слагаемым, а затем полученное вновь вернуть в старую систему побитной инверсией.

И вуаля, смена исходных критериев истины с 0-ложь, 1-истина, на противоположные с возвратом все на место после сложения, в итоге выдает результат как вычитание. Хитро?Очень хитро.

Вот и формулка, упрощенная…А-Б=i(iA+B)где A и В двоичные числа, а i — операция побитной инверсии (он же допкод).

Но ни один математик вам не объяснит в чем истинная сущность допкода и на каком основании что то «левое» вдруг является неотъемлемой частью вычислительной операции.Но это далеко не вся истина, которая скрывается за системными операциями с нулем. Мы же так и не ответили почему умножение на ноль приводит N к аннигиляции. Но это в следующий раз. ..если материал наберет достаточно просмотров.

Деление на ноль | зеркало лурк Lurkmore

Материал из Lurkmore

У этой страницы нет проверенных версий, вероятно, её качество не оценивалось.

Перейти к: навигация, поиск

«	Это уникальный случай умножения нуля на бесконечность, представленный на целом машинописном листе.	»
— Татьяныч

«	Деление на ноль это как секс. Всем можно, а школьникам нет.	»
— Анонимус

«	Hmmm… no, no… that’s wrong… that’s not right, either… a divide by zero error here… hmmm… you don’t seem to have the intelligence necessary to grasp higher mathematics.	»
— Проконсул Грегори из Fallout 2, проверяя результаты испытания ГГ

«	— Этой ночью, Люся, мы с тобой будем делать то, чего делать нельзя!. . — На ноль делить, что ли?	»
— Анекдот

«	На ноль делить нельзя. Потому что так сказал калькулятор.	»
— Анекдот

«	Можно сдохнуть, пытаясь делить разные числа на ноль.	»
— Кровосток

Деление на ноль (Дивайд бай зиро) — невозможное математическое действие.

OH SHI~

Содержание 1 Деление на ноль как мем 2 Деление на ноль в математике 2.1 Алгебра 2.2 Делить на бесконечно малую 2.3 Нестандартный анализ 2.4 Теория функций комплексной переменной 2.5 Точка зрения прикладной алгебры 2.6 Алгебра, она такая алгебра… 2.7 Мнение Wolfram|Alpha 2.8 Мнение ГСМ-небыдла 3 Деление на ноль в программировании 4 Деление на ноль в образной логике 5 Тривия 6 Помножить на ноль 7 Bash. org.ru о делении на ноль 8 Галерея 9 См. также 10 Примечания 11 Ссылки

Деление на ноль как мем

«	Эта грустная история о прекрасной восточной девушке Наноль, которая любит двоих прекрасных и мужественных юношей и не может выбрать. Юноши тоже любят ее. Казалось бы, в нынешние-то времена, зажить бы им простой и дружной семьей. Но трагедия в том, что Наноль делить нельзя.	»
— Смехуёчки

«	Я спускаюсь один в глубину ночных кварталов. Сам себе господин, нас таких осталось мало. Я забыл свою роль, я начальник всей Вселенной. Мне неведома боль, я делил все на ноль.	»
— группа «Технология»

Физически (или физиологически) пребывать в процессе деления на ноль вполне можно. Стой себе и дели, никто же законодательно не запрещал. Проблема обычно заключается в том, чтобы получить из этого процесса хоть какой-то обоснованный наукой результат (или создать потом Вселенную заново). Проще говоря, делить на ноль можно, разделить — нельзя.

И даже в этом вашем ХоНе

Деление на ноль давно стало одним из классических образцов математического юмора, поскольку в среде математиков считается, что попытка представить получающуюся в итоге актуальную бесконечность (неотъемлемая часть успешного деления на ноль, в противоположность потенциальной бесконечности из теории пределов) ведёт к сумасшествию совершившего это. И нуля-то самого никто никогда не видел (даже математики), «а тут такоє»… Алсо, в обществе прикладных математиков пожелание «делись оно всё на ноль» является аналогом широко известного рецепта «ебись оно всё конём». Поскольку численность математик-кунов в среде компьютерщиков и истинных хакеров составляет лишь чуть менее, чем 42%, этот мем проник и туда, а с возникновением форчана обогатился представлением о том, что удачное деление на ноль неотвратимо вызывает не только безумие самого экспериментатора, но и создание сингулярной аномалии бесконечной массы в точке пространства, где было произведено удачное деление. Со всеми вытекающими последствиями.

Среди менее продвинутых товарищей деление на ноль упоминается в том же смысле, что и умножение на него же. Хуже того, в очень многих статьях этого сайта можно найти это словосочетание именно в ошибочном смысле, противоположном истинному. Это ещё один аргумент в пользу ввода матан-капчи. Или против неё.


Деление на ноль в математике

ACHTUNG! Опасно для моска! Министерство здравоохранения Луркмора предупреждает: вдумчивое чтение нижеследующего текста способно нанести непоправимый ущерб рассудку. Вас предупреждали.

Не понял…

Поле действительных чисел, помимо всего прочего, как и любое другое поле, является аддитивной группой, и ноль — нейтральный элемент этой группы. Множество ненулевых действительных чисел, снабжённое операцией умножения, является мультипликативной группой. Поэтому запиливая ноль в эту группу, мы превращаем её во что-то группой не являющееся, ибо понадобилось бы как минимум запилить туда обратный нулю элемент, который, очевидно, не может быть действительным числом, а если запилить НЁХ как обратку, то ещё больше проблем будет, так как остальные элементы действительные, и понадобилось бы прописать, как они взаимодействуют с обраткой, и даже если всё цивильно получится, то полученное множество уже не будет даже изоморфно привычному множеству действительных чисел и вообще не будет кольцом. Такие дела.

Алгебра

А настоящие быдломатематики знают, что если определить операцию деления на ноль, то тогда выходит, что все числа совпадают и равны 1, так что лучше на ноль не делить вовсе…

Действительно, для любого числа a верно:

0 ∙ a = 0

Разделив на ноль получим:

а = 1

Проблема лишь в том, что 0 нами тоже признан числом и мы только что доказали, что

0 = 1

,

что по крайней мере не так с точки зрения умножения, ибо умножение на 1 дает исходное число, а умножение на 0 дает 0. Впрочем, если все числа одинаковые, то это одно и то же. Хотя есть теория, что все числа делятся (в прямом и переносном смыслах) на 0, 1 и прочие числа.

Действительно, пусть у нас есть два произвольных разных числа, a и b, и мы умеем делить на ноль:

0 ∙ a = 0
0 ∙ b = 0
0 ∙ a = 0 ∙ b
делим на 0, и получается
a = b

Таким образом «доказывается», что 2 + 2 = n. (где n — любое число)

(2+2)∙0 = 0
n∙0 = 0
(2 + 2) ∙ 0 = n ∙ 0
делим на 0, и получается
2 + 2 = n

Или, например, что 1=2:

х²—х²=х²—х²
x(x—x)=(x+x)(x—x)
x=2x
1=2

(спойлер: {{{1}}})


А суть в некорректно поданном развязании. Допустим

0 • 0 = 0
0 ∙ a = 0
0 ∙ b = 0
0 ∙ a = 0 ∙ b
разбиваем на
(a ∙ 0) ÷ 0 = (a ∙ 0) ÷ (0 • 0) = (a ÷ 0) ∙ (0 ÷ 0)
(b ∙ 0) ÷ 0 = (b ∙ 0) ÷ (0 • 0) = (b ÷ 0) ∙ (0 ÷ 0)
после чего совершается деление на ноль приводящее к неопределённости (от слова «не определено»).

При этом следует отметить, что для получения запрета деления на ноль достаточно взять множество, определить на нём обратимую операцию сложения с нейтральным элементом (нулём), обратимую же операцию умножения со своим нейтральным элементом (единицей) и стандартную аксиому дистрибутивности (a(b+c)=ab+ac) о связи между этими операциями. То есть деление на ноль неопределено не только для чисел известным всем, но так же и в кольцах вычетов, и для матриц, и для комплексных чисел, и для любого другого множества с двумя обратимыми операциями, связанными дистрибутивностью. Неопределённость (как невозможность непротиворечиво определить операцию деления) возникает несмотря на наличие/отсутствие коммутативности, ассоциативности и прочих няшных свойств операций. Проблема в том, что если очень захотеть алгебру с делением на ноль (то есть с двумя обратимыми операциями, но без «распределительного закона»), как следствие получим, что в общем случае даже 0 • 0 может быть не равен нулю, и вообще теряется какой-либо смысл сложения и умножения.

Делить на бесконечно малую

Делить на бесконечно малую функцию можно, при этом получается бесконечно большая функция. То есть за результат деления на такой «ноль» можно принять предел. Засада в том, что этот предел может не существовать (получатся бесконечности разных знаков при стремлении к нулю с разных сторон, либо вообще какая-нибудь хуйня), и для каждой такой функции он свой. В общем, не ноль, а где-то рядом.

Например, 1/x стремится к +∞ при x→+0 и -∞ при x→-0. Однако, если по условиям задачи мы стремимся к нулю определенным образом (и предел существует), «деление» вполне дает результат. Например, время, за которое мы пройдем расстояние в 100 километров со скоростью v, равно 100/v. При устремлении v к +0 время, за которое мы пройдем вперёд сотню километров стоя, будет +∞.

Нестандартный анализ

Для тех, кому на ноль делить все-таки очень уж хочется, в нестандартном анализе придумали гипердействительные числа; так, например, существуют нестандартные числа не равные нулю, но меньшие всех стандартных действительных чисел по модулю. При этом, на ноль делить все равно нельзя. Школьные знания здесь не помогут.

Теория функций комплексной переменной

В расширенной комплексной плоскости делить на ноль можно. Это связано с тем, что в ней бесконечность — не предельно-недостижимое значение, а вполне конкретная точка, соответствующая точке (0, 0, 1) в стереографической проекции. Правда, при этом подобное множество внезапно перестает быть полем, но это мало кого волнует.

Точка зрения прикладной алгебры

Деление — это не атомарная операция, а макрос — взятие обратного по умножению от делителя и умножение на делимое. Например, обратный двойке по умножению — это 2^-1, 3/2 = 2^-1 ∙ 3 и т. д. Операция взятия обратного по умножению определена для всех чисел, кроме нуля (говорят — нуля по сложению). Деление на ноль на самом деле не запрещено, эта операция просто не определена, как перемножение паровоза на самовар. Так-то.

Алгебра, она такая алгебра…

Отсутствие обратного элемента для нуля это ещё полбеды. В целых числах тоже нет обратного, скажем, к 42, но это не мешает найти его в рациональных (1/42). Главная проблема здесь в том, что ноль является делителем нуля, а значит на него нельзя сокращать: из тождества «0 ∙ x = 0 ∙ y» ни разу не следует, что «x = y». Причём, если в хороших числовых системах такие корчи происходят только с нулём, то уже в седенионах или ещё проще функциях на отрезке корчи случаются на каждом шагу: вы ничего не можете сказать о функциях, для которых f(x) ∙ g(x) = 0.

Мнение Wolfram|Alpha

Если ввести в Вольфрам 1/0, то получим ~∞, а если 0/0 — INDETERMINATE.
На запрос x=(0/0=1)*1 он отвечает… x=0 (он воспринимает сабж как логическое выражение по типу языка С и таки да: 0/0 не равно единице, что он и возвращает нулем…булевым)

Мнение ГСМ-небыдла

На самом деле, вопрос о делении на ноль вещественного числа (ну или там мнимого, в общем, отличного от нуля) не имеет смысла. Почему-то большинство людей воспринимают ноль как какое-то очень-очень маленькое, но все-таки имеющее невообразимо ничтожное значение число. Тащемта, да, но нет. Если мы имеем дело с теорией пределов, то 0 — это не ничто и не отсутствие значения, а неопределенная бесконечно малая величина. Вследствие этого операция 0/0 и не имеет смысла, так как оба операнда представляют из себя неопределенные величины, а следовательно, нельзя сделать вывод об их равенстве или неравенстве.

Что тогда получается? Допустим, мы делим 8 на 2. При этом мы считаем, сколько нужно взять двоек, чтобы получить восемь. Ответ очевиден — двойку надо взять четыре раза. А если мы делим 8 на 0, то нам нужно посчитать, сколько нужно взять нулей, чтобы получить восемь. Ответ — да нисколько. Сколько бы мы нулей не взяли, хоть сто миллионов, хоть бесконечность, хоть сто миллионов бесконечностей, мы никогда не получим вещественного числа. Из ничего нельзя получить что-то вещественное, как ни старайся. Короче, в человеческом языке и сознании не существует терминов для обозначения количества нулей, которые могут превратиться в восьмерку, или например 9000. Именно поэтому математики и договорились не ебать мозга друг другу и считать этот вопрос бессмысленным.

Зато ноль на ноль умножать можно вполне! Сколько раз нужно взять ноль, чтобы получить ноль? Да сколько угодно! 0*8=0. 0*100500=0, не так ли? Вот, поэтому неопределенность типа 0/0 может равняться чему угодно!

Деление на ноль в программировании

В программировании числа целого типа (попытаться) поделить на ноль в принципе можно, но получается какая-то хуита: процессор x86 при попытке выполнить операцию целочисленного деления на ноль формирует особый случай (исключение) с номером 0, вектор которого также находится по адресу 0. Другими словами, процессор славное действие деления на ноль до конца не доводит, а перескакивает в другое место, обычно сообщая юзеру о внезапном просирании всех полимеров. На самом деле, поскольку деление целых чисел осуществляется на микропрограммном уровне как вычитание со сдвигом и при этом признаком окончания процесса является обнуление остатка от делимого, нулевой делитель означает бесконечное число циклов с одинаковым ненулевым результатом. Ч.т.д. А вот и нет. Делимое списывается в остаток и возвращается −1. Так-то!

Зато числа с плавающей запятой делить на ноль можно невозбранно. При аффинном представлении бесконечностей получается плюс бесконечность (+INF) или минус бесконечность (-INF) — зависит от знака делимого числа. При проективном представлении — беззнаковая бесконечность (INF) в любом случае. Самое интересное происходит при делении на ноль самого ноля: результатом будет специально зарезервированное для подобных ситуаций (вроде извлечения квадратного корня из отрицательного числа или умножения нуля на бесконечность) значение «Не Число» (NaN, Not a Number).

Альзо, в одной книжке по процессорам Intel сказано, что NaN и Inf — вполне обычные числа. Если не обращать внимания на исключения, то с ними можно производить операции: NaN + p = NaN, NaN*p = NaN и т. д. и т. п., однако p^NaN = 1, так как корень нулевой степени из p⁰ таки равен единице (конечно же, при p != 0).

В КофеСкрипте при делении числа на ноль возвращается «Infinity».

Также, в лаконичном языке программирования J сабж даёт бесконечность, обозначаемую как «_». Адепты данного языка ехидно заявляют, что ошибка при делении на ноль возникает исключительно в головах быдлокодеров, пытающихся освоить мозголомный синтаксис J.

Деление на ноль в образной логике

Если попытаться с помощью образной логики изобразить такой математический процесс как деление, то получится раздача неких предметов неким субъектам. Например: 10 делим на 2 = мать раздаёт 10 яблок двум своим детям поровну, и у каждого в руках оказывается по 5 штук. Поэтому с точки зрения образной логики «деление на ноль» это «отсутствие деления». Скажем, 10 : 0 это 10 яблок, которые никто никому не раздаёт. Деление же ноля на ноль это «пустая корзина, в ней нет ни одного яблока, вот потому их никто никому не раздаёт».

Осталось только объяснить, почему «10 ∙ 0» равно нулю, а не отсутствию умножения. Добавим правило «от перестановки мест множителей итог не меняется» и получим «ноль, повторённый десять раз», а он равен нулю.

Если 10 яблок раздать 0 человек(ни дать никому), то это можно сделать(ни дать никому) сколь угодное число раз, поэтому результат будет, как при использовании пределов, бесконечность. Аналогично можно представить, что мы можем 10 раз взять 0(ничего), либо 0(ни разу) (не)взять по 10, итог один(sic!) — 0.

Алсо, если считать на палочках (как в детском саду считали), то в такой арифметике будут не все операции деления и нельзя будет вычесть из меньшего числа большее — поскольку нет дробных палочек и отрицательных палочек тоже нет.

Тривия

• В рассказе Леонида Каганова «Гамлет на дне» главный герой под воздействием сектантов ушёл в подземелье и делил на ноль долгое время, пока не появился чудо-спасатель.
• «Two Divided By Zero» — песня из дебютного альбома расово британского синтипоп-дуэта Pet Shop Boys ([1]). Примечателен факт, что металлический голос, произносящий во время песни одну и ту же фразу «two divided by…», принадлежит электронному «говорящему» калькулятору, который вокалист группы, Нил Теннант, решил подарить своему отцу^[1]
• ВИА «Кровосток» в тексте, простите, песни «Сдохнуть» как бы предупреждает: «можно сдохнуть пытаясь делить разные числа на ноль».
• У группы gastel?o есть песня «:0». Текст песни подтверждает [2], что его придумавший явно изящно поделил…
• Деление на ноль — это еще ничего. Для умножения на ноль уже придумали водородные и атомные бомбы типа Fat Boy.
• На испытаниях Су-24 регулярно случался отказ аппаратуры бомбометания. Причем происходило это только в том случае, если на цель заходил летчик-испытатель Ильюшин. Причина оказалось тоже не сложной. Только он заходил на цель с точностью, превышавшей машинную точность. Получался «машинный нуль», после чего шел сбой из-за попытки деления на ноль.
• В интернетах гуляет байка об аналогичном случае: мотороловцы клеили истребитель для Израиля, и он над Мертвым морем (высота над уровнем моря — нулевая или отрицательная) пытался делать сабж и самовыпиливался
• При выводе на орбиту одной космической кастрюли, созданной в лабораториях NASA, системы телеметрии в какой-то момент внезапно начали заполнять экраны мониторов сообщениями «Ошибка деления на ноль». В результате персонал был слегка обеспокоен, потому как все выглядело так, что спутник придется слить. Однако разработчик соответствующей подсистемы храбро заявил: «Я понимаю, что происходит. Это сейчас пройдет. Беру всю ответственность на себя». Самая мякотка тут в том, что этим самым разработчиком был один из Summer Student, подрабатывавший в NASA во время летних каникул. Правда, история закончилась обычным пиндосским хэппи-эндом, и в дальнейшем подобных проблем не возникало.
• Алсо, существует одноименный фантастический рассказ за авторством Теда Чана. Текст повествует об учёном-математике, который тронулся умом, внезапно обнаружив полную несостоятельность любимой науки. Мораль проста — гиковство в любой форме до добра не доводит. Такие дела.
• Алсо, у пейссателя есть книжка, где одна зверушка с IQ > 9000 способна буквально войти в кому, пытаясь в уме произвести операцию деления на ноль.
• В эпичной игре «Ядерный Титбит» свою роль в развязке сюжета сыграл суперробот, по всемогуществу сравнимый с Богом. «Когда его включили он начал смеяться. И не перестает до сих пор… Он может вообще все, но его волнует один единственный вопрос: Что будет, если единицу разделить на ноль». Для устранения бага требовались внеземные технологии и человеческий мозг, так как только люди могут держать иррациональность в голове, не сходя с ума.
• Алсо, у этого вашего Алистера Кроули есть

Каждое число равно бесконечности: в них нет различия

• А еще это умеет делать калькулятор андроида (пруфлинк для скачивания) — при делении любого числа на ноль он выдает бесконечность. (При делении ноля на ноль он честно пишет «Ошибка». Проверено на 2.3.3 — NaN)
• А в HL2 есть оружие, делящее на ноль всех (в цитадели гравиган меняет цвет и боевые параметры). И AR2 тоже делит, шариком.
• В винрарном квесте «The Longest Journey» можно в прямом и переносном смысле поделить на ноль темного колдуна при помощи калькулятора.
• В махо-сейнен манге Mahou Senki Lyrical Nanoha Force у одного из главных героев есть магическое устройство Devider и заклинание Divide by Zero.

Деление на ноль (iPod Touch)

Деление на ноль (Facit ESA-01)

• При попытке деления на ноль встроенным калькулятором телефона Sony Ericsson и Nokia всплывает окошко, которое гласит «деление на ноль запрещено». Видимо, сони с нокой решили не мучать себе моск, да и другим тоже. Motorola ZN5 с английским языком при делении на 0 пишет E. Что означает Error — Ошибка — с расово-верного пиндосского языка.
• Встроенный калькулятор Windows 7 знает, что деление на ноль невозможно. Теперь и ты это знаешь. Однако, 0/0 сделать пытается, как всегда, безрезультатно.
• Встроенный калькулятор Mac OS X при делении на ноль, так и пишет: «деление на ноль». Но в последней версии, OS X Lion — «Не число».
• В расово математическом Emacs Calc при делении на ноль получаются интересные числа вида «2/0», которые при определенном умении можно даже превратить во что-то вроде «3 (2/0 + 1)». Однако попытка умножить, например, 5 на 1/0 все же заканчивается ошибкой «Division by zero».
• Первые олдскульные советские программируемые калькуляторы типа МК-52 были способны выполнять операцию деления на ноль, после чего их цифровой дисплей становился способным показывать некоторые буквенные символы, что активно использовалось продвинутыми юзерами таких калькуляторов для создания различных надписей на экране с целью их показывания друг другу и для написания экранных сообщений псевдоигровых программ в рамках возможностей данного вида калькуляторов.
• У братьев Стругацких в «Понедельнике…» делением ноля на ноль (причём с помощью настольных арифмометров) занимается целый отдел Абсолютного Знания. Что характерно, кстати, на настольном арифмометре поделить на ноль чисто технически возможно — просто после этого каретка уходила до предела вправо и там задумчиво останавливалась. Ну вроде как сейчас на калькуляторе MA ERROR пишется. Получалось, стало быть, что сотрудники отдела АЗ просто хуи на работе пинали, а не занимались антинаучной хуйнёй. Поэтому в более поздних изданиях «Понедельника…» они уже умножали ноль на бесконечность — вот этот подвиг повторить что на арифмометре, что на калькуляторе уже затруднительно будет, нес па?
• Один из первых процессоров серии Pentium при выполнении операции «деление на ноль» просто напросто зависал; приходилось перезагружать компьютер чудо-кнопкой Reset. Запрос деления на ноль мог возникать в случае коряво написанных программ или же мог быть вызван искуственно посредством Windows-калькулятора. Ошибка была исправлена в следующей модели пня.
• Олимпиады и ногомячные чемпионаты являются вовсе не попыткой создания благоприятной распильной среды, а результатом деления на ноль бюджета этой страны.
• У попсовой группы ВиаГра есть песня «Но я играю эту роль…». Так вот, анонимус однажды IRL слышал, как незнакомая красивая тян исполняла пародию на эту песню, и один из рефренов этой пародии звучал так: «Но я играю эту роль, Делю трёхзначные на ноль, В науке я неутомима. Мне теорема по плечу, Но я бессмертья не хочу, Вези в дурдом меня, любимый!» (Другие рефрены были еще более доставляющими: «…курю табак, пью алкоголь, И мне становится голимо…», «…я из ружья стреляю в моль, Но почему-то чаще мимо…»).
• Формально такими операциями, как деление и умножение на ноль (обычно алиенов, мутантов, роботов и прочей подобной пиздобратии), занимаются герои 95% быдло-фантастических книжонок и YOBA-игр. Пипл хавает и просит добавки.
• У американской панк-рок группы The Offspring есть песня Dividing By Zero.
• Тема деления на ноль чуть боле чем полностью раскрыта в аниме Cardcaptor Sakura Movie 2: The Sealed Card. Этой сп

Деление — значение, шаги, алгоритм, примеры

Деление — одна из четырех основных математических операций, три другие — сложение, вычитание и умножение. Проще говоря, деление можно определить как разбиение большой группы на более мелкие группы таким образом, чтобы в каждой группе было равное количество элементов. Это операция, используемая для равного группирования и равного распределения в математике. Давайте подробно узнаем об операции деления в математике в этой статье.

1.	Что такое дивизия?
2.	Части отдела
3.	Алгоритм деления
4.	Как сделать Раздел?
5.	Деление с остатками
6.	Имущество подразделения
7.	Часто задаваемые вопросы по подразделению

Что такое деление?

Деление — одна из основных арифметических операций в математике, при которой большее число разбивается на меньшие группы с одинаковым количеством элементов. Например, для спортивного мероприятия, если 30 студентов нужно разделить на группы по 5 человек, то сколько всего групп будет сформировано? Такие задачи легко решаются с помощью операции деления. Здесь нам нужно разделить 30 на 5. В результате получится 30 ÷ 5 = 6. Итак, будет 6 групп по 5 учеников в каждой. Вы можете проверить это значение, умножив 6 и 5, что даст вам исходное число 30.

Деление Определение

Деление — это процесс повторяющегося вычитания. Это обратная операция умножения. Он определяется как акт формирования равных групп. При делении чисел мы разбиваем большее число на более мелкие так, чтобы умножение этих меньших чисел было равно большему взятому числу. Например, 4 ÷ 2 = 2. Это можно записать как факт умножения 2 × 2 = 4.

Символ деления

Деление обозначается математическим символом, состоящим из маленькой горизонтальной линии с точкой над каждой. и ниже линии. Есть два основных символа деления, которые обозначают деление двух чисел. их ÷ и /. Например, 4 ÷ 2 = 2 и 4/2 = 2.

Части отдела

Части деления означают названия терминов, связанных с процессом деления. Есть четыре части деления: делимое, делитель, частное и остаток. Давайте посмотрим на пример деления, приведенный ниже, и поймем значения этих четырех частей деления.

Здесь, когда мы делим 105 на 8, мы получаем значения делителя, делимого, частного и остатка. Посмотрите на таблицу ниже, чтобы понять значение этих терминов.

Условия	Описания	Значения
Дивиденд	Число, которое нужно разделить	105
Делитель	Количество равных групп, которые необходимо составить, или число, на которое мы делим делимое	8
Частное	Значение/ответ, полученный после выполнения деления	13
Остаток	Оставшееся или пропущенное значение, не входящее ни в одну группу	1

На изображении выше написано, что «Дивиденд = Делитель × Частное + Остаток». Это уравнение удовлетворяет приведенным выше значениям, но будет ли оно удовлетворять значениям делимого, делителя, частного и остатка при каждом делении? Давай выясним.

Алгоритм деления

Алгоритм деления представляет собой уравнение, которое формирует связь между всеми четырьмя частями деления. В любом факте деления произведение делителя на частное, прибавленное к остатку, всегда равно значению делимого. Таким образом, общая формула деления: Дивиденд = (Делитель × Частное) + Остаток . Это известно как алгоритм деления.

Приведенная выше формула помогает нам проверить значения частного и остатка, полученные после выполнения деления. Мы можем подставить значения частного, остатка и делителя в приведенное выше уравнение и проверить, совпадает ли результат с делимым или нет. Если мы получили дивиденд, значит, мы правильно выполнили шаги деления. Если нет, значит, в наших расчетах есть ошибка, которую нужно исправить. Давайте возьмем один пример и посмотрим, удовлетворяет ли он приведенному выше алгоритму деления или нет. Разделите 17 на 3. Разделив 17 на 3, мы получим 5 в частном и 2 в остатке.

Делимое = (Делитель × Частное) + Остаток

17 = (3 × 5) + 2

17 = 15 + 2

17 = 17

Следовательно, проверено.

Как сделать Раздел?

Однозначное деление можно выполнить с помощью таблицы умножения. Например, чтобы решить 24 ÷ 6, нам просто нужно посмотреть, что нам нужно умножить на 6, чтобы получить 24 в качестве ответа. Ясно, что 6 × 4 = 24, следовательно, 24 ÷ 6 = 4. Когда дело доходит до деления чисел на большие числа, то мы можем использовать метод деления в длину. Давайте возьмем пример 65, разделенного на 5, чтобы понять это. Выполните следующие действия, чтобы научиться выполнять деление:

• Шаг 1: Нарисуйте символ деления ⟌ и напишите делитель (5) слева от него и делимое (65), заключенное под этим символом.
• Шаг 2: Возьмите первую слева цифру делимого (6). Проверьте, больше ли эта цифра делителя или равна ему. [Если первая цифра делимого меньше делителя, то считаем первые две цифры делимого]
• Шаг 3: Затем разделите на делитель и запишите ответ сверху как частное. Здесь частное 6 ÷ 5 равно 1,
• Шаг 4: Вычтите произведение делителя и цифры, записанной в частном (5 × 1), из первой цифры делимого и запишите разницу ниже. Здесь разница 6 — 5 = 1.
• Шаг 5: Запишите следующую цифру делимого (если она есть). Следующая цифра в делимом 5.
• Шаг 6: Повторяйте тот же процесс, пока не получите остаток меньше делителя.

Посмотрите на приведенное ниже изображение, показывающее вышеуказанные этапы деления.

Разделение с остатками

Не всегда обязательно иметь в остатке 0. Если делимое не кратно делителю, то получаем ненулевой остаток. Когда мы получаем ненулевой остаток при делении одного числа на другое, это называется делением с остатками. Возьмем пример раздачи 9 воздушных шаров 2 детям поровну так, чтобы у обоих детей было равное количество воздушных шаров. Можно ли это сделать, не получая остатка?

Разделив 9 на 2, мы получим 4 в частном и 1 в остатке. Мы можем сделать 2 группы по 4 шарика в каждой, но останется 1 шарик. Посмотрите на изображение ниже, на котором показано деление с остатком (9 ÷ 2).

Попробуйте ответить на следующие вопросы на деление и посмотрите, получится ли у вас ненулевой остаток или нет: 63 ÷ 9, 76 ÷ 13, 89 ÷ 8, 34 ÷ 5 и 27 ÷ 3.

Свойства отдела

Теперь давайте рассмотрим некоторые свойства операции деления, которые помогут вам лучше понять эту операцию. Ниже перечислены некоторые свойства деления:

• Деление на 1: Любое число, деленное на 1, дает само число. Другими словами, если делитель = 1, то делимое = частное.
• Деление на 0: Значение числа, деленного на 0, не определено, т. е. n/0 = не определено, где n — любое число.
• Деление само на себя: Если мы разделим число само на себя, мы всегда получим 1 в качестве ответа. Другими словами, если делимое = делителю, то частное = 1,
.
• Деление 0 на любое число: 0 деление на любое число всегда дает 0. Некоторые примеры: 0 ÷ 4 = 0, 0 ÷ 9 = 0, 0 ÷ 5754 = 0 и т. д.
• Деление на 10: Если мы разделим число на 10, то цифра, стоящая на месте единиц, всегда будет остатком, а оставшиеся слева цифры будут частным. Например, 579 ÷ 10 = 57 р 9.
• Деление на 100: Если мы разделим число на 100, то число, составленное из разрядов единиц и разрядов десятков, всегда будет остатком, а оставшиеся слева цифры будут частным. Например, 8709÷ 100 = 87 р 9.

☛ Статьи по теме

Чтобы узнать больше о фактах разделения, ознакомьтесь с еще несколькими интересными статьями, перечисленными ниже, и изучите основы.

• Двоичный раздел
• Деление дробей
• Калькулятор длинного деления

 

Примеры разделов

1. Пример 1: У Лизы 2 щенка. Она купила 8 жевательных костей, чтобы накормить их обоих поровну. Сколько костей достанется каждому щенку?

   Решение:

   Дано, количество щенков = 2, а количество костей = 8. Таким образом, количество костей у каждого щенка = 8 ÷ 2 = 4. Таким образом, каждый щенок получит 4 кости.

2. Пример 2: Отец Евы испек для нее печенье. Пал и Эйкон, ее лучшие друзья, решили преподнести ей сюрприз, навестив ее без предупреждения. Если было 9 печенек, то сколько отец Евы дал Еве, Палу и Эйкону, чтобы они были разделены поровну? Используйте алгоритм деления, чтобы проверить свой ответ.

   Решение:

   Учитывая, что количество файлов cookie = 9, а количество людей, которым нужно поделиться файлами cookie = 3. Количество файлов cookie, разделенных поровну между Евой, Палом и Эйконом = 9 ÷ 3 = 3. Чтобы проверить деление, мы поместите значения в формулу, Делимое = (Делитель × Частное) + Остаток. Итак, 9 = 3 × 3 + 0 = 9. Значит, проверено.

3. Пример 3: Найдите значение частного и остатка при делении 75 на 3? Проверьте ответы, используя алгоритм деления.

   Решение:

   Здесь мы должны разделить 75 на 3. Таким образом, делимое = 75 и делитель = 3. Разделим 75 на 3, используя шаги деления.
   

   Следовательно, мы получаем, Частное = 25 и Остаток = 0.
   Чтобы проверить деление, мы подставим значения в формулу Делимое = (Делитель × Частное) + Остаток. Итак, 75 = 3 × 25 + 0 = 75. Значит, проверено.

перейти к слайдуперейти к слайдуперейти к слайду

Как ваш ребенок может освоить математические понятия?

Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу с Cuemath.

Записаться на бесплатный пробный урок

Практические вопросы отдела

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по подразделению

Что такое деление в математике?

В математике есть четыре основных арифметических действия: сложение, вычитание, умножение и деление. Среди этих четырех операций деление является одной из основных операций, которые мы используем в нашей повседневной деятельности. Это процесс разделения большой группы на равные меньшие группы. Например, разделите 25 на 5. Факт деления для этого примера будет 25 ÷ 5 = 5,9.0005

Какие существуют два типа разделения?

Подразделение разделено на две части: частичных и квотных моделей. Partitive используется при делении числа на известное количество слотов. Например, если мы разделим 4 на 2 слота, то сможем узнать, сколько предметов будет в каждом слоте. Quotative деление используется при делении числа на слоты измеряемой величины. Например, когда мы делим 4 на слоты по 2, мы можем определить, сколько слотов можно создать.

Что такое три части деления?

Тремя основными частями деления являются делимое, частное и делитель. В дополнение к этому, когда делитель не является делимым, мы получаем ненулевой остаток, который является четвертой частью деления.

Что такое метод длинного деления?

Метод длинного деления является наиболее распространенным методом, используемым для решения задач на деление. В этом процессе делитель записывается вне символа деления, а делимое помещается внутри. Частное пишется над чертой над делимым.

Каковы этапы отдела?

Шаги для деления перечислены ниже:

• Шаг 1: Возьмите первую цифру делимого. Проверьте, больше ли эта цифра делителя или равна ему.
• Шаг 2: Затем разделите на делитель и сверху напишите ответ.
• Шаг 3: Вычтите результат из цифры и запишите ниже.
• Шаг 4: Снова повторите тот же процесс.

Как делить, если делитель больше дивиденда?

В этом случае деления мы можем просто продолжать добавлять нули справа от делимого, пока не станет целесообразным дальнейшее деление. Кроме того, мы можем разделить частное на те же степени 10 для получения окончательного ответа, как только мы правильно выполним деление.

Как делить десятичные дроби?

Деление десятичных дробей так же просто, как и любое другое число. Все, что вам нужно сделать, это умножить десятичную дробь на степени десяти, пока не получите целое число. Затем вы можете выполнить обычный процесс деления. Получив окончательный ответ, обязательно разделите его на те же степени 10, на которые вы делили ранее.

Как пользоваться калькулятором делений?

Калькулятор деления — это инструмент, который используется для быстрого решения задач на деление в течение нескольких секунд. Попробуйте сейчас калькулятор деления Cuemath для решения задач, основанных на делении, и получите ответы за считанные секунды одним щелчком мыши.

Какие правила умножения и деления целых чисел?

Ниже приведены правила умножения и деления целых чисел:

• Положительный ÷ / × положительный = положительный
• Отрицательный ÷ / × отрицательный = положительный
• Отрицательный ÷ / × положительный = отрицательный
• Положительный ÷ / × отрицательный = отрицательный

Что такое символ деления?

Есть два символа деления: ÷ и /. ÷ рисуется путем размещения двух маленьких точек сверху и снизу небольшой горизонтальной линии. И знак / используется в основном с дробями, отношениями и процентами.

Почему деление на ноль не определено?

Деление на ноль не определено, потому что нельзя делить любое число на ноль. Это потому, что когда любое число умножается на ноль, ответ равен 0. Теперь подумайте об обратном. 1/0 будет иметь бесконечное значение. Мы не можем количественно определить это значение в математике. Следовательно, деление любого числа на ноль неопределенно.

Разделить Определение и значение | Dictionary.com

• Основные определения
• Синонимы
• Викторина
• Похожие материалы
• Примеры
• Британский
• Медицинский
• Научный

Показывает уровень сложности слова.

[ дих-вахид ]

/ dɪˈvaɪd /

Сохрани это слово!

См. синонимы для: разделить / разделить / разделить на Thesaurus.com

Показывает уровень оценки в зависимости от сложности слова.

---

Определение слова делить

глагол (используется с дополнением), разделять, разделять.

для разделения на части, группы, секции и т.п.

отделить или отделить от чего-то другого; разделитель; отрезать.

раздавать по частям; распределить по акциям; распределять.

для расщепления; часть.

разделить мнение или чувство; причина несогласия: вопрос разделил сенаторов.

различать виды; классифицировать.

Математика.

1. разделить на равные части методом математического деления; применить математический процесс деления к: восемь разделить на четыре равно два.
2. быть делителем без остатка.

для разметки единой шкалы на (линейке, термометре и т.п.).

Правительство Великобритании. разделить (законодательный орган, собрание и т. д.) на две группы при установлении голосования по вопросу.

глагол (используется без объекта), разделенный, разделенный.

разделить или отделить.

, чтобы поделиться чем-то с другими.

расходиться; ответвляться; fork: Дорога разделяет шесть миль отсюда.

для выполнения математического процесса деления: Он мог складывать и вычитать, но не научился делить.

Правительство Великобритании. проголосовать, разделившись на две группы.

сущ.

а дивизия: разделение на дороге.

Физическая география. линия или зона возвышенности между двумя соседними ручьями или водосборными бассейнами.

Архаичный. акт о разделе.

ДРУГИЕ СЛОВА СЛОВА разделить

2 разрезать, срезать.

3 перегородка, часть.

5 отчуждать, отчуждать.

6 сортировать, упорядочивать, распределять.

См. синонимы к слову разделить на Thesaurus.com

ПРОТИВОПОЛОЖНОСТИ ДЛЯ ДЕЛИТЬ

1 объединить.

См. антонимы слова «делить» на Thesaurus.com

ВИКТОРИНА

Сыграем ли мы «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?

Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!

Вопрос 1 из 6

Какая форма используется для указания обязательства или обязанности кого-либо?

Происхождение разделения

Впервые записано в 1325–1375 гг. ; Среднеанглийское (от англо-французского divider), от латинского dīvidere «отделять, разделять»

исследование синонимов слова «разделять»

1. См. отдельный.

ДРУГИЕ СЛОВА ОТ ОТДЕЛИТЬ

mis·di·vide, глагол, mis·di·vide, mis·di·vid·ing.pre·di·vide, глагол (используется с дополнением), pre·di·vid ·ed, pre·di·viding.re·di·vide, глагол, re·di·ed, re·di·viding.un·di·vid·ing, прилагательное

Слова, расположенные рядом с разделяющими

отчуждение, дайв-таблица, разделяй, разделяй, разделяемый, разделяй, разделяй и властвуй, разделяй, разделенное шоссе, дивиденд, покрытие дивидендов

Dictionary.com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc., 2022

Слова, связанные со словом делить

ломать, ломать, вырезать, резать, изолировать, разделять, отделять, разделять, подразделять, рвать, делить, сдвигать, нарезать, упорядочивать, разделять, разбивать, различать, варьировать, делить пополам, разветвлять

Как использовать разделять в предложении

• Некоторые школьные округа быстро мобилизовались, чтобы преодолеть этот цифровой разрыв.

  Творческие школьные планы могут противостоять неравенству, выявленному COVID-19|Суджата Гупта|8 сентября 2020 г.|Новости науки

• Я хочу сказать, что за период пандемии между имущими и неимущие.

  Подкаст: Как закон 135-летней давности позволяет Индии отключить интернет|Энтони Грин|2 сентября 2020 г.|MIT Technology Review

• Одно из самых важных противоречий в политике Миннесоты — это разногласия между разнообразными космополитическими городами-побратимами и «Большой Миннесотой», жители которой часто чувствуют себя обделенными по сравнению с метро.

  Почему Миннесота может стать следующим штатом Среднего Запада, который станет красным | Натаниэль Ракич ([email protected])|31 августа 2020 г.|FiveThirtyEight помогает преодолеть разрыв.

  Полная расшифровка: Шон Спайсер на «Шоу Карлоса Уотсона»|Дэниел Маллой|26 августа 2020 г.|Ози

• На самом деле игнорируется то, что мы уже знаем, а именно то, что пандемия обнажила все эти цифровые разрывы в образование.

  Трагедия на экзаменах в Великобритании напоминает нам, что алгоритмы не могут починить сломанные системы|Карен Хао|20 августа 2020 г.|MIT Technology Review

• Преодоление разрыва между полицией и теми, кто им не доверяет, потребует большего, чем протесты и символические жесты.

  Как разрешить полицейский кризис|Кели Гофф|5 января 2015 г.|DAILY BEAST

• Разложите тесто по подготовленным формочкам, поставьте формочки на противень и выпекайте около 20 минут.

  Приготовьте липкий карамельный пудинг Карлы Холл «The Chew’s»|Карла Холл|28 декабря 2014 г.|DAILY BEAST

• Разделите тесто пополам и очень аккуратно скатайте каждую половинку в круглый диск толщиной 1 дюйм.

  Приготовить пирог с тыквой и орехами от Карлы Холл «The Chew’s»|Карла Холл|26 декабря 2014 г.|DAILY BEAST

• «Вы можете бичевать лидеров; вы можете попробовать разделить нас на поколения», — сказал он.

  Шарптон вспоминает о борьбе за гражданские права в округе Колумбия против насилия со стороны полиции|Бен Джейкобс|13 декабря 2014 г. |DAILY BEAST

• В стране наблюдается крайняя демонстрация этого разделения.

  Пивные страны против винных стран|Клайв Ирвинг|7 декабря 2014|DAILY BEAST

• Его голова безвольно упала на руку Макрея, а остальная часть сообщения пошла вместе с игрой старого голландца через большой водораздел.

  Необработанное золото|Бертран В. Синклер

• Все еще дрожа на рассвете, я оседлал и поскакал к гребню ближайшего водораздела, чтобы насладиться первыми солнечными лучами.

  Необработанное золото|Бертран В. Синклер

• Я помню, как он однажды сказал — это было в Зоопарке — как жаль, что у него недостаточно денег, чтобы разделить их между всем кабинетом.

  Первые пьесы|А. A. Milne

• В случае роспуска ассоциации ее члены могут разделить ее имущество между собой.

  Удобная книга законов Патнэма для неспециалистов|Альберт Сидни Боллес

• Иногда в одной из этих ассоциаций возникает ссора, члены расходятся, кому достанется собственность?

  Удобная юридическая книга Патнэма для неспециалистов|Альберт Сидни Боллес

Британский словарь определений слова «разделить»

«разделить»

/ (dɪˈvaɪd) /

---

разделить на 5 частей или разделить на группы 900; разделить; часть

разделить или разделить по частям; распространять

, чтобы расходиться или вызывать расхождение во мнениях или целях. голосовать, разделившись на две группы

по категориям; классифицировать

для расчета частного (одного числа или количества) и (другого числа или количества) путем деления 50 на 10; разделить 10 на 50; делить на 10

(intr) для разделения дорог

(tr) для обозначения приращений (длины, угла и т. д.) с помощью гравировального станка

сущ. ; водоразделСм. также континентальный водораздел

а участок; разделить

Производные формы слова разделить

делимый, прилагательное

Происхождение слова разделить

C14: от латинского dīvidere разъединить, от di- ² + vid- отделить, от источника viduus скорбящий, vidua widow

Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Издательства 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012

Медицинские определения делить

делить

[ди-вид’

---

В. группы или ответвления.

Разбить на единицы измерения; выпускник.

Разделить и сгруппировать по виду; классифицировать.

Разветвляться, как кровеносный сосуд.

Для деления клеток.

Медицинский словарь Стедмана The American Heritage® Copyright © 2002, 2001, 1995, компания Houghton Mifflin. Опубликовано компанией Houghton Mifflin.

Научные определения деления

деления

[ ди-вид’ ]

---

Подвергнуть (число) процессу деления.

Быть делителем.

Использовать (число) как делитель.

Для выполнения операции деления.

Для деления клеток.

Научный словарь American Heritage® Copyright © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.

Люди в странах с развитой экономикой говорят, что их общество более разделено, чем до пандемии

Общественность расходится во мнениях относительно того, достаточно ли далеко зашли ограничения на общественную деятельность для борьбы с COVID-19

Пешеход спорит с полицейским в Памплоне, Испания, май 2020 г. (Иранзу Ларрасоана Онека/NurPhoto через Getty Images)

В этом анализе основное внимание уделяется отношению общественности к пандемии COVID-19 в 17 странах с развитой экономикой в ​​Северной Америке, Европе и Азиатско-Тихоокеанском регионе. Что касается данных за пределами США, отчет основан на общенациональных репрезентативных опросах 16 254 взрослых с 12 марта по 26 мая 2021 года в 16 публичных местах. Все опросы проводились по телефону со взрослыми в Канаде, Бельгии, Франции, Германии, Греции, Италии, Нидерландах, Испании, Швеции, Великобритании, Австралии, Японии, Новой Зеландии, Сингапуре, Южной Корее и Тайване. Общие выводы включают анализ тенденций в 13 странах, опрошенных как в 2021 г., так и летом 2020 г.

В Соединенных Штатах мы опросили 2596 взрослых американцев с 1 по 7 февраля 2021 года. Все, кто принял участие в этом опросе, являются членами Центра American Trends Panel (ATP), группы онлайн-опросов, которая набирается через национальные , случайная выборка адресов проживания. Таким образом, почти все взрослые американцы имеют возможность выбора. Опрос взвешен, чтобы быть репрезентативным для взрослого населения США по полу, расе, этнической принадлежности, партийной принадлежности, образованию и другим категориям.

Это исследование было проведено в странах, где можно проводить телефонные опросы, репрезентативные на национальном уровне. Из-за вспышки коронавируса личное собеседование в настоящее время невозможно во многих частях мира.

Чтобы учесть тот факт, что некоторые люди по-разному относятся к коронавирусу, в Южной Корее в опросе задавался вопрос о «вспышке Corona19». В Японии опрос задавался вопросом о «новой вспышке коронавируса». В Греции опрос задавался вопросом о «пандемии коронавируса». В Австралии, Канаде, Новой Зеландии и Тайване в опросе задавался вопрос о «COVID-19вспышка.» Во всех остальных опросах использовался термин «вспышка коронавируса».

Вот вопросы, использованные в отчете, вместе с ответами. Дополнительную информацию о методах опроса за пределами США см. в нашей базе данных методологий. Для респондентов в США см. дополнительную информацию о методологии ATP.

В связи с тем, что вспышка коронавируса уже второй год нарушает жизнь во всем мире, большинство людей считают, что их общество сейчас более разделено, чем до пандемии, согласно новому исследованию Pew Research Center, проведенному в 17 странах с развитой экономикой. В то время как в среднем 34% чувствуют себя более сплоченными, примерно шесть из десяти сообщают, что национальные разногласия ухудшились с начала вспышки. В 12 из 13 стран, опрошенных как в 2020, так и в 2021 году, чувство разделения значительно усилилось, в некоторых случаях более чем на 30 процентных пунктов.

Один из источников этих разногласий проявляется в том, как люди относятся к социальным ограничениям, с которыми они столкнулись во время пандемии, таким как приказы оставаться дома или предписания носить маски в общественных местах. В целом примерно четверо из десяти высказывают мнение, что в ходе пандемии уровень ограничений на общественную деятельность был примерно правильным. Почти такая же доля считает, что для сдерживания распространения вируса должно было быть введено на 90 724 больше 90 725 ограничений. Меньшинство населения считает, что их должно было быть 9.0724 меньше ограничений .

Выделяется Азиатско-Тихоокеанский регион: общественность там, скорее всего, считает ограничения на социальную активность правильными, в среднем 63% придерживаются этой точки зрения. С другой стороны, жители Северной Америки и Западной Европы чаще считают, что в их собственных странах ограничения не зашли достаточно далеко.

С идеологической точки зрения в большинстве стран те, кто идентифицирует себя как правый политический спектр, с большей вероятностью, чем те, кто слева, поддерживают меньше ограничений для сдерживания вируса.

Точно так же неоднозначны оценки экономических последствий пандемии. В среднем 46% говорят, что их экономика восстанавливается от последствий вспышки коронавируса, что свидетельствует о сильных сторонах экономической системы. Почти такое же количество респондентов считают, что неспособность их экономики восстановиться свидетельствует о слабости их экономики в целом. Это негативное мнение более распространено среди тех, кто хотел меньше ограничений во время пандемии.

В частности, в Западной Европе общественность несколько обеспокоена тем, достаточно ли далеко зашла экономическая помощь от Европейского Союза, чтобы смягчить последствия пандемии. Среди восьми государств-членов ЕС в среднем 48% говорят, что уровень экономической помощи на данный момент находится на должном уровне, а 40% говорят, что он недостаточен. Греки и испанцы больше всего обеспокоены тем, что усилия ЕС по оказанию помощи не зашли достаточно далеко.

Большинство людей в 17 населенных пунктах относительно удовлетворены общей реакцией на пандемию там, где они живут, хотя со временем во многих местах она снизилась. В среднем 60% считают, что их собственное общество хорошо справилось с коронавирусом, а 40% считают, что плохо. Многие люди в Азиатско-Тихоокеанском регионе, где показатели заболеваемости коронавирусом гораздо ниже, чем где-либо еще, особенно склонны говорить, что стратегии оказались успешными. Однако в нескольких странах, опрошенных как в 2020, так и в 2021 году, всего за год снизилась доля положительно оценивающих свои собственные ответные меры на пандемию. В Германии, например, 88% немцев в 2020 году одобряли реакцию своей страны на вирус, в то время как сейчас этого мнения придерживается только 51%, что на 37 процентных пунктов меньше. Снижение как минимум на 20 пунктов также отмечается в Нидерландах, Канаде и Японии.

Существует тесная взаимосвязь между тем, насколько положительно человек оценивает свое отношение к пандемии, и количеством смертей, связанных с вирусом, в этом обществе. Например, в Сингапуре, Новой Зеландии и Тайване зарегистрировано менее 100 смертей от COVID-19 (по состоянию на 15 мая 2021 г.). Эта общественность также имеет одни из самых положительных отзывов о мерах реагирования на пандемию там, где они живут: более девяти из десяти в каждом говорят, что их общество хорошо справилось со вспышкой. На другом конце спектра в середине мая в США погибло более полумиллиона человек, и менее половины американцев говорят, что их страна хорошо справилась с пандемией.

Однако, размышляя о будущих чрезвычайных ситуациях в области общественного здравоохранения, большинство опрошенных жителей выражают уверенность в том, что их система здравоохранения сможет справиться с такой ситуацией.

На индивидуальном уровне люди в 17 опрошенных странах с развитой экономикой теперь ощущают большее влияние в своей повседневной жизни. В среднем 65% говорят, что пандемия сильно или изрядно повлияла на их повседневную жизнь, и большинство населения придерживается этого мнения, за исключением Новой Зеландии и Австралии. В 10 из 13 стран, опрошенных как в 2020, так и в 2021 году, этот показатель значительно увеличился в ходе пандемии. Молодые люди, в частности, чаще всего сообщают, что их жизнь изменилась непосредственно из-за коронавируса.

Таковы результаты нового опроса Pew Research Center, проведенного с 1 февраля по 26 мая 2021 года среди 18 850 взрослых в 17 странах с развитой экономикой.

Коронавирус оставил неизгладимые следы в мире множеством способов, и международная деятельность Исследовательского центра Пью также ощутила на себе эти последствия. В начале пандемии Центр столкнулся с последствиями вспышки и решил приостановить всю очную работу на местах во имя безопасности как интервьюеров, так и респондентов. Однако, поскольку мы продолжаем адаптироваться к новой реальности опросов в условиях пандемии, мы также должны учитывать постоянно меняющуюся ситуацию на местах в местах, которые мы обследуем, и то, как это влияет на формирование общественного мнения.

Полевые работы для этого исследования совпали с несколькими крупными событиями, связанными с ограничениями на национальном уровне и распространением вакцины по всему миру. Многие европейские страны ввели новые блокировки или сняли ограничения по мере проведения опроса. Канада и каждая из стран Европейского союза провели опрос о приостановке использования вакцины «АстраЗенека» по крайней мере для части своего населения; ЕС также подал в суд на фармацевтическую компанию в это время. Несколько стран отложили развертывание вакцины Johnson & Johnson/Janssen.

Люди, опрошенные в Азиатско-Тихоокеанском регионе, обычно имели дело с меньшим количеством или более короткими ограничениями из-за меньшей распространенности вируса на тот момент. Тем не менее, Япония объявила чрезвычайное положение в Токио и нескольких префектурах во время опроса, и, поскольку полевые исследования закончились, ситуация теперь выглядит более серьезной. В более поздней части полевых исследований внимание было обращено на растущую вспышку в Индии (страна, не включенная в этот обзор) и усилия международной помощи по сдерживанию болезни. Тайвань и Сингапур также столкнулись с внезапным появлением новых случаев, которых они ранее избегали, хотя это произошло в основном после завершения полевых исследований.

Опрос в США проводился онлайн и завершился раньше, чем остальные опросы, а полевые исследования проводились с 1 по 7 февраля 2021 г. В стране было введено более 26 миллионов доз вакцины, но еще не было приостановлено использование вакцины Johnson & & Co. Вакцина Джонсона/Янссена. Третий раунд проверок стимулов, являющийся частью пакета помощи COVID-19 на сумму 1,9 триллиона долларов, еще не дошел до американцев.

Этот отчет дает представление о том, как 17 представителей общественности думали о пандемии в определенный момент времени. Подобно тому, как пандемия изменилась, иногда быстро, за последний год, изменилось и отношение общественности к связанным с ней темам, таким как национальное единство, ограничения и то, как их правительства справляются с постоянно меняющейся ситуацией.

Пандемия коронавируса усилила социальные разногласия во многих опрошенных группах населения. В среднем 61% во всех 17 странах с развитой экономикой говорят, что сейчас они более разделены, чем до вспышки, а 34% считают себя более сплоченными.

Настроения особенно негативны в США: 88% американцев говорят, что они более разделены, чем до пандемии, что является самым высоким показателем среди всех опрошенных. Большинство канадцев также говорят, что их страна более разделена.

В Европе большинство в семи из девяти опрошенных стран говорят, что они более разделены, чем до пандемии. Пессимистические взгляды особенно распространены в Нидерландах, Германии и Испании, где примерно восемь из десяти сообщают о большем разделении. Только в Швеции и Великобритании примерно четверо из десяти считают, что они более сплочены, чем до вспышки.

Мнения опрошенных жителей Азиатско-Тихоокеанского региона значительно различаются. Большинство жителей Австралии, Тайваня, Новой Зеландии и Сингапура говорят, что они более сплочены, чем до вспышки коронавируса. С другой стороны, большинство в Японии и Южной Корее чувствуют себя более разделенными.

Мнение о том, что общества скорее разделены, чем едины, значительно возросло во всех, кроме одной, из 13 стран, также включенных в опрос, проведенный исследовательским центром Pew Research Center летом 2020 года.

Доля тех, кто говорит, что теперь они более разделены, чем до вспышки, увеличилась на 20 процентных пунктов или более в Канаде (+32 пункта), Японии (+32), Нидерландах (+30), Южной Корее (+25) и Германия (+23).

В то же время резко упал процент тех, кто считает, что их общественность стала более сплоченной. В Канаде, например, 66% сказали, что они были более сплоченными, чем до пандемии летом 2020 года. Этой весной то же самое сказали 36%, снижение на 30 процентных пунктов. Большое снижение также наблюдается в Нидерландах (-29баллов), Южной Корее (-22), Германии (-21), Японии (-18) и Испании (-18).

Австралийцы во многом придерживаются тех же взглядов на национальное единство, что и прошлым летом. Большинство австралийцев говорят, что их страна стала более сплоченной, что всего на 5% выше, чем 49% прошлым летом, и взгляды на общенациональные разногласия остались в основном прежними.

Те, кто негативно относится к экономике, с большей вероятностью, чем те, кто считает, что экономика находится в хорошем состоянии, говорят, что их общество сейчас более разделено, чем до вспышки коронавируса. Эта закономерность наблюдается во всех местах, включенных в исследование. Для некоторых различия существенны: в Швеции, например, те, кто говорит, что их экономическое положение плохое, на 35 процентных пунктов чаще, чем те, кто говорит, что это хорошо, считают, что их общественность более разделена (83% против 48%, соответственно). ).

Отношение к ограничениям общественной деятельности зависит от того, чувствуют ли люди разделение. В некоторых из опрошенных стран с развитой экономикой те, кто говорит, что ограничений должно было быть меньше, с большей вероятностью считают, что их общественность стала более разделенной, чем до вспышки коронавируса, чем те, кто считал, что ограничений должно было быть больше, или что ограничения были правильными. . В Новой Зеландии, например, 58% тех, кто говорит, что ограничений на общественную деятельность должно быть меньше, также говорят, что их общественность более разделена, по сравнению с 15% тех, кто считает, что ограничений должно быть больше.

Большинство жителей Азиатско-Тихоокеанского региона говорят, что ограничения, связанные с пандемией, были правильными, но европейцы более разделены. Значительная доля — 37% — считают, что дополнительные ограничения были бы уместны. Только 18% говорят, что в период вспышки коронавируса ограничений на общественную деятельность должно было быть меньше.

Греция — единственная опрошенная страна, где большинство взрослых (43%) выступают за меньшее количество ограничений.

Половина или больше представителей некоторых слоев населения считают, что ограничения, введенные в связи с COVID-19, были слишком ограниченными за последние полтора года. Например, 62% взрослых японцев считают, что ограничений должно быть больше, как и 56% взрослых американцев. (Япония и США также получили одни из худших оценок за реакцию на коронавирус от своей общественности.)

Тем не менее, многие люди считают, что их правительства ввели правильные ограничения на общественную деятельность. В Новой Зеландии, которая заслужила похвалу за свою реакцию на коронавирус и на момент написания статьи было зарегистрировано всего 26 смертей, связанных с коронавирусом, самая высокая доля тех, кто говорит, что ограничения были правильными — 80%. Большинство на Тайване, в Австралии и Сингапуре также считают, что ограничения на коронавирус были правильными.

Поддержка правых популистских партий также связана со взглядами на ограничения из-за коронавируса. В Нидерландах 42% респондентов, поддерживающих правую партию «Форум за демократию» (FvD), говорят, что во время вспышки коронавируса ограничений на общественную деятельность должно было быть меньше. Только 17% тех, кто отрицательно относится к FvD, разделяют это мнение. Подобные расколы возникают между сторонниками и противниками «Альтернативы для Германии», «Лиги» и «Forza Italia» в Италии, «Vox» в Испании, «Партии свободы» в Нидерландах, «Шведских демократов», «Греческого решения» и «Реформы Великобритании».

В большинстве опрошенных идеологически правые значительно чаще, чем левые, говорят, что ограничений должно быть меньше. В США 52% консерваторов считают, что ограничений должно быть меньше; только 7% либералов говорят то же самое. Греция — единственная опрошенная общественность, где левые чаще, чем правые, говорят, что ограничений должно было быть меньше (55% и 34% соответственно).

Многие в США, Европе и Японии говорят, что пандемия выявила слабые стороны их экономической системы

Вспышка коронавируса нанесла ущерб мировой экономике, сведя на нет многолетний прогресс в борьбе с глобальной бедностью и вытеснив миллионы людей из мирового среднего класса. Но экономические последствия пандемии не были одинаковыми, и мнения людей о том, как люди оценивают устойчивость своей экономической системы, сильно различаются.

В Европе мнения в основном пессимистичны: в среднем 58% говорят, что их экономика не может оправиться от последствий вспышки коронавируса, что свидетельствует о слабости их экономической системы. (В ЕС два квартала подряд фиксируется отрицательный рост валового внутреннего продукта после резкого восстановления в третьем квартале 2020 года.) Мнения особенно негативны в Испании и Италии, примерно три четверти или более придерживаются этого мнения.

Швеция, отказавшаяся от широкомасштабных карантинных мер, является исключением в Европе: три четверти населения говорят, что экономика восстанавливается таким образом, что это демонстрирует сильные стороны ее экономической системы. Взрослые голландцы также настроены оптимистично, а мнения в Великобритании и Германии разделились.

Мнения в Азиатско-Тихоокеанском регионе более позитивны: большинство почти всех опрошенных заявили, что их экономика восстанавливается таким образом, что это демонстрирует сильные стороны их системы. Опять же, мнение японцев является исключением в регионе: 77% взрослых говорят, что их экономика не может оправиться от последствий вспышки коронавируса. Экономика Японии сократилась в годовом исчислении на 5,1% в первом квартале 2021 года после роста на 11,6% в предыдущем квартале.

Отношение к восстановлению экономики очень тесно связано с мнением о целесообразности ограничений, связанных с коронавирусом. В большинстве опрошенных людей люди, которые считают, что ограничений из-за COVID-19 должно быть меньше, с большей вероятностью, чем те, кто считает, что ограничения были правильными, настроены пессимистично в отношении восстановления своей экономики.

Те, кто говорит, что их текущая экономическая ситуация плохая, гораздо чаще говорят, что их экономика не может оправиться от последствий вспышки коронавируса в каждом опрошенном обществе.

Экономический ответ ЕС на пандемию получил неоднозначные отзывы

В то время как большинство или большинство в половине из восьми опрошенных стран Европейского Союза говорят, что усилия ЕС по оказанию экономической помощи были примерно правильными, многие в нескольких странах считают, что усилия не зашли достаточно далеко. В среднем 48% в этих странах считают, что усилия были правильными, в то время как в среднем 40% считают, что усилия по оказанию помощи не увенчались успехом. В среднем всего 6% говорят, что усилия зашли слишком далеко.

Удовлетворенность усилиями блока по оказанию экономической помощи, включая пакет стимулирующих мер на сумму 750 миллиардов евро (858 миллиардов долларов), согласованный в июле 2020 года, является самым высоким в Швеции, где 65% согласны с тем, что эти усилия были уместными. Шесть из десяти в Италии и Нидерландах говорят то же самое.

Тем не менее, в странах-членах ЕС, включенных в опрос, удовлетворенность не является широко распространенной, поскольку правительства стран-членов продолжают решать, как лучше всего потратить стимулирующие деньги. В Греции, например, 60% говорят, что усилия по оказанию экономической помощи не зашли достаточно далеко, и это самая высокая доля тех, кто выражает такое недовольство. В то время как все страны ЕС испытали экономические трудности в результате пандемии, Греция пострадала особенно сильно. Согласно экономическому прогнозу Европейской комиссии на осень 2020 года, ВВП Греции сократится примерно на 9%.%, одно из самых больших сокращений, прогнозируемых во всех странах-членах ЕС. Общественность в Бельгии и Испании примерно разделена на тех, кто говорит, что экономическая реакция ЕС была адекватной, и тех, кто говорит, что она не зашла достаточно далеко.

Взгляды на текущую экономическую ситуацию также влияют на удовлетворенность экономической помощью ЕС. Во всех опрошенных странах ЕС те, кто говорит, что экономическая ситуация плохая, с большей вероятностью, чем те, кто говорит, что ситуация хорошая, считают, что ЕС не зашел достаточно далеко в своих усилиях по оказанию помощи. В Греции, например, 68% тех, кто говорит, что экономическая ситуация плохая, говорят, что усилия ЕС по оказанию помощи не зашли достаточно далеко, по сравнению с 39%% греков, считающих экономическую ситуацию хорошей.

В нескольких странах-членах сторонники правых популистских партий чаще, чем противники, говорят, что усилия ЕС по оказанию помощи не зашли достаточно далеко. Например, в Италии сторонники Forza Italia на 18 процентных пунктов чаще, чем противники, считают, что экономическая помощь ЕС не увенчалась успехом (50% против 32% соответственно).

Реагирование на коронавирус вызывает неоднозначные отзывы общественности, более низкие оценки, чем летом 2020 г.

В отличие от реакции США и Китая на вспышку коронавируса, взрослые в основном высоко оценивают реакцию на коронавирус там, где они живут, особенно среди опрошенных жителей Азиатско-Тихоокеанского региона.

Например, почти все взрослые в Сингапуре и Новой Зеландии говорят, что их собственные страны хорошо справились со вспышкой коронавируса (97% и 96% соответственно), в том числе более семи из десяти говорят, что ответные меры было очень хорошо. Около девяти из десяти жителей Австралии и Тайваня и семь из десяти жителей Южной Кореи положительно оценивают свою реакцию на вспышку коронавируса.

Япония является исключением в Азиатско-Тихоокеанском регионе: 64% опрошенных заявили, что Япония плохо справляется со вспышкой коронавируса. Около половины или более жителей США, Испании, Франции, Бельгии и Германии также отрицательно оценивают свои ответные меры на пандемию.

Во многих странах рейтинги реагирования на коронавирус значительно снизились с лета 2020 года. Это особенно верно в отношении Германии, где доля немцев, считающих, что их страна хорошо справилась со вспышкой коронавируса, упала на 37 процентных пунктов с 88%. летом 2020 г. до 51% весной 2021 г. Положительные рейтинги также упали на двузначное число в Нидерландах, Канаде, Японии, Южной Корее, Италии, Франции, Бельгии и Испании.

Великобритания, которая провела одну из самых быстрых и успешных кампаний вакцинации в мире, — единственное место, где рейтинги улучшились. Летом 2020 года 46% британцев положительно оценили свою национальную реакцию; сегодня так делают 64%.

Экономическая уверенность связана с тем, как люди оценивают меры своей страны по борьбе с пандемией. В каждом опрошенном обществе те, кто считает текущую экономическую ситуацию хорошей, с большей вероятностью говорят, что реакция их общества на COVID-19 была хорошей.

Верно и обратное: те, кто считает текущую экономическую ситуацию плохой, также склонны негативно оценивать свою национальную реакцию. Этот разрыв наиболее велик в Греции, где 92% тех, кто считает текущую экономическую ситуацию хорошей, и 48% тех, кто считает текущую экономическую ситуацию плохой, положительно оценивают реакцию Греции на коронавирус, разница составляет 44 процентных пункта.

Многие говорят, что пандемия коронавируса повлияла на их жизнь

Спустя год после того, как в мире впервые возникла вспышка коронавируса, больше людей в 17 опрошенных сообществах считают, что их жизнь изменилась в результате пандемии, чем нет. В среднем 65% говорят, что их жизнь сильно или существенно изменилась в результате вспышки коронавируса, от 33% в Новой Зеландии до 87% в Южной Корее.

Примерно семь из десяти жителей США и Канады считают, что пандемия изменила их жизнь, по крайней мере, в значительной степени, в то время как примерно три из десяти говорят, что их жизнь не изменилась или изменилась совсем. В девяти опрошенных европейских странах в среднем 65% говорят, что их жизнь изменилась. Такого мнения придерживается большинство в этих девяти странах, в том числе более восьми из десяти в Греции.

Ответы на воздействие вспышки на жизнь людей более разнообразны в шести странах Азиатско-Тихоокеанского региона, включенных в опрос. Менее четырех из десяти жителей Австралии и Новой Зеландии считают, что пандемия изменила их жизнь, однако большинство жителей Тайваня, Сингапура, Японии и Южной Кореи говорят, что это повлияло на их жизнь.

Две страны выделяются тем, что сообщают об относительно небольших изменениях в результате пандемии: Австралия и Новая Зеландия. Большинство в каждом из них говорят, что их жизнь изменилась не сильно или совсем не изменилась. Обе страны остались относительно защищенными от худших последствий пандемии благодаря строгим карантинным мерам, повсеместному тестированию, отслеживанию контактов и соблюдению населением мер сдерживания, а также по географическому признаку. Во время полевых работ Австралия и Новая Зеландия открыли свои границы для жителей другой страны, что позволило посетителям из каждой страны путешествовать без карантинного периода.

Представление о том, что жизнь не сильно изменилась во время пандемии, резко падает за пределами Австралии и Новой Зеландии. Следующей по величине долей сторонников этой точки зрения являются немцы (43%).

Среди большинства из 12 стран, опрошенных как летом 2020 года, так и этой весной, сейчас больше тех, кто говорит, что их жизнь изменилась значительно или изрядно, чем говорит обратное. В среднем 58% в этих 12 странах прошлым летом сказали, что их жизнь изменилась, по крайней мере, изрядно, в то время как в среднем 67% в той же группе стран говорят то же самое в этом году.

Доля тех, кто говорит, что их жизнь изменилась в результате вспышки коронавируса, значительно увеличилась в восьми из 12 стран, включенных в оба опроса (исключениями являются Япония, Швеция и Великобритания), при этом в Италии увеличилась двузначная цифра (+18 процентных пунктов), Германии (+18), Франции (+15), Бельгии (+14), Нидерландов (+12) и Испании (+12).

Единственным местом, где доля тех, кто считает, что их жизнь изменилась, значительно снизилась, является Австралия, где 38% говорят, что их жизнь изменилась по крайней мере изрядно в этом году, что на 10 процентных пунктов меньше, чем 48%, которые сказали то же самое в лето 2020.

Хотя многие говорят, что пандемия COVID-19 повлияла на их жизнь, молодые люди особенно склонны выражать это мнение. За последний год молодые люди столкнулись с уникальными проблемами, в том числе срывами учебы и карьерными возможностями. Взрослые в возрасте от 18 до 29 лет во многих опрошенных группах чаще, чем люди в возрасте 65 лет и старше, говорят, что их жизнь изменилась в результате вспышки коронавируса. В Нидерландах, например, молодые люди на 28 процентных пунктов чаще, чем их сверстники старшего возраста, говорят, что их жизнь изменилась в результате вируса. Точно так же большие различия между молодыми и пожилыми людьми наблюдаются в Новой Зеландии (+27 баллов), Италии (+25), Австралии (+21), Бельгии (+21) и Франции (+21).

Отношение к экономике связано с восприятием изменений из-за пандемии в большинстве стран с развитой экономикой: те, кто говорит, что текущая экономическая ситуация в их стране плохая, с большей вероятностью скажут, что их жизнь изменилась. На Тайване, например, 72% тех, кто считает текущую экономическую ситуацию плохой, считают, что их жизнь изменилась в результате вспышки коронавируса, по сравнению с 49%, которые считают экономическую ситуацию хорошей. Двузначные различия были обнаружены в восьми других странах с развитой экономикой.

Оптимизм в отношении того, что системы здравоохранения могут справиться с будущими чрезвычайными ситуациями

Большинство 17 респондентов, принявших участие в этом опросе, выражают уверенность в том, что их системы здравоохранения справятся с будущими глобальными чрезвычайными ситуациями в области здравоохранения. В целом такого мнения придерживаются в среднем 75%.

Жители Азиатско-Тихоокеанского региона верят в свои системы здравоохранения с большим отрывом: в среднем 83% уверены, что система сможет справиться с будущей глобальной чрезвычайной ситуацией в области общественного здравоохранения. Примерно восемь из десяти или более говорят об этом в Сингапуре, Тайване, Австралии, Южной Корее и Новой Зеландии. Примечательно, что 60% сингапурцев выражают очень много уверенности, как и примерно четыре из десяти в Австралии и на Тайване.

Европейцы также положительно оценивают способность своей национальной системы здравоохранения справиться с гипотетической чрезвычайной ситуацией в области общественного здравоохранения. В среднем 75 % в девяти европейских странах, в которых проводился опрос, доверяют голосу, а 25 % — нет. У жителей Швеции и Великобритании самый высокий уровень доверия среди опрошенных европейских стран. А о четырех из десяти в Испании, Великобритании и Германии сообщают 9.0724 большое доверие к своим национальным системам здравоохранения.

Канадцы также высоко оценивают систему здравоохранения своей страны перед лицом будущей глобальной чрезвычайной ситуации в области здравоохранения. Однако это не так в США, где самая низкая доля среди 17 респондентов выражает доверие. Это может быть связано с характером американской системы здравоохранения; это единственная страна с развитой экономикой в ​​обзоре (и в мире) без всеобщего медицинского страхования и часто занимает последнее место в сравнительном анализе систем здравоохранения в странах с высоким уровнем дохода.

Почему минута делится на 60 секунд, час на 60 минут, а в сутках всего 24 часа?

Майкл А. Ломбарди, метролог отдела времени и частоты Национального института стандартов и технологий в Боулдере, штат Колорадо, берется за дело.

В современном мире наиболее широко используемой системой счисления является десятичная (с основанием 10), система, которая, вероятно, возникла потому, что людям было легко считать с помощью пальцев. Однако цивилизации, впервые разделившие день на более мелкие части, использовали разные системы счисления, в частности двенадцатеричную (с основанием 12) и шестидесятеричную (с основанием 60).

Благодаря документальным свидетельствам использования египтянами солнечных часов, большинство историков считают, что они были первой цивилизацией, разделившей день на более мелкие части. Первые солнечные часы представляли собой просто колышки, вкопанные в землю, которые указывали время по длине и направлению образующейся тени. Еще в 1500 году до нашей эры египтяне разработали более совершенные солнечные часы. Т-образный стержень, помещенный в землю, был откалиброван таким образом, чтобы разделить интервал между восходом и заходом солнца на 12 частей. Это деление отражало использование египтянами двенадцатеричной системы: важность числа 12 обычно приписывают либо тому факту, что оно равно числу лунных циклов в году, либо количеству суставов пальцев на каждой руке (по три на каждой руке). четыре пальца, исключая большой), что позволяет считать до 12 большим пальцем. Солнечные часы следующего поколения, вероятно, стали первым представлением того, что мы сейчас называем часом. Хотя часы в пределах данного дня были примерно равными, их продолжительность менялась в течение года, причем летние часы были намного длиннее зимних.

Без искусственного освещения люди этого временного периода рассматривали солнечные и темные периоды как два противоположных царства, а не как часть одного и того же дня. Без помощи солнечных часов разделить темный интервал между закатом и восходом было сложнее, чем разделить солнечный период. Однако в эпоху, когда впервые использовались солнечные часы, египетские астрономы также впервые наблюдали набор из 36 звезд, которые делили небесный круг на равные части. Прохождение ночи могло быть отмечено появлением 18 таких звезд, по три из которых относились к каждому из двух периодов сумерек, когда звезды было трудно разглядеть. Период полной темноты был отмечен оставшимися 12 звездами, что снова привело к 12 делениям ночи (еще один поклон двенадцатеричной системе). Во времена Нового царства (1550–1070 гг. до н. э.) эта система измерения была упрощена, чтобы использовать набор из 24 звезд, 12 из которых отмечали прохождение ночи. Клепсидра, или водяные часы, также использовалась для записи времени в ночное время и была, пожалуй, самым точным устройством для измерения времени в древнем мире. Часы, образец которых был найден в храме Аммона в Карнаке и датирован 1400 г. до н. 12 частей в разные месяцы.

Как только светлый и темный часы были разделены на 12 частей, появилась концепция 24-часового дня. Однако концепция часов фиксированной продолжительности возникла только в эллинистический период, когда греческие астрономы начали использовать такую ​​систему для своих теоретических расчетов. Гиппарх, чья работа в основном имела место между 147 и 127 г. до н.э., предложил делить день на 24 часа равноденствия, исходя из 12 часов дневного света и 12 часов темноты, наблюдаемых в дни равноденствия. Несмотря на это предположение, миряне продолжали использовать часы, меняющиеся в зависимости от сезона, на протяжении многих веков. (Часы фиксированной длины стали обычным явлением только после того, как в 14 веке в Европе впервые появились механические часы.)

Гиппарх и другие греческие астрономы использовали астрономические методы, ранее разработанные вавилонянами, проживавшими в Месопотамии. Вавилоняне производили астрономические расчеты в шестидесятеричной системе (с основанием 60), унаследованной ими от шумеров, разработавших ее около 2000 г. до н.э. Хотя неизвестно, почему было выбрано число 60, оно особенно удобно для выражения дробей, поскольку 60 — это наименьшее число, которое делится на первые шесть счетных чисел, а также на 10, 12, 15, 20 и 30.

Хотя шестидесятеричная система больше не используется для общих вычислений, она по-прежнему используется для измерения углов, географических координат и времени. На самом деле и круглый циферблат часов, и сфера земного шара обязаны своим делением 4000-летней системе счисления вавилонян.

Греческий астроном Эратосфен (который жил примерно с 276 по 194 г. до н.э.) использовал шестидесятеричную систему счисления, чтобы разделить круг на 60 частей, чтобы разработать раннюю географическую систему широты, с горизонтальными линиями, проходящими через хорошо известные места на Земле. в это время. Столетие спустя Гиппарх нормализовал линии широты, сделав их параллельными и послушными геометрии Земли. Он также разработал систему линий долготы, охватывающих 360 градусов и проходящих с севера на юг, от полюса к полюсу. В своем трактате г. Альмагеста г. (около 150 г. н.э.) Клавдий Птолемей объяснил и расширил работу Гиппарха, разделив каждый из 360 градусов широты и долготы на более мелкие сегменты. Каждая ступень делилась на 60 частей, каждая из которых снова подразделялась на 60 меньших частей. Первое деление, partes minutae primae, или первая минута, стало известно просто как «минута». Вторая сегментация, partes minutae secundae, или «вторая минута», стала известна как вторая.

Минуты и секунды, однако, не использовались для повседневного измерения времени до тех пор, пока спустя много столетий после Альмагеста. Индикация часов делила час на половины, трети, четверти, а иногда даже на 12 частей, но никогда на 60. На самом деле под часом обычно не понималась продолжительность 60 минут. Для широкой публики было непрактично считать минуты, пока первые механические часы, показывающие минуты, не появились ближе к концу 16 века. Даже сегодня многие часы и наручные часы имеют разрешение всего одну минуту и ​​не показывают секунды.

Благодаря древним цивилизациям, которые определили и сохранили деление времени, современное общество до сих пор считает день равным 24 часам, часу — 60 минут и минуте — 60 секундам. Однако достижения в области хронометрии изменили определение этих единиц. Секунды когда-то были получены путем деления астрономических событий на более мелкие части, при этом Международная система единиц (СИ) одно время определяла секунду как долю среднего солнечного дня, а затем связывала ее с тропическим годом. Это изменилось в 1967, когда секунда была переопределена как продолжительность 9 192 631 770 энергетических переходов атома цезия. Эта переквалификация открыла эру атомного хронометража и всемирного координированного времени (UTC).

Интересно, что для того, чтобы согласовать атомное время с астрономическим временем, к UTC иногда нужно добавлять дополнительные секунды. Таким образом, не все минуты содержат 60 секунд. Несколько редких минут, происходящих с частотой около восьми за десятилетие, на самом деле содержат 61.

Ссылки

• Маятник времени. Джо Эллен Барнетт. Пленум Пресс, 1998.
.
• История математики. Флориан Каджори. Макмиллан и Ко, 1894.
• История часа. Герхард Дорн-ван Россум. Издательство Чикагского университета, 1996.
.

Кольцевая структура FtsZ, связанная с делением Escherichia coli

Сохранить цитату в файл

Формат: Резюме (текст)PubMedPMIDAbstract (текст)CSV

Добавить в коллекции

• Создать новую коллекцию
• Добавить в существующую коллекцию

Назовите свою коллекцию:

Имя должно содержать менее 100 символов

Выберите коллекцию:

Не удалось загрузить вашу коллекцию из-за ошибки
Повторите попытку

Добавить в мою библиографию

• Моя библиография

Не удалось загрузить делегатов из-за ошибки
Повторите попытку

Ваш сохраненный поиск

Название сохраненного поиска:

Условия поиска:

Тестовые условия поиска

Эл. адрес: (изменить)

Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый рабочий день

Который день? ВоскресеньеПонедельникВторникСредаЧетвергПятницаСуббота

Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed

Отправить максимум: 1 штука5 штук10 штук20 штук50 штук100 штук200 штук

Отправить, даже если нет новых результатов

Необязательный текст в электронном письме:

Создайте файл для внешнего программного обеспечения для управления цитированием

. 1991 14 ноября; 354 ​​(6349): 161-4.

дои: 10.1038/354161a0.

ЭФ Би ¹ , J Lutkenhaus

принадлежность

• ¹ Отделение микробиологии, Медицинский центр Канзасского университета, Канзас-Сити 66103.
• PMID: 1944597
• DOI: 10.1038/354161а0

E F Bi et al. Природа. 1991 .

. 1991 14 ноября; 354 ​​(6349): 161-4.

дои: 10.1038/354161a0.

Авторы

ЭФ Би ¹ , Дж. Люткенхаус

принадлежность

• ¹ Отделение микробиологии, Медицинский центр Канзасского университета, Канзас-Сити 66103.
• PMID: 1944597
• DOI: 10.1038/354161а0

Абстрактный

Гены клеточного деления были идентифицированы у Escherichia coli путем выделения условно летальных мутаций, которые блокируют клеточное деление, но не влияют на репликацию или сегрегацию ДНК. Из этих генов большой интерес представляет ftsZ, так как он действует на самом раннем пути деления, является важным, его уровень определяет частоту делений, и считается, что он является мишенью для двух ингибиторов клеточного деления, SulA, вырабатываемых в ответ на повреждение ДНК и MinCD, препятствующий делению на старых сайтах. Здесь мы использовали иммуноэлектронную микроскопию для локализации белка FtsZ в месте деления. Результаты предполагают, что FtsZ самостоятельно собирается в кольцевую структуру в месте будущего деления и может функционировать как элемент цитоскелета. Формирование этого кольца может быть точкой, в которой регулируется деление.

Похожие статьи

• Ингибиторы клеточного деления SulA и MinCD предотвращают образование кольца FtsZ.

  Bi E, Луткенхаус Дж. Би Э и др. J Бактериол. 1993 г., февраль; 175(4):1118-25. doi: 10.1128/jb.175.4.1118-1125.1993. J Бактериол. 1993. PMID: 8432706 Бесплатная статья ЧВК.

• Существенный белок деления бактериальной клетки FtsZ представляет собой GTPase.

  де Бур П. , Кроссли Р., Ротфилд Л. де Бур П. и др. Природа. 1992 г., 17 сентября; 359(6392):254-6. дои: 10.1038/359254a0. Природа. 1992. PMID: 1528268

• Ингибиторы клеточного деления SulA и MinC/MinD блокируют образование перегородки на разных этапах сборки механизма деления Escherichia coli.

  Джастис С.С., Гарсия-Лара Дж., Ротфилд Л.И. Джастис С.С. и др. Мол микробиол. 2000 г., июль; 37(2):410-23. дои: 10.1046/j.1365-2958.2000.02007.х. Мол микробиол. 2000. PMID: 10931335

• Деление бактериальной клетки: механизм и его особенности.

  Гарри Э., Монахан Л., Томпсон Л. Гарри Э. и др. Int Rev Cytol. 2006; 253:27-94. doi: 10.1016/S0074-7696(06)53002-5. Int Rev Cytol. 2006. PMID: 17098054 Обзор.

• Деление бактериальных клеток и септальное кольцо.

  Вайс ДС. Вайс ДС. Мол микробиол. 2004 г., ноябрь; 54 (3): 588-97. doi: 10.1111/j.1365-2958.2004.04283.x. Мол микробиол. 2004. PMID: 15491352 Обзор.

Посмотреть все похожие статьи

Цитируется

• Регуляция литических механизмов комплексом FtsEX в бактериальной дивисоме.

  Алькорло М., Мартинес-Кабальеро С., Молина Р., Эрмосо Х.А. Алькорло М. и др. Субклеточная биохимия. 2022;99:285-315. doi: 10.1007/978-3-031-00793-4_9. Субклеточная биохимия. 2022. PMID: 36151380

• Локализованный синтез кардиолипина необходим для сборки MreB во время деления поляризованных клеток Chlamydia trachomatis.

  Ouellette SP, Fisher-Marvin LA, Harpring M, Lee J, Rucks EA, Cox JV. Уэллетт С.П. и др. PLoS Патог. 2022 12 сентября; 18 (9): e1010836. doi: 10.1371/journal.ppat.1010836. электронная коллекция 2022 сент. PLoS Патог. 2022. PMID: 36095021 Бесплатная статья ЧВК.

• Поиск антибактериальных ингибиторов, нацеленных на белок клеточного деления FtsZ в его нуклеотидных и аллостерических сайтах связывания.

  Андреу Х.М., Уэкас С., Араужо-Базан Л., Васкес-Вилья Х., Мартин-Фонтеча М. Андреу Дж. М. и соавт. Биомедицины. 2022 28 июля; 10 (8): 1825. doi: 10.3390/biomedics10081825. Биомедицины. 2022. PMID: 36009372 Бесплатная статья ЧВК. Обзор.

• Эволюция продольного деления у многоклеточных бактерий семейства Neisseriaceae.

  Ньонгеса С., Вебер П.М., Бернет Э., Пулидо Ф., Ньевес С., Никкарц М., Делаби М., Фибек Т., Краузе Н., Ривера-Милло А., Накамура А., Вишер Н.О. С, Верье Ф.Дж. Ньонгеса С. и др. Нац коммун. 2022 22 августа; 13 (1): 4853. doi: 10.1038/s41467-022-32260-w. Нац коммун. 2022. PMID: 35995772 Бесплатная статья ЧВК.

• Приближаемся к расшифровке фазовых переходов бактериальных биомолекул.

  Солтыс К., Тарчевска А., Быстроновска Д., Созанска Н. Солтыс К. и соавт. Биомолекулы. 2022 28 июня; 12 (7): 907. doi: 10.3390/biom12070907. Биомолекулы. 2022. PMID: 35883463 Бесплатная статья ЧВК. Обзор.

Просмотреть все статьи «Цитируется по»

Типы публикаций

термины MeSH

вещества

Полнотекстовые ссылки

Издательская группа «Природа»

Укажите

Формат: ААД АПА МДА НЛМ

Отправить по номеру

Как делить десятичные дроби — пустышки

Авторы: Марк Зегарелли и

Обновлено: 24 июля 2021 г. Для чайников с онлайн-практикой

Изучить книгу Купить на Amazon

Деление десятичных дробей похоже на деление целых чисел, за исключением того, что перед делением необходимо обработать десятичную точку. Вот как делить десятичные дроби шаг за шагом:

1. Переместить десятичную точку в делителе и делимом.

   Превратите делитель (число, на которое вы делите) в целое число, переместив десятичную точку до упора вправо. При этом переместите запятую в делимом (число, которое вы делите) на такое же количество знаков вправо.

2. Поместите десятичную точку в частное (ответ) непосредственно над тем местом, где теперь стоит десятичная точка в делимом.

3. Разделите как обычно, тщательно выстраивая частное так, чтобы десятичная точка встала на свое место.

   Выровняйте каждую цифру частного сразу после последней цифры делимого, используемого в этом цикле.

Как и в случае деления целых чисел, иногда десятичное деление не работает равномерно в конце. Однако с десятичными дробями вы никогда не записываете остаток. Вместо этого добавьте достаточно нулей в конце, чтобы округлить частное до определенного числа знаков после запятой. Цифра справа от цифры, до которой вы округляете, говорит вам, нужно ли округлять в большую или меньшую сторону, поэтому вам всегда нужно вычислять деление до одного дополнительного разряда.

См. следующую диаграмму:

Чтобы округлить десятичную дробь до	Заполнить дивиденд нулями до
Целое число	Один десятичный знак
Один десятичный знак	Два десятичных знака
Два десятичных знака	Три десятичных знака

Примеры вопросов

1. Разделите следующее: 9,152 / 0,8 = ?

   11.44 . Для начала напишите задачу как обычно:

   Превратите 0,8 в целое число 8, переместив запятую на одну позицию вправо. При этом запятую в числе 9,1526 переместите на один разряд вправо. Поставьте запятую в частном прямо над тем местом, где она попадает в 91,25:

   .

   Теперь вы готовы делить. Просто будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.

2. Разделите следующее: 21,9/ 0,015 = ?

   1460. Настройте проблему как обычно:

   Обратите внимание, что к делимому добавлены два завершающих нуля, потому что вам нужно переместить десятичные точки в каждом числе на три позиции вправо. Снова поместите десятичную точку в частном непосредственно над тем местом, где она теперь появляется в делимом, 21900:

   .

   Теперь вы готовы делить. Тщательно выровняйте частное, чтобы десятичная точка встала на свое место:

   Несмотря на то, что деление получается даже после того, как вы вписываете цифру 6 в частное, вам все равно нужно добавить замещающий ноль, чтобы десятичная точка стояла в правильном месте.

Практические вопросы

1. Разделите эти два десятичных знака: 9,345 / 0,05 = ?

2. Решите следующее деление: 3,15 / 0,021 = ?

3. Выполните следующее десятичное деление, округлив до одного знака после запятой: 6,7 / 10,1.

4. Найдите решение, округлив до сотых: 9.13 / 4.25.

Ниже приведены ответы на практические вопросы:

1. 9,345/0,05 = 186,9. Для начала напишите задачу как обычно:

   Превратите делитель (0,05) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9,345) на два знака вправо. Поместите десятичную точку в частное прямо над тем местом, где она теперь появляется в делимом:

   Теперь вы готовы делить. Будьте осторожны, чтобы правильно выстроить частное, чтобы десятичная точка встала на свое место.

2. 3,15 / 0,021 = 150. Напишите задачу как обычно:

   Вам нужно переместить десятичную точку в делителе (0,021) на три знака вправо, поэтому добавьте дополнительный нуль в конце делимого (3,15), чтобы расширить его до трех знаков после запятой:

   Теперь вы можете переместить обе десятичные точки на три позиции вправо. Поместите запятую в частном над запятой в делимом:

   Разделите, соблюдая правильное построение частного:

   Не забудьте вставить в частное замещающий ноль, чтобы десятичная точка оказалась в правильном месте.

3. 6,7/10,1 = 0,7. Для начала напишите задачу как обычно:

   Превратите делитель (10.1) в целое число, переместив запятую на один разряд вправо. При этом переместите запятую в делимом (6.7) на один разряд вправо:

   Задача требует округлить частное до одного знака после запятой, поэтому заполните делимое нулями в конце до двух знаков после запятой:

   Теперь можно делить:

   Округлить частное до одного десятичного знака:

4. 9,13/4,25 = 2,15. Сначала напишите задачу как обычно:

   Превратите делитель (4.25) в целое число, переместив запятую на два знака вправо. При этом переместите запятую в делимом (9.13) на два знака вправо:

   В задаче предлагается округлить частное до сотых, поэтому заполните делимое нулями в конце до трех знаков после запятой:

   Теперь разделите, тщательно выстраивая частное:

   Округлить частное до сотых:

Об этой статье

Эта статья взята из книги:

• Рабочая тетрадь по базовой математике и алгебре для чайников с онлайн-практикой,

Об авторе книги:

Марк Зегарелли — учитель математики и подготовки к экзаменам, который написал множество книг по базовой математике и предварительной алгебре в For Dummies 9.

No related posts.