Формулы для первой производной функции
y есть функция y = y(x)
C = постоянная, производная (y’) постоянной есть 0
y = C => y’ = 0
пример: y = 5, y’ = 0
Если y есть функцией типа y = xn, формула для производной есть:
y = xn => y’ = nxn-1
пример: y = x3 y’ = 3x3-1 = 3x2
y = x-3 y’ = -3x-4
Из вышеприведенной формулы мы можем сказать, что для производной y’ функции y = x = x1 that:
если y = x тогда y’=1
y = f1(x) + f2(x) + f3(x) …=>
y’ = f’1(x) + f’2(x) + f’3(x) …
Эта формула представляет производную функции, являющейся суммой функций.
Пример: Если мы имеем две функции f(x) = x2 + x + 1 и
g(x) = x5 + 7 и y = f(x) + g(x) тогда y’ = f'(x) + g'(x) =>
y’ = (x2
Если функция есть произведением двух функций, формула производной выглядит так:
y = f(x). g(x) => y’ = f'(x)g(x) + f(x)g'(x)
g(x) => y’ = f'(x)g(x) + f(x)g'(x)
Если f(x) = C(C есть постоянной) и y = f(x)g(x)
y = Cg(x) y’=C’.g(x) + C.g'(x) = 0 + C.g'(x) = C.g'(x)
y = Cf(x) => y’ = C.f'(x)
Формулы вычисления производной
| y = | y’ = |
|
y = ln x => y’ = 1/x
y = ex => y’ = ex
y = sin x => y’ = cos x
y = cos x => y’ = -sin x
y = tg x => y’ = 1/cos2x
y = ctg x => y’ = —
1/sin2xесли функция есть функцией функции: u = u(x)
y = f(u) => y’ = f'(u).u’
Пример. Пусть у нас есть функция y = sin(x2)
в этом случае u = x2, f(u) = sin(u), производные есть f'(u) = cos(u), u’ = 2x
y’ = (sin(u))’.u’ = cos(x2). 2x = 2.x.cos(x2)
2x = 2.x.cos(x2)
Задачи с производными
1) f(x) = 10x + 4y. Найдите первую производную f'(x)
ОТВЕТ: Мы можем использовать формулу нахождения производной для суммы функций
f(x) = f1(x) + f2(x), f1(x) = 10x, f2(x) = 4y
для функции f2(x) = 4y, y есть постоянной, потому что аргумент f2(x) есть x.
Поэтому f’2(x) = (4y)’ = 0. Отсюда производная функции f(x) есть: f'(x) = 10 + 0 = 10.
| 2) Вычислите производную f(x) = |
ОТВЕТ: у нас есть две функции h(x) = x10 и g(x) = 4.15 + cos x
функция f(x) есть h(x), разделенная на g(x). h'(x) = 10x9 g'(x) = 0 — sin x = -sin x
| f'(x) = |
|
| f'(x) = |
| = |
|
3) f(x) = ln(sinx). Какая производная функции f(x)?
ОТВЕТ: Чтобы решить эту задачу, мы можем использовать последнюю формулу.
Как мы видим, f(x) есть функцией двух функций:
f(x) = h(g(x)), где h = ln и g = sin x
Подробнее о производных на страницах математического форума
Форум о производных
Билеты по математике для устного экзамена и задачи по теме билеты по математике
Вопросы по алгебре (устный экзамен) Тригонометрия: основные тригонометрические тождества; доказательство формул; мнемоническое правило. Свойства тригонометрических функций: sin x, y= cos x, y= tg x, y= ctg x. Их графики. Определения синуса, косинуса, тангенса и котангенса через тригонометрический круг.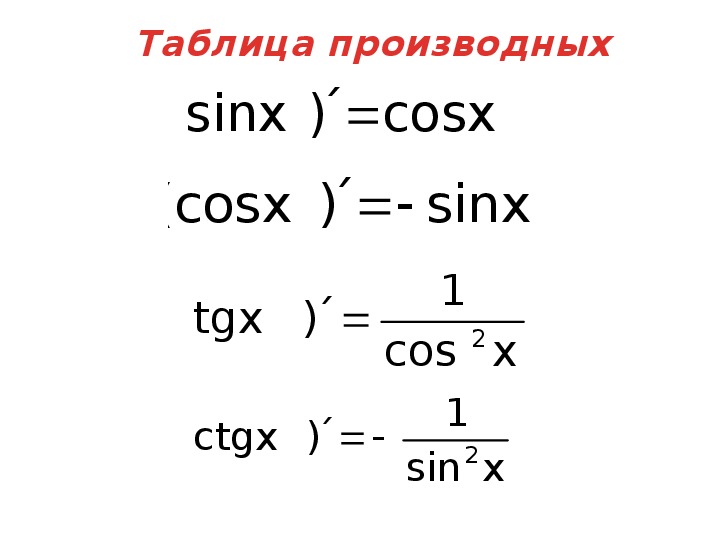 Простейшие тригонометрические уравнения. Определения и свойства обратных тригонометрических функций: y= arcsin x, y= arccos x, y= arctg x, y= arcctg x. Их графики. Простейшие тригонометрические неравенства (sin x < a). Любая производная из листа, таблицы. Правила вычисления производной (Лагранж). Геометрический смысл производной: производная в данной точке; уравнение касательной; угол между прямыми. Физический смысл производной. Экстремумы функций. Правила нахождения их с помощью производной. Возрастание и убывание функции. Правило Лагранжа. Наибольшее и наименьшее значение функции. Правила. На эту тему. Многочлены. Теорема Безу, ее доказательство. Правила нахождения рациональных корней, доказательство. Четность, периодичность. Вычислить cos 22,5 F 0B 0 sin(arcsin11/12)-cos(arccos1/6) tg(arcsin21/29) tg(arccos1/4) tg(arcctg7) sin(arccos1/3)-cos(arcsin(-1/3)) sin(arctg12)+cos(arcctg(-2)) cos(arctg(-5))-sin(arctg3) cos( F 07 0/2+arcsin3/4) cos( F 07 0-arctg17) cos(3 F 07 0/2+arcctg(-4)) cos(2 F 07 0-2arccos(- F 0 D 63/2)) sin( F 07 0/2-arccos1/10) sin( F 07 0+arctg F 0 D 63/7) sin(3 F 07 0/2-arcctg81) sin(2 F 07 0-3arcsin F 0 D 62/2) tg( F 07 0/2-arccos(-1/3)) tg(3 F 07 0/2+4arctg F 0 D 63/3) tg( F 07 0+arcsin(-2/17)) tg(2 F 07 0-arcctg(-5)) arcsin(- F 0D 63/2) arcsin1 arcsin(-1) arccos(- F 0D 63/2) arccos0 arccos(-1) arctg(-1/ F 0D 63) arctg(-1) arctg1 arcctg(-1/ F 0D 63) arcctg(-1) arcctg0 cos(arctg2) sin(arctg(-3/4)) tg(arcctg(-3)) sin(arcctg p) tg(arcsin p), -1<p<1 ctg(arctg p), p F 0B 90 arcsin(- F 0D 63/2)+arcctg(-1)+arccos(1/ F 0 D 62)+1/2arccos(-1) sin(1/2arcctg(-3/4)) Решить уравнения: sin(x2 + x) =1/2; 4 — сos2 x = 4sinx 5 — 2cosx = 5 F 0D 62sin(x/2) cos4x = cos2x sin4x + cos4x = sin2x-1/2 sin2x + 3sin2x — 2сos2x = 2 cos(x/2) + 3/2sinx + 5sin2(x/2) = 3 sinx — 2cosx = 1 cos6x + sin6x — cos22x = 1/16 cos2x — sin3x F 0D 7cosx + 1 = sin2x + sinx F 0 D 7cos3x tgx — tg2x = sinx 2sin3x — cos2x — sinx = 0 2cos2x = F 0D 6 (cosx — sinx) 1 — sinx = cosx — sin2x 2 F 0D 63sin2(x/2) + 2 = 2sin2x + F 0 D 63 1 + cos(x2 + 1) = sin2(x2 + 1) 2sinx F 0D 7cos2x + cos4x = 2sinx + cos2x + cos2x tg2x + ctg2x + 3tgx + 3ctgx +4 = 0 1 + cos(x/2) + cosx = 0 1 — sin(x/2) = cosx 2sin2x + cos4x = 0 sin4x + 2cos2x = 1 5sinx — 4ctgx = 0 3cosx + 2tgx = 0 1 + 4cosx = cos2x 2cos2x + 5sinx + 1 = 0 cos2x + 3 F 0D 62sinx — 3 = 0 2cos2x + 4cosx =sin2x 2cos2x + sin3x = 2 cos4x + 4sin2x = 1 + 2sin22x 4 — 6cosx = 3 sin2x — sin2(x/2) 5 + 2sin2x — 5cosx = 5sinx cos4x + 8sin2x — 2 = 6cos2x — 8 cos4x 4 — 3cos4x = 10sinx F 0D 7cosx sin4x = (1 + F 0D 62)(sin2x + cos2x — 1) cos(10x + 12) + 4 F 0D 62sin(5x + 6) = 4 sin3x + cos3x = 1 — 1/2sin2x ctg2x — tg2x = 16cos2x 1 + sinx + cosx + sin2x + cos2x = 0 1/2(cos2x + cos22x) — 1 = 2sin2x — 2sinx — sinx — sin2x tg( F 07 0/2 F 0 D 7cosx) = ctg( F 0 7 0/2 F 0 D 7sinx) sin3x — sinx + cos2x = 1 2cos2x + 3sinx = 0 2sin2x + 1/cos2x = 3 2sin2x + F 0D 63cosx = 0 F 0 D 61 + sinx F 0 A 2+ cosx = 0 sin4x + cos4x = sin2x 4cos4x + 6sin22x + 5cos2x = 0 cos2x + 4sin3x = 1 1 — sin2x = -(sinx + cosx) 4sin22x — 2cos22x = cos8x 8sin4x + 13cos2x = 7 2sinx + 3sin2x = 0 cos(x/2) = 1 + cosx sin2x = 1 + F 0D 62cosx + cos2x sin2x = F 0D 63sinx 2cos23x — cos3x = 0 F 0 D 63sin2x = 2cos2x 3sin2x — cos2x — 1 = 0 F 0 D 63sin2x — cos2x = F 0 D 63 Доказать: tg208 F 0B 0<sin492 F 0 B 0 Что больше: sin1 или cos1 tg1 или tg2
Простейшие тригонометрические уравнения. Определения и свойства обратных тригонометрических функций: y= arcsin x, y= arccos x, y= arctg x, y= arcctg x. Их графики. Простейшие тригонометрические неравенства (sin x < a). Любая производная из листа, таблицы. Правила вычисления производной (Лагранж). Геометрический смысл производной: производная в данной точке; уравнение касательной; угол между прямыми. Физический смысл производной. Экстремумы функций. Правила нахождения их с помощью производной. Возрастание и убывание функции. Правило Лагранжа. Наибольшее и наименьшее значение функции. Правила. На эту тему. Многочлены. Теорема Безу, ее доказательство. Правила нахождения рациональных корней, доказательство. Четность, периодичность. Вычислить cos 22,5 F 0B 0 sin(arcsin11/12)-cos(arccos1/6) tg(arcsin21/29) tg(arccos1/4) tg(arcctg7) sin(arccos1/3)-cos(arcsin(-1/3)) sin(arctg12)+cos(arcctg(-2)) cos(arctg(-5))-sin(arctg3) cos( F 07 0/2+arcsin3/4) cos( F 07 0-arctg17) cos(3 F 07 0/2+arcctg(-4)) cos(2 F 07 0-2arccos(- F 0 D 63/2)) sin( F 07 0/2-arccos1/10) sin( F 07 0+arctg F 0 D 63/7) sin(3 F 07 0/2-arcctg81) sin(2 F 07 0-3arcsin F 0 D 62/2) tg( F 07 0/2-arccos(-1/3)) tg(3 F 07 0/2+4arctg F 0 D 63/3) tg( F 07 0+arcsin(-2/17)) tg(2 F 07 0-arcctg(-5)) arcsin(- F 0D 63/2) arcsin1 arcsin(-1) arccos(- F 0D 63/2) arccos0 arccos(-1) arctg(-1/ F 0D 63) arctg(-1) arctg1 arcctg(-1/ F 0D 63) arcctg(-1) arcctg0 cos(arctg2) sin(arctg(-3/4)) tg(arcctg(-3)) sin(arcctg p) tg(arcsin p), -1<p<1 ctg(arctg p), p F 0B 90 arcsin(- F 0D 63/2)+arcctg(-1)+arccos(1/ F 0 D 62)+1/2arccos(-1) sin(1/2arcctg(-3/4)) Решить уравнения: sin(x2 + x) =1/2; 4 — сos2 x = 4sinx 5 — 2cosx = 5 F 0D 62sin(x/2) cos4x = cos2x sin4x + cos4x = sin2x-1/2 sin2x + 3sin2x — 2сos2x = 2 cos(x/2) + 3/2sinx + 5sin2(x/2) = 3 sinx — 2cosx = 1 cos6x + sin6x — cos22x = 1/16 cos2x — sin3x F 0D 7cosx + 1 = sin2x + sinx F 0 D 7cos3x tgx — tg2x = sinx 2sin3x — cos2x — sinx = 0 2cos2x = F 0D 6 (cosx — sinx) 1 — sinx = cosx — sin2x 2 F 0D 63sin2(x/2) + 2 = 2sin2x + F 0 D 63 1 + cos(x2 + 1) = sin2(x2 + 1) 2sinx F 0D 7cos2x + cos4x = 2sinx + cos2x + cos2x tg2x + ctg2x + 3tgx + 3ctgx +4 = 0 1 + cos(x/2) + cosx = 0 1 — sin(x/2) = cosx 2sin2x + cos4x = 0 sin4x + 2cos2x = 1 5sinx — 4ctgx = 0 3cosx + 2tgx = 0 1 + 4cosx = cos2x 2cos2x + 5sinx + 1 = 0 cos2x + 3 F 0D 62sinx — 3 = 0 2cos2x + 4cosx =sin2x 2cos2x + sin3x = 2 cos4x + 4sin2x = 1 + 2sin22x 4 — 6cosx = 3 sin2x — sin2(x/2) 5 + 2sin2x — 5cosx = 5sinx cos4x + 8sin2x — 2 = 6cos2x — 8 cos4x 4 — 3cos4x = 10sinx F 0D 7cosx sin4x = (1 + F 0D 62)(sin2x + cos2x — 1) cos(10x + 12) + 4 F 0D 62sin(5x + 6) = 4 sin3x + cos3x = 1 — 1/2sin2x ctg2x — tg2x = 16cos2x 1 + sinx + cosx + sin2x + cos2x = 0 1/2(cos2x + cos22x) — 1 = 2sin2x — 2sinx — sinx — sin2x tg( F 07 0/2 F 0 D 7cosx) = ctg( F 0 7 0/2 F 0 D 7sinx) sin3x — sinx + cos2x = 1 2cos2x + 3sinx = 0 2sin2x + 1/cos2x = 3 2sin2x + F 0D 63cosx = 0 F 0 D 61 + sinx F 0 A 2+ cosx = 0 sin4x + cos4x = sin2x 4cos4x + 6sin22x + 5cos2x = 0 cos2x + 4sin3x = 1 1 — sin2x = -(sinx + cosx) 4sin22x — 2cos22x = cos8x 8sin4x + 13cos2x = 7 2sinx + 3sin2x = 0 cos(x/2) = 1 + cosx sin2x = 1 + F 0D 62cosx + cos2x sin2x = F 0D 63sinx 2cos23x — cos3x = 0 F 0 D 63sin2x = 2cos2x 3sin2x — cos2x — 1 = 0 F 0 D 63sin2x — cos2x = F 0 D 63 Доказать: tg208 F 0B 0<sin492 F 0 B 0 Что больше: sin1 или cos1 tg1 или tg2
9.
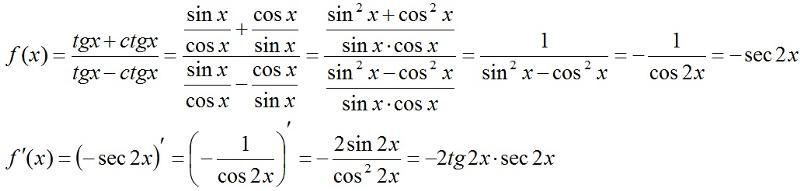 Найти дифференциал функции
Найти дифференциал функцииПример 9.1. Найти дифференциал функции y = ctg3x
►Пользуясь тем, что dy = y`(x)dx найдем dy
dy = – , xk/3, kZ.◄
Пример 9.2. Найти дифференциал функции y=ln| |
► Используя определение дифференциала, находим
.◄
1) y = arccos(89log56(8x+4x9) ) 2) y = tg(exp(5x+x7))
3) y = cos(log3(2x+x4)) 4) y = tg(5log4(7x+x3))
5) y = arctg7log8(9x+x2)) 6) y = log3(5log4(7x)+6x8))
7) y = exp(6log7(16+2x5
9) y = arcctg(8log12(13x)) 10) y = cos(exp(2x+x4))
11) y = arcsin(log3(6x+12(x7)3)) 12) y = (67log11(2x+33x77))
13) y = 45log12(x+2x12) 14)y = (34log9(11x+66×9))3
15) y = (23log3(7x+77×5))5 16) y = ln|x+|
17) y = xex 18) y = tg(exp(16x+x9))
19) y = arctg(3log5(2x+4x3)) 20) y = arcctg(2log6(7x+2x4))
21) y = arcsin(ln(6x2)) 22) y = arccos
23) y = arcsin 24) y = x2ln2x
25) y = 26) y =
27) y = sinx – xcosx+4 28) y = x + -5
29) y = xlnx-x+1 30) y = xarcsinx+
10.
 Вычислить значение функции используя формулу малых приращений
Вычислить значение функции используя формулу малых приращенийПример 10.1. Вычислить
► Рассмотрим функцию y = . Вычислим ее производную в точке x = 1: y`(1) = 1/3.
По формуле малых приращений имеем (x = 0,02):
◄
Пример 10.2. Вычислить sin 290
► Рассмотрим функцию y = sinx. Ее производная в точке x = /6 = 300 равна . Тогда по формуле малых приращений получим (x =-/180)
sin29 = sin(/6-/180) sin/6 – = 1/2(1 – ) = 0,484 … .◄
1) sin60015′ 2) cos60015′ 3) tg60015′ 4) ctg60015′
5) 20.013‘ 6) 50.012 7) 90.501 8) 2.013
9) 5.012 10) 91/3 11) 801/4 12) 1001/8
 05 16) sin46
05 16) sin4617) cos 44 18) (7.01)3 19) (7.01)4 20) (7.01)7
21) arcsin0.99 22) arccos0.09 23) cos29 24) tg44
25) ctg46 26) arctg0.99 27) 28)
29) 160.503 30) sin14.5cos14.5
11. Найти уравнение касательной к графику функции y=f(x) в точке с абсциссой x0 . Сколько общих точек имеет график данной функции с искомой касательной
Пример 11.1. y = x2/2 x0 = 0
► y`=x по формуле уравнения касательной получим y = 0 + 0 = 0 y = 0.
Найдем точки пересечения графика функции и касательной
x2/2 = 0 x = 0 единственная точка совпадения графика функции с касательной – точка (0,0).◄
Пример 11.2.y = sinx, x0 = /2.
►y`=cosx,
y(x0)=1,
y`(x0)
= 0.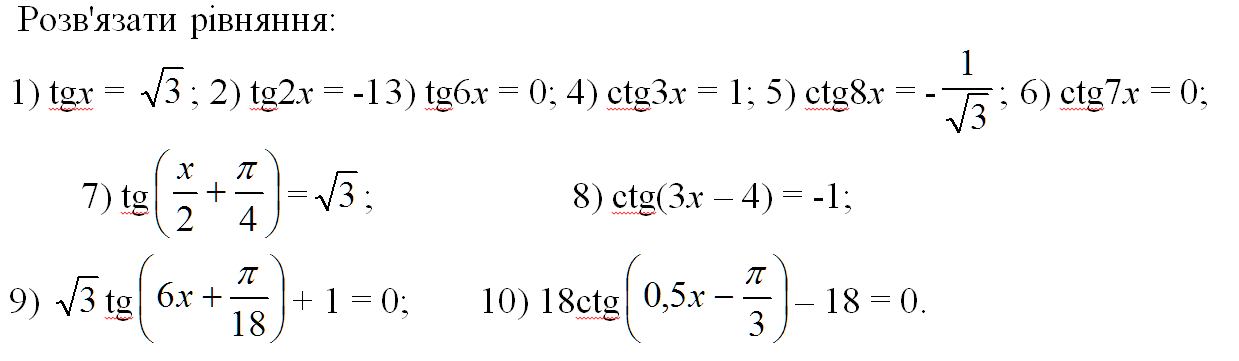 Запишем
уравнение касательной y
= 1. Таким образом в точках пересечения
графика функции и касательной получаем
уравнение
Запишем
уравнение касательной y
= 1. Таким образом в точках пересечения
графика функции и касательной получаем
уравнение
sinx = 1 x = /2+2k, kZ.
То есть, график функции имеет бесконечное число общих точек со своей касательной. Легче было решить эту задачу графически, так как, очевидно, что прямая y =1 будет касаться графика y = sinx во всех его «верхних» точках, а таких точек на всей числовой оси бесконечно много. ◄
1) y = sin3x +2, при x0 = 0. 2) y = cos5px +6 , при x0 = 1
3) y = sin5(x — 2) , при x0 = 2 4) y = cos5px +8 , при x0 = 1
7) y = arctg2x +4 , при x0 = 1 8) y= arcctg3x +6, при x0 = 1/6
9) y = ax2+bx +c, при x0 = –b/(2a) 10) y = ax+b, при x0 = –b/(2a)
11) y = 1/x2, при x0 = –1 12) y = x3+bx +c, при x0 = 0
13) y = (x+1)/(x-1), при x0 = –1/2 14) y = x2/(1+x), при x0 = –1
15) y = (x+1)/(3-x)1/3, при x0 = 2 16) y = sin4x – 1 , при x0 = /8
17) y = sin2(x — 1), при x0 = 3 18) y = cos2x +3 , при x0 = 0
19) y = tg4px +2, при x0 = 1 20) y= ctg(3px/2) +2, при x0 = 1
21) y = arctgx/2 +1, при, x0 = 1 22) y= arcctg3x/4 +6, при x
0 = 1/823) y = 3/2x2, при x0 = 7/2 24) y = x2+5x +23/24, при x0 = 5/4
25) y = (2x+3)/(7x-15), при x0 = 7/5 26) y = x4/2(4+2x), при x0 = 1/2
27) y = tg46x –1/e, при x0 = 2e 28) y = ctg(3x/8) -5, при x0 = 1
29) y = (3x+9)/(6-2x)1/5, при x0 =–2/3 30) y = sin4x/11 – 2 , при x0 = 11/8
12. Найти k-ю
производную от функции y
= f(x)
Найти k-ю
производную от функции y
= f(x)
Пример 12.1. y=ax—m, k=3
► Последовательно дифференцируя, имеем:
y` = –max-m-1;
y« = –ma(x-m-1)` = am(m+1)x-m-2;
y«` = am(m+1)(x-m-2
Пример 12.2. y= , k = 100.
► Преобразуем данную функцию к удобному для дифференцирования виду
y = 2(1-x)-1/2-(1-x)1/2
После 100-кратного дифференцирования получаем:
◄
1) k = 38, y = xex 2) k = 45, y = ex2
3) k = 30, y = sinx +ex 4) k = 39, y = cosx+ex
5) k = 68, y = cos2x +ex 6) k = 100, y = ln2x +ex
7) k = 50, y = 2x +ex 8) k = 618, y = (3x)121 +ex
9) k = 63, y = 1+ex 10) k = 87, y = +ex+1/(x+1)
11) k = 88, y = 1/(1-x2)+ex 12) k = 98, y = 1/x+ex
13) k = 78, y = 756x8+56x6+ex 14) k = 6, y = 1+cos(x)ex
15) k = 5, y = +sin(x)ex 16) k = 6, y = x(2x–1)2(x+3)3
17) k = 3, y = 18) k = 100, y =
19) k = 20, y = x2e2x 20) k = 10, y =
21) k = 6, y = sin2xlnx 22) k =100, y = xshx
23) k = 10, y = sinxsin2xsin3x 24) k = 50, y = x2sin2x
25) k = 5, y = xlnx 26) k = 5, y =
27) k = 8, y = 28) k = 10, y =
29) k = 6, y = cosxchx 30) k = 10, y = (2x–1)23x32x
13. С
помощью правила ЛОПИТАЛЯ найти предел
функции y =f(x) при x x0 .
С
помощью правила ЛОПИТАЛЯ найти предел
функции y =f(x) при x x0 .
Пример 13.1.
►Непосредственное применение правила Лопиталя не эффективно, поэтому, произведя замену 1/x2 = y и применив правило Лопиталя к полученному выражению получим
◄
Пример 13.2.
► Здесь имеется неопределенность вида 00, поэтому предварительно воспользуемся представлением (u>0, v>0), а также соотношением , вытекающим из непрерывности функции ex.
После очевидных преобразований и применения правила Лопиталя получаем
◄
1) x0 = +0 y = xx . 2) x0 = a y = (ax–xa)/(x–a)
3)
x0 = п/2
y = tg(3x)/tgx . 4) x0 = 0 y = (tg(x)–x)/(x–sinx) .
5) x0 = 0 y = sinax/sinbx . 6) x0 =1 y = x1/(1–x) .
7) x0 = +0 y = (ln(1/x))x . 8) x0 = 0 y = xalnx (a>0).
9) x0 = 0 y = ((1+x)1/x-e)/x . 10) x0 = 0 y = (1-cos(x2))/(x2sin(x2)) .
11) x0 = y = lnx/xa (a>0) . 12) x0 = 0 y = sinax/tgbx .
13) x0=0 y = ln(sin(ax))/ln(sin(bx)) . 14) x0 = 0 y = ln(cos(bx))/ln(cos(ax))
15) x0 = 0 y = (cos(sinx))-cosx)/x4 . 16) x0 = 0 y =
17) x0=0 y= 18) x0 = 1 – 0 y = lnxln(1-x)
19) x0=0 y= 20) x0 + y = (thx)x
21) x0 = 0 y = 22) x0 = 0 y =
23) x0 = 0 y = 24) x0 = 0 y =
25) x0 = 0 y = 26) x0 = 0 y =
27) x0 = 1 y = 28) x0 = 0 y =
29) x0 = +0 y = -1 30) x0 = /4 y = (tgx)tg2x
14.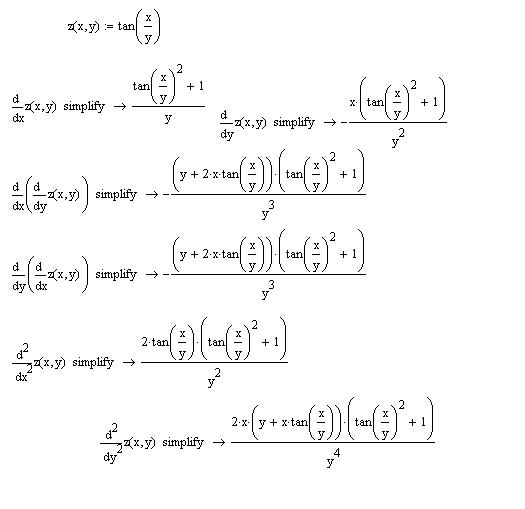 Найти
второй
дифференциал функции y = f(x) определяемой
уравнением
Найти
второй
дифференциал функции y = f(x) определяемой
уравнением
Пример 14.1. y=lnx
► Находим последовательно
dy = – dx/x;
◄
Пример 14.2. y = f(x) , где x – функция от некоторой независимой переменной.
► Исходя из определения дифференциалов высших порядков, имеем:
dy = f`dx; d2y = d(f`dx) = f«(dx)2 + f`d2x;
d3y = d(f«(dx)2 + f`d2x) =
f«`(dx)3 + 2f«dxd2x + f«dxd2x + f`d3x = f«`(dx)3 + 3d2xdxf« + f`d3x.◄
1) sin(x + y) =y 2) tg(x + y) = y
3) exy + x + y = 0 4) log3(x + y) = x + y
5) log4(x2 + y) = 1-y 6) arccos(3x4 + y2) = y
7) (1 + x2 + y2)1/3 = x-y2 8) arctg(x4 + 3y) = x + y6
9) arcctg(x5 + 2y) = x + y3 10) 2xy + y = xy + x
11) 31/(x + y) = xy 12) xy = x + y
13) yx = x2 + y3 14) (x + y)(x + y) = x4 + y7
15) logxy = x+y2 16) sin2(x + y) = 3y
17) logxy = (x+y)2 18) 3x + y + 2x + 5y = 0
19) y3 = x3 + 3y 20) arctg(x – y) = x + y
21) x2y = xx 22) ln(2x + 3y) = x – 2y2
23) = x2-y2 24) cos(xy) = sin(x + y)
25) tg(cosxy) = lnx3 26) (x + y)3 = xy
27) log3xx + y = y2 28) 2x + y = xy
29) lncos(x3 + y) = x + y5 30) x3x + y3 = 2xy
2} x}} {{\ Delta x}} \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {\ left [{\ tan \ left ({x + \ Delta x} \ right) + \ tan x} \ right] \ left [{\ tan \ left ({x + \ Delta x} \ right) — \ tan x} \ right]}} {{\ Delta x}} \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {\ left [{\ tan \ left ({x + \ Delta x} \ right) + \ tan x} \ right]}} {{\ Delta x}} \ left [{\ frac {{\ sin \ left ({x + \ Delta x} \ right)}} {{\ cos \ left ({x + \ Delta x} \ right)}} — \ frac {{\ sin x}} {{\ cos x}}} \ right] \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{\ left [{\ tan \ left ({x + \ Delta x} \ right) + \ tan x} \ right]}} {{\ Delta x}} \ left [{\ frac {{\ sin \ left ({x + \ Delta x} \ right) \ cos x — \ cos \ left ({x + \ Delta x} \ right) \ sin x}} {{\ cos \ left ({x + \ Delta x} \ right) \ cos x}}} \ right] \\ \ end {собрано} \] Используя формулу из тригонометрии \ [\ sin \ alpha \ cos \ beta — \ cos \ alpha \ sin \ beta = \ sin \ left ({\ alpha — \ beta} \ right) \]
\ [\ begin { } \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{\ left [{\ tan \ left ({x + \ Delta x} \ right) + \ tan x} \ right]}} {{\ Delta x}} \ left [{\ frac {{\ sin \ left ({x + \ Delta x — x} \ right)}} {{\ cos \ left ({x + \ Delta x} \ right) \ cos x}}} \ right] \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Дельта x \ к 0} \ frac {{\ left [{\ tan \ left ({x + \ Delta x} \ right) + \ tan x} \ right]}} {{\ cos \ left ({x + \ Delta x} \ right) \ cos x}} \ left [{\ frac {{\ sin \ left ({\ Delta x} \ right)}} {{\ Delta x}}} \ right] \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ frac {{\ left [{\ tan \ left ({x + \ Delta x} \ right ) + \ tan x} \ right]}} {{\ cos \ left ({x + \ Delta x} \ right) \ cos x}} \ mathop {\ lim} \ limits _ {\ Delta x \ to 0} \ left [{\ frac {{\ sin \ left ({\ Delta x} \ right)}} {{\ Delta x}}} \ right] \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ f rac {{\ left [{\ tan \ left ({x + 0} \ right) + \ tan x} \ right]}} {{\ cos \ left ({x + 0} \ right) \ cos x}} \ left (1 \ right) \\ \ Rightarrow \ frac {{dy}} {{dx}} = \ frac {{2 \ tan x}} {{{{\ cos} ^ 2} x}} \\ \ Стрелка вправо \ frac {{dy}} {{dx}} = 2 \ tan x {\ sec ^ 2} x \\ \ end {gather} \]
Пример : Найдите производную от \ [y = f \ left (x \ right) = {\ tan ^ 2} \ left ({{x ^ 2} + 1} \ right) \]
У нас есть заданная функция как
\ [y = {\ tan ^ 2} \ left ({{x ^ 2} + 1} \ right) \]
Дифференцируя по переменной $$ x $$, получаем
\ [\ frac {{dy}} {{dx}} = \ frac {d} {{dx}} {\ tan ^ 2} \ left ({ {x ^ 2} + 1} \ right) \]
Используя правило $$ \ frac {d} {{dx}} {\ tan ^ 2} x = 2 \ tan x {\ sec ^ 2} x $$, получаем
\ [\ begin {gather} \ frac {{dy}} {{dx}} = 2 \ tan \ left ({{x ^ 2} + 1} \ right) {\ sec ^ 2} \ left ({{x ^ 2} + 1} \ right ) \ frac {d} {{dx}} \ left ({{x ^ 2} + 1} \ right) \\ \ Rightarrow \ frac {{dy}} {{dx}} = 2 \ tan \ left ({ {x ^ 2} + 1} \ right) {\ sec ^ 2} \ left ({{x ^ 2} + 1} \ right) \ left ({2x} \ right) \\ \ Rightarrow \ frac {{dy }} {{dx}} = 4x \ tan \ left ({{x ^ 2} + 1} \ right) {\ sec ^ 2} \ left ({{x ^ 2} + 1} \ right) \\ \ конец \]
Производные от тригонометрических функций
Основные тригонометрические функции включают следующие \ (6 \) функции: синус \ (\ left (\ sin x \ right), \) косинус \ (\ left (\ cos x \ right), \) тангенс \ (\ left (\ tan x \ right), \) котангенс \ (\ left (\ cot x \ right), \) секанс \ (\ left (\ sec x \ right) \) и косеканс \ (\ left (\ csc x \ верно). \ prime} = {1 \ cdot \ sin x + x \ cdot \ cos x + \ left ({- \ sin x} \ right)} = {\ cancel {\ sin x} + x \ cos x — \ cancel { \ sin х}} = {х \ соз х.} \]
\ prime} = {1 \ cdot \ sin x + x \ cdot \ cos x + \ left ({- \ sin x} \ right)} = {\ cancel {\ sin x} + x \ cos x — \ cancel { \ sin х}} = {х \ соз х.} \]
Дифференциальное исчисление
Дифференциальное исчислениеEngineering ToolBox — ресурсы, инструменты и основная информация для проектирования и разработки технических приложений!
– поиск — самый эффективный способ навигации по Engineering ToolBox!
Производные и дифференцирование
1 1 y = сек (Θ)| Выражение | Производные | |
|---|---|---|
| y = x n | dy / dx = nx n-1 n | dy / dx = тревога n-1 |
| f (x) = ax n | f ‘(x) = тревога n-1 | |
| y = e x | dy / dx = e x | |
| y = e ax | dy / d ax = y = a x | dy / dx = a x ln (a) |
| y = ln (x) | dy / dx = 1 / x | |
| y = грех (Θ) 903 21 | dy / dΘ = cos (Θ) | |
| y = cos (Θ) | dy / dΘ = — sin (Θ) | |
| y = tan (Θ) 90 | dy / dΘ = сек 2 (Θ) | |
| y = детская кроватка (Θ) | dy / dΘ = cosec 2 (Θ) | |
| dy / dΘ = tan (Θ) sec (Θ) = sin (Θ) / cos 2 (Θ) | ||
| y = cosec (Θ) | dy / dΘ = — cot (Θ) cosec (Θ) = — cos (Θ) / sin 2 (Θ) | |
| y = sin -1 (x / a) | dy / dx = 1 / (a 2 — x 2 ) 1/2 | |
| y = cos -1 ( x / a) | dy / dx = — 1 / (a 2 — x 2 ) 1/2 | |
| y = tan -1 (x / a) | dy / dx = a / (a 2 + x 2 ) | |
| y = детская кроватка -1 (x / a) | dy / dx = — a / (a 2 + x 2 ) | |
| y = sec — 1 (x / a) | dy / dx = a / (x (x 2 — a 2 ) 1/2 ) | |
| y = cosec -1 ( x / a) | dy / dx = — a / (x (x 2 — a 2 ) 1/2 ) |
Связанные темы
Связанные документы
Поиск по тегам
- ru: дифференциальное исчисление производных
Перевести эту страницу на
О Engineering ToolBox!
Мы не собираем информацию от наших пользователей. В нашем архиве хранятся только письма и ответы. Файлы cookie используются в браузере только для улучшения взаимодействия с пользователем.
В нашем архиве хранятся только письма и ответы. Файлы cookie используются в браузере только для улучшения взаимодействия с пользователем.
Некоторые из наших калькуляторов и приложений позволяют сохранять данные приложений на локальном компьютере. Эти приложения — из-за ограничений браузера — будут отправлять данные между вашим браузером и нашим сервером. Мы не сохраняем эти данные.
Google использует файлы cookie для показа нашей рекламы и обработки статистики посетителей. Пожалуйста, прочтите Условия использования Google для получения дополнительной информации о том, как вы можете контролировать показ рекламы и собираемую информацию.
AddThis использует файлы cookie для обработки ссылок на социальные сети. Пожалуйста, прочтите AddThis Privacy для получения дополнительной информации.
Цитирование
Эту страницу можно цитировать как
- Engineering ToolBox, (2011). Дифференциальное исчисление . [онлайн] Доступно по адресу: https://www.
 engineeringtoolbox.com/derivatives-differential-calculus-d_1766.html [день доступа, пн. год].
engineeringtoolbox.com/derivatives-differential-calculus-d_1766.html [день доступа, пн. год].
Изменить дату доступа.
. .закрыть
Научный онлайн-калькулятор
5 19
.Функция обратной касательной
Функция обратной касательнойФункция y = tan
-1 x = arctan x и ее график:Поскольку y = tan -1 x является обратной функцией y = tan x, функция y = tan -1 x тогда и только тогда, когда tan y = x . Но, поскольку y = tan x не является взаимно однозначным, его область должна быть ограничена, чтобы y = tan -1 x была функцией. Чтобы получить график y = tan -1 x, начните с графика y = tan x. (Окно справа — [-2, 2] x [-4, 4].) | |
Ограничить область действия функции однозначной областью — обычно используется (выделено справа) для tan -1 x. Это оставляет диапазон ограниченной функции неизменным как. Это оставляет диапазон ограниченной функции неизменным как. | |
Отразите этот график через линию y = x, чтобы получить график y = tan -1 x (y = arctan x), самая толстая черная кривая справа. Обратите внимание, что y = tan -1 x имеет домен и диапазон. Он строго увеличивается на всей своей территории. | |
| Итак, когда вы попросите калькулятор построить график y = tan -1 x, вы получите график, показанный справа. (Окно просмотра составляет [-2, 2] x [-4, 4].) |
Производная y = tan -1 x:
Производная y = tan -1 x: (Щелкните здесь, чтобы получить вывод.)
Графики y = tan -1 x и его производной показаны ниже. Область y ‘есть. Поскольку y = tan -1 x всегда увеличивается, y ‘> 0 для всех x в своей области.
Интегралы, содержащие обратную касательную функцию
Вот типичная проблема:
Какая площадь находится под графиком на [0,10]?
График этого региона показан справа.Площадь этого региона:
Теперь мы знаем, что:
Сравнение того, что мы знаем, с тем, что нам нужно знать, показывает, что мы принимаем u 2 = 4x 2 :
последнее обновление 30 марта 2010 г., Джерри Л. Стэнбро
% PDF-1.3
%
24 0 obj>
эндобдж
xref
24 92
0000000016 00000 н.
0000002646 00000 н.
0000002726 00000 н.
0000002905 00000 н.
0000003300 00000 н.
0000003802 00000 н.
0000004314 00000 н.
0000004540 00000 н.
0000004970 00000 п.
0000005599 00000 н.
0000006113 00000 п.
0000006816 00000 н.
0000006870 00000 н.
0000007026 00000 н.
0000011865 00000 п.
0000011899 00000 п. 0000011946 00000 п.
0000012005 00000 п.
0000012065 00000 п.
0000012460 00000 п.
0000012513 00000 п.
0000012567 00000 п.
0000012952 00000 п.
0000013219 00000 п.
0000014576 00000 п.
0000014826 00000 п.
0000015161 00000 п.
0000015259 00000 п.
0000016557 00000 п.
0000016939 00000 п.
0000017253 00000 п.
0000017622 00000 п.
0000017813 00000 п.
0000017888 00000 п.
0000020050 00000 п.
0000020343 00000 п.
0000020662 00000 п.
0000020838 00000 п.
0000022880 00000 п.
0000023162 00000 п.
0000023539 00000 п.
0000023689 00000 п.
0000026117 00000 п.
0000026435 00000 п.
0000028072 00000 п.
0000028264 00000 п.
0000028641 00000 п.
0000028696 00000 п.
0000028743 00000 п.
0000029652 00000 п.
0000029894 00000 п.
0000029977 00000 н.
0000030710 00000 п.
0000030959 00000 п.
0000031263 00000 п.
0000031334 00000 п.
0000031410 00000 п.
0000031741 00000 п.
0000033658 00000 п.
0000035965 00000 п.
0000038180 00000 п.
0000040394 00000 п.
0000040761 00000 п.
0000040815 00000 п.
0000011946 00000 п.
0000012005 00000 п.
0000012065 00000 п.
0000012460 00000 п.
0000012513 00000 п.
0000012567 00000 п.
0000012952 00000 п.
0000013219 00000 п.
0000014576 00000 п.
0000014826 00000 п.
0000015161 00000 п.
0000015259 00000 п.
0000016557 00000 п.
0000016939 00000 п.
0000017253 00000 п.
0000017622 00000 п.
0000017813 00000 п.
0000017888 00000 п.
0000020050 00000 п.
0000020343 00000 п.
0000020662 00000 п.
0000020838 00000 п.
0000022880 00000 п.
0000023162 00000 п.
0000023539 00000 п.
0000023689 00000 п.
0000026117 00000 п.
0000026435 00000 п.
0000028072 00000 п.
0000028264 00000 п.
0000028641 00000 п.
0000028696 00000 п.
0000028743 00000 п.
0000029652 00000 п.
0000029894 00000 п.
0000029977 00000 н.
0000030710 00000 п.
0000030959 00000 п.
0000031263 00000 п.
0000031334 00000 п.
0000031410 00000 п.
0000031741 00000 п.
0000033658 00000 п.
0000035965 00000 п.
0000038180 00000 п.
0000040394 00000 п.
0000040761 00000 п.
0000040815 00000 п.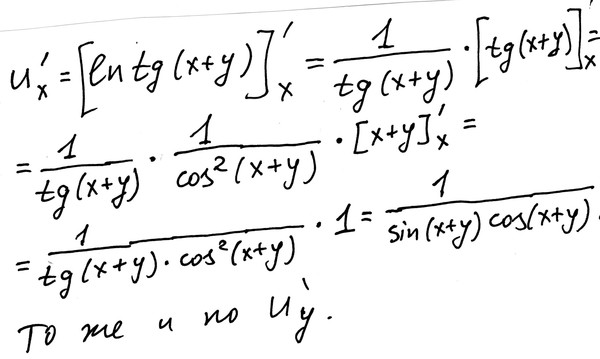 2 + 3)`.2 + 3) `
2 + 3)`.2 + 3) `
cos x 2 + 3
не равно
cos ( x 2 + 3).
Кронштейны имеют большое значение. У многих студентов с этим возникают проблемы.
Вот графики y = cos x 2 + 3 (зеленый) и y = cos ( x 2 + 3) (показаны синим).
Первый, y = cos x 2 + 3 или y = (cos x 2 ) + 3, означает взять кривую y = cos x 2 и переместите его вверх на «3» единицы.2sin x`
6. Найдите производную неявной функции
x cos 2 y + sin x cos y = 1.
Ответ
Неявная функция:
`x \ cos 2y + sin x \ cos y = 1`
Мы дифференцируем каждый термин слева направо:
`x (-2 \ sin 2y) ((dy) / (dx))` `+ (cos 2y) (1)` `+ sin x (-sin y (dy) / (dx))` `+ cos у \ соз х`
`= 0`
Так
`(-2x \ sin 2y-sin x \ sin y) ((dy) / (dx))` `= -cos 2y-cos y \ cos x`
Решение для `dy / dx` дает нам:
`(dy) / (dx) = (- cos 2y-cos y \ cos x) / (- 2x \ sin 2y-sin x \ sin y)`
`= (cos 2y + cos x \ cos y) / (2x \ sin 2y + sin x \ sin y)`
7. 2`
2`
Когда x = 0,15 (конечно, в радианах), это выражение (которое дает нам наклон) равен «-2,65».
Вот график нашей ситуации. Показана касательная к кривой в точке, где x = 0,15. Его наклон равен «-2,65».
8. Ток (в амперах) в цепи усилителя как функция времени t (в секундах) определяется как
`i = 0.10 cos (120πt + π / 6)`.
Найдите выражение для напряжения на 2.2x + загар x`
См. Также: Производная квадратного корня из синуса x по первым принципам.
РЕШЕНИЕ: Найдите площадь области, ограниченную…
Стенограмма видео
здесь мы хотим найти площадь области, ограниченную кривыми. Десять x загар в квадрате X для X между нулевой степенью для Итак, вот приблизительный набросок графиков, и позвольте мне объяснить, почему Итак, во-первых, мы знаем, что может и дубль в квадрате или оба нуля на X ноль, и они оба выигрывают, когда избыточная мощность на данный момент между бывшими между нулевым пирометром, потому что у нас есть числа. Итак, у нас есть желто-коричневый квадрат. Итак, у нас на ноль меньше, чем у наших людей, на два десятка яиц меньше, чем на единицу на интервале. Раньше это была ваша собственная империя, и я знаю, что когда вы берете число от нуля до единицы и возводите его в более высокую степень, их число становится меньше. Итак, поскольку синий график является большей степенью того же числа десять, он будет меньше красного графика. Итак, чтобы убедиться в этом, перейдем к настоящему графическому калькулятору. Так что просто это перед самой красной рукой, самой синей рукой в квадрате и от нуля до примерно степени, потому что мы видим, что красный график находится над синим эталоном, так что это хорошо нам говорит.Прежде всего, у нас будет формула для площади .Итак, давайте запишем это. Эта площадь является интегралом A, чтобы быть таким здесь. Нулевая мощность перед абсолютным значением десяти яиц Квадрат Линуса Тана. По нашим предыдущим наблюдениям, мы заметили, что квадрат загара был меньше или равен десяти яйцам.
Итак, у нас есть желто-коричневый квадрат. Итак, у нас на ноль меньше, чем у наших людей, на два десятка яиц меньше, чем на единицу на интервале. Раньше это была ваша собственная империя, и я знаю, что когда вы берете число от нуля до единицы и возводите его в более высокую степень, их число становится меньше. Итак, поскольку синий график является большей степенью того же числа десять, он будет меньше красного графика. Итак, чтобы убедиться в этом, перейдем к настоящему графическому калькулятору. Так что просто это перед самой красной рукой, самой синей рукой в квадрате и от нуля до примерно степени, потому что мы видим, что красный график находится над синим эталоном, так что это хорошо нам говорит.Прежде всего, у нас будет формула для площади .Итак, давайте запишем это. Эта площадь является интегралом A, чтобы быть таким здесь. Нулевая мощность перед абсолютным значением десяти яиц Квадрат Линуса Тана. По нашим предыдущим наблюдениям, мы заметили, что квадрат загара был меньше или равен десяти яйцам. Это говорит нам о том, что коричневые яйца минус десять квадратных Dex положительно. И мы можем использовать это, потому что если это так, если это положительное значение, это означает, что абсолютное значение — это само по себе. Таким образом, мы можем записать это так, как в девочке нулевая степень перед десятью яйцами минус десять в квадрате. Теперь давайте продолжим и перепишем эту нулевую степень для CNX минус поиск и возведем в квадрат X минус один.Итак, мы здесь использовали идентификацию пути Agron, чтобы переписать Tan Square как сикха и возвести его в квадрат минус один. Мы можем оценить все эти антипроизводные. Производная тангенса — это натуральный логарифм абсолютного значения C не может. Здесь у нас есть минус загар X, и это становится так, что у нас есть двойная минус их своего рода плюс X и rn указывает на нулевую мощность для Итак, это идет и подключает эти конечные точки. Таким образом, Пи играет за четыре первых поиска Пайпер в естественном бревне для своего маршрута.
Это говорит нам о том, что коричневые яйца минус десять квадратных Dex положительно. И мы можем использовать это, потому что если это так, если это положительное значение, это означает, что абсолютное значение — это само по себе. Таким образом, мы можем записать это так, как в девочке нулевая степень перед десятью яйцами минус десять в квадрате. Теперь давайте продолжим и перепишем эту нулевую степень для CNX минус поиск и возведем в квадрат X минус один.Итак, мы здесь использовали идентификацию пути Agron, чтобы переписать Tan Square как сикха и возвести его в квадрат минус один. Мы можем оценить все эти антипроизводные. Производная тангенса — это натуральный логарифм абсолютного значения C не может. Здесь у нас есть минус загар X, и это становится так, что у нас есть двойная минус их своего рода плюс X и rn указывает на нулевую мощность для Итак, это идет и подключает эти конечные точки. Таким образом, Пи играет за четыре первых поиска Пайпер в естественном бревне для своего маршрута. Поскольку он положительный, мы можем тут же опустить абсолютное значение, а затем касательная друг к другу, прежде чем будет равна единице плюс x.Итак, плюс мощность для, а затем, когда мы подключаем ноль, у нас есть натуральный логарифм, и поиск нуля — это одна касательная к нулю, а затем плюс ноль. И мы знаем этот натуральный логарифм одного нуля, поэтому мы можем игнорировать весь второй член. И мы остались с нашим окончательным ответом. Эллен Рут тоже минус один плюс пират для Так что это наша территория, и это наш окончательный ответ.
Поскольку он положительный, мы можем тут же опустить абсолютное значение, а затем касательная друг к другу, прежде чем будет равна единице плюс x.Итак, плюс мощность для, а затем, когда мы подключаем ноль, у нас есть натуральный логарифм, и поиск нуля — это одна касательная к нулю, а затем плюс ноль. И мы знаем этот натуральный логарифм одного нуля, поэтому мы можем игнорировать весь второй член. И мы остались с нашим окончательным ответом. Эллен Рут тоже минус один плюс пират для Так что это наша территория, и это наш окончательный ответ.
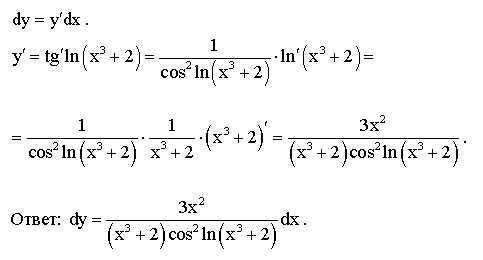

 15 + cos x) — x10(-sin x)
15 + cos x) — x10(-sin x) engineeringtoolbox.com/derivatives-differential-calculus-d_1766.html [день доступа, пн. год].
engineeringtoolbox.com/derivatives-differential-calculus-d_1766.html [день доступа, пн. год].