Парабола y 2 3x – Парабола, квадратичная функция. Как решаются квадратные уравнения?

Содержание

x y 2 парабола

Вы искали x y 2 парабола? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y 1 3x 2 парабола, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x y 2 парабола».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как x y 2 парабола,y 1 3x 2 парабола,y 1 4x 2 парабола,y 2x 2 парабола,y 2×2 парабола,y 3x 2 парабола,ветви параболы,график функции y x2 парабола,как найти дополнительные точки параболы,как начертить параболу,как параболу чертить,как по уравнению построить параболу,как построить парабола,как построить параболу,как построить параболу по уравнению,как решать параболу,как рисовать параболу,как сделать параболу,как строится парабола,как строить парабола,как строить параболу,как строить параболы,как чертить параболу,отрицательная парабола,парабола 2 x,парабола 2 х 2,парабола x 2 y,парабола x y 2,парабола x y в квадрате,парабола x y в квадрате y,парабола y 1 2×2,парабола y 2 2x,парабола y 2 3x,парабола y 2 x 2,парабола y 2×2,парабола y 3x 2,парабола алгебра,парабола как построить,парабола как строится,парабола как строить,парабола отрицательная,парабола построение,парабола х в квадрате,парабола х2,парабола х2 у,параболу как сделать,параболы решение,построение параболы,построить параболу по уравнению,сколько нужно точек для построения параболы,сколько точек нужно для построения параболы,таблица параболы,точки для параболы,точки параболы,формула график параболы,формула параболы график,х в квадрате парабола,шаблон параболы y 2x в квадрате,шаблон параболы y x в квадрате. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и x y 2 парабола. Просто введите задачу в окошко и нажмите «решить» здесь или введите в окно ввода ниже свой запрос (например, y 1 4x 2 парабола).

Где можно решить любую задачу по математике, а так же x y 2 парабола Онлайн?

Решить задачу x y 2 парабола вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на этой странице.

www.pocketteacher.ru

Квадратичная функция. Как построить параболу?

Квадратичная функция – это функция вида $y=ax^2+bx+c$. График квадратичной функции – парабола.

Примеры:

$y= x^2+6x+5$		$y=x^2-4x+5$
$y=-2x^2-4x+4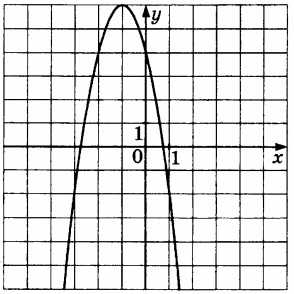$		$y=-3x^2+21x-34$

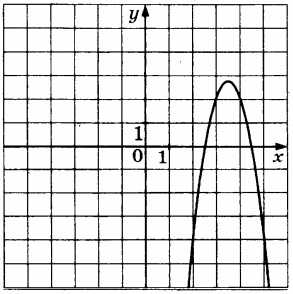«Анатомия» квадратичной функции:

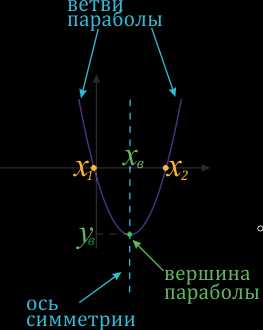
$x_в$ и $y_в$ – координаты вершины параболы. $x_в$ можно найти с помощью формулы: $x_в=\frac{-b}{2a}$. $y_в$ можно найти подставив в формулу квадратичной функции вместо $x$ значение $x_в: y_в=ax_в^2+bx_в+с$
Ось симметрии проходит через вершину параболы и параллельна оси $y$ (ординат). $x_1$ и $x_2$ – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.

3 параметра позволяющих сопоставить формулу квадратичной функции и график:

1.	$a>0$ — ветви параболы направлены вверх
1.	$a<0$ — ветви параболы направлены вниз
2.	$c$ равна ординате точки пересечения графика с осью $y$
3.	координата вершины параболы $x_в=-\frac{b}{2a}$

Пример (задание из ОГЭ). На рисунке изображён график квадратичной функции $y=ax^2+bx+c$

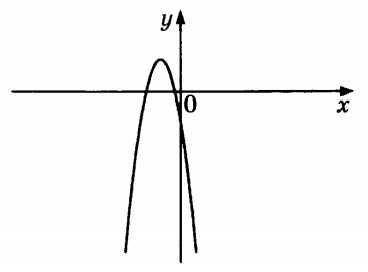
Какие знаки параметров $a$ и $c$?

Решение:

Ветви параболы направлены вниз, значит $a<0$
График функции пересекает ось $y$ в точке лежащий ниже оси $x$, значит $c<0$

Ответ: $a<0$,$c<0$

Пример (задание из ОГЭ). Установите соответствие между квадратичными функциями и их графиками:

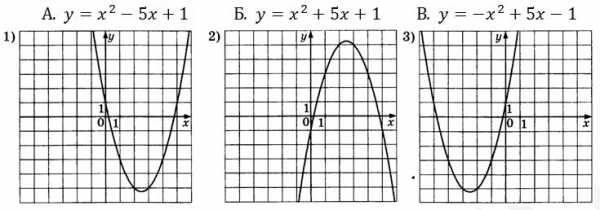
Решение:
Во втором графике ветви параболы направлены вниз, значит $a<0$. Под этот график подходит только функция под буквой В.
Во втором и третьем графике $a>0,c=1$ – по этим параметрам нам определить их функции. Тогда найдем $x_в$ функций под буквой А и Б:

А. $y=x^2-5x+1$ $x_в=\frac{5}{2}=2,5$ так же как на графике 1
Б. $y=x^2+5x+1$ $x_в= \frac{-5}{2}=-2,5$ так же как на графике 3

Ответ:

Как построить график квадратичной функции (параболу)?

Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно.

Найдите координаты вершины параболы. Поставьте точку вершины на координатной плоскости и проведите через неё ось симметрии параболы.
Найдите точку пересечения графика с осью $y$: $x=0;y=c$. Постройте точку симметричную точке $(0;c)$ относительно оси параболы.
Найдите координату целой точки, лежащей вблизи оси параболы. Отметьте симметричную ей точку на плоскости.

Соедините точки плавной линией.

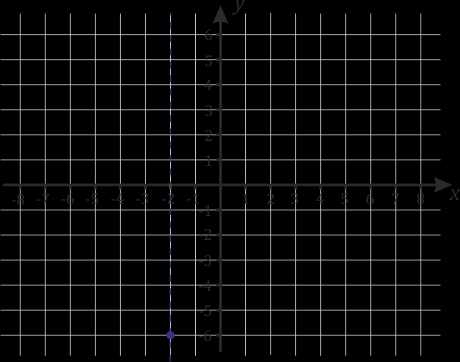
$a=2$, $b=8$, $c=2$ 1. $x_в=\frac{-b}{2a}=\frac{-8}{2 \cdot 2}=-2$ $y_в=2 \cdot (-2)^2+8 \cdot (-2)+2=2 \cdot 4-16+2=-6$
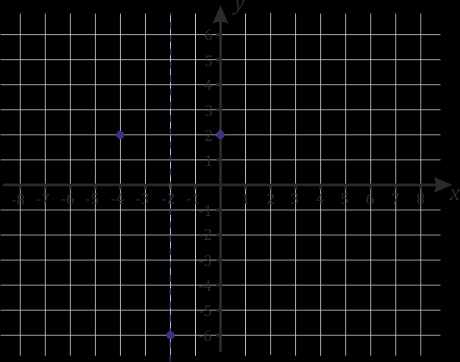
2. $x=0, y=2$
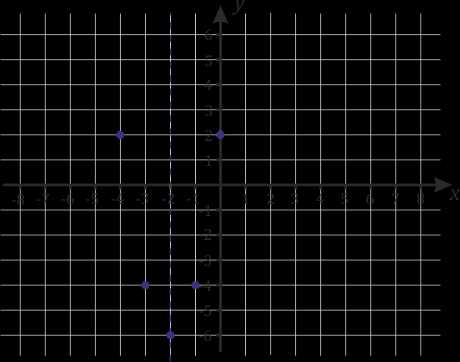
3. При $x=-3$, $y=2 \cdot (-3)^2+8 \cdot (-3)+2=2 \cdot 9-24+2=20-24=-4$
Готово!

Связь квадратичной функции и квадратных уравнений:

Давайте сравним общий вид квадратичной функции и общий вид квадратного уравнения:

$y=ax^2+bx+c$

$ax^2+bx+c=0$

И там, и там есть квадратный трехчлен $ax^2+bx+c$. Разница в том, что в функции мы исследуем все возможные значения трехчлена, а в уравнении мы ищем $x$, при которых значение трехчлена будет равно нулю или при каких $x$, $y=0$. Поэтому по графику функции $y=ax^2+bx+c$ легко определить корни уравнения $ax^2+bx+c=0$.

Пример:

$y=x^2+6x+5$	$y=x^2-4x+5$

Судя по графику, корнями уравне- ния $x^2+6x+5=0$ будут $x_1=-5$ и $x_2=-1$	У уравнения $x^2-4x+5=0$ нет корней, т.к. нету $x$ при которых y будет равен нулю (функция не пересекает ось $x$)

Смотрите также:
Линейная функция
Виды графиков функций
Квадратные неравенства

Скачать статью

cos-cos.ru

Ответы@Mail.Ru: куда смещена парабола y=-x^2+3?

Парабола с ветками вниз, смещенная на 3 вверх

в верх по оси игрик на три пункта!!!

на три клетки вверх

она перевернута вниз «рожками» и ее вершина поднята на 3 пункта по оси У

Вверх на три единицы.

Это просто. Подставь несколько значений Х, найди У и построй график. Центр параболы будет в точке ( 0, 3 ), ветви пойдут вверх, т. к. даже при отрицательном Х функция У будет положительной.

Вершина на три единицы вверх по оси У, ветви вверх, и сжата к оси У

touch.otvet.mail.ru

Парабола

Определение 1

Парабола — это кривая, образованная геометрическим множеством точек, равноудалённых от точки $F$, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.

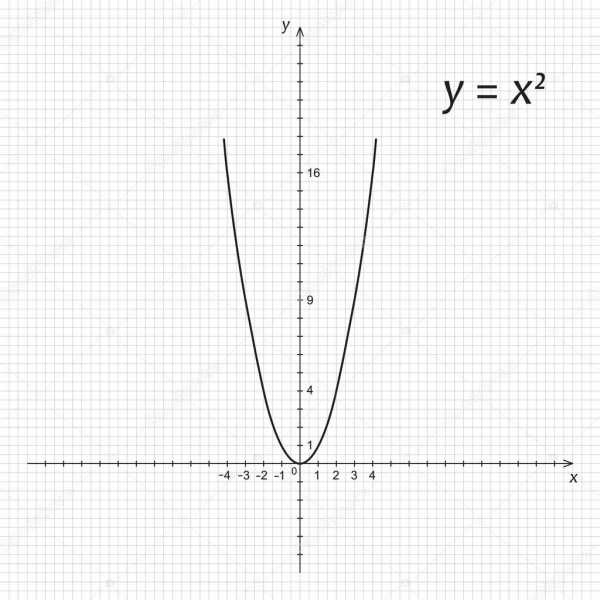
Рисунок 1. Парабола в прямоугольной системе координат

Парабола наряду с окружностью, эллипсом и гиперболой является одним из сечений конуса.

Парабола симметрична относительно своей оси, и поэтому можно построить сначала одну половину параболы, а затем, отложив симметричные этой половине точки, уже другую.

Определение 2

Классическая парабола описывается уравнением, оно имеет следующий вид:

$y^2 = 2px$, где число $p$ должно быть больше нуля.

Это уравнение является каноническим уравнением параболы и описывает вид параболы в прямоугольной системе координат.

Чаще всего приходится иметь дело с уравнениями параболы с вершиной, располагающейся не на пересечении осей координат, их общий вид представлен формулой: $y = ax^2 + bx + c$.

Кто придумал параболу

Парабола известна математикам уже очень давно, а название этой функции дал древнегреческий математик Аполлоний Пергский в III в. до н.э., изучавший свойства сечений конуса.

Также изучением параболы занимались Архимед и Папп Александрийский.

В дальнейшем разные учёные показали, что многие явления можно описать параболой, так, например, была открыта траектория движения снаряда.

Основные определения и строение параболы

Вершина параболы — это точка, находящаяся на минимальном расстоянии от директрисы параболы $d$.

Фокус $F$ параболы — это точка, через которую проходит ось симметрии параболы, перпендикулярная прямой, находящаяся на расстоянии $d$. Фокус расположен на расстоянии $\frac{p}{2}$ от вершины. Координаты фокуса классической параболы можно определить из её уравнения.

Фокус и вершина являются основными точками, характеризующими параболу.

Параметр $p$ параболы иначе называется фокальным параметром и является расстоянием между фокусом и директрисой. Чтобы найти фокальный параметр параболы, нужно выразить $p$ из формулы канонического уравнения параболы:

$p = \frac{y^2}{2x}$, где $x$ и $y$ — координаты точки, лежащей на параболе. Координаты фокуса параболы определяются через значение фокального параметра и равны ($\frac{p}{2};0)$.

Анализ уравнения и описание параболы

Сначала необходимо обратить внимание на коэффициент $a$ при $x^2$. Если он отрицательный, то парабола перевёрнутая по отношению к обычной и её ветви смотрят вниз, а если положительный – то её ветви смотрят вверх. Также модуль коэффициента $a$ влияет на степень пологости (ширину) параболы, чем меньше модуль $a$, тем парабола более широкая (пологая), и чем больше модуль $a$, тем она более узкая (крутая).
Далее необходимо посмотреть на коэффициент $c$. Коэффициент $c$ обозначает смещение по оси $OY$ относительно пересечения осей координат. Это легко проверить, если приравнять $x$ к нулю в имеющемся уравнении. Если коэффициент $c$ — положительный, то парабола смещена вверх относительно точки $(0;0)$, а если отрицательный – то вниз. В случае если $c=0$ — парабола проходит через точку начала координат.
Теперь можно найти вершину параболы, её координаты вычисляются по формуле:
$x = — \frac{b}{2a}$ (1).

Чтобы найти $y$, нужно подставить полученный по формуле $x$ в уравнение.

Пример 1

Рассмотрим уравнение параболы $y = x^2 + 2x + 3$

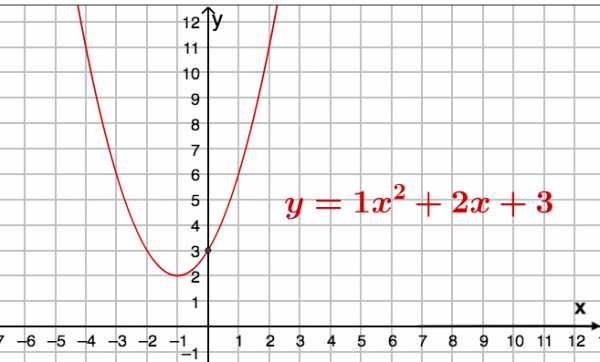
Рисунок 2. Анализ уравнения параболы, график и примеры решения

Коэффициент при $a$ положительный, значит, ветви параболы смотрят вверх.
Теперь смотрим на коэффициент $c$, он равен 3, значит, парабола пересекается с осью ординат в точке $(0; 3)$.
Найдём координату $x$ вершины параболы по формуле (1), она равна $x = — \frac{2}{2} = -1$. Теперь найдём значение $y$, подставив значение $x$ в уравнение: $y = 1^2 +(-1) \cdot 2 + 3 = 2$. Координаты вершины равны $(-1; 2)$.

spravochnick.ru

\(y= x^2+6x+5\)		\(y=x^2-4x+5\)
\(y=-2x^2-4x+4\)		\(y=-3x^2+21x-34\)

\(a=2\), \(b=8\), \(c=2\) 1. \(x_в=\frac{-b}{2a}=\frac{-8}{2 \cdot 2}=-2\) \(y_в=2 \cdot (-2)^2+8 \cdot (-2)+2=2 \cdot 4-16+2=-6\)
2. \(x=0, y=2\)
3. При \(x=-3\), \(y=2 \cdot (-3)^2+8 \cdot (-3)+2=2 \cdot 9-24+2=20-24=-4\)
Готово!

\(y=x^2+6x+5\)	\(y=x^2-4x+5\)

Судя по графику, корнями уравне- ния \(x^2+6x+5=0\) будут \(x_1=-5\) и \(x_2=-1\)	У уравнения \(x^2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\))