Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Схема метода Феррари
Целью данного раздела является изложение метода Феррари, с помощью которого можно решать уравнения четвёртой степени
| a0x4 + a1x3 + a2x2 + + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем 
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x4 + ax3 + bx2 + + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
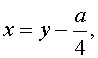 | (3) |
где y – новая переменная.
Тогда, поскольку
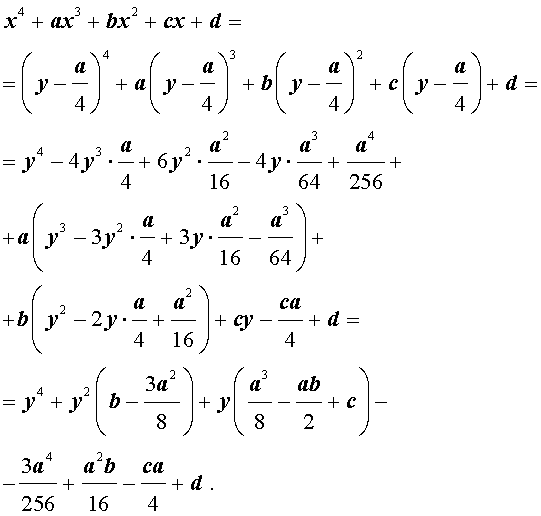
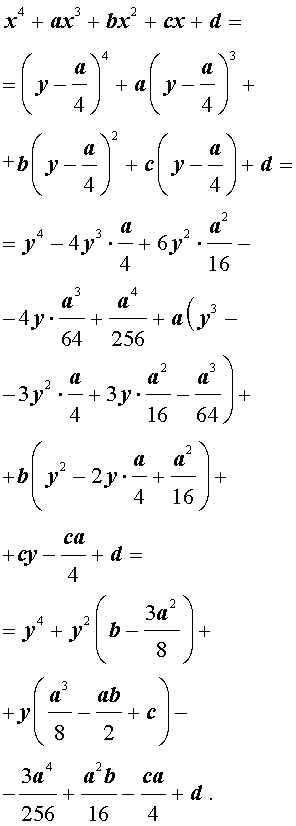
то уравнение (2) принимает вид
В результате уравнение (2) принимает вид
Если ввести обозначения
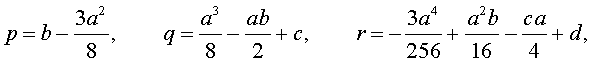
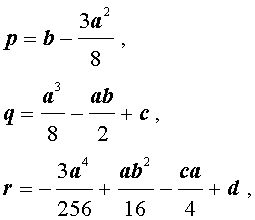
то уравнение (4) примет вид
| y4 + py2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
2sy2 + s2,
где s – некоторое число, которое мы определим чуть позже, из (5) получим
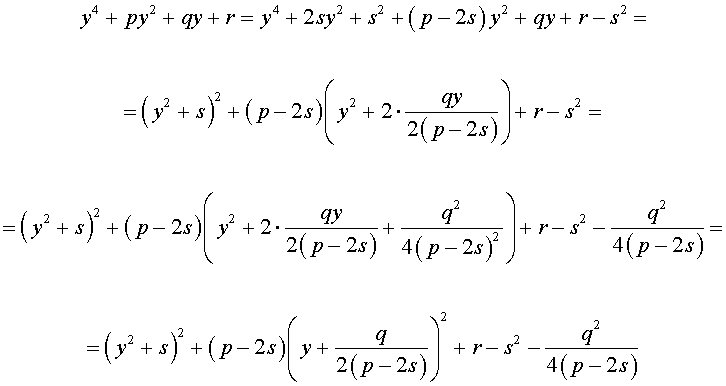
Следовательно, уравнение (5) принимает вид
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
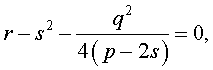  | (7) |
то уравнение (6) примет вид
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
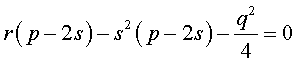
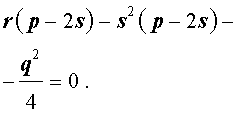
или, раскрыв скобки, — в виде
  | (9) |
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Действительно,
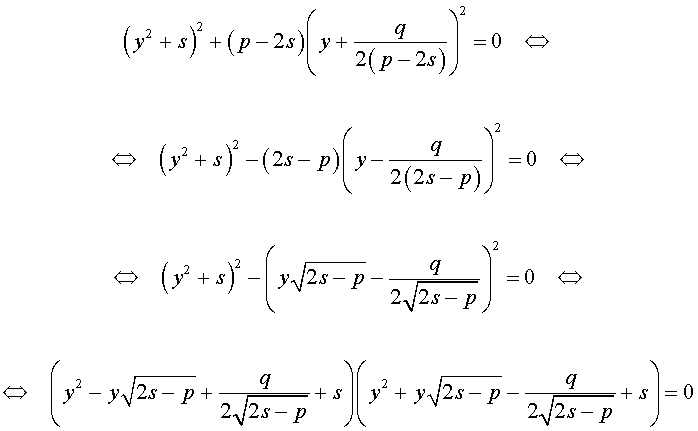
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
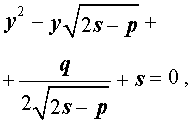  | (10) |
а также квадратное уравнение
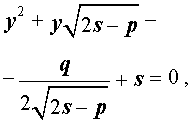  | (11) |
Вывод метода Феррари завершен.
Пример решения уравнения 4-ой степени
Пример. Решить уравнение
| x4 + 4x3 – 4x2 – – 20x – 5 = 0. | (12) |
Решение. В соответствии с (3) сделаем в уравнении (12) замену
Поскольку
x4 + 4x3 – 4x2 – 20x – 5 =
= (y – 1)4 + 4(y – 1)3 –
– 4(y – 1)2 – 20(y – 1)– 5 =
= y4 – 4y3 + 6y2 – 4y + 1 +
+ 4y3 – 12y2 + 12y – 4 –
– 4y2 + 8y – 4 –
– 20y + 20 – 5 =
= y4 – 10y2 – 4y + 8,
то в результате замены (13) уравнение (12) принимает вид
| y4 – 10y2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
| p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
2s3 + 10s2 – 16s – 84 = 0,
которое при сокращении на 2 принимает вид:
| s3 + 5s2 – 8s – 42 = 0. | (16) |
Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
y2 – 2y – 4 = 0,
корни которого имеют вид:
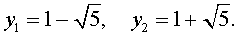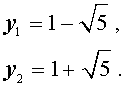  | (18) |
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
y2 + 2y – 2 = 0,
корни которого имеют вид:
  | (19) |
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
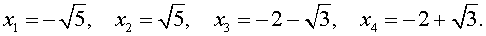
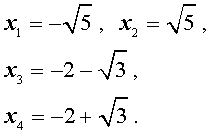
Ответ.
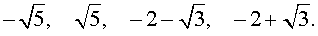
Замечание. При решении примера мы попутно получили разложение левой части уравнения (14) на множители:
| y4 – 10y2 – 4y + 8 = = (y2 – 2y – 4) (y2 + + 2y – 2). | (20) |
Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.
Решение уравнений четвертой степени
В общем случае решение уравнения четвёртой степени осуществляется с использованием методов решения уравнений для высших степеней, например, методом Феррари или с помощью схемы Горнера. Но некоторые уравнения 4-ой степени имеют более простое решение.
Существует несколько особых типов уравнений четвертой степени, со способами решения которых вы познакомитесь ниже:
- Биквадратное уравнения $ax^4+bx^2+c=0$;
- Возвратные уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$;
- Уравнения вида $ax^4+b=0$.
Решение биквадратных уравнений четвёртой степени
Биквадратные уравнения $ax^4+bx^2+c=0$ сводятся к квадратным путём замены переменной $x^2$ на новую, например, на $y$. После замены решается новое полученное уравнение, а затем значение найденной переменной подставляется в уравнение $x^2=y$. Результатом решения будут корни уравнения $x^2=y$.
Пример 1
Решите уравнение $x(x-1)(x-2)(x-3)=24$:
Раскроем скобки в многочлене:
$(x^2-3x)(x^2-3x+2)=24$
В таком виде становится очевидно, что в качестве новой переменной можно выбрать выражение $y=x^2-3x$, подставим её:
$y \cdot (y+2)=24$
$y^2+2y-24=0$
$y_1=4;y_2=-6$.
Теперь решим два квадратных уравнения $x^2-3x=-4$ и $x^2-3x=-6$.
Корни первого уравнения $x_1{1,2}=4;-1$, второе решений не имеет.
Готовые работы на аналогичную тему
Решение возвратных уравнений 4 степени
Эти уравнения вида $ax^4+bx^3+cx^2 +bx+ a=0$ повторяют своими коэффициентами при младших членах коэффициенты при многочленах со старшими степенями. Для решения такого уравнения сначала делят его на $x^2$:
$ax^4+bx^3+cx^2 +bx+ a=0|:x^2$
$ax^2+bx+c+\frac{b}{x} + \frac{a}{x^2}=0$
$a(x^2+\frac{1}{x^2})+b(x+\frac{1}{x}) + c=0$
Затем заменяют $(x+\frac{1}{x})$ на новую переменную, тогда $(x^2+\frac{1}{x^2})=y^2-2$, после подстановки получаем следующее квадратное уравнение:
$a(y^2-2)+by+c=0$
После этого ищем корни уравнений $x+\frac{1}{x}=y_1$ и $x+\frac{1}{x}=y_2$.
Аналогичным методом решаются возвратные уравнения вида $ax^4+bx^3+cx^2 +kbx+ k^2a=0$.
Пример 2
Решите уравнение:
$3x^4-2x^3-9x^2-4x+12=0$
Данное уравнение – возвратное уравнение вида $ax^4+bx^3+cx^2 +kbx+ k^2a=0$. Поэтому разделим всё уравнение на $x^2$:
$3x^2-2x-9 \cdot \frac{2 \cdot 2}{x}+3 \cdot (\frac{2}{x})^2=0$
$3(x^2+\frac{4}{x^2})-2(x+\frac{2}{x}-9=0$
Произведём замену выражения $x+\frac{2}{x}$: $3(y^2-4)-2y-9=0$
Рассчитаем корни данного уравнения, они равны $y_1=3$ и $y_2=-\frac{7}{3}$.
Соответственно, теперь необходимо решить два уравнения $x+\frac{2}{x}=3$ и $x+\frac{2}{x}=-\frac{7}{3}$. Решение первого уравнения — $x_1=1, x_2=2$, второе уравнение не имеет корней.
Следовательно, корнями исходного уравнения являются $x_1=1, x_2=2$.
Уравнения вида $ax^4+b=0$
Корни уравнения такой разновидности находятся с помощью применения формул сокращённого умножения.
Алгебраические уравнения и способы их решения. Уравнения третьей и четвертой степени
Что делать, если вам – например, на Профильном ЕГЭ по математике – встретилось не квадратное уравнение, а кубическое? Или даже уравнение четвертой степени? Ведь для уравнений третьей, четвертой и более высоких степеней нет таких простых формул, как для квадратного уравнения.
В этой статье – способы решения сложных алгебраических уравнений. Замена переменной, использование симметрии и даже деление многочлена на многочлен.
Вспомним основные понятия.
Корень уравнения – такое число, которое мы можем подставить вместо переменной в уравнение и получить истинное равенство.
Например, число 3 – корень уравнения 2x = 6.
Решить уравнение – значит найти его корни или доказать, что их нет.
Равносильными называются уравнения, множества решений которых совпадают. Другими словами, у них одни и те же корни.
Например, уравнения и равносильны. Их корни совпадают: или
Замена переменной – ключ к решению многих задач.
Решим уравнение:
Если приводить обе части к одному знаменателю, получим уравнение четвертой степени. Вряд ли мы с ним справимся.
Сделаем замену Тогда
С новой переменной уравнение стало проще:
Умножим обе части на 10t. Получим квадратное уравнение:
Корни этого уравнения: или
Вернемся к переменной
Если , то
Отсюда
Дискриминант этого уравнения отрицателен, корней нет.
Если , то Получим квадратное уравнение для :
У этого уравнения два корня: или Это ответ.
Решим уравнение
Не будем спешить раскрывать скобки. Ведь раскрыв их, мы получили бы уравнение четвертной степени.
Посмотрим на уравнение внимательно.
На координатной прямой точки 1; 3; –5; –7 расположены симметрично относительно точки
Сделаем замену , тогда .
Тогда:
Мы выразили все «скобки», то есть все множители, через новую переменную. Вот что это дает:
И еще одна замена: .
Обычное квадратное уравнение. Замечательно!
Подберем его корни по теореме Виета. Заметим, что
; отсюда , .
Если , то нет решений.
Если , то Тогда или
Если , то .
Если , то .
Ответ: 4; –8.
Дальше – еще интереснее.
3. Решите уравнение
Сделаем замену . То, что в правой части в скобках, заменили на новую переменную.
.
Получили квадратное уравнение:
Если , то
Если , то
Ответ:
Следующее уравнение решим с помощью группировки слагаемых.
4. Решите уравнение
Разложим левую часть уравнения на множители. Сгруппируем слагаемые:
Первые два слагаемых – сумма кубов. Применим формулу: . Получим:
.
Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Записывается это так:
Ответ: -2; 1; 4.
У нас появилось новое обозначение: — знак совокупности.
Такой знак означает «или».
Запись читается как « или или ».
Решая уравнения и особенно неравенства, мы будем постоянно пользоваться знаками системы и совокупности. Мы записываем решения в виде цепочки равносильных переходов. Для сложных уравнений и неравенств это единственный способ прийти к ответу и не запутаться.
5. Решите уравнение
Разложить левую часть на множители с первой попытки не удается.
Оказывается, если уравнение третьей (четвертой, пятой…) степени имеет целые корни, то находятся они среди делителей свободного члена (слагаемого, не содержащего x). В данном случае – среди целых делителей числа 24.
Выпишем целые делители числа 24:
1; –1; 2; –2; 3; –3; 4; –4; 6; –6; 8; –8; 12; –12; 24; –24
Подставляя их по очереди в уравнение, при получаем верное равенство:
Это значит, что левую часть уравнения можно разложить на множители:
, где .
Чтобы найти , поделим выражение на . В столбик. Так же, как мы делим друг на друга числа.
Немного непривычно, да? Потренируйтесь – у вас получится!
Ответ: 2; 3; 4.
6. Решите уравнение
группируем слагаемые:
А если сделать замену ?
Тогда .
Получаем квадратное уравнение: . Удачная замена!
Если , то 
, нет решений.
Если , то
, .
Ответ: .
7. Решите уравнение
Разложить на множители? Но как? И замена не видна сразу. Посмотрим на уравнение внимательно. Его коэффициенты: 1, — 5, 4, — 5, 1.
Такое уравнение называется симметрическим.
Разделим обе его части на . Мы можем это сделать, поскольку не является корнем нашего уравнения.
Теперь группируем слагаемые:
Сделаем замену .
Тогда
Получили уравнение . Легко!
Ответ:
Схема (метод) Горнера. Примеры. Решение уравнений четвертой степени
РЕШЕНИЕ УРАВНЕНИЙ 4-ОЙ СТЕПЕНИ ПО СХЕМЕ ГОРНЕРА
2x4 + 5x3 — 11x2 — 20x + 12 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:
1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена
-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена
Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
| Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | |
| 2 ∙ 2 + 5 = 9 | |
| 2 ∙ 9 — 11 = 7 | |
| 2 ∙ 7 — 20 = -6 | |
| 2 ∙ (-6) + 12 = 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Таким образом мы исходный многочлен разложили на множители:
2x4 + 5x3 — 11x2 — 20x + 12 = (x — 2)(2x3 + 9x2 + 7x — 6)
Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x3 + 9x2 + 7x — 6.
Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6.
1: 2 + 9 + 7 — 6 = 12 ⇒ число 1 не является корнем многочлена
-1: -2 + 9 — 7 — 6 = -6 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 — 6 = 60 ⇒ число 2 не является корнем многочлена
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) — 6 = 0 ⇒ число -2 является корнем многочлена
Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:
| Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. | |
| -2 ∙ 2 + 9 = 5 | |
| -2 ∙ 5 + 7 = -3 | |
| -2 ∙ (-3) — 6 = 0 |
Таким образом мы исходный многочлен разложили на множители:
2x4 + 5x3 — 11x2 — 20x + 12 = (x — 2)(x + 2)(2x2 + 5x — 3)
Многочлен 2x2 + 5x — 3 тоже можно разложить на множители. Для этого можно решить квадратное уравнение через дискриминант, а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3
| Во вторую ячейку четвертой строки запишем число 2, просто перенеся его из соответствующей ячейки третьей строки. | ||||||||||||||||||||||||
| -3 ∙ 2 + 5 = -1 | ||||||||||||||||||||||||
| -3 ∙ (-1) — 3 = 0 |
Таким образом мы исходный многочлен разложили на линейные множители:
2x4 + 5x3 — 11x2 — 20x + 12 = (x — 2)(x + 2)(x + 3)(2x — 1)
А корнями уравнения являются:
x = ±2; 3; 0.5
Найти уравнение четвертой степени онлайн
Равенство, содержащее неизвестное число, которое обозначено буквой, называется уравнением. Решение уравнения предполагает нахождение всех значений неизвестного (неизвестных), при которых соблюдается верное равенство. Такие значения неизвестного (неизвестных) являются корнями или решением уравнения.
Уравнение вида ах4 + bх3 + сх2 + dх + е = 0 называется уравнением 4-й степени с одним неизвестным. В результате решения уравнения получается 4 комплексных или вещественных корня.
Для решения приведенного уравнения 4-й степени вида: х4 + Ах3 + Вх2 +Сх + D = 0 можно воспользоваться методом Феррари.
Составим кубическое уравнение: у3 — Ву2 + (АС — 4D)у — А2D + 4ВD — С2 = 0.
Решаем полученное уравнение, находим один из его вещественных корней у0, который используем для дальнейшего нахождения корней квадратных уравнений.
Получаем и решаем два квадратных уравнения: 
. Корни уравнений будут корнями первоначального уравнения 4-й степени.
Если дано биквадратное уравнение 4-й степени вида: Ах4 + Вх2 + С = 0 и нужно найти его корни, можно свести его к квадратному, заменив переменную х2 на у (у = х2). В результате получим уравнение вида: Ау2 + Ву + С = 0. Далее решаем квадратное уравнение через дискриминант.
Если дано возвратное уравнение 4-й степени вида: Ах4 + Вх3 + Сх2 + Вх + А = 0 и нужно найти его корни, следует разделить уравнение на х2, получим:
Ах2 + Вх + С + В / х + А / х2 = 0.
Группируем и выносим коэффициенты за скобки: Ах2 + А / х2 + Вх + В / х + С = 0; А(х2 + 1 / х2) + В(х + 1 / х) + С = 0.
Произведем замену переменных: х + 1 / х = у; х2 + 1 / х2 = у2 — 2, получим: А(у2 — 2) + Ву + С = 0.
Сводим уравнение 4-й степени к квадратному уравнению и решаем его через дискриминант Ау2 + Ву + С — 2А = 0.
Находим у1 и у2, после чего возвращаемся к замене и находим корни.
Быстро решить любое уравнение вы сможете с помощью представленного на сайте онлайн калькулятора.
Уравнение четвёртой степени — Википедия
Уравнение четвёртой степени — в математике алгебраическое уравнение вида:
- f ( x ) = a x 4 + b x 3 + c x 2 + d x + e = 0 , a ≠ 0. {\displaystyle f(x)=ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0.}
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любом значении коэффициентов).
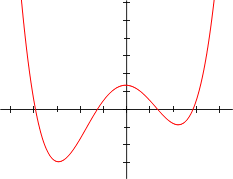
Так как f ( x ) {\displaystyle f(x)} является многочленом чётной степени, она имеет один и тот же предел при стремлении к плюс и к минус бесконечности. Если a > 0 {\displaystyle a>0} , то функция возрастает до плюс бесконечности с обеих сторон, таким образом, функция имеет глобальный минимум. Аналогично, если a < 0 {\displaystyle a<0} , то функция убывает до минус бесконечности с обеих сторон, таким образом, функция имеет глобальный максимум
Теорема Виета для уравнения четвёртой степени
Корни уравнения четвёртой степени x 1 , x 2 , x 3 , x 4 {\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами a , b , c , d , e {\displaystyle a,\,b,\,c,\,d,\,e} следующим образом:
- x 1 + x 2 + x 3 + x 4 = − b a , {\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}
- x 1 x 2 + x 1 x 3 + x 1 x 4 + x 2 x 3 + x 2 x 4 + x 3 x 4 = c a , {\displaystyle x_{1}\,x_{2}+x_{1}\,x_{3}+x_{1}\,x_{4}+x_{2}\,x_{3}+x_{2}\,x_{4}+x_{3}\,x_{4}={\frac {c}{a}},}
- x 1 x 2 x 3 + x 1 x 2 x 4 + x 1 x 3 x 4 + x 2 x 3 x 4 = − d a , {\displaystyle x_{1}\,x_{2}\,x_{3}+x_{1}\,x_{2}\,x_{4}+x_{1}\,x_{3}\,x_{4}+x_{2}\,x_{3}\,x_{4}=-{\frac {d}{a}},}
- x 1 x 2 x 3 x 4 = e a . {\displaystyle x_{1}\,x_{2}\,x_{3}\,x_{4}={\frac {e}{a}}.}
История
Уравнения четвёртой степени впервые были рассмотрены древнеиндийскими математиками между IV в. до н. э. и II в. н. э.
Лодовико Феррари приписывается получение решения уравнения четвёртой степени в 1540 году, но его работа опиралась на решение кубического уравнения, которого у него не было, поэтому сразу это решение не было опубликовано,
То, что это наибольшая степень уравнения, для которого можно указать общую формулу решения, было доказано в теореме Абеля — Руффини в 1824. Записки, оставленные Галуа, позже привели к элегантной теории корней многочленов, одним из результатов которой была эта теорема.[3]
Решения
Через резольвенту
Решение уравнения четвёртой степени
- x 4 + p x 2 + q x + r = 0 {\displaystyle x^{4}+px^{2}+qx+r=0}
сводится к решению кубической резольвенты
- y 3 − 2 p y 2 + ( p 2 − 4 r ) y + q 2 = 0 {\displaystyle y^{3}-2py^{2}+(p^{2}-4r)y+q^{2}=0}
Корни резольвенты
y
1
,
y
2
,
y
3
{\displaystyle y_{1},y_{2},y_{3}}
связаны с корнями исходного уравнения
x
1
,
x
2
,
x
3
,
x
4
{\displaystyle x_{1},x_{2},x_{3},x_{4}}
(которые и нужно найти) следующими соотношениями:
- y 1 = ( x 1 + x 2 ) ( x 3 + x 4 ) {\displaystyle y_{1}=(x_{1}+x_{2})(x_{3}+x_{4})}
- y 2 = ( x 1 + x 3 ) ( x 2 + x 4 ) {\displaystyle y_{2}=(x_{1}+x_{3})(x_{2}+x_{4})}
- y 3 = ( x 1 + x 4 ) ( x 2 + x 3 ) {\displaystyle y_{3}=(x_{1}+x_{4})(x_{2}+x_{3})}
Корни резольвенты могут быть решены по формуле Кардано. Три формулы соотношений между y i {\displaystyle y_{i}} и x i {\displaystyle x_{i}} вместе с исходным уравнением дают систему из 4 алгебраических уравнений с 4 неизвестными, которая легко решается.
Решение Декарта — Эйлера
В уравнении четвёртой степени
- a x 4 + b x 3 + c x 2 + d x + e = 0 , a ≠ 0 {\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0,\quad a\neq 0}
сделаем подстановку x = y − b 4 a {\displaystyle x=y-{\frac {b}{4a}}} , получим уравнение в следующем виде (оно называется «неполным»):
- y 4 + p y 2 + q y + r = 0 , {\displaystyle y^{4}+py^{2}+qy+r=0,}
где
- p = 8 a c − 3 b 2 8 a 2 , {\displaystyle p={\frac {8ac-3b^{2}}{8a^{2}}},}
- q = 8 a 2 d + b 3 − 4 a b c 8 a 3 , {\displaystyle q={\frac {8a^{2}d+b^{3}-4abc}{8a^{3}}},}
- r = 16 a b 2 c − 64 a 2 b d − 3 b 4 + 256 a 3 e 256 a 4 . {\displaystyle r={\frac {16ab^{2}c-64a^{2}bd-3b^{4}+256a^{3}e}{256a^{4}}}.}
Корни y 1 , y 2 , y 3 , y 4 {\displaystyle y_{1},\,y_{2},\,y_{3},\,y_{4}} такого уравнения равны одному из следующих выражений:
- ± z 1 {\displaystyle \pm {\sqrt {z_{1}}}} ± z 2 {\displaystyle \pm {\sqrt {z_{2}}}} ± z 3 , {\displaystyle \pm {\sqrt {z_{3}}},}
в которых сочетания знаков выбираются таким образом, чтобы выполнялось следующее соотношение:
- ( ± z 1 ) ( ± z 2 ) ( ± z 3 ) = − q 8 , {\displaystyle (\pm {\sqrt {z_{1}}})(\pm {\sqrt {z_{2}}})(\pm {\sqrt {z_{3}}})=-{\frac {q}{8}},}
причём z 1 , z 2 , z 3 {\displaystyle z_{1},\,z_{2},\,z_{3}} — это корни кубического уравнения
- z 3 + p 2 z 2 + p 2 − 4 r 16 z − q 2 64 = 0. {\displaystyle z^{3}+{\frac {p}{2}}z^{2}+{\frac {p^{2}-4r}{16}}z-{\frac {q^{2}}{64}}=0.}
Решение Феррари
Решение уравнения четвёртой степени вида x 4 + a x 3 + b x 2 + c x + d = 0 {\displaystyle x^{4}+ax^{3}+bx^{2}+cx+d=0} может быть найдено по методу Феррари. Если y 1 {\displaystyle y_{1}} — произвольный корень кубического уравнения
| y 3 − b y 2 + ( a c − 4 d ) y − a 2 d + 4 b d − c 2 = 0 , {\displaystyle y^{3}-by^{2}+(ac-4d)y-a^{2}d+4bd-c^{2}=0,} | (2) |
(резольвенты основного уравнения), то четыре корня исходного уравнения находятся как корни двух квадратных уравнений
- x 2 + a 2 x + y 1 2 = ± ( a 2 4 − b + y 1 ) x 2 + ( a 2 y 1 − c ) x + y 1 2 4 − d {\displaystyle x^{2}+{\frac {a}{2}}x+{\frac {y_{1}}{2}}=\pm {\sqrt {\left({\frac {a^{2}}{4}}-b+y_{1}\right)x^{2}+\left({\frac {a}{2}}y_{1}-c\right)x+{\frac {y_{1}^{2}}{4}}-d}}}
где подкоренное выражение в правой части является полным квадратом.
Биквадратное уравнение
Биквадратное уравнение[4] — уравнение четвёртой степени вида a x 4 + b x 2 + c = 0 {\displaystyle ax^{4}+bx^{2}+c=0} , где a , b , c {\displaystyle a,b,c} — заданные комплексные числа и a ≠ 0 {\displaystyle a\not =0} . Подстановкой y = x 2 ; y ⩾ 0 {\displaystyle y=x^{2};y\geqslant 0} оно сводится к квадратному уравнению относительно y {\displaystyle y} .
Четыре его корня находятся по формуле
- x 1 , 2 , 3 , 4 = ± − b ± b 2 − 4 a c 2 a . {\displaystyle x_{1,2,3,4}=\pm {\sqrt {\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}.}
Возвратные уравнения четвёртой степени
Возвратное уравнение четвёртой степени является также относительно легко решаемым: для a x 4 + b x 3 + c x 2 + b x + a = 0 {\displaystyle ax^{4}+bx^{3}+cx^{2}+bx+a=0} такого, что a ≠ 0 {\displaystyle a\neq 0} , решение находится приведением к виду:
- a ( x 2 + 1 x 2 ) + b ( x + 1 x ) + c = 0 {\displaystyle a\left(x^{2}+{1 \over x^{2}}\right)+b\left(x+{1 \over x}\right)+c=0} ,
После замены t = x + 1 x {\displaystyle t={x+{1 \over x}}} ищется решение квадратного уравнения a t 2 + b t + c − 2 a = 0 {\displaystyle at^{2}+bt+c-2a=0} , а затем — квадратного уравнения x 2 − t x + 1 = 0 {\displaystyle x^{2}-tx+1=0} .
Примечания
- ↑ Ferrari biography
- ↑ «Великое искусство» (Ars magna, 1545)
- ↑ Стюарт, Ян. Теория Галуа, издание третье (Chapman & Hall/CRC Mathematics, 2004) (англ.)
- ↑ В литературе до середины XX века биквадратным также могли называть уравнение четвёртой степени общего вида
Литература
Ссылки
Калькулятор уравнения четвертой степени
Уравнения четвертой степени имеет вид ах4; + bх3 + сх2 + ах + е = 0. Общее уравнение четвертой степени (также называемый биквадратным) является четвертой степени полиномиального уравнения. Бесплатный онлайн калькулятор расчета уравнения четвертой степени, используемый для нахождения корней уравнения.
Вычисление корней:
Например, Введите a=3, b=6, c=-123, d=-126 и e=1080
Формула уравнения четвертой степени:
ax4 + bx3 + cx2 + dx + e = 0
- Примечание : Допустим что p и q квадратные корни из 2 ненулевых корней.
- p = sqrt(y1)
- q = sqrt(y3)
- r = -g / (8pq)
- s = b / (4a)
- x1 = p + q + r — s
- x2 = p — q — r — s
- x3> = -p + q — r — s
- x4 = -p — q + r — s
Уравнением четвертой степени называется полиномиальное уравнение четвертого порядка вида, ax4+ bx3 + cx2 + dx + e = 0:
Формула уравнения четвертой степени:
ax4 + bx3+ cx2 + dx + e = 0
где,
- a = коэффициент для x4
- b = коэффициент для x3
- c = коэффициент для x2
- d = коэффициент для x
- e = константа.
Решение уравнения четвертой степени:
- x1 = p + q + r — s
- x2 = p — q — r — s
- x3 = -p + q — r — s
- x4 = -p — q + r — s
Пример 1:
Вычислить корни (x1, x2, x3, x4) уравнения четвертой степени, 3X4 + 6X3 — 123X2 — 126X + 1080 = 0
Шаг 1:
Из приведенного выше уравнения, значения a=3, b=6, c=-123, d=-126, e=1080.
Шаг 2:
Найдем x : Подставьте значения в приведенных ниже формул.
- f = c — ( 3b ² / 8 )
- g = d + ( b ³ / 8 ) — ( b x c / 2 )
- h = e — ( 3 x b4 / 256 ) + ( b ² x c / 16 ) — ( b x d / 4 )
Шаг 3:
Представим как уравнение третьей степени : y ³ + ( f / 2 ) y ² + (( f ² — 4 x h ) / 16 ) y — g ² / 64 = 0
где,
- a = коэффициент для y ³
- b = коэффициент для y²
- c = коэффициент для y
- d = константа
Шаг 4:
Из приведенного выше уравнения, значения:
- a = 1,
- b = f/2,
- c = (( f ² — 4 x h ) / 16 ),
- d = — g² / 64.
Шаг 5:
Найдем y: Подставьте значения в формулу, чтобы найти корни.
дискриминант (Δ) = q3 + r2
- q = (3c — b2) / 9
- r = -27d + b(9c — 2b2)
- s = r +√ (дискриминант)
- t = r — √(дискриминант)
- term1 = √(3.0) * ((-t + s) / 2)
- r13 = 2 * √(q)
- y1 = (- term1 + r13*cos(q3/3) )
- y2 = (- term1 + r13*cos(q3+(2∏)/3) )
- y3 = (- term1 + r13*cos(q3+(4∏)/3) )
Шаг 6:
Получим корни, y1 = 20.25 , y2 = 0 и y3 = 1.
Шаг 7:
После решения уравнения третьей степени решим уравнение четвертой степени.
Подставим y1, y2, y3 в p, q, r, s.
Примечание : Пусть p и q квадратные корни 2 ненулевых корней.
- p = sqrt(y1) = 4.5
- q = sqrt(y3) = 1
- r = -g / (8pq) = 0
- s = b / (4a) = 0.5
Шаг 8:
Мы получили корни, x1 = 5, x2 = 3, x3 = -4 и x4 = -6.
Практический пример решения уравнения четвертой степени.
Было ли это полезно?
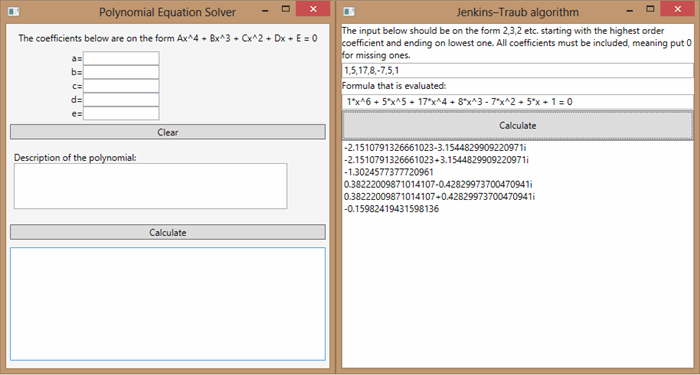
Программа для решения полиномиальных уравнений— CodeProject
Введение
Недавно я столкнулся с ситуацией, когда мне нужно было решить полиномиальное уравнение 4-й степени в .NET, и, к своему удивлению, я не смог найти ни одного кода, написанного на C # или VB .NET, который содержал либо явные алгебраические формулы, либо числовые алгоритм Дженкинса-Трауба. (Однако я нашел несколько переводов алгоритма Дженкинса-Трауба, написанного Дженкинсом Хаймелфом на ФОРТРАНЕ (все еще можно скачать здесь, Netlib).Однако мне удалось перепутать реализации, сделанные на C ++, которые я перевел на C # и VB.NET. В свою защиту я перевел и тот, что написал Лоран Бартольди, но он не был включен в статью. Я использовал один алгоритм C ++, переведенный Дэвидом Биннером только для реальных коэффициентов. Примите мои искренние извинения за эту ошибку. C ++, на который я полагался для сложных коэффициентов, был написан Хенриком Вестермарком. Оба этих приложения преобразованы мной из C ++ и C в код C # и VB.
NB: К алгоритму Джеркинса-Трауба может быть приложена лицензия для коммерческого использования. Пожалуйста, проверьте это, прежде чем использовать его в программе, которую вы хотите продавать другим. Для повторного поиска и личного использования нет проблем.Явные алгебраические формулы, которые также реализованы, отвратительны и определенно засорят ваш день, если вам когда-нибудь понадобится такая, поэтому я решил поделиться ею с вами. Я внес некоторые исправления в формулу благодаря приведенному ниже комментарию Бенуа Андриё.
У меня также есть довольно длинный рассказ, чтобы следить за ним, так как я прочитал «Уравнение, которое не может быть решено» Марио Ливио. Название книги отсылает к истории неразрешимости полиномиального уравнения 5-й степени, но оно также проходит через историческое развитие решений полиномиальных уравнений более низкой степени.
Я не буду давать никаких объяснений того, как были получены эти формулы, поскольку формулы становятся довольно длинными, настолько длинными, что даже у Тартальи (одного из людей, принимавших участие в решении кубического уравнения) были проблемы с запоминанием всего. правила, которые он открыл.
Что касается числового алгоритма Jenkins-Traub, он был полностью переведен мной из версий C ++ и C в VB.NET и C #, и, насколько я его тестировал, похоже, он работает нормально. Следует отметить, что алгоритм Дженкинса-Трауба обычно использует явные формулы для 1-й и 2-й степени, а численное приближение — для 3-й степени и выше.
Полиномиальное уравнение 1-й степени
Это довольно легко решить математически, поэтому, если у вас возникли проблемы, вам, вероятно, не следует загружать код.Я, конечно, говорю об уравнениях в форме 2x + 3 = 7, а простое уравнение называется линейными уравнениями, так как они могут быть представлены линиями при построении графика (или рисовании).
Однако история, лежащая в основе уравнений, довольно интересна, поэтому я собираюсь вернуть вас в 2000 г. до н.э. — 600 г. до н.э., к вавилонской цивилизации в Месопотамии. Слово уравнение следует использовать в этом контексте с осторожностью, поскольку вавилоняне на самом деле не использовали алгебру для решения этих уравнений, а вместо этого отважились на длительные дебаты и логику для решения проблем.Это может быть способом сделать математику еще более сложной и непонятной, чем когда-либо, особенно когда мы имеем дело с полиномиальными уравнениями более высокого порядка.
Результат такого способа решения математических задач без использования алгебры означал, что вавилоняне не могли найти никаких общих закономерностей или формул, лежащих в основе различных математических задач. Несмотря на громоздкие формулировки математических задач, им удалось решить пары (то есть уравнения с неизвестными x и y) линейных уравнений.
Вавилоняне, похоже, не были так заинтересованы в создании большого количества текстов с уравнением 1-й степени, как, например, египтяне, поскольку кажется, что вавилоняне считали это слишком элементарным для любого подробного обсуждения. Однако в Египте существуют большие рукописи на эту тему, в которых представлены математические «рецепты» с решением некоторых проблем, как своего рода кулинарная книга.
Следует отметить, что в китайском сборнике «Девять глав по математическому искусству» (Jiu zhang suan shu) можно найти решения не менее чем трех линейных уравнений с тремя неизвестными, что является большим подвигом, учитывая, насколько громоздкой была процедура.2 — x = 870 и может найти положительное решение, поскольку решение предназначалось для использования, например, в измерениях земли и подобных задачах. Однако они проигнорировали уравнения этого типа, у которых было два положительных решения, поскольку они считались нелогичными. Это также верно в отношении очень раннего греческого математика Евклида, поскольку он решает квадратное уравнение, используя геометрию, а не алгебру. Чтобы сравнить математические знания в древнем мире, египтяне, с другой стороны, знали только, как решать уравнения в форме x ^ 2 = 4, а не как решать x ^ 2 + x = 4, и они также могли только найти положительное решение.
Греческой цивилизации вскоре удалось решить некоторые проблемы с помощью блестящего математика Диафаноуса. Он эффективно продвинул способ представления решений, сделав промежуточный пункт между вавилонскими формулировками уравнений и современным способом использования алгебры. Его книга «Арифметика» показывает решения трех различных типов квадратных уравнений, а также знаменитых уравнений Диафаноуса, примером которых является Великая теорема Ферма. Фактически Ферма читал «Аритметику», и именно в этой книге Диафануса он написал свою знаменитую последнюю теорему на полях.Что касается самого Диафануса, то на самом деле мы знаем о нем очень мало, невозможно даже представить себе занавес, когда он действительно жил, за исключением того, что это, вероятно, было в Александрии в период между 200 и 214-284 или 298 годами нашей эры.
С падением греческой цивилизации математический прогресс на западе остановился и впал в спячку почти на тысячелетие. Прогресс математики теперь повернулся на восток, и один из великих математиков его возраста, Брахмагупта из Индии, сумел решить некоторые из уравнений Диафаноуса, а также первым дал решения полиномиальных уравнений 2-й степени, которые также включали отрицательные числа.Он понял, что отрицательные числа можно рассматривать как «долги», а положительные числа — как «состояние», как это сделал бы сегодня бухгалтер, и таким образом совершил огромный прорыв в математике.
Следующим крупным шагом в решении уравнений стало развитие алгебры, получившее свое название от арабского математика Мухаммада ибн Мусы аль-Хорезми, а точнее его книги «Китаб аль-Джабр ва аль-мукабала», относящейся к слово аль-джабр как основа современной алгебры слов. Аль-Джабр означает «восстановление» или «завершение», что вполне соответствует важности математического развития, которое это повлечет за собой.Его книги не были новаторскими в плане нового материала; вместо этого именно систематическое рассмотрение решений квадратного уравнения было настоящим гением в этой области. Однако полный набор решений квадратного уравнения появился в Европе только в XII веке в Испании.
Однако реализация формулы квадратичного уравнения на компьютере не так проста, как может показаться на первый взгляд. Принимаем уравнение в виде:
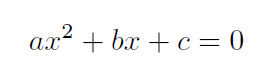
Решением является хорошо известная формула, и я, конечно, думаю об этом:
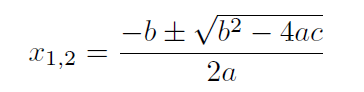
Однако у вас могут возникнуть проблемы, если вы действительно реализовали эту формулу на компьютере.Причина в том, что если коэффициенты a или c очень близки к нулю, вы можете получить большие ошибки усечения. Правильная реализация для поиска корней на компьютере:
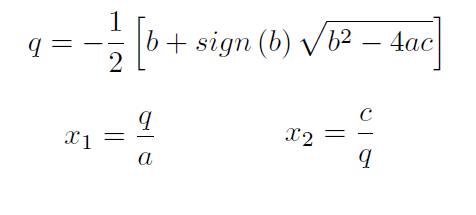
Даже если коэффициенты сложны, компьютерная формула все еще верна, хотя нужно учитывать, как брать знак квадратного корня:
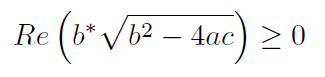
В приведенной выше формуле Re означает действительную часть решения, а звездочка — комплексное сопряжение комплексного числа.
Полиномиальное уравнение 3-й и 4-й степени
Это часто называют кубическим или четвертым уравнением или функцией, и неудивительно, что оно появляется, когда мы хотим найти объем чего-либо. Фактическое общее уравнение не было решено до шестнадцатого века, хотя несколько частных случаев были решены вавилонянами, а еще несколько были даны персидским поэтом Омаром Хайямом в двенадцатом веке. Однако реальной ощутимой необходимости в решении кубического уравнения не было.Никто не ждал, когда это будет открыто, это было скорее умственное испытание, своего рода Олимпийские игры по математике, которые определят величайший интеллект его времени.
Первое частное решение кубического уравнения могло быть получено в старейшем в настоящее время открытом университете, Болонском университете, который был открыт с момента его основания в 1088 году. После того, как в 1501 году ему была поставлена задача, связанная с полиномиальными уравнениями третьей степени, Сципионе дель Ферро решил поработать над проблемой.И примерно в 1515 году ему удалось найти метод решения кубических уравнений, который имел вид x3 + mx = n. Дель Ферро не опубликовал свой результат, который, к сожалению, был вполне нормальным в те дни, и только рассказал своему ученику Антонио Фиоре и его зятю о своем открытии на собственном смертном одре. Тогда Фиоре, похоже, подумал, что формула была его, чтобы использовать с этого момента, как ему заблагорассудится, но не опубликовал ее сразу, а вместо этого дождался подходящего момента, чтобы появиться.
Итак, когда Никколо Тарталья в 1530 году объявил, что он может решить некоторые проблемы, касающиеся кубических уравнений, Фиоре решил, что его момент настал, и вызвал Тарталью на математический спор.Каждый участник давал другому 30 задач для решения, а проигравший платил победителю денежную цену. У каждого из них будет сорок или пятьдесят дней на решение проблем.
К тому времени, как задачи были переданы Тарталье, он сумел решить их все за два часа! И Фиоре не мог решить ни одну из поставленных ему задач, и он не знал уравнений в форме x3 + mx2 = n, поэтому Тарталья выиграл соревнование.
В 1539 году, после масштабной кампании по сохранению, персонаж по имени Джероламо Кардано (на самом деле он получал свое пособие, играя в азартные игры, когда был студентом, и был известен тем, что был грубым и грубым по отношению к окружающим), сумел убедить Тарталья раскрыть формулу при условии, что Кардано не раскроет ее.Однако Кардано узнал о решениях дель Ферро от зятя дель Ферро и решил, что он не связан соглашением с Тартальей, поскольку он представит решение дель Ферро, а не Тарталья, поэтому он опубликовал результат в своей книге Ars Magna. Многие современные математики считают эту книгу началом современной алгебры, и она включает решения с комплексными числами, хотя Кардано не понимал этого в деталях, так как некоторая часть этого была взята из решений Тартальи, включающих квадратный корень из отрицательного числа. .(Рафаэля Бомбелли часто считают первооткрывателем комплексных чисел, поскольку он провел гораздо больше исследований по этому предмету.) После того, как книга была опубликована, Тарталья немедленно бросил вызов Кардано, который был довольно плохим математиком по стандартам Тартальи: и он сразу отказался. Однако ученик Кардано, Лодовико Феррари, отправил Тарталье многочисленные публичные вызовы, которые Тарталья отрицал. В конце концов Тарталье предложили работу в университете, учитывая, что он победит Феррари в споре.Феррари открыл общий способ решения кубического уравнения, который не был известен Тарталье, он также нашел решение уравнения четвертой степени еще в 1540 году, но для этого требовалось решение кубического уравнения, поэтому оно не было опубликовано, пока Кардано не нашел о решениях дель Ферро.
Ferrari выиграла спор с Тартальей, который ушел незадолго до того, как закончился первый день спора. (Феррари был настоящим персонажем, поскольку в семнадцатилетнем возрасте в драке он потерял все пальцы на правой руке).С этого момента его карьера резко пошла вверх, хотя, как утверждается, позже он был отравлен своей сестрой и умер.
Настоящий первооткрыватель формулы третьей степени, как вы понимаете, довольно сложен, хотя решение уравнения 4-й степени, похоже, является делом только Феррари.
Формулы обычно не реализуются на компьютере, так как решения, найденные численным методом, почти всегда лучше с ними. Если вы все же хотите использовать явные формулы, вам следует реализовать формулу Вите, которая использует тригонометрические функции вместо решений Феррари.
Полиномиальные уравнения высшей степени
После того, как квадратное уравнение было решено с помощью алгебры, многие пытались решить полиномиальное уравнение пятой степени или пятой степени, но все они потерпели неудачу. Это не было доказано до тех пор, пока в 1823 году Авель не нашел общего доказательства этого, в котором говорилось, что на самом деле это невозможно. Теорема известна сегодня как теорема Абеля – Руффини или как теорема невозможности Абеля. Причина двойного названия в том, что Руффини дал неполное доказательство теоремы в 1799 году, о котором Абель не знал до 1826 года.Прочитав ее и изучив, он сказал, что работа Руффини была настолько сложной для понимания, что он не был уверен, правильна ли она.
Однако важно знать, что на самом деле означает доказательство, и что особенно важно, что оно не означает. Доказательство Абеля просто утверждает, что нельзя найти общее решение для всех корней в квинтике или любом полиномиальном уравнении более высокого порядка с помощью алгебры. Абель использовал обобщение интегралов Эйлера, чтобы доказать это, и немецкий математик Якоби был вне себя от того, что это открытие осталось незамеченным математическим сообществом.
Однако можно найти решение уравнений 5-й степени с помощью численных методов (Ньютона-Рэпсона) или с помощью эллиптических интегралов. Если использовать теорию Эвариста Галуа, можно также выяснить, какие решения можно было бы найти. Эварист Галуа также доказал, что полиномиальное уравнение 5-й степени не может быть решено независимо от работ Абеля и Руффини, и его доказательство было опубликовано посмертно в 1846 г.
.Задача с явными формулами
Существуют проблемы с явными формулами, которые связаны с ограниченным пространством памяти на компьютере, которое в некоторых случаях может давать такую высокую ошибку, что может привести к тому, что вычисленные решения будут далеки от истинных значений.На практике решения для 3-го и выше почти всегда лучше с алгоритмом Дженкинса-Трауба или другими подобными методами, чем решения, рассчитанные с помощью явных формул.
Однако существуют проблемы с численной оценкой полинома, поскольку любой человек, обладающий достаточным пониманием лежащих в основе алгоритмов, легко может построить пример, который не сойдется. Возьмите уравнение (1) ниже:
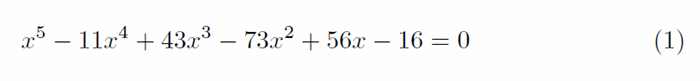
Учитывая, что это полиномиальные решения 5-й степени, можно найти только с помощью численного алгоритма, но мы знаем из Фундаментальной теоремы алгебры, что уравнение будет иметь ровно 5 действительных или комплексных решений, как доказали Гаусс и другие.Точные решения уравнения 1: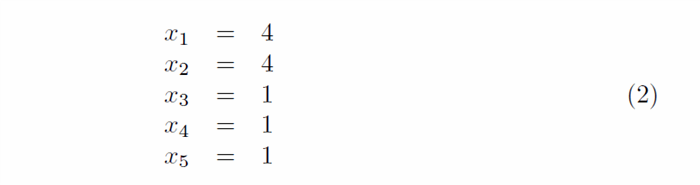 
Проблема с этим примером заключается в том, что реализованный Jenkins-Traub в C # и VB не сходится (скорее всего, с двойной точностью, которая выбрана для хранения данных, а также значения epsilon, min и max, которые были «экспортированы» из библиотеки float в VC ++). На самом деле, для такого алгоритма всегда может быть проблематично сойтись, учитывая количество множественных корней. Причина в том, что алгоритм извлекает найденные корни из исходного уравнения и при слишком большой числовой ошибке может привести к тому, что другие решения не будут найдены.Так что обратите внимание на тот факт, что любой метод, использующий итерации типа Ньютона, может иметь проблемы с несколькими корнями. Это также применимо к обстоятельствам, когда корни находятся близко друг от друга (или очень далеко друг от друга).
Jenkins-Traub действительно использует метод типа Ньютона для поиска корней, и это также может иметь другие проблемы. Если полином без линейного члена равен нулю в нуле, итерационный метод не сможет сойтись, учитывая, что и функция, и ее производная равны нулю в нуле.
Есть еще одна довольно удивительная особенность многочленов, имеющих кратные корни. дело в том, что у производного многочлена будет на один корень меньше. Возьмите пример формы уравнения 1, если мы выведем уравнение, мы получим:
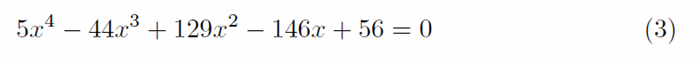
И когда мы пытаемся решить это уравнение, используя тот же алгоритм Дженкинса-Трауба, что и раньше, мы обнаруживаем, что действительно те же корни все еще существуют, с дополнительным, который не был. Решения можно легко проверить, подставив значения в исходное уравнение (1):
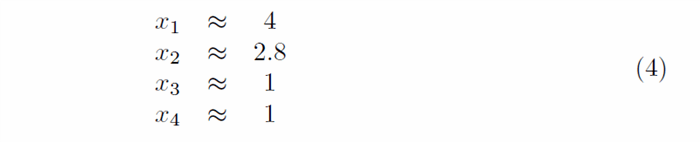
Фактический код стал настолько сложным, что объяснить все это трудно, а то и невозможно.Вместо этого я направлю вас к процедуре Дженкинса-Трауба, описанной в Википедии.
Однако важно знать, что алгоритм Дженкинса-Трауба де-факто считается способом численного вычисления корней многочлена. Он тщательно протестирован, а также внедрен во многие продукты, которые используются в коммерческих целях (например, Matematica и другие).
Что касается явных формул, их следует использовать с осторожностью, и нельзя предполагать, что они дают правильные результаты для любых реальных коэффициентов, которые вы вводите, хотя описание, данное в программе, должно указывать, является ли это распознанным типом, и если описание вывода соответствует вычисленным корням.Для нахождения корней используются несколько различных методов, среди которых уравнение Феррари, двуквадратное уравнение с депрессией и многие другие.
Список литературы
Сайт Wolfram, на котором представлены некоторые используемые формулы и другие ссылки на используемый числовой алгоритм:
Исходный код C ++:
Книг:
Другие ссылки:
.Калькулятор уравнений четвертой степени — Расчет с высокой точностью
- Цель использования
- Попытка найти решение ошибки
- Комментарий / Запрос
- неплохо
[1] 2020/07/11 01:47 Женский / Моложе 20 лет / Высшая школа / Университет / Аспирант / Очень /
- Цель использования
- Кому рассчитать высоту вынужденного вихря
[2] 07.07.07 20:40 Мужчина / Уровень 20 лет / Инженер / Полезно /
- Цель использования
- Помощь в исчислении
[3] 2020/05/21 06:42 Женский / До 20 лет / Высшая школа / Университет / Аспирант / Немного /
- Цель использования
- Физика частиц
- Комментарий / запрос
- Можете ли вы сделать ваши сообщения об ошибках более конкретными?
[4] 2020/04/21 06:48 Мужчина / 60 лет и старше / Учитель / Исследователь / Полезно /
- Цель использования
- просто возился, пытаясь решить неприятную Преобразование Лапласа.
[5] 2020/04/21 04:42 Мужской / 20-летний уровень / Старшая школа / Университет / аспирант / Немного /
- Цель использования
- Попытка уместить данные COVID-19 для Пенсильвании в кривую найти, когда возникает апекс.
[6] 2020/04/19 06:05 Мужчина / 60 лет и старше / Пенсионер / Полезный /
- Цель использования
- Помогая с hw
[7] 2020/01/24 23:06 Женский / До 20 лет / Старшая школа / Университет / аспирант / Очень /
- Цель использования
- Тестирование моего собственного решателя четвертичной системы
[8] 2020/01/20 19:48 Мужской / До 20 лет / Старшая школа / Университет / аспирант / Полезно /
- Цель использования
- Проверка моих ответов и получение общего представления о форме кривых для моего домашнего задания.Также намного лучше, чем использовать MATLAB, чтобы просто увидеть форму кривой.
[9] 2019/11/27 01:14 Мужской / 20-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Найдите x, когда ln (x) = 1 / x
Использовали ряд Тейлора с n-3, решенное уравнение Квартика. Точность 0,05.
Отличная задача для продвинутых студентов.
[10] 2019/05/07 11:56 Мужчина / 60 лет и старше / Пенсионер / Очень /