Презентация «Решение простых задач» — 1 класс
Простые задачи
1 класс, 3 четверть, ч. 2
МБОУ «СОШ № 6 имени Н. З. Ульяненко» учитель начальных классов Дубовцева Е. В.
1. У Лены 3 астры, а у Гали 5 роз. Сколько всего цветов у девочек ?
ч.
ч.
5
3
?
ц.
1) 3 + 5 = 8(ц.) -всего.
Ответ: всего 8 цветов.
2. У Миши было 8 машинок. 1 машинку он подарил своему другу. Сколько машинок осталось у Миши?
ц.
8
1
?
ч.
ч.
1) 8 – 1 = 7(м.) -осталось.
Ответ: осталось 7 машинок.
3. На пеньке сидело 4 майских жука.
ч.
ч.
3
4
?
ц.
1) 4 + 3 = 7(ж.) -стало.
Ответ: стало 7 жуков.
4. В магазине было 6 тортов. 3 торта продали . Сколько тортов осталось в магазине?
ц.
6
3
?
ч.
ч.
1) 6 – 3 = 3(т.) -осталось.
Ответ: осталось 3 торта.
5. Караван из 3 верблюдов догнали ещё 2 верблюда. Сколько верблюдов стало в караване?
ч.
ч.
2
3
?
ц.
1) 3 + 2 = 5(в.) -стало.
Ответ: стало 5 верблюдов.
6.
У Нади было 8 мармеладок. 3 мармеладки она отдала подругам. Сколько мармеладок осталось у Нади?
ц.
8
3
?
ч.
ч.
1) 8 – 3 = 5(м.) -осталось.
Ответ: осталось 5 мармеладок.
7. Шли по тропе 6 белых носорогов и повстречали 3 чёрных носорогов. Сколько носорогов встретились на тропе?
ч.
ч.
3
6
?
ц.
1) 6 + 3 = 9(н.) -стало.
Ответ: стало 9 носорогов.
8. На тропе встретились 9 носорогов. 6 носорогов были белые, а остальные – чёрные. Сколько чёрных носорогов?
ц.
3
?
ч.
ч.
1) 9 – 3 = 6(н.) -чёрных.
Ответ: 6 чёрных носорогов.
9. У фокусника было 2 зонтика от дождя и 3 зонтика от солнца. Сколько всего зонтиков было у фокусника?
ч.
ч.
3
2
?
ц.
1) 2 + 3 = 5(з.) -всего.
Ответ: всего 5 зонтиков.
10. На тарелке лежало 10 шоколадок. За обедом 4 шоколадки съели. Сколько осталось шоколадок?
ц.
10
4
?
ч.
ч.
1) 1 0 – 4 = 6(ш.) -осталось.
Ответ: 6 шоколадок осталось.
11.
На баобабе сидело 5 обезьян. Потом ещё 2 обезьяны залезли на дерево. Сколько всего обезьян стало на дереве?ч.
ч.
2
5
?
ц.
1) 5 + 2 = 7(об.
) -всего.
Ответ: всего стало7 обезьян.
12. 6 утят плавали в пруду. 4 из них поплыли к берегу. Сколько утят осталось в пруду?
ц.
6
4
?
ч.
ч.
1) 6 – 4 = 2(ут.) -осталось.
Ответ: 2 утят осталось.
13. На столе лежали 3 столовые ложки и 5 чайных. Сколько всего ложек лежало на столе?
ч.
ч.
5
3
?
ц.
1) 3 + 5 = 8(л.) -всего.
Ответ: всего лежало8 ложек.
14. На тарелке лежало 9 ватрушек. Вова съел 1 ватрушку. Сколько ватрушек осталось на тарелке?
ц.
9
1
?
ч.
ч.
1) 9 – 1 = 8(в.
) -осталось.
Ответ: осталось 8 ватрушек.
15. Около школы растут 4 липы и 2 рябины. Сколько всего деревьев растёт около школы?
ч.
ч.
2
4
?
ц.
1) 4 + 2= 6(д.) -всего.
Ответ: всего растёт 6 деревьев.
16. Поезд состоит из 9 вагонов. На станции от поезда отцепили 2
вагона . Сколько вагонов осталось ?ц.
9
2
?
ч.
ч.
1) 9 – 2 = 7(в.) -осталось.
Ответ: осталось 7 вагонов.
17. Во дворе гуляют 5 кур и 3 утки. Сколько всего птиц во дворе?
ч.
ч.
3
5
?
ц.
1) 5 + 3 = 8(п.) -всего.
Ответ: всего 8 птиц во дворе.
18. У кормушки было 6 лебедей. 2 лебедя уплыли . Сколько лебедей осталось ?
ц.
6
2
?
ч.
ч.
1) 6 – 2 = 4(л.) -осталось.
Ответ: осталось 4 лебедя.
Пышкало Анатолий Михайлович / Авторы, персоны / Указатели // Библиотека Mathedu.Ru
Пышкало Анатолий Михайлович / Авторы, персоны / Указатели // Библиотека Mathedu.RuПышкало Анатолий Михайлович
(23.05.1919 — 02.04.2000)
(все публикации)Авторские труды (37)Книги (2)Авторефераты (1)Диафильмы (33)Статьи/произведения (1)Составление, редактирование, переводы (14)Диссертации (9)Диафильмы (5)Литература о персоне и её трудах (1)Пышкало А. М. Геометрия в I—IV классах. — 1968 Пышкало А. М. Геометрия в I—IV классах : (проблемы формирования геометрических представлений у младших школьников) / Акад.
пед. наук РСФСР, Ин-т общего и политехн. образования. — 2-е изд., испр. и доп. — М. : Просвещение, 1968. — 263 с. — Библиогр. в прим.Пышкало А. М. Методика обучения элементам геометрии в начальных классах. — 1973 Пышкало А. М. Методика обучения элементам геометрии в начальных классах : пособие для учителей. — 2-е изд., испр. и доп. — М. : Просвещение, 1973. — 208 с. — Библиогр.: с. 205.Пышкало А. М. Вопросы формирования геометрических представлений у младших школьников. — 1966 Пышкало А. М. Вопросы формирования геометрических представлений у младших школьников : автореф. дис. по книге «Геометрия в I—IV классах» … канд. пед. наук / АПН РСФСР. Науч.-исслед. ин-т общего и политехн. образования. — М., 1966. — 24 с.Макарычев Ю. Н., Пышкало А. М. Параллельный перенос. — 1966 Макарычев Ю. Н., Пышкало А. М. Параллельный перенос : диафильм по математике для средней школы. — М. : студия «Диафильм», 1966. — [3], 40 кадров.Нешков К. И., Пышкало А. М. Геометрические фигуры и их взаимное расположение.
— 1965 Нешков К. И., Пышкало А. М. Геометрические фигуры и их взаимное расположение : диафильм по математике для 4—6 классов. — М. : студия «Диафильм», 1965. — [3], 38 кадров.Пышкало А. М. 8 задач по геометрии. — 1972 
Страница
Продолжая использовать данный сайт, вы выражаете согласие с условиями его использования
Как преподавать задачи на сложение и вычитание
Мои ученики мучились с тем, как решать задачи на сложение и вычитание , казалось, целую вечность.
Они могли подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа вместе, не понимая смысла задачи.
Тьфу.
Вы можете рассказать?
Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении словесным задачам на сложение и вычитание с использованием любого ресурса.
Итак, как мне учить текстовые задачи? Это довольно сложно, но так весело, как только вы войдете в него.
Как преподавать задачи на сложение и вычитание
Основные компоненты обучения задачам на сложение и вычитание включают:
- Обучение соотношению чисел s – Как учитель, знайте тип задач и помогайте учащимся решать действие в задаче
- Дифференцируйте числа – Дайте учащимся только правильные числа, чтобы они могли прочитать задачу, не увязая в вычислениях
- Используйте академический словарь — и будьте последовательны в том, что вы используете.
- Остановить поиск «Ответа» — дело не в ответе; речь идет о процессе
- Различие между моделями и стратегиями – одна связана с отношениями между числами, а другая – с тем, как учащиеся «решают» или вычисляют задачу.
Я большой сторонник НЕ изучения списков ключевых слов. Это просто не работает последовательно во всех проблемах. Это короткий путь, ведущий к сбоям в математическом мышлении. Вы также не должны просто давать учащимся рабочие листы с текстовыми задачами и заставлять их искать ключевые слова для текстовых задач. Я более подробно рассказываю о том, почему это не работает, в статье «Проблема с использованием ключевых слов для решения текстовых задач».
Научите соотношению чисел в математических задачах со словами
Один из способов помочь вашим ученикам решать задачи со словами — научить их отношениям между числами. Другими словами, помогите им понять, что числа в задаче каким-то образом связаны друг с другом.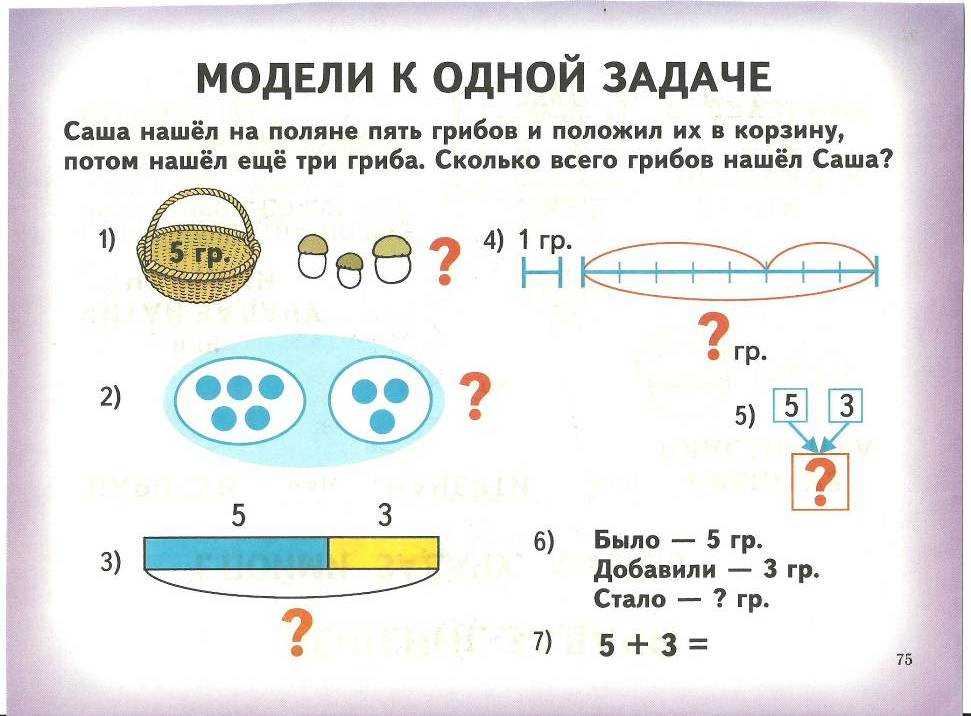
Я учу текстовые задачи, убирая числа. Звучит странно, верно?
Устранение отвлекающих факторов на числа помогает учащимся сосредоточиться на проблемной ситуации и понять действие или взаимосвязь чисел. Это также удерживает учащихся от решения задачи до того, как мы поговорим о взаимосвязи чисел.
Когда я преподаю текстовые задачи, я даю ученикам задачи с пробелами и без чисел. Сначала поговорим о действии в задаче. Мы определяем, добавляется ли что-то к чему-то другому или отнимается от чего-то другого. Это становится нашим уравнением. Мы определяем, что нам нужно решить, и составляем уравнение с пробелами и квадратом для неизвестного числа.
___ + ___ = неизвестно
Хотите бесплатный образец текстовых задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже. БЕСПЛАТНЫЙ образец текстовых задач по типу задачи
Различие чисел в задачах Word
Только после того, как мы обсудим задачу, я даю ученикам числа.
Я различаю числа в зависимости от потребностей учащихся. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что ученики понимают процесс.
После того, как учащиеся ознакомятся с процессом, я начинаю давать разным учащимся разные числа в зависимости от их уровня математического мышления.
Я также меняю номера в течение года с однозначных на двузначные. Прелесть пустых мест в том, что я могу вставить в задачу любые числа, которые захочу, чтобы попрактиковаться в стратегиях, над которыми мы работали в классе.
В какой-то момент мы создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, соединяют ли эти действия что-то или разделяют. Сколько вы можете придумать?
Вот несколько идей:
Присоединяйтесь: положил, получил, взял, купил, сделал
Разделить: съел, потерял, положил, уронил, использовал
Не бойтесь использовать академическую лексику при обучении словесным задачам
Я учу своих учеников определять начало проблемы, изменение проблемы и результат проблемы.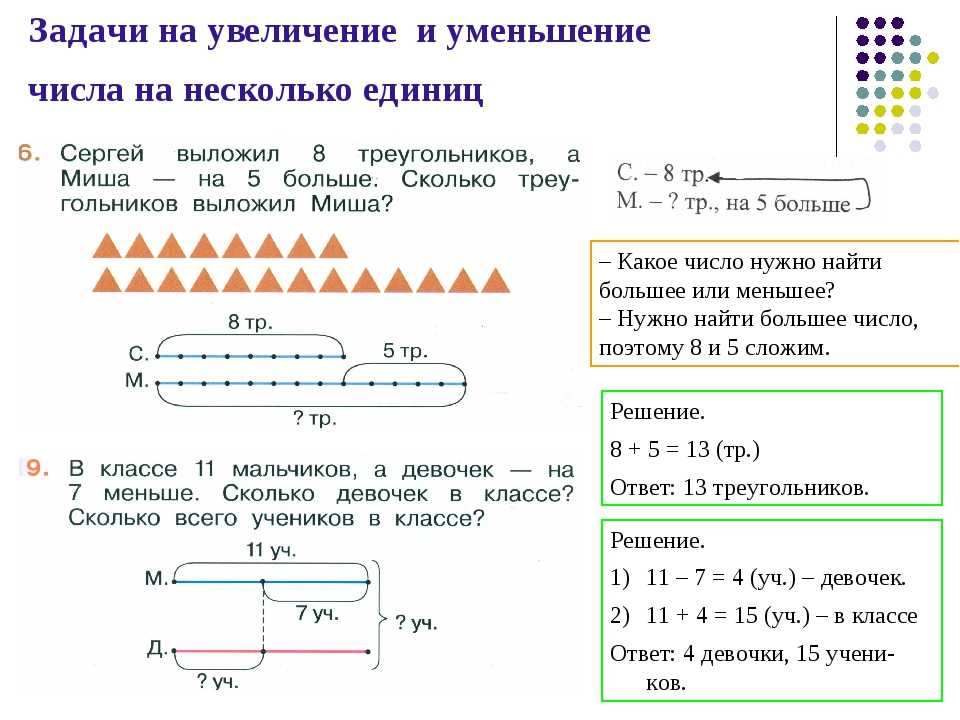
Я учу их искать неизвестных .
Все эти слова мы используем при решении задач, и мы изучаем структуру словесной задачи через словарный запас и взаимосвязь чисел.
На самом деле, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.
Возьмите эти примеры, можете ли вы определить запуск, изменение и результат в каждой проблеме? Подсказка: посмотрите на код, используемый для типа проблемы в правом нижнем углу.
Для сравнения задач мы используем термины больше , меньше , больше и меньше . Попробуйте решить эти задачи и посмотрите, сможете ли вы определить компоненты словесных задач.
Перестаньте искать «ответ» при решении текстовых задач
Это заблуждение труднее всего разрушить.
Учащиеся не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, , я хочу, чтобы ученики могли объяснить свой процесс и понять глубину словесных задач.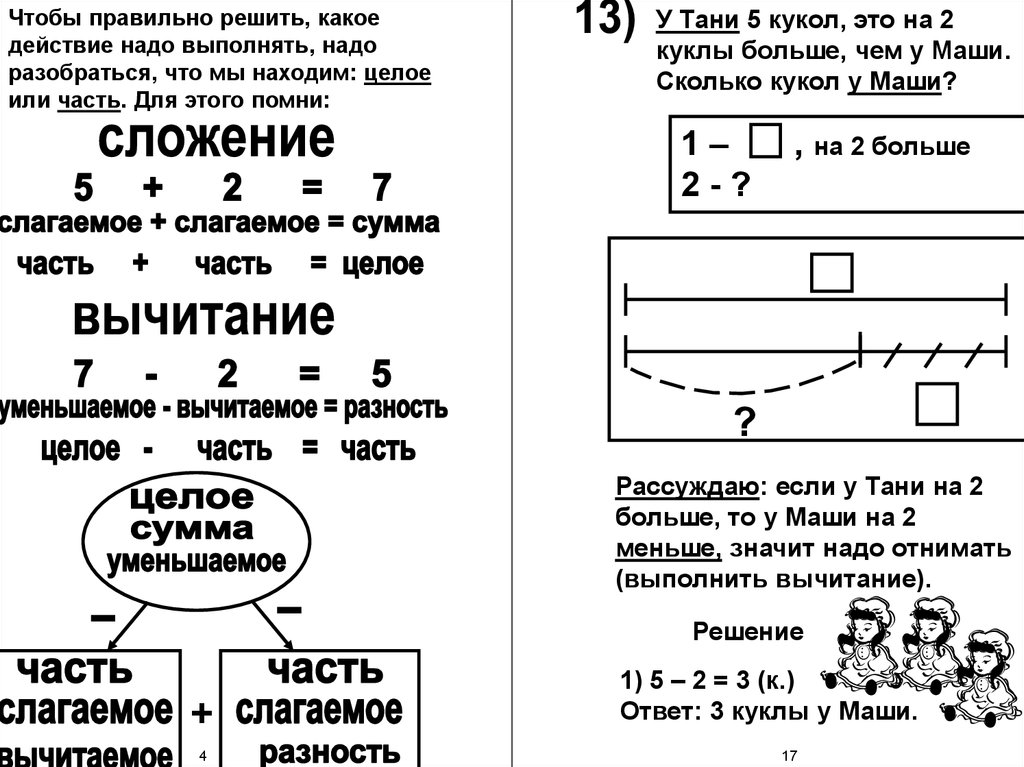
Ладно, это первоклассники и второклассники. Я знаю.
Мои студенты все еще могут объяснить после обучения, что они начинают изд с одной цифры. Проблема результат ed в прочем другой номер. Затем учащиеся узнают, что они ищут замену на между этими двумя числами.
Все дело в отношениях.
Различие между моделями и стратегиями
Пару лет назад я наткнулся на эту статью о необходимости помочь учащимся разработать адекватные модели для понимания связи чисел в задаче.
У меня в голове взорвалась лампочка. Мне нужно было провести различие между модели, которые студенты используют для понимания соотношения чисел в задаче, и стратегии для решения вычислений в задаче. Модели и стратегии работают в тандеме, но очень разные.
Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми учащийся решает задачу, складывая и разбирая числа.
Самое главное в моделях — отойти от них. Я знаю, это звучит странно.
Вы так долго обучаете студентов пользоваться моделями, а потом не хотите, чтобы они использовали модели. Ну, на самом деле, вы хотите, чтобы студенты двигались к эффективности.
Младшие школьники будут разыгрывать задачи, рисовать задачи с изображениями и рисовать задачи с кругами или линиями. Направьте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять отношение чисел
Это яркий пример перехода от модели перевернутой v к модели столбцов.
Ученик переходит от рисования кругов к использованию перевернутой буквы v.
Учащиеся должны полностью использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока выясняют сходство между моделями.
Студенты также должны иметь возможность создавать свои собственные модели. Вы увидите, как я иногда давал студентам копии модели, которые они могли вклеить в свои тетради, а иногда студенты рисовали свою собственную модель.
Они должны нести ответственность за выбор того, что лучше всего подходит для них. Начните обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них для использования. Всегда подталкивайте учащихся к более эффективным моделям.
То же самое касается стратегий для вычислений. Сначала обучайте стратегиям с помощью математических фактов, а затем применяйте их к текстовым задачам, чтобы учащиеся понимали стратегии и могли быстро выбрать одну из них для использования. При обучении сосредоточьтесь на одной или двух стратегиях. Как только учащиеся овладеют некоторыми стратегиями, попросите их выбрать стратегии, которые работают для решения различных задач.
Какие числа вы вставляете в пробелы?
Будьте целеустремленны в числах, которые вы выбираете для своих текстовых задач. Разные наборы чисел подходят для разных стратегий и разных моделей. Используйте числовые наборы, которые учащиеся уже использовали в вычислениях.
Если вас учили составлять 10, используйте числа, которые составляют 10.
Если вы работаете над сложением без перегруппировки, используйте эти наборы чисел. Чем больше связей вы сможете установить между вычислениями и решением задачи, тем лучше.
Приведенные выше примеры в основном предназначены для задач объединения и разделения. Неудивительно, что у наших студентов такие трудности с задачами на сравнение, поскольку мы не учим их в той же степени, что и задачи на соединение и разделение.
Нашим ученикам нужно еще больше практиковаться в решении подобных задач, потому что отношение чисел более абстрактно. Однако я собираюсь оставить это для другого поста в блоге.
Вы хотите получить БЕСПЛАТНЫЙ образец ресурса, который я использую для обучения задачам на сложение и вычитание по типу задач ? Нажмите на эту ссылку или изображение ниже.
Как приобрести задачи на сложение и вычитание
Полный ресурс также доступен для покупки в моем магазине и на сайте Teachers Pay Teachers.
Дополнительные идеи для обучения словесным задачам
Используйте сложение и вычитание в пределах 20 для решения словесных задач1, включающих ситуации сложения, отнимания, сложения, разъединения и сравнения с неизвестными во всех положениях, например, с использованием предметов, рисунки и уравнения с символом неизвестного числа для представления задачи (1Учащиеся не обязаны самостоятельно читать словесные задачи.
)- Дом CPALMS
- Информация о стандартах. & Ресурсы
- Описание курсов и каталог
- Ресурсы проверены коллегами и экспертами
- Программы PD Самостоятельное обучение
- Об инициативах и партнерстве CPALMS
- Платформа iCPALMS во Флориде
Экспорт
Распечатать
Связанные точки доступа
Альтернативная версия этого теста для учащихся с серьезными когнитивными нарушениями.
Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом эталонном тесте.
Уроки STEM — Активность по моделированию
Fill It Up — Piñatas!:
Этот MEA фокусируется на навыках решения проблем учащихся. После прочтения рассказа о том, что находится в пиньяте, студентов просят помочь компании найти лучший способ заполнить пиньяту. Основное внимание уделяется математическим навыкам, включая счет и сложение трех чисел, чтобы получить 20.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Квадраты для квилтинга:
Учащиеся будут использовать блоки выкройки, чтобы создать квадрат для квилтинга для Общества быстрых квилтеров.
Им придется учитывать информацию на диаграмме данных, чтобы помочь им создать свои квадраты. Им также придется добавить стоимость, чтобы сделать свой квадрат.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для того, чтобы выявить мысли учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Формирующие оценки MFAS
Добавить к (изменить неизвестное) словесные задачи:
Ученикам предлагается решить две словесные задачи «Добавить к (изменить неизвестное)», используя карандаш и бумагу или другие подходящие манипуляторы.
Словесные задачи на добавление (результат неизвестен):
Учащимся предлагается решить две задачи на добавление (результат неизвестен), используя карандаш и бумагу или другие подходящие манипуляторы.
Словесные задачи «Добавить к (Начало неизвестно)»:
Ученикам предлагается решить две задачи «Добавить к (Начало неизвестно)», используя карандаш и бумагу или другие подходящие манипуляторы.
Птицы на ветке:
Учащимся предлагается решить две словесные задачи «Взять из (Заменить неизвестно)», используя карандаш и бумагу или другие подходящие манипуляторы.
Словесные задачи на сравнение (большее неизвестное):
Учащимся предлагается решить две задачи на сравнение (большее неизвестное), представленные с использованием терминов больше чем и меньше чем.
Сравнить (разница неизвестна) словесные задачи:
Ученикам предлагается решить две словесные задачи на сравнение (разница неизвестна) в пределах 20, используя карандаш и бумагу или другие подходящие манипуляции.
Задачи на сравнение (меньшее неизвестное) со словами:
Учащимся предлагается решить две задачи на сравнение (меньшее неизвестное) со словами, используя карандаш и бумагу или другие подходящие манипуляторы.
Рыба в пруду:
Учащиеся решают словесную задачу «Возьми откуда (начало неизвестно)».
Сколько M&M’s?:
Учащимся предлагается решить две задачи на сравнение, представленные с использованием терминов больше, чем и меньше, чем .
Сколько еще наклеек?:
Учащимся предлагается решить задачу «Сравнить (разница неизвестна)», используя карандаш и бумагу или другие подходящие манипуляторы.
Еще Добавить в (Изменить неизвестно) Проблемы:
Учащихся просят решить две словесные задачи «Добавить в (изменить неизвестное)», используя карандаш и бумагу или другие подходящие манипуляторы.
Составить/Разобрать (Добавить Неизвестно) Словесная задача:
Учащихся просят решить две Составить/Разобрать (Сложить Неизвестно) словесную задачу, используя карандаш и бумагу или другие подходящие манипуляции.
Собрать/разобрать (оба слагаемых неизвестны) Словесные задачи:
Учащимся предлагается решить словесную задачу «Сложить/разобрать» (оба сложения неизвестны), используя карандаш и бумагу или другие подходящие манипуляторы.
Собери/Разбери (Всего Неизвестно):
Учащихся просят решить две словесные задачи «Собери/Разбери» (Всего Неизвестно), используя карандаш и бумагу или другие подходящие манипуляции.
Red Birds и Blue Birds:
Учащихся просят решить две словесные задачи «Соедини/Разбери» (добавить неизвестное) с помощью карандаша и бумаги или других подходящих манипуляторов.
Словесные задачи «Взять из (Заменить неизвестно)»:
Учащимся предлагается решить две задачи «Взять из (Заменить неизвестно)», используя карандаш и бумагу или другие подходящие манипуляторы.
Take From (Результат неизвестен):
Учащихся просят решить две словесные задачи на Take From (результат неизвестен), используя карандаш и бумагу или другие подходящие манипуляторы.
Take From (Начало неизвестно):
Учащихся просят решить две словесные задачи на Take From (Начало неизвестно), используя карандаш и бумагу или другие подходящие манипуляторы.
Задача о кексах:
Учащимся предлагается решить две словесные задачи «Взять из (Начало неизвестно)», используя карандаш и бумагу или другие подходящие манипуляторы.
Поезда и скакалки:
Учащимся предлагается решить две задачи на сравнение, представленные с использованием терминов больше и меньше.
Оригинальные учебники для учащихся по математике — классы K-5
День рождения: Дополнение:
Присоединяйтесь к Джулиане на ее 8-й день рождения! Научитесь решать задачи на сложение в пределах 20, используя объекты и создавая рисунки в этом интерактивном учебном пособии для учащихся.
Задачи на сложение в зоопарке. Часть 1:
Помогите Марио и Гретхен смоделировать и написать уравнения для задач на сложение в этом интерактивном учебном пособии.
Это первая часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Часть 1: Задания на сложение в зоопарке (этот)
Часть 2: Задачи на вычитание в зоопарке
Часть 3: Задания на сложение в зоопарке
Задачи на вычитание в зоопарке — Часть 2:
Помогите Марио и Гретхен смоделировать и написать уравнения для задач на вычитание в этом интерактивном учебном пособии.
Это вторая часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Часть 1. Задачи на сложение в зоопарке
Часть 2. Задачи на вычитание в окрестностях зоопарка (эта) В этом интерактивном уроке Гретхен и Марио различают задачи на сложение и вычитание во время экскурсии в зоопарк.
Это третья часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Часть 1: Задачи на сложение в зоопарке
Часть 2: Задачи на вычитание в зоопарке
Часть 3: Задачи на сложение в зоопарке (этот)
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения понятий и навыков в этом бенчмарке.
Оригинальные учебные пособия для студентов
День рождения: Дополнение:
Присоединяйтесь к Джулиане на ее 8-й день рождения! Научитесь решать задачи на сложение в пределах 20, используя объекты и создавая рисунки в этом интерактивном учебном пособии для учащихся.
Тип: Оригинальное учебное пособие для учащихся
Задачи на вычитание Вокруг зоопарка. Часть 2:
Помогите Марио и Гретхен смоделировать и написать уравнения для задач на вычитание в этом интерактивном учебном пособии.
Это вторая часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Часть 1: Задания на сложение в зоопарке
Часть 2: Задачи на вычитание в зоопарке (эта)
Часть 3: Задания на сложение в зоопарке
Тип: Оригинальное учебное пособие для учащихся
Задачи на вычитание в зоопарке — Часть 3:
Помогите Гретхен и Марио различать задачи на сложение и вычитание во время их экскурсии в зоопарк с помощью этого интерактивного руководства.
Это третья часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Часть 1: Задания на сложение в зоопарке
Часть 2: Задачи на вычитание в районе зоопарка
Часть 3: Задачи на сложение в районе зоопарка (эта)
Тип: оригинальное учебное пособие для учащихся
Задачи на сложение в зоопарке — часть 1:
Помогите Марио и Гретхен смоделировать и написать уравнения для задач на сложение в этом интерактивном руководстве.
Это первая часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Часть 1: Словесные задачи на сложение в зоопарке (эта)
Часть 2. Задачи на вычитание в зоопарке
Часть 3. Задания на вычитание в зоопарке
Тип: оригинальное учебное пособие для учащихся
Задачи решения проблем
Поиск стула:
Эти задачи явно описывают взаимно-однозначные соответствия без использования языка сравнения. Такие задачи учащимся решать легче, чем задачи, в которых используется язык сравнения, например «Сколько еще?» или «Насколько меньше».
Тип: Задание на решение проблем
Мальчики и девочки, Вариант 2:
Это задание представляет собой задание «Собери/Разбери» с неизвестным контекстом обоих сложений для сложения и вычитания. Как только учащийся находит один правильный ответ, его/ее можно побудить найти другой.
Попросите учащегося использовать предметы, картинки или уравнения для представления каждого ответа.
Тип: Задание на решение задач
Мальчики и девочки, Вариант 1:
Учащиеся могут использовать сложение или вычитание для решения этих типов текстовых задач, причем сложение связано с действием сложения, а вычитание связано с действием разбирать. В зависимости от того, как учащиеся думают об этих текстовых задачах, любая из них подходит для задач на «добавление неизвестных». Взгляд на это в обоих направлениях подчеркивает связь между сложением и вычитанием.
Тип: Задача решения проблем
В парке:
Эта задача включает три разных типа задач, использующих контекст «Добавить в» с дискретным количеством.
Тип: Задание на решение задач
Шарики Марии:
Ученикам полезно решать задачи одного типа, ограниченные небольшим числом, и разрабатывать стратегии для этого типа задач до того, как они столкнутся со смешанными наборами задач и большими числами, которые отвлекают учащегося от основного сама проблема.
Со временем они смогут различать типы проблем в смешанных наборах и применять соответствующую стратегию для решения каждого из них.
Тип: Задание на решение задач
Домашняя змея:
Цель этого задания — дать учащимся лучшее понимание измерений на примере роста домашней змеи.
Тип: Задание на решение задач
Школьные принадлежности:
Это задание можно использовать как в учебных, так и в оценочных целях, в зависимости от того, на каком этапе понимания сложения находятся учащиеся и как их поддерживает учитель. Показанное решение очень краткое; стратегии решения студентов, вероятно, будут гораздо более разнообразными.
Тип: Задача решения проблем
Маркеры общего доступа:
Эти типы задач представляют контексты «Взять из» для сложения и вычитания. Эта задача включает в себя три разных типа проблем с использованием контекста «Взять из»: неизвестный результат, неизвестное изменение и неизвестное начало.
Студентам нужен опыт и практика со всеми тремя типами.
Тип: задача решения проблем
Учебники
Упражнение с гориллами:
В этом обучающем видео от Академии Хана задача со словами решается с помощью единичных кубов, а также с отсутствующим уравнением сложения сложения и уравнением вычитания.
Тип: Учебное пособие
Обезьяны для вечеринки:
В этом учебном видео от Академии Хана исследуются отношения разрядов с десятками и единицами в пределах 20.
В этом уроке вы научитесь решать задачи с неизвестными словами: 10 — 2 = ?.
Тип: Учебное пособие
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Задачи решения проблем
Поиск стула:
Эти задачи явно описывают взаимно-однозначные соответствия без использования языка сравнения.
Такие задачи учащимся решать легче, чем задачи, в которых используется язык сравнения, например «Сколько еще?» или «Насколько меньше».
Тип: Задание на решение задач
Полевой день Дефицит:
Цель этого задания состоит в том, чтобы учащиеся связали задачи на сложение и вычитание с деньгами в контексте, знакомящем с понятием дефицита. Дефицит возникает, когда вы хотите или нуждаетесь в большем, чем можете иметь. Студенты могут захотеть купить все, но обнаружат, что всего за 7 долларов это невозможно, и им придется принимать решения.
Тип: Задача-решение
Мальчики и девочки, Вариант 2:
Эта задача представляет собой операцию «Собрать/разобрать» с неизвестным контекстом обоих сложений для сложения и вычитания. Как только учащийся находит один правильный ответ, его/ее можно побудить найти другой. Попросите учащегося использовать предметы, картинки или уравнения для представления каждого ответа.
Тип: Задание на решение задач
Мальчики и девочки, Вариант 1:
Учащиеся могут использовать сложение или вычитание для решения этих типов текстовых задач, причем сложение связано с действием сложения, а вычитание связано с действием разбирать. В зависимости от того, как учащиеся думают об этих текстовых задачах, любая из них подходит для задач на «добавление неизвестных». Взгляд на это в обоих направлениях подчеркивает связь между сложением и вычитанием.
Тип: Задача решения проблем
В парке:
Эта задача включает три разных типа задач, использующих контекст «Добавить в» с дискретным количеством.
Тип: Задание на решение задач
Шарики Марии:
Ученикам полезно решать задачи одного типа, ограниченные небольшим числом, и разрабатывать стратегии для этого типа задач до того, как они столкнутся со смешанными наборами задач и большими числами, которые отвлекают учащегося от основного сама проблема.
Со временем они смогут различать типы проблем в смешанных наборах и применять соответствующую стратегию для решения каждого из них.
Тип: Задание на решение задач
Измерение кубиков:
В этом задании учащиеся работают в парах, чтобы измерить кубик с помощью скрепок.
Тип: Задание на решение задач
Домашняя змея:
Цель этого задания — дать учащимся лучшее понимание измерений на примере роста домашней змеи.
Тип: Задание на решение задач
Школьные принадлежности:
Это задание можно использовать как в учебных, так и в оценочных целях, в зависимости от того, на каком этапе понимания сложения находятся учащиеся и как их поддерживает учитель. Показанное решение очень краткое; стратегии решения студентов, вероятно, будут гораздо более разнообразными.
Тип: Задача решения проблем
Маркеры общего доступа:
Эти типы задач представляют контексты «Взять из» для сложения и вычитания.