Проверить определитель матрицы онлайн: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

Линейная алгебра на Python. [Урок 4]. Определитель матрицы

Четвертый урок из цикла “Линейная алгебра на Python“, посвящен понятию определителя матрицы и его свойствам.

Определитель матрицы

Определитель матрицы размера (n-го порядка) является одной из ее численных характеристик. Определитель матрицы A обозначается как |A| или det(A), его также называют детерминантом. Рассмотрим квадратную матрицу 2×2 в общем виде:

Определитель такой матрицы вычисляется следующим образом:

➣ Численный пример

Перед тем, как привести методику расчета определителя в общем виде, введем понятие минора элемента определителя. Минор элемента определителя – это определитель, полученный из данного, путем вычеркивания всех элементов строки и столбца, на пересечении которых стоит данный элемент. Для матрицы 3×3 следующего вида:

Минор M₂₃ будет выглядеть так:

Введем еще одно понятие – алгебраическое дополнение элемента определителя – это минор этого элемента, взятый со знаком плюс или минус:

В общем виде вычислить определитель матрицы можно через разложение определителя по элементам строки или столбца.

Суть в том, что определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения. Для матрицы 3×3 это правило будет выполняться следующим образом:

Это правило распространяется на матрицы любой размерности.

➣ Численный пример

➤ Пример на Python

На Python определитель посчитать очень просто. Создадим матрицу A размера 3×3 из приведенного выше численного примера:

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

 

Для вычисления определителя этой матрицы воспользуемся функцией det() из пакета linalg.

>>> np.linalg.det(A)
-14.000000000000009

 

Мы уже говорили про особенность работы

Python с числами с плавающей точкой, поэтому можете полученное значение округлить до -14.

Свойства определителя матрицы.

Свойство 1. Определитель матрицы остается неизменным при ее транспонировании:

➤Пример на Python

Для округления чисел будем использовать функцию round().

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(A.T)
[[-4 10 8]
[-1 4 3]
[ 2 -1 1]]

>>> det_A = round(np.linalg.det(A), 3)
>>> det_A_t = round(np.linalg.det(A.T), 3)
>>> print(det_A)
-14.0
>>> print(det_A_t)
-14.0

 

Свойство 2. Если у матрицы есть строка или столбец, состоящие из нулей, то определитель такой матрицы равен нулю:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 0 0 0; 8 3 1')
>>> print(A)
[[-4 -1 2]
[ 0 0 0]
[ 8 3 1]]
>>> np. linalg.det(A)
0.0

 

Свойство 3. При перестановке строк матрицы знак ее определителя меняется на противоположный:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

>>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1')
>>> print(B)
[[10 4 -1]
[-4 -1 2]
[ 8 3 1]]

>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
14.0

 

Свойство 4. Если у матрицы есть две одинаковые строки, то ее определитель равен нулю:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> np.linalg.det(A)
0.0

 

Свойство 5. Если все элементы строки или столбца матрицы умножить на какое-то число, то и определитель будет умножен на это число:

➤ Пример на Python

>>> A = np. matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

>>> k = 2
>>> B = A.copy()
>>> B[2, :] = k * B[2, :]
>>> print(B)
[[-4 -1 2]
[10 4 -1]
[16 6 2]]

>>> det_A = round(np.linalg.det(A), 3)
>>> det_B = round(np.linalg.det(B), 3)

>>> det_A * k
-28.0
>>> det_B
-28.0

 

Свойство 6. Если все элементы строки или столбца можно представить как сумму двух слагаемых, то определитель такой матрицы равен сумме определителей двух соответствующих матриц:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> B = np.matrix('-4 -1 2; 8 3 2; 8 3 1')
>>> C = A.copy()
>>> C[1, :] += B[1, :]
>>> print(C)
[[-4 -1 2]
[ 4 2 4]
[ 8 3 1]]
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 8 3 2]
[ 8 3 1]]
>>> round(np.
  linalg.det(C), 3)
4.0
>>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3)
4.0

 

Свойство 7. Если к элементам одной строки прибавить элементы другой строки, умноженные на одно и тоже число, то определитель матрицы не изменится:

 

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> k = 2
>>> B = A.copy()
>>> B[1, :] = B[1, :] + k * B[0, :]
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 2 2 3]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
-14.0

 

Свойство 8. Если строка или столбец матрицы является линейной комбинацией других строк (столбцов), то определитель такой матрицы равен нулю:

➤ Пример на Python

>>> A = np. matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]

>>> k = 2
>>> A[1, :] = A[0, :] + k * A[2, :]
>>> round(np.linalg.det(A), 3)
0.0

 

Свойство 9. Если матрица содержит пропорциональные строки, то ее определитель равен нулю:

➤ Пример на Python

>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = k * A[0, :]
>>> print(A)
[[-4 -1 2]
[-8 -2 4]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
0.0

 

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.   Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Определитель, детерминант матрицы — онлайн справочник для студентов

ОПРЕДЕЛЕНИЕ

Определителем или определителем квадратной матрицы \(\ A=\left\|a_{i j}\right\|_{n \times n} \) является число, присвоенное этой матрице.

Определитель матрицы \(\ A \) обозначается вертикальными полосами \(\ |A| \) или греческой буквой \(\ \Delta \) или \(\ \operatorname{det} A \).

Способы вычисления определителя матрицы

Определителем матрицы второго порядка является число, равное

\(\ \left|\begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right|=a_{11} \cdot a_{22}-a_{21} \cdot a_{12} \)

ПРИМЕР 1

Задача

Вычислить определитель второго порядка

\(\ \Delta=\left|\begin{array}{cc}{1} & {-1} \\ {2} & {3}\end{array}\right| \)

Решение

По определению определитель второго порядка

\(\ \Delta=\left|\begin{array}{cc}{1} & {-1} \\ {2} & {3}\end{array}\right|=1 \cdot 3-2 \cdot(-1)=3+2=5 \)

Ответ

\(\ \Delta=5 \)

Определитель матрицы третьего порядка

Определитель матрицы третьего порядка может быть вычислен с использованием правила треугольника или правила Сарруса.

Правило треугольника. Определитель матрицы третьего порядка можно вычислить по формуле

\(\ \left|\begin{array}{lll}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=a_{11} \cdot a_{22} \cdot a_{33}+a_{31} \cdot a_{12} \cdot a_{23}+a_{21} \cdot a_{13} \cdot a_{32}-a_{31} \cdot a_{22} \cdot a_{13}-a_{21} \cdot a_{12} \cdot a_{33}-a_{11} \cdot a_{23} \cdot a_{32} \)

Это правило можно схематически изобразить следующим образом.

ПРИМЕР 2

Задача

Вычислить определитель третьего порядка по правилу треугольника

\(\ \Delta=\left|\begin{array}{ccc}{1} & {2} & {-4} \\ {2} & {3} & {1} \\ {3} & {-1} & {2}\end{array}\right| \)

Решение

Согласно правилу треугольника определитель третьего порядка равен

\(\ \Delta=\left|\begin{array}{ccc}{1} & {2} & {-4} \\ {2} & {3} & {1} \\ {3} & {-1} & {2}\end{array}\right|=1.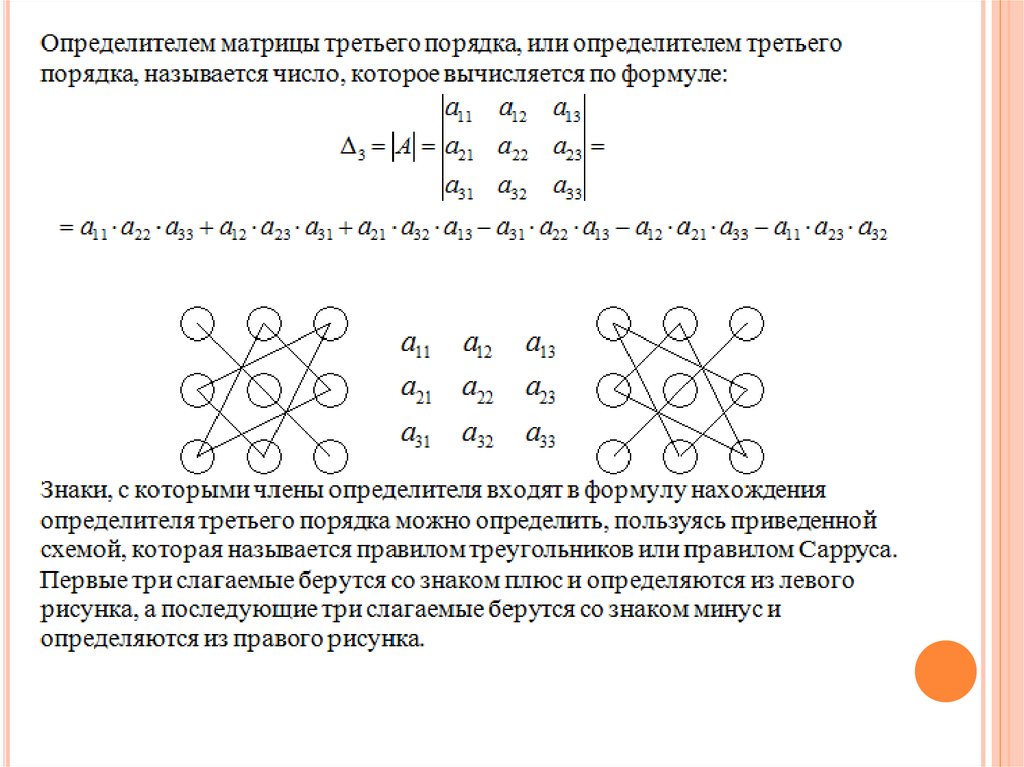 3 \cdot 2+3 \cdot 2 \cdot 1+2 \cdot(-4) \cdot(-1)-3 \cdot 3 \cdot(-4)-2 \cdot 2 \cdot 2-1 \cdot 1 \cdot(-1)=49 \)

Ответ

\(\ \Delta=49 \)

Правило Сарруса. Чтобы вычислить детерминант третьего порядка, мы добавим первые два столбца и умножим диагональные элементы, взяв произведение со знаком плюс, если диагональ является главной или параллельной ему и взяв произведение с знаком минус, если диагональ равна стороны или параллели, мы получаем

ПРИМЕР 3

Задача

Вычислить определитель третьего порядка из примера 2 в соответствии с правилом Сарруса

\(\ \Delta=\left|\begin{array}{ccc}{1} & {2} & {-4} \\ {2} & {3} & {1} \\ {3} & {-1} & {2}\end{array}\right| \)

Решение.

Согласно правилу Сарруса, необходимо написать первые два столбца этого определителя справа от вычисленного определителя и умножить диагональные элементы. Взяв эти произведения с соответствующими знаками, получим, что искомый определитель третьего порядка

\(\ \Delta= \begin{array}{|ccc|cc}{1} & {2} & {-4} & {1} & {2} \\ {2} & {3} & {1} & {2} & {3} \\ {3} & {-1} & {2} & {3} & {-1}\end{array}=1 \cdot 3 \cdot 2+2 \cdot 1 \cdot 3+(-4) \cdot 2 \cdot(-1)-3 \cdot 3 \cdot(-4)-(-1) \cdot 1 \cdot 1-2 \cdot 2 \cdot 2=49 \)

Ответ

\(\ \Delta=49 \)

Вычисление детерминантов более высокого порядка

Для расчета детерминантов высших порядков используется метод разложения определителя в строке или столбце. Это позволяет нам представить детерминант квадратной матрицы как сумму произведений элементов любой из ее строк или столбцов для их алгебраических дополнений. В этом случае вычисление детерминанта n-го порядка сводится к вычислению детерминантов n-1-го порядка.

Теорема

Теорема о разложении определителя на элементы строки. Детерминант матрицы \(\ \mathrm{A} \) равен сумме произведений элементов строки и их алгебраических дополнений.

\(\ \operatorname{det} A=a_{i 1} A_{i 1}+a_{i 2} A_{i 2}+\ldots+a_{i n} A_{i n} \)

Теорема

Теорема о разложении определителя на элементы столбца. Определитель матрицы \(\ \mathrm{A} \) равен сумме произведений элементов столбца и их алгебраических дополнений.

\(\ \operatorname{det} A=a_{1 j} A_{1 j}+a_{2 j} A_{2 j}+\ldots+a_{n j} A_{n j} \)

ПРИМЕР 4

Задача

Вычислить определитель 4-го порядка двумя способами:

а) выкладка на 1-й линии;

б) расширение на 1-й столбец

\(\ \Delta=\left|\begin{array}{cccc}{2} & {1} & {0} & {2} \\ {3} & {2} & {1} & {0} \\ {-1} & {0} & {1} & {3} \\ {-1} & {2} & {1} & {3}\end{array}\right| \)

Решение

а) По теореме о разложении определителя на элементы строки этот определитель разбивается на первую строку следующим образом

\(\ \Delta=a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}+a_{14} A_{14} \)

С учетом формулы для вычисления алгебраических дополнений \(\ A_{i j}=(-1)^{i+j} M_{i j} \) Здесь \(\ M_{i j} \) является минором элемента \(\ a_{i j} \) , равным определителю, полученному из данного определителя, путем пересечения i-й строки и j-го столбца. {1+4}\left|\begin{array}{ccc}{3} & {2} & {1} \\ {-1} & {0} & {1} \\ {-1} & {2} & {1}\end{array}\right|=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{3} & {1} & {0} \\ {-1} & {1} & {3} \\ {-1} & {1} & {3}\end{array}\right|-2 \cdot\left|\begin{array}{ccc}{3} & {2} & {1} \\ {-1} & {0} & {1} \\ {-1} & {2} & {1}\end{array}\right| \)

Полученные детерминанты третьего порядка вычислимы по правилу треугольника \(\ \Delta=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{3} & {1} & {0} \\ {-1} & {1} & {3} \\ {-1} & {1} & {3}\end{array}\right|-2 \cdot\left|\begin{array}{ccc}{3} & {2} & {1} \\ {-1} & {0} & {1} \\ {-1} & {2} & {1}\end{array}\right|=2(6+6+0-0-0-6)-(9-3+0-0+3-9)-2(0-2-2-0+2-6)= \)

б) По теореме о разложении определителя на элементы столбца этот определитель разбивается на первый столбец следующим образом

\(\ \Delta=a_{11} A_{11}+a_{21} A_{21}+a_{31} A_{31}+a_{41} A_{41}=2 \cdot(-1)^{1+1}\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|+3 \cdot(-1)^{2+1}\left|\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|+(-1) \cdot(-1)^{3+1}\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {2} & {1} & {3}\end{array}\right|+ \)

\(\ +(-1) \cdot(-1)^{4+1}\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {0} & {1} & {3}\end{array}\right|=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-3 \cdot\left|\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {2} & {1} & {3}\end{array}\right|+\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {0} & {1} & {3}\end{array}\right| \)

Полученные детерминанты третьего порядка вычислимы по правилу треугольника

\(\ \Delta=2 \cdot\left|\begin{array}{ccc}{2} & {1} & {0} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-3 \cdot\left|\begin{array}{ccc}{1} & {0} & {2} \\ {0} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right|-\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {2} & {1} & {3}\end{array}\right|+\left|\begin{array}{ccc}{1} & {0} & {2} \\ {2} & {1} & {0} \\ {0} & {1} & {3}\end{array}\right|=2 \cdot(6+6+0-0-0-6)- 3 \cdot(3+0+0-4-0-3)-(3+0+4-4-0-0)+(3+0+4-0-0-0)=28 \)

Ответ

\(\ \Delta=28 \)

Свойства определителя матрицы

Определитель любого порядка может быть вычислен с использованием свойств определителя:

детерминант не изменяется при элементарных преобразованиях строк или столбцов;

при перестановке строк или столбцов знак детерминанта меняется на обратный;

Определитель треугольной матрицы равен произведению элементов, расположенных на диагонали. Например, для верхней треугольной матрицы

\(\ A=\left(\begin{array}{cccc}{a_{11}} & {a_{12}} & {\dots} & {a_{1 n}} \\ {0} & {a_{22}} & {\dots} & {a_{2 n}} \\ {\cdots} & {\cdots} & {\cdots} & {\cdots} \\ {0} & {0} & {\dots} & {a_{n n}}\end{array}\right) \)

детерминантом является \(\ \operatorname{det} A=a_{11} \cdot a_{22} \cdot \ldots \cdot a_{n n} \)

ПРИМЕР 5

Задача

Вычислить определитель 4-го порядка, используя свойства определителя

\(\ \Delta=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {-2} & {1} & {5} & {6} \\ {-3} & {-5} & {1} & {7} \\ {-4} & {-6} & {-7} & {1}\end{array}\right| \)

Решение.

Приведем этот определитель, используя элементарные преобразования в верхнюю треугольную форму. Для этого добавьте первый, умноженный, соответственно, на 2, 3 и 4 на вторую, третью и четвертую строки.

\(\ \Delta=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {-2} & {1} & {5} & {6} \\ {-3} & {-5} & {1} & {7} \\ {-4} & {-6} & {-7} & {1}\end{array}\right|=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {5} & {11} & {14} \\ {0} & {1} & {10} & {19} \\ {0} & {2} & {5} & {17}\end{array}\right| \)

Измените вторую и третью строки в некоторых местах, а знак детерминанта изменится на противоположное

\(\ \Delta=\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {5} & {11} & {14} \\ {0} & {1} & {10} & {19} \\ {0} & {2} & {5} & {17}\end{array}\right|=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {5} & {11} & {14} \\ {0} & {2} & {5} & {17}\end{array}\right| \)

Рядом с третьей строкой добавьте вторую, умноженную на (-5), а на четвертую добавьте вторую, умноженную на (-2). Получите

\(\ \Delta=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {5} & {11} & {14} \\ {0} & {2} & {5} & {17}\end{array}\right|=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {0} & {-39} & {-81} \\ {0} & {0} & {-15} & {-21}\end{array}\right| \)

Добавьте к последней строке третий, умноженный на \(\ (-38) \)

\(\ \Delta=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {5} & {11} & {14} \\ {0} & {2} & {5} & {17}\end{array}\right|=-\left|\begin{array}{cccc}{1} & {2} & {3} & {4} \\ {0} & {1} & {10} & {19} \\ {0} & {0} & {-39} & {-81} \\ {0} & {0} & {0} & {\frac{396}{39}}\end{array}\right| \)

Теперь определитель равен произведению элементов на главной диагонали

\(\ \Delta=-\left(1 \cdot 1 \cdot(-39) \cdot \frac{396}{39}\right)=396 \)

Ответ

\(\ \Delta=396 \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Умножение матриц Сравнение бесконечно малых функций Бесконечно малые функции Непрерывность функции в точке и на промежутке

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Калькулятор определителя матрицы — Определитель матрицы 2×2 3×3 4×4

Введение в калькулятор определителя матрицы

Калькулятор определителя матрицы представляет собой онлайн-инструмент для вычисления определителя матрицы для нахождения скалярного значения. Он использует метод расширения, чтобы найти одно значение квадратной матрицы. Он также использует метод редукции и находит скалярное значение.

Мы обычно применяем сложение, вычитание и умножение в матричной алгебре на матрицах. Определитель необходим для вычисления единственного решения системы нелинейных уравнений. Вот почему мы представляем 9Калькулятор определителя матрицы 0005 3×3 с шагами , который может легко вычислять определители, используя как методы расширения, так и методы сокращения.

Формула, используемая калькулятором формулы определителя матрицы

Этот калькулятор определителя матрицы с шагами использует две формулы для вычисления определителя матрицы порядка 2, 3 или 4. Это:

1. Определитель играет важную роль при решении системы линейных уравнений и нахождении обратной матрицы, тогда определитель матрицы 2×2:

   $$ А \;=\; \begin{bmatrix} a & b \\ c & d \end{bmatrix} $$ $$ |A| «=» \begin{vmatrix} a & b \\ c & d \end{vmatrix} \;=\; (а \ раз с) \;-\; (б\умножить на г) $$

2. Если A определитель матрицы A, то определитель матрицы 3×3.

   $$ \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{bmatrix} $$ $$ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \\ \end{vmatrix} $$ $$ |A| «=» a \begin{vmatrix} e & f \\ h & i \end{vmatrix} \;-\; б \begin{vmatrix} d & f \\ g & i \end{vmatrix} \;-\; c \begin{vmatrix} d & e \\ g & h \end{vmatrix} $$
3. Определитель матрицы 4-by-by можно решить, сократив ее строку столбца или приведя матрицу к треугольной форме.

Как пользоваться калькулятором определителя матрицы 4х4?

Этот калькулятор определительной матрицы можно использовать, выполнив следующие шаги:

1. На первом этапе вам необходимо ввести количество строк и столбцов для матрицы.
2. Теперь подставьте значения всех элементов матрицы.
3. Или вы можете использовать случайную кнопку, чтобы выбрать случайную матрицу.
4. Теперь нажмите кнопку расчета.

Вы получите решение в течение нескольких секунд после нажатия на кнопку расчета. Определитель матричного калькулятора даст вам пошаговое решение, которое вы сможете использовать для обучения и практики.

Зачем использовать калькулятор определительной матрицы?

В математике матрица важна для решения системы линейных уравнений. Некоторые операции применяются для решения системы линейных уравнений. Таким образом, определитель является важной операцией. Решатель определителя матрицы можно использовать для решения многих задач.

Пока вы вычисляете определитель матрицы высшего порядка, вы не можете решить ее только с помощью расширения. Вы должны уменьшить порядок матрицы, используя редуцированную эшелонированную форму, что является сложной процедурой.

Таким образом, существует потребность в калькуляторе определителя матрицы 4×4 с шагами , который может легко уменьшить потребность в матрице. Вот почему вам нужно использовать определитель матрицы, который поможет вам найти определитель матрицы 2×2.

Преимущества использования калькулятора определителя с шагами

Определитель матрицы представляет собой скалярное значение, вычисленное из квадратной матрицы. Полезно найти единственное решение системы уравнений. Калькулятор определителя матрицы с переменными полезен для нахождения этого решения, потому что он может легко обрабатывать матрицы более высокого порядка. Некоторые другие преимущества этого инструмента приведены ниже:

1. Он предоставляет пошаговое объяснение определителя матрицы, так что вы можете понять каждый шаг, чтобы найти определитель матрицы 3×3.
2. Экономит ваше время, быстро и эффективно вычисляя определители.
3. Калькулятор формулы определителя матрицы удобен для вас благодаря простому и уникальному интерфейсу.
4. Позволяет выбирать случайные значения для матрицы, чтобы можно было потренироваться на случайных примерах и найти определитель матрицы 4×4.
5. Калькулятор определителя матрицы дает пошаговое решение, которое помогает понять каждый шаг.

Как найти определитель матрицы 3×3 калькулятором?

Найти определитель матричного калькулятора просто и легко. Есть два способа, с помощью которых вы можете получить к нему доступ.

1. Найдите в Google или любой другой поисковой системе, набрав вычислитель определителя матрицы с шагами и найдите наш инструмент в результатах.
2. Откройте сайт calculatees.com и найдите здесь «определитель матричного калькулятора 3×3».

Прочие сопутствующие инструменты

На этом сайте есть и другие полезные матричные калькуляторы, которые вы можете использовать бесплатно. Эти инструменты

• калькулятор формулы транспонирования матрицы
• найти ранг матрицы с помощью калькулятора формы эшелона
Матрица
• в степени -1
• Калькулятор метода Гаусса-Джордана
• онлайн калькулятор обратной матрицы с шагами
• Калькулятор собственных значений 3×3 с шагами
Калькулятор обнуления матрицы
• с шагами
• калькулятор след матрицы
• lu калькулятор разложения для систем линейных уравнений
Калькулятор собственного вектора матрицы
• шаг за шагом
• сопряжение матричного калькулятора с шагами
• Калькулятор умножения матриц

Часто задаваемые вопросы

Является ли калькулятор определителя 3×3 с шагом точным?

Да, этот определитель матричного калькулятора проверен и одобрен старшими математиками. Вы можете использовать этот инструмент, так как он дает точные результаты.

Калькулятор определителя матрицы 4×4 с шагами предоставляет бесплатные шаги?

Да, определитель матрицы предоставляет пошаговые результаты бесплатно. Вы можете использовать этот инструмент для обучения и практики онлайн.

Хамза Харун

Последнее обновление 05 апреля 2022 г.

Я автор контента и создатель контента. Мне нравится писать контент на разные темы. Помимо писательства, я SEO-ASO-SMM специалист и любитель футбола.

Калькулятор детерминанта матрицы

Создано Maciej Kowalski, кандидатом наук

Отредактировано Анной Щепанек, доктором наук и Джеком Боутером

Последнее обновление: 03 декабря 2022 г.

Содержание:

• Что такое определитель?
• Общая формула определителя
• Определитель матрицы 2×2, 3×3 и 4×4
• Свойства определителя
• Пример: использование калькулятора определителя матрицы

Добро пожаловать в 9Калькулятор определителя матрицы 0005 , где у вас будет возможность вычислить определители матрицы, используя простую в использовании формулу определителя для любой квадратной матрицы размером до 4×4. Кроме того, мы рассмотрим некоторые из основных свойств определителей , которые могут помочь в решении более крупных, таких как определитель матрицы 4×4.

» Что такое определитель и зачем мне это? » Через некоторое время мы покажем вам определение определителя, но давайте просто скажем, что, помимо прочего, он чрезвычайно полезен при работе с системами уравнений. — проверьте наш калькулятор системы уравнений для более подробной информации. В основном как решить систему из трех уравнений так же, как найти определитель матрицы 3×3 .

Убежден? Воодушевлен? Взволнованный? Тогда давайте двигаться дальше, хорошо?

Что такое определитель?

Почему бы нам не начать с , что такое матрица ? Хотите верьте, хотите нет, но это не только классика научной фантастики 90-х. В математике это имя, которое мы даем массиву элементов (обычно чисел) с заданным количеством строк и столбцов . Пример матрицы:

A=[3−1021−1]A = \begin{bmatrix} 3 & -1 \\ 0 и 2\\ 1 и -1 \end{bmatrix}A=⎣

⎡​301​−12−1​⎦

⎤​

Как видите, числа заключены в две большие квадратные скобки, [[[ и ]]]. Также мы говорим, что, например, число 222 равно в ячейке во второй строке и во втором столбце .

Определение определителя гласит, что это число, полученное путем умножения и сложения ячеек квадратной матрицы в соответствии с заданным правилом . Давайте подробнее рассмотрим несколько важных вещей здесь.

• Как следует из определения определителя, нам нужна квадратная матрица даже для начала вычислений. Это означает, что мы можем найти определитель матрицы 2×2 или определитель матрицы 4×4, но не, например, чего-то похожего на AAA выше, то есть 3×2 (три строки и две строки). столбцы) матрица;
• Формула определителя для больших матриц становится довольно сложной . Количество его слагаемых равно количеству перестановок числа, являющегося стороной матрицы. Это означает, что определитель матрицы 2×2 имеет только два слагаемых, но для матриц 5×5 мы получаем 120 слагаемых;
• Есть способы упростить вычисления . Например, нахождение определителя матрицы 4×4 можно превратить в задачу о том, как найти определитель матрицы 3×3. Мы рассмотрим некоторые такие свойства определителей в разделе «Свойства определителей»; и
• Определитель матрицы , AAA, обозначается ∣A∣|A|∣A∣ (просто замените квадратные скобки матрицы вертикальными линиями ∣|∣) или det⁡(A)\det(A) дет (А). Не перепутайте первое обозначение с абсолютным значением! В общем случае определитель может быть отрицательным числом .

Итак, что такое определитель? Это число; мы так многому научились. Но почему это полезно? Где он появляется?

Определитель матрицы чрезвычайно полезный и часто используемый инструмент по линейной алгебре. Всякий раз, когда у нас есть матрица и мы хотим понять ее, определитель — это одна из первых вещей, к которым мы обращаемся. Например, любую систему линейных уравнений можно описать матрицей. Его определители помогают нам найти решение, например, с помощью правила Крамера, которое вы можете найти в нашем калькуляторе правил Крамера. Более того, когда мы используем матрицы для описания линейного преобразования, часто лучше всего диагонализовать их . Как мы это делаем? С определителями, конечно.
Определитель матрицы также говорит нам, есть ли у матрицы обратная и должна ли обратная быть аппроксимирована псевдообратной Муром-Пенроузом.
Наконец, нам обычно нужны собственные значения такого преобразования. Да, как вы уже догадались — для этого мы также используем определители .

🙋 Чтобы найти собственные значения и соответствующие собственные векторы любой матрицы, не стесняйтесь использовать калькулятор собственных значений и собственных векторов Omni

Надеюсь, нам удалось убедить вас в том, что стоит изучить определение определителя. Но как его рассчитать? Есть ли какая-нибудь короткая, аккуратная формула определителя для повседневного использования?

Общая формула определителя

Прежде чем мы рассмотрим некоторые конкретные примеры, например, как найти определитель матрицы 3×3, давайте взглянем на чудовище, которым является общее определение определителя .

Пусть AAA — квадратная матрица размера nnn, где nnn — некоторое натуральное число. Обозначим ячейки ААА через ai,ja_{i,j}ai,j​, где iii — номер строки, а jjj — номер столбца. Тогда: 9{\ mathrm {sign} (\ sigma)} \ prod a_ {i, \ sigma (i)}, ∣A∣ = ∑ (−1) sgn (σ) ∏ai, σ (i)​,

, где:

• ∑\sum∑ сумма всех перестановок множества {1,2…,n}\{1,2\ldots,n\}{1,2…,n}; и
• ∏\prod∏ — произведение iii-s от 111 до nnn.

Красиво, не так ли? Если перевести забавные символы на нечто более понятное, то это означает примерно следующее:

💡 Чтобы вычислить определитель, посмотрите на свою матрицу, возьмите nnn чисел, по одному из каждой строки и каждого столбца, и перемножьте их между собой. Возьмите все такие nnn-наборы, иногда меняйте их знак и просуммируйте.

Не беспокойтесь; теперь, когда мы выложили это общее определение детерминанта в открытый доступ, мы больше не будем о нем думать . Мы будем придерживаться простых случаев , где матрица не слишком велика, чтобы показать, что это на самом деле означает.

Определитель матрицы 2×2, 3×3 и 4×4

Как это часто бывает в жизни, размер имеет значение. В данном конкретном случае чем меньше матрица, тем проще формула определителя . Для согласованности мы используем обозначение ниже, как в калькуляторе определителя матрицы.

Если

A=[a1a2b1b2]A = \begin{bmatrix} а_1 и а_2 \\ б_1 и б_2 \end{bmatrix}A=[a1​b1​​a2​b2​​]

, тогда определитель числа AAA равен

∣A∣=a1⋅b2−a2⋅b1|A| = a_1 \cdot b_2 — a_2 \cdot b_1∣A∣=a1​⋅b2​−a2​⋅b1​.

Обратите внимание, что это эквивалентно взятию чисел одной из диагоналей квадратной матрицы (из левого верхнего угла в правый нижний) минус другой (из правого верхнего угла в левый нижний).

Далее, если

B=[a1b1c1a2b2c2a3b3c3]B = \begin{bmatrix} а_1 и б_1 и с_1 \\ а_2 и б_2 и с_2 \\ а_3 и б_3 и с_3 \end{bmatrix}B=⎣

⎡​a1​a2​a3​b1​b2​b3​​c1​c2​c3​​⎦

⎤​

тогда определитель BBB:

∣B∣=a1⋅b2⋅c3+a2⋅b3⋅c1+a3⋅b1⋅c2−a3⋅b2⋅c1−a1⋅b3⋅c2−a2⋅b1⋅c3. \footnotesize \начать{разделить} |Б| =&\, a_1 \!\cdot\! b_2 \!\cdot\! c_3 + a_2 \!\cdot\! b_3 \!\cdot\! c_1 + a_3 \!\cdot\! b_1 \!\cdot\! с_2 \\ &-\!a_3 \!\cdot\! b_2 \!\cdot\! c_1 — a_1 \!\cdot\! b_3 \!\cdot\! c_2 — a_2 \!\cdot\! b_1 \!\cdot\! с_3. \end{split}∣B∣=​a1​⋅b2​⋅c3​+a2​⋅b3​⋅c1​+a3​⋅b1​⋅c2​−a3​⋅b2​⋅c1​−a1​⋅b3 ​⋅c2​−a2​⋅b1​⋅c3​.​

Здесь снова мы можем использовать несколько диагоналей, чтобы запомнить формулу. Чтобы это было ясно, давайте снова запишем две верхние строки под матрицей:

∣a1b1c1a2b2c2a3b3c3∣a1b1c1a2b2c2\begin{vmatrix} а_1 и б_1 и с_1 \\ а_2 и б_2 и с_2 \\ а_3 и б_3 и с_3 \end{vmatrix}\\ \керн{.4em} \begin{матрица} а_1 и б_1 и с_1 \\ а_2 и б_2 и с_2 \end{matrix}∣

∣​a1​a2​a3​b1​b2​b3​c1​c2​c3​∣

∣​a1​a2​​b1​b2​​c1​c2​​

Теперь, как и в случае 2×2, начнем с диагонали исходной квадратной матрицы, идущей из левого верхнего угла в правый нижний — это первое слагаемое, a1⋅b2⋅c3a_1 \cdot b_2 \cdot c_3a1​⋅b2​⋅c3​. Затем берем всю эту диагональ и перемещаем ее на один шаг вниз , т. е. в каждом столбце берем элемент под тем, который мы взяли раньше. Здесь расширенный массив, который мы нарисовали выше, помогает нам увидеть, что это дает второе слагаемое, a2⋅b3⋅c1a_2 \cdot b_3 \cdot c_1a2​⋅b3​⋅c1​. Делаем это еще раз, чтобы получить a3⋅b1⋅c2a_3 \cdot b_1 \cdot c_2a3​⋅b1​⋅c2​ и это завершает диагонали справа внизу и слагаемые, которые появляются с плюсом .

Далее, переходим на другую диагональ исходной матрицы (из правого верхнего угла в левый нижний) и получаем первое отрицательное слагаемое в формуле, a3⋅b2⋅c1a_3 \cdot b_2 \cdot c_1a3​ ⋅b2​⋅c1​. Делаем то же самое, что и раньше — перемещаем по диагонали вниз . Расширенная форма выше позволяет легко увидеть, что это дает два других отрицательных слагаемых, a1⋅b3⋅c2a_1 \cdot b_3 \cdot c_2a1​⋅b3​⋅c2​ и a2⋅b1⋅c3a_2 \cdot b_1 \cdot c_3a2​⋅b1 ​⋅с3​.

Наконец, если

C=[a1b1c1d1a2b2c2d2a3b3c3d3a4b4c4d4]C = \begin{bmatrix} a_1 & b_1 & c_1 & d_1 \\ а_2 и б_2 и с_2 и d_2 \\ a_3 & b_3 & c_3 & d_3 \\ а_4 и б_4 и с_4 и d_4 \\ \end{bmatrix}C=⎣

⎡​a1​a2​a3​a4​​b1​b2​b3​b4​​c1​c2​c3​c4​​d1​d2​d3​d4​​⎦

⎤​

, то определитель такой матрицы 4×4: ⋅c2⋅d4+a2⋅b3⋅c1⋅d4−a3⋅b2⋅c1⋅d4+a3⋅b2⋅c4⋅d1−a2⋅b3⋅c4⋅d1+a4⋅b3⋅c2⋅d1−a3⋅b4⋅c2 ⋅d1+a2⋅b4⋅c3⋅d1−a4⋅b2⋅c3⋅d1+a4⋅b1⋅c3⋅d2−a1⋅b4⋅c3⋅d2+a3⋅b4⋅c1⋅d2−a4⋅b3⋅c1⋅d2 +a1⋅b3⋅c4⋅d2−a3⋅b1⋅c4⋅d2+a2⋅b1⋅c4⋅d3−a1⋅b2⋅c4⋅d3+a4⋅b2⋅c1⋅d3−a2⋅b4⋅c1⋅d3+a1 ⋅b4⋅c2⋅d3−a4⋅b1⋅c2⋅d3. \scriptsize \начать{разделить} \!|С| \!=&\керн{.9em} a_1 \!\cdot\! b_2 \!\cdot\! c_3 \!\cdot\! d_4 — a_2 \!\cdot\! b_1 \!\cdot\! c_3 \!\cdot\! d_4 + a_3 \!\cdot\! b_1 \!\cdot\! c_2 \!\cdot\! д_4\\ &\! — а_1 \!\cdot\! b_3 \!\cdot\! c_2 \!\cdot\! d_4 + a_2 \!\cdot\! b_3 \!\cdot\! c_1 \!\cdot\! d_4 — a_3 \!\cdot\! b_2 \!\cdot\! c_1 \!\cdot\! д_4\ &\! + a_3 \!\cdot\! b_2 \!\cdot\! c_4 \!\cdot\! d_1 — a_2 \!\cdot\! b_3 \!\cdot\! c_4 \!\cdot\! d_1 + a_4 \!\cdot\! b_3 \!\cdot\! c_2 \!\cdot\! д_1 \\ &\! — а_3 \!\cdot\! b_4 \!\cdot\! c_2 \!\cdot\! d_1 + a_2 \!\cdot\! b_4 \!\cdot\! c_3 \!\cdot\! d_1 — a_4 \!\cdot\! b_2 \!\cdot\! c_3 \!\cdot\! д_1 \\ &\! + a_4 \!\cdot\! b_1 \!\cdot\! c_3 \!\cdot\! d_2 — a_1 \!\cdot\! b_4 \!\cdot\! c_3 \!\cdot\! d_2 + a_3 \!\cdot\! b_4 \!\cdot\! c_1 \!\cdot\! д_2 \\ &\! — а_4 \!\cdot\! b_3 \!\cdot\! c_1 \!\cdot\! d_2 + a_1 \!\cdot\! b_3 \!\cdot\! c_4 \!\cdot\! d_2 — a_3 \!\cdot\! b_1 \!\cdot\! c_4 \!\cdot\! д_2 \\ &\! + a_2 \!\cdot\! b_1 \!\cdot\! c_4 \!\cdot\! d_3 — a_1 \!\cdot\! b_2 \!\cdot\! c_4 \!\cdot\! d_3 + a_4 \!\cdot\! b_2 \!\cdot\! c_1 \!\cdot\! д_3\ &\! — а_2 \!\cdot\! b_4 \!\cdot\! c_1 \!\cdot\! d_3 + a_1 \!\cdot\! b_4 \!\cdot\! c_2 \!\cdot\! d_3 — a_4 \!\cdot\! b_1 \!\cdot\! c_2 \!\cdot\! д_3. \end{split}∣C∣=​a1​⋅b2​⋅c3​⋅d4​−a2​⋅b1​⋅c3​⋅d4​+a3​⋅b1​⋅c2​⋅d4​−a1​⋅b3 ​⋅c2​⋅d4​+a2​⋅b3​⋅c1​⋅d4​−a3​⋅b2​⋅c1​⋅d4​+a3​⋅b2​⋅c4​⋅d1​−a2​⋅b3​⋅ c4​⋅d1​+a4​⋅b3​⋅c2​⋅d1​−a3​⋅b4​⋅c2​⋅d1​+a2​⋅b4​⋅c3​⋅d1​−a4​⋅b2​⋅c3​ ⋅d1​+a4​⋅b1​⋅c3​⋅d2​−a1​⋅b4​⋅c3​⋅d2​+a3​⋅b4​⋅c1​⋅d2​−a4​⋅b3​⋅c1​⋅d2 ​+a1​⋅b3​⋅c4​⋅d2​−a3​⋅b1​⋅c4​⋅d2​+a2​⋅b1​⋅c4​⋅d3​−a1​⋅b2​⋅c4​⋅d3​+ a4​⋅b2​⋅c1​⋅d3​−a2​⋅b4​⋅c1​⋅d3​+a1​⋅b4​⋅c2​⋅d3​−a4​⋅b1​⋅c2​⋅d3​.​

Фу, это было длинно, не так ли? Теперь вы видите, что найти определитель матрицы 2×2 очень просто, и мы можем научиться находить определитель матрицы 3×3 примерно за час. Но определитель матрицы 4×4 — это совершенно новая проблема . Не поймите нас неправильно, это вполне выполнимо, но кто нам заплатит за то время, которое мы потратили на вычисления, а затем на поиски того, где мы взяли a1a_1a1​ вместо a2a_2a2​?

Итак, как здесь использовать диагональный трюк? Ответ прост: мы не . К сожалению, это не работает для матриц размером 4 или больше.

» Итак, как я могу эффективно вычислить определитель 4×4? Или 5×5? «Ну, как удобно с твоей стороны спросить! Мы покажем вам это в следующем разделе.

Свойства определителей

Теперь мы перечислим несколько важных свойств определителей , которые могут оказаться полезными. Начнем с простых и в самом конце выведем большие пушки.

1. Определитель произведения есть произведение определителей. Другими словами, если мы перемножаем две квадратные матрицы и хотим найти определитель результата, то мы можем получить ответ, вычислив определители факторов и перемножив их между собой.

2. Определитель матрицы равен определителю ее транспонирования. В сущности, если вместо матрицы, с которой мы начали, мы «перевернём» её так, чтобы её первая строка была первым столбцом, первый столбец был первой строкой и т. д. (это называется транспонированием матрицы ), то их определители будут одинаковыми. Например:

∣14−102−36115∣=∣1064211−1−35∣\begin{vmatrix} 1 и 4 и -1 \\ 0 и 2 и -3 \\ 6 и 11 и 5 \end{vmatrix} «=» \begin{vmatrix} 1 и 0 и 6 \\ 4 и 2 и 11 \\ -1 и -3 и 5 \end{vmatrix}∣

∣​106​4211​−1−35​∣

∣​=∣

∣​14−1​02−3​6115​∣

∣​ 900 07

3. Если если поменять местами две строки или два столбца, определитель останется тот же, но с обратным знаком. Это означает, что, например, если мы хотим узнать, как найти определитель матрицы 3×3, то мы можем поменять местами, скажем, ее первый столбец с третьим, чтобы получить то же число, но с другим знаком (см. пример ниже):

∣14−102−36115∣=− ⁣∣−141−3205116∣\begin{vmatrix} 1 и 4 и -1 \\ 0 и 2 и -3 \\ 6 и 11 и 5 \end{vmatrix} «=» \begin{vmatrix} -1 и 4 и 1 \\ -3 & 2 & 0 \\ 5 и 11 и 6 \end{vmatrix}∣

∣​106​4211​−1−35​∣

∣​=−∣

∣​−1−35​4211​106​∣

∣​

4. 9 0005 Мы можем добавить любое ненулевое кратное строки в какую-либо другую строку (или столбца в столбец) и не менять определитель . Это похоже на то, что мы делаем при исключении Гаусса, когда хотим найти эшелонированную форму строки системы уравнений, за исключением того, что там мы имели дело только со строками (которые соответствовали уравнениям). Наш калькулятор формы уменьшенного эшелона строк использует это свойство. Это значит, что если мы прибавим, скажем, два экземпляра первой строки ко второй, то получим матрицу с тем же определителем. Например:

∣14−102−36115∣=∣14−10+2⋅12+2⋅4−3+2⋅(−1)6115∣\footnotesize \begin{vmatrix} 1 &\! 4 &\! -1\ 0 &\! 2 &\! -3\ 6 &\! 11 &\! 5 \end{vmatrix} «=» \begin{vmatrix} 1 &\! 4 &\! -1\ 0\!+\!2\!\cdot\!1 &\! 2\!+\!2\!\cdot\!4 &\! -3\!+\!2\!\cdot\!(-\!1) \\ 6 &\! 11 &\! 5 \end{vmatrix}∣

∣​106​4211​−1−35​∣

∣​=∣

∣​10+2⋅16​42+2⋅411​−1−3+2⋅( −1)5​∣

∣​

что дает:

∣14−102−36115∣=∣14−1210−56115∣\begin{vmatrix} 1 и 4 и -1 \\ 0 и 2 и -3 \\ 6 и 11 и 5 \end{vmatrix} «=» \begin{vmatrix} 1 и 4 и -1 \\ 2&10&-5\ 6 и 11 и 5 \end{vmatrix}∣

∣​106​4211​−1−35​∣

∣​=∣

∣​126​41011​−1−55​∣

∣​ 90 007

5. ( Лаплас расширение ) Помните вопрос « Что такое определитель матрицы 5×5? » из предыдущего раздела? Наконец, мы можем коснуться этой темы и представить мощный инструмент , который поможет нам с формулой определителя. {3+3} \!\cdot\! 5 \!\cdot\! \begin{vmatrix} 1 и 4 \\ 0 и 2 \end{vmatrix} \конец{разделить} ∣

   ∣​106​4211​−1−35​∣

   ∣​=++​(−1)3+1⋅6⋅∣

   ∣​42​−1−3​∣

   ∣​( −1) 3+2 %11t∣

   ∣ 10 −1–3 ∣

   ∣ (−1) 3+3om5 ∣

   ∣ 10 42 ∣

   ∣​

   Должно быть, ушла целая вечность, чтобы прочитать всю эту теорию! Если вы хотите узнать больше, посетите наш специальный калькулятор расширения кофактора. И наконец посмотрим на примере .

   Пример: использование калькулятора определителя матрицы

   Скажите, что вы хотите вычислить определитель следующей матрицы :

   A=[2513417968327814]A = \begin{bmatrix} 2 и 5 и 1 и 3 \\ 4 и 1 и 7 и 9 \\ 6 и 8 и 3 и 2 \\ 7 и 8 и 1 и 4 \end{bmatrix}A=⎣

   ⎡​2467​5188​1731​3924​⎦

   ⎤​

   Определитель матрицы 4×4 , да? Формулу определителя единицы мы видели в разделе «Определитель матрицы 2×2, 3×3 и 4×4», так что мы знаем, что это будет не очень интересно , не так ли? Но с тех пор мы узнали некоторые свойства определителей, так почему бы нам не заставить их работать в нашу пользу ?

   Прежде чем мы это сделаем, давайте воспользуемся калькулятором определителя матрицы , чтобы посмотреть, как наш инструмент упрощает такие задачи. Прежде всего, мы имеем дело с матрицей 4×4, поэтому нам нужно сообщить об этом калькулятору , выбрав соответствующую опцию в разделе « Размер матрицы ».

   Это покажет нам пример такой матрицы с условное обозначение его элементов . Как мы видим, a1a_1a1​, b1b_1b1​, c1c_1c1​ и d1d_1d1​ обозначают числа в первой строке, поэтому давайте прокрутим туда, где мы вводим данные, и загрузим калькулятор определителя матрицы тем, что у нас есть в нашем упражнении:

   • a1=2a_1=2a1​=2, b1=5b_1=5b1​=5, c1=1c_1=1c1​=1, d1=3d_1=3d1​=3.

   Аналогично, для остальных строк имеем:

   • a2=4a_2=4a2​=4, b2=1b_2=1b2​=1, c2=7c_2=7c2​=7, d2=9d_2=9d2​=9 ;
   • a3=6a_3=6a3​=6, b3=8b_3=8b3​=8, c3=3c_3=3c3​=3, d3=2d_3=2d3​=2;
   • a4=7a_4=7a4​=7, b4=8b_4=8b4​=8, c4=1c_4=1c4​=1, d4=4d_4=4d4​=4.

   В тот момент, когда мы запишем последнее число, калькулятор определителя матрицы сделает свое волшебство и выдаст ответ :

   ∣A∣=630|A| = 630∣А∣=630.

   Хорошо, теперь, когда у нас есть этот спойлер ответа, давайте посмотрим, как мы можем получить этот ответ вручную . Очевидно, что один из способов — просто использовать формулу определителя с 24 членами, но мы хотели бы получить дополнительные баллы за творческий подход и использовать свойства определителей .

   Мы воспользуемся разложением Лапласа, но по-умному. Мы выбираем произвольную строку или столбец, скажем, первую строку матрицы, и пытаемся сделать расширение немного проще. Ведь если мы воспользуемся формулой сразу, то получим сумму четырех определителей 3×3. Не ужасно, но и не здорово. Однако мы можем кое-что сделать сначала — использовать элементарные операции со столбцами .

   В предыдущем разделе мы видели, что определитель останется прежним, если мы добавим любое ненулевое число, кратное столбцу, к другому столбцу. Так почему бы нам не добавить (−2)(-2)(−2) -кратное третьего столбца к первому ?

   ∣A∣=∣2 ⁣+ ⁣(−2) ⁣⋅ ⁣15134 ⁣+ ⁣(−2) ⁣⋅ ⁣71796 ⁣+ ⁣(−2) ⁣ ⋅ ⁣38327 ⁣+ ⁣(−2) ⁣⋅ ⁣1814∣|А| «=» \begin{vmatrix} 2\!+\!(-2)\!\cdot\!1 & 5 & 1 & 3 \\ 4\!+\!(-2)\!\cdot\!7 и 1 и 7 и 9 \\ 6\!+\!(-2)\!\cdot\!3 & 8 & 3 & 2 \\ 7\!+\!(-2)\!\cdot\!1 и 8 и 1 и 4 \end{vmatrix}∣A∣=∣

   ∣​2+(−2)⋅14+(−2)⋅76+(−2)⋅37+(−2)⋅1​5188​1731​3924​ ∣

   ∣​

   что дает:

   ∣A∣=∣0513−1017908325814∣|A| «=» \begin{vmatrix} 0 и 5 и 1 и 3 \\ -10&1&7&9\ 0 и 8 и 3 и 2 \\ 5 и 8 и 1 и 4 \end{vmatrix}∣A∣=∣

   ∣​0−1005​5188​1731​3924​∣

   ∣​

   И зачем мы это сделали? Вспомните, что в разложении Лапласа слагаемые были такими: (-1)(-1)(-1) в некоторой степени, умноженное на элемент выбранной строки или столбца, умноженный на меньший определитель. Следовательно, если мы теперь разложим ∣A∣|A|∣A∣ по первой строке, слагаемое, соответствующее первой ячейке в первой строке, будет (−1)(−1)(−1) в некоторой степени умножить на 000 умножить на какой-то определитель. И это ноль , потому что все, что умножается на ноль, равно нулю.

   Отлично, мы уменьшили количество слагаемых на единицу! Так как насчет того, чтобы повторить процедуру и получить еще меньше ? Для этого нам нужно, чтобы в первой строке было больше нулей, поэтому давайте превратим 555 и 333 в 000-е. Как и раньше, мы добавляем к этим столбцам правое кратное третьего столбца (тот, что со 111):

   ∣A∣=∣05+(−5)⋅113+(−3)⋅1−101 +(−5)⋅779+(−3)⋅708+(−5)⋅332+(−3)⋅358+(−5)⋅114+(−3)⋅1∣\footnotesize |А| «=» \begin{vmatrix} 0 и 5\!+\!(-5)\!\cdot\!1 & 1 & 3\!+\!(-3)\!\cdot\!1 \\ -10 и 1\!+\!(-5)\!\cdot\!7 и 7 и 9\!+\!(-3)\!\cdot\!7 \\ 0 и 8\!+\!(-5)\!\cdot\!3 & 3 & 2\!+\!(-3)\!\cdot\!3 \\ 5 и 8\!+\!(-5)\!\cdot\!1 & 1 & 4\!+\!(-3)\!\cdot\!1 \end{vmatrix}∣A∣=∣

   ∣​0−1005​5+(−5)⋅11+(−5)⋅78+(−5)⋅38+(−5)⋅1​1731​ 3+(−3)⋅19+(−3)⋅72+(−3)⋅34+(−3)⋅1​∣

   ∣​

   что дает:

   ∣A∣=∣0010−10 −347−120−73−75311∣|А| «=» \begin{vmatrix} 0 и 0 и 1 и 0 \\ -10&-34&7&-12\ 0 и -7 и 3 и -7 \\ 5 и 3 и 1 и 1 \end{vmatrix}∣A∣=∣ 9{1+3} \!\cdot\! 1 \!\cdot\! \begin{vmatrix} -10 &\! -34 &\! -12\ 0 &\! -7 &\! -7\\ 5 &\! 3 &\! 1 \end{vmatrix}∣A∣=(−1)1+3⋅1⋅∣

   ∣​−1005​−34−73​−12−71​∣

   ∣​

   И мы хорошо знаем, как найти определитель матрицы 3×3, не так ли? Но помните, что если вы хотите повеселиться , вы можете снова использовать разложение Лапласа, чтобы получить определитель матрицы 2×2.

   No related posts.