Простое ли число — онлайн калькулятор CALC.WS
Простое число — натуральное (целое положительное) число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Другими словами, число х является простым, если оно больше 1 и при этом делится без остатка только на 1 и на x. К примеру, 5 — простое число, а 6 не является простым числом, так как, помимо 1 и 6, оно также делится на 2 и на 3.
C помощью данного калькулятора, вы можете проверить, является ли число простым
Является ли число простым?
Оно имеет следующие делители:
Найти все простые числа до Разложить на простые множители
Предыдущее просто число:
Следующее простое число:
Свойство числа быть простым называется простотой. Простой, но медленный метод проверки простоты заданного числа n известен как перебор делителей.
Простой, но медленный метод проверки простоты заданного числа n известен как перебор делителей.
Основная теорема арифметики утверждает, что каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей. Таким образом, простые числа являются элементарными «строительными блоками» натуральных чисел.
Вопрос определения того, является ли натуральное число N простым, известен как проблема простоты.
Тестом простоты (или проверкой простоты) называется алгоритм, который, приняв на входе число N, позволяет либо не подтвердить предположение о составности числа, либо точно утверждать его простоту. Во втором случае он называется истинным тестом простоты. Таким образом, тест простоты представляет собой только гипотезу о том, что если алгоритм не подтвердил предположение о составности числа N, то это число может являться простым с определённой вероятностью.
Первые 500 простых чисел
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 |
| 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 |
| 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 |
| 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 | 1009 | 1013 | 1019 | 1021 | 1031 | 1033 | 1039 | 1049 | 1051 | 1061 | 1063 | 1069 |
| 1087 | 1091 | 1093 | 1097 | 1103 | 1109 | 1117 | 1123 | 1129 | 1151 | 1153 | 1163 | 1171 | 1181 | 1187 | 1193 | 1201 | 1213 | 1217 | 1223 |
| 1229 | 1231 | 1237 | 1249 | 1259 | 1277 | 1279 | 1283 | 1289 | 1291 | 1297 | 1301 | 1303 | 1307 | 1319 | 1321 | 1327 | 1361 | 1367 | 1373 |
| 1381 | 1399 | 1409 | 1423 | 1427 | 1429 | 1433 | 1439 | 1447 | 1451 | 1453 | 1459 | 1471 | 1481 | 1483 | 1487 | 1489 | 1493 | 1499 | 1511 |
| 1523 | 1531 | 1543 | 1549 | 1553 | 1559 | 1567 | 1571 | 1579 | 1583 | 1597 | 1601 | 1607 | 1609 | 1613 | 1619 | 1621 | 1627 | 1637 | 1657 |
| 1663 | 1667 | 1669 | 1693 | 1697 | 1699 | 1709 | 1721 | 1723 | 1733 | 1741 | 1747 | 1753 | 1759 | 1777 | 1783 | 1787 | 1789 | 1801 | 1811 |
| 1823 | 1831 | 1847 | 1861 | 1867 | 1871 | 1873 | 1877 | 1879 | 1889 | 1901 | 1907 | 1913 | 1931 | 1933 | 1949 | 1951 | 1973 | 1979 | 1987 |
| 1993 | 1997 | 1999 | 2003 | 2011 | 2017 | 2027 | 2029 | 2039 | 2053 | 2063 | 2069 | 2081 | 2083 | 2087 | 2089 | 2099 | 2111 | 2113 | 2129 |
| 2131 | 2137 | 2141 | 2143 | 2153 | 2161 | 2179 | 2203 | 2207 | 2213 | 2221 | 2237 | 2239 | 2243 | 2251 | 2267 | 2269 | 2273 | 2281 | 2287 |
| 2293 | 2297 | 2309 | 2311 | 2333 | 2339 | 2341 | 2347 | 2351 | 2357 | 2371 | 2377 | 2381 | 2383 | 2389 | 2393 | 2399 | 2411 | 2417 | 2423 |
| 2437 | 2441 | 2447 | 2459 | 2467 | 2473 | 2477 | 2503 | 2521 | 2531 | 2539 | 2543 | 2549 | 2551 | 2557 | 2579 | 2591 | 2593 | 2609 | 2617 |
| 2621 | 2633 | 2647 | 2657 | 2659 | 2663 | 2671 | 2677 | 2683 | 2687 | 2689 | 2693 | 2699 | 2707 | 2711 | 2713 | 2719 | 2729 | 2731 | 2741 |
| 2749 | 2753 | 2767 | 2777 | 2789 | 2791 | 2797 | 2801 | 2803 | 2819 | 2833 | 2837 | 2843 | 2851 | 2857 | 2861 | 2879 | 2887 | 2897 | 2903 |
| 2909 | 2917 | 2927 | 2939 | 2953 | 2957 | 2963 | 2969 | 2971 | 2999 | 3001 | 3011 | 3019 | 3023 | 3037 | 3041 | 3049 | 3061 | 3067 | 3079 |
| 3083 | 3089 | 3109 | 3119 | 3121 | 3137 | 3163 | 3167 | 3169 | 3181 | 3187 | 3191 | 3203 | 3209 | 3217 | 3221 | 3229 | 3251 | 3253 | 3257 |
| 3259 | 3271 | 3299 | 3301 | 3307 | 3313 | 3319 | 3323 | 3329 | 3331 | 3343 | 3347 | 3359 | 3361 | 3371 | 3373 | 3389 | 3391 | 3407 | 3413 |
| 3433 | 3449 | 3457 | 3461 | 3463 | 3467 | 3469 | 3491 | 3499 | 3511 | 3517 | 3527 | 3529 | 3533 | 3539 | 3541 | 3547 | 3557 | 3559 | 3571 |
Примеры
-
Задание: 2021 — простое число или нет
Решение: Число 2021 — составное, так как делится на 43 и 47
-
Задание: Являются ли простыми числа 998 999 1000:
Решение: Пользуемся онлайн расчетом, получаем, что 998 — составное (делится на 2 и 499), 999 — составное (делится на 3, 9, 27,37,111,333), а 1000 — тоже составное (очень много делителей).
 Ближайшее простое — 1009
Ближайшее простое — 1009 -
Решение: Число 1571 — простое, так как делится только на 1 и само себя
Проверка простых чисел | Защита информации
Общее
В данной статье вы увидите обзор известных алгоритмов проверки чисел на простоту. На сегодня не существует единого алгоритма для определения всех простых чисел. Все методы проверки делят на две группы: вероятностные проверки и детерминированные. Детерминированные методы определяют точно, является ли число простым. Вероятностные проверки определяют число на простоту с некой вероятностью ошибки. Многократное повторение для одного числа, но с разными переменными, разрешает сделать вероятность ошибки сколь угодно малой величины.
Быстрые тесты для малых чисел и вероятно простые числа
Малые простые числа
Пока не было нужды в генерации больших простых чисел, можно было реализовывать методы проверки без применения вычислительной техники. Первым из таких методов является полный перебор всех возможных делителей. Есть модификация, которая не хуже всего перебора, называется — пробное деление. Он заключается в делении на предыдущие простые числа либо равные корню из этого числа. Для такого метода можно использовать решето Эратосфена.
Первым из таких методов является полный перебор всех возможных делителей. Есть модификация, которая не хуже всего перебора, называется — пробное деление. Он заключается в делении на предыдущие простые числа либо равные корню из этого числа. Для такого метода можно использовать решето Эратосфена.
Малая теорема Ферма
Французский математик Пьер Ферма в 17 веке выдал закономерность, которая лежит в основе почти всех методов проверки на простоту.
Малая теорема Ферма — Если P простое и A — любое целое, то AP = A (mod P). Если P не делит А, то АP-1 = 1 (mod P). На основе такой теоремы, можно создать мощный алгоритм на простоту:
- Тест Ферма: Для n > 1 выбираем a > и вычисляем An-1 mod n, если результат не 1, то n составное число, если 1, то n — слабо возможно простое по основанию a (a-PRP)
Часть чисел проходящие Тест Ферма являются составными, и их называют псевдопростыми.
Тест Рабина-Миллера
Можно улучшить тест Ферма, заметив, что если n — простое нечетное, то для 1 есть только два квадратных корня по модулю n: 1 и -1. По этому квадратный корень из An-1, A(n-1)/2 равен минус или плюс еденице. Если (n-1)/2 опять нечетно, то можно снова извлечь корень и тд. Первый вариант алгоритма определяет только одно деление:
- Тест Леманна: Если для любого целого числа А меньшего n не выполняется условие A(n-1)/2 = ± 1 (mod n), то число n — составное. Если это условие выполнено, то число n — возможно простое с вероятностью ошибки не больше 50%.
- Тест Рабина-Миллера: Запишем (n-1) в виде 2sd, где d нечетно, а s — неотрицательно: n называют сильно возможно простым по основанию A (A-SPRP), если реализуется одно из двух условий:
- Ad = 1 (mod n)
- (Ad)2r = -1 (mod n), для любого неотрицательного r < s
В 1980 году была доказана вероятность ошибки теста Рабина-Миллера не превышающая 1/4. Реализуя этот тест T раз для разных оснований, мы получим вероятность ошибки 2-2t
Реализуя этот тест T раз для разных оснований, мы получим вероятность ошибки 2-2t
Объединение тестов
Классические тесты
Проверки чисел вида n + 1
Тест заключается в том, что мы должны знать частичное или полное разложение на множители числа n — 1. Разложение на множители n — 1 просто найти, если n имеет определенный вид.
- Тест Лукаса: N ≥ 3. Если для каждого простого q, делящего n — 1 есть целое А такое что:
- An-1 = 1 (mod n) и
- A(n-1)/q ≠ 1 (mod n), то n — простое
Для такой проверки нужно знать полное разложение n — 1 на простые множители. Более мощная версия определяет знание не полного, а частичного разложения n — 1 на простые множители. Такой вариант алгоритма был выдан Поклингтоном в 1914 году.
- Тест Поклингтона: N ≥ 3 и n = FR + 1 (F делит n-1), причем F > R, НОД (F,R) = 1 и известно разложение F на простые множители. Тогда, если для любого простого q, делящего F есть такое целое A > 1, что:
- An-1 = 1 (mod n) и
- НОД (A(n-1)/q — 1, n) = 1
- Теорема Пепина: пусть Fn это n-е число Ферма и n > 1, тогда Fn — простое тогда и только тогда, когда 3(Fn — 1)/2 = 1 (mod Fn
- Теорема Прота: Пусть n = h × 2k + 1, причем 2k > h.
 Если есть такое целое A, что A(n-1)/2 = -1 (mod n), то n — простое
Если есть такое целое A, что A(n-1)/2 = -1 (mod n), то n — простое
На основе теоремы Прота было найдено пятое по величине из известных простых чисел — 28433 × 27830457
Проверки чисел вида n — 1
Здесь рассмотрим числа только определенного вида. 7 из первых 10 позиций по самым большим известным простым числам были найдены с помощью чисел Мерсенна. Числа Мерсенна называют числа вида 2s -1.
Лукасом и Лемером в 1930 году было создано следующее утверждение: пусть s — простое, тогда число Мерсенна n = 2s — 1 является простым тогда, когда S (n — 2) = 0, где S(0) = 4 и S(k+1) = S(k)2 — 2 (mod n). На основе такого факта можно создать проверку на простоту, которая точно скажет нам, является ли для заданного s число Мерсенна простым.
- Тест Лукаса-Лемера:
- С помощью пробного деления проверяем, является ли данное s простым, если нет, то получившееся число Мерсенна — составное
- Задаем S(0) = 4
- Для k от 1 до s — 2 вычисляем S(k) = S(k-1)2 — 2 (mod n)
- Если в результате получился 0, то число Мерсенна простое
Неоклассические алгоритмы ARP и ARP-CL
Можно рассматривать числа в виде n2 + n + 1 или n2 — n + 1. А можно рассмотреть число вида nm — 1 для больших m. Тогда любое просто число q такое, что q — 1 делит m, по малой теореме Ферма будет делить nm — 1.
А можно рассмотреть число вида nm — 1 для больших m. Тогда любое просто число q такое, что q — 1 делит m, по малой теореме Ферма будет делить nm — 1.
Было представлено, что всегда существует целое число m:
- m < (log n)log log log n
Эллиптические кривые: ECPP
Современные вариант проверок на простоту основан на теореме Поклингтона, но для эллиптических кривых. Смысл алгоритма заключается в переходе от групп порядка n — 1 и n + 1 к достаточно большему диапазону размеров групп.
AKS
В 2002 году летом индийские математики Аграавал, Саксен и Кайал нашли полиномиальный детерминированный алгоритм проверки числа на простоту. Их метод основан на версии малой теоремы Ферма:
- Теорема: Пусть A и P взаимно простые целые числа и P > 1. Число P является простым, когда (x — a)p = (xp — a) (mod p)
- Доказательство: Если p — простое, то p делит биномиальные коэффициенты pCr для r = 1,2 .
 .p-1. Пусть p — составное, и пусть q — простой делитель p. Пусть qk максимальная степень q которая делит p. Тогда qk не делит pCr и взаимно просто с Ap-q. Отсюда, коэффициент перед xq в левой части требуемого равенства не равен нулю, а в правой равен. Алгоритм для числа n ≥ 23 (странное число получается из одного из требований для корректной работы алгоритма)
.p-1. Пусть p — составное, и пусть q — простой делитель p. Пусть qk максимальная степень q которая делит p. Тогда qk не делит pCr и взаимно просто с Ap-q. Отсюда, коэффициент перед xq в левой части требуемого равенства не равен нулю, а в правой равен. Алгоритм для числа n ≥ 23 (странное число получается из одного из требований для корректной работы алгоритма)
if (n is has the form ab with b > 1) then output COMPOSITE
r := 2
while (r < n) {
if (gcd(n,r) is not 1) then output COMPOSITE
if (r is prime greater than 2) then {
let q be the largest factor of r-1
if (q > 4sqrt(r)log n) and (n(r-1)/q is not 1 (mod r)) then
break
}
r := r+1
}
for a = 1 to 2sqrt(r)log n {
if ( (x-a)n is not (xn-a) (mod xr-1,n) ) then output COMPOSITE
}
output PRIME;
Итоги
| Тест | Тип теста | Где используется |
|---|---|---|
| Пробное деление | детерминированный | Из-за большой вычислительной сложности в чистом виде не используется. Пробное деление на маленькие простые числа реализуется во многих тестах как один из шагов Пробное деление на маленькие простые числа реализуется во многих тестах как один из шагов |
| Ферма | вероятностный | В чистом виде не реализуется. Может быть одним из первых шагов на проверку простоты для очень больших чисел |
| Леманна | верляьнлсьный | Не используется |
| Рабина-Миллера | вероятностный | В чистом виде может реализовываться в криптосистемах с открытым ключом для реализации простых ключей длиной 512, 1024 и 2048 бит. |
| Миллера | детерминированный | На практике не используется, так как пока не доказана расширенная гипотеза Римана |
| Лукаса | детерминированный | Для получения больших простых чисел определенного вида |
| Поклингтона | детерминированный | Для получения больших чисел с частично известной факторизацией n — 1 |
| Петина | детерминированный | Для получения больших простых чисел Ферма |
| Прота | детерминированный | Для получения больших простых чисел определенного вида |
| Лукаса-Лемера | детерминированный | Для получения больших простых чисел Мерсенна |
| APR | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| ECPP | детерминированный | В качестве детерминированной быстрой проверки на простоту |
| AKS | детерминированный | В качестве детерминированной полиномиальной проверки на простоту |
Из таблицы видно, что разные методы проверки на простоту служат для двух целей:
- для получения очень больших целый чисел
- для генерации простых чисел определенного размера для реализации в криптографии
Аналитическую работу провел студент (ГУ МФТИ) кафедры радиотехники Кучин Борис.
Оценка статьи:
Загрузка…
Поделиться с друзьями:
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 9 из 39Следующая ⇒ Проверку числа на простоту оформим в виде функции, которая будет возвращать True для простых чисел и False для составных. Наивный алгоритм заключается в том, что будем перебирать числа, начиная с 2, пока не не найдем делитель числа n. Если этот делитель будет равен n, то число будет простым, иначе у n есть нетривиальный делитель и число n будет составным. Запишем алгоритм в виде функции IsPrime (по-английски простое число — prime number, составное число — composite number). def IsPrime(n): d = 2 while n % d != 0: d += 1 return d == n В данной записи алгоритма реализована идея линейного поиска с барьерным элементом. Мы хотим найти наименьший делитель числа n. Для этого берем число d и пока n не делится на d переходим к следующему возможному делителю. Сложность этого алгоритма — O(n). Однако данный алгоритм можно оптимизировать, если заметить, что у любого составного числа есть собственный (то есть не равный 1) делитель, не превосходящий квадратного корня из числа. Это позволит сократить сложность алгоритма до O(n√): def IsPrime(n): d = 2 while d * d <= n and n % d != 0: d += 1 return d * d > n Соответственно, такой алгоритм заканчивает работу либо при нахождении делителя, либо если проверяемый делитель станет больше корня из n. Чиcло n является простым, если алгоритм закончился по причине того, что проверяемый делитель стал больше, чем корень из n. ПЕРЕБОР ТОЛЬКО НЕЧЕТНЫХ ДЕЛИТЕЛЕЙ Сделаем ещё одну оптимизацию — будем перебирать только нечетные делители, если число не делится на два. def isPrime(n): d = 3 while d * d <= n and n % d != 0: d += 2 return d * d > n ПРОГРАММА: (0 — признак конца ввода) sum_int = 0 counter = 0 x = int(input()) while x != 0: sum_int += x counter += 1 x = int(input()) print(sum_int / counter) ОДНОПРОХОДНАЯ ПРОГРАММА: summa = 0 summa_2 = 0 kolichestvo = 0 x = int(input()) while x != 0: summa += x summa_2 += x*x kolichestvo += 1 x = int(input()) srednee = summa/kolichestvo srednee_2 = summa_2/kolichestvo otklonenie = (srednee_2 — srednee**2)**0. Цикл for в Python Цикл for, также называемый циклом с параметром, в языке Питон богат возможностями. В цикле forуказывается переменная и множество значений, по которому будет пробегать переменная. Множество значений может быть задано списком, кортежем, строкой или диапазоном. Вот простейший пример использования цикла, где в качестве множества значений используется кортеж: i = 1 В этом примере переменная color последовательно принимает значения ‘red’, ‘orange’ и т.д. В теле цикла выводится сообщение, которое содержит название цвета, то есть значение переменной color, а также номер итерации цикла – число, которое сначала равно 1, а потом увеличивается на один (инструкцией i += 1 с каждым проходом цикла). В списке значений могут быть выражения различных типов, например: for i in 1, 2, 3, ‘one’, ‘two’, ‘three’: При первых трех итерациях цикла переменная i будет принимать значение типа int, при последующих трех — типа str. ФУНКЦИЯ RANGE Как правило, циклы for используются либо для повторения какой-либо последовательности действий заданное число раз, либо для изменения значения переменной в цикле от некоторого начального значения до некоторого конечного. Для повторения цикла некоторое заданное число раз n можно использовать цикл for вместе с функциейrange: for i in range(n): В качестве n может использоваться числовая константа, переменная или произвольное арифметическое выражение (например, 2 ** 10). Если значение n равно нулю или отрицательное, то тело цикла не выполнится ни разу. Если задать цикл таким образом: for i in range(a, b): то индексная переменная i будеть принимать значения от a до b – 1, то есть первый параметр функции range, вызываемой с двумя параметрами, задает начальное значение индексной переменной, а второй параметр — значение, которая индексная переменная принимать не будет. sum = 0 В этом примере переменная i принимает значения 1, 2, …, n, и значение переменной sum последовательно увеличивается на указанные значения. Наконец, чтобы организовать цикл, в котором индексная переменная будет уменьшаться, необходимо использовать функцию range с тремя параметрами. Первый параметр задает начальное значение индексной переменной, второй параметр — значение, до которого будет изменяться индексная переменная (не включая его!), а третий параметр — величину изменения индексной переменной. Например, сделать цикл по всем нечетным числам от 1 до 99 можно при помощи функции range(1, 100, 2), а сделать цикл по всем числам от 100 до 1 можно при помощи range(100, 0, -1). Более формально, цикл for i in range(a, b, d) при d > 0 задает значения индексной переменной i = a, i = a + d, i = a + 2 * d и так для всех значений, для которых i < b. Фильтрация потока чисел Пусть на вход программы подаются числа, подлежащие обработке, причем из них нужно использовать только те, которые удовлетворяют некоторому условию. Например, если требуется просуммировать только четные числа, это можно сделать так (0 — признак конца ввода): sum_even = 0 x = int(input()) while x != 0: if x % 2 == 0: sum_even += x x = int(input()) print(sum_even) Или же, если требуется найти произведение только отрицательных чисел: product = 1 x = int(input()) while x != 0: if x < 0: product *= x x = int(input()) print(product) Может потребоваться подсчитать количество определенных (например, четных) чисел: counter = 0 x = int(input()) while x != 0: if x % 2 == 0: counter += 1 x = int(input()) print(counter) Например, это может понадобиться для того, чтобы найти среднее арифметическое только четных чисел: sum_even = 0 counter = 0 x = int(input()) while x != 0: if x % 2 == 0: sum_even += x counter += 1 x = int(input()) print(sum_even / counter) ⇐ Предыдущая45678910111213Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 2312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Проверить, является ли число простым
Скоро Эти математические инструменты уже в пути
Функции построения графиков
Рисовать графики математических функций.
Рисование формулы LaTeX
Создание изображения из выражения LaTeX.
Найти n-ю цифру
Вычислить n-ю цифру числа Эйлера.
Найти n-ю цифру золотого сечения
Вычислить n-ю цифру золотого сечения.
Найти n-ю цифру числа пи
Вычислить n-ю цифру числа пи.
Вычислить сумму e цифр
Найти сумму e цифр.
Вычислить сумму цифр золотого сечения
Найти сумму цифр золотого сечения.
Вычислить сумму пи цифр
Найти сумму пи цифр.
Генерировать цифры Чамперноуна
Генерировать цифры константы Чамперноуна.
Найти n-ю цифру Чамперноуна
Вычислить n-ю цифру константы Чамперноуна.
Декодирование последовательности «посмотри и скажи»
Выполните обратную операцию над последовательностью «посмотри и скажи».
Генерация P-адических расширений
Вычисление p-адических расширений произвольных чисел.
Создать последовательность панцифровых чисел
Создать список панцифровых чисел.
Создать последовательность номеров Стэнли
Создать список номеров Стэнли.
Создать последовательность номеров звонков
Создать список номеров звонков.
Генерация последовательности номеров Кармайкла
Создание списка номеров Чармичел.
Создать последовательность каталонских номеров
Создайте список каталонских номеров.
Создать последовательность треугольных чисел
Создать список треугольных чисел.
Создать последовательность составных чисел
Создать список составных чисел.
Создать последовательность секущих чисел
Создать список секущих чисел.
Создать последовательность чисел Голомба
Создать список чисел Голомба-Сильвермана.
Создать последовательность чисел Эйлера Тотиент
Создать список фи-чисел Эйлера.
Создать последовательность номеров жонглеров
Создать список номеров жонглеров.
Создать последовательность счастливых номеров
Создать список счастливых номеров.
Создать последовательность номеров Моцкина
Создать список номеров Моцкина.
Создать последовательность номеров Padovan
Создать список номеров Padovan.
Создать последовательность псевдосовершенных чисел
Создать список полусовершенных чисел.
Создать последовательность чисел Улама
Создать список номеров Улама.
Создать последовательность странных чисел
Создать список странных чисел.
Создать последовательность суперсовершенных чисел
Создать список суперсовершенных чисел.
Продолжить числовую последовательность
Найти закономерность в числовой последовательности и расширить ее.
Разбить число
Найти все разбиения данного целого числа.
Создать последовательность номеров разделов
Создать список номеров функций разделов.
Создать арифметическую прогрессию
Создать арифметическую последовательность чисел.
Создание геометрической прогрессии
Создание геометрической последовательности чисел.
Создание полиномиальной прогрессии
Создание полиномиальной последовательности чисел.
Создать последовательность натуральных чисел
Создать список натуральных чисел.
Создание степеней двойки
Создание списка чисел степеней двойки.
Создание сил десяти
Создать список чисел степени десятки.
Создание плотной матрицы
Создание матрицы с очень небольшим количеством нулевых элементов.
Создать разреженную матрицу
Создать матрицу с очень небольшим количеством ненулевых элементов.
Умножение матрицы на скаляр
Умножение всех элементов матрицы на число.
Проверить, является ли матрица единственной.
Определить, является ли матрица вырожденной.
Найти матрицу кофакторов
Для заданной матрицы найти ее матрицу кофакторов.
Найдите вспомогательную матрицу
По заданной матрице найдите ее дополнение.
LU Factor a Matrix
Разложить матрицу на LU-факторы.
Найти собственные значения матрицы
Найти собственные значения матрицы.
Украсьте матрицу
Украсьте матрицу, аккуратно выровняв все ее столбцы.
Переформатировать матрицу
Преобразовать матрицу из одного формата в другой формат.
Рисование архимедовой спирали
Создание архимедовой спирали.
Рисование спирали Эйлера
Создание кривой спирали Корню (полиномиальной спирали).
Рисование спирали Фибоначчи
Создание кривой спирали Фибоначчи.
Рисование спирали Теодора
Создание спирали квадратного корня.
Нарисуйте спираль Ферма
Создайте кривую в виде параболической спирали.
Рисование прямоугольников Фибоначчи
Создание рисунка прямоугольников Фибоначчи.
Нарисуйте головку семени Фибоначчи
Создайте головку цветка Фибоначчи.
Нарисовать фрактал Падована
Создать фрактал равнобуквенных треугольников Падована.
Нарисуйте аполлонову прокладку
Создайте фрактал аполлоновой прокладки.
Нарисовать фрактал Мандельброта
Создать фрактал Мандельброта.
Нарисовать фрактал Юлии
Создать фрактал Джулии.
Нарисовать фрактал Рози
Создать фрактал Рози.
Нарисовать кривую фрактала Бланманже
Создать фрактал Бланманже.
Рисование функции Вейерштрасса
Создание фрактала Вейерштрасса.
Нарисовать кривую Минковского в виде вопросительного знака
Создать фрактал Минковского в виде вопросительного знака.
Нарисуйте функцию Тома
Создайте функцию Тома (также известную как функция попкорна или капли дождя).
Нарисовать функцию Дирихле
Нарисовать функцию Дирихле.
Нарисуйте рог Гавриила
Нарисуйте геометрическую фигуру с бесконечной площадью поверхности и конечным объемом.
Преобразование слов в числа
Преобразование чисел из английского текста в реальные цифры.
Преобразование чисел в слова
Преобразование чисел в письменный текст на английском языке.
Преобразование десятичной записи в экспоненциальную запись
Преобразование чисел, записанных в десятичной форме, в экспоненциальную форму.
Преобразование научной записи в десятичную.
Преобразование чисел, записанных в научной форме, в десятичную форму.
Округление чисел вверх
Применение операции ceil к числам.
Округление чисел в меньшую сторону
Применить к числам операцию нижнего предела.
Анализ чисел
Подсчитайте, сколько раз встречается каждое число.
Преобразование числа в виде суммы
Создайте сумму, которая в сумме равна заданному числу.
Создать таблицу умножения
Нарисовать таблицу умножения n×m.
Нарисовать круговую диаграмму
Нарисовать круговую диаграмму и показать относительные размеры данных.
Визуализация процентов
Нарисуйте диаграмму, показывающую проценты.
Подбросьте монетку
Подбросьте монетку и выпадет орел или решка.
Бросьте кубик
Бросьте кубик и получите число на его стороне.
Тест на простоту номера — онлайн-инструменты для работы с номерами
Скоро Эти числовые инструменты уже в пути
Создание номеров Numberwang
Создание списка номеров Numberwang.
Переписать числа
Учитывая числа и грамматику, рекурсивно переписать их.
Создать число с плавающей запятой 9б форма.
Преобразование научной записи в число
Преобразование числа в научной записи в обычное число.
Создать символьную нумерацию
Создать список буквенных чисел (a, b, c, …, z, aa, ab, …).
Создать римскую нумерацию
Создать список римских цифр (i, ii, iii, iv, v…).
Создать нумерацию Брайля
Создать список цифр Брайля (⠂, ⠆, ⠒, ⠲, ⠢, …).
Генерация случайных двоичных чисел
Создать список случайных двоичных чисел.
Создание случайных восьмеричных чисел
Создание списка случайных восьмеричных чисел.
Создание случайных десятичных чисел
Создание списка случайных десятичных чисел.
Создание случайных шестнадцатеричных чисел
Создание списка случайных шестнадцатеричных чисел.
Вычислить текущую сумму
Вычислить кумулятивную сумму списка чисел.
Вычисление текущего произведения
Вычисление кумулятивного произведения списка чисел.
Вычислить факториал
Найти факториал числа.
Создание числовых анаграмм
Создание одной или нескольких числовых анаграмм.
Создание числовых биграмм
Создание списка цифровых биграмм из числа.
Создание числовых триграмм
Создание списка цифровых триграмм из числа.
Генерация числовых N-грамм
Создание списка цифровых nграмм из числа.
Создание полиномиальной последовательности
Создать список чисел полиномиальной прогрессии.
Создание префиксов SI
Создание списка префиксов метрик.
Анализ числа
Сообщить, сколько цифр встречается сколько раз.
Преобразование числа в порядковое
Преобразование количественного числительного в порядковое.
Преобразование порядкового числа в число
Преобразование порядкового числа в количественное.
Преобразование числа в римское число
Преобразование арабских цифр в римские.
Преобразование римских чисел в обычные числа
Преобразование римских цифр в арабские.
Создание чисел Негафибоначчи
Вычисление серии расширенных чисел Фибоначчи.
Генерация простых чисел Фибоначчи
Поиск чисел, которые являются одновременно числами Фибоначчи и простыми числами.
Проверка числа Фибоначчи
Проверка, является ли число числом Фибоначчи.
Проверка простых чисел Фибоначчи
Проверяет, является ли число одновременно числом Фибоначчи и простым числом.
Построить слова Фибоначчи
Создать последовательность слов Фибоначчи.
Создать слова Трибоначчи
Создать последовательность слов Трибоначчи.
Генерировать числа Негалука
Вычислить серию расширенных чисел Лукаса.
Генерировать простые числа Лукаса
Вычислить серию расширенных чисел Лукаса.
Lucas Prime Test
Проверить, является ли число одновременно числом Лукаса и простым числом.
Вычисление следа матрицы
Найдите сумму элементов главной диагонали матрицы.
Вычислить собственные значения матрицы
Найти собственные значения матрицы.
Умножение матриц
Вычисление произведения двух матриц.
Добавить матрицы
Вычислить сумму двух матриц.
Вычитание матриц
Вычисление разности двух матриц.
Генерация чисел Мозера де Брюйна
Вычисление последовательности чисел Мозера-Брейна.
Сгенерировать числа Колакоски
Вычислить последовательность чисел Ольденбургера-Колакоски.
Сгенерировать числа Стэнли
Вычислить последовательность чисел Стэнли.
Генерировать числа Гийсвейта
Вычислить последовательность самоописывающих чисел Гийсвейта.
Сгенерировать числа Рудина-Шапиро
Вычислить последовательность чисел Русина-Шапиро.
Генерация чисел Баума-Свита
Вычисление последовательности чисел Баума-Свита.
Генерация последовательности Туэ-Морса
Вычисление членов ряда чисел Туэ-Морса.
Создание идеальных чисел
Создание списка совершенных чисел.
Создание почти идеальных чисел
Создание списка почти идеальных чисел.
Создать последовательность избыточных чисел
Вычислить последовательность избыточных чисел.
Создать последовательность неполных чисел
Вычислить последовательность неполных чисел.
Расчет чисел кривой дракона
Создать список порядковых номеров для складывания бумаги.
Создание составных чисел
Создание списка чисел, которые не являются простыми.
Нарисовать таблицу чисел
Создать таблицу чисел.
Проверить, является ли число совершенным
Проверить, является ли заданное число совершенным числом.
Проверить, является ли число обильным
Проверить, является ли данное число обильным числом.
Проверить, является ли число недостаточным
Проверить, является ли данное число недостаточным.
Вычислить модуль
Найти модуль числа.
Группировка цифр числа
Группировка цифр числа.
Разделить число на цифры
Создать список цифр из числа.
Printf Numbers
Применение функций sprintf или printf к числам.
Создайте номера Zalgo
Позвольте Zalgo уничтожить ваши номера.
Повторить номер
Повторить номер несколько раз.
Зеркальное число
Создать зеркальную копию номера.
Дополнение числа нулями
Добавление нулей к числу.
Обратный порядок цифр
Обратный порядок цифр в числе.
Поворот числа
Циклический поворот цифр числа влево или вправо.
Увеличить число
Добавить единицу к заданному числу.
Увеличить все цифры в числе
Добавить единицу к каждой цифре в числе.
Уменьшить число
Вычесть единицу из заданного числа.
Уменьшить все цифры в числе
Вычесть единицу из каждой цифры в числе.
Находить закономерности в числах
Находить закономерности в последовательностях чисел.
Подсчет числа вхождений
Узнайте, как часто встречаются числовые значения.
Вычисление процентов
Найти x% числа.
Создание больших чисел
Создание списка больших чисел.
Генерация малых чисел
Создать список маленьких чисел.
Создание натуральных чисел
Создание списка натуральных чисел.
Создание рациональных чисел
Создание списка рациональных чисел.
Создать последовательность констант
Создать серию чисел, в которой все термины одинаковы.
Создание действительных чисел
Создание последовательности действительных чисел.
Создание комплексных чисел
Создание списка комплексных чисел.
Создать двоичные числа
Создать последовательность двоичных чисел.
Создание пар чисел
Создание последовательности пар чисел.
Создание троек чисел
Создание последовательности троек чисел.
Создание кортежей чисел
Создание последовательности n-кортежей чисел.
Переплетение чисел
Переплетение двух или более чисел поразрядно.
Найти десятичное представление числа
Переписать число в десятичной форме.
Преобразование дроби в десятичную
Преобразование дроби в десятичное число.
Преобразование десятичного числа в дробь
Преобразование десятичного числа в дробь.
Преобразование двоичного числа в восьмеричное
Преобразование числа с основанием два в число с основанием восемь.
Преобразование двоичного числа в десятичное число
Преобразование числа с основанием два в число с основанием десять.
Преобразование двоичного числа в шестнадцатеричное
Преобразование числа с основанием два в число с основанием шестнадцать.
Преобразование восьмеричного числа в двоичное
Преобразование числа с основанием восемь в число с основанием два.
Преобразование восьмеричного числа в десятичное
Преобразование числа с основанием восемь в число с основанием десять.
Преобразование восьмеричного числа в шестнадцатеричное
Преобразование числа с основанием восемь в число с основанием шестнадцать.
Преобразование десятичного числа в двоичное
Преобразование числа с основанием десять в число с основанием два.
Преобразование десятичного числа в восьмеричное число
Преобразование десятичного числа в восьмеричное.
Преобразование десятичного числа в шестнадцатеричное
Преобразование числа с основанием десять в число с основанием шестнадцать.
Преобразование шестнадцатеричного числа в двоичное число
Преобразование числа с основанием шестнадцать в число с основанием два.
Преобразование шестнадцатеричного числа в восьмеричное
Преобразование числа с основанием шестнадцать в число с основанием восемь.
Преобразование шестнадцатеричного числа в десятичное число
Преобразование числа с основанием шестнадцать в число с основанием десять.
Преобразование любого числа в любое основание
Преобразование любого числа в любом основании в любое другое основание.
Изменение мантиссы числа
Изменение значения числа.
Изменить показатель степени числа
Изменить степень числа.
Замена цифр буквами
Замена цифр в числе буквами алфавита.
Создание спирали чисел
Создание спирали из цифр числа.
Удалить десятичную точку
Удалить десятичный разделитель из десятичного числа.
Проверка числа Numberwang
Проверка, является ли данный номер числом numberwang.
Проверка простых чисел
Опубликовано Кэтрин Митчелл
Зачем использовать онлайн-проверку простых чисел?
Вас заинтриговал вопрос: «Это простое число ?» Вам трудно идентифицировать большие простые числа? Не беспокойтесь больше! онлайн Проверка простых чисел — это все, что вам нужно! Это экономит ваше время и дает вам самые надежные ответы. С помощью программы проверки простых чисел идентифицировать простые числа несложно.
Программа проверки простых чисел упрощает выполнение задач
Онлайн-проверка простых чисел используется для определения того, является ли натуральное число простым или составным. Простое число — это такое натуральное число, которое делится только на единицу и на само число. Они используются в различных местах и имеют жизненно важное значение. Определение простого числа размером до 23 456 789это трудно. Однако большая программа для проверки простых чисел может сделать это в мгновение ока! Итак, используйте эту легкую проверку простых чисел сегодня и получите 100 в своем тесте на простые числа! Преподаватели, студенты и любой желающий могут получить доступ к удобной онлайн-проверке простых чисел!
Простое число — это такое натуральное число, которое делится только на единицу и на само число. Они используются в различных местах и имеют жизненно важное значение. Определение простого числа размером до 23 456 789это трудно. Однако большая программа для проверки простых чисел может сделать это в мгновение ока! Итак, используйте эту легкую проверку простых чисел сегодня и получите 100 в своем тесте на простые числа! Преподаватели, студенты и любой желающий могут получить доступ к удобной онлайн-проверке простых чисел!
Проверьте свой номер
Инструкции по использованию онлайн-проверки простых чисел
Онлайн-проверка простых чисел выполняет все расчеты за экраном и предоставляет вам надежный результат в течение нескольких секунд.
Все, что вам нужно сделать, это ввести номер в поле. Нажмите кнопку «Рассчитать» и получите результат! Результаты онлайн-проверки простых чисел на Convert For Free абсолютно безошибочны. Посетите сайт сегодня!
Посетите сайт сегодня!
История проверки простых чисел:
Самые ранние сохранившиеся записи манифестного изучения простых чисел восходят к древнегреческой математике. Математический папирус Райнда также работал и изучал эту тему. Это наглядно свидетельствует о том, что даже древние люди стремились найти простые числа и использовали различные собственные методы. Этого факта достаточно, чтобы доказать важность простых чисел, и, следовательно, проверка простых чисел !
Методы онлайн-проверки простых чисел
Методы, используемые онлайн-проверкой простых чисел для вычисления простоты определенного числа, включают:
- Пробное деление:.
- Эвристический тест:
- Теоретико-числовые методы:
Пример работы программы проверки простых чисел:
Например, подумайте о числе. Давайте выберем 337. Это 9?0779 простое число ? Мы узнаем очень скоро.
Это 9?0779 простое число ? Мы узнаем очень скоро.
Шаг 1: 19 ¿ квадратный корень (337). Простые числа меньше 19 — это 2, 3, 5, 7, 11, 13, 17.
Шаг 2: 337 не делится ни на одно из них.
Применение проверки простых чисел:
- Многие современные компьютерные криптографии работают с использованием простых множителей больших чисел.
- Простые числа имеют огромное значение для теоретиков чисел. Они являются краеугольным камнем целых чисел. Они важны для мира, потому что их уникальные математические свойства делают их лучшими для нашего текущего использования.
Следовательно, средство проверки простых чисел упрощает задачу, определяя простые числа за считанные секунды!
Конвертировать бесплатно — лучшая программа для проверки простых чисел:Посетите: http://www.convertforfree.com/prime-number-checker/
Это откроет дверь в совершенно новый упрощенный мир математики. Наша большая программа проверки простых чисел позволяет вам проверять числа до
Наша большая программа проверки простых чисел позволяет вам проверять числа до
Опубликовано Кэтрин Митчелл
Проверка простых чисел Простые числа — краеугольный камень проверки простых чисел. Простое число — это такое натуральное число, которое делится только на два числа, равные единице, и на само число. А простое число никогда не является произведением двух маленьких натуральных чисел. Простые числа всегда больше 1.Преимущества программы проверки простых чисел
Обычно математика считается сложным предметом. Старшеклассникам становится трудно выучить формулы или даже выучить простые числа наизусть. Можете ли вы определить, является ли это простым числом: 23 456 789? Считаете ли вы математику тревожной и отнимающей много времени? Не беспокойтесь больше! С Prime Number Checker в качестве вашего компаньона упростил задачу. Вы можете легко воспользоваться помощью онлайн простого числа, чтобы перепроверить тест на простое число! Вот некоторые другие преимущества проверки простых чисел
Старшеклассникам становится трудно выучить формулы или даже выучить простые числа наизусть. Можете ли вы определить, является ли это простым числом: 23 456 789? Считаете ли вы математику тревожной и отнимающей много времени? Не беспокойтесь больше! С Prime Number Checker в качестве вашего компаньона упростил задачу. Вы можете легко воспользоваться помощью онлайн простого числа, чтобы перепроверить тест на простое число! Вот некоторые другие преимущества проверки простых чисел
1) Это экономит время. Вы получаете результат всего за несколько кликов!
2) Надежно! Хотите, чтобы ваши ответы проверил эксперт? Проверка простых чисел — ваш лучший помощник!
3) Это большая программа для проверки простых чисел. 12 345 678,987 654 321 — простое число.
Нам бы, конечно, потребовалось много времени, чтобы идентифицировать его самостоятельно. Но с проверкой Prime Number это проще простого!
Это причина, по которой так много доверяют онлайн-проверке номеров. Будь то студенты, учителя или кто угодно; эта простая в использовании программа проверки приходит на помощь каждому. Посетите веб-сайт сегодня, чтобы получить доступ к бесплатной онлайн-проверке простых чисел !
Будь то студенты, учителя или кто угодно; эта простая в использовании программа проверки приходит на помощь каждому. Посетите веб-сайт сегодня, чтобы получить доступ к бесплатной онлайн-проверке простых чисел !
Пошаговое руководство по онлайн-проверке простых чисел
Онлайн-проверка простых чисел — это ответ на все ваши вопросы « — это простое число »! Следуйте этим простым шагам, чтобы получить надежные результаты простой в использовании программы проверки простых чисел .
3) Получите результаты теста на простые числа в мгновение ока!
4) Вы можете нажать на вкладку сброса. Это позволит вам проверить больше простых чисел!
Факты о простых числах, которые нам сообщает программа проверки простых чисел!
Простые числа исследовались давно. Они были даже примечательной темой в 19 веке! Из Проверки простых чисел мы узнаем
1) 1 — исключительный случай. Это строительный блок составных и простых чисел
Это строительный блок составных и простых чисел
2) Число 2 является единственным четным числом, которое считается простым числом!
3) Число 2 — наименьшее простое число 9.0003
4) Ноль не считается простым числом /
Упростите свои сложные математические и информационные задачи уже сегодня! Веб-сайт Convert For Free является центром конверсии. Он предлагает простой в использовании помех. Кроме того, он позволяет вам получить доступ к проверке простых чисел с любого устройства! Вам не нужно ничего скачивать, чтобы получить доступ к этому сайту. Кроме того, 9Результаты калькулятора 0779 тщательно проверены и изучены. Это делает результаты безошибочными! Convert For Free — это надежный и бесплатный веб-сайт! Итак, посетите сайт сегодня и используйте идеальную программу проверки простых чисел !
Попробуйте бесплатно : http://www.convertforfree.com/prime-number-checker/
Tagged бесплатная проверка простых чисел, Бесплатные инструменты, большая проверка простых чисел, наибольшее простое число, онлайн проверка простых чисел, Проверка простых чисел, проверка простых чисел онлайн, проверка простых чисел, проверка простых чиселОставить комментарийОпубликовано Кэтрин Митчелл
Проверка простых чиселПРОСТЫЕ ЧИСЛА И ПРОВЕРКА ПРОСТЫХ ЧИСЕЛ
Конвертировать бесплатно Проверка простых чисел – это онлайн-решение для простых чисел. Простые числа — это натуральные числа, имеющие только два делителя: 1 и само себя. Это положительные целые числа, имеющие только два делителя. Числа, имеющие более двух делителей, называются составными числами. Простые числа занимают центральное место в теории чисел.
Греки не считали 1 за простое число , поэтому его первозданность подвергалась сомнению. Следовательно, он стал строительной единицей всех простых и составных чисел. Число 2 также является единственным исключением для четного числа. Это потому, что это наименьшее простое число, а также единственное четное простое число. Первые 10 простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29.
КАК ПРОВЕРКА ПРОСТЫХ ЧИСЕЛ ПОМОГАЕТ ПОЛЬЗОВАТЕЛЯМ
Простые числа сложнее вычислить, так как цифры в цифре увеличивать. Чтобы упростить проверку простых чисел. Конвертировать бесплатно предоставляет пользователям онлайн-калькулятор . Этот калькулятор помогает пользователям определить, является ли большое число простым или нет. Трех- или четырехзначные числа бывает трудно вычислить, и велика вероятность ошибок. Это идеальное решение для упрощения математики в мире технологий. Программное обеспечение помогает пользователям выполнять сложные вычисления простых чисел.
Чтобы упростить проверку простых чисел. Конвертировать бесплатно предоставляет пользователям онлайн-калькулятор . Этот калькулятор помогает пользователям определить, является ли большое число простым или нет. Трех- или четырехзначные числа бывает трудно вычислить, и велика вероятность ошибок. Это идеальное решение для упрощения математики в мире технологий. Программное обеспечение помогает пользователям выполнять сложные вычисления простых чисел.
Большой калькулятор простых чисел делает ненавистную большинству тему немного более терпимой. Это помогает избежать рисков и сократить скорость расчета до секунды. Конвертировать бесплатно онлайн Проверка простых чисел — простое решение. Преподаватели, студенты и все остальные пользователи доверяют конвертировать бесплатно.
ЭТО ПРОСТОЕ ЧИСЛО? КАК ПРОВЕРИТЬ С ПОМОЩЬЮ ПРОВЕРКИ ПРОСТЫХ ЧИСЕЛ
Сложные и большие числа трудно проверить на простоту. Ошибки весьма вероятны, а проверка, в общем-то, длительный и утомительный процесс. Чтобы избежать всех этих проблем, этот калькулятор простых чисел здесь, чтобы помочь. Это простое решение для учителей, студентов и всех, у кого есть Интернет. Это делает большие числа одним щелчком мыши. Онлайн 9Калькулятор простого числа 0779 ответит на все ваши вопросы о том, является ли это простым числом. Единственным ограничением для этого большого калькулятора является максимум
Ошибки весьма вероятны, а проверка, в общем-то, длительный и утомительный процесс. Чтобы избежать всех этих проблем, этот калькулятор простых чисел здесь, чтобы помочь. Это простое решение для учителей, студентов и всех, у кого есть Интернет. Это делает большие числа одним щелчком мыши. Онлайн 9Калькулятор простого числа 0779 ответит на все ваши вопросы о том, является ли это простым числом. Единственным ограничением для этого большого калькулятора является максимум
Чтобы легко проверить комплексные числа, войдите на сайт www.convertforfree.com. Перейти к проверке простых чисел. Это очень удобный и простой в обращении. Просто введите свой номер в соответствующее поле и нажмите «Рассчитать». Онлайн-калькулятор мгновенно сгенерирует ваши результаты. Для дополнительных расчетов нажмите кнопку сброса, чтобы очистить все поля.
Для дополнительных расчетов нажмите кнопку сброса, чтобы очистить все поля.
ПОЧЕМУ КОНВЕРТИРОВАТЬ БЕСПЛАТНО: ПРОВЕРКА ПРОСТЫХ ЧИСЕЛ — ЛУЧШИЙ
Конвертировать бесплатно онлайн калькулятор простых чисел является одним из наиболее часто используемых среди других. Он известен своей безошибочной природой, в то время как другие программы проверки могут давать неверные результаты. Он удобен и прост в использовании. Инструменту доверяют пользователи по всему миру независимо от возраста и профессии. Преобразование бесплатно всегда был известен своими быстрыми, простыми и бесплатными онлайн-калькуляторами. Этот большой 9Калькулятор простого числа 0779 является одной из причин доверия.
Простой и удобный калькулятор. Он был проверен на точность несколько раз и не разочаровал. Это самое большое преимущество, помимо точных результатов, — это бесплатность. Когда может потребоваться покупка других шашек, онлайн или иным образом. Преобразование бесплатно предоставляет бесплатное решение. Он доступен для всех и любых пользователей во всем мире онлайн с доступом в Интернет. Это не ограничивается только студентами или учителями. Вы можете быть учеником, учителем или родителем, объясняя это своему ребенку. Преобразование по свободной воле оказывает помощь независимо от того, кто. Большой плюс 9Программа проверки простых чисел 0779 заключается в том, что она абсолютно бесплатна.
Преобразование бесплатно предоставляет бесплатное решение. Он доступен для всех и любых пользователей во всем мире онлайн с доступом в Интернет. Это не ограничивается только студентами или учителями. Вы можете быть учеником, учителем или родителем, объясняя это своему ребенку. Преобразование по свободной воле оказывает помощь независимо от того, кто. Большой плюс 9Программа проверки простых чисел 0779 заключается в том, что она абсолютно бесплатна.
Чтобы упростить расчеты, получите результат в один клик на Convert бесплатно!
Этот пост изначально появился по адресу http://www.convertforfree.com/prime-number-checker/
Tagged бесплатная проверка простых чисел, Бесплатные инструменты, большая проверка простых чисел, наибольшее простое число, онлайн проверка простых чисел, Проверка простых чисел, проверка простых чисел онлайн, проверка простых чисел, проверка простых чиселОставить комментарийОпубликовано Кэтрин Митчелл
Программа проверки простых чисел КАК ЭТА ПРОВЕРКА ПРОСТЫХ ЧИСЕЛ ПОМОГАЕТ ПОЛЬЗОВАТЕЛЯМ?
Насколько можно вспомнить, математика всегда была сложным предметом для многих. Длинные вычисления, числа , разные типы чисел. Все они могут быть очень запутанными и разочаровывающими. Будучи человеком, человек никогда не был безошибочен, особенно при вычислениях. Математика — это предмет, который много раз демонстрирует именно эту слабость. Чтобы решить эту проблему, Конвертировать бесплатно решил сделать решение. Он вступил в игру с онлайн-проверкой простых чисел. Это простое решение для всех, чтобы сделать расчеты немного проще.
Простые числа — это целые положительные числа, имеющие только два делителя. Они могут быть только произведением и делиться только на 1 и на самих себя. Каждое число, имеющее только два делителя, считается простым числом. Однако цифра один не является ни простым, ни составным числом. Он считается строительным блоком обоих типов чисел. Простые числа — знакомое понятие, которому учат в школе. Однако расчеты «является ли это простым числом» могут усложняться по мере роста цифр. Трех- или четырехзначные числа трудно проверить на простоту. Вот где эта большая 9Появляется программа проверки простых чисел 0779 . Она помогает пользователям запускать тесты простоты одним щелчком мыши.
Он считается строительным блоком обоих типов чисел. Простые числа — знакомое понятие, которому учат в школе. Однако расчеты «является ли это простым числом» могут усложняться по мере роста цифр. Трех- или четырехзначные числа трудно проверить на простоту. Вот где эта большая 9Появляется программа проверки простых чисел 0779 . Она помогает пользователям запускать тесты простоты одним щелчком мыши.
Проверьте свой номер
КАК ПОЛЬЗОВАТЬСЯ ОНЛАЙН-ПРОВЕРКОЙ ПРОСТЫХ ЧИСЕЛ
Выполнение тестов простого числа удобно с помощью онлайн-инструмента. Это поможет вам проверить простоту больших чисел за считанные секунды. Его легко и быстро использовать, даже если вы никогда раньше не пользовались таким инструментом.
- Чтобы выполнить проверку простых чисел с помощью большой программы проверки простых чисел:
○ Введите свой номер в указанное поле.
○ Нажмите «Рассчитать», чтобы программа сгенерировала результаты за считанные секунды.
○ Чтобы пересчитать с другим числом, нажмите «Сброс», чтобы очистить все поля.
ЧТО ДЕЛАЕТ ЭТУ ПРОВЕРКУ ПРОСТЫХ ЧИСЕЛ ЛУЧШИМИ
Есть много причин, по которым convert for free известен тем, что предоставляет своим пользователям лучшие услуги. Имея в виду этот особый блок проверки больших чисел , конечным преимуществом является то, что инструмент является бесплатным. Он доступен для всех и любых пользователей без каких-либо хлопот с платежами. Вам также не нужно загружать какие-либо приложения для расчета. Он доступен для любого онлайн с подключением к Интернету, независимо от того, кто. Калькулятор проверен на точность несколько раз. 9Программа проверки простых чисел 0779 отказывается разочаровывать. Он известен точными расчетами и никогда не разочаровывал. Это заслуживающее доверия имя для учителей, студентов и даже родителей, обучающих своих детей. Он выполняет большие вычисления всего одним щелчком мыши. Единственным ограничением для этой большой программы проверки простых чисел является максимум
99254740992. Она также существует только из-за программных ограничений . Это простое, быстрое и простое в использовании решение. Это помогает избежать ошибок и вычисляет комплексные числа за считанные секунды. Это облегчает работу родителей, учителей и учеников. Чтобы упростить ваши тесты на простоту. Получите расчет с конвертировать бесплатно проверка простых чисел сейчас! CONVERT FOR FREE — ЛУЧШАЯ ПРОВЕРКА ПРОСТЫХ ЧИСЕЛ
Она также существует только из-за программных ограничений . Это простое, быстрое и простое в использовании решение. Это помогает избежать ошибок и вычисляет комплексные числа за считанные секунды. Это облегчает работу родителей, учителей и учеников. Чтобы упростить ваши тесты на простоту. Получите расчет с конвертировать бесплатно проверка простых чисел сейчас! CONVERT FOR FREE — ЛУЧШАЯ ПРОВЕРКА ПРОСТЫХ ЧИСЕЛ
Convert For Free предоставляет наиболее легкодоступные онлайн-калькуляторы . Удобная в использовании программа для проверки простых чисел упрощает выполнение сложных задач. Вам даже не нужно ничего скачивать или устанавливать. Посетите веб-сайт сегодня для лучших расчетов!
Попробуйте прямо сейчас : http://www.convertforfree.com/prime-number-checker/
Метки: бесплатная проверка простых чисел, бесплатные инструменты, большая проверка простых чисел, наибольшее простое число, онлайн проверка простых чисел, проверка простых чисел, проверка простых чисел онлайн, проверка простых чисел, проверка простых чиселОставить комментарийОпубликовано

 Ближайшее простое — 1009
Ближайшее простое — 1009 Если есть такое целое A, что A(n-1)/2 = -1 (mod n), то n — простое
Если есть такое целое A, что A(n-1)/2 = -1 (mod n), то n — простое .p-1. Пусть p — составное, и пусть q — простой делитель p. Пусть qk максимальная степень q которая делит p. Тогда qk не делит pCr и взаимно просто с Ap-q. Отсюда, коэффициент перед xq в левой части требуемого равенства не равен нулю, а в правой равен. Алгоритм для числа n ≥ 23 (странное число получается из одного из требований для корректной работы алгоритма)
.p-1. Пусть p — составное, и пусть q — простой делитель p. Пусть qk максимальная степень q которая делит p. Тогда qk не делит pCr и взаимно просто с Ap-q. Отсюда, коэффициент перед xq в левой части требуемого равенства не равен нулю, а в правой равен. Алгоритм для числа n ≥ 23 (странное число получается из одного из требований для корректной работы алгоритма) Все правила по сольфеджио
Все правила по сольфеджио
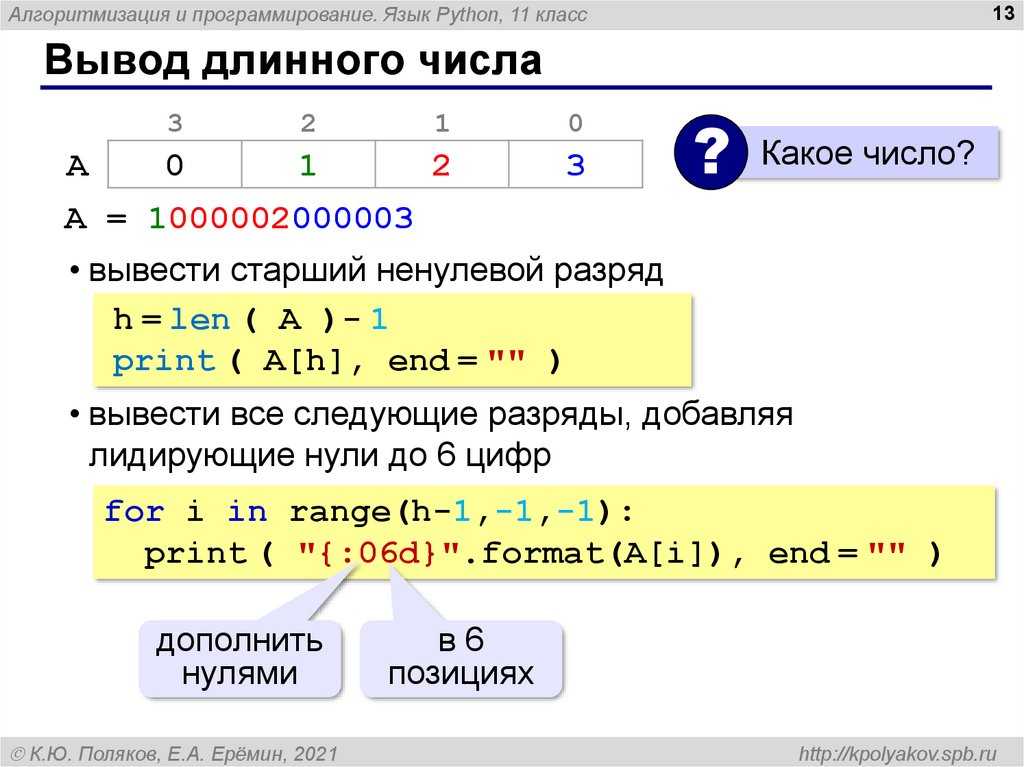 Алгоритм остановится на числе, которое будет делителем числа n. Если алгоритм остановился на числе n, то число n простое, иначе — составное.
Алгоритм остановится на числе, которое будет делителем числа n. Если алгоритм остановился на числе n, то число n простое, иначе — составное. 5 print(‘Среднее значение:’, srednee, ‘+-‘, otklonenie)
5 print(‘Среднее значение:’, srednee, ‘+-‘, otklonenie)
 Если же a≥b, то цикл не будет выполнен ни разу. Например, для того, чтобы просуммировать значения чисел от 1 до n можно воспользоваться следующей программой:
Если же a≥b, то цикл не будет выполнен ни разу. Например, для того, чтобы просуммировать значения чисел от 1 до n можно воспользоваться следующей программой: Если же d < 0, то переменная цикла принимает все значения i > b.
Если же d < 0, то переменная цикла принимает все значения i > b. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.008 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.008 с.)