Сенсация! Прямой угол равен тупому!
Анна Малкова (автор книги для подготовки к ЕГЭ, ведущая годового Онлайн-курса подготовки к ЕГЭ на 100 баллов, руководитель компании «ЕГЭ-студия» (Курсы ЕГЭ)).
Все мы знаем, что такое прямой угол и тупой угол, но не все знают, что они равны друг другу. И сейчас я вам это докажу. В моем доказательстве не будет ошибок. И оно будет полностью соответствовать чертежу.
Проведем отрезок АВ. Отложим прямой угол САВ. Проверим вместе – он действительно прямой. Построим тупой угол АВД. И тоже проверим. Он больше прямого, значит – он тупой. И сделаем отрезки АС и ВД одинаковой длины. Проверяем. Оба они по 20 см.
Соединяем точки С и Д. Если вам показалось, что СД параллельно АВ, то, конечно, это не так, потому что если мы их продлим, то увидим, что они вовсе не параллельны, а пересекаются. Они и не могут быть параллельными, потому что угол А – прямой, а угол В – тупой.
Теперь находим середины АВ и СД и строим серединные перпендикуляры к отрезкам АВ и СД.
Запишем, что АС = ВД. Н – серединный перпендикуляр к АВ, м – серединный перпендикуляр к СД. И пусть м пересекает н в точке О.
Если вам кажется, что серединные перпендикуляры м и н не должны пересекаться, то это значит, что они параллельны, и значит АВ параллельно СД, но мы знаем, что это не так.
Давайте проверим, что мы провели перпендикуляры именно в серединах и именно под прямым углом. Проверили, все правильно.
Теперь соединяем точку О с вершинами четырехугольника АВДС.
Построение окончено. Дальше – доказательство.
Мы сказали, что АС = ВД, и даже проверили это.
Теперь скажем, что отрезки АО и ОВ тоже равны. Давайте на них посмотрим.
АО = ОВ, т. к. треугольник АОВ – равнобедренный.
Действительно, вот серединный перпендикуляр, обозначим его ОН, а выше поставим точку М.
ОН – высота и медиана треугольника АОВ. А если в треугольнике высота является медианой, то этот треугольник равнобедренный.
Аналогично мы скажем, что треугольник СОД тоже равнобедренный. СО = ОД, т. к. треугольник СОД – равнобедренный. И в нем ОМ – высота и медиана, по построению.
Мы получили, что АС = ВД, АО = ОВ, ОС = ОД.
Отсюда следует, что треугольники АОС и ВОД – равны по трем сторонам. Это один из признаков равенства треугольников.
Если эти треугольники равны, тогда большие углы этих треугольников, лежащие напротив больших сторон, тоже равны. Угол ОАС = углу ОВД.
Конечно, в равных треугольниках равные углы, лежащие напротив соответственных сторон.
А из чего же складывается угол ОАС? Из угла ОАВ и угла ВАС. ОАС=ОАВ+ВАС.
Из чего складывается угол ОВД? Из угла ОВА и угла АВД. ОВД=ОВА+АВД.
Но мы сказали, что треугольник АОВ – равнобедренный. И ОА=ОВ, значит углы при основании тоже равны. Угол ОАВ = углу ОВА.
Тогда мы получаем, что угол ОАВ + угол ВАС = угол ОВА + угол АВД. Угол ОАВ = углу ОВА, значит угол ВАС = углу АВД. Посмотрим это на чертеже. Прямой угол равен тупому углу, что и требовалось доказать. Парадоксально, правда?
Парадоксально, правда?
Сколько новых теорем можно будет вывести на основе этого полезного факта. Можно построить совсем другую геометрию, которая отличается от той, что нас учили в школе. Но как же тогда школьные учебники? Пишите в комментариях! Подписывайтесь на мой канал!
Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Сенсация! Прямой угол равен тупому!» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.01.2023
Немножко тупой угол: rimmavologdina — LiveJournal
?- catIsShown({ humanName: ‘наука’ })» data-human-name=»наука»> Наука
- Cancel
рассмотрим вот такой прямоугольник ABCD:
EF- серединный перпендикуляр. Я, уж извините, на глазок рисую, так что не придирайтесь, плиз.
Теперь давайте отложим тупой угол (подчеркиваю, слегка тупой угол) КDC,причем, |KD| = |DA| по построению.
KD — отрезок. Он ступеньками получился из-за моего кривого владения Paint. Короче говоря, в пианиста просьба не стрелять.
Дальше, соединим точки К и В и построим серединный перпендикуляр RL к отрезку КВ. L — точка пересечения прямой EF и серединного перпендикуляра к КВ.
А теперь, дамы и господа, ловкость рук и никакого мошенничества, рассмотрим треугольники KDL и LBC.
Как легко видеть — треугольники KDL и LBC конгруэнтны по трём сторонам, т.е., проще говоря, равны. ( |KD| = |CB| по постороению, |DL| = |CL|, поскольку FL — срединный перпендикуляр к отрезку DC, а |KL| = |BL|, т.к. RL — серединный перпендикуляр к КВ). Тогда угол KDL равен углу LCB. А т.к. углы LDF и LCF равны ( треугольник DCL равнобедренный), то из этого следует, что прямой угол FCB равен тупому углу KDF.
Ну и какая после этого математика точная наука? Математика получилась лишь немножко точной наукой:) Ну что, найдутся рыцари у дамы Математики, вступятся за честь?:)
Комментарии изначально скрываю. И открываю только комментарии, не содержащие корректного опровержения. Уже все открыла.
Tags: задачко
Subscribe
Дела дачные
Кто-нибудь догадайтесь, пожалуйста, что это за сосуд. Или, может, кто знает: Мне муж загадал, а я не знаю) Подсказка: емкость резиновая.
 …
…(no subject)
На мат. кружке для шестиклассников в 57-ой школе дали вот такую задачку: «Хулиган Вася живет в 20-этажном доме. После того, как Вася однажды…
Задачка
И пункта А в пункт Б едет машина со скоростью 60 км в час. Расстояние между пунктами 60 км. Во сколько раз надо увеличить скорость, чтобы на каждом…
Photo
Hint http://pics.livejournal.com/igrick/pic/000r1edq
Дела дачные
Кто-нибудь догадайтесь, пожалуйста, что это за сосуд. Или, может, кто знает: Мне муж загадал, а я не знаю) Подсказка: емкость резиновая.…
(no subject)
На мат. кружке для шестиклассников в 57-ой школе дали вот такую задачку: «Хулиган Вася живет в 20-этажном доме. После того, как Вася однажды…
Задачка
И пункта А в пункт Б едет машина со скоростью 60 км в час. Расстояние между пунктами 60 км. Во сколько раз надо увеличить скорость, чтобы на каждом…
Прямоугольные, тупоугольные и остроугольные треугольники – Математические истории для вас
Счастливый мистер Пауэр означал сложный урок
Мистер Джон Пауэр снова выглядел очень счастливым. Многие студенты начали думать, что у него, должно быть, что-то в рукаве. Последний класс пришел с таким же счастливым лицом, он попросил класс определить значение числа пи с помощью тригонометрии. Все недоумевали, что он придумал на этот раз.
Многие студенты начали думать, что у него, должно быть, что-то в рукаве. Последний класс пришел с таким же счастливым лицом, он попросил класс определить значение числа пи с помощью тригонометрии. Все недоумевали, что он придумал на этот раз.
Мистер Пауэр: Сегодня мы будем изучать прямоугольный, тупоугольный и остроугольный треугольники. Тинку, что такое прямоугольный треугольник?
Тинку позабавился тем, насколько простым был этот вопрос, и выпалил: Прямой угол — это треугольник, в котором один из углов — прямой угол, равный 90°.
Мистер Пауэр: Кто мне скажет, что такое тупоугольные и остроугольные треугольники?
Несколько студентов подняли руки, но мистер Пауэр спросил Трейси.
Трейси: В тупоугольном треугольнике один из углов больше 90°, а в остроугольном все три угла меньше 90°.
Классификация треугольников по косинусам
Мистер Пауэр: Сара, пожалуйста, напишите тригонометрические функции трех типов треугольников.
Сара подошла к доске и составила таблицу для наибольшего угла (ВАС) в каждом типе треугольника (см. рисунок).
рисунок).
| Тупой | Прямой угол | Острый | |
| Грех БАК | >0, но <1 | 1 | >0, но <1 |
| Кос БАК | <0 (отрицательный) | 0 | >0, но <1 |
| Желто-коричневый BAC | <0 (отрицательный) | ∞ | >0, но < ∞ |
Мистер Пауэр: Хорошая работа, Сара. Теперь, если вам нужно определить три типа треугольников на основе тригонометрических отношений, какую функцию вы выберете?
Сара: Потому что это просто: минус для тупого угла, 0 для прямого угла и плюс для остроугольного треугольника.
Многие студенты были поражены тем, как можно использовать тригонометрию для определения трех типов треугольников.
Алгебраическая классификация
Мистер Пауэр еще не закончил. Он спросил, помнит ли кто-нибудь теорему Пифагора, которую они выучили в геометрии. Многие студенты подняли руки, и он призвал студентку по имени Трейси описать теорему.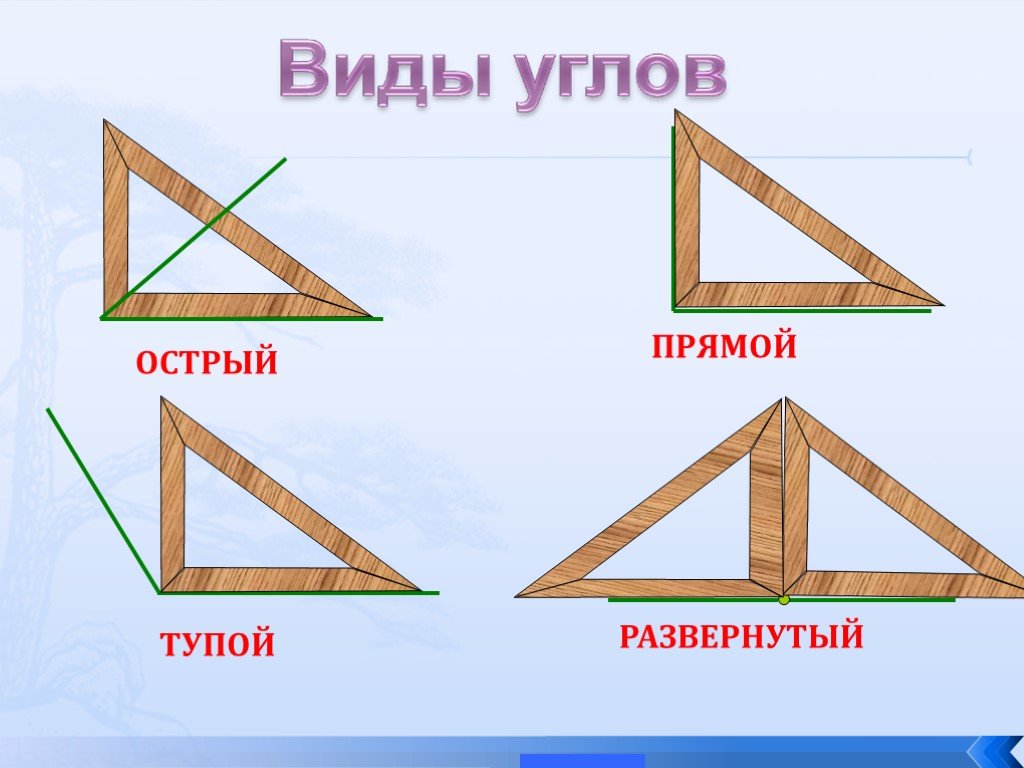
Мистер Пауэр: Если длина гипотенузы равна c, а длины других сторон равны a и b, вы бы сказали, что тогда c 2 = а 2 + б 2 ?
Трейси: Да, мистер Пауэр.
Работает ли c 2 = a 2 + b 2 для тупоугольных треугольников
Мистер Сила: Хорошо класс. Я хочу, чтобы вы сели в группы по три человека и решили, применимо ли это соотношение к треугольникам с тупыми углами, у которых длина наибольшей стороны равна c, а две другие стороны равны a и b. Я дам вам подсказку. В треугольниках ABC на доске проведите вертикальную линию от угла C к основанию AB.
Примерно через 10 минут группа Томми сообщила, что они выяснили, что для тупоугольного треугольника c 2 > a 2 + b 2 . Он подошел к доске и написал это.
Для тупоугольного треугольника ABC длина стороны BC, противоположной тупому углу, равна c, основание AB равно a, а сторона AC равна b.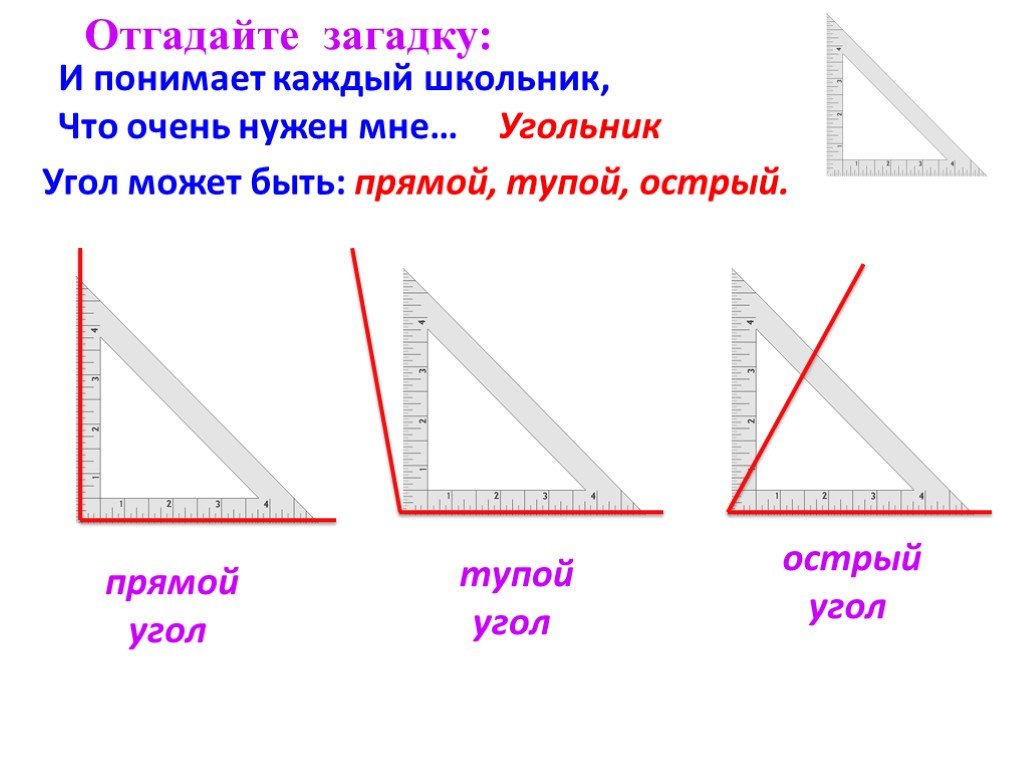
Тогда из большого прямоугольного треугольника DCB, h 2 = с 2 – (а+х) 2 .
Из треугольника DAC, h 2 = b 2 – x 2 .
Следовательно, c 2 – (a+x) 2 = b 2 -x 2 .
Прибавив (a+x) 2 к обеим частям уравнения, мы получим c 2 = (a+x) 2 + b 2 -x 2 , что равно
c 2 90 = а 2 +2ax +x 2 + b 2 -x 2 или с 2 = а 2 + b 2 +2ах.
Поскольку a, b, c и x положительны c 2 > a 2 + b 2 .
Мистер Пауэр вместе с большинством студентов принял доказательство и был впечатлен.
Описание типов треугольников с помощью алгебраических уравнений
Мистер Пауэр: Молодцы, Томми и ваши партнеры Сара и Джонни показали, что в тупоугольном треугольнике c 2 > a2 + b 2 .
Помните, Трейси сказала, что для прямоугольного треугольника c 2 = a2 + b 2 . Я собираюсь добавить, что для остроугольного треугольника с наибольшей стороной, имеющей длину c, c 2 < a2 + b 2 , и ваша домашняя работа — доказать это.
Для тупоугольного, прямоугольного и остроугольного треугольников косинус угла, противоположного большей стороне, будет отрицательным, равным 0 и положительным соответственно. Я собираюсь добавить, что мы могли бы написать, что c
| Тупой | Прямой угол | Острый | |
| Кос БАК | <0 (отрицательный) | 0 | >0, но <1 |
| Значение наибольшей стороны c | с 2 > а2 + b 2 | с 2 = а2 + б 2 | с 2 < а2 + b 2 |
Задача
Докажите, что для остроугольного треугольника со сторонами длины a, b и c и наибольшей стороной c, c 2 < a2 + b 2 .
Решение:
Дано: остроугольный треугольник ABC, сторона BC — наибольшая сторона длины c, длина стороны AB = a и AC = b.
Проведите вертикальную линию BD, которая пересекает основание в точке D. Пусть длина BD равна h, а BD равна x, тогда AD длины = a-x.
Из правого угольного треугольника BCD, C 2 = H 2 + x 2
Из правого треугольника ACD, B 2 = H 2 + (A-X) 2 = H 2 + (A-X) 2 = H 2 + (A-X) 2 = H 2 + (A-X) 2 . or h 2 = b 2 – (a-x) 2
Therefore c 2 = b 2 – (a-x) 2 + x 2 or c 2 = b 2 + x 2 – a 2 – x 2 +2ax
x 2 или C 2 = B 2 — A 2 +2AX или C 2 = B 2 +A 2 — 2A 2 +2AX или
C 2 2 2 +2AX или
C 2 2 2 +2AX или
C 2 2 2 +2AX OR b 2 + a 2 – 2a (a – x)
Поскольку a больше x, a–x положительны, и, следовательно,
c 2 < (a 2 + b 2 9008).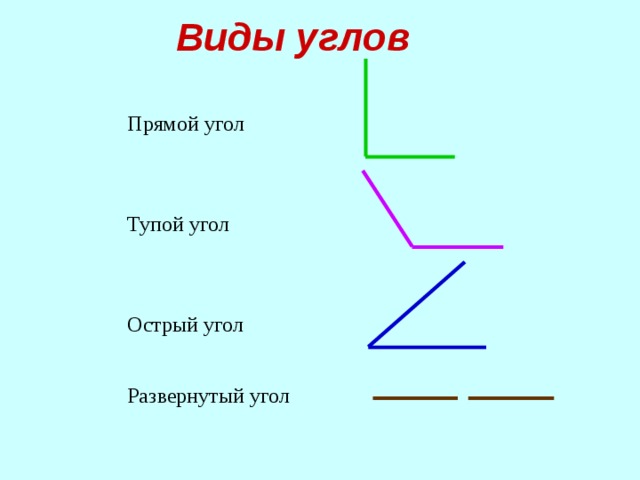
Нравится:
Нравится Загрузка…
Что такое углы? Острые, тупые, прямые углы и многое другое
Здесь вы можете узнать о различных углах, когда их изучают в начальной и средней школе, и о том, как вы можете помочь детям понять их в процессе изучения математики дома.
Учащиеся неформально начинают изучение углов в начальных классах с определения форм. Хотя на этом этапе не ожидается, что они будут использовать названия углов, это закладывает основу, например, для словаря прямых углов.
Учащиеся полностью изучат углы в начальной школе, где им нужно будет точно нарисовать их с помощью транспортира и идентифицировать их с виду.
Что такое угол?
Угол — это пространство между двумя пересекающимися прямыми, где они соединяются в одной точке. Величина угла измеряется в градусах.
В зависимости от числового диапазона «пространства» между наборами пересекающихся прямых, углы можно разделить на различные типы углов: острые, тупые или прямые.
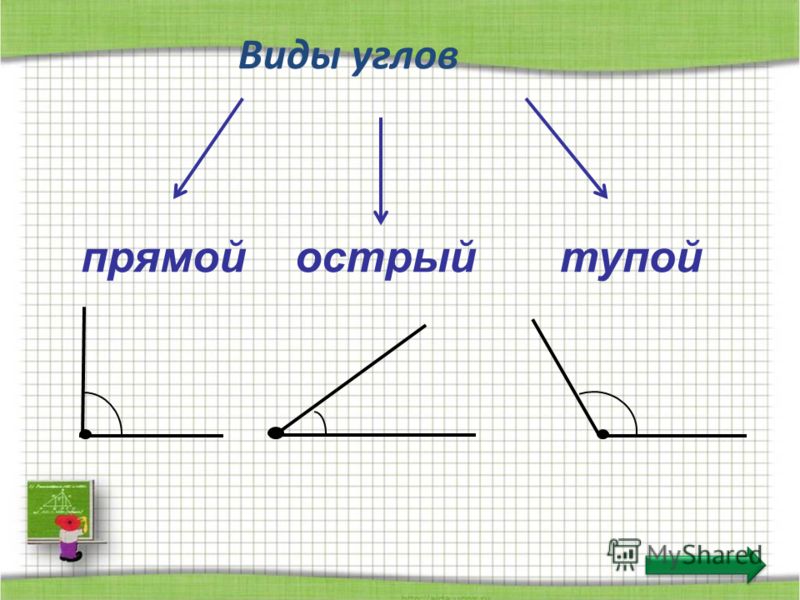
Виды углов
Что такое прямой угол?
Прямой угол образуется, когда две пересекающиеся линии встречаются точно под углом 90 градусов. Это часто рассматривается как четверть оборота, поскольку четыре четверти оборота дадут целый оборот. Прямой угол обозначается между двумя пересекающимися линиями с помощью квадрата.
Пример прямого угла.Что такое острый угол?
Острый угол – это расстояние между двумя пересекающимися линиями в диапазоне от 1 до 89 градусов.градусов.
Пример острого угла.Что такое тупой угол?
Тупой угол — это когда расстояние между двумя пересекающимися линиями составляет от 91 до 179 градусов.
Пример тупого угла.Что такое прямая?
Прямая линия — это угол, равный ровно 180 градусам. Он представляет собой изменение в противоположном направлении. Обратите внимание, что дополнительные углы — это два угла, которые в сумме дают 180 градусов.
Прямая линия, показывающая угол 180 градусов.
Что такое полный оборот?
Полный оборот представляет собой поворот на 360 градусов, при котором пространство между пересекающимися линиями возвращается в исходное положение.
Когда дети узнают об углах в школе?
Школы, следующие Common Core:
Неформально учащиеся начинают изучать углы в 1-м классе, где их учат двумерным и трехмерным формам. Ожидается, что учащиеся составят двухмерные фигуры, такие как полукруги и четверть круга.
Хотя термин «прямой угол» не используется для описания четверти окружности, это будет первое знакомство студента с этим углом.
Углы для 2-го класса
Это дополняется во 2-м классе, когда учащиеся должны «узнавать и рисовать фигуры, имеющие определенные атрибуты, такие как заданное количество углов или заданное количество равных граней».
На этом этапе , студенты не должны знать измерение угла в градусах или знать формальное определение того, что такое «угол».
3-й класс Углы
В 3-м классе учащиеся применяют знания, полученные в группах предыдущего года, для описания свойств формы.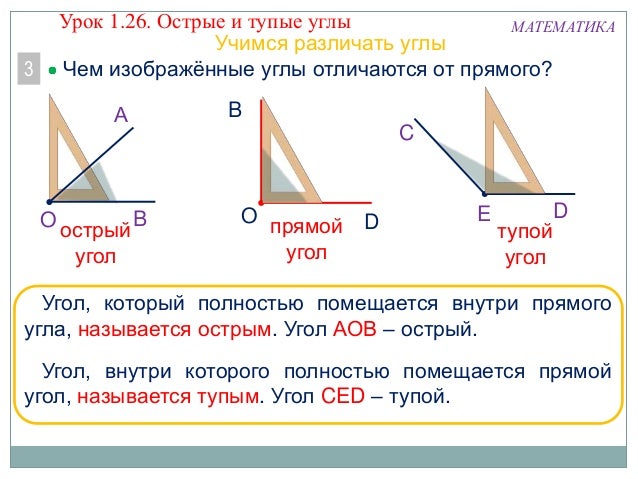 Ожидается, что их будет:
Ожидается, что их будет:
- Поймите, что фигуры в разных категориях (например, ромбы, прямоугольники и другие) могут иметь общие атрибуты (например, иметь четыре стороны) и что общие атрибуты могут определять более крупную категорию (например, четырехугольники).
- Распознавать ромбы, прямоугольники и квадраты как примеры четырехугольников и рисовать примеры четырехугольников, не принадлежащих ни к одной из этих подкатегорий.
Именно в этот момент, вероятно, будет введено формальное определение «угла», но в настоящее время им не нужно будет знать техническое название острого или тупого угла.
Углы 4 класса
В 4 классе учащиеся расширят свои знания об углах, изучив термины острый угол и тупой угол. Ожидания в отношении того, что учащиеся должны знать и уметь делать с углами, значительно возрастают в 4-м классе, где они должны знать следующее:
- Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать концепции измерения угла:
- Измерьте углы в целых числах градусов с помощью транспортира.
 Эскиз углов заданной меры.
Эскиз углов заданной меры. - Рисование точек, прямых, отрезков, лучей, углов (прямых, острых, тупых), перпендикулярных и параллельных прямых. Определите их на двумерных фигурах.
- Классифицировать двухмерные фигуры на основе наличия или отсутствия параллельных или перпендикулярных линий, а также наличия или отсутствия углов заданной величины. Распознавать прямоугольные треугольники как категорию и определять прямоугольные треугольники.
- Распознать угловую меру как аддитивную. Когда угол разлагается на непересекающиеся части, угловая мера целого равна сумме угловых мер частей.
- Решите задачи на сложение и вычитание, чтобы найти неизвестные углы на диаграмме в реальном мире и математические задачи, например, используя уравнение с символом для неизвестной меры угла.
5-й класс Углы
Наконец, в 5-м классе больше внимания уделяется применению знаний об углах для выполнения следующих действий:
- Понимание того, что атрибуты, принадлежащие к категории двумерных фигур, также принадлежат ко всем подкатегориям этой категории .
 Например, все прямоугольники имеют четыре прямых угла, а квадраты являются прямоугольниками, поэтому все квадраты имеют четыре прямых угла.
Например, все прямоугольники имеют четыре прямых угла, а квадраты являются прямоугольниками, поэтому все квадраты имеют четыре прямых угла. - Классифицировать двухмерные фигуры в иерархии на основе свойств.
- Сравнивать и классифицировать геометрические фигуры на основе их свойств и размеров и находить неизвестные углы в любых треугольниках, четырехугольниках и правильных многоугольниках
Другие школы:
В школьных округах и школах, которые следуют стандартам, отличным от Единых базовых государственных стандартов, эти понятия могут преподаваться в другом порядке или в разное время. Обратитесь к стандартам, установленным вашей школой, чтобы узнать, когда эти концепции обсуждаются в школе вашего ребенка.
Как это связано с другими областями математики?
Углы связаны с другими областями евклидовой геометрии, такими как форма. Обязательным условием для понимания и расчета углов является свободное владение арифметическими навыками. Особенно при вычитании нескольких чисел из 90, 180 или 360.
Особенно при вычитании нескольких чисел из 90, 180 или 360.
Как это соотносится с реальной жизнью?
Знание углов важно, так как их применение имеет множество применений. Большая часть строительной отрасли полагается на то, чтобы здания были структурно прочными, используя свои знания об углах.
Игроки в бильярд полагаются на углы, чтобы предсказать реакцию двух шаров. Аналоговые часы могут показывать любой угол до 360 градусов! Углы вокруг нас!
Примеры обработанных углов
1) Какие углы меньше прямого угла?
Чтобы ответить на этот вопрос, учащиеся должны знать, что прямой угол равен 90 градусам, и уметь представить, как это выглядит, поскольку изображение нарисовано не в масштабе.
Имея прочную мысленную модель того, как выглядит прямой угол, учащиеся смогут сделать вывод, что углы «а» и «с» меньше прямого угла.
2) Это поворот на три четверти. Сколько градусов составляет «х»?
Отвечая на этот вопрос, учащиеся должны знать, что поворот на три четверти градуса равен 270 градусам.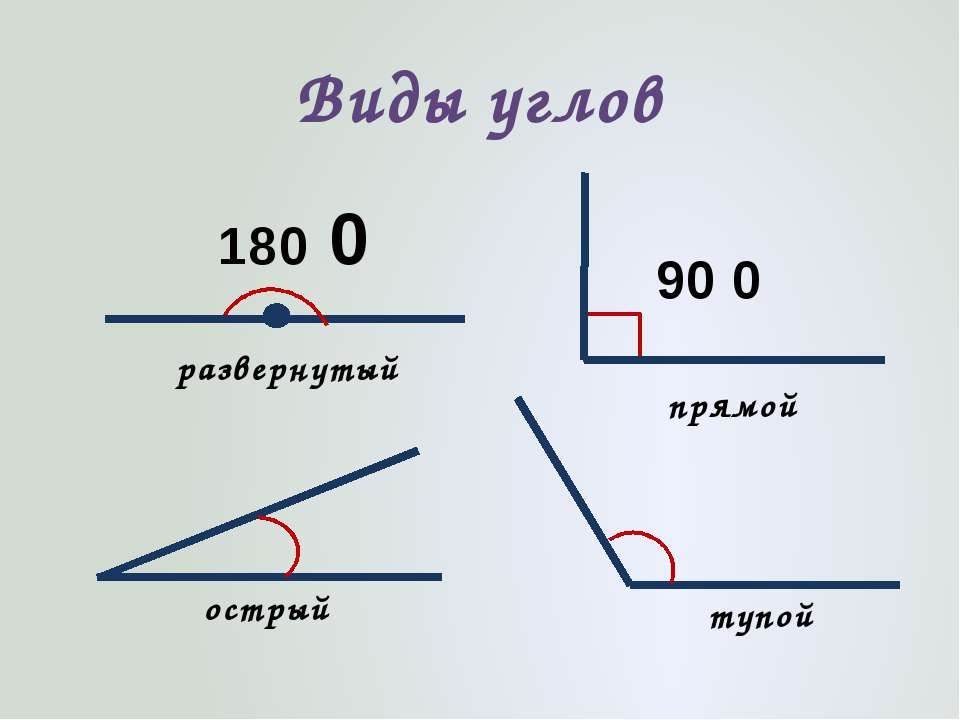 Некоторые студенты могут знать этот факт наизусть.
Некоторые студенты могут знать этот факт наизусть.
Некоторые учащиеся могут умножить 90 (четверть оборота) на 3, чтобы получить 270 градусов, или вычесть 90 градусов из 360 (полный оборот или 4 четверти).
3) Найдите недостающий угол ‘y
Этот вопрос требует от учащихся применения своих знаний и понимания различных аспектов изучения углов и арифметики. Они должны знать, что углы на прямой составляют в сумме 180 градусов.
Они также должны сделать вывод, что квадрат на вершине двух линий представляет собой прямой угол, а это означает 90 градусов. Им придется использовать эти знания для вычисления y. Это можно сделать следующим образом:
65 + 90 = 155
180 – 155 = 25
y = 25
Практические вопросы по углам
1. Найдите тупые углы.
2. Для каждой фигуры напишите, сколько у нее прямых углов.
3. Вычислите размер «x».
4. С помощью транспортира начертите острый угол.
С помощью транспортира начертите острый угол.
5. С помощью транспортира начертите угол, равный 105 градусам.
Хотите знать, как объяснить своим детям другие ключевые слова по математике? Ознакомьтесь с нашим математическим словарем для детей или попробуйте другие блоги:
- Что такое овладение математикой?
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.

 …
… Эскиз углов заданной меры.
Эскиз углов заданной меры.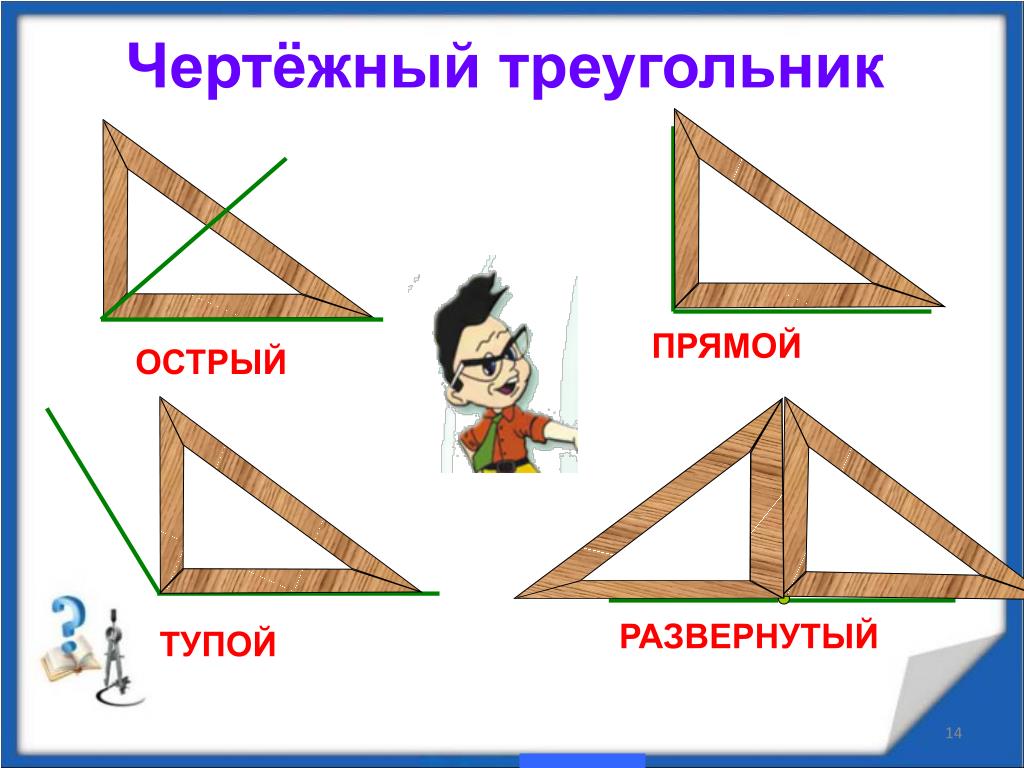 Например, все прямоугольники имеют четыре прямых угла, а квадраты являются прямоугольниками, поэтому все квадраты имеют четыре прямых угла.
Например, все прямоугольники имеют четыре прямых угла, а квадраты являются прямоугольниками, поэтому все квадраты имеют четыре прямых угла.