Календарь Формулы 1 2022 — расписание Гран При, даты, Время проведения Гран При
Фильтры:
Год Тип события
2022
Гонки чемпионата
2023 2022 2021 2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 2000 1999 1998 1997 1996 1995 1994 1993 1992 1991 1990 1989 1988 1987 1986 1985 1984 1983 1982 1981 1980 1979 1978 1977 1976 1975 1974 1973 1972 1971 1970 1969 1968 1967 1966 1965 1964 1963 1962 1961 1960 1959 1958 1957 1956 1955 1954 1953 1952 1951 1950 1949 1948 1939 1938 1937 1936 1935 1933 1931 1921 1914 1913
Гонки чемпионата Все события
Subscribe to calendar
Местное время Ваше время
25
февр. 25 * февр. | Предсезонные тесты в БарселонеНовости Фото Результаты | Закончено | |||
12 мар. 12 * мар. | Предсезонные тесты в БахрейнеНовости Фото Результаты | Закончено | |||
20
мар. | Гран При БахрейнаНовости Фото Результаты Прямой эфир | Закончено | |||
27 мар. | Гран При Саудовской АравииНовости Фото Результаты Прямой эфир | Закончено | |||
10
апр. | Гран При АвстралииНовости Фото Результаты Прямой эфир | Закончено | |||
24 апр. | Гран При Эмилии-РоманьиНовости Фото Результаты Прямой эфир | Закончено | |||
08 мая | Гран При МайамиНовости Фото Результаты | Закончено | |||
22 мая | Гран При ИспанииНовости Фото Результаты | Закончено | |||
29 мая | Гран При МонакоНовости Фото Видео Результаты | Закончено | |||
12
июн. | Гран При АзербайджанаНовости Фото Результаты | Закончено | |||
19 июн. | Гран При КанадыНовости Фото Результаты | Закончено | |||
03
июл. | Гран При ВеликобританииНовости Фото Результаты | Закончено | |||
10 июл. | Гран При АвстрииНовости Фото Результаты | Закончено | |||
24
июл. | Гран При ФранцииНовости Фото Результаты | Закончено | |||
31 июл. | Гран При ВенгрииНовости Фото Результаты | Закончено | |||
28
авг. | Гран При БельгииНовости Фото Результаты | Закончено | |||
04 сент. | Гран При НидерландовНовости Фото Результаты | Закончено | |||
11
сент. | Гран При ИталииНовости Фото Результаты | Закончено | |||
25 сент. 25 * сент. | Гран При РоссииНовости | Отменен | |||
02
окт. | Гран При СингапураНовости Фото Результаты | Закончено | |||
09 окт. | Гран При ЯпонииНовости Фото Результаты | Закончено | |||
23
окт. | Гран При СШАНовости Фото Результаты | Закончено | |||
30 окт. | Гран При МексикиНовости Фото Результаты | Закончено | |||
13
нояб. | Гран При БразилииНовости Фото Результаты | Закончено | |||
20 нояб. | Гран При Абу-ДабиНовости Фото Результаты | Закончено | |||
00:30
18:41
00:00
02:45
01:21
Календарь гонок – Формула-1.
 СПОРТ-ЭКСПРЕСС Календарь гонок – Формула-1. СПОРТ-ЭКСПРЕСС
СПОРТ-ЭКСПРЕСС Календарь гонок – Формула-1. СПОРТ-ЭКСПРЕСС
Лента новостей
Читать все новости
Дата
Гонка
Трасса
Победитель
Длина
Круги
Дистанция
20.03.2022 18:00
Гран-при Бахрейна
Манама. Bahrain International Circuit
Шарль Леклер
5408 м
57
308.238 км
27.03.2022 20:00
Гран-при Саудовской Аравии
Джедда. Гран-при Саудовской Аравии
Макс Ферстаппен
6169 м
50
308.450 км
10.04.2022 08:00
Гран-при Австралии
Мельбурн. Melbourne Grand Prix Circuit
Melbourne Grand Prix Circuit
Шарль Леклер
5303 м
58
307.574 км
24.04.2022 16:00
Гран-при Эмилии-Романьи
Имола. Autodromo Enzo e Dino Ferrari
Макс Ферстаппен
4906 м
63
309.049 км
08.05.2022 22:30
Гран-при Майами
Майами. International Autodrome
Макс Ферстаппен
5410 м
57
308.370 км
22.05.2022 16:00
Гран-при Испании
Барселона. Circuit de Barcelona-Catalunya
Circuit de Barcelona-Catalunya
Макс Ферстаппен
4673 м
66
308.424 км
29.05.2022 16:00
Гран-при Монако
Монте-Карло. Circuit de Monaco
Серхио Перес
3337 м
78
260.286 км
12.06.2022 14:00
Гран-при Азербайджана
Баку. Baku City Circuit
Макс Ферстаппен
6001 м
51
306.049 км
19.06.2022 21:00
Гран-при Канады
Монреаль. Circuit Gilles Villeneuve
Макс Ферстаппен
4361 м
70
305. 270 км
270 км
03.07.2022 17:00
Гран-при Великобритании
Silverstone Circuit
Карлос Сайнс
5888 м
52
306.198 км
10.07.2022 16:00
Гран-при Австрии
Red Bull Ring
Шарль Леклер
4316 м
71
306.452 км
24.07.2022 16:00
Гран-при Франции
Circuit Paul Ricard
Макс Ферстаппен
5843 м
53
309.690 км
31.07.2022 16:00
Гран-при Венгрии
Hungaroring
Макс Ферстаппен
4380 м
70
306. 630 км
630 км
28.08.2022 16:00
Гран-при Бельгии
Circuit de Spa-Francorchamps
Макс Ферстаппен
7001 м
44
308.052 км
04.09.2022 16:00
Гран-при Нидерландов
Circuit Park Zandvoort
Макс Ферстаппен
4258 м
72
306.587 км
11.09.2022 16:00
Гран-при Италии
Монца. Autodromo Nazionale Monza
Макс Ферстаппен
5787 м
53
306.720 км
02.10.2022 15:00
Гран-при Сингапура
Сингапур. Marina Bay Street Circuit
Marina Bay Street Circuit
Серхио Перес
5061 м
61
308.706 км
09.10.2022 10:35
Гран-при Японии
Suzuka International Racing Course
Макс Ферстаппен
5801 м
53
307.471 км
23.10.2022 22:00
Гран-при США
Остин. Circuit of The Americas
Макс Ферстаппен
5507 м
56
308.405 км
30.10.2022 23:00
Гран-при Мексики
Мехико. Autodromo Hermanos Rodriguez
Макс Ферстаппен
4301 м
71
305. 354 км
354 км
13.11.2022 21:00
Гран-при Бразилии
Сан-Паулу. Autodromo Jose Carlos Pace
Джордж Расселл
4308 м
71
305.879 км
20.11.2022 16:00
Гран-при Абу-Даби
Yas Marina Circuit
Макс Ферстаппен
5279 м
58
306.183 км
FV = P (1 + r/n) Yn где P — начальная сумма долга, r — годовая процентная ставка, Y — количество лет инвестирования, а n — количество периодов начисления процентов в год.
FV — это будущая стоимость, то есть сумма, до которой основная сумма вырастет через Y лет.
Понимание формулыПредположим, вы открываете счет, по которому ежегодно выплачивается гарантированная процентная ставка. Вы больше не делаете взносов; вы просто оставляете свои деньги в покое и позволяете сложным процентам творить чудеса. Баланс, до которого ваш счет вырос в какой-то момент в будущем, известен как будущей стоимости вашего начального основного долга. Чтобы найти формулу для будущей стоимости, мы напишем P для вашей начальной основной суммы и r для нормы прибыли, выраженной в виде десятичной дроби. (Так что, если процентная ставка составляет 5%, r равно 0,05). Ваш баланс будет расти по следующему графику:
Это начинает становиться грязным в спешке.
Если вы будете следовать этой схеме в течение Y лет, вы получите общую формулу будущей стоимости:
Это для соединения один раз в год. В более общем случае, если вы хотите составлять n раз в год, вы используете:
ПримерДопустим, вы хотите инвестировать 1000 долларов под 5% годовых с начислением сложных процентов. Через десять лет ваш баланс будет
что равняется $1628,89. Если бы проценты начислялись ежемесячно, а не ежегодно, вы бы получили
что равно $1647,01.
Философское отступление о процентах В какой-то момент вы должны спросить себя, почему вообще существуют проценты, то есть почему вы можете положить деньги на банковский счет, а затем заработать больше денег, не работая.
Ответ заключается в том, что деньги — полезная вещь, а проценты — это рента, которую банк платит владельцу денег (то есть вам) за привилегию пользоваться ими. Что касается сложных процентов (получение «процентов на ваши проценты») — предположим, вы кладете 1000 долларов на банковский счет, который ежегодно выплачивает пять процентов. В конце года ваш баланс вырастет на 50 долларов (это пять процентов от вашей начальной тысячи) до 1050 долларов. Если вы оставите все 1050 долларов на своем счете, проценты, которые вы получите в течение следующего года, будут больше — пять процентов от всех 1050 долларов. Так что в сложных процентах нет ничего таинственного; это просто фиксированная ставка «арендной платы» на ваш постоянно растущий основной капитал.
(Люди любят говорить, что Эйнштейн считал сложные проценты интересной концепцией.
Еще одно экономическое отступление В разгар Великой депрессии Джон Мейнард Кейнс сказал, что «проценты обычно рассматривались как награда за [сбережения], тогда как на самом деле это награда за отказ от накопления».
Под «накоплением» он имел в виду привычку людей прятать деньги в матрасах вместо того, чтобы класть их на банковский счет, из страха, что банкротство банка может уничтожить их сбережения.
Накопление, возможно, было разумным поведением для отдельных людей, но это было плохой новостью для экономики, потому что все эти потенциально полезные деньги были спрятаны там, где их нельзя было использовать.
Сегодня эта проблема решена: FDIC страхует банковские счета (до определенного предела), что делает накопление в старом стиле устаревшим.
Создание FDIC является примером правильной государственной политики: она привела в соответствие личные цели людей (сохранить свои деньги в безопасности) с национальными экономическими интересами (сохранить богатство страны для продуктивного использования). (Также смотрите больше сложных процентов для периодического или непрерывного начисления процентов, и базовые инвестиции под сложные проценты с ежегодными дополнениями, плюс калькулятор простых процентов.)
|
График удобочитаемости Фрая – удобочитаемый
Что такое формула удобочитаемости Фрая?Фрай — это формула, используемая для расчета уровня успеваемости в США, необходимого для понимания фрагмента текста. Это цель большинства формул удобочитаемости. Что отличает Фрай от других формул, так это то, как он рассчитывает уровень успеваемости.
Фрай — это графическая формула. Он использует предложения и слоги в качестве переменных. Фрай наносит текст на график, соответствующий счету. Первоначально это было определено путем выборки отрывков из текстов.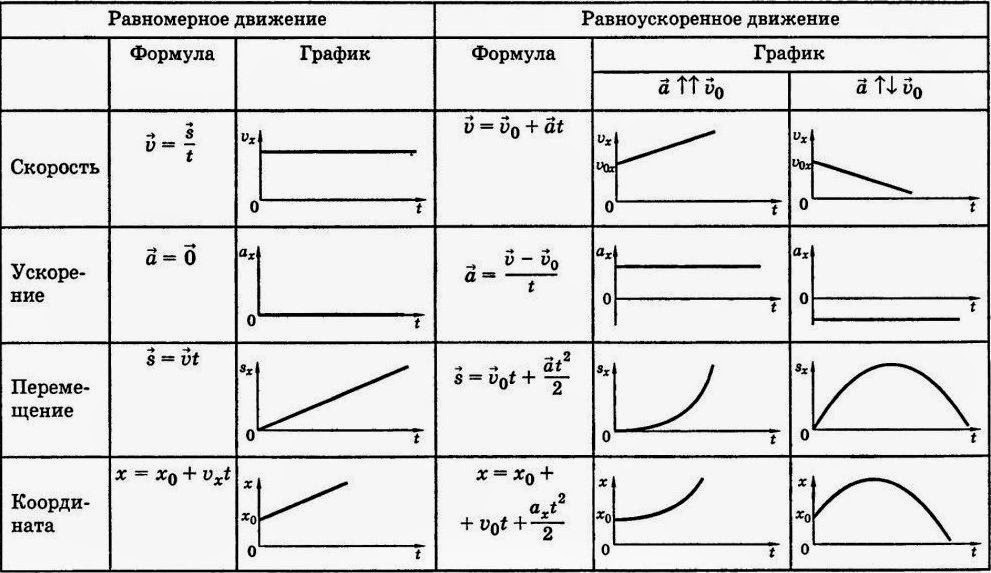 Это было три набора из 100 слов. Затем брались средние предложения и средние слоги.
Это было три набора из 100 слов. Затем брались средние предложения и средние слоги.
Затем эти две цифры были нанесены на график. Пересечение двух линий является приблизительным уровнем чтения текста.
Откуда взялся график удобочитаемости Фрая?Формула удобочитаемости Фрая была создана Эдвардом Фраем в 1968 году. Фрай внес большой вклад в исследования чтения и удобочитаемости. Он был президентом Национальной конференции по чтению.
На протяжении всей своей карьеры он стал авторитетом в том, как люди учатся читать.
Он также поддерживал развитие грамотности на международном уровне. Преподавая в Уганде, он создал Фрая как «формулу экономии времени». График обещал «разумную точность и необыкновенную простоту». Он уточнил, что точность находится в пределах класса. Это полезно для педагогов или библиотекарей, рассчитывающих возраст чтения.
Он также хорошо сочетается с другими популярными формулами, такими как Dale-Chall, Flesch Reading Ease и Spache.
График Фрая изначально был рассчитан следующим образом:
- Выберите три отрывка из ста слов из начала, середины и конца книги. Пропустить все имена собственные.
- Подсчитайте общее количество предложений в каждом отрывке из ста слов (с точностью до ближайшей десятой части предложения). Усредните эти три числа.
- Подсчитайте общее количество слогов в каждой выборке из ста слов. Для каждого гласного звука есть слог; например кот, черный дрозд, конт-ин-энталь. Не обманывайтесь размером слова; например по-ли-о, через.
- Окончания -y, -ed, -el или -le обычно образуют слог, например: read-y, bott-le.
- Сосчитайте каждый слог больше одного в каждом слове и прибавьте 100. Усредните общее количество слогов для трех образцов.
- Нанесите на график среднее количество предложений на сто слов и среднее количество слогов на сто слов. Большинство точек графика находятся рядом с жирной изогнутой линией.
 Перпендикулярные линии обозначают области приблизительного уровня обучения.
Перпендикулярные линии обозначают области приблизительного уровня обучения.
На первый взгляд это выглядит сложно. Но это был более простой процесс, чем многие формулы того времени. К счастью, теперь рассчитать формулу Фрая стало еще проще. Readable анализирует весь текст. Это дает вам ваш балл Фрая как уровень обучения в США в течение нескольких секунд.
Когда формула Фрая наиболее полезна?Сам Фрай указал на множество применений Фрая и других формул. Among other uses, Fry can be used for:
- Libraries and schools
- Technical manuals
- Businesses
- Insurance
- Banks
- Advertising
- Publishing
- Law
- Healthcare
- Government
- Military
Неудивительно, что формула Фрая особенно полезна в образовании. Благодаря широкому диапазону оценок его можно использовать для текстов от начальной школы до уровня колледжа.
Реальное применение
Фрай также является одной из нескольких формул, используемых в здравоохранении. Четкое общение имеет ключевое значение, независимо от того, используется ли оно при диагностике или в текущей переписке. Исследования показали, что пациенты, не разбирающиеся в медицинской литературе, с меньшей вероятностью будут следовать инструкциям. Поэтому они могут не до конца понимать свою болезнь.
Четкое общение имеет ключевое значение, независимо от того, используется ли оно при диагностике или в текущей переписке. Исследования показали, что пациенты, не разбирающиеся в медицинской литературе, с меньшей вероятностью будут следовать инструкциям. Поэтому они могут не до конца понимать свою болезнь.
Формула Фрая также важна в юриспруденции. Фрай отмечает, что вопрос удобочитаемости поднимался в судебных делах. В своем примере он обсуждает судебное дело относительно страховых полисов. Истец даже близко не получил выплату, на которую он имел право, из-за формулировки страхового полиса. Это вызывало особую озабоченность, поскольку заявитель был пожилым человеком. Юридические службы указали, что чуть менее половины пожилого населения Нью-Йорка имеют образование ниже девятого класса.
Эдвард Фрай показал, что их документы были написаны на уровне колледжа. Страховая компания подрывала права граждан на достоверную информацию. Им пришлось принять «оперативные меры», чтобы улучшить читаемость своих документов.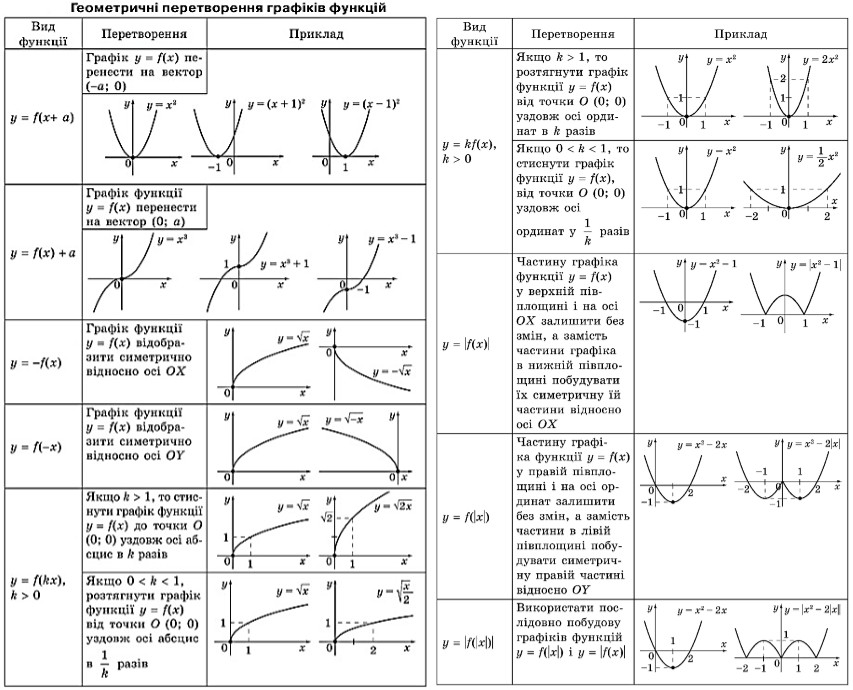



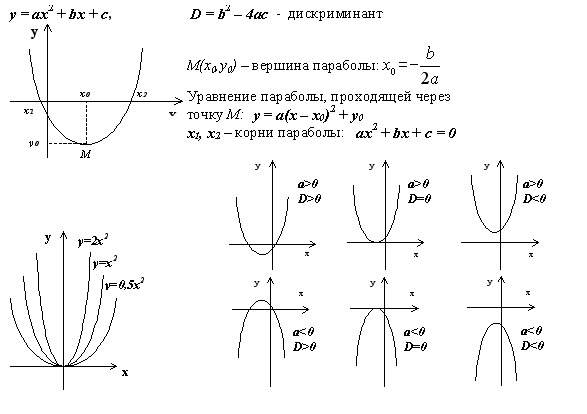


 Но вы можете упростить его, заметив, что вы можете продолжать вытягивать множители (1 + r) из каждой строки.
Если вы сделаете это, балансы рухнут до простого шаблона:
Но вы можете упростить его, заметив, что вы можете продолжать вытягивать множители (1 + r) из каждой строки.
Если вы сделаете это, балансы рухнут до простого шаблона:
 Типичный способ, которым они будут его использовать, — это сдать его в аренду кому-то другому, например, в виде ипотеки или автокредита.
Пока арендная плата, которую они получают, выше, чем арендная плата, которую они платят вам, все будет хорошо.
Типичный способ, которым они будут его использовать, — это сдать его в аренду кому-то другому, например, в виде ипотеки или автокредита.
Пока арендная плата, которую они получают, выше, чем арендная плата, которую они платят вам, все будет хорошо. Ну… возможно, кто-то по имени Эл Эйнштейн действительно так думал, но он не был умным чуваком с сумасшедшей прической.
Сложные проценты — это не что иное, как аренда денег.)
Ну… возможно, кто-то по имени Эл Эйнштейн действительно так думал, но он не был умным чуваком с сумасшедшей прической.
Сложные проценты — это не что иное, как аренда денег.)
 Перпендикулярные линии обозначают области приблизительного уровня обучения.
Перпендикулярные линии обозначают области приблизительного уровня обучения.