Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей
Многоугольники. Выпуклый многоугольник. Четырехугольник.
Треугольник – это частный случай многоугольника.
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник – фигуру с пятью углами.
Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.
Иными словами, например, когда говорят о пятиугольнике А1А2А3А4А5, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника.
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Периметр многоугольника – сумма длин сторон многоугольника.
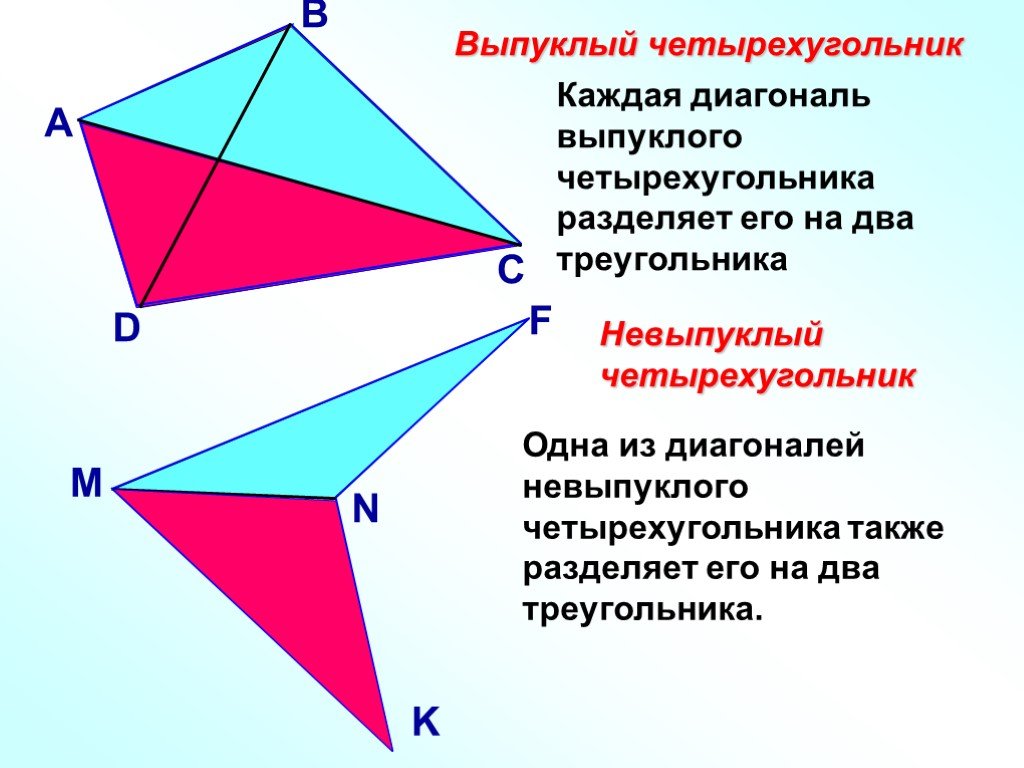
Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника.
Многоугольники делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на рисунке выше, является выпуклым, а на рисунке ниже – невыпуклым.
Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой.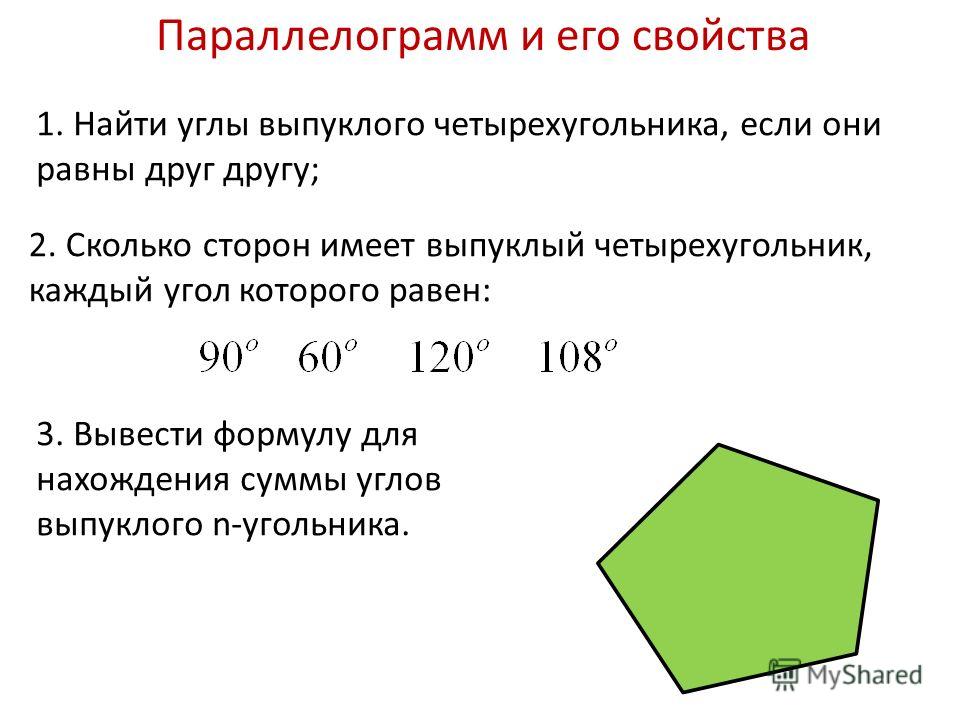 Невыпуклыми являются все остальные многоугольники.
Невыпуклыми являются все остальные многоугольники.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.
Существенное отличие четырехугольника от треугольника в том, что он может быть выпуклым или невыпуклым.
Очень важное различие, о котором знает каждый плотник, состоит в том, что треугольник – «жесткая» фигура, а четырехугольник (как и все остальные многоугольники) – «нежесткая».
У треугольника невозможно изменить его форму, не изменив длин сторон. При этом у любого четырехугольника можно изменить его форму, не меняя длины сторон. На практике это будет означать, что треугольник, сколоченный из трех дощечек, будет жестким, не будет сминаться даже при сильных воздействиях, а четырехугольник при достаточной нагрузке со стороны изменит свою форму.
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольникаитеорема о сумме внешних углов выпуклого многоугольника.
Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).
Сумма углов n-угольника равна 180°·(n-2).
Математическая запись: ∠A1+∠A2+…+∠An=180°(n-2), где n – количество его углов (сторон).
Вспомним, что любой четырехугольник состоит из двух треугольников (достаточно провести диагональ). Но сумма углов каждого из них одинакова и равна 1800, значит, сумма углов четырехугольника 3600.
Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).
∠1’+∠2’+…+∠n’=360°, где n – количество его углов (сторон), а ∠1′,…,∠n’ – внешние углы, по одному от каждой вершины.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Геометрия (Планиметрия) | Четырехугольники |
| Типы четырехугольников |
| Типы параллелограмов |
| Типы трапеций |
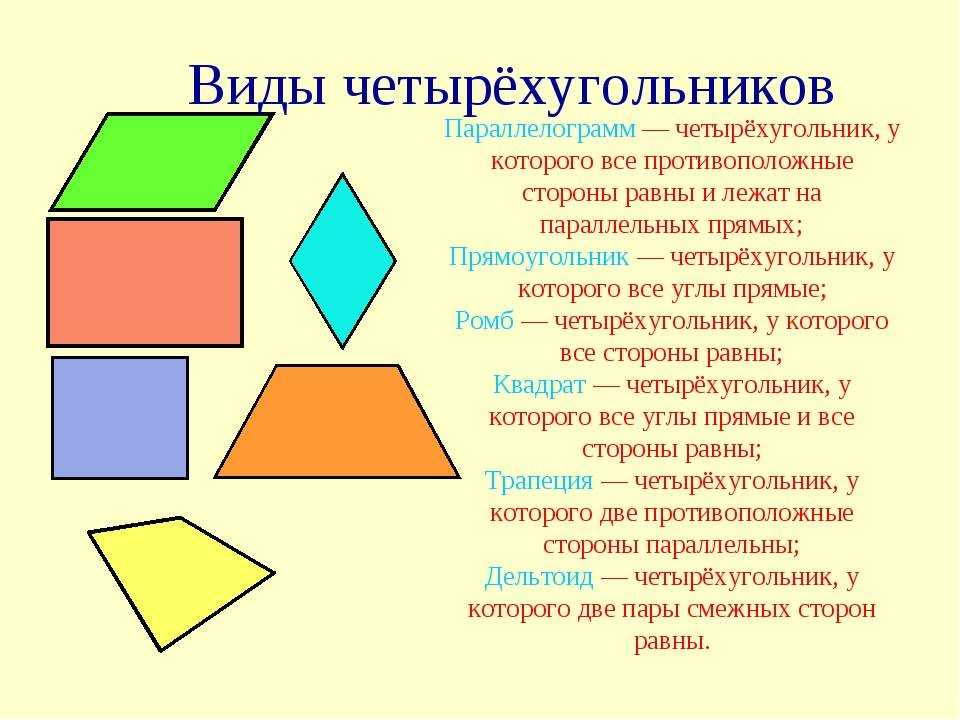
Типы четырёхугольников
Классификация треугольников изложена в разделе нашего справочника «Типы треугольников».
Целью данного раздела является классификация четырёхугольников.
Классификация четырёхугольников по типам представлена на схеме 1.
Схема 1
Рисунки и определения фигур, представленных на схеме 1, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Четырёхугольник | Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. | |
| Выпуклый четырёхугольник | Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках | |
| Невыпуклый четырёхугольник | Четырёхугольник называют невыпуклым, если он не является выпуклым. | |
| Параллелограмм | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны | |
| Трапеция | Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). | |
| Дельтоид | Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
| Четырёхугольник |
Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. |
| Выпуклый четырёхугольник |
Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках |
| Невыпуклый четырёхугольник |
Четырёхугольник называют невыпуклым, если он не является выпуклым. |
| Параллелограмм |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Трапеция |
Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). |
| Дельтоид |
Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
Типы параллелограммов
На схеме 2 представлена классификация параллелограммов.
Схема 2
Рисунки и определения фигур, представленных на схеме 2, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Прямоугольник | Прямоугольник – это параллелограмм, у которого все углы прямые. | |
| Ромб | Ромб – это параллелограмм, у которого все стороны равны. | |
| Квадрат | Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. | |
| Параллелограмм общего вида | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Прямоугольник |
Прямоугольник – это параллелограмм, у которого все углы прямые. |
| Ромб |
Ромб – это параллелограмм, у которого все стороны равны. |
| Квадрат |
Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. |
| Параллелограмм общего вида |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
Типы трапеций
На схеме 3 представлена классификация трапеций.
Схема 3
Рисунки и определения фигур, представленных на схеме 3, даны в следующей таблице.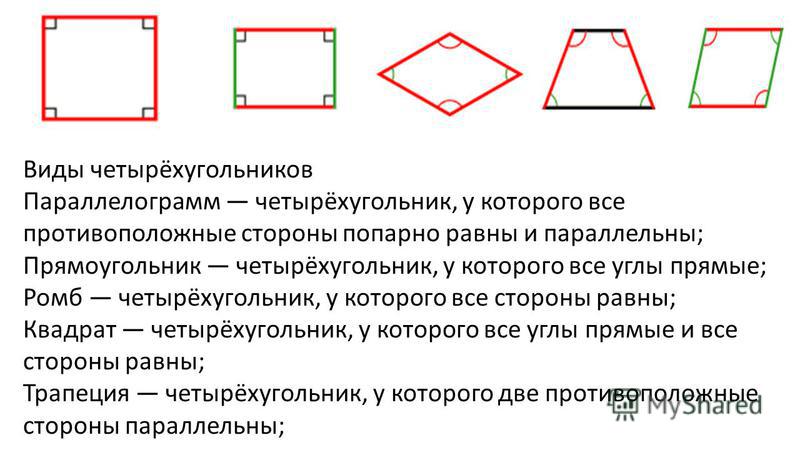
| Фигура | Рисунок | Определение |
| Равнобедренная (равнобочная) трапеция | Равнобедренной называют трапецию, у которой боковые стороны равны. | |
| Прямоугольная трапеция | Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. | |
| Трапеция общего вида | Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
| Равнобедренная (равнобочная) трапеция |
Равнобедренной называют трапецию, у которой боковые стороны равны. |
| Прямоугольная трапеция |
Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. |
| Трапеция общего вида |
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Q5 Объясните, почему прямоугольник является выпуклым четырехугольником…
Перейти к
- Упражнение 3.1
- Упражнение 3.
 2
2 - Упражнение 3.3
- Упражнение 3.4
- Рациональное число
- Линейные уравнения с одной переменной
- Практическая геометрия
- Обработка данных
- Квадраты и квадратные корни
- Кубы и кубические корни
- Сравнение количеств
- Алгебраические выражения и тождества
- Визуализация твердых фигур
- Измерение
- Показатели и силы
- Прямые и обратные пропорции
- Факторизация
- Введение в графики
- Игра с числами
Главная >
Решения НЦЭРТ
Класс 8
Математика
>
Глава 3. Понимание четырехугольников
>
Упражнение 3.4
>
Вопрос 16
Понимание четырехугольников
>
Упражнение 3.4
>
Вопрос 16
Вопрос 16 Упражнение 3.4
В5) Объясните, почему прямоугольник является выпуклым четырехугольником.
Ответ:
Решение:
Прямоугольник является выпуклым четырехугольником, так как его вершина приподнята и обе его диагонали лежат внутри него.
Связанные вопросы
**Укажите, верно это или нет:** **Все ромбы — воздушные змеи.**
**Укажите, верно это или нет:** **Все параллелограммы являются трапециями.**
**Укажите, верно это или нет:** **Все прямоугольники являются квадратами.**
**Укажите, верно это или нет:** **Все ромбы являются параллелограммами.**
**Укажите, верно это или нет:** **Все квадраты не являются параллелограммами. **
**
**Укажите, верно это или нет:** **Все воздушные змеи представляют собой ромбы.**
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 3.1
Упражнение 3.2
Упражнение 3.3
Упражнение 3.4
Главы
Рациональные числа
Линейные уравнения в одной вариабельной
СПАСИДЕНИЯ
ПРАКТИЧЕСКАЯ ГЕЙОМЕТРИЯ
Data Handling Handling Handladlals
. Корни
Кубы и кубические корни
Сравнение величин
Алгебраические выражения и идентичности
Визуализация твердых форм
Mensuration
Экспоненты и мощности
Прямые и обратные пропорции
Фактор
Введение в графики
играют с номерами
. n — 1
$
прямоугольники на каждом шаге моего алгоритма (см. рисунки ниже). Я утверждаю, что $A_{x_n} \ge a_n$ (и $a_n$ также описывается ниже и сходится к $1$ с разумной скоростью).
n — 1
$
прямоугольники на каждом шаге моего алгоритма (см. рисунки ниже). Я утверждаю, что $A_{x_n} \ge a_n$ (и $a_n$ также описывается ниже и сходится к $1$ с разумной скоростью).Пусть $\mathrm{diam}(O)$ — диаметр $O$, и пусть две точки $x$ и $y$ на $\partial O$ такие, что $\| х — у \| = \mathrm{диам}(O)$. (Функция, которая берет две точки в $O$ и выводит их расстояние, непрерывна, а $\partial O$ компактна, так что у нас действительно есть такая пара $(x,y)$.) Это означает, что в точке $x $ касательная, параллельная $\partial O$, проходящая через $x$, ортогональна прямой, проходящей из $x$ в $y$. См. рисунок ниже.
Теперь, поскольку $x$ и $y$ выбраны так, чтобы расстояние между ними было максимальным, векторы, касающиеся $\partial O$ в точках $x$ и $y$, в обоих направлениях «вверх» и «вниз» (см. рисунки) будут указывать внутрь (поскольку они имеют максимальное расстояние), так что «высота» точек на $\partial O$ относительно оси $x-y$ будет вогнутой функцией (минус выпуклая функция) , поэтому имеет максимум.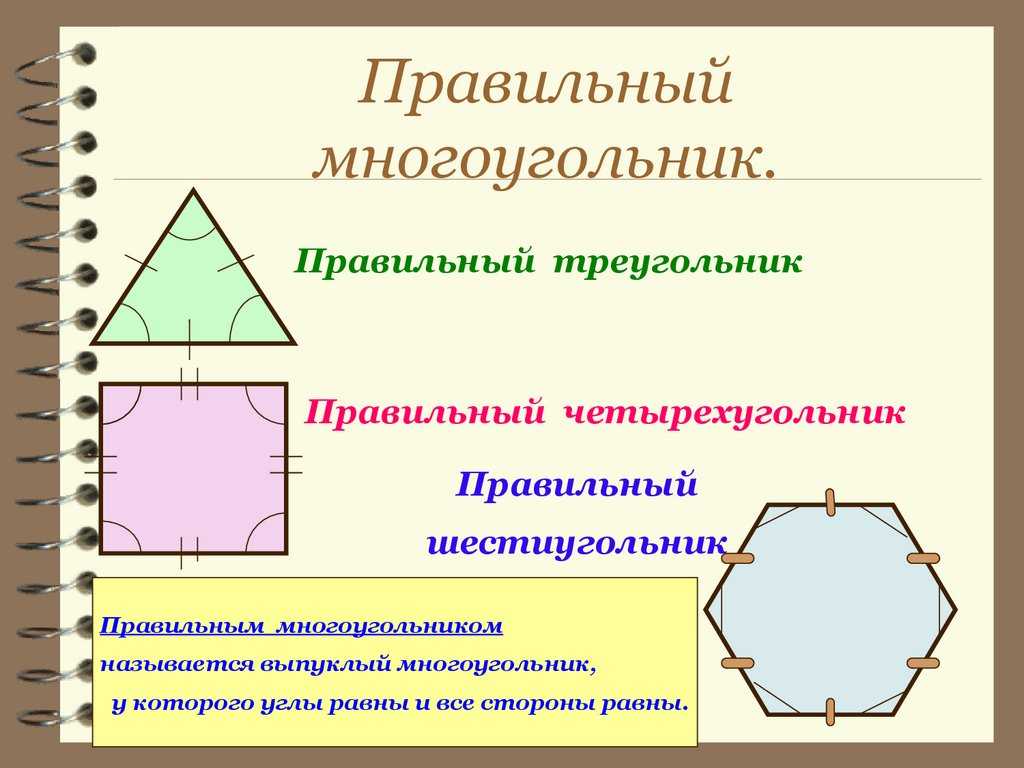
На рисунке я определяю $f(t)$ как площадь определенного прямоугольника. Я определяю $f : (0,a) \to \mathbb R$, полагая $t$ расстоянием от пересечения между осью $x-y$ и точкой, опущенной ортогонально из $z_2$ (которая является нижней точкой) и некоторая точка слева от этой точки на оси $x-y$. Чтобы нарисовать прямоугольник, вы опускаетесь вертикально вниз, затем поворачиваетесь ортогонально, пока не достигнете границы, а затем поворачиваетесь ортогонально и снова останавливаетесь на оси $x-y$. Я определяю прямоугольник таким образом, потому что наихудшее выпуклое множество, имеющее $x$, $y$ и $z$ в этих местах, — это просто два треугольника, следовательно, площадь будет минимальной, и я получу нижнюю границу.
Используя геометрию, вы можете легко увидеть, что
$$
f(t) = (t+\beta)(h-\alpha) = \left(t+\frac{t(d-a)}a \right)\left(h — \frac{ht}a \right) = \frac {dh}a \left( t \left( 1 — \frac ta \right) \right). $$
что дает максимум при $t = \frac a2$ (естественно, не так ли) и максимум при $\frac{3}{16} dh.
$$
что дает максимум при $t = \frac a2$ (естественно, не так ли) и максимум при $\frac{3}{16} dh.
Теперь площадь обоих прямоугольников равна $\frac{3}{16}dh_1 +\frac{3}{16}dh_2 = \frac{3}{16}(d(h_1+h_2)) \ge \frac {3}{16}$, а неравенство возникает из-за того, что выпуклое множество можно заключить в прямоугольник шириной $d$ и высотой $h_1+h_2$, где $h_1$ – максимальная высота одной из конструкций, а $h_2$ — другой.
На шаге $1$ я удалил как минимум $r=3/16$ из множества $O$ с 2 прямоугольниками. Оставшееся пространство (представьте себе круг с вписанным в него квадратом, осталось $4$ зон… это новые выпуклые множества, которые я перебираю). Теперь из оставшейся области $(1-r)$ я могу удалить как минимум $3/16$, следовательно, теперь удалена область $r + (1-r)r$. Итерируя таким образом, я получаю
$$
a_1 = r, \qquad a_n = a_{n-1} + (1-a_{n-1})r
$$
а так как эта последовательность явно возрастает и ограничена сверху, то она сходится, и, допуская предел $a = a + (1-a)r$, получаем $a = 1$.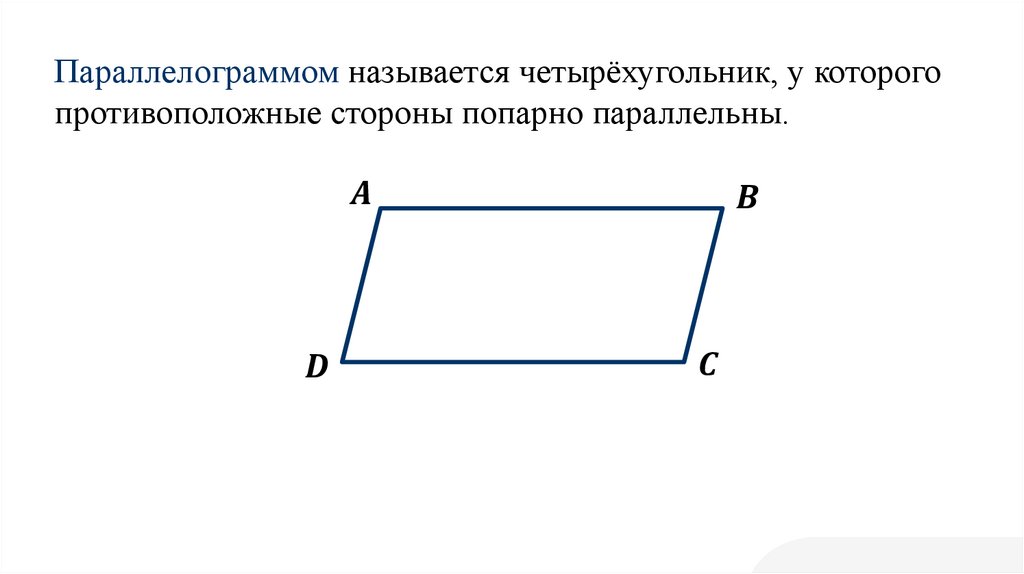



 2
2