Как решать график параболы: Построение графика квадратичной функции — урок. Алгебра, 8 класс.

alexxlab / / Разное

Портфолио проекта «Графики квадратичной функции в зависимости от чисел a, b и c»

Содержание

  • Портфолио проекта «Графики квадратичной функции в зависимости от чисел a, b и c»

  • Тема проекта

  • Предмет, класс

  • Краткая аннотация проекта

  • Вопросы, направляющие проект

  • Основополагающий вопрос

  • Проблемные вопросы:

  • План проведения проекта

  • Визитная карточка проекта

  • Дидактические цели и ожидаемые результаты обучения

  • Презентация учителя для выявления представлений и интересов учащихся

  • Пример продукта проектной деятельности учащихся

  • Материалы по формирующему и итоговому оцениванию

  • Описание методов оценивания

  • Ученик, для которого язык изучения не является родным

  • Полезные ресурсы

  • Используемые ресурсы

Бондарчук Светлана Николаевна и Богословская Александра Михайловна

Графики квадратичной функции в зависимости от чисел a, b и c

алгебра, 8 класс.

Данный проект ориентирован на учеников 8 класса базового уровня. Выбранная тема представлена в образовательном стандарте в разделе Алгебра «Числовые функции». В рамках данной темы рассматриваются такие вопросы как:

квадратичная функция, график квадратичной функции, парабола; координаты вершины параболы; ось симметрии.

От чего зависит расположение графика квадратичной функции?

1)от чего зависит направления ветвей параболы?

2)от чего зависит форма параболы?

3)от чего зависит место нахождения вершины параболы?

1. Подготовительный этап (определение целей и задач проекта; составление общего плана проекта).

2. Начало проекта (актуализация знаний учащихся с помощью проблемной ситуации; разбиение учеников на группы и распределение вопросов и тем проекта; обсуждение возможных источников информации).

3. Развитие проекта (поиск и подбор материалов; выдвижение гипотез; проведение исследования; оформление результата исследования в виде обобщенной презентации и решения проблемной задачи; самооценка вклада каждого ученика в коллективную работу).

4. Заключительный этап (защита проделанной работы на итоговой конференции;итоговая рефлексия). Схема проведения проекта

Обучающие цели

*Изучить расположение графиков квадратичной функции в зависимости от чисел а, b и с;

Воспитательные цели

  Формирование навыков коллективной и самостоятельной работы.
  Расширение кругозора учащихся.
  Развитие умений сравнивать, обобщать, анализировать.
  Развитие умения правильно обобщить данные и сделать вывод.

Развивающие цели:

развитие умения работать с Интернет-ресурсами;
развитие умения строить графики квадратичной функции ;
развитие познавательного интереса;
развитие умения работать с большим количеством информации по рассматриваемой проблеме.

Ожидаемые результаты обучения:

По окончанию проекта ученики смогут:

самостоятельно решать жизненного характера с помощью графика квадратичной функции;
ориентироваться в большом количестве разнообразной информации по рассматриваемой проблеме;
критически оценивать свои возможности;
оформлять компьютерные презентации по теме проекта.

123.odp

исследовательская_работа.odp

критерии_оценивания_wiki-статьи.odt

критерии_оценивания_итоговой_презентации.odt

оценка_работы_группы.odt

самооценка_ученика.odt

тест онлайн: http://madam-fonova.ucoz.ru/publ/testy_po_algebre_8_klass/test_3/test_3_variant_2_8_klass/29-1-0-42

тестирование: расставьте знаки >,< или = в исходя из предложенных графиков квадратичной функции

Мотивирующие:

Опрос сопровождающий вводную презентацию;
Мозговой штурм.

Формирующие:

План проекта;
Самооценка и рефлексия;
Наблюдения групп;
Тест.

Итоговые:

Портфолио;
Представление продуктов проектной деятельности на конференции.
====== Материалы по сопровождению и оценке проектной деятельности ======

Одаренный ученик

анализ_статьи.odt

диалог.odt

  Сопровождение информации картинками;
  
  Книги по математике на родном языке.

http://ru.wikipedia.org/wiki/%CA%E2%E0%E4%F0%E0%F2%E8%F7%ED%E0%FF_%F4%F3%ED%EA%F6%E8%FF

1. http://www.slideboom.com/presentations/416064/%D0%A1%D0%BA%D0%B0%D0%B7%D0%BA%D0%B0-%D0%BE-%D0%9F%D0%B0%D1%80%D0%B0%D0%B1%D0%BE%D0%BB%D0%B8%D0%BA%D0%B5

2. Диалоги о параболе http://festival.1september.ru/articles/517395/

3. Онлайн тестирование http://madam-fonova.ucoz.ru/publ/testy_po_algebre_8_klass/test_3/test_3_variant_2_8_klass/29-1-0-42

Математика Земли

Дом / Обзор Темы

А парабола, которая раскрывается, имеет самую низкую точку, а парабола, которая раскрывается вниз имеет наивысшую точку. Самая высокая или самая низкая точка параболы называется вершиной . Парабола симметрична относительно вертикальная линия, проходящая через его вершину, называемая осью симметрии . На рисунке ниже показана раскрывающаяся парабола с вершиной (0,75, 0,875). и ось симметрии x = 0,75.

Вершина Форма квадратичной функции

Для нахождения вершины параболы напишем функцию по форме

. В качестве примера рассмотрим функцию . Сначала заполняем квадрат с правой стороны:

f(x) = 2(x 2 — 4x) + 7 (вычтите 2 из слагаемых 2x 2 — 8х)

= 2(х 2 — 4х + 4) + 7 — 8       (заполните квадрат x 2 — 4 шт.)

= 2(х — 2) 2 — 1 (фактор совершенный квадрат и упрощение.)

Уведомление что для всех значений x. Таким образом, f(x) = 2(x — 2) 2 — 1 -1 для всех значений x и минимальное значение функции равно -1, когда x = 2.

Точка (2, -1) является самой нижней точкой на графике, поэтому она является вершиной параболы. Вертикальная линия x = 2 является осью симметрии. См. график ниже.

В общем случае  называется вершинной формой квадратичного функция. Когда квадратичная функция записывается в вершинной форме, мы можем легко определить вершину (h, k). Если коэффициент a > 0 , то парабола открывается вверх и вершина самая нижняя точка параболы. Мы говорим, что к это минимум значение квадратичной функции. С другой стороны, если коэффициент a < 0 , то парабола открывается вниз и вершина высшая точка параболы. В этом случае

к является максимальным значение квадратичной функции. Изучите роль каждого коэффициента в следующем интерактивном примере.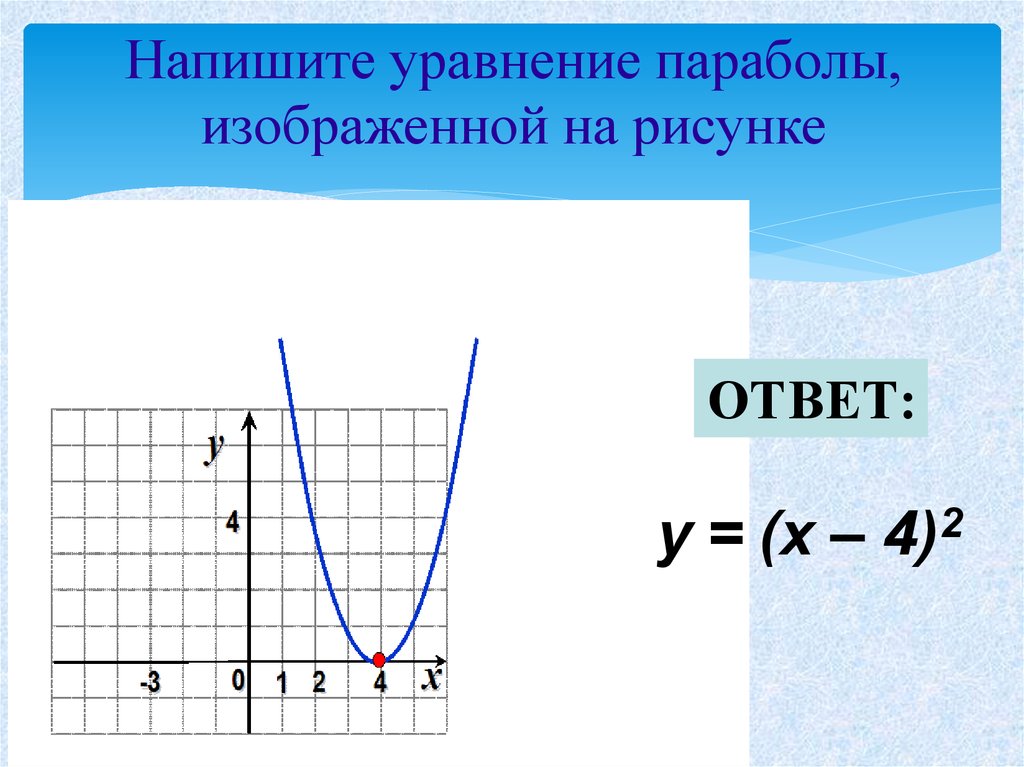

Пример

Запись квадратичная функция в вершинной форме. Определить вершину и максимум или минимальное значение функции.

Решение

Заполним квадрат до запишите функцию в виде вершины:

Форма вершины , поэтому вершина (3, -11) . Так как а < 0, парабола открывается вниз и вершина – самая высокая точка. Функция имеет максимальное значение 11. Его график показан ниже.

Зная вершину параболы, мы можем определить диапазон квадратичной функции. Рассмотрим функцию . Ранее мы определили, что парабола имеет минимальное значение -1, возникающее при x = 2. Таким образом, диапазон квадратичная функция равна {y y -1}.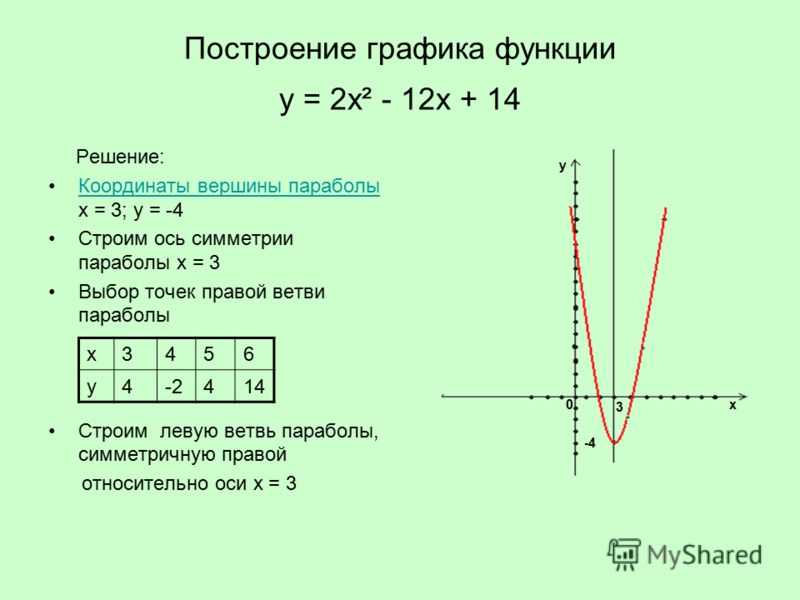 В качестве другого примера, давайте вернуться к функции в приведенном выше примере. График этой функции — парабола, развернутая вниз, и максимальное значение функции равно 11. Следовательно, диапазон квадратичной функции равен

Нахождение вершина Алгебраически

вершина квадратичной функции также может быть определена алгебраически. Мы первые предположим, что квадратичная функция имеет две точки пересечения по оси x. Затем график представляет собой параболу, пересекающую ось x в двух различных точках. Так как парабола симметрична относительно вертикали, проходящей через его вершина (ось симметрии) x-координата вершины равна всегда на полпути между двумя x-перехватами. По квадратичной формуле два x-перехвата равны

Обратите внимание, что одно и то же число прибавляется и вычитается из .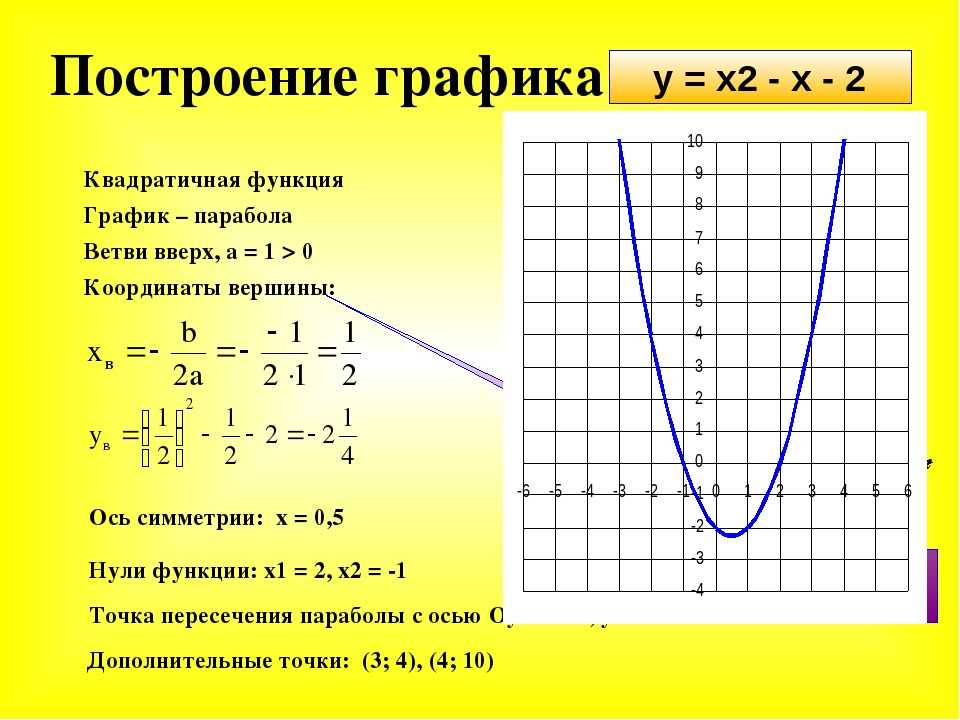 Отсюда следует, что число  находится посередине между  Это означает, что x-координата вершины это . Затем мы можем найти y-координату вершины путем вычисления  Хотя мы предполагали, что квадратичная функция имел два x-пересечения, когда мы выводили нашу вершинную формулу, она также верна в двух других случаях, когда парабола имеет одну точку пересечения с абсциссой или вообще не имеет ее.

Пример

Найти вершина квадратичной функции . Используйте вершину, чтобы определить максимум или минимум значение функции и найти ее диапазон.

Решение

Вершина формула дает  Чтобы найти вторую координату вершины, мы оцениваем Вершина параболы (3, 53). С года < 0 , парабола открывается вниз, а вершина является самой высокой точка. Это дает максимальное значение 53 и диапазон функции  Ниже показан график функции.

Вызов функция , описывающая высоту в футов мяча через t секунд после того, как он был брошен вверх с вершины здание высотой 200 футов. Теперь мы можем определить, когда мяч попадает земли и максимальной высоты, на которую он достигает, а также время, когда он достигает этой максимальной высоты. Когда мяч коснется земли, его высота над землей будет равна нулю. Это дает квадратное уравнение . Используя квадратичную формулу, находим, что решения:

и  

(округлено до два десятичных знака). Поскольку время не может быть отрицательным, мы видим, что мяч ударяется о землю через 5,21 секунды. Максимальная высота шара будет задан второй координатой вершины и время будет первой координатой. Используя вершинную формулу, мы найти это  (округлено  до двух знаков после запятой). Следующий мы оцениваем  Это означает, что мяч достигает своего максимума высота 231,64 фута через 1,41 секунды.

Как найти уравнение параболы с двумя точками и осью симметрии, но без вершины?

Предварительный расчет

Дэвид Дж.

спросил 03.04.19

У меня есть то, что он проходит через 1,4 и 2,7 и что у него есть ось симметрии в точке х = 0, но больше ничего

Подписаться І 1

Подробнее

Отчет

2 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Морис Г. ответил 04.04.19

Репетитор

5,0 (145)

Инженер по образованию, учитель наизусть

Об этом репетиторе ›

Об этом репетиторе ›

Используя форму вершины параболы f(x) = a (x — h ) 2 + k где (h,k) — вершина параболы

Ось симметрии равна x = 0, поэтому h также равно 0

. Подставим каждую точку параболы в форму вершины:

4 = a(1 — 0) 2 + k

4 = а(1) + к

4 = а + к

7 = а(2 — 0) 2 + к

7 = а(4) + к

7 = 4а + к

Нам известна линейная система:

4 = a + k

7 = 4a + k

Вычитание двух уравнений дает нам:

-3 = -3a

a = 1

0

7 90 значение в первое уравнение линейной системы:

4 = 1 + k

k = 3

f(x) = (x — 0) 2 + 3

f( 1 ) = 4 = ( 1 — 0) 2 + 91 f( 3

7 2 ) = 7 = ( 2 — 0) 2 + 3 = 4 + 3

Уравнение параболы через заданные точки и ось симметрии:

f(219) = 90 (х — 0) 2 + 3 = х 2 + 3

Голосовать за 1 Понизить голос

Подробнее

Отчет

Марк М. ответил 03.04.19

Репетитор

5,0 (270)

Учитель математики — высококвалифицированный специалист NCLB

Об этом репетиторе ›

Об этом репетиторе ›

4 = a(x — 1) + k

7 = a(x — 2) + k

Найти a, т. е. исключить k

Подставить любую точку и в любое уравнение со значением «a» и решить для к.

Голосовать за 1 Понизить голос

Подробнее

Отчет

Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *