Плоские геометрические фигуры
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Пономарев П.В. 1
1МБОУ «Школа № 91 с углубленным изучением отдельных предметов»
Калина О.В. 1
1ФГБОУ ВО «Нижегородский государственный архитектурно-строительный университет»
Автор работы награжден дипломом победителя III степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Геометрия – одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания.
В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий – понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии – теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).
На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям. Таким образом, актуальным становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества [1]. Таким образом, целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Таким образом, целью данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Объект исследования: Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.
Задачи исследования: Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.
Теоретическая и практическая значимость исследования состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.
Объем и структура исследования:
Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.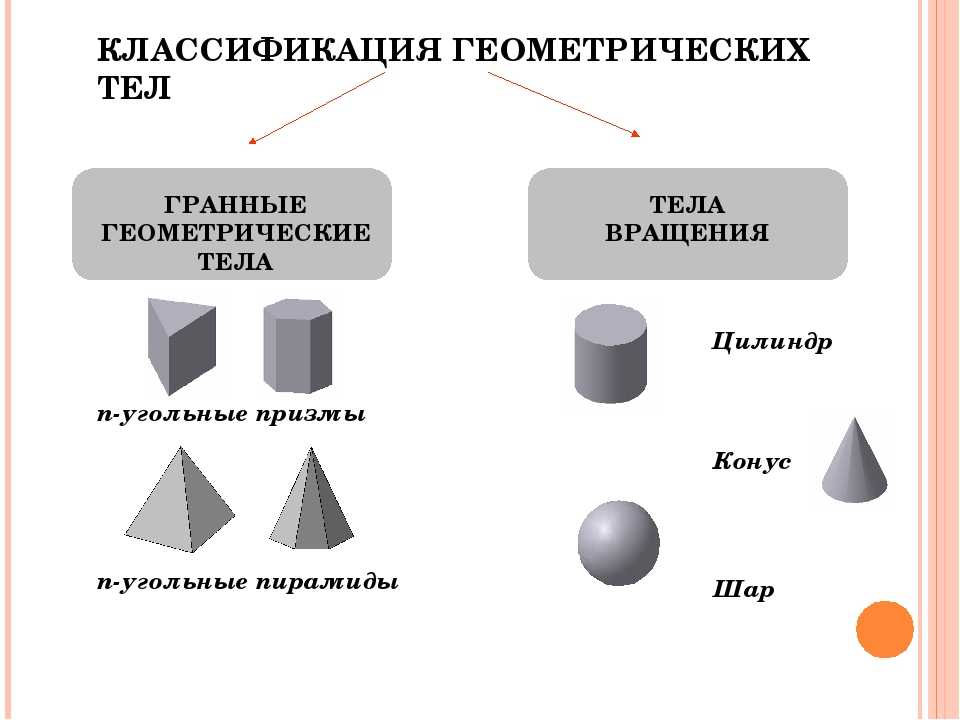
Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1. Основные геометрические фигуры в архитектуре зданий и сооружений
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии – планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.
Самой простой геометрической фигурой является
Прямая— одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой). Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):
Прямые
Таблица 1
|
Параллельные прямые |
Свойства параллельных прямых |
Примеры в архитектуре зданий и сооружений |
|
Если прямые параллельны, то их одноименные проекции параллельны: |
Ессентуки, здание грязелечебницы (фото автора) |
|
|
Пересекающиеся прямые |
Свойства пересекающихся прямых |
Примеры в архитектуре зданий и сооружений |
|
Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи: |
Здания «горы» на Тайване https://www. |
|
|
Скрещивающиеся прямые |
Свойства скрещивающихся прямых |
Примеры в архитектуре зданий и сооружений |
|
Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. , ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях. |
Робер, Гюбер – Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287 |
1. 2. Плоские геометрические фигуры. Свойства и определения
2. Плоские геометрические фигуры. Свойства и определения
Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.
Четырехугольники:
Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник – параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник – параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Трапеция— это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Треугольник — это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:
|
«Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения, лежат, на одной окружности». |
|
|
Рис. 1.Окружность девяти точек |
|
Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.
|
Тем удивительнее было открытие, сделанное американским математиком Франком Морли. Он доказал, что если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника (1899). |
|
|
Рис. 2.Открытие Франка Морли |
Многоуго́льник — это геометрическая фигура, обычно определяемая как замкнутая ломаная.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.
Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.
Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.
Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».
И первой задачей, которую я нашел, была головоломка «Танграм».
Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» ( греч. — «буква»).
Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5, квадрат 6 и параллелограмм 7. Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.
Рис.3. Элементы игры «Танграм» и геометрические фигуры
Рис.4. Задания «Танграм»
Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.
Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.
Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).
Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.
Рис. 5. Приёмы разрезаний
На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.
Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части[1].
Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части[1].
Рис.6.Примеры задач на разрезание:
—— — воссозданный квадрат; — разрез ножницами;
— основная фигура
2.2.Равновеликие и равносоставленные фигуры
Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.
|
На рисунке 6 показано как разбить многоугольники на одинаковое число соответственно равных частей (равные части отмечены одинаковыми цифрами). Эти два многоугольника являются равносоставленными[2]. |
|
|
Рис.6. Равносоставленные многоугольники |
Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.
Отсюда вытекает следующая теорема: равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.
На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).
А Б
Рис.7. Преобразование «греческого креста»
В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).
Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).
На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики — вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет[1].
Рис.8. Паркет, собранный из греческого креста
Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).
|
Зная формулу площади прямоугольника, находим, что площадь параллелограмма равна произведению длин его стороны и соответствующей высоты. |
|
|
Рис.9. Равносоставленные параллелограмм и прямоугольник |
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.
|
Еще одну интересную задачу на равносотавленный треугольник и параллелограмм, можно использовапть для вычисления площадей многоугольников, способ этот был известен еще Евклиду, который жил более 2000 лет назад. |
|
|
Рис.10. Равносоставленные треугольник и параллелограмм |
Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.
Из этого положения легко выводится формула площади треугольника.
Отметим, что для приведенной выше теоремы справедлива и обратная теорема: если два многоугольника равновелики, то они равносоставлены.
Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.
Заключение
В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.
Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.
В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».
Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае — ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.
Библиографический список
1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. – Нижний Новгород: Изд-во НГТУ, 2002. – 73 с.
2. Энциклопедический словарь юного математика /Сост. А.П. Савин. – М.: Педагогика, 1985. – 352 с.
Савин. – М.: Педагогика, 1985. – 352 с.
3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053
Приложение 1
Анкета-опросник для одноклассников
1. Знаете ли вы, что такое головоломка «Танграм»?
2. Что такое «греческий крест»?
3. Было бы вам интересно узнать, что такое «Танграм»?
4. Было бы вам интересно узнать, что такое «греческий крест»?
Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки «Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.
Приложение 2
Элементы игры «Танграм» и геометрические фигуры
Преобразование «греческого креста»
Просмотров работы: 6825
Геометрические фигуры — 43 фото
Арт
Автомобили
Аниме
Девушки
Дети
Животные
Знаменитости
Игры
Красота
Мужчины
Природа
Фантастика
Фильмы
Фэнтези
Разное 4 127 5 января 2020
1
Геометрические фигуры для детей
2
Геометрические фигугуры
3
Биометрические фигуры
4
Геометрические фигуры для дошкольников
5
Геометрические фигурки
6
Геометрические фигугуры
7
Биометрические фигуры
8
Разноцветные геометрические фигуры
9
Геометрические фигуры объемные
10
Геометрические фигугуры
11
Биометрические фигуры
12
Геометрические горы
13
Геометрические фигурки
14
Геометрические фигуры для малышей
15
Цветные геометрические фигуры
16
Геометрические игры
17
Геометрические фигуры для детей
18
Геометрические фигуры для дошкольников
19
Геометрические фигуры вырезать
20
Геометрические фигуры раскраска
21
Биометрические фигуры
22
Геометрические фигуры объемные
23
Объемные геометрические фигу
24
Геометрические горы
25
Геометрические фигуры для малышей
26
Геометрические фигуры для детей раскраска
27
Геометрические фигуры для дошкольников
28
Раскраска фигуры для малышей
29
Биометрические фигуры
30
Геометрические фигурки
31
Геометрические фигуры для дошкольников
32
Геометрические горы
33
Плоские геометрические фигуры
34
Геомантические фигуры
35
Геометрические фигуры для детей
36
Плоскостные геометрические фигуры
37
Куб Призма пирамида конус цилиндр шар
38
Геометрические тела куб шар цилиндр конус Призма
39
Объемные фигуры
40
Биометрические фигуры
41
Геометрические фигугуры
42
Биометрические фигуры
Оцени фото:
Комментарии (0)
Оставить комментарий
Жалоба!
Еще арты и фото:
Шикарные обои на самого высокого качества! Выберайте обои и сохраняйте себе на рабочий стол или мобильный телефон — есть все разрешения! Огромная коллекция по самым разным тематикам только у нас! Чтобы быстро найти нужное изображение, воспользутесь поиском по сайту. В нашей базе уже более 400 000 шикарных картинок для рабочего стола! Не забывайте оставльять отзывы под понравившимися изображениями.
В нашей базе уже более 400 000 шикарных картинок для рабочего стола! Не забывайте оставльять отзывы под понравившимися изображениями.
- абстракция
автомобили
аниме
арт
девушки
дети
еда и напитки
животные
знаменитости
игры
красота
места
мотоциклы
мужчины
общество
природа
постапокалипсис
праздники
растения
разное
собаки
текстуры
техника
фантастика
фэнтези
фильмы
фоны
красивых фотографий геометрии в природе
красивая фотография геометрии в природе Значок поискаУвеличительное стекло. Это означает: «Нажмите, чтобы выполнить поиск». Значок шевронаОн указывает на расширяемый раздел или меню, а иногда и на предыдущие/следующие параметры навигации.ДОМАШНЯЯ СТРАНИЦАПутешествовать
Значок «Сохранить статью» Значок «Закладка» Значок «Поделиться» Изогнутая стрелка, указывающая вправо.
Скачать приложение
Каждый год в саду появляются миллионы цветов. Ив Херман/Reuters- Природа – это дом идеальной формы и ярких цветов.
- Если смотреть вблизи, снежинки имеют невероятно совершенную геометрическую форму.
- Круги можно найти на пнях и в океанах, а прямые линии — на пляжах и полях.
- Посетите домашнюю страницу Insider, чтобы узнать больше.
Спасибо за регистрацию!
Получайте доступ к своим любимым темам в персонализированной ленте, пока вы в пути.
Природа действительно является домом для оптических иллюзий, достопримечательностей и многого другого.
Иногда вы даже можете найти формы, скрытые в природе — радугу, которая представляет собой идеальный полукруг или шестиугольные соты.
Мы собрали фотографии естественных и искусственных форм, которые можно найти во внешнем мире.
Некоторые из них более совершенны, чем другие, но нельзя отрицать, что все эти изображения захватывают дух.
Эти соты недалеко от Кольмара, Франция, имеют идеальную шестиугольную форму, но пчеловоды озадачены оттенками меда в них.
В 2012 году неестественные оттенки повлияли на пчелиные скопления по всему региону Эльзас. Винсент Кесслер/Reuters
Винсент Кесслер/ReutersПчеловоды на северо-востоке Франции были встревожены, когда пчелы начали производить мед в оттенках синего и зеленого. В конце концов они приписали мед необычного цвета остаткам из контейнеров с конфетами M&M, которые перерабатываются на биогазовом заводе рядом с ульями.
Эти каплевидные листья происходят от растения алоэ вера.
Растение алоэ. Сабина Хортебуш/Shutterstock
Сабина Хортебуш/ShutterstockАлоэ вера может помочь при ряде заболеваний, включая солнечные ожоги.
Это пример мозаичного покрытия в Тасмании, Австралия.
Мозаичный тротуар в Тасмании, Австралия. Викимедиа/Джей Джей Харрисон «Мозаичный тротуар» возникает естественным образом, когда эрозия приводит к тому, что плоские поверхности скал образуют почти идеальные прямоугольники.
Безумно думать, что эту замысловатую паутину, полную форм и форм, создал паук.
Потрясающая паутина в Косово. Хазир Река/ReutersЭта паутина была найдена в деревне Акарева в Косово.
Эта удивительная двойная радуга появилась после сильных муссонных штормов.
 Ниптон-роуд в городе Серчлайт, штат Невада.
Джин Блевинс/Reuters
Ниптон-роуд в городе Серчлайт, штат Невада.
Джин Блевинс/ReutersБыл замечен в Неваде в 2012 году.
У деревьев идеально круглые кольца.
Кольца деревьев. Игорь Чери/Shutterstock
Игорь Чери/ShutterstockДендрохронология, или датировка по кольцам деревьев, — это научный метод, использующий эти кольца для определения возраста дерева.
На этой фотографии крупным планом показан спил ясеня.
Если смотреть вблизи, снежинки имеют невероятно совершенную геометрическую форму.
Снежинка. Майк Сегар/Reuters Снежинки вблизи действительно невероятны.
Если смотреть в безветренный день, когда вода внизу неподвижна, создается впечатление, что Ракотцбрюке образует идеальный круг благодаря своему отражению.
Мост проходит через озеро Ракоцзе в Габленце, Германия. Лукаш Стефанск/Shutterstock Построенный во второй половине 19 века, потрясающий Ракоцбрюкке получил свое второе название от старой легенды, согласно которой опасные мосты, такие как этот, был построены дьяволом.
Эти длинные прямоугольные полосы образуют овощное поле в таиландской провинции Патхумтхани.
Фермеры работают в поле. Чайват Субпрасом/ReutersЭто фото было сделано в октябре 2011 года, после того как сильное наводнение накрыло треть страны.
Эта плантация пальмового масла в индонезийской провинции Южная Суматра выглядит как четыре идеальных треугольника сверху.
 Эта фотография была сделана в 2010 году.
Бовихарта/Рейтер
Эта фотография была сделана в 2010 году.
Бовихарта/РейтерИндонезия является крупнейшим в мире производителем пальмового масла.
На этой недатированной фотографии НАСА показаны Луна, а также границы тропосферы, тропопаузы и атмосферы Земли.
Фотография была сделана экипажем 28-й экспедиции на борту Международной космической станции. НАСА/Рейтер
НАСА/РейтерНа этой фотографии тропосфера выделена оранжевым цветом. Это самая нижняя и самая плотная часть атмосферы Земли. Тропосфера резко заканчивается в тропопаузе, которая выглядит на фотографии как резкая граница между оранжевой и синей атмосферой.
Прямые линии пересекают заснеженные поля в Мюлетурнене, недалеко от Берна, Швейцария.
Это похоже на одну холодную верховую езду. Майкл Бухольцер/Reuters
Майкл Бухольцер/ReutersПохоже, ясный холодный день.
Лодочные тропы могут выглядеть как искусство с высоты.
Лодки в океане. Иван Брчич/iStock Две лодки делают круги в океане недалеко от Хорватии.
Эти сферы не НЛО — на самом деле это облака.
Полуостров Камчатка в России. Михаил Дорогович/ShutterstockОблака, изображенные выше, называются линзовидными облаками. Когда температура падает достаточно низко, эти стационарные облака часто образуются на нижней стороне горного хребта.
На этом фото ровные ряды — это тюки сена, сформированные благодаря трактору.
 Поле во Франции.
Паскаль Россиньоль/Reuters
Поле во Франции.
Паскаль Россиньоль/ReutersЭта фотография была сделана в Кокеле, недалеко от города Кале на севере Франции.
Когда Солнце и Луна выровнялись над Землей в мае 2012 года, Солнце на короткое время превратилось в это кольцо.
Солнечное затмение из начальной школы Хираи Дайни в Токио, Япония.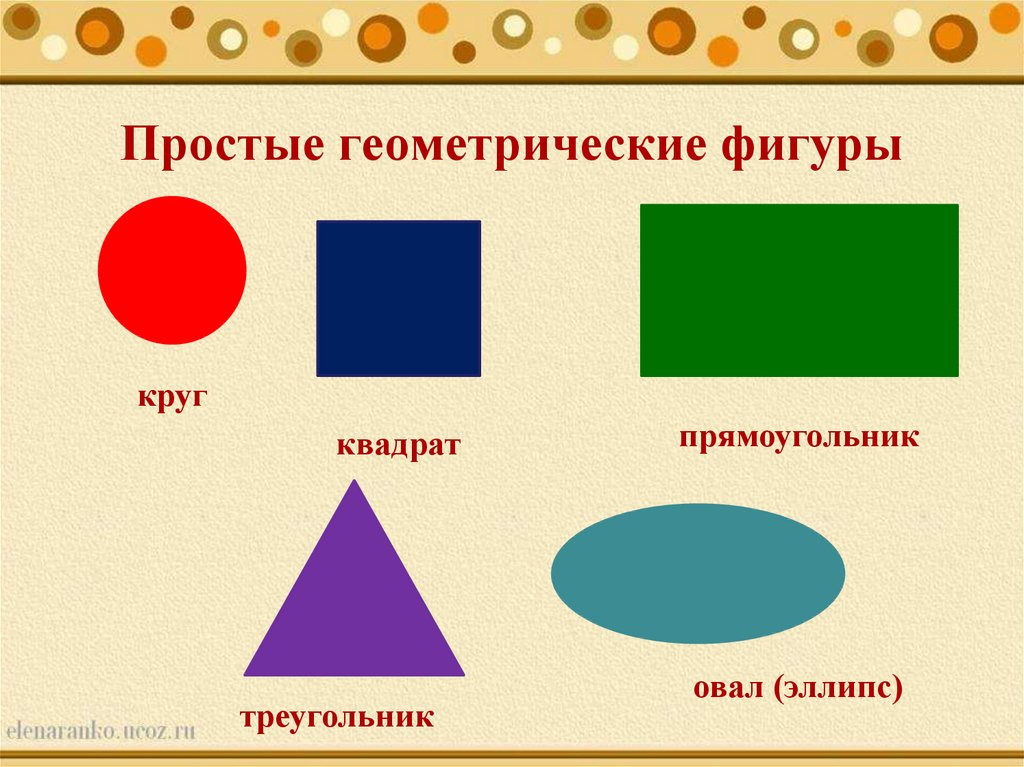 Иссей Като/Reuters
900:16 Солнечное затмение затемнило небо над частями Северной Америки и Азии.
Иссей Като/Reuters
900:16 Солнечное затмение затемнило небо над частями Северной Америки и Азии.
Парк Кекенхоф расположен в городе Лиссе в Нидерландах и считается самым большим цветочным садом в мире. Его чистые границы и яркие цвета поражают.
Каждый год в саду появляются миллионы цветов. Ив Херман/Reuters В Кёкенхоф работает около 30 садовников. В этом году вы можете совершить поездку по нему виртуально.
В этом году вы можете совершить поездку по нему виртуально.
Colle des Mees — крупнейшая во Франции солнечная электростанция. На ферме установлено 112 780 солнечных модулей, расположенных на территории почти 500 акров.
Ферма расположена в Les Mees на юге Франции. Жан-Поль Пелисье/Reuters Солнечные панели производят возобновляемую энергию и обеспечивают мощность 100 МВт.
Эта геометрическая туристическая достопримечательность занимает площадь более 300 акров и расположена в небольшой деревне в Китае.
Аттракцион расположен в Цзуньи в китайской провинции Гуйчжоу. VCG / Getty Images Местные жители сами построили аттракцион из сорго, а также персиковых и сливовых деревьев менее чем за восемь месяцев.
Дизайн известен как гигантский багуа — восьмигранная диаграмма, символизирующая древнюю китайскую энергетическую карту.
В сентябре 2015 года произошло редкое идеально круглое «суперлуние».
Тень Земли отбрасывала на Луну красноватое свечение. Мэтт Карди / Getty Images Суперлуние произошло в результате лунного затмения, совпавшего с ближайшим к Земле полнолунием.
Эти нарциссы почти подходят друг к другу.
Нарциссы. Тоби Мелвилл/ReutersЦветы были замечены на выставке цветов RHS в Челси в Лондоне.
Эти прямоугольные участки составляют региональное предприятие по очистке сточных вод Фресно-Кловис во Фресно, Калифорния.
Региональные очистные сооружения Фресно-Кловис. Люси Николсон/Reuters
Люси Николсон/ReutersЭта фотография была сделана в 2015 году.
Эти круглые формы созданы морским льдом, образующимся над Северным Ледовитым океаном.
Арктические льды истончаются. Кэтрин Хансен/НАСА/Reuters На фотографии выше показаны два члена катера береговой охраны США Хили, поднимающие припасы, сброшенные на парашютах летом 2011 года.
Красные песчаные дюны Намибии создают красивые формы.
Пустынные дюны. Shutterstock.comРябь, создаваемая ветром, создает еще больше узоров.
Читать далее
Функции Фотографии ПриродаКаковы примеры геометрических фигур в реальной жизни?
Описание
Примеры геометрических форм в уличных знаках
Источник
KTSDESIGN / Science Photo Library / Getty Images
Разрешение
.
 Куда бы вы ни посмотрели, почти все состоит из двухмерных (2D) и трехмерных (3D) геометрических фигур. Продолжайте читать, чтобы узнать о реальных примерах геометрических фигур, из которых состоит окружающий нас мир.
Куда бы вы ни посмотрели, почти все состоит из двухмерных (2D) и трехмерных (3D) геометрических фигур. Продолжайте читать, чтобы узнать о реальных примерах геометрических фигур, из которых состоит окружающий нас мир.Примеры двумерных геометрических фигур
Двумерные фигуры — это плоские фигуры, которые имеют ширину и высоту, но не имеют глубины. Круги, квадраты, треугольники и прямоугольники — это все типы двухмерных геометрических фигур. Ознакомьтесь со списком различных 2D-геометрических фигур, а также описанием и примерами их применения в повседневной жизни.
Имейте в виду, что все эти фигуры представляют собой плоские фигуры без глубины. Это означает, что вы можете сфотографировать эти предметы и определить их форму. То же самое не верно для трехмерных форм.
Реклама
Описание
2D Геометрические фигуры в реальной жизни
Источник
BurwellPhotography / E+ / Getty Images, Khaffizzul Hakim Al-Jalil Abdullah / Eyememe / Getty Images, raimund Kochl Images, Westend61 / Getty Images, Pongnathee Kluaythong / EyeEm / Getty Images, artpartner-images / The Image Ban.
 ..
..РАЗРЕШЕНИЕ
Используется по лицензии Getty Images
Примеры кругов
Круг — это круглая форма с одинаковым радиусом от фиксированной точки в центре. Примеры кругов в реальной жизни:
- пироги с пиццей
- печенье
- колеса велосипеда
- циферблаты часов
- обеденные тарелки
Примеры квадратов
Четыре равных прямых угла образуют квадрат с четырьмя прямыми сторонами. Некоторые реальные примеры квадратов:
- квадратные резиновые штампы
- квадратные плитки на полу
- квадратные бумажные салфетки
- шахматные доски
- клавиши виртуальной клавиатуры
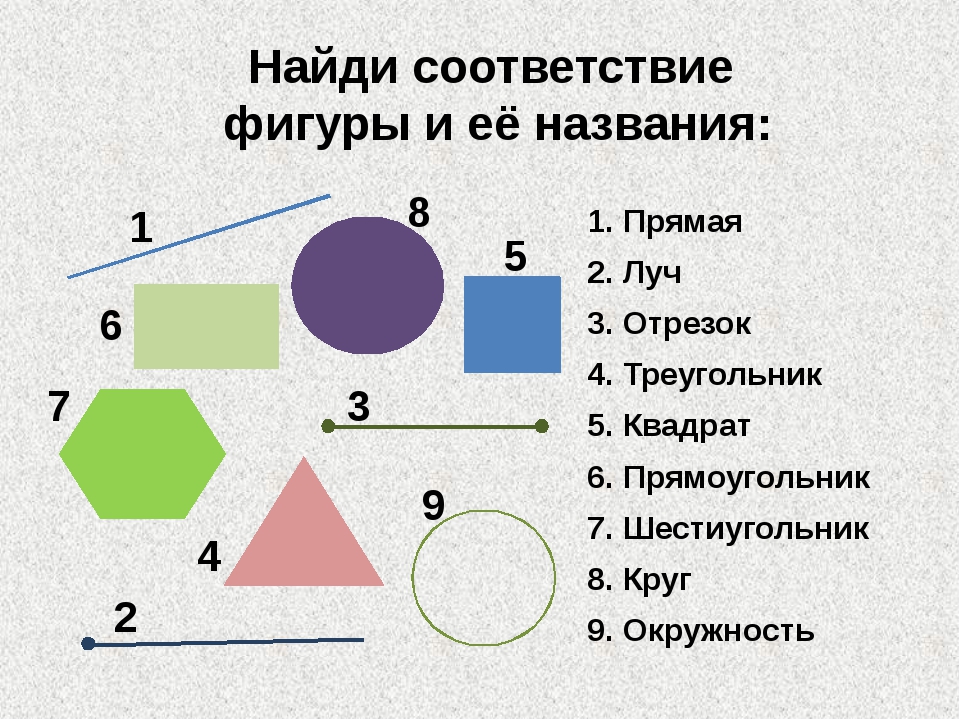
Примеры треугольников
Треугольники — это трехсторонние фигуры с прямыми сторонами. Существует множество различных типов треугольников, в зависимости от их углов. Примеры треугольников в реальной жизни:
- кусочки пиццы
- бутерброд, разрезанный по диагонали
- чипсы из тортильи
- паруса на лодке
- уступайте дорожные знаки
Примеры прямоугольников
Как и квадрат, прямоугольник имеет четыре прямые стороны и четыре прямых угла.
 Однако две стороны короче двух других сторон. Посмотрите на эти примеры реальных прямоугольников:
Однако две стороны короче двух других сторон. Посмотрите на эти примеры реальных прямоугольников: - обложки книг
- сотовые телефоны
- рамки для фотографий
- долларовые купюры
- сэндвичи с мороженым0016 Пятиугольники — фигуры с пятью сторонами одинаковой длины. Они менее распространены, чем четырехугольники, которые имеют четыре стороны, но все же встречаются в реальной жизни. Некоторые примеры пятиугольников:
- Здание Пентагона
- черные секции на футбольных мячах
- домашняя табличка в бейсболе
- знаки перехода
Примеры шестиугольников
шестиугольник. Шестиугольник имеет шесть прямых сторон одинаковой длины. Посмотрите на эти примеры реальных шестиугольников:
- кристаллы льда
- снежинки
- ячейки улья
- контур металлического ореха
- белые участки на футбольных мячах
восьмиугольник Примеры
равные по длине восемь сторонВ реальной жизни они встречаются чаще, чем вы думаете.
 Некоторые примеры восьмиугольников:
Некоторые примеры восьмиугольников:- знаки остановки
- открытые зонты
- Кольцо UFC
- покерные столы
Реклама
Примеры трапеций
Трапеция — это четырехсторонняя фигура, у которой всего одна пара параллельных сторон. Вы можете найти трапеции в следующих примерах:
- Торзы на мостах
- Некоторые стороны сумочки
- Полуготанный кусок пиццы
- Musical Dulcimer
Описание
GEOMETRIC SHAPES SHAPES.
ModernewWorld / DigitalVision / Getty Images, mtreasure / iStock / Getty Images Plus
РАЗРЕШЕНИЕ
Используется по лицензии Getty Images
Примеры трехмерных геометрических фигур
В отличие от двумерных фигур трехмерные фигуры имеют ширину, высоту и глубину. Примеры трехмерных фигур включают пирамиды, сферы и кубы. Взгляните на эти повседневные примеры трехмерных геометрических фигур.
Конечно, некоторые из этих форм взаимозаменяемы.
 Например, сумка не всегда может быть параллелограммом, поскольку, безусловно, возможны круглые сумки и другие типы. Этот список также не является исчерпывающим, так как существует множество других двухмерных и трехмерных геометрических фигур.
Например, сумка не всегда может быть параллелограммом, поскольку, безусловно, возможны круглые сумки и другие типы. Этот список также не является исчерпывающим, так как существует множество других двухмерных и трехмерных геометрических фигур.Реклама
ОПИСАНИЕ
Трехмерные геометрические фигуры в реальной жизни Dazeley / The Image Bank / Getty Images, Lenny Tam / EyeEm / Getty Images, frankwright / E+ / Getty Images
РАЗРЕШЕНИЕ
Используется по лицензии Getty Images
Примеры сфер
Сферы представляют собой круглые сплошные фигуры. Как и у кругов, у них есть радиус в центре, который равноудален от каждой точки на сфере. Однако, в отличие от кругов, они имеют объем и глубину. Примеры реальных сфер:
- баскетбольных мячей
- планет
- апельсинов
- шариков
- теннисных мячей
Примеры кубов
Каждая из шести граней является квадратом куба.
 Когда они соединяются в форме трехмерного куба, также известного как квадратная призма, они создают глубину. Вот некоторые примеры кубов:
Когда они соединяются в форме трехмерного куба, также известного как квадратная призма, они создают глубину. Вот некоторые примеры кубов:- шестигранные игральные кости
- кубики сахара
- квадратные строительные блоки
- кубики Rubix
- квадратные упаковочные коробки
Примеры конусов
Конус имеет одно круглое основание, которое сужается к одному круглому концу. Конусы очень распространены в предметах повседневного обихода, в том числе:
- дорожные конусы
- вафельные рожки для мороженого
- шляпы для вечеринок
- рождественские елки
- воронки
реклама
9024 цилиндры0248Цилиндры представляют собой объемные фигуры с параллельными сторонами и круглым поперечным сечением. Примеры цилиндров из реальной жизни:
- картонная трубка для бумажных полотенец
- прямые трубы
- стаканы для питья
- тюбики для гигиенических помад
- банки
эллипсоид сплющена с двух сторон.
 Также известный как сфероид, эллипсоид создает эффект трехмерного овала. Некоторые примеры эллипсоидов:
Также известный как сфероид, эллипсоид создает эффект трехмерного овала. Некоторые примеры эллипсоидов:- футбольных мячей
- яиц
- некоторые спутники Сатурна (Мимас, Энцелад, Тефия)
Примеры прямоугольной призмы , параллельные стороны. У них четыре прямоугольные грани и две квадратные грани. Вы можете найти прямоугольные призмы в следующих примерах:
- палочки масла
- кирпичи
- камеры
- коробки с хлопьями
- прямоугольные упаковочные коробки
Реклама
Треугольная призма
Треугольные призмы похожи на прямоугольные, за исключением того, что их квадратные грани представляют собой треугольники, что делает их трехгранными призмами. Примеры реальных треугольных призм включают:
- палатки
- дольки арбуза
- дольки сыра
- кусочки торта
Пирамида Примеры
Трехмерная фигура с одной плоской стороной и складывающейся трехмерной фигурой.


 sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane Эта окружность получила название «окружности девяти точек». Ее центр оказался в середине отрезка, соединяющего точку пересечения высот с центром описанной окружности.
Эта окружность получила название «окружности девяти точек». Ее центр оказался в середине отрезка, соединяющего точку пересечения высот с центром описанной окружности.

 Куда бы вы ни посмотрели, почти все состоит из двухмерных (2D) и трехмерных (3D) геометрических фигур. Продолжайте читать, чтобы узнать о реальных примерах геометрических фигур, из которых состоит окружающий нас мир.
Куда бы вы ни посмотрели, почти все состоит из двухмерных (2D) и трехмерных (3D) геометрических фигур. Продолжайте читать, чтобы узнать о реальных примерах геометрических фигур, из которых состоит окружающий нас мир.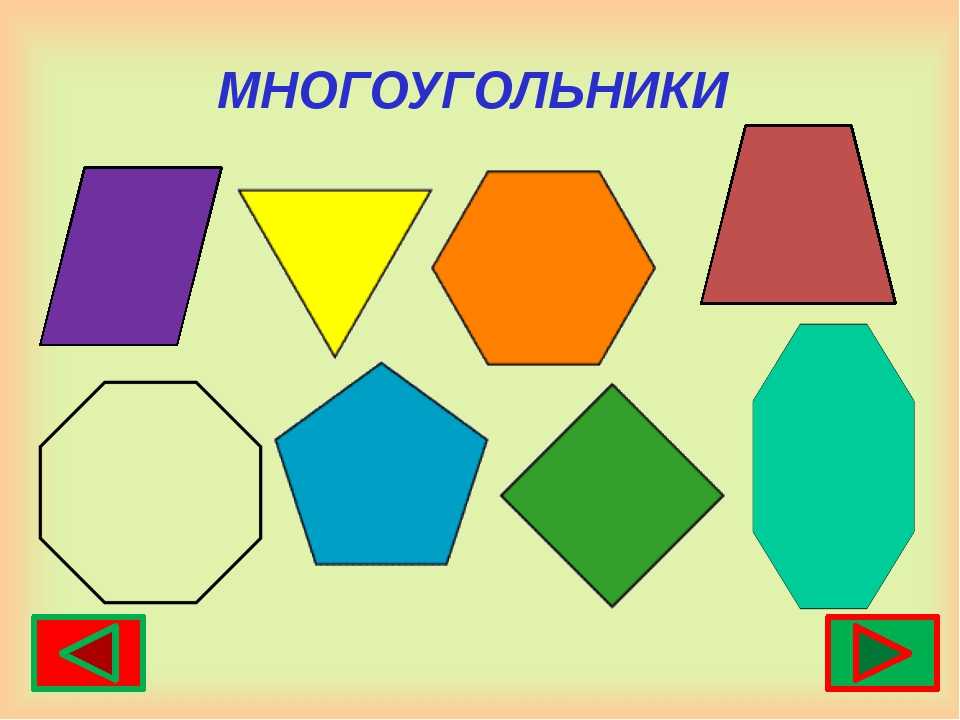 ..
.. Однако две стороны короче двух других сторон. Посмотрите на эти примеры реальных прямоугольников:
Однако две стороны короче двух других сторон. Посмотрите на эти примеры реальных прямоугольников:  Некоторые примеры восьмиугольников:
Некоторые примеры восьмиугольников: Например, сумка не всегда может быть параллелограммом, поскольку, безусловно, возможны круглые сумки и другие типы. Этот список также не является исчерпывающим, так как существует множество других двухмерных и трехмерных геометрических фигур.
Например, сумка не всегда может быть параллелограммом, поскольку, безусловно, возможны круглые сумки и другие типы. Этот список также не является исчерпывающим, так как существует множество других двухмерных и трехмерных геометрических фигур. Когда они соединяются в форме трехмерного куба, также известного как квадратная призма, они создают глубину. Вот некоторые примеры кубов:
Когда они соединяются в форме трехмерного куба, также известного как квадратная призма, они создают глубину. Вот некоторые примеры кубов: Также известный как сфероид, эллипсоид создает эффект трехмерного овала. Некоторые примеры эллипсоидов:
Также известный как сфероид, эллипсоид создает эффект трехмерного овала. Некоторые примеры эллипсоидов: