Конечные графы и сети
Конечные графы и сети
ОглавлениеОТ РЕДАКТОРА ПЕРЕВОДАЧАСТЬ I. ОСНОВЫ ТЕОРИИ Глава 1. ОСНОВНЫЕ ПОНЯТИЯ: НЕОРИЕНТИРОВАННЫЕ ГРАФЫ 1.2. Геометрические графы 1.3. Абстрактные графы 1.4. Изоморфизмы и реализации 1.5. Термины, описывающие локальные свойства 1.6. Маршруты, цепи и циклы 1.7. Связность 1.8. Деревья и леса 1.9. Разделяющие множества и разрезы 1.10. Некоторые специальные классы графов Глава 2. ОСНОВНЫЕ ПОНЯТИЯ: ОРИЕНТИРОВАННЫЕ ГРАФЫ 2.3. Термины для описания локальной структуры 2.4. Ориентированные маршруты, пути и контуры 2.5. Сильная связность 2.6. Деревья и разрезы 2.7. Ориентированные графы и бинарные отношения Глава 3. РАЗБИЕНИЯ И РАССТОЯНИЯ НА ГРАФАХ 3.2. Разбиения ребер 3.3. Разбиения дуг 3.4. Гамильтоновы цепи и циклы 3.5. Разбиения вершин Графы: 3.6. Радиус и диаметр 3.7. Задачи о минимальных расстояниях Глава 4. ПЛОСКИЕ И НЕПЛОСКИЕ ГРАФЫ.  ТЕОРЕМА О РАСКРАСКЕ4.2. Плоские графы Двойственный граф Многогранные графы 4.3. Дополнительный граф 4.4. Раскраска ребер графа 4.5. Раскраска граней и вершин. Задача о четырех красках 4.6. Графы и поверхности Глава 5. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ГРАФОВ 5.2. Матрица инциденций 5.3. Матрица циклов 5.4. Матрица разрезов 5.5. Матрица смежности вершин 5.6. Матрица путей 5.7. Реализуемость матриц циклов и разрезов 5.8. Матрица графов и комбинаторная топология ЧАСТЬ II. ПРИЛОЖЕНИЯ ТЕОРИИ ГРАФОВ Глава 6. ПРИКЛАДНЫЕ ЗАДАЧИ ТЕОРИИ ГРАФОВ ПРИЛОЖЕНИЯ К ЭКОНОМИКЕ И ИССЛЕДОВАНИЮ ОПЕРАЦИЙ 6.3. Линейное программирование и потоки в сетях КОМБИНАТОРНЫЕ ЗАДАЧИ 6.5. Примеры комбинаторных задач в теории графов Применение теоремы Пойя к задачам перечисления 6.6. Минимальное число аварий на кирпичном заводе 6.7. Минимальное число пересечений в полных графах ГОЛОВОЛОМКИ И ИГРЫ 6.8. Задача соединения раскрашенных кубов [7] 6.  9. Задачи изменения состояний системы6.10. Матричная форма задачи о переправе 6.11. Задача деления треугольника 6.12. Игра двух лиц 6.13. Игры на шахматной доске ПАРОСОЧЕТАНИЯ 6.14. Максимальные паросочетания ТЕХНИЧЕСКИЕ ПРИЛОЖЕНИЯ 6.15. Анализ технических систем 6.16. Сети связи 6.17. Граф потока сигналов 6.18. Переключательные сети (схемы) 6.19. Объединение электростанций в энергосистему 6.20. Печатные схемы ЕСТЕСТВЕННЫЕ НАУКИ 6.21. Идентификация в химии 6.22. Простая модель из органической химии 6.23. Два примера из статистической механики 6.24. Генетическая задача ЗАДАЧИ ИЗУЧЕНИЯ ЧЕЛОВЕКА И ОБЩЕСТВА 6.25. Графы и кибернетика 6.26. Применения в социологии 6.27. Математические модели разоружения 6.28. Лингвистика ДОПОЛНИТЕЛЬНЫЕ ПРИЛОЖЕНИЯ 6.29. Математические машины и цепи Маркова 6.30. Группы и обыкновенные графы 6.31. Построение деревьев минимальной общей длины 6.32. Графы и собственные значения неотрицательных матриц 6.  33. Задача ранжированияГлава 7. ПОТОКИ В СЕТЯХ 7.3. Отношения между потоками и операции над ними 7.4. Простые потоки 7.5. Другое представление потока 7.6. Потоки с ограничениями на дугах 7.7. Максимальный поток в транспортной сети 7.8. Максимальные потоки в сетях общего вида с ограниченными пропускными способностями дуг 7.9. Потоки минимальной стоимости 7.11. Задачи о многопродуктовых потоках 7.12. Стохастические потоки в сетях КРАТКИЙ ТЕРМИНОЛОГИЧЕСКИЙ СЛОВАРЬ |
Урок математики по теме «Радиус и диаметр»
Цель урока: познакомить учащихся с понятиями радиус и диаметр.
Задачи урока: сформировать понятия : радиус и диаметр; совершенствовать умение работать циркулем; развивать логическое мышление, творческие способности. память, воображение; воспитание аккуратности, культуры общения и поведения в учебном процессе
Ход урока
1.
Организационный момент.
2. Устные упражнения.
Учитель. Сегодня наш урок мы начнём с решения кроссворда. Решив его, мы узнаем ещё одно слово, связанное с понятием “круг” и “окружность”. Вы готовы приступить к этой работе?
Дети. Да.
(Приложение. Слайд 1)
Учитель.
- Единица измерения длины, которую можно заменить 10 сантиметрами. (Дециметр.)
- Чертёжный инструмент, при помощи которого можно построить окружность. (Циркуль.)
- Отрезок соединяющий центр и любую точку лежащую на окружности. (Радиус.)
- Сотая доля метра. (Сантиметр.)
- Место, в котором находится иголка циркуля, называется …(Центр.)
- Основная единица длины. (Метр.)
- Часть плоскости, ограниченная окружностью. (Круг.)
Учитель. Прочитайте, какое слово получилось. Сегодня тема нашего урока: “Радиус и диаметр”(Слайд 2)
3.
Работа над новым материалом. Работа с учебником
Учитель. Откройте учебники на странице 50. Прочитайте задание № 1.
Дети читают задание.
Учитель. Что необходимо сделать для выполнения этого задания?
Дети. Нужно построить окружность и провести два радиуса так, чтобы они находились на одной прямой.
Что необходимо сделать, прежде чем начинать работу с циркулем?
Дети. Отметить центр окружности.
Дети самостоятельно выполняют построение окружности, проводят радиусы.
Учитель. Обведите красным карандашом отрезок, образованный этими двумя радиусами. Этот отрезок называется ДИАМЕТРОМ данной окружности. А теперь внимательно посмотрите на эти чертежи (Слайд 3). На каком из них изображен диаметр окружности
Дети. На окружности под № 2.
Учитель. Сделайте такой же чертёж у себя в тетради.
Учащиеся выполняют построение.
Учитель. Теперь нам предстоит выполнить задание повышенной сложности,
но я думаю, что вы с ним обязательно справитесь.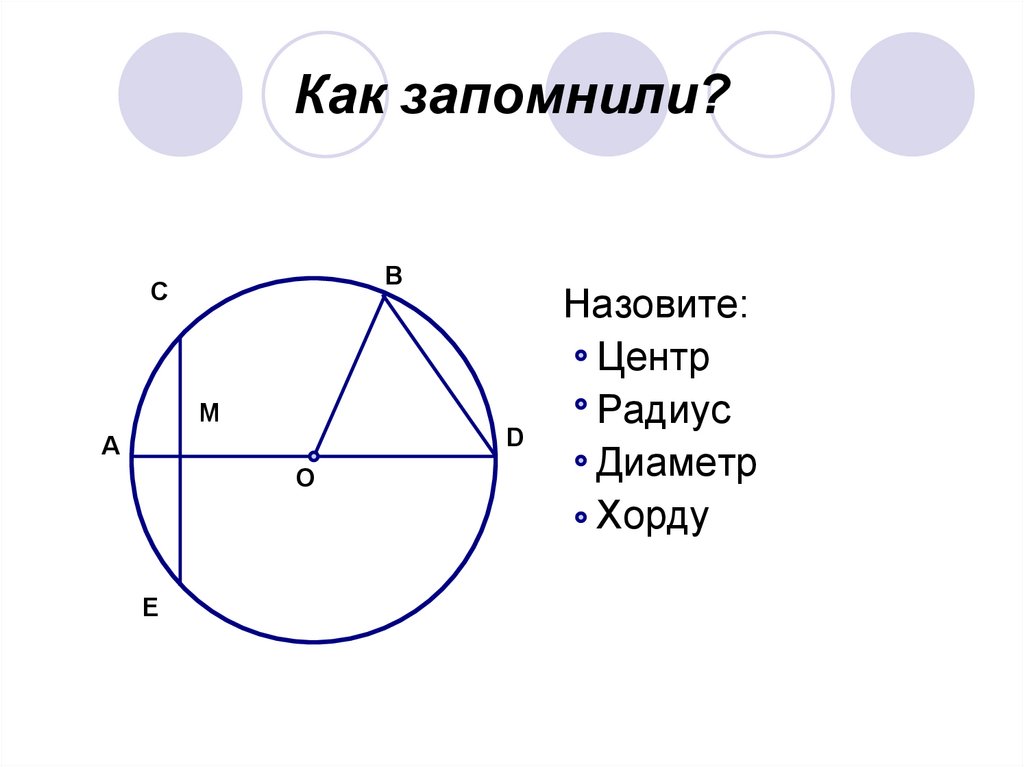
Учащиеся читают задание № 3.
Учитель. Ребята, я предлагаю вам сначала выполнить первую часть задания и построить окружность с радиусом 3 сантиметра.
Дети выполняют первую часть задания.
Учитель. А теперь давайте вспомним, что такое диаметр.
Дети. Диаметр – это отрезок образованный двумя радиусами.
Учитель. Если один радиус окружности будет иметь длину 3 сантиметра, то чему будет равен второй радиус?
Дети. Тоже 3 сантиметрам.
Учитель. Тогда чему будет равен диаметр?
Дети. Диаметр будет равен 6 сантиметрам.
Учитель. Начертите круг. Отметьте центр этого круга. Проведите в нём два диаметра так, чтобы они пересекались под прямым углом. На сколько частей эти диаметры делят круг? Равны ли эти части? Как это можно доказать?
Учащиеся делают свои предположения.
Учитель. Прочитайте задание № 5. Как мы можем ответить на вопросы
задания.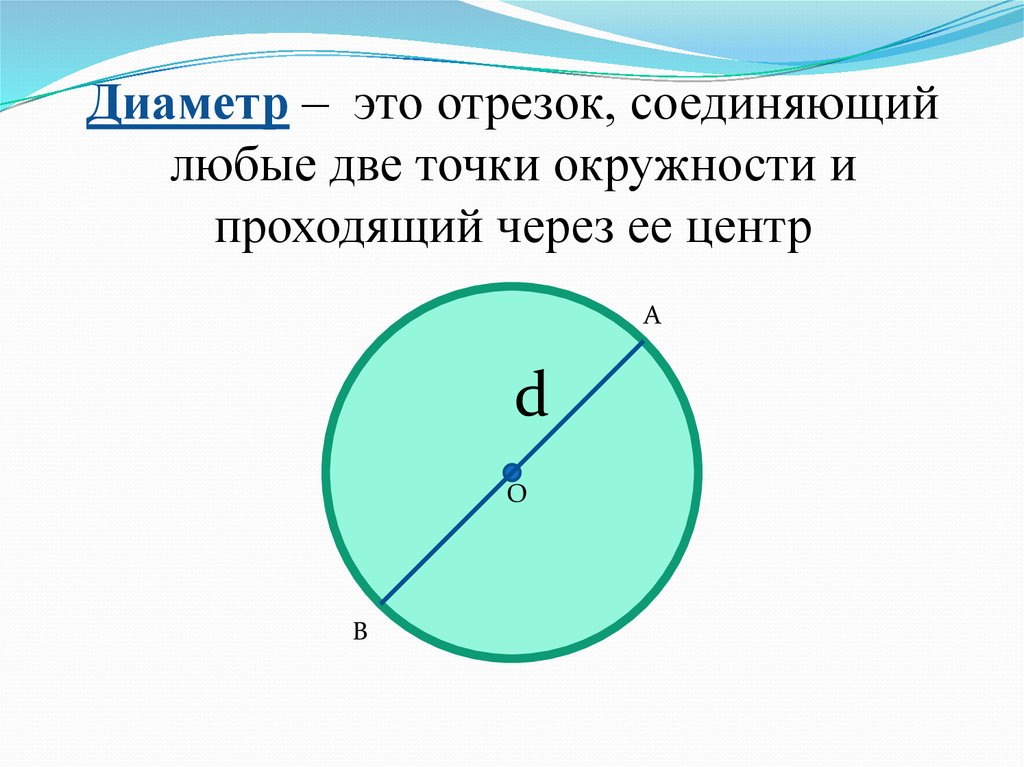
Дети. В круге проведено 4 диаметра и 8 радиусов.
Учитель. Первая окружность имеет радиус 5 см. Вторая окружность имеет диаметр 8 см. У какой окружности диаметр больше и на сколько сантиметров больше? Всё ли нам известно, для того чтобы сравнить диаметры этих окружностей?
Дети. Нам неизвестно чему равен диаметр первой окружности.
Учитель. Мы это можем узнать?
Дети. Да. Если мы сложим два радиуса, то получим диаметр. 5+5=10см
Учитель. А теперь мы можем сравнить диаметры этих окружностей?
Дети. Да. Диаметр второй окружности меньше диаметра первой на 2 см.
Учитель. Как вы это узнали?
Дети. Мы из десяти вычли восемь. Получилось два сантиметра. Значит на два сантиметра диаметр второй окружности меньше, чем диаметр первой.
4. Домашнее задание.
Учитель. Дома вам предстоит выполнить задание в тетради на печатной
основе на странице 27.
№ 1, № 2.
В № 1 Вам необходимо будет начертить окружность и провести в ней диаметр.
В № 2 – вычислить значение числовых выражений.
5. Итог урока.
Учитель. Сегодня на уроке вы познакомились с новым понятием “диаметр окружности”. Давайте ещё раз повторим, что означает это понятие (Слайд 4)
Дети читают определение.
Вам понравился урок? Покажите с помощью “человечков”, какое у вас сейчас настроение. Спасибо за урок.
Как обозначаются радиус и диаметр?
Символ диаметра — символ, указывающий, что размер показывает диаметр окружности. Используемый символ — греческая буква фи Ø
|
Посмотреть полный ответ на mcgill.ca
Что такое символ радиуса?
Радиус круга
Радиус обозначается строчной буквой r.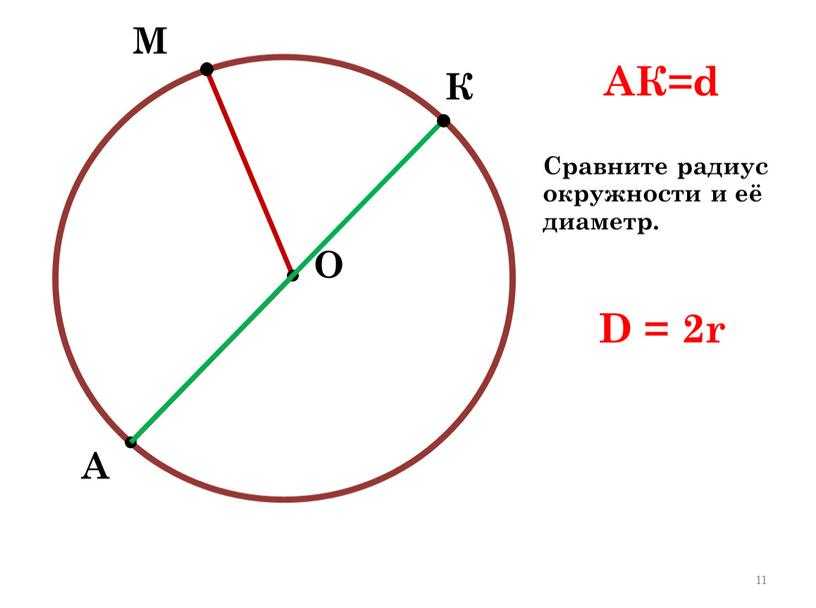
|
Посмотреть полный ответ на сайте mometrix.com
Радиус — это диаметр или R?
Хорда, проходящая через центр окружности, называется диаметром окружности и является наибольшей хордой окружности. Этот диаметр в два раза больше радиуса окружности, т. е. D=2r, где «D» — диаметр, а «r» — радиус.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Является ли диаметр большой D?
Диаметр обычно обозначается строчной буквой d или символом ⊘. Диаметр круга — это расстояние линии, проходящей через центр круга от одного края круга до другого.
Запрос на удаление |
Посмотреть полный ответ на сайте Study.com
Для чего используется символ Ø?
Ø (или минускул: ø) — буква, используемая в датском, норвежском, фарерском и южных саамских языках.
Он в основном используется для обозначения закругленных гласных среднего переднего ряда, таких как [ø] (слушаю) и [œ] (слушаю), за исключением южных саамов, где он используется как дифтонг [oe].
|
Посмотреть полный ответ на en.wikipedia.org
Что такое радиус круга? | Что такое диаметр круга? | Объяснение радиуса и диаметра
Является ли Ø диаметром?
Измерение, используемое для обозначения размера круга на основе длины прямой линии, которая начинается и заканчивается на краю круга, а также проходит через центр круга. Диаметр обозначается символом Ø и обычно обозначается аббревиатурой «диаметр» или «d».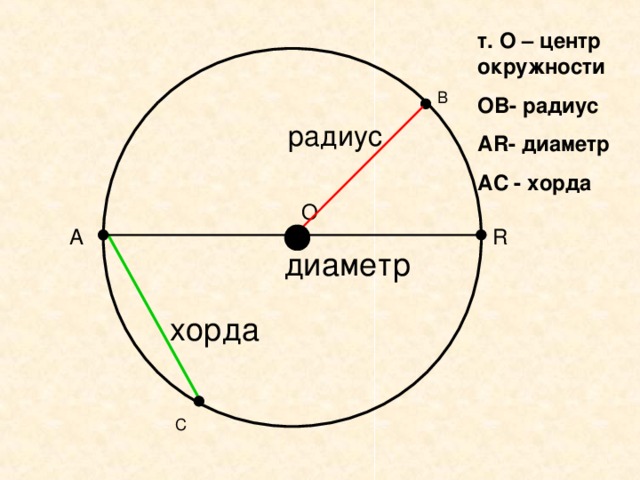
|
Посмотреть полный ответ на labelplanet.co.uk
Как написать радиус?
Когда диаметр известен, формула Радиус = Диаметр/2. Когда известна длина окружности, формула Радиус = Длина окружности/2π. Когда площадь известна, формула для радиуса: Радиус = ⎷(Площадь круга/π).
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Как написать диаметр?
Символ или переменная диаметра ⌀ иногда используется в технических чертежах или спецификациях в качестве префикса или суффикса для числа (например, «⌀ 55 мм»), указывая на то, что он представляет собой диаметр.
Запрос на удаление |
Посмотреть полный ответ на en.wikipedia.org
R означает диаметр?
Последнее число, 15, — это диаметр обода колеса, на которое поместится шина.
Буквенное значение шины относится к конструкции шины: R — радиальная, D — диагональная и RF — Run-Flat.
|
Посмотреть полный ответ на Tireagent.com
Является ли R диаметром?
r — радиус окружности. d — диаметр окружности. С — длина окружности.
Запрос на удаление |
Посмотреть полный ответ на byjus.com
Что означает круг?
Окружность (символ О) — это множество всех точек на плоскости, которые находятся на фиксированном расстоянии от данной точки, известной как центр окружности. Радиус — это отрезок, соединяющий центр окружности с точкой на окружности.
Запрос на удаление |
Посмотреть полный ответ на math.uh.edu
Что такое R в круговой математике?
Радиус окружности – это расстояние от центра до края окружности.
Это 1 / 2 диаметра и обозначено символом r. Если вы измерите длину окружности и диаметр окружности и разделите длину окружности на диаметр, вы получите число Пи, равное примерно 3,14.
|
Посмотреть полный ответ на rasmus.is
Какова единица измерения радиуса?
радиан. Дуга окружности той же длины, что и радиус этой окружности, образует угол в 1 радиан. Окружность образует угол 2π радиан. Общая информация. Система единиц.
Запрос на удаление |
Посмотреть полный ответ на en.wikipedia.org
Как написать диаметр круга?
Каков диаметр этого круга? Чтобы решить это, вспомните уравнение d=2r d = 2 r . По определению длина диаметра этой окружности будет в два раза больше радиуса.
Запрос на удаление |
Посмотреть полный ответ на сайте Study.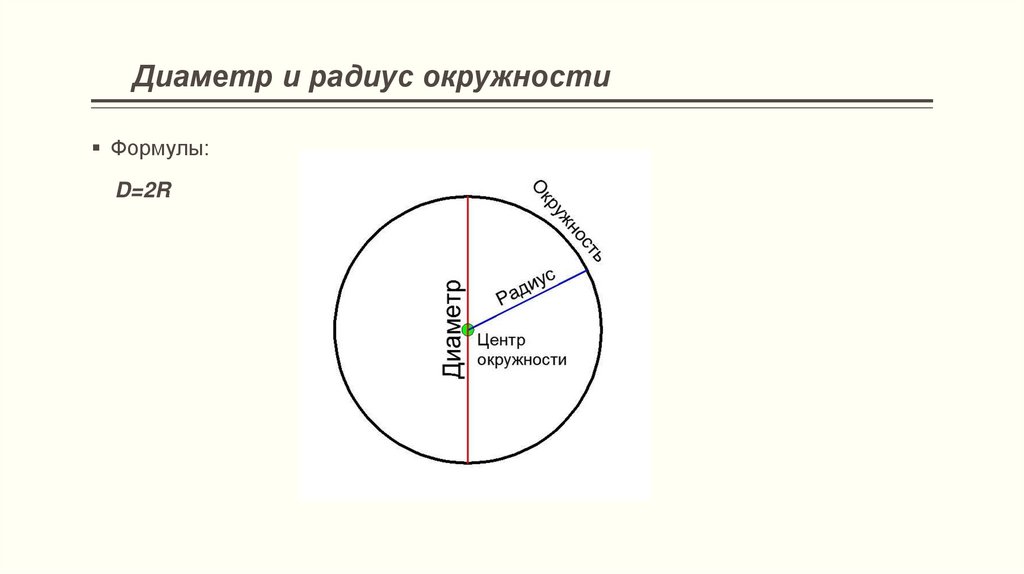
com
Радиус диаметра * 2?
Диаметр в два раза больше радиуса, поэтому уравнение для длины окружности с использованием радиуса равно удвоенному пи, умноженному на радиус.
Запрос на удаление |
Посмотреть полный ответ на flexbooks.ck12.org
Как нарисовать радиус в математике?
Шаг 1: Определите заданное значение радиуса или диаметра окружности. Шаг 2: Отрегулируйте стрелки компаса по радиусу окружности. Поместите иглу в центр круга и поверните ручку карандаша на бумаге на 360°. Вы получите круг заданного радиуса.
Запрос на удаление |
Полный ответ см. на сайте Study.com
Почему радиус — это тире?
Подтвержденный экспертом ответ
Если вы поместите два радиуса в один конец в круг, вы получите ту же длину, что и один диаметр. Таким образом, диаметр круга в два раза больше радиуса.
Следовательно, диаметр круга в два раза больше его радиуса.
|
Посмотреть полный ответ на brainly.in
Что такое краткая форма радиуса?
Типичное сокращение и имя математической переменной для радиуса — R или r.
Запрос на удаление |
Посмотреть полный ответ на en.wikipedia.org
Означает ли φ диаметр?
Символ диаметра в технике ⌀ часто ошибочно называют «фи», а символ диаметра иногда ошибочно набирают как Φ. Этот символ используется для обозначения диаметра круглого сечения; например, «⌀14» означает, что диаметр круга равен 14 единицам.
Запрос на удаление |
Посмотреть полный ответ на en.wikipedia.org
Что такое Ø В круге?
Символ диаметра (⌀), U+2300 в Unicode.
Запрос на удаление |
Полный ответ см.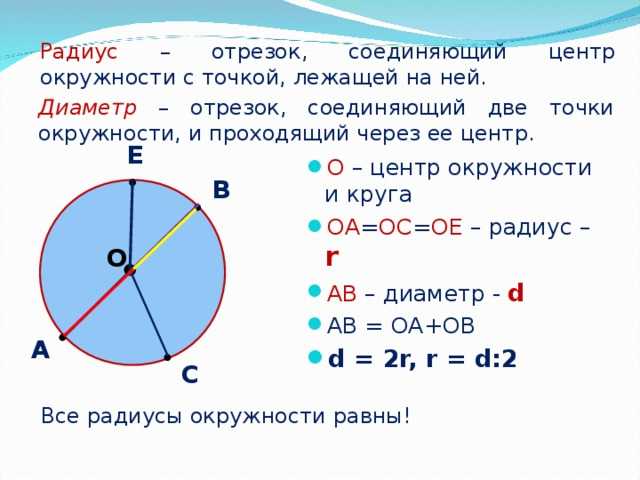
на en.wikipedia.org
Является ли Ø таким же, как Ø?
Ø эквивалентен гласной и букве Ö в исландском, шведском, эстонском и финском алфавитах и языках. Буква Ø также используется в орфографии некоторых африканских языков, таких как ленду, на котором говорят в Конго-Киншасе, и кунзиме, на котором говорят в Камеруне.
Запрос на удаление |
Посмотреть полный ответ на openspace.sfmoma.org
← Предыдущий вопрос
Есть ли 12-летние принцессы?
Следующий вопрос →
Содержит ли топленое масло витамин B12?
| Изменить радиус/диаметр | На панели направляющих введите Измерение. | |
| Переместите точку стрелки |
| |
| Переместите точку текста |
| |
| Переместить текст из центра | Нажмите и перетащите Расстояние | Отредактируйте параметр Distance в панели управления |
| Переместите центральную точку |
| |
| Отметить центр крестиком | На панели управления выберите Отметить Центр. | |
| Добавить этикетку |
|
