Онлайн калькулятор решение кубических уравнений: Решение кубических уравнений онлайн

Литры в миллиметры кубические — Онлайн-калькулятор

Литры в миллиметры кубические

28.11.2022

Миллиметры и литры представляют собой две меры измерения показателей, однако первые зачастую используются для обозначения длины, тогда как вторые для указания количества жидкости. В математических уравнениях, которые предоставляются студентам и школьникам нередко требуется совершить преобразование л в мм3. Для этого рекомендуется использовать онлайн калькуляторы, которые помогут быстро и правильно провести решение уравнения.

1 литр = 1000 миллилитров

Однако прежде чем приступить к решению, необходимо понимать сколько кубических миллиметров в литре, соотношение показателей составляет 1:1e-6. Поэтому, чтобы провести расчеты и правильно записать уравнение нужно использовать формулу разделения 1/1e-6, которая в примерах будет выглядеть следующим образом: если в условии задания указывает 12 или 34 миллиметров, то решение будет таким: 12/1e+6 = 1,2e-5 или 34/1e+6 = 3,4e-5. Если же нужно наоборот перевести л в мм3, тогда необходимо использовать умножение 1х1e+6, возьмем те же показатели миллиметров, поменяем на литры и получим формулы: 12х1е+6 = 1,2е+7, а 34х1е+6 = 3,4е+7.

Перевести из

метры кубическиемиллиметры кубическиесантиметры кубическиелитрымиллилитрыдюймы кубическиефуты кубическиеярды кубическиеАнглийская системажидкие минимыжидкая драхмажидкие унциипинтаджиллквартагаллонбаррел (нефть)бушельпекАмериканская система (liquid)жидкие минимыжидкая драхмажидкие унциипинтаджиллквартагаллонбаррель (нефть)Американская система (Dry)пинтаквартгаллонпекбушелькорд1 чайная ложка1 столовая ложкачашкастакан

Перевести в

метры кубическиемиллиметры кубическиесантиметры кубическиелитрымиллилитрыдюймы кубическиефуты кубическиеярды кубическиеАнглийская системажидкие минимыжидкая драхмажидкие унциипинтаджиллквартагаллонбаррел (нефть)бушельпекАмериканская система (liquid)жидкие минимыжидкая драхмажидкие унциипинтаджиллквартагаллонбаррель (нефть)Американская система (Dry)пинтаквартгаллонпекбушелькорд1 чайная ложка1 столовая ложкачашкастакан

Метры кубические

(м³)

Миллиметры кубические

(мм³)

Сантиметры кубические

(см³)

Литры

л

Миллилитры

мл

Дюймы кубические

(дюйм³)

Фут кубический

(фут³)

Ярд кубический

(ярд³)

Жидкие минимы

fl min (UK)

Жидкая драхма

fl dr (UK)

Жидкая унция

fl oz (UK)

Пинта

pt (UK)

Джиллы

gi (UK)

Кварты

qt (UK)

Галлоны

gal (UK)

Баррель нефтяной

bbl (oil UK)

Бушель

bu (UK)

Пек

(pk)

Жидкие минимы

fl min (US liq)

Жидкая драхма

fl dr (US liq)

Жидкие унции

fl oz (US liq)

Пинта

pt (US liq)

Джиллы

gi (US liq)

Кварты

qt (US liq)

Галлоны

gal (US liq)

Баррель нефтяной

bbl (oil US)

Пинта

pt (US dry)

Кварта

qt (US dry)

Галлоны

gal (US dry)

Пек

pk (US dry)

Бушель

bu (US dry)

Корд

cd (firewood)

Чайная ложка

штук

Столовая ложка

штук

Чашка

штук

Стакан

штук

Теорема Виета по алгебре 8 класса: формула, уравнения, примеры

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.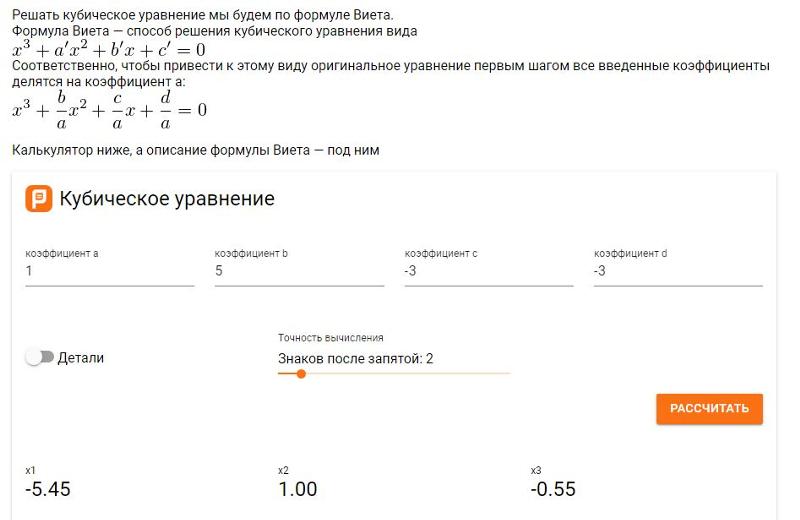 ru Математика Алгебра Теорема Виета: для квадратного/кубического уравнения, обратная

В данной публикации мы рассмотрим теорему Виета, определяющую взаимосвязи между коэффициентами многочлена и его корнями, а также, научимся применять ее на практике для решения задач.

• Формулировка теоремы
  • Квадратное уравнение
  • Кубическое уравнение
• Обратная теорема
• Примеры задач

Формулировка теоремы

Если c₁, c₂…, c_n являются корнями многочлена

xⁿ + a₁xⁿ⁻¹ + a₂xⁿ⁻² + … + a_n, где каждый корень взят соответствующее его кратности число раз, то:

коэффициенты a₁, a₂…, a_n можно выразить в виде симметрических многочленов от корней, т. е.:

• a₁ = −(c₁ + c₂ + … + c_n)
• a₂ = c₁c₂ + c₁c₃ + … + c₁c_n + c₂c₃ + … + c_n−1c_n
• a₃ = −(c₁c₂c₃ + c₁c₂c₄ + … + c_n−2c_n−1c_n)
• a_n−1 = (−1)ⁿ⁻¹(c₁c₂ … c_n−1 + c
  1c₂ … c_n−2c_n + … + c₂c₃ … c_n
• a_n = (−1)ⁿc₁c₂ … c_n

Другими словами, (−1)^ka_k равняется сумме всех возможных произведений из k корней.

Примечание: теорема названа в честь французского маетиматика Франсуа Виета.

Квадратное уравнение

Для квадратного уравнения ax² + bx + c = 0 с корнями x₁ и x₂ справедливо:

Если уравнение имеет вид x² + px + c = 0 (приведенная форма при a = 1), то:

Кубическое уравнение

Для кубического уравнения p(x) = ax³ + bx² + cx + d = 0 с корнями x₁, x₂ и x₃ справедливо:

Обратная теорема

Если для чисел x₁ и x₂ справедливы соотношения x₁ + x₂ = −p, а x₁x₂ = q, значит они являются корнями приведенного квадратного уравнения x² + px + c = 0.

Примеры задач

Задание 1
Дано квадратное уравнение x² − 70x + 600 = 0. Найдите его корни, используя теорему Виета.

Решение:
Используем соотношение корней для приведенного уравнения (т.к. a = 1):
x₁ + x₂ = 70
x₁x₂ = 600
Остается только подобрать числа x₁ и x₂, которые будут одновременно соответствовать данным уравнениям. В нашем случае – это 10 и 60.

Задание 2

Составьте уравнение, если известно, что его корни x₁ и x₂ равны 2 и −6, соответственно.

Решение:
Допустим, что у нас приведенное квадратное уравнение вида x² + px + c = 0. В этом случае, исходя из установленных для него соотношений корней получаем:
p = −(x₁ + x₂) = −(2 + (−6)) = 4
q = x₁x₂ = 2 ⋅ (−6) = −12
Получаем уравнение, подставив найденные значения в формулу общего вида: x² + 4x − 12 = 0.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Калькулятор кубических уравнений

| Taskvio

Как использовать этот инструмент кубического уравнения купить Taskvio.

com

Кубическое уравнение всегда с одной переменной является уравнением формы или Третьей степени, и уравнение это.

ax3 + bx2 + cx + d= 0 (где a не равно нулю)

Решения этого уравнения называются корнями кубической функции, определяемой левой частью уравнения. Если все коэффициенты a, b, c и d кубического уравнения являются действительными числами, то это минимум одного действительного корня (это верно для всех полиномиальных функций нечетной степени). Все корни кубического уравнения часто находятся следующими способами:

Алгебраически, то есть они будут выражены кубической формулой, включающей четыре коэффициента, четыре основных арифметических действия и корни n-й степени (радикалы). (Дополнительно это верно для квадратных (второй степени) и четвертых (четвертой степени) уравнений, но не для уравнений более высоких степеней, оно основано на теореме Абеля–Раффинга.)

Тригонометрически численные аппроксимации корней часто найдены с использованием алгоритмов поиска корней, таких как метод Ньютона.

Как решить кубическое уравнение?

Традиционный способ решения кубического уравнения состоит в том, чтобы уменьшить его до квадратного, а затем решить либо с помощью факторизации, либо по квадратной формуле.

Подобно тому, как квадратное уравнение имеет два действительных корня, кубическое уравнение может иметь, возможно, три действительных корня. Но в отличие от квадратного уравнения, которое может иметь любое действительное решение, кубическое уравнение имеет минимум один действительный корень.

Два других корня могут быть действительными или мнимыми.

Всякий раз, когда вам дают кубическое уравнение или любое уравнение, вам обычно нужно сначала привести его в стандартную форму.

Например, если вам дано что-то вроде этого, 3×2 + x – 3 = 2/x, вы перестроите его в форму качества и запишете так: 3×3 + x2 – 3x – 2 = 0. Тогда вы решите это любым подходящим методом.

Примеры кубического уравнения, которые помогут вам хорошо понять его, чтобы вы могли сделать это вручную. Предположим, у вас нет нашего инструмента или любого другого инструмента, который поможет вам решить вашу проблему. Так что в таком случае это вам очень поможет.

Теперь определите корни кубического уравнения вот так: 2×3 + 3×2 – 11x – 6 = 0

Теперь вот решение, внимательно прочитайте его, чтобы правильно понять.

Итак, если d = 6, то возможные множители равны 1, 2, 3 и 6.

Теперь примените теорему о множителях, чтобы методом проб и ошибок увидеть возможные значения.

f (1) = 2 + 3 – 11 – 6 ≠ 0

f (–1) = –2 + 3 + 11 – 6 ≠ 0

f (2) = 16 + 12 – 22 – 6 = 0

Следовательно, x = 2 — это первый корень.

Теперь мы собираемся получить противоположные корни уравнения, используя метод синтетического деления.

= (x – 2) (ax2 + bx + c)

= (x – 2) (2×2 + bx + 3)

= (x – 2) (2×2 + 7x + 3)

= (x – 2) (2x + 1) (x +3)

Следовательно, решения равны x = 2, x = -1/2 и x = -3.

Как использовать этот инструмент кубического уравнения купить Taskvio. com

Инструмент кубического уравнения от taskvio действительно отличный и очень полезный, он поможет вам решить ваши проблемы. Хотя этот инструмент является полностью бесплатным веб-инструментом, и вы можете использовать его из любого места, даже на своем телефоне. Вам не нужно носить с собой калькулятор и даже не нужно беспокоиться о формуле.

Независимо от того, знаете вы математику или нет, вы сможете использовать этот инструмент по всему миру, так что вам не о чем беспокоиться.

Теперь посмотрим, как использовать наш инструмент;

Итак, как вы можете видеть на своем экране, мы предоставили все поля, связанные с ним, например, каково значение a, b, c, d.

Вы должны ввести указанное значение в каждое из полей.

После того, как вы введете значение, вам просто нужно нажать на кнопку решения, и тогда вы получите ответ.

Вот что вам нужно сделать.

Find-The Remating-Factors of the Polynomial-Calculator-Google Suce

ALLBILDERVIDEOSBüchermapsNewshopping

Sucoptionen

44. Factory Polynomials Calculator-emathhelp 9000

4. › facto…

Калькулятор попытается разложить на множители любой полином (биномиальный, трехчленный, квадратичный и т. д.) с показанными шагами. Используются следующие методы: факторинговые мономы.

Калькулятор факторизации полиномов — показывает все шаги — MathPortal

www.mathportal.org › Решатели полиномов › полиномы…

Этот онлайн-калькулятор дает пошаговое объяснение того, как факторизовать многочлен. Он также поддерживает полиномы с более чем одной переменной. — QuickMath решатель. … Если мы выделим a из оставшихся двух членов, мы получим a (ax + 2y).

Ähnliche Fragen

Как найти остаток многочлена на калькуляторе?

Калькулятор факторинга — MathPapa

www.mathpapa.com › factoring-calculator

Пошаговый алгоритм расчета выражений! Этот калькулятор решит ваши проблемы.

Калькулятор коэффициентов — Symbolab

www. symbolab.com › … › Алгебра › Основные операции

Бесплатный калькулятор коэффициентов — квадратные уравнения сомножителей шаг за шагом. … упростить, решить, расширить, факторизовать, рационализировать. Просмотреть все, чередующийся тест, область …

Калькулятор факторинга — Wolfram|Alpha

www.wolframalpha.com › калькуляторы › факторинг-ка…

Бесплатный онлайн-решатель факторинга поможет вам факторизовать, расширить или упростить многочлены. Ответы, графики, альтернативные формы. Работает на платформе Wolfram|Alpha.

Калькулятор теоремы об остатках — Теорема о остатках с шагами мудрый …

Калькулятор факторинга — Mathway

www.mathway.com › Калькулятор › факторинг-калькулятор

Калькулятор факторинга преобразует сложные выражения в произведение простых множителей. Он может разлагать выражения с полиномами, включающими любое число …

Калькулятор факторинга полиномов — Бесплатный онлайн-калькулятор — Byju’s

byjus.