Радиус описанной около треугольника окружности: онлайн-калькулятор, формула
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
В публикации представлены онлайн-калькуляторы и формулы для расчета радиуса окружности, описанной около треугольника: произвольного, прямоугольного и равностороннего (правильного).
- Расчет радиуса окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Через катеты
- Через гипотенузу
- Равносторонний (правильный) треугольник
На рисунке ниже в качестве примера изображена окружность, описанная вокруг произвольного треугольника.
Инструкция по использованию: введите требуемые стороны треугольника (зависит от его вида), затем нажмите кнопку 
В результате будет вычислен радиус (R) окружности, описанной около фигуры.
Произвольный треугольник
Формула расчета
Прямоугольный треугольник
Через катеты
Формула расчета
Через гипотенузу
Формула расчета
Равносторонний (правильный) треугольник
Формула расчета
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Онлайн калькулятор длины окружности
org/BreadcrumbList»>С помощью данного бесплатного онлайн калькулятора вы сможете узнать длину окружности по радиусу или диаметру. Преимуществом сервиса является то, что перевод (конвертация) осуществляется автоматически. Просто вводите значения в соответствующие поля.
Длина окружности по радиусу
Радиус
Длина окружности 0.00
Длина окружности по диаметру
Диаметр
Длина окружности 0.00
Округлять до знаков после запятой (от 0 до 10)
Как узнать длину окружности
Чтобы вычислить длину окружности достаточно воспользоваться следующими формулами.
1. Формула длины для радиуса
ДЛИНА = 2 * π * РАДИУС
2.
Формула длины для диаметра
ДЛИНА = π * ДИАМЕТР
где π = 3.14159 (примерно равно; часто для простоты используют и вовсе 3.14)
Теперь, у вас всегда есть под рукой удобный и легкий онлайн калькулятор.
☕ Понравился обзор? Поделитесь с друзьями!
- Калькулятор скидок онлайн
- Онлайн калькулятор объема цилиндра
Добавить комментарий / отзыв
VK
Задать вопрос ⚑
Свежие обзоры
- Синтаксис (языки программирования): что это такое? Что такое?
- Что такое Скетч и Скетчинг? Что такое?
- Нужен ли дома мощный компьютер? Технические советы
- Рекурсия: что это такое? Что такое?
Программы (Freeware, OpenSource.
..)
- Безопасность
- Интернет и Сеть
- Мультимедиа
- Оптимизация
- Офис
- Разработка
- Жесткий диск и файлы
- Система
Еще программы / обзоры
-
✎
Перевод унций в граммы и обратно (Авердюпуа и Тройская) Конвертеры -
✎
Перевод пинт в литры и обратно Конвертеры -
✎
Перевод ярдов в метры и обратно Конвертеры -
✎
Перевод галлонов в литры и обратно Конвертеры -
✎
Перевод секунд в часы и обратно Конвертеры -
✎
Перевод секунд в минуты и обратно Конвертеры
Калькулятор радиуса окружности
РЕКЛАМА
Указано:
Окружность (C) Площадь (A) Диаметр (D)
Окружность (C)
MMCMDMMKMINFTYDMINMI
(A)
9000mm MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM MM El (C).
РЕКЛАМА
РЕКЛАМА
Содержание
Получите виджет!
Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Получить код
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
ОБРАТНАЯ СВЯЗЬ
Наш калькулятор радиуса круга в основном предназначен для нахождения радиуса круга по значениям длины окружности, площади или диаметра.
Что такое радиус круга?Все вы, возможно, знакомы с кругом, хорошо известной и широко используемой геометрической фигурой.
«Расстояние от центра окружности до любой из ее точек на окружности называется радиусом»
Как найти радиус окружности?
В геометрии окружность определяется многими связанными объектами.
И если вы хотите найти его радиус при разных параметрах, то к ним относятся: 9{2}=24,840\)
\(r=\sqrt{24,840}\)
\(r=4,983\)
Как работает калькулятор радиуса окружности?По правде говоря, наш калькулятор довольно прост в использовании, если вы придерживаетесь следующего руководства по использованию!
Ввод:
- Из первого выпадающего списка выберите параметр, с которым вы хотите провести расчеты
- После этого введите его значение вместе с единицей измерения, выбранной из следующего списка
- Наконец-то попал в калькукатре вутон
Вывод:
- Радиус, площадь, диаметр и длина окружности
Из источника Википедии: Радиус, Формула, Использование в системах координат
Из источника Академии Хана: Радиус, диаметр, длина окружности и π, Маркировка, Площадь частей кругов источник Lumen Learning: Круги, Уравнение круга в стандартной форме, Общая форма круга
Положение точки относительно окружности
Учитывая уравнение окружности и координаты точки, как мы узнаем, что точка находится внутри, снаружи или на окружности?
Этот урок ответит именно на этот вопрос.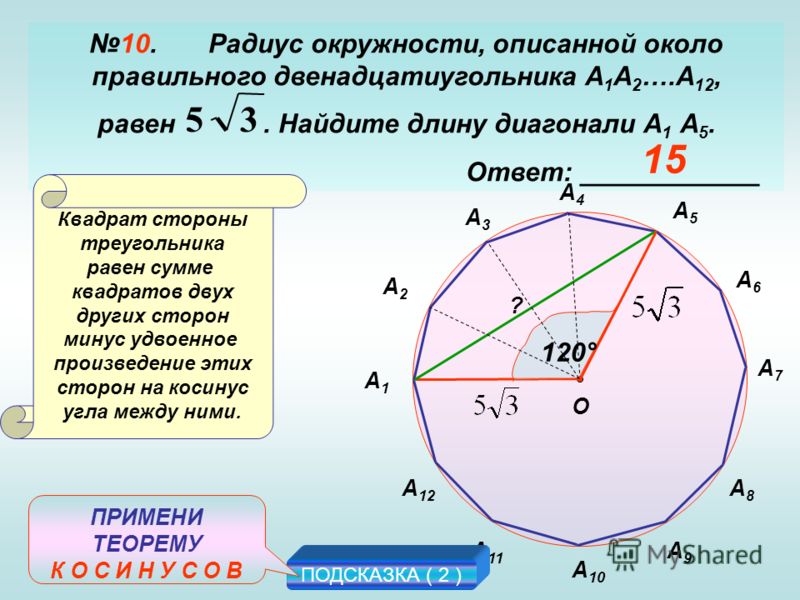
2} \)
Теперь точка будет лежать снаружи, внутри или внутри круга, когда CP > r , CP = r или CP < r соответственно. По перераспределению терминов, мы получаем необходимые условия как
Вне: x 1 2 + Y 1 2 — R 2 > 0
ON: x 1 > 00006
ON: x 1 > 00006
ON + y 1 2 – r 2 = 0
Внутри: x 1 2 + y 1 2 – r 2 < 0
Это эквивалентно подстановке координат точки в уравнение окружности и проверке ее знака.
Если полученное выражение положительное, то точка лежит вне круга, если ноль, то на окружности, а если отрицательное, то внутри круга. Аккуратный.
Теперь перейдем к общему уравнению: x 2 + y 2 + 2gx + 2fy + c = 0 92} \).
Comparing this with the radius, we get the conditions as:
Outside: x 1 2 + y 1 2 + 2gx 1 + 2fy 1 + c > 0
ON: x 1 2 + Y 1 2 + 2GX 1 + 2FY 1 + C = 0
Внутри: x 1 + 9999999.9019 29 29 29 29 2902.19 29 29 2 2
Хм. Получаем снова что-то подобное. Выражение, знак которого мы проверяем, находится в левой части уравнения окружности, в котором координаты (x 1 , y 1 ) подставлены вместо (x, y) . .
На самом деле, это выражение будет представлять для нас большой интерес на протяжении всего нашего путешествия по коническим сечениям.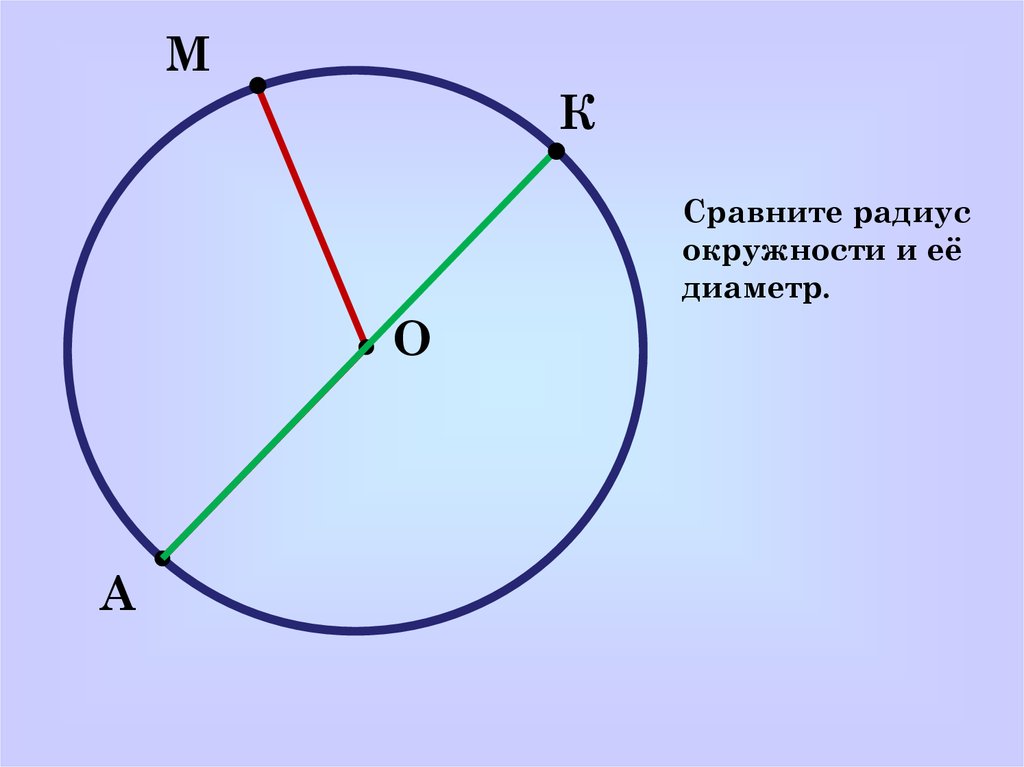
Итак, мы дадим ему имя: S 1
Пусть S = x 2 + y 2 + 2gx + 2fy + c , а P — точка (x 1 , y 1 ) . Тогда S 1 = x 1 2 + y 1 2 + 2gx 1 + 2fy 1 + c 90.
А положение точки P определяется проверкой знака S 1 , как показано выше!
- Точка (x 1 , y 1 ) лежит снаружи, на или внутри круга x 2 + y 2 — R 2 = 0 Соответственно, как выражение x 1 2 + Y 1 2 — R 2 9020 9 . Zero . Zero . или OKEL IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS IS OLTID69 .
