Ранг матрицы методом элементарных преобразований: Элементарные преобразования. Ранг матрицы. Решение однородных систем уравнений.

15. Вычисление ранга матрицы методом элементарных преобразований.

II. Метод элементарных преобразований

Элементарными преобразованиями матрицы называют следующие:

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число, отличное от нуля.

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число.

4. Вычёркивание строки (столбца), все элементы которой равны нулю.

З а м е ч а н и е . 1) Элементарные преобразования не меняют ранга матрицы; 2) матрицы, полученные одна из другой путём элементарных преобразований, называются эквивалентными (обозначаются A ~В).

Чтобы вычислить ранг матрицы А, путём элементарных преобразований сводим её к ступенчатому виду (в частности к треугольному), выделяя наибольший минор, отличный от нуля.

A~

rangA = rangB= k

Пример 2.  Найти ранг матрицы

Решение. 1) переставим строки матрицы: 

2) первую строку умножим на 2 и сложим со второй:  ,

3)  первую строку умножим на 3 и сложим с третьей, одновременно вторую строку   прибавим к четвёртой:

,

4) умножим вторую строку на   ,  третью на   , пятую на   ,четвёртую вычеркнем :

,

5) прибавим вторую строку к третьей и четвёртой:

~  ,

Ранг последней матрицы, а значит и исходной, равен двум: rangA = 2.

Пример 3. Найти ранг матрицы

rang A=2

Над матрицей А были проведены следующие преобразования:

а) Первая строка матрицы А умножается на (- 2) и прибавляется ко второй.

б ) Первая строка матрицы А умножается на (- 1) и прибавляется к последней.

в) Вторая строка матрицы А умножается на (- 2) и прибавляется к третьей.

г) Нулевая строка вычёркивается.

Оставшаяся матрица содержит миноры второго порядка отличные от нуля. Строки такой матрицы называются линейно независимыми, их число равно рангу матрицы

16. Теорема Кронекера-Капелли. Решение систем на основе теоремы Кронекера-Капелли.

Теорема Кронекера-Капелли

Матрица, получающаяся конкатенацией матрицы   и столбца правых частей 

называется расширенной матрицей системы линейных уравнений.

Т

Теорема [Кронекер, Капелли]. Система совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:

При выполнении этого условия, система имеет единственное решение, если число неизвестных   совпадает с общим значением ранга

  , и бесконечное множество решений, если   меньше этого значения.

Доказательство необходимости. Пусть существует решение   системы, тогда

т.е. столбец   линейно выражается через столбцы  . Но тогда

Следовательно  .

Доказательство достаточности проводится в следующем пункте. ♦

§

Обозначение   для ранга матрицы   соответствует по смыслу этому же обозначению в методе Гаусса: после приведения к трапециевидному (или треугольному) виду в системе л.у. должно остаться ровно   линейно независимых уравнений, явно содержащих неизвестные. Это утверждение вытекает из способа вычисления ранга матрицы по методу элементарных преобразований

.

П

Пример. Исследовать совместность системы уравнений

в зависимости от значения параметра  .

Решение.  В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы  . Если он отличен от нуля — система совместна.

. По теореме Крамера при   и при   решение системы единственно:

Осталось исследовать критические случаи:   и  : определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При   имеем

и система совместна. Она эквивалентна единственному уравнению

которое имеет бесконечно много решений.

При  :

и система несовместна.

Ответ. Система несовместна при  ; она имеет бесконечное множество решений при   и единственное решение при  .

!

Что можно сказать о совместности или несовместности случайным образом составленной системы из   линейных уравнений относительно  неизвестных? При   система, 

как правило, совместна и имеет бесконечное множество решений. В самом деле, если выбрать минор порядка   в матрице системы  , элементы которой считаются случайными, то этот минор будет «с вероятностью 1» отличен от нуля (см. рассуждения в предыдущем пункте о совместности системы л.у. при  ). Таким образом,  , и автоматически получаем, что   (поскольку ранг не может больше количества строк матрицы). Если же   то такаяпереопределенная система, как правило, несовместна. Рассуждения для доказательства правдоподобия этого утверждения могут быть следующими. Выберем произвольным образом в рассматриваемой системе какую-то подсистему, состоящую из   уравнений. Она, как правило, будет иметь единственное решение. Теперь составим другую подсистему, хотя бы одним уравнением отличающуюся от предыдущей (поскольку   такое всегда можно сделать). Новая подсистема снова, как правило, будет иметь единственное решение. Однако решения этих двух подсистем будут, как правило, различными и, следовательно, сама основная система не будет иметь решения. В этом последнем случае переопределенной системы имеется, однако, важный исключительный, который рассмотрим ☞ 

НИЖЕ.

=>

Система однородных уравнений

всегда совместна: она имеет тривиальное решение  . Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.

П

Пример. Найти условие, при котором три точки плоскости с координатами   и   лежат на одной прямой.

Решение. Будем искать уравнение прямой в виде   при неопределенных коэффициентах  . Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений:

Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора   при хотя бы одном из чисел отличном от нуля):

?

Доказать, что для совместности системы

необходимо, чтобы было выполнено условие

Является ли это условие достаточным для совместности?

И

Исторический комментарий. Понятие ранга матрицы и результат, известный в литературе как «теорема Кронекера–Капелли», были открыты несколькими независимыми исследователями. Первое доказательство этой теоремы принадлежит Ч.

Л.Додсону, оно было напечатано им в 1867 г. в книге

Источник.  An elementary treatise on determinants

в следующей формулировке.

Теорема. Для того чтобы система   неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.

понятие, как вычислить, методы нахождения, пример

Содержание:

• Что такое ранг матрицы — понятие, для чего используется
• Как определить ранг матрицы, примеры
  • Нахождение ранга матрицы по определению
  • Нахождение ранга матрицы методом окаймляющих миноров
  • Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)

Содержание

• Что такое ранг матрицы — понятие, для чего используется
• Как определить ранг матрицы, примеры
  • Нахождение ранга матрицы по определению
  • Нахождение ранга матрицы методом окаймляющих миноров
  • Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)

Что такое ранг матрицы — понятие, для чего используется

Возьмем случайную матрицу \(\underset{m\times n}A\) и натуральное число k, меньшее или равное числам m и n. k\) миноров k-го порядка.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Например, из \(\underset{3\times 4}A\) мы получим 12 миноров 1-го порядка, 18 — 2-го и 4 — 3-го. 
Если среди матричных элементов \(a_{ij}\) (i = 1, 2 … m; j = 1, 2 … n) есть отличные от нуля, то существует натуральное число r, которое обладает следующими свойствами:

1. У матрицы А есть ненулевой минор r-го порядка.
2. Любой из миноров этой матрицы порядка r + 1 или выше будет нулевым.

Число r с такими характеристиками — ранг матрицы A. 

Ранг матрицы — это наивысший порядок ее ненулевых миноров.

Устоявшегося обозначения ранга не существует, чаще всего его записывают как \(r (A)\) или rang A, где А — обозначение матрицы. Понятие ранга обычно используют в ситуациях, когда необходима проверка совместимости системы линейных уравнений.

В случае, когда базисный минор матрицы \(\underset{3\times 4}A\) имеет порядок r < m, то как минимум одна ее строка будет не базисной. Согласно теореме о базисном миноре, в таком случае строки рассматриваемой матрицы \(\underset{3\times 4}A\) линейно зависимы. В случае, когда r = m, все строки являются базисными и линейно независимыми.

Из этого можно сделать следующие выводы:

1. Когда ранг матрицы A меньше числа ее строк, они линейно зависимы. В случае, когда он равен числу строк, все они линейно независимы.
2. Всякие r + 1 строк матрицы A ранга r линейно зависимы.
3. Ранг любой матрицы равняется максимальному числу ее линейно независимых строк.

Теорема 1

Максимальное число линейно независимых столбцов матрицы равно максимальному количеству ее линейно независимых строк и равно ее рангу.

Следствие

Ранг не меняется при транспонировании.

Как определить ранг матрицы, примеры

Нахождение ранга матрицы по определению

Определить ранг можно, перебрав все миноры.

Теорема 2

Если из элементов матрицы можно составить ненулевой минор n-го порядка, то ранг равен n.

С учетом данной теоремы перебор производится по следующему алгоритму:

1. Перебрать миноры 1-го порядка. Если наличествует хоть один ненулевой минор 1-го порядка, ранг как минимум равен 1.
2. Перебрать миноры 2-го порядка. Если все они нулевые, ранг — единичный. В противном случае переходим к пункту 3.
3. Перебрать миноры 3-го порядка. Если все они нулевые, ранг — два. В противном случае переходим к минорам 4-го, 5-го порядков и т. д.

Нахождение ранга матрицы методом окаймляющих миноров

Этот метод дает возможность сократить вычисления.

Окаймляющий минор — минор (n+1)-го порядка матрицы А. Он окаймляет минор n-го порядка, если матрица, соответствующая минору (n+1)-го порядка, содержит матрицу, которая соответствует упомянутому минору n-го порядка. Таким образом, чтобы получить окаймляемый минор, надо взять окаймляющий его и вычеркнуть одну строку и один столбец.

Пример № 1

Вычислить ранг матрицы

\(\begin{pmatrix}2&3&7&11\\1&2&4&7\\5&0&10&5\end{pmatrix}.\)

Решение:

В матрице есть элементы, отличные от нуля, значит, ее ранг больше единицы.

\(М_2\;=\;\begin{pmatrix}2&3\\1&2\end{pmatrix}\;=\;4\;-\;3\;=\;1\; \neq 0. \)

Раз ранг больше двух, нужно рассмотреть миноры 3-го порядка, содержащие вышеприведенный минор \(М_2.\)

\(М_3\;=\;\begin{pmatrix}2&3&7\\1&2&4\\5&0&10\end{pmatrix}\;=\;5\;\times\;\begin{pmatrix}3&7\\2&4\end{pmatrix}\;+\;10\;\times\;\begin{pmatrix}2&3\\1&2\end{pmatrix}=\;5\;\times\;(12\;-\;14)\;+\;10\;\times\;(4\;-\;3)\;=\;-\;10\;+\;10\;=\;0. \)

\(М_3\;=\;\begin{pmatrix}2&3&11\\1&2&7\\5&0&5\end{pmatrix}\;=\;5\;\times\;\begin{pmatrix}3&11\\2&7\end{pmatrix}\;+\;5\;\times\;\begin{pmatrix}2&3\\1&2\end{pmatrix}=\;5\;\times\;(21\;-\;22)\;+\;5\;\times\;(4\;-\;3)\;=\;-\;5\;+\;5\;=\;0.\)

Как мы видим, все миноры 3-го порядка нулевые, значит, наибольший ненулевой минор относится ко 2-му порядку.

Ответ: 2.

Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)

В большинстве случаев нахождение ранга перебором миноров требует долгих вычислений. Более простой способ решения этой задачи базируется на элементарных преобразованиях по методу Гаусса, сохраняющих ранг исходной матрицы A и приводящих ее к ступенчатому виду. К таким преобразованиям относятся:

1. Вычеркивание нулевой строки или столбца. Нулевая строка не может быть базисной строкой, ведь в таком случае базисные строки были бы линейно зависимы, а это противоречит теореме о базисном миноре.
2. Перестановка двух строк между собой. Другие строки в этом случае не меняются. Это утверждение непосредственно следует из теоремы о базисном миноре, согласно которой ранг равняется максимальному числу линейно независимых строк.
3. Умножение любой строки на число\( \lambda \neq 0\). 
4. Вычеркивание строки, которая является линейной комбинацией других строк.
5. Прибавление к одной строке другой строки, умноженной на число \(\lambda \neq 0\).
6. Транспонирование.

Проведем подробный разбор пункта 5. Представим, что к q-й строке прибавлена p-я строка, умноженная на \(\lambda \neq 0\). В итоге появится новая матрица A′. Если q-я и p-я строки — базисные, это преобразование не изменит значения базисного минора. В случае, когда только p-я строка — базисная, q-я строка является их линейной комбинацией. Умножение на \(\lambda\) это не изменит, и такую строку допустимо удалить при преобразовании.

Если q-я строка — базисная, а p-я — нет, то после преобразования \(r_{q} \rightarrow r_{q} + \lambda r_{p}\) базисный минор \(\triangle_{r}\) перейдет в минор \(\triangle’_{r}\) матрицы A′, который отличается от \(\triangle_{r}\) тем, что вместо элементов строки \(r_{q}\) содержит элементы строки\( r_{q} + \lambda r_{p}\). {(1)} = \triangle_r.\)
Как мы видим, при преобразовании\( r_{q} \rightarrow r_{q} + \lambda r_{p}\) базисный минор ни при каких условиях не изменяется. Из этого делаем вывод, что r (A) = r (A′).

Примечание

Матрицы A и B эквивалентны по рангу и обозначаются A ∼ B в том случае, когда B можно получить из A путем элементарных преобразований, перечисленных выше.

Пример № 2

Вычислить ранг матрицы

\(В\;=\;\begin{pmatrix}4&0&-1\\0&2&4\\4&4&1\end{pmatrix}.\)

Решение:

Прибавим первую строку матрицы B, умноженную на -1, к ее третьей строке. После произведения необходимых расчетов получим:

\(В\;\sim\;\begin{pmatrix}4&0&-1\\0&2&4\\0&4&2\end{pmatrix}.\)

Умножим вторую строку получившейся матрицы на -2 и прибавим результат умножения к третьей строке:

\(В\;\sim\;\begin{pmatrix}4&0&-1\\0&2&4\\0&0&-6\end{pmatrix}. \)

Итак, исходная матрица 3-го порядка является невырожденной, поскольку ее определитель равен

\(4 \times 2 \times (-6) = -48 \neq 0.\)

Ответ: 3.

Насколько полезной была для вас статья?

Рейтинг: 2.33 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Элементарные преобразования матрицы: Решенные примеры задач

с ответами, Решение — Элементарные преобразования матрицы: Решенные примеры задач | 12-я математика: БЛОК 1: Применение матриц и определителей

Глава:

12-я математика: БЛОК 1: Применение матриц и определителей

ранжирование матриц методом минора , ранг матриц методом редукции строк , обратная матриц методом Гаусса-Жордана

Форма строки-эшелона

Пример 1.13

Приведите матрицу к форме строки-эшелона.

Решение

Примечание

Это тоже строково-ступенчатая форма данной матрицы.

Таким образом, ступенчатая форма матрицы не обязательно уникальна.

 

Пример 1.14

Приведите матрицу к строчно-эшелонной форме.

Решение

Ранг матрицы

Пример 1.15

Найдите ранг каждой из следующих матриц:

Решение

(i) Пусть A =. Тогда A — матрица порядка 3 × 3. Значит, ρ(A) ≤ min {3, 3}  = 3. Наивысший порядок миноров матрицы A равен 3 . Существует только один минор третьего порядка A .

 = 3 (6−6) − 2 (6−6) + 5 (3 − 3) = 0. Итак, ρ(A) < 3.

 Далее рассмотрим миноры второго порядка A .

Мы находим, что минор второго порядка = 3 − 2 = 1 ≠ 0 . Итак, р(А) = 2.

(ii) Пусть A = . Тогда A — матрица порядка 3×4. Таким образом, ρ(A) ≤ min {3, 4}  = 3.

Наивысший порядок миноров A равен 3 . Мы ищем ненулевой минор третьего порядка A . Но

мы обнаруживаем, что все они исчезают. На самом деле у нас есть

Итак, ρ( A ) < 3. Далее мы ищем ненулевой минор второго порядка для A .

Мы находим, что  = -4+9 =5 ≠ 0 . Итак, р(А) = 2.

Примечание

Нахождение ранга матрицы путем поиска ненулевого минора высшего порядка довольно утомительно, когда порядок матрицы достаточно велик. Есть еще один простой способ найти ранг матрицы, даже если порядок матрицы довольно высок. Этот метод заключается в вычислении ранга эквивалентной ступенчато-строковой формы матрицы. Если матрица представлена ​​в виде ступенчатой ​​строки, то все элементы ниже главной диагонали (это линия, соединяющая позиции диагональных элементов  а 11, а 22, а 33, л. матрицы) равны нулю. Итак, проверить, равен ли минор нулю, довольно просто.

 

. ) Пусть А = . Тогда A — матрица порядка 3 3 × и ρ(A) ≤ 3

 Минор третьего порядка |A| =   = (2) (3)( 1) = 6 ≠ 0 . Итак, р(А) = 3.

Пример 1.17

Найдите ранг матрицы, приведя ее к строчно-эшелонной форме.

Решение

Пусть A = . Применяя элементарные операции со строками, получаем

Последняя эквивалентная матрица имеет строчно-эшелонную форму. Он имеет две ненулевые строки. Итак, ρ (A)= 2.

 

Пример 1.18

Найдите ранг матрицы, приведя ее к строчно-эшелонному виду.

Решение

Пусть A — матрица. Выполняя элементарные операции над строками, получаем

Последняя эквивалентная матрица имеет форму строки-эшелона. Он имеет три ненулевых строки. Итак, ρ( A ) = 3.

Элементарные операции со строками над матрицей могут быть выполнены путем предварительного умножения данной матрицы на особый класс матриц, называемых элементарными матрицами.

Пример 1.19

Показать, что матрица невырожденная, и свести ее к единичной матрице с помощью элементарных преобразований строк.

Решение

Пусть A = . Тогда |A| = 3 (0+2) – 1(2+5) + 4(4-0) = 6-7+16 ≠ 0. Итак, A неособо. Сохраняя в качестве нашей цели единичную матрицу, мы последовательно выполняем операции со строками над A следующим образом:

Метод Гаусса-Жордана

Пример 1.20

Найдите обратную неособую матрицу A = методом Гаусса-Жордана.

Решение

Применяя метод Гаусса-Жордана, получаем Метод Гаусса-Жордана.

Решение

Применяя метод Гаусса-Жордана, получаем

• Предыдущая страница
• Следующая страница

Теги : с ответами, решение , 12th Mathematics : UNIT 1 : Применение матриц и определителей Применение матриц и определителей: элементарные преобразования матрицы: решенные примеры задач | с ответами, решение

Элементарное преобразование матрицы — введение, определение, методы, расчет и решенные примеры

Матрица — это прямоугольное расположение чисел, символов или символов, представляющее набор данных в любой системе.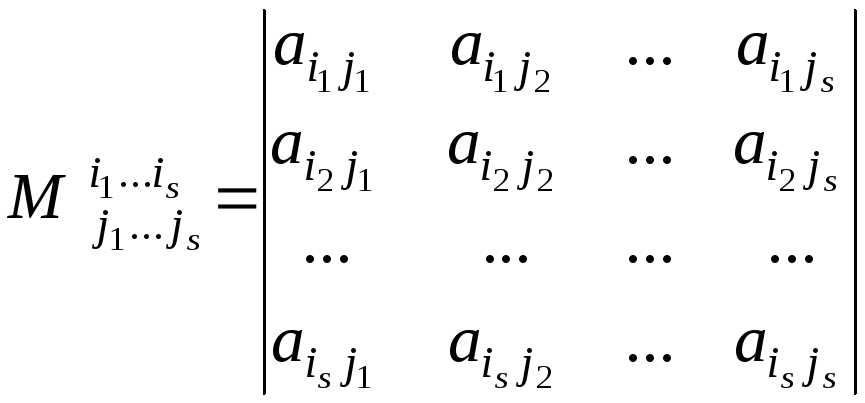 Элементы матрицы расположены в строках и столбцах. Порядок матрицы — это представление количества ее строк и столбцов в виде MxN, где m — количество строк, а n — количество столбцов. Две матрицы называются равными, если они имеют одинаковый порядок и их элементы одинаковы. Существует разница между терминами «равные матрицы» и «эквивалентные матрицы». Эквивалентность двух матриц обозначается символом «~». Две матрицы называются эквивалентными, если одну матрицу можно изменить элементарным преобразованием матрицы, чтобы получить другую матрицу.

Что такое элементарное преобразование матрицы?

Элементарные преобразования — это операции, выполняемые над строками и столбцами матриц для преобразования их в другую форму, чтобы упростить вычисления. Понятие «Что такое элементарные преобразования» используется в методе Гаусса для решения линейных уравнений, определения ступенчатой ​​формы матрицы и других операций, связанных с матричным представлением системы уравнений. Он также используется для нахождения обратных матриц, определителей матриц и решения системы линейных уравнений. Для выполнения элементарных преобразований между любыми двумя матрицами порядок двух матриц должен быть одинаковым.

Элементарные преобразования строк

Преобразования строк выполняются только на основе нескольких наборов правил. Индивидуум не может выполнять какие-либо другие операции со строками, кроме указанных ниже правил. Существует три вида элементарных преобразований строк.

1. Замена строк в матрице: В этой операции вся строка в матрице заменяется другой строкой. Это символически представлено как Ri ↔ Rj, где i и j — два разных номера строки.

2. Масштабирование всей строки с ненулевым числом: Вся строка умножается на одно и то же ненулевое число. Это символически представлено как Ri → k Ri, что указывает на то, что каждый элемент строки масштабируется с коэффициентом «k».

3. Добавление одной строки к другой строке, умноженное на ненулевое число: Каждый элемент строки заменяется числом, полученным путем прибавления его к масштабированному элементу другой строки. Он символически представляется как Ri → Ri + k Rj.

Две матрицы называются эквивалентными по строкам тогда и только тогда, когда одна матрица может быть получена из другой путем выполнения любого из приведенных выше элементарных преобразований строк.

Пример для матриц, эквивалентных строкам

1. Покажите, что матрицы A и B эквивалентны строкам, если 

\[A=\begin{bmatrix}1 & -1 & 0 \\2 & 1 & 1\end{bmatrix} \textrm{and B}=\begin{bmatrix}3 & 0 & 1 \\0 & 3 & 1\end{bmatrix}\] 

Решение:

Рассмотрим матрицу A. Примените преобразование строк так, чтобы R1 → R1 + Р2

Применение преобразования строки к первой строке, A11 = 1 + 2, A12 = -1 + 1 и A13 = 0 + 1

Таким образом, матрица A будет равна  

\[\begin{bmatrix}3 & 0 & 1 \\2 & 1 & 1\end{bmatrix}\]

Теперь давайте сохраним первую строку и применим преобразование строки ко второй строке, так что

R2 → 3 R2 — R1

Итак, элементы второй строки в A будет дано следующим образом:

A21 = 2 x 3 — 3 = 3

A22 = 1 x 3 — 0 = 3

A23 = 1 x 3 — 1 = 2

Таким образом, матрица A будет равна R1 и примените преобразование строки к R2 так, чтобы R2 → R2 — R1.

A21 = 3 — 3 = 0

A22 = 3 — 0 = 3

A23 = 2 — 1 = 1

Таким образом, матрица A будет равна матрице B.

\[\begin{bmatrix}3 & 0 & 1 \\0 & 3 & 1\end{bmatrix}\]

Отсюда мы можем заключить, что матрицы A и B эквивалентны по строкам.

Элементарные преобразования столбцов

Существует также несколько наборов правил, которым необходимо следовать при выполнении преобразований столбцов. Существует три различных формы преобразования элементарных столбцов. Никакие другие преобразования столбцов, кроме этих трех, не допускаются.

1. Замена столбцов в матрице: В этой операции весь столбец в матрице заменяется другим столбцом. Он символически представлен как Ci ↔ Cj, где i и j — два разных номера столбца.

2. Умножение всего столбца на ненулевое число: Весь столбец умножается или делится на одно и то же ненулевое число. Он символически представлен как Ci → k Ci, что указывает на то, что каждый элемент столбца умножается на коэффициент масштабирования «k».

3. Добавить один столбец к другому столбцу, масштабированному ненулевым числом: каждый элемент столбца заменяется числом, полученным путем добавления его к масштабированному элементу другого столбца. Он символически представляется как Ci → Ci + k Cj.

Две матрицы называются эквивалентными по столбцам тогда и только тогда, когда одна матрица может быть получена из другой путем выполнения любого из приведенных выше преобразований элементарных столбцов.

Интересные факты

• Равные матрицы имеют одинаковый порядок и одинаковые элементы.

• Эквивалентные матрицы — это матрицы с одинаковым порядком и сходными элементами.

  No related posts.