Расчет диаметра окружности через длину окружности: Онлайн калькулятор диаметра круга. Как узнать диаметр круга, окружности.

Длина окружности онлайн, формулы и примеры

Окружность представляет собой замкнутую кривую, все точки которой находятся на одинаковом расстоянии от центра. Центр окружности – это точка, которая находится на равном расстоянии от всех точек, расположенных на одной прямой. Также стоит различать два понятия: окружность и круг. Круг – это просто часть некого пространства, которое ограничено окружностью. А окружностью представляет собой совокупность точек на одной прямой. Понятия связаны, но имеют существенные различия.

• Длина окружности через радиус
• Длина окружности через диаметр
• Длина окружности через площадь круга

Через радиус

Для начала стоит сказать, что R- радиус окружности, Р – длина (периметр) окружности. Одним из самых простых способов для ее вычисления является следующий:

Р = 2R * π

где R — Радиус.

Радиус (R):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Дана окружность. Учащемуся требуется найти длину окружности, когда у него есть только радиус. Радиус равен 15 см, тогда длина окружности? Решение. Находим неизвестную величину по вышеупомянутой формуле: Р = 2R * π, восполняя данные, которые были указаны в условии. К слову, π — это постоянная математическая величина. Чаще всего в ответах к заданиям она и остается в таком виде, хотя у нее есть числовое значение, которое равно 3,14. Р = 2 * 15 * 3,14 = 9 см. см. Решение не вызывает никаких вопросов, так как для нахождения неизвестной требуется только радиус окружности.

Через диаметр

Диаметр – это радиус, который увеличили в два раза. Он тоже проходит через центр окружности и касается контура, только уже в двух местах.

Но через диаметр можно найти переменную – длину (периметр) окружности. Это действие выполнимо благодаря следующей формуле:

P = D * π

где D – это диаметр окружности.

Диаметр (D):

ммсмдмм

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Учащемуся необходимо найти длину (периметр) окружности. Из известных данных только диаметр (D), который равен 20 см. Решение. Используем формулу, которая была указана выше и подставим известные данные: Р = 20 * 3,14 = 6 см.

Через площадь окружности

Есть еще один способ, который поможет найти длину окружности. Этот способ основан на площади окружности. Стоит упомянуть, что площадь можно найти по следующей формуле: S= πR², где S – это площадь окружности, а R – радиус окружности. А длину окружности находят следующим образом:

P = √(S * 4π)

где S — это площадь окружности.

Площадь круга (S):

мм²см²дм²м²

Цифр после запятой:

012345678910Результат в: ммсмдмм

Пример. Дана окружность, а учащемуся требуется найти ее длину (периметр). Он имеет следующие данные: R = 3 см. Тогда чему равна длина окружности. Решение. Сначала требуется найти площадь вышеуказанной фигуры: S = πR² = 3,14 * 9 = 28,26 см. Далее можно уже находить и длину окружности, подставляя все уже известные данные в формулу, которая была упомянута выше: P = √(S * 4π) = √(28,26 * 4 * 3,14) = 1,9 см.

Каждая окружность обладает некоторыми переменными, которые можно и нужно уметь различать. Например, радиус – это расстояние от центра окружности до любой точки, которая лежит на окружности. Диаметр – это то понятие, которое связано с радиусом. Он представляет собой отрезок, который проходит через центр окружности и соединяет точки на этой же окружности, которые лежат напротив друг друга. Диаметр – это увеличенный вдвое радиус. Любая фигура имеет площадь. Окружность не является исключением. Таким образом, окружность является довольно важной фигурой, которая имеет множество составляющих, которые позволяют находить ее длину несколькими способами.

Определение диаметра по длине окружности онлайн. Как рассчитать длину окружности, если не указан диаметр и радиус круга

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415 .

Определение периметра круга

Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)

Формула периметра круга

Периметр круга радиуса \(r\) :

\[ \LARGE{P} = 2 \cdot \pi \cdot r \]

\[ \LARGE{P} = \pi \cdot d \]

\(P \) – периметр (длина окружности). 0}{n}}=\frac{2τ}{2τ»} \)

Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть

\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)

С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:

\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)

Из последних двух равенств получим, что

\(\frac{C}{C»}=\frac{2τ}{2τ»} \)

\(\frac{C}{2τ}=\frac{C»}{2τ»} \)

Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть

\(\frac{C}{2τ}=const \)

Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом

\(\frac{C}{2τ}=π \)

Окончательно, получим, что длина окружности (периметр круга) определяется формулой

\(C=2πτ \)

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.

У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.

• Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
• Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
• Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.

Как узнать длину окружности? Сейчас выясним.

Длина окружности: формула

Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:

Задача 1

У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?

1. Итак, формула для вычисления окружности — p= πd
2. Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724

Ответ: длина окружности основания колокола 20,7 метра.

Задача 2

Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?

1. 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
2. 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
3. 3.P=2*3,14*6690=42013,2

Ответ: длина круговой орбиты спутника Земли 42013,2 км.

Способы измерения длины окружности

Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.

Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.

Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.

Характеристики фигуры

Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.

В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.

Основные термины окружности

Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.

Основные формулы для вычислений

Параметры используются в формулах вычислений величин окружности:

Диаметр в формулах вычисления

В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.

Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.

Расчёты по радиусу

Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.

Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?

Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.

Подручные способы вычисления

Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:

• При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
• Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
• Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.

Круглые предметы в истории человеческой жизни

Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.

Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.

Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.

Существует несколько определений этой геометрической фигуры.

• Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
• Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
• Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
• Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.

Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.

Определение окружности

Формулы

Как вычислить длину окружности через радиус? Это делается по простой формуле:

где L – искомая величина,

π – число пи, примерно равное 3,1413926.

Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.

Обозначения

Для нахождения через диаметр существует следующая формула:

Если L уже известно, можно легко узнать радиус или диаметр.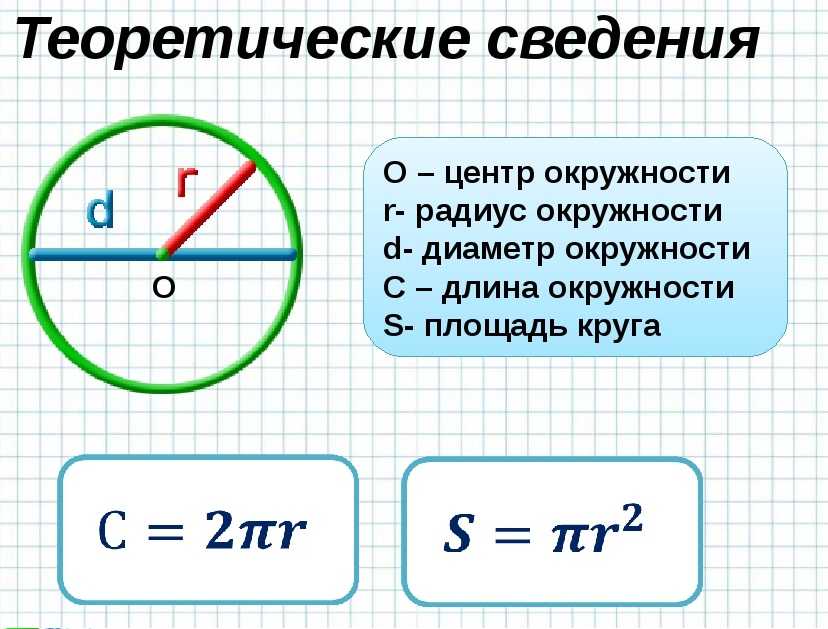 Для этого L нужно поделить на 2π или на π соответственно.

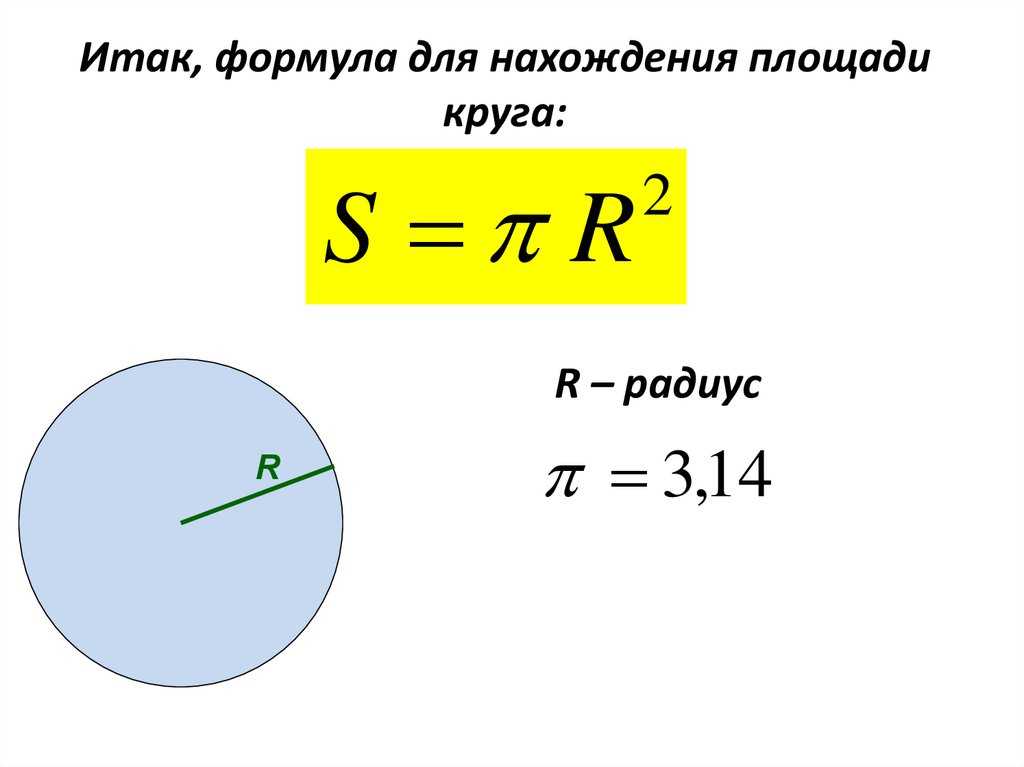
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда

L = 2πR = 2π√(S/π) = 2√(Sπ).

Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)

Резюмируя, можно сказать, что существует три основных формулы:

• через радиус – L = 2πR;
• через диаметр – L = πD;
• через площадь круга – L = 2√(Sπ).

Число пи

Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.

Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.

Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.

Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.

Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.

Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.

Полезное видео: длина окружности

Практическое применение

Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:

L = πD = 3,14 * 20 = 62,8 см.

Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:

L = 2πR = 2 * 3,14 * 13 = 81,68 м.

Полезное видео: круг — радиус, диаметр, длина окружности

Итог

Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.

Окружность формулы круга, примеры

Во-первых, мы должны понять, что такое круг. Простыми геометрическими словами, круг — это замкнутая круглая фигура, образованная путем соединения всех точек на плоскости на заданном расстоянии от определенной точки, известной как центр. Окружность круга является важным элементом для круга. Следовательно, мы должны знать все детали относительно окружности круга.

Окружность любой формы в математике определяет путь или границу, которая ее окружает. Другими словами, окружность, также известная как периметр, используется для определения длины границы любой формы. Поэтому длина окружности любой формы играет существенную роль при расчете ее граничных размеров.

Окружность — это измерение границ круга. Когда мы разрезаем круг и проводим через него прямую линию, эта длина называется его окружностью или периметром.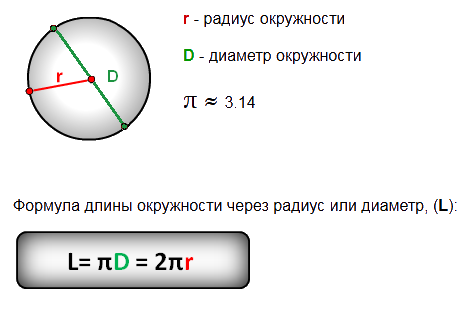 Он обычно выражается в таких единицах, как сантиметры, метры или другие соответствующие единицы длины.

Радиус окружности также учитывается при нахождении длины окружности. Таким образом, чтобы вычислить периметр круга, мы должны сначала определить радиус или диаметр этого круга.

Окружность относится к расстоянию по окружности. Это одномерное измерение границы любой двумерной круглой поверхности. Таким образом, нахождение длины окружности обычно называют вычислением периметра круга, поскольку оно следует тому же принципу, что и нахождение периметра любого многоугольника.

Окружность представляет собой простую круглую геометрическую форму, а значение Pi(π) приблизительно равно 3,1415926535897………… мы используем греческую букву, чтобы описать это значение как бесконечное.

Для окружности, показанной ниже, длина окружности и диаметр равны:

Другими словами, длина окружности — это расстояние вокруг окружности. Диаметр круга — это расстояние поперек круга от его центра до двух точек на его периферии. Отношение периметра круга к его диаметру равно π. В результате мы получаем значение, достаточно близкое к значению pi(π), когда делим длину окружности на диаметр любого круга. Таким образом, для описания этой связи можно использовать следующую формулу:

C/D = π, где C обозначает длину окружности, а D — диаметр.

 C= πD — это другой способ записи этой формулы, когда нам нужно найти длину окружности и задан диаметр окружности.

Таким образом, длина окружности включает различные другие факторы. Три наиболее важных фактора окружности — это центр, диаметр и радиус.

Центр: Центр — это место на окружности на заданном расстоянии от любой другой точки.

Диаметр: Диаметр круга — это расстояние от одного конца круга до точки на другом конце круга, проходящее через центр.

Радиус: Радиус круга — это расстояние между центром круга и любой точкой по его периметру.

Окружность формулы круга

Радиус «r» круга и значение «пи» могут определить длину окружности формулы круга.

Длина окружности по формуле = 2πR

Где,

• Радиус круга R
• π — математическая константа, имеющая приблизительное значение 3,14

Кроме того, Пи (π) представляет собой отношение длины окружности к диаметру любого круга.

Следовательно, C = πD

Где,

• Длина окружности обозначается C
• Диаметр представлен D

Различные формулы для нахождения длины окружности

Чтобы найти периметр круга, мы можем использовать три различные формулы

1. Когда радиус (R) круга известен, тогда формула:

     Длина окружности = 2πR

2. Если известен диаметр (D) окружности, формула будет следующей:

        Окружность = πD

3. Если площадь (A) круга известна, то формула:

         Окружность = 4πA, где A — площадь круга.

  Длина окружности к диаметру

Радиус окружности в два раза больше ее диаметра, что означает D = 2R       

Кроме того, отношение длины окружности к ее диаметру равно Pi(π). Следовательно, мы можем сказать, что это определение pi(π).

т. е. C = 2πR

=>   C = πD (поскольку D = 2R)                                                                        

Теперь, если мы разделим обе части на D (диаметр), мы получим значение, очень близкое к приблизительному значению пи (π).

Это означает, что C/D = π

Как найти длину окружности?

Метод 1:

Мы не можем физически измерить длину круга с помощью весов, потому что это изогнутая поверхность. Однако это возможно только для многоугольников, таких как квадраты, треугольники и прямоугольники. Вместо этого мы можем использовать нить для измерения окружности круга. Используя нить, мы можем проследить кривую траекторию круга и отметить места на нити. Для измерения этой длины можно использовать обычную линейку.

Метод 2:

Вычисление длины окружности является наиболее точным способом ее определения. Для этого метода необходимо знать радиус окружности. На рисунке ниже показана окружность с радиусом R и центром O. Его диаметр в два раза больше радиуса.

Следовательно, мы можем заключить, что длина окружности является важным элементом для измерения размеров круга. Теперь нам также ясно, что длина окружности есть произведение константы π и диаметра окружности. Итак, теперь, если кто-то спросит, какова длина окружности? Или как найти длину окружности? Вы можете ответить на них, не сталкиваясь с какими-либо трудностями.

  Вот несколько примеров, которые помогут вам лучше понять концепцию.

Решение:

Из вопроса диаметр нам известен, поэтому радиус(R) = 7/2 см = 3,5 см

Отсюда длина окружности = 2πR = 2 х 3,14 х 3,5 = 21,98 см

Пример 2: Найдите радиус окружности, где C = 80 см.

Решение:

Итак, длина окружности дана = 80 см

Формула, которую мы знаем, C = 2πR

                   Отсюда следует, что 80 = 2πR

                                      =>80/2 = 2πR/2

                                  =>40 = πR

                                     => R = 40/π

Следовательно, радиус окружности равен 40/ π, что равно 12,74

Пример 3: Найдите периметр круга, радиус которого равен 9 см?

Решение:

В предыдущем вопросе нам дан радиус, R = 9 см

Итак, формула длины окружности нам известна, а периметр известен также как длина окружности. Следовательно, формула для периметра круга C = 2πR

.

Теперь, подставив в этот вопрос значение R, то есть 9 см, получим:

                          C = (2 x 3,14 x 9) см

                             = 56,52 см

Пример 4: Вычислите периметр круга с точки зрения π, имеющего диаметр 20 см.

Решение:

Дан диаметр круга, равный 20 см.

Следовательно, радиус круга равен R = 20/2 см = 10 см.

Мы знаем, что формула длины окружности: C = 2πR

Итак, C для этого круга = (2 x π x 10) = 20π см

Пример 5: Каков будет диаметр круга с длиной окружности 8 см?

Решение:

В этом вопросе известна длина окружности (С), равная 8 см.

Мы знаем, что C = 2πR

                =>C = πD (поскольку D=2R)

                 => D = C/π = (8/3,14) см = 2,55 см

Следовательно, диаметр данного круга при известной длине окружности равен 2,55 см.

Пример 6: Если окружность имеет длину 16 см, каков будет радиус этой окружности?

Решение:

Здесь задана длина окружности 16 см

Нам известна формула C = 2πR

              Итак, радиус R = C/2π = (16)/(2 x 3,14) см = 2,547 см

 

Найдите длину окружности круг

Найдите площадь круга

Свойства кругов изучались более [латекс]2000[/латекс] лет. Все круги имеют одинаковую форму, но на их размеры влияет длина радиуса, отрезка прямой от центра до любой точки на круге. Отрезок, проходящий через центр окружности и соединяющий две точки окружности, называется диаметром. Диаметр в два раза больше радиуса. См. изображение ниже.

Размер круга можно измерить двумя способами. Расстояние вокруг окружности называется ее окружностью.

Архимед обнаружил, что для кругов всех размеров деление длины окружности на диаметр всегда дает одно и то же число. Значение этого числа — пи, символизируемое греческой буквой [латекс]\пи [/латекс] (произносится как «пирог»). Однако точное значение [latex]\pi [/latex] не может быть вычислено, так как десятичная дробь никогда не заканчивается и не повторяется (мы узнаем больше о подобных числах в разделе «Свойства действительных чисел»). Лаборатория поможет вам лучше понять число Пи.

Если нам нужна точная длина окружности или площадь круга, мы оставляем в ответе символ [латекс]\пи [/латекс]. Мы можем получить приблизительный ответ, подставив [латекс]3.14[/латекс] в качестве значения [латекс]\пи [/латекс]. Мы используем символ [латекс]\приблизительно [/латекс], чтобы показать, что результат приблизительный, а не точный.

Свойства окружностей

[latex]\begin{array}{c}r\text{ длина радиуса.}\hfill \\ d\text{ длина диаметра.}\hfill \end {массив}[/латекс] 9{2}\text{)}\hfill \\ A=\pi \cdot 100\hfill \end{array}[/latex]

Мы пишем [latex]\pi [/latex] после [latex]100[ /латекс].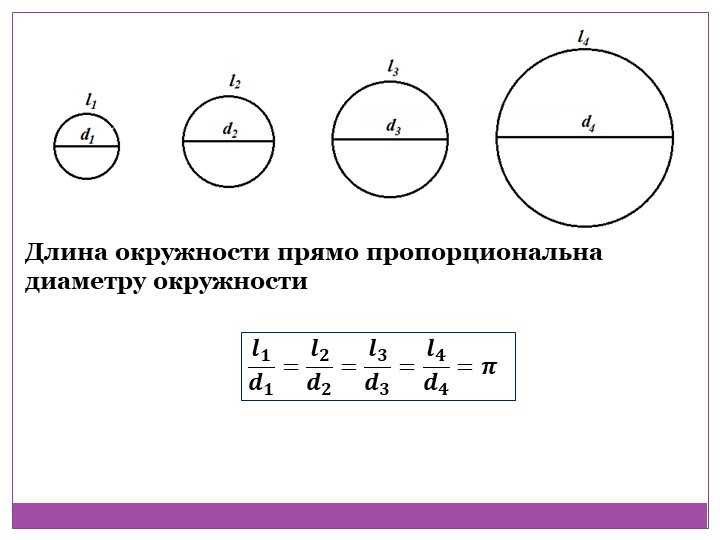 Таким образом, точное значение площади равно [латекс]А=100\пи [/латекс] квадратных дюймов.
Чтобы приблизить площадь, мы должны заменить [латекс]\пи \приблизительно 3,14[/латекс].

[латекс]\begin{array}{ccc}A& =& 100\pi \hfill \\ \\ & \приблизительно & 100\cdot 3.14\hfill \\ & \приблизительно & 314\текст{квадратный дюйм}\hfill \end{array}[/latex]

Не забывайте использовать квадратные единицы измерения, такие как квадратные дюймы, при вычислении площади.

пример

Круг имеет радиус [латекс]10[/латекс] сантиметров. Приблизительно вычислите его длину окружности и площадь.

Решение

1. Найдите длину окружности, когда [латекс]r=10[/латекс].
Напишите формулу длины окружности.	[латекс] C = 2 \ pi \ mathit {\ text {r}} [/ латекс]
Замените [латекс]3.14[/латекс] на [латекс]\pi [/латекс] и 10 на , [латекс]r[/латекс] .	[латекс]C\ок 2\влево(3,14\вправо)\влево(10\вправо)[/латекс] 9{2}[/латекс]
Умножение.	[латекс]А\примерно 314\текст{квадратный сантиметр}[/латекс]

 

попробуйте

 

пример

Круг имеет радиус [латекс]42,5[/латекс] сантиметра. Приблизительно его окружность и площадь.

Показать решение

 

попробуйте

Посмотрите следующее видео, чтобы увидеть еще один пример того, как найти длину окружности.

В следующем видео примере мы находим площадь круга.

Преобразуйте дробь [латекс]{\большой\фрак{22}{7}}[/латекс] в десятичную. Если вы используете свой калькулятор, десятичное число заполнит дисплей и покажет [латекс]3,14285714[/латекс].