Расчет медианой группы чисел
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 for Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Mac 2011 Еще…Меньше
Предположим, что вы хотите узнать, что такое средний балл в распределении о оценкам учащихся или в образце данных для контроля качества. Чтобы вычислить медиану группы чисел, используйте функцию МЕДИАНА.
Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
-
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество.

-
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
-
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.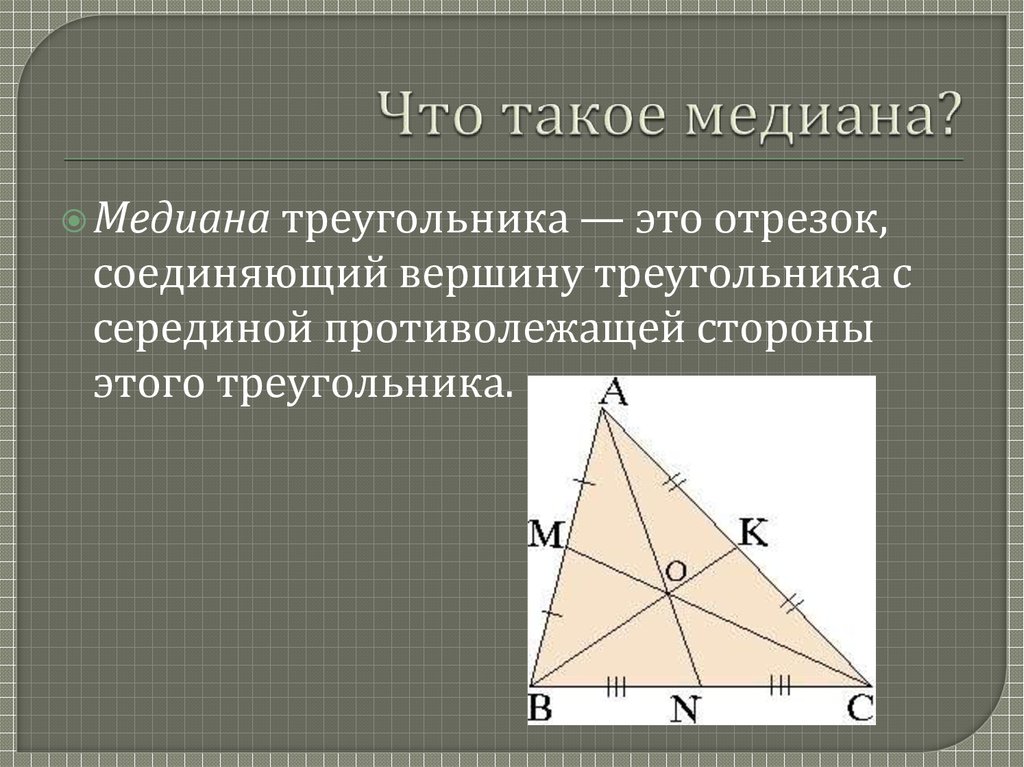
Снимки экрана в этой статье получены в Excel 2016. Если вы используете другую версию, интерфейс может немного отличаться, но функции будут такими же.
Пример
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
-
Откройте пустую книгу или лист.
-
Копирование примера
Выберите пример ниже.
Примечание: Не выделяйте заголовки строк или столбцов.
1
2
34
5
6
7
A
10
7
9
27
0
4
Выделение примера в справке
- org/ListItem»>
Нажмите клавиши CTRL+C.
-
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
-
Щелкните в пустой ячейке.
-
На вкладке Формула нажмите кнопку Автосводка > дополнительные функции.
-
Введите МЕДИАНА в поле Поиск функции: и нажмите кнопку ОК.

-
Введите A1:A7 в поле Число1.
В этом примере в ячейке должен быть ответ 8.
Совет: Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите клавиши CTRL+` (знак ударения) или на вкладке
Пример
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
-
Откройте пустую книгу или лист.

-
Копирование примера
Выберите пример ниже.
Примечание: Не выделяйте заголовки строк или столбцов.
1
2
3
4
5
6
7
A
10
7
9
27
0
4
Выделение примера в справке
- org/ListItem»>
Нажмите клавиши CTRL+C.
-
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
-
Щелкните в пустой ячейке.
-
На вкладке Формула нажмите кнопку Автосводка > дополнительные функции.
-
В области построитель формул введите МЕДИАНА в поле Поиск и нажмите кнопку Вставить функцию.

-
Убедитесь, что диапазон ячейки в поле Число1 совпадает с вашими данными (в данном случае A1:A7).
В этом примере в ячейке должен быть ответ 8.
Совет: Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите клавиши CTRL+` (знак ударения) или на вкладке Формулы в группе Зависимости формул нажмите кнопку Показывать формулы.
Функция МЕДИАНА
Как в Excel посчитать медиану
Автор Елизавета КМ На чтение 5 мин Опубликовано
Чтобы рассчитать медиану в Эксель, можно воспользоваться встроенной функцией МЕДИАНА. Попытаемся разобраться, что такое медиана и рассмотрим методы ее вычисления для выборки или распределения случайных чисел.
Содержание
- Медиана выборки
- Медиана непрерывного распределения
- Функция МЕДИАНА
- Среднее значение ряда чисел
- Вычисление значений непрерывного ряда
- Среднее взвешенное значение
- Вычисление без учета нулевых значений
- Полезные видео
Медиана выборки
Итак, медиана представляет собой число, которое выражает середину множества определенного ряда чисел. Таким образом, половина чисел указанного ряда будет больше значения вычисленной медианы, а вторая половина числового ряда – меньше. Для того чтобы определить медиану, нужно отсортировать числовые значения выборки. В итоге медианой выборки цифр 2, 2, 3, 5, 6, 7, 8 будет 5. В данном случае выборка состоит из семи значений – три цифры больше полученной медианы и три – меньше.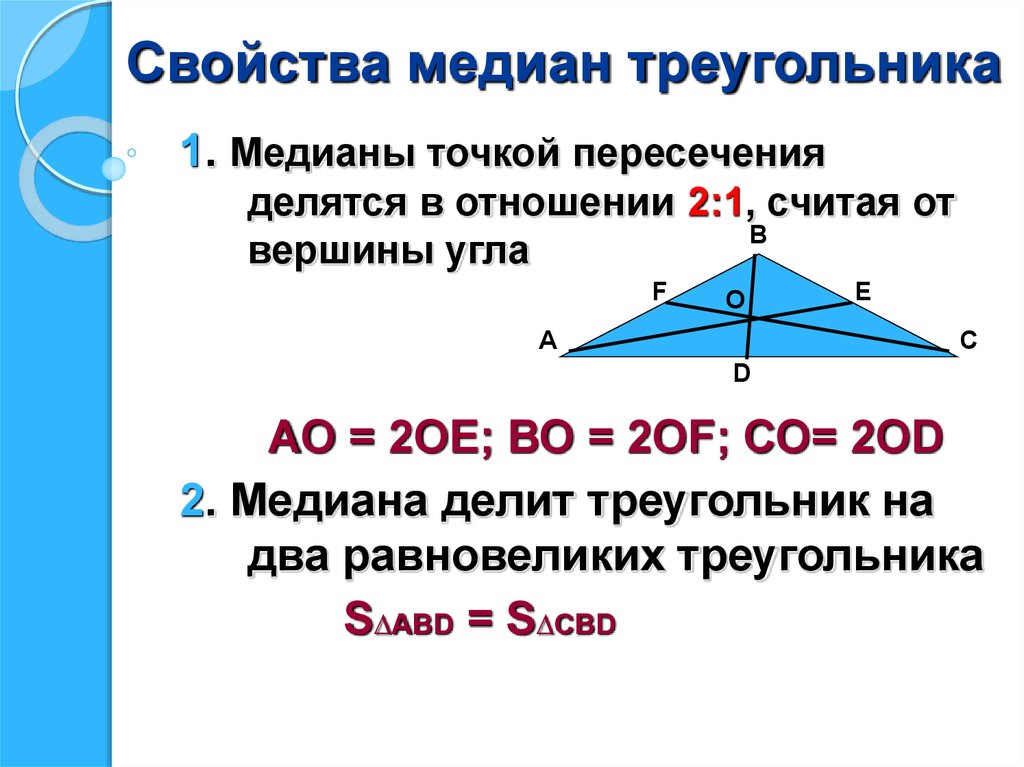
Важно! Если выборка состоит четного количества целых цифровых значений, то медиана будет представлена в виде десятичной дроби. Так, медиана выборки ряда 2, 2, 3, 5, 6, 7, 8, 10 составляет 5,5.
Вычисление медианы выборке через возможности Excel осуществляется при помощи соответствующей функции МЕДИАНА. В скобках формулы можно проставить до 255 значений, из которых необходимо вычислить медиану.
Функция МЕДИАНА с выборкой из семи чиселМедиана не всегда совпадает со средним цифровым значением из представленного ряда. Как правило, совпадение бывает только при симметричном тождестве относительно среднего показателя.
Разница между медианой и средним значением ряда чиселОбратите внимание! Медиана – это не то же самое, что среднее значение. Средний показатель выборки чисел 2, 2, 3, 5, 6, 7, 300 соответствует значению 46,42857, медиана при этом все еще равна 5, так как соотношение чисел больше 5 и меньше не изменилось.
Медиана непрерывного распределения
Теперь рассмотрим расчет медианы в случае непрерывного распределения. Показатель медианы – это результат решения функции распределения случайных непрерывных числовых величин. Если показатель функции распределения (т.е. функция плотности) известен, то значение медианы можно вычислить по такой формуле:
Показатель медианы – это результат решения функции распределения случайных непрерывных числовых величин. Если показатель функции распределения (т.е. функция плотности) известен, то значение медианы можно вычислить по такой формуле:
При решении данного уравнения аналитическим методом при логнормальном распределении LnN (µ; σ; 2), значение медианы модно вычислить благодаря формуле =EXP (µ). При условии, что µ=0, медиана будет равна 1. В программе Excel результат медианы для логнормального распределения, представленная формулой LnN (0; 1) вычисляется через функцию =ЛОГНОРМ.ОБР (0,5; 0; 1).
Вычисление медианы через функцию ЛОГНОРМ.ОБРФункция МЕДИАНА
Применяя функцию МЕДИАНА в Эксель, можно вычислить значение середины числового множества. Синтаксическое выражение представляет собой формулу =МЕДИАНА (число 1; [число 2]…). Аргументы «Число 1», «Число 2» и так далее до «Число 255». Первое значение – это обязательное значение, последующие – необязательные, но именно они помогают вычислить медиану.
Следует отметить! В качестве аргументов могут использоваться не только числовые значение, но и ссылки, имена, массивы. Если ссылка или массив частично представлены в виде текста или в выборке есть пустые ячейки, то эти значения не учитываются в процессе вычислений. Использование текстового формата в аргументах приводят к ошибкам в работе функции.
Среднее значение ряда чисел
Рассмотрим вариант расчета средних значений определенного ряда чисел. Например, это может быть средняя температура воздуха в конкретный день года, выполнение поставленных задач сотрудниками и так далее. Для выполнения данного вычисления потребуются три важных параметра:
- Медиана – среднее значение числового ряда. При этом половина чисел больше показателя медианы, а вторая половина – меньше. Например, медиана числового ряда 2, 2, 3, 5, 6, 7, 9 равняется 5.
- Среднее значение – это среднеарифметический показатель, который вычисляется суммированием всех чисел определенного ряда и деления этой суммы на количество показателей, то есть 2+2+3+5+6+7+9=34/7.
 В данном случае среднее значение соответствует показателю 4,857143.
В данном случае среднее значение соответствует показателю 4,857143. - Показатель Режим – это выделение числа, которое чаще других встречается в числовом ряде. В представленном ряду чисел 2, 2, 3, 5, 6, 7, 9 этот показатель соответствует цифре 2.
Указанные параметры при симметричном распределении числового ряда своих значений не меняют, а при асимметричном распределении они могут меняться.
Вычисление значений непрерывного ряда
При определении среднего значения непрерывного числового ряда необходимо осуществить определенный порядок действия:
- Следует активировать ячейку справа или ниже от ряда или строки, в котором представлены значения.
- На «Главной» вкладке выбираем параметр «Автосумма», который можно найти в группе инструментов «Редактирование».
- Также данную функцию можно обнаружить во вкладке «Формулы».
- Рядом с кнопкой «Автосумма», которая обозначается значком Σ, есть стрелочка с встроенным меню.
 Выбираем показатель «Среднее». Данное значение также можно получить, выполнив функцию СРЗНАЧ.
Выбираем показатель «Среднее». Данное значение также можно получить, выполнив функцию СРЗНАЧ.
Среднее взвешенное значение
Здесь случае придется использовать несколько функций – СУММ и СУММПРОИЗВ. Попробуем рассчитать среднюю стоимость единицы товара при наличии трех товаров и количества проведенных продаж. Синтаксис формулы выглядит таким образом: =СУММПРОИЗВ (R[-3]C : R[-3]C[1] : R[-1]C[1]) / СУММ (R[-3]C[1] : R[-1]C[1]). После выполнения данной функции получим среднее значение стоимости одной единицы товара 184,5238095
Формула для определения средней стоимости товаров с разной ценой и разным количеством продажВычисление без учета нулевых значений
Чтобы в процессе вычислений не учитывались нулевые значения, необходимо воспользоваться двумя функциями – ЕСЛИ и СРЗНАЧ. Рассмотрим пример. В представленном числовом ряду 4, 6, 8, 0, 5, 8 необходимо найти среднее значение, но с условием исключения нулевого значения. Функция будет иметь такой синтаксис: =СРЗНАЧЕСЛИ (А2:А7; “<>0”). В итоге результат функции без нуля будет равен 6,2.
Рассмотрим пример. В представленном числовом ряду 4, 6, 8, 0, 5, 8 необходимо найти среднее значение, но с условием исключения нулевого значения. Функция будет иметь такой синтаксис: =СРЗНАЧЕСЛИ (А2:А7; “<>0”). В итоге результат функции без нуля будет равен 6,2.
Полезные видео
Ознакомиться с основными принципами вычисления медианы в программе Excel можно, просмотрев несколько обучающих роликов в YouTube
Оцените качество статьи. Нам важно ваше мнение:
Нам важно ваше мнение:
T-SQL | Медианы
116
Работа с базами данных в .NET Framework — Оконные функции T-SQL — Медианы
Исходник базы данных
Ранее я рассказывал, как вычисляются процентили. Я говорил, что 50-й процентиль обычно называется медианой и, грубо говоря, представляет собой такое значение из набора, для которого 50% всех остальных значений набора данных меньше этого значения. Я показал решения для вычисления любых процентилей как в SQL Server 2012, так и предыдущих версиях SQL Server. Здесь я только напомню вам решение в SQL Server 2012 с использованием функции PERCENTILE_CONT (CONT здесь означает модель непрерывного распределения), а затем покажу интересные решения для вычисления медианы в более ранних версиях SQL Server.
В качестве тестовых данных я воспользуюсь таблицей Stats.Scores, содержащей результаты экзаменов студентов. Допустим, нам нужно для каждого экзамена вычислить медиану результатов в предположении модели непрерывного распределения. Если число результатов в определенном экзамене нечетное, нужно вернуть средний результат. Если же число результатов четное, нужно вернуть среднее значение для двух средних результатов. Вот ожидаемый результат для наших тестовых данных:
Если число результатов в определенном экзамене нечетное, нужно вернуть средний результат. Если же число результатов четное, нужно вернуть среднее значение для двух средних результатов. Вот ожидаемый результат для наших тестовых данных:
Как уже говорилось ранее, функция PERCENTILE_CONT появилась в SQL Server 2012 и служит для вычисления процентилей в предположении модели непрерывного распределения. Однако она реализована как оконная функция, а не как функция, в которой используется сгруппированные упорядоченные наборы. Это означает, что можно использовать ее для получения процентиля вместе со строками данных, но для получения этой информации только раз в группе, нужно добавить определенную логику фильтрации. Например, можно вычислять номера строк с применением того же определения секционирования окон, что и в функции PERCENTILE_CONT, и произвольного упорядочения, а затем фильтром отобрать только строки с номером равным единице. Вот полное решение задачи вычисления медианы результатов экзаменов:
WITH C AS
(
SELECT testid,
ROW_NUMBER() OVER(PARTITION BY testid ORDER BY (SELECT NULL)) AS rownum,
PERCENTILE_CONT(0. 5) WITHIN GROUP(ORDER BY score) OVER(PARTITION BY testid) AS median
FROM Stats.Scores
)
SELECT testid, median
FROM C
WHERE rownum = 1;
5) WITHIN GROUP(ORDER BY score) OVER(PARTITION BY testid) AS median
FROM Stats.Scores
)
SELECT testid, median
FROM C
WHERE rownum = 1;Оно немного неуклюжее, но свою работу делает.
До SQL Server 2012 приходилось быть более изобретательным, тем не менее для решения этой задачи все равно можно было использовать оконные функции. Одно из решений заключалось в вычислении для каждой строки ее позиции в результатах экзамена при упорядочении по оценкам (назовем это pos) и числу результатов для соответствующего экзамена (назовем это cnt). Для вычисления pos применяется функция ROW_NUMBER, а для расчета cnt — оконная функция агрегирования COUNT. Затем отбираются только строки, которые должны участвовать в вычислении медианы, а именно строки, у которых pos равно (cnt + 1) / 2 или (cnt + 2) / 2. Заметьте, что в этих выражениях используется целочисленное деление, а дробная часть отбрасывается. При нечетном числе элементов оба выражения возвращают одинаковое срединное значение.
Например, если в группе 9 элементов, оба выражения возвращают 5. При четном числе элементов оба выражения возвращают два срединных значения. Например, если в группе 10 элементов, выражения вернут 5 и 6. После фильтрации нужных строк остается выполнить их группировку по идентификатору экзамена и вернуть средний результат для каждого экзамена. Вот готовое решение:
WITH C AS
(
SELECT testid, score,
ROW_NUMBER() OVER(PARTITION BY testid ORDER BY score) AS pos,
COUNT(*) OVER(PARTITION BY testid) AS cnt
FROM Stats.Scores
)
SELECT testid, AVG(1. * score) AS median
FROM C
WHERE pos IN( (cnt + 1) / 2, (cnt + 2) / 2 )
GROUP BY testid;
Другое интересное решение задачи в версиях, предшествующих SQL Server 2012, предусматривает вычисление двух номеров строк: первый при упорядочении по возрастанию по score и studentid (studentid добавлено для детерминизма), а второй — при упорядочении по убыванию. Вот код вычисления этих номеров и результат работы запроса:
SELECT testid, score, ROW_NUMBER() OVER(PARTITION BY testid ORDER BY score, studentid) AS rna, ROW_NUMBER() OVER(PARTITION BY testid ORDER BY score DESC, studentid DESC) AS rnd FROM Stats.Scores;
Можно ли обобщить правило, определяющее строки, которые должны участвовать в вычислении медианы?
Заметим, что при нечетном количестве строк, медиана располагается там, где номера строк совпадают. При четном числе элементов медиана находится там, где разница между двумя номерами строк равна единице. Объединить два правила можно так: медиана находится в строках, где абсолютная разница между номерами строк меньше или равна единице. Вот готовое решение, основанное на этом обобщенном правиле:
WITH C AS
(
SELECT testid, score,
ROW_NUMBER() OVER(PARTITION BY testid ORDER BY score, studentid) AS rna,
ROW_NUMBER() OVER(PARTITION BY testid ORDER BY score DESC, studentid DESC) AS rnd
FROM Stats.Scores
)
SELECT testid, AVG(1. * score) AS median
FROM C
WHERE ABS(rna - rnd) <= 1
GROUP BY testid;Функция МЕДИАНА в Excel для выполнения статистического анализа
Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.
То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.
Примеры использования функции МЕДИАНА в Excel
Пример 1. При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.
Исходные данные:
Формула для расчета:
Описание аргумента:
- B3:B15 – диапазон исследуемых возрастов.
Полученный результат:
То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.
Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения
Пример 2. Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.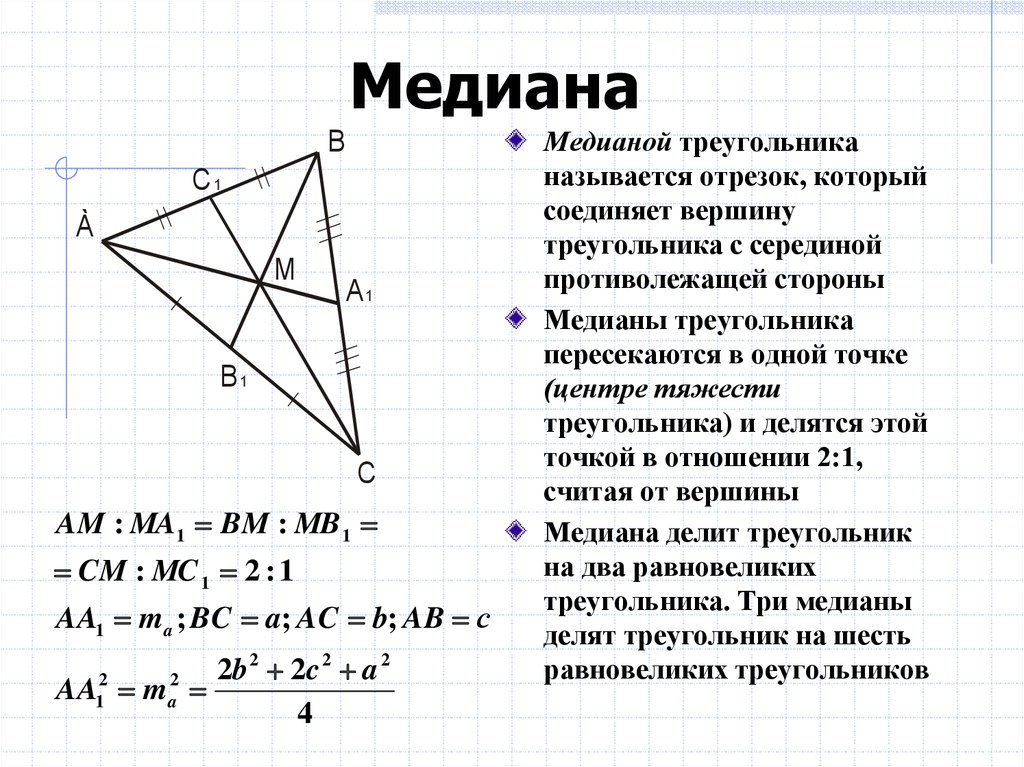
Исходные данные:
Формула для нахождения среднего значения:
Формула для нахождения медианы:
Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.
Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:
То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.
Пример расчета медианы при статистическом анализе в Excel
Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.
По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.
Исходная таблица данных:
Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:
Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:
- av – среднее значение;
- med – медиана;
- mod – мода.
Рассчитаем значение коэффициента x для первого продавца:
Аналогично проведем расчеты для остальных продавцов. Полученные результаты:
Определим продавца, которому будет выдана премия:
Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.
Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.
Особенности использования функции МЕДИАНА в Excel
Функция имеет следующий синтаксис:
=МЕДИАНА(число1;[число2];…)
Описание аргументов:
- число1 – обязательный аргумент, характеризующий первое числовое значение, содержащееся в исследуемом диапазоне;
- [число2] – необязательный второй (и последующие аргументы, всего до 255 аргументов), характеризующий второе и последующие значения исследуемого диапазона.
Примечания 1:
- При расчетах удобнее передавать сразу весь диапазон исследуемых значений вместо последовательного ввода аргументов.
- В качестве аргументов принимаются данные числового типа, имена, содержащие числа, данные ссылочного типа и массивы (например, =МЕДИАНА({1;2;3;5;7;10})).

- При расчете медианы учитываются ячейки, содержащие пустые значения или логические ИСТИНА, ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно. Например, результат выполнения функции с логическими значениями в аргументах (ИСТИНА;ЛОЖЬ) эквивалентен результату выполнения с аргументами (1;0) и равен 0,5.
- Если один или несколько аргументов функции принимают текстовые значения, которые не могут быть преобразованы в числовые, или содержат коды ошибок, результатом выполнения функции будет код ошибки #ЗНАЧ!.
- Для определения медианы выборки могут быть использованы другие функции Excel: ПРОЦЕНТИЛЬ.ВКЛ, КВАРТИЛЬ.ВКЛ, НАИБОЛЬШИЙ Примеры использования:
- =ПРОЦЕНТИЛЬ.ВКЛ(A1:A10;0,5), поскольку по определению медиана – 50-я процентиль.
- =КВАРТИЛЬ.ВКЛ(A1:A10;2), так как медиана – 2-я квартиль.
- =НАИБОЛЬШИЙ(A1:A9;СЧЁТ(A1:A9)/2), но только если количество чисел в диапазоне является нечетным числом.
Примечания 2:
- Если в исследуемом диапазоне все числа распределены симметрично относительно среднего значения, среднее арифметическое и медиана для данного диапазона будут эквивалентны.

- При больших отклонениях данных в диапазоне («разбросе» значений) медиана лучше отражает тенденцию распределения значений, чем среднее арифметическое. Отличным примером является использование медианы для определения реального уровня зарплат у населения государства, в котором чиновники получают на порядок больше обычных граждан.
- Диапазон исследуемых значений может содержать:
Скачать примеры функции МЕДИАНА для статистического анализа в Excel
- Нечетное количество чисел. В этом случае медианой будет являться единственное число, разделяющее диапазон на два подмножества больших и меньших значений соответственно;
- Четное количество чисел. Тогда медиана вычисляется как среднее арифметическое для двух числовых значений, разделяющих множество на два указанных выше подмножества.
3.2. Расчет медианы в дискретных и интервальных рядах по накопленным частотам
1). В
дискретном вариационном ряду распределения
(ДВР) медиана определяется по ряду накопленных частот.
Поиск медианы разбивается на два шага:
1 шаг. Определяется середина вариационного ряда, т.е. порядковый номер (местоположение) медианы в дискретном вариационном ряду:
. (5.15)
2 шаг. Если порядковый номер медианы – целое число, то значение признака у выявленной единицы и является медианой. Если порядковый номер медианы – нецелое число, то медианой является варианта, рассчитанная как среднее арифметическое простое из двух смежных центральных вариант в дискретном ряду.
В нашем примере число единиц совокупности четное – 30 компаний (табл. 3.3′, дополнительно в графах 5, 6 рассчитаны накопленные частоты и частости).
Таблица 3.3′.
Дискретный ряд распределения 30 компаний мира 2008 г. по размеру годового дохода
Номер группы j | Группы компаний
по размеру годового дохода (100 млн. xj | Число компаний в группе | Накопленные частоты Fj | Накопленные частости, % Dj | |
абсолютное (частота) fj | относительное (частость), % dj | ||||
1 | 2 | 3 | 4 | 5 | 6 |
1 | 0,95 | 1 | 3,3 | 1 | 3,3 |
2 | 0,98 | 2 | 6,7 | 3 | 10 |
3 | 0,99 | 2 | 6,7 | 5 | 16,7 |
4 | 1,00 | 1 | 3,3 | 6 | 20 |
5 | 1,02 | 1 | 3,3 | 7 | 23,3 |
6 | 1,03 | 1 | 3,3 | 8 | 26,7 |
7 | 1,04 | 2 | 6,7 | 10 | 33,3 |
8 | 1,05 | 2 | 6,7 | 12 | 40 |
9 | 1,06 | 2 | 6,7 | 14 | 46,7 |
10 | 1,08 | 1 | 3,3 | 15 | 50 |
11 | 1,10 | 1 | 3,3 | 16 | 53,3 |
12 | 1,14 | 1 | 3,3 | 17 | 56,7 |
13 | 1,16 | 2 | 6,7 | 19 | 63,3 |
14 | 1,17 | 1 | 3,3 | 20 | 66,7 |
15 | 1,18 | 1 | 3,3 | 21 | 70 |
16 | 1,19 | 2 | 6,7 | 23 | 76,7 |
17 | 1,21 | 1 | 3,3 | 24 | 80 |
18 | 1,23 | 1 | 3,3 | 25 | 83,3 |
19 | 1,30 | 1 | 3,3 | 26 | 86,7 |
20 | 1,33 | 1 | 3,3 | 27 | 90 |
21 | 1,38 | 1 | 3,3 | 28 | 93,3 |
=22 | 1,41 | 2 | 6,7 | 30 | 100 |
ВСЕГО | п=30 | 100 | – | – | |
1 шаг. Определение
номера медианы по формуле (5.15):
Определение
номера медианы по формуле (5.15):
компаний. Таким образом, медиана попадает в середину между компаниями № 15 и 16: компании с 1 по 15 включительно входят в первую половину совокупности, компании с 16 по 30 – во вторую половину совокупности.
2 шаг. Расчет медианы по формуле средней арифметической простой.
Значение годового дохода 15 и 16 компаний, согласно ряду накопленных частот (частостей), составляет 1,08 и 1,10 сотен млн. $. Тогда медиана равна:
сотен млн. $.
Вывод: половина компаний, стоящих в ранжированном массиве до 15, имеют размер годового дохода менее 1,09 сотен млн. $, половина компаний, стоящих в ряду после 15, – более 1,09 сотен млн. $.
2). В интервальном вариационном ряду распределения (ИВР) медиана определяется по ряду накопленных частот.
Поиск медианы разбивается на три шага:
1 шаг. Определяется
середина вариационного ряда, т.е.
местоположение (порядковый номер)
медианы в ИВР по формуле (5.15).
Определяется
середина вариационного ряда, т.е.
местоположение (порядковый номер)
медианы в ИВР по формуле (5.15).
2 шаг. Определяется номер медианного интервала по ряду накопленных частот.
Медианным называется интервал, кумулятивная (накопленная) частота которого равна или впервые превышает номер медианы.
3 шаг. Определяется численное значение медианы в медианном интервале по формуле:
, (5.16)
где – нижняя граница медианного интервала;
– ширина медианного интервала;
– частота каждого -го интервала;
– частота медианного интервала;
– накопленная частота интервала, предшествующего медианному;
Пример. Рассчитаем медиану по накопленным частотам на основании данных таблицы 3.4′.
1 шаг.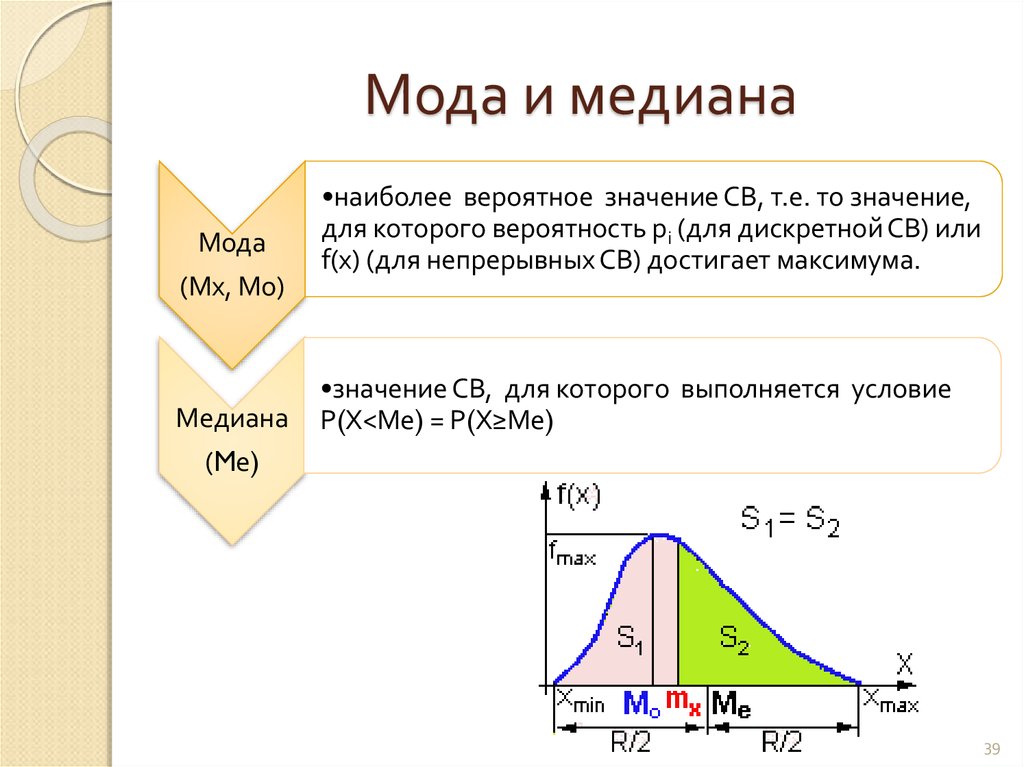 Определим
порядковый номер медианы в ИВР по формуле
(5.15):
Определим
порядковый номер медианы в ИВР по формуле
(5.15):
.
2 шаг. Определим номер медианного интервала по ряду накопленных частот. По данным столбца 4 таблицы 3.4′ видно, что накопленная частота второго интервала впервые превышает номер медианы (,5). Значит, медианным является интервал №2.
3 шаг. Определим численное значение медианы в медианном интервале по формуле (5.16):
Вывод: половина компаний, стоящих в ранжированном массиве до 15, имеют размер годового дохода меньше 1,101 сотен млн. $. Половина компаний, стоящих в ряду после 16 включительно, имеют размер годового дохода больше 1,101 сотен млн. $.
Сведем результаты всех расчетов в статистическую таблицу 5.1.
Таблица 5.1.
Значения средней, моды и медианы размера годового дохода 30 компаний мира для различных типов данных, сотни млн. $
Показатель | Массив исходных (несгруппированных) и массив ранжированных данных (МИД и МРД) | Ряды распределения | |
Дискретный вариационный ряд (ДВР) | Равноинтервальный вариационный ряд (ИВР) | ||
1 | 2 | 3 | 4 |
Среднее значение признака | 1,129 (средняя арифметическая простая) | 1,129 (средняя арифметическая взвешенная) | 1,134 (средняя арифметическая взвешенная) |
Мода — по частотам | Мода не определяется по причине отсутствия частот | 0,98; 0,99; 1,04; 1,05; … ; 1,41 | 1,057 |
Медиана — по накопленным частотам | Медина не определяется по причине отсутствия частот и накопленных частот | 1,09 | 1,101 |
Вывод. Как
видно из таблицы 5.1, средние, модальные
и медианные значения признака для
массивов несгруппированных и ранжированных
данных, а также для различных видов
рядов распределения (ДВР, ИВР) не
совпадают. Это объясняется тем, что при
вычислении указанных величин по
интервальным рядам распределения в
формулах принимают участие границы
интервалов, что снижает точность
расчетов. Наиболее
достоверные значения средней, моды и
медианы признака дают несгруппированные
и ранжированные данные, а также дискретные
вариационные ряды.
Как
видно из таблицы 5.1, средние, модальные
и медианные значения признака для
массивов несгруппированных и ранжированных
данных, а также для различных видов
рядов распределения (ДВР, ИВР) не
совпадают. Это объясняется тем, что при
вычислении указанных величин по
интервальным рядам распределения в
формулах принимают участие границы
интервалов, что снижает точность
расчетов. Наиболее
достоверные значения средней, моды и
медианы признака дают несгруппированные
и ранжированные данные, а также дискретные
вариационные ряды.
Вычисление среднего, медианы и моды в Python
Введение Когда мы пытаемся описать и обобщить выборку данных, мы, вероятно, начинаем с нахождения среднего [https://en.wikipedia.org/wiki/Mean] (или среднего), медианы [https: // en .wikipedia.org / wiki / Median] и режим [https://en.wikipedia.org/wiki/Mode_(statistics)] данных. Это центральная тенденция [https://en.wikipedia.org/wiki/Central_tendency] меры и часто первый взгляд на набор данных.
 В этом руководстве мы узнаем, как найти или вычислить среднее значение, медиану,
В этом руководстве мы узнаем, как найти или вычислить среднее значение, медиану,Вступление
Когда мы пытаемся описать и обобщить выборку данных, мы, вероятно, начинаем с нахождения среднего (или среднего), медианы и режима данных. Это основные меры тенденций, которые часто являются нашим первым взглядом на набор данных.
В этом руководстве мы узнаем, как найти или вычислить среднее значение,
медиану и режим в Python. Сначала мы закодируем функцию Python для
каждой меры, а затем воспользуемся statistics Python для выполнения той же задачи.
Обладая этими знаниями, мы сможем быстро взглянуть на наши наборы данных и получить представление об общей тенденции данных.
Оглавление
- Вычисление среднего значения выборки
- Расчет среднего с помощью Python
- Использование Python mean ()
- Нахождение медианы выборки
- Поиск медианы с помощью Python
- Использование медианы Python ()
- Нахождение моды образца
- Поиск режима с помощью Python
- Использование режима Python ()
Расчет среднего значения выборки
Если у нас есть выборка числовых значений, то ее среднее или среднее
- это общая сумма значений (или наблюдений), деленная на количество
значений.

Допустим, у нас есть образец [4, 8, 6, 5, 3, 2, 8, 9, 2, 5] . Мы можем
вычислить его среднее значение, выполнив операцию:
(4 + 8 + 6 + 5 + 3 + 2 + 8 + 9 + 2 + 5) / 10 = 5,2
Среднее арифметическое — это общее описание наших данных. Предположим, вы купили 10 фунтов помидоров. Если пересчитать дома помидоры, получится 25 помидоров. В этом случае вы можете сказать, что средний вес помидора составляет 0,4 фунта. Это было бы хорошее описание ваших помидоров.
Среднее также может быть плохим описанием выборки данных. Допустим, вы анализируете группу собак. Если вы возьмете совокупный вес всех собак и разделите его на количество собак, то это, вероятно, будет плохим описанием веса отдельной собаки, поскольку разные породы собак могут иметь очень разные размеры и вес.
Насколько хорошо или плохо среднее значение описывает выборку, зависит
от того, насколько разбросаны данные. В случае помидоров, они почти
одинакового веса, и среднее значение является хорошим их описанием. В
случае с собаками нет актуальных собак. Они могут варьироваться от
крошечного чихуахуа до гигантского немецкого мастифа. Итак, среднее само
по себе в данном случае не очень хорошее описание.
В
случае с собаками нет актуальных собак. Они могут варьироваться от
крошечного чихуахуа до гигантского немецкого мастифа. Итак, среднее само
по себе в данном случае не очень хорошее описание.
Теперь пора приступить к делу и узнать, как вычислить среднее значение с помощью Python.
Расчет среднего с помощью Python
Чтобы вычислить среднее значение выборки числовых данных, мы будем использовать две встроенные функции Python. Один для вычисления общей суммы значений, а другой для вычисления длины выборки.
Первая функция — это sum() . Эта
встроенная функция принимает итерацию числовых значений и возвращает их
общую сумму.
Вторая функция — len() . Эта
встроенная функция возвращает длину объекта. len() может принимать в
качестве аргумента последовательности (строка, байты, кортеж, список или
диапазон) или коллекции (словарь, набор или замороженный набор).
Вот как мы можем вычислить среднее значение:
>>> def my_mean(sample): ... return sum(sample) / len(sample) ... >>> my_mean([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 5.2
Сначала мы суммируем значения в sample используя sum() . Затем мы
делим эту сумму на длину sample , которая является результирующим
значением len(sample) .
Использование Python
mean ()Поскольку вычисление среднего — это обычная операция, Python включает
эту функцию в модуль statistics Он предоставляет некоторые функции для
расчета базовой статистики по наборам данных. Функция statistics.mean() берет образец числовых данных (любых итерируемых) и возвращает их
среднее значение.
Вот как работает функция mean() Python:
>>> import statistics >>> statistics.mean([4, 8, 6, 5, 3, 2, 8, 9, 2, 5]) 5.2
Нам просто нужно
импортировать statistics а затем вызвать mean() с нашим образцом в качестве аргумента. Это
вернет среднее значение выборки. Это быстрый способ найти среднее
значение с помощью Python.
Это
вернет среднее значение выборки. Это быстрый способ найти среднее
значение с помощью Python.
Нахождение медианы выборки
Медиана выборки числовых данных — это значение, которое находится посередине при сортировке данных. Данные могут быть отсортированы по возрастанию или убыванию, медиана остается прежней.
Чтобы найти медиану, нам необходимо:
- Отсортировать образец
- Найдите значение в середине отсортированного образца
При нахождении числа в центре отсортированной выборки мы можем столкнуться с двумя типами ситуаций:
- Если в выборке есть нечетное количество наблюдений , то среднее значение в отсортированной выборке — это медиана.
- Если в выборке есть четное количество наблюдений , нам нужно вычислить среднее из двух средних значений в отсортированной выборке.
Если у нас есть выборка [3, 5, 1, 4, 2] и мы хотим найти ее медиану,
то сначала мы сортируем выборку по [1, 2, 3, 4, 5] . Медиана будет
равна
Медиана будет
равна 3 поскольку это значение посередине.
С другой стороны, если у нас есть выборка [1, 2, 3, 4, 5, 6] , то ее
медиана будет (3 + 4) / 2 = 3.5 .
Давайте посмотрим, как мы можем использовать Python для вычисления медианы.
Поиск медианы с помощью Python
Чтобы найти медиану, нам сначала нужно отсортировать значения в нашей
выборке . Этого можно
добиться с помощью встроенной функции sorted() sorted() принимает итерацию и возвращает отсортированный list содержащий те же значения, что и исходная итерация.
Второй шаг — найти значение, которое находится в середине отсортированной выборки. Чтобы найти это значение в выборке с нечетным количеством наблюдений, мы можем разделить количество наблюдений на 2. Результатом будет индекс значения в середине отсортированной выборки.
Поскольку оператор деления ( / ) возвращает число с плавающей запятой,
нам нужно использовать оператор деления этажа ( // ),
чтобы получить целое число. Итак, мы можем использовать его как индекс в
операции индексации (
Итак, мы можем использовать его как индекс в
операции индексации ( [] ).
Если в выборке есть четное количество наблюдений, нам нужно найти два
средних значения. Скажем, у нас есть образец [1, 2, 3, 4, 5, 6] . Если
мы разделим его длину ( 6 ) на 2 с помощью деления пола, то получим 3 . Это индекс нашего верхнего среднего значения ( 4 ). Чтобы найти
индекс нашего нижнего среднего значения ( 3 ), мы можем уменьшить
индекс верхнего среднего значения на 1 .
Давайте объединим все это в функцию, которая вычисляет медиану выборки. Вот возможная реализация:
>>> def my_median(sample): ... n = len(sample) ... index = n // 2 ... # Sample with an odd number of observations ... if n % 2: ... return sorted(sample)[index] ... # Sample with an even number of observations ... return sum(sorted(sample)[index - 1:index + 1]) / 2 ... >>> my_median([3, 5, 1, 4, 2]) 3 >>> my_median([3, 5, 1, 4, 2, 6]) 3.5
Эта функция берет образец числовых значений и возвращает их медиану.
Сначала мы находим длину образца n . Затем мы вычисляем индекс
среднего значения (или верхнего среднего значения) путем деления n на 2 .
Оператор if проверяет, есть ли в имеющейся выборке нечетное количество
наблюдений. Если да, то медиана — это значение index .
Окончательный return выполняется, если в выборке есть четное
количество наблюдений. В этом случае мы находим медиану, вычисляя
среднее из двух средних значений.
Обратите внимание, что операция
нарезки [index - 1:index + 1] получает два значения. Значение в index - 1 и
значение в index поскольку операции нарезки исключают значение в
конечном индексе ( index + 1 ).
Использование
медианы Python ()Функция Python statistics.median() берет выборку данных и возвращает
ее медиану. Вот как работает метод:
Вот как работает метод:
>>> import statistics >>> statistics.median([3, 5, 1, 4, 2]) 3 >>> statistics.median([3, 5, 1, 4, 2, 6]) 3.5
Обратите внимание, что median() автоматически обрабатывает вычисление
медианы для выборок с нечетным или четным числом наблюдений.
Поиск режима образца
Режим — это наиболее частое наблюдение (или наблюдения) в выборке.
Если у нас есть образец [4, 1, 2, 2, 3, 5] , то его режим равен 2 потому что 2 появляется в образце два раза, тогда как другие элементы
появляются только один раз.
Режим не обязательно должен быть уникальным. Некоторые образцы имеют
более одного режима. Скажем, у нас есть образец [4, 1, 2, 2, 3, 5, 4] . В этом примере есть два режима — 2 и 4 потому что эти значения
появляются чаще и оба появляются одинаковое количество раз.
Этот режим обычно используется для категориальных данных. Распространенными категориальными типами данных являются:
Распространенными категориальными типами данных являются:
- логическое значение — может принимать только два значения,
например
trueилиfalse,maleилиfemale - номинальный — может принимать более двух значений, например,
American - European - Asian - African - порядковый — может принимать более двух значений, но значения
имеют логический порядок, например,
few - some - many
Когда мы анализируем набор категориальных данных, мы можем использовать этот режим, чтобы узнать, какая категория является наиболее распространенной в наших данных.
Мы можем найти образцы, у которых нет режима. Если все наблюдения уникальны (нет повторяющихся наблюдений), то в вашей выборке не будет режима.
Теперь, когда мы знаем основы режима, давайте посмотрим, как его найти с помощью Python.
Поиск режима с помощью Python
Чтобы найти режим с помощью Python, мы начнем с подсчета количества
вхождений каждого значения в рассматриваемом примере. Затем мы получим
значения с большим количеством вхождений.
Затем мы получим
значения с большим количеством вхождений.
Поскольку подсчет объектов — обычная операция, Python предоставляет
класс collections.Counter Этот класс специально разработан для подсчета предметов.
Класс Counter предоставляет метод, определенный как .most_common([n]) . Этот метод возвращает list кортежей из двух
элементов с n более общими элементами и их соответствующими
счетчиками. Если n опущено или None , то .most_common() возвращает
все элементы.
Давайте воспользуемся Counter и .most_common() чтобы закодировать
функцию, которая берет образец данных и возвращает свой режим.
Вот возможная реализация:
>>> from collections import Counter >>> def my_mode(sample): ... c = Counter(sample) ... return [k for k, v in c.items() if v == c.most_common(1)[0][1]] ... >>> my_mode(["male", "male", "female", "male"]) ['male'] >>> my_mode(["few", "few", "many", "some", "many"]) ['few', 'many'] >>> my_mode([4, 1, 2, 2, 3, 5]) [2] >>> my_mode([4, 1, 2, 2, 3, 5, 4]) [4, 2]
Сначала мы подсчитываем наблюдения в sample с помощью объекта Counter c ). Затем мы используем составление
списка, чтобы создать
Затем мы используем составление
списка, чтобы создать list содержащий наблюдения, которые встречаются в выборке одинаковое
количество раз.
Поскольку .most_common(1) возвращает list с одним tuple формы (observation, count) , нам нужно получить наблюдение с индексом 0 в list а затем элемент с индексом 1 во вложенном tuple . Это можно
сделать с помощью выражения c.most_common(1)[0][1] . Это значение
является первым режимом нашего образца.
Обратите внимание, что условие понимания сравнивает счетчик каждого
наблюдения ( v ) со счетчиком наиболее распространенного наблюдения ( c.most_common(1)[0][1] ). Это позволит нам получить несколько
наблюдений ( k ) с одним и тем же подсчетом в случае многомодовой
выборки.
Использование
режима Python ()Python statistics.mode() принимает некоторые data и возвращает свой
(первый) режим.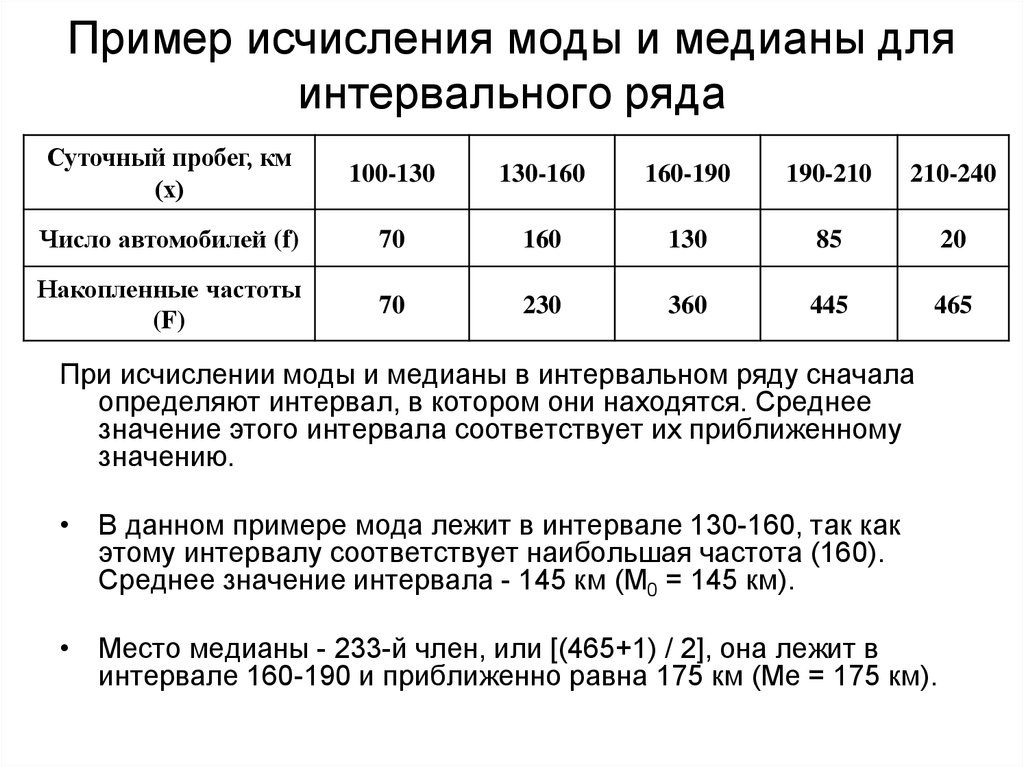 Посмотрим, как это можно использовать:
Посмотрим, как это можно использовать:
>>> import statistics >>> statistics.mode([4, 1, 2, 2, 3, 5]) 2 >>> statistics.mode([4, 1, 2, 2, 3, 5, 4]) 4 >>> st.mode(["few", "few", "many", "some", "many"]) 'few'
В одномодовом примере функция Python mode() возвращает наиболее
распространенное значение 2 . Однако в следующих двух примерах он
вернул 4 и few . В этих образцах были другие элементы, встречающиеся
такое же количество раз, но они не были включены.
Начиная с Python
3.8 мы также
можем использовать statistics.multimode() который принимает итерацию и
возвращает list режимов.
Вот пример использования multimode() :
>>> import statistics >>> statistics.multimode([4, 1, 2, 2, 3, 5, 4]) [4, 2] >>> statistics.multimode(["few", "few", "many", "some", "many"]) ['few', 'many'] >>> st.multimode([4, 1, 2, 2, 3, 5]) [2]
Примечание . Функция всегда возвращает list , даже если вы
передаете одномодовый образец.
Заключение
Среднее (или среднее), медиана и мода обычно являются нашим первым взглядом на выборку данных, когда мы пытаемся понять центральную тенденцию данных.
В этом руководстве мы узнали, как найти или вычислить среднее значение,
медиану и режим с помощью Python. Сначала мы пошагово рассмотрели, как
создавать наши собственные функции для их вычисления, а затем как
использовать statistics Python как быстрый способ найти эти
показатели.
Калькулятор среднего, медианы, режима
Использование калькулятора
Расчет среднего, медианы, режима, а также минимума, максимума, диапазона, числа и суммы для набора данных.
Введите значения, разделенные запятыми или пробелами. Вы также можете копировать и вставлять строки данных из электронных таблиц или текстовых документов. См. все допустимые форматы в таблице ниже.
Вы также можете копировать и вставлять строки данных из электронных таблиц или текстовых документов. См. все допустимые форматы в таблице ниже.
Что такое средняя медиана и мода?
Среднее значение, медиана и мода — все это меры центральной тенденции в статистике. Каждый из них по-разному сообщает нам, какое значение в наборе данных является типичным или репрезентативным для набора данных.
Среднее значение совпадает со средним значением набора данных и определяется с помощью вычислений. Сложите все числа и разделите на количество чисел в наборе данных.
Медиана — это центральное число набора данных. Расположите точки данных от наименьшего к наибольшему и найдите центральное число. Это медиана. Если в середине есть 2 числа, медиана является средним значением этих 2 чисел.
Мода — это наиболее часто встречающееся число в наборе данных. Подсчитайте, сколько раз каждое число встречается в наборе данных. Мода — это число с наибольшим значением. Это нормально, если есть более одного режима. {n}x_i}{n} \]
{n}x_i}{n} \]
Как найти медиану
Медиана \( \widetilde{x} \) — это значение данных, отделяющее верхнюю половину набора данных от нижней половины.
- Упорядочить значения данных от наименьшего к наибольшему значению
- Медиана — это значение данных в середине набора
- Если в середине есть 2 значения данных, медиана является средним значением этих 2 значений.
Пример медианы
Для набора данных 1, 1, 2, 5 , 6, 6, 9 медиана равна 5.
Для набора данных 1, 1, 2 , 6 , 6, 9 медиана равна 4. Возьмите среднее 2 и 6 или (2+6)/2 = 4.
Формула медианы
Заказ набора данных x 1 ≤ x 2 ≤ x 3 ≤ … ≤ x n от наименьшего к наибольшему значению, медиана \( \widetilde{x} \) — точка данных, отделяющая верхнюю половину значений данных из нижней половины.
Если размер набора данных n нечетный, медианой является значение в позиции p , где
\[ p = \dfrac{n + 1}{2} \] \[ \widetilde{x} = x_p \]
Если n четное, то медиана представляет собой среднее значений на позициях p и р + 1 где
\[ p = \dfrac{n}{2} \] \[ \widetilde{x} = \dfrac{x_{p} + x_{p+1}}{2} \]
Как найти моду
Мода — это значение или значения в наборе данных, которые встречаются чаще всего.
Для набора данных 1 , 1 , 2, 5, 6 , 6 , 9 мода равна 1, а также 6.
Межквартильный диапазон
IQR = Q 3 — Q 1
Выбросы
Потенциал Выбросы – это значения, лежащие выше или ниже нижнего предела набора образцов.
Верхний забор = Q 3 + 1,5 × межквартильный диапазон
Нижняя граница = Q 1 − 1,5 × межквартильный размах
Калькуляторы соответствующей статистики и анализа данных
- Калькулятор статистики
- Калькулятор описательной статистики
- Генератор стеблей и листьев
- Формулы статистики
Допустимые форматы данных
Столбец (новые строки)
42
54
65
47
59
40
53
42, 54, 65, 47, 59, 40, 53
Через запятую
42,
54, г.
65, г.
47, г.
59, г.
40, г.
53, г.
или
42, 54, 65, 47, 59, 40, 53
42, 54, 65, 47, 59, 40, 53
Пробелы
42 54
65 47
59 40
53
или
42 54 65 47 59 40 53
42, 54, 65, 47, 59, 40, 53
Смешанные разделители
42
54 65, 47,59,
40 53
42, 54, 65, 47, 59, 40, 53
Медиана: как найти, определение и примеры
Содержание:
- Определение и формула медианы.

- Расчет для нечетных наборов чисел.
- Расчет для четного набора чисел .
- Среднее значение против медианы.
- Расчет группового частотного распределения.
- Инструкции Excel
- Медиана в Minitab (видео)
Посмотрите видео, чтобы узнать, как вычислить медиану:
Режим среднего медианы
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Медиана показывает, где находится середина набора данных. Он используется во многих реальных ситуациях, таких как закон о банкротстве, где вы можете подать заявление о банкротстве только в том случае, если ваш доход ниже среднего в вашем штате.
Формула медианы равна {(n + 1) ÷ 2}th, где «n» — это количество элементов в наборе, а «th» означает только (n)-е число.
Чтобы найти медиану , сначала упорядочить числа от меньшего к большему. Затем найдите среднее число. Например, середина для этого набора чисел — 5, потому что 5 находится прямо посередине:
Затем найдите среднее число. Например, середина для этого набора чисел — 5, потому что 5 находится прямо посередине:
1, 2, 3, 5, 6, 7, 9.
Вы получите тот же результат с формулой. В наборе 7 чисел, поэтому n = 7:
- {(7 + 1) ÷ 2}-й
- = {(8) ÷ 2}
- = {4}-й
4-е число в 1, 2, 3, 5, 6, 7, 9 равно 5.
Предупреждение с использованием формулы медианы: Шаги немного различаются в зависимости от того, у вас четная или нечетная сумма чисел в вашем наборе данных.
Найдите медиану для числа
нечетный набор чисел Пример вопроса: Найдите медиану для следующего набора данных:
102, 56, 34, 99, 89, 101, 10.
Шаг 1: Отсортируйте данные по наименьшему числу до максимального числа . Для этого примера набора данных порядок следующий:
10, 34, 56, 89, 99, 101, 102.
Шаг 2: Найдите число в середине (где есть равное количество точек данных выше и под номером):
10, 34, 56, 89 , 99, 101, 102.
Медиана равна 89.
Совет : Если у вас большой набор данных, разделите число в наборе на 2. Это говорит вам, сколько чисел должно быть выше и как многие цифры должны быть ниже. Например, 10 1/2 = 55,5. Не обращайте внимания на десятичную дробь; 55 номеров должны быть выше и 55 ниже.
Найдите медиану для
четного набора чисел Пример вопроса: Найдите медиану для следующего набора данных:
102, 56, 34, 99, 89, 101, 10, 54.
Шаг 1: Разместите данные в порядке возрастания (от меньшего к большему).
10, 34, 54, 56, 89, 99, 101, 102.
Шаг 2: Найдите ДВА числа в середине (где есть равное количество точек данных над и под двумя средними числами ).
10, 34, 54, 56, 89 , 99, 101, 102
Шаг 3: Сложите два средних числа и затем разделите на два, , чтобы получить среднее значение:
- 56 + 89= 145
- 145/2 = 72,5.

Медиана 72,5.
Совет: Для больших наборов данных разделите количество элементов на 2, затем вычтите 1, чтобы найти число, которое должно быть выше, и число, которое должно быть ниже. Например, 100/2 = 50. 50 – 1 = 49. Два средних числа будут иметь 49 элементов вверху и 49 внизу.
Вот и все!
Медиана очень полезна для описания таких вещей, как заработная плата, где большие цифры могут отклонить среднее значение. Средняя зарплата в США по состоянию на 2012 год составляла 51 017 долларов. Если бы использовалось среднее значение, эти американские миллиардеры могли бы исказить эту цифру в большую сторону.
Допустим, вы хотите работать в небольшой юридической фирме, которая платит 11 сотрудникам среднюю зарплату более 73 000 долларов. Вы можете подумать, что у вас есть хорошие шансы найти хорошо оплачиваемую работу. Но взгляните внимательнее на то, как рассчитывается среднее значение для этих одиннадцати сотрудников:
| Сотрудник | Зарплата |
| Сэмюэл | 28 000 долларов США |
| Кэндис | 17 400 долларов США |
| Томас | 22 000 долларов |
| Тед | 300 000 долларов США |
| Карли | 300 000 долларов США |
| Шаванна | 20 500 долларов США |
| Чан | 18 500 долларов США |
| Джанин | 27 000 долларов США |
| Барбара | 21 000 долларов США |
| Анна | 29 000 долларов США |
| Джим | 20 000 долларов США |
Среднее (среднее) =
(28 000 долл. США + 17 400 долл. США + 22 000 долл. США + 300 000 долл. США + 300 000 долл. США + 20 500 долл. США + 18 500 долл. США + 27 000 долл. США + 21 000 долл. США + 29 000 долл. США + 20 000 долл. США) / 11 = долл. США 73 000
США + 17 400 долл. США + 22 000 долл. США + 300 000 долл. США + 300 000 долл. США + 20 500 долл. США + 18 500 долл. США + 27 000 долл. США + 21 000 долл. США + 29 000 долл. США + 20 000 долл. США) / 11 = долл. США 73 000
. Два партнера в фирме — Carly. большая часть заработной платы, выплачиваемой в фирме.
Видите, как «средний» может вводить в заблуждение?
Лучший способ описать доход — вычислить медиану — или среднюю заработную плату. Если вы возьмете тот же список доходов и найдете медиану, вы получите более реалистичное представление о доходах. Медиана — это среднее число, поэтому, если вы поместите все доходы в список (от наименьшего к наибольшему), вы получите:
17 400 долларов, 18 500 долларов, 20 000 долларов, 20 500 долларов 21 000 долларов, 22 000 долларов, 27 000 долларов, 28 000 долларов, 29 000 долларов, 300 000 долларов, 300 000 долларов
Это более точное представление того, сколько людям на самом деле платят.
Простой способ приблизить медиану (MD) для сгруппированного частотного распределения — использовать среднюю точку интервала. Если вам нужно что-то более точное, используйте формулу:
MD = нижнее значение + (B ÷ D) x C.
Шаг 1: Используйте (n + 1) / 2, чтобы узнать, какой интервал имеет MD. Например, если у вас 11 интервалов, то MD находится в шестом интервале: (11 + 1)/2 = 12/2 = 6. Этот интервал называется группой MD.
Шаг 2: Рассчитайте «A»: кумулятивный процент для интервала непосредственно перед медианной группой.
Шаг 3: Рассчитайте «В»: вычтите значение шага 2 из 50%. Например, если кумулятивный процент равен 45%, то B равно 50% — 45% = 65%.
Шаг 4: Найдите «C»: диапазон (сколько чисел в интервале).
Шаг 5: Найдите «D»: процент медианного интервала.
Шаг 7: Найдите медиану: Медиана = нижнее значение + (B ÷ D) x C.
Вот и все!
Содержание :
- Excel 2013.

- Excel 2007-2010.
Excel 2013
Посмотрите видео или прочитайте шаги ниже:
Как найти медиану в Excel 2013
Посмотрите это видео на YouTube.
Есть два способа найти медиану в Excel — с помощью функции или с помощью инструмента анализа данных. Пакет инструментов анализа данных имеет несколько преимуществ по сравнению с простым вводом формул. Во-первых, он дает вам доступ ко многим функциям, которых нет в стандартном пакете Excel (например, к гистограммам). Во-вторых, вам не придется запоминать формулы, так как Toolpak представляет собой интерфейс Click and Go.
Функция МЕДИАНА
Шаг 1: Введите «=МЕДИАНА (A1:A12)» в пустую ячейку, где «A1:A12» — это расположение ваших данных. Например, если вы ввели данные в поля от D1 до D12, измените их на «=MEDIAN(D1:D12)».
Шаг 2: Нажмите «Ввод».
Пакет инструментов для анализа данных
Шаг 1. Перейдите на вкладку «Данные», а затем нажмите «Анализ данных».
Шаг 2: Нажмите «Описательная статистика», а затем нажмите «ОК».
Шаг 3. Щелкните поле «Входной диапазон» и введите местоположение для ваших данных. Например, если вы ввели данные в ячейки от A1 до A10, введите в это поле «A1:A10».0121 Шаг 4: Щелкните переключатель для строк или столбцов, в зависимости от того, как расположены ваши данные.
Шаг 5. Установите флажок «Ярлыки в первой строке», если ваши данные содержат заголовки столбцов.
Шаг 6: Установите флажок «Описательная статистика».
Шаг 7: Выберите место для вывода. Например, щелкните переключатель «Новый рабочий лист».
Шаг 8: Нажмите «ОК».
Медиана в Excel 2007-2010.
Медиана в Excel 2007
Посмотрите это видео на YouTube.
Пример вопроса: Найдите медиану для следующего набора: 123, 563, 567, 22, 498, 593, 947, 4, 46, 876, 223, 567,1, 222,22.
Шаг 1: Введите данные в один столбец. В этом примере введите «123» в ячейку A1, нажмите «Ввод» и продолжайте вводить числа вниз по столбцу от A1 до A13.
Шаг 2: Щелкните пустую ячейку.
Шаг 3: Перейдите на вкладку «Формулы» , а затем нажмите «Вставить функцию».
Шаг 4: Введите «Медиана» в текстовое поле «Поиск функции» , а затем нажмите «Перейти». Медиана должна быть выделена в списке результатов. Нажмите «ОК».
Шаг 5: Введите диапазон ячеек в ячейку «Число1» . В большинстве случаев Excel уже автоматически заполнит этот список вашим списком. Если это не так, введите «A1: A13» в поле Number1, где «A1: A13» — фактическое местоположение ваших данных.
Шаг 6: Нажмите «ОК ». Ответ будет отображаться в ячейке, которую вы выбрали на шаге 2. Для этого примера медиана равна 498.
Чтобы упорядочить данные:
- Щелкните букву в верхней части столбца, где вы хотите расположить упорядоченные номера. В этом примере нажмите «А».
- Щелкните стрелки справа от раскрывающихся списков, чтобы изменить параметры.
 Например, вы можете выбрать «Порядок» как «от меньшего к большему» или «от большего к меньшему».
Например, вы можете выбрать «Порядок» как «от меньшего к большему» или «от большего к меньшему». - Нажмите «ОК».
В этом видео показано, как найти медиану в Minitab менее чем за минуту:
Как найти медиану в Minitab
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Медиана: как найти, определение и примеры» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/median/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Медиана | Что это такое и как его найти?
Опубликован в 2 октября 2020 г. по Прита Бхандари. Отредактировано 23 мая 2022 г.
Медиана — это значение, которое находится точно в середине набора данных, когда он упорядочен. Это мера центральной тенденции, которая отделяет самые низкие 50% от самых высоких 50% значений.
Действия по нахождению медианы различаются в зависимости от того, четное или нечетное количество точек данных. Если в середине набора данных есть два числа, их среднее значение является медианой.
Медиана обычно используется с количественными данными (где значения являются числовыми), но иногда вы также можете найти медиану для порядкового набора данных (где значения являются ранжированными категориями).
Содержание
- Найти медиану с нечетным набором данных
- Найти медиану с четным набором данных
- Найти медиану с порядковым номером
- Когда следует использовать медиану?
- Часто задаваемые вопросы о медиане
Найти медиану с нечетным набором данных
Мы пройдемся по шагам, используя небольшой примерный набор данных с еженедельной оплатой 5 человек.
| Еженедельная оплата (доллары США) | 350 | 800 | 220 | 500 | 130 |
|---|
| Еженедельная оплата (долл. США) | 130 | 220 | 350 | 500 | 800 |
|---|
Используйте формулу , где n — это количество значений в вашем наборе данных.
Вычисление среднего положения| Формула | Расчет |
|---|---|
| |
Медиана — это значение в 3-й позиции .
Шаг 3: Найдите значение в средней позиции. Нахождение медианы Еженедельная заработная плата (долл. США) США) | 130 | 220 | 350 | 500 | 800 |
|---|
Средняя недельная заработная плата составляет 350 долларов США.
Найти медиану с четным набором данных
В наборе данных с четным номером нет ни одного значения в середине набора данных, поэтому мы должны следовать немного другой процедуре.
Давайте добавим еще одно значение в набор данных. Теперь у вас есть 6 значений.
Набор данных| Еженедельная оплата (долл. США) | 350 | 800 | 220 | 500 | 130 | 1150 |
|---|
| Еженедельная оплата (долл. США) | 130 | 220 | 350 | 500 | 800 | 1150 |
|---|
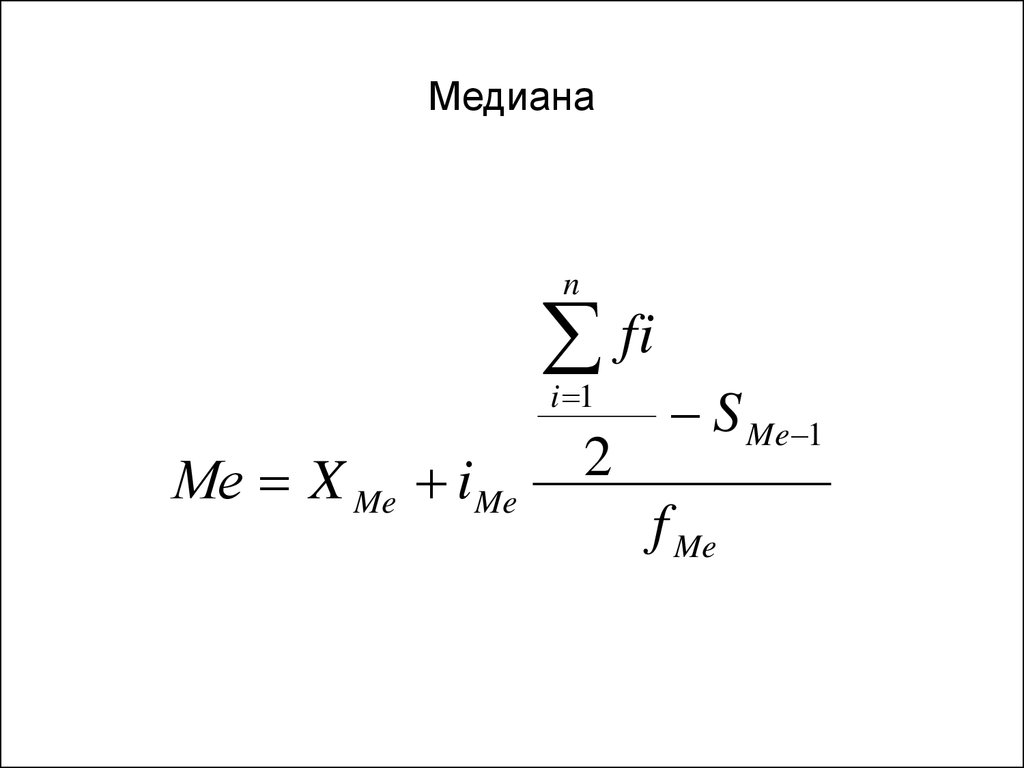
Средние позиции находятся по формулам и , где n — это количество значений в вашем наборе данных.
Вычисление средних позиций| Формула | Расчет |
|---|---|
| | |
| |
Средние значения находятся на 3-й и 4-й позициях.
Шаг 3: Найдите два средних значения.
Средние значения| Еженедельная оплата (долл. США) | 130 | 220 | 350 | 500 | 800 | 1150 |
|---|
Средние значения: 350 и 500 .
Шаг 4: Найдите среднее значение двух средних значений.
Чтобы найти медиану, вычислите среднее значение, сложив средние значения и разделив их на два.
Расчет медианыМедиана: Средняя еженедельная оплата для этого набора данных составляет 425 долларов США.
Получение отзывов о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
- Академический стиль
- Расплывчатые предложения
- Грамматика
- Согласованность стиля
См. пример
Найти медиану с порядковыми данными
Медиана обычно используется для количественных данных, что означает, что значения в наборе данных являются числовыми. Но иногда вы также можете определить медиану для порядковых данных.
Порядковые данные организованы в категории с порядком ранжирования — например, уровень владения языком (начальный, средний или свободный) или уровень согласия (полностью согласен, согласен и т. д.).
Процесс нахождения медианы почти такой же.
Набор данных с нечетным номером
Мы рассмотрим шаги для нечетного порядкового набора данных с 7 значениями.
Вы делите время реакции участников на 3 группы: медленная, средняя или быстрая.
Сначала расположите все значения в порядке возрастания.
Заказанный набор данных| Скорость реакции | Медленный | Медленный | Средний | Средний | Быстро | Быстро | Быстро |
|---|
Затем найдите среднее значение, используя , где n — количество значений в наборе данных.
Вычисление среднего положения| Формула | Расчет |
|---|---|
| |
Медиана — это значение на 4-й позиции.
Нахождение медианы| Скорость реакции | Медленный | Медленный | Средний | Средний | Быстро | Быстро | Быстро |
|---|
Средняя скорость реакции Средняя .
Можете ли вы найти медиану для четного порядкового набора данных?
Невозможно рассчитать среднее значение для порядковых данных, поэтому невозможно найти медиану для набора данных с четным номером.
Например, если два средних значения — «медленный» и «средний», вы не можете вычислить среднее значение этих значений.
На практике порядковые данные иногда для удобства преобразуются в числовой формат и обрабатываются как количественные данные. Затем можно вычислить среднее значение средних значений, чтобы найти медиану.
Хотя это считается приемлемым в некоторых контекстах, это не всегда считается правильным.
Когда следует использовать медиану?
Медиана является наиболее информативной мерой центральной тенденции для асимметричных распределений или распределений с выбросами.
В асимметричных распределениях по одну сторону от центра приходится больше значений, чем по другую, а среднее значение, медиана и мода отличаются друг от друга.
В распределении с положительной асимметрией имеется группа более низких оценок и растянутый хвост справа.
В распределении с отрицательной асимметрией есть кластер с более высокими оценками и разбросанный хвост слева.
Поскольку медиана использует только одно или два значения из середины набора данных, на нее не влияют экстремальные выбросы или несимметричное распределение оценок. Напротив, положения среднего значения и моды могут варьироваться в асимметричных распределениях.
По этой причине медиану часто называют мерой центральной тенденции для таких переменных, как доход, поскольку эти распределения обычно имеют положительную асимметрию.
Уровень измерения вашей переменной также определяет, можно ли использовать медиану. Медиану можно использовать только для данных, которые можно упорядочить, то есть из порядковых, интервальных и относительных уровней измерения.
Часто задаваемые вопросы о медиане
- Что такое меры центральной тенденции?
- org/Answer»>
Меры центральной тенденции помогают найти середину или среднее значение набора данных.
Тремя наиболее распространенными показателями центральной тенденции являются среднее значение, медиана и мода.
- Режим является наиболее частым значением.
- Медиана — это среднее число в упорядоченном наборе данных.
- Среднее значение — это сумма всех значений, деленная на общее количество значений.
- Как найти медиану?
Чтобы найти медиану, сначала упорядочите свои данные. Затем вычислите среднюю позицию на основе n , количество значений в вашем наборе данных.
- Если n — нечетное число, медиана лежит в позиции .

- Если n — четное число, медиана — это среднее значение значений в позициях и .
- Если n — нечетное число, медиана лежит в позиции .
- Когда следует использовать медиану?
Медиана является наиболее информативной мерой центральной тенденции для асимметричных распределений или распределений с выбросами. Например, медиана часто используется как мера центральной тенденции распределения доходов, которое обычно сильно асимметрично.
Поскольку медиана использует только одно или два значения, на нее не влияют экстремальные выбросы или несимметричное распределение оценок. Напротив, среднее значение и мода могут различаться в асимметричных распределениях.
Полезна ли эта статья?
Вы уже проголосовали. Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса…
Спасибо 🙂
Ваш голос сохранен 🙂
Обработка вашего голоса…
Прита имеет академическое образование в области английского языка, психологии и когнитивной нейробиологии. Как междисциплинарный исследователь, она любит писать статьи, объясняющие сложные исследовательские концепции для студентов и ученых.
4.4.2 Расчет медианы
Содержание
Текст начинается
Тематическая навигация
- 4 Исследование данных
- 4.4 Меры центральной тенденции
- 4.4.1 Вычисление среднего
- 4.4.2 Расчет медианы
- 4.4.3 Расчет режима
- 4.4 Меры центральной тенденции
Медиана — это значение в середине набора данных, означающее, что 50 % точек данных имеют значение, меньшее или равное медиане, а 50 % точек данных имеют значение выше или равное медиане. Для небольшого набора данных вы сначала подсчитываете количество точек данных (n) и упорядочиваете точки данных в порядке возрастания. Если количество точек данных нечетное, вы добавляете 1 к количеству точек и делите результат на 2, чтобы получить ранг точки данных, значение которой является медианой. Ранг — это положение точки данных после того, как набор данных был упорядочен в порядке возрастания: наименьшее значение — ранг 1, второе наименьшее значение — ранг 2 и т. д.
Для небольшого набора данных вы сначала подсчитываете количество точек данных (n) и упорядочиваете точки данных в порядке возрастания. Если количество точек данных нечетное, вы добавляете 1 к количеству точек и делите результат на 2, чтобы получить ранг точки данных, значение которой является медианой. Ранг — это положение точки данных после того, как набор данных был упорядочен в порядке возрастания: наименьшее значение — ранг 1, второе наименьшее значение — ранг 2 и т. д.
Пример 1. Среднее время на 200 м спортсмена-лидера
Представьте, что лучший спортсмен на типичной тренировке на 200 метров бежит за следующие времена: 26,1 секунды, 25,6 секунды, 25,7 секунды, 25,2 секунды, 25,0 секунды, 27,8 секунды и 24,1 секунды. Как бы вы рассчитали его среднее время?
Начнем с расположения значений в порядке возрастания:
| Ранг | Раз (в секундах) |
|---|---|
| 1 | 24,1 |
| 2 | 25,0 |
| 3 | 25,2 |
| 4 | 25,6 |
| 5 | 25,7 |
| 6 | 26,1 |
| 7 | 27,8 |
Имеется n = 7 точек данных, что является нечетным числом. Медиана будет значением точек данных ранга 9.0005
Медиана будет значением точек данных ранга 9.0005
(n + 1) ÷ 2 = (7 + 1) ÷ 2 = 4.
Среднее время составляет 25,6 секунды.
Если количество точек данных четное, медианой будет среднее значение точки данных ранга n ÷ 2 и точки данных ранга (n ÷ 2) + 1. лучший бегун (часть 2)
Теперь предположим, что спортсмен пробежал свой восьмой забег на 200 метров со временем 24,7 секунды. Каково его среднее время сейчас?
| Ранг | Раз (в секундах) |
|---|---|
| 1 | 24,1 |
| 2 | 24,7 |
| 3 | 25,0 |
| 4 | 25,2 |
| 5 | 25,6 |
| 6 | 25,7 |
| 7 | 26,1 |
| 8 | 27,8 |
Теперь имеется n = 8 точек данных, четное число. Медиана представляет собой среднее значение между точкой данных ранга
Медиана представляет собой среднее значение между точкой данных ранга
n ÷ 2 = 8 ÷ 2 = 4
и точкой данных ранга
(n ÷ 2) + 1 = (8 ÷ 2) +1 = 5
Следовательно, среднее время равно (25,2 + 25,6) ÷ 2 = 25,4 секунды.
Для больших наборов данных кумулятивное относительное частотное распределение может быть полезным для определения медианы. Медиана — это наименьшее значение, для которого кумулятивная относительная частота составляет не менее 50 %. Однако, когда это возможно, лучше использовать базовую статистическую функцию, доступную в электронной таблице или статистическом приложении, потому что тогда результаты будут более надежными.
Пример 3 – Средний размер домохозяйства учащихся класса
Представьте, что вы спрашиваете 30 учеников вашего класса, сколько человек проживает в их семьях. Вы суммируете данные, которые вы собрали, в таблице частот, в которую вы включаете относительные частоты и кумулятивные относительные частоты.
| Размер семьи | Периодичность (количество студентов) | Относительная частота (%) | Суммарная частота (количество учащихся) | Кумулятивная относительная частота (%) |
|---|---|---|---|---|
| 2 | 3 | 10,0 | 3 | 10,0 |
| 3 | 4 | 13,3 | 7 | 23,3 |
| 4 | 10 | 33,3 | 17 | 56,7 |
| 5 | 4 | 13,3 | 21 | 70,0 |
| 6 | 2 | 6,7 | 23 | 76,7 |
| 7 | 3 | 10,0 | 26 | 86,7 |
| 8 | 1 | 3,3 | 27 | 90,0 |
| 9 | 2 | 6,7 | 29 | 96,7 |
| 10 | 1 | 3,3 | 30 | 100,0 |
Вы можете видеть, что 10 % учащихся (3 учащихся) живут в домохозяйстве размера 2, 23 % учащихся (7 учащихся) живут в домашнем хозяйстве 3-го размера или меньше и 57 % учащихся (17 учащихся) жить в домохозяйстве размером 4 или меньше. Медиана будет равна 4, поскольку это наименьшее значение, для которого кумулятивная относительная частота превышает 50%. Это станет еще более очевидным, если вы представите кумулятивную относительную частоту на гистограмме, как на диаграмме 4.4.2.1. Пунктирная линия указывает кумулятивную относительную частоту 50%.
Медиана будет равна 4, поскольку это наименьшее значение, для которого кумулятивная относительная частота превышает 50%. Это станет еще более очевидным, если вы представите кумулятивную относительную частоту на гистограмме, как на диаграмме 4.4.2.1. Пунктирная линия указывает кумулятивную относительную частоту 50%.
| Размер семьи | Кумулятивная относительная частота (%) |
|---|---|
| 2 | 10,0 |
| 3 | 23,3 |
| 4 | 56,7 |
| 5 | 70,0 |
| 6 | 76,7 |
| 7 | 86,7 |
| 8 | 90,0 |
| 9 | 96,7 |
| 10 | 100,0 |
Среднее значение равно общему количеству людей в домохозяйствах учащихся:
2 × 3 + 3 × 4 + 4 × 10 + 5 × 4 + 6 × 2 + 7 × 3 + 8 × 1 + 9 × 2 + 10 × 1 = 147
разделить на количество учащихся, равное 30. Результат: 147 ÷ 30 = 4,9 человека на домохозяйство.
Результат: 147 ÷ 30 = 4,9 человека на домохозяйство.
В этом примере медиана (4) ниже среднего (4.9).
Преимущество использования медианы вместо среднего заключается в том, что медиана является более надежной, а это означает, что экстремальное значение, добавленное к одному краю распределения, не оказывает на медиану такого же сильного влияния, как влияние на среднее значение. Поэтому важно проверить, содержит ли набор данных экстремальные значения, прежде чем выбирать меру центральной тенденции. Это будет проиллюстрировано следующим примером.
Пример 4 – Средний размер домохозяйств учащихся в классе (Часть 2)
Недавно к вашему классу присоединился новый ученик. Вы решаете спросить его, каков размер его семьи, чтобы обновить свои результаты. Он отвечает вам, что живет в большом многоквартирном доме, в котором проживает 18 человек!
После обновления среднее значение составляет (147 + 18) ÷ 31 = 5,3 человека на домохозяйство. Простое добавление одного нового ученика увеличило среднее значение на 0,4 (5,3–4,9). Медиана такая же после обновления. Теперь 7 ÷ 31 = 22,6% учащихся в домохозяйстве размером 3 или меньше, и 17 ÷ 31 = 54,8% учащихся, проживающих в домохозяйстве размером 4 или меньше. Значение 4 по-прежнему является наименьшим значением с совокупной относительной частотой не менее 50%.
Медиана такая же после обновления. Теперь 7 ÷ 31 = 22,6% учащихся в домохозяйстве размером 3 или меньше, и 17 ÷ 31 = 54,8% учащихся, проживающих в домохозяйстве размером 4 или меньше. Значение 4 по-прежнему является наименьшим значением с совокупной относительной частотой не менее 50%.
- Статистика: сила данных! — Главная страница
- 1 Данные, статистическая информация и статистика
- 2 Источники данных
- 3 Сбор и обработка данных
- 4 Исследование данных
- 5 Визуализация данных
- Библиография
- Глоссарий
Что-то не работает? Есть ли устаревшая информация? Не можете найти то, что ищете?
Пожалуйста, свяжитесь с нами и дайте нам знать, как мы можем вам помочь.
Уведомление о конфиденциальности
- Дата изменения:
Медиана в Excel (формула, пример)
Медиана Excel Формула (Оглавление)
- Формула медианы в Excel
- Как рассчитать медиану в Excel с помощью формулы?
Формула медианы в Excel является одним из основных элементов статистической меры центральной тенденции (остальные два — среднее значение и мода). Это дает более достойный подход к нахождению среднего значения для заданных данных.
Это дает более достойный подход к нахождению среднего значения для заданных данных.
Если у нас есть группа наблюдений, расположенных в порядке возрастания или убывания, то медиана этой группы будет самым средним значением. Это означает, что ровно 50% (половина наблюдений) выше среднего значения и ровно 50% (или половина наблюдений) ниже среднего значения.
Если набор данных содержит нечетное количество наблюдений, медианой будет среднее наблюдение. Если набор данных содержит четное количество наблюдений, медиана будет средним значением двух средних наблюдений.
В случаях, когда нам нужно рассчитать точный центр данных, например. Расчеты, содержащие данные о заработной плате, — это те, где среднего значения не было бы с такой эффективностью. Причина этого в том, что наше среднее значение может иметь чрезвычайно низкие или высокие значения, что может повлиять на среднюю заработную плату. Однако медиана менее всего подвержена влиянию таких экстремальных наблюдений, из-за чего мы предпочитаем ее вычислять.
В Microsoft Excel мы можем вычислить медиану, используя функцию МЕДИАНА. Это встроенная в Excel функция, которая работает с рядом данных и вычисляет медиану для этой группы.
Формула для функции МЕДИАНА в Excel выглядит следующим образом:
Где число1, число2 … — аргументы функции. Формула МЕДИАНА Excel может принимать числа, массивы, именованные диапазоны, даты или ссылки на ячейки в качестве входных аргументов. Эта функция требует по крайней мере один аргумент для обеспечения вывода (т. е. номер 1 является фиксированным/обязательным аргументом, все остальные необязательны).
Как рассчитать медиану в Excel с помощью формулы?Вычислить медиану в Excel с помощью формулы очень просто и легко. Давайте разберемся, как рассчитать медиану в Excel на нескольких примерах.
Вы можете скачать этот шаблон формулы медианы в Excel здесь — Шаблон формулы медианы в Excel
Пример № 1 — Группа с нечетным числом наблюдений
Предположим, у меня есть данные о продажах автомобилей в миллионах с 2010 по 2018 год для США. (9общее количество наблюдений, что является нечетным числом).
(9общее количество наблюдений, что является нечетным числом).
На изображении ниже видно, что наблюдения перечислены в порядке возрастания по годам.
Поместите следующую формулу в ячейку B12. то есть = МЕДИАНА (B2: B10). См. рисунок ниже:
Какой результат вы ожидаете получить, используя эту формулу?
Как вы могли правильно догадаться, эта функция позволяет Excel печатать значение медианы для заданного диапазона (B2:B10), которое в данном случае равно 202.
- Нажмите клавишу ВВОД, когда закончите с формулой, и вы получите следующий вывод:
Год, связанный со средним значением, можно рассматривать как Медианный год (в данном случае 2014 г.). Кажется логичным, правда?
Обратите внимание, что мы расположили данные по годам, а не по продажам. Поэтому не смущайтесь, если значение продаж кажется не в порядке возрастания или убывания.
А что, если у меня четное количество наблюдений?
Пример № 2 — Группа с четным числом наблюдений
Предположим, у меня есть данные о продажах еще для одного года 2019. Это означает четное количество (10) наблюдений. Давайте посмотрим, как формула медианы работает с такими данными.
Это означает четное количество (10) наблюдений. Давайте посмотрим, как формула медианы работает с такими данными.
Предположим, у меня есть данные, как показано ниже:
В ячейке D2 введите формулу =МЕДИАНА (B2:B11)
После завершения нажмите Enter и посмотрите результат.
При наличии четного числа наблюдений Медиана представляет собой среднее двух самых средних значений.
Формула условной медианы
Работая над функцией СРЗНАЧ в Excel, вы, возможно, видели некоторые настраиваемые формулы, такие как СРЗНАЧЕСЛИ и СРЗНАЧСЛИМН, которые позволяют настраивать функцию СРЗНАЧ на основе условия/условий. Это означает предоставление среднего значения группы в соответствии с определенными критериями. К сожалению, для МЕДИАНЫ нет такой индивидуальной формулы в готовом виде в Excel. Однако вы можете использовать свою собственную логику и создать одну из таких условных формул для расчета медианы группы наблюдений.
Ниже приведена формула, которую можно использовать:
Пример № 3. Медиана Excel Если формула
Предположим, у вас есть данные о типах автомобилей и их стоимости в лакхах, как показано ниже:
Тип автомобиля Седан в ваших данных; что ты можешь сделать?
Для этого поместите значения типа автомобиля в отдельный столбец, скажем, столбец D.
Используйте приведенную ниже условную формулу:
=МЕДИАНА(ЕСЛИ($A$2:$A$13 = $D$2, $ Б$2:$Б$13))
См. изображение ниже:
Нажмите Ctrl + Shift + Enter одновременно после завершения формулы.
Поскольку вы работаете с диапазоном ячеек (например, с массивом), знак доллара ($) делает диапазоны ячеек абсолютными и полезен, когда у вас есть одинаковый диапазон данных для разных других категорий.
Более того, как видно из формулы, вы работаете с диапазоном ячеек, который сейчас является массивом, чтобы заставить формулу массива работать, вам нужно нажать Ctrl + Shift + Enter.
Что эта формула сделала, так это выбрала все седаны и их стоимость в лакхах, расположила их в порядке возрастания (что по умолчанию), а затем выбрала медиану из доступного набора значений.
Проделайте ту же процедуру для других ячеек в столбце D (ячейки D3, D4, D5, D6).
Вы также можете добавить несколько условий в эту формулу и заставить ее работать как СРЗНАЧЕСЛИМН.
Вот это из этой статьи. Давайте завершим кое-что, что нужно запомнить.
Что нужно помнить О формуле медианы в Excel- Когда группа наблюдений имеет нечетное количество значений, формула МЕДИАНА рассматривает самое среднее значение как медиану. Если группа наблюдений имеет четное количество значений, формула МЕДИАНА рассматривает среднее значение двух самых средних значений в качестве медианы.
- Прежде чем вы начнете использовать эту формулу, ваша группа наблюдения должна быть отсортирована в порядке возрастания или убывания.

- Если какая-либо ячейка имеет нулевое значение, она все равно является частью расчета медианы.
- В большинстве случаев медиана имеет преимущество перед средним значением. Потому что на него меньше всего влияют экстремально низкие/высокие значения.
- При вычислении пустых ячеек автоматически игнорируются ячейки с текстом или логическими значениями.
- Excel 2003 и более ранние версии позволяют использовать 30 аргументов в формуле для функции МЕДИАНА. В Excel 2007, 2010, 2013, 2016 это ограничение было увеличено с 30 до 255. Это означает, что вы можете передавать до 255 аргументов.
- Логические значения ИСТИНА и ЛОЖЬ учитываются в формуле МЕДИАНА. Например, МЕДИАНА(ЛОЖЬ, ИСТИНА, 2, 3) будет выводить 1,5 в качестве медианы, которая является не чем иным, как средним логическим значением ИСТИНА (ИСТИНА = 1) и числом 2.
Рекомендуемые статьи
Это руководство по формуле медианы в Excel. Здесь мы обсуждаем, как рассчитать медиану в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть другие наши рекомендуемые статьи —
Вы также можете просмотреть другие наши рекомендуемые статьи —
- Формула частоты Excel
- Формула FV Excel
- Статистика в Excel
- Как найти среднее значение в Excel
Медиана — формула, значение, пример
Медиана представляет среднее значение для любой группы. Это точка, в которой половина данных больше, а половина данных меньше. Медиана помогает представить большое количество точек данных с помощью одной точки данных. Медиана является самой простой статистической мерой для вычисления. Для расчета медианы данные должны быть расположены в порядке возрастания, а затем самая средняя точка данных представляет медиана данных .
Кроме того, расчет медианы зависит от количества точек данных. Для нечетного числа данных медиана — это самые средние данные, а для четного числа данных — среднее значение двух средних значений. Давайте узнаем больше о медиане, расчете медианы для четно-нечетного количества точек данных и формуле медианы в следующих разделах.
| 1. | Что такое медиана? |
| 2. | Медианная формула |
| 3. | Как найти медиану? |
| 4. | Часто задаваемые вопросы о том, как найти медиану |
Что такое медиана?
Медиана — одна из трех мер центральной тенденции. При описании набора данных определяется центральное положение набора данных. Это известно как мера центральной тенденции. Тремя наиболее распространенными показателями центральной тенденции являются среднее, медиана, и мода.
Определение медианы
Значение самого среднего наблюдения, полученного после упорядочивания данных в порядке возрастания, называется медианой данных. Во многих случаях трудно учесть полные данные для представления, и здесь полезна медиана. Среди статистических сводных метрик медиану легко вычислить. Медиану также называют средним значением по месту, так как данные, помещенные в середину последовательности, берутся за медиану.
Медиану также называют средним значением по месту, так как данные, помещенные в середину последовательности, берутся за медиану.
Пример медианы
Давайте рассмотрим пример, чтобы выяснить, что такое медиана для заданного набора данных.
- Шаг 1: Рассмотрим данные: 4, 4, 6, 3 и 2. Расположим эти данные в порядке возрастания: 2, 3, 4, 4, 6.
- Шаг 2: Подсчитайте количество значений. Есть 5 значений.
- Шаг 3: Найдите среднее значение. Среднее значение является медианой. Таким образом, медиана = 4, .
Медианная формула
Используя формулу медианы, можно вычислить среднее значение упорядоченного набора чисел. Для нахождения этой меры центральной тенденции необходимо расписать компоненты группы в порядке возрастания. Формула медианы варьируется в зависимости от количества наблюдений и от того, являются ли они нечетными или четными. Следующий набор формул поможет найти медиану данных.
Формула медианы для разгруппированных данных
Следующие шаги полезны при применении формулы медианы для разгруппированных данных.
- Шаг 1: Расположите данные в порядке возрастания или убывания.
- Шаг 2: Во-вторых, подсчитайте общее количество наблюдений ‘n’.
- Шаг 3: Проверьте, является ли число наблюдений n четным или нечетным.
Формула медианы при нечетном n
Формула медианы заданного набора чисел, скажем, имеющего ‘n’ нечетное число наблюдений, может быть выражена следующим образом:
Медиана = [(n + 1)/2] th термин
Формула медианы, когда n четно
Формула медианы заданного набора чисел, скажем, имеющего ‘n’ четное число наблюдений, может быть выражена следующим образом:
Медиана = [(n/2) th член + (( n/2) + 1) й термин]/2
Пример: Ниже указан возраст членов команды, играющей в покер на выходных. Найдите медиану вышеуказанного множества.
{42, 40, 50, 60, 35, 58, 32}
Решение:
Шаг 1. Расположите элементы данных в порядке возрастания.
Расположите элементы данных в порядке возрастания.
Исходный набор: {42, 40, 50, 60, 35, 58, 32}
Заказной набор: {32, 35, 40, 42, 50, 58, 60}
Шаг 2: Подсчитайте количество наблюдений . Если количество наблюдений нечетное, то мы будем использовать следующую формулу: Медиана = [(n + 1)/2] th term
Шаг 3: Рассчитайте медиану по формуле.
Медиана = [(n + 1)/2] th термин
= (7 + 1)/2 th термин = 4 th термин = 42
Медиана = 42
Формула медианы для сгруппированных данных
Когда данные являются непрерывными и представлены в виде частотного распределения, медиана вычисляется с помощью следующей последовательности шагов.
- Шаг 1: Найдите общее количество наблюдений (n).
- Шаг 2: Определите размер класса (h) и разделите данные на разные классы.
- Шаг 3: Рассчитайте совокупную частоту каждого класса.
- Шаг 4: Определите класс, к которому относится медиана.
 (Медианный класс — это класс, в котором находится n/2.)
(Медианный класс — это класс, в котором находится n/2.) - Шаг 5: Найдите нижний предел медианного класса (l) и кумулятивную частоту класса, предшествующего среднему классу (c).
Теперь используйте следующую формулу, чтобы найти среднее значение.
Применение формулы медианы
Давайте воспользуемся приведенными выше шагами на следующей практической иллюстрации, чтобы понять применение формулы медианы.
Иллюстрация: В организации 5 сотрудников высшего руководства. Заработная плата сотрудников составляет 5000, 6000, 4000, 8000 и 7500 долларов. Используя формулу медианы, рассчитывается медианная заработная плата.
Решение: Мы будем следовать данным шагам, чтобы найти медианную зарплату.
- Шаг 1: Сортировка данных в порядке возрастания: 4000, 5000, 6000, 7500 и 8000 долларов.
- Шаг 2: Общее количество наблюдений = 5
- Шаг 3: Заданное количество наблюдений нечетное.

- Шаг 4: Использование формулы медианы для нечетного наблюдения, Медиана = [(n + 1)/2] -й термин
- Медиана = [(5+1)/2] th год. = 6/3 = 3 рд терм. Третий срок — 6000 долларов.
Средняя зарплата составляет 6000 долларов.
Как найти медиану?
Мы используем формулу медианы, чтобы найти среднее значение заданных данных. Для набора разгруппированных данных мы можем выполнить приведенные ниже шаги, чтобы найти медианное значение.
- Шаг 1: Отсортируйте данные в порядке возрастания.
- Шаг 2: Подсчитайте количество наблюдений.
- Шаг 3: Если количество наблюдений нечетное, используйте формулу медианы: Медиана = [(n + 1)/2] th term
- Шаг 4: Если количество наблюдений четное, используйте формулу медианы: Медиана = [(n/2) -й -й термин + (n/2 + 1) -й -й термин]/2
Пример: Ниже указан рост (в сантиметрах) членов школьной футбольной команды.
{142, 140, 130, 150, 160,135, 158,132}
Найдите медиану приведенного выше множества.
Решение:
Шаг 1:
Расположите элементы данных в порядке возрастания.
Оригинальный набор: {142, 140, 130, 150, 160, 135, 158,132}
Заказанный набор: {130, 132, 135, 140, 142, 150, 158, 160}
. 2:
Подсчитайте количество наблюдений.
Количество наблюдений, n = 8
Если количество наблюдений четное, то будем использовать следующую формулу:
Медиана = [(n/2) -й -й член + ((n/2) + 1) -й -й термин]/2
Шаг 3:
Рассчитайте медиану, используя формулу.
Медиана = [(n/2) -й -й термин + ((n/2) + 1) -й -й термин]/2
Медиана = [(8/2) -й -й термин + ((8/ 2) + 1) -й -й термин]/2
= (4 -й -й термин + 5 -й -й термин)/2
= (140 + 142)/2
= 141
5 Для набора из 90 сгруппированные данные , мы можем выполнить следующие шаги, чтобы найти медиану:
Когда данные непрерывны и представлены в виде частотного распределения, медиана вычисляется с помощью следующей последовательности шагов.
- Шаг 1: Найдите общее количество наблюдений (n).
- Шаг 2: Определите размер класса (h) и разделите данные на разные классы.
- Шаг 3: Рассчитайте совокупную частоту каждого класса.
- Шаг 4: Определите класс, к которому относится медиана. (Медианный класс — это класс, в котором находится n/2.)
- Шаг 5: Найдите нижний предел медианного класса (l) и кумулятивной частоты (c).
- Шаг 6. Примените формулу медианы для сгруппированных данных: Медиана \(= l + [\dfrac {\dfrac{n}{2}-c}{f}]\times h\)
В предыдущем разделе мы видели примеры поиска медианы для разгруппированных данных. Вот пример расчета медианы для сгруппированных данных.
Пример: Рассчитайте медиану для следующих данных:
| Марки | 0 — 20 | 20 — 40 | 40 — 60 | 60 — 80 | 80 — 100 |
| Количество студентов | 5 | 20 | 35 | 7 | 3 |
Решение:
Нам нужно вычислить кумулятивные частоты, чтобы найти медиану.
| Знаки | Количество студентов | Суммарная частота | |
| 0 — 20 | 5 | 0 + 5 | 5 |
| 20 — 40 | 20 | 5 + 20 | 25 |
| 40 — 60 | 35 | 25 + 35 | 60 |
| 60 — 80 | 7 | 60 + 7 | 67 |
| 80 — 100 | 3 | 67 + 3 | 70 |
N = \(\sum f_i\) = 70
N/2 = 70/2 = 35
Медианный класс 40 — 60
l = 40, f = 35, c = 25, h = 20 \(\)
Используя формулу медианы:
Медиана \(= l + [\dfrac {\dfrac{n}{2}-c}{f}]\times h\)
= 40 + [(35 — 25)/35] × 20
= 40 + (10/35) × 20
= 40 + (40/7)
Медиана двух чисел
В упорядоченном ряду медиана — это число, которое находится посередине между крайними значениями диапазона. Обычно оно не совпадает со средним значением. Давайте разберемся, как найти медиану. Для набора из двух значений медиана будет такой же, как среднее или среднее арифметическое. Например, числа 2 и 10 имеют среднее значение и медиану 6. Обратите внимание, что медиана — это значение в средней точке набора данных, а не в средней точке значений. Среднее значение — это среднее арифметическое: (10 + 2)/2 = 6. Что, если мы добавим еще два числа, скажем, 3 и 4? Медиана будет 3,5, а среднее будет (2 + 3 + 4 + 10)/4 = 4,75
Обычно оно не совпадает со средним значением. Давайте разберемся, как найти медиану. Для набора из двух значений медиана будет такой же, как среднее или среднее арифметическое. Например, числа 2 и 10 имеют среднее значение и медиану 6. Обратите внимание, что медиана — это значение в средней точке набора данных, а не в средней точке значений. Среднее значение — это среднее арифметическое: (10 + 2)/2 = 6. Что, если мы добавим еще два числа, скажем, 3 и 4? Медиана будет 3,5, а среднее будет (2 + 3 + 4 + 10)/4 = 4,75
Важные примечания о медиане:
Вышеупомянутое содержание для нахождения медианы было обобщено в виде следующих пунктов.
- Медиана — это центральное значение данных (среднее позиционное).
- Данные должны быть расположены в порядке возрастания/убывания, чтобы найти среднее значение или медиану.
- При расчете медианы учитывается не каждое значение.
- Медиана не зависит от экстремумов.
Нестандартное мышление:
Теперь пришло время применить изученные концепции медианы. Вот вам вопрос!
Вот вам вопрос!
Вопрос: Определите медиану первых пяти целых чисел. В компании для каждого из 10 сотрудников, участвующих в процессе обновления услуг, количество проданных обновлений услуг составляет: 34, 26, 30, 21, 25, 12, 18, 20, 19, 15. среднее количество обновлений услуг, проданных 10 сотрудниками?
Связанные темы по медиане:
- Режим
- Средний
- Среднее
- Среднее геометрическое
Часто задаваемые вопросы о медиане
Что означает медиана в статистике?
Значение самого среднего наблюдения, полученного после упорядочивания данных в порядке возрастания или убывания, называется медианой данных . При описании набора данных определяется центральное положение набора данных, которое далее используется в формуле медианы. Это известно как мера центральной тенденции. Медиана является важным показателем центральной тенденции.
Что такое формула медианы для негруппированных данных?
Формула медианы для негруппированных данных полностью зависит от количества наблюдений (n). Если количество наблюдений нечетное, то формула медианы такова: [медиана = {(n + 1)/2} -й термин]. Если количество наблюдений четное, то формула медианы будет [медиана = ((n/2) th член + (n/2 + 1) th член)/2]
Если количество наблюдений нечетное, то формула медианы такова: [медиана = {(n + 1)/2} -й термин]. Если количество наблюдений четное, то формула медианы будет [медиана = ((n/2) th член + (n/2 + 1) th член)/2]
Что такое формула медианы при числе наблюдений четно?
Когда количество наблюдений четное (n = четное), тогда формула медианы будет [Median = ((n/2) -й терм + (n/2 + 1) -й терм)/2]
Какая формула медианы при нечетном числе наблюдений?
Когда число наблюдений нечетное (n = нечетное), тогда формула медианы будет [Median = {(n + 1)/2} th term]
В чем разница между средним значением, медианой, модой и Диапазон?
Среднее значение — это среднее арифметическое заданного набора данных. Медиана — это средний балл в наборе заданных чисел. Мода — это наиболее часто встречающееся значение в наборе заданных чисел. Диапазон — это разница между самым высоким и самым низким значениями.
Как найти среднее, моду и диапазон?
Режим относится к наиболее повторяющемуся числу в данном наборе данных. Среднее значение — это среднее всех чисел: сложите все значения и разделите сумму на количество значений. Диапазон — это разница между самым высоким и самым низким значениями.
Как рассчитать медиану?
Медиана набора данных вычисляется в два простых шага. Сначала расположите данные в порядке возрастания. Далее нам нужно выбрать самые средние данные.
- Для четного числа точек данных есть два средних значения, и нам нужно взять среднее этих двух средних значений.
- Для нечетного числа точек данных существует только одна средняя точка данных, и мы можем принять ее как медиану данных.
Что такое среднее и медиана?
Среднее значение данных — это среднее значение данных, равное сумме всех значений данных, деленной на количество точек данных. Медиана данных — это среднее значение данных после упорядочения данных в порядке возрастания.
Медиана равна среднему значению?
Медиана данных отличается от среднего. Медиана — это среднее значение заданных точек данных, а среднее значение — это значение, полученное путем деления суммы значений данных на количество точек данных. Но для равноотстоящих чисел, таких как 2, 4, 6, 8, 10, медиана и среднее совпадают, то есть 6.
Каково применение медианы?
Медиана — важный статистический показатель, помогающий представить одно значение для большого количества точек данных. Например, данные о росте или возрасте учащихся в классе представлены одним медианным значением данных.
Как расположить данные в порядке возрастания?
Для упорядочивания данных в порядке возрастания нам необходимо записать данные, начиная с наименьших значений, и далее включать точки данных в порядке возрастания их значения.
Почему медиану называют позиционной средней?
Медиана попадает в середину, когда данные располагаются в возрастающем или убывающем порядке.




 В данном случае среднее значение соответствует показателю 4,857143.
В данном случае среднее значение соответствует показателю 4,857143. Выбираем показатель «Среднее». Данное значение также можно получить, выполнив функцию СРЗНАЧ.
Выбираем показатель «Среднее». Данное значение также можно получить, выполнив функцию СРЗНАЧ.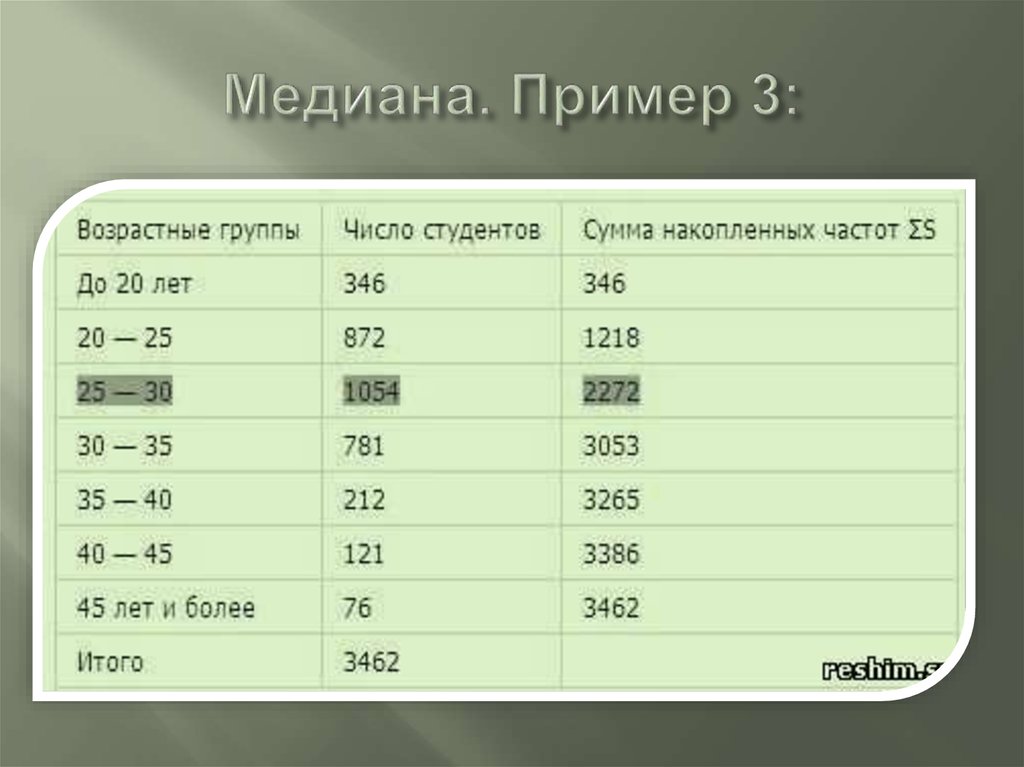 5) WITHIN GROUP(ORDER BY score) OVER(PARTITION BY testid) AS median
FROM Stats.Scores
)
SELECT testid, median
FROM C
WHERE rownum = 1;
5) WITHIN GROUP(ORDER BY score) OVER(PARTITION BY testid) AS median
FROM Stats.Scores
)
SELECT testid, median
FROM C
WHERE rownum = 1;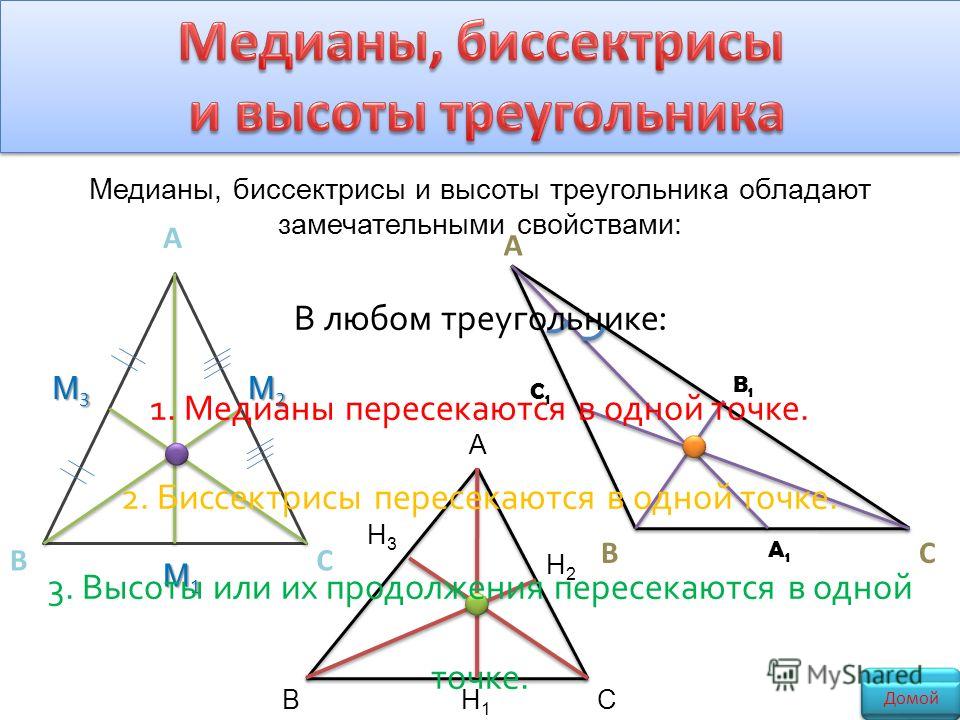 Scores;
Scores;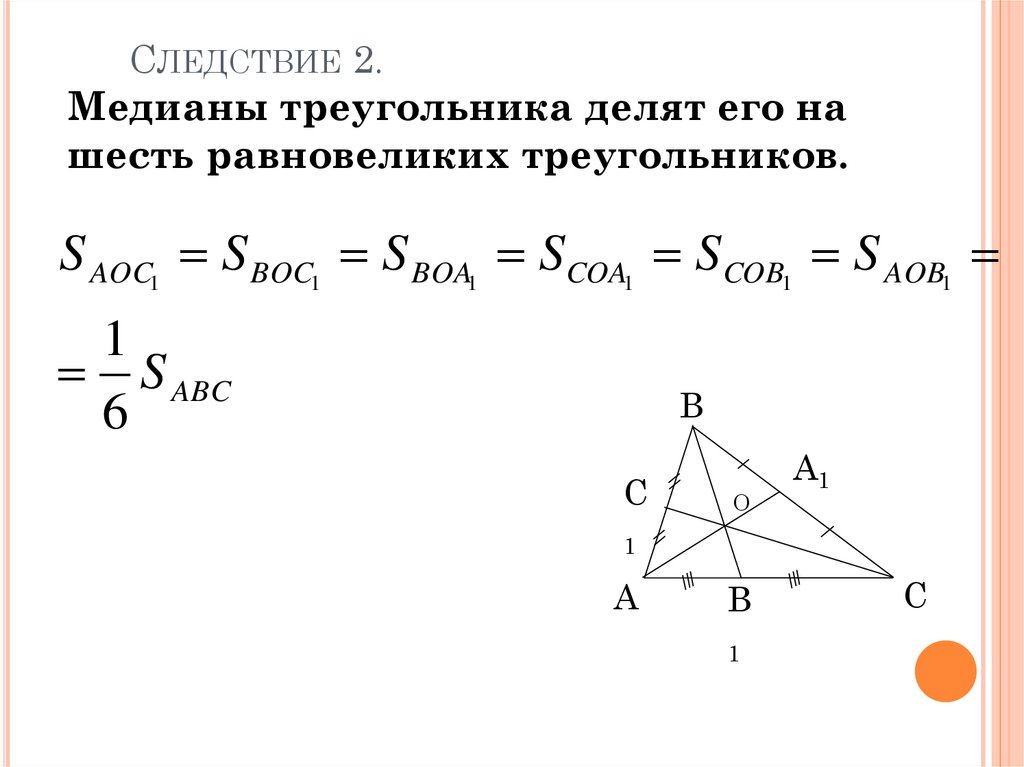

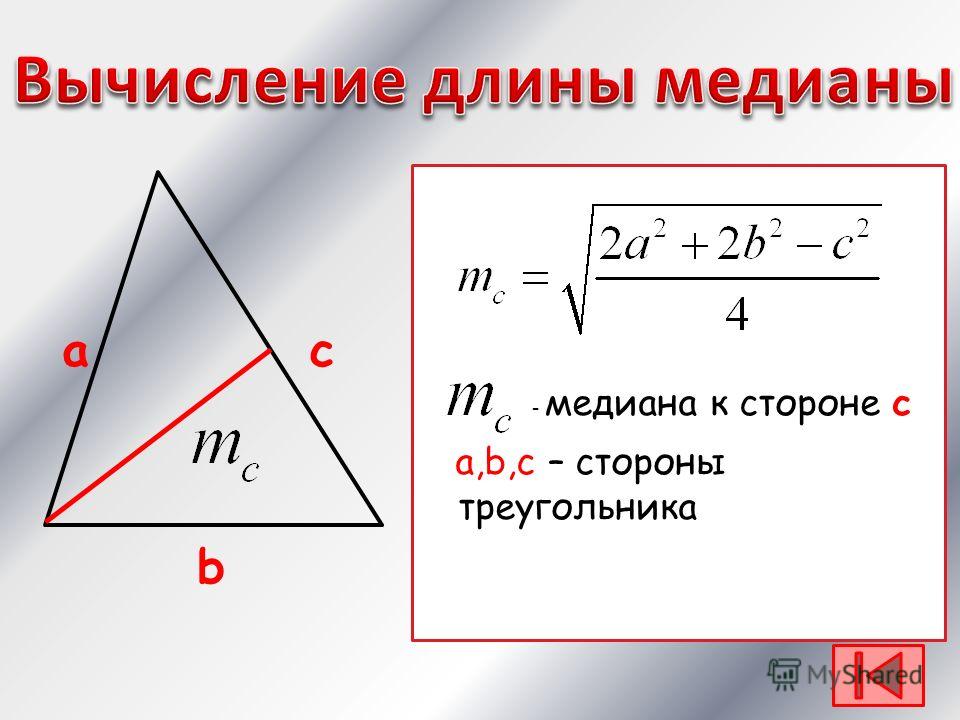 $)
$)
 .. return sum(sample) / len(sample)
...
>>> my_mean([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
5.2
.. return sum(sample) / len(sample)
...
>>> my_mean([4, 8, 6, 5, 3, 2, 8, 9, 2, 5])
5.2
 5
5
 multimode([4, 1, 2, 2, 3, 5])
[2]
multimode([4, 1, 2, 2, 3, 5])
[2]



 Например, вы можете выбрать «Порядок» как «от меньшего к большему» или «от большего к меньшему».
Например, вы можете выбрать «Порядок» как «от меньшего к большему» или «от большего к меньшему».