Вычислите площадь фигуры ограниченной линиями y x 2 1: Найдите площадь фигуры ограниченной линиями y=x^2+1,x=2,x=0,y=0

2,y=…

Лучший ответ по мнению автора

11. 05.17 Лучший ответ по мнению автора

Евгений Читать ответы

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Решено

Площадь треугольника ABC равна 31, DE — средняя линия, параллельная стороне AB. 2 x))/log_31 (корень из 2 *Cosx)

Решено

Последовательность задана условиями b1=-6,bn+1=-3×1/bn.найдите b3.

Пользуйтесь нашим приложением

Площадь фигуры ограниченной кривыми в прямоугольных координатах

Площадь фигуры между двумя кривыми в прямоугольных координатах определяется интегралом
от разницы кривых, где одна из них всегда принимает не меньшие значения чем другая , а также кривые непрерывны.
Пределы интегрирования — прямые x₁=a, x₂=b — ограничивают фигуру (a<b чаще всего это точки пересечения заданных кривых).
Данный цикл задач в первую очередь подойдет студентам мех-мата Львовского национального университета имени Ивана Франко для прохождения практикума из математического анализа.
Студенты других Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления.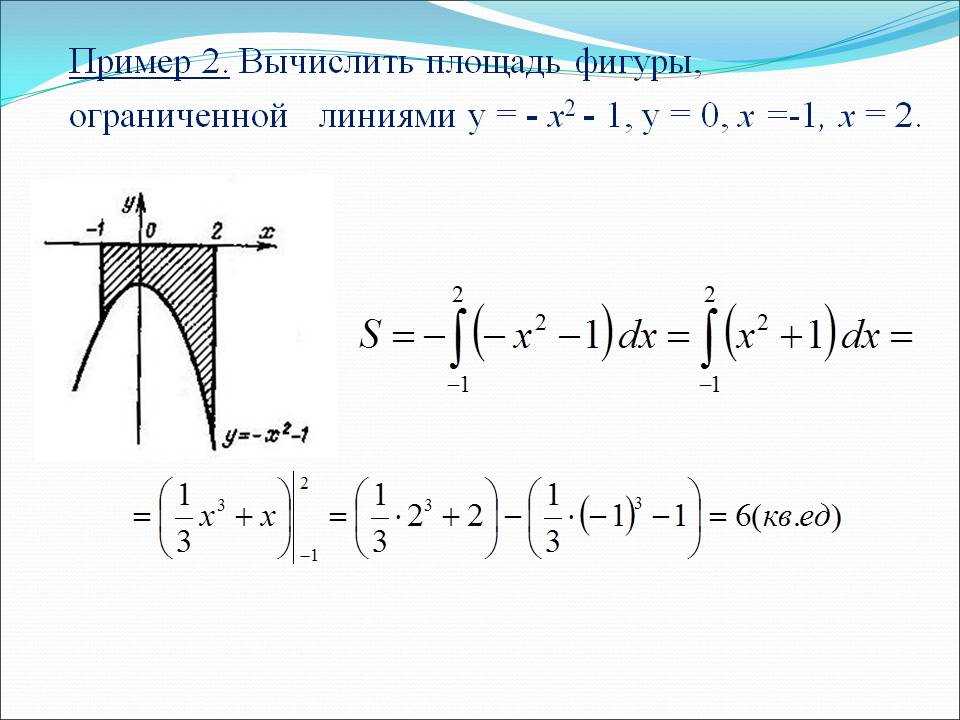
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича). 

 

Пример 2.81 (2397). Найти площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах ax=y², ay=x²,(a>0).

Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:

На графике они будут иметь следующий вид

Площадь между кривыми и нужно найти. Как правило, Вам редко будет известно сам график, поэтому в заданиях где не заданы области на которой находить площадь в первую очередь необходимо найти точки пересечения кривых.
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций y₁(x)=y₂(x):

Как видите таким условием есть условие равенства функций.
Из последнего уравнения получим две точки x₁=0, x₂=a.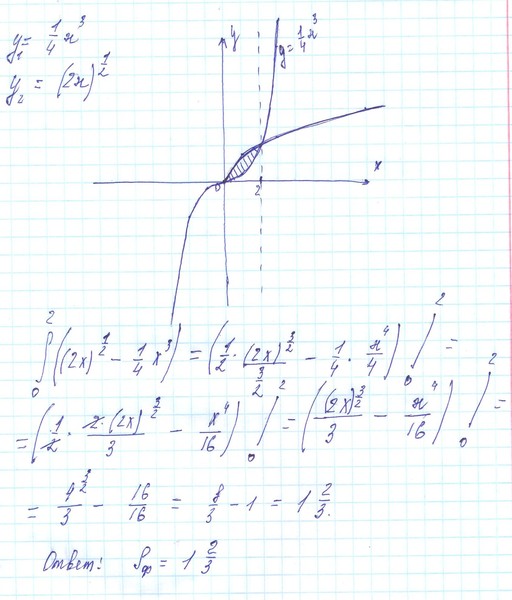
Дальше, когда Вы не видите графика функций необходимо установить какая из кривых принимает большие значения. Это нужно лишь для того, чтобы с первого раза получить положительное значение площади фигуры. Поскольку площадь всегда больше нуля, а интеграл может принимать произвольные значения, то без проверки следующего условия для нахождения площади интеграл нужно брать за модулем.
Выбираем произвольную точку из отрезка интегрирования [0;a] и убеждаемся в правильности неравенства , то есть проверяем которая из кривых принимает большее значения .
Как отмечалось выше, это нужно для того, чтобы после интегрирования получить положительную площадь фигуры между кривыми.
Вычисляем площадь фигуры, которая ограничена заданными кривыми интегрированиям:

Здесь мы имели достаточно простые функции, поэтому возведя их к табличным интегралам найти площадь достаточно легко. Следующие примеры будут содержать все более тяжелые функции, для интегрирования которых нужно применять знание практически всех формул интегрирования.
Следует заметить: значения площадей (во всех заданиях) измеряются в квадратных единицах (кв. од.), об этом Вы должны помнить, однако для экономии места и времени здесь будут приведены лишь значения определенных интегралов.

 

Пример 2.82 (2398) Вычислить площадь фигуры, ограниченной кривыми y=x², x+y=2.
Вычисление: По методике записываем уравнение кривых, которые ограничивают площадь фигуры:
y₁(x)=x², y₂(x)=2-x.
Здесь функции выразить достаточно просто.
Вычислим пределы интегрирования, приравняв между собой функции y₁(x)=y₂(x):
x²=2-x.
Переносим переменные по одну сторону от знака равенства и решаем квадратное уравнение
x²+x-2=0;
(x+2)(x-1)=0.
Следовательно, корни уравнения x₁=-2, x₂=1.
Сам график кривых и фигуры, площадь которой ищем, приведен на рисунку

Подстановкой любой точки из промежутка [-2;1], например x=0 в функции убеждаемся, что выполняется неравенство
, поэтому .
Площадь фигуры вычисляем интегрированием разницы кривых в найденных пределах:

Площадь равна S=4,5 квадратных единиц.
По физическому содержанию площадь фигуры равна разнице площадей двух криволинейных трапеций. Первая отвечает за верхний график y₂(x), нижняя криволинейная трапеция за функцию, которая принимает меньшие значения y₂(x). Разница заключается в том, что здесь еще нужно определять пределы интегрирования.

 

Пример 2.83 (2399) Найти площадь фигуры, ограниченной кривыми y=2x-x², x+y=0.
Вычисление: Запишем уравнение кривых, которые ограничивают искомую фигуру:
y₁(x)=-x, y₂(x)=2x-x².
Из условия равенства функций y₁(x)=y₂(x) найдем пределы интегрирования:
2x-x²=-x;
x²-3x=0;
x (x-3) =0.
Следовательно, x₁=0, x₂=3.
Подстановкой единицы видим, что на промежутке [0;3] исполняется неравенство
, то есть .

Находим площадь фигуры ограниченной заданными кривыми:

Под интегралом простая квадратичная функция, поэтому само интегрирование не сложно.
Следующие функции будут более сложными в плане интегрирования, однако используя табличные интегралы площадь найти удается.

 

Пример 2.84 (2400) Найти площадь фигуры, ограниченной кривыми y=2^x, y=2, x=0.
Вычисление: Запишем подынтегральные функции:
y₁(x)=2^x, y₂(x)=2, а также прямую x₁=0 (ограничивает фигуру по оси абсцисс).
Найдем вторую границу интегрирования из условия равенства функций y₁(x)=y₂(x):
2^x=2, 2^x=2¹, отсюда имеем вторую точку x₁=1.
На промежутке [0;1] исполняется неравенство , поэтому .
График  степенной функции и прямой приведен ниже.

Площадь фигуры, которая ограничена кривыми равна интегралу:

При интегрировании получим логарифм.
На калькуляторах можете проверить, что площадь положительна.

 

Пример 2.85 (2401) Вычислить площадь фигуры, ограниченной кривыми y=x, y=x+sin²x, .

Вычисление: Запишем уравнение кривых, которые ограничивают площадь фигуры:
y₁(x)=x, y₂(x)=x+sin²x.
Дальше пределы интегрирования:
x₁=0, x₂=Pi (это известно нам по условию).
На промежутке справедливо неравенство
, поэтому .

Если бы существовала дополнительная точка пересечения, то площадь была бы равна сумме двух интегралов.
Площадь фигуры вычисляем интегрированием: квадрат синуса под интегралом понижаем и выражаем с помощью косинуса двойного угла, а дальше за классической формулой интегрирования

Площадь равна Pi/2, что приблизительно равно 1,5708.

 

Пример 2.86 (2402) Найти площадь фигуры, ограниченной кривыми
Вычисление: Переписываем функции

Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций из условия y₁(x)=y₂(x):
Поскольку функция парная

то найдем половину площади и результат умножим на двойку.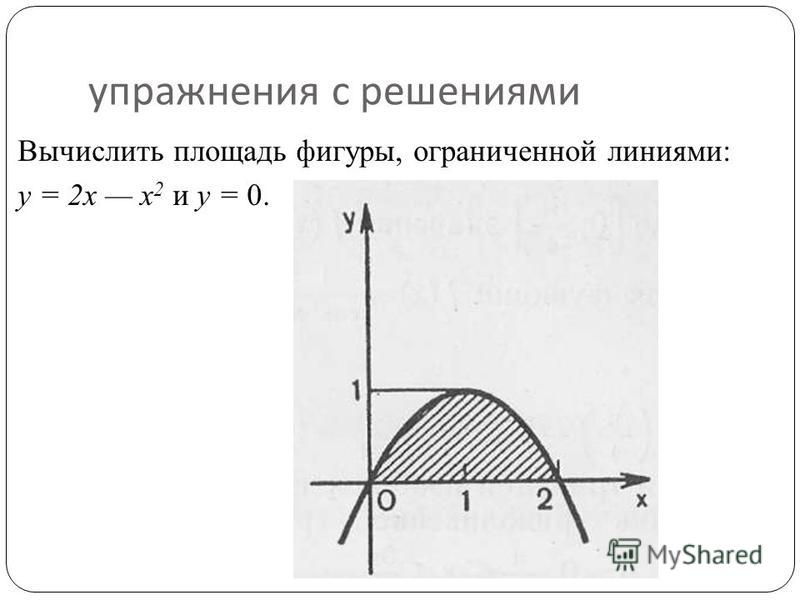
Из условия находим

что пределы равны плюс, минус бесконечности.
Чтобы легко представить, что мы интегрируем наведем график подынтегральных функций

Учитывая четность функции интегрировать будем от 0 к бесконечности , а полученное значение умножим на двойку.
Получим несвойственный интеграл первого рода (детальнее о нем в части ІІІ).
Площадь фигуры вычисляем через предел интеграла:

В результате интегрирования получим арктангенс, который в предельном случае стремится к Pi/2.
Конечная формула достаточно компактна и удобна для расчетов, хотя с таким типом интегралов Вы знакомитесь впервые.

 

Пример 2.87 (2403) Вычислить площадь фигуры, ограниченной кривыми

Вычисление: Все Вы должны знать, что такой формулой задается уравнение эллипса.
Так как оси эллипса в канонической системе координат являются его осями симметрии, то эти оси делят эллипс на 4 равные части. Поэтому будем рассматривать часть эллипса, который находится в первом квадранте канонической (прямоугольной) системы координат.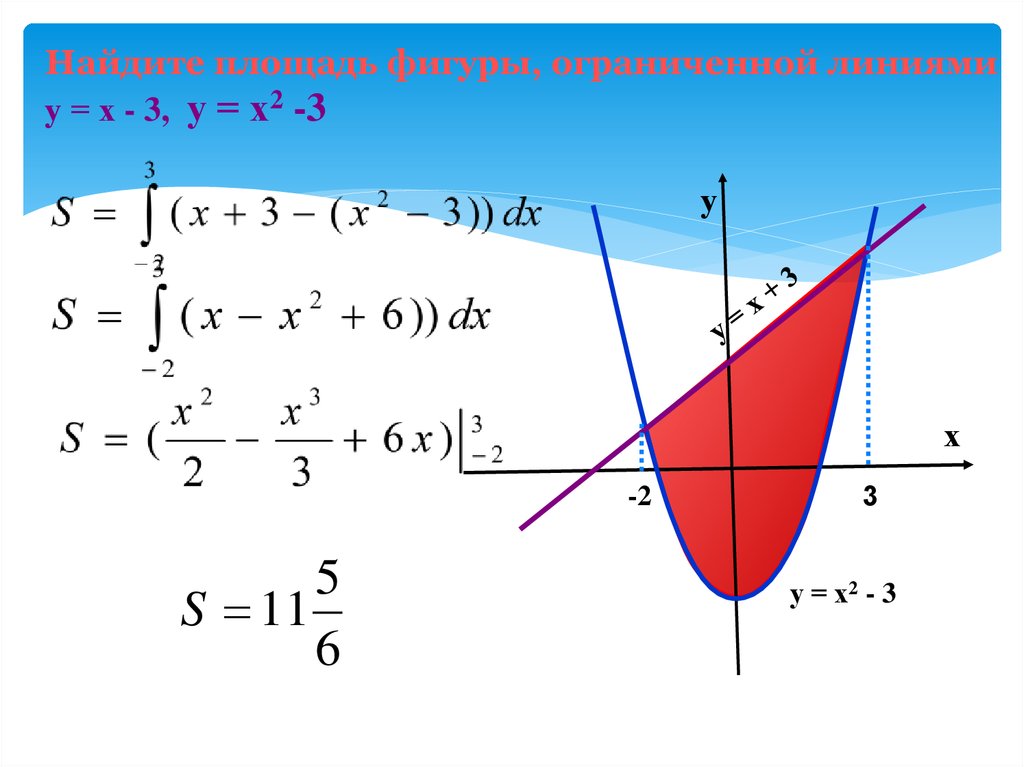
Выражаем уравнение функции, которая ограничивает искомую площадь (четверть эллипса):

Запишем пределы интегрирования: из аналитической геометрии известно, что четверть эллипса ограничена прямыми x₁=0, x₂=a.

Для вычисления площади эллипса в самом интеграле необходимо выполнить замену переменных, что в свою очередь ведет к изменению пределов интегрирование. При этом придем к квадрату косинуса, который понижаем через косинус двойного угла.
В конце манипуляций приходим к табличным интегралам, которые легко интегрируем и подставляем пределы:

Получили классическую формулу площади эллипса S=Pi*a*b .
Видим, если эллипс вырождается в круг при (a=b=R), тогда формула площади круга S=Pi*R².

 

Пример 2.88 (2404) Вычислить площадь фигуры, ограниченной кривыми y²=x²(a²-x²).
Вычисление: Так как все переменные в заданном уравнении входят в квадратах, то оси прямоугольной системы координат являются осями симметрии фигуры, которая ограничена этой линией, потому эти оси делят заданную фигуру на 4 равных части. Достаточно рассмотреть часть фигуры, которая заходиться в первом квадранте прямоугольной системы координат.
Построим график функции, которая ограничивает искомую площадь четвертины фигуры:

График неизвестной фигуры подобен на крылья бабочки.

При y=0 имеем два корня уравнения x₁=0 и x₂=a.
Площадь фигуры равна 4 умножить на интеграл с найденными пределами.
Во время интегрирования выполняем замену переменных и пределов интегрирования

Это позволяет перейти к показательной функции, которая легко интегрируется.
Всегда помните, что замена переменных под интегралом ведет к изменению пределов интегрирования.

 

Пример 2.89 Найти площадь фигуры, ограниченную линиями

Вычисление: Запишем графику функций, которые ограничивают искомую площадь фигуры:

Определим пределы интегрирования из условия y₁(x)=y₂(x):
 отсюда x₁=0 и x₂=1.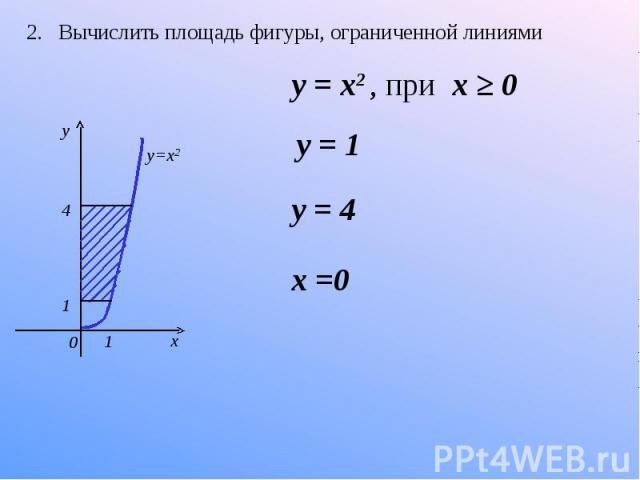
Между функциями справедлива зависимость на [0;1], поэтому .
График функций, что анализируем следующий

Площадь фигуры через определенный интеграл равна 1/3 (сравните 2.81 при a=1) :

 

Пример 2.90 Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Вычислим пределы интегрирования из условия равенства функций y₁(x)=y₂(x):

Из биквадратного уравнения получим значение точек пересечения:
 x₁=-1 и x₂=1.
Сами же функции в прямоугольных координатах будут иметь вид

Интегрированием находим площадь фигуры (смотри рисунок и образец 2.89) :

Первый интеграл даст арктангенс, запомните хорошо эту формулу.

 

Пример 2.91 Вычислить площадь фигуры, ограниченной кривыми y=e^x, y=e^-x,x=1.
Вычисление: Из условия, которое Вы из-за повторяемости должны выучить y₁(x)=y₂(x) находим точки пересечения кривых:
e^x=e^-x,x=-x, 2x=0, следовательно, x₁=0.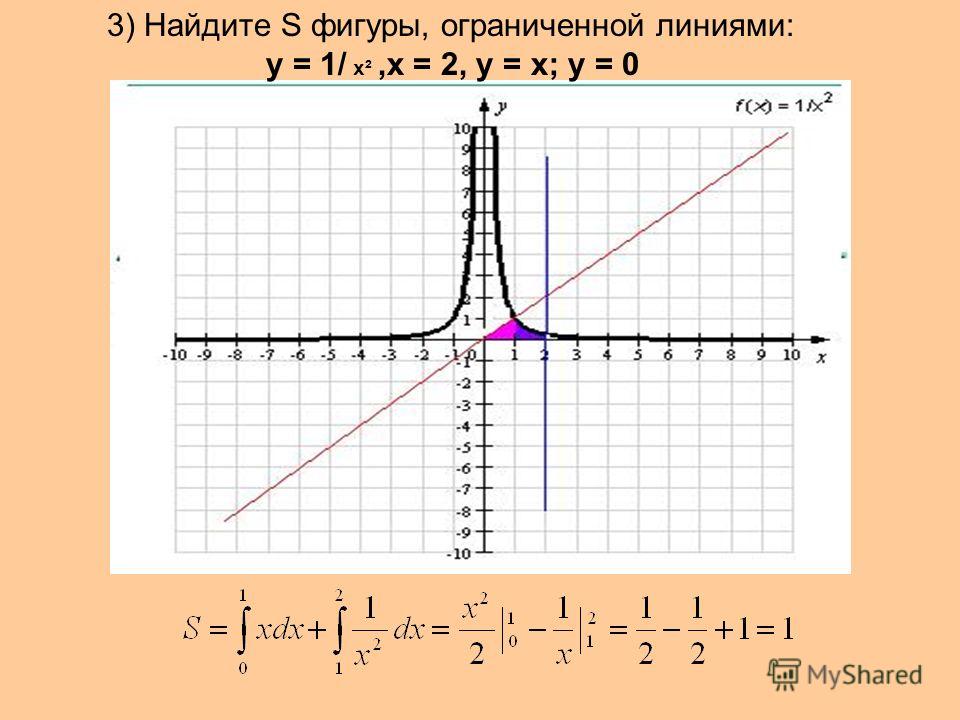
x₂=1 (известно за условием).
График функций следующий

Экспоненту интегрировать не трудно, а площадь фигуры выражается формулой (смотри рисунок и образец 2.84) :

 

Пример 2.92 Найти площадь фигуры, ограниченной кривыми y=ln(x), y=ln²(x).
Вычисление: Пределы интегрирования из условия равенства функций y=ln(x), y=ln²(x) равны x₁=1 и x₂=e.

Интегрированием логарифмов находим площадь фигуры (смотри рисунок):

Здесь надо проинтегрировать по частям, положив ln(x) =u, (ln²(x)=u) и dx=dv. Попробуйте промежуточные действия провести самостоятельно.

 

Пример 2.93 Вычислить площадь фигуры, ограниченной кривыми
y=ln(x), y=ln(a), y=ln(b), x=0, где 0<a<b.
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
x (y) =e^y (то есть обратная функция к заданной функции y(x)=ln(x)) .
Такой прием применяют, когда пределы интегрирования параллельны оси Оx, то есть y=const.
Запишем пределы интегрирования:
y₁=ln(a), y₂=ln(b) (берем из начального условия).
График искомой фигуры следующий

Площадь фигуры, которая ограничена заданными кривыми:

 

Пример 2.94 Найти площадь фигуры, ограниченной кривыми
Вычисление: Пределы интегрирования в формуле площади находим из условия y₁(x)=y₂(x):
ln(x)/(4x)=x*ln(x).
Упростив на логарифм (если он больше нуля), получим
1=4x²; 4x²-1=0, x₁=1/2.
Из условия на логарифм (=0) получим
ln(x) =0; x₂=1.
ОДЗ: x>0.
График фигуры в прямоугольных координатах следующий

Площадь фигуры между кривыми (на [0,5;1]) находим интегрированием:
для вычисления интегралов используем метод замены переменных

Вычисление не так просты, поэтому с превращениями попробуйте разобраться самостоятельно.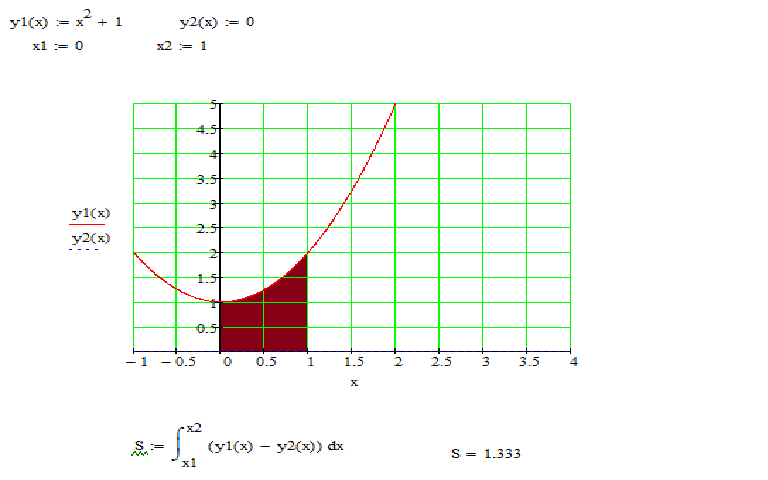

 

Пример 2.95 Вычислить площадь фигуры, ограниченной кривыми y=arcsin(x), y=arccos(x), y=0.
Вычисление: Находим точки пересечения кривых из равенства x₁(y)=x₂(y):
sin(x)=cos(y), отсюда y₁=0 (известно за условием) и y₁=Pi/4 (образец 2.93).
На графике это выглядит следующим образом

Учитывая справедливость неравенства вычисляем площадь фигуры:

Думаю, что с такими заданиями на экзамене или модулях Вы справитесь.

 

Пример 2.96 Найти площадь фигуры, ограниченной кривыми y=tg(x), y=2/3*cos(x), x=0.
Вычисление: Найдем пределы интегрирования, то есть абсциссы точек  пересечения заданных функций y₁(x)=y₂(x):
tg(x)=2/3*cos(x), отсюда
(вторая точка известна за условием).
Кривые на плоскости имеют вид

Площадь фигуры, которая ограничена заданными кривыми () равна интегралу:

 

Пример 2.97 (2400) Вычислить площадь фигуры, ограниченной кривыми y=|ln(x)|, y=0, x=0,1; x=10.
Вычисление: Выписываем пределы интегрирования x₁=0,1; x₂=10 из начального условия.
Как строить модуль от логарифма Вы, по-видимому, еще не забыли

Площадь фигуры равна сумме двух интегралов, причем первый берем со знаком минус ():

Во время интегрирования использовали интегрирование частями.

 

Пример 2.98 (2400) Найти площадь фигуры, ограниченной кривыми y=(x+1)², x=sin(Pi*y), y=0 .
Вычисление: Построим график функций, которые ограничивают искомую площадь фигуры:
(здесь взяли обратную функцию к заданной y₁(x)=(x+1)²), x₂=sin(Pi*y).
Выпишем пределы интегрирования:
y₁=0; y₂=1 (известно за условием).
График функций приведен ниже

Неизвестную площадь фигуры вычисляем интегрированием ():

 

Пример 2.99 Вычислить площадь фигуры, ограниченной кривыми y=sin(x), y=cos(x), y=0
Вычисление: Из рисунку видно, что площадь S лучше разбить на две части: S=S₁+S₂.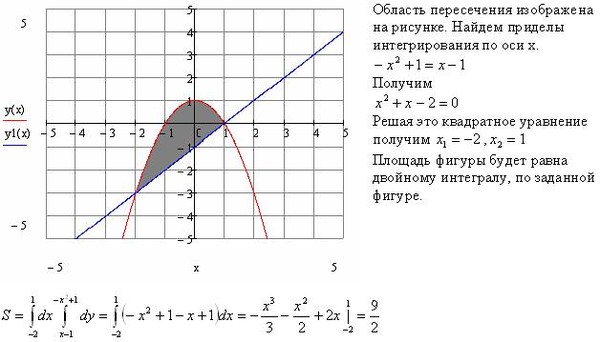

Запишем уравнение функций, которые ограничивают искомую площадь фигуры:

Интегрируем синус и косинус функции и находим площадь.

Второй вариант заключается в интегрировании разницы обратных функций по y.

 

Пример 2407 Найти площадь фигуры, ограниченной кривыми (циссоида Диокла) x=2a (a>0).
Вычисление: Поскольку график функции симметричен относительно оси Ox, то будем рассматривать половину площади фигуры (над осью Ox) и результат умножим на 2.
В точке x=2a функция не определена, поэтому будем иметь интеграл второго рода (детальнее смотрите часть ІІІ), он совпадает и, следовательно, площадь будет выражена числом.
Запишем пределы интегрирования:
x₁=0 (потому что ) x₂=2a (за условием).
График функций следующий

Площадь фигуры, что ограниченна заданной кривой находится достаточно непростым интегрированием



Здесь пришлось трижды выполнять замену переменных, чтобы прийти к правильному ответу.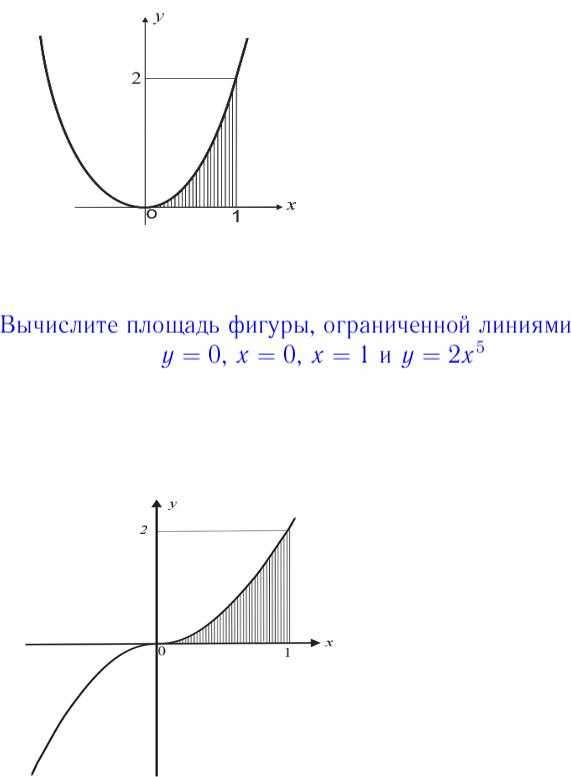
Еще раз внимательно разберите интеграл.

 

Пример 2408 Вычислить площадь фигуры, ограниченной кривыми (трактриса), y=0.
Вычисление: Трактриса — кривая, по которой двигается объект, когда его тянуть по горизонтальной плоскости за бечевку фиксированной длины, если направление движения тягача является ортогональным к начальному положению бечевки и скорость тягача бесконечно малая величина.
Очевидно, что (смотри рисунок).

Принимая к сведению, что положительному приросту x отвечает отрицательный прирост y, и что фигура не квадрируема (в общем понимании), допускаем

где дифференциал за x находим через производную

Площадь фигуры через определенный интеграл равна

Следующим идет материал из которого Вы научитесь находить площадь фигуры, ограниченной кривыми заданными параметрически.

Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)

В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:

S(G)=∫abf(x)dx  для непрерывной и неотрицательной функции y=f(x) на отрезке [a;b],

S(G)=-∫abf(x)dx  для непрерывной и неположительной функции y=f(x) на отрезке [a;b].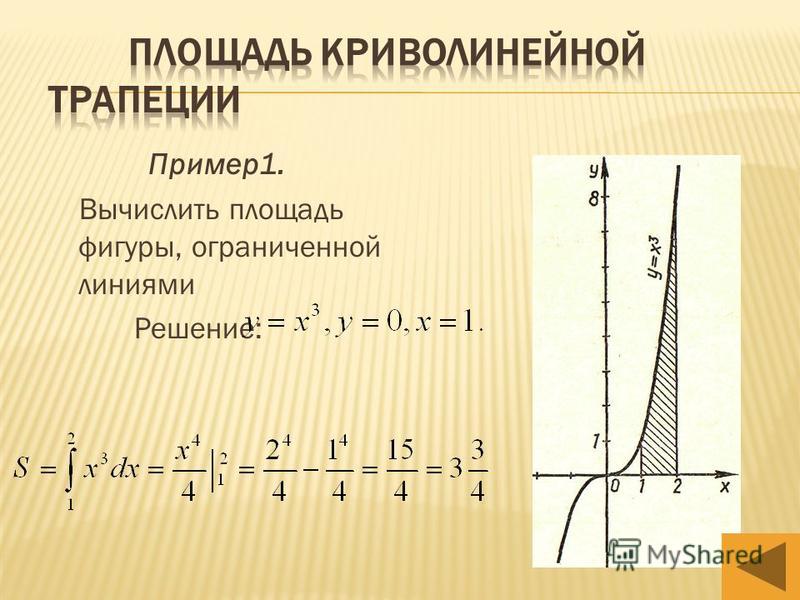

Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y=f(x) или x=g(y).

Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)

Теорема

Пусть функции y=f1(x)  и y=f2(x) определены и непрерывны на отрезке [a;b], причем f1(x)≤f2(x) для любого значения x из [a;b]. Тогда формула для вычисления площади фигуры G, ограниченной линиями x=a, x=b, y=f1(x)  и y=f2(x) будет иметь вид S(G)=∫abf2(x)-f1(x)dx.

Похожая формула будет применима для площади фигуры, ограниченной линиями y=c, y=d, x=g1(y) и x=g2(y): S(G)=∫cd(g2(y)-g1(y)dy.

Доказательство

Разберем три случая, для которых формула будет справедлива.

В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G1 равна площади фигуры G2. Это значит, что

Поэтому, S(G)=S(G2)-S(G1)=∫abf2(x)dx-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx.

Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.

Во втором случае справедливо равенство: S(G)=S(G2)+S(G1)=∫abf2(x)dx+-∫abf1(x)dx=∫ab(f2(x)-f1(x))dx

Графическая иллюстрация будет иметь вид:

Если обе функции неположительные, получаем: S(G)=S(G2)-S(G1)=-∫abf2(x)dx—∫abf1(x)dx=∫ab(f2(x)-f1(x))dx . Графическая иллюстрация будет иметь вид:

Перейдем к рассмотрению общего случая, когда  y=f1(x)  и y=f2(x) пересекают ось Ox.

Точки пересечения мы обозначим как  xi, i=1, 2,…, n-1. Эти точки разбивают отрезок [a; b] на n частей xi-1; xi, i=1, 2,…, n, где α=x0<x1<x2<…<xn-1<xn=b. Фигуру G можно представить объединением фигур Gi, i=1, 2,…, n. Очевидно, что на своем интервале Gi попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S(Gi)=∫xi-1xi(f2(x)-f1(x))dx, i=1, 2,.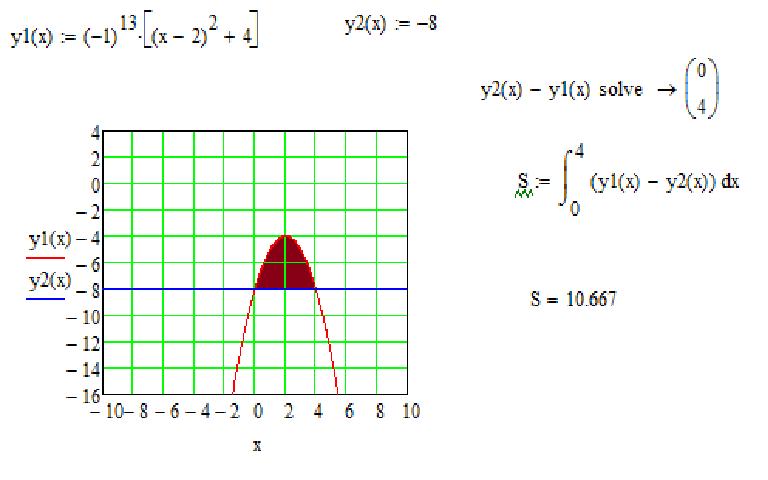 .., n

Следовательно, 

S(G)=∑i=1nS(Gi)=∑i=1n∫xixif2(x)-f1(x))dx==∫x0xn(f2(x)-f(x))dx=∫abf2(x)-f1(x)dx

Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.

Проиллюстрируем на графике общий случай.

Формулу S(G)=∫abf2(x)-f1(x)dx можно считать доказанной.

А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y=f(x) и x=g(y).

Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)

Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.

Пример 1

Необходимо определить площадь фигуры, которая ограничена параболой y=-x2+6x-5 и прямыми линиями y=-13x-12, x=1, x=4.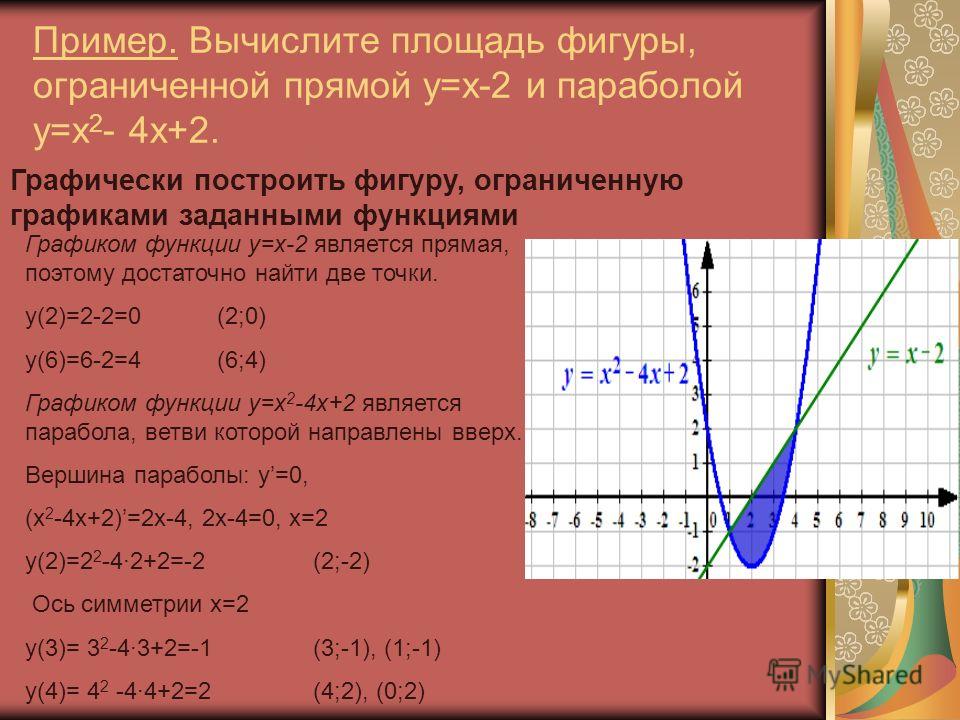

Решение

Изобразим линии на графике в декартовой системе координат.

На отрезке [1;4] график параболы y=-x2+6x-5 расположен выше прямой y=-13x-12. В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по  формуле Ньютона-Лейбница:

S(G)=∫14-x2+6x-5—13x-12dx==∫14-x2+193x-92dx=-13×3+196×2-92×14==-13·43+196·42-92·4—13·13+196·12-92·1==-643+1523-18+13-196+92=13

Ответ: S(G)=13

Рассмотрим более сложный пример.

Пример 2

Необходимо вычислить площадь фигуры, которая ограничена линиями y=x+2, y=x, x=7.

Решение

В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x=7. Это требует от нас найти второй предел интегрирования самостоятельно.

Построим график и нанесем на него линии, данные в условии задачи.

Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y=x и полу параболы y=x+2. Для нахождения абсциссы используем равенства:

y=x+2ОДЗ: x≥-2×2=x+22×2-x-2=0D=(-1)2-4·1·(-2)=9×1=1+92=2∈ОДЗx2=1-92=-1∉ОДЗ

Получается, что абсциссой точки пересечения является x=2.

Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y=x+2 , y=x пересекаются в точке (2;2), поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.

На интервале [2;7] график функции y=x расположен выше графика функции y=x+2 . Применим формулу для вычисления площади:

S(G)=∫27(x-x+2)dx=x22-23·(x+2)3227==722-23·(7+2)32-222-23·2+232==492-18-2+163=596

Ответ: S(G)=596

Пример 3

Необходимо вычислить площадь фигуры, которая ограничена графиками функций y=1x и y=-x2+4x-2.

Решение

Нанесем линии на график.

Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1x  и -x2+4x-2. При условии, что x не равно нулю, равенство 1x=-x2+4x-2становится эквивалентным уравнению третьей степени -x3+4×2-2x-1=0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».

Корнем этого уравнения является х=1: -13+4·12-2·1-1=0.

Разделив выражение -x3+4×2-2x-1 на двучлен x-1, получаем: -x3+4×2-2x-1⇔-(x-1)(x2-3x-1)=0

Оставшиеся корни мы можем найти из уравнения x2-3x-1=0:

x2-3x-1=0D=(-3)2-4·1·(-1)=13×1=3+132≈3.3 ; x2=3-132≈-0.3

Мы нашли интервал x∈1; 3+132, на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:

S(G)=∫13+132-x2+4x-2-1xdx=-x33+2×2-2x-ln x13+132==-3+13233+2·3+1322-2·3+132-ln3+132—133+2·12-2·1-ln 1=7+133-ln3+132

Ответ: S(G)=7+133-ln3+132

Пример 4

Необходимо вычислить площадь фигуры, которая ограничена кривыми y=x3, y=-log2x+1 и осью абсцисс.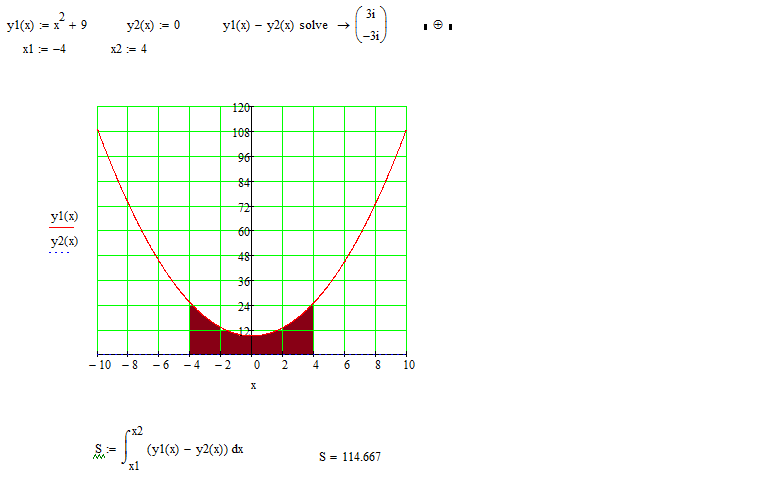

Решение

Нанесем все линии на график. Мы можем получить график функции y=-log2x+1 из графика y=log2x, если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у=0.

Обозначим точки пересечения линий.

Как видно из рисунка, графики функций y=x3 и y=0 пересекаются в точке (0;0). Так получается потому, что х=0 является единственным действительным корнем уравнения x3=0.

x=2 является единственным корнем уравнения -log2x+1=0, поэтому графики функций y=-log2x+1  и y=0 пересекаются в точке (2;0).

x=1 является единственным корнем уравнения x3=-log2x+1. В связи с этим графики функций y=x3 и y=-log2x+1 пересекаются в точке (1;1). Последнее утверждение может быть неочевидным, но уравнение x3=-log2x+1 не может иметь более одного корня, так как функция y=x3 является строго возрастающей, а функция y=-log2x+1 строго убывающей.

Дальнейшее решение предполагает несколько вариантов.

Вариант №1

Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x∈0; 1, а вторая ниже красной линии на отрезке x∈1;2. Это значит, что площадь будет равна S(G)=∫01x3dx+∫12(-log2x+1)dx.

Вариант №2

Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x∈0; 2, а вторая между красной и синей линиями на отрезке x∈1; 2. Это позволяет нам найти площадь следующим образом:

S(G)=∫02x3dx-∫12×3-(-log2x+1)dx

В этом случае для нахождения площади придется использовать формулу вида S(G)=∫cd(g2(y)-g1(y))dy.  Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y.

Разрешим уравнения y=x3 и -log2x+1 относительно x: 

y=x3⇒x=y3y=-log2x+1⇒log2x=1-y⇒x=21-y

Получим искомую площадь:

S(G)=∫01(21-y-y3)dy=-21-yln 2-y4401==-21-1ln 2-144—21-0ln 2-044=-1ln 2-14+2ln 2=1ln 2-14

Ответ: S(G)=1ln 2-14

Пример 5

Необходимо вычислить площадь фигуры, которая ограничена линиями y=x, y=23x-3, y=-12x+4.

Решение

Красной линией нанесем на график линию, заданную функцией y=x. Синим цветом нанесем линию y=-12x+4, черным цветом обозначим линию y=23x-3.

Отметим точки пересечения.

Найдем точки пересечения графиков функций y=x и y=-12x+4 :

x=-12x+4ОДЗ: x≥0x=-12x+42⇒x=14×2-4x+16⇔x2-20x+64=0D=(-20)2-4·1·64=144×1=20+1442=16; x2=20-1442=4Проверка:x1=16=4, -12×1+4=-12·16+4=-4⇒x1=16 не является решением уравненияx2=4=2, -12×2+4=-12·4+4=2⇒x2=4 является решением уравниния ⇒(4; 2) точка пересечения y=x и y=-12x+4

Найдем точку пересечения графиков функций y=x  и y=23x-3:

x=23x-3ОДЗ: x≥0x=23x-32⇔x=49×2-4x+9⇔4×2-45x+81=0D=(-45)2-4·4·81=729×1=45+7298=9, x245-7298=94Проверка:x1=9=3, 23×1-3=23·9-3=3⇒x1=9 является решением уравнения ⇒(9; 3) точка пересечания y=x и y=23x-3×2=94=32, 23×1-3=23·94-3=-32⇒x2=94 не является решением уравнения

Найдем точку пересечения линий y=-12x+4  и y=23x-3:

-12x+4=23x-3⇔-3x+24=4x-18⇔7x=42⇔x=6-12·6+4=23·6-3=1⇒(6; 1) точка пересечения y=-12x+4 и y=23x-3

Дальше мы можем продолжить вычисления двумя способами.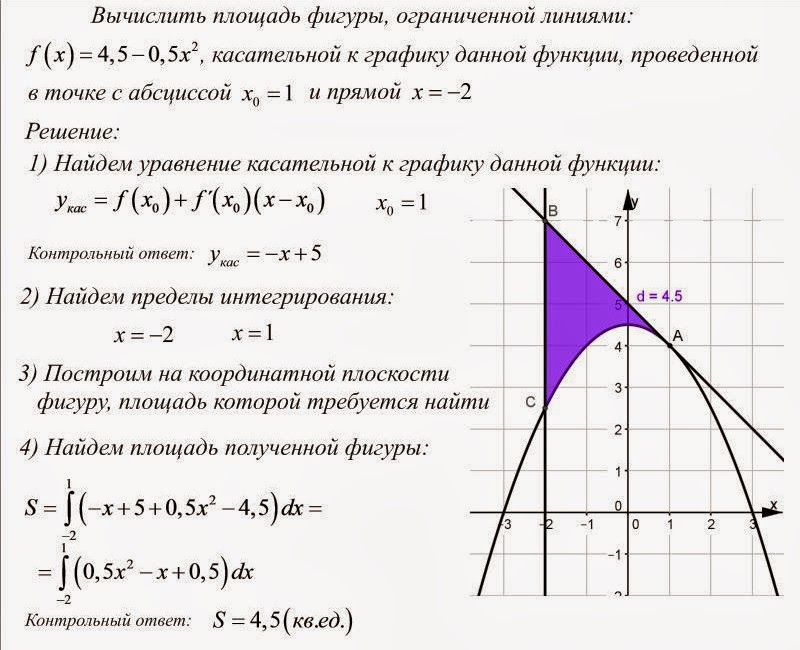

Способ №1

Представим площадь искомой фигуры как сумму площадей отдельных фигур.

Тогда площадь фигуры равна:

S(G)=∫46x—12x+4dx+∫69x-23x-3dx==23×32+x24-4×46+23×32-x23+3×69==23·632+624-4·6-23·432+424-4·4++23·932-923+3·9-23·632-623+3·6==-253+46+-46+12=113

Способ №2

Площадь исходной фигуры можно представить как сумму двух других фигур.

Тогда решим уравнение линии относительно x, а только после этого применим формулу вычисления площади фигуры.

y=x⇒x=y2 красная линияy=23x-3⇒x=32y+92 черная линияy=-12x+4⇒x=-2y+8 синяя линия

Таким образом, площадь равна:

S(G)=∫1232y+92—2y+8dy+∫2332y+92-y2dy==∫1272y-72dy+∫2332y+92-y2dy==74y2-74y12+-y33+3y24+92y23=74·22-74·2-74·12-74·1++-333+3·324+92·3—233+3·224+92·2==74+2312=113

Как видите, значения совпадают.

Ответ: S(G)=113

Итоги

Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

вычисление площади фигуры ограниченной линиями

Вы искали вычисление площади фигуры ограниченной линиями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление площади фигуры ограниченной линиями онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление площади фигуры ограниченной линиями».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление площади фигуры ограниченной линиями,вычисление площади фигуры ограниченной линиями онлайн,вычислите площадь фигуры,вычислите площадь фигуры ограниченной,вычислите площадь фигуры ограниченной линиями,вычислите площадь фигуры ограниченной линиями y,вычислите площадь фигуры ограниченной линиями y 0 x 1 y x,вычислите площадь фигуры ограниченной линиями онлайн,вычислите площадь фигуры ограниченной линиями онлайн решение,вычислите площадь фигуры ограниченной линиями у 1 x y 2 x 2,вычислить онлайн площадь ограниченную линиями,вычислить площади фигур ограниченных линиями,вычислить площадь ограниченную линиями,вычислить площадь ограниченную линиями онлайн,вычислить площадь плоской фигуры ограниченной заданными кривыми онлайн,вычислить площадь плоской фигуры ограниченной линиями,вычислить площадь плоской фигуры ограниченной линиями онлайн с решением,вычислить площадь фигур ограниченных линиями онлайн,вычислить площадь фигуры,вычислить площадь фигуры ограниченной,вычислить площадь фигуры ограниченной графиками функций,вычислить площадь фигуры ограниченной графиками функций онлайн,вычислить площадь фигуры ограниченной графиками функций онлайн решение,вычислить площадь фигуры ограниченной линиями,вычислить площадь фигуры ограниченной линиями y,вычислить площадь фигуры ограниченной линиями y x 2 1 y x 1,вычислить площадь фигуры ограниченной линиями y x 2 y 2 x,вычислить площадь фигуры ограниченной линиями y x 2 y x,вычислить площадь фигуры ограниченной линиями онлайн,вычислить площадь фигуры ограниченной линиями онлайн калькулятор,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с графиком,вычислить площадь фигуры ограниченной линиями онлайн калькулятор с решением,вычислить площадь фигуры ограниченной линиями онлайн подробное решение,вычислить площадь фигуры ограниченной линиями онлайн с решением калькулятор,вычислить площадь фигуры ограниченной линиями примеры решения,вычислить площадь фигуры ограниченной указанными линиями сделать чертеж,вычислить площадь фигуры онлайн,заштрихуй фигуры ограниченные двумя линиями,заштрихуй фигуры ограниченные линиями,как найти площадь фигуры ограниченной графиками функций,как найти площадь фигуры ограниченной линиями,калькулятор вычислить площадь фигуры ограниченной линиями онлайн с решением,калькулятор онлайн площадь фигуры,найдите площадь плоской фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями,найдите площадь фигуры ограниченной линиями y 5 x 2 y 1,найдите площадь фигуры ограниченной линиями y x 2 1 y 1 x,найдите площадь фигуры ограниченной линиями онлайн,найдите площадь фигуры ограниченной линиями онлайн калькулятор,найдите площадь фигуры ограниченной указанными линиями,найти площадь криволинейной трапеции ограниченной линиями онлайн,найти площадь криволинейной трапеции онлайн,найти площадь области ограниченной линиями онлайн,найти площадь ограниченной фигуры,найти площадь ограниченную линиями,найти площадь ограниченную линиями онлайн калькулятор,найти площадь плоской фигуры ограниченной линиями,найти площадь плоской фигуры ограниченной линиями онлайн,найти площадь фигуры,найти площадь фигуры ограниченной,найти площадь фигуры ограниченной графиками функций,найти площадь фигуры ограниченной кривыми,найти площадь фигуры ограниченной линиями,найти площадь фигуры ограниченной линиями онлайн,найти площадь фигуры ограниченной линиями онлайн калькулятор,найти площадь фигуры ограниченной линиями онлайн калькулятор подробно,найти площадь фигуры ограниченной линиями онлайн решение,найти площадь фигуры ограниченной линиями онлайн с подробным решением,найти площадь фигуры ограниченной линиями примеры решения,найти площадь фигуры ограниченной линиями с помощью определенного интеграла сделать иллюстрацию,найти площадь фигуры ограниченной указанными линиями,найти площадь фигуры онлайн,нахождение площади фигуры ограниченной линиями,нахождение площади фигуры ограниченной линиями онлайн,онлайн вычисление площади фигуры ограниченной линиями,онлайн вычислить площадь фигуры ограниченной графиками функций онлайн,онлайн калькулятор площадь фигуры ограниченной линиями,онлайн нахождение площади фигуры ограниченной линиями,онлайн площадь фигуры,площадь криволинейной трапеции онлайн,площадь ограниченная линиями,площадь плоской фигуры ограниченной линиями онлайн,площадь под графиком,площадь фигуры ограниченной графиками функций,площадь фигуры ограниченной линиями,площадь фигуры ограниченной линиями онлайн,площадь фигуры ограниченной линиями онлайн калькулятор,площадь фигуры онлайн,построить фигуру ограниченную линиями онлайн,сделайте чертеж и вычислите площадь фигуры ограниченной данными линиями,фигуры ограниченные двумя линиями,фигуры ограниченные линиями. 2+x+6 и y=0 Вычислить площадь фигуры, ограниченной линиями — Учеба и наука

Ответы

26. 02.17

Евгений Читать ответы

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0. 75 . Найдите АС.

Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81%

Дано: геометрическая прогрессия (bn) задана условиями: b1=-2 , bn+1=3bn. Найдите b6. Объясните пожалуйста, как это решить?

Решено

в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?

Решено

дана арифмитическая прогрессия (аn)в которой a9=-22,2,a23=-41,8 найдите разность прогрессии

Пользуйтесь нашим приложением

Как вычислить площадь фигуры ограниченной линиями ℹ️ примеры

Общие сведения

Вычислить площадь фигуры на плоскости считается довольно простой операцией. Для ее выполнения необходимо знать только формулу. Существенно усложняет задачу фигура, ограниченная прямыми.

Одной из них считается криволинейная трапеция. Ее площадь можно определить только при нахождении значений определенного интеграла.

Операция интегрирования считается довольно сложной, поскольку необходимо знать основные правила. Перед нахождением площади криволинейной трапеции специалисты рекомендуют внимательно изучить и освоить правила интегрирования основных функций.

Разбирается неопределенный интеграл, а затем осуществляется переход к более сложным операциям.

Информация об интегралах

С понятием интеграла связано много направлений научных отраслей. Обозначается он символом «∫». С помощью интеграла открываются большие возможности по быстрому и эффективному нахождению значений следующих величин: площади криволинейной трапеции, объема тела вращения, поверхности, пути при неравномерном движении, массы неоднородного физического тела и так далее.

Упрощенный вариант представления и определения интеграла — сумма бесконечно малых слагаемых. Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:

1. Неопределенный.
2. Определенный.

Операция нахождения первого типа значительно проще второго. Это объясняется тем, что во втором случае следует не только найти первообразную, но и выполнить правильную подстановку значений.

Неопределенным интегралом функции вида f(х) называется такая первообразная функция F(х), производная которой равна подинтегральному выражению. Записывается это таким образом: ∫(f(x)) = F(х) + С.

Последняя величина является константой, поскольку при выполнении операции нахождения производной константа равна 0.

Для нахождения первообразной используется специальная таблица интегралов:

Рисунок 1. Таблица интегралов и их первообразные.

В таблице приведены простые функции. Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).

Криволинейные фигуры

Криволинейная фигура (трапеция) — класс плоских фигур, которые ограничены графиком неотрицательной и непрерывной функции, а также осью ОУ и прямыми (х = а, х = b). Она изображена на рисунке 2. Для нахождения ее площади следует использовать определенный интеграл.

Рисунок 2. Фигуры с криволинейными сторонами.

Интегрирование разбивает фигуру на прямоугольные части. Длина каждой из них равна ординате y = f(х) через промежутки, которые очень малы, по оси декартовой системы координат (есть еще и полярная) ОХ на отрезке [a;b]. Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.

Криволинейная трапеция — геометрическая фигура с неровными сторонами, которые образовались в результате пересечения графика непрерывной функции с осями абсцисс и ординат.

Применение обыкновенных методов нахождения площади этой фигуры невозможно, поскольку она обладает одной или несколькими неровными сторонами (кривыми линиями).

Способы вычисления и рекомендации

Для расчетов площади криволинейной трапеции используется несколько методов. Их условно можно разделить на следующие: автоматизированные и ручные. Первый из них выполняется при помощи специализированного программного обеспечения (ПО). Примером является онлайн-калькулятор, который не только находит площадь заданной фигуры, но и изображает ее в декартовой системе координат.

Существует и другое ПО, которое является более «мощным». К нему можно отнести наиболее популярные среды: Maple и Matlab. Однако существует множество программ, написанных на языке программирования Python. Программы нужны также при освоении темы интегрирования. Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.

Новичку для автоматизированных вычислений рекомендуется применять различные онлайн-калькуляторы. Однако следует выделить неплохую программу, которая обладает довольно неплохими функциональными возможностями.

Она называется Integral calculator и представляет собой очень удобное приложение для Android-устройств. Кроме того, можно скачать подобное ПО для Linux, Mac и Windows.

Программа — это калькулятор, который используется для нахождения интегралов и производных, а также его можно применять для решения уравнений интегрального и дифференциального типов. Integral calculator обладает такими функциональными возможностями:

1. Вычисление производных.
2. Нахождения первообразных для определенных и неопределенных интегралов.
3. Решение систем уравнений.
4. Выполнения операций над матрицами и определителями.
5. Построение графиков заданных функций в 2D и 3D.
6. Расчет точек перегиба.
7. Вычисление рядов Фурье.
8. Решение дифференциальных уравнений линейного типа первого и второго порядков.

Однако специалисты не рекомендуют использовать приложения такого типа, поскольку нужно уметь решать подобные задачи самостоятельно. Любые математические операции развивают мышление, а злоупотребление ПО приводит к значительной деградации. Решать какие-либо задачи рекомендуется также людям, которые не имеют отношения к математической сфере.

Основной алгоритм

При нахождении площади криволинейной трапеции рекомендуется следовать определенному алгоритму. Он поможет избежать ошибок, поскольку задача разбивается на несколько простых подзадач, решение которых довольно просто контролировать. Алгоритм имеет следующий вид:

1. Нужно прочитать и понять условие задачи.
2. Начертить декартовую систему координат.
3. Построить график заданной функции.
4. Изобразить линии, ограничивающие фигуру.
5. После определения границ нужно аккуратно заштриховать фигуру.
6. Вычислить неопределенный интеграл функции, которая дана в условии.
7. Посчитать площадь, подставив значения ограничивающих прямых в первообразную.
8. Проверить решение задачи при помощи программы.

Первый пункт — внимательное чтение условия задачи. Этап считается очень важным, поскольку формирует дальнейший алгоритм. Необходимо выписать все известные данные, а затем подумать над дальнейшим решением задачи. Следует обратить особое внимание на график функции, который при возможности нужно упростить. Далее следует выписать линии, которые будут ограничивать фигуру.

Следующий пункт считается наиболее простым, поскольку нужно начертить обыкновенную систему координат. В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.

Третий пункт алгоритма — правильное построение графика функции. В этом случае нет необходимости составлять таблицу зависимости значения функции от аргумента. График должен быть схематичным. Например, если это парабола, то нужно ее изобразить. В этом случае необходимо ознакомиться с основными базовыми функциями и их графиками.

Следующим шагом является правильное изображение прямых. Если ее уравнение имеет следующий вид «x = 5» или что-то подобное, то она будет проходить параллельно оси ОУ. Например, при y = 10 прямая проходит параллельно оси ОХ. В других случаях нужно составить таблицу зависимостей значений уравнения прямой от переменной. Следует брать всего два значения аргумента, поскольку их достаточно для проведения прямой.

После всех операций образуется фигура, которая ограничена линиями. Ее необходимо заштриховать. После этого вычисляется неопределенный интеграл заданной функции. Необходимо воспользоваться табличными значениями первообразных на рисунке 2. Однако здесь есть небольшой нюанс: константу записывать нет необходимости. Она «уничтожается» при подстановке в формулу Ньютона-Лейбница.

В полученное значение следует подставить значения границ. 2) / 2) + (-1)] = 3 — 0,75 = 2,25 (кв. ед.).

Для определения значения площади криволинейной фигуры (трапеции) необходимо использовать определенные интегралы. При решении нужно внимательно следить за знаками и первообразными из таблицы на рисунке 1.

2-1|-3|x|+3)dx$$

Правильно? Помогите пожалуйста с правильным решением.

Не знаю, как вычислить $\int|x|dx.$

исчисление интегрирование области определенных интегралов

$\endgroup$

2

$\begingroup$

Прежде чем решать задачи такого типа, вы должны тщательно нарисовать графики двух заданных кривых, а для этого вам нужно найти точки, в которых они пересекаются. Давайте сделаем это 92-2)dx$$

$\endgroup$

6

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Обязательно, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

6.

1: Области между кривыми — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

2519

• Гилберт Странг и Эдвин «Джед» Герман
• OpenStax

Цели обучения

• Определить площадь области между двумя кривыми путем интегрирования по независимой переменной.
• Найдите площадь составной области.
• Определите площадь области между двумя кривыми путем интегрирования по зависимой переменной.

В разделе «Введение в интегрирование» мы разработали концепцию определенного интеграла для вычисления площади под кривой на заданном интервале. В этом разделе мы расширим эту идею, чтобы вычислить площадь более сложных регионов. Начнем с нахождения площади между двумя кривыми, являющимися функциями \(\displaystyle x\), начиная с простого случая, когда значение одной функции всегда больше другого. Затем рассмотрим случаи, когда графики функций пересекаются. Наконец, мы рассмотрим, как вычислить площадь между двумя кривыми, которые являются функциями \(\displaystyle y\).

Площадь области между двумя кривыми

Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции на интервале \(\displaystyle [a,b]\), такие что \(\displaystyle f(x)≥g(x)\) на \(\displaystyle [a,b]\). Нам нужно найти площадь между графиками функций, как показано на рисунке \(\PageIndex{1}\).

Рисунок \(\PageIndex{1}\): Площадь между графиками двух функций, \(\displaystyle f(x)\) и \(\displaystyle g(x)\), на интервале \( \displaystyle [а,б]\) 9b_a[f(x)−g(x)]dx. \nonumber \]

Эти результаты резюмируются в следующей теореме.

Нахождение площади между двумя кривыми

Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции такие, что \(\displaystyle f(x)≥g(x) \) на интервале [\(\displaystyle a,b]\). Обозначим через R область, ограниченную сверху графиком \(\displaystyle f(x)\), снизу графиком \(\displaystyle g(x)\), а слева и справа линиями \(\ displaystyle x=a\) и \(\displaystyle x=b\) соответственно. Тогда площадь \(\textbf{R}\) равна 9b_a[f(x)−g(x)]dx. \nonumber \]

Применим эту теорему в следующем примере.

Пример \(\PageIndex{1}\): нахождение площади области между двумя кривыми I

Если \(\textbf{R}\) — это область, ограниченная сверху графиком функции \(\displaystyle f(x)=x+4\) и ниже по графику функции \(\displaystyle g(x)=3−\dfrac{x}{2}\) на интервале \(\displaystyle [1,4 ]\), найдите площадь области \(\textbf{R}\).

Раствор

92\).

Упражнение \(\PageIndex{1}\)

Если \(\textbf{R}\) область, ограниченная графиками функций \(\displaystyle f(x)=\dfrac{x}{2 }+5\) и \(\displaystyle g(x)=x+\dfrac{1}{2}\) на интервале \(\displaystyle [1,5]\), найти площадь области \(\textbf {Р}\).

Подсказка

Нарисуйте графики функций, чтобы определить, график какой функции образует верхнюю границу, а график нижней границы, затем выполните процесс, описанный в примере.

Ответить

\(\displaystyle 12\) единиц ²

В примере \(\PageIndex{1}\) мы определили интересующий интервал как часть условия задачи. Однако довольно часто мы хотим определить интересующий нас интервал на основе того, где пересекаются графики двух функций. Это показано в следующем примере.

Пример \(\PageIndex{2}\): нахождение площади области между двумя кривыми II 92\) и ниже по графику функции \(\displaystyle g(x)=6−x\) найти площадь области \(\textbf{R}\).

Решение

Область изображена на следующем рисунке.

Рисунок \(\PageIndex{4}\): на этом графике показана область ниже графика \(\displaystyle f(x)\) и выше графика \(\displaystyle g(x).\)

Сначала мы необходимо вычислить, где пересекаются графики функций. Установив \(\displaystyle f(x)=g(x),\), получим

\[ \begin{align*} \displaystyle f(x) =g(x) \\[4pt] 94\), найдите площадь области \(\textbf{R}\).

Подсказка

Используйте процесс из примера \(\PageIndex{2}\).

Ответить

\(\displaystyle \dfrac{3}{10}\) ед. ²

Площади составных областей

До сих пор нам требовалось \(\displaystyle f(x)≥g(x)\) на всем интересующем интервале, но что, если мы хотим посмотреть на области, ограниченные графами пересекающиеся друг с другом функции? В этом случае мы модифицируем процесс, который мы только что разработали, используя функцию абсолютного значения. 9b_a|f(x)−g(x)|dx. \nonumber \]

На практике применение этой теоремы требует, чтобы мы разбивали интервал \(\displaystyle [a,b]\) и вычисляли несколько интегралов, в зависимости от того, какое из значений функции больше на данной части интервал. Изучим этот процесс на следующем примере.

Пример \(\PageIndex{3}\): нахождение площади области, ограниченной пересекающимися функциями

Если \(\textbf{R}\) — это область между графиками функций \(\displaystyle f (x)=\sin x \) и \(\displaystyle g(x)=\cos x\) на интервале \(\displaystyle [0,π]\), найти площадь области \(\textbf{R }\).

Решение

Область изображена на следующем рисунке.

Рисунок \(\PageIndex{5}\): Область между двумя кривыми может быть разбита на две подобласти.

Графики функций пересекаются в точке \(\displaystyle x=π/4\). Для \(\displaystyle x∈[0,π/4], \cos x≥\sin x,\) поэтому

\(\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .\)

С другой стороны, для \(\displaystyle x∈[π/4,π], \sin x ≥\cos x,\), поэтому

9π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \end{align*}\]

Площадь области составляет \(\displaystyle 2\sqrt{2}\) единиц ^₂ .

Упражнение \(\PageIndex{3}\)

Если \(\textbf{R}\) область между графиками функций \(\displaystyle f(x)=\sin x \) и \( \displaystyle g(x)=\cos x\) на интервале \(\displaystyle [π/2,2π]\), найти площадь области \(\textbf{R}\).

Подсказка

Две кривые пересекаются в точке \(\displaystyle x=(5π)/4. \)

Ответить

\(\displaystyle 2+2\sqrt{2}\) единиц ²

Пример \(\PageIndex{4}\): определение площади сложной области

Рассмотрим область, изображенную на рисунке \(\PageIndex{6}\). Найдите площадь \(\textbf{R}\).

Рисунок \(\PageIndex{6}\): Для вычисления площади этой области требуются два интеграла. 92_1=\dfrac{1}{2}.\)

Складывая эти области вместе, мы получаем

\(\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2 }=\dfrac{5}{6}.\)

Площадь области составляет \(\displaystyle 5/6\) единиц ^{2 .}

Упражнение \(\PageIndex{4}\)

Рассмотрим область, изображенную на следующем рисунке. Найдите площадь \(\textbf{R}\).

Подсказка

Две кривые пересекаются в точке х=1

Ответить

\(\displaystyle \dfrac{5}{3}\) единиц ²

Области, определенные относительно y

В примере \(\PageIndex{4}\) нам пришлось вычислить два отдельных интеграла для вычисления площади области. 2\) как функции \(\displaystyle y \).Однако, судя по графику, нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но также легко может быть представлен функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл. Разработаем формулу для этого типа интеграции.

Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции на интервале \(\displaystyle [c,d]\) такие, что \(\displaystyle u(y) )≥v(y)\) для всех \(\displaystyle y∈[c,d]\). Мы хотим найти площадь между графиками функций, как показано на рисунке \(\PageIndex{7}\).

Рисунок \(\PageIndex{7}\): Мы можем найти площадь между графиками двух функций, \(\displaystyle u(y)\) и \(\displaystyle v(y)\).

На этот раз мы собираемся разбить интервал на 9d_c[u(y)−v(y)]dy. \end{align*}\]

Эти результаты резюмируются в следующей теореме.

Нахождение площади между двумя кривыми, интегрирование по оси Y

Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции, такие что \(\displaystyle u( y)≥v(y) \) для всех \(\displaystyle y∈[c,d]\). Пусть \(\textbf{R}\) обозначает область, ограниченную справа графиком \(\displaystyle u(y)\), слева графиком \(\displaystyle v(y)\ ), а сверху и снизу строками \(\displaystyle y=d\) и \(\displaystyle y=c\) соответственно. Тогда площадь \(\textbf{R}\) равна 9d_c[u(y)−v(y)]dy. \nonumber \]

Пример \(\PageIndex{5}\): интегрирование по y

Вернемся к примеру \(\PageIndex{4}\), только на этот раз интегрируем по \(\displaystyle y \). Пусть \(\textbf{R}\) будет регионом, изображенным на рисунке \(\PageIndex{9}\). Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).

Рисунок \(\PageIndex{9}\): Площадь области \(\textbf{R}\) можно вычислить с помощью одного интеграла, только если кривые рассматриваются как функции \(\displaystyle y\).

Решение

Сначала мы должны представить графики как функции \(\displaystyle y\). Как мы видели в начале этого раздела, кривая слева может быть представлена ​​функцией \(\displaystyle x=v(y)=\sqrt{y}\), а кривая справа может быть представлена ​​функцией функция \(\displaystyle x=u(y)=2−y\).

Теперь нам нужно определить пределы интегрирования. Область ограничена снизу осью x, поэтому нижний предел интегрирования равен \(\displaystyle y=0\). Верхний предел интегрирования определяется точкой пересечения двух графиков, которая является точкой \(\displaystyle (1,1)\), поэтому верхний предел интегрирования равен \(\displaystyle y=1\). Таким образом, мы имеем \(\displaystyle [c,d]=[0,1]\). 91_0\\[4pt] =\dfrac{5}{6}. \end{align*}\]

Площадь области составляет \(\displaystyle 5/6\) единиц ² .

Упражнение \(\PageIndex{5}\)

Давайте вернемся к контрольной точке, связанной с примером \(\PageIndex{4}\), только на этот раз давайте проинтегрируем относительно \(\displaystyle y\). Пусть \(\textbf{R}\) будет областью, изображенной на следующем рисунке. Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).

Подсказка

Повторите процесс из предыдущего примера.

Ответить

\(\displaystyle \dfrac{5}{3}\) единиц ²

Ключевые понятия

• Определенные интегралы можно использовать не только для нахождения площади под кривой, но и для нахождения площади между двумя кривыми.
• Чтобы найти площадь между двумя кривыми, заданными функциями, проинтегрируйте разность функций.
• Если графики функций пересекаются или область является сложной, используйте абсолютное значение разности функций. В этом случае может потребоваться вычислить два или более интеграла и сложить результаты, чтобы найти площадь области.
• Иногда проще интегрировать по y, чтобы найти площадь. Принципы одни и те же независимо от того, какая переменная используется в качестве переменной интегрирования.

Ключевые уравнения

9d_c[u(y)−v(y)]dy\)

---

Эта страница под названием 6.1: Области между кривыми распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   ОпенСтакс

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

2. Метки

   1. ОБЛАСТЬ МЕЖДУ ДВУМЯ КРИВЫМИ
   2. Площадь между двумя кривыми, интегрированная по оси x
   3. Площадь между двумя кривыми, интегрированная по оси Y
   4. Площади составных регионов
   5. автор @ Эдвин «Джед» Герман
   6. автор@Гилберт Странг
   7. источник@https://openstax. org/details/books/calculus-volume-1

Площадь области, ограниченной кривыми

Площадь в прямоугольных координатах

Напомним, что площадь под графиком непрерывной функции f ( х ) между вертикальными линиями х = 9b {f\left( x \right)dx} = F\left( b \right) — F\left( a \right),\]

, где F ( x ) — любая производная от f ( x ).

Рисунок 1.

Мы можем расширить понятие площади под кривой и рассмотреть площадь области между двумя кривыми.

Если \(f\left( x \right)\) и \(g\left( x \right)\) две непрерывные функции и \(f\left( x \right) \ge g\left( x \ справа)\) на отрезке \(\left[ {a,b} \right],\) то площадь между кривыми \(y = f\left( x \right)\) и \(y = g \left( x \right)\) в этом интервале равно 9б {\ влево [ {е \ влево ( х \ вправо) — г \ влево ( х \ вправо)} \ вправо] dx} = F \ влево ( б \ вправо) — G \ влево ( б \ вправо) — F \ влево( а \вправо) + G\влево( а \вправо),\]

где \(F\left( x \right)\) и \(G\left( x \right)\) — первообразные функций \(f\left( x \right)\) и \(g\left ( x \right),\) соответственно.

Обратите внимание, что эта площадь всегда будет неотрицательной, как \(f\left( x \right) — g\left( x \right) \ge 0\) для всех \(x \in \left[ {a,b } \справа].\)

При наличии точек пересечения следует разбить интервал на несколько подинтервалов и определить, какая кривая больше на каждом подинтервале. Затем мы можем определить площадь каждой области, интегрируя разность большей и меньшей функций. 9\prime\left( t \right),\) \(y\left( t \right)\) здесь предполагаются непрерывными на отрезке \(\left[ {a,b} \right].\) Кроме того что функция \(x\left( t \right),\) должна быть монотонной на этом интервале.

Рис. 5.

Если \(x = x\left( t \right),\) \(y = y\left( t \right),\) \(0 \le t \le T\) параметрические уравнения гладкая кусочно-замкнутая кривая \(С\), проходимая против часовой стрелки и ограничивающая область слева (рис. \(5\)), то площадь области определяется следующими интегралами: 92}\) на отрезке \(\left[{1,b}\right]\) равно \(1?\)

Пример 3

Найдите координату точки \(a\), которая разбивает площадь под корневой функцией \(y = \sqrt{x}\) на отрезке \(\left[{0,4}\right]\) на равные части.

Пример 4

Область ограничена вертикальными линиями \(x = t\), \(x = t + \frac{\pi }{2}\), осью \(x-\) и кривая \(y = a + \cos x,\), где \(a \ge 1.\) Определите значение \(t\), при котором область имеет наибольшую площадь. 9{t + \frac{\pi} {2}} = a\left( {t + \frac{\pi} {2}} \right) + \sin \left( {t + \frac{\pi} }{ 2}} \right) — at — \sin t = \cancel{at} + \frac{{a\pi}}{2} + \sin \left( {t + \frac{\pi }{2}} \right) — \cancel{at} — \sin t = \frac{{a\pi}}{2} + \sin \left( {t + \frac{\pi }{2}} \right) — \ sin т.\]

Использование разности синусов тождества

\[\sin\alpha — \sin\beta = 2\cos\frac{{\alpha + \beta}}{2}\sin\frac{{\alpha — \beta}}{2},\]

получаем

\[A = \frac{{a\pi}}{2} + 2\cos \frac{{t + \frac{\pi} {2} + t}}{2}\sin \frac{{\ cancel{t} + \frac{\pi }{2} — \cancel{t}}}{2} = \frac{{a\pi}}{2} + 2\cos \left( {t + \frac {\pi} {4}} \right)\sin \frac{\pi}}{4} = \frac{{a\pi}}{2} + 2\cos \left( {t + \frac{\pi }{4}} \right) \cdot \frac{{\sqrt 2 }}{2} = \frac{{a\pi}}{2} + \sqrt 2 \cos \left( {t + \frac{ \pi }{4}} \справа). \]

Область имеет наибольшую площадь, когда \(\cos \left( {t + \frac{\pi }{4}} \right) = -1.\)

Решая это уравнение, находим

\[\cos \left( {t + \frac{\pi }{4}} \right) = — 1,\;\; \Rightarrow t + \frac{\pi }{4} = \pi + 2\pi n,\;\; \Rightarrow t = \frac{{3\pi }}{4} + 2\pi n,\,n \in \mathbb{Z}.\]

Дополнительные проблемы см. на стр. 2.

9.1 Площадь между кривыми

Мы видели, как с помощью интегрирования можно найти область между кривая и ось $x$. С очень небольшим изменением мы можем найти некоторые области между кривыми; действительно, площадь между кривой и осью $x$ может интерпретируется как площадь между кривой и второй «кривой». с уравнением $y=0$. В самых простых случаях идея довольно проста чтобы понять. 92\кр &={16\более4}-{64\более3}+28-4-({1\более4}-{8\более3}+7-2)\кр &=23-{56\over3}-{1\over4}={49\over12}.\cr }$$ $\квадрат$

Стоит рассмотреть эту проблему немного подробнее. Мы видели один из способов посмотрите на него, рассматривая желаемую область как большую область минус маленькую площади, что естественным образом приводит к различию между двумя интегралы. Но поучительно рассмотреть, как мы могли бы найти желаемая область напрямую. Мы можем аппроксимировать площадь, разделив площадь на тонкие срезы и аппроксимируя площадь каждого среза на прямоугольник, как показано на цифра 92 = 1$. Обратите внимание: $t$ фиксировано, плоскость $x$-$y$.

Пример 9.1.15 Докажите, что площадь $R$ равна $t$.

Область между двумя функциями | Superprof

В этой статье мы обсудим, как вычислить площадь между двумя функциями. Мы специально сосредоточимся на том, как вычислить площадь между кривой и прямой линией, а также площадь между двумя кривыми.

Площадь между двумя функциями

Площадь между двумя функциями равна площади функции, расположенной выше, за вычетом площади функции, расположенной ниже. Математически мы можем обозначить эту область так:

 

Лучшие репетиторы по математике

Поехали

Площадь между кривой и прямой

Теперь давайте разберемся, как вычислить площадь между кривой и прямой на следующих примерах

Пример 1

Найдите площадь пространства, ограниченного параболой и прямой, проходящей через точки A(−1, 0) и B(1, 4).

Решение

Шаг 1 — Найдите уравнение прямой

На этом шаге мы вычислим уравнение прямой, проходящей через две точки A и B. Для этого сначала мы должны вычислить наклон прямой, проходящей через точки A(-1, 0) и В(1, 4). Для расчета наклона мы будем использовать следующую формулу:

Подставим значения точек A и B в приведенную выше формулу:

Теперь подставим этот наклон в уравнение точки пересечения ниже:

Следовательно, уравнение прямой линии имеет вид y = 2x + 2.

Шаг 2. Нарисуйте график 

На этом этапе мы нарисуем график функции и линии следующим образом:

Шаг 3. Расчет границ

Точки, в которых линия пересекает параболы, будут границами или пределами функции. Как видно из приведенного выше графика, линия пересекает параболу в точках и . Следовательно, это пределы функции.

Шаг 4. Вычисление определенного интеграла

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов, чтобы записать функции в следующей форме:

правило суммы/разности определенных интегралов, подобное этому:

Чтобы вычислить определенный интеграл, мы сначала найдем первообразную функции. Первообразная функции равна

Теперь воспользуемся фундаментальной теоремой исчисления:

Подставим 2 и 0 в первообразную функции, например: линии y = x, при x = 0 и x = 2.

Решение

Шаг 1. Нарисуйте график

В этом примере нам уже дано уравнение линии y = x. Следовательно, нам не нужно его вычислять. Мы просто начнем с построения графика функций и .

На приведенном выше графике видно, что от x = 0 до x = 1 прямая линия находится выше параболы, а от x = 1 до x = 2 прямая линия находится ниже параболы. Следовательно, мы будем вычислять площади, используя эти пределы выше и ниже параболы отдельно.

 

Шаг 2. Вычисление границ

В этом примере уже заданы границы или пределы графика, которые равны 0 и 1.

Шаг 3. Вычисление определенного интеграла

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов, чтобы записать функции в следующем виде:

Площадь, где прямая проходит над параболой:

Найдите первообразную функции . Первопроизводная функции равна

Используйте основную теорему исчисления:

Подставьте 1 и 0 в первообразную функции следующим образом:

93}{3} —

 

В следующем разделе мы увидим, как вычислить площадь между двумя кривыми, зная их уравнения.

 

Площадь между двумя кривыми

Следующие примеры помогут вам понять, как вычислить площадь между двумя кривыми.

Пример 1

Найдите площадь, ограниченную графиками функций и

Решение

Шаг 1 — Нарисуйте график

Шаг 2 — Найдите границы

Чтобы определить, где графики двух кривых пересекаются друг друга, мы приравниваем уравнения двух кривых:

или

Следовательно, границы — и 0,

Шаг 3. — Вычислить определенный интеграл

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов, чтобы записать функции в следующем виде:

Найдите первообразную функции. Первопроизводная функции равна

. Используйте основную теорему исчисления:

. Подставив 0 в первообразную функции, получим следующее значение площади:

Пример 2

Найдите площадь между двумя кривые и.

Решение

Выполните следующие действия, чтобы рассчитать площадь.

Шаг 1. Нарисуйте график

График двух кривых приведен ниже:

Шаг 2. Найдите границы

Вычислите границы функции по уравнению:

или

Следовательно, границы функции равны 5 и 902.

Шаг 3. Вычисление определенного интеграла

Чтобы вычислить определенный интеграл, сначала используйте информацию из предыдущих шагов, чтобы записать функции в следующем виде:

Найдите первообразную функции. Первопроизводная функции равна

Используйте основную теорему исчисления:

Подставьте 2 и 0 в первообразную функции:

 

9002 Исчисление I -0 Онлайн-заметки Пола
Главная / Исчисление I / Приложения интегралов / Площадь между кривыми

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 6-2: Площадь между кривыми

В этом разделе мы рассмотрим нахождение площади между двумя кривыми. На самом деле есть два случая, которые мы собираемся рассмотреть.

В первом случае мы хотим определить площадь между \(y = f\left( x \right)\) и \(y = g\left( x \right)\) на интервале \(\left[ {яркий]\). Мы также собираемся предположить, что \(f\left( x \right) \ge g\left( x \right)\). Взгляните на следующий эскиз, чтобы получить представление о том, на что мы изначально собираемся смотреть.

В разделе «Формулы площади и объема» главы «Дополнительно» мы вывели следующую формулу для площади в этом случае. {{\,b}}{{f\left(x\right) — g\left(x\right)\,dx}} \метка{уравнение:уравнение1}\конец{уравнение}\] 9{{\,d}}{{f\left(y\right) — g\left(y\right)\,dy}}\label{eq:eq2}\end{equation}\]

Теперь \(\eqref{eq:eq1}\) и \(\eqref{eq:eq2}\) вполне пригодные формулы, однако иногда легко забыть, что они всегда требуют, чтобы первая функция была больше из двух функций. Таким образом, вместо этих формул мы будем использовать следующие «словесные» формулы, чтобы убедиться, что мы помним, что площадь всегда представляет собой «большую» функцию минус «меньшую» функцию. 9{{\,d}}{{\left(\begin{array}{c}{\mbox{right}}\\ {\mbox{function}}\end{array} \right) — \left(\begin {массив} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5 дюйма} c \ le y \ le d \ метка{уравнение:уравнение4}\конец{уравнение}\]

Использование этих формул всегда заставит нас думать о том, что происходит с каждой задачей, и убедиться, что мы получили правильный порядок функций, когда переходим к использованию формулы. 2}\) и \(y = \sqrt x \).

Показать решение

Прежде всего, что мы подразумеваем под «окруженной областью». Это означает, что интересующая нас область должна иметь одну из двух кривых на каждой границе области. Итак, вот график двух функций с заштрихованной областью.

Обратите внимание, что мы не берем какую-либо часть области справа от крайней правой точки пересечения этих двух графиков. В этой области нет границы с правой стороны, поэтому эта область не является частью замкнутой области. Помните, что одна из заданных функций должна находиться на границе замкнутой области. 92}\) является верхней функцией, и они подходят для подавляющего большинства \(x\). Однако в данном случае это младшая из двух функций.

Пределы интегрирования для этого будут точками пересечения двух кривых. В этом случае довольно легко увидеть, что они пересекаются в точках \(x = 0\) и \(x = 1\), так что это пределы интегрирования.

Итак, интеграл, который нам нужно вычислить, чтобы найти площадь, равен

. 1\\ & = \frac{1}{3}\end{align*}\]

Прежде чем перейти к следующему примеру, следует отметить пару важных моментов.

Во-первых, почти во всех этих задачах требуется граф. Часто граничную область, которая дает пределы интегрирования, трудно определить без графика.

Кроме того, без графика часто бывает трудно определить, какая из функций является верхней, а какая — нижней. Это особенно верно в случаях, подобных последнему примеру, где ответ на этот вопрос на самом деле зависел от диапазона \(x\), который мы использовали.

Наконец, в отличие от площади под кривой, которую мы рассматривали в предыдущей главе, площадь между двумя кривыми всегда будет положительной. Если мы получим отрицательное число или ноль, мы можем быть уверены, что где-то допустили ошибку, и нам нужно будет вернуться и найти ее.

Также обратите внимание, что иногда вместо слова «область, заключенная в», мы будем говорить «область, ограниченная». Они означают одно и то же.

Давайте рассмотрим еще несколько примеров. 2}}}\), \(y = x + 1\), \(x = 2\) и ось \(y\).

Показать решение

В этом случае две последние части информации, \(x = 2\) и ось \(y\), говорят нам о правой и левой границах области. Также напомним, что ось \(y\) задается линией \(x = 0\). Вот график с заштрихованной областью.

Здесь, в отличие от первого примера, две кривые не пересекаются. Вместо этого мы полагаемся на две вертикальные линии, чтобы ограничить левую и правую стороны области, как мы отметили выше

92} + 10\) и \(у = 4х + 16\).

Показать решение

В этом случае точки пересечения (которые нам в конечном итоге потребуются) будет нелегко определить на графике, поэтому давайте продолжим и получим их сейчас. Обратите внимание, что для большинства этих задач вы не сможете точно идентифицировать точки пересечения на графике, поэтому вам нужно уметь определять их вручную. В этом случае мы можем получить точки пересечения, приравняв два уравнения. 92} — 4x — 6 & = 0\\ 2\left( {x + 1} \right)\left( {x — 3} \right) & = 0\end{align*}\]

Получается, что две кривые пересекаются в точках \(x = — 1\) и \(x = 3\). Если они нам нужны, мы можем получить значения \(y\), соответствующие каждому из них, подставив значения обратно в любое из уравнений. Мы предоставим вам проверить, что координаты двух точек пересечения на графике равны \(\left( { — 1,12} \right)\) и \(\left( {3,28} \right )\). 92} + 10\), \(у = 4х + 16\), \(х = — 2\) и \(х = 5\).

Показать решение

Итак, функции, используемые в этой задаче, идентичны функциям из первой задачи. Разница в том, что мы расширили ограниченную область от точек пересечения. Поскольку это те же самые функции, которые мы использовали в предыдущем примере, мы не будем снова искать точки пересечения.

Вот график этого региона.

Итак, у нас есть небольшая проблема. Наша формула требует, чтобы одна функция всегда была верхней функцией, а другая функция всегда была нижней функцией, чего здесь явно нет. Однако на самом деле это не проблема, как может показаться на первый взгляд. Есть три области, в которых одна функция всегда является верхней функцией, а другая всегда нижней функцией. Итак, все, что нам нужно сделать, это найти площадь каждой из трех областей, что мы можем сделать, а затем сложить их все. 95\\ & = \frac{{14}}{3} + \frac{{64}}{3} + \frac{{64}}{3}\\ & = \frac{{142}}{3 }\конец{выравнивание*}\]

Пример 5. Определите площадь области, заключенной в \(y = \sin x\), \(y = \cos x\), \(x = \frac{\pi }{2}\), и \( у\)-ось.

Показать решение

Сначала создадим график региона.

Итак, у нас есть еще одна ситуация, когда нам нужно будет сделать два интеграла, чтобы получить площадь. Точка пересечения будет там, где 92} — 3\) и \(у = х — 1\).

Показать решение

Не позволяйте первому уравнению вас расстроить. 2} — 2y — 8\\ 0 & = \left( {y — 4} \right)\left( {y + 2} \right)\end{align*}\]

Итак, похоже, что две кривые будут пересекаться в точках \(y = — 2\) и \(y = 4\) или, если нам нужны полные координаты, они будут: \(\left( { — 1, — 2} \справа)\) и \(\слева({5,4} \справа)\).

Вот эскиз двух кривых.

Теперь у нас будут серьезные проблемы, если мы не будем осторожны. До сих пор мы использовали верхнюю функцию и нижнюю функцию. Для этого обратите внимание на то, что на самом деле есть две части области, которые будут иметь разные нижние функции. В диапазоне \(\left[ { — 3, — 1} \right]\) парабола фактически является как верхней, так и нижней функцией.

Чтобы использовать формулу, которую мы использовали до сих пор, нам нужно решить параболу для \(y\). Это дает,

\[y = \pm \sqrt {2x + 6} \]

, где «+» обозначает верхнюю часть параболы, а «-» — нижнюю часть.

Вот набросок полной области с заштрихованными областями, которые нам понадобятся, если мы собираемся использовать первую формулу.

Тогда интегралы площади будут равны 9{{\,d}}{{\left(\begin{array}{c}{\mbox{right}}\\ {\mbox{function}}\end{array} \right) — \left(\begin {массив} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5 дюйма} c \ le y \ le d \ ]

и в нашем случае у нас есть одна функция, которая всегда слева, а другая всегда справа. Так что в данном случае это определенно выход. Обратите внимание, что нам нужно будет переписать уравнение прямой, поскольку оно должно быть в форме \(x = f\left( y \right)\), но это достаточно легко сделать. Вот график для использования этой формулы. 94\\ & = 18\конец{выравнивание*}\]

Это то же самое, что мы получили, используя первую формулу, и это было определенно проще, чем первый метод.

Итак, в этом последнем примере мы видели случай, когда мы могли использовать любую формулу для нахождения площади. Однако второе было определенно легче.

Студенты часто приходят на занятия по математическому анализу с идеей, что единственный простой способ работать с функциями — использовать их в виде \(y = f\left( x \right)\).

No related posts.