Параллельное соединение резисторов онлайн калькулятор
Random converter. Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно. Введите величины сопротивлений в поля R 1 , R 2 и т.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Онлайн калькулятор для параллельного соединения резисторов
- Калькулятор резисторов
- Параллельное соединение резисторов, онлайн расчет
- Параллельное соединение резистора
- калькулятор параллельного соединения резисторов онлайн
- Расчет сопротивления параллельного соединения резисторов
- Parallel Resistor Calculator
- Онлайн-калькулятор параллельного соединения резисторов
- Радиолюбительский калькулятор
- Подарки и советы
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: физика ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ 8 класс
youtube.com/embed/agBsAVKl19o» frameborder=»0″ allowfullscreen=»»/>Онлайн калькулятор для параллельного соединения резисторов
Собирая самостоятельные схемы, начинающие радиолюбители сталкиваются с необходимостью установить то или иное сопротивление, величины которого нет в стандартном ряде или на руках. Поэтому нужная величина импеданса подбирается путём параллельного или последовательного соединения элементов. Для правильного вычисления эквивалентного значения проще всего воспользоваться калькулятором для сопротивления, но можно и провести вычисления самостоятельно по несложным формулам.
Практически ни одно электронное устройство не обходится в своей схеме без резисторов. Являясь пассивными элементами, они имеют основное предназначение — ограничивать величину тока в электрической цепи. Кроме токоограничения, они служат делителями напряжения или шунтами в измерительных приборах. Электрическое сопротивление — это величина, имеющая физическую природу и характеризующая возможность проводника пропускать электрический ток.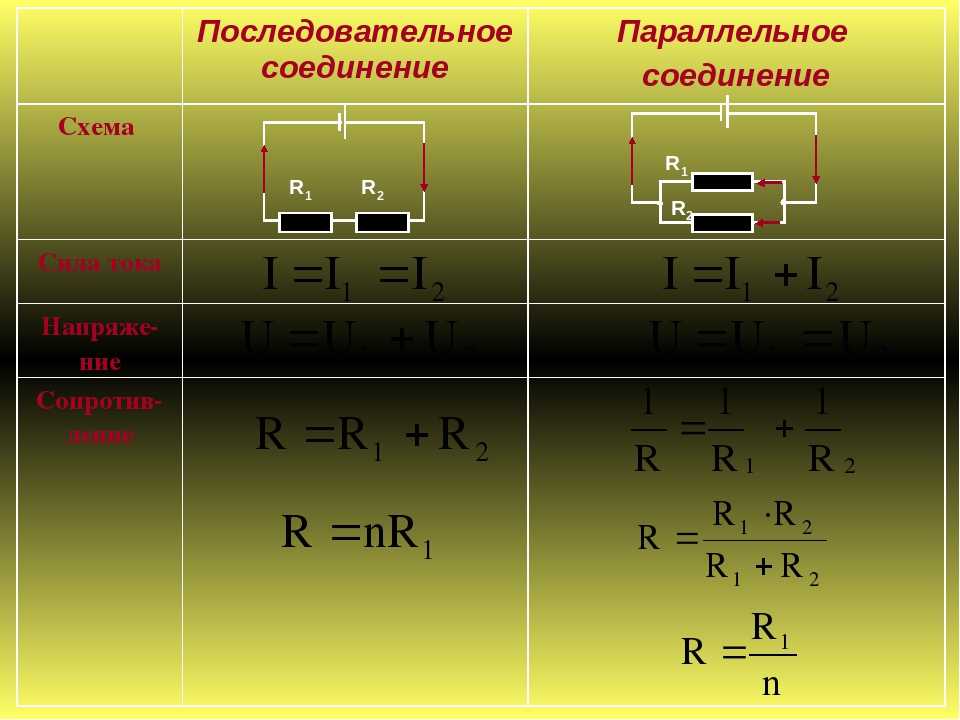
Принцип работы резистора был описан выдающимся экспериментатором Омом. Позже в его честь и была названа единица измерения электрического сопротивления — Ом. Учёный, проводя ряд экспериментов, установил зависимость между силой тока, напряжением и сопротивлением в проводнике.
Позже устройства, использующиеся только в качестве элементов сопротивления в электрических цепях, получили название — резисторы. Полученная величина измеряется в Ваттах. В схемотехнике используется как параллельное, так и последовательное соединение проводников. В зависимости от этого изменяется и величина импеданса участка цепи. Вид соединения, если он не используется для подбора нужного значения, как раз и характеризует применение резисторов в первом случае как токоограничителей, а во втором — как делителей напряжения.
На схемах резисторы обозначаются в виде прямоугольника и подписываются латинской буквой R. Рядом указывается порядковый номер и значение сопротивления. Например, R23 1k обозначает, что резистор с номером 23 имеет сопротивление, равное одному килоОму.
Полоски, изображённые внутри прямоугольника, характеризуют мощность, рассеиваемую на проводнике. Фундаментальный закон сохранения энергии гласит: энергия никуда не исчезает и из ниоткуда не появляется, а только изменяет форму.
Поэтому при ограничении тока часть энергии трансформируется в тепло. Именно эту часть и называют мощностью рассеивания резистора, т. Сам по себе резистор может иметь различную конструкцию и вид. Например, быть проволочным, керамическим, слюдяным и т.
Маркируется он тремя способами:. Поэтому видя, какие резисторы установлены в схеме, даже начинающему радиолюбителю не составит труда рассчитать общее сопротивление, особенно используя онлайн-калькулятор параллельного соединения резисторов или последовательного.
В случае невозможности различить маркировку на корпусе его сопротивление возможно измерить мультиметром. Но опытные электротехники знают, что для точного измерения понадобится один вывод сопротивления отсоединить от схемы.
Связано это как раз с видом подключения проводника. Такое соединение резисторов получается путём объединения двух и более электрических устройств, при котором их одни выводы соединяются друг с другом и образовывают первую общую точку, а другие, аналогично первым, образовывают вторую общую точку.
Такое соединение резисторов получается путём объединения двух и более электрических устройств, при котором их одни выводы соединяются друг с другом и образовывают первую общую точку, а другие, аналогично первым, образовывают вторую общую точку.
В этом случае напряжение на всех элементах одинаковое, а проходящая сила тока зависит от их импеданса. Исходя из этого, при параллельном соединении результирующий импеданс двух и более резисторов будет меньше самого меньшего значения сопротивления в соединении.
При этом когда параллельно включены только два резистора, имеющие одинаковый номинал, то их можно заменить эквивалентом, равным одной второй от величины этого номинала. Так можно соединить и сотню резисторов, тогда эквивалентное сопротивление определяется как сотая часть от номинала. Важно отметить, что при таком соединении величина тока поделится на каждый элемент, поэтому и резисторы можно применить меньшей мощности, чем если бы использовался эквивалент, заменяющий всё параллельное подключение.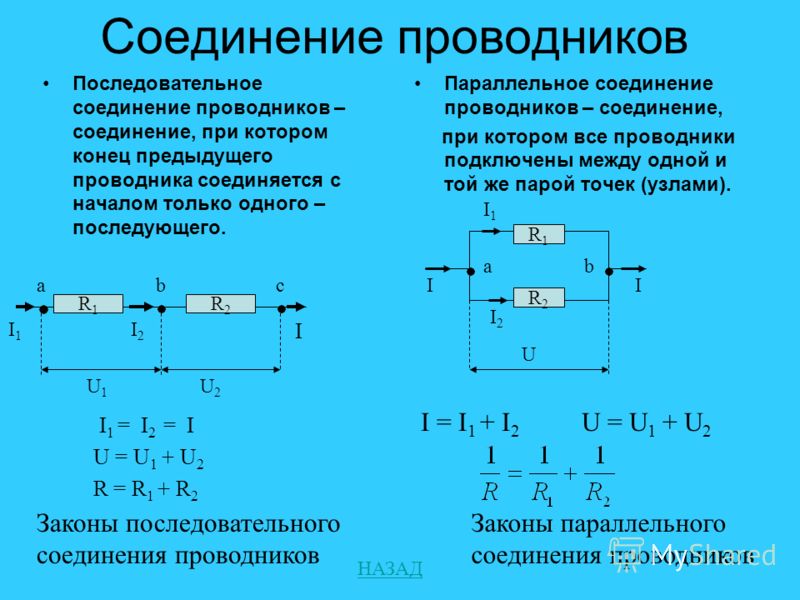
При разработке прибора возникла потребность использовать на участке цепи резистор с сопротивлением 6 Ом. При изучении номинального ряда стандартных значений, выпускаемых промышленностью, можно отметить, что резистора на 6 Ом в нём нет. Для получения нужного значения понадобится воспользоваться параллельным включением двух элементов. Эквивалентное значение сопротивления для двух резисторов в таком случае находится в следующем порядке:.
Из решения видно, что если R1 совпадает по номиналу с R2, то общая величина сопротивления равна половине значения одного из элементов. Таким образом, решением поставленной задачи будет параллельное включение двух резисторов с величиной сопротивления, равной 12 Ом. Пусть существует схема с тремя параллельно включёнными резисторами и для её упрощения необходимо заменить их одним элементом. Для решения задачи используется уже известная формула:.
Перед тем как подставлять величины в формулу , их все понадобится привести к международной системе единиц СИ.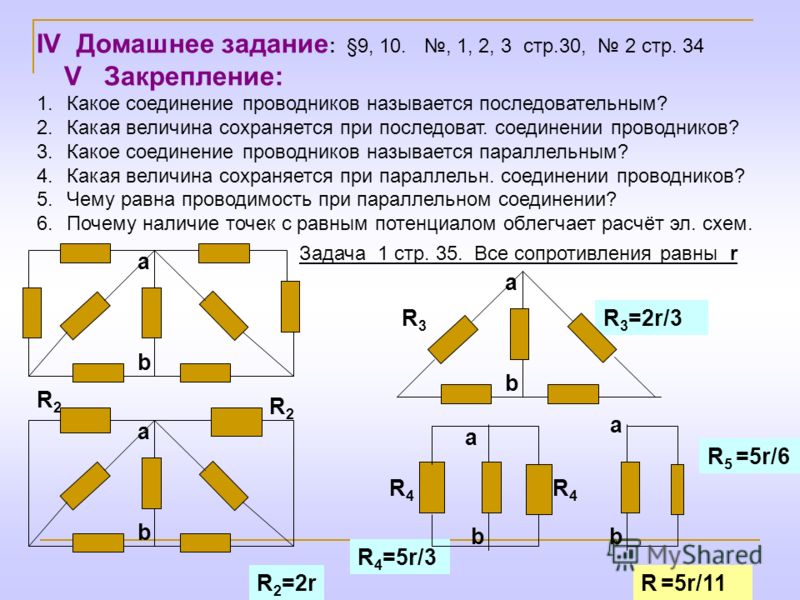 Такая методика расчёта применяется для любого количества параллельно соединённых резисторов. Такой вид включения подразумевает вид соединения, когда резисторы соединяются между собой только одним выводом, образовывая цепочку, при этом между её началом и концом отсутствует проводимость, соответствующая режиму короткого замыкания. При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников.
Такая методика расчёта применяется для любого количества параллельно соединённых резисторов. Такой вид включения подразумевает вид соединения, когда резисторы соединяются между собой только одним выводом, образовывая цепочку, при этом между её началом и концом отсутствует проводимость, соответствующая режиму короткого замыкания. При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников.
В этом случае на участке схемы используется комбинация параллельного и последовательного включения элементов. Такое соединение часто называется параллельно-последовательным:. Используя эти правила, которые справедливы для любого числа соединённых проводников в схеме, определяется общее значение импеданса для любого вида подключения.
Для того чтобы определить эквивалентное значение сопротивления параллельно-последовательного соединения, участок схемы делится на небольшие группы из параллельно или последовательно включённых резисторов. Затем используется алгоритм, помогающий оптимально посчитать значение эквивалента:.
Затем используется алгоритм, помогающий оптимально посчитать значение эквивалента:.
Поэтому импеданс на этом участке будет равен:. Так шаг за шагом вычисляется эквивалентное значение любой сложности схемы. При множестве проводников, входящих в электрическую цепь, нетрудно ошибиться при расчётах, поэтому все операции выполняются аккуратно или используются онлайн-калькуляторы.
Создано множество интернет-страниц, позволяющих найти сопротивление параллельных резисторов за несколько секунд, используя в своих вычислительных алгоритмах формулы для расчёта параллельного соединения. Такие калькуляторы достаточно полезны радиолюбителям-конструкторам или специалистам РЭА при возникновении затруднения с выбором нужного номинала резистора для замены его в цепи электронного устройства.
Внешний вид онлайн-приложений может отличаться друг от друга, а вот принцип работы одинаков. Немаловажным является в работе программ тот факт, что алгоритмы их вычисления используют разную точность в округлении результата, поэтому ответ в некоторых программах при сравнении может немного отличаться.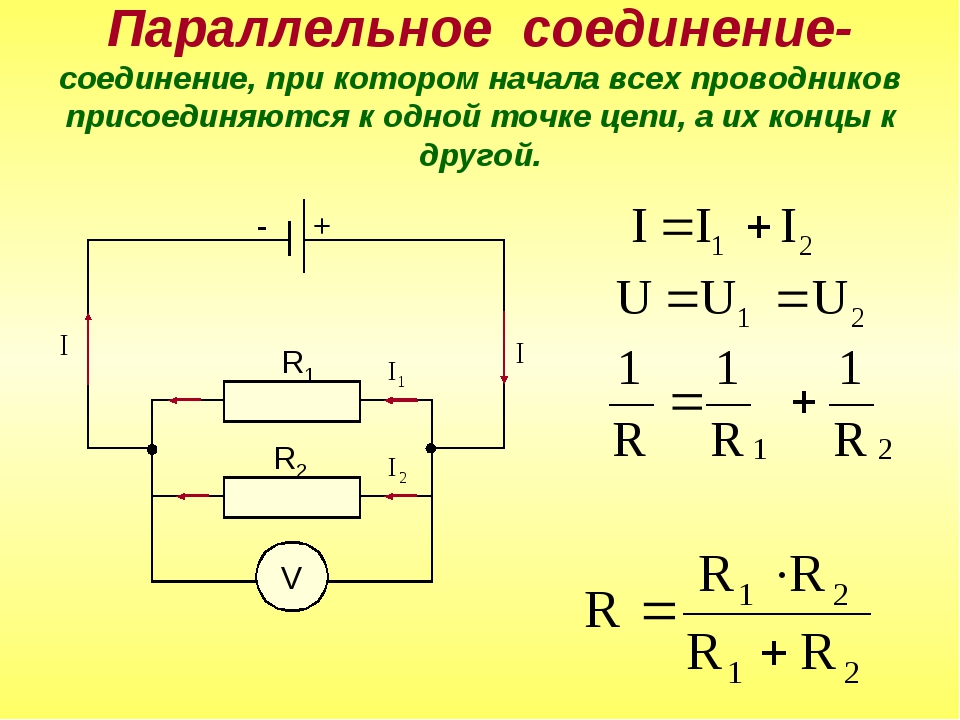
Само приложение обычно представляет собой ячейки, в которые вносится величина значений резисторов в международной системе измерений.
Ответ рассчитывается в Омах. В некоторых приложениях функциональность может быть расширена, это такие возможности, как автоматический перевод значений резисторов в систему СИ, отображение наиближайшего стандартного значения сопротивления из номинального ряда, близкого к полученному ответу.
Полезной функцией может быть и обратный переход, когда вводится эквивалентное сопротивление, а в ответе выдаётся комбинация номиналов проводника для параллельного включения. Таким образом, расчёт с использованием онлайн-калькуляторов помогает решить задачу не только быстро, но и безошибочно, чем часто пользуются не только радиолюбители, но и профессионалы.
Автор: chebo Распечатать Оцените статью:. Расшифровка маркировки номиналов smd резисторов. Сопротивление изоляции кабеля: измерение и норма.
Как проверить работоспособность резисторов и диодов тестером.
Калькулятор резисторов
Расчёт сопротивления резисторов в параллельном включении. Подбор нужного значения из стандартных номиналов. Иногда проще вписать значения, чем выбирать селектором… Результат получаем кликом мыши в любом месте таблицы. Получим варианты параллельного соединения резисторов R1 и R2. Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств. Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться.
Параллельное соединение резисторов, онлайн расчет поможет вам рассчитать полное сопротивление электрической цепи с параллельным.
Параллельное соединение резисторов, онлайн расчет
В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы. Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами. При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений. При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.
Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы. Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами. При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений. При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.
Параллельное соединение резистора
Как оставлять свои сообщения Предупреждение и вечный бан для постоянных нарушителей. Автор Шурик Регуляторы тембра и громкости. Автор Horri Радиодетали и компоненты. Автор WolfTheGrey Компьютерный раздел. Клуб DiyAudio Звук в твоих руках!
Для того чтобы определить общее эквивалентное сопротивление , можно воспользоваться точным и удобным калькулятором.
калькулятор параллельного соединения резисторов онлайн
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:. Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:. Ток, протекающий через отдельно взятый резистор, согласно закону Ома , можно найти по формуле:. При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.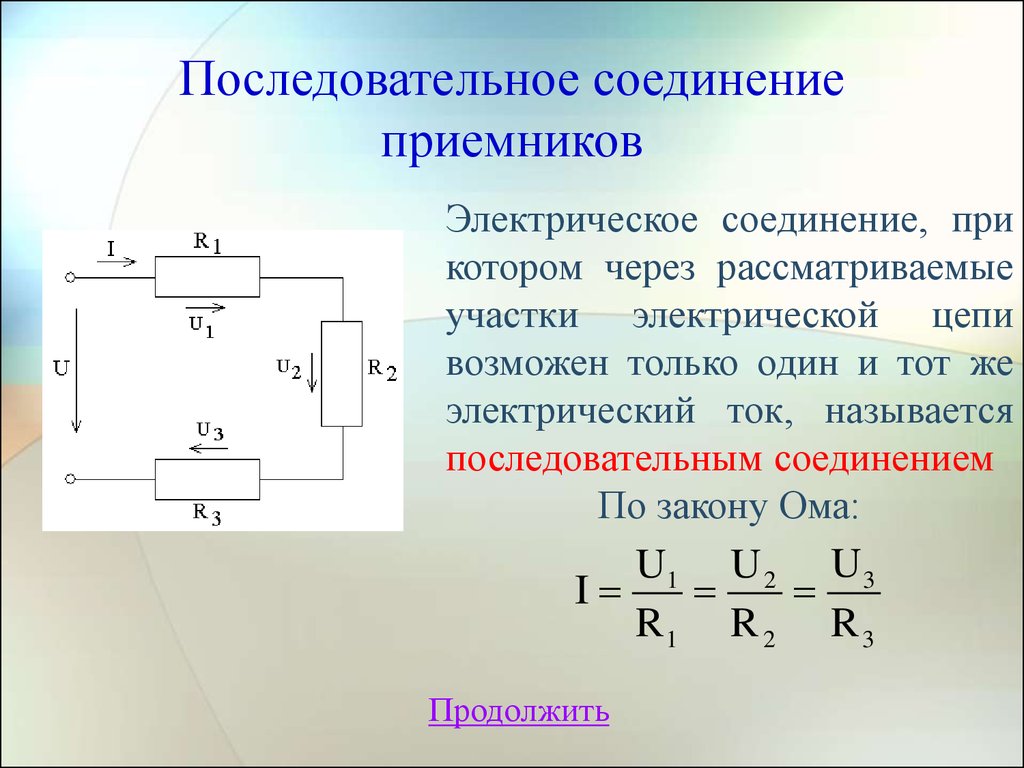 Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Расчет сопротивления параллельного соединения резисторов
Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Онлайн калькулятор для резисторов, соединенных параллельно: для чего используют параллельное соединение, как рассчитывается параллельное.
Parallel Resistor Calculator
Портал QRZ. RU существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Мы стараемся размещать только релевантную рекламу, которая будет интересна не только рекламодателям, но и нашим читателям.
RU существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Мы стараемся размещать только релевантную рекламу, которая будет интересна не только рекламодателям, но и нашим читателям.
Онлайн-калькулятор параллельного соединения резисторов
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:. Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:. При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора.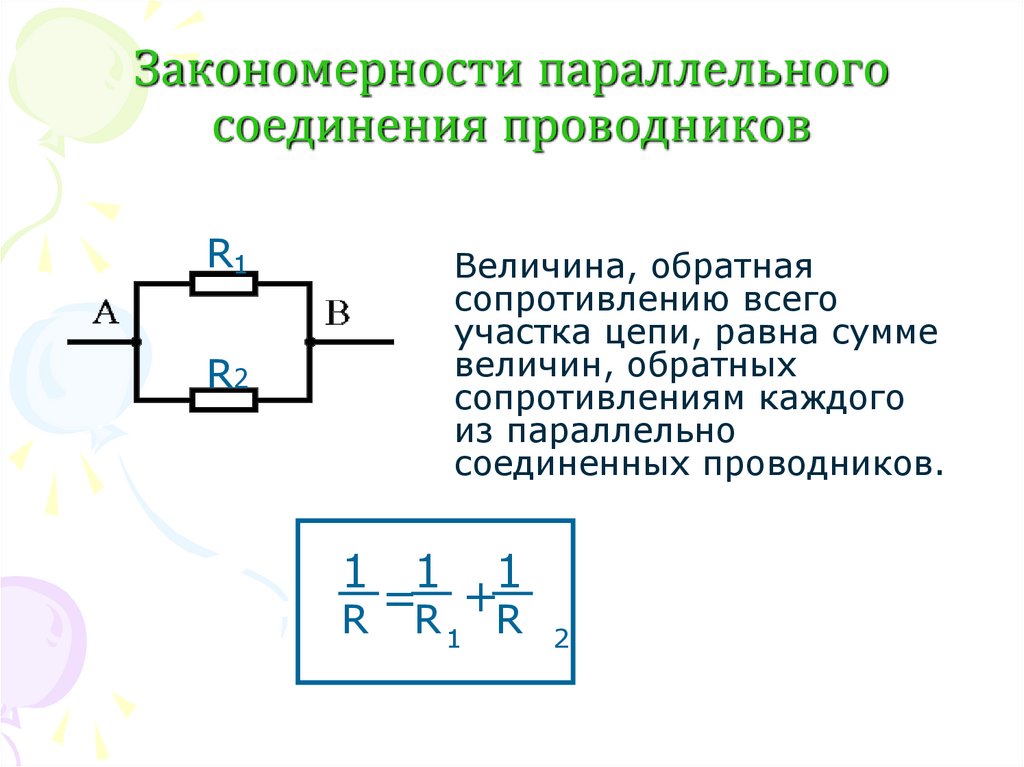
Радиолюбительский калькулятор
R1 Ohm :. R2 Ohm :. Оставить комментарий. Обнаружен блокировщик рекламы. Сайт Паяльник существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Как это сделать?
Подарки и советы
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:. Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:.
Параллельное соединение резисторов калькулятор онлайн
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома. С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов. В данной статье речь пойдёт о расчёте физических параметров, характеризующих цепь.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Параллельное соединение сопротивлений, формула
- Параллельное соединение резисторов
- Параллельное соединение резисторов, калькулятор
- Онлайн-калькулятор параллельного соединения резисторов
- Подарки и советы
- калькулятор параллельного соединения резисторов онлайн
- Расчет сопротивления параллельного соединения резисторов
- Параллельное соединение резисторов
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Последовательное и параллельное подключение резисторов.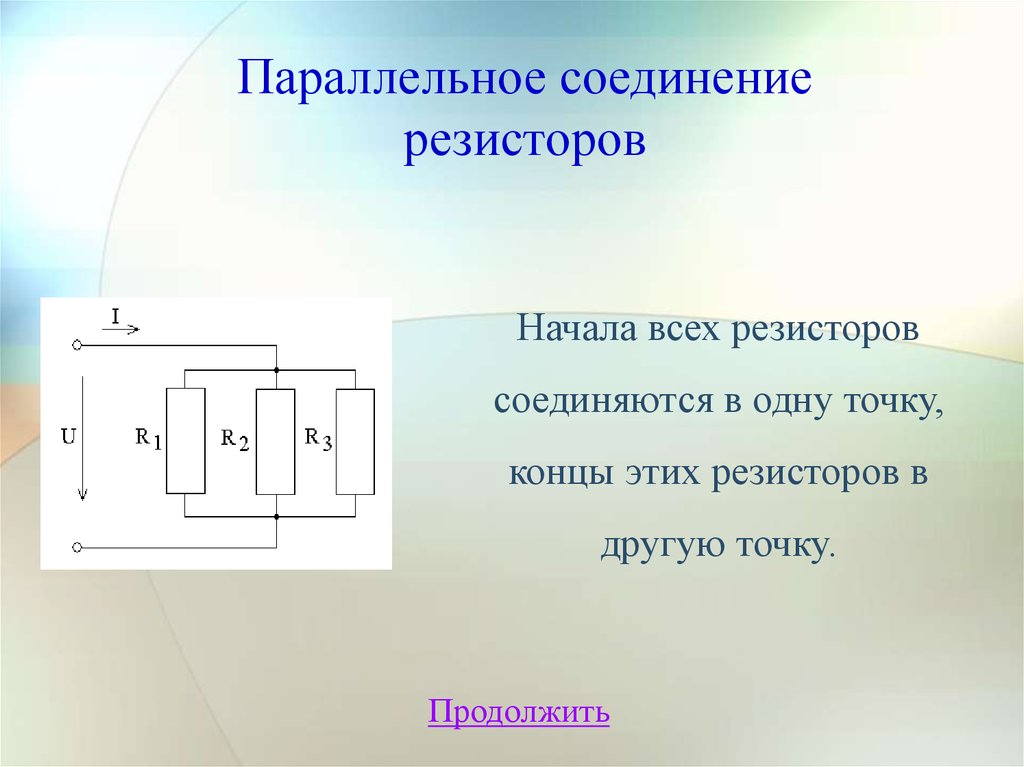 Как рассчитать с помощью формул?
Как рассчитать с помощью формул?
Параллельное соединение сопротивлений, формула
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей. При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей.
Собирая самостоятельные схемы, начинающие радиолюбители сталкиваются с необходимостью установить то или иное сопротивление, величины которого нет в стандартном ряде или на руках. Поэтому нужная величина импеданса подбирается путём параллельного или последовательного соединения элементов.
Для правильного вычисления эквивалентного значения проще всего воспользоваться калькулятором для сопротивления, но можно и провести вычисления самостоятельно по несложным формулам.
Практически ни одно электронное устройство не обходится в своей схеме без резисторов. Являясь пассивными элементами, они имеют основное предназначение — ограничивать величину тока в электрической цепи. Кроме токоограничения, они служат делителями напряжения или шунтами в измерительных приборах. Электрическое сопротивление — это величина, имеющая физическую природу и характеризующая возможность проводника пропускать электрический ток.
Являясь пассивными элементами, они имеют основное предназначение — ограничивать величину тока в электрической цепи. Кроме токоограничения, они служат делителями напряжения или шунтами в измерительных приборах. Электрическое сопротивление — это величина, имеющая физическую природу и характеризующая возможность проводника пропускать электрический ток.
Принцип работы резистора был описан выдающимся экспериментатором Омом. Позже в его честь и была названа единица измерения электрического сопротивления — Ом. Учёный, проводя ряд экспериментов, установил зависимость между силой тока, напряжением и сопротивлением в проводнике.
Позже устройства, использующиеся только в качестве элементов сопротивления в электрических цепях, получили название — резисторы. Полученная величина измеряется в Ваттах. В схемотехнике используется как параллельное, так и последовательное соединение проводников. В зависимости от этого изменяется и величина импеданса участка цепи. Вид соединения, если он не используется для подбора нужного значения, как раз и характеризует применение резисторов в первом случае как токоограничителей, а во втором — как делителей напряжения.
На схемах резисторы обозначаются в виде прямоугольника и подписываются латинской буквой R. Рядом указывается порядковый номер и значение сопротивления. Например, R23 1k обозначает, что резистор с номером 23 имеет сопротивление, равное одному килоОму.
Полоски, изображённые внутри прямоугольника, характеризуют мощность, рассеиваемую на проводнике. Фундаментальный закон сохранения энергии гласит: энергия никуда не исчезает и из ниоткуда не появляется, а только изменяет форму.
Поэтому при ограничении тока часть энергии трансформируется в тепло. Именно эту часть и называют мощностью рассеивания резистора, т. Сам по себе резистор может иметь различную конструкцию и вид. Например, быть проволочным, керамическим, слюдяным и т. Маркируется он тремя способами:.
Цветной полосочной системой. Каждая полоска отвечает за определённый множитель. Расшифровку полосок можно взять из справочников или онлайн-калькуляторов. Цифрами и буквами. Число указывает непосредственно значение сопротивления, а буква — множитель.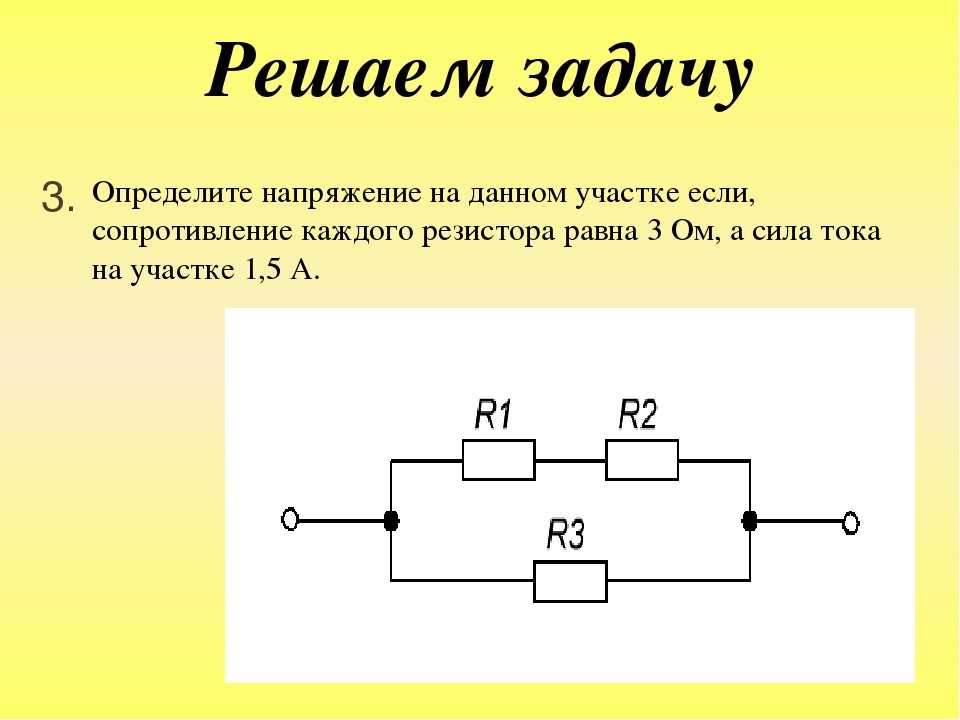 Например,15M — пятнадцать мегаОм. Обычно используются три цифры, первая и вторая обозначают значение сопротивления, а последняя — множитель.
Например,15M — пятнадцать мегаОм. Обычно используются три цифры, первая и вторая обозначают значение сопротивления, а последняя — множитель.
Например, — десять килоОм. Поэтому видя, какие резисторы установлены в схеме, даже начинающему радиолюбителю не составит труда рассчитать общее сопротивление, особенно используя онлайн-калькулятор параллельного соединения резисторов или последовательного. В случае невозможности различить маркировку на корпусе его сопротивление возможно измерить мультиметром.
Но опытные электротехники знают, что для точного измерения понадобится один вывод сопротивления отсоединить от схемы. Связано это как раз с видом подключения проводника. Такое соединение резисторов получается путём объединения двух и более электрических устройств, при котором их одни выводы соединяются друг с другом и образовывают первую общую точку, а другие, аналогично первым, образовывают вторую общую точку. В этом случае напряжение на всех элементах одинаковое, а проходящая сила тока зависит от их импеданса.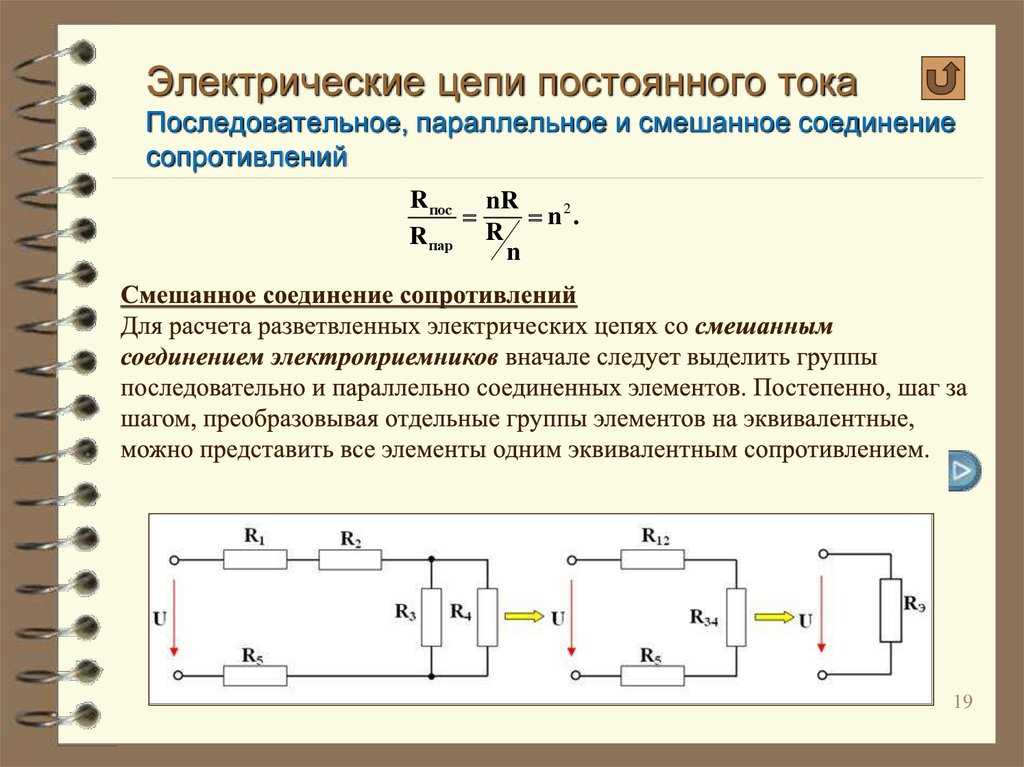
Исходя из этого, при параллельном соединении результирующий импеданс двух и более резисторов будет меньше самого меньшего значения сопротивления в соединении. При этом когда параллельно включены только два резистора, имеющие одинаковый номинал, то их можно заменить эквивалентом, равным одной второй от величины этого номинала. Так можно соединить и сотню резисторов, тогда эквивалентное сопротивление определяется как сотая часть от номинала.
Важно отметить, что при таком соединении величина тока поделится на каждый элемент, поэтому и резисторы можно применить меньшей мощности, чем если бы использовался эквивалент, заменяющий всё параллельное подключение. При разработке прибора возникла потребность использовать на участке цепи резистор с сопротивлением 6 Ом.
При изучении номинального ряда стандартных значений, выпускаемых промышленностью, можно отметить, что резистора на 6 Ом в нём нет. Для получения нужного значения понадобится воспользоваться параллельным включением двух элементов.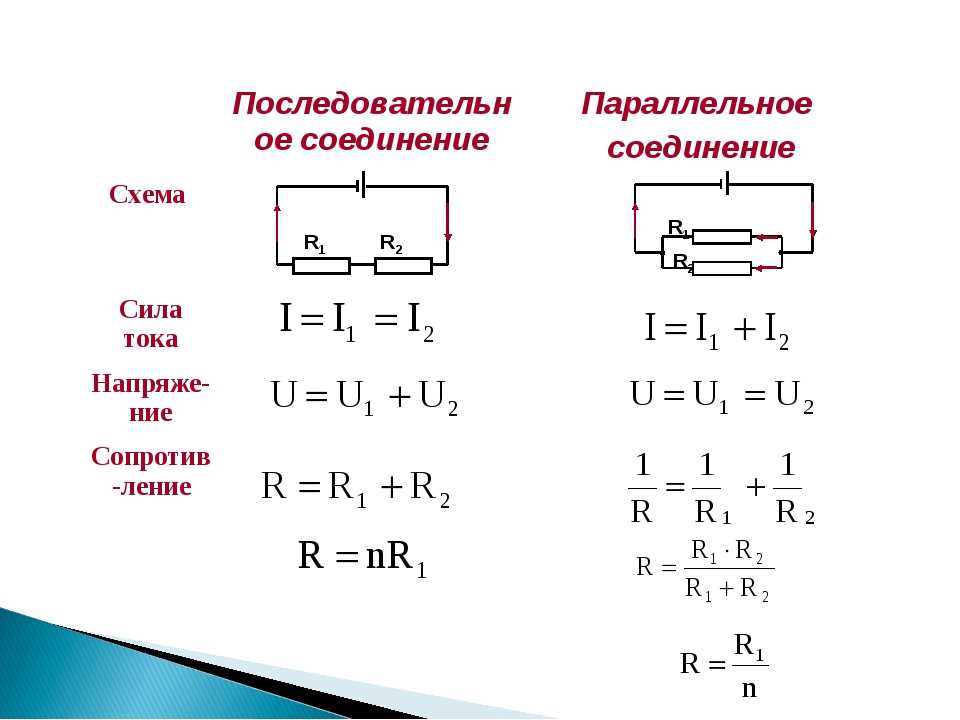 Эквивалентное значение сопротивления для двух резисторов в таком случае находится в следующем порядке:.
Эквивалентное значение сопротивления для двух резисторов в таком случае находится в следующем порядке:.
Из решения видно, что если R1 совпадает по номиналу с R2, то общая величина сопротивления равна половине значения одного из элементов. Таким образом, решением поставленной задачи будет параллельное включение двух резисторов с величиной сопротивления, равной 12 Ом.
Пусть существует схема с тремя параллельно включёнными резисторами и для её упрощения необходимо заменить их одним элементом.
Для решения задачи используется уже известная формула:. Перед тем как подставлять величины в формулу , их все понадобится привести к международной системе единиц СИ. Такая методика расчёта применяется для любого количества параллельно соединённых резисторов.
Такой вид включения подразумевает вид соединения, когда резисторы соединяются между собой только одним выводом, образовывая цепочку, при этом между её началом и концом отсутствует проводимость, соответствующая режиму короткого замыкания. При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников.
При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников.
В этом случае на участке схемы используется комбинация параллельного и последовательного включения элементов. Такое соединение часто называется параллельно-последовательным:. Используя эти правила, которые справедливы для любого числа соединённых проводников в схеме, определяется общее значение импеданса для любого вида подключения.
Для того чтобы определить эквивалентное значение сопротивления параллельно-последовательного соединения, участок схемы делится на небольшие группы из параллельно или последовательно включённых резисторов.
Затем используется алгоритм, помогающий оптимально посчитать значение эквивалента:. Поэтому импеданс на этом участке будет равен:. Так шаг за шагом вычисляется эквивалентное значение любой сложности схемы. При множестве проводников, входящих в электрическую цепь, нетрудно ошибиться при расчётах, поэтому все операции выполняются аккуратно или используются онлайн-калькуляторы.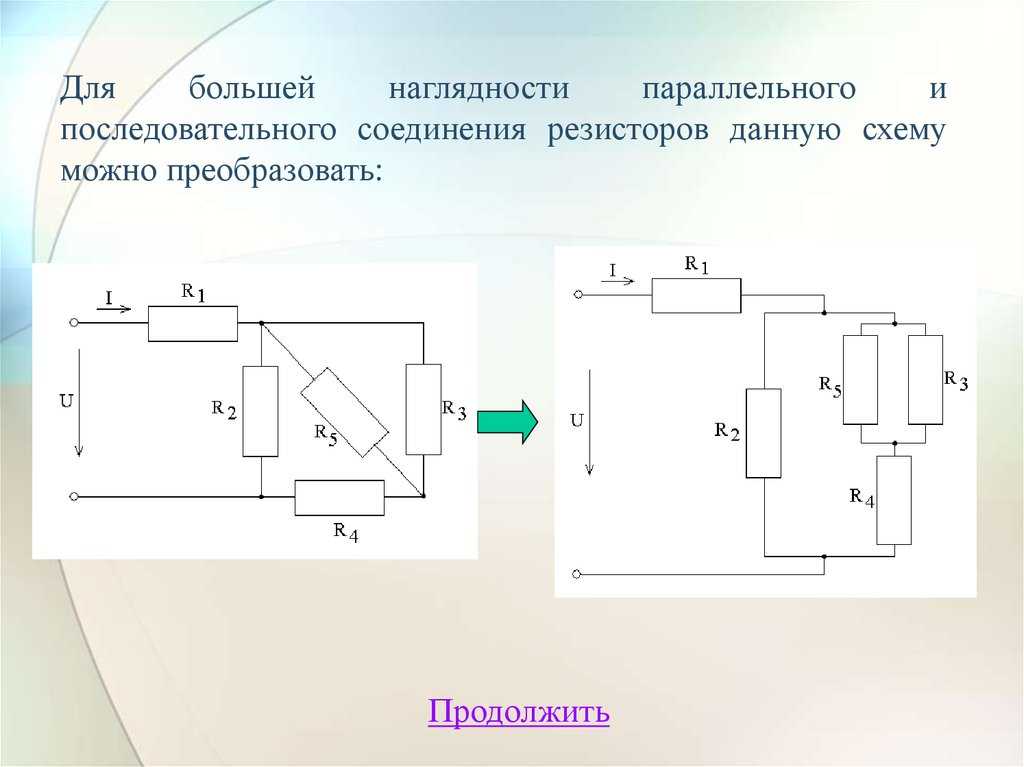 Создано множество интернет-страниц, позволяющих найти сопротивление параллельных резисторов за несколько секунд, используя в своих вычислительных алгоритмах формулы для расчёта параллельного соединения.
Создано множество интернет-страниц, позволяющих найти сопротивление параллельных резисторов за несколько секунд, используя в своих вычислительных алгоритмах формулы для расчёта параллельного соединения.
Такие калькуляторы достаточно полезны радиолюбителям-конструкторам или специалистам РЭА при возникновении затруднения с выбором нужного номинала резистора для замены его в цепи электронного устройства. Внешний вид онлайн-приложений может отличаться друг от друга, а вот принцип работы одинаков. Немаловажным является в работе программ тот факт, что алгоритмы их вычисления используют разную точность в округлении результата, поэтому ответ в некоторых программах при сравнении может немного отличаться.
Само приложение обычно представляет собой ячейки, в которые вносится величина значений резисторов в международной системе измерений.
Ответ рассчитывается в Омах. В некоторых приложениях функциональность может быть расширена, это такие возможности, как автоматический перевод значений резисторов в систему СИ, отображение наиближайшего стандартного значения сопротивления из номинального ряда, близкого к полученному ответу.
Полезной функцией может быть и обратный переход, когда вводится эквивалентное сопротивление, а в ответе выдаётся комбинация номиналов проводника для параллельного включения. Таким образом, расчёт с использованием онлайн-калькуляторов помогает решить задачу не только быстро, но и безошибочно, чем часто пользуются не только радиолюбители, но и профессионалы.
Данный калькулятор можно смело назвать одним из самых простых и эффективных. В результате вы сможете получить точно сопротивление резисторов в сети. Калькулятор для расчета параллельного сопротивления позволит безошибочно все определить, а это очень важно, так как ручной расчет считается достаточно сложным и трудоемким процессом. Наш калькулятор с легкостью поможет вам справиться со всем.
Главная Инструменты Параллельно соединенные резисторы калькулятор Содержание Параллельное соединение двух сопротивлений Параллельное соединение двух сопротивлений Назначение и определение импеданса Параллельное соединение Пример подбора замены Задача на нахождение эквивалента Последовательное включение Смешанное подключение Онлайн-расчёт на калькуляторе. Оценка статьи:. Пока оценок нет.
Оценка статьи:. Пока оценок нет.
Параллельное соединение резисторов
Расчёт сопротивления резисторов в параллельном включении. Подбор нужного значения из стандартных номиналов. Иногда проще вписать значения, чем выбирать селектором… Результат получаем кликом мыши в любом месте таблицы. Получим варианты параллельного соединения резисторов R1 и R2. Калькуляторы могут быть полезны радиолюбителям-конструкторам, а так же ремонтникам РЭА при затруднении с выбором нужных номиналов резисторов для замены их в цепях электронных устройств. Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться.
двух и более резисторов, онлайн калькулятором.
Параллельное соединение резисторов, калькулятор
Из закона Ома и первого и второго правил Кирхгофа следует:. При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей. При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей. Формулы и расчеты онлайн — Fxyz. Домой Формулы по физике Электричество Цепи постоянного тока Соединение сопротивлений Параллельное соединение сопротивлений. Добавить ячейку. Последовательное соединение сопротивлений Электрическое сопротивление, Закон Ома Мощность электрического тока Соединение сопротивлений Делитель напряжения Кило, Мега, Гига, мили, микро, нано, пико — Приставки к единицам СИ Параллельное соединение конденсаторов, Емкость параллельно соединенных конденсаторов.
При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей. Формулы и расчеты онлайн — Fxyz. Домой Формулы по физике Электричество Цепи постоянного тока Соединение сопротивлений Параллельное соединение сопротивлений. Добавить ячейку. Последовательное соединение сопротивлений Электрическое сопротивление, Закон Ома Мощность электрического тока Соединение сопротивлений Делитель напряжения Кило, Мега, Гига, мили, микро, нано, пико — Приставки к единицам СИ Параллельное соединение конденсаторов, Емкость параллельно соединенных конденсаторов.
Онлайн-калькулятор параллельного соединения резисторов
Каждый в этой жизни сталкивался с резисторами. Люди с гуманитарными профессиями, как и все, изучали в школе на уроках физики проводники электрического тока и закон Ома. С резисторами также имеют дело студенты технических университетов и инженеры различных производственных предприятий. Перед всеми этими людьми, так или иначе, вставала задача расчёта электрической цепи при различных видах соединения резисторов.
Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:.
Подарки и советы
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом. Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель. Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
калькулятор параллельного соединения резисторов онлайн
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей. При параллельном соединении полное сопротивление цепи меньше самого малого из сопротивлений ветвей. Собирая самостоятельные схемы, начинающие радиолюбители сталкиваются с необходимостью установить то или иное сопротивление, величины которого нет в стандартном ряде или на руках. Поэтому нужная величина импеданса подбирается путём параллельного или последовательного соединения элементов. Для правильного вычисления эквивалентного значения проще всего воспользоваться калькулятором для сопротивления, но можно и провести вычисления самостоятельно по несложным формулам.
Калькулятор онлайн для параллельного соединения резисторов: общие сведения, формулы расчета В каждой электрической схеме присутствует.
Расчет сопротивления параллельного соединения резисторов
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом. Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом. Несмотря на то что для резисторов предусмотрены различные номиналы , может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Параллельное соединение резисторов
ВИДЕО ПО ТЕМЕ: физика ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ПРОВОДНИКОВ 8 класс
Попробуйте удобное мобильное приложение для Android: cкачать. Вы искали калькулятор параллельного соединения резисторов онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и онлайн калькулятор параллельного соединения резисторов, не исключение.
Внимание покупателей подшипников.
Давно хотел заиметь калькулятор для расчета общей величины сопротивления при параллельном соединении резисторов. Калькулятор, который я хочу предложить вам сейчас, может считать в обе стороны, т. Данный калькулятор может работать с дробными числами, разделителем целой части числа и дробью является точка. Но и в таком виде калькулятор намного упрощает нудные расчеты-перерасчеты. Ниже вы видите скриншот калькулятора. Калькулятор можно скачать себе. Файл имеет расширение html и открывается любым браузеров.
Соединение резисторов, при котором одноименные выводы каждого из элементов собираются в одну точку, называется параллельным. При этом ко всем резисторам подводится один и тот же потенциал, но величина тока через каждый из них будет отличаться. Для составления схем или при замене резисторов в уже существующих цепях важно знать их суммарное сопротивление, как показано на рисунке:. Данный калькулятор позволяет рассчитать суммарное сопротивление параллельно соединенных резисторов с любым количеством элементов.
Параллельное соединение резисторов: расчет и формулы
В случае последовательного соединения прохождение тока осуществляется только через один проводник. Параллельное соединение резисторов предполагает распределение электрического тока среди нескольких проводников. При добавлении еще одного резистора в электрическую цепь, ток будет частично проходить через разные резисторы.
Содержание
Схемы последовательного и параллельного соединения
Если рассматривать соединение на примере громкоговорителя, то при последовательном соединении с усилителем мощности подключается только один динамик, поскольку прохождение тока осуществляется только через один проводник. Подключение второго громкоговорителя может быть выполнено разными способами.
При последовательном соединении по обоим устройствам будет протекать одинаковый ток. В этом случае общее сопротивление приборов представляет собой сумму отдельно взятых сопротивлений.
При параллельном соединении протекание тока будет происходить по двум направлениям. Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.
Здесь общее значение сопротивления в отличие от последовательного соединения, наоборот, будет уменьшаться. То есть, при параллельном соединении двух сопротивлений, их общее значение будет составлять половину каждого из них.
Если последовательное и параллельное соединение резисторов рассматривается с точки зрения радиоэлектроники, необходимо четко представлять себе, что представляет собой данный элемент и какова его роль в электронных схемах. Эта деталь является неотъемлемой частью многих устройств, благодаря такому свойству, как сопротивление электрическому току. Резисторы могут быть двух типов – постоянными и переменными, то есть подстроечными. При создании тех или иных электрических схем требуется резистор установленного номинала, которого в данный момент может не оказаться в наличии. Поэтому приходится использовать элементы с другими номинальными значениями, формула для каждого из которых подтверждает их физические свойства.
Последовательное соединение считается наиболее простым.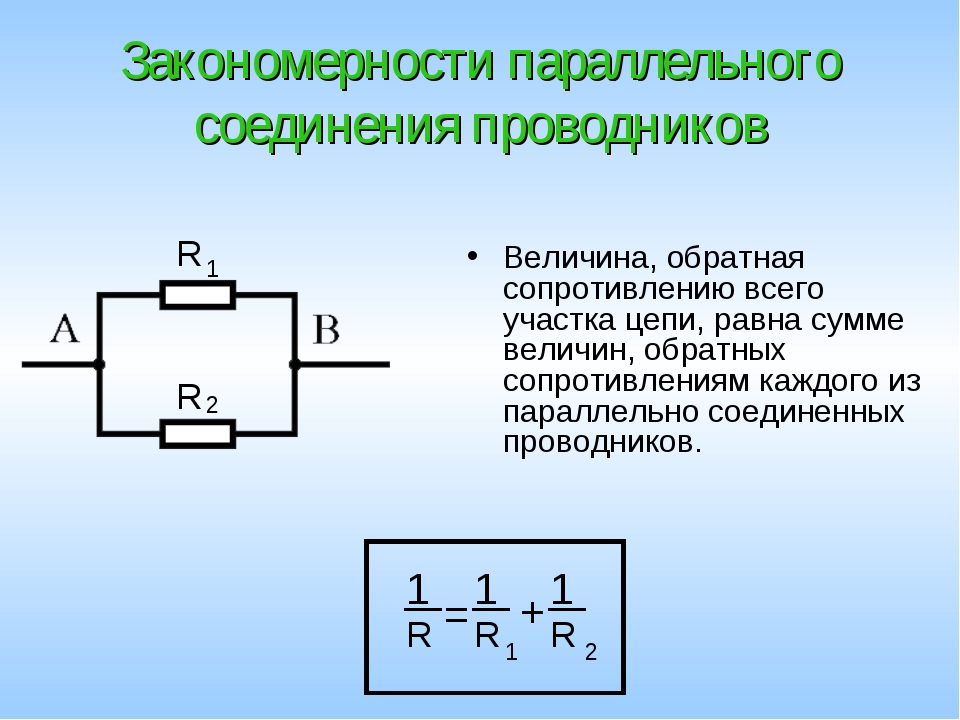 Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.
Оно используется, когда необходимо увеличить общее сопротивление электрической цепи. В этом случае все сопротивления резисторов просто складываются и дают общую сумму. При параллельном соединении, наоборот, можно снизить результирующее сопротивление или увеличить мощность за счет нескольких подключенных резисторов.
Отличие параллельного и последовательного соединения
Последовательное и параллельное соединение резисторов отличаются между собой значениями напряжения. В каждой части параллельных контуров этот показатель будет одинаковым. Однако, при одном и том же напряжении, сила тока в контурах будет разной. Кроме того, сопротивление резисторов при параллельном соединении будет существенно отличаться от того же показателя при последовательном соединении.
В процессе использования последовательной схемы наблюдаются обратные явления. Сила тока в каждом сопротивлении будет одна и та же, а напряжение на каждом участке будет отличаться. Это связано с тем, что во время протекания тока, каждый резистор частично забирает приложенное напряжение.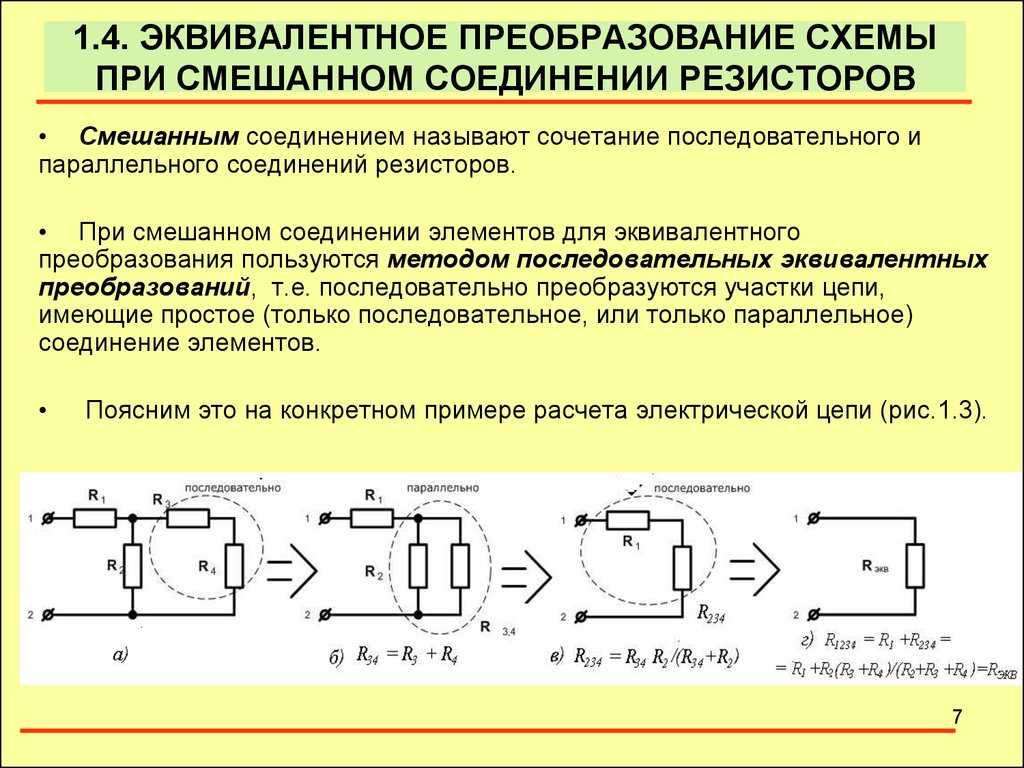 Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.
Из-за различного сопротивления резисторов, при последовательном соединении, напряжение в цепи может падать. Для того чтобы подтвердить данное явление, выполняется расчет сопротивления. Все падения напряжения в общей сумме равняются общему напряжению, которое было приложено. Для проведения вычислений используются формулы, с помощью которых можно получить наиболее точные результаты.
Таким образом, параллельное соединение резисторов, находящихся под одинаковым напряжением, не влияет на режим работы каждого из них. То есть, они совершенно не зависят друг от друга, и ток, проходящий по одному приемнику, не может существенно влиять на другие приемники.
Формула расчета параллельного соединения резисторов
Свои особенности имеет и ток при параллельном соединении резисторов. Попадая в первый узел соединения, он разделяется на столько частей, сколько имеется резисторов, подключенных параллельно. То есть, через сопротивление R1 будет протекать ток I1, а через R2 – ток I2. При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.
При попадании во второй узел, они вновь соединяются в один общий ток: I = I1 + I2.
Если какой-либо резистор вышел из строя, то остальные будут нормально функционировать. В этом заключается основное преимущество параллельного соединения. Особенно, это касается двигателей и электрических ламп, работающих от определенного номинального напряжения.
Расчет общего номинального сопротивления осуществляется с помощью формулы: R(общ)=1/(1/R1+1/R2+1/R3+1/R n), где R(общ) – является общим сопротивлением, а R1, R2, R3 и Rn – параллельно подключенными резисторами. Если выполняется параллельное соединение двух резисторов, при котором используется всего лишь два элемента, то в этом случае для расчетов используется следующая схема: R(общ)=R1хR2/R1+R2.
Очень часто в радиоэлектронике приходится пользоваться следующим правилом: если резисторы, подключенные параллельно, имеют один и тот же номинал, то итоговое сопротивление высчитывается путем деления номинала на число подключенных элементов.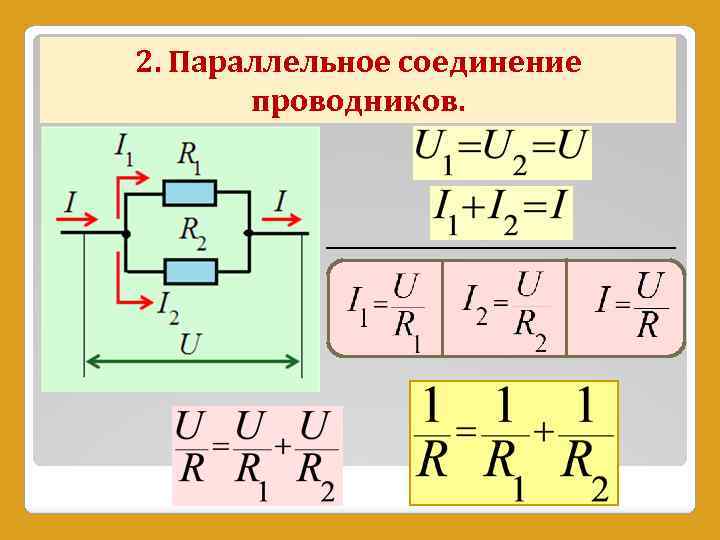 Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1\n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.
Такое параллельное соединение резисторов формула представляется следующим образом: R(общ)=R1\n, где R(общ) представляет собой сопротивление, R – номинал параллельно подключенного резистора, n – число подключенных элементов.
Для того чтобы рассчитать параллельное соединение резисторов, следует учитывать, что итоговое сопротивление всех подключенных элементов будет всегда ниже, чем сопротивление резистора с самым низким номиналом. В качестве примера можно рассмотреть схему с тремя резисторами, сопротивления которых составляют 30, 100 и 150 Ом. При использовании основной формулы будет получен следующий результат: R(общ)=1/(1/30+1/100+1/150) =1/(0,03+0,01+0,007)=1/0,047=21,28Ом. Таким образом, три резистора, соединенные параллельно, с минимальным номиналом 30 Ом, в итоге дадут общее сопротивление электрической цепи 21,28 Ом.
Онлайн калькулятор
общие сведения, формулы расчета • Мир электрики
Содержание
- Видео: Последовательное и параллельное соединение проводников
- Параллельное соединение: общая информация
- Расчет сопротивления
- Видео: Пример расчёта сопротивления
- Пример расчёта
- Важные нюансы
- Видео: Правильное подключение светодиодов
В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току.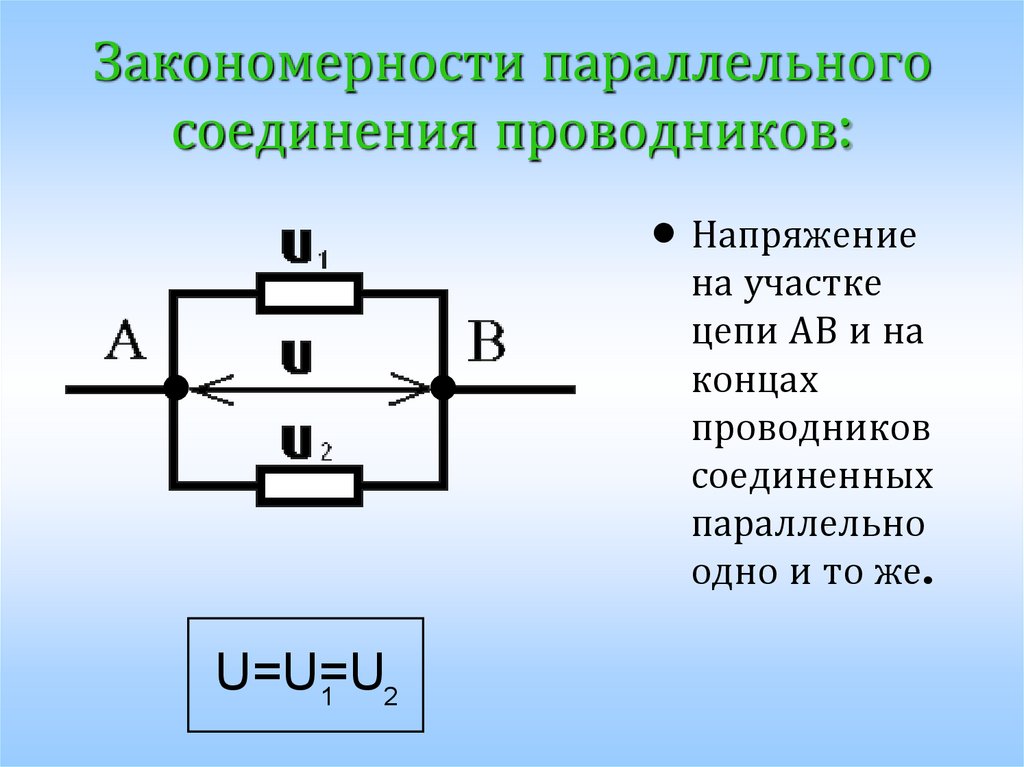 Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.
Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.
Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.
Видео: Последовательное и параллельное соединение проводников
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи.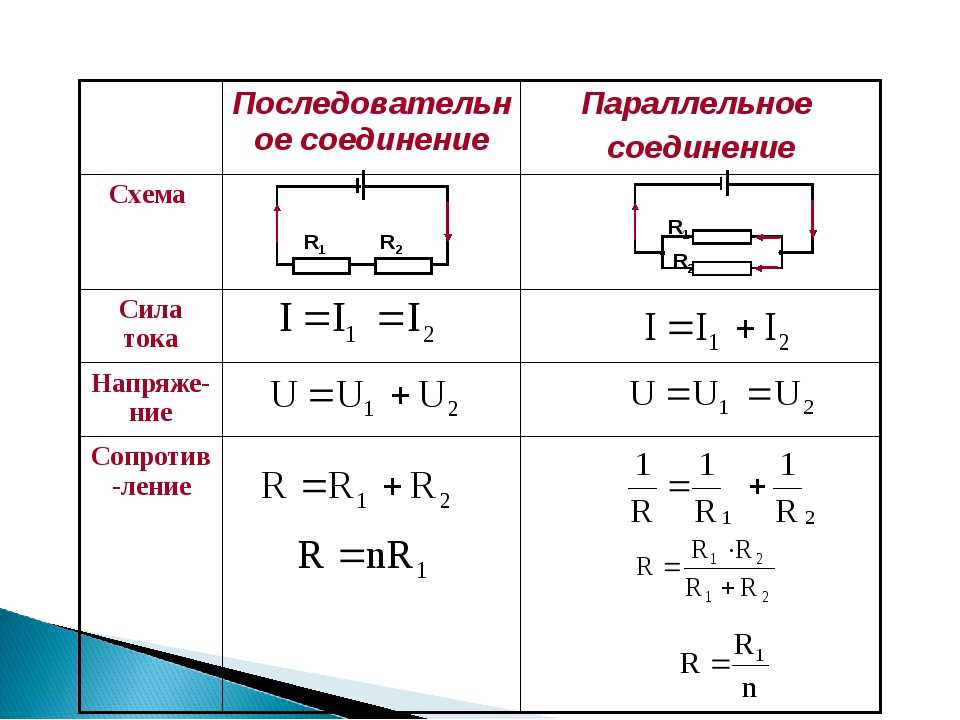 Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.
К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.
Расчет сопротивления
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:
R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).
причем :
- R(общ) – суммарное значение сопротивления;
- R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.
Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:
R(общ)=R1*R2/R1+R2.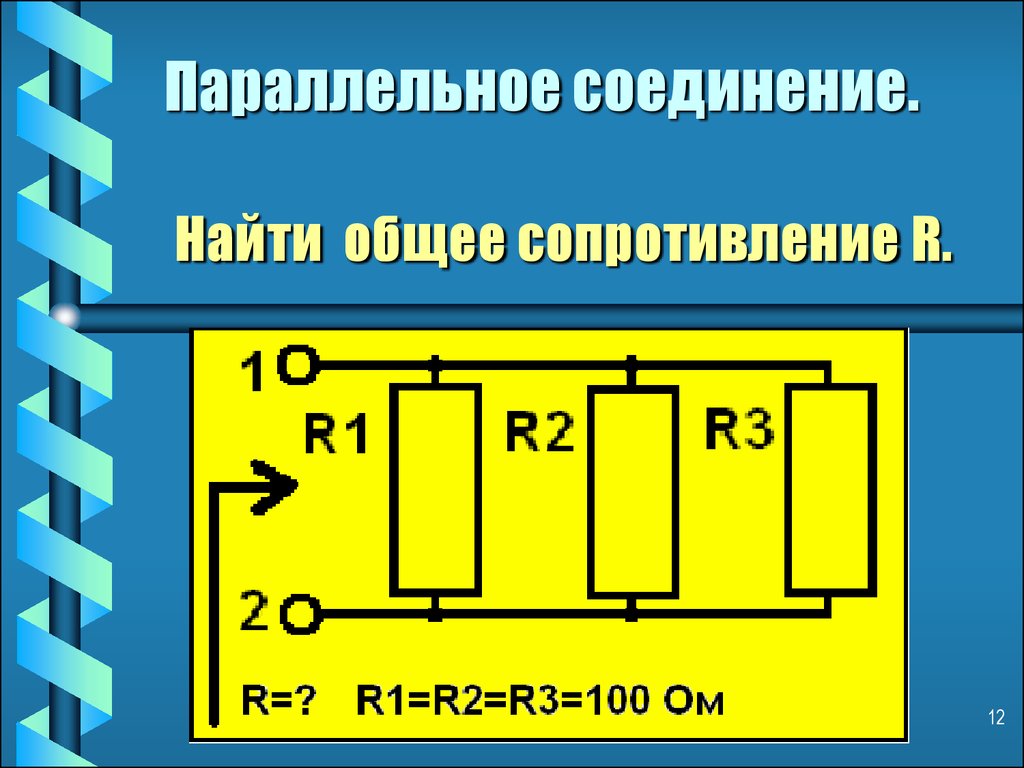
причем:
- R(общ) – суммарное сопротивление;
- R1 и R2 – резисторы, подсоединенные по параллельной схеме.
Видео: Пример расчёта сопротивления
Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:
R(общ)=R1n.
причем :
- R(общ) – суммарное значение сопротивления;
- R – номинал резистора, подсоединенного по параллельной схеме;
- n – число подключенных узлов.
Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше по сравнению с номиналом любого элемента, подключаемого в цепь.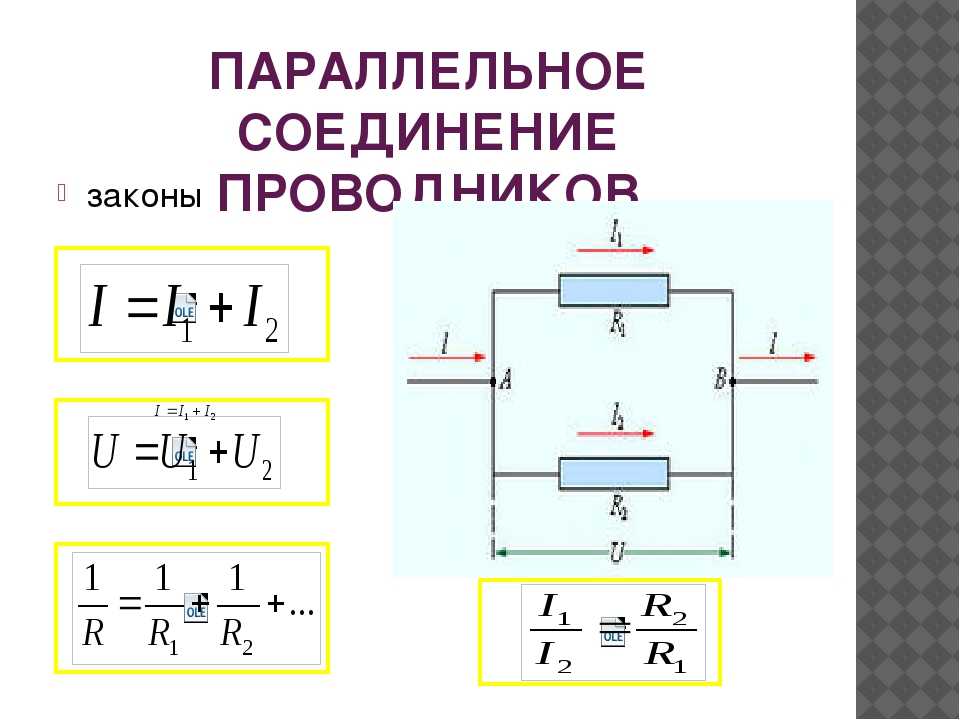
Пример расчёта
Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:
R(общ)=1/(1/100+1/150+1/30)=
1/(0,01+0,007+0,03)=1/0,047=21,28Ом.
Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.
Важные нюансы
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Последовательное и параллельное соединение проводников, резисторов,конденсаторов и катушек индуктивности. Онлайн расчёт.
«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно.
Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным
да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»
Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно
набросаю пару-тройку калькуляторов на заданную тему.
Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи
равно сумме напряжений на концах каждого из проводников.
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для
всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то
оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном
соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
А есть возможность не вводить…
Короче, все вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников
| Тип соединения |   ПараллельноеПоследовательное | |
| Сопротивление резистора R1 | ОмкОм МОм | |
| Сопротивление резистора R2 | ОмкОм МОм | |
| Сопротивление резистора R3* | ОмкОм МОм | |
| Сопротивление резистора R4* | ОмкОм МОм | |
| Общее напряжение в цепи (В)* | ||
| Общее сопротивление цепи R | ||
| Общий ток в цепи I | ||
| Напряжение на резисторе R1 (U1) | ||
| Ток через резистор R1 (I1) | ||
| Напряжение на резисторе R2 (U2) | ||
| Ток через резистор R2 (I2) | ||
| Напряжение на резисторе R3 (U3) | ||
| Ток через резистор R3 (I3) | ||
| Напряжение на резисторе R4 (U4) | ||
| Ток через резистор R4 (I4) |
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение
напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
Почему переменными?
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность,
а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную
зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и
катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения
реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников
и резисторов. А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.
А в качестве общего напряжения в цепи — подставлять действующее значение амплитуды переменного тока.
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и
параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
С = С1+ С2+….+ Сn и
1/L = 1/L1+ 1/L2 +…+ 1/Ln
для параллельных цепей и
L = L1 + L2 +….+ Ln и
1/С = 1/С1+ 1/С2+…+ 1/Сn для последовательных.
Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов
| Тип соединения |   ПараллельноеПоследовательное | |
| Ёмкость конденсатора С1 | пФнФ МкФ | |
| Ёмкость конденсатора С2 | пФнФ МкФ | |
| Ёмкость конденсатора С3* | пФнФ МкФ | |
| Ёмкость конденсатора С4* | пФнФ МкФ | |
| Общая ёмкость цепи С |
Ну и в завершении ещё одна таблица.
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек
| Тип соединения |   ПараллельноеПоследовательное | |
| Индуктивность катушки L1 | мкГнмГн Гн | |
| Индуктивность катушки L2 | мкГнмГн Гн | |
| Индуктивность катушки L3 | мкГнмГн Гн | |
| Индуктивность катушки L4 | мкГнмГн Гн | |
| Общая индуктивность цепи L |
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек,
то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание,
пересечения взаимных магнитных полей.
Соединение резисторов последовательное, параллельное, смешанное. Пример расчета
Соединение резисторов — это взаимное расположение данных элементов в цепи относительно друг друга и источника питания. Можно по отдельности выделить последовательное и параллельное соединение резисторов. Когда в схеме присутствуют оба варианта, то такое соединение называется смешанным.
Нам известно, что резистор — это электронный компонент, который обладает электрическим сопротивлением и мощностью рассеивания. Если в цепи имеется несколько резисторов, то для получения общего сопротивления прибегают к расчетам по правилам последовательного или параллельного соединения. Помимо общего сопротивления, группы резисторов по закону Ома влияют на напряжение и силу тока на участках цепи. И в данном обзоре будет доступно рассмотрена методика расчета общего сопротивления при различных видах соединения резисторов. Также будет рассмотрен наглядный пример со смешанным соединением резисторов, где помимо сопротивлений будут просчитаны напряжения и сила тока на разных участках.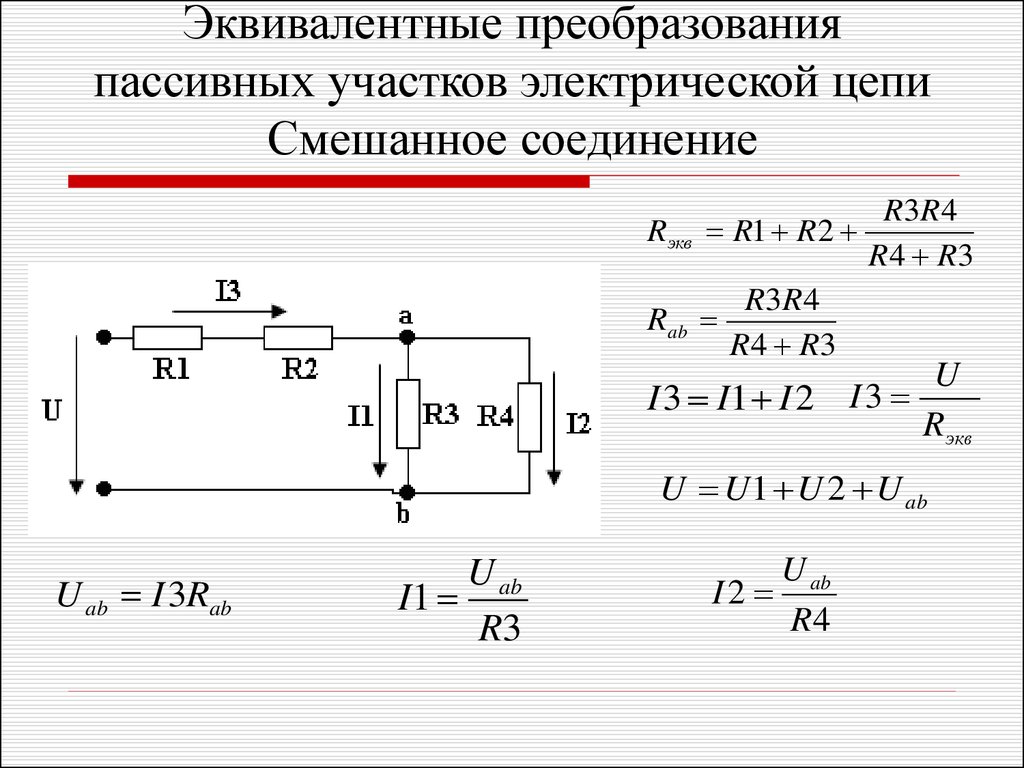
Стоит сразу отметить, что в данной теме рассеивающая мощность резисторов вынесена за скобки. Мощность важна при подборе и комбинировании резисторов в схеме, но это уже отдельная тема. К тому же все рассмотренные примеры взяты с учетом источника переменного напряжения 220 В. Почему так? Об этом вы узнаете в последнем пункте публикации.
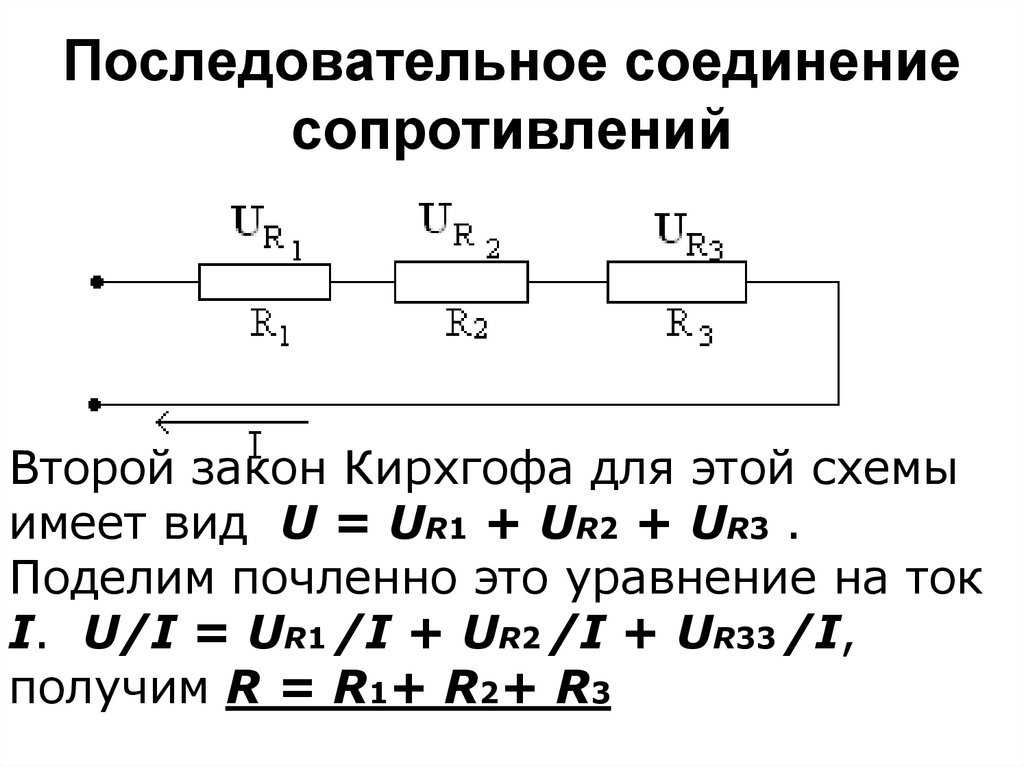
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
R = R1 + R2 + R3 + … + Rn.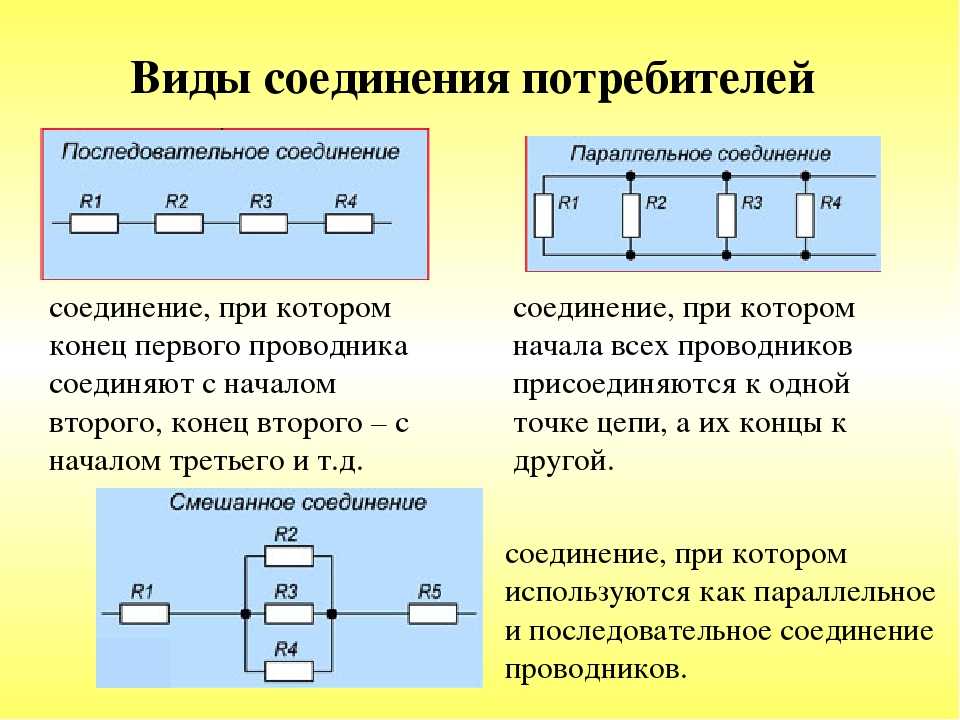
R = 20 + 70 + 10 = 100 Ом.
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
I = U / R = U / (R1 + R2 + R3 + … + Rn).
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
- U1 = I × R1.
- U2 = I × R2.
- U3 = I × R3.
- Un = I × Rn.
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).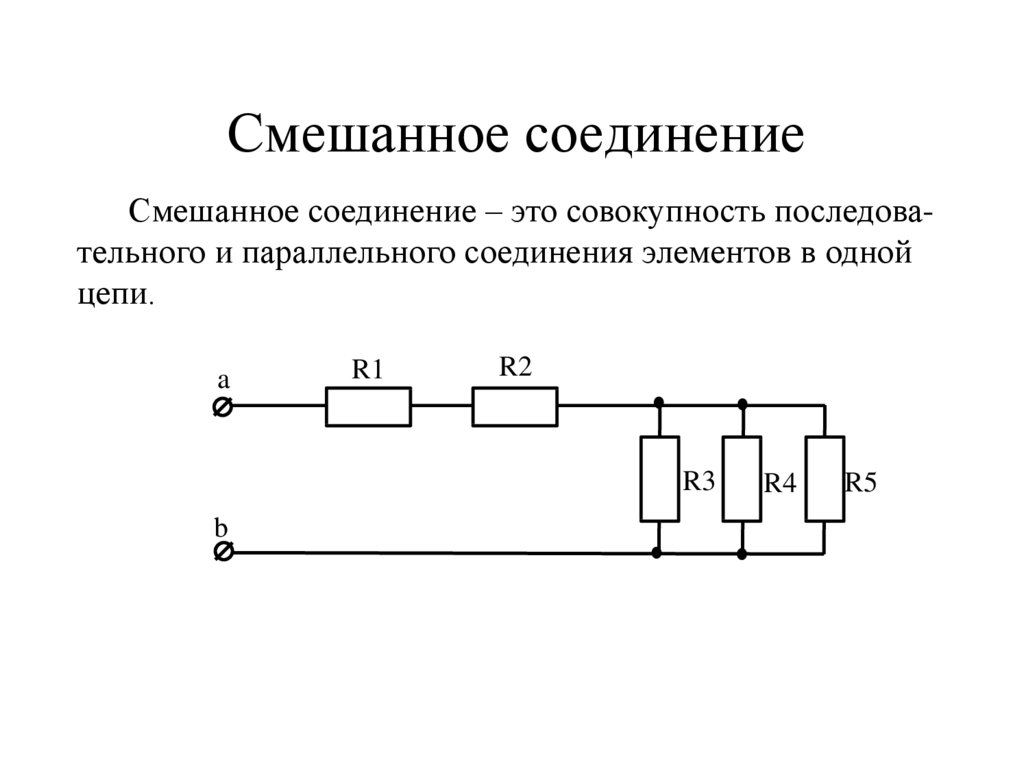
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.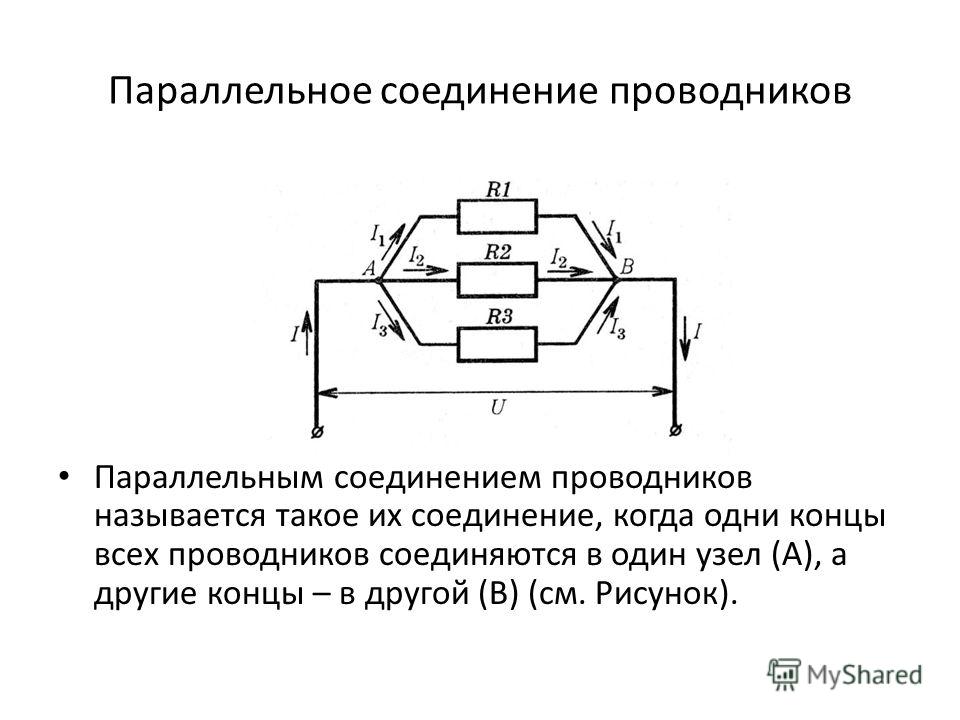
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
R ≈ 1 / 0,164 ≈ 6,097 Ом.
Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):
Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.

- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
| Определяется общее сопротивление участков с параллельным соединением резисторов. | |
| Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление. | |
После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений.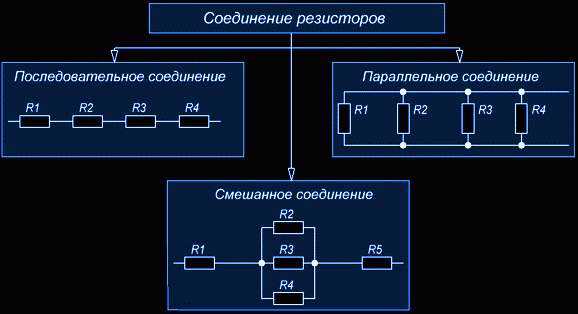 | |
| Далее рассчитывается сопротивление полученной простой схемы. |
Видео соединение резисторов
Соединение резисторов — пример расчета
В качестве примера смешанного соединения резисторов рассмотрим систему распределения электроэнергии и систему заземления в частном доме. Несмотря на то, что данная схема отношения к электронике не имеет, а в качестве резисторов выступают контуры заземления, все же принципы одни и те же. К тому же, вместо того, чтобы рассматривать произвольную цепь, намного интересней и познавательней дополнительно разобраться в вопросах электричества в быту.
На приведенной выше схеме показана система распределения электроэнергии по системе TN-C-S. Слева направо:
- Источник питания U = 220 В (распределительный трансформатор) с глухозаземленной нейтралью R1 = 2 Ом.
- Далее R2 = 4000 Ом — это имитация прикосновения человека к зануленному корпусу, находящемуся в доме с системой заземления TN-C-S.

- R3 = 30 Ом — повторное заземление в доме с системой TN-C-S.
- R4 = 4 Ом — сопротивление контура заземления (система TT) в соседнем доме.
В доме с системой заземления TT смоделирован пробой фазы на корпус при неработающей автоматике отключения питания. Поэтому потенциал через землю направился к нейтрали трансформатора по трем путям (участок параллельного соединения):
- Через заземление 30 Ом соединенное с нейтралью (рабочий нулевой проводник).
- Через землю — пол — человека — зануленный прибор (4000 Ом).
- Через заземление нейтрали трансформатора 2 Ом.
Получаем параллельное соединение резисторов — R1, R2, R3, и последовательное соединение — R4 и группа с параллельным соединением.
Прежде чем переходить к расчету в цепи со смешанным соединением резисторов, отметим, о чем данная симуляция свидетельствует. Нельзя допускать в одной системе распределения электроэнергии наличия различных систем заземления. Так, согласно приведенной модели, при пробое фазы на корпус в системе TT произошел вынос опасного потенциала 70 В на корпус прибора в соседнем доме с системой заземления TN-C-S. Выносимый потенциал будет снижаться, если в цепи с параллельным соединением будет снижаться общее сопротивление.
Выносимый потенциал будет снижаться, если в цепи с параллельным соединением будет снижаться общее сопротивление.
Рассчитаем, на сколько снизится выносимый потенциал (напряжение), если добавить в участок с параллельным соединением еще 29 домов с системой заземления TN-C-S (сопротивление повторного заземления каждого дома 30 Ом).
Согласно методике расчета в первую очередь определим общее сопротивление на участке с параллельным соединением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + 1 / R4 = 1 / 2 + 1 / 4000 + 1 / 30 + 29 / 30 = 1,5 Ом.
R = 1 / 1,5 = 0,67 Ом.
Теперь можно рассмотреть последовательное соединение с резисторами R123(+29 по 30 Ом) = 0,67 Ом и R4 = 4 Ом. R = R123(+29 по 30 Ом) + R4 = 4,67. Зная напряжение, находим силу тока:
I = U / R = 220 / (4 ,67) = 47,1 A.
Зная силу тока, найдем напряжение на участке с параллельным соединением резисторов (где общее сопротивление 0,67 Ом):
U123(+29 по 30 Ом) = R123(+29 по 30 Ом) × I = 0,67 × 47,1 = 31,5 В.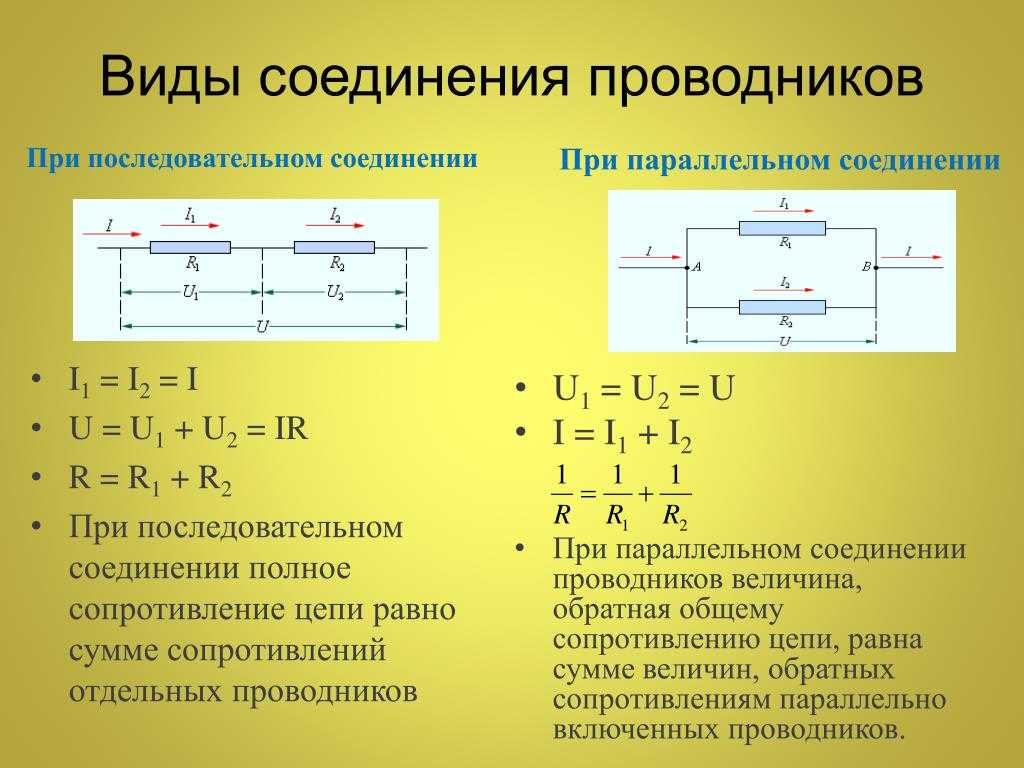
Как видно с добавлением в участок с параллельным соединением 29 дополнительных резисторов с сопротивлением каждого 30 Ом общее сопротивление и напряжение снизились. И, несмотря на то, что ток всей цепи возрос, ток проходящий через человека (R2 = 4000 Ом) значительно снизился за счет снижения напряжения участка цепи. Если посмотреть схему, то изначально через тело человека проходило 17,6 mA. После добавления 29 резисторов это значение снизилось: I2 = U123(+29 по 30 Ом) / R2 = 31,5 / 4000 = 0,0078 A = 7,8 mA.
Подведем итог. При различном соединении резисторов расчет их общих сопротивлений выполняется в соответствии с простыми формулами. И помимо изменения сопротивления в цепи, согласно закону Ома можно проанализировать также такие параметры, как сила тока и напряжение на различных участках.
Калькулятор параллельного резистора — Как решить сложные параллельные цепи
Вы чувствуете препятствие для расчета эквивалентного или отсутствующего сопротивления параллельной цепи? Перестаньте беспокоиться и начните использовать наш бесплатный калькулятор параллельных резисторов, который делает то же самое.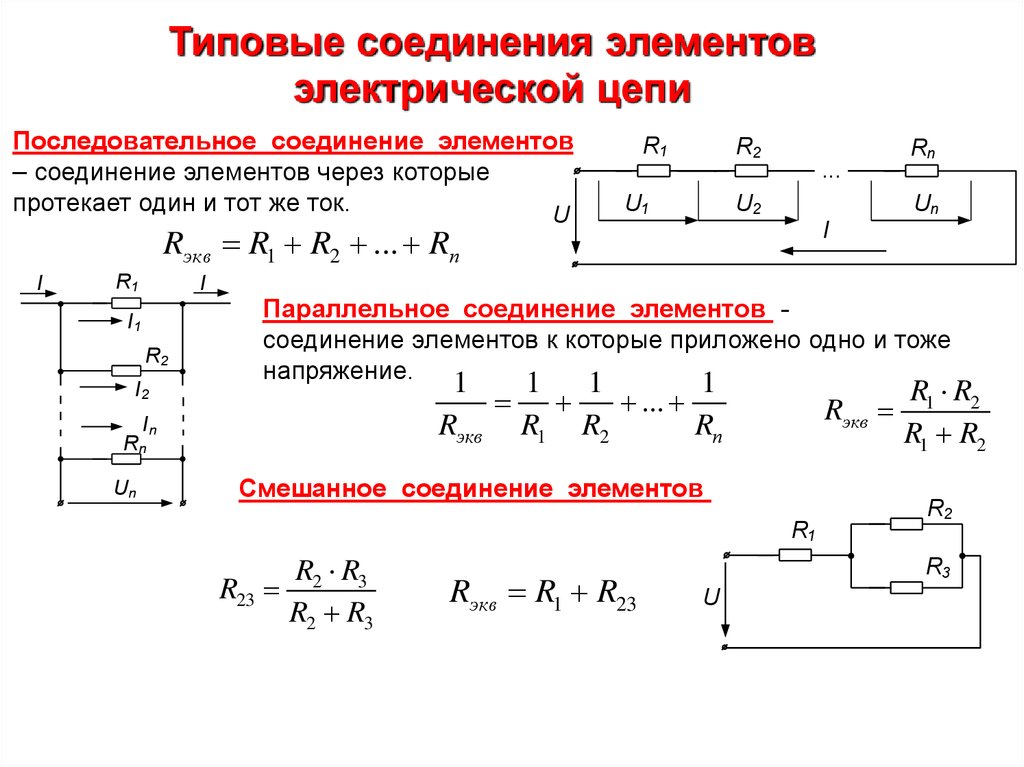 Да, вы были бы поражены тем фактом, что этот калькулятор позволит вам сравнить сопротивления в электрической цепи, чтобы вычислить общее сопротивление цепи, необходимое для ее бесперебойной работы.
Да, вы были бы поражены тем фактом, что этот калькулятор позволит вам сравнить сопротивления в электрической цепи, чтобы вычислить общее сопротивление цепи, необходимое для ее бесперебойной работы.
Переходя к делу, давайте продолжим, чтобы узнать больше о сопротивлении цепи.
Держись!
Что такое сопротивление?
«Противодействие протеканию тока внутри цепи называется сопротивлением цепи»
Обозначение:
Основной символ, используемый для обозначения резистора: обе клеммы которого подключены к одному узлу, называется параллельным сопротивлением»
В электрической сети, содержащей параллельные резисторы, ток всей цепи будет эквивалентен сумме всех токов, протекающих через каждый отдельный резистор. и когда дело доходит до вычисления его значения, бесплатный онлайн-калькулятор параллельного резистора — единственный вариант, который у вас остался.
Формула параллельного сопротивления:
В параллельной цепи каждый подключенный резистор имеет определенную разность потенциалов (падение напряжения) на своих концах. И это вызывает большое падение напряжения в каждом узле сети электронных схем. Вот почему становится очень важным вычислить, сколько потерь в нем в целом. И это можно рассчитать, только если вы используете следующие параллельные резисторы в параллельной формуле:
И это вызывает большое падение напряжения в каждом узле сети электронных схем. Вот почему становится очень важным вычислить, сколько потерь в нем в целом. И это можно рассчитать, только если вы используете следующие параллельные резисторы в параллельной формуле:
$$ R_{eq} = \frac{V}{I_{total}} = \frac{V}{(\frac{V} {R_1} + \frac{V}{R_2} + \frac{V}{R_3} + … + \frac{V}{R_n})} $$
Взяв LCM приведенного выше выражения, его можно привести к простейшей форме:
$$ R_{eq} = \frac{1}{(\frac{1}{R_1} + \frac{1}{ R_2} + \frac{1}{R_3} + … + \frac{1}{R_n})} $$
А наиболее упрощенная запись приведенного выше выражения может быть записана как:
$$ \frac{1 }{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
Калькулятор свободных параллельных резисторов также учитывает следующую формулу для расчета эквивалентного сопротивления всей электрической сети. .
Как найти сопротивление в параллельной цепи?
Чаще всего при работе со сложными электрическими сетями на ум приходит вопрос «как решить сложные параллельные схемы». Единственный ответ на эту проблему — использовать любую формулу параллельного резистора для этого онлайн-калькулятора параллельного резистора.
Единственный ответ на эту проблему — использовать любую формулу параллельного резистора для этого онлайн-калькулятора параллельного резистора.
Иллюстрация:
Посмотрите на рисунок ниже:
В этой цепи три резистора соединены параллельно, чтобы отклонить путь тока, тем самым уменьшая его потенциал. Предполагая, что к нему подключена идеальная нагрузка, как рассчитать сопротивление в параллельной цепи по заданной схеме?
Решение:
Используя формулу параллельного сопротивления:
$$ \frac{1}{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
$ $ \frac{1}{R_{eq}} = \frac{1}{10 + 2 + 1} $$
$$ \frac{1}{R_{eq}} = \frac{1}{10 } + \frac{1}{2} +\frac{1}{1} $$
$$ \frac{1}{R_{eq}} = 0,1 + 0,5 + 1 $$
$$ \frac {1}{R_{eq}} = 1,6 кОм $$
Какой идентификатор является требуемым ответом, а также может быть проверен с помощью этого калькулятора параллельного сопротивления.
Иллюстрация № 02:
Как найти полное сопротивление в параллельной цепи, в которой следующие резисторы соединены параллельно?
- 25 кОм
- 52 кОм
- 785 кОм
- 65 кОм
Решение:
Используя резисторы в параллельной формуле:
$$ \frac{1}{R_{eq}} = \frac{1}{R_1 + R_2 + R_3 + … + R_n} $$
$$ \frac{1}{R_{eq}} = \frac{1}{25 + 52 + 785 + 65} $$
$$ \frac{1}{R_{eq}} = \frac{1}{927} $$
$$ \frac{1}{R_{eq}} = 0,001 кОм $$
Как параллельно Калькулятор резисторов работает?
Вам просто нужно выполнить следующие шаги, чтобы рассчитать эквивалентное сопротивление параллельной цепи с помощью нашего онлайн-калькулятора резисторов в параллельной цепи:
Ввод:
- В первом раскрывающемся списке выберите сопротивление, которое вы хотите найти
При выборе эквивалентного сопротивления:
- Добавьте значения сопротивлений в соответствующие поля.
 Вы также можете добавить до 30 сопротивлений
Вы также можете добавить до 30 сопротивлений - После того, как вы закончите, нажмите кнопку расчета
Если выбрать «Отсутствует сопротивление»:
- Введите значение желаемого общего сопротивления и количество сопротивлений, подключенных к цепи
- Теперь нажмите кнопку расчета
Вывод:
Калькулятор параллельных цепей за несколько секунд выполняет следующие вычисления:
- Расчет эквивалентного и недостающего сопротивления в параллельной цепи
Часто задаваемые вопросы:
Что происходит при параллельном подключении резистора?
Добавление дополнительных резисторов в электрическую сеть открывает новые пути для прохождения токов. Вот почему добавление резисторов прямо пропорционально увеличению потока заряда.
Как узнать, параллельны ли два резистора?
Два сопротивления будут считаться соединенными параллельно, если узлы на обоих концах резисторов одинаковы.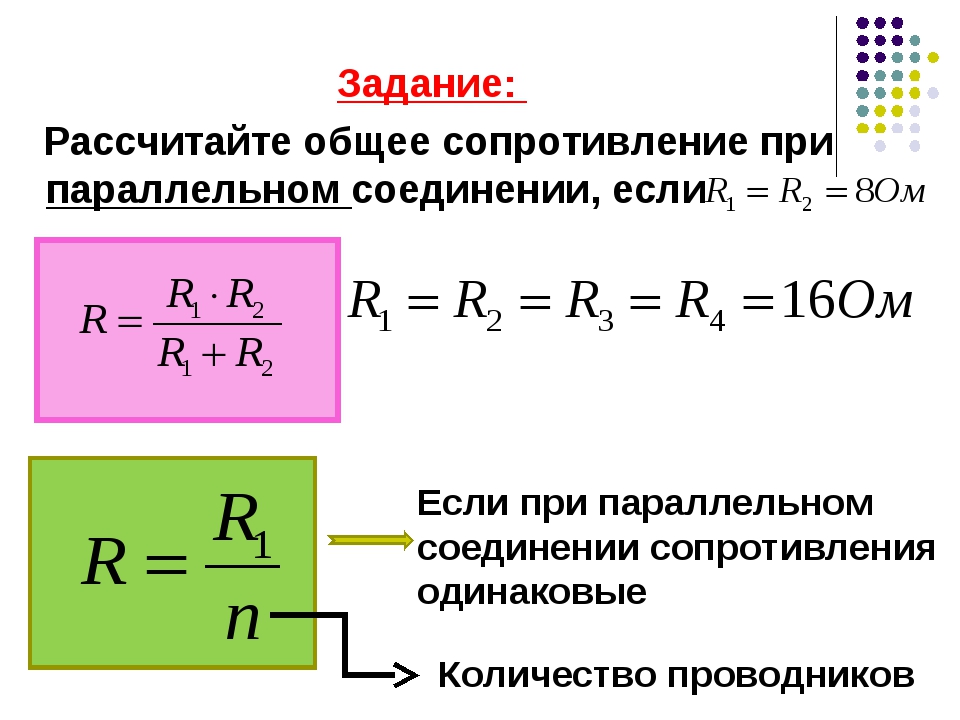 В этом случае сопротивления R_1 и R_2 будут параллельны, так что (R_1||R_2) . А если есть еще общее сопротивление R_3 , то оно будет последовательно с параллельным соединением этих двух резисторов.
В этом случае сопротивления R_1 и R_2 будут параллельны, так что (R_1||R_2) . А если есть еще общее сопротивление R_3 , то оно будет последовательно с параллельным соединением этих двух резисторов.
Параллельное напряжение одинаковое?
Да, при параллельной схеме общее напряжение сети всегда одинаково. Вы можете лучше понять соотношение между напряжением и током любой цепи или отдельного проводника, используя калькулятор закона Ома.
Что такое закон сопротивления?
Закон сопротивления гласит:
«Сопротивление проводника прямо пропорционально длине проводника при сохранении постоянной температуры и физического состояния».
Что называется проводимостью?
Электропроводность — это особое свойство материалов, таких как металлы или неметаллы, благодаря которому электрический ток протекает по электрической сети. Обозначается символом G.
Почему мы предпочитаем параллельное подключение дома?
Параллельные соединения позволяют подавать ток без каких-либо помех для работающих приборов.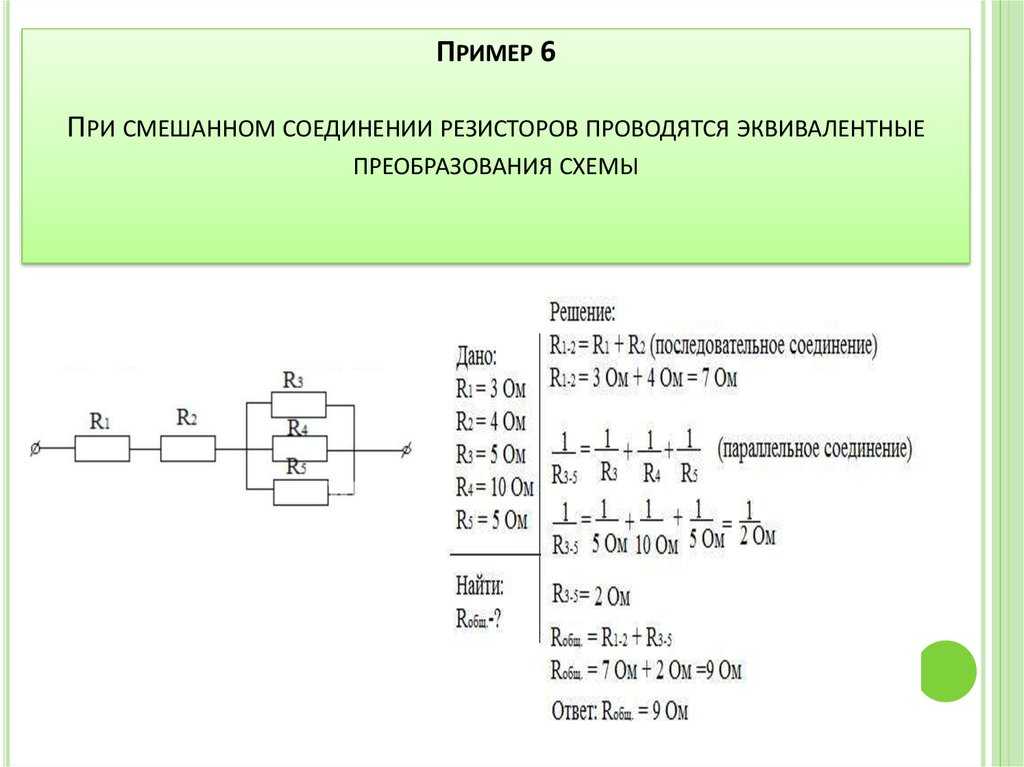 А по закону Джоуля, когда теплопотерь не будет, шансы короткого замыкания минимальны. Это позволяет им работать без возгорания.
А по закону Джоуля, когда теплопотерь не будет, шансы короткого замыкания минимальны. Это позволяет им работать без возгорания.
Вывод:
Параллельные сопротивления допускают напряжение в электрических сетях при одинаковом потенциале. И именно поэтому это конкретное соединение в цепи предохраняет устройства от возгорания.
Каталожные номера:
Из источника Википедии: Последовательные и параллельные цепи, Параллельные цепи, Объединение проводимостей, Обозначения, Приложения
Из источника Академии Хана: Резисторы последовательно и параллельно, Резисторные сети, Резисторная схема с двумя батареями
Из источника изучения люменов: Резисторы последовательно и параллельно, Комбинации последовательно и параллельно, Практические последствия
Калькулятор параллельных резисторов — [100% бесплатно]
Вычисление эквивалентного сопротивления или REQ параллельных резисторов вручную может быть довольно утомительным. К счастью, этот калькулятор параллельных резисторов может помочь вам в расчетах независимо от того, сколько резисторов у вас подключено параллельно. Вы также можете выполнить расчеты вручную, а затем использовать калькулятор параллельных цепей, чтобы проверить свой ответ.
Вы также можете выполнить расчеты вручную, а затем использовать калькулятор параллельных цепей, чтобы проверить свой ответ.
Загрузка калькулятора…
Содержание
Как пользоваться калькулятором параллельных резисторов?
Какими бы пугающими ни казались расчеты параллельных резисторов, использование этого калькулятора параллельных резисторов дает полную противоположность. Этот онлайн-инструмент очень прост в использовании и понимании. Вот шаги, которые необходимо выполнить для использования этого калькулятора эквивалентного сопротивления или калькулятора параллельного сопротивления:
- Сначала введите значение резистора 1.
- Затем введите значения резистора 2, резистора 3, резистора 4 и резистора 5.
- После ввода всех необходимых значений калькулятор параллельных цепей автоматически сгенерирует нужный вам результат. Поскольку единицей измерения всех номиналов резисторов является Ω, окончательный результат также имеет ту же единицу измерения.

Что такое параллельный резистор?
Когда вы соединяете обе клеммы резисторов вместе параллельно, это означает, что вы соответственно соединили каждую из клемм с другим резистором или резисторами. В отличие от других схем, вы также можете классифицировать схему с параллельными резисторами как делитель тока.
Это связано с тем, что параллельные цепи резисторов могут иметь более одного пути, поскольку они имеют несколько путей для прохождения тока. Поскольку этот тип цепи обеспечивает несколько путей для протекания источника тока, сила тока может быть неодинаковой во всех ответвлениях или путях.
Но падение напряжения на всех резисторах в параллельной цепи остается одинаковым. Это означает, что параллельные резисторы имеют общее напряжение, и этот факт относится ко всем элементам, соединенным параллельно.
По определению, параллельная резистивная цепь — это цепь, в которой резисторы соединены параллельно или имеют общие узлы или точки соединения. Кроме того, этот тип схемы имеет более одного пути, подключенного к одному источнику напряжения.
Кроме того, этот тип схемы имеет более одного пути, подключенного к одному источнику напряжения.
Как рассчитать сопротивление в параллельной цепи?
Основным признаком, характеризующим параллельную цепь, является общее напряжение или разность потенциалов на концах всех резисторов. Даже не используя калькулятор эквивалентного сопротивления, вы можете рассчитать эквивалентное сопротивление для этого типа цепи по этой формуле:
1/r = 1/R1 + 1/R2 +… + 1/RN
Где:
R относится к эквивалентному параллельному сопротивлению
R1, R2,… RN. относится к сопротивлениям отдельных резисторов с номерами 1…n .
Единицей измерения всех этих значений является Ом или Ом . По определению, один Ом — это электрическое сопротивление между двумя заданными точками. При подаче на эти точки разности потенциалов в 1 вольт возникает ток силой 1 ампер. Следовательно: 92) в базовых единицах СИ
Следовательно: 92) в базовых единицах СИ
Вот несколько шагов для расчета параллельного сопротивления без использования калькулятора параллельного сопротивления:
- Сначала определите значения сопротивления всех параллельно соединенных резисторов. Например, пусть у нас есть три номинала резисторов: 4 Ом , 3 Ом и 6 Ом .
- Подставьте эти значения в приведенную выше формулу:
1/R = 1/4 + 1/3 +1/6
поэтому , 1/R = 0,75, а R = 1,33
- Чтобы проверить правильность ответа, введите значения в параллель калькулятор резисторов.
Как рассчитать сопротивление?
Прежде чем вы сможете выполнить расчет, вы должны иметь хорошее представление о параллельных цепях. Помните, что такая схема делится на несколько путей, а затем снова объединяется. Кроме того, имейте в виду, что ток протекает через каждый из отдельных путей цепи.
Кроме того, имейте в виду, что ток протекает через каждый из отдельных путей цепи.
Если основная ветвь цепи снабжена резисторами или если одна ветвь имеет более одного резистора, следует выполнить другой расчет. Решите общее сопротивление, используя значение сопротивления каждой из ветвей. Каждый из резисторов замедляет ток, проходящий через одну ветвь.
Но резисторы не так сильно влияют на общее сопротивление цепи. Следовательно, вы должны использовать формулу полного сопротивления:
1/RT = 1/R1 + 1/R2 + 1/R3 + 1/R4 … 1/Rn
где:
1-я ветвь сопротивления 70 R1 R2 относится к сопротивлению 2-й ветви
R3 относится к сопротивлению 3-й ветви
R4 относится к сопротивлению 4-й ветви
и так далее, пока не дойдете до конечной ветви Rn .
Это самый простой способ расчета сопротивления.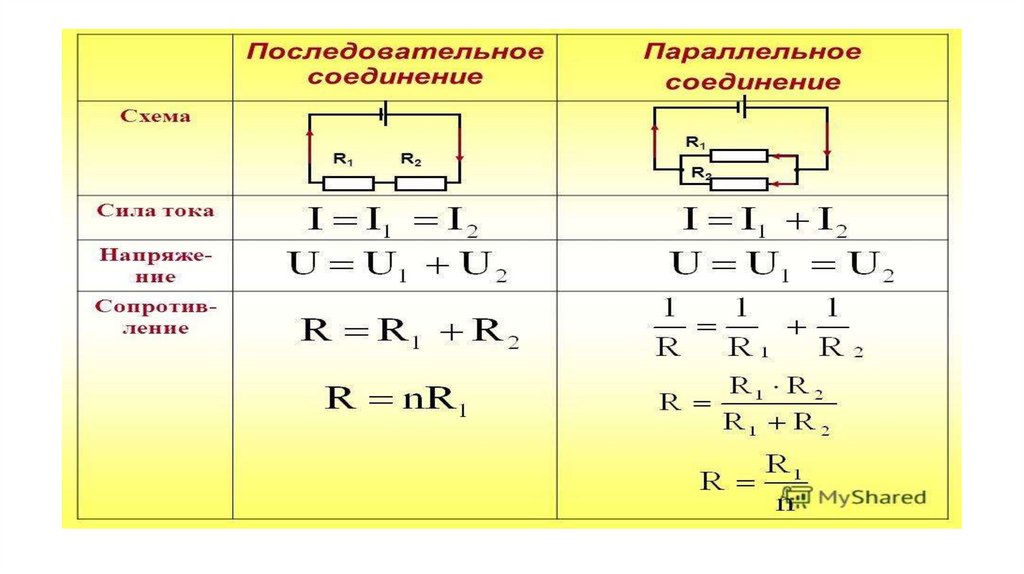 Но в некоторых случаях у вас может не быть значений отдельных сопротивлений. В таком случае вам нужно вместо этого использовать напряжение и ток. Вот шаги, которые необходимо выполнить:
Но в некоторых случаях у вас может не быть значений отдельных сопротивлений. В таком случае вам нужно вместо этого использовать напряжение и ток. Вот шаги, которые необходимо выполнить:
- В параллельных цепях напряжение на одной ветви имеет то же значение, что и общее напряжение, протекающее по всей цепи. Если известно значение напряжения одной из ветвей, можно выполнить расчет.
- Вы также можете найти значение общего напряжения, поскольку оно равно источнику питания схемы, например, батареи. В параллельных цепях токи отличаются от одной ветви к другой. Вы должны знать значение полного тока. Без него нельзя рассчитать полное сопротивление.
- Как только у вас есть общее напряжение и ток, вы можете вычислить общее сопротивление по закону Ома:
R = V / I. сопротивление. Если параллельная цепь имеет одну такую ветвь, то весь ток протекает через эту ветвь и сопротивление становится равным нулю.
Почему при параллельном эквивалентном сопротивлении меньше?
Продолжая добавлять резисторы в параллельную цепь, это уменьшает эквивалентное сопротивление всей цепи. Однако это также увеличивает общий ток цепи. Это происходит потому, что параллельное добавление резисторов обеспечивает в цепях больше путей для протекания тока.
Серияи параллельные резисторы
Google Ads
- Изучив этот раздел, вы сможете:
- Расчет значений полного сопротивления в сетях с последовательным сопротивлением.
- Используйте соответствующие формулы для расчета сопротивления в сетях с параллельным сопротивлением.
- • Обратное значение суммы обратных чисел.
- • Произведение сверх суммы.
- Расчет значений общего сопротивления в последовательно/параллельно соединенных сетях.
Расчеты в последовательном и параллельном соединении резисторов
Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:
ПОСЛЕДОВАТЕЛЬНО, так что через все компоненты протекает одинаковый ток, но разность потенциалов (напряжение) различна.
может существовать в каждом из них.
ПАРАЛЛЕЛЬНО, так что на всех компонентах существует одинаковая разность потенциалов (напряжение), но каждый компонент может проводить разный ток.
Рис. 4.2.1 Резисторы, включенные последовательно
Рис. 4.2.2 Резисторы, соединенные параллельно
В любом случае (для резисторов) общее сопротивление части цепи, содержащей резисторы, может быть рассчитано с использованием методов, описанных ниже. .
Способность таким образом вычислять комбинированное (общее) значение резисторов позволяет легко определять неизвестные значения сопротивления, тока и напряжения для довольно сложных цепей с использованием относительно простых методов. Это очень полезно при поиске неисправностей.
ПРЕЖДЕ ЧЕМ ПРОДОЛЖАТЬ ПРОДОЛЖЕНИЕ, ПОПРАКТИЧЕСКИ ИСПОЛЬЗУЙТЕ ФОРМУЛЫ ДЛЯ РАСЧЕТА СУММАРНЫХ ЗНАЧЕНИЙ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.
Для резисторов, соединенных последовательно:
Общее сопротивление двух или более резисторов, соединенных последовательно , определяется простым сложением значений отдельных резисторов, чтобы найти общую сумму (R TOT ):
Для резисторов параллельно:
Для расчета общего сопротивления цепи с параллельными резисторами можно использовать следующую формулу.
Однако обратите внимание, что эта формула НЕ дает вам общее сопротивление R TOT . Это дает вам ОБРАТНУЮ величину R TOT или:
Это совсем другое значение — и НЕ полное сопротивление. Это 1, деленное на R TOT . Чтобы получить правильное значение для R TOT (которое будет обратным 1/R TOT , т. е. R TOT /1, просто нажмите кнопку обратного вычисления на вашем калькуляторе (обозначена 1/x или x-1)
Другой способ расчета параллельных цепей.
Общее сопротивление двух резисторов, включенных параллельно , без учета обратных величин, определяется по формуле:
Эту формулу часто называют «произведением на сумму».
Он рассчитывает только ДВА резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и вычислите общее сопротивление для этих двух, а затем используйте это общее сопротивление, как если бы это был один резистор, и сделайте еще одну пару с третьим резистором.
Вычислите новую сумму и так далее, пока не включите все параллельные резисторы в эту конкретную сеть.
О, еще кое-что, что нужно помнить о произведении на сумму, видите скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это ДО того, как будете использовать его для деления продукта (верхней части) на . Если вы этого не сделаете, ваш ответ будет неправильным.
Звучит сложно? На самом деле нет, это просто вопрос повторения, и на практике вы не часто сталкиваетесь с множеством параллельных сетей с гораздо большим количеством резисторов, чем с двумя. Тем не менее, какую формулу вы выберете, зависит от вас, обратные или произведение на сумму.
Советы
Использование метода обратной величины
Если вы используете МЕТОД обратной величины для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы сложите обратные величины отдельных резисторов — вы должны снова найти обратную величину.1/R1+1/R2 +1/R3 = 1/R TOT , и чтобы найти R TOT , вы должны найти обратную величину 1/R TOT .
Упрощение цепей
Для комбинированных последовательных и параллельных цепей сначала разработайте участок цепи (последовательный или параллельный). Затем перерисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, в которой нужно найти R ТОТ .
Вы можете использовать формулу «произведение на сумму»:
Для цепей с более чем двумя параллельными резисторами просто определите два параллельных резистора, используя формулу произведения на сумму, а затем перерисуйте схему, заменив два резисторы с одним резистором, значение которого является комбинированным сопротивлением двух.
Теперь вы можете использовать первое комбинированное значение в качестве одного резистора со следующим параллельным резистором и так далее. Таким образом, можно вычислить большое количество параллельных резисторов, используя произведение на сумму.
Когда все параллельные резисторы имеют одинаковое значение.
Если несколько одинаковых параллельных резисторов подключены, общее сопротивление будет равно значению резистора, умноженному на обратную величину количества резисторов.
т. е. два резистора 12 кОм, соединенные параллельно, имеют суммарное сопротивление
12 кОм x 1/2 = 6 кОм
Три резистора по 12 кОм, соединенные параллельно, имеют суммарное сопротивление
12 кОм x 1/3 = 0 кОм 9002 и т. д.
Рисунок 2. Три резистора, соединенные последовательно с батареей (слева) и эквивалентное одиночное или последовательное сопротивление (справа).Проверка вашего ответа
Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.
Комбинированное последовательное и параллельное соединение
Попробуйте выполнить несколько расчетов, основанных на последовательном и параллельном соединении резисторов. Для этого вам просто нужно использовать информацию на этой странице и на странице «Советы по расчету резисторов». Вас просят определить общее сопротивление для каждой цепи.
Вы можете выбрать, какую формулу использовать
Вы также можете получить помощь по математике, загрузив нашу бесплатную брошюру «Советы по математике».
Прежде чем начать, подумайте об этих нескольких советах. Они облегчат проблемы, если вы будете внимательно следовать им.
1. Подготовьте ответы с помощью карандаша и бумаги; перерисуйте схему, над которой вы работаете.
2. Конечно, ответом будет не просто число, это будет определенное количество Ом, не забудьте указать правильную единицу измерения (например, Ом, кОм или МОм), иначе ваш ответ не имеет смысла.
3. При вводе значений в калькулятор конвертируйте все значения кОм или МОм в омы с помощью клавиши EXP. Если вы ошибетесь здесь, это даст действительно глупые ответы, в тысячи раз большие или слишком маленькие.
Итак, вы прочитали эти инструкции и готовы приступить к работе. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.
Пример последовательной и параллельной цепи.
Хорошо, здесь есть что вспомнить, так почему бы не попробовать несколько практических вопросов в модуле «Резисторы 4.5» по нахождению общего сопротивления некоторых резисторных цепей?
Google Реклама
Калькулятор параллельных резисторов
- Анкета
- Сохранить
Цепи последовательных и параллельных резисторов являются частью стандартного научного исследования. Проблемы обычно требуют, чтобы вы рассчитали общее сопротивление цепи или запросили эквивалентное сопротивление, используя наилучшую комбинацию резисторов.
Наш Калькулятор параллельных резисторов поможет вам найти общее эквивалентное сопротивление в параллельной цепи или ряду резисторов. Просто введите сопротивления, разделенные запятыми, чтобы получить результат.
Для тех, кто только учится, мы подготовили исчерпывающие вопросы и ответы для нашего калькулятора параллельного сопротивления. Мы охватываем основы резисторов, расчет сопротивления и многое другое.
ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ
Что может вычислитель параллельного резистора?
В электронных схемах резисторы имеют множество применений. Они используются для уменьшения тока, регулировки уровней сигнала и завершения линий передачи. Есть много других применений.
Любое электрическое устройство сегодня может иметь сотни цепей. Вычисление мощности, силы тока, сопротивления и напряжения вручную утомительно и подвержено ошибкам.
Наш параллельный калькулятор резисторов устраняет ошибки в транскрипции и помогает вам проверить свои ответы. Это даст вам эквивалентное сопротивление для резисторов, соединенных параллельно или последовательно.
Мы надеемся, что это краткое объяснение и наш калькулятор будут вам полезны. Сохраните эту страницу на главном экране вашего смартфона, чтобы получить быстрый и легкий доступ к этому замечательному инструменту.
Что такое параллельные и последовательные резисторы?
Прежде чем погрузиться в изучение, важно сначала понять, что такое отдельный резистор.
Это двухконтактный электрический компонент.
Это часть цепи, реализующая электрическое сопротивление. Он потребляет, но не производит энергию.
Параллельные резисторы создаются, когда цепь разделяет два пути тока (или более) к общему источнику питания. Например, четыре резистора, соединенные параллельно с батареей:
Ток течет к резисторам R1, R2, R3 и R4 от положительной клеммы батареи. Узел, который соединяет R1 с батареей, также соединяет R2, R3 и R4. Другие концы этих резисторов подключаются аналогичным образом, а затем подключаются к отрицательному полюсу батареи.
Существует четыре уникальных пути, по которым может пройти ток, прежде чем он вернется в батарею. Резисторы считаются параллельными. Все параллельные компоненты имеют одинаковое падение напряжения, ток между резисторами может быть разным.
Характеристики резисторов, соединенных параллельно:
- Параллельная цепь имеет два или более пути прохождения тока
- Падение напряжения одинаково на каждом компоненте параллельной цепи
- Общий ток равен сумме каждого пути тока
- Если один из путей в параллельной цепи разорван, ток продолжает течь по оставшимся путям
Это отличается от последовательной цепи.
Характеристики резисторов в последовательной цепи:
- В последовательной цепи есть один путь для протекания тока
- Если цепь разорвана в какой-либо точке, ток не течет
- Общее сопротивление последовательной цепи равно сумма индивидуальных сопротивлений. Всего R = R1 + R2 + R3…
- Напряжение, подаваемое на последовательную цепь, равно сумме отдельных падений напряжения
Какова формула для резисторов в параллельной цепи?
Формула полного сопротивления в параллельной цепи рассчитывается следующим образом:
1/Rt = 1/R1 + 1/R2 + 1/R3 +…
Rt = Rобщ.
Пример
Рассчитаем сопротивление параллельной цепи с тремя дорожками (это может быть любое число больше двух). Источник питания обеспечивает 9вольт и номинал резисторов 4 Ом, 4 Ом и 2 Ом.
- E = 9 В
- R1 = 4 Ом
- R2 = 4 Ом
- R3 = 2 Ом
Уравнение
Решите:
1/Rt = 1/4 + 1/4 + 1/2
1/Rt = 1
Rt = 1 Ом
Какие другие задачи может решить параллельное сопротивление?
Зная общее сопротивление цепи, можно рассчитать силу тока с помощью Закон Ома .
Возвращаясь к приведенному выше примеру, вы можете использовать закон Ома, чтобы вычислить общую силу тока (I):
I = напряжение / сопротивление
I = 9 В / 1 Ом
= 9 ампер
Суммарная сила тока между тремя ответвления резисторов должны быть равны 9 Ампер. Чтобы выяснить, что тянет каждая ветвь, снова используйте закон Ома.
Напоминание: напряжение везде одинаково в параллельной цепи. Итак, мы знаем напряжение и сопротивление:
I1 = 9V / 2 Ом = 4,5 А
I2 = 9 В / 4 Ом = 2,25 А
I3 = 9 В / 4 Ом = 2,25 А
Чтобы перепроверить свой ответ, возьмите сумму I выше и подставьте свои цифры.
It = I1 + I2 + I3…
9 Ампер = 4,5 А + 2,25 А + 2,25 А эти переменные.
P = I (ток) * E (напряжение)
P = E2 / R (сопротивление)
P = I2 * R
P (всего) = P1 + P2 + P3 …
Конечно, используйте второе уравнение или онлайн-калькулятор, чтобы проверить свои ответы.
Расскажите о нас своим друзьям!
Series and Parallel — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
AP Physics 1 Справка » Электричество и волны » Электричество » Схемы » Серия и параллель
Цепь имеет резистор с сопротивлением , за которым следуют три параллельных ответвления, каждое из которых содержит резистор с сопротивлением .
Чему равно полное эквивалентное сопротивление цепи?
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, нам нужно рассчитать эквивалентное сопротивление трех параллельно соединенных резисторов. Для этого воспользуемся следующим уравнением:
Теперь, чтобы получить общее эквивалентное сопротивление, мы можем просто сложить два оставшихся значения, так как они идут последовательно:
Сообщить об ошибке приложено к точкам A и B так, что ток течет от A к R2, а затем к B. Каково значение этого напряжения, если ток через R2 равен 4A?
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, нам нужно рассчитать ток, протекающий через резистор R2 без дополнительного напряжения.
Нам нужно будет рассчитать полное эквивалентное сопротивление цепи. Поскольку два резистора включены последовательно, мы можем просто добавить их.
Затем мы можем использовать закон Ома для расчета тока в цепи:
Теперь, когда у нас есть ток, мы можем рассчитать дополнительный ток, который вносит новое напряжение:
На пути нового напряжения есть только один резистор (R2), поэтому мы можем рассчитать, каким должно быть это напряжение для подачи нового тока:
Сообщить об ошибке
Каково эффективное сопротивление этой цепи постоянного тока?
Возможные ответы:
Нет других ответов
Правильный ответ: 0003
Объяснение:
Во-первых, давайте напомним себе, что эффективное сопротивление последовательно соединенных резисторов равно и эффективное сопротивление параллельно подключенных резисторов равно .
Начните эту задачу с определения эффективного сопротивления резисторов 2, 3 и 4:
(Это потому, что эти три резистора включены последовательно.)
Теперь схему можно упростить до следующего:
Далее нам нужно будет определить эффективное сопротивление резисторов 6 и 9.0003
Опять же, схему можно упростить:
Отсюда можно определить эффективное сопротивление цепи постоянного тока, вычислив эффективное сопротивление резисторов , 1 и 5:
Сообщить об ошибке
Две лампочки, одна из которых имеет класс , а другая – , последовательно подключены к батарее. Какой из них будет ярче? А если их подключить параллельно?
Возможные ответы:
Недостаточно информации для решения этой задачи
Series:
Параллель:
Серия:
Параллель:
Серия:
Параллель:
Серия:
Параллель:
Серия:
Параллель:
.
:
Параллельный:
Объяснение:
Первый шаг к решению этой проблемы — выяснить, как сопротивление лампочки соотносится с номинальной мощностью. Для резистора рассеиваемая мощность равна:
Таким образом, существует обратная зависимость между сопротивлением лампочки и номинальной мощностью.
Вторым шагом является рассмотрение элементов схемы, соединенных последовательно и параллельно. Последовательно они имеют один и тот же ток; параллельно они делят одно и то же напряжение. Таким образом, для двух последовательно соединенных лампочек ярче будет та, у которой больше сопротивление (меньшая мощность), а для параллельной конфигурации ярче будет лампочка с меньшим сопротивлением (больше мощность).
Сообщить об ошибке
Если у нас есть 3 последовательно соединенных резистора, причем резистор 1 имеет сопротивление , резистор 2 имеет сопротивление , а резистор 3 имеет сопротивление , каково эквивалентное сопротивление серии?
Возможные ответы:
Правильный ответ:
Пояснение:
Общее сопротивление последовательно соединенных резисторов равно сумме их индивидуальных сопротивлений.
В этом случае
Сообщить об ошибке
Вам представлены три резистора, каждый размер . В чем разница между общим сопротивлением резисторов, соединенных последовательно, и полным сопротивлением резисторов, соединенных параллельно?
Возможные ответы:
Правильный ответ:
Объяснение:
Резисторы последовательно:
Параллельные резисторы:
Сообщить об ошибке
Каково общее сопротивление трех резисторов, , , и , включенных параллельно?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение эквивалентного сопротивления для нескольких резисторов, включенных параллельно:
Подставьте известные значения и решите.
Обратите внимание, что для параллельных резисторов общее сопротивление никогда не превышает сопротивления наименьшего элемента.
Сообщить об ошибке
Цепь создается с использованием батареи и 3-х одинаковых резисторов, как показано на рисунке. Каждый из резисторов имеет сопротивление . Если резистор удалить из цепи, как это повлияет на ток через резистор?
Возможных ответов:
Проходной ток увеличится в два раза
Проходной ток останется прежним
Проходной ток уменьшится
Проходной ток увеличится в четыре раза
Невозможно определить, не зная удельного сопротивления провода
Правильный ответ:
Ток через уменьшится
Объяснение:
Поскольку резисторы и образуют параллельную сеть, удаление из цепи увеличивает сопротивление этой части цепи.
Поскольку новая схема представляет собой последовательную комбинацию и , увеличенное сопротивление приводит к снижению тока в каждом из этих резисторов.
Сообщить об ошибке
Определите общий заряд, хранящийся в цепи с двумя одинаковыми плоскопараллельными конденсаторами, соединенными параллельно, с площадью и расстоянием между параллельными пластинами. Предположим, что пространство между параллельными пластинами представляет собой вакуум. Схема показывает разницу напряжений 10 В.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить общий накопленный заряд, нам нужно сложить емкость каждого конденсатора (поскольку они соединены параллельно) и умножить на разницу напряжений. Напомним, что для конденсаторов
Для конденсаторов с параллельными пластинами:
Здесь, , которая представляет собой диэлектрическую проницаемость пустого пространства, является диэлектрической проницаемостью, которая из-за присутствия только вакуума, , которая представляет собой площадь параллельных пластин, и , что является расстоянием между пластинами.
Подставьте известные значения для определения емкости.
Каждый из двух конденсаторов имеет емкость
Поскольку конденсаторы подключены параллельно, общая емкость представляет собой сумму емкостей каждого из них. Общая емкость в цепи определяется как:
Подставьте это значение в наше первое уравнение и найдите общий накопленный заряд.
, где — общий заряд, хранящийся в конденсаторе. Начиная с
Сообщить об ошибке
Каков общий ток, протекающий через систему с 2 параллельными резисторами с сопротивлением и и аккумулятором с разностью напряжений 10 В?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала нам нужно определить общее сопротивление цепи, прежде чем мы узнаем, какой ток протекает через нее. Поскольку резисторы подключены параллельно, их сопротивления складываются обратно:
, где — общее сопротивление цепи.
Теперь, когда мы решили для , мы знаем, что ток, протекающий через цепь, можно найти с помощью закона Ома:
Сообщить об ошибке
← Предыдущий 1 2 Далее →
Уведомление об авторских правах
Все ресурсы AP Physics 1
7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept
21.1 Резисторы, включенные последовательно и параллельно — College Physics
Глава 21 Цепи и приборы постоянного тока
Резюме
- Нарисуйте цепь с параллельными и последовательными резисторами.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Сравните способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему общее сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, содержащей смесь резисторов, соединенных последовательно и параллельно.
Большинство схем имеют более одного компонента, называемого резистор , ограничивающий поток заряда в цепи. Мера этого предела потока заряда называется сопротивлением . Простейшими комбинациями резисторов являются последовательное и параллельное соединения, показанные на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от того, как они соединены.
Рис. 1. (а) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.Когда резисторы в серия ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, в землю, то [латекс]{R_1}[/латекс] на рис.
1(а) может быть сопротивлением стержня отвертки, [латекс]{R_2}[ /latex] сопротивление ручки, [latex]{R_3}[/latex] сопротивление тела человека и [latex]{R_4}[/latex] сопротивление его обуви.
На рис. 2 показаны резисторы, последовательно соединенные с
.0011 напряжение
источник. Кажется разумным, что общее сопротивление представляет собой сумму отдельных сопротивлений, учитывая, что ток должен последовательно проходить через каждый резистор. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев высокоомную обувь на резиновой подошве. Это могло бы быть недостатком, если бы одним из сопротивлений был неисправный высокоомный шнур для прибор, снижающий рабочий ток.) Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потери электроэнергии, называемые падением напряжения , в каждом резисторе на рисунке 2.
В соответствии с законом
Ома падение напряжения [латекс]{В}[/латекс] на резисторе при протекании через него тока рассчитывается по уравнению [латекс]{В = IR}[/латекс], где [латекс]{I}[/латекс] равен току в амперах (А), а [латекс]{R}[/латекс] — сопротивление в омах [латекс]{(\Omega )}[/латекс]. Другой способ представить это так: [латекс]{V}[/латекс] — это напряжение, необходимое для протекания тока [латекс]{I}[/латекс] через сопротивление [латекс]{R}[/латекс] .Таким образом, падение напряжения на [латексе]{R_1}[/латексе] равно [латексу]{V_1 = IR_1}[/латексу], а на [латексе]{R_2}[/латексе] равно [латексу]{V_2 = IR_2 }[/latex], а через [latex]{R_3}[/latex] — [latex]{V_3 = IR_3}[/latex]. Сумма этих напряжений равна выходному напряжению источника; то есть
[латекс] {V = V_1 + V_2 + V_3}.[/латекс]
Это уравнение основано на законах сохранения энергии и сохранения заряда. Электрическая потенциальная энергия может быть описана уравнением [латекс]{PE = qV}[/латекс], где [латекс]{q}[/латекс] представляет собой электрический заряд, а [латекс]{В}[/латекс] представляет собой Напряжение.
Таким образом, энергия, подаваемая источником, равна [латекс]{qV}[/латекс], а энергия, рассеиваемая резисторами, равна
[латекс]{qV_1 + qV_2 + qV_3}.[/латекс]
Соединения: законы сохранения
Выводы выражений для последовательного и параллельного сопротивления основаны на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно связаны со всеми электрическими явлениями и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого места назначения энергии. Таким образом, [латекс]{qV = qV_1 + qV_2 + qV_3}[/латекс]. Заряд [латекс]{q}[/латекс] отменяется, что дает [латекс]{V = V_1 + V_2 + V_3}[/латекс], как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для накопления заряда, нет места для утечки заряда, и заряд сохраняется.
)
Теперь подстановка значений отдельных напряжений дает
[латекс] {V = IR_1 + IR_2 + IR_3 = I(R_1+R_2+R_3)}.[/латекс]
Обратите внимание, что для эквивалентного последовательного сопротивления [латекс]{R_s}[/латекс] мы имеем
[латекс]{V = IR_s}.[/латекс]
Это означает, что общее или эквивалентное последовательное сопротивление [латекс]{R_s}[/латекс] трех резисторов равно
.[латекс]{R_s = R_1 + R_2 + R_3}[/латекс].
Эта логика действительна в целом для любого количества последовательно соединенных резисторов; таким образом, общее сопротивление [латекс]{R_s}[/латекс] последовательного соединения равно
[латекс]{R_s = R_1 + R_2 + R_3 + \dots}[/латекс]
, как было предложено. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого из них, а последовательные сопротивления просто складываются.
Пример 1: расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рис.
], а сопротивления равны [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/латекс] и [латекс]{R_3 = 13,0 \; \Омега }[/латекс]. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление представляет собой просто сумму индивидуальных сопротивлений, определяемую следующим уравнением:
[латекс]\begin{array}{r @{{}={} } l} {R_s} & {R_1 + R_2 + R_3} \\[1em] & {1.00 \;\Omega + 6.00 \;\Omega + 13.0 \;\Omega} \\[1em] & {20.0 \;\ Омега}. \end{array}[/latex]
Стратегия и решение для (b)
Ток определяется по закону Ома, [latex]{V = IR}[/latex]. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {R_s}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {12,0 \; \text{V}}{20,0 \;\Omega}}[/latex] [латекс]{= 0,600 \;\textbf{A}}.
[/latex]
Стратегия и решение для (c)
Падение напряжения — или [латекс] {IR} [/латекс] — на резисторе определяется законом Ома. Ввод тока и значения первого сопротивления дает
[латекс]{V_1 = IR_1 = (0,600 \;\textbf{A})(1,0 \;\Omega) = 0,600 \;\text{V}}.[ /латекс]
Аналогично,
[латекс]{V_2 = IR_2 = (0,600 \;\textbf{A})(6,0 \;\Omega) = 3,60 \;\text{V}}[/латекс]
и
[латекс]{ V_3 = IR_3 = (0,600 \;\textbf{A})(13,0 \;\Omega) = 7,80 \;\text{V}}.[/latex]
Обсуждение для (c)
Три [ латекс] {ИК}[/латекс] капли добавляют к [латексу]{12,0 \;\текст{V}}[/латекс], как и прогнозировалось:
[латекс]{V_1 + V_2 + V_3 = (0,600 + 3,60 + 7.80) \;\text{V} = 12,0 \;\text{V}}.[/latex]
Стратегия и решение для (d) 92}{R}}[/latex], где [latex]{V}[/latex] — падение напряжения на резисторе (не полное напряжение источника). Будут получены одинаковые значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать [латекс]{P = IV}[/латекс], где [латекс]{V}[/латекс] является напряжением источника.
Это дает
[латекс]{P = (0,600 \;\textbf{A})(12,0 \;\text{V}) = 7,20 \;\text{W}}.[/latex]
Обсуждение для д)
Обратите внимание, по совпадению, что общая мощность, рассеиваемая резисторами, также составляет 7,20 Вт, как и мощность, выдаваемая источником. То есть
[латекс]{P_1 + P_2 + P_3 = (0,360 + 2,16 + 4,68) \;\text{W} = 7,20 \;\text{W}}.[/latex]
Мощность – это энергия на единицу единица времени (ватты), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Сопротивления серии добавить: [латекс]{R_s = R_1 + R_2 + R_3 + \dots}[/латекс] .
- Один и тот же ток протекает через каждый резистор последовательно.
- Отдельные последовательно соединенные резисторы не получают общее напряжение источника, а делят его.
На рис. 3 показаны резисторы параллельно , подключенные к источнику напряжения.
Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радиоприемник и т. д. соединены параллельно, так что они используют полное напряжение источника и могут работать совершенно независимо. То же самое верно и в вашем доме, или в любом здании. (См. рис. 3(b).)
Рисунок 3. (a) Три резистора, подключенные параллельно к батарее, и эквивалентное одиночное или параллельное сопротивление. (b) Установка электроснабжения в доме. (кредит: Дмитрий Г., Wikimedia Commons)Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс]{R_{\textbf{p}}}[/латекс], давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением.
Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [latex]{I_1 = \frac{V}{R_1}}[/latex], [latex]{I_2 = \frac{V} {R_2}}[/latex] и [латекс]{I_3 = \frac{V}{R_3}}[/latex]. Сохранение заряда подразумевает, что полный ток [латекс]{I}[/латекс], производимый источником, представляет собой сумму этих токов:
[латекс] {I = I_1 + I_2 + I_3}.[/латекс]
Подстановка выражений для отдельных токов дает
[латекс] {I =} [/ латекс] [латекс] {\ гидроразрыва {V} {R_1}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {V} {R_2 }}[/латекс] [латекс]{+}[/латекс] [латекс]{\ гидроразрыва {V} {R_3}}[/латекс] [латекс] {= V}[/латекс] [латекс] {(\ frac{1}{R_1}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{R_2}}[/latex] [латекс]{+}[/latex] [ латекс] {\ гидроразрыва {1} {R_3})}. [/латекс]
Обратите внимание, что закон Ома для эквивалентного единичного сопротивления дает
[латекс] {I =}[/латекс] [латекс]{\ гидроразрыва {V} {R_p}} [/ латекс] [латекс] {= V} [/латекс] [латекс] {(\ гидроразрыва {1} {R_p})}.
[/латекс]
Члены в скобках в последних двух уравнениях должны быть равны. Обобщая любое количество резисторов, общее сопротивление [латекс]{R_p}[/латекс] параллельного соединения связано с отдельными сопротивлениями как
.[латекс] {\ гидроразрыва {1} {R_p}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {R_1}} [/ латекс] [латекс] {+ } [/латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3}} [/ латекс] [ латекс]{+ \cdots}[/латекс]
Это соотношение приводит к тому, что общее сопротивление [латекс]{R_p}[/латекс] меньше, чем наименьшее из отдельных сопротивлений. (Это видно в следующем примере.) Когда резисторы соединены параллельно, от источника протекает больший ток, чем для любого из них по отдельности, и поэтому общее сопротивление ниже.
Пример 2: расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления при параллельном соединении на рис.
3 будут такими же, как и при последовательном соединении, рассмотренном ранее: [ латекс]{V = 12,0 \;\text{V}}[/латекс], [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/ латекс] и [латекс]{R_3 = 13,0 \;\Omega}[/латекс]. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
Стратегия и решение для (a)
Общее сопротивление для параллельной комбинации резисторов определяется с помощью приведенного ниже уравнения. Ввод известных значений дает
[латекс] {\ гидроразрыва {1} {R_p}} [/латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1} {R_1}} [/латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {1,00 \; \ Omega}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ frac{1}{6.
00 \;\Omega}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{13.0 \;\Omega}}.[/latex]
Таким образом,
[латекс] {\ гидроразрыва {1} {R_p}} [/латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1.00} {\ Omega}} [/латекс ] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {0,1667} {\ Omega}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {0,07692} {\ Omega}}[/latex] [latex]{=}[/latex] [latex]{\frac{1.2436}{\Omega}}[/latex]
(Обратите внимание, что в этих расчетах каждый промежуточный ответ показан с дополнительная цифра.)
Мы должны инвертировать это, чтобы найти полное сопротивление [латекс]{R_p}[/латекс]. Это дает
[латекс] {R_p =} [/латекс] [латекс] {\ гидроразрыва {1} {1.2436}} [/ латекс] [латекс] {\ Omega = 0,8041 \; \ Omega}. [/latex]
Общее сопротивление с правильным количеством значащих цифр равно [латекс]{R_p = 0,804 \;\Омега}[/латекс]
Обсуждение для (а)
[латекс]{R_p}[/латекс] как и предсказывалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, подставив [латекс]{R_p}[/латекс] вместо полного сопротивления. Это дает
[латекс] {I =} [/латекс] [латекс] {\ гидроразрыва {V} {R_p}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {12,0 \;\text{V}}{0,8041 \;\Omega}}[/latex] [латекс]{= 14,92 \;\textbf{A}}[/latex]
Обсуждение для (b)
Ток [latex]{I}[/latex] для каждого устройства намного больше, чем для тех же устройств, соединенных последовательно ( см. предыдущий пример). Цепь с параллельными соединениями имеет меньшее общее сопротивление, чем резисторы, соединенные последовательно.
Стратегия и решение для (c)
Индивидуальные токи легко рассчитать по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
[латекс] {I_1 =} [/латекс] [латекс] {\ гидроразрыва {V} {R_1}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {12,0 \; \text{V}}{1.
00 \;\Omega}}[/latex] [латекс]{= 12.0 \;\textbf{A}}.[/latex]
Аналогично,
[латекс]{I_2 =} [/латекс] [латекс] {\ гидроразрыва {V} {R_2}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {12,0 \; \ текст {V}} {6,00 \ ;\Omega}}[/латекс] [латекс]{= 2,00 \;\textbf{A}}[/латекс]
и
[латекс]{I_3 =}[/латекс] [латекс]{\ гидроразрыва{ V} {R_3}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {12,0 \; \ текст {V}} {13,0 \; \ Омега}} [/ латекс] [латекс ] {= 0,92 \;\textbf{A}}.[/latex]
Обсуждение для (c)
Общий ток представляет собой сумму отдельных токов:
[латекс]{I_1 + I_2 + I_3 = 14,92 \ ;\textbf{A}}.[/latex]
Это соответствует закону сохранения заряда.
Стратегия и решение для (d)
Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.
2}{R}}[/latex], поскольку на каждый резистор подается полное напряжение. Таким образом, 92}{13.0 \;\Omega}}[/latex] [latex]{= 11.1 \;\text{W}} .[/latex]
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении значительно выше, чем при последовательном подключении к одному и тому же источнику напряжения.
Стратегия и решение для (e)
Общая мощность также может быть рассчитана несколькими способами. Выбор [латекс]{P = IV}[/латекс] и ввод общего тока дает
[латекс]{P = IV = (14,92 \;\textbf{A})(12,0 \;\text{V} ) = 179\;\text{W}}.[/latex]
Обсуждение для (e)
Суммарная мощность, рассеиваемая резисторами, также составляет 179 Вт:
[латекс]{P_1 + P_2 + P_3 = 144 \; \text{W} + 24,0 \;\text{W} + 11,1 \;\text{W} = 179 \;\text{W}}.[/latex]
Это согласуется с законом сохранения энергии .
Общее обсуждение
Обратите внимание, что и токи, и мощности при параллельном соединении больше, чем у тех же устройств, соединенных последовательно.
Основные характеристики резисторов, включенных параллельно
- Параллельное сопротивление находится из [латекс] {\ гидроразрыва {1} {R_p} = \ гидроразрыва {1} {R_1} + \ гидроразрыва {1} {R_2} + \ гидроразрыва {1 }{R_3} + \cdots }[/latex], и оно меньше любого отдельного сопротивления в комбинации.
- К каждому параллельно подключенному резистору приложено одинаковое полное напряжение источника. (Системы распределения электроэнергии чаще всего используют параллельные соединения для питания множества устройств, обслуживаемых одним и тем же напряжением, и позволяют им работать независимо.)
- Параллельные резисторы не получают суммарный ток каждый; они его делят.
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Они часто встречаются, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения могут быть сведены к одному эквивалентному сопротивлению с помощью метода, показанного на рисунке 4. Различные части обозначены как последовательные или параллельные, приведены к их эквивалентам и далее уменьшены до тех пор, пока не останется одно сопротивление. Процесс скорее трудоемкий, чем сложный.
Рисунок 4. Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единое эквивалентное сопротивление.Простейшая комбинация последовательного и параллельного сопротивлений, показанная на рис. 5, также является наиболее поучительной, поскольку она встречается во многих приложениях. Например, [латекс]{R_1}[/латекс] может быть сопротивлением проводов от автомобильного аккумулятора до его электрических устройств, которые включены параллельно.
[латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс] могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3. Расчет сопротивления, [латекс]{IR}[/латекс] падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей последовательно и параллельно. Мы можем рассматривать [латекс]{R_1}[/латекс] как сопротивление проводов, ведущих к [латексу]{R_2}[/латексу] и [латексу]{R_3}[/латексу]. а) Найдите полное сопротивление. (b) Каково снижение [латекса]{IR}[/латекса] в [латексе]{R_1}[/латекс]? (c) Найдите текущий [латекс]{I_2}[/латекс] через [латекс]{R_2}[/латекс]. (d) Какая мощность рассеивается [латексом]{R_2}[/латексом]?
Рисунок 5. Эти три резистора подключены к источнику напряжения таким образом, что R 2 и R 3 параллельны друг другу, а эта комбинация последовательно1 907 9012 1 .Стратегия и решение для (a)
Чтобы найти полное сопротивление, заметим, что [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс] параллельны, и их комбинация [латекс ]{R_p}[/latex] идет последовательно с [latex]{R_1}[/latex]. Таким образом, общее (эквивалентное) сопротивление этой комбинации равно
[латекс]{R_{\text{tot}} = R_1 + R_p}.[/latex]
Сначала находим [латекс]{R_p}[/латекс], используя уравнение для параллельно включенных резисторов и вводя известные значения:
[латекс]{\ гидроразрыва {1} {R_p}} [/латекс] [латекс] {=}[/латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/латекс] [латекс ] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {6,00 \; \ Омега }}[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{1}{13,0 \;\Омега}}[/латекс] [латекс]{=}[/латекс] [латекс] {\ гидроразрыва {0,2436} {\ Omega}}.[/латекс]
Инвертирование дает
[латекс] {R_p =} [/латекс] [латекс] {\ гидроразрыва {1} {0,2436}} [/латекс] [латекс] {\ Omega = 4,11 \; \ Omega}.
[/ латекс]
Таким образом, общее сопротивление равно
[латекс]{R_{\text{tot}} = R_1 + R_p = 1,00 \;\Omega + 4,11 \;\Omega = 5,11 \;\Omega}.[/latex ]
Обсуждение для (a)
Суммарное сопротивление этой комбинации является промежуточным между чистыми последовательными и чисто параллельными значениями ([латекс]{20,0 \;\Омега}[/латекс] и [латекс]{0,804 \ ;\Omega}[/latex] соответственно), найденные для тех же резисторов в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение [latex]{IR}[/latex] в [latex]{R_1}[/latex], заметим, что полный текущий [latex]{I }[/latex] проходит через [latex]{R_1}[/latex]. Таким образом, его [латекс]{IR}[/латекс] равен
[латекс]{V_1 = IR_1}.[/латекс]
Мы должны найти [латекс]{I}[/латекс], прежде чем мы сможем вычислить [латекс ]{V_1}[/латекс]. Полный ток [латекс]{I}[/латекс] находится по закону Ома для цепи. То есть
[латекс] {I =}[/латекс] [латекс] {\ гидроразрыва {V} {R _ {\ текст {tot}}}} [/латекс] [латекс] {=}[/латекс] [латекс]{\ гидроразрыва {12,0 \;\текст{V}}{5,11 \;\Омега}}[/латекс] [латекс]{= 2,35 \;\textbf{A}}.
[/латекс]
Подставив это в выражение выше, мы получим
[латекс]{V_1 = IR_1 = (2,35 \;\textbf{A})(1,00 \;\Omega) = 2,35 \;\text{V}}.[ /latex]
Обсуждение для (b)
Напряжение, подаваемое на [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс], меньше общего напряжения на величину [латекс ]{V_1}[/латекс]. Когда сопротивление проводов велико, это может существенно повлиять на работу устройств, представленных [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс].
Стратегия и решение для (c)
Чтобы найти ток через [латекс]{R_2}[/латекс], мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение [латекс] {V _ {\ textbf {p}}} [/латекс], потому что оно приложено к параллельной комбинации резисторов. Напряжение, подаваемое как на [латекс]{R_2}[/латекс], так и на [латекс]{R_3}[/латекс], уменьшается на величину [латекс]{V_1}[/латекс], поэтому оно составляет
[латекс]. ]{V_p = V — V_1 = 12,0 \;\text{V} — 2,35 \;\text{V} = 9,65 \;\text{V}}.
[/latex]
Теперь ток [латекс]{I_2}[/латекс] через сопротивление [латекс]{R_2}[/латекс] находится по закону Ома:
[латекс]{I_2 =}[/латекс] [латекс]{ \frac{V_p}{R_2}}[/latex] [латекс]{=}[/latex] [латекс]{\frac{9,65 \;\text{V}}{6,00 \;\Omega}}[/latex ] [latex]{ = 1,61 \;\textbf{A}}[/latex]
Обсуждение для (c)
Ток меньше, чем 2,00 A, протекающих через R2R2 размера 12{R rSub { размера 8 {2} } } {} при параллельном подключении к аккумулятору в предыдущем примере с параллельной схемой. 92(6,00 \;\Omega) = 15,5 \;\text{W}}.[/latex]
Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источник 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах уменьшает ток и мощность, подаваемые на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными.
Если потребляется большой ток, падение [латекс]{ИК}[/латекс] в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается двигатель, освещение холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
То, что происходит в этих сильноточных ситуациях, показано на рис. 6. Устройство, представленное [латекс]{R_3}[/латекс], имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Это увеличение тока вызывает большее [латекс]{IR}[/латекс] падение в проводах, представленных [латекс]{R_1}[/латекс], уменьшая напряжение на лампочке (которое составляет [латекс]{R_2}[ /latex]), который затем заметно тускнеет.
Рисунок 6. Почему гаснет свет при включении большого электроприбора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на светильнике.Стратегии решения проблем с последовательными и параллельными резисторами
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает в себя список известных проблем, поскольку они помечены на вашей принципиальной схеме.
- Точно определите, что нужно определить в задаче (идентифицируйте неизвестные). Письменный список полезен.
- Определите, подключены ли резисторы последовательно, параллельно или как последовательно, так и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий и другой для параллельных. Если в вашей задаче сочетаются последовательные и параллельные соединения, уменьшите ее пошагово, рассмотрев отдельные группы последовательных или параллельных соединений, как это делается в этом модуле и в примерах.
Особое примечание: при поиске[/latex]латекса{R_p}[/latex] следует проявлять осторожность.
- Проверьте, разумны ли и последовательны ли ответы. Единицы и численные результаты должны быть разумными. Например, общее последовательное сопротивление должно быть больше, тогда как общее параллельное сопротивление должно быть меньше. Мощность должна быть больше для тех же устройств, соединенных параллельно, по сравнению с последовательными и т.д.
- Общее сопротивление электрической цепи с последовательно соединенными резисторами представляет собой сумму отдельных сопротивлений: [latex]{R_s = R_1 + R_2 + R_3 + \cdots}[/latex]
- Через каждый резистор в последовательной цепи протекает одинаковый ток.
- Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различны, и их общая сумма составляет входную мощность источника питания.
- Общее сопротивление электрической цепи с параллельно соединенными резисторами меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле:
[латекс] {\ гидроразрыва {1} {R _ {\ textbf {p}}}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1} {R_1}} [/ латекс] [латекс] {+}[/ латекс] [латекс] {\ гидроразрыва {1} {R_2}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {R_3 }}[/латекс] [латекс]{+ \;\cdots}[/латекс]
- К каждому резистору в параллельной цепи приложено одинаковое полное напряжение источника.
- Ток, протекающий через каждый резистор в параллельной цепи, различен в зависимости от сопротивления.
- Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного сопротивления, его можно свести к единому эквивалентному сопротивлению, обозначив различные его части как последовательные или параллельные, сведя каждую к эквиваленту и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление. .
Концептуальные вопросы
1: Выключатель имеет переменное сопротивление, близкое к нулю в закрытом состоянии и очень большое в разомкнутом, и он включен последовательно с устройством, которым он управляет. Объясните влияние переключателя на рисунке 7 на ток в разомкнутом и замкнутом состоянии.
Рисунок 7. Переключатель обычно подключается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в закрытом состоянии, но чрезвычайно большое сопротивление в разомкнутом состоянии.(Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)
2: Какое напряжение на разомкнутом выключателе на рисунке 7?
3: На разомкнутом ключе есть напряжение, как на рис. 7. Почему же тогда мощность, рассеиваемая разомкнутым ключом, мала?
4: Почему мощность, рассеиваемая замкнутым выключателем, таким как на рисунке 7, мала?
5: Студент в лаборатории физики по ошибке подключил лампочку, батарею и выключатель, как показано на рис. 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и выключается, когда выключатель замкнут. (Не пытайтесь это сделать — это плохо для батареи!)
Рисунок 8. Ошибка проводки поставила этот переключатель параллельно с устройством, представленным R . (Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)
6: Зная, что сила удара зависит от силы тока, протекающего через ваше тело, вы бы предпочли быть включенным последовательно или параллельно с сопротивлением, например, с нагревательным элементом тостера, если оно поражено им? Объяснять.
7: Погасли бы фары при запуске двигателя автомобиля, если бы провода в автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объясните.
8: Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые разрывали электрическое соединение, как разомкнутый выключатель, когда они перегорали. Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампочки, у которых короткое замыкание, как у замкнутого выключателя, когда они перегорают.
Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 39остальные одинаковые лампочки, какое тогда рабочее напряжение у каждой?
9: Если две бытовые лампочки мощностью 60 Вт и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10: Предположим, вы выполняете лабораторную работу по физике, в которой вас просят включить резистор в цепь, но все поставляемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее требуемое значение?
11: Перед Второй мировой войной некоторые радиоприемники получали питание через «резистивный шнур», который имел значительное сопротивление. Такой шнур сопротивления снижает напряжение до желаемого уровня для радиоламп и т.п., а также экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и расходуют энергию, когда радио включено.
12: Некоторые лампочки имеют три настройки мощности (не включая нулевую), полученные от нескольких нитей накала, которые включаются по отдельности и соединяются параллельно. Какое минимальное количество нитей необходимо для трех режимов мощности? 92 — \;\Omega}[/latex] a [латекс]{2.50 — \;\text{k} \Omega}[/latex] и [латекс]{4.00 — \;\text{k} \Omega }[/latex] резистор соединен последовательно? б) Параллельно?
3: Какое наибольшее и наименьшее сопротивление можно получить, соединив [латекс]{36.0 — \;\Omega}[/латекс], [латекс]{50.0 — \;\Омега}[/латекс ], и резистор [латекс]{700 — \;\Омега}[/латекс] вместе?
4: Тостер мощностью 1800 Вт, электрическая сковорода мощностью 1400 Вт и лампа мощностью 75 Вт подключены к одной розетке в сети 15 А, 120 В. (Три устройства подключены параллельно, когда они подключены к одной и той же розетке.). а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5: Фара вашего автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в системе 12,0 В.
Какую мощность будет потреблять одна фара и стартер при последовательном подключении к аккумулятору 12,0 В? (Любым другим сопротивлением в цепи и любым изменением сопротивления в двух устройствах пренебречь). и [латекс]{96.0 — \;\Омега}[/латекс] резисторы, найдите ток и мощность для каждого из них при последовательном соединении. (b) Повторите, когда сопротивления параллельны.
7: Ссылаясь на пример объединения последовательных и параллельных цепей и рисунок 5, рассчитайте [латекс]{I_3}[/латекс] двумя следующими способами: (а) по известным значениям [латекс]{I }[/латекс] и [латекс]{I_2}[/латекс]; (б) с использованием закона Ома для [латекса]{R_3}[/латекс]. В обеих частях подробно показано, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
8: Ссылаясь на рисунок 5: (a) Рассчитайте [латекс]{P_3}[/латекс] и обратите внимание, как это соотносится с [латексом]{P_3}[/латекс], обнаруженным в первых двух примерах задач в этом модуль.
Рис. 9. Высоковольтная линия электропередачи (240 кВ), по которой проходит 5,00 × 10 2 Линия подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает 1,00 × 10 9 Ом сопротивления каждого.9- \;\Omega}[/latex] сопротивление. Рис. 9. (а) Каково сопротивление заземления 100 таких изоляторов? б) Рассчитайте мощность, рассеиваемую 100 из них. в) Какую долю мощности несет линия? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
11: Покажите, что если объединить два резистора [латекс]{R_1}[/латекс] и [латекс]{R_2}[/латекс] и один из них намного больше другого ([латекс]{R_1 >> R_2 }[/latex]): (a) Их последовательное сопротивление почти равно большему сопротивлению [latex]{R_1}[/latex]. (b) Их параллельное сопротивление почти равно меньшему сопротивлению [латекс]{R_2}[/латекс].

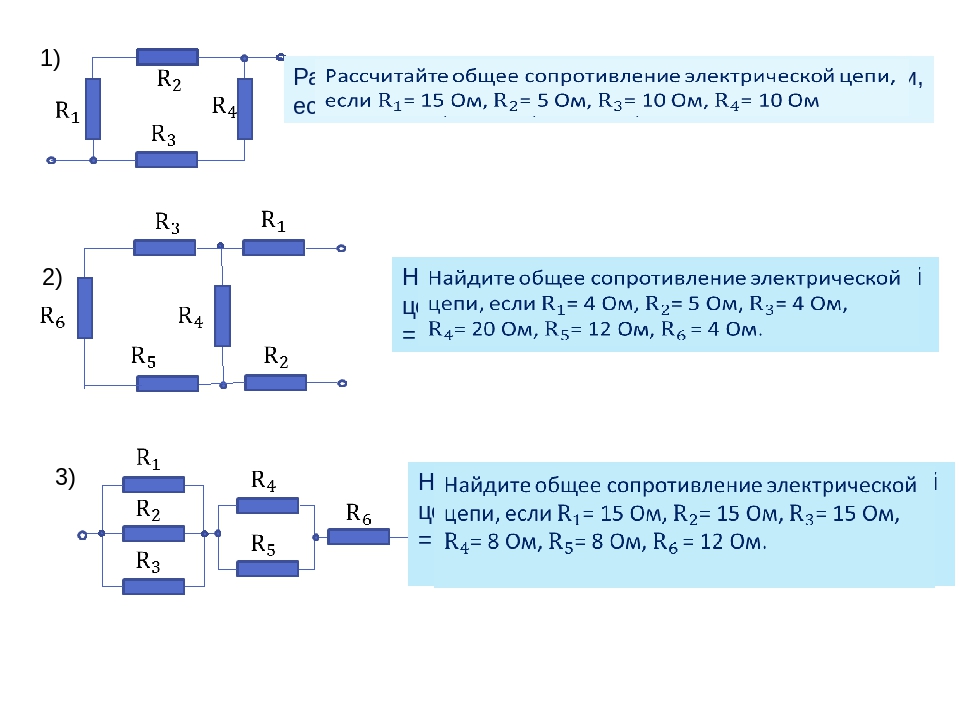
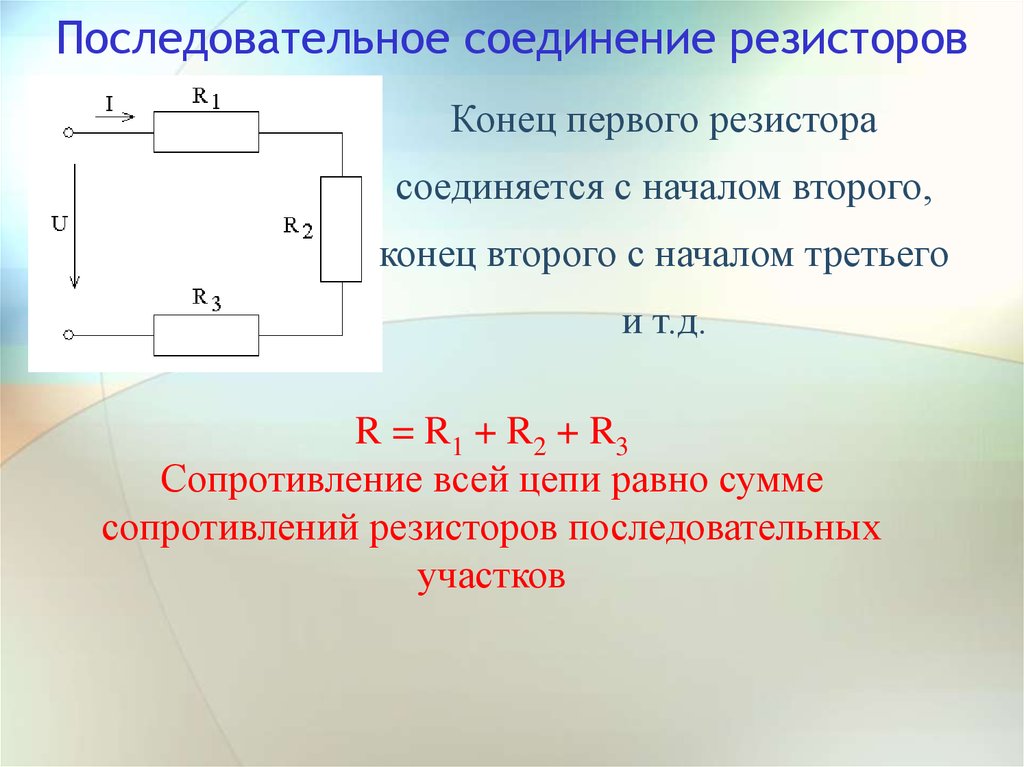

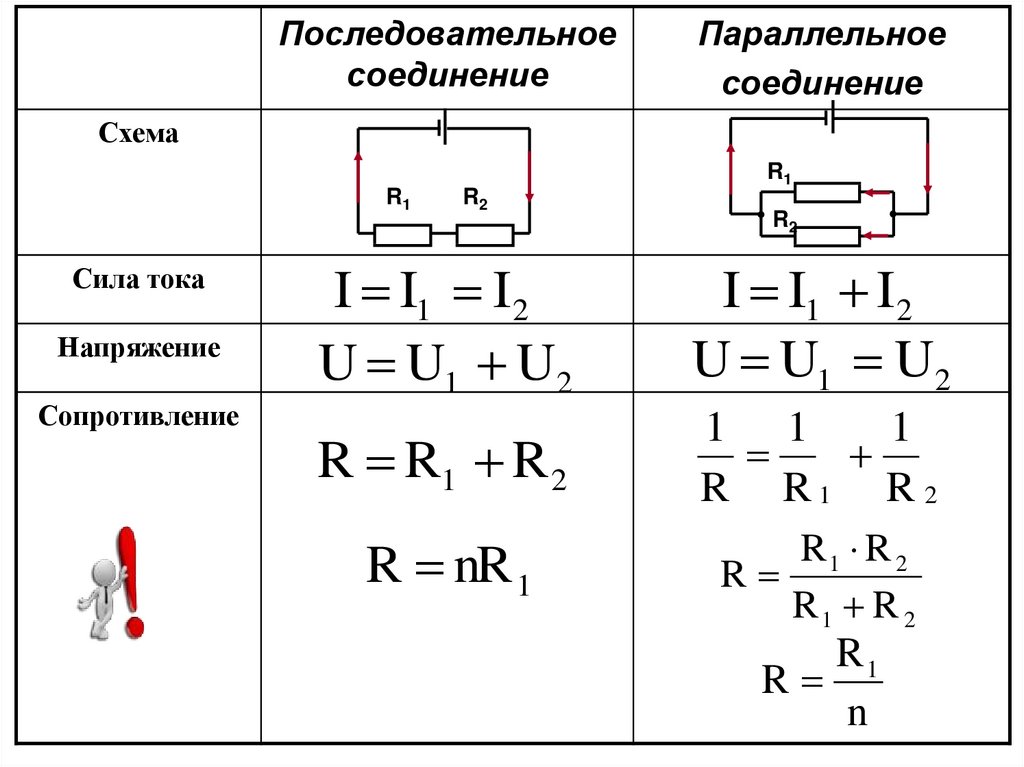 Вы также можете добавить до 30 сопротивлений
Вы также можете добавить до 30 сопротивлений
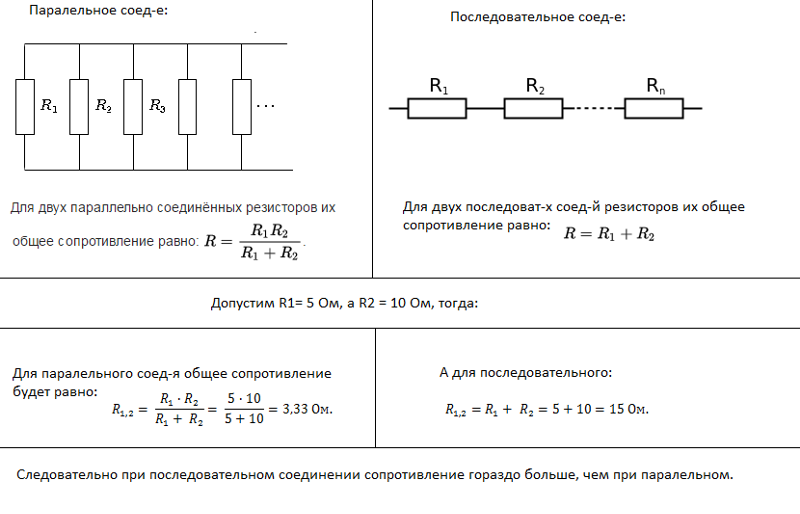
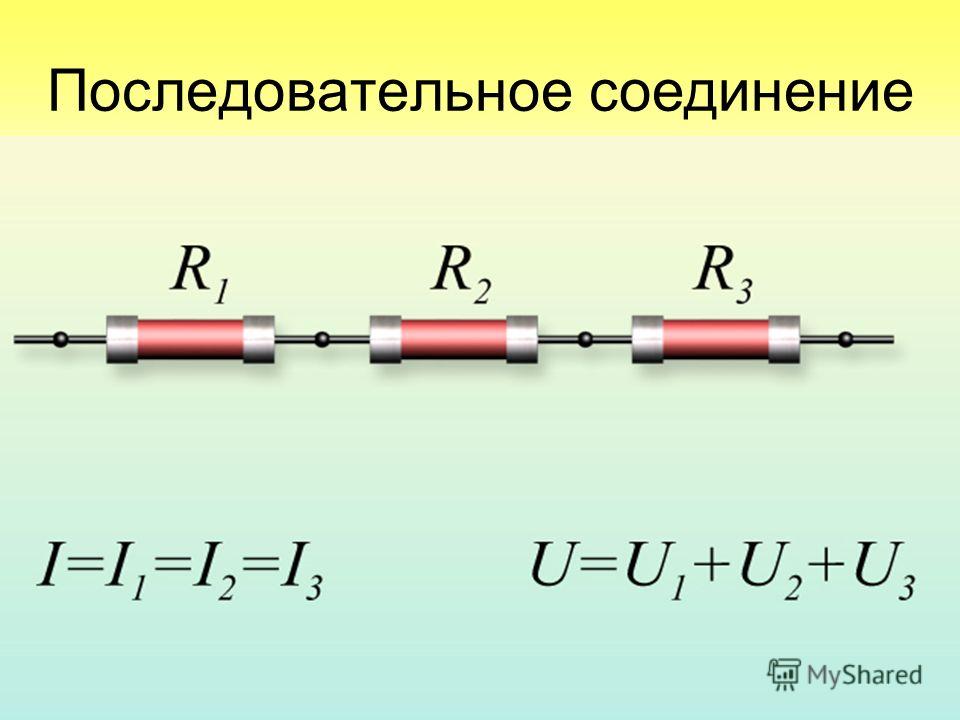 может существовать в каждом из них.
может существовать в каждом из них. 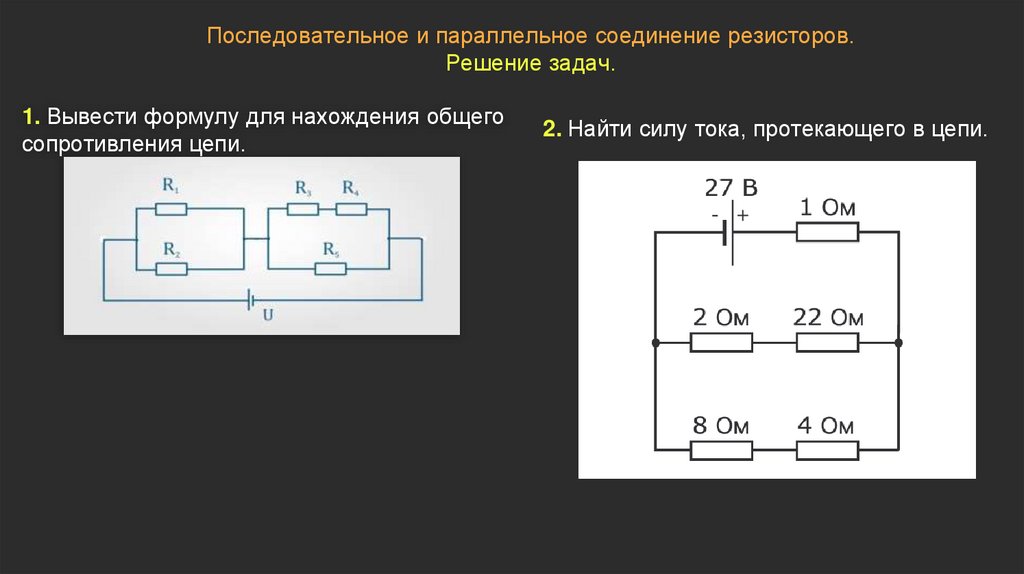
 Вычислите новую сумму и так далее, пока не включите все параллельные резисторы в эту конкретную сеть.
Вычислите новую сумму и так далее, пока не включите все параллельные резисторы в эту конкретную сеть.

 Вы можете выбрать, какую формулу использовать
Вы можете выбрать, какую формулу использовать
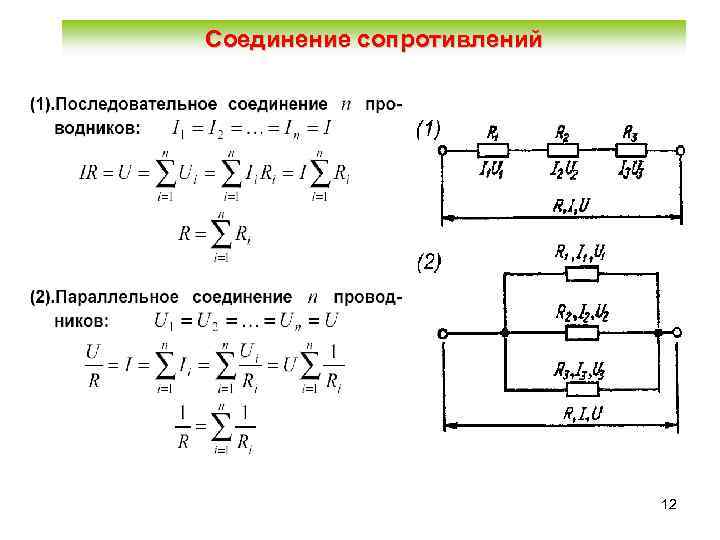 Это двухконтактный электрический компонент.
Это двухконтактный электрический компонент.

 Чему равно полное эквивалентное сопротивление цепи?
Чему равно полное эквивалентное сопротивление цепи?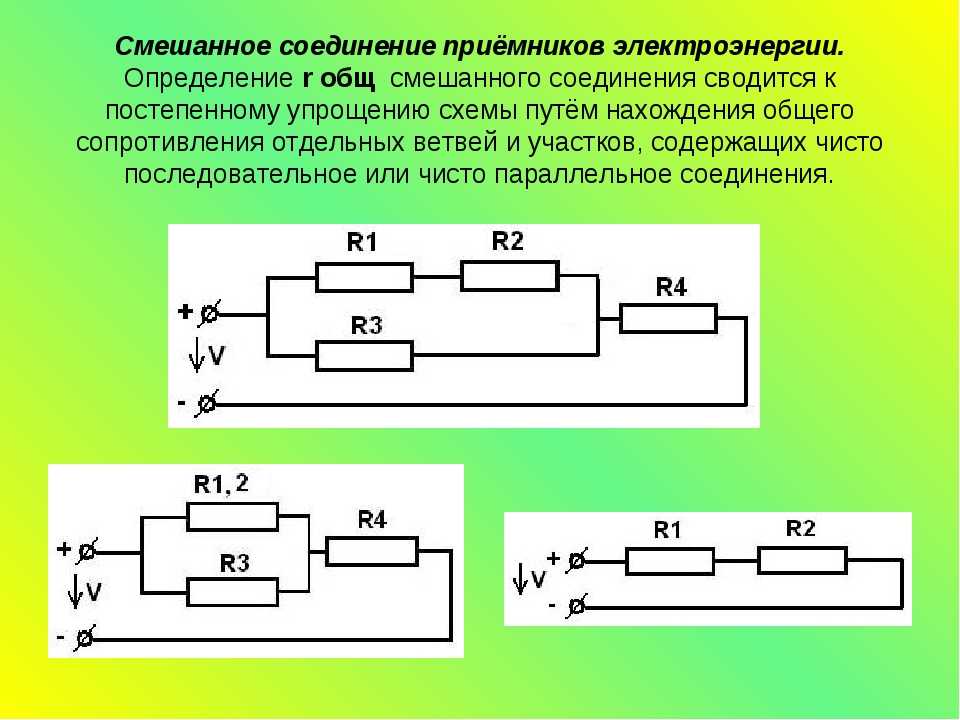 Нам нужно будет рассчитать полное эквивалентное сопротивление цепи. Поскольку два резистора включены последовательно, мы можем просто добавить их.
Нам нужно будет рассчитать полное эквивалентное сопротивление цепи. Поскольку два резистора включены последовательно, мы можем просто добавить их.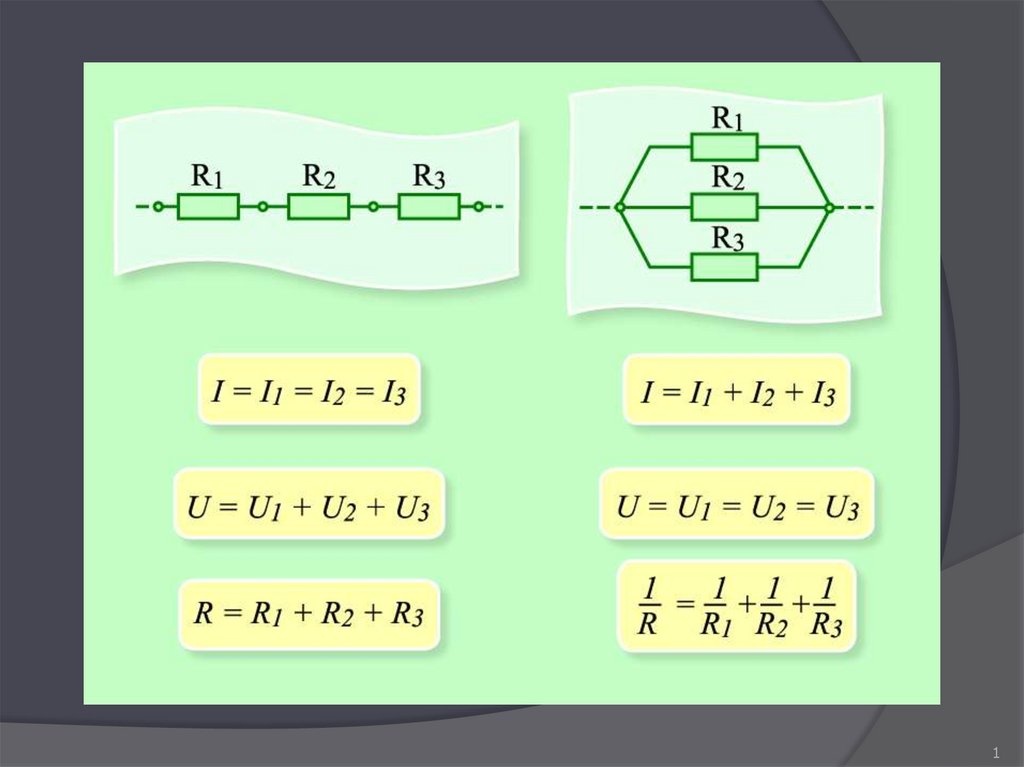
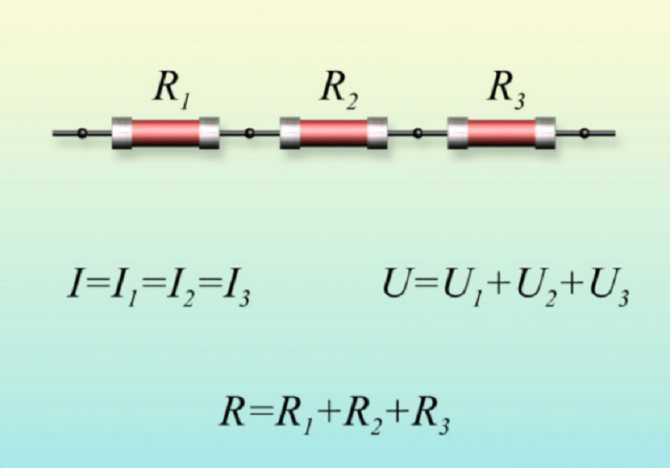 :
: В этом случае
В этом случае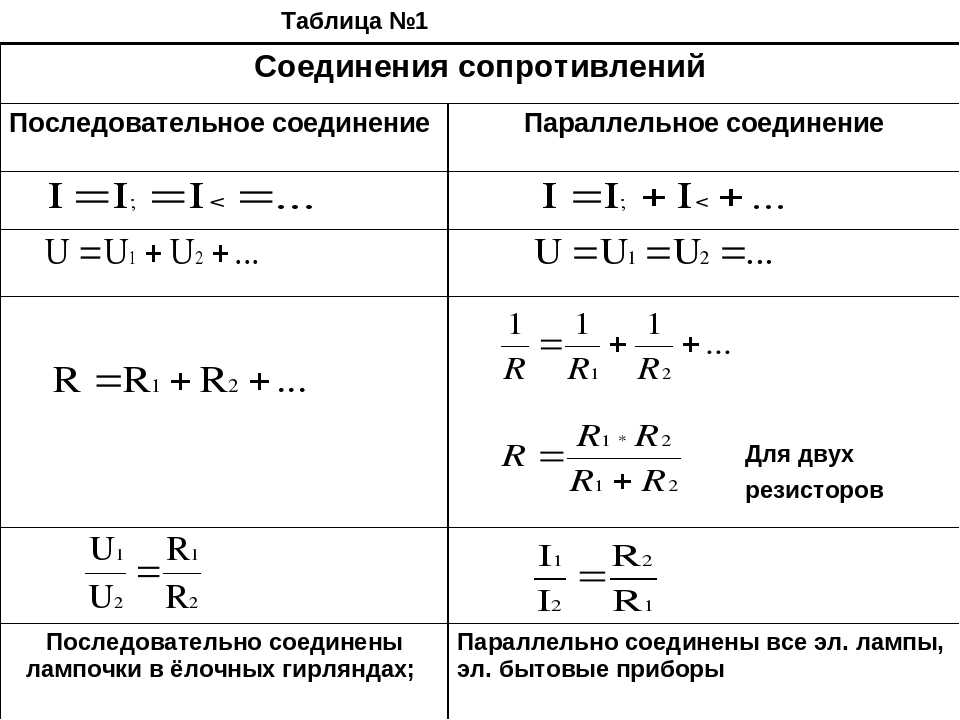
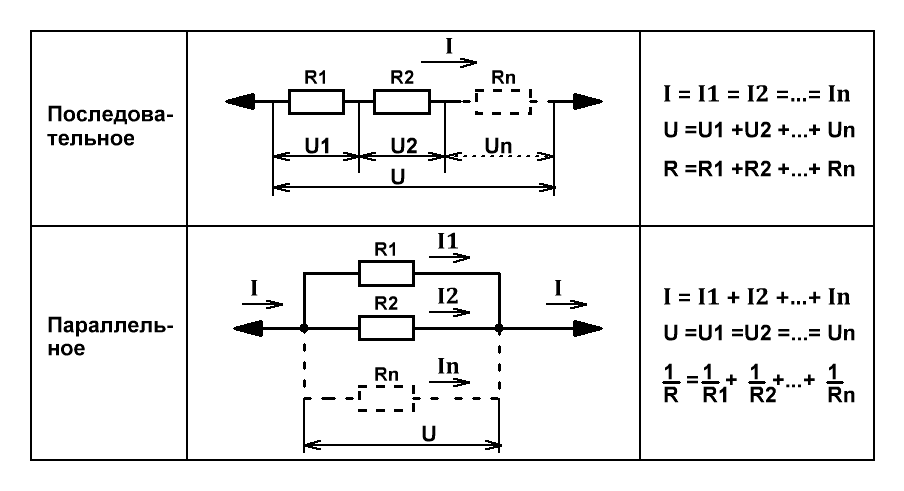 Поскольку новая схема представляет собой последовательную комбинацию и , увеличенное сопротивление приводит к снижению тока в каждом из этих резисторов.
Поскольку новая схема представляет собой последовательную комбинацию и , увеличенное сопротивление приводит к снижению тока в каждом из этих резисторов.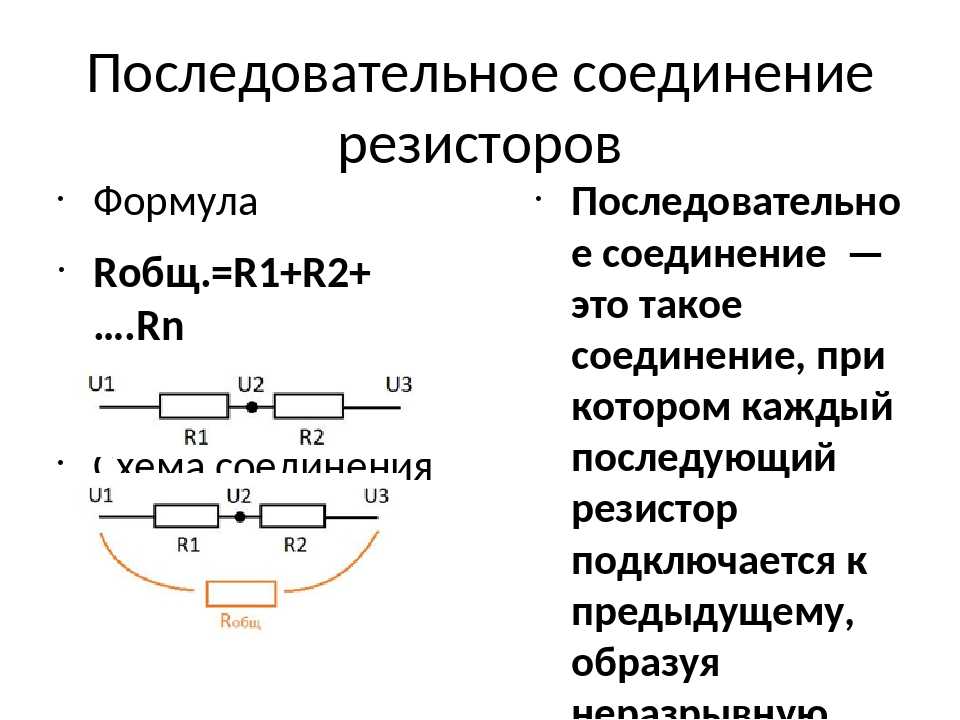
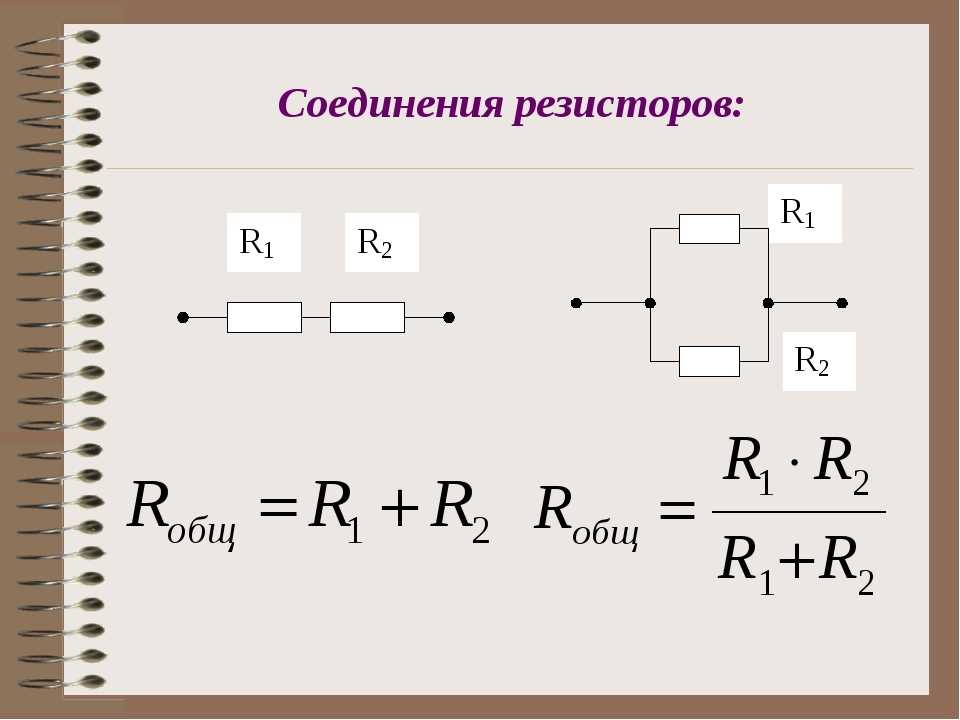
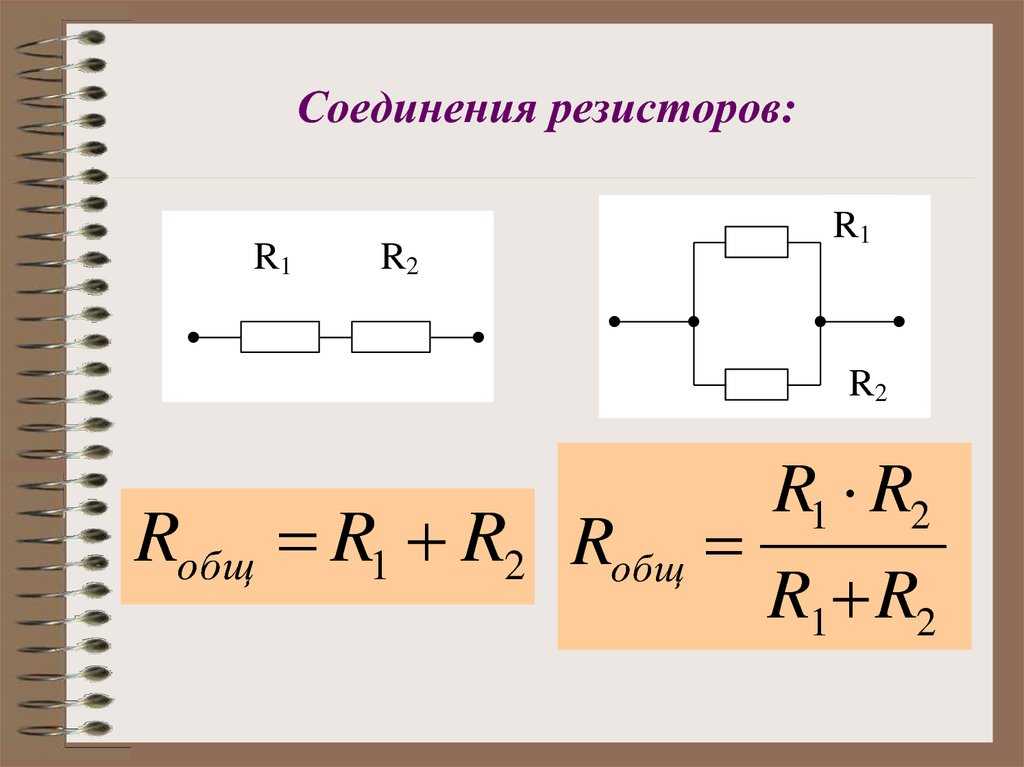
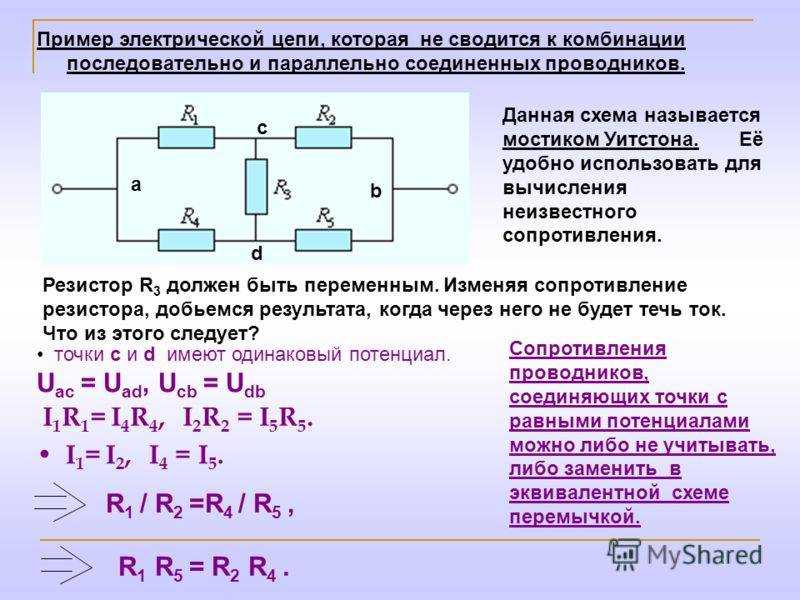 1(а) может быть сопротивлением стержня отвертки, [латекс]{R_2}[ /latex] сопротивление ручки, [latex]{R_3}[/latex] сопротивление тела человека и [latex]{R_4}[/latex] сопротивление его обуви.
1(а) может быть сопротивлением стержня отвертки, [латекс]{R_2}[ /latex] сопротивление ручки, [latex]{R_3}[/latex] сопротивление тела человека и [latex]{R_4}[/latex] сопротивление его обуви.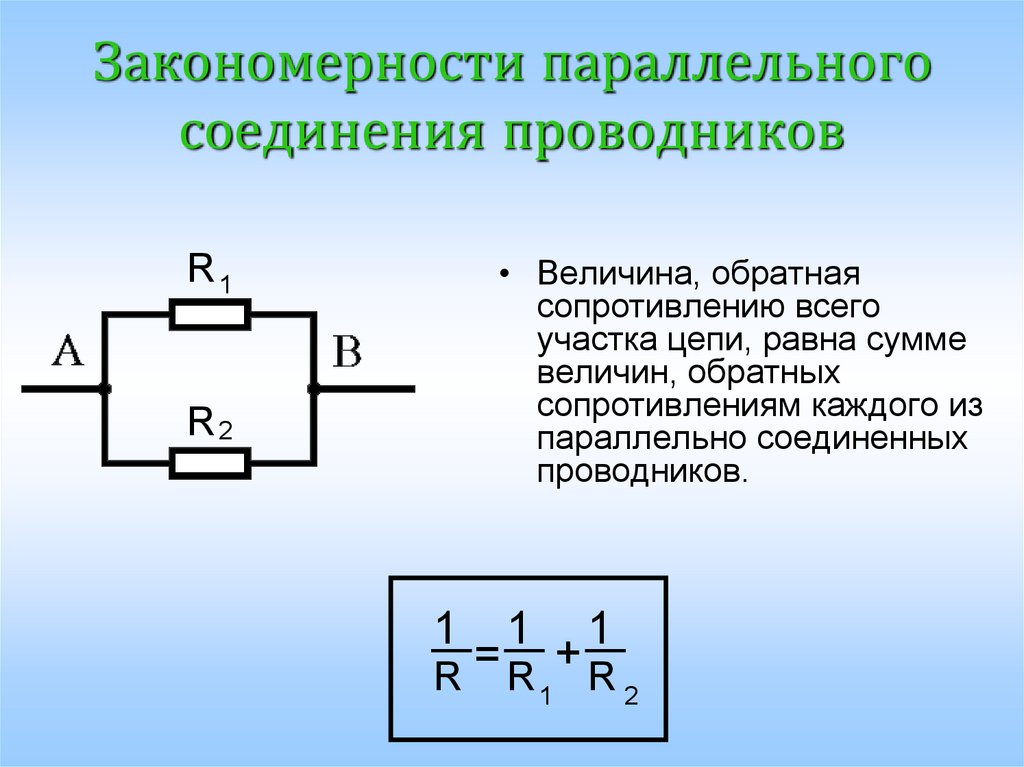
 Таким образом, энергия, подаваемая источником, равна [латекс]{qV}[/латекс], а энергия, рассеиваемая резисторами, равна
Таким образом, энергия, подаваемая источником, равна [латекс]{qV}[/латекс], а энергия, рассеиваемая резисторами, равна )
)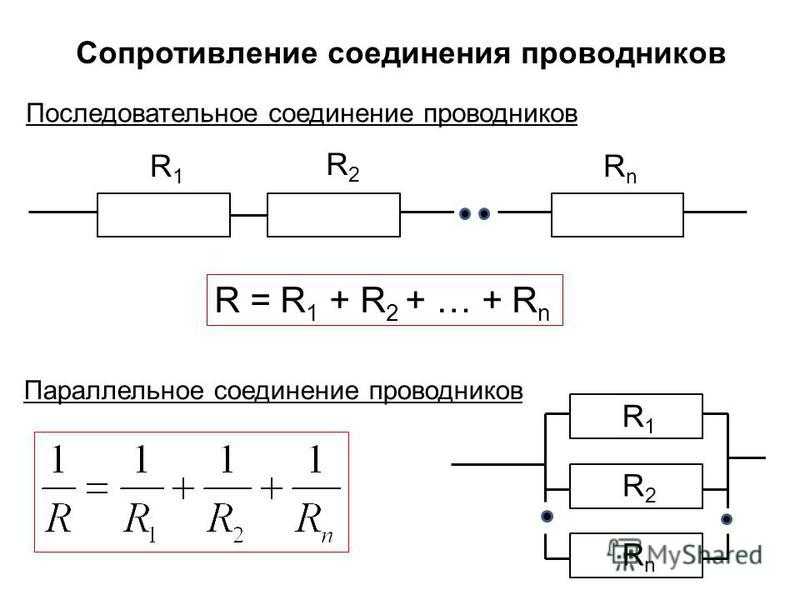 ], а сопротивления равны [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/латекс] и [латекс]{R_3 = 13,0 \; \Омега }[/латекс]. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
], а сопротивления равны [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/латекс] и [латекс]{R_3 = 13,0 \; \Омега }[/латекс]. а) Чему равно полное сопротивление? б) Найдите силу тока. (c) Рассчитайте падение напряжения на каждом резисторе и покажите, что их сумма равна выходному напряжению источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.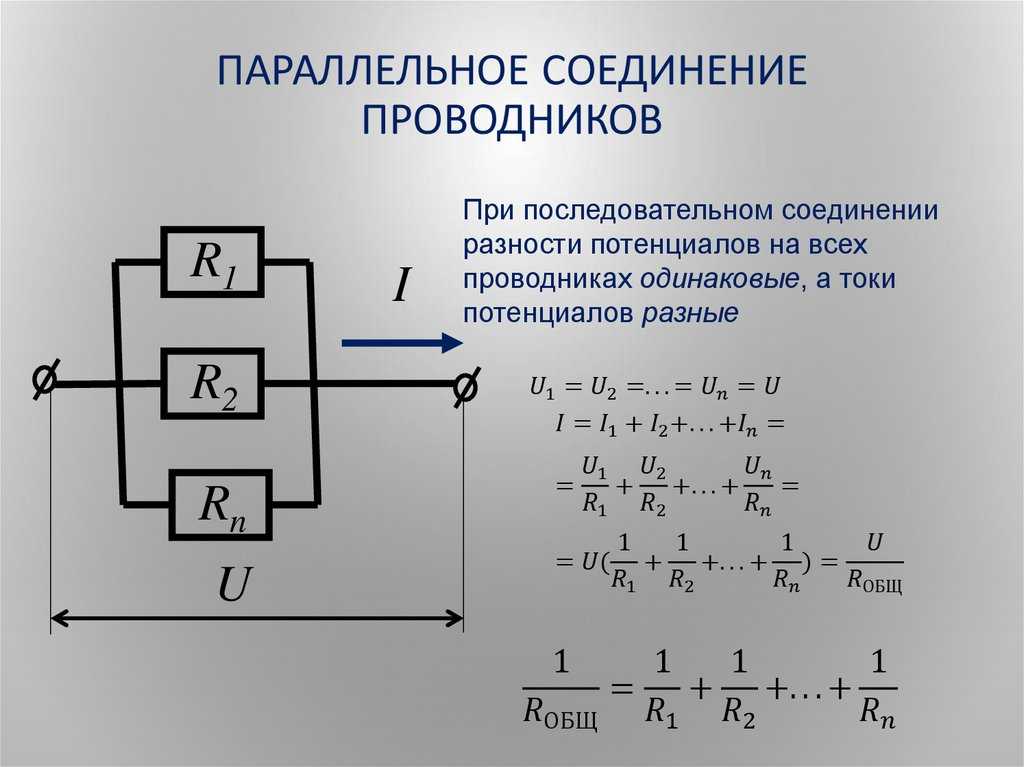 [/latex]
[/latex]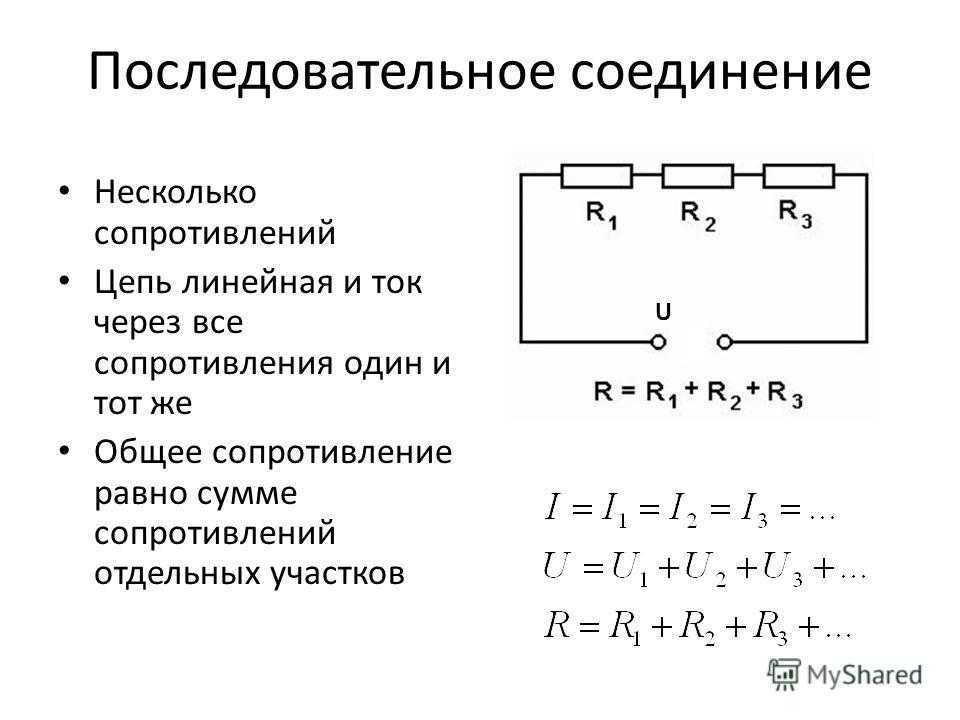 Это дает
Это дает Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.
Резисторы параллельны, когда каждый резистор подключен непосредственно к источнику напряжения соединительными проводами, имеющими незначительное сопротивление. Таким образом, к каждому резистору приложено полное напряжение источника.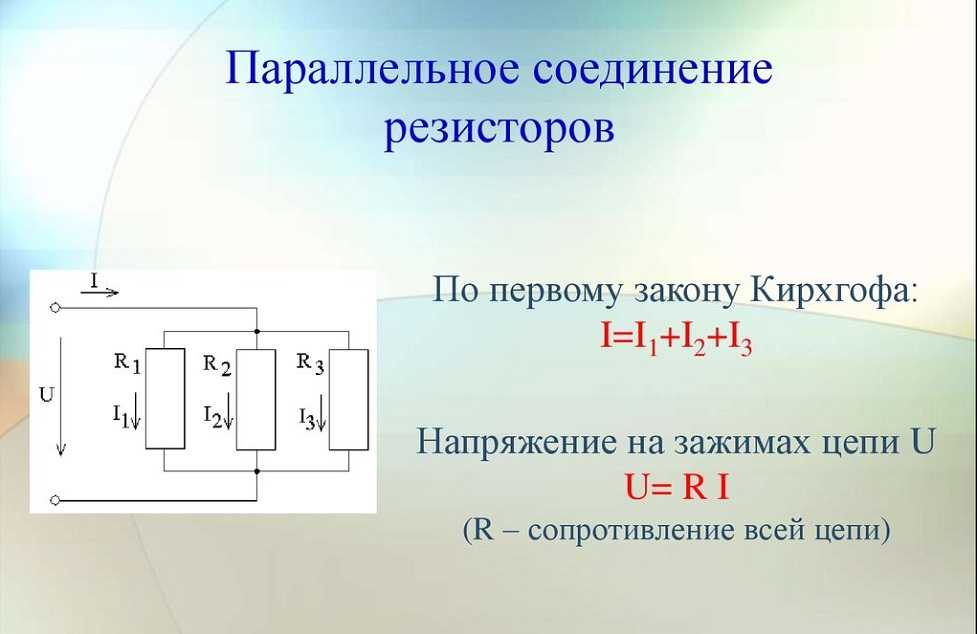 Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [latex]{I_1 = \frac{V}{R_1}}[/latex], [latex]{I_2 = \frac{V} {R_2}}[/latex] и [латекс]{I_3 = \frac{V}{R_3}}[/latex]. Сохранение заряда подразумевает, что полный ток [латекс]{I}[/латекс], производимый источником, представляет собой сумму этих токов:
Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [latex]{I_1 = \frac{V}{R_1}}[/latex], [latex]{I_2 = \frac{V} {R_2}}[/latex] и [латекс]{I_3 = \frac{V}{R_3}}[/latex]. Сохранение заряда подразумевает, что полный ток [латекс]{I}[/латекс], производимый источником, представляет собой сумму этих токов: [/латекс]
[/латекс]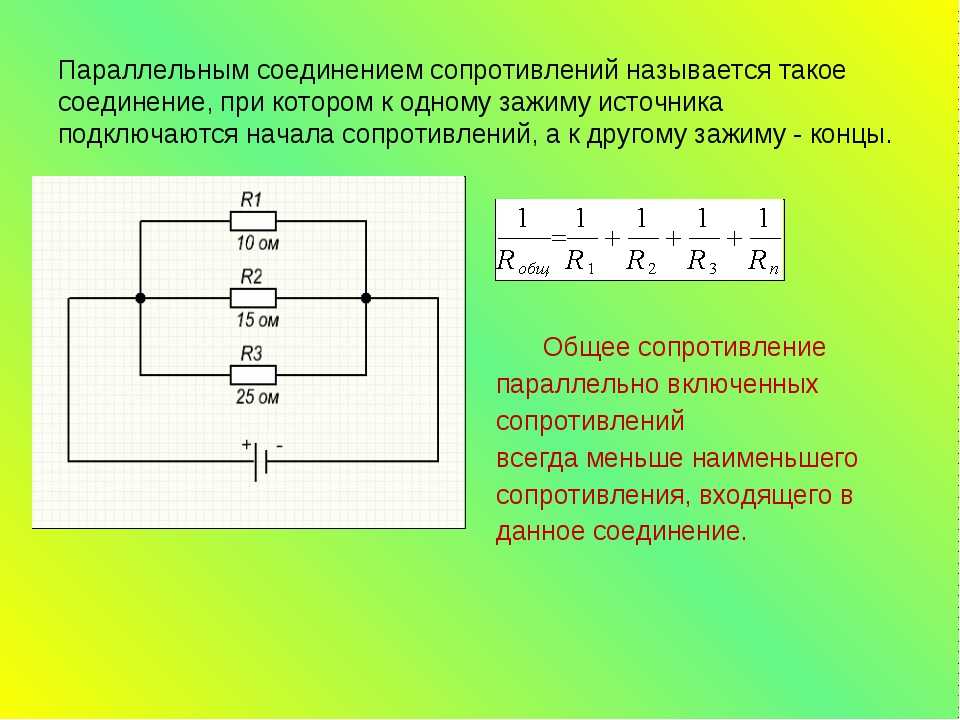 3 будут такими же, как и при последовательном соединении, рассмотренном ранее: [ латекс]{V = 12,0 \;\text{V}}[/латекс], [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/ латекс] и [латекс]{R_3 = 13,0 \;\Omega}[/латекс]. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами.
3 будут такими же, как и при последовательном соединении, рассмотренном ранее: [ латекс]{V = 12,0 \;\text{V}}[/латекс], [латекс]{R_1 = 1,00 \;\Omega}[/латекс], [латекс]{R_2 = 6,00 \;\Omega}[/ латекс] и [латекс]{R_3 = 13,0 \;\Omega}[/латекс]. а) Чему равно полное сопротивление? б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, что их сумма равна общему выходному току источника. г) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна полной мощности, рассеиваемой резисторами. 00 \;\Omega}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{13.0 \;\Omega}}.[/latex]
00 \;\Omega}}[/latex] [латекс]{+}[/latex] [латекс]{\frac{1}{13.0 \;\Omega}}.[/latex]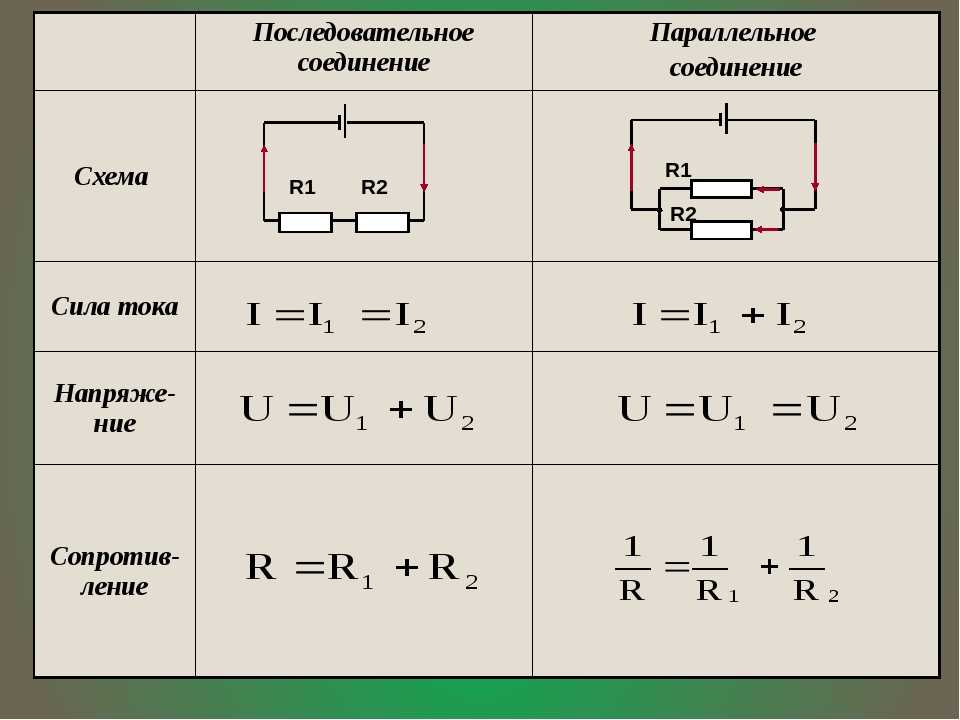
 00 \;\Omega}}[/latex] [латекс]{= 12.0 \;\textbf{A}}.[/latex]
00 \;\Omega}}[/latex] [латекс]{= 12.0 \;\textbf{A}}.[/latex]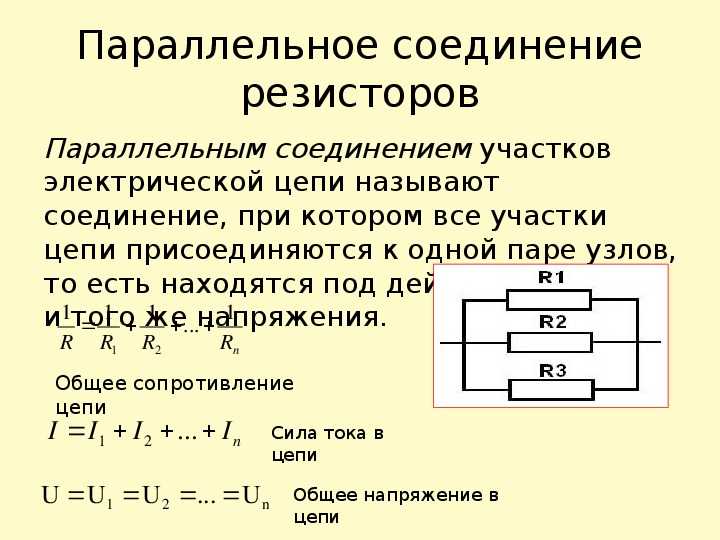 2}{R}}[/latex], поскольку на каждый резистор подается полное напряжение. Таким образом, 92}{13.0 \;\Omega}}[/latex] [latex]{= 11.1 \;\text{W}} .[/latex]
2}{R}}[/latex], поскольку на каждый резистор подается полное напряжение. Таким образом, 92}{13.0 \;\Omega}}[/latex] [latex]{= 11.1 \;\text{W}} .[/latex]
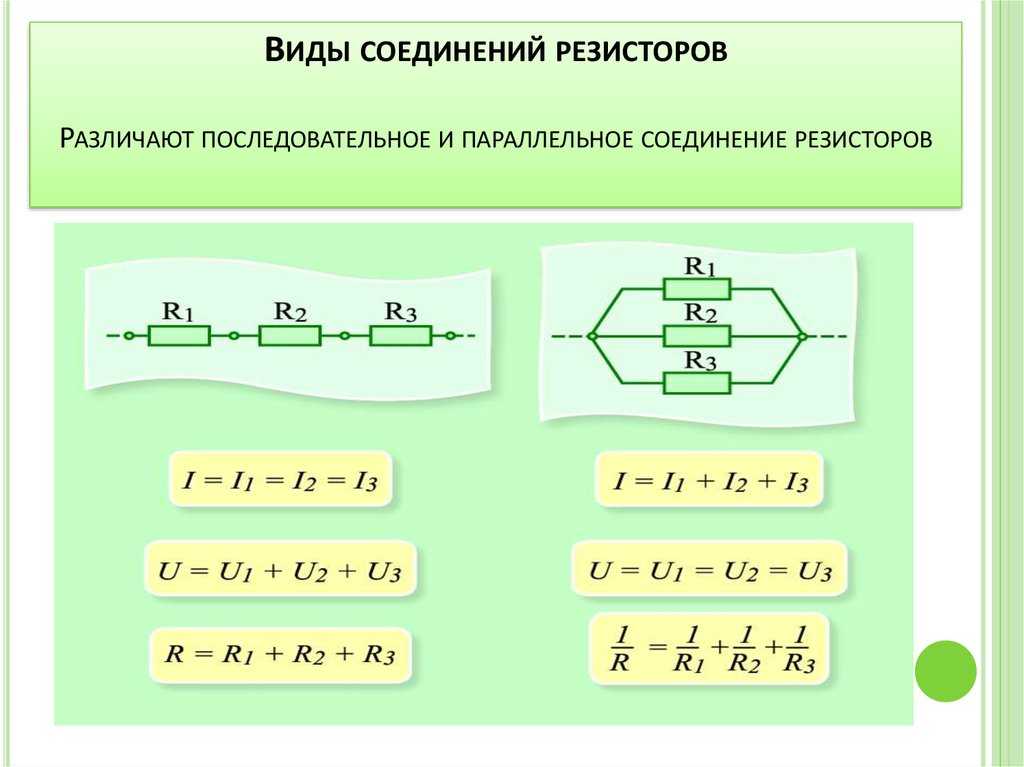
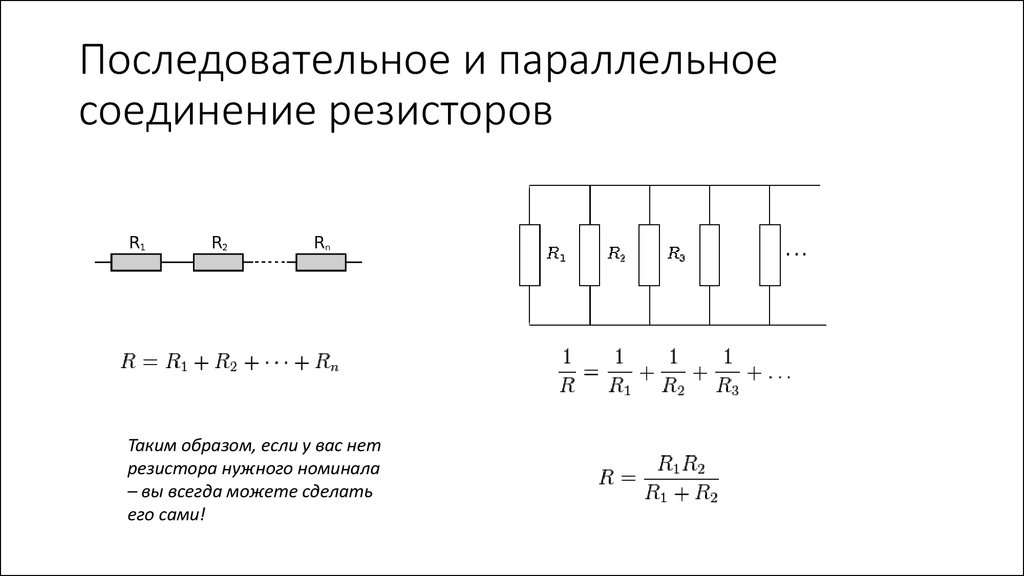 [латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс] могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.
[латекс]{R_2}[/латекс] и [латекс]{R_3}[/латекс] могут быть стартером и освещением салона. Ранее мы предполагали, что сопротивление провода пренебрежимо мало, но когда это не так, оно имеет важные последствия, как показывает следующий пример.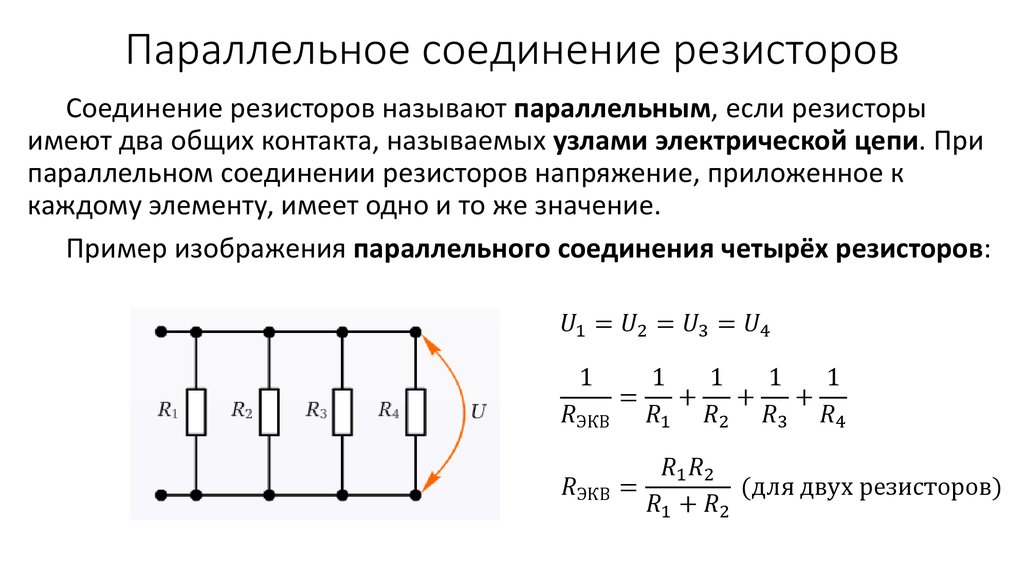
 [/ латекс]
[/ латекс] [/латекс]
[/латекс] [/latex]
[/latex] Если потребляется большой ток, падение [латекс]{ИК}[/латекс] в проводах также может быть значительным.
Если потребляется большой ток, падение [латекс]{ИК}[/латекс] в проводах также может быть значительным.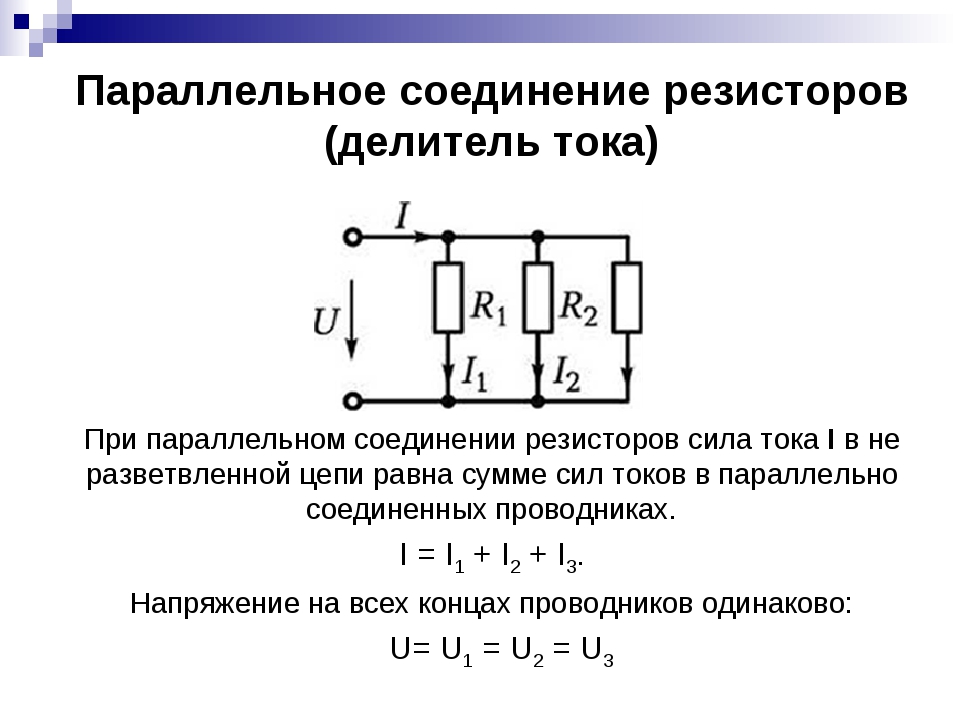
 Особое примечание: при поиске[/latex]латекса{R_p}[/latex] следует проявлять осторожность.
Особое примечание: при поиске[/latex]латекса{R_p}[/latex] следует проявлять осторожность.
 (Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)
(Обратите внимание, что на этой диаграмме буква E представляет напряжение (или электродвижущую силу) батареи.)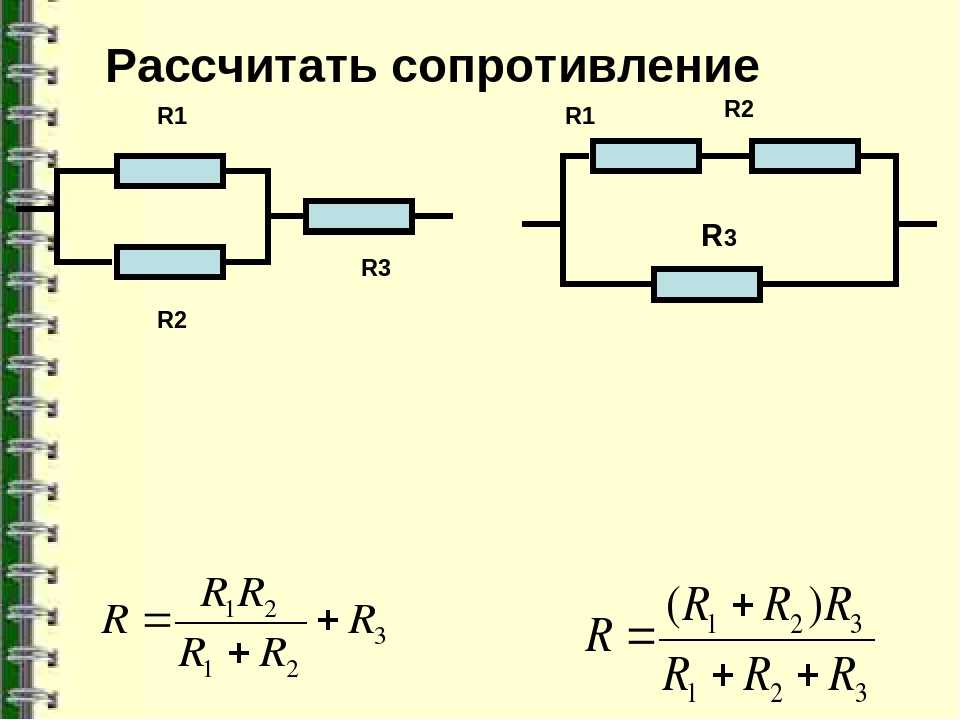 )
) Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 39остальные одинаковые лампочки, какое тогда рабочее напряжение у каждой?
Если перегорит одна такая лампочка, что будет с остальными? Если такая цепочка работает от 120 В и имеет 39остальные одинаковые лампочки, какое тогда рабочее напряжение у каждой?
 Какую мощность будет потреблять одна фара и стартер при последовательном подключении к аккумулятору 12,0 В? (Любым другим сопротивлением в цепи и любым изменением сопротивления в двух устройствах пренебречь). и [латекс]{96.0 — \;\Омега}[/латекс] резисторы, найдите ток и мощность для каждого из них при последовательном соединении. (b) Повторите, когда сопротивления параллельны.
Какую мощность будет потреблять одна фара и стартер при последовательном подключении к аккумулятору 12,0 В? (Любым другим сопротивлением в цепи и любым изменением сопротивления в двух устройствах пренебречь). и [латекс]{96.0 — \;\Омега}[/латекс] резисторы, найдите ток и мощность для каждого из них при последовательном соединении. (b) Повторите, когда сопротивления параллельны.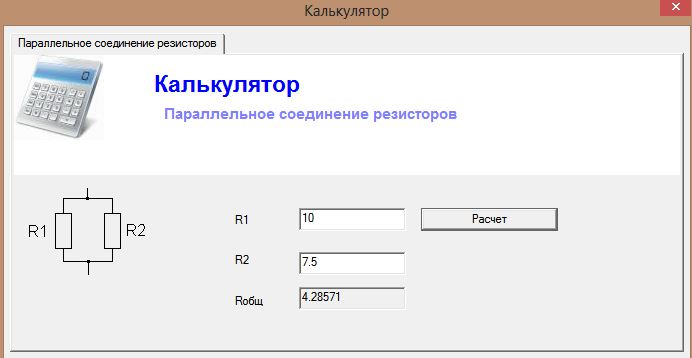 9- \;\Omega}[/latex] сопротивление. Рис. 9. (а) Каково сопротивление заземления 100 таких изоляторов? б) Рассчитайте мощность, рассеиваемую 100 из них. в) Какую долю мощности несет линия? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».
9- \;\Omega}[/latex] сопротивление. Рис. 9. (а) Каково сопротивление заземления 100 таких изоляторов? б) Рассчитайте мощность, рассеиваемую 100 из них. в) Какую долю мощности несет линия? Подробно покажите, как вы следуете шагам, описанным в разделе «Стратегии решения проблем для последовательных и параллельных резисторов».