Формула Бернулли. Решение задач
Схема Бернулли возникает при повторных независимых испытаниях. Независимыми испытаниями называются такие, которые зависят друг от друга, и от результатов предыдущих испытаний. Они могут проводиться как в однотипных условиях, так и в разных. В первом случае вероятность появления какого-либо события во всех испытаниях одна и та же, во втором случае она меняется от опыта к опыту.
Пусть для каждого опыта вероятность появления события равна , вероятность противоположного события определяется зависимостью
Нужно найти вероятность появления события ровно раз в серии из испытаний. При этом следует отметить, что событие в серии опытов может чередоваться любым способом, главное чтобы исполнилась ровно раз.
Результаты испытаний для удобства обозначаем буквой в случае появления события и для противоположного.
Испытания в которых происходит раз и не происходит () раз по определению будут благоприятными. Их количество равно количеству способов выбора элементов с и определяется по формуле сочетания
Определим вероятность благоприятной комбинации (в серии из испытаний появления события ровно раз). Для простоты записи, рассмотрим случай, когда событие произошло в первых опытах и не состоялось в остальных . Схематично его можно обозначить следующим образом, а вероятность найти по теореме умножения вероятностей
Для простоты записи, рассмотрим случай, когда событие произошло в первых опытах и не состоялось в остальных . Схематично его можно обозначить следующим образом, а вероятность найти по теореме умножения вероятностей
для других благоприятных испытаний и вероятности будут такие же, только порядок их в серии из экспериментов будет постоянно меняться
Все благоприятные испытания являются попарно несовместимы, поэтому для нахождения общей вероятности их нужно просуммировать
или
Вывел ее впервые швейцарский математик Якоб Бернулли (1654 г.-1705 г.).
Если просуммировать вероятности всех испытаний в которых событие может произойти от нуля до раз в серии испытаний, то получим полную вероятность
Слагаемые этой суммы совпадают по виду с расписанием бинома Ньютона
Легко убедится, что
В литературе можно встретить термин «биномиальное распределение вероятностей», это как раз множество всех вероятностей, которые просуммированы выше.
Как последствия, из формулы Бернулли выводятся следующие формулы для популярных для практики задач:
1) вероятность появления события «хотя бы один раз» в серии из испытаний
2) вероятность появления события «хотя бы определенное количество раз» в серии из испытаний вычисляют по формуле
или согласно свойству биномиального разложения вероятностей
На основе данной зависимости вводят в рассмотрение сквозную функцию, которая дает возможность определить возможное количество появления события в серии из испытаний
По свойству сквозной функции множители при степени переменной () равны вероятности появления события в серии из опытов ровно раз. Это легко проследить по формуле суммирования вероятностей всех возможных испытаний по схеме Бернулли.
Если вероятности появления события в каждом опыте разные , а противоположного равны то по свойствам сквозной функции вероятность события произойти раз в серии из опытов равна множителю при в расписании функции по степеням
Она достаточно часто встречается при решении задач, в которых вероятности появления события в каждом последующем опыте меняются и позволяет при небольшом количестве появления события быстро найти вероятность (решение задачи).
Вероятное количество появлений события в схеме Бернулли лежит в интервале
Для применения схемы Бернулли нужно, чтобы выполнялись три условия:
1) опыты должны быть независимы между собой;
2) каждый опыт должен иметь два результата , и никаких других вариантов;
3) вероятность появления события должна быть одинаковой для каждого следующего опыта.
Рассмотрим решения типичных для данной схемы задач.
——————————
Пример 1. В тире стрелок проводит 7 выстрелов по мишени с вероятностью попадания каждого 0,8. Какова вероятность того, что будет: а) ровно 4 попадания б) не менее 5 попаданий в) не более двух попаданий.
Решение. а) проводится независимых друг от друга испытаний с вероятностью попадания в мишень в каждом из них . Вероятность того, что будет точно попаданий вычисляем по формуле Бернулли:
б) событие , которое заключается в том, что при выстрелах будет не менее 5 попаданий, можно рассматривать как сумму трех несовместных событий: – 5 попаданий из 7, событие – 6 попаданий с 7 и – все 7 выстрелов метки.
По формуле Бернулли находим вероятности событий
Тогда вероятность события равна сумме найденных вероятностей
в) Подобным образом, вероятность события – не более двух попаданий при семи выстрелах можно вычислить, как сумму вероятностей трех событий:
– 2 попадания из 7,
– 1 из 7 ,
– ни одного попадания из 7 выстрелов (7 промахов).
На практике студенты часто забывают рассматривать событие — подобное отсутствию попадений , поэтому не делайте подобных ошибок и хорошо запомните возможность возникновения такого варианта. Вероятности находим по знакомой уже формуле
Суммируя вероятности получим
Однако, события (не более двух попаданий при семи выстрелах) и (не менее 5 попаданий при семи выстрелах) противоположны друг другу, поэтому
——————————
Пример 2. Монета подбрасывают пять раз. Найти вероятность того, что герб выпадет не более трех раз.
Решение. Вероятность выпадения герба или решки считаем независимым событием с вероятностью . По аналогии с предыдущей задачей, искомая вероятность равна сумме трех следующих
Чтобы не искать столько слагаемых, из приведенных выше формул получим простую
——————————
Пример 3. Вероятность появления события в одном опыте равна 0,4. Сколько нужно провести опытов, чтобы вероятное количество появления события была равна 20.
Решение. Согласно условия выписываем данные
и проводим расчеты согласно неравенству
С него получим
три числа 49,50,51.
——————————
Пример 4. Три биатлониста независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого равна 0,9, для второго — 0,85, для третьего — 0,8. Найти вероятность того, что будут закрыты две мишени из трех.
Решение. Вероятности попадания для стрелков разные, поэтому применяем образующую функцию. Для нее входные данные примут значения
Для нее входные данные примут значения
После подстановки и разложения в ряд получим
Искомая вероятность входит в расписание множителем при
Из этого примера также легко убедиться, что сумма всех множителей при степенях равна полной вероятности (единицы).
——————————
Схема Бернулли на практике не сложная, важно уловить как в вычислениях реализовать задачи вида «не более раз», «не менее раз», «ровно раз» с . Как только Вы это поймете, все остальное сведется к суммирования, умножению и возведения в степень.
Формула Бернулли и следствие из нее.
*Событие – результат (исход) испытания.
*Вероятность события-число характеризующее степень объективной возможности появл-я событий в опыте.
Пусть производятся n независимых опытов,в кажд из кот событие А может появиться с вероятностью р. Тогда вероятность того,что в серии из n независ опытов событие А появится ровно m раз определиться по формуле.
Pn(m)=Сnm×Pm(1-p)n—m
Все из событий А появл ровно n раз
С-число сочетаний из n-опытов по m
С=n!:(m!(n-m)!)
m-число появлений события А
р-вероятность появл событий в одном опыте.
Пример:
1) По цели пороизв 5 независ выстрелов. Вероятность попад-я при кажд выстреле 0,8. Определить вероятность поражения цели 3 выстрелами.
n=5
h=0,8
P(3)=?
1. Сост расчет формулу:
Р5(3)=С53×р3(1-р)2
С53=5!:(3!(5×3)!)=10
Р5(3)=10×0,83(1-0,8)2=0,2048(20%)
Следствие 1
Вероятность появл-я события хотя бы 1 раз в серии из n испытаний определяется по формуле:
Pn(m>=1)=1-(1-p)n
Р-вероятность попадания при 1 выстреле
1-р-вероятность промаха -//-
Следствие 2
Кол-во испытаний, опытов n необходимых д/появления события А хотя бы 1 раз с задан вероятностью опред по формуле:
(1-p)n =1-Pn(m>=1)
Pn(m>=1)-надежность
n×lg(1-p)=lg(1-Pn(m>=1))
n=(lg(1-Pn(m>=1)): lg(1-p)
Дискретные СВ и законы их распределения.
cB-величина, кот в рез-те опыта может принимать то или иное значение неизвестно заранее какое именно(№:выпадание чисел при брос игральн карты)
Примеры случайных величин:
1. Число выпавших очков при подбрасывании игральной кости (значения: 0,1, 2, 3, 4, 5, 6).
2. Число попаданий в цель при n выстрелах (значения: 0, 1, 2,…, n).
3. Количество бракованных изделий в партии (значения: 0, 1, 2,…, n).
4. Ошибки при измерении физической величины.
Виды СВ:
1. Дискретные
2. Непрерывные
Дискретные-величина,кот в рез-те опыта может принимать только конечное или счетное число значений(№:выпад чисел при однократ бросании кости)
Примеры дискретных случайных величин:
— число попаданий при n выстрелах: Х={0,1,2…n};
— число очков при бросании игральной кости: Х={0,1,2,3,4,5,6}
Непрерывная-величина.кот может принимать любое знач-е в пределах некоторого промежутка(№:отклонение снаряда от цели при 1 выстреле)
Полной, исчерпывающей хар-кой CB явл закон распредел-я СВ
Закон распредел-я СВ-соотношение, устанавливающее связь м/д возможными значениями случ величины и отличающими их вероятностями.
Формы законов распределения СВ
Для дискретных СВ сущ формы:
Ряд распределения
| Х | х1 | Х2 | … | хn |
| pi | p1 | p2 | … | pn |
-возможные значения вероятностей
-событий
2. Многоугольник распределения-графическое изображение выражения ряда распределения.
3. Функция распределения-вероятность события сост в том, что случайная величина Х примет значение меньшее фиксируемого значения х.
*вероятность не м.б. >1
Свойства:
1. Возрастающая по своему физическому смыслу
2. F(-∞)=0
F(+∞)=1
3. F(x1)= P(Х<x1)=Р(-∞<X<х1)
F(x2)= P(Х<x2)=Р(-∞<X<х2)
Р(х1<=X<x2)= F(x2)-F(x1)
Законы распределения наиболее часто встречающихся на практике СВ.
Закон распределения дискретных СВ.
Биномиальный закон (Я.Бернулли)
Дискретная СВ X имеет биномиальное распределение, если ее возможные значения 0,1,2,n (конечно число значений) и отвечающие им вероятности рассчит по формуле:
Рm=P(X=m)=Cnmpmqn—m
P(X=m)-вероятность того,что СВ примет значение равное m
р-вероятность появления события А в одном опыте
q=(1-р)-вероятность не появл-я -//-
n-число проведенных опытов
*Р-не изм в каждом опыте. Все проводимые опыты должны провод в одинак условиях. №: на практике при контроле партии: выним из коробки,проверяют,записывают,кладут обратно в коробку. Затем берут др и тд. Если брак запис и возвр в контрол партию, тогда число подчин биномиальн закону.
Хар-ки закона:
M(x)=n*p-мат ожидание
Dx=h*p*q-дисперсия
σх=√ h*p*q-среднее квадратическое отклонение
Закон Пуассона
Распределение Пуассона-предельное распределение,к кот стремится биномиальное распределение. При увел числа n опытов и одновременном уменьшении вероятности появления события в одном опыте.
При увел числа n опытов и одновременном уменьшении вероятности появления события в одном опыте.
n→∞, p→0
закон Пуассона часто называют ЗАКОНОМ РЕДКИХ СОБЫТИЙ, т.к. вероятность столь мала.
СВ X имеет распределение Пуассона если ее возможные значения в серии из n испытаний: X 0,1,2,…m, … а соответствующие им вероятности: Рm= P(X=m)=(am:m!)×e—a
a-параметр закона Пуассона a=n*p
e-иррац число (2ой замечат предел) 2<e<3
n-число которое примет х
Хар-ки закона:
M(x)=a-мат ожидание
Dx=a-дисперсия
σч=√ a-среднее квадратическое отклонение
на практике данный закон применяется при многократном контроле продукции прибором высокой надежности (многокр контроль m
Примеры решения задач на тему «Случайные величины»
Примеры
решения задач на тему «Случайные величины».
Задача 1. В лотерее выпущено 100 билетов. Разыгрывался один выигрыш в 50 у.е. и десять выигрышей по 10 у.е. Найти закон распределения величины X – стоимости возможного выигрыша.
Решение. Возможные значения величины X: x1 = 0; x2 = 10 и x3 = 50. Так как «пустых» билетов – 89, то p1 = 0,89, вероятность выигрыша 10 у.е. (10 билетов) – p2 = 0,10 и для выигрыша 50 у.е. – p3 = 0,01. Таким образом:
|
X |
0 |
10 |
50 |
|
P |
0,89 |
0,10 |
0,01 |
Легко проконтролировать:.
Задача 2. Вероятность того,
что покупатель ознакомился заранее с рекламой товара равна 0,6 (р=0,6). Осуществляется выборочный контроль
качества рекламы путем опроса покупателей до первого, изучившего рекламу заранее.
Составить ряд распределения количества опрошенных покупателей.
Вероятность того,
что покупатель ознакомился заранее с рекламой товара равна 0,6 (р=0,6). Осуществляется выборочный контроль
качества рекламы путем опроса покупателей до первого, изучившего рекламу заранее.
Составить ряд распределения количества опрошенных покупателей.
Решение. Согласно условию задачи р = 0,6. Откуда: q=1-p = 0,4. Подставив данные значения, получим: и построим ряд распределения:
Х |
1 |
2 |
… |
m |
… |
|
pi |
0,6 |
0,24 |
… |
|
… |
Задача 3. Компьютер состоит из трех независимо работающих элементов:
системного блока, монитора и клавиатуры. При однократном резком повышении
напряжения вероятность отказа каждого элемента равна 0,1. Исходя из распределения
Бернулли составить закон распределения числа отказавших элементов при скачке
напряжения в сети.
Компьютер состоит из трех независимо работающих элементов:
системного блока, монитора и клавиатуры. При однократном резком повышении
напряжения вероятность отказа каждого элемента равна 0,1. Исходя из распределения
Бернулли составить закон распределения числа отказавших элементов при скачке
напряжения в сети.
Решение. Рассмотрим распределение Бернулли (или биномиальное): вероятность того, что в n испытаниях событие А появится ровно k раз: , или:
|
X |
0 |
1 |
… |
… |
n |
|
|
P |
qn |
|
… |
|
… |
pn |
Вернёмся к задаче.
Возможные значения величины X (число отказов):
x0 =0 – ни один из элементов не отказал;
x1 =1 – отказ одного элемента;
x2 =2 – отказ двух элементов;
x3 =3 – отказ всех элементов.
Так как, по условию, p = 0,1, то q = 1 – p = 0,9. Используя формулу Бернулли, получим
, ,
, .
Контроль: .
Следовательно, искомый закон распределения:
|
X |
0 |
1 |
2 |
3 |
|
p |
0,729 |
0,243 |
0,027 |
0,001 |
Задача 4. Произведено 5000 патронов.
Вероятность того, что один патрон бракованный . Какова вероятность того, что во всей партии будет ровно 3
бракованных патрона?
Произведено 5000 патронов.
Вероятность того, что один патрон бракованный . Какова вероятность того, что во всей партии будет ровно 3
бракованных патрона?
Решение. Применим распределение Пуассона: это распределение используется для определения вероятности того, что при очень большом
количестве испытаний (массовые испытания), в каждом из которых вероятность события A очень мала, событие A наступит k раз: , где .
Здесь n = 5000, p = 0,0002, k = 3. Находим , тогда искомая вероятность: .
Задача 5. При стрельбе до первого попадания с вероятностью попадания p = 0,6 при выстреле надо найти вероятность того, что попадание произойдет при третьем выстреле.
Решение. Применим геометрическое
распределение: пусть производятся независимые испытания, в каждом из которых
событие A имеет вероятность появления p (и непоявления
q = 1 – p). Испытания заканчиваются, как только произойдет
событие A.
Испытания заканчиваются, как только произойдет
событие A.
При таких условиях вероятность того, что событие A произойдет на k-ом испытании, определяется по формуле: . Здесь p = 0,6; q = 1 – 0,6 = 0,4; k = 3. Следовательно, .
Задача 6. Пусть задан закон распределения случайной величины X:
|
X |
1 |
2 |
|
P |
0,2 |
0,8 |
Найти математическое ожидание.
Решение. .
Заметим, что вероятностный смысл математического ожидания – это среднее значение случайной величины.
Задача 7. Найти дисперсию случайной величины X со следующим законом распределения:
|
X |
2 |
3 |
5 |
|
P |
0,1 |
0,6 |
0,3 |
Решение. Здесь .
Здесь .
Закон распределения квадрата величины X2:
|
X2 |
4 |
9 |
25 |
|
P |
0,1 |
0,6 |
0,3 |
.
Искомая дисперсия: .
Дисперсия характеризует меру отклонения (рассеяния) случайной величины от её математического ожидания.
Задача 8. Пусть случайная величина задается распределением:
|
X |
2м |
3м |
10м |
|
P |
0,1 |
0,4 |
0,5 |
Найти
её числовые характеристики.
Решение: м, м2,
м2, м.
Про случайную величину X можно сказать либо – ее математическое ожидание 6,4 м с дисперсией 13,04 м2, либо – ее математическое ожидание 6,4 м с отклонением м. Вторая формулировка, очевидно, нагляднее.
Задача 9. Случайная величина X задана функцией распределения: .
Найти вероятность того, что в результате испытания величина X примет значение, заключенное в интервале .
Решение. Вероятность того, что X примет значение из заданного интервала, равно приращению интегральной функции в этом интервале, т.е. . В нашем случае и , поэтому
.
Задача 10. Дискретная случайная величина X задана законом распределения:
|
X |
2 |
5 |
8 |
|
P |
0,6 |
0,1 |
0,3 |
Найти
функцию распределения F(x) и построить ее график.
Решение. Так как функция распределения,
для , то
при ;
при ;
при ;
при ;
Соответствующий график:
Задача 11. Непрерывная случайная величина X задана дифференциальной функцией распределения: .
Найти вероятность попадания X в интервал
.
Решение. Заметим, что это частный случай показательного закона распределения.
Воспользуемся формулой: .
.
Задача 12. Найти числовые характеристики дискретной случайной величины X, заданной законом распределения:
|
X |
–5 |
2 |
3 |
4 |
|
p |
0,4 |
0,3 |
0,1 |
0,2 |
Решение. Математическое ожидание:
Математическое ожидание:
.
Запишем закон распределения X2:
|
X2 |
25 |
4 |
9 |
16 |
|
p |
0,4 |
0,3 |
0,1 |
0,2 |
Математическое ожидание:
.
Находим дисперсию:
, .
Задача 13. Непрерывная случайная величина задана на интервале плотностью
распределения , а вне этого интервала . Найти ее числовые характеристики.
Найти ее числовые характеристики.
Решение. Математическое ожидание:
.
Дисперсия: .
Среднее квадратическое отклонение: .
Задача 14. Найти числовые характеристики случайной величины X, равномерно распределенной на интервале .
Решение. Для случайной величины, равномерно распределеной на интервале , плотность распределения: ,
поэтому: ; ; .
Задача 15. Математическое ожидание нормально распределенной случайной величины , а среднее квадратическое отклонение — . Найти вероятность того, что в результате испытания X примет значение из интервала и записать закон распределения.
Решение. Запишем вначале закон распределения. Общая формула имеет вид: .
Подставляя и , получим: .
Вероятность того, что X примет значение из интервала имеет вид:
, где – функция Лапласа.
Значения этой функции находятся с помощью таблицы.
В нашем случае: .
По таблице находим: , следовательно:
.
Схема Бернулли. Примеры решения задач
Формула Бернулли — формула в теории вероятностей , позволяющая находить вероятность появления события A {\displaystyle A} при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли , который вывел эту формулу.
Энциклопедичный YouTube
1 / 3
✪ Теория вероятностей. 22. Формула Бернулли. Решение задач
✪ Формула Бернулли
✪ 20 Повторение испытаний Формула Бернулли
Субтитры
Формулировка
Теорема.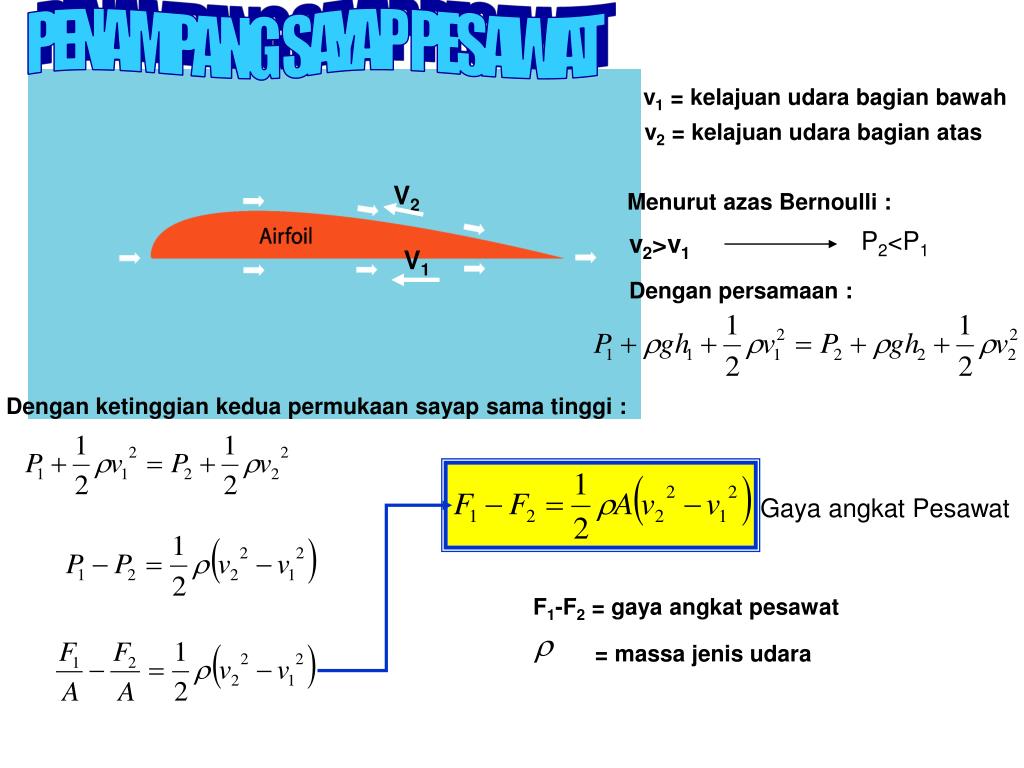 {n-k}}
, где
q
=
1
−
p
{\displaystyle q=1-p}
.
{n-k}}
, где
q
=
1
−
p
{\displaystyle q=1-p}
.
Доказательство
Пусть проводится n {\displaystyle n} независимых испытаний, причём известно, что в результате каждого испытания событие A {\displaystyle A} наступает с вероятностью P (A) = p {\displaystyle P\left(A\right)=p} и, следовательно, не наступает с вероятностью P (A ¯) = 1 − p = q {\displaystyle P\left({\bar {A}}\right)=1-p=q} . Пусть, так же, в ходе испытаний вероятности p {\displaystyle p} и q {\displaystyle q} остаются неизменными. Какова вероятность того, что в результате n {\displaystyle n} независимых испытаний, событие A {\displaystyle A} наступит ровно k {\displaystyle k} раз?
Оказывается можно точно подсчитать число «удачных» комбинаций исходов испытаний, для которых событие A {\displaystyle A} наступает k {\displaystyle k} раз в n {\displaystyle n} независимых испытаниях, — в точности это количество сочетаний из n {\displaystyle n} по k {\displaystyle k} :
C
n
(k)
=
n
!
k
!
(n
−
k)
!
{\displaystyle C_{n}(k)={\frac {n!}{k!\left(n-k\right)!}}}
. {n}(P_{k,n})=1}
.
{n}(P_{k,n})=1}
.
При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться событие А , причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас интересует не результат каждого выстрела, а общее число попаданий. Такие задачи решаются достаточно просто, если опыты являются независимыми .
Определение . Независимыми относительно события А испытаниями называются такие, в которых вероятность события А в каждом испытании не зависит от исходов других испытаний.
Пример. Несколько последовательных выниманий карты из колоды представляют собой независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются; в противном случае это – зависимые опыты.
Пример . Несколько выстрелов представляют собой независимые опыты только в случае, если прицеливание производится заново перед каждым выстрелом; в случае, когда прицеливание производится один раз перед всей стрельбой или непрерывно осуществляется в процессе стрельбы (стрельба очередью, бомбометание серией), выстрелы представляют собой зависимые опыты.
Независимые испытания могут производиться в одинаковых или различных условиях. В первом случае вероятность события А во всех опытах одна и та же, во втором случае вероятность события А меняется от опыта к опыту. Первый случай связан со многими задачами теории надежности, теории стрельбы и приводит к так называемой схеме Бернулли , которая состоит в следующем:
1) проводится последовательность n независимых испытаний, в каждом из которых событие А может появиться, либо не появиться;
2) вероятность появления события А в каждом испытании постоянна и равна , как и вероятность его не появления .
Формула Бернулли, с помощью которой находится вероятность появления события А k раз в n независимых испытаниях, в каждом из которых событие А появляется с вероятностью p :
. (1)
Замечание 1 . С возрастанием n и k применение формулы Бернулли связано с вычислительными трудностями, поэтому формула (1) применяется, в основном, если k не превосходит 5 и n не велико.
Замечание 2. В связи с тем, что вероятности по форме представляют собой члены разложения бинома , распределение вероятностей вида (1) называется биномиальным распределением.
Пример . Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность пяти попаданий при шести выстрелах.
Решение. Так как , то , кроме того и . Пользуясь формулой Бернулли, получим:
Пример . Производится четыре независимых выстрела по одной и той же цели с различных расстояний. Вероятности попадания при этих выстрелах равны соответственно:
Найти вероятности ни одного, одного, двух, трех и четырех попаданий:
Решение. Составляем производящую функцию:
Составляем производящую функцию:
Пример . Производится пять независимых выстрелов по цели, вероятность попадания в которую равна 0,2. Для разрушения цели достаточно трех попаданий. Найти вероятность того, что цель будет разрушена.
Решение. Вероятность разрушения цели вычисляем по формуле:
Пример . Производится десять независимых выстрелов по цели, вероятность попадания в которую при одном выстреле равна 0,1. Для поражения цели достаточно одного попадания. Найти вероятность поражения цели.
Решение. Вероятность хотя бы одного попадания вычисляем по формуле:
3. Локальная теорема Муавра-Лапласа
В приложениях часто приходится вычислять вероятности различных событий, связанных с числом появлений события в n испытаниях схемы Бернулли при больших значениях n . В этом случае вычисления по формуле (1) становятся затруднительными. Трудности возрастают, когда приходится ещё суммировать эти вероятности. Затруднения при вычислениях возникают также при малых значениях p или q .
Затруднения при вычислениях возникают также при малых значениях p или q .
Лаплас получил важную приближенную формулу для вероятности появления события А точно m раз, если — достаточно большое число, то есть при .
Локальная теорема Муавра – Лапласа . Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы , , величина ограничена равномерно по m и n, то вероятность появления события А ровно m раз в n независимых испытаниях приближенно равна
Пусть относительно события А проводится n испытаний. Введем события: Аk — событие А осуществилось при k-том испытании, $ k=1,2,\dots , n$. Тогда $\bar{A}_{k} $ — противоположное событие (событие А не осуществилось при k-том испытании, $k=1,2,\dots , n$).
Что такое однотипные и независимые испытания
Определение
Испытания называются однотипными по отношению к событию А, если вероятности событий $А1, А2, \dots , Аn$ совпадают: $Р(А1)=Р(А2)= \dots =Р(Аn)$ (т.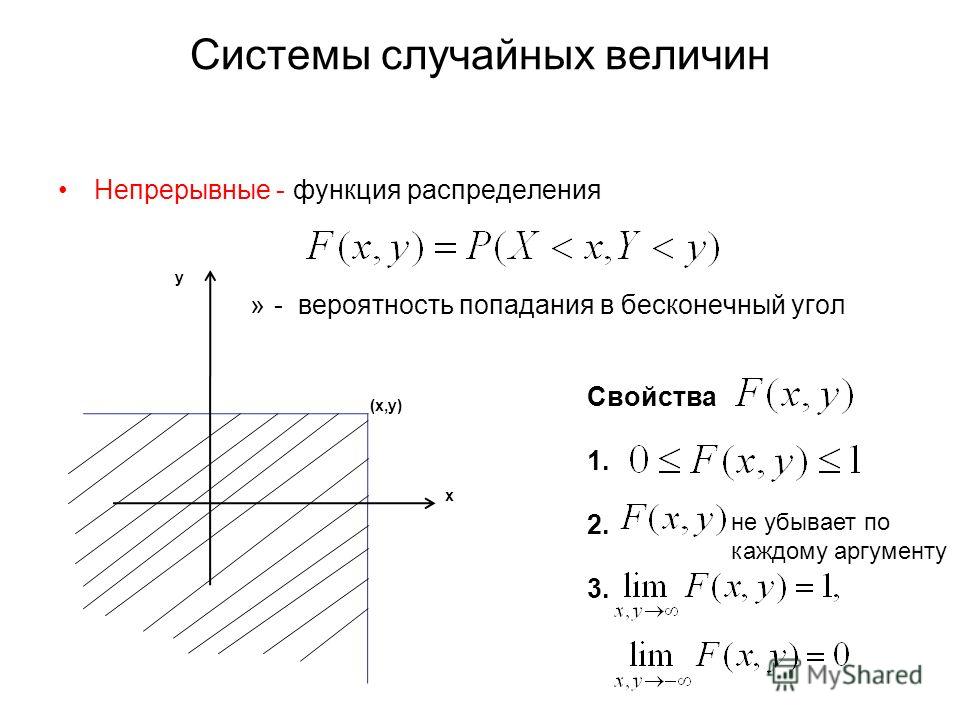 {5} =\frac{1}{32} $,
{5} =\frac{1}{32} $,
\ \ \
Следовательно, искомая вероятность $D =D_{5} (0)+D_{5} (1)+D_{5} (2)+D_{5} (3)=\frac{13}{16} $.
Ответ: $\frac{13}{16} $.
Пример 4
Первый стрeлок при одном выстриле может попасть в десятку с вероятностью 0,6 в девятку с вероятностью 0,3, а в восьмерку с вероятностью 0,1. Какая вероятность того, что при 10 выстрелах он попадет в десятку шесть раз, в девятку три раза и в восьмерку 1 раз?
Производится n опытов по схеме Бернулли с вероятностью успеха p . Пусть X — число успехов. Случайная величина X имеет область значений {0,1,2,…,n}. Вероятности этих значений можно найти по формуле:
, где C m n — число сочетаний из n по m .
Ряд распределения имеет вид:
| x | 0 | 1 | … | m | n |
| p | (1-p) n | np(1-p) n-1 | … | C m n p m (1-p) n-m | p n |
Этот закон распределения называется биноминальным .
Назначение сервиса . Онлайн-калькулятор используется для построения биноминальным ряда распределения и вычисления всех характеристик ряда: математического ожидания, дисперсии и среднеквадратического отклонения. Отчет с решением оформляется в формате Word (пример).
Число испытаний: n = , Вероятность p =При малой вероятности p и большом количестве n (np формула Пуассона.
Видеоинструкция
Схема испытаний Бернулли
Числовые характеристики случайной величины, распределенной по биноминальному закону
Математическое ожидание случайной величины Х, распределенной по биноминальному закону.
M[X]=np
Дисперсия случайной величины Х, распределенной по биноминальному закону.
D[X]=npq
Пример №1
. Изделие может оказаться дефектным с вероятностью р = 0.3 каждое. Из партии выбирают три изделия. Х – число дефектных деталей среди отобранных. Найти (все ответы вводить в виде десятичных дробей): а) ряд распределения Х; б) функцию распределения F(x) .
Решение . Случайная величина X имеет область значений {0,1,2,3}.
Найдем ряд распределения X.
P 3 (0) = (1-p) n = (1-0.3) 3 = 0.34
P 3 (1) = np(1-p) n-1 = 3(1-0.3) 3-1 = 0.44
P 3 (3) = p n = 0.3 3 = 0.027
| x i | 0 | 1 | 2 | 3 |
| p i | 0.34 | 0.44 | 0.19 | 0.027 |
Математическое ожидание находим по формуле M[X]= np = 3*0.3 = 0.9
Проверка: m = ∑x i p i .
Математическое ожидание M[X] .
M[x] = 0*0.34 + 1*0.44 + 2*0.19 + 3*0.027 = 0.9
Дисперсию находим по формуле D[X]=npq = 3*0.3*(1-0.3) = 0.63
Проверка: d = ∑x 2 i p i — M[x] 2 .
Дисперсия D[X] .
D[X] = 0 2 *0.34 + 1 2 *0.44 + 2 2 *0.19 + 3 2 *0. 027 — 0.9 2 = 0.63
027 — 0.9 2 = 0.63
Среднее квадратическое отклонение σ(x) .
Функция распределения F(X) .
F(xF(0F(1F(2F(x>3) = 1
- Вероятность появления события в одном испытании равна 0.6 . Производится 5 испытаний. Составить закон распределения случайной величины Х – числа появлений события.
- Составить закон распределения случайной величины Х числа попаданий при четырех выстрелах, если вероятность попадания в цель при одном выстреле равна 0.8 .
- Монету подбрасывают 7 раз. Найти математическое ожидание и дисперсию числа появлений герба. Примечание: здесь вероятность появление герба равна p = 1/2 (т.к. у монеты две стороны).
Пример №2 . Вероятность появления события в отдельном испытании равна 0.6 . Применяя теорему Бернулли, определите число независимых испытаний, начиная с которого вероятность отклонения частоты события от его вероятности по абсолютной величине меньше 0.1 , больше 0.97 . (Ответ: 801)
Пример №3
. Студенты выполняют контрольную работу в классе информатики. Работа состоит из трех задач. Для получения хорошей оценки нужно найти правильные ответы не меньше чем на две задачи. К каждой задаче дается 5 ответов из которых только одна правильная. Студент выбирает ответ наугад. Какая вероятность того, что он получит хорошую оценку?
Работа состоит из трех задач. Для получения хорошей оценки нужно найти правильные ответы не меньше чем на две задачи. К каждой задаче дается 5 ответов из которых только одна правильная. Студент выбирает ответ наугад. Какая вероятность того, что он получит хорошую оценку?
Решение . Вероятность правильно ответить на вопрос: p=1/5=0.2; n=3.
Эти данные необходимо ввести в калькулятор. В ответ см. для P(2)+P(3).
Пример №4 . Вероятность попадания стрелка в мишень при одном выстреле равна (m+n)/(m+n+2) . Производится n+4 выстрела. Найти вероятность того, что он промахнется не более двух раз.
Примечание . Вероятность того, что он промахнется не более двух раз включает в себя следующие события: ни разу не промахнется P(4), промахнется один раз P(3), промахнется два раза P(2).
Пример №5
. Определите распределение вероятностей числа отказавших самолётов, если влетает 4 машины. Вероятность безотказной работы самолета Р=0.99 . Число отказавших в каждом вылете самолётов распределено по биноминальному закону.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А .
В разных независимых испытаниях событие А может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие А имеет одну и ту же вероятность.
Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми .
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Условимся считать, что вероятность события A в каждом испытании одна и та же, а именно равна р . Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 — p .
Поставим перед собой задачу вычислить вероятность того, что при n испытаниях событие А осуществится ровно k раз и, следовательно, не осуществится n — k раз. Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно k раз в определенной последовательности.
Важно подчеркнуть, что не требуется, чтобы событие А повторилось ровно k раз в определенной последовательности.
Например, если речь идет о появлении события А три раза в четырех испытаниях, то возможны следующие сложные события: ААА, ААА, ААА, ААА . Запись ААА означает, что в первом, втором и третьем испытаниях событие А наступило, а в четвертом испытании оно не появилось, т.е. наступило противоположное событие А; соответственный смысл имеют и другие записи.
Искомую вероятность обозначим Р п (k) . Например, символ Р 5 (3) означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
Вывод формулы Бернулли . Вероятность одного сложного события, состоящего в том, что в п испытаниях событие А наступит k раз и не наступит п — k раз, по теореме умножения вероятностей независимых событий равна p k q n — k .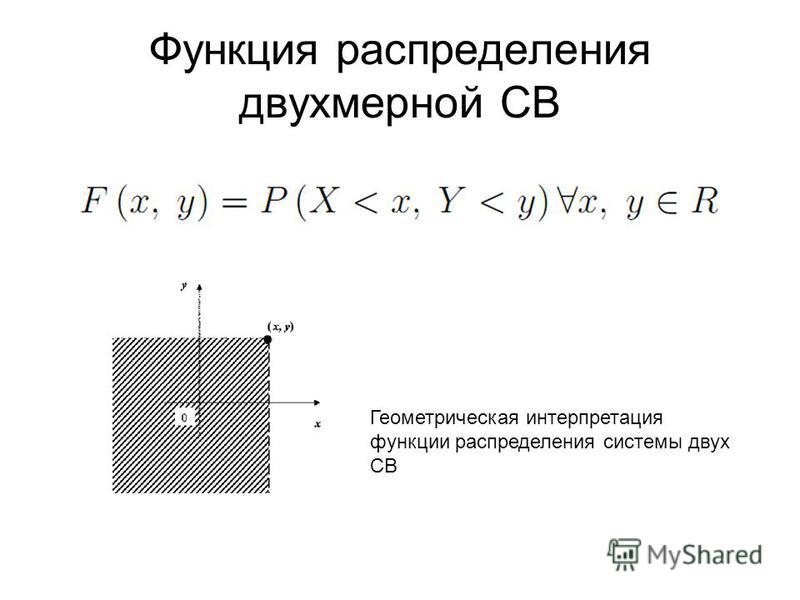 Таких сложных событий может быть столько, сколько можно составить сочетаний из п элементов по k элементов, т.е. С n k .
Таких сложных событий может быть столько, сколько можно составить сочетаний из п элементов по k элементов, т.е. С n k .
Так как эти сложные события несовместны , то по теореме сложения вероятностей несовместных событий искомая вероятность равна сумме вероятностей всех возможных сложных событий . Поскольку же вероятности всех этих сложных событий одинаковы, то искомая вероятность (появления k раз события А в п испытаниях) равна вероятности одного сложного события, умноженной на их число:
Полученную формулу называют формулой Бернулли .
Пример 1 . Вероятность того, что расход электроэнергии в течение одних суток не превысит установленной нормы, равна р = 0,75 . Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение . Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна р = 0,75 . Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1 — р = 1 — 0,75 = 0,25.
Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1 — р = 1 — 0,75 = 0,25.
Искомая вероятность по формуле Бернулли равна:
Схема Бернулли
Если производится несколько испытаний (опытов), причем вероятность события A в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события A.
Биноминальное распределение
В схеме Я. Бернулли рассматривается серия, состоящая из n независимых испытаний, каждое из которых имеет лишь два исхода: наступление какого-то события (успех) или его не наступление (неудача). Причем вероятность успеха при одном испытании равна – постоянна и не зависит от номера испытания. Следовательно, вероятность неуспеха — тоже постоянна.
Сформулируем задачу – вычислить вероятность того, что при испытаниях событие осуществится ровно раз и, следовательно, не осуществится – раз. Чтобы стало понятнее сделаю схематический чертеж:
По теореме умножения вероятностей независимых событий искомая вероятность будет равна:
Однако интересующее нас событие ( успехов при опытах) может произойти не только одним способом. Число возможных вариантов (комбинаций) выборки элементов из вычисляется по формуле:
Число возможных вариантов (комбинаций) выборки элементов из вычисляется по формуле:
Окончательно получим
Это и есть формула Бернулли (биномиальное распределение). Вспомним формулу бинома Ньютона:
Отсюда, и непосредственно из формулы Бернулли следует:
Очевидно этот же результат получится, если учтем, что для получим полную группу событий, вероятность которых равна 1.
Теперь давайте все эти сперва непонятные формулы рассмотрим на примере.
ПРИМЕР 1. В семье 10 детей. Считая, что вероятность рождения мальчика равна 0,5, найдем вероятность того, что в семье имеются 0, 1, …, 10 мальчиков.
Решение
Отметим, что в силу предположения и равенства имеют место равенства: . Отсюда получим:
,
,
,
,
,
ОТВЕТ
В многодетной семье с десятью детьми мальчиков и девочек будет поровну с вероятностью ≈ 0,25. Вероятность того, что в семье будут дети одного пола (мальчики или девочки) – чуть меньше одной пятисотой.
Вероятность того, что в семье будут дети одного пола (мальчики или девочки) – чуть меньше одной пятисотой.
График биноминального распределения
Введем следующее обозначение, пусть означает вероятность того, что в испытаниях схемы Бернулли успех наступит не менее чем раз, и не более чем раз . Так как события, соответствующие различному числу успехов попарно несовместны, то имеет место формула:
.
Вероятность того, что в результате испытаний, успех наступит хотя бы один раз, вычисляется по формуле:
Типичный график биномиального распределения для :
Заострять внимание на графике, думаю, не нужно так как все предельно ясно, график очень похож на параболу, имеет свой максимум, в котором вероятность успеха будет максимальной. Поэтому лучше поработаем дальше с формулами, с которыми все немного сложнее.
Сформулируем задачу: необходимо найти — наивероятнейшее число успехов, то есть такое , вероятность которого максимальна.
Запишем условия максимума вероятности (их два):
а) ; б) .
Запишем неравенства а) и б) в явном виде:
а) , ;
б) , .
Учитывая оба неравенства, окончательно получим
В испытаниях схемы Бернулли с вероятностью успеха наиболее вероятным числом успехов является:
- единственное число , если число не целое;
- два числа и , если число целое.
При достаточно большом числе испытаний из полученного выше выражения, получим — статистическое определение вероятности.
При больших значениях наиболее вероятная относительная частота успеха совпадает (равна) вероятности успеха при одном испытании.
ПРИМЕР 2. Вероятность того, что расход электроэнергии на продолжении одних суток не превышает установленной нормы, равна . Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение
Вероятность нормального расхода . Вероятность перерасхода .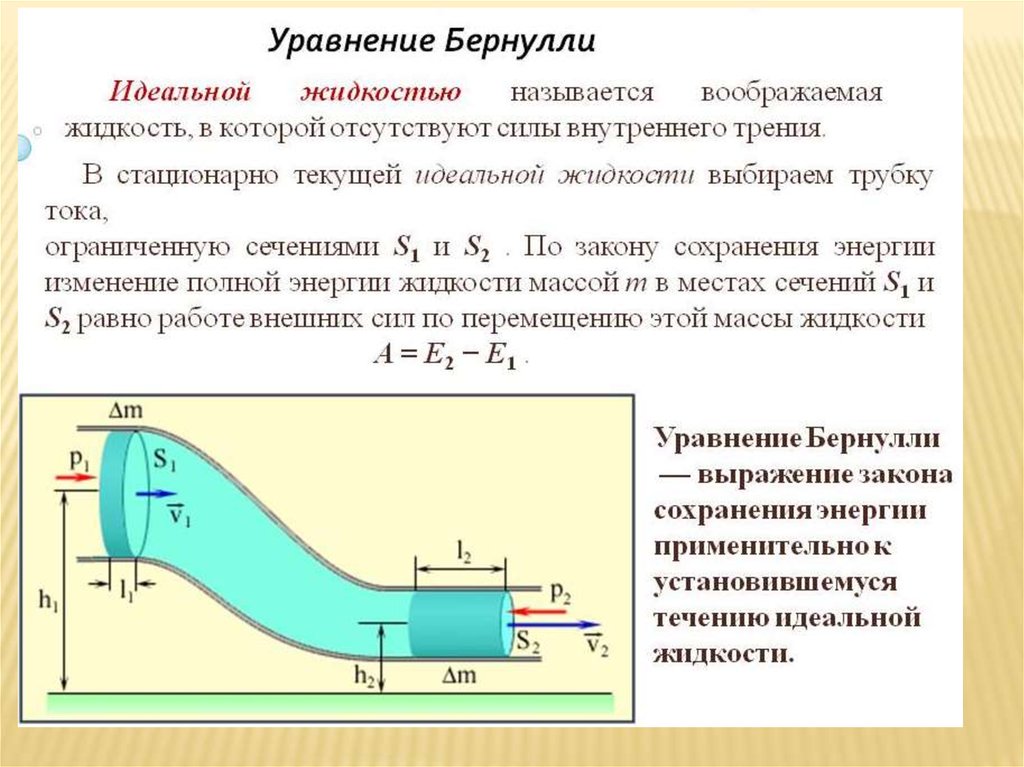 Искомая вероятность по формуле Бернулли:
Искомая вероятность по формуле Бернулли:
ОТВЕТ: Вероятность того, что расход э/э не превысит нормы составляет примерно 0,3 или 30%.
Обобщение схемы Бернулли
Рассмотрим обобщение схемы Бернулли. Пусть производится независимых испытаний, каждое из которых имеет попарно несовместных и возможных исходов, которые обозначим . События составляют полную группу событий. Вероятности наступления каждого события — в общем случаи различны и удовлетворяют условию . В этих условиях для произвольно заданных целых неотрицательных чисел таких, что , определим вероятность того, что при испытаниях исход наступит ровно раз, исход раз и т.д., исход произойдет раз:
Данное выражение носит название формула полиномиального распределения.
ПРИМЕР 3. Игральная кость подбрасывается 15 раз. Какова вероятность события – выпало ровно десять шестерок и три единицы?
Решение
Вероятности выпадения шестерки и единицы равны 1/ 6, а вероятность третьего исхода (выпали любые другие грани) равна 4/ 6 . Тогда вероятность получить 10 шестерок, 3 единицы и 2 других значения чисел равна:
Тогда вероятность получить 10 шестерок, 3 единицы и 2 других значения чисел равна:
ОТВЕТ. Вероятность выпадения десяти шестерок и трех единиц ничтожно мала и составляет примерно 0,0001022%
Ну вроде на этом можно пока закончить, далее будем рассматривать теоремы Пуассона и теоремы Муавра-Лапласа.
0 | 1 | 2 | … | k | … | N | |||
Вероятность | 0 | 1 | |||||||
Вероятность | q | p | 1 | 2 | 3 | 4 | 5 | 6 | |
Вероятность | 1 | 2 | 3 | 4 | 5 | 6 | |||
Вероятность | х | 0 | 1 | 2 | … | k | … | N | |
Вероятность | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Вероятность | 0,004 | 0,031 | 0,109 | 0,219 | 0,273 | 0,219 | 0,109 | 0,031 | 0,004 | 0 | 1 | 2 | … | k | … | N |
Вероятность | 0 | 1 | 2 | 3 | 4 | 5 | |||
Вероятность | 0,078 | 0,259 | 0,346 | 0,23 | 0,077 | 0,01 |
Что это? [С примерами]
Распределение — это основная концепция в области анализа данных, науки о данных и машинного обучения. Он закладывает основу для статистического анализа данного набора данных и обеспечивает основу для определенных моделей машинного обучения.
Он закладывает основу для статистического анализа данного набора данных и обеспечивает основу для определенных моделей машинного обучения.
Одним из самых простых, но важных типов распределения, с которым нужно разобраться, является распределение Бернулли, названное в честь швейцарского математика Якоба Бернулли. В этом посте мы предоставим мягкое, но подробное введение в распределение Бернулли и испытания Бернулли. К концу у вас будет четкое представление о том, что на самом деле означает распределение Бернулли и как оно вписывается в более широкий контекст анализа данных.
Мы рассмотрим:
- Что такое распределения в статистике?
- Что такое распределение Бернулли?
- Примеры распределения Бернулли
- Каковы условия распределения Бернулли?
- Какое место занимает распределение Бернулли в анализе данных, науке о данных и машинном обучении?
- Ключевые выводы и дополнительное чтение
Прежде чем мы углубимся в распределение Бернулли, давайте сначала вспомним, что означает распределение в мире статистики. Если вы уже знакомы с концепцией распространения, просто пропустите вперед, используя интерактивное меню.
Если вы уже знакомы с концепцией распространения, просто пропустите вперед, используя интерактивное меню.
В статистике распределение — это функция, которая показывает возможные значения переменной и то, как часто они встречаются в заданном наборе данных. Это позволяет вам рассчитать вероятность возникновения определенных результатов и понять, насколько велика вариация в вашем наборе данных.
Предположим, вы собрали данные о занятости 500 человек, проживающих в Нью-Йорке. Различные возможные результаты — это все различные названия должностей в вашем наборе данных. Поскольку род занятий является категориальным по своей природе (т. е. не числовым), распределение вашего набора данных покажет вам, сколько (или какой процент) людей в вашей выборке попадают в каждую группу. Например, 20 % выборки — юристы, 10 % — учителя, 5 % — медсестры и так далее.
С числовыми данными распределение упорядочивает данные от наименьшего к наибольшему значению. В этом случае распределение представляется в виде графика или диаграммы. Натренированный глаз может затем взглянуть на форму графика, чтобы сразу увидеть, как распределяются данные. Так называемое нормальное распределение создает на графике симметричную колоколообразную кривую. Это указывает на то, что большинство наблюдений из данных группируются вокруг центра (т. е. среднего значения), и лишь несколько более экстремальных наблюдений отклоняются от среднего значения в обоих направлениях. Нормальное распределение также известно как распределение Гаусса или, в зависимости от формы графика, колоколообразная кривая. По сути, нормальное распределение говорит вам, что большинство наблюдений (например, высота) будут находиться в пределах или близко к среднему значению, с несколькими выбросами.
Натренированный глаз может затем взглянуть на форму графика, чтобы сразу увидеть, как распределяются данные. Так называемое нормальное распределение создает на графике симметричную колоколообразную кривую. Это указывает на то, что большинство наблюдений из данных группируются вокруг центра (т. е. среднего значения), и лишь несколько более экстремальных наблюдений отклоняются от среднего значения в обоих направлениях. Нормальное распределение также известно как распределение Гаусса или, в зависимости от формы графика, колоколообразная кривая. По сути, нормальное распределение говорит вам, что большинство наблюдений (например, высота) будут находиться в пределах или близко к среднему значению, с несколькими выбросами.
Нормальное распределение — это лишь один из множества различных типов распределений. В этом руководстве мы сосредоточимся на распределении Бернулли.
2. Что такое распределение Бернулли?
Распределение Бернулли — это дискретное распределение вероятностей , что означает, что оно связано с дискретными случайными величинами. Дискретная случайная величина — это величина, имеющая конечное или исчисляемое число возможных значений — количество выпавших орлов при одновременном подбрасывании трех монет или количество учеников в классе.
Дискретная случайная величина — это величина, имеющая конечное или исчисляемое число возможных значений — количество выпавших орлов при одновременном подбрасывании трех монет или количество учеников в классе.
Итак: Дискретное распределение вероятностей описывает вероятность появления каждого возможного значения дискретной случайной величины, например вероятность выпадения шестерки при бросании игральной кости. При работе с дискретными переменными вероятность каждого значения находится в диапазоне от 0 до 1, а сумма всех вероятностей равна 1. Итак, в примере с игральной костью, предполагая, что мы используем стандартную игральную кость, вероятность броска шесть составляет 0,167, или 16,7%. Это основано на делении 1 (сумма всех вероятностей) на 6 (количество возможных исходов).
Вкратце это дискретное распределение вероятностей. А как же распределение Бернулли?
Распределение Бернулли и объяснение испытаний Бернулли
Распределение Бернулли применяется к событиям, которые имеют одно испытание и два возможных исхода . Они известны как испытания Бернулли. Подумайте о любом эксперименте, который задает вопрос «да» или «нет» — например, упадет ли эта монета решкой, когда я ее подброшу? Выкину ли я шестерку этим кубиком? Выберу ли я туза из этой колоды карт? Будет ли избиратель X голосовать «за» на политическом референдуме? Сдаст ли студент Y тест по математике?
Они известны как испытания Бернулли. Подумайте о любом эксперименте, который задает вопрос «да» или «нет» — например, упадет ли эта монета решкой, когда я ее подброшу? Выкину ли я шестерку этим кубиком? Выберу ли я туза из этой колоды карт? Будет ли избиратель X голосовать «за» на политическом референдуме? Сдаст ли студент Y тест по математике?
Вы поняли. В испытаниях Бернулли два возможных исхода можно рассматривать как «успех» или «неудача», но эти ярлыки не следует воспринимать буквально. В этом контексте «успех» просто означает получение результата «да» (например, выпадение шестерки, выпадение туза и т. д.).
Распределение Бернулли — это, по сути, вычисление, позволяющее создать модель набора возможных результатов испытания Бернулли. Таким образом, если у вас есть событие, имеющее только два возможных исхода, распределение Бернулли позволяет рассчитать вероятность каждого исхода.
В чем разница между распределением Бернулли и биномиальным распределением?
Занимаясь распределением Бернулли, вы, вероятно, встречали другой термин: биномиальное распределение. Так в чем же разница между ними и как они соотносятся друг с другом?
Так в чем же разница между ними и как они соотносятся друг с другом?
Проще говоря, распределение Бернулли — это тип биномиального распределения. Мы знаем, что распределение Бернулли применимо к событиям, которые имеют одно испытание (n = 1) и два возможных исхода, например, одно подбрасывание монеты (это испытание) и исход либо орел, либо решка. Когда у нас есть более одного испытания — скажем, мы подбрасываем монету пять раз — биномиальное распределение дает дискретное распределение вероятностей числа «успехов» в этой последовательности независимых подбрасываний монеты (или испытаний).
Итак, продолжим пример с подбрасыванием монеты: распределение Бернулли дает вам вероятность «успеха» (скажем, выпадения орла) при подбрасывании монеты только один раз (это ваше испытание Бернулли). Если вы подбросите монету пять раз, биномиальное распределение рассчитает вероятность успеха (выпадение орла) для всех пяти подбрасываний монеты.
Это очень упрощенный обзор — здесь вы найдете более подробное объяснение биномиального распределения. А пока давайте вернемся к распределению Бернулли с некоторыми примерами.
А пока давайте вернемся к распределению Бернулли с некоторыми примерами.
3. Примеры распределения Бернулли
Пример распределения Бернулли: подбрасывание монеты
Пример с подбрасыванием монеты, пожалуй, самый простой способ объяснить распределение Бернулли. Предположим, что исход «орел» — это «успех», а исход «решка» — «неудача». В этом случае:
- Вероятность удачного исхода (выпадение решки) записывается как p
- Вероятность неудачи (выпадение решки) записывается как q , рассчитывается как 1 ** – ** p
. Итак, в этом случае:
- P = 0,5
- Q = 1 — ** 0,5
SO, в нашем примере броска монеты, оба P и Q = 0,5 . . На графике вы бы представили вероятность неудачи как «0», а вероятность успеха как «1», обе по оси Y.
Другие примеры распределения Бернулли
Пример с подбрасыванием монеты очень прост, но на самом деле в жизни есть много сценариев, которые имеют исход «да-нет». Например:
- Пройдете вы тест или нет?
- Ваша любимая спортивная команда выиграет или проиграет свой следующий матч?
- Будете ли вы приняты или отклонены на работу, на которую вы претендуете?
- Выпадет ли шестерка в первом раунде вашей любимой настольной игры?
- Вы выиграете или проиграете в лотерею?
В этой статье Swizec Teller объясняет, как испытания Бернулли и распределение Бернулли могут помочь вам определить, сколько заявлений о приеме на работу вам нужно разослать, прежде чем вы получите работу. Распределение Бернулли также используется в медицине и клинических испытаниях для моделирования вероятности успеха определенного лекарства или исхода клинического испытания. Например, при разработке нового лекарства ученые-фармацевты могут использовать распределение Бернулли для расчета вероятности того, что человек вылечится или не вылечится с помощью нового лекарства. Распределения Бернулли также используются в логистической регрессии для моделирования возникновения заболеваний. Вы можете узнать больше о логистической регрессии в этом посте.
Распределения Бернулли также используются в логистической регрессии для моделирования возникновения заболеваний. Вы можете узнать больше о логистической регрессии в этом посте.
4. Каковы условия распределения Бернулли?
Чтобы помочь вам понять, когда и как применяется распределение Бернулли, полезно рассмотреть условия испытаний Бернулли. Событие или эксперимент можно считать испытанием Бернулли (и, следовательно, иметь отношение к распределению Бернулли), только если оно соответствует следующим критериям:
- Возможны только два исхода испытания. Другой способ думать об этом — с точки зрения «успеха» или «неудачи» — другими словами, задает ли ваш эксперимент вопрос «да или нет»? Вспомните наши предыдущие примеры, такие как «Сдаст ли ученик X контрольную по математике?» или «Вылечится ли пациент Y, если примет это лекарство?»
- Каждый из двух исходов имеет фиксированную вероятность возникновения. Другими словами, независимо от того, сколько раз вы подбрасываете монету, вероятность выпадения орла фиксирована.
 Говоря математическим языком, вероятность успеха всегда p , а вероятность неудачи всегда 1 – p.
Говоря математическим языком, вероятность успеха всегда p , а вероятность неудачи всегда 1 – p. - Испытания полностью независимы друг от друга. Результат одного испытания (скажем, первого подбрасывания монеты) абсолютно не влияет на результат любых последующих подбрасываний монеты.
Если сценарий соответствует всем трем критериям, его можно считать испытанием Бернулли. Теперь, когда мы знакомы с распределением Бернулли, давайте рассмотрим, где оно играет роль в более широких областях анализа данных, науки о данных и машинного обучения.
5. Распределение Бернулли в анализе данных, науке о данных и машинном обучении
Вероятностные распределения, такие как распределение Бернулли, полезны не только для математиков и статистиков; они также играют решающую роль в анализе данных, науке о данных и машинном обучении. Аналитики данных и специалисты по данным работают с большими объемами данных, и изучение распределения данного набора данных является важной частью исследовательского анализа данных, то есть получения первоначального понимания ваших данных перед дальнейшим исследованием.
В машинном обучении многие модели работают на основе предположений о распределении, а распределение Бернулли (и другие дискретные распределения вероятностей) в основном используются при моделировании задач бинарной и многоклассовой классификации. Некоторые примеры моделей бинарной классификации включают спам-фильтры, которые определяют, следует ли классифицировать электронное письмо как «спам» или «не спам», модели, которые могут предсказать, предпримет ли клиент определенное действие или нет, или классифицирующие продукт, скажем, как книга или фильм. Примером многоклассовой модели классификации может быть модель, которая определяет, какая категория продуктов будет наиболее актуальной для конкретного покупателя.
Как одно из самых простых распределений, распределение Бернулли часто служит отправной точкой для более сложных распределений. Например, процесс Бернулли закладывает основу для биномиального распределения, геометрического распределения и отрицательного биномиального распределения — все они играют решающую роль в глубоком обучении. Вы можете узнать больше о глубоком обучении (и чем оно отличается от машинного обучения) в этом руководстве.
Вы можете узнать больше о глубоком обучении (и чем оно отличается от машинного обучения) в этом руководстве.
Итак, если вы хотите глубже погрузиться в аналитику данных, науку о данных или машинное обучение, распределения вероятностей, такие как распределение Бернулли, — хорошее место для начала.
6. Основные выводы и дополнительная литература
В этом посте мы представили распределение Бернулли — концепцию, с которой стоит разобраться, если вы планируете карьеру в какой-либо области, связанной с данными. Напомним:
- Распределение Бернулли — это дискретное распределение вероятностей
- Оно описывает вероятность достижения «успеха» или «неудачи» в испытании Бернулли
- отказ). Например, упадет ли монета орлом (успех) или решкой (неудача)?
- Распределение Бернулли — это тип биномиального распределения
Если вы изучаете статистику с целью начать работу в индустрии данных, почему бы не попробовать бесплатный краткий вводный курс по аналитике данных? А для получения дополнительных вводных руководств ознакомьтесь со следующим:
- В чем разница между описательной и логической статистикой?
- Введение в многофакторный анализ
- В чем разница между регрессией и классификацией?
Биномиальное распределение VS Бернулли | Харшит Давар | The Startup
Этот блог призван объяснить разницу между одним из наиболее часто встречающихся распределений в мире науки о данных, то есть биномиальным распределением и распределением Бернулли, на реальных примерах.
 Источник изображения
Источник изображения Будь то вероятность, статистика, наука о данных, машинное обучение, глубокое обучение или любая другая подобная область, знание распределения данных является обязательным или решающим, поскольку оно помогает в работе с данными. .
Поскольку оба распределения (биномиальное и бернуллиевское) поначалу сбивают с толку большинство людей, они не пытаются их изучить и понять. Кроме того, еще один фактор заключается в том, что в большинстве источников контента не приведены примеры из реальной жизни, чтобы сделать объяснение более реалистичным. Вот почему этот блог призван объяснить разницу между двумя дистрибутивами на реальных примерах.
Теперь, как говорится, давайте сначала объясним распределение Бернулли.
Это распределение имеет дело с данными, которые имеют только 1 испытание и только 2 возможных результата. Все, кроме этого, не подпадает под категорию распределения Бернулли.
Способ представить Испытание/Событие Бернулли!
Хотя любой может использовать любой символ для представления распределения ради упрощения, оно было представлено как:
Бернулли Событие/Испытание Представление! [Изображение автора] На изображении выше «p» представляет вероятность возникновения события; Например, вероятность выпадения орла при подбрасывании монеты.
Пример распределения Бернулли!
В качестве примера из реальной жизни рассмотрим ситуацию сдачи или провала экзамена. Предположим, что вероятность сдать экзамен равна 95%, следовательно, вероятность провала составит 5%.
В этом случае, если рассматривается событие сдать экзамен, то событие Бернулли будет содержать вероятность сдачи экзамена. Точно так же и за провал на экзамене.
Это набор испытаний Бернулли для одного и того же события, т. е. содержит более 1 события Бернулли для одного и того же сценария, для которого вычисляется испытание Бернулли.
Способ представления биномиального распределения!
Его можно представить двумя вещами:
- Количество испытаний Бернулли.
- Вероятность события в каждом испытании.
На изображении выше «n» соответствует количеству испытаний Бернулли, а «p» соответствует вероятности события в каждом испытании.
Функция вероятности для расчета биномиального распределения!
Когда требуется рассчитать вероятность возникновения какого-либо события определенное количество раз из фиксированного количества раз, используется приведенная ниже формула.
Функция вероятности для биномиального распределения! [Изображение автора]В приведенном выше уравнении:
- «n» — это общее количество испытаний события.
- «с» соответствует количеству раз, которое должно произойти событие.
- «p» — вероятность того, что событие произойдет.
- «(1 — p)» — вероятность того, что событие не произойдет.
- Термин «C» предназначен для комбинаций.
Пример биномиального распределения!
Рассматривая тот же пример распределения Бернулли, давайте создадим биномиальное распределение из этого примера.
Принимая во внимание 95% и 5% за сдачу и провал экзамена для студента соответственно. Если мы хотим рассчитать вероятность того, что студент сдаст ровно 5 экзаменов из 5 экзаменов, на которых он появился, с помощью приведенной выше формулы вероятности ее можно легко вычислить. 9(0)
9(0)
=> 0,774
Следовательно, вероятность того, что студент сдаст все 5 экзаменов, составляет примерно 77,4 %.
- Бернулли имеет дело с исходом одного испытания события, тогда как Биномиальный имеет дело с исходом нескольких испытаний одного события.
- Бернулли используется, когда результат события требуется только один раз, тогда как биномиальный используется, когда результат события требуется несколько раз.
Это все для того, чтобы объяснить разницу между распределением Бернулли и биномиальным распределением на реальных примерах.
Я надеюсь, что моя статья объясняет все и все, что связано с темой, со всеми глубокими концепциями и объяснениями. Большое спасибо за то, что потратили свое время на чтение моего блога и пополнили свои знания. Если вам нравится моя работа, я прошу вас поаплодировать этому блогу и подписаться на меня на Medium и GitHub !
Распределение Бернулли в R — GeeksforGeeks
Распределение Бернулли является частным случаем Биномиального распределения , когда выполняется только одно испытание. Это дискретное распределение вероятностей для испытания Бернулли (испытания, которое имеет только два исхода, то есть либо успех, либо неудачу). Например, это можно представить как подбрасывание монеты, где вероятность выпадения орла равна 0,5, а выпадения решки — 0,5. Это распределение вероятностей случайной величины, которая принимает значение 1 с вероятностью p и значение 0 с вероятностью q=1-p . Распределение Бернулли является частным случаем биномиального распределения с n=1.
Это дискретное распределение вероятностей для испытания Бернулли (испытания, которое имеет только два исхода, то есть либо успех, либо неудачу). Например, это можно представить как подбрасывание монеты, где вероятность выпадения орла равна 0,5, а выпадения решки — 0,5. Это распределение вероятностей случайной величины, которая принимает значение 1 с вероятностью p и значение 0 с вероятностью q=1-p . Распределение Бернулли является частным случаем биномиального распределения с n=1.
Функция массы вероятности f этого распределения по возможным исходам k определяется как: 4 встроенные функции для распределения Бернулли, и все они обсуждаются ниже.
Функция dbern()dbern() в программировании на языке R измеряет функцию плотности распределения Бернулли.
Синтаксис: Dbern (x, prob, log = false)
Параметр:
- x: Вектор квантиля
- SRE: вероятность из каждого испытания
- SRE: вероятность из каждого испытания
- SRE: вероятность из каждого испытания
- .
логический; если TRUE, вероятности p задаются как log(p)
In statistics, it is given by below formula:
Example:
R
|
Output:
pbern() pbern( ) function in R programming giver the distribution function for the Bernoulli distribution.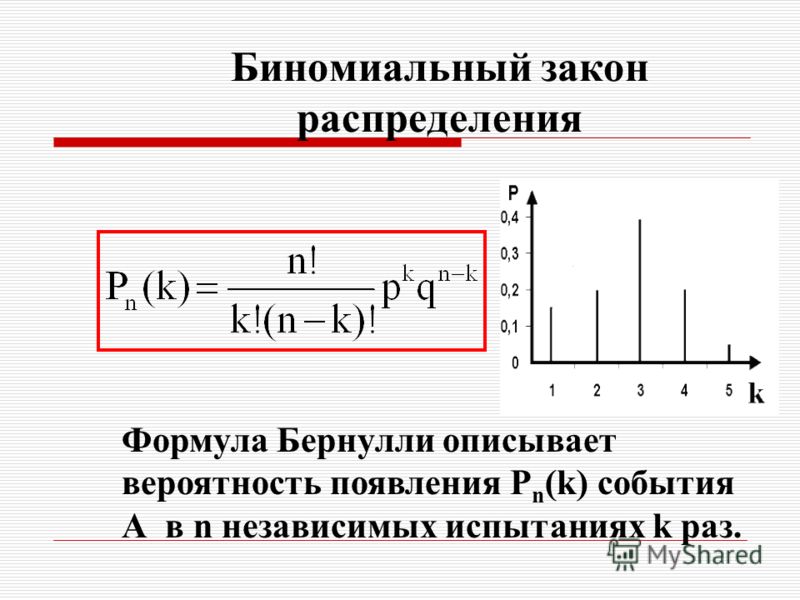 Функция распределения, или кумулятивная функция распределения (CDF), или кумулятивная функция частоты, описывает вероятность того, что переменная X примет значение, меньшее или равное числу x.
Функция распределения, или кумулятивная функция распределения (CDF), или кумулятивная функция частоты, описывает вероятность того, что переменная X примет значение, меньшее или равное числу x.
Синтаксис: pbern(q, prob, lower.tail = TRUE, log.p = FALSE)
Параметр:
- q: вектор квантилей
- prob:
- 300389 вероятность успеха в каждом испытании lowe.tail:
логический- log.p: логический; если TRUE, вероятности p задаются как log(p).
Пример:
R
|
.
qbern()qbern() дает функцию квантиля для распределения Бернулли. Квантильная функция в статистических терминах определяет значение случайной величины так, что вероятность того, что переменная меньше или равна этому значению, равна заданной вероятности.
Синтаксис: qbern(p, prob, lower.tail = TRUE, log.p = FALSE)
Параметр:
- p: вектор вероятностей.
- prob: вероятность успеха в каждом испытании.
- нижний.хвост: логический
- лог.p: логический; если TRUE, вероятности p задаются как log(p).
Example:
R
|
Выход:
RBE случайных чисел, распределенных Бернулли.
Синтаксис: rbern(n, prob)
Параметр:
- n: количество наблюдений.
- prob : количество наблюдений.
Example:
R
|
Выход:
[1] 0 0 1 0 0 0 0 0 0 0 1 0 1 0 1 0 10002 1 1 0 1 0 1 1 0 1 0 1 1 0 1 1 1 1 0 1 0 0 0 0 1 1 1 0 1 1 1 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1
[68] 1 1 1 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 1 1 0 1 0 0 0 0 1 0 0 1 1 0 0 0 0 0 1 0 1 0 0 1 0 1 0 1 0 1 1 1 0 1
[135] 0 0 0 0 0 1 1 0 1 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 0 1 1 0 0 1 0 0 1 0 1 1 0 1 1 0 1 1 1 1 1 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0
[202] 1 1 1 1 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 1 1 0 0 1 0 0 1 1 1 0 1 1 0 1 1 0 0 0 0 0 0 0 1 1 0 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 0
[269] 0 0 1 1 0 1 0 1 0 1 0 0 0 0 1 1 0 0 1 1 1 1 0 0 1 0 0 1 0 0 0 0 0 1 1 0 0 1 0 0 1 0 1 0 1 0 1 0 0 0 1 0 0 1 1 0 1 0 1 0 0 0 0 1 0 0 0
[336] 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 0 1 1 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 0 1 1 0 1 0 1 0 0 1 0 1 1 0 1 1 1 0 0 1 0 1 1 0 0 0
[403] 1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 1 0 1 0 1 0 0 0 0 1 1 0 0 0 0 1 1 1 1 1 0 0 1 0 0 1 0 0 0 0 1 0 1 1 0 0 0 1 1 0 1 1 1 0 1 0 1
[470] 1 0 1 1 1 0 0 0 0 1 0 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0
[537] 0 0 1 0 0 0 1 1 0 0 1 0 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 0 1 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 0 0 1 0
[604] 1 0 1 0 1 1 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 1 0 0 1 0 0 0 1 0 1 0 1 1 0 1 1 1 0 1 1 1 0 1 0 1 1 0 0 0 0 1 0 0 1 0 1 0 1 1
[671] 0 0 0 1 0 1 0 0 1 0 0 0 0 1 1 1 0 1 0 1 1 0 1 1 1 0 1 1 0 1 0 0 0 0 0 0 1 0 0 1 1 0 1 1 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 1 1
[738] 1 0 0 1 1 1 1 1 0 0 1 0 1 0 0 0 1 1 0 0 0 1 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1
[805] 0 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 1 0 0 1 1 0 0 1 1 0 0 0 1 1 1 0 0 1 0 1 0 0 0 0 1 0 1 1 0 0 0 0 1 1 0 1 0 1 1 0 1 0 1 1 1 1
[872] 1 1 0 1 0 0 1 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 0 0
[939] 1 1 1 1 0 1 0 0 1 1 1 0 1 0 0 1 1 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 1 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1
Приведенный выше график представляет случайный рисунок Числа распределения Бернулли в R.
Распределение Бернулли - определение, формула, среднее/дисперсия, график
Распределение Бернулли — это дискретное одномерное распределение вероятностей. Испытание или эксперимент Бернулли приводит к бинарным результатам: успех или неудача (0 или 1). Успех испытания обозначается как p (x=1), а неудача выражается как 1-p (x=0).
Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство?0003
Это распределение вероятностей широко применяется в машинном обучении, анализе данных, науке о данных, медицине и финансах. Кроме того, он считается удобным методом определения вероятности в реальных сценариях. Например, он может определить успех или неудачу медицинского теста, студенческого экзамена или отбора на собеседование.
Содержание
- Определение распределения Бернулли
- Объяснение распределения Бернулли
- Среднее значение и дисперсия распределения Бернулли
- Примеры
- График
- Приложения
- Часто задаваемые вопросы (FAQ)
- Рекомендуемые статьи
- 900 Индикатор вероятности является дискретным индикатором распределения Бернулли.
- Отличается от биномиального распределения, которое определяет вероятность нескольких биномиальных испытаний.
- Распределение Бернулли для события рассчитывается по следующей формуле:
 Он используется для определения возможного исхода одиночного случайного эксперимента (испытания Бернулли). Такое испытание может иметь только два результата: успех или неудачу.
Он используется для определения возможного исхода одиночного случайного эксперимента (испытания Бернулли). Такое испытание может иметь только два результата: успех или неудачу.Распределение Бернулли выполняется, когда исследователи хотят найти вероятность достижения бинарного результата — из одного испытания Бернулли или случайного эксперимента. . Результатом может быть успех: x или n = 1, или это может быть провал: x или n = 0.
Швейцарский математик Якоб Бернулли предложил распределение вероятностей Бернулли. Он был опубликован посмертно в 1713 г.
Следующие функции отличают вероятность Бернулли от других распределений вероятностей:
- Во-первых, это одномерное распределение вероятностей.

- Во-вторых, это дискретный случайный эксперимент.
- В-третьих, каждое испытание Бернулли не зависит друг от друга.
- Наконец, возможные результаты являются бинарными, то есть успех или неудача.
Распределение Бернулли имеет следующие свойства:
- Испытание Бернулли может дать только два вероятных исхода — 0 или 1, т. е. неудачу или успех.
- Вероятность успеха обозначается как p, а вероятность неудачи выражается как q или 1-p.
- Сумма двух исходов должна равняться 1, т. е. p + q = 1.
- Распределение вероятностей остается постоянным в каждом последующем испытании Бернулли независимо друг от друга.
- Ожидаемое среднее значение распределения Бернулли обозначается как E[X] = p. Здесь X — случайная величина.
- Дисперсия распределения Бернулли для случайной величины выражается как Var[X] = p (1 – p).
Метод Бернулли более удобен, чем другие методы, когда определяется вероятность реального сценария. Это связано с тем, что когда аналитики определяют вероятность реальных сценариев, успех относится к ожидаемому результату, а неудача — к противоположному.
Это связано с тем, что когда аналитики определяют вероятность реальных сценариев, успех относится к ожидаемому результату, а неудача — к противоположному.
Вероятность Бернулли обозначается буквой P; он дает только два типа выводов: успех или неудача. Он рассчитывается по следующей формуле.
- Здесь «x» — исход, который может быть либо успехом (x=1), либо неудачей, ( x=0)
- «p» — вероятность успеха.
- q = 1-p, и это обозначает вероятность отказа.
- Значение p равно 0 < p < 1.
Ожидаемое среднее значение распределения Бернулли получается как среднее арифметическое нескольких независимых результатов (для случайной величины X). Теперь давайте разберемся со средней формулой:
Согласно предыдущей формуле: P (X=1) = p
P (X=0) = q = 1-p
E (X) = P (X=1) × 1 + P (X= 0) × 0
E (X) = p × 1 + (1-p) × 0
E (X) = p
Следовательно, ожидаемое среднее значение распределения Бернулли равно p.
С помощью среднего мы можем вычислить дисперсию распределения Бернулли. Это разница между ожидаемым средним значением X2 и ожидаемым средним квадратом. Посмотрим на его математическое представление:
Var (X) = E (X2) – (E (X)) 2
E (X2) = ∑x 2 P (X=x)
E (X2) = 12 × P (X = 1) + 02 × P (X = 0)
E (X2) ) = 1 × p + 0 × (1-p)
E (X2) = p
Var (X) = p – (p) 2 = p(1-p) = pq
Таким образом, дисперсия распределения Бернулли равна pq.
Примеры
Давайте рассмотрим несколько примеров распределения Бернулли, чтобы понять концепцию:
Пример #1Предположим, что из каждых 50 человек в городе 1 является владельцем бизнеса. Итак, если случайным образом выбран один гражданин, каково распределение владельцев бизнеса?
Решение :
Дано:
p = 1/50
P (X = x) = p x (1-p) (1-x)
Таким образом, P (X = x) = (1/50 ) x (1 – 1/50) (1-x)
Вычислим для x = 0, 1
- Если x = 1
Тогда P (X = 1) = 1/50 = 0,02
- Если, x = 0
Тогда P (X = 0) = q = 1 – p = 1 – 1/50 = 49/50 = 0,98
Таким образом, вероятность успеха, т. е. гражданин, являющийся владельцем бизнеса, составляет 0,02, а вероятность отказа, т. е. того, что выбранный гражданин не является владельцем бизнеса, составляет 0,9.8.
е. гражданин, являющийся владельцем бизнеса, составляет 0,02, а вероятность отказа, т. е. того, что выбранный гражданин не является владельцем бизнеса, составляет 0,9.8.
Если 1 из каждых 15 акций в портфеле демонстрирует исключительную динамику, то какова будет эффективность акции, случайно выбранной из портфеля?
Решение :
Дано:
p = 1/15
P (X = x) = p x (1-p) (1-x)
Таким образом, P (X = x) = (1/15 ) x (1 – 1/15) (1-x)
Вычислим для x = 0, 1
- Если x = 1
Тогда P (X = 1) = 1/15 = 0,07
- Если, x = 0
Тогда P (X = 0) = q = 1 – p = 1 – 1/15 = 14/15 = 0,93
Таким образом, вероятность получения чрезвычайно эффективной акции (успех) составляет 0,07. Точно так же вероятность того, что акции не будут работать чрезвычайно (провал), равна 0,93.
Пример №3 При медицинском осмотре вероятность ошибки составляет 15%. Теперь найдите распределение Бернулли, если из 60 пациентов случайным образом выбран один пациент.
Теперь найдите распределение Бернулли, если из 60 пациентов случайным образом выбран один пациент.
Решение :
Количество отчетов об ошибках при обследовании 60 пациентов = 15% от 60 = 9 пациентов
Таким образом, количество пациентов, получивших правильные отчеты = 60 – 9 = 51
p = 51/60 = 17 /20
P (X = x) = p x (1-p) (1-x)
Таким образом, P (X = x) = (17/20) x (1 – 17/20) (1-x )
Вычисление x = 0, 1
- Если x = 1
Тогда P (X = 1) = 17/20 = 0,85
- Тогда x = 80 0 902 = 0) = q = 1 – p = 1 – 17/20 = 3/20 = 0,15
Таким образом, вероятность получения успешного результата медицинского освидетельствования равна 0,85, а вероятность ошибки (неудачи) - 0,15.
График
Построим приведенный выше пример на графике:
Учитывая, что p = 0,85 и q или 1-p = 0,15.
Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство?0003
д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство?0003
Приведенный выше график распределения Бернулли показывает шансы на успех или неудачу при медицинском осмотре.
ПриложенияМетод Бернулли прост в применении, особенно когда одно испытание дает только два результата — успех или неудачу. Этот метод применяется в науке о данных, майнинге, машинном обучении, аналитике, медицине, финансах, статистике и спорте.
Например, с помощью этого инструмента можно измерить вероятность побочных эффектов, вызванных новым лекарством. Он может определить вероятность успеха или неудачи медицинского теста. Он используется для оценки вероятности того, что электронное письмо является спамом. В маркетинге эта теорема предсказывает вероятность того, что клиент купит или не купит определенный продукт.
Этот метод эффективно предсказывает вероятность того, что учащийся сдаст или не сдаст тест. Исследователь может определить шансы выбора или отклонения новобранца. Он также может предсказать вероятность выигрыша или проигрыша ставки.
Он также может предсказать вероятность выигрыша или проигрыша ставки.
1. Является ли распределение Бернулли дискретным или непрерывным?
Распределение Бернулли — это одномерная дискретная вероятность, при которой случайный эксперимент дает только два возможных результата — успех или неудачу.
2. Когда использовать распределение Бернулли?
Используется для одиночных случайных испытаний Бернулли, когда событие может иметь только два возможных исхода — успех или неудачу. Он широко применяется в статистике, машинном обучении, науке о данных, аналитике, финансах, медицине и т. д.
3 . В чем разница между распределением Бернулли и биномиальным распределением?
Распределение Бернулли определяет вероятность одного случайного эксперимента или испытания Бернулли. Биномиальное распределение определяет вероятность N числа испытаний Бернулли.
Биномиальное распределение определяет вероятность N числа испытаний Бернулли.
Рекомендуемые статьи
Эта статья представляет собой руководство по распределению Бернулли и его определению. Мы объясняем его среднее значение и дисперсию, формулу, приложения и график с примерами. Вы можете узнать больше об этом из следующих статей –
- Распределение вероятностей
- Независимая переменная
- Среднеквадратичное значение
Испытания Бернулли и биномиальное распределение – условия, примеры, свойства и формулы
Распределение Бернулли и испытание, биномиальное распределения кратко описаны в этой статье. Давайте сначала узнаем об испытаниях Бернулли. Испытания Бернулли также известны как биномиальные испытания, поскольку в испытаниях Бернулли возможны только результаты, то есть успех и неудача, тогда как в биномиальном распределении мы получаем ряд успехов в серии независимых экспериментов. Распределение Бернулли — это распределение вероятностей для серии испытаний Бернулли, в которых возможны только два исхода. В этой статье мы обсудим биномиальное распределение испытания Бернулли, формулу испытания Бернулли, пример испытания Бернулли, распределение Бернулли, примеры распределения Бернулли, свойства распределения Бернулли, как испытание Бернулли связано с биномиальным распределением и т. д.
В этой статье мы обсудим биномиальное распределение испытания Бернулли, формулу испытания Бернулли, пример испытания Бернулли, распределение Бернулли, примеры распределения Бернулли, свойства распределения Бернулли, как испытание Бернулли связано с биномиальным распределением и т. д.
Испытания Бернулли
В области вероятности эксперименты с различными концепциями привели к основным математическим теориям. Предположим один эксперимент, число которых будет конечным. Он должен иметь только два результата, так как результат один будет называться успехом, а другой - неудачей. И во всех условиях эксперимента вероятность неудачи и успеха событий не меняется. Эта постановка эксперимента известна как испытание Бернулли. Это было создано Якобом Бернулли, швейцарским математиком, и опубликовано в его книге Ars Conjectandi в 1713 году. Это помогло нам лучше понять природу вероятности.
Определение
Последовательное событие в последовательности независимых экспериментов, где есть только два возможных исхода, и вероятность исходов остается неизменной в каждом событии. Когда мы проводим эти события последовательно конечное число раз, тогда серия опытов называется испытаниями Бернулли.
Когда мы проводим эти события последовательно конечное число раз, тогда серия опытов называется испытаниями Бернулли.
Биномиальное распределение
Биномиальное распределение представляет собой графическое представление результатов испытаний Бернулли. Это дает нам представление о вероятности событий во всей последовательности эксперимента. Это также можно сказать как частотное распределение вероятности данного числа успехов в случайном числе повторных независимых испытаний Бернулли. Если испытания Бернулли являются экспериментом, то биномиальную теорему можно назвать результатом или выводом эксперимента.
Использование
Допустим, нам нужно найти вероятность выпадения орла при подбрасывании монеты, тогда мы можем легко найти ее, используя формулу успеха, деленную на число выборок, и то же самое можно сказать о вероятности выпадения двух орлов в двух последовательных подбрасывает монеты. Если нам нужно найти вероятность двух орлов и трех решек при 5 последовательных подбрасываниях монеты, то это будет сложно, но решаемо описанным выше методом, но сложность очень велика. Но скажем, нам нужно найти вероятность того, что даже при 20 последовательных подбрасываниях монеты не будет подсчитано ни одного орла. Для нас будет почти невозможно финансировать вероятность вышеуказанным методом. В этих сложных случаях нам придется использовать формулу биномиального распределения, которая поможет нам найти вероятность сложных предсказуемых проблем. 9{n-r}\]
Но скажем, нам нужно найти вероятность того, что даже при 20 последовательных подбрасываниях монеты не будет подсчитано ни одного орла. Для нас будет почти невозможно финансировать вероятность вышеуказанным методом. В этих сложных случаях нам придется использовать формулу биномиального распределения, которая поможет нам найти вероятность сложных предсказуемых проблем. 9{n-r}\]
n= количество попыток
r= количество успешных попыток
p= вероятность успеха
q=вероятность неудачи
Подробнее о биномиальном распределении
Биномиальное распределение является разновидностью распределения вероятностей что имеет два возможных исхода. В теории вероятностей биномиальные распределения имеют два параметра, таких как n и p.
Распределение вероятностей становится биномиальным, когда оно удовлетворяет следующим критериям.
Количество попыток должно быть фиксированным.

Испытания независимы друг от друга.
Успех вероятности остается одинаковым для каждого испытания.
Каждое испытание имеет только два результата: успех или неудачу.
(Изображение будет загружено в ближайшее время)
Испытание Бернулли
Случайный эксперимент, который имеет только два взаимоисключающих результата, таких как «успех» и «неуспех», известен как дихотомический эксперимент.
Если дихотомический эксперимент повторяется много раз и если в каждом испытании вы обнаружите, что вероятность успеха p (0 Поскольку испытание Бернулли имеет только два возможных результата, его можно легко сформулировать как вопросы «да» или «нет» Пример испытания Бернулли объяснит концепцию испытания Бернулли в двух различных ситуациях: Случайным образом извлекаются 8 шаров, из них 10 белых и 10 черных. В первом испытании, когда шар вытягивается с возвратом, вероятность успеха (скажем, черного шара) равна 10/20 = ½, что одинаково для всех 8 испытаний. Следовательно, испытания, включающие розыгрыш шаров с возвратом, считаются испытаниями Бернулли. Во втором испытании при вытягивании без возвращения вероятность успеха (скажем, черных шаров) изменяется с числом испытаний =10/20 = ½ для вторых испытаний вероятность успеха p =9/19, что не похоже на первое испытание. Таким образом, следы, включающие вытягивание шаров без замены, не считаются испытанием Бернулли Испытание Бернулли имеет только два возможных исхода: успех или неудачу. Вероятность успеха и неудачи остается неизменной на протяжении всех испытаний. Испытания Бернулли не зависят друг от друга. Количество попыток фиксировано. Если x - вероятность успеха, то вероятность неудачи равна 1-x. Здесь вы можете увидеть формулу испытаний Бернулли в математике Бернулли. Возьмем пример, когда проводятся n испытаний Бернулли, тогда вероятность получения r успехов в n испытаниях может быть получена по приведенной ниже формуле испытаний Бернулли. P(r) = Cn pr qn-r Термин n! / г!(п!-р!)! называется биномиальным коэффициентом. Учащийся сможет разработать испытание или эксперимент Бернулли Учащийся сможет легко использовать биномиальную формулу распределения Учащиеся смогут вычислять приложения, включая испытания Бернулли и биномиальное распределение' Распределение Бернулли в математике Бернулли — это распределение вероятностей для серии испытаний Бернулли, где есть только два возможных исхода. Некоторые из примеров распределения Бернулли, приведенные в математике Бернулли, приведены ниже: Новорожденный ребенок — либо девочка, либо мальчик (здесь вероятность того, что ребенок будет мальчиком, составляет примерно 0,5) Ученик сдает или не сдает экзамен Теннисист либо выигрывает, либо проигрывает в матче Подбрасывание монеты либо орел, либо решка. Здесь вы можете найти некоторые свойства распределения Бернулли в математике Бернулли. Ожидаемое значение распределения Бернулли приведено ниже. E(X) = 0 * (1-P) + 1 * p = p Дисперсия распределения Бернулли вычисляется как Var (X) = E(X²) -E (X²) = 1² * p +0² * (1-p) - p² = p - p² = p (1-p) Мода, значение с наибольшей вероятностью появления распределения Бернулли равно 1, если p > 0,5, и 0, если < 0,5, успех и неудача равновероятны, и как 0, так и 1 считаются модами. Основные свойства распределения Бернулли можно вычислить, рассматривая вероятность n=1. Более 1 Более 2 ровно 1 ровно 2 2. Какова будет дисперсия испытаний в Бернулли, если вероятность успеха испытания Бернулла будет 0,3. 0,3 0,7 0,21 0,09 3. Среднее значение и дисперсию равны бинеальным распределениям. Верно Неверно 1. Решение: Вероятность того, что лампочка неисправна, p = 0,8 0.2 2. На экзамене задается 10 вопросов с несколькими вариантами ответов, из которых только один из четырех правилен. Найдите вероятность правильного ответа на 5 из 10 вопросов в листе ответов. Решение: Вероятность получить правильный ответ, p = ¼ Вероятность получить неправильный ответ, q = 1-p = 1 Вероятность получить 5 правильных ответов, P(X=5) = (0,25 )5 ( 0,75)5 = 0,5839920044 3. Подбросить монету 12 раз. Какова вероятность того, что выпадет 7 решек? Решения: Количество попыток (N) = 12 Количество успешных попыток (r) = 7 Вероятность единственной попытки (P) = ½ = 0,5 nCr = n!r! н!р! * (н-р)! 12!7! (12-7)! = 95040120 = 792 pr= 0,57= 0,0078125 Чтобы найти (1-p)n-r, вычислить (1-p) и (n-r) = 9 P 101023. = 792 * 0,0078125 * 0,03125 = 0,193359375 Вероятность выпадения 7 решек равна 0,19 Пример испытания Бернулли
 Проверьте, являются ли испытания испытаниями Бернулли, если шары переставлены и не заменены.
Проверьте, являются ли испытания испытаниями Бернулли, если шары переставлены и не заменены. Условия испытаний Бернулли

Формула испытаний Бернулли
Испытания Бернулли и биномиальное распределение
Распределение Бернулли
 Это своего рода дискретное распределение вероятностей, при котором возможны только определенные значения. В таком случае возможны только два значения: e ( n=0 в случае неудачи и n=1 в случае успеха). Это делает распределение Бернулли простейшей формой сохраняющегося распределения вероятностей.
Это своего рода дискретное распределение вероятностей, при котором возможны только определенные значения. В таком случае возможны только два значения: e ( n=0 в случае неудачи и n=1 в случае успеха). Это делает распределение Бернулли простейшей формой сохраняющегося распределения вероятностей. Примеры распределения Бернулли

Свойства распределения Бернулли

Решаемые примеры
 Если вероятность неисправности лампочки равна 0,8, то найти вероятность того, что лампочка не неисправна.
Если вероятность неисправности лампочки равна 0,8, то найти вероятность того, что лампочка не неисправна. пр. (1-p)n-r
пр. (1-p)n-r Распределение Бернулли. Редакция Towards AI
Источник: Unsplash Учебное пособие по распределению Бернулли — погружение в дискретное распределение вероятностей случайной величины с примерами на Python В этой серии руководств мы подробно рассмотрим распределения вероятностей. Мы не просто продемонстрируем формулы, но вместо этого мы увидим, как каждая из формул выводится из их основных определений (поскольку важно понимать математику, стоящую за выводами), и мы продемонстрируем это, используя некоторые примеры в Python.
Код этого руководства доступен по адресу Github , а его полная реализация также доступна по адресу Google Colab .
Содержание:
- Что такое случайная величина?
- Дискретная случайная величина.

- Непрерывная случайная величина.
- Вероятностные распределения.
- Распределение Бернулли.
- Функция массы вероятности (PMF).
- Среднее значение распределения Бернулли.
- Дисперсия распределения Бернулли.
- Стандартное отклонение распределения Бернулли.
- Среднее отклонение распределения Бернулли.
- Генерирующая функция момента для распределения Бернулли.
- Кумулятивная функция плотности (CDF) для распределения Бернулли.
- Реализация Python.
- Краткое изложение распределения Бернулли.
- Ресурсы.
- Ссылки.
📚 Ознакомьтесь с нашим учебным пособием по функции генерации момента с помощью Python. 📚
Прежде чем углубляться в распределение вероятностей, давайте сначала разберемся с некоторыми основными терминами, касающимися случайной величины.
Рисунок 1: Основные типы данных Переменная называется случайной, если ее значение неизвестно. Другими словами, переменная является случайной величиной, если мы не можем получить ту же самую переменную, используя какую-либо функцию.
Другими словами, переменная является случайной величиной, если мы не можем получить ту же самую переменную, используя какую-либо функцию.
Случайная величина — это переменная, возможные значения которой являются числовыми результатами случайного явления.
Свойства случайной величины:
- Мы обозначаем случайные величины с большой буквы.
- Случайные величины могут быть дискретными или непрерывными.
Примеры:
- Подбрасывание правильной монеты:
На рисунке 1 показано, что результат не зависит ни от каких других переменных. Таким образом, результат подбрасывания монеты будет случайным.
2. Бросание игральной кости:
Рисунок 3: Бросание игральной кости. На рисунке 2 видно, что выход кубика нельзя предсказать заранее, и он не зависит ни от каких других переменных. Таким образом, мы можем сказать, что вывод будет случайным.
Теперь давайте кратко рассмотрим неслучайные переменные.
Рисунок 4: Неслучайные события.В приведенном выше примере мы видим, что в примере 1 мы можем быстро получить значение переменной x, вычитая единицу с обеих сторон. Следовательно, значение x не случайно, а фиксировано. Во втором примере мы видим, что значение переменной y зависит от значения переменной x, где мы можем заметить, что значение y изменяется в соответствии со значением x. Мы можем сгенерировать ту же выходную переменную y, когда мы вставляем то же значение x. Таким образом, переменная y вовсе не случайна. В распределениях вероятностей мы будем работать со случайными величинами.
Случайная величина называется дискретной случайной величиной, если ее значения могут быть получены путем подсчета . Дискретные переменные можно посчитать за конечное количество времени. Здесь важно отметить, что дискретные переменные не обязательно должны быть целыми числами. У нас могут быть дискретные случайные величины, которые являются конечными значениями с плавающей запятой.
Примеры:
- Количество учащихся в школьном автобусе.
- Количество печенья на тарелке.
- Количество орлов при подбрасывании монеты.
- Количество планет вокруг звезды.
- Чистый доход членов семьи.
Случайная величина называется непрерывной случайной величиной, если ее значения могут быть получены путем измерения . Мы не можем считать непрерывные переменные за конечное время. Другими словами, мы можем сказать, что для подсчета непрерывных переменных потребуется бесконечное количество времени.
Примеры:
- Точный вес случайного животного во вселенной.
- Точный рост случайно выбранного ученика.
- Точное расстояние, пройденное за час.
- Точное количество еды, съеденной вчера.
- Точное время победы спортсмена.
Важно отметить, что здесь мы упоминаем слово «Точный» . Это означает, что все измерения, которые мы проводим, имеют абсолютную точность.
Например, если мы измеряем время завершения гонки для спортсмена, мы можем сказать, что он завершил гонку за 9,5 секунды. Если быть точнее, то можно сказать, что он завершил гонку за 9,52 секунды. Если быть точнее, то можно сказать, что спортсмен преодолел дистанцию за 9,523 секунды. Чтобы добавить больше точности в затраченное время, мы также можем сказать, что он завершил гонку за 9,5238 секунды. Если мы продолжим это делать, мы сможем довести эту вещь до бесконечного уровня точности, и нам потребуется бесконечное количество времени, чтобы измерить ее. Вот почему она называется непрерывной переменной.
Пример: Ваш текущий возраст?
Что вы думаете об этом? Это непрерывная переменная или дискретная переменная? Пожалуйста, найдите минутку, чтобы подумать об этом.
Пример относится к группе непрерывных переменных. Как обсуждалось выше, мы можем сказать о вашем возрасте следующее:
Рисунок 6: Текущий возраст с точностью.
Обратите внимание, что мы можем продолжать писать возраст с большей и большей точностью. Поэтому мы не можем посчитать точный возраст человека за конечное время. Вот почему это непрерывная переменная.
С другой стороны, если бы вопрос был, каков ваш текущий возраст в годах?». Тогда в этом случае переменная может быть отнесена к группе дискретных переменных. Поскольку мы уже знаем, что мой возраст на данный момент составляет «X лет».
Теперь давайте обсудим распределения вероятностей. Распределения вероятностей основаны на типах данных и могут быть либо дискретными, либо непрерывными.
Рисунок 7: Типы вероятностных распределений.Распределение вероятностей — это математическая функция, которая определяет вероятности появления различных возможных результатов эксперимента. [1]
Условия для распределения Бернулли
- Должно быть только одно испытание.
- В испытании должно быть только два возможных исхода, один называется успехом, а другой — неудачей.

- P(Успех) = p
- P(Неудача) = 1 — p = q
- Обычно мы присваиваем значение 1 событию с вероятностью p и значение 0 событию с вероятностью 1 — p.
- Условно имеем p>1 — p. По-другому мы можем сказать, что мы принимаем вероятность успеха (1) как p и вероятность неудачи (0) как 1 — p, так что P (успех)> P (неудача).
- У нас должна быть вероятность одного из событий (Успеха или Неудачи) или какие-то прошлые данные, которые указывают на экспериментальную вероятность.
Если наши данные удовлетворяют приведенным выше условиям, то:
Рисунок 8: Дискретная случайная величина X подчиняется распределению Бернулли с вероятностью успеха=p.
Визуальное представление распределения Бернулли:
Примеры:
Рисунок 10: Примеры распределения Бернулли.Например:
На выборах есть только два кандидата: Патрик и Гэри, и мы можем голосовать либо за Патрика, либо за Гэри.
- P(Успех) = P(1) = Голосование за Патрика = 0,7
- P(Неудача) = P(0) = Голосование за Гэри = 0,3
Здесь у нас есть только одно испытание и только два возможных исхода. Таким образом, мы можем сказать, что данные следуют распределению Бернулли. Чтобы визуализировать это:
Рис. 11: Пример графика распределения Бернулли.Массовая функция вероятности дискретной случайной величины X присваивает вероятности каждому из возможных значений случайной величины. Используя PMF, мы можем получить вероятности каждой случайной величины. [ 6 ]
Пусть X — дискретная случайная величина, возможные значения которой обозначены x1, x2, x3, …, xn. Функция массы вероятности (PMF) должна удовлетворять следующим условиям:
Свойства PMF:
- Сумма всех вероятностей в данной PMF должна быть равна 1.
2. Все возможные значения вероятности должны быть больше или равны 0.
Давайте визуализируем функцию:
Рисунок 15: Визуализация распределения Бернулли.Среднее значение дискретной случайной величины X является средневзвешенным. Его вероятность взвешивает каждое значение случайной величины X. В распределении Бернулли случайная величина X может принимать только два значения: 0 и 1, и мы можем быстро получить вес, используя функцию массы вероятности (PMF).
Среднее: Среднее значение распределения вероятностей — это долгосрочное среднее арифметическое значение случайной величины, имеющей это распределение.
Ожидаемое значение E[X] выражает вероятность желаемого события.
Рисунок 16: Ожидаемое значение E[X}.Ожидаемое значение или среднее значение распределения Бернулли определяется как:
Рисунок 17: Среднее значение распределения Бернулли.
Среднее значение распределения Бернулли:
Рисунок 18: Доказательство среднего значения распределения Бернулли.Дисперсия (σ2) — это мера того, насколько далеко каждое число из набора случайных чисел от среднего. Квадратный корень из дисперсии называется стандартным отклонением.
На основании определения:
Рисунок 19: Формула дисперсии.Дисперсия дискретного распределения вероятностей:
Рисунок 20; Дисперсия для дискретного распределения вероятностей.В нашем случае переменная x может принимать только два значения: 0 и 1.
Рисунок 21: Дисперсия для распределения Бернулли.Дисперсия распределения Бернулли:
Рисунок 22: Доказательство дисперсии распределения Бернулли.Существует более популярная форма для поиска дисперсии в статистике:
Рисунок 23: Популярная форма формулы дисперсии.Давайте посмотрим, как это появилось.
Обычно дисперсия представляет собой ожидаемое значение квадрата разницы между каждым значением и средним значением распределения.
[ 7 ]
Из определения дисперсии мы можем тогда:
Рисунок 24: Доказательство формулы дисперсии.Нахождение дисперсии по этой формуле:
Рисунок 25: Доказательство дисперсии для распределения Бернулли.На рисунке 25 видно, что дисперсия распределения Бернулли одинакова независимо от используемой формулы.
Стандартное отклонение — это число, используемое для определения того, как измерения для группы отличаются от среднего (среднее или ожидаемое значение) [ 8 ].
Низкое стандартное отклонение означает, что большинство чисел близки к среднему, а высокое стандартное отклонение означает, что числа более разбросаны.
Рисунок 26: Стандартное отклонение для распределения Бернулли.Среднее отклонение — это среднее абсолютных отклонений набора данных относительно среднего значения данных.
На основе определения:
Рисунок 27: Формула среднего отклонения.
Для дискретного распределения вероятностей:
Рисунок 28: Среднее отклонение для распределения вероятностей.Нахождение среднего отклонения для распределения Бернулли:
Рисунок 29: Среднее отклонение для распределения Бернулли.Рисунок 30; Резюме взаимосвязи между центральным и необработанным моментами.Для следующих выводов мы будем использовать формулы, полученные в предыдущем уроке. Поэтому мы рекомендуем вам ознакомиться с нашим руководством по функции генерации момента.
Рис. 31: Определение производящей функции момента.Функция генерации момента:
Рис. 32: Функция генерации момента для распределения Бернулли.Поиск сырых моментов:
1. Первый момент:
a. Первый необработанный момент:
Рисунок 33: Первый необработанный момент.2. Второй момент:
а. Второй необработанный момент:
Рисунок 34: Второй необработанный момент.б. Второй центральный момент (дисперсия):
Рисунок 35: Второй центральный момент.
3. Третий момент:
а. Третий необработанный момент:
Рисунок 36: Третий необработанный момент.б. Третий центральный момент:
Рисунок 37: Третий центральный момент.г. Третий стандартизированный момент: (асимметрия)
Рисунок 38: Третий стандартизированный момент (асимметрия).4. Четвертый момент:
а. Четвертый необработанный момент:
Рисунок 39; Четвертый сырой момент.б. Четвертый центральный момент:
Рис. 40: Четвертый центральный момент.с. Четвертый стандартизованный момент: (эксцесс):
Рисунок 41: Четвертый стандартизированный момент (эксцесс). Рисунок 42: Четвертый стандартизированный момент (избыточный эксцесс). Рисунок 43: Определение функции кумулятивной плотности.На основе функции массы вероятности (PMF) мы можем записать кумулятивную функцию распределения (CDF) для распределения Бернулли следующим образом:
Рисунок 44: Кумулятивная функция плотности для распределения Бернулли.
После самой интересной части давайте перейдем к ее реализации на Python.
- Импорт необходимых библиотек:
2. Найдите моменты:
Рисунок 46: Нахождение моментов для распределения Бернулли с p-значением 0,7.3. Получите среднее значение:
Рисунок 47: Среднее значение для p=0,7.4. Получите медианное значение:
Рисунок 48: Медиана для p=0,7.5. Получите значение дисперсии:
Рисунок 49: Дисперсия для p=0,7.6. Получите значение стандартного отклонения:
Рисунок 50: Стандартное отклонение для p=0,7.7. Функция массы вероятности (PMF):
Рисунок 51: Функция массы вероятности для p = 0,7.8. График PMF:
Рисунок 52: Диаграмма рассеяния PMF для p=0,7.9. Кумулятивная функция плотности (CDF):
Рисунок 53: Кумулятивная функция плотности для p=0,7.10. Постройте CDF:
Рисунок 54: Диаграмма рассеяния CDF для p=0,7.11. Постройте гистограмму для PMF:
Рисунок 55: Гистограмма для PMF при значении p 0,7.
12. Постройте гистограмму CDF:
Рисунок 56: Гистограмма CDF для значения p 0,7.13. Выходные данные для различных экспериментов:
Рисунок 57: Генерация выходных данных для различных экспериментов Бернулли. Рисунок 58: Сводная информация о распределении Бернулли.Это учебник по дистрибутиву Бернулли. Мы надеемся, что вам понравилось читать и вы узнали что-то новое. В будущем мы постараемся более подробно рассмотреть распределения вероятностей. Любые предложения или отзывы имеют решающее значение для дальнейшего улучшения. Пожалуйста, дайте нам знать в комментариях, если они у вас есть.
Купи Pratik a Coffee! ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ: Мнения, выраженные в этой статье, принадлежат автору (авторам) и не отражают точку зрения Университета Карнеги-Меллона или других компаний (прямо или косвенно), связанных с автором (авторами). Эти работы не претендуют на то, чтобы быть конечными продуктами, а скорее отражают текущее мышление, а также служат катализатором для обсуждения и улучшения.








 е. событие А наступит ровно k раз)?
е. событие А наступит ровно k раз)? Поскольку все отдельные опыты в любой серии независимы, то вероятность любой последовательности из k успехов и (N — k) неудач может быть найдена по формуле .
Поскольку все отдельные опыты в любой серии независимы, то вероятность любой последовательности из k успехов и (N — k) неудач может быть найдена по формуле .
 Договоримся считать значение 1 – успехом, а значение 0 – неудачей. Тогда, как легко сообразить, число успехов в N испытаниях выражается случайной величиной , равной сумме величин : .
Договоримся считать значение 1 – успехом, а значение 0 – неудачей. Тогда, как легко сообразить, число успехов в N испытаниях выражается случайной величиной , равной сумме величин : . Вот так будут выглядеть полигоны частот для биноминальных распределений с равными вероятностями и возрастающими значениями N:
Вот так будут выглядеть полигоны частот для биноминальных распределений с равными вероятностями и возрастающими значениями N: Снова тестирование. Экзамен состоит из 16 вопросов. К каждому вопросу предлагается 4 варианта ответа, из которых ровно один верный. Положительная оценка ставится, если ученик ответил хотя бы на 5 вопросов. С какой вероятностью ученик, не знающий предмета, сдаст экзамен?
Снова тестирование. Экзамен состоит из 16 вопросов. К каждому вопросу предлагается 4 варианта ответа, из которых ровно один верный. Положительная оценка ставится, если ученик ответил хотя бы на 5 вопросов. С какой вероятностью ученик, не знающий предмета, сдаст экзамен?


 Для этого можно воспользоваться тем, что случайная величина является суммой N независимых случайных величин: .
Для этого можно воспользоваться тем, что случайная величина является суммой N независимых случайных величин: . Мишень установлена так, что может вращаться вокруг оси. При достаточно большой угловой скорости вращения стрелок не в состоянии различать цифры, выписанные по одной на секторах. Он вынужден стрелять наугад. При попадании в сектор 1 стрелок получает 1 р., в сектор 2 – 2 р., в сектор 3 – 3 р. и т.д., в сектор 8 – 8 р.. Стоит ли ему участвовать в такой игре, если за право стрелять один раз надо платить 5 р.?
Мишень установлена так, что может вращаться вокруг оси. При достаточно большой угловой скорости вращения стрелок не в состоянии различать цифры, выписанные по одной на секторах. Он вынужден стрелять наугад. При попадании в сектор 1 стрелок получает 1 р., в сектор 2 – 2 р., в сектор 3 – 3 р. и т.д., в сектор 8 – 8 р.. Стоит ли ему участвовать в такой игре, если за право стрелять один раз надо платить 5 р.? Найдем ожидаемое среднее число удач при n = 20 испытаниях Бернулли с вероятностью успеха p = 0,4 в одном испытании.
Найдем ожидаемое среднее число удач при n = 20 испытаниях Бернулли с вероятностью успеха p = 0,4 в одном испытании.


 При заполнении хотя бы двух отсеков крейсер тонет. Вычислите вероятность гибели крейсера.
При заполнении хотя бы двух отсеков крейсер тонет. Вычислите вероятность гибели крейсера.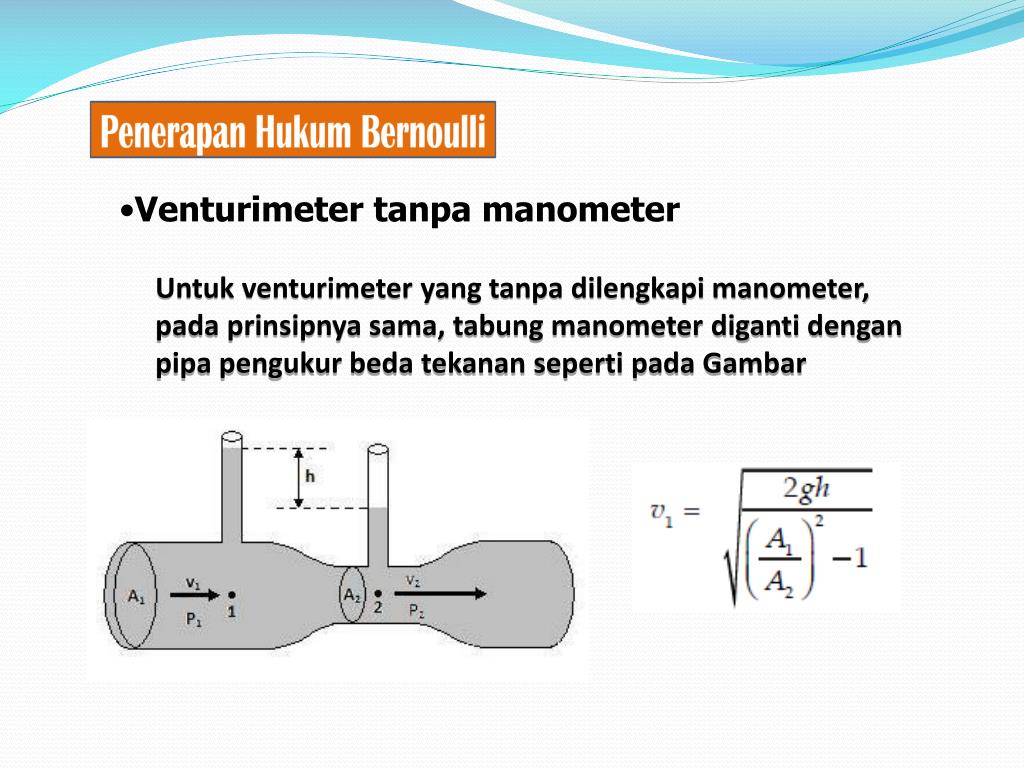


 А. Бунимович, В.А. Булычев. Вероятность и статистика в курсе математики общеобразовательной школы: лекции 5 – 8. – М.: Педагогический университет «Первое сентября», 2006.
А. Бунимович, В.А. Булычев. Вероятность и статистика в курсе математики общеобразовательной школы: лекции 5 – 8. – М.: Педагогический университет «Первое сентября», 2006. Успехом будем считать выпадение шестерки. Неудачей – выпадение иного числа очков. Таким образом, . Найдите вероятность того, что бросив кость 8 раз, мы выбросим шестерку не менее 4, но не более 6 раз.
Успехом будем считать выпадение шестерки. Неудачей – выпадение иного числа очков. Таким образом, . Найдите вероятность того, что бросив кость 8 раз, мы выбросим шестерку не менее 4, но не более 6 раз. Говоря математическим языком, вероятность успеха всегда p , а вероятность неудачи всегда 1 – p.
Говоря математическим языком, вероятность успеха всегда p , а вероятность неудачи всегда 1 – p.  логический; если TRUE, вероятности p задаются как log(p)
логический; если TRUE, вероятности p задаются как log(p) 7)
7)  5,lower.tail =
5,lower.tail =  5)
5) 

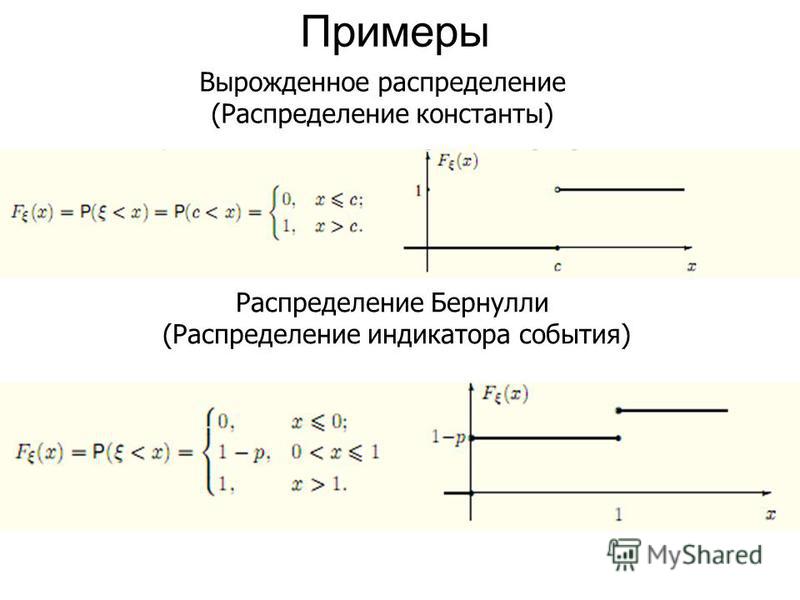

 [ 7 ]
[ 7 ]