Треугольник равносторонний: свойства, признаки, площадь, периметр
В школьном курсе геометрии огромное количество времени уделяется изучению треугольников. Ученики вычисляют углы, строят биссектрисы и высоты, выясняют, чем фигуры отличаются друг от друга, и как проще всего найти их площадь и периметр. Кажется, что это никак не пригодится в жизни, но иногда все-таки полезно узнать, например, как определить, что треугольник равносторонний или тупоугольный. Как же это сделать?
Типы треугольников
Три точки, которые не лежат на одной прямой, и отрезки, которые их соединяют. Кажется, что эта фигура — самая простая. Какими могут быть треугольники, если у них всего три стороны? На самом деле вариантов довольно большое количество, и некоторым из них уделяется особое внимание в рамках школьного курса геометрии. Правильный треугольник — равносторонний, то есть все его углы и стороны равны. Он обладает рядом примечательных свойств, о которых речь пойдет дальше.
У равнобедренного равны только две стороны, и он также довольно интересен. У прямоугольного и тупоугольного треугольников, как несложно догадаться, соответственно, один из углов прямой или тупой. При этом они также могут равнобедренными.
У прямоугольного и тупоугольного треугольников, как несложно догадаться, соответственно, один из углов прямой или тупой. При этом они также могут равнобедренными.
Существует и особый вид треугольника, называемый египетским. Его стороны равны 3, 4 и 5 единицам. При этом он является прямоугольным. Считается, что такой треугольник активно использовался египетскими землемерами и архитекторами для построения прямых углов. Есть мнение, что с его помощью были возведены знаменитые пирамиды.
И все-таки все вершины треугольника могут лежать на одной прямой. В этом случае он будет называться вырожденным, в то время как все остальные — невырожденными. Именно они и являются одним из предметов изучения геометрии.
Треугольник равносторонний
Разумеется, правильные фигуры вызывают всегда наибольший интерес. Они кажутся более совершенными, более изящными. Формулы вычисления их характеристик зачастую проще и короче, чем для обычных фигур. Это относится и к треугольникам. Неудивительно, что при изучении геометрии им уделяется достаточно много внимания: школьников учат отличать правильные фигуры от остальных, а также рассказывают о некоторых их интересных характеристиках.
Признаки и свойства
Как нетрудно догадаться из названия, каждая сторона равностороннего треугольника равна двум другим. Кроме того, он обладает рядом признаков, благодаря которым можно определить, правильная ли фигура или нет.
- все его углы равны, их величина составляет 60 градусов;
- биссектрисы, высоты и медианы, проведенные из каждой вершины, совпадают;
- правильный треугольник имеет 3 оси симметрии, он не изменяется при повороте на 120 градусов.
- центр вписанной окружности также является центром описанной окружности и точкой пересечения медиан, биссектрис, высот и срединных перпендикуляров.
Если наблюдается хотя бы один из вышеперечисленных признаков, то треугольник — равносторонний. Для правильной фигуры справедливы все упомянутые утверждения.
Все треугольники обладают рядом примечательных свойств. Во-первых, средняя линия, то есть отрезок, делящий две стороны пополам и параллельный третьей, равна половине основания. Во-вторых, сумма всех углов этой фигуры всегда равна 180 градусам. Кроме того, в треугольниках наблюдается еще одна любопытная взаимосвязь. Так, против большей стороны лежит больший угол и наоборот. Но это, конечно, к равностороннему треугольнику отношения не имеет, ведь у него все углы равны.
Кроме того, в треугольниках наблюдается еще одна любопытная взаимосвязь. Так, против большей стороны лежит больший угол и наоборот. Но это, конечно, к равностороннему треугольнику отношения не имеет, ведь у него все углы равны.
Вписанные и описанные окружности
Нередко в курсе геометрии учащиеся также изучают то, как фигуры могут взаимодействовать друг с другом. В частности, изучаются окружности, вписанные в многоугольники или описанные около них. О чем идет речь?
Вписанной называют такую окружность, для которой все стороны многоугольника являются касательными. Описанной — ту, которая имеет точки соприкосновения со всеми углами. Для каждого треугольника всегда можно построить как первую, так и вторую окружность, но только одну каждого вида. Доказательства двух этих
теорем приводятся в школьном курсе геометрии.
Помимо вычисления параметров самих треугольников, некоторые задачи также подразумевают расчет радиусов этих окружностей.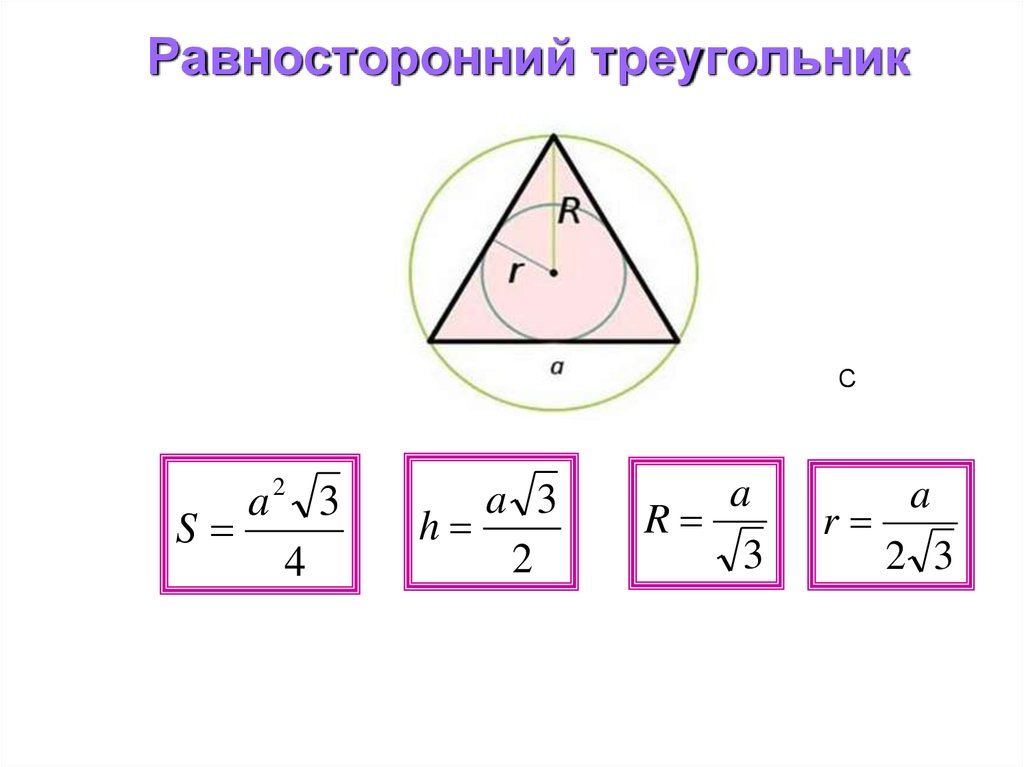 И формулы применительно к
И формулы применительно к
равностороннему треугольнику выглядят следующим образом:
r = a/√ ̅3;
R = a/2√ ̅3;
где r — радиус вписанной окружности, R — радиус описанной окружности, a — длина стороны треугольника.
Вычисление высоты, периметра и площади
Основные параметры, вычислением которых занимаются школьники во время изучения геометрии, остаются неизменными практически для любых фигур. Это периметр, площадь и высота. Для простоты расчетов существуют различные формулы.
Так, периметр, то есть длина всех сторон, вычисляется следующими способами:
P = 3a = 3√ ̅3R = 6√ ̅3r, где a — сторона правильного треугольника, R — радиус описанной окружности, r — вписанной.
Высота:
h = (√ ̅3/2)*a, где a — длина стороны.
Наконец, формула площади равностороннего треугольника выводится из стандартной, то есть произведения половины основания на его высоту.
S = (√ ̅3/4)*a2, где a — длина стороны.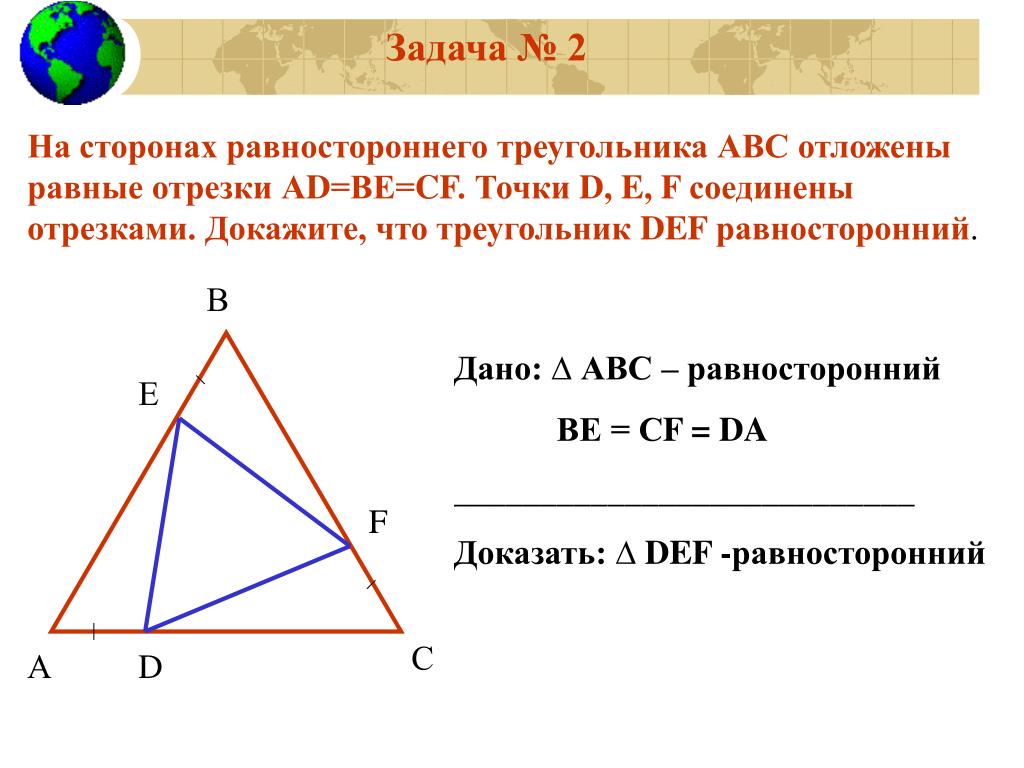
Также эта величина может быть вычислена через параметры описанной или вписанной окружности. Для этого также существуют специальные формулы:
S = 3√ ̅3r2 = (3√ ̅3/4)*R2, где r и R — соответственно радиусы вписанной и описанной окружностей.
Построение
Еще один интересный тип задач, касающийся в том числе и треугольников, связан с необходимостью начертить ту или иную фигуру, используя минимальный набор
инструментов: циркуль и линейку без делений.
Для того чтобы построить правильный треугольник с помощью только этих приспособлений, необходимо выполнить несколько шагов.
- Нужно начертить окружность с любым радиусом и с центром в произвольно взятой точке А. Ее необходимо отметить.
- Далее нужно провести прямую через эту точку.
- Пересечения окружности и прямой необходимо обозначить как В и С. Все построения должны проводиться с максимально возможной точностью.
- Далее надо построить еще одну окружность с тем же радиусом и центром в точке С или дугу с соответствующими параметрами.
 Места пересечения будут обозначены как D и F.
Места пересечения будут обозначены как D и F. - Точки B, F, D необходимо соединить отрезками. Равносторонний треугольник построен.
Решение подобных задач обычно представляет для школьников проблему, но это умение может пригодиться и в обычной жизни.
Равносторонний остроугольный треугольник. Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника — формулы вычисления, прямоугольный треугольник, равнобедренн. Какая фигур
Деление треугольников на остроугольные, прямоугольные и тупоугольные. Классификация по соотношению сторон делит треугольники на разносторонние, равносторонние и равнобедренные. Причем каждый треугольник одновременно принадлежит к двум . Например, он может быть прямоугольным и разносторонним одновременно.
Определяя вид по типу углов, очень внимательны. Тупоугольным будет называться такой треугольник, у которого один из углов является , то есть составляет боле 90 градусов. Прямоугольный треугольник может быть вычислен по наличию одного прямого (равного 90 градусам) угла. Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла острыми.
Прямоугольный треугольник может быть вычислен по наличию одного прямого (равного 90 градусам) угла. Однако чтобы классифицировать треугольник как остроугольный, вам нужно будет убедиться, что все три его угла острыми.
Определяя вид треугольника по соотношению сторон, для начала вам придется узнать длины всех трех сторон. Однако если по условию длины сторон вам не даны, помочь вам смогут углы. Разносторонним будет являться треугольник, все три стороны которого имеют разную длину. Если длины сторон неизвестны, то треугольник может быть классифицирован как разносторонний в случае, если все три его угла являются разными. Разносторонний треугольник может быть тупоугольным, прямоугольным и остроугольным.
Равнобедренным будет являться треугольник, две из трех сторон которого равны между собой. Если длины сторон вам не даны, ориентируйтесь по двум равным между собой углам. Равнобедренный треугольник, как и разносторонний, может быть и тупоугольным, и прямоугольным и остроугольным.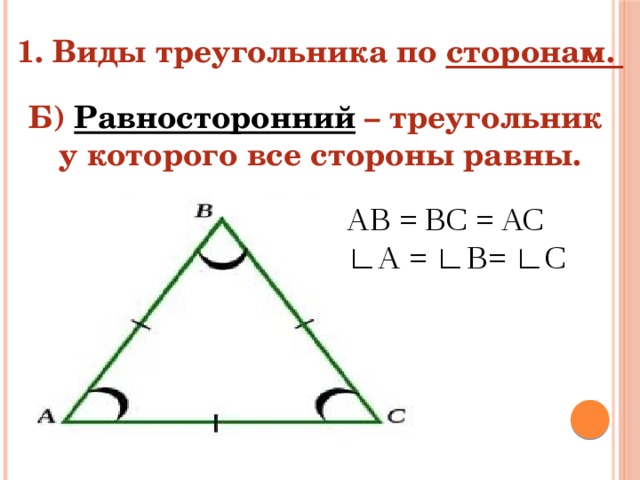
Равносторонним может быть только такой треугольник, все три стороны которого имеют одинаковую длину. Все его углы также равны между собой, и каждый из них равен 60-ти градусам. Отсюда ясно, что равносторонние треугольники всегда являются остроугольными.
Простейший из многоугольников – это треугольник. Он образуется при помощи трех точек, лежащих в одной плоскости, но не лежащих на одной прямой, попарно соединенных отрезками. Тем не менее, треугольники бывают разных типов, а значит, обладают разными свойствами.
Инструкция
Принято выделять три типа : тупоугольные, остроугольные и прямоугольные. Это по типу углов. Тупоугольным называется треугольник, у которого один из углов является тупым. Тупым называется угол, имеющий величину больше девяноста градусов, но меньше ста восьмидесяти. Например, в треугольнике ABC угол ABC равен 65°, угол BCA равен 95°, угол CAB равен 20°. Углы ABC и CAB меньше 90°, но угол BCA больше, значит, треугольник тупоугольный.
Остроугольным называется треугольник, у которого все углы являются острыми.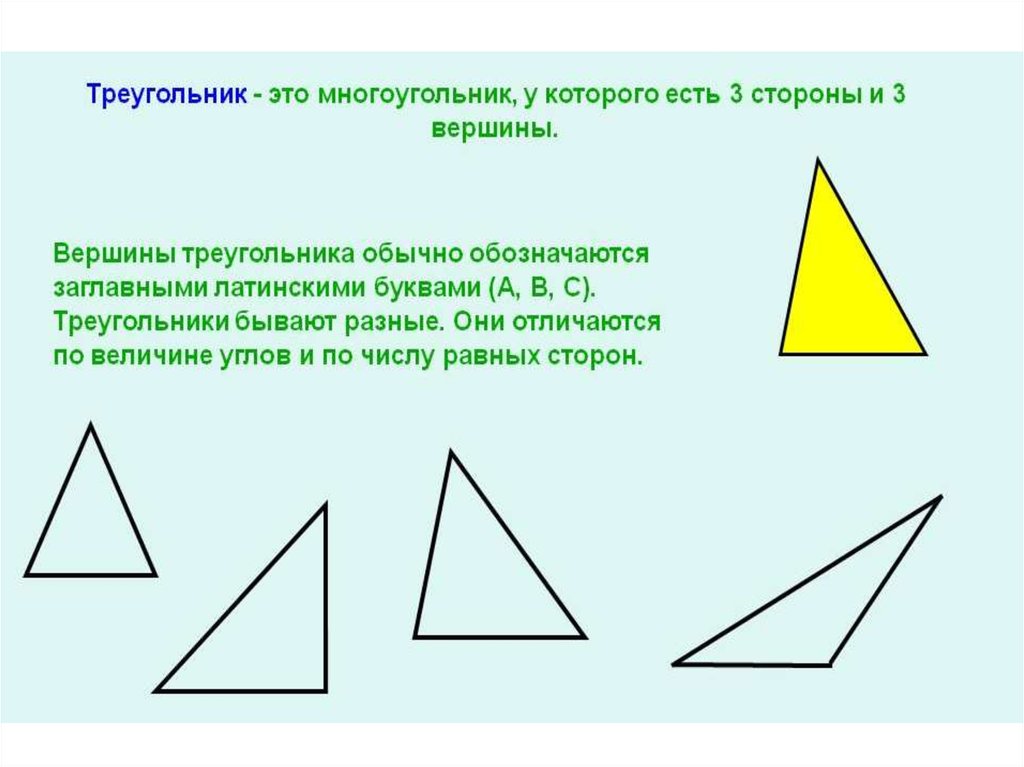 Острым называется угол, имеющий величину меньше девяноста и больше нуля градусов. Например, в треугольнике ABC угол ABC равен 60°, угол BCA равен 70°, угол CAB равен 50°. Все три угла меньше 90°, значит треугольник . Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.
Острым называется угол, имеющий величину меньше девяноста и больше нуля градусов. Например, в треугольнике ABC угол ABC равен 60°, угол BCA равен 70°, угол CAB равен 50°. Все три угла меньше 90°, значит треугольник . Если вам известно, что у треугольника все стороны равны, это значит, что все углы у него тоже равны между собой, при этом равны шестидесяти градусам. Соответственно, все углы в таком треугольнике меньше девяноста градусов, а следовательно такой треугольник является остроугольным.
Если в треугольнике один из углов равен девяноста градусам, это значит, что он не относится ни широкоугольному типу, ни к остроугольному. Это прямоугольный треугольник.
Если вид треугольника определять по соотношению сторон, они будут равносторонние, разносторонние и равнобедренные. В равностороннем треугольнике все стороны равны, а это, как вы выяснили, говорит о том, что треугольник остроугольный. Если у треугольника равны только две стороны или стороны не равны между собой, он может быть и тупоугольным, и прямоугольным, и остроугольным.
Видео по теме
Источники:
- тупоугольный треугольник
Равенство двух или более треугольников соответствует случаю, когда все стороны и углы данных треугольников равны. Однако существует ряд более простых критериев для доказательства данного равенства.
Вам понадобится
- Учебник по геометрии, лист бумаги, простой карандаш, транспортир, линейка.
Инструкция
Откройте учебник по геометрии седьмого класса на параграфе о признаках равенства треугольников. Вы увидите, что существует ряд основных признаков, доказывающих равенство двух треугольников. Если два треугольника, равенство которых проверяется, являются произвольными, то для них существует три основных признака равенства. Если же известна какая-то дополнительная информация о треугольниках, то основные три признака дополняются еще несколькими. Это относится, например, к случаю равенства прямоугольных треугольников.
Прочитайте первое правило о равенстве треугольников. Как известно, оно позволяет считать треугольники равными, если можно доказать, что какой-либо один угол и две прилегающие к нему стороны двух треугольников равны. Для того чтобы понять, данный закон, начертите на листе бумаги с помощью транспортира два одинаковых определенных угла, образованных двумя лучами, исходящими из одной точки. Отмерьте линейкой одинаковые стороны от вершины нарисованного угла в обоих случаях. Используя транспортир, измерьте величины полученных углов двух образованных треугольников, убедитесь, что они равны.
Для того чтобы не прибегать к таким практическим мерам для понимания признака равенства треугольников, прочитайте доказательство первого признака равенства. Дело в том, что каждое правило о равенстве треугольников имеет строгое теоретическое доказательство, просто его не удобно использовать в целях запоминания правил.
Прочитайте второй признак равенства треугольников. Он гласит, что два треугольника будут равны в том случае, если какая-либо одна сторона и два прилегающие к ней угла двух таких треугольников равны. Для того чтобы запомнить данное правило, представьте нарисованную сторону треугольника и два прилежащих к ней угла. Представьте, что длины сторон углов постепенно увеличиваются. В конце концов, они пересекутся, образуя третий угол. В данной мысленной задаче важным является то, что точка пересечения сторон, которые мысленно увеличиваются, а также полученный угол однозначно определяются третьей стороной и двумя прилегающими к ней углами.
Для того чтобы запомнить данное правило, представьте нарисованную сторону треугольника и два прилежащих к ней угла. Представьте, что длины сторон углов постепенно увеличиваются. В конце концов, они пересекутся, образуя третий угол. В данной мысленной задаче важным является то, что точка пересечения сторон, которые мысленно увеличиваются, а также полученный угол однозначно определяются третьей стороной и двумя прилегающими к ней углами.
Если вам не дана никакая информация об углах исследуемых треугольников, то используйте третий признак равенства треугольников. По данному правилу, два треугольника считаются равными, если все три стороны одно из них равны соответствующим трем сторонам другого. Таким образом, данное правило говорит о том, что длины сторон треугольника однозначно определяют все углы треугольника, а значит, они однозначно определяют и сам треугольник.
Видео по теме
Треугольники
Треугольником называется
фигура, которая состоит из трёх точек,
не лежащих на одной прямой, и трёх
отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника,
а отрезки — его сторонами.
Точки называются вершинами треугольника,
а отрезки — его сторонами.
Виды треугольников
Треугольник называется равнобедренным, если у него две сторны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Треугольник, у которого все сторны равны, называется равносторонним
или правильным.Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Основные линии треугольника
Медиана
Медиана треугольника
— это отрезок, соединяющий верщину
треугольника с серединой противолежащей
стороны этого треугольника.
Свойства медиан треугольника
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Биссектриса
Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
Высота
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Свойства высот треугольника
В прямоугольном
треугольнике высота, проведенная из вершины прямого
угла, разбивает его на два треугольника, подобные исходному.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Срединный перпендикуляр
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника .
Средняя линия
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника
Средняя
линия треугольника параллельна одной
из его сторон и равна половине этой
стороны.
Формулы и соотношения
Признаки равенства треугольников
Два треугольника равны, если у них соответственно равны:
две стороны и угол между ними;
два угла и прилежащая к ним сторона;
три стороны.
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, если у них соответственно равны:
гипотенуза и острый угол;
катет и противолежащий угол;
катет и прилежащий угол;
два катета ;
гипотенуза и катет .
Подобие треугольников
Два треугольника подобны, если выполняется одно из следующих условий, называемых признаками подобия:
два угла одного треугольника равны двум углам другого треугольника;
две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны;
три
стороны одного треугольника соответственно
пропорциональны трем сторонам другого
треугольника.
В подобных треугольниках соответствующие линии (высоты , медианы , биссектрисы и т. п.) пропорциональны.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов, причем коэффициент пропорциональности равен диаметру описанной около треугольника окружности :
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a 2 = b 2 + c 2 — 2bc cos
Формулы площади треугольника
Произвольный треугольник
a, b, c — стороны; — угол между сторонамиa и b ;- полупериметр;R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; h a — высота, проведенная к стороне a .
При изучении математики ученики начинаются знакомиться с различными видами геометрических фигур.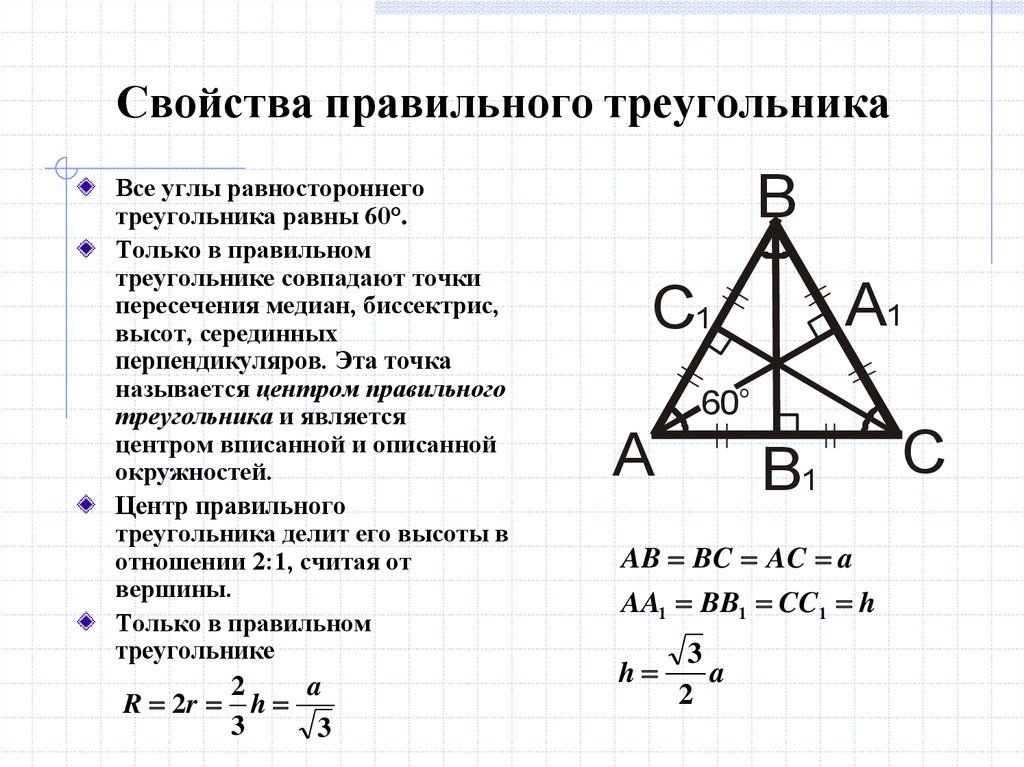 Сегодня речь пойдет о различных видах треугольников.
Сегодня речь пойдет о различных видах треугольников.
Определение
Геометрические фигуры, которые состоят из трех точек, которые не находятся на одной прямой, называются треугольниками.
Отрезки, соединяющие точки, называются сторонами, а точки – вершинами. Вершины обозначаются большими латинскими буквами, например: A, B, C.
Стороны обозначаются названиями двух точек, из которых они состоят – AB, BC, AC. Пересекаясь, стороны образуют углы. Нижняя сторона считается основанием фигуры.
Рис. 1. Треугольник ABC.
Виды треугольников
Треугольники классифицируют по углам и сторонам. Каждый из видов треугольника имеет свои свойства.
Существует три вида треугольников по углам:
- остроугольные;
- прямоугольные;
- тупоугольные.
Все углы остроугольного треугольника острые, то есть градусная мера каждого составляет не более 90 0 .
Прямоугольный треугольник содержит прямой угол. Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.
Два других угла всегда будут острыми, так как иначе сумма углов треугольника превысит 180 градусов, а это невозможно. Сторона, которая, находится напротив прямого угла, называется гипотенузой, а две другие катетами. Гипотенуза всегда больше катета.
Тупоугольный треугольник содержит тупой угол. То есть угол, величиной больше 90 градусов. Два других угла в таком треугольника будут острыми.
Рис. 2. Виды треугольников по углам.
Пифагоровым треугольником называется прямоугольник, стороны которого равны 3, 4, 5.
Причем, большая сторона является гипотенузой.
Такие треугольники часто используются для составления простых задач в геометрии. Поэтому, запомните: если две стороны треугольника равны 3, то третья обязательно будет 5. Это упростит расчеты.
Виды треугольников по сторонам:
- равносторонние;
- равнобедренные;
- разносторонние.
Равносторонний треугольник – это треугольник, у которого все стороны равны.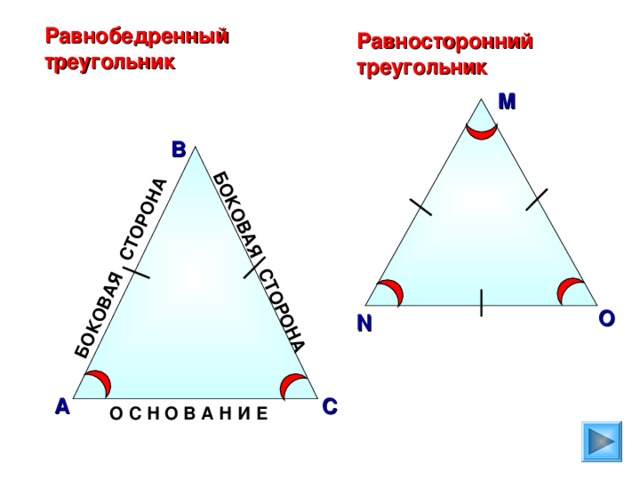 Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.
Все углы такого треугольника равны 60 0 , то есть он всегда является остроугольным.
Равнобедренный треугольник – треугольник, у которого только две стороны равны. Эти стороны называются боковыми, а третья – основанием. Кроме того, углы при основании равнобедренного треугольника равны и всегда являются острыми.
Разносторонним или произвольным треугольником называется треугольник, у которого все длины и все углы не равны между собой.
Если в задаче нет никаких уточнений по поводу фигуры, то принято считать, что речь идет о произвольном треугольнике.
Рис. 3. Виды треугольников по сторонам.
Сумма всех углов треугольника, независимо от его вида, равна 1800.
Напротив большего угла находится большая сторона. А также длина любой стороны всегда меньше суммы двух других его сторон. Эти свойства подтверждаются теоремой о неравенстве треугольника.
Существует понятие золотого треугольника. Это равнобедренный треугольник, у которого две боковые стороны пропорциональны основе и равны определенному числу. В такой фигуре углы пропорциональны соотношению 2:2:1.
В такой фигуре углы пропорциональны соотношению 2:2:1.
Задача:
Существует ли треугольник, стороны которого равны 6 см., 3 см., 4 см.?
Решение:
Для решения данного задания нужно использовать неравенство a
Что мы узнали?
Из данного материала из курса математики 5 класса, мы узнали, что треугольники классифицируются по сторонам и величине углов. Треугольники имеют определенные свойства, которые можно использовать при решении заданий.
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.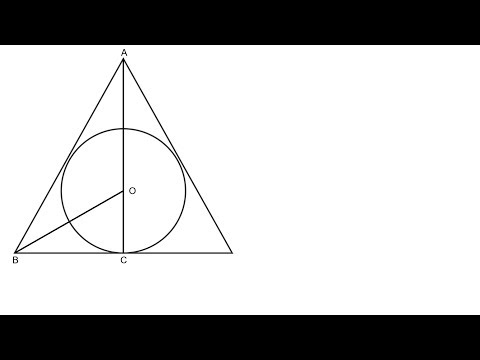
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.
Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне.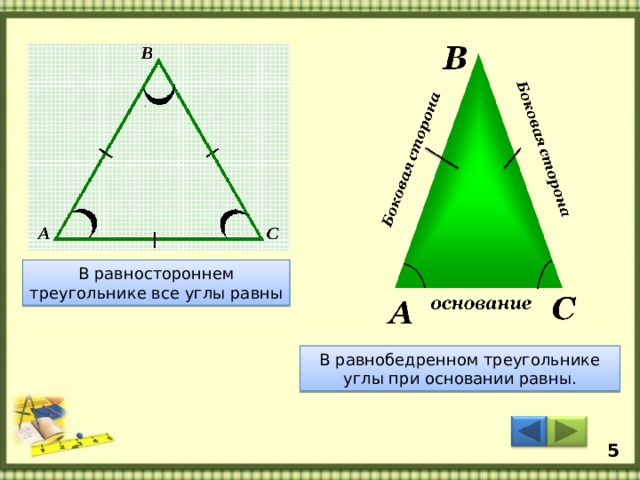 Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.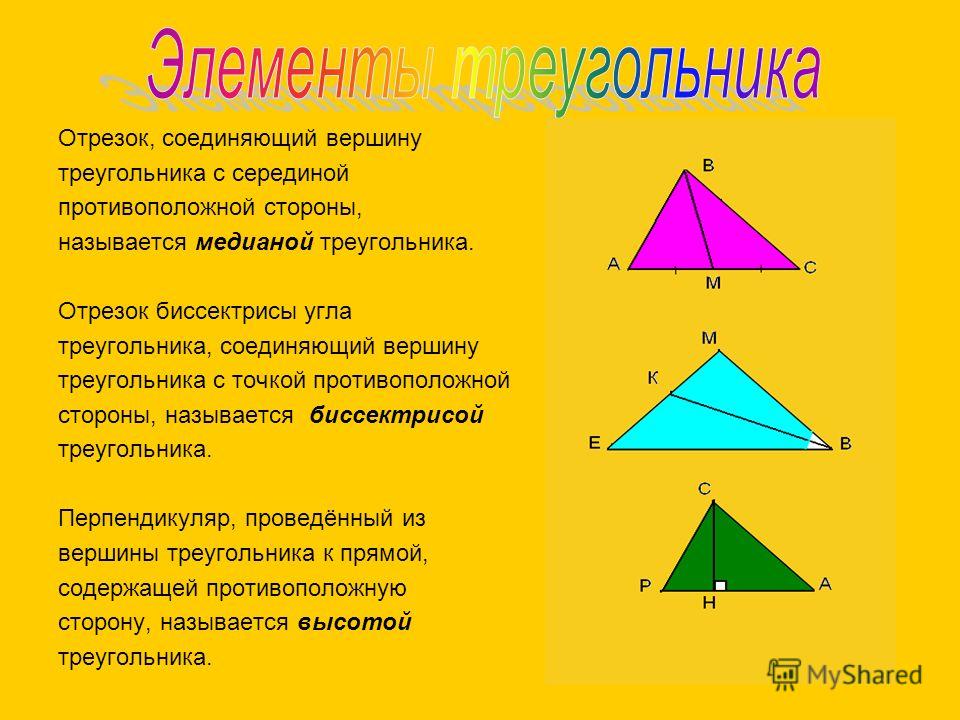
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности).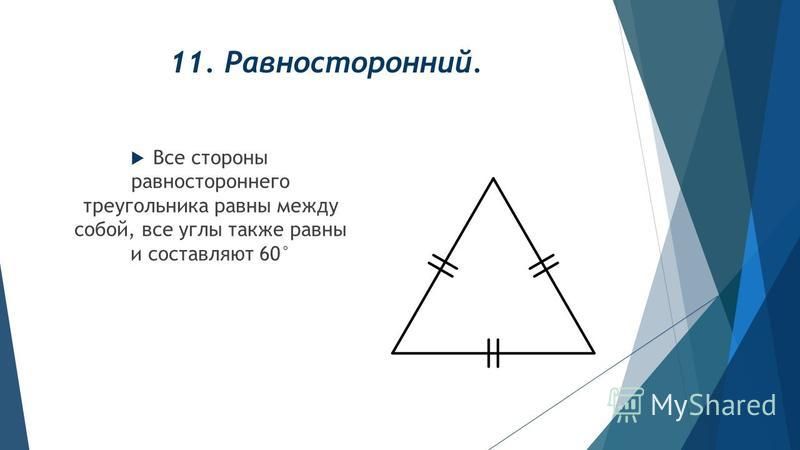 То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.
Сегодня мы отправляемся в страну Геометрия, где познакомимся с различными видами треугольников.
Рассмотрите геометрические фигуры и найдите среди них «лишнюю» (рис. 1).
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 — четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника , отрезки — его сторонами .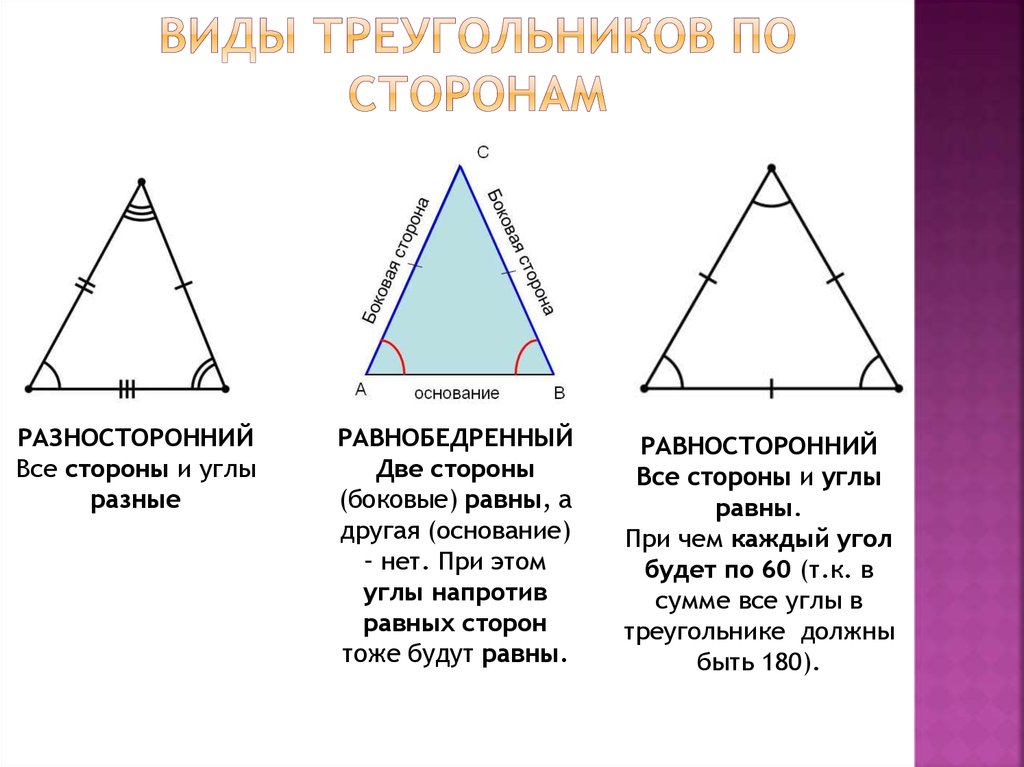 Стороны треугольника образуют в вершинах треугольника три угла.
Стороны треугольника образуют в вершинах треугольника три угла.
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Равнобедренный треугольник
Эти стороны называются боковыми , третья сторона — основанием . В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны . Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Рассмотрите рисунки.
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются … , отрезки — его … . Стороны треугольника образуют в вершинах треугольника ….
Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
2. Начертите
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Как рисовать остроугольный треугольник. Как построить равнобедренный треугольник
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.

Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию.
 Обозначаем его буквами АС.
Обозначаем его буквами АС. - Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам.
 Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. - Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.
Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.
Инструкция
Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.
В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.
Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.
В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.
Получив все три вершины, соедините их прямыми линиями с помощью любой ровной поверхности (лучше линейки). Треугольник ABC построен.
Если окружность касается всех трех сторон данного треугольника, а её центр находится внутри треугольника, то ее называют вписанной в треугольник.
Вам понадобится
- линейка, циркуль
Инструкция
Из вершин треугольника (стороны противоположной делимому углу) циркулем проводят дуги окружности произвольного радиуса до пересечения их между собой;
Точку пересечения дуг по линейке соединяют с вершиной делимого угла;
Тоже самое проделывают с любым другим углом;
Радиусом вписанной в треугольник окружности будет отношение площади треугольника и его полупериметра: r=S/p , где S — площадь треугольника, а p=(a+b+c)/2 — полупериметр треугольника.
Радиус вписанной в треугольник окружности равноудален от всех сторон треугольника.
Источники:
- http://www.alleng.ru/d/math/math52.htm
Рассмотрим задачу построения треугольника при условии, что известны три его стороны или одна сторона и два угла.
Вам понадобится
- — циркуль
- — линейка
- — транспортир
Инструкция
Допустим, даны три стороны : a, b и с. Пользуясь , несложно с такими сторонами. Для начала выберем самую длинную из этих сторон, пусть это будет сторона с, и начертим ее. Затем установим раствор циркуля на величину другой стороны, стороны a, и начертим циркулем окружность радиуса a с центром на одном из концов стороны c. Теперь установим раствор циркуля на величину стороны b и начертим окружность с центром на другом конце стороны c. Радиус этой окружности равен b. Соединим точку пересечения окружностей с центрами и получим треугольник с искомыми сторонами.
Чтобы начертить треугольник с заданной стороной и двумя прилегающими углами, возьмите транспортир. Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Видео по теме
Обратите внимание
Для сторон треугольника справедливо следующее утверждение: сумма длин двух любых сторон должна быть больше третьей. Если это не выполняется, то построить такой треугольник невозможно.
Окружности в шаге 1 пересекаются в двух точках. Можно выбрать любую, треугольники будут равными.
Правильный треугольник — тот, у которого все стороны обладают одинаковой длиной. Исходя из этого определения, построение подобной разновидности треугольника является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
С помощью линейки соединить отмеченные на листке точки последовательно, друг за другом так, как это показано на рисунке 2.
Обратите внимание
В правильном (равностороннем) треугольнике все углы равны 60 градусам.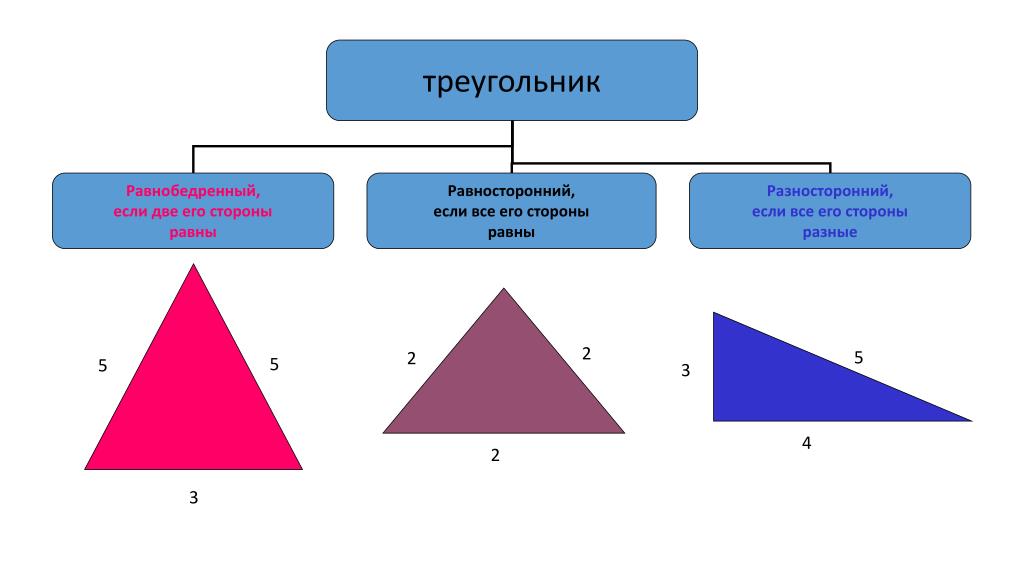
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это означает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Любой правильный треугольник является равнобедренным, в то время как обратное утверждение не верно.
У любого равностороннего треугольника одинаковы не только стороны, но и углы, каждый из которых равен 60 градусам. Однако чертеж такого треугольника, построенный при помощи транспортира, не будет обладать высокой точностью. Поэтому для построения данной фигуры лучше воспользоваться циркулем.
Вам понадобится
- Карандаш, линейка, циркуль
Инструкция
Затем возьмите циркуль, установите его в из концов (будущей вершине треугольника) и проведите окружность с радиусом, равным длине этого отрезка. Можно не проводить окружность целиком, а начертить лишь ее четверть, от противоположного края отрезка.
Теперь переставьте циркуль в другой конец отрезка и снова начертите окружность того же радиуса.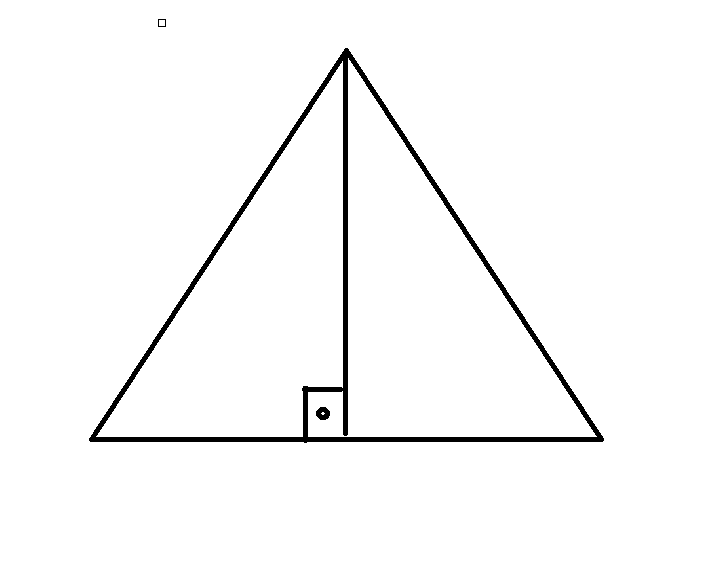 Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Чтобы закончить построение, снова возьмите линейку с карандашом и соедините точку пересечения двух окружностей с обоими концами отрезка. Вы получите треугольник, все три стороны которого абсолютно равны, – это можно будет легко проверить с помощью линейки.
Видео по теме
Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.
Вам понадобится
- Линейка, циркуль.
Инструкция
С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.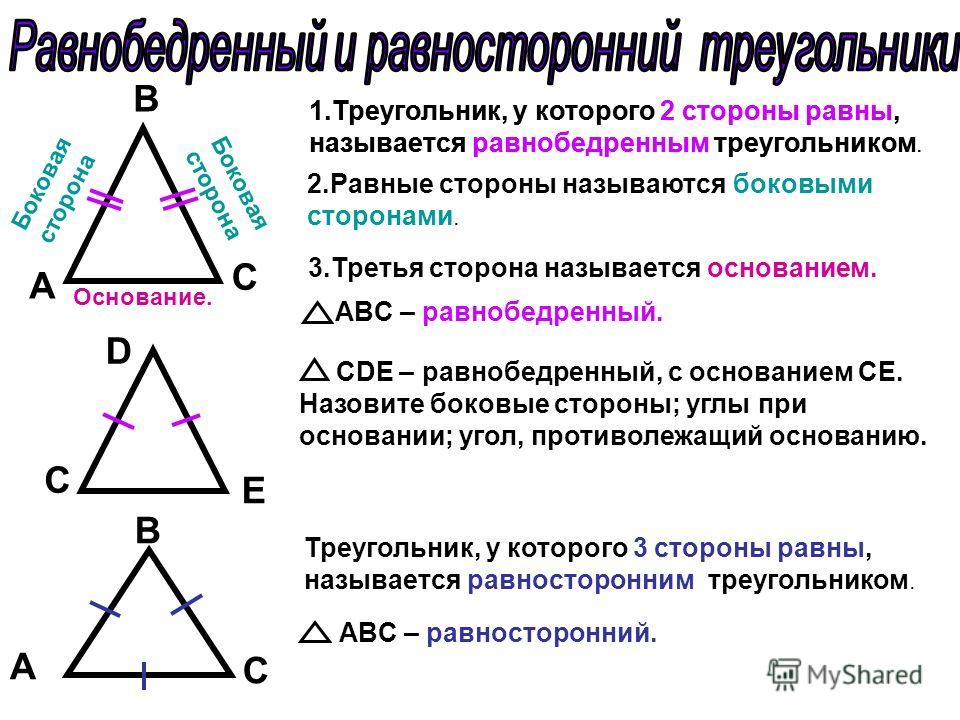
Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.
Не сдвигая линейки после построения отрезка ОК, приложите перпендикулярно к ней еще одну линейку. Проведите прямую m пересекающую отрезок ОК в середине.
С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.
Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.
Обратите внимание
Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.
Полезный совет
Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки.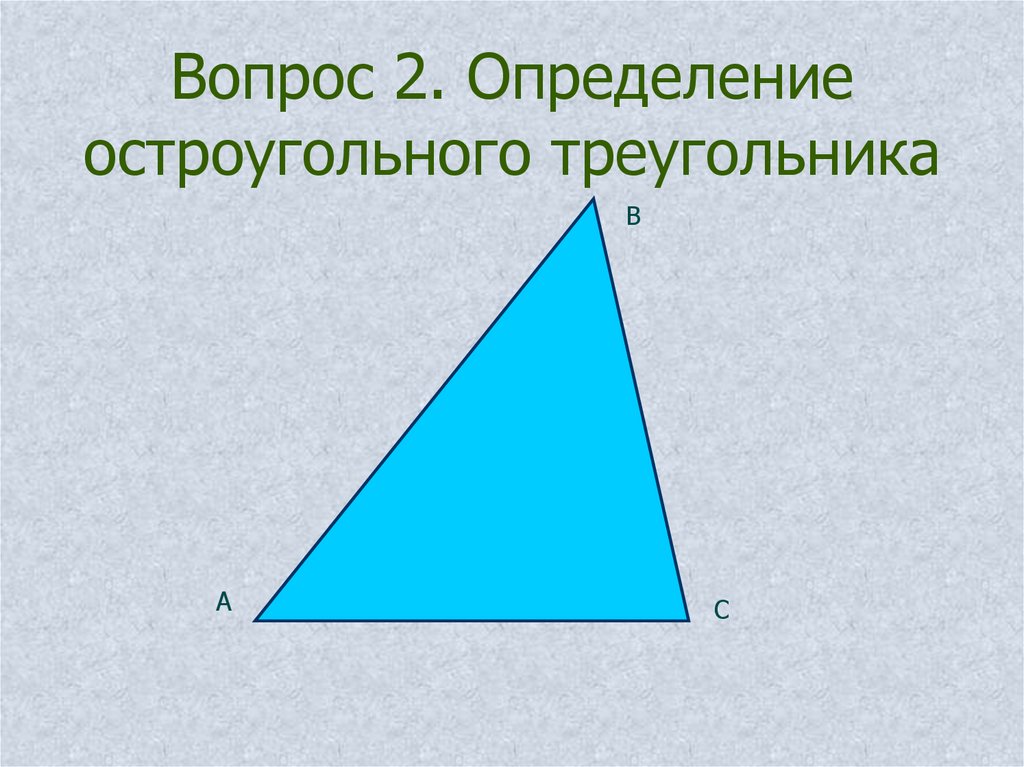 Вместо другой линейки используйте перпендикулярные линии.
Вместо другой линейки используйте перпендикулярные линии.
Источники:
- Классификация треугольников. Равносторонние треугольники
- Что такое треугольник
- построение правильного треугольника
Вписанным называется такой треугольник, все вершины которого находятся на окружности. Построить его можно, если знать хотя бы одну сторону и угол. Окружность называется описанной, и она будет единственной для данного треугольника.
Вам понадобится
- — окружность;
- — сторона и угол треугольника;
- — лист бумаги;
- — циркуль;
- — линейка;
- — транспортир;
- — калькулятор.
Инструкция
От точки А с помощью транспортира отложите заданный угол. Продолжите сторону угла до пересечения с окружностью и поставьте точку С. Соедините точки В и С. У вас получился треугольник АВС. Он может быть любого типа. Центр окружности у остроугольного треугольника него, у тупоугольного — вне, а у прямоугольного — на гипотенузе.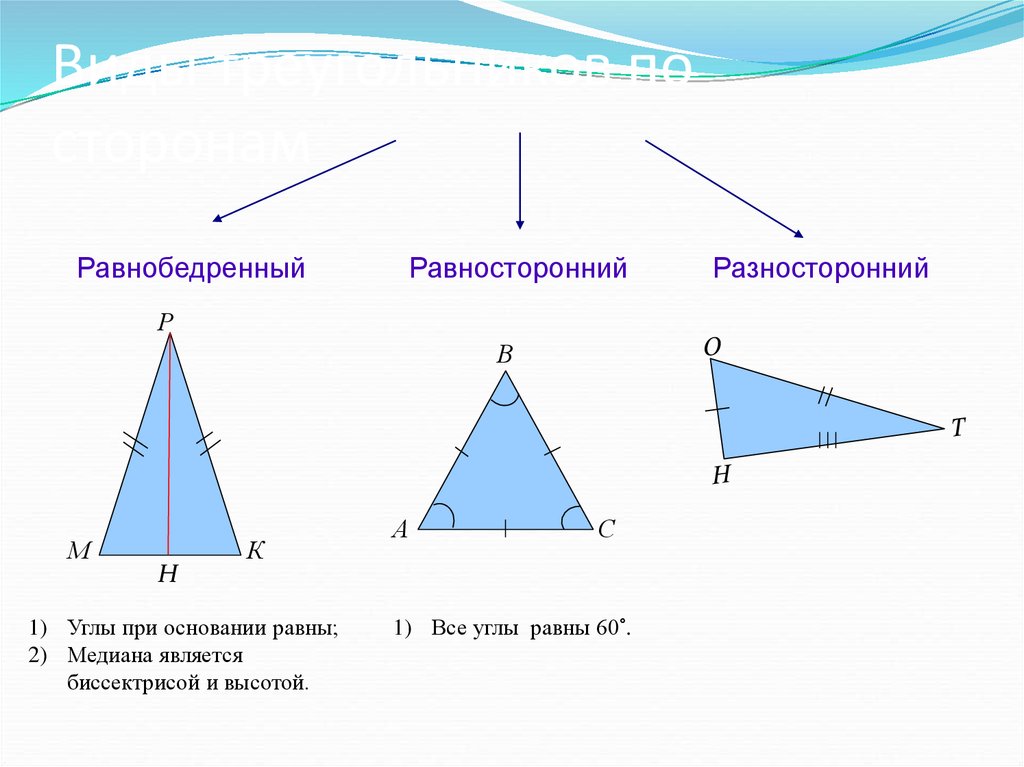 Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Значительно чаще приходится иметь дело с обратным построением, когда задан треугольник и надо вокруг него описать окружность. Вычислите его радиус. Сделать это можно по нескольким формулам, в зависимости от того, что вам дано. Радиус можно найти, например, по стороне и синусу противолежащего угла. В этом случае он равен длине стороны, разделенной на удвоенный синус противолежащего угла. То есть R=a/2sinCAB. Можно его выразить и через произведение сторон, в этом случае R=abc/√(a+b+c)(a+b-c)(a+c-b)(b+c-a).
Определите центр окружности. Разделите все стороны пополам и проведите серединам перпендикуляры. Точка их пересечения и будет центром окружности. Начертите ее так, чтобы она пересекла все вершины углов.
Две короткие стороны прямоугольного треугольника, которые принято называть катетами, по определению должны быть перпендикулярны между собой.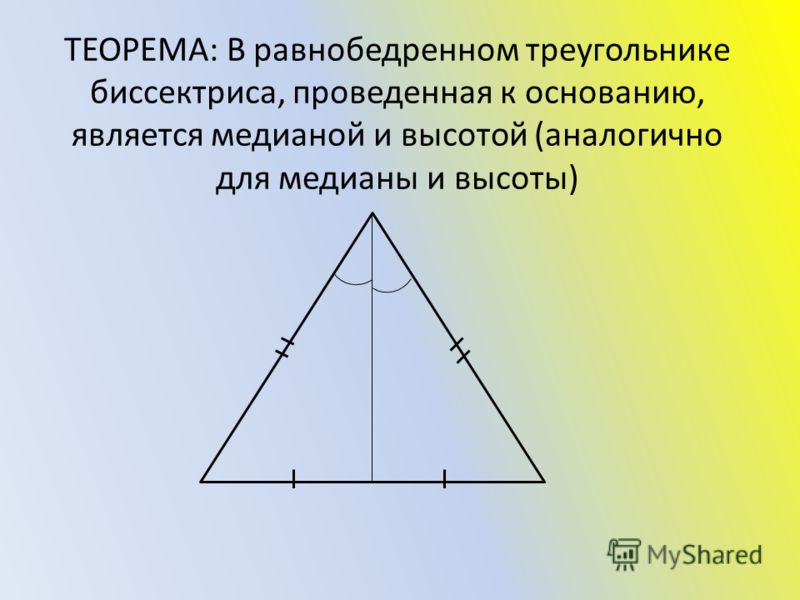 Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Вам понадобится
- Бумага, карандаш, линейка, транспортир, циркуль, угольник.
Как рассчитать площадь равностороннего треугольника формула. Площадь равностороннего треугольника
Найти площадь равностороннего треугольника можно по любой формуле для произвольной фигуры данного типа или воспользоваться теми, в которых уже учтена особенность именно этой фигуры и математические выражения существенно упрощены.
Первый случай только требует замены всех сторон одинаковым значением и учета того, что все углы у треугольника равны 60º. Потом останется провести несложные преобразования, которые и приведут к формулам, данным в готовом виде немного ниже.
Формула 1: известна сторона
В этой и последующих формулах приняты стандартные обозначения величин треугольника.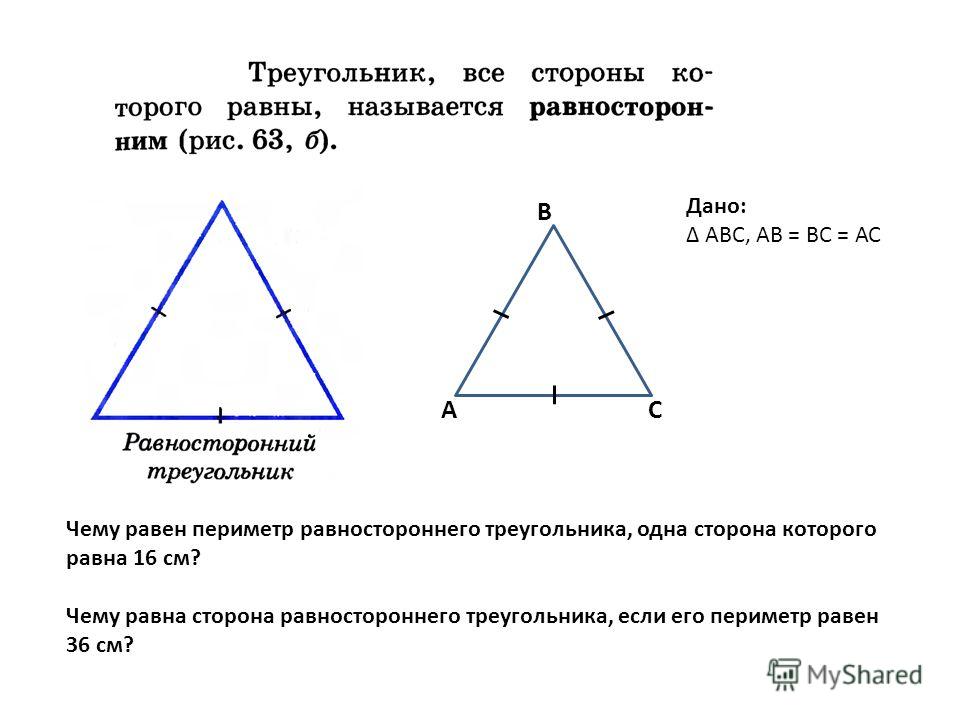 Подробнее их можно посмотреть в предложенной таблице.
Подробнее их можно посмотреть в предложенной таблице.
Расчет площади треугольника в этом случае будет осуществляться по формуле:
S = √3/4 * а 2 .
Она легко получается из той, которая известна для произвольной фигуры с тремя сторонами. Просто в формуле нужно учесть то, что все стороны у треугольника равны.
Если говорить более точно, то потребуется формула Герона: S = √(p(p-a)(p-b)(p-c)). Значение полупериметра для равностороннего треугольника будет равно 3а/2. Таким образом, в каждой скобке под корнем получится выражение ((3а/2) — а). Оно даст после преобразования а/2.
Так как скобок три, то у этого выражения появится третья степень. А значит, оно преобразится в а 3 /8.
Его еще нужно умножить на полупериметр, который определяется как сумма сторон, разделенная на 2. Получится выражение: 3а 4 /16. После извлечения квадратного корня как раз и останется то выражение, что дано в первой формуле для площади равностороннего треугольника.
Поэтому нет необходимости запоминать много формул. Можно просто запомнить одну — Герона. Из нее путем простых математических преобразований получаются все остальные, например, для равностороннего треугольника.
Можно просто запомнить одну — Герона. Из нее путем простых математических преобразований получаются все остальные, например, для равностороннего треугольника.
Формула 2: дан радиус вписанной окружности
Это выражение очень напоминает предыдущую запись. Но все же есть существенные отличия: используется другая буква, иррациональность ушла в знаменатель, появился множитель 3 и исчезла цифра 4. В общем, ее легко запомнить.
S = 3√3 * r 2 .
Эту формулу тоже легко получить из той, которая дана для произвольного треугольника. В ней радиус умножается на сумму сторон и делится на 4. Поскольку стороны имеют одинаковое значение, что сумма заменится на 3а. Теперь нужно убрать «а», чтобы осталось только значение радиуса. Для этого потребуется выражение, в котором сторона делится на произведение 2 и синуса противолежащего стороне угла. Так как угол равен 60º, то значение синуса будет √3/2. Тогда сторона выразится через радиус так: а = √3R. После несложного преобразования можно прийти к тому выражению для площади, которое дано вначале.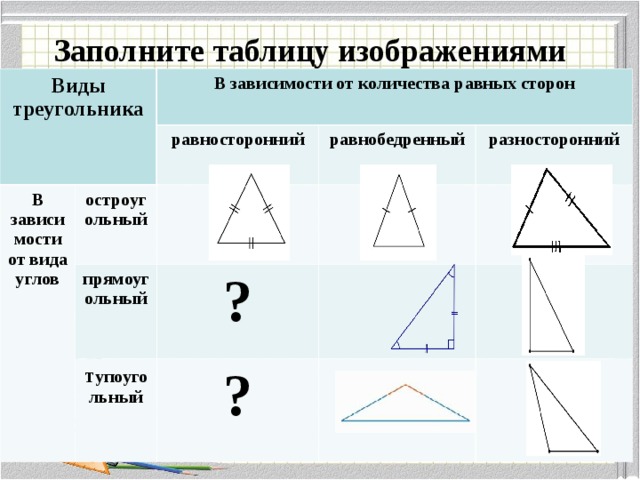
Формула 3: дана описанная окружность и ее радиус
Она очень похожа на первую. Только в ее числителе появляется цифра 3 и поменялась буква на R.
S = 3√3/4 * R 2 .
Поскольку радиус в два раза больше того, который рассматривался в предыдущем пункте, то понятно, как она получается. В ней просто вместо r ставится R/2. И проводятся необходимые преобразования.
Поэтому формулу можно не запоминать. Только держать в памяти соотношение радиусов вписанной и описанной около равностороннего треугольника окружностей.
Формула 4: известна высота
В этом случае площадь равностороннего треугольника равна:
S = н 2 / √3.
Чтобы понять, как получается такая формула, потребуется опять воспользоваться общей для всех треугольников. Она выглядит как произведение стороны на высоту и на ½. Теперь, чтобы узнать площадь равностороннего треугольника, придется вспомнить или вывести математическое выражение для высоты.
Ее несложно узнать, если воспользоваться тем фактом, что высота образует прямоугольный треугольник. Значит, высота может быть найдена как катет — из теоремы Пифагора. Второй катет будет равен половине стороны, так как высота является еще и медианой (это известное свойство равностороннего треугольника). Тогда высота будет определяться как квадратный корень из разности двух квадратов. Первый «а», а второй «а/2». После возведения во вторую степень и извлечения корня остается: н = (√3/2)*а. Из него а = 2н/√3. После подстановки его в основную для всех треугольников формулу получится то выражение, которое указано в начале раздела.
Значит, высота может быть найдена как катет — из теоремы Пифагора. Второй катет будет равен половине стороны, так как высота является еще и медианой (это известное свойство равностороннего треугольника). Тогда высота будет определяться как квадратный корень из разности двух квадратов. Первый «а», а второй «а/2». После возведения во вторую степень и извлечения корня остается: н = (√3/2)*а. Из него а = 2н/√3. После подстановки его в основную для всех треугольников формулу получится то выражение, которое указано в начале раздела.
Пример №1
Условие. Вычислить площадь равностороннего треугольника, если известно, что его сторона имеет значение 4 см.
Решение. Поскольку известно значение сторон фигуры, то необходимо пользоваться первой формулой.
Сначала потребуется возвести в квадрат число 4. От этого действия получится число 16. Теперь оно сокращается с четверкой, стоящей в знаменателе. И в итоге в числителе остается 4 и √3, а знаменатель становится равным единице, значит, его можно просто не записывать. Это результат, который и требовалось найти в задаче.
Это результат, который и требовалось найти в задаче.
Ответ: 4√3 см 2 .
Пример №2
Условие. Все стороны равностороннего треугольника равны 2√2 дм. Вычислить его площадь.
Решение. Рассуждения такие же, как в первой задаче. Только значение квадрата стороны будет другим. В нем нужно отдельно возвести во вторую степень 2 и иррациональность. И результат будет таким: 4*2 = 8. После сокращения со знаменателем остается 2 и √3 в числителе дроби, а знаменатель исчезает.
Ответ: 2√3 дм 2 .
Пример №3
Условие. В равносторонний треугольник вписана окружность, ее радиус 2,5 см. Необходимо вычислить площадь треугольника.
Решение. Для расчета искомой величины потребуется воспользоваться второй формулой.
Сначала значение радиуса нужно возвести в квадрат. Получится 6,25. Потом это значение требуется умножить на 3. Результатом этого действия станет число 18,75. Но это еще не конечное значение: в нем будет множитель √3, который присутствует в используемой формуле.
Ответ: 18,75√3 см 2 .
Пример №4
Условие. Требуется определить, чему равна площадь равностороннего треугольника, если известна его высота — 3 дм.
Решение. Естественно, что выбрать нужно четвертую формулу. С ее помощью проще всего найти ответ этой задачи.
Достаточно только возвести в квадрат число 3, то есть высоту, что даст значение 9. А потом разделить его на √3, стоящий в формуле.
Поскольку в математике не принято оставлять иррациональность в знаменателе ответа, то от нее нужно избавиться. Для этого дробь 9/√3 потребуется умножить на дробь с одинаковыми числителем и знаменателем, а именно √3/√3. От этого действия в числителе появится значение 9√3, а в знаменателе появится число 3.
Эту дробь можно и нужно сократить на 3. Это конечный результат.
Ответ: площадь — 3√3 дм 2 .
Пример №5
Условие. Дан равносторонний треугольник, площадь которого равна 27 см 2 . По этой величине нужно узнать длину стороны фигуры.
Решение. Поскольку речь идет о стороне, то подойдет первая формула. Из нее можно сразу вывести математическое выражение, которое позволит определить сторону треугольника.
Для этого площадь нужно умножить на 4 и разделить на квадратный корень из трех. Так получится значение для стороны в квадрате. Чтобы получить просто сторону, нужно извлечь корень. Выражение для стороны будет выглядеть так: а = 2 * √(S/√3).
Так как площадь известна, то можно сразу приступать к вычислениям. Подкоренное выражение выглядит как частное 27 и √3. Нужно избавиться от иррациональности в знаменателе. Получится 27√3, разделенное на 3. После сокращения в знаменателе остается 1, которую можно не писать, а в числителе остается 9√3.
Следующим действием будет извлечение корня из получившегося выражения. Первый множитель дает значение 3. А вот второй — √3 — требует к себе внимания. Чтобы упростить задачу, можно извлечь эти корни и округлить значения.
√3 = 1,73; теперь из него еще раз извлекаем корень и получаем 1,32.
Осталось только умножить его на 2 и получить искомый результат.
Ответ: сторона равна 2,64 см.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Среди геометрических фигур, которые рассматриваются в разделе геометрия, наиболее часто приходится сталкиваться при решении тех или иных задач с треугольником. Он представляет собой образованную тремя прямыми. Они в одной точке не пересекаются и не являются параллельными. Можно дать иное определение: треугольник представляет собой ломаную замкнутую линию, состоящую из трех звеньев, где ее начало и конец соединяются в одной точке. Если все три стороны имеют равную величину, то это правильный треугольник, или, как говорят, равносторонний.
Как же определить Для решения подобных задач необходимо знать некоторые свойства этой геометрической фигуры. Во-первых, у данного все углы равны. Во-вторых, высота, которая опускается с вершины на основание, является одновременно и медианой, и высотой. Это говорит о том, что высота делит вершину треугольника на два равных угла, а противоположную сторону — на два равных отрезка. Так как равносторонний треугольник состоит из двух то при определении искомой величины необходимо использовать теорему Пифагора.
Расчет площади треугольника можно произвести различными способами, в зависимости от известных величин.
1. Рассмотрим равносторонний треугольник с известными стороной b и высотой h. Площадь треугольника в этом случае будет равна одной второй произведения стороны и высоты. В виде формулы это будет выглядеть так:
Говоря словами, площадь равностороннего треугольника равна одной второй произведения его стороны и высоты.
2. Если известна только величина стороны, то прежде, чем искать площадь, необходимо вычислить его высоту. Для этого рассмотрим половину треугольника, в котором высота будет одним из катетов, гипотенуза — это сторона треугольника, а второй катет — половина стороны треугольника согласно его свойствам. Все из той же теоремы Пифагора Как из нее известно, квадрат гипотенузы соответствует сумме квадратов катетов. Если рассматривать половину треугольника, то в данном случае сторона является гипотенузой, половина стороны — одним катетом, а высота — вторым.
Для этого рассмотрим половину треугольника, в котором высота будет одним из катетов, гипотенуза — это сторона треугольника, а второй катет — половина стороны треугольника согласно его свойствам. Все из той же теоремы Пифагора Как из нее известно, квадрат гипотенузы соответствует сумме квадратов катетов. Если рассматривать половину треугольника, то в данном случае сторона является гипотенузой, половина стороны — одним катетом, а высота — вторым.
(b/2)²+ h3= b² , отсюда
h²= b²-(b/2)². Приведем к общему знаменателю:
Как видим, высота рассматриваемой фигуры равна произведению половины его стороны и корня из трех.
Подставим в формулу и увидим: S=1/2* b* b/2√3= b²/4√3.
То есть, площадь равностороннего треугольника равна произведению четвертой части квадрата стороны и корня из трех.
3. Есть и такие задачи, где необходимо определить площадь равностороннего треугольника при известной высоте. И это оказывается проще простого. Мы уже вывели в предыдущем случае, что h²= 3 b²/4. Дальше необходимо отсюда вывести сторону и подставить в формулу площади. Выглядеть это будет так:
Дальше необходимо отсюда вывести сторону и подставить в формулу площади. Выглядеть это будет так:
b²=4/3* h², отсюда b=2h/√3. Подставив в формулу, по которой находится площадь, получим:
S=1/2* h*2h/√3, отсюда S= h²/√3.
Имеют место задачи, когда необходимо найти площадь равностороннего треугольника по радиусу вписанной или описанной окружности. Для этого расчета также существуют определенные формулы, которые выглядят следующим образом: r = √3* b/6, R=√3* b/3.
Действуем уже по знакомому нам принципу. При известном радиусе, выводим из формулы сторону и вычисляем ее, подставив известную величину радиуса. Полученное значение подставляем в уже известную формулу для расчета площади правильного треугольника, проводим арифметические вычисления и находим искомую величину.
Как видим, для того, чтобы решить аналогичные задачи, необходимо знать не только свойства правильного треугольника, а и теорему Пифагора, и радиус описанной и вписанной окружности. Для владеющих этими знаниями решение подобных задач не будет представлять особого труда.
В элементарной геометрии равносторонним треугольником считается правильный многоугольник, имеющий три стороны. Если несколько расширить и конкретизировать это определение, то получится, что треугольник является правильным в том случае, если все его стороны имеют одинаковую длину, а углы равны 60° . Тому, как найти , учат на уроках геометрии в средней школе, а на практике эти знания нередко приходится применять инженерам-конструкторам и архитекторам.
Вычисление площади равностороннего треугольника
| S | = | ah |
a — сторона треугольника
h — высотат треугольника
S — площадь
Зодчим площадь равностороннего треугольника приходится находить в том случае, если такую форму имеют элементы зданий, проектированием которых они занимаются. Таковыми могут быть нестандартные окна (как обычные, так и мансардные), которые нередко встречаются в зданиях, имеющих оригинальное архитектурное решение. Их проектировщикам формула площади равностороннего треугольника требуется для того, чтобы выяснить, достаточный ли размер будет иметь окно для того, чтобы через него в помещение проникало необходимое количество дневного света. Кроме того, форму равносторонних треугольников достаточно часто имеют фронтоны тех жилых загородных домов и коттеджей, а также хозяйственных построек, скаты крыш которых иногда располагаются под углом 60° .
Их проектировщикам формула площади равностороннего треугольника требуется для того, чтобы выяснить, достаточный ли размер будет иметь окно для того, чтобы через него в помещение проникало необходимое количество дневного света. Кроме того, форму равносторонних треугольников достаточно часто имеют фронтоны тех жилых загородных домов и коттеджей, а также хозяйственных построек, скаты крыш которых иногда располагаются под углом 60° .
Равносторонние треугольники нередко можно встретить в составе различных технических устройств и инструментов. Например, такую форму имеют сменные пластины проходных твердосплавных токарных резцов. На державке они устанавливаются путем установки на специальную ось, а фиксируются при помощи клиновидного стального элемента, прижим которого осуществляется за счет резьбового соединения. После того, как одна из граней вставки затупляется в процессе резания, пластина снимается, поворачивается на 60° , фиксируется заново, в результате чего может использоваться другая, острая грань. Таким образом, за счет того, что твердосплавная пластина имеет форму равностороннего треугольника, такая переустановка может совершаться три раза. Заточке затупившиеся грани не подлежат, и эти элементы режущего инструмента утилизируются путем переплавки.
Таким образом, за счет того, что твердосплавная пластина имеет форму равностороннего треугольника, такая переустановка может совершаться три раза. Заточке затупившиеся грани не подлежат, и эти элементы режущего инструмента утилизируются путем переплавки.
Как автомобилистам, так и пешеходам отлично известны дорожные знаки, представляющие собой равносторонние треугольники. Такая форма делает их более заметными, и поэтому они в большинстве своем являются предупреждающими. Само собой разумеется, что в процессе их разработки и написания соответствующей нормативно-технической документации приходилось использовать формулу расчета площади равностороннего треугольника .
Великолепно знают, что такое равносторонний треугольник , любители такой популярной игры, как бильярд. При помощи специальных рамок, имеющих соответствующую форму, происходит установка шаров в определенном порядке перед началом каждой партии. Производятся эти изделия из древесины, пластических масс или металлов.
В школьном курсе геометрии огромное количество времени уделяется изучению треугольников. Ученики вычисляют углы, строят биссектрисы и высоты, выясняют, чем фигуры отличаются друг от друга, и как проще всего найти их площадь и периметр. Кажется, что это никак не пригодится в жизни, но иногда все-таки полезно узнать, например, как определить, что треугольник равносторонний или тупоугольный. Как же это сделать?
Типы треугольников
Три точки, которые не лежат на одной прямой, и отрезки, которые их соединяют. Кажется, что эта фигура — самая простая. Какими могут быть треугольники, если у них всего три стороны? На самом деле вариантов довольно большое количество, и некоторым из них уделяется особое внимание в рамках школьного курса геометрии. Правильный треугольник — равносторонний, то есть все его углы и стороны равны. Он обладает рядом примечательных свойств, о которых речь пойдет дальше.
У равнобедренного равны только две стороны, и он также довольно интересен. У прямоугольного и как несложно догадаться, соответственно, один из углов прямой или тупой.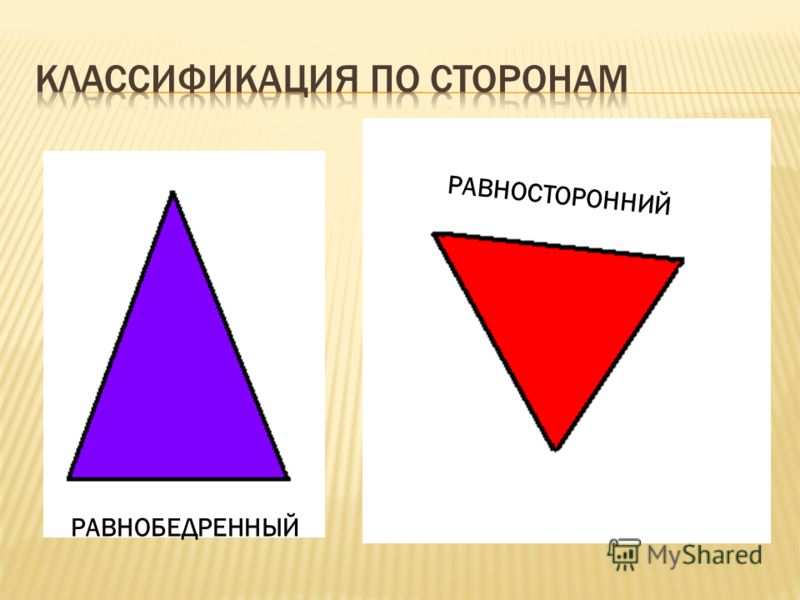 При этом они также могут равнобедренными.
При этом они также могут равнобедренными.
Существует и особый называемый египетским. Его стороны равны 3, 4 и 5 единицам. При этом он является прямоугольным. Считается, активно использовался египетскими землемерами и архитекторами для построения прямых углов. Есть мнение, что с его помощью были возведены знаменитые пирамиды.
И все-таки все вершины треугольника могут лежать на одной прямой. В этом случае он будет называться вырожденным, в то время как все остальные — невырожденными. Именно они и являются одним из предметов изучения геометрии.
Треугольник равносторонний
Разумеется, правильные фигуры вызывают всегда наибольший интерес. Они кажутся более совершенными, более изящными. Формулы вычисления их характеристик зачастую проще и короче, чем для обычных фигур. Это относится и к треугольникам. Неудивительно, что при изучении геометрии им уделяется достаточно много внимания: школьников учат отличать правильные фигуры от остальных, а также рассказывают о некоторых их интересных характеристиках.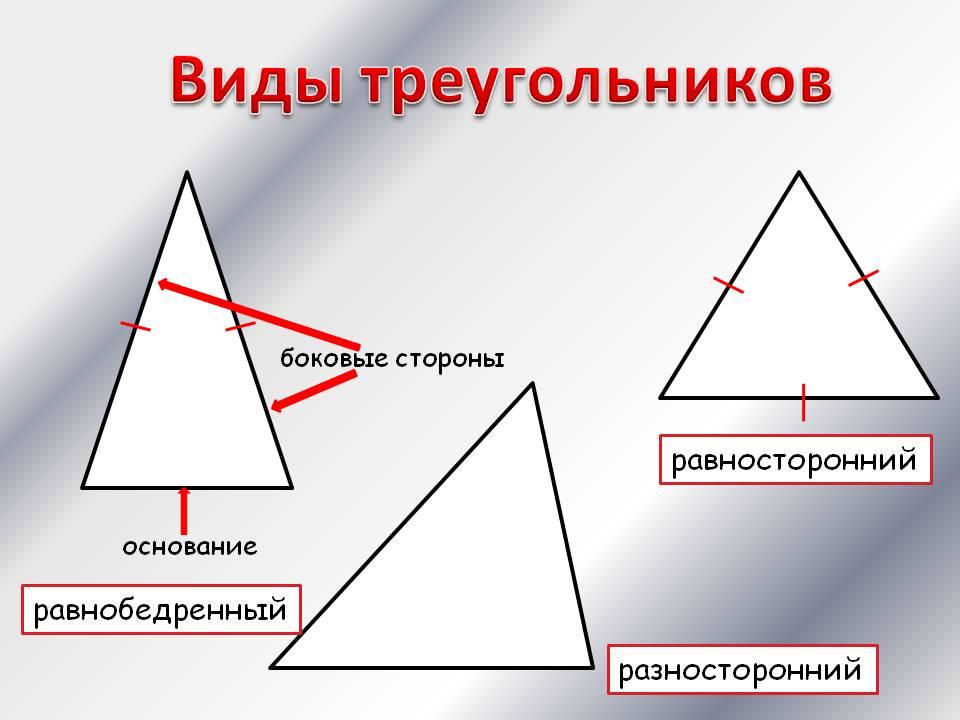
Признаки и свойства
Как нетрудно догадаться из названия, каждая сторона равностороннего треугольника равна двум другим. Кроме того, он обладает рядом признаков, благодаря которым можно определить, правильная ли фигура или нет.
Если наблюдается хотя бы один из вышеперечисленных признаков, то треугольник — равносторонний. Для правильной фигуры справедливы все упомянутые утверждения.
Все треугольники обладают рядом примечательных свойств. Во-первых, средняя линия, то есть отрезок, делящий две стороны пополам и параллельный третьей, равна половине основания. Во-вторых, сумма всех углов этой фигуры всегда равна 180 градусам. Кроме того, в треугольниках наблюдается еще одна любопытная взаимосвязь. Так, против большей стороны лежит больший угол и наоборот. Но это, конечно, к равностороннему треугольнику отношения не имеет, ведь у него все углы равны.
Вписанные и описанные окружности
Нередко в курсе геометрии учащиеся также изучают то, как фигуры могут взаимодействовать друг с другом. В частности, изучаются окружности, вписанные в многоугольники или описанные около них. О чем идет речь?
В частности, изучаются окружности, вписанные в многоугольники или описанные около них. О чем идет речь?
Вписанной называют такую окружность, для которой все стороны многоугольника являются касательными. Описанной — ту, которая имеет точки соприкосновения со всеми углами. Для каждого треугольника всегда можно построить как первую, так и вторую окружность, но только одну каждого вида. Доказательства двух этих
теорем приводятся в школьном курсе геометрии.
Помимо вычисления параметров самих треугольников, некоторые задачи также подразумевают расчет радиусов этих окружностей. И формулы применительно к
равностороннему треугольнику выглядят следующим образом:
где r — радиус вписанной окружности, R — радиус описанной окружности, a — длина стороны треугольника.
Вычисление высоты, периметра и площади
Основные параметры, вычислением которых занимаются школьники во время изучения геометрии, остаются неизменными практически для любых фигур. Это периметр, площадь и высота.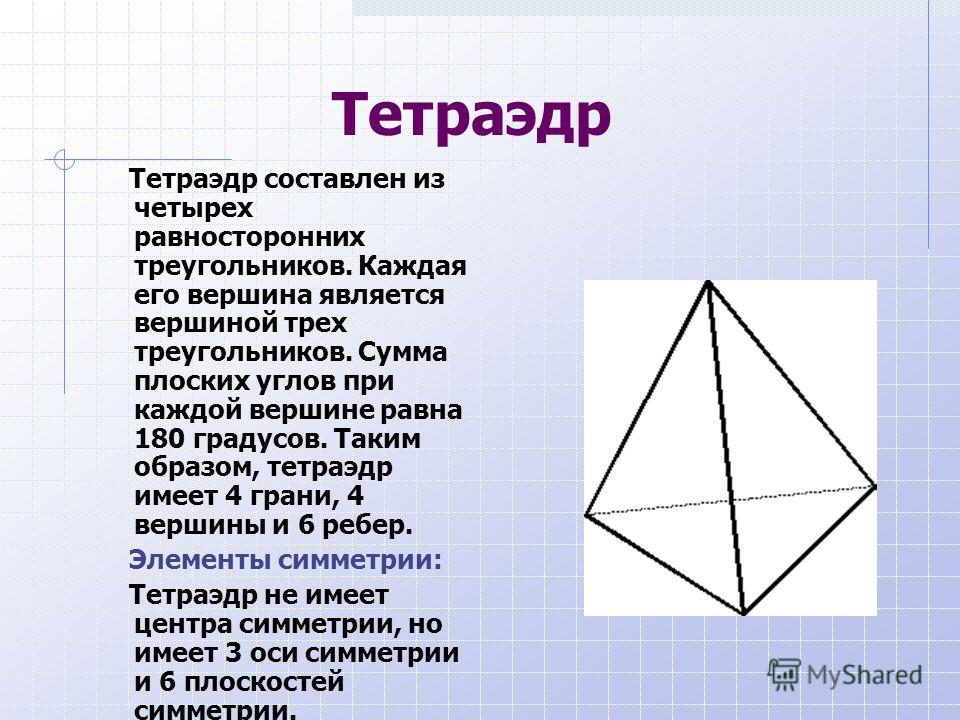 Для простоты расчетов существуют различные формулы.
Для простоты расчетов существуют различные формулы.
Так, периметр, то есть длина всех сторон, вычисляется следующими способами:
P = 3a = 3√ ̅3R = 6√ ̅3r, где a — сторона правильного треугольника, R — радиус описанной окружности, r — вписанной.
h = (√ ̅3/2)*a, где a — длина стороны.
Наконец, формула выводится из стандартной, то есть произведения половины основания на его высоту.
S = (√ ̅3/4)*a 2 , где a — длина стороны.
Также эта величина может быть вычислена через параметры описанной или вписанной окружности. Для этого также существуют специальные формулы:
S = 3√ ̅3r 2 = (3√ ̅3/4)*R 2 , где r и R — соответственно радиусы вписанной и описанной окружностей.
Построение
Еще один интересный тип задач, касающийся в том числе и треугольников, связан с необходимостью начертить ту или иную фигуру, используя минимальный набор
инструментов: циркуль и линейку без делений.
Для того чтобы построить правильный треугольник с помощью только этих приспособлений, необходимо выполнить несколько шагов.
- Нужно начертить окружность с любым радиусом и с центром в произвольно взятой точке А. Ее необходимо отметить.
- Далее нужно провести прямую через эту точку.
- Пересечения окружности и прямой необходимо обозначить как В и С. Все построения должны проводиться с максимально возможной точностью.
- Далее надо построить еще одну окружность с тем же радиусом и центром в точке С или дугу с соответствующими параметрами. Места пересечения будут обозначены как D и F.
- Точки B, F, D необходимо соединить отрезками. Равносторонний треугольник построен.
Решение подобных задач обычно представляет для школьников проблему, но это умение может пригодиться и в обычной жизни.
как найти площадь, чему равна сторона, формулы, расчет по высоте и через окружности
Треугольник – геометрическая фигура, сформированная 3 отрезками, соединенными между собой 3 точками. При этом все углы у нее расположены внутри. Равносторонний или равноугольный треугольник – многоугольник правильной формы с равными сторонами и углами (по 60°).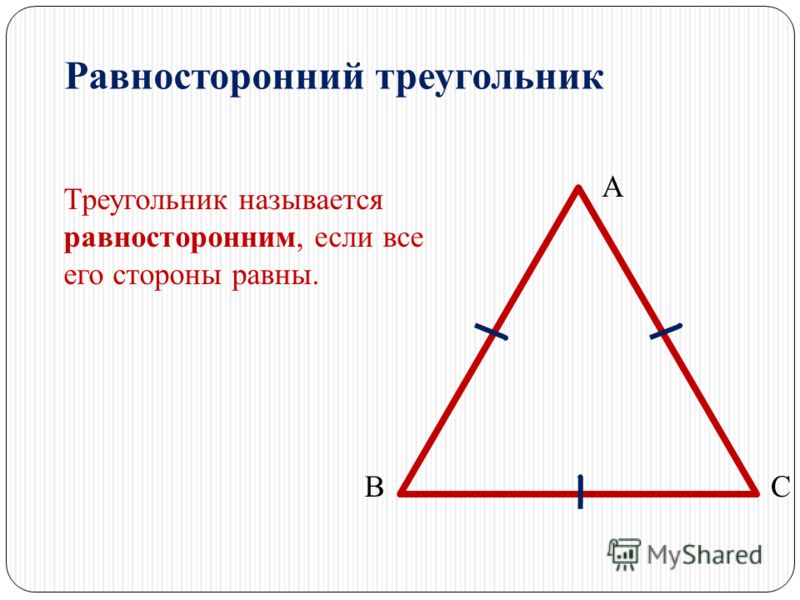 В этой фигуре высота выступает одновременно и медианой, и биссектрисой. Площадь равностороннего треугольника можно просчитать через сторону, высоту, через сторону и высоту.
В этой фигуре высота выступает одновременно и медианой, и биссектрисой. Площадь равностороннего треугольника можно просчитать через сторону, высоту, через сторону и высоту.
Геометрия – это раздел математики, который занимается изучением фигур в пространстве и на плоскости, а также вычислением их площади, объема и прочих показателей. Впервые как наука она появилась в Древней Греции. Изучением занимался ученый Евклид. Позже было создано еще несколько видов геометрии – проективная, начертательная, дифференциальная и аналитическая.
Геометрия окружает человека каждый день. Если оглянуться вокруг, то можно увидеть, что вокруг расположены не просто предметы, а геометрические фигуры. Например, монитор, кровать, стол и даже стены в комнате. Поэтому важно изучить хотя бы ее основы. Одной из самых популярных фигур, которые можно встретить в повседневной жизни, является треугольник.
Признаки и свойства
Треугольник представляет собой геометрическую фигуру, состоящую из трех точек, не располагающихся на одной прямой линии.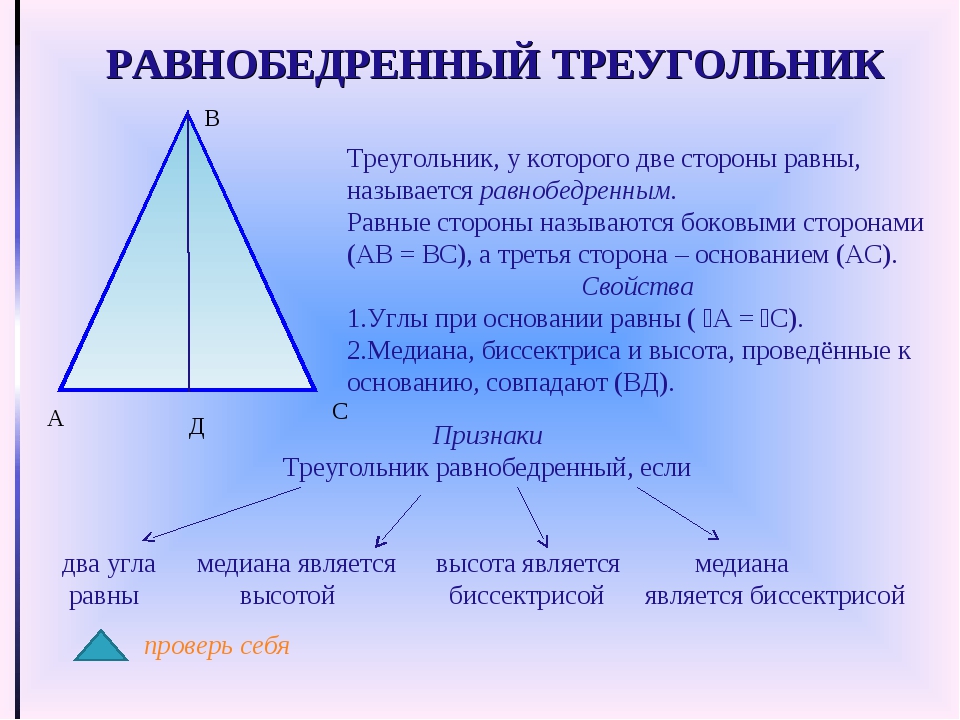 Отрезки, которые из соединяют, называются стороны. Точки их соединения – это вершины. В геометрии принято обозначать их латинскими буквами. К примеру, так – А, В, С. Стороны указывают названиями двух точек (вершин) из которых они состоят – АВ, ВС, АС. В тех местах, где они соединяются, формируются углы. Нижний отрезок называют основанием.
Отрезки, которые из соединяют, называются стороны. Точки их соединения – это вершины. В геометрии принято обозначать их латинскими буквами. К примеру, так – А, В, С. Стороны указывают названиями двух точек (вершин) из которых они состоят – АВ, ВС, АС. В тех местах, где они соединяются, формируются углы. Нижний отрезок называют основанием.
Многоугольники классифицируют по нескольким признакам. Каждый из них имеет свои определенные свойства.
Классификация по углам (∠):
- тупоугольные. Имеют один тупой ∠, градусная мера которого более 90 градусов. Остальные 2 острые;
- остроугольные. Все углы острые и градусная мера каждого не превышает 90 градусов;
- прямоугольные. Есть один прямой ∠ и 2 острых. В общей сложности сумма их градусных мер не превышает 180 градусов. Та сторона, которая локализуется прямо напротив прямого называется гипотенузой, а две других – это катеты.
Виды треугольника по сторонам:
- равнобедренный. У данного многоугольника 2 стороны равны.
 Их называют боковыми. Третья – это основание;
Их называют боковыми. Третья – это основание; - разносторонний. Также его называют произвольным. У данного многоугольника нет равных отрезков – они все разные;
- равносторонний. Его можно также назвать правильным. В этом многоугольнике все отрезки равны. Фигура оптимальная для проведения различных вычислений.
Для того чтобы рассчитать площадь равностороннего треугольника необходимо понимать свойства и признаки, которыми он обладает. Выделяют следующие основные признаки этой фигуры:
- Значение величины его углов одинаково во всех случаях и равняется 60 градусам, вне зависимости от размера сторон.
- Биссектриса, высота и медиана будут совпадать.
- Любой отрезок равностороннего треугольника равен двум другим.
- Центр равностороннего треугольника будет являться центром для вписанной и описанной окружности (ВО и ОО).
- Является частным случаем равнобедренного треугольника.
[stop]Если хотя бы один из этих признаков соблюдается, значит, треугольник является равносторонним. [/stop]
[/stop]
Дополнительно этот многоугольник обладает следующими свойствами:
- средняя линия, которая делит два боковых отрезка пополам, равняется половине основания, параллельно которому она располагается;
- сумма всех его ∠ не превышает 180 градусов;
- радиус ВО рассчитывается так r = , а ОО согласно выражению R = ;
- радиус ОО в равностороннем треугольнике в 2 раза больше радиуса вписанной.
Как выглядит равносторонний треугольник
Расчет через сторону
Существует множество способов вычисления площади (S) этой фигуры. Все они имеют свои преимущества и недостатки. Применяются в зависимости от условий, представленных задаче. Самый популярный способ найти искомое значение для равностороннего треугольника вычисляется через произведение половины сторон и синуса угла между ними, выглядит это следующим образом:
, где, a и b – стороны, α – ∠ между ними.
В случае с равносторонним, этот способ упрощается в значительной степени.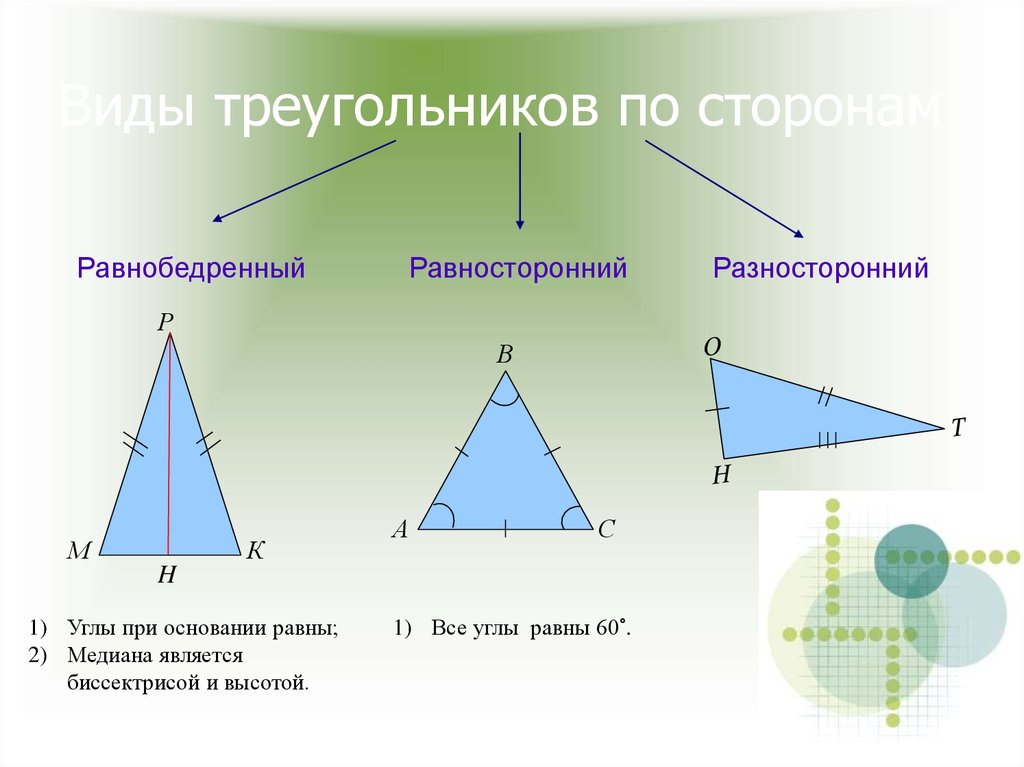 Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все ∠ = 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется
Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все ∠ = 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется
, преобразовав исходное выражение получаем следующее значение: .
Учитывая то, что все отрезки равны, то преобразованное выражение даст такой результат:
.
Данная формула отлично подойдет в случае, если известна величина стороны. В таком виде вычислять показатель гораздо легче и быстрее.
Те, кто помнит формулу Герона, знают, как найти площадь. В процессе преобразования выражение изменится в представленное выше. Площадь по Герону рассчитывается так:
, где, a, b, c —стороны, а p — полупериметр (). Преобразовывается данное выражение просто. Необходимо подставить вместо значения p расчет полупериметра и постепенно начать сокращать выражение. Сумму сторон представить в виде суммы трех одинаковых сторон и довести сокращения до конца. Математически это выглядит так:
Математически это выглядит так:
;
;
;
.
Полученная формула площади и представленные ниже функции могут быть использованы только, в случае, если фигура является правильной, в ином случае не будет давать правильный ответ.
Вычисление площади треугольника по его стороне
Расчет по высоте
Вычислить площадь равностороннего многоугольника также есть возможность, если известна его высота и сторона. Половина длины высоты (h) умножается на сторону, выбрана может быть любая h и сторона, ведь согласно свойствам, они все одинаковые:
, где a – это длина стороны. Формулу площади легко запомнить, однако, на практике она применяется редко.
Если в задаче указана информация о том, что многоугольник с 3 углами является равносторонним и известна величина h, чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее определить.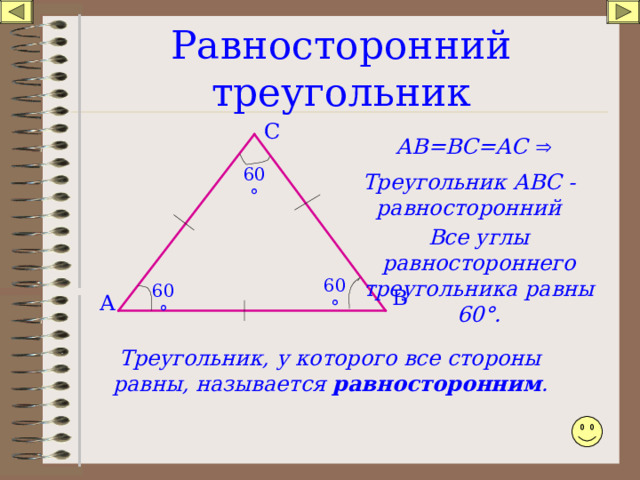 Найти сторону есть возможность, разделив двойную величину h на корень квадратный из трех, математически выглядит следующим образом:
Найти сторону есть возможность, разделив двойную величину h на корень квадратный из трех, математически выглядит следующим образом:
. После этого применяется формула площади, где вычисления производятся через сторону, она описана в предыдущем пункте.
Для того чтобы не делать лишних подсчетов выводят формулу этого показателя сразу же через h. Квадрат h делится на корень квадратный из трех. Она будет выглядеть так:
. В этом случае для определения площади не нужно применять формулу равностороннего треугольника через сторону.
Вычисление площади треугольника по его стороне и высоте
Расчет через окружности
В математике популярен также прием вычисления, рассматриваемого в статье значения, через помещение фигуры в окружность или наоборот. Такая окр-ть называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.
ОО обязательно должна проходить через все вершины, ВО должна проходить через стороны только в одной точке по касательной.
Если в условии задачи дан радиус вписанной (r) и описанной (R) окр-ти, то из них также допустимо составить выражение, так как вместе они дадут суммарную длину h. Как рассчитывается площадь при ее помощи, показано выше: h = R + r .
Преобразовав формулу
, применив h = R + r, получаем следующее значение: . Данную формулу можно упростить еще больше, ведь R описанной окр-ти можно выразить через r вписанной. Согласно свойствам этих окр-тей R = 2r, где r — это радиус вписанной окр-ти, R — это радиус описанной. Соответственно площадь равностороннего Δ будет высчитываться так: .
Если же будет дан размер R ОО, то выражение будет выглядеть следующим образом:
.
Использование этих свойств пригодится для расчета стороны. Для того чтобы ее определить нужно воспользоваться выражением
для ОО, и для ВО.
Учитывая R описанной окр-ти определяют искомое значение при помощи возведения стороны в куб, после чего результат делится на R, увеличенный в 4 раза. Математически его записывают следующим образом:
.
Процесс вычисления, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.
[warning]Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть.[/warning]
Как найти площадь равностороннего треугольника смотрите в видео:
Также смотрите в видео как найти площадь равностороннего треугольника, вписанного в окружность:
youtube.com/embed/xLQo4eQlFwk» frameborder=»0″ allowfullscreen=»allowfullscreen»/>Применив логическое мышление, расчеты с легкостью преобразовываются в частные случаи, коих гораздо больше. Нецелесообразно забивать голову большим количеством нерелевантной информации, лучше развивать причинно-следственную связь для преобразования выражений.
Геометрия — это точная наука, которая не терпит отклонений и недочетов. Для ее изучения нужно запастись колоссальным терпением и быть очень внимательным. То, что на первый взгляд кажется непостижимым и непонятным, после освоения азов станет легким и доступным для понимания. Но все же особое внимание необходимо уделить изучению теорем и формул, так как они являются основой для вычислений таких важных показателей, как объем или площадь. Ее изучение и нужно начинать с таких простых и правильных фигур, как равносторонний треугольник. Он поможет понять основы и не потерять интерес к науке в целом.
Как найти площадь и сторону равностороннего треугольника, вписанного в окружность, формула
Равносторонний треугольник — это самый простой правильный многоугольник из возможных. При нахождении его площади возникают частные варианты его расчета. Важно знать и понимать признаки и свойства этого вида фигур, для более легкого вычисления этого параметра. Все методы, представленные ниже, достаточно просты в применении, и не потребуют глубокого осмысления….
При нахождении его площади возникают частные варианты его расчета. Важно знать и понимать признаки и свойства этого вида фигур, для более легкого вычисления этого параметра. Все методы, представленные ниже, достаточно просты в применении, и не потребуют глубокого осмысления….
Содержание
Признаки и свойства фигуры
Для того чтобы рассчитать его площадь необходимо понимать свойства и признаки, которыми он обладает. Можно выделить следующие основные признаки этой фигуры:
- Значение величины его углов одинаково во всех случаях и равняется 60 градусам, вне зависимости от размера сторон.
- Биссектриса, высота и медиана выпущенные из одного угла будут совпадать.
- Любая сторона равностороннего треугольника равна двум другим.
- Центр правильного треугольника будет являться центром для вписанной и описанной окружности.
- Является частным случаем равнобедренного треугольника.
Важно! Если хотя бы один из этих признаков соблюдается, значит, треугольник является равносторонним.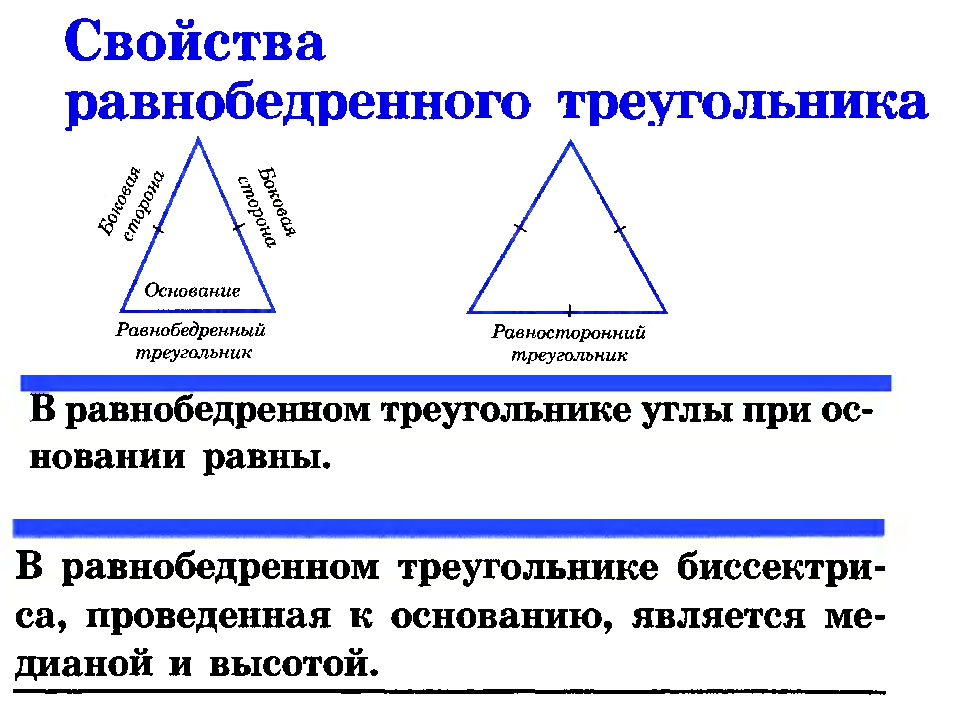 Равносторонний треугольник
Равносторонний треугольник
Дополнительно этот частный случай фигуры обладает следующими свойствами:
- Средняя линия, которая делит две боковые стороны пополам, равняется половине основания, параллельно которому она располагается.
- Сумма всех его углов не превышает 180 градусов.
- Радиус вписанной окружности рассчитывается по следующей формуле r = , а описанной согласно выражению R = .
- Радиус описанной окружности в правильном треугольнике в 2 раза больше радиуса вписанной.
Расчет через сторону
Существует множество способов расчета площади этой фигуры. Все они имеют свои преимущества и недостатки. Применяются в зависимости от условий, представленных задаче. Самая популярный способ найти искомое значение для равностороннего треугольника вычисляется через произведение половины сторон и синуса угла между ними, выглядит это следующим образом: , где, a и b – стороны, α – угол между ними.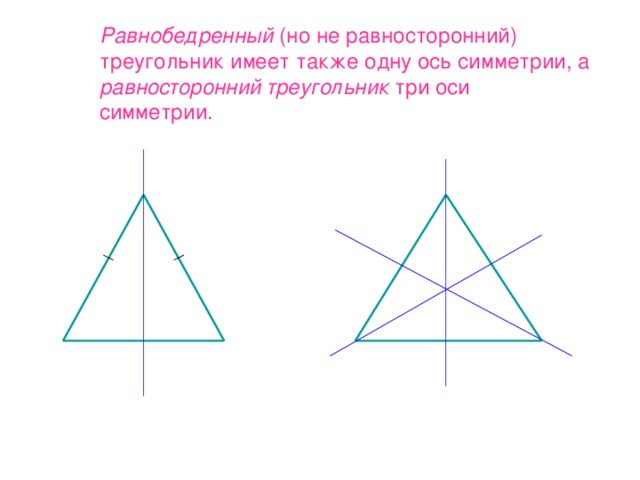
В случае с равносторонним, этот способ упрощается в значительной степени. Для этого нужно обратиться к рассмотренным выше признакам и свойствам. Исходя из того, что все углы этой фигуры равны, и равняются 60 градусам. Синус 60 градусов, согласно таблице Брадиса, равняется , преобразовав исходное выражение получаем следующее значение: .
Учитывая то, что все стороны этой фигуры равны, то преобразованное выражение даст такой результат: .
Данная формула отлично подойдет в случае, если известна величина стороны этой фигуры. В таком виде вычислять данный показатель гораздо легче и быстрее.
Те, кто помнит формула Герона, знают, как найти площадь этой фигуры. В процессе преобразования выражение изменится в представленное выше. Площадь этой фигуры по Герону рассчитывается так: , где, a, b, c —стороны, а p — полупериметр (). Преобразовывается данное выражение достаточно просто. Необходимо подставить вместо значения p расчет полупериметра и постепенно начать сокращать выражение. Сумму сторон можно представить в виде суммы трех одинаковых сторон и довести сокращения до конца. Математически это выглядит так:
Сумму сторон можно представить в виде суммы трех одинаковых сторон и довести сокращения до конца. Математически это выглядит так:
,
,
,
.
Полученная формула площади и представленные ниже функции могут быть использованы только, в случае, если фигура является правильной, в ином случае не будет давать правильный ответ.
Вычисление площади треугольника по его стороне
Расчет по высоте
Найти площадь равностороннего треугольника можно также, если известна его высота и сторона. Половина длины высоты умножается на сторону, выбрана может быть любая высота и сторона, ведь согласно свойствам, они все одинаковые: , где a – это длина стороны. Ее легко запомнить, однако, на практике она применяется достаточно редко.
Если в задаче указана информация о том, что треугольник является равносторонним и известна величина высоты. А чему равна длина стороны неизвестно, то можно воспользоваться формулой, позволяющей ее рассчитать. Найти сторону можно разделив двойную величину высоты на корень квадратный из трех, математически выглядит следующим образом: . После этого применяется формула площади, где расчеты производятся через сторону, она описана в предыдущем пункте.
Найти сторону можно разделив двойную величину высоты на корень квадратный из трех, математически выглядит следующим образом: . После этого применяется формула площади, где расчеты производятся через сторону, она описана в предыдущем пункте.
Для того чтобы не делать лишних расчетов можно вывести формулу этого показателя сразу же через высоту. Квадрат высоты делится на корень квадратный из трех. Она будет выглядеть так: . В этом случае можно не применять формулу равнобедренного треугольника через сторону.
Вычисление площади треугольника по его стороне и высоте
Расчет через окружности
В математике популярен также прием расчета, рассматриваемого в статье, значения через помещение фигуры в окружность или наоборот. Такая окружность называется описанной. Если она находится внутри, то она называется вписанной. Именно в этом разделе возникает большинство вопросов, как найти площадь равностороннего многоугольника с тремя углами.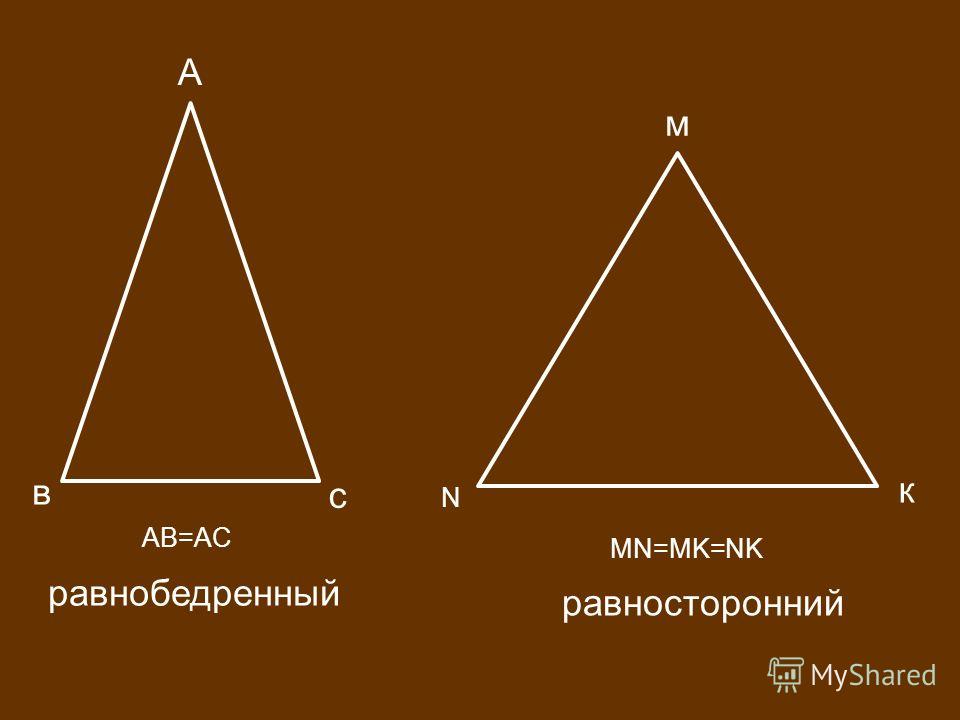
Описанная окружность обязательно должна проходить через все вершины, вписанная должна проходить через стороны только в одной точке по касательной.
Чертеж равностороннего треугольника, описанного или вписанного в окружность
Если в условии задачи дан радиус вписанной и описанной окружности, то из них также можно составить выражение, так как вместе они дадут суммарную длину высоты. Как рассчитывается площадь при ее помощи, показано выше: h = R + r .
Преобразовав формулу , применив расчет высоты h = R + r, можно получить следующее значение: . Данную формула можно упростить еще больше, ведь радиус описанной окружности можно выразить через радиус вписанной. Согласно свойствам этих окружностей R = 2r, где r — это радиус вписанной окружности, R — это радиус описанной. Соответственно площадь правильного треугольника будет высчитываться так: .
Если же будет дан размер радиуса описанной окружности, то выражение будет выглядеть следующим образом: .
Использование этих свойств пригодится для расчета стороны фигуры. Для того чтобы ее найти можно воспользоваться выражением для описанной окружности, и для вписанной.
Учитывая радиус описанной окружности можно найти искомое значение при помощи возведения стороны в куб, после чего результат делится на радиус, увеличенный в 4 раза. Математически его можно записать следующим образом: .
Процесс расчета, чему равен показатель площади равностороннего треугольника через любую из предложенных формул не должен вызывать особых затруднений. Для того чтобы успешно справиться с этой задачей не нужно запоминать все указанные способы, достаточно запомнить основные общие формулы расчета, а также свойства и признаки этой фигуры.
Внимание! Для проверки правильности расчетов можно воспользоваться несколькими способами, результаты должны совпасть.
Площадь равностороннего треугольника
Площадь равностороннего треугольника, вписанного в окружность
youtube.com/embed/xLQo4eQlFwk» frameborder=»0″ allowfullscreen=»allowfullscreen»>Что такое равносторонний треугольник? — Определение, факты и примеры
Определение равностороннего треугольника
В геометрии равносторонним треугольником называется треугольник, все три стороны которого имеют одинаковую длину. Стороны равностороннего треугольника равны, что означает, что все стороны имеют одинаковую длину. Все внутренние углы равны (60 градусов).
Термин «равносторонний» состоит из слов «экви», что означает «равный», и «латеральный», что означает «сторона». Итак, треугольник с равными сторонами называется равносторонним треугольником.
История равносторонних треугольников
Следы треугольников можно найти во всем мире, особенно в строительстве. Их любили древние египтяне. Лица знаменитых египетских пирамид треугольные. Пирамиды Гизы – самые известные пирамиды, построенные египтянами во втором веке до нашей эры. Египтяне думали, что треугольная форма пирамиды символизирует местопребывание их бога Солнца Ра на земле.
Равносторонние треугольники, используемые в реальной жизни
- Дорожные знаки, которые мы видим на дороге, имеют форму равносторонних треугольников. В следующий раз, когда вы отправитесь кататься на машине, обратите внимание, что все три стороны вывески кажутся одинаковой длины.
- Стойки, используемые для установки бильярдного стола с шарами, представляют собой равносторонние треугольники. Всего в них помещается 15 шаров, образуя идеальный равносторонний треугольник.
- Начос, обычная закуска, также имеют треугольную форму. Некоторые из них действительно равносторонние.
Что НЕ является равносторонним треугольником?
- Поверхность дорожного конуса не является равносторонним треугольником, потому что все три стороны не равны. Дорожный конус имеет удлиненные стороны с меньшим основанием.
- Паруса на парусной лодке не являются равносторонними треугольниками, так как стороны не равны по длине.
 Две стороны длиннее, чем оставшаяся сторона.
Две стороны длиннее, чем оставшаяся сторона.
Свойства равносторонних треугольников
- Все стороны имеют одинаковую длину «а»
- Все внутренние углы равны 60 градусам.
- Равносторонний треугольник симметричен, а это означает, что если вы сложите его, чтобы соединить его вершины, он сложится так, что две половинки будут идеально перекрывать друг друга.
Периметр и площадь равностороннего треугольника
- Вы можете рассчитать периметр (длину всей границы) равностороннего треугольника, сложив длины всех трех сторон. В равностороннем треугольнике со стороной «а» длины сторон равны. Таким образом, периметр равностороннего треугольника = a + a + a = 3.a 92$; где а — сторона равностороннего треугольника.
Забавные факты о равностороннем треугольнике
- Грани пирамид Гизы в Египте — один из старейших и крупнейших в мире примеров равносторонних треугольников. Они были построены в 26 веке до н.
 э. и являются совершенно равносторонними.
э. и являются совершенно равносторонними. - Равносторонний треугольник — это особый равнобедренный треугольник, у которого все три стороны равны.
Решенные примеры
Q1. Чему будет равен периметр равностороннего треугольника, если предположить, что все его стороны имеют длину 30 дюймов?
Решение :
Вы знаете, что периметр равностороннего треугольника в 3 раза больше длины стороны. В вопросе указано, что длина стороны = 30 дюймов.
Следовательно, периметр равностороннего треугольника будет 3 × 30 = 90 дюймов.
Q2. Чему будут равны периметр и полупериметр равностороннего треугольника, сторона которого равна 10 единицам?
Решение :
Вы знаете, что периметр равностороннего треугольника в 3 раза больше длины стороны, а полупериметр равен половине периметра. 9{2}$ = $100\sqrt{3}$ квадратных дюймов
Часто задаваемые вопросы
Что мы подразумеваем под равносторонним?
Термин «равносторонний» состоит из слов «экви», что означает «равный», и «латеральный», что означает «сторона». Итак, если фигура имеет все стороны одинаковой длины, она называется равносторонней.
Итак, если фигура имеет все стороны одинаковой длины, она называется равносторонней.
Каковы свойства равностороннего треугольника?
Три свойства равностороннего треугольника:
- Все три стороны равны.
- Все три угла равны.
- Фигура имеет три оси симметрии.
Как узнать, является ли треугольник равносторонним?
Вы можете узнать, что треугольник равносторонний, измерив его стороны. Если они одинаковой длины, то треугольник равносторонний.
Может ли прямоугольный треугольник быть равносторонним?
Равносторонний треугольник никогда не может быть прямоугольным, так как в прямоугольном треугольнике один из углов равен 90°, тогда как в равностороннем треугольнике все углы равны 60°
Является ли равносторонний треугольник равнобедренным?
Равносторонний треугольник является частным случаем равнобедренного треугольника, у которого равны не две, а все три стороны и углы.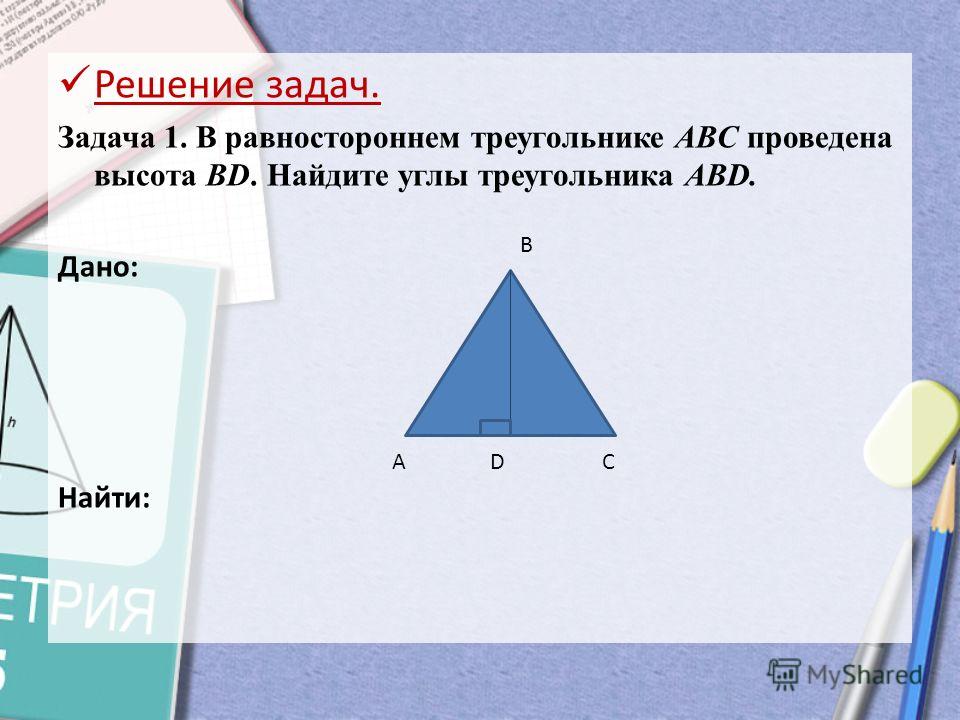
Равносторонние треугольники: значение, формула и свойства
Вокруг нас много объектов, имеющих форму треугольников, таких как кусочки пиццы, вершины и крыши башен, баннеры ко дню рождения. Но иногда мы сталкиваемся с треугольными фигурами, которые выглядят одинаково в любом направлении, в котором мы их вращаем, как чипсы для начо или дорожные знаки. Это какая-то особая форма треугольников? Действительно ли они равны во всех отношениях? Давай выясним.
В геометрии треугольники можно разделить на различные формы в зависимости от их сторон и углов. И одна из таких форм – равносторонний треугольник. В этом разделе мы разберемся с понятием равностороннего треугольника и увидим его свойства и основанные на нем формулы.
Треугольник является равносторонним треугольником , если у него три равные стороны. Другими словами, если все три стороны треугольника имеют одинаковую длину, то это равносторонний треугольник .
Таким образом, название «равносторонний» происходит от equi , что означает равные, и lateral, означает стороны.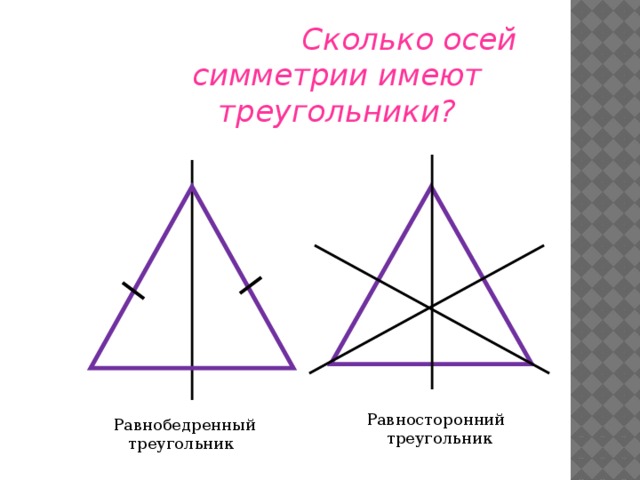
Равносторонний треугольник с конгруэнтными сторонами, Мули-Хавия — StudySmarter Originals
Равносторонние треугольники и углы
Равносторонние треугольники также можно классифицировать по их углам.
Равносторонний треугольник — это треугольник, у которого все три внутренних угла конгруэнтны и равны .
Равносторонний треугольник с одинаковыми углами, Мули-Хавия — StudySmarter Originals
Следствия о равносторонних треугольниках
Давайте рассмотрим некоторые важные утверждения о равносторонних треугольниках
Следствие 1
Утверждение : Каждый угол равностороннего треугольника равен.
Доказательство : Чтобы доказать этот равносторонний треугольник.
Теперь равносторонний треугольник также считается равнобедренным треугольником. Таким образом, мы можем применить свойства равнобедренного треугольника к равностороннему треугольнику.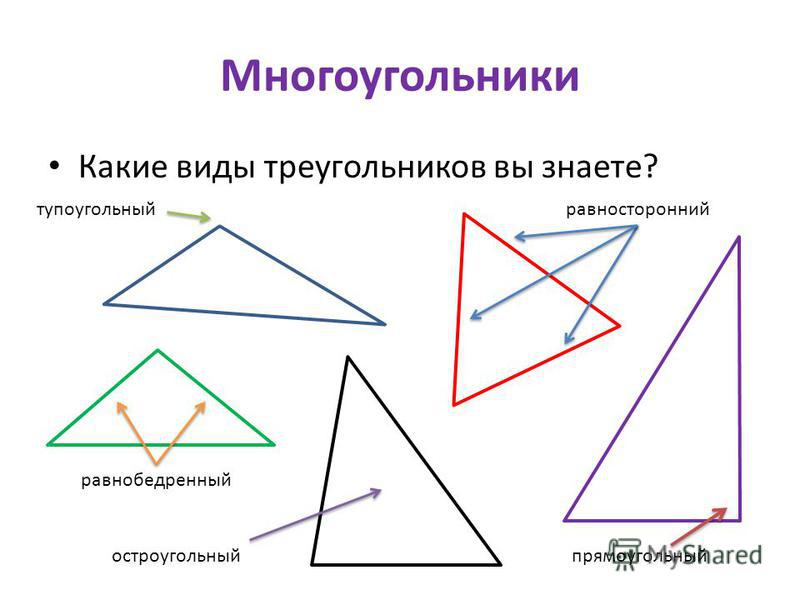 Здесь мы используем теорему о равнобедренном треугольнике.
Здесь мы используем теорему о равнобедренном треугольнике.
Для этого возьмите:
и
и
Теперь рассмотрим одно из свойств треугольника, которое гласит, что сумма всех внутренних углов треугольника равна:
Так как все три угла равны , мы можем просто рассмотреть один из них вместо всех.
Итак, .
Следовательно, мы можем сказать, что равносторонний треугольник — это равносторонний треугольник .
Теорема о равнобедренном треугольнике утверждает, что углы, противоположные двум сторонам треугольника, равны, если эти две стороны равны.
Из этого следствия мы приходим к следующему следствию.
Следствие 2
Утверждение : Треугольник равноугольный тогда и только тогда, когда он равносторонний.
Свойства равностороннего треугольника
Вот некоторые свойства равносторонних треугольников:
Равносторонний треугольник является правильным многоугольником, поскольку он имеет три стороны.

Все стороны и углы равносторонних треугольников равны.
Перпендикуляр, проведенный из любой вершины равностороннего треугольника к его противоположной стороне, делит пополам и сторону, и угол.
Эта перпендикулярная линия (как упоминалось выше) является той же линией для высоты, медианы, биссектрисы перпендикуляра и биссектрисы угла для одной и той же стороны.
Линиями симметрии в равносторонних треугольниках являются три упомянутые линии с каждой стороны.
В равносторонних треугольниках центр тяжести, ортоцентр, центр описанной окружности и центр вписанной окружности находятся в одной и той же точке.
Помните, что разделить пополам означает разделить на две равные части.
Формулы равностороннего треугольника
Давайте обсудим несколько формул, относящихся к равносторонним треугольникам, в том числе его:
- Периметр
- Площадь
- Высота
Периметр равен сумме104 всех сторон равностороннего треугольника 9042.
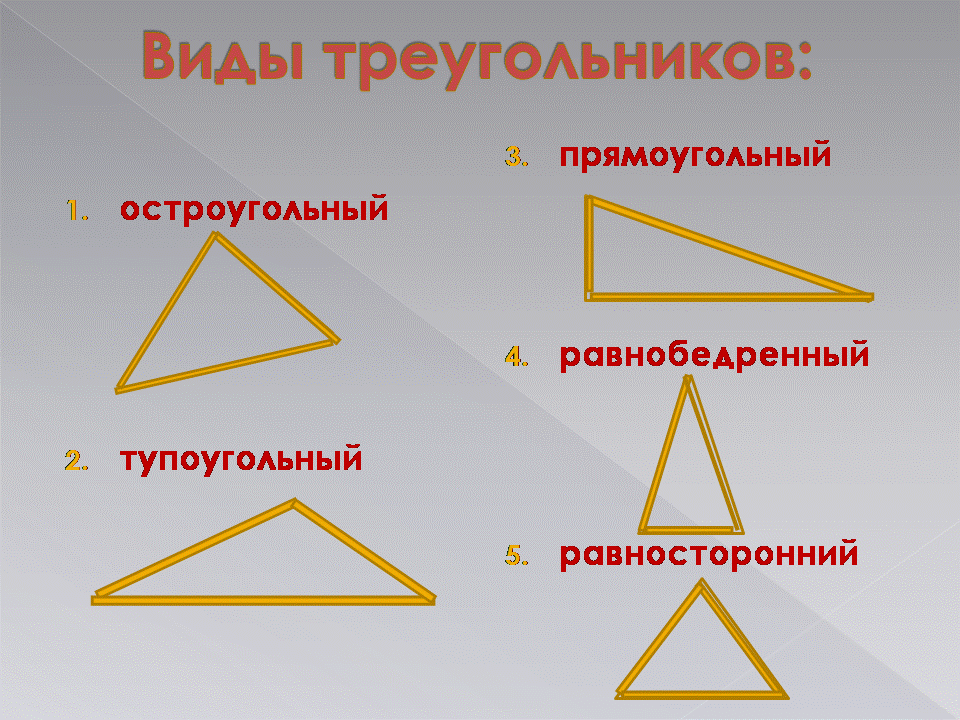 А так как речь идет о равностороннем треугольнике, то здесь все стороны равны. Таким образом, периметр равностороннего треугольника в три раза больше длины одной стороны.
А так как речь идет о равностороннем треугольнике, то здесь все стороны равны. Таким образом, периметр равностороннего треугольника в три раза больше длины одной стороны.Периметр равностороннего треугольника. Вот длина стороны.
Из этого мы можем вывести формулу полупериметра. Полупериметр — это половина периметра равностороннего треугольника, и мы можем рассчитать его следующим образом.
Полупериметр равностороннего треугольника
Мы обычно используем полупериметр для вычисления площади треугольника по формуле Герона.
Чему равен периметр данного равностороннего треугольника со стороной 6 см? Кроме того, найдите для него полупериметр.
Равносторонний треугольник, Мули-Хавия — StudySmarter Originals
Решение: здесь. Итак применяя формулу периметра, получаем:
Периметр равностороннего треугольника.
Полупериметр равностороннего треугольника.
Площадь равностороннего треугольника
Площадь рассчитывается для измерения пространства, занимаемого сторонами многоугольника в 2D-плоскости.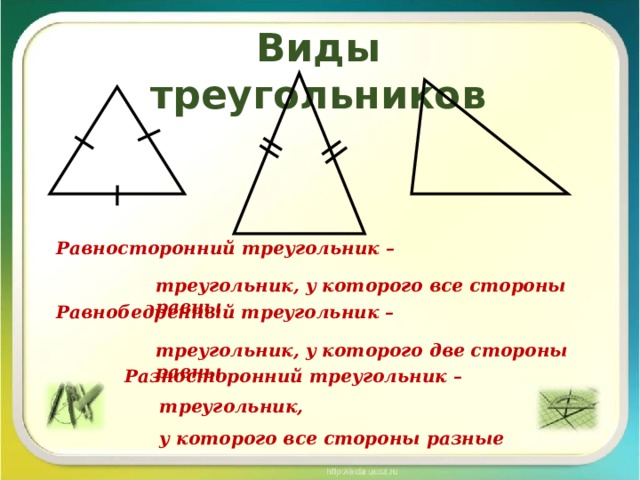 Формула для нахождения площади равностороннего треугольника выглядит следующим образом.
Формула для нахождения площади равностороннего треугольника выглядит следующим образом.
Площадь равностороннего треугольника , где длина стороны.
Мы также можем вычислить площадь по формуле Герона, если задан полупериметр. Формула Герона выглядит следующим образом.
Площадь равностороннего треугольника, , где а — длина стороны, а s — полупериметр треугольника.
Вычислите площадь равностороннего треугольника со стороной 5 см.
Равносторонний треугольник, Мули-Хавия — StudySmarter Originals
Решение: здесь
Площадь равностороннего треугольника
Следовательно, площадь данного равностороннего треугольника равна
Высота равностороннего треугольника
Высота равностороннего треугольника — это расстояние по перпендикуляру от вершины этого треугольника до его противоположной стороны.
Высота равностороннего треугольника, Мули-Хавия — StudySmarter Originals
Формула для расчета высоты равностороннего треугольника приведена ниже.
Высота равностороннего треугольника, где длина стороны.
Найдите высоту равностороннего треугольника со стороной 15 см.
Решение: Используя формулу высоты, мы можем сказать:
Высота равностороннего треугольника
Следовательно, высота (или высота) равностороннего треугольника равна 12,12 см.
Примеры равносторонних треугольников
Теперь мы работаем над некоторыми примерами, основанными на приведенной выше теории.
Найдите площадь равностороннего треугольника с периметром 18 см.
Решение: Чтобы найти площадь равностороннего треугольника, нам нужно знать длины его сторон. Итак, сначала найдем длину стороны, используя периметр. Мы знаем, что формула периметра равностороннего треугольника такова. В вопросе также указано значение периметра, которое равно 18 см.
Теперь, когда мы нашли длину стороны, мы можем использовать ее в формуле площади для ее расчета.
Площадь равностороннего треугольника
Следовательно, равносторонний треугольник с периметром 18 см имеет площадь 15,58 см 2 .
Дан равносторонний треугольник с двумя длинами сторон. Длина одной стороны равна, а длина другой стороны равна. Чему равна длина стороны этого равностороннего треугольника? Также найдите периметр этого треугольника.
Решение: Поскольку данный треугольник является равносторонним, мы знаем, что все его стороны равны. Таким образом, заданные длины двух сторон равны, и уравнения также можно считать равными друг другу.
Чтобы определить длину стороны, решаем приведенное выше уравнение и находим значение x.
Теперь, поскольку обе стороны равны, мы подставляем значение x в любую из длин сторон.
Подставив, получим
.
Мы можем проверить правильность найденного значения x, подставив x в обе длины сторон. Если оба значения длин сторон равны, значение x верное.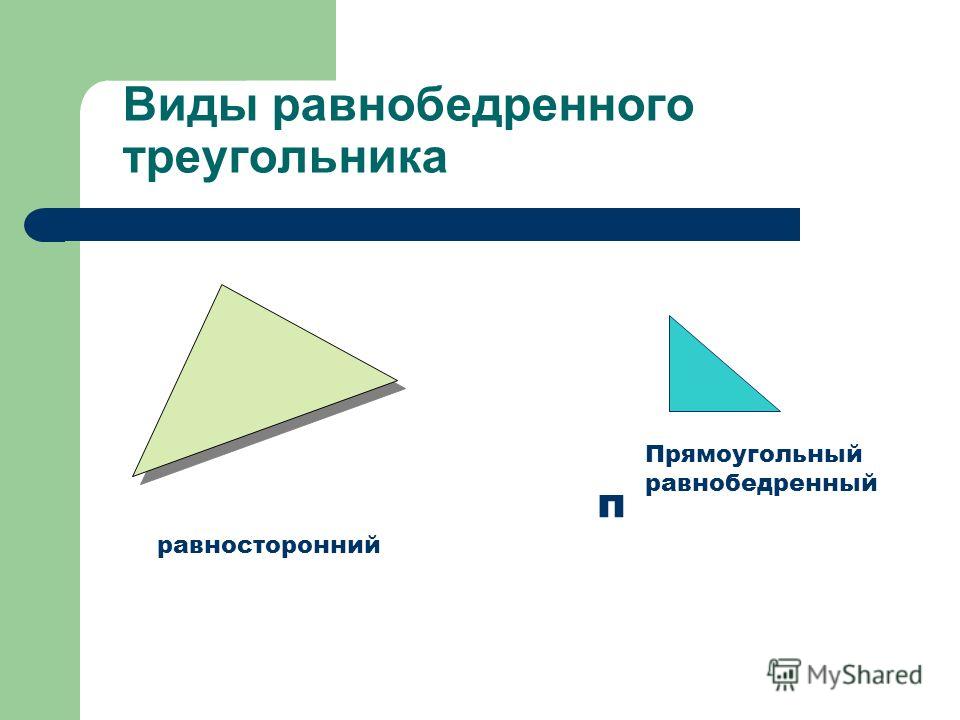 Посмотрим для нашего случая. Мы уже нашли значение одной из длин сторон. Найдем длину другой стороны и сравним ее.
Посмотрим для нашего случая. Мы уже нашли значение одной из длин сторон. Найдем длину другой стороны и сравним ее.
Подставив x в , мы снова получим значение 11. Следовательно, поскольку оба значения длины стороны равны, наше вычисленное значение x верно!
Теперь, когда у нас есть длина сторон, мы можем легко вычислить периметр равностороннего треугольника.
Периметр равностороннего треугольника. Здесь.
.
Итак, периметр данного равностороннего треугольника равен 33см.
Равносторонние треугольники. Ключевые выводы
- Треугольник является равносторонним, если у него три равные стороны.
- Равносторонний треугольник — это треугольник, у которого все три внутренних угла конгруэнтны и равны .
- Треугольник равноугольный тогда и только тогда, когда он равносторонний.
- Периметр равностороннего треугольника равен .
- Полупериметр равностороннего треугольника.
- Площадь равностороннего треугольника.

- Площадь равностороннего треугольника (по формуле Герона) равна .
- Высота равностороннего треугольника.
Равносторонние треугольники — Математика верхнего уровня ISEE
Все математические ресурсы верхнего уровня ISEE
6 диагностических тестов 244 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 Следующая →
Справка по математике верхнего уровня ISEE » Геометрия » Плоская геометрия » Треугольники » Равносторонние треугольники
Для равностороннего треугольника стороны A измеряют и стороны B измеряют . Какова длина стороны А?
Возможные ответы:
Правильный ответ:
8
Пояснение:
Прежде всего вам нужно понять, что у равностороннего треугольника все три стороны имеют одинаковую длину.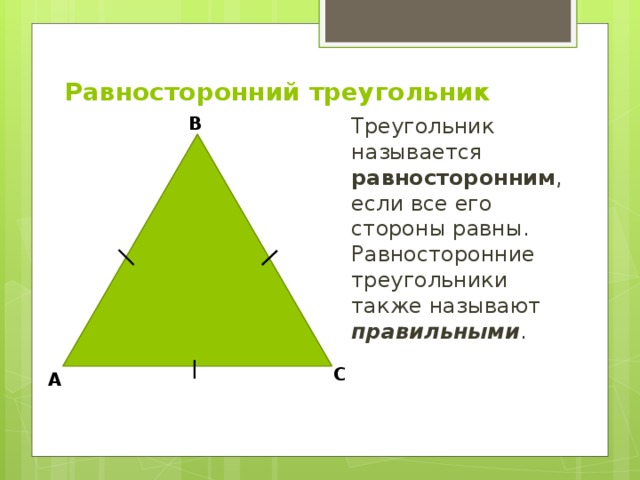
Это означает, что вы можете установить два значения для сторон A и B равными друг другу, поскольку они измеряют одинаковую длину, чтобы найти .
Теперь вы это знаете, но это не ваш ответ. Вопрос касается длины стороны А, поэтому вам нужно подставить 3 в это уравнение.
Таким образом, длина стороны A (и стороны B в этом отношении) равна 8.
Сообщить об ошибке
Один угол равностороннего треугольника равен 60 градусам. Одна сторона этого треугольника равна 12 см. Чему равны два других угла и две другие стороны?
Возможные ответы:
45 градусов, 75 градусов, 12 сантиметров, 13 сантиметров
90 градусов, 30 градусов, 12 сантиметров, 12 сантиметров
50 градусов, 70 градусов, 5 сантиметров, 12 сантиметров 6
5 , 60 градусов, 12 сантиметров, 12 сантиметров
55 градусов, 65 градусов, 12 сантиметров, 13 сантиметров
Правильный ответ:
60 градусов, 60 градусов, 12 сантиметров, 12 сантиметров
Пояснение:
Равносторонний треугольник — это треугольник, у которого все три стороны равны.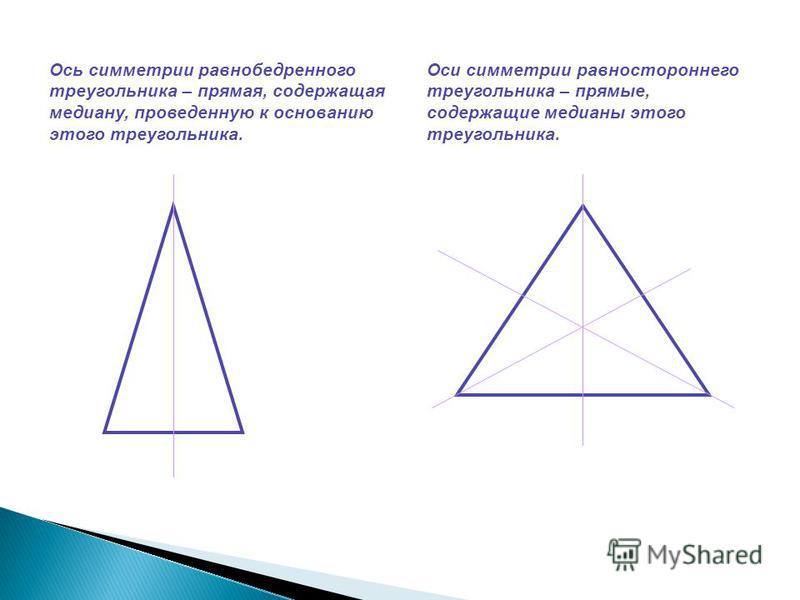 Он также обладает тем свойством, что все три внутренних угла равны. Другими словами, все три угла равностороннего треугольника всегда равны 60°. Поскольку все стороны равны, две другие стороны равны 12 сантиметрам.
Он также обладает тем свойством, что все три внутренних угла равны. Другими словами, все три угла равностороннего треугольника всегда равны 60°. Поскольку все стороны равны, две другие стороны равны 12 сантиметрам.
Сообщить об ошибке
Если периметр равностороннего треугольника равен 18 дюймов, какова длина одной стороны?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти периметр равностороннего треугольника, воспользуемся следующей формулой:
, где a — длина любой стороны треугольника. Поскольку у равностороннего треугольника 3 равные стороны, мы можем использовать любую сторону в формуле. Чтобы найти длину одной стороны треугольника, мы найдем a .
Теперь мы знаем, что периметр равностороннего треугольника равен 18 дюймам. Итак, будем заменять.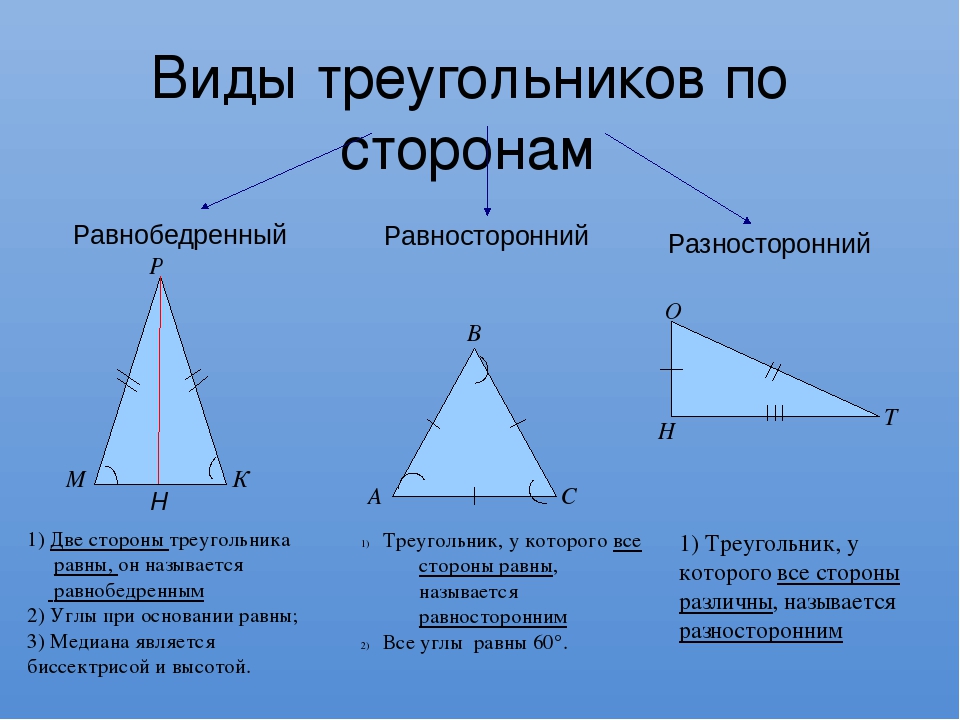
Следовательно, длина одной стороны равностороннего треугольника равна 6 дюймов.
Сообщить об ошибке
Периметр равностороннего треугольника равен 39 дюймов. Найдите длину одной стороны.
Возможные ответы:
Правильный ответ:
Объяснение:
Равносторонний треугольник имеет 3 равные стороны. Итак, чтобы найти длину одной стороны, воспользуемся тем, что знаем. Мы знаем, что периметр равностороннего треугольника равен 39 дм. Итак, рассмотрим формулу периметра. Получаем
, где — длина одной стороны треугольника. Итак, чтобы найти длину одной стороны, мы найдем для . Теперь, как было сказано ранее, мы знаем, что периметр треугольника равен 39 дюймов. Итак, подставим и решим на и . Получаем
Следовательно, длина одной стороны равностороннего треугольника равна 13 дюймов.
Сообщить об ошибке
Длина одной стороны равностороннего треугольника составляет 6 дюймов. Укажите площадь треугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
,
где и – длины двух сторон треугольника, а – величина угла.
В равностороннем треугольнике все стороны имеют одинаковую длину, а все три угла всегда равны .
Сообщить об ошибке
Периметр равностороннего треугольника . Укажите его площадь.
Возможные ответы:
Правильный ответ:
Пояснение:
Равносторонний треугольник с периметром имеет три конгруэнтные стороны длины 9. Укажите его площадь.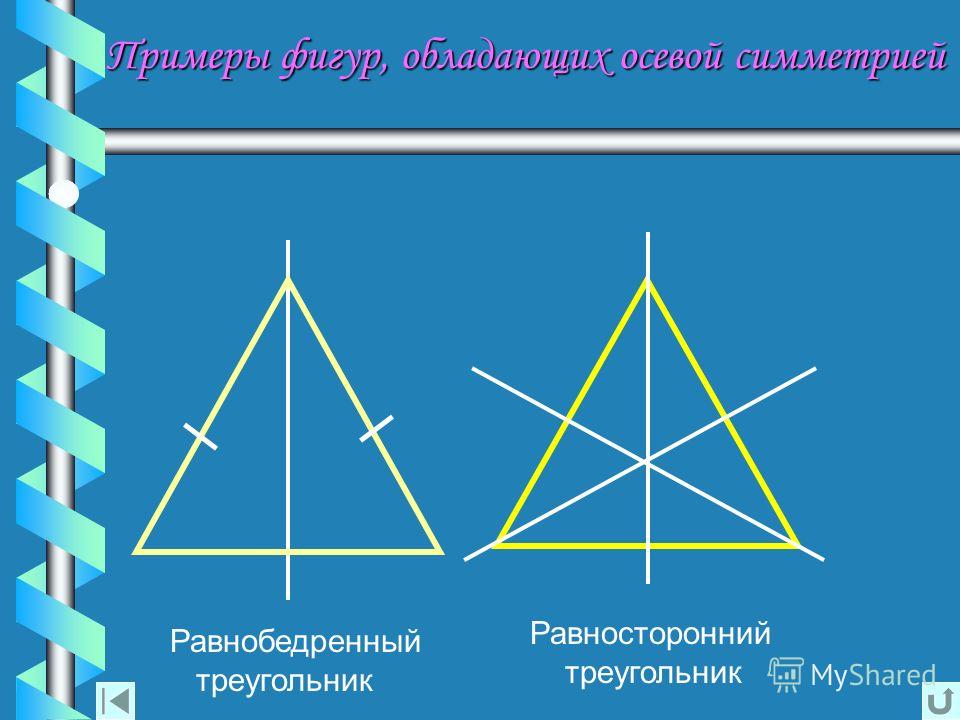
Возможные ответы:
Правильный ответ отсутствует среди других четырех вариантов.
Правильный ответ:
Пояснение:
Равносторонний треугольник с периметром имеет три конгруэнтные стороны длины
Площадь этого треугольника
Сообщить об ошибке
Периметр равностороннего треугольника . Выразите его площадь через .
Возможные ответы:
Правильный ответ:
Объяснение:
Равносторонний треугольник с периметром имеет три равные стороны по длине. Подставьте это вместо в следующей формуле площади:
Сообщить об ошибке
В круг радиуса 8 вписан равносторонний треугольник.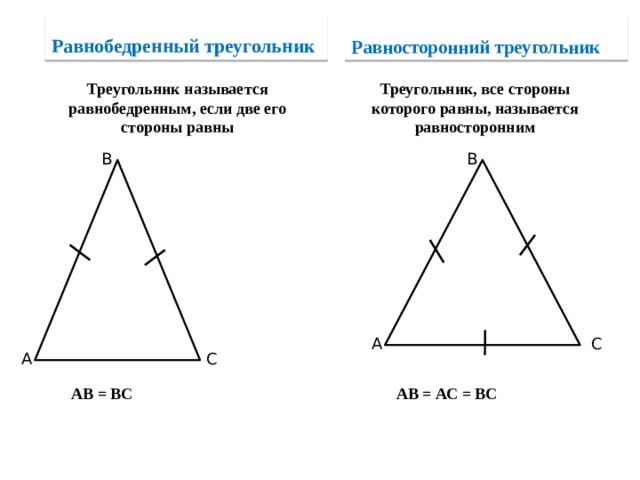 Укажите его площадь.
Укажите его площадь.
Возможные ответы:
Правильный ответ:
Объяснение:
Хитрость заключается в том, чтобы знать, что описанная окружность или описанная окружность имеет своим центром пересечение трех высот треугольника, и что этот центр или описанная окружность , делит каждую высоту на два сегмента, один из которых в два раза длиннее другого, причем более длинный из них является радиусом. Из-за этого мы можем построить следующее:
Каждый из шести меньших треугольников является треугольником 30-60-90, и все шесть равны.
Мы найдем площадь и умножим ее на 6.
По теореме 30-60-90, площадь равна
.
Шесть раз это — — площадь .
Сообщить об ошибке
Периметр равностороннего треугольника равен . Укажите его площадь.
Возможные ответы:
Правильный ответ:
Объяснение:
Равномерный треугольник с периметром 36 имеет три конгруэнтные стороны длины
Площадь этого треугольника —
Отчет о ошибке
← Предыдущий 1 2 3 Следующий →
.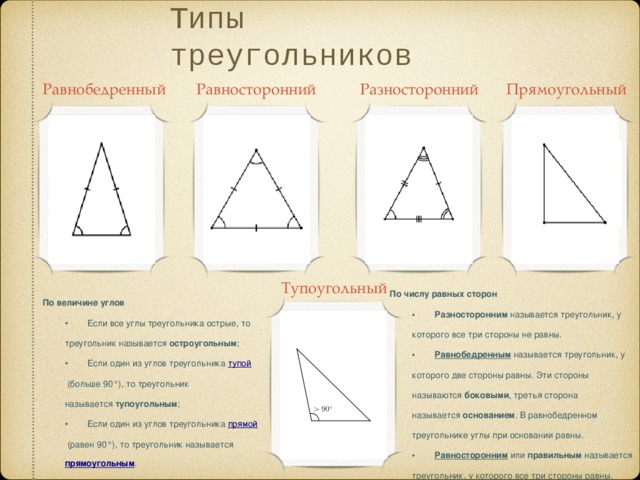 Копират. Обратите внимание
Копират. Обратите внимание
6 диагностических тестов 244 практических теста Вопрос дня Карточки Учитесь по концепции
терминология — Может ли равносторонний треугольник быть равнобедренным треугольником?
Спросил
Изменено 2 года, 10 месяцев назад
Просмотрено 38 тысяч раз
$\begingroup$
Я прочитал в учебнике по математике, что у равнобедренного треугольника по крайней мере две конгруэнтные стороны. Я также знаю, что слова «по крайней мере» означают этот символ: $\ge$, что означает «больше или равно» или «не меньше».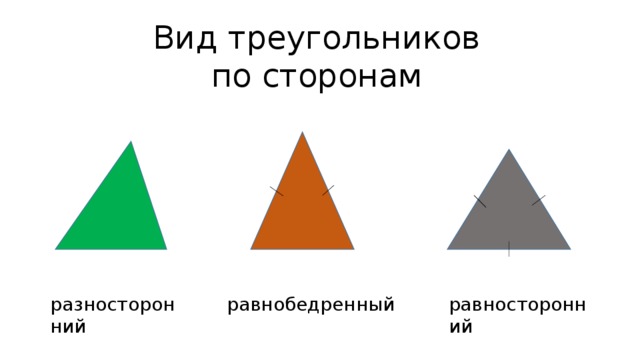 Это навело меня на мысль, что равнобедренные треугольники также могут быть равнобедренными, но так ли это?
Это навело меня на мысль, что равнобедренные треугольники также могут быть равнобедренными, но так ли это?
- терминология
- определение
- треугольники
$\endgroup$
7
$\begingroup$
NB: Я представляю этот ответ как вызов кадра. Основная мотивация этого ответа состоит в том, чтобы сделать более постоянными некоторые комментарии, оставленные в ответ на вопрос и другие ответы, а также включить некоторые идеи из уже удаленного ответа.
Важность определений
Математика – это человеческая деятельность. Слова, которые мы используем для описания математических идей, являются человеческим изобретением, поэтому важно понимать, что разные люди могут использовать одно и то же слово для описания разных идей или разные слова для описания одной и той же идеи. Когда кто-то пытается понять математическую идею, представленную другим, важно понимать определения докладчика.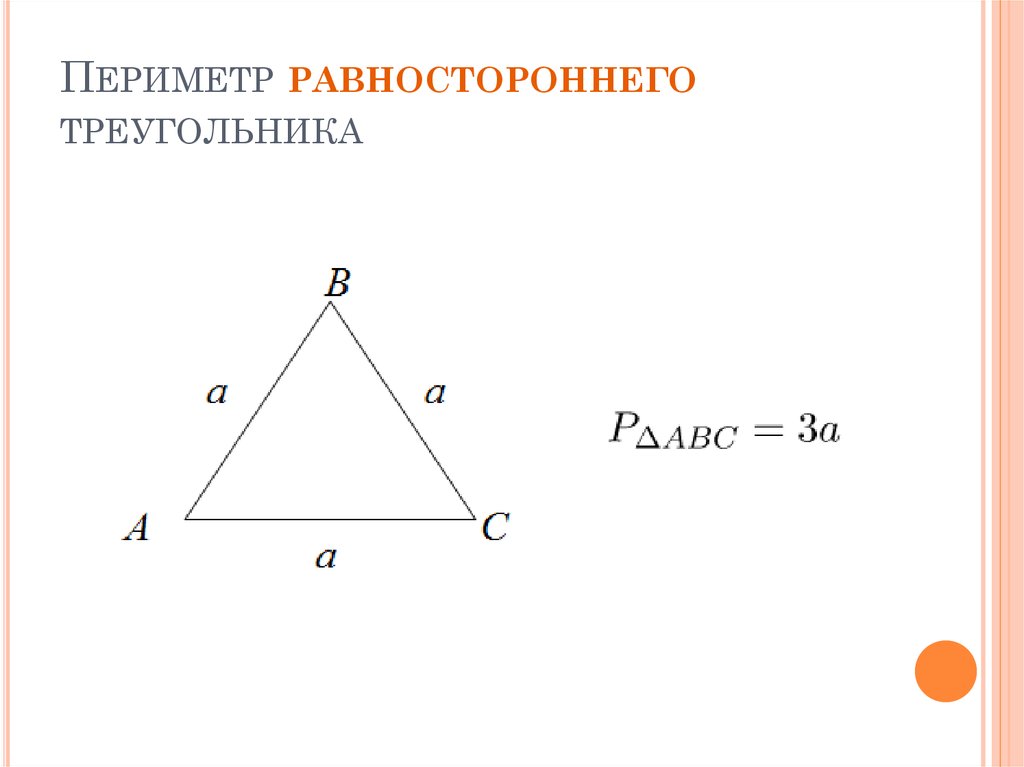 Из определений можно сделать дальнейшие выводы.
Из определений можно сделать дальнейшие выводы.
Например, в вопросе выше у нас есть определение:
Определение: Равнобедренный треугольник — это треугольник, у которого по крайней мере две конгруэнтные стороны.
Равносторонний треугольник имеет три конгруэнтные стороны, а три «по крайней мере» два. Следовательно, согласно этому определению, каждый равносторонний треугольник должен быть равнобедренным.
Однако есть авторы, которые дают другое определение равнобедренных треугольников. Джоэл Рейес Нош отмечает, что многие учителя начальных классов определяют равнобедренный треугольник как треугольник с 9 сторонами.0194 ровно две конгруэнтные стороны. Ведь это определение дал сам Евклид!:
- Кроме того, из трехсторонних фигур равносторонний треугольник — это тот, у которого три стороны равны, равнобедренный треугольник — тот, у которого две стороны равны, а разносторонний треугольник — тот, у которого три стороны не равны.
. [Euclid’s Elements , как переведено Томасом Хитом]
Согласно этому определению, ни один равнобедренный треугольник не является равносторонним, и ни один равносторонний треугольник не является равнобедренным.
$\endgroup$
$\begingroup$
Равносторонний треугольник — это треугольник с тремя равными сторонами. Равнобедренный треугольник – это треугольник с двумя равными сторонами.
Следовательно, каждый равносторонний треугольник равнобедренный, но не всякий равнобедренный треугольник равносторонний.
Пока так бронируй. Однако согласно Википедии определение равнобедренного треугольника иногда указывает, что у него должно быть две и только две равных сторон. Согласно этому (необычному) определению равносторонний треугольник с тремя равными сторонами, конечно, не будет равнобедренным.
$\endgroup$
11
$\begingroup$
Из Шанхая (Китай) я должен сказать, что равносторонний треугольник — это частный случай равнобедренного треугольника. Период.
Период.
$\endgroup$
$\begingroup$
Все равносторонние треугольники равнобедренные, потому что у них две равные стороны и два равных угла
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
ТОП 8 как выглядит равносторонний треугольник САМЫЙ ЛУЧШИЙ и НОВЫЙ
Вы задаетесь вопросом как выглядит равносторонний треугольник но на данный момент нет ответа, поэтому пусть kienthuctudonghoa.com обобщить и перечислить основные статьи с вопросом. ответьте на вопрос, как выглядит равносторонний треугольник, что поможет вам получить наиболее точный ответ. Следующая статья призвана помочь вам сделать правильный выбор и получить больше полезной информации.
Mục lục
- 1 1. Как выглядит равносторонний треугольник? – Сократ
- 2 2.Треугольники – Равносторонний, равнобедренный и разносторонний – YouTube
- 3 3.Как выглядит равносторонний треугольник [Решено] – Cuemath
- 4 4. Равносторонний треугольник — Википедия
- 5 5. Равносторонний треугольник — из Wolfram MathWorld
- 6 6. Равносторонний треугольник | Углы, градусы и измерения — Study.
 com
com - 7 7. Равносторонний треугольник — определение, свойства, формулы и примеры
- 8 8. Равносторонний треугольник — Math.net
1. Как выглядит равносторонний треугольник? – Socratic
- Автор: socratic.org
- Дата публикации: 22 вчера
- Рейтинг: 1 (1383 Обзоры)
- Высокий рейтинг: 4
- Низкий рейтинг: 3
- Суммар. ) тот, у которого все стороны конгруэнтны (равны по длине).
Подробнее
2.Треугольники – Равнобедренные, Равнобедренные и Разносторонние – YouTube
- Автор: www.youtube.com
- Дата публикации: 9 вчера
- Рейтинг: 5 (1059 обзоров)
- Высокий рейтинг: 3
- Низкий рейтинг: 2
- SEEL: 4 2
- .
 Как выглядит равносторонний треугольник [Решено]0064 3
Как выглядит равносторонний треугольник [Решено]0064 3 - Низкий рейтинг: 3
- Резюме: Ответ: Равносторонний треугольник — это трехсторонний многоугольник, у которого все 3 стороны и 3 угла равны. Давайте разберемся с концепцией с изображением.
See Details
4.Equilateral triangle – Wikipedia
- Author: en.wikipedia.org
- Post date: 15 yesterday
- Rating: 2(788 reviews)
- Highest rating : 4
- Низкий рейтинг: 1
- Резюме: Равносторонний треугольник в геометрии — это треугольник, в котором все три стороны имеют одинаковую длину. В знакомой евклидовой геометрии, равенственная…
См. Подробности
5. Обязательный треугольник — от Wolfram Mathworld
- Автор: MathWorld.Wolfram.
 com
com - POST Дата: 26 26 Вчера 6666699
- Post Дата: 26 26 26 26666666669
- . 1(1596 отзывов)
- Наивысшая оценка: 4
- Низкая оценка: 3
- Резюме: Равносторонний треугольник — это треугольник, все три стороны которого имеют одинаковую длину a, соответствующий тому, что также можно назвать «правильным» треугольником. .
Подробнее
6. Равносторонний треугольник | Углы, градусы и измерения – Study.com
- Автор: Study.com
- Дата публикации: 7 вчера
- Рейтинг: 3 (обзоры 1928 г.)
- Высокий рейтинг: 3
- Низкий рейтинг: 1
- Сводка:
. См. Детали
9006 7.conater.- Автор: byjus.
 com
com - Дата поста: 23 вчера
- Рейтинг: 1 (1813 Обзоры)
- Высокий рейтинг: 4
- .0064 1
- Сводка:
См. Подробная информация
8. Обязательный треугольник — Math.net
- Автор: WWW.Math.NET
- POST Дата: 21 216 2166669.NET
- POST Дата: 21 216 216666669. NET
- . 5(1377 отзывов)
- Самый высокий рейтинг: 5
- Низкий рейтинг: 2
- Итог: Равносторонний треугольник также называют равноугольным треугольником, так как три его угла равны 60°. В равнобедренном треугольнике углы при основании равны.
См. подробности
Информация, представленная выше о вопросе как выглядит равносторонний треугольник , безусловно, помогла вам получить желаемый ответ, пожалуйста, поделитесь этой статьей со всеми.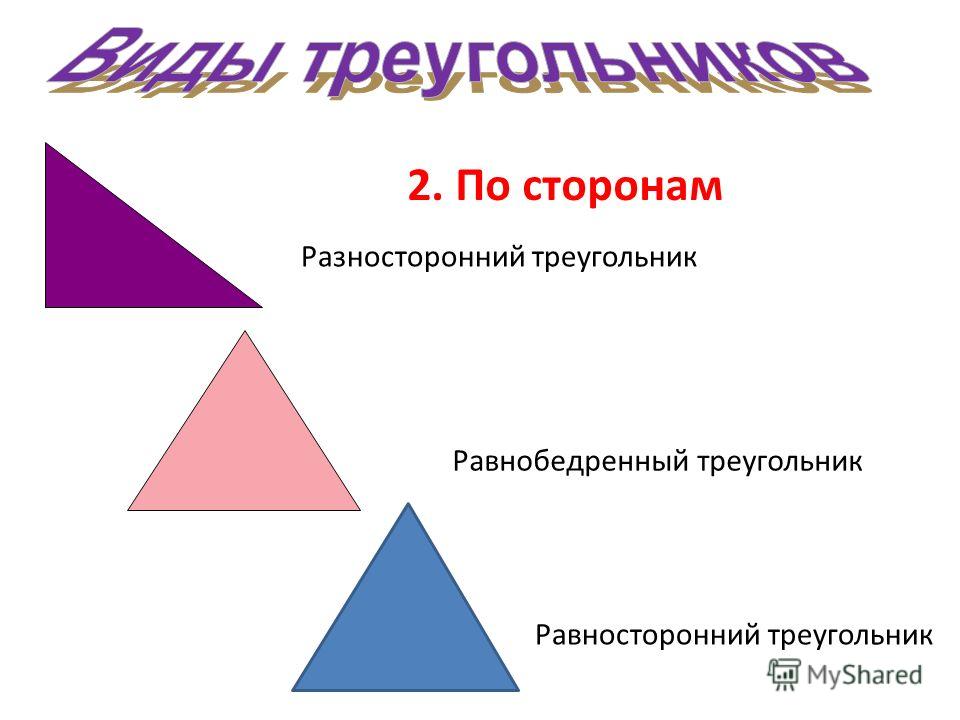 так что каждый может знать эту полезную информацию. Желаю тебе хорошего дня!
так что каждый может знать эту полезную информацию. Желаю тебе хорошего дня!
Факты о равностороннем треугольнике для детей, которые обожают уроки геометрии
Факты о равностороннем треугольнике для детей, которые обожают уроки геометрии | КидадльПоследние поиски (0)
ДЛЯ ВОЗРАСТА ОТ 3 ЛЕТ ДО 18 ЛЕТ
Автор:
Таня Парки
21 февраля 2022 г.
; Обновлено
14 сентября 2022 г.
Подредактировано
Кэтрин Кук
12 апреля 2022 г.
; Факт проверен
Аматулла Гулбаргавала
4 июля 2022 г.
6 минут до прочтения
Arts & Crafts
Узнайте больше
Чтение и написание
Узнайте больше
Math & Logic
Узнайте больше
Sports & Active
.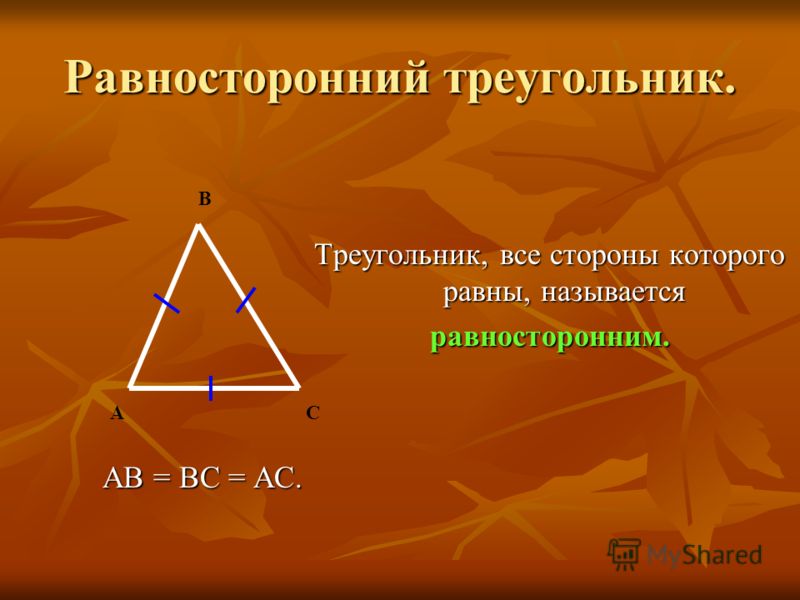 подробнее
подробнее
Социальные сети и сообщества
Узнать больше
Внимательность и размышления
Узнать больше
На открытом воздухе и на природе
Узнать больше
Автор:
Таня Парки
Опубликовано 21 февраля 2022 г.
6 минут на чтение
Kidadl Статья Стандарты проверки фактов
В Kidadl мы гордимся тем, что предлагаем семьям оригинальные идеи, чтобы максимально использовать время, проведенное вместе дома или на улице, где бы вы ни находились. Мы стремимся рекомендовать самые лучшие вещи, предложенные нашим сообществом, и то, что мы сделали бы сами — наша цель — быть надежным другом для родителей.
Мы стараемся изо всех сил, но не можем гарантировать совершенство. Мы всегда будем стремиться предоставить вам точную информацию на дату публикации, однако информация может меняться, поэтому важно, чтобы вы провели собственное исследование, перепроверили и приняли решение, подходящее для вашей семьи.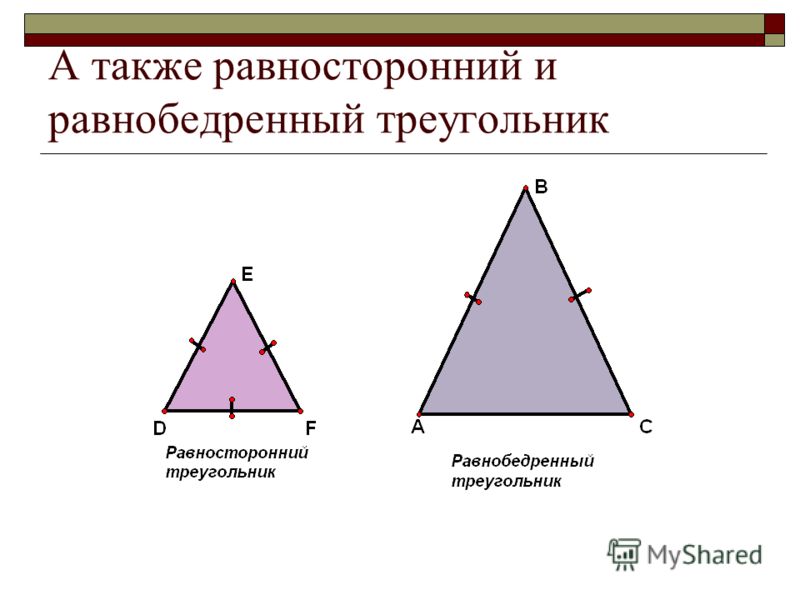
Kidadl вдохновляет детей развлекать и обучать их. Мы понимаем, что не все виды деятельности и идеи подходят и подходят для всех детей и семей или во всех обстоятельствах. Наши рекомендуемые занятия основаны на возрасте, но это ориентир. Мы рекомендуем использовать эти идеи в качестве вдохновения, чтобы идеи воплощались в жизнь под надлежащим наблюдением взрослых, и чтобы каждый взрослый использовал свое собственное усмотрение и знания своих детей для рассмотрения безопасности и пригодности.
Kidadl не может взять на себя ответственность за реализацию этих идей, поэтому рекомендуется постоянно находиться под присмотром родителей, так как безопасность превыше всего. Любой, кто использует информацию, предоставленную Kidadl, делает это на свой страх и риск, и мы не несем ответственности, если что-то пойдет не так.
» класс = ‘мв-видео-цель’ данные-автовоспроизведение = «ложь» данные-автовставка = «истина» данные-отключить-jsonld=»true»>
Равносторонний треугольник — одна из самых узнаваемых фигур в геометрии.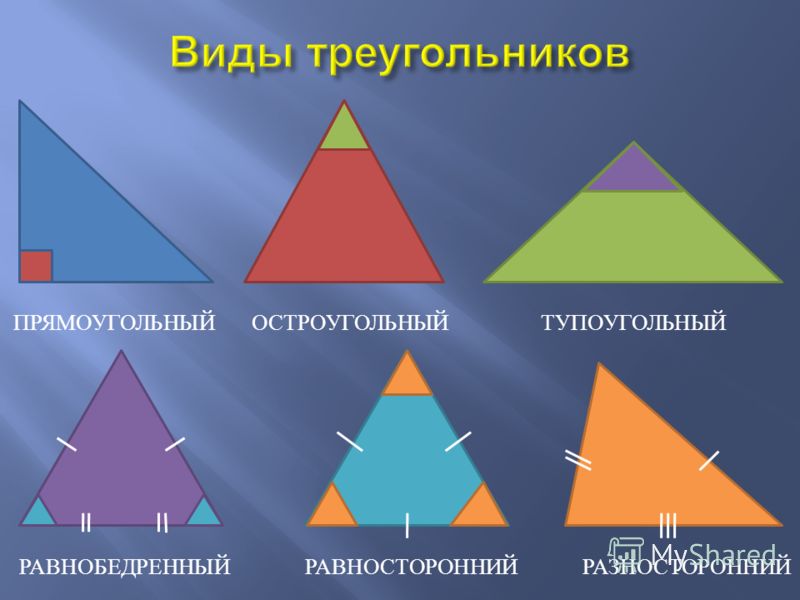
Этот треугольник, как вы могли догадаться из названия, известен равными сторонами и равными углами! Это делает этот треугольник довольно простым для рисования, и он обычно используется в проектах, узорах и строительных работах.
Равносторонний треугольник обладает множеством интересных свойств, о которых вы узнаете из этой статьи! Читайте дальше, чтобы узнать больше о захватывающем равностороннем треугольнике!
Значение равностороннего треугольникаРавносторонний треугольник — это тип треугольника с тремя сторонами одинаковой длины. Эта форма обладает особыми свойствами, которых нет у других треугольников, и может использоваться по-разному. Вот некоторые интересные факты о равносторонних треугольниках:
- Это единственный тип треугольника, который имеет равные углы по 60 градусов каждый.
- Все стороны треугольника имеют одинаковую длину и всегда имеют отношение 1:1:1.
- Этот треугольник имеет три линии симметрии, т.
 е. линии, которые делят его на идеальные половины. Каждая точка симметрии расположена в середине каждой стороны. Линия проходит от вершины треугольника до середины противоположной стороны.
е. линии, которые делят его на идеальные половины. Каждая точка симметрии расположена в середине каждой стороны. Линия проходит от вершины треугольника до середины противоположной стороны. - Как и любой другой треугольник, он имеет три вершины.
- Периметр равен 3а, где а — длина сторон.
- Вы можете нарисовать круг внутри равностороннего треугольника так, чтобы стороны круга касались всех сторон треугольника. Это известно как вписанный круг! Геометрический центр вписанной окружности и треугольника будет совпадать.
- Прямая линия из центра в вершины равностороннего треугольника будет иметь такой же радиус окружности.
- Точно так же можно нарисовать описанную окружность. Вершины треугольника будут касаться круга, а треугольник будет внутри круга!
- Хотя трудно найти примеры равносторонних треугольников в природе, вы можете попытаться найти их в повседневной жизни! Ищите специальные чипсы из тортильи, кусочки пиццы или знаки остановки. Попробуйте визуализировать и посмотреть, совпадают ли длины сторон.
 Если да, то у вас получился равносторонний треугольник!
Если да, то у вас получился равносторонний треугольник! - Равносторонние треугольники можно использовать для различных целей. Их можно использовать в геометрических рисунках, логотипах или символах, в художественных проектах, таких как картины или скульптуры, а также в математических задачах и головоломках. Эти треугольники также используются для строительства таких вещей, как мосты и здания, потому что они прочные.
- Слово «экви» означает «равный». Если треугольник называется равносторонним, то три стороны треугольника равны. Это также работает и для других форм!
- Например, у равностороннего пятиугольника пять равных сторон. А квадрат? У него четыре равные стороны, значит, это равносторонний четырехугольник!
- Равносторонний треугольник — это фигура с наименьшим возможным числом сторон, поскольку никакая фигура не может состоять только из двух сторон! Итак, треугольники совершенно особенные!
В настоящее время существует около шести различных типов треугольников: равнобедренный, равносторонний, разносторонний, прямоугольный, остроугольный и тупоугольный. Каждый тип треугольника имеет свой особый набор характеристик.
Каждый тип треугольника имеет свой особый набор характеристик.
- Наиболее симметричным из всех треугольных форм является равносторонний треугольник. У него три стороны одинаковой длины и все углы равны 60 градусов.
- Равнобедренный треугольник тоже достаточно симметричен. У него две равные стороны и углы.
- Разносторонний треугольник является наименее симметричным типом треугольника. Он имеет три неравные стороны и углы в диапазоне от 0 до 180 градусов.
- Прямоугольный треугольник называется так, потому что один из его углов (прямой) равен 90 градусов. Эта форма треугольника занимает особое место в математике, поскольку с ее помощью можно вычислить отношения между двумя связанными величинами.
- Остроугольный треугольник — это треугольник, углы которого меньше 90 градусов. Эти треугольники часто используются для строительных проектов, таких как строительство домов и мостов.
- Тупоугольный треугольник — это треугольник, угол которого больше 90 градусов, но меньше 180, что делает эту форму очень асимметричной.

Равносторонний треугольник имеет три равные стороны и три угла, каждый из которых равен 60 градусов.
- Длина каждой стороны равностороннего треугольника одинакова, и периметр (расстояние вокруг треугольника) также одинаков.
- Площадь равностороннего треугольника всегда составляет одну треть площади квадрата с таким же периметром. Если вы хотите найти площадь равностороннего треугольника, вы можете просто умножить длину одной стороны на саму себя, а затем разделить ее на три.
- Равносторонние треугольники обладают несколькими интересными математическими свойствами, включая возможность разбиения на более мелкие равносторонние треугольники.
- На самом деле, любой многоугольник (форма, состоящая из прямых линий) может быть разбит на все меньшие и меньшие многоугольники, если каждый новый многоугольник состоит из прямых линий.
- Равносторонние треугольники также очень полезны в геометрии, потому что они могут решать проблемы.

- Например, если вам дали задачу, в которой нужно найти длину одной стороны треугольника, гораздо проще выяснить, известна ли уже длина другой стороны.
- Это потому, что у равностороннего треугольника три стороны одинаковой длины, что позволяет легко вычислить длину любой стороны.
- Вычисление площади и других параметров также становится намного проще с помощью этого треугольника. Равносторонний треугольник также намного легче визуализировать из-за его простой формы. Это делает его хорошим выбором для многих людей при строительстве и проектировании.
Существуют разные способы вычисления площади треугольника. Используя эти базовые формулы, вы также можете легко вычислить площадь равностороннего треугольника.
- Лучший способ вычислить это — использовать формулу площади 1/2*основание*высота, где высота и основание известны.
- Другим способом является использование формулы Герона, которая имеет вид длины трех сторон треугольника.
 2).
2). - Независимо от того, как вы вычисляете площадь, важно убедиться, что все ваши измерения выражены в одних и тех же единицах измерения (например, в дюймах, футах или м). В противном случае ваши расчеты будут неверными.
- Итак, если вы работаете с треугольником, площадь которого указана в метрах, убедитесь, что все ваши измерения указаны в метрах!
Прочитайте заявление об отказе от ответственности
Заявление об отказе от ответственности
В Kidadl мы гордимся тем, что предлагаем семьям оригинальные идеи, чтобы максимально использовать время, проведенное вместе дома или на улице, где бы вы ни находились. Мы стремимся рекомендовать самые лучшие вещи, предложенные нашим сообществом, и то, что мы сделали бы сами — наша цель — быть надежным другом для родителей.
Мы стараемся изо всех сил, но не можем гарантировать совершенство. Мы всегда будем стремиться предоставить вам точную информацию на дату публикации, однако информация может меняться, поэтому важно, чтобы вы провели собственное исследование, перепроверили и приняли решение, подходящее для вашей семьи.
Kidadl вдохновляет детей развлекать и обучать их. Мы понимаем, что не все виды деятельности и идеи подходят и подходят для всех детей и семей или во всех обстоятельствах. Наши рекомендуемые занятия основаны на возрасте, но это ориентир. Мы рекомендуем использовать эти идеи в качестве вдохновения, чтобы идеи воплощались в жизнь под надлежащим наблюдением взрослых, и чтобы каждый взрослый использовал свое собственное усмотрение и знания своих детей для рассмотрения безопасности и пригодности.
Kidadl не может взять на себя ответственность за реализацию этих идей, поэтому рекомендуется постоянно находиться под присмотром родителей, так как безопасность превыше всего. Любой, кто использует информацию, предоставленную Kidadl, делает это на свой страх и риск, и мы не несем ответственности, если что-то пойдет не так.
Политика в отношении спонсорства и рекламы
Kidadl является независимой организацией, и чтобы сделать наши услуги бесплатными для вас, читатель, мы поддерживаем рекламу.
Надеемся, вам понравились наши рекомендации по продуктам и услугам! То, что мы предлагаем, выбирается независимо командой Kidadl. Если вы совершаете покупку с помощью кнопки «Купить сейчас», мы можем получить небольшую комиссию. Это не влияет на наш выбор. Обратите внимание: цены указаны правильно, а товары есть в наличии на момент публикации статьи.
У Kidadl есть ряд партнеров, с которыми мы работаем, включая Amazon. Обратите внимание, что Kidadl является участником партнерской программы Amazon Services LLC, партнерской рекламной программы, предназначенной для предоставления сайтам средств для получения платы за рекламу за счет рекламы и ссылок на Amazon.
Мы также ссылаемся на другие веб-сайты, но не несем ответственности за их содержание.
Ознакомьтесь с нашей Политикой в отношении спонсорства и рекламы
Поделитесь этой статьей с друзьями и семьей
- фейсбук
- твиттер
- связан в
- реддит
- скопируй ссылку
- электронная почта
- еще
Мы пришлем вам кучу вдохновения, чтобы помочь вам найти скрытую жемчужину в вашем районе или спланировать большой день.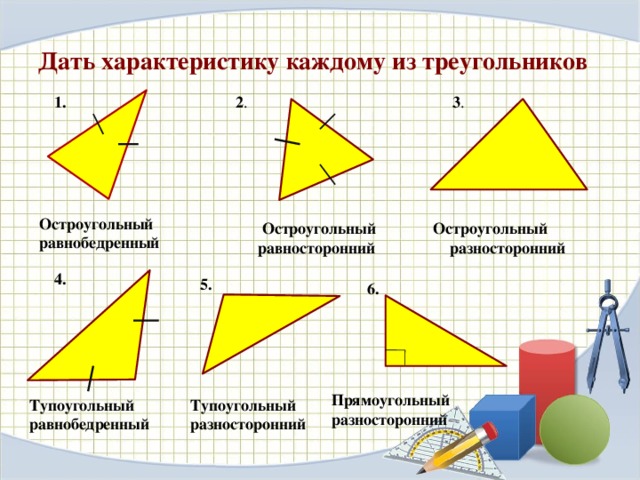

 Места пересечения будут обозначены как D и F.
Места пересечения будут обозначены как D и F.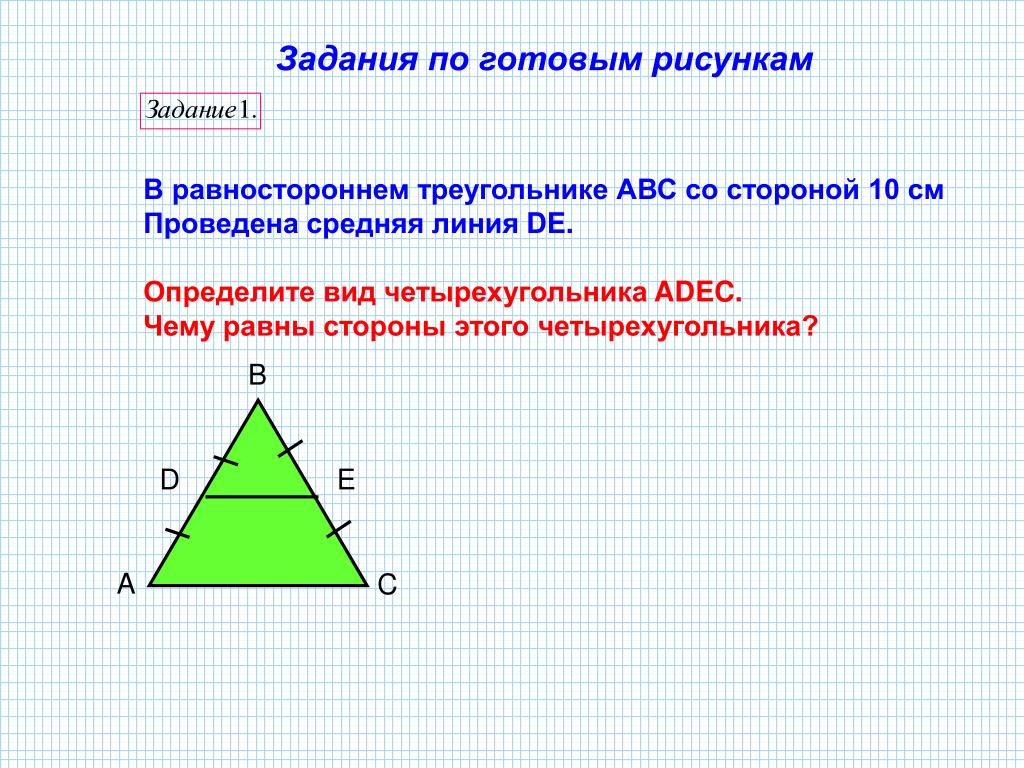
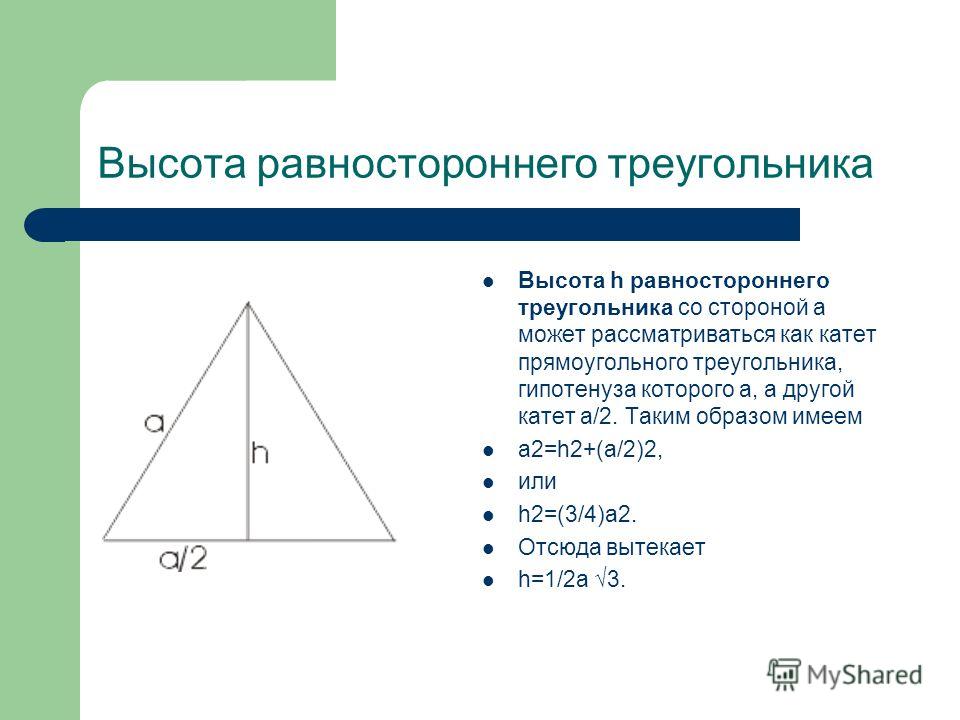 Обозначаем его буквами АС.
Обозначаем его буквами АС.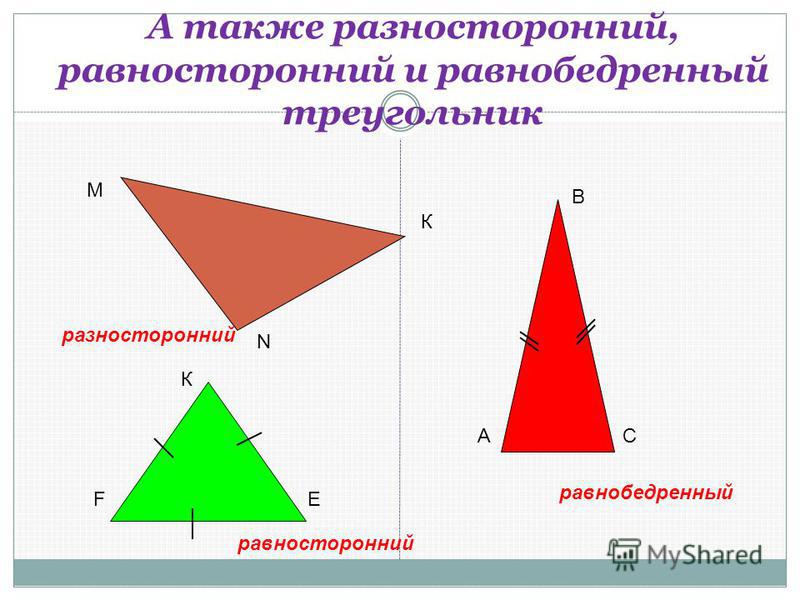 Соедините полученные точки. У нас получился искомый треугольник.
Соедините полученные точки. У нас получился искомый треугольник. Их называют боковыми. Третья – это основание;
Их называют боковыми. Третья – это основание; Две стороны длиннее, чем оставшаяся сторона.
Две стороны длиннее, чем оставшаяся сторона.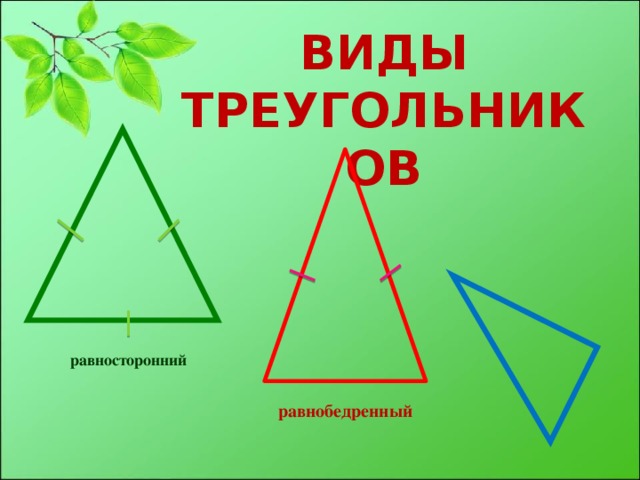 э. и являются совершенно равносторонними.
э. и являются совершенно равносторонними.
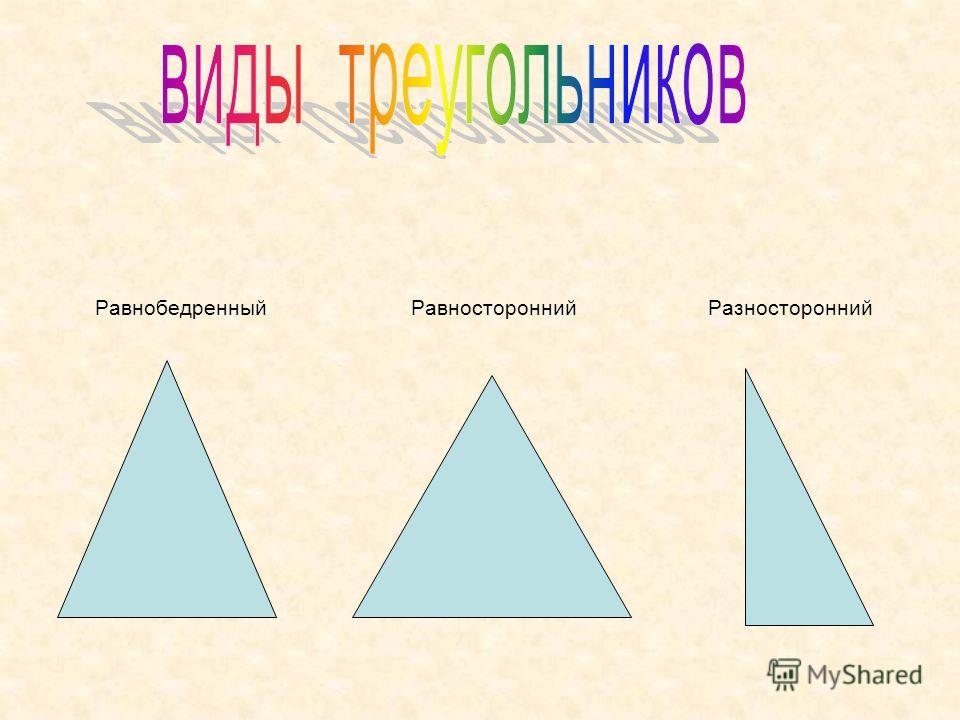
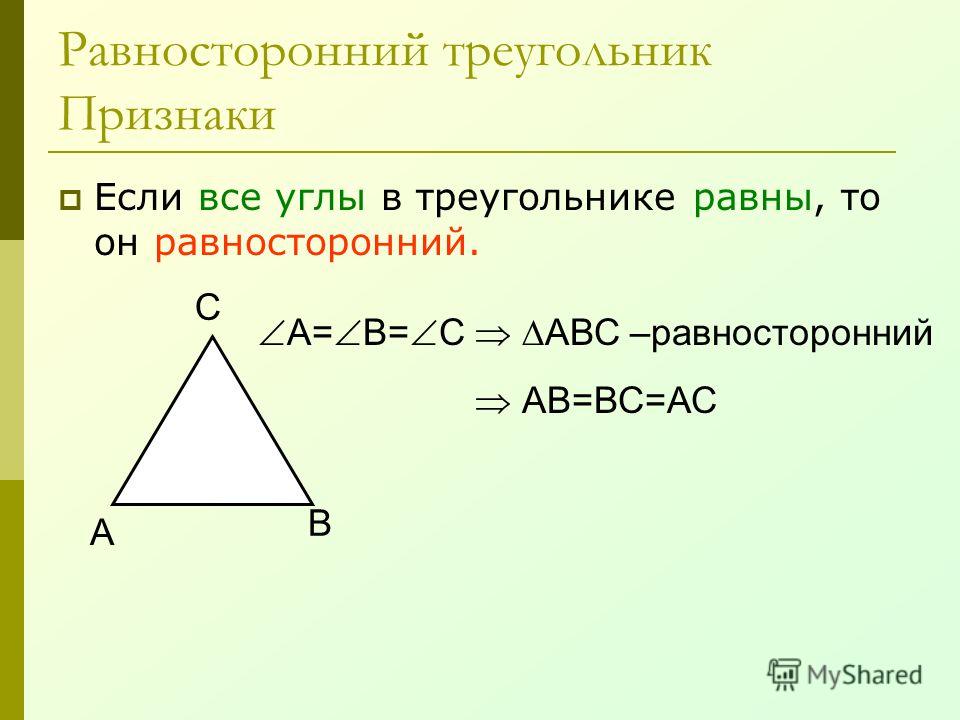 . [Euclid’s Elements , как переведено Томасом Хитом]
. [Euclid’s Elements , как переведено Томасом Хитом] com
com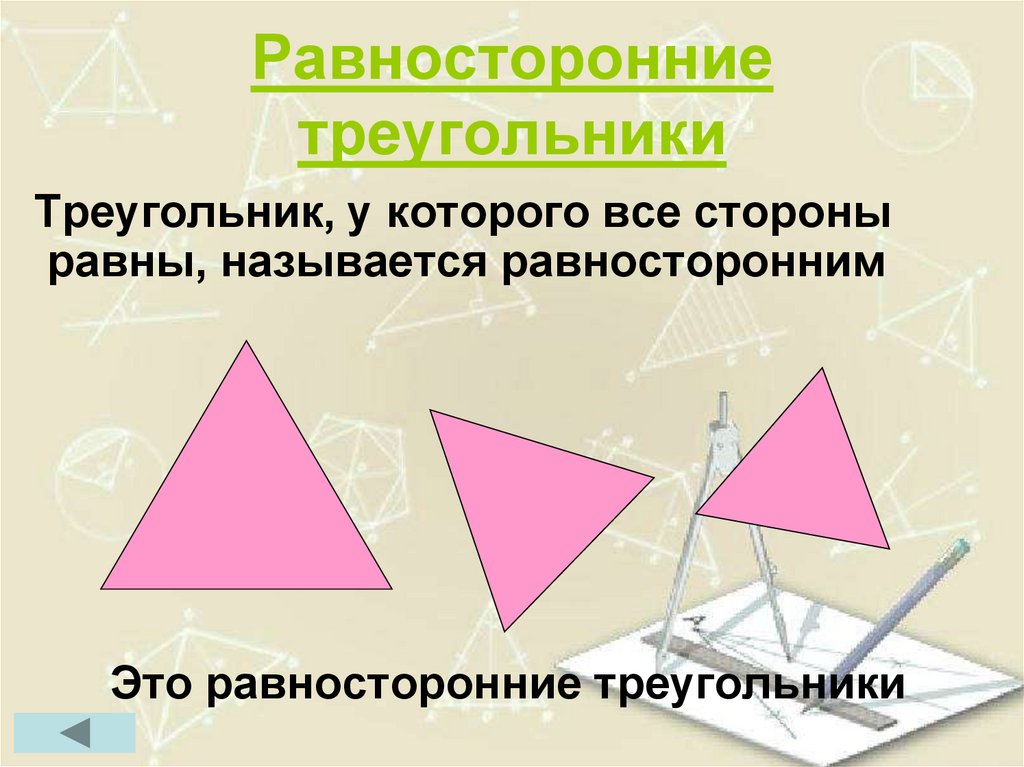 Как выглядит равносторонний треугольник [Решено]0064 3
Как выглядит равносторонний треугольник [Решено]0064 3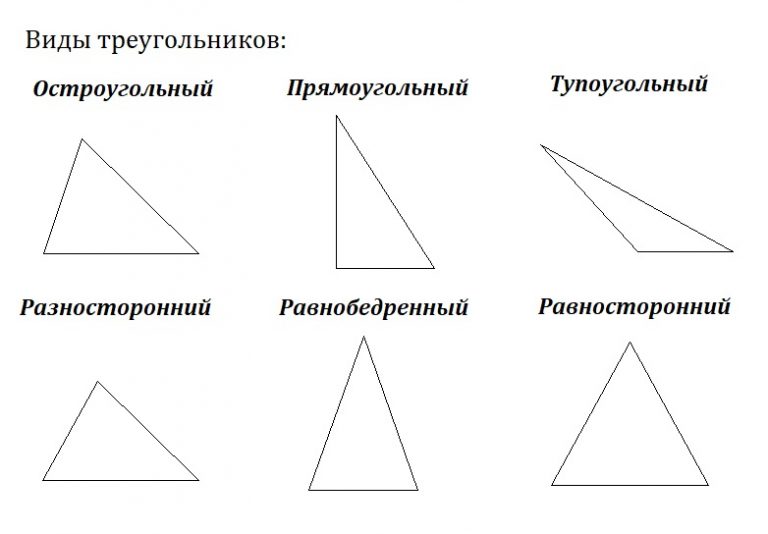 com
com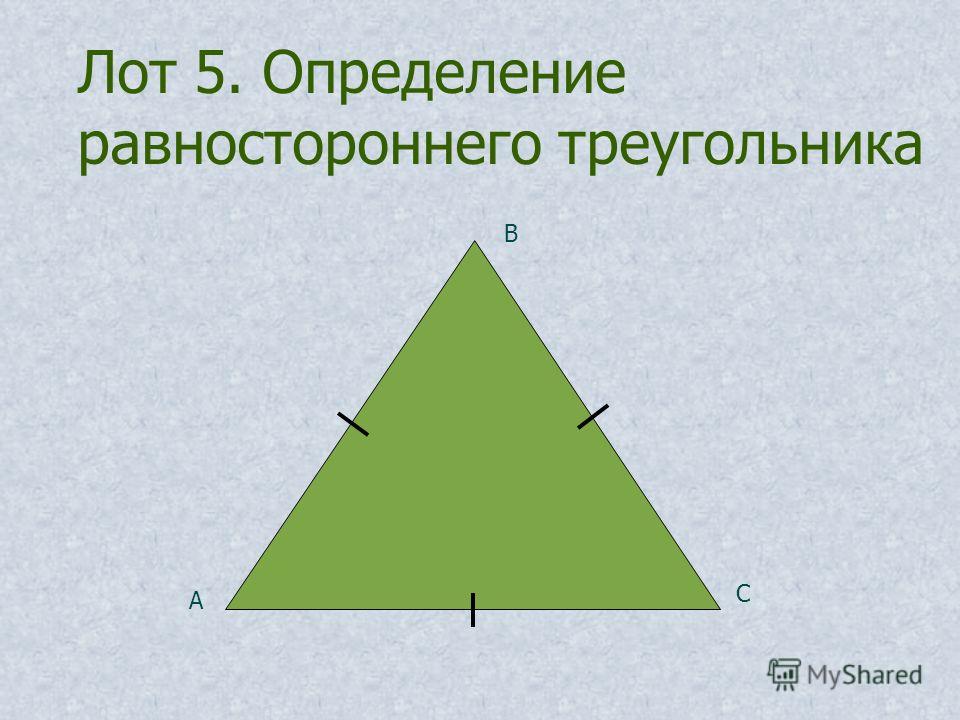 com
com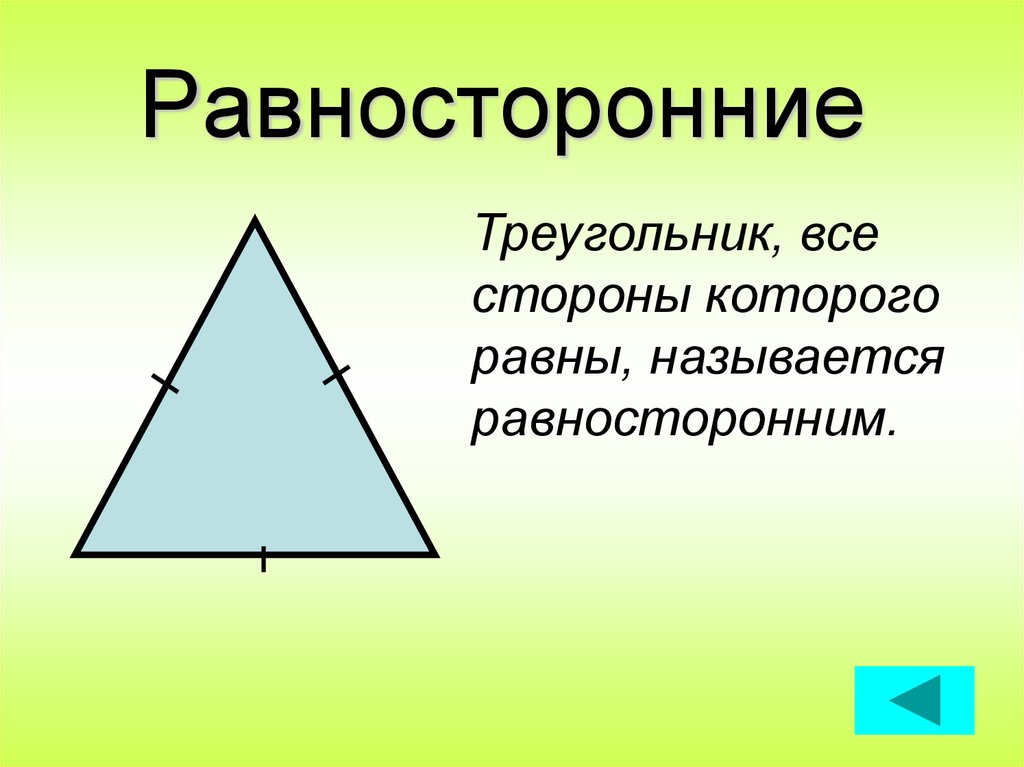 е. линии, которые делят его на идеальные половины. Каждая точка симметрии расположена в середине каждой стороны. Линия проходит от вершины треугольника до середины противоположной стороны.
е. линии, которые делят его на идеальные половины. Каждая точка симметрии расположена в середине каждой стороны. Линия проходит от вершины треугольника до середины противоположной стороны. Если да, то у вас получился равносторонний треугольник!
Если да, то у вас получился равносторонний треугольник!
 2).
2).