Распределение эквивалентных пар случайным образом это: Объект психологического исследования. — КиберПедия

alexxlab / / Разное

Тема 3.

1.Определите, о каком компоненте исследования идет речь: «Особенности агрессивного поведения подростка»

  1. +Предмет исследования

  2. + Объект исследования

2. Определите вид следующей гипотезы: «Существуют различия в стилях управления мужчин и женщин» +Корреляционная гипотеза

3. Какой вид гипотезы изучает причинно-следственные связи между явлениями

  1. +Каузальная гипотеза

4.Определить вид гипотезы: «При введении легких физических нагрузок, работоспособность нервной системы обучающихся повышается»

3. +Каузальная гипотеза

5. Сущностью экспериментальной гипотезы являет­ся:

+б) система научных догадок, основанная на кос­венных эмпирических и теоретических сведениях;

6

. К целям психологического исследования не принадлежит:

+3.Проведение эксперимента

7. Выделите цели психологического исследования

  1. +Определение психологических характеристик конкретных явлений

  2. +Выявление взаимосвязи между психологическими явлениями

8. Определите вид следующей гипотезы: «Существует взаимосвязь между поло-возрастными характеристиками и уровнем развития чувства ответственности»

  1. +Корреляционная гипотеза

9. Определите, о каком компоненте исследования идет речь: «Проведение эксперимента» +Этап исследовательской работы

10. Теоретический или фактический вопрос, требующий разрешения. +Проблема

11. Постановка научной проблемы предполагает определенную последовательность действий:

  1. +Обнаружение дефицита информации.

  2. +Осознание потребности в устранении этого дефицита.

  3. +Описание (вербализация) проблемной ситуации на естественном языке.

  4. +Формулирование проблемы в научных категориях и терминах.

  5. Формулирование объекта и предмета

12. Выделите цели психологического исследования

  1. +Адаптация новых методик

  2. +Установление причинной зависимости между переменными

1.Естественное множество индивидов, обладающих определенным набором свойств, потенциальные участники исследования, часть генеральной совокупности. +Популяция

2. Множество испытуемых, выбранных для участия в исследовании с помощью определенной процедуры (чаще — рандомизации) из генеральной совокупности

  1. +Выборка

  2. +Респондент

3. Число испытуемых, включенных в выборочную совокупность. +Объем выборки

4. К какому типу выборки испытуемых относится «Выборка испытуемых, исследуемые характеристики которой идентичны экспериментальной выборке»?

  1. +Контрольная выборка

  2. +Эквивалентная выборка

5. Требования к выборке

  1. +Репрезентативность

  2. +Адекватность

6. Стратегии

формирования выборки

  1. +Рандомизация

  2. +Попарный отбор

  3. +Стратометрический отбор

  4. +Привлечение реальных групп

7. Факторы, нарушающие внутреннюю валидность выборки

1. + Селекция

2. + Статистическая регрессия

3. + Естественное развитие

8. Стратегия случайного отбора или распределения испытуемых, при кото­рой все субъекты имеют равные шансы попасть в группу называется +Рандомизация

9. Соответствие свойств исследуемой выборки свойствам генеральной совокупности называется +Репрезентативность выборки

10. К какому типу выборки испытуемых относится следующее суждение: «Выборка испытуемых, на кото­рую направлено экспериментальное воздействие»?

+б) экспериментальная выборка;

11. К какому типу выборки испытуемых относится следующее суждение: «Выборка испытуемых, на кото­рую не направлено воздействие независимой перемен­ной»?

+в) контрольная выборка;

12. К какому типу выборки испытуемых относится следующее суждение: «Выборка испытуемых, отра­жающая качественные и количественные характери­стики генеральной совокупности»? +а) репрезентативная выборка;

12.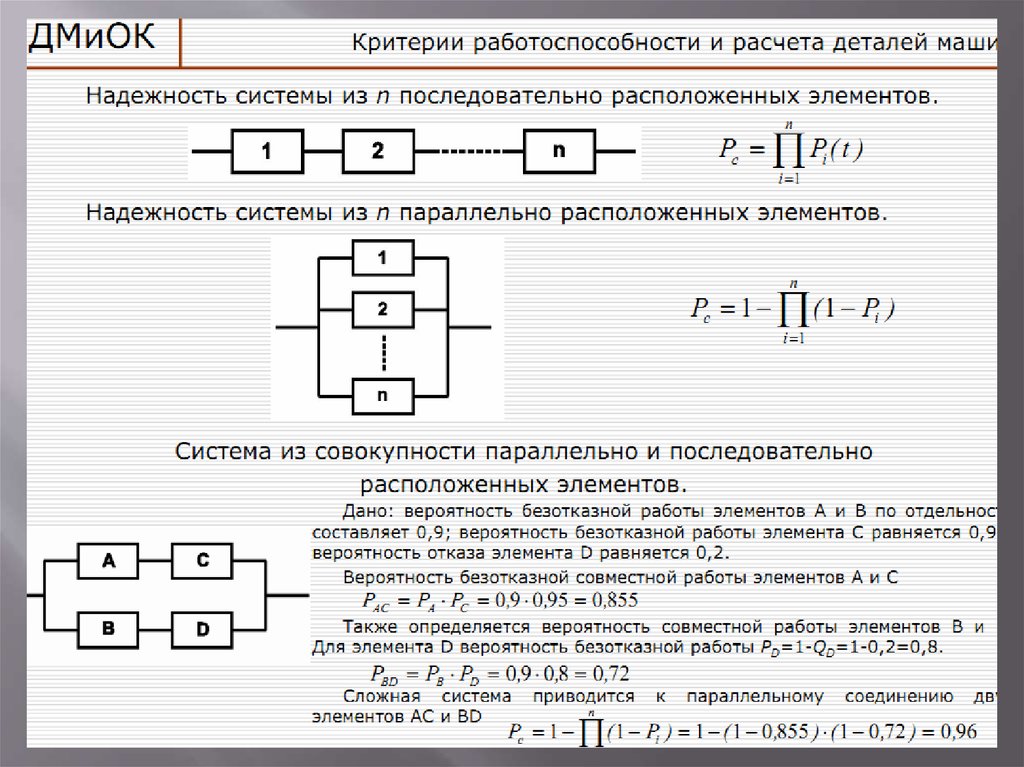 Выявите номер определения, который адекватно бы соответствовал стратегиям формирования экспери­ментальной и контрольной выборок испытуемых:

Стратегии форми­рования выборки:

Определение стратегий:

а) рандомизация;

б) попарный отбор;

в) попарный отбор с последующей рандомизацией;

г) стратометрический отбор;

д) приближенное моделирование вы­борки;

е) репрезентатив­ное моделирование выборки;

ж) привлечение реальных групп;

з) привлечение добровольцев или принудительное участие.

1) распределение эквивалент­ных пар;

2) соответствие структуры выборки структуре популя­ции;

3) случайным образом из раз­личных социальных страт формируется выборка;

4) распределение случайным образом;

5) смещение выборки при ис­пользовании добровольцев или принуждение к участию;

6) привлечение реальных кол­лективов;

7) распределение эквивалент­ных пар случайным образом;

8) приближенная представленность в выборке.

Ответ:

А- 4

Б – 1

В — 7

Г – 3

Д – 8

Е – 2

Ж – 6

З – 5

13. Способ привлечения испытуемых, позволяющий обеспечить представленность изучаемой популяции. + Отбор

14. Контингент потенциальных испытуемых, объединенных общей возрастной, профессиональной или другой принадлежностью, изучаемой в экспериментальном исследовании .+ популяция

15. Система случайного выбора испытуемых для участия в эксперименте . +Рандомизация

16. Способ организации экспериментальных групп из имеющихся в наличии испытуемых. +Распределение испытуемых

17. Степень адекватности отражения свойств и характеристик изучаемой популяции в выборке испытуемых, привлеченных для эксперимента. . +Репрезентативность выборки

18. Эксперимент с одним испытуемым проводится:

  1. + индивидуальными различиями можно пренебречь, исследование чрезвычайно велико по объему и включает множество экспериментальных проб;

  2. + испытуемый — уникальный объект;

  3. + от испытуемого требуется особая компетентность при проведении исследования;

  4. + повторение данного эксперимента с уча­стием других испытуемых невозможно;

19. Наилучшая внешняя и внутренняя валидность достигается при :

1. +Стратегии подбора эквивалентных пар

2. +Стратометрической рандомизации

20. Достаточное количество испытуемых для проведения эксперимента

1. +Адекватность выборки

21. Рандомизация — + Случайный подбор испытуемых

Объект психологического исследования. — КиберПедия

Навигация:

Главная Случайная страница Обратная связь ТОП Интересно знать Избранные

Топ:

Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования…

Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного…

Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь…

Интересное:

Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным…

Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является. ..

Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории…

Дисциплины:

Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

⇐ ПредыдущаяСтр 3 из 5Следующая ⇒

Экспериментальная выборка

Психологические аспекты экспериментальной выборки представляют собой объект исследования.

В качестве выборки может выступать один человек или группа испытуемых. Одиночный испытуемый в качестве объекта экспериментального воздействия используется в ситуациях, во-первых, когда индивидуальными различиями можно пренебречь или исследование велико по объему и требуется множество экспериментальных проб (типичный представитель). Во-вторых, когда испытуемый является уникальным объектом (талантливый музыкант, художник, писатель, уникальный больной). В-третьих, когда от испытуемого требуется особая компетентность (специальная обученность, профессиональное мастерство). В-четвертых, когда повторение данного эксперимента с участием других испытуемых невозможно.

Экспериментальная группа может комплектоваться по следующим схемам:

а) схема формирования экспериментальной и контрольной групп, которые распределяются по различным режимам эксперимента;

б) схема исследования одной группы в экспериментальном и контрольном режимах;

в) схема «парного дизайна», когда по итогам предварительного тестирования подбираются эквивалентные пары испытуемых с последующим распределением по режимам эксперимента;

г) «смешанная» схема, когда все группы распределяются по различным режимам эксперимента, то есть проверяется влияние независимой переменной на зависимую переменную в различных условиях.

Среди критериев формирования экспериментальной выборки наиболее значимыми являются: содержательный, эквивалентности и репрезентативности.

1. Содержательный критерий (критерий операционной валидности).

Выборка должна соответствовать содержанию гипотезы. Например, обучаемость обычно исследуется на учениках школы или студентах вуза, дисциплинированность изучается на экспериментальной выборке военнослужащих и т.д.

2. Критерий эквивалентности испытуемых (критерий внутренней валидности).

Результаты выборки должны распространяться на каждого члена выборки, то есть, необходимо учитывать все значимые характеристики объекта исследования, различия выраженности которых могут значительно повлиять на зависимую переменную.

Например, при исследовании «тревожности» в ходе обучения необходимо подбирать группу примерно с равными интеллектуальными характеристиками (по IQ-тестам).

3. Критерий репрезентативности (критерий внешней валидности).

Выборка должна представлять генеральную совокупность качественно (по возрасту, полу, образованию, социально-демографическим характеристикам и т. д.) и количественно.

При формировании выборки используются следующие стратегии:

1. Рандомизация представляет собой распределение испытуемых по группам случайным образом. Впервые эту стратегию использовал в своих исследованиях Р.Фишер.

2. Парный отбор — составление эквивалентных пар и распределение их по разным группам исследователем.

3. Парный отбор с последующей рандомизацией — это составление эквивалентных пар и распределение их случайным образом по группам и режимам эксперимента. Кэмпбелл указывал, что это наиболее предпочтительный способ формирования экспериментальной выборки.

4. Стратометрический отбор представляет собой формирования групп при помощи рандомизации из различных социальных страт.

5. Приближенное моделирование экспериментальных групп есть приблизительная представленность в выборке характеристик популяции.

6. Репрезентативное моделирование применяется в форме конструирования структуры выборки в соответствии со структурой реальной популяции.

7. Привлечение реальных групп для проведения эксперимента производится, когда конструирование выборки осложнено организационно. В данных условиях в качестве экспериментальной и контрольной групп используются реальные социальные совокупности.

8. Привлечение добровольцев и принудительное участие испытуемых в качестве объектов эксперимента имеют ряд недостатков, которые «смещают выборку». В первом случае добровольно стремятся к участию в психологическом эксперименте люди, обладающие определенными «специфическими» характерологическими особенностями. Во втором — в ходе эксперимента имеет место «специфический» эмоциональный фон. И тот и другой варианты могут стать причиной артефактов.

⇐ Предыдущая12345Следующая ⇒

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой…

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства. ..

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций…

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни…



python — перетасовка с ограничениями на пары

Задай вопрос

спросил

Изменено 3 года, 11 месяцев назад

Просмотрено 287 раз

У меня есть n списков, каждый из которых имеет длину м . предположим, что н*м четно. я хочу получить случайно перетасованный список со всеми элементами при условии, что элементы в местах i,i+1 , где i=0,2,. ..,n*m-2 , никогда не происходят из одного и того же список. редактировать: кроме этого ограничения, я не хочу смещать распределение случайных списков. то есть решение должно быть эквивалентно полному случайному выбору, который перетасовывается до тех пор, пока ограничение не будет выполнено.

пример:

список1: a1,a2

список2: b1,b2

список3: c1,c2

разрешено: b1,c1,c2,a2,a1,b2

запрещено: b1,c1,c2,b2,a1,a2

  • 8 python

    перемешивание

3

Возможное решение состоит в том, чтобы думать о наборе чисел как о n кусках элемента, каждый из которых имеет длину m. Если вы случайным образом выберете для каждого чанка ровно один элемент из каждого списка, то вы никогда не зайдёте в тупик. Просто убедитесь, что первый элемент в каждом фрагменте (кроме первого фрагмента) будет из другого списка, чем последний элемент предыдущего фрагмента.

Вы также можете повторно рандомизировать числа, всегда убедившись, что вы выбираете из списка, отличного от предыдущего числа, но тогда вы можете зайти в тупик.

Наконец, еще одно возможное решение — рандомизировать число на каждой позиции последовательно, но только из тех, которые «можно туда поставить», то есть если поставить число, то ни одно из ограничений не будет нарушено, т. е. вы будет иметь по крайней мере возможное решение.

2

Разновидность вышеприведенного варианта b, позволяющая избежать тупиков: на каждом шаге вы выбираете дважды. Во-первых, случайным образом выбрал предмет. Во-вторых, случайным образом выберите, где его разместить. На K-м шаге есть k дополнительных мест для размещения предмета (новый предмет можно вставить между двумя существующими предметами). Естественно, вы выбираете только из разрешенных мест. Деньги!

6

  1. упорядочить списки в список списков
  2. сохранить каждый элемент в списке как кортеж с индексом списка в списке списков
  3. петля п*м раз
  4. при четных поворотах — свести в один список и просто рандомно вытащить — получить элемент и группу элементов
  5. при нечетных ходах — временно удалить последнюю группу предметов и вытолкнуть как раньше — в конце добавить удаленную группу обратно

важно — как избежать взаимоблокировок?

тупиковая ситуация может возникнуть, если все оставшиеся элементы принадлежат только одной группе.
чтобы избежать этого, проверяйте на каждой итерации длины всех списков
и проверяйте, длиннее ли самый длинный список, чем сумма всех остальных .
если правда — потяните за этот список

таким образом вы никогда не останетесь только с одним полным списком

вот суть с попыткой решить это в питоне https://gist.github.com/YontiLevin/bd32815a0ec62b920bed214921a96c9d

0

Очень быстрый и простой метод, который я пробую:

 случайное перемешивание
цикл по парам в списке:
   если пара плохая:
   цикл по парам в списке:
      если оба элемента новой пары отличаются от плохой пары:
         поменять местами вторые элементы
         сломать

всегда ли это найдет решение? будут ли решения иметь то же распределение, что и наивная перетасовка, пока не будет найдено законное решение?

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

python — Создать случайный порядок пар (x, y) без повторения/последующего x

Скажем, у меня есть список действительных X = [1, 2, 3, 4, 5] и список действительных Y = [1, 2, 3, 4, 5] .

Мне нужно сгенерировать все комбинации каждого элемента в X и каждого элемента в Y (в данном случае 25) и получить эти комбинации в случайном порядке.

Само по себе это было бы просто, но есть дополнительное требование: в этом случайном порядке не может быть повторения одних и тех же x подряд. Например, это нормально:

 [1, 3]
[2, 5]
[1, 2]
...
[1, 4]

Это не:

 [1, 3]
[1, 2] <== "1" не может повториться, потому что он уже был раньше
[2, 5]
...
[1, 4]

Наименее эффективной идеей было бы просто рандомизировать полный набор до тех пор, пока не будет больше повторений. Мой подход был немного другим: я неоднократно создавал перетасованный вариант X и список всех Y * X , а затем выбирал случайный следующий из них. До сих пор я придумал это:

 import random
вывод = []
число_х = 5
число_у = 5
all_ys = список (xrange (1, num_y + 1)) * num_x
пока верно:
    # конец, если больше нет доступных
    если len(выход) == num_x * num_y:
        сломать
    xs = список (xrange (1, num_x + 1))
    в то время как лен(хз):
        следующий_x = случайный. выбор(xs)
        следующий_y = случайный.выбор(all_ys)
        если [next_x, next_y] не выводится:
            хз.удалить(следующий_х)
            all_ys.remove (следующий_y)
            output.append([next_x, next_y])
печать (отсортировано (вывод))

Но я уверен, что это можно сделать еще более эффективно или более лаконично?

Кроме того, мое решение сначала проходит через все значения X , прежде чем снова перейти к полному набору, который не является совершенно случайным . Я могу жить с этим для моего конкретного случая применения.

  • питон

15

Простое решение для обеспечения средней сложности O(N*M) :

 определение псевдослучайного (M, N):
    l=[(x+1,y+1) для x в диапазоне (N) для y в диапазоне (M)]
    случайный.перетасовка(l)
    для я в диапазоне (M * N-1):
            для j в диапазоне (i+1,M*N): # найти совместимый ...
                если l[i][0] != l[j][0]:
                    l[i+1],l[j] = l[j],l[i+1]
                    сломать
            else: # или вставьте иначе. 
                пока верно:
                    л[я],л[я-1] = л[я-1],л[я]
                    я-=1
                    если l[i][0] != l[i-1][0]: сломать
    вернуть л

Некоторые тесты:

 В [354]: print(псевдослучайный(5,5))
[(2, 2), (3, 1), (5, 1), (1, 1), (3, 2), (1, 2), (3, 5), (1, 5), ( 5, 4),\
(1, 3), (5, 2), (3, 4), (5, 3), (4, 5), (5, 5), (1, 4), (2, 5), (4) , 4), (2, 4),\
(4, 2), (2, 1), (4, 3), (2, 3), (4, 1), (3, 3)]
В [355]: %timeit псевдослучайный(100,100)
10 циклов, лучший из 3: 41,3 мс на цикл

2

Вот мое решение. Сначала выбираются кортежи среди тех, у которых значение x отличается от предыдущего выбранного кортежа. Но я заметил, что вы должны подготовить последний трюк для случая, когда у вас есть только кортежи с плохими значениями для размещения в конце.

 случайный импорт
число_х = 5
число_у = 5
all_ys = диапазон (1, num_y+1)*num_x
all_xs = отсортировано (диапазон (1, num_x + 1) * num_y)
вывод = []
последний_х = -1
для я в диапазоне (0, num_x * num_y):
    #получить список возможных кортежей для размещения
    all_ind = диапазон (0, длина (all_xs))
    all_ind_ok = [k вместо k в all_ind, если all_xs[k]!=last_x]
    ind = случайный. выбор(all_ind_ok)
    last_x = all_xs[ind]
    output.append([all_xs.pop(ind),all_ys.pop(ind)])
    if(all_xs.count(last_x)==len(all_xs)):#если только кортежи last_x,
        сломать
if len(all_xs)>0: # если есть еще кортежи, они размещаются случайным образом
    nb_to_place = len(all_xs)
    в то время как (длина (all_xs)> 0):
        место = random.randint(0,len(выход)-1)
        если вывод[место]==last_x:
            Продолжить
        если место>0:
            если вывод [место-1] == last_x:
                Продолжить
        output.insert (место, [all_xs.pop(), all_ys.pop()])
вывод на печать

4

Вот решение с использованием NumPy

 def generate_pairs(xs, ys):
    n = длина (xs)
    м = лен(г)
    индексы = np.arange(n)
    массив = np.tile (ys, (n, 1))
    [np.random.shuffle (массив [i]) для i в диапазоне (n)]
    количество = np.full_like (xs, m)
    я = -1
    для _ в диапазоне (n * m):
        веса = np. array (количество, dtype = float)
        если я != -1:
            веса [я] = 0
        веса /= np.sum (веса)
        i = np.random.choice(индексы, p=веса)
        количество [я] -= 1
        пара = xs[i], массив[i, количество[i]]
        доходная пара
 92 м)  
 
 Но время выполнения является детерминированным, а накладные расходы невелики. И я почти уверен, что он генерирует все правовые последовательности с равной вероятностью. 
 
 Интересный вопрос! Вот мое решение. Он имеет следующие свойства: 
 
     
  •  Если нет правильного решения, он должен обнаружить это и сообщить вам 
    • 
 
  •  Итерация гарантированно завершится, поэтому она никогда не застрянет в бесконечном цикле 
    • 
 
  •  Любое возможное решение достижимо с ненулевой вероятностью 
    • 
 
 
 Распределение вывода по всем возможным решениям я не знаю, но думаю, что оно должно быть равномерным, так как в алгоритме нет явной асимметрии. Я был бы удивлен и рад, если бы мне показали обратное! 
 
 случайный импорт
def random_without_repeats (xs, ys):
    пары = [[x,y] для x в xs для y в ys]
    вывод = [[объект()], [объект()]]
    видел = установить ()
    пока пары:
        # выбираем случайную пару из оставшихся
        индексы = список (набор (xrange (длина (пары))) - просмотрено)
        пытаться:
            индекс = случайный.  выбор (индексы)
        кроме IndexError:
            поднять исключение («Нет допустимого решения!»)
        # первый элемент нашей случайно выбранной пары
        х = пары [индекс] [0]
        # ищем допустимое место в выводе, куда мы его вставляем
        для i в xrange (len (выход) - 1):
            слева, справа = выход[i], выход[i+1]
            если x != left[0] и x != right[0]:
                output.insert (я + 1, пары.поп (индекс))
                видел = установить ()
                сломать
        еще:
            # убедитесь, что мы случайно не выбрали такую ​​плохую пару снова
            замечено |= {i для i в индексах if pairs[i][0] == x}
    # обрезаем часовых
    вывод = вывод[1:-1]
    утверждать len(выход) == len(xs) * len(ys)
    утверждать не любой (L == R для L, R в zip (выход [:-1], вывод [1:]))
    возвратный вывод
nx, ny = 5, 5 # Пример ОП
# nx, ny = 2, 10 # вывод должен чередоваться в 1-м индексе
# nx, ny = 4, 13 # перетасовать "колоду карт" без повторяющейся масти
# nx, ny = 1, 5 # должно подняться "Нет допустимого решения!" исключение
xs = диапазон (1, nx+1)
ys = диапазон (1, ny + 1)
для пары в random_without_repeats(xs, ys):
    печатная пара
 
 11
 Это должно делать то, что вы хотите.
  random  никогда не будет генерировать один и тот же X дважды подряд, но я понял, что  возможно  (хотя кажется маловероятным, поскольку я никогда не замечал, чтобы это происходило примерно 10 раз, когда я запускал без дополнительной проверки) что из-за потенциального отбрасывания повторяющихся пар это может произойти с предыдущим X. О! Но я думаю, что понял это ... обновлю свой ответ через мгновение.
 случайный импорт
Х = [1,2,3,4,5]
Y = [1,2,3,4,5]
Def rando (выбор_один, выбор_два):
    last_x = случайный.выбор(выбор_один)
    пока верно:
        выход last_x, random.choice(choice_two)
        возможно_x = выбор_один[:]
        возможно_x.удалить (последний_x)
        last_x = random.choice(possible_x)
all_pairs = набор (itertools.product (X, Y))
результат = []
г = случайный (X, Y)
в то время как набор (результат) != all_pairs:
    пара = следующая (г)
    если пара не в результате:
        если результат и результат[-1][0] == пара[0]:
            Продолжить
        результат. добавить(пара)
импорт pprint
pprint.pprint(результат)
 
 2
 Для полноты картины я добавлю супер-наивное решение "просто перетасовывай, пока не получишь". Не гарантируется, что он завершится, но если это произойдет, он будет иметь хорошую степень случайности, и вы сказали, что одним из желаемых качеств является лаконичность, и это точно лаконичность:
 import itertools
импортировать случайный
x = range(5) # это список в Python 2
у = диапазон (5)
all_pairs = список (itertools.product (x, y))
s = list(all_pairs) # делаем рабочую копию
в то время как any(s[i][0] == s[i + 1][0] для i в диапазоне (len(s) - 1)):
    случайное перемешивание(я)
печать с
 
 Как было отмечено, для небольших значений  x  и  y  (особенно  y  !), это на самом деле достаточно быстрое решение. Ваш пример из 5 для каждого завершается в среднем за время «сразу». Пример колоды карт (4 и 13) может занять гораздо больше времени, потому что обычно требуется сотни тысяч тасовок. (И опять же,  не гарантирует, что  вообще завершится.)
 5
 Равномерно распределите значения  x  (каждое значение по 5 раз) по выходным данным:
 import random
def random_combo_without_x_repeats (xvals, yvals):
    # произвести все допустимые комбинации, но сгруппировать по `x` и перетасовать `y`
    grouped = [[x, random.sample(yvals, len(yvals))] для x в xvals]
    last_x = object() # часовой не равен чему-либо
    while grouped[0][1]: # еще осталось `y`
        для _ в диапазоне (len (xvals)):
            # перетасовать `x, но пропустить любой порядок, который
            # производить последовательные `x`.
            random.shuffle(сгруппировано)
            если сгруппировано[0][0] != last_x:
                сломать
        еще:
            # мы пытались перетасовать N раз, но получили одно и то же значение `x`
            # в первой позиции каждый раз. Это довольно маловероятно, но
            # если это произойдет, мы спасаемся и просто меняем порядок.  Это
            # более чем достаточно.
            сгруппировано = сгруппировано[::-1]
        # получить набор пар (x, y) для каждого уникального x
        # Выберите один y (из предварительно перетасованных групп по x
        для x, ys в группе:
            выход x, ys.pop()
        последний_х = х
 
 Сначала перемешиваются значения  y  на  x , а затем выдается комбинация  и   x, y  на каждые  x  . Порядок, в котором выдаются  x  s, перемешивается на каждой итерации, где вы проверяете ограничение.
 Это случайное число, но вы получите все числа от 1 до 5 в позиции  x , прежде чем снова увидите то же число:
 >>> list(random_combo_without_x_repeats(range(1, 6), range (1, 6)))
[(2, 1), (3, 2), (1, 5), (5, 1), (4, 1),
 (2, 4), (3, 1), (4, 3), (5, 5), (1, 4),
 (5, 2), (1, 1), (3, 3), (4, 4), (2, 5),
 (3, 5), (2, 3), (4, 2), (1, 2), (5, 4),
 (2, 2), (3, 4), (1, 3), (4, 5), (5, 3)]
 
 (я вручную сгруппировал их в наборы по 5 штук).  В целом  , это обеспечивает довольно хорошую случайную перетасовку фиксированного входного набора с вашим ограничением.
 Это тоже эффективно; поскольку вероятность того, что вам придется перетасовывать порядок  x , составляет всего 1 из  N , вы должны увидеть, что в среднем происходит только одна перетасовка во время полного запуска алгоритма. Таким образом, весь алгоритм остается в пределах O(N*M), что в значительной степени идеально подходит для чего-то, что производит  N  раз  M  элементов вывода. Поскольку мы ограничиваем перетасовку максимум N раз, прежде чем вернуться к простому реверсу, мы избегаем (крайне маловероятной) возможности бесконечной перетасовки.
 Единственным недостатком является то, что он должен создать  N  копий  M  значений y заранее.
 2
 Вот эволюционный алгоритм. Сначала он создает список, в котором элементы 9Каждый из 0013 X  повторяется  len(Y)  раз, а затем он случайным образом заполняет каждый элемент  Y  len(X) раз. Полученные заказы кажутся довольно случайными:
 import random
#следующие меры фитнес-функции
#количество раз, когда
#последовательные элементы в списке
#равны
определение числа повторений (x):
    п = длина (х)
    если n < 2: вернуть 0
    повторы = 0
    для я в диапазоне (n-1):
        если x[i] == x[i+1]: повторы += 1
    возвращение повторяется
деф мутировать (xs):
    #меняет местами случайные пары элементов
    # возвращает новый список
    #выбирается один из двух индексов так, что
    #это в повторяющейся паре
    #и замененный элемент отличается
    n = длина (xs)
    Repeats = [i для i в диапазоне (n), если (i > 0 и xs[i] == xs[i-1]) или (i   Останавливается, когда найдено идеальное решение
    Предполагается, что #popsize кратен 10
    население = []
    для i в диапазоне (popSize):
        колода = xs[:]
        random.shuffle(колода)
        пригодность = количество повторений (колода)
        если пригодность == 0: вернуть колоду
        населения.append((фитнес,колода))
    для i в диапазоне (numGens):
        населения.sort (ключ = (лямбда р: р [0]))
        новыйПоп = []
        для i в диапазоне (popSize//10):
            подходит, колода = население [я]
            newPop.append((подходит,колода))
            для j в диапазоне (9):
                newDeck = мутировать (колода)
                пригодность = количество повторений (новая колода)
                если пригодность == 0: вернуть newDeck
                newPop.append((фитнес,новая колода))
        население = новое население
    #если вы доберетесь сюда :
    return [] #специального перемешивания не найдено
#следующая функция принимает список x
#с n различными элементами (n>1) и целым числом k
#и возвращает случайный список длины nk
#где последовательные элементы не совпадают
def specialShuffle(x,k):
    п = длина (х)
    если п == 2:
        если random. random() <0,5:
            а, б = х
        еще:
            б, а = х
        вернуть [а, б] * к
    еще:
        колода = х*к
        вернуться к эволюции в случайном порядке (колода)
Def randOrder (x, y):
    xs = specialShuffle (x, len (y))
    д = {}
    для я в х:
        у = у [:]
        случайный.перемешать(г)
        d[i] = итер (ys)
    пары = []
    для я в хз:
        пары.добавлять((я,следующий(д[я])))
    обратные пары
 
 например:
 >>> случайный порядок([1,2,3,4,5],[1,2,3,4,5])
[(1, 4), (3, 1), (4, 5), (2, 2), (4, 3), (5, 3), (2, 1), (3, 3), ( 1, 1), (5, 2), (1, 3), (2, 5), (1, 5), (3, 5), (5, 5), (4, 4), (2, 3), (3, 2), (5, 4), (2, 4), (4, 2), (1, 2), (5, 1), (4, 1), (3, 4) ]
 
 Чем больше  len(X)  и  len(Y) , тем труднее найти решение (и в этом случае он предназначен для возврата пустого списка), и в этом случае параметры  popSize  и  numGens  можно увеличить. Как таковой, он может очень быстро находить решения 20x20. Это занимает около минуты, когда  X  и  Y  имеют размер 100, но даже тогда он может найти решение (в то время, когда я его запускал).
 Интересное ограничение! Вероятно, я слишком много думал об этом, решая более общую проблему: перетасовывать произвольный список последовательностей так, чтобы (если возможно) никакие две соседние последовательности не имели общего первого элемента.
 из продукта импорта itertools
из случайного выбора импорта, случайного выбора, перемешивания
деф комбинат (* последовательности):
    вернуть список воспроизведения (продукт (* последовательности))
список воспроизведения (последовательность):
    r'''Перемешать набор последовательностей, избегая повторяющихся первых элементов.
    '''#"""#'''
    результат = список (последовательность)
    длина = длина (результат)
    если длина < 2:
        # Перестановка невозможна.
        вернуть результат
    деф своп (а, б):
        если а != б:
            результат[а], результат[б] = результат[б], результат[а]
    своп (0, ранжирование (длина))
    для n в диапазоне (1, длина):
        предыдущий = результат[n-1][0]
        варианты = [x для x в диапазоне (n, длина), если результат [x][0] != предыдущий]
        если не выбор:
            # Застрял в углу: осталось слишком много одинаковых предметов. 
            # Возврат, насколько это необходимо, для чередования других элементов.
            минор = 0
            мажор = длина - п
            при n > 0:
                п -= 1
                если результат[n][0] == предыдущий:
                    мажор += 1
                еще:
                    минор += 1
                если минор == мажор - 1:
                    если n == 0 или результат[n-1][0] != предыдущий:
                        сломать
            еще:
                # Требование не может быть выполнено,
                # потому что слишком много одного элемента.
                перемешать (результат)
                сломать
            # Чередуйте основной элемент с другими элементами.
            major = [элемент для элемента в результате[n:], если элемент[0] == предыдущий]
            второстепенный = [элемент для элемента в результате [n:] если элемент [0] != предыдущий]
            перетасовать (основной)
            перемешивание (минор)
            результат[n] = мажор. поп(0)
            п += 1
            в то время как n <длина:
                результат[n] = минор.поп(0)
                п += 1
                результат[n] = мажор.поп(0)
                п += 1
            сломать
        поменять местами (n, выбор (выбор))
    вернуть результат
 
 Все начинается просто, но когда он обнаруживает, что не может найти элемент с другим первым элементом, он выясняет, как далеко нужно вернуться назад, чтобы чередовать этот элемент с чем-то другим. Таким образом, основной цикл обходит массив не более трех раз (один раз в обратном направлении), но обычно только один раз. Конечно, каждая итерация первого прямого прохода проверяет каждый оставшийся элемент в массиве, а сам массив содержит каждую пару, поэтому общее время выполнения составляет  O((NM)**2)  .
 Для вашей конкретной проблемы:
 >>> X = Y = [1, 2, 3, 4, 5]
>>> объединить (X, Y)
[(3, 5), (1, 1), (4, 4), (1, 2), (3, 4),
 (2, 3), (5, 4), (1, 5), (2, 4), (5, 5),
 (4, 1), (2, 2), (1, 4), (4, 2), (5, 2),
 (2, 1), (3, 3), (2, 5), (3, 2), (1, 3),
 (4, 3), (5, 3), (4, 5), (5, 1), (3, 1)]
 
 Кстати, это сравнивает значения x по равенству, а не по положению в массиве X, что может иметь значение, если массив может содержать дубликаты.
No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *