Формула Пуассона онлайн
Закон Пуассона , где λ равна среднему числу появления событий в одинаковых независимых испытаниях, т.е. λ = n × p, где p – вероятность события при одном испытании, e = 2,71828.Ряд распределения закона Пуассона имеет вид:
| X | 0 | 1 | 2 | … | m | … |
| P | e-λ | λe-λ | … | … |
Назначение сервиса. Онлайн-калькулятор используется для построения Пуассоновского распределения и вычисления всех характеристик ряда: математического ожидания, дисперсии и среднеквадратического отклонения. Отчет с решением оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
Вычислить вероятность для: m =
наступит раз
не менее раз
более раз
не более раз
не менее и не более раз
наступит хотя бы один раз
В случае, когда n велико, а λ = p·n > 10 формула Пуассона дает очень грубое приближение и для расчета Pn(m) используют локальную и интегральную теоремы Муавра-Лапласа.
M[X] = λ
Дисперсия распределения Пуассона
D[X] = λ
Пример №1. Семена содержат 0.1% сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 5 семян сорняков?
Решение.
Вероятность р мала, а число n велико. np = 2 P(5) = λ5e-5/5! = 0.03609
Математическое ожидание: M[X] = λ = 2
Пример №2. Среди семян ржи имеется 0.4% семян сорняков. Составить закон распределения числа сорняков при случайном отборе 5000 семян. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Математическое ожидание: M[X] = λ = 0.004*5000 = 20. Дисперсия: D[X] = λ = 20
Закон распределения:
| X | 0 | 1 | 2 | … | m | … |
| P | e-20 | 20e-20 | 200e-20 | … | 20me-20/m! | … |
Пример №3.
На телефонной станции неправильное соединение происходит с вероятностью 1/200. Найдите вероятность того, что среди 200 соединений произойдет:
б) меньше чем три неправильных соединения;
в) больше чем два неправильных соединения.
Решение. По условию задачи вероятность события мала, поэтому используем формулу Пуассона (15).
а) Задано: n = 200, p = 1/200, k = 1. Найдем P200(1).
Получаем: . Тогда P200(1) ≈ e-1≈ 0,3679.
б) Задано: n = 200, p = 1/200, k < 3. Найдем P200(k < 3).
Имеем: a = 1.
в) Задано: n = 200, p = 1/200, k > 2. Найдем P200(k > 2).
Эту задачу можно решить проще: найти вероятность противоположного события, так как в этом случае нужно вычислить меньше слагаемых. Принимая во внимание предыдущий случай, имеем
P200(k>2) = 1-P200(k≤2) = 1-P200(kРассмотрим случай, когда n является достаточно большим, а p — достаточно малым; положим np = a, где a — некоторое число.
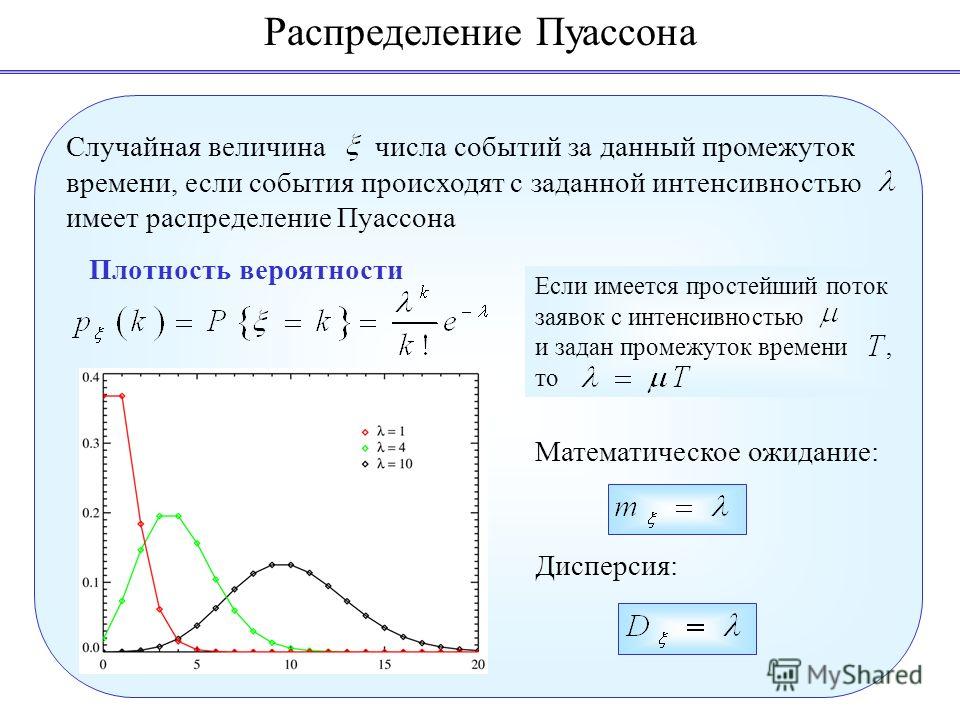В этом случае искомая вероятность определяется формулой Пуассона:
Вероятность появления k событий за время длительностью t можно также найти по формуле Пуассона:
где λ — интенсивность потока событий, то есть среднее число событий, которые появляются в единицу времени.
Пример №4. Вероятность того, что деталь бракованная, равна 0.005. проверяется 400 деталей. Укажите формулу вычисления вероятности того, что больше 3 деталей оказались с браком.
Пример №5. Вероятность появления бракованных деталей при их массовом производстве равна p. определить вероятность того, что в партии из N деталей содержится а) ровно три детали; б) не более трех бракованных деталей.
p=0,001; N = 4500
Решение.
Вероятность р мала, а число n велико. np = 4.5 < 10. Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон.
,m). Вероятности этих значений можно найти по формуле:
Найдем ряд распределения X.
Здесь λ = np = 4500*0.001 = 4.5
P(0) = e— λ = e-4.5 = 0.01111
P(1) = λe-λ = 4.5e-4.5 = 0.04999
Тогда вероятность того, что в партии из N деталей содержится ровно три детали, равна:
Тогда вероятность того, что в партии из N деталей содержится не более трех бракованных деталей:
P(x<3) = P(0) + P(1) + P(2) = 0,01111 + 0,04999 + 0,1125 = 0,1736
Пример №6. Автоматическая телефонная станция получает в среднем за час N вызовов. Определить вероятность того, что за данную минуту она получит: а) ровно два вызова; б) более двух вызовов.
Решение.
За одну минуту АТС в среднем получает λ = 18/60 мин. = 0,3
Считая, что случайное число X вызовов, поступивших на АТС за одну минуту,
подчиняется закону Пуассона, по формуле найдем искомую вероятность
Найдем ряд распределения X.
Здесь λ = 0.3
P(0) = e— λ = e-0.3 = 0.7408
P(1) = λe-λ = 0.3e-0.3 = 0.2222
Вероятность того, что за данную минуту она получит ровно два вызова:
P(2) = 0,03334
Вероятность того, что за данную минуту она получит более двух вызовов:
P(x>2) = 1 – 0,7408 – 0,2222 – 0,03334 = 0,00366
Пример №7. Рассматриваются два элемента, работающих независимо друг от друга. Продолжительность времени безотказной работы имеет показательное распределение с параметром λ1 = 0,02 для первого элемента и λ2 = 0,05 для второго элемента. Найти вероятность того, что за 10 часов: а) оба элемента будут работать безотказно; б) только Вероятность того, что за 10 часов элемент №1 не выйдет из строя:
P1(0) = e-λ1*t = e-0.02*10 = 0,8187
Вероятность того, что за 10 часов элемент №2 не выйдет из строя:
P2(0) = e-λ2*t = e-0.
05*10 = 0,6065
а) оба элемента будут работать безотказно;
P(2) = P1(0)*P2(0) = 0,8187*0,6065 = 0,4966
б) только один элемент выйдет из строя.
P(1) = P1(0)*(1-P2(0)) + (1-P1(0))*P2(0) = 0.8187*(1-0.6065) + (1-0.8187)*0.6065 = 0.4321
Пример №7. Производство даёт 1% брака. Какова вероятность того, что из взятых на исследование 1100 изделий выбраковано будет не больше 17?
Примечание: поскольку здесь n*p=1100*0.01=11 > 10, то необходимо использовать теорему Лапласа.
распределение Пуассона Калькулятор | Вычислить распределение Пуассона
✖Среднее значение распределения — это долгосрочное среднее арифметическое значение случайной величины, имеющей это распределение.ⓘ Среднее распределение [μ] | +10% -10% | ||
✖Конкретные исходы в испытаниях — это количество раз, когда определенный результат имел место в рамках данной группы испытаний. | +10% -10% |
ⓘ Конкретные исходы в испытаниях [x]|
|
⎘ копия |
👎
Формула
сбросить
👍
распределение Пуассона Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
(-μ)/(x!)
Что такое распределение вероятностей Пуассона?
Распределение вероятностей Пуассона — это дискретное распределение вероятностей количества событий, происходящих в заданный период времени, с учетом среднего количества раз, когда событие происходит за этот период времени. Распределение Пуассона используется для описания распределения редких событий в большой популяции. Распределение Пуассона описывает распределение двоичных данных из бесконечной выборки. Таким образом, это дает вероятность получить r событий в популяции.
Share
Copied!
ХИМИЧЕСКИЙ / МОЛЯРНЫЙ КАЛЬКУЛЯТОР — молярность, разбавление, поглощение и т.д.
Определения и формулы
Определения основных терминов
Моль
Моль является единицей измерения количества вещества. Он определяется как ровно 6,02214076×10 23 (постоянная Авогадро) частицы, которые могут быть атомами, молекулами, ионами или электронами.
Молярная масса
Молярная масса – это масса 1 моля вещества, выраженная в г/моль. Значение молярной массы конкретного вещество почти идентично его молекулярной массе (MW или M.W., иногда также называют формулой веса — FW или F.W.), хотя последняя используется либо без каких-либо единицей или с единицей, называемой Дальтон (Да).
Растворенное вещество
Растворенное вещество — это вещество, растворенное в другом веществе, известное как растворитель.
Растворитель
Растворитель – это вещество, растворяющее растворенное вещество с образованием раствора.
Раствор
Раствор в химии представляет собой гомогенную смесь, состоящую из двух или более веществ. В такой смеси образуется растворенное вещество — это вещество, растворенное в другом веществе, известное как растворитель.
Концентрация
Концентрация раствора – это количество растворенного вещества, растворенного в единице объема раствора.
Эта сумма может
выражаться в молях, единицах массы или процентах.
Молярная концентрация (молярность)
Молярная концентрация (также называемая молярностью) – это число молекул вещества, выраженное в молярных единицах (см. выше), присутствующих в определенном объеме раствора. Наиболее часто используемой единицей молярности является число молей на литр, имеющее символ единицы моль/л или моль⋅дм −3 . Значение молярности также часто выражается как «х-моль», например 2,5 М (читается как «2,5-моль»), где «М» означает моль/л.
Моляльность
Моляльность – это количество молей растворенного вещества, присутствующего в 1 кг растворителя. Это контрастирует с определение молярности, основанное на указанном объеме раствора.
Массовая концентрация
Массовая концентрация представляет собой отношение массы растворенного вещества к объему раствора, обычно выражаемое в грамм на литр (г/л).
Процентная концентрация
Процентная концентрация раствора может быть выражена как масса на массу (масса/масса или масса/масса), масса на объем (масса/объем),
или объем на объем (об.
/об.) в процентах.
Процент по массе (или весу), м/м или вес/вес — это масса растворенного вещества, деленная на общую массу раствора,
умножается на 100 %.
Массовые проценты на объем (w/v) — это количество граммов растворенного вещества в 100 мл раствора.
Процент по объему (v/v) — это объем растворенного вещества, деленный на общий объем раствора, умноженный на 100.
%.
Исходный раствор
Исходный раствор — это концентрированный раствор, который будет разбавлен до более низкой концентрации, что часто называется рабочей или конечной концентрацией для фактического использования. Стандартные растворы используются для экономии подготовки время, уменьшить пространство для хранения и повысить точность, с которой рабочие растворы с более низкой концентрацией готовый.
Поглощение
Поглощение – это число, которое измеряет ослабление мощности прошедшего света в растворе. Это
определяется как десятичный логарифм отношения мощности падающего света к мощности прошедшего через раствор.
Молярный коэффициент экстинкции
Молярный коэффициент экстинкции или молярный коэффициент ослабления является измерением того, насколько сильно химический вид ослабляет свет на данной длине волны. Единицей молярного коэффициента затухания в СИ является квадратный метр на моль (м 2 /моль), но на практике количества обычно выражают в единицах М -1 см -1 или лмоль -1 см -1 .
Расчеты
В расчетных формулах будут использоваться следующие символы (единицы измерения в квадратных скобках):
| нет | — | количество молей [моль] |
| М | — | молярная масса [г/моль] |
| с | — | молярная концентрация [моль/л] |
| м | — | масса [г] |
| В | — | объем [л] |
| C б/об | — | процентная концентрация (вес/объем) [%] |
| С в/в | — | процентная концентрация (об. /об.) [%] |
| р | — | массовая плотность [кг/л] |
| А | — | абсорбция |
| ε | — | молярный коэффициент экстинкции [лмоль -1 см -1 ] |
| л | — | оптический путь [см] |
Вы можете использовать калькулятор молярности, расположенный вверху страницы, для расчета массы, объем или концентрация, необходимые для приготовления раствора соединения известная молекулярная масса. Для этого будут использованы следующие формулы:
Как рассчитать молярность раствора?
Молярность раствора рассчитывается непосредственно из определяющей формулы; разделить массу вещества на его молярная масса и объем раствора:
| c | = | = | м М × В |
Как рассчитать массу вещества, необходимого для приготовления раствора определенной молярности в данной объем?
Просто умножьте молярность, молярную массу и объем раствора:
m = c × M × V
Как рассчитать объем раствора, необходимый для получения желаемой молярной концентрации после растворения определенная масса вещества?
Разделите значение массы на произведение молярной массы и молярной концентрации:
| V | = | м М × в |
Вы можете использовать второй калькулятор (сверху страницы) для преобразования между
процентная концентрация и молярная концентрация.
Для этого будут использованы следующие формулы:
Как перевести проценты в молярность?
Чтобы найти молярную концентрацию, чтобы определить процентное соотношение масса/объем, умножьте значение процентной концентрации на 10, чтобы получить массу вещества в 1 литре и затем разделить на молярную массу вещества:
| c | = | 10 × C б/об M |
Для определения процентного соотношения объем/объем умножьте 10-кратное значение процентной концентрации на массовую плотность раствора, чтобы получить массу вещества в 1 л и затем разделить на молярную массу вещества:
| с | = | 10 × C об./об. × ρ M |
Как преобразовать молярность в процентную концентрацию?
Чтобы получить процентное содержание массы/объема, умножьте молярность на молярную массу вещества и разделите на 10.
| C масса/объем | = | с × M 10 |
Чтобы получить объемное соотношение, умножьте молярность на молярную массу вещества и разделите массовую плотность на 10.
решения.
| С в/в | = | с × M 10 × р |
Вы можете использовать третий калькулятор (сверху страницы) для расчета разведение или приготовление маточного раствора. Для этого будут использоваться следующие формулы:
Как рассчитать концентрацию маточного раствора, необходимую для получения желаемой конечной (рабочей) концентрации после разбавления заданного объема маточного раствора до заданного конечного объема?
Умножьте соотношение объемов конечного и основного раствора на требуемую конечную концентрацию:
| c исходный | = | c окончательный | × | В окончательный В сток |
Как рассчитать конечную концентрацию, полученную путем разбавления заданного объема исходного раствора в с учетом конечного объема?
Умножьте соотношение объемов исходного и конечного растворов на концентрацию исходного раствора:
| с окончательная | = | c на складе | × | В сток В окончание |
Как рассчитать объем маточного раствора, необходимый для получения желаемой конечной (рабочей) концентрации после разбавления маточного раствора до заданного конечного объема?
Умножьте отношение концентраций конечного и исходного раствора на конечный объем раствора:
| V склад | = | В окончательный | × | c окончательный c склад |
Как рассчитать конечный объем раствора, необходимый для получения желаемой конечной концентрации после разбавление указанного объема исходного раствора?
Умножьте отношение концентраций исходного и конечного растворов на объем исходного раствора:
| В окончательный | = | В на складе | × | c сток c окончание |
Вы можете использовать четвертый калькулятор (сверху страницы) для расчета
разбавление всего раствора, необходимое для доведения его концентрации до желаемого значения.
Для этого будут использоваться следующие формулы:
Как рассчитать объем, который необходимо добавить для достижения заданной концентрации после разбавления?
Умножить начальный объем на отношение начальной и конечной концентраций, уменьшенное на 1:
| V добавить | = | В начальный | × | ( | c начальный c окончательный | — 1 | ) |
Как рассчитать начальный объем раствора, если известны коэффициент разбавления и объем добавлен?
Коэффициент разбавления – это отношение начальной и конечной концентраций. Разделите добавляемый объем на разбавление значение коэффициента уменьшено на 1:
| V начальный | = | В добавить | / | ( | c начальный c окончательный | — 1 | ) |
Как рассчитать конечную концентрацию раствора, полученного добавлением определенного объема растворителя к раствор известной начальной концентрации и объема?
Разделить исходное значение концентрации на отношение объемов плюс один:
| c конечное | = | c начальный | / | ( | В добавить В начальный | + 1 | ) |
Как рассчитать начальную концентрацию раствора до того, как он будет разбавлен добавлением указанного объем растворителя для получения известной конечной концентрации?
Умножьте конечное значение концентрации на отношение добавленного и начального объемов плюс один:
| c начальный | = | c окончательный | × | ( | В добавить В начальный | + 1 | ) |
Вы можете использовать пятый калькулятор (сверху страницы) для расчета
поглощения раствора заданной концентрации или наоборот.
Для этого будут использованы следующие формулы:
Как рассчитать оптическую плотность раствора по его концентрации?
Поглощение подчиняется закону Бера-Ламберта:
A = ε × l × c
Как рассчитать концентрацию раствора по его поглощению?
Преобразовывая закон Бера-Ламберта, получаем формулу:
| c | = | А ε × l |
КОМБИНАТОРИКА
Комбинаторика Калькулятор
Бесплатный онлайн-инструмент для подсчета количества комбинаций и перестановки.
Очистить
Вычислить
Перестановки без повторения
k-перестановки, или частичные перестановки, представляют собой упорядоченные расположения k отдельные элементы, выбранные из набора S из n уникальных элементов. Когда k равно размер n набора, это перестановки набора и их количество равно н! (н факториал). Если k < n , количество всех возможных k -перестановок равно:
| n P k | = | н! (н-к)! |
Калькулятор (заполните оба поля и нажмите «Рассчитать»):
Общее количество элементов:n =
Сколько выбрать:k =
Количество перестановок:
В экспоненциальном представлении:
Очистить 90 011
Рассчитать
Перестановки с повторением
Упорядоченные расположения длиной k элементов из набора S где одинаковые
элемент может встречаться более одного раза, называются k -кортежами, но иногда их называют
перестановки с повторением.
Их также называют словами над алфавитом S в некоторых контекстах. Если
набор S имеет n элементов, количество k -кортежей более S это:
| P k (n) | = | н к |
Калькулятор (заполните оба поля и нажмите «Рассчитать»):
Общее количество элементов:n =
Сколько выбрать:k =
Количество перестановок:
В экспоненциальном представлении:
Очистить 90 011
Вычислить
Комбинации без повторения
Комбинация — это способ выбора элементов из набора, такой, что (в отличие от перестановок) порядок выбора значения не имеет. Если в наборе н элементы, количество к -сочетания (подмножества с k элементами) это:
| n C k | = | н! к!(н — к)! | = | ( | ) |
Калькулятор (заполните оба поля и нажмите «Рассчитать»):
Общее количество предметов:n =
Сколько выбрать:k =
Количество комбинаций:
В экспоненциальном представлении:
Очистить
Рассчитать
Комбинации с повторением
A k -комбинация с повторением или мультиподмножество размера k 90 610 из набора S задается последовательностью из k элементов S , где один и тот же элемент может встречаться более одного раза
и порядок значения не имеет.