Многогранник с 6 гранями: 8.2. Тетраэдр, гексаэдр, октаэдр

Гармония правильных многогранников / Этюды // Математические этюды

Гармония правильных многогранников / Этюды // Математические этюды

Математические этюды

К списку

Пра­виль­ные многогран­ники инте­ре­со­вали многих вели­ких учё­ных. И этот инте­рес выхо­дил далеко за пре­делы матема­тики. Пла­тон (427 до н.э. — 347 до н.э.) рас­смат­ри­вал их как основу стро­е­ния Все­лен­ной, Кеплер (1571—1630) пытался свя­зать пра­виль­ные многогран­ники с движе­нием пла­нет Сол­неч­ной системы (кото­рых в его время было известно пять). Возможно, именно кра­сота и гар­мо­ния пра­виль­ных многогран­ни­ков застав­ляла вели­ких учё­ных прошлого предпо­лагать какое-то более глу­бо­кое их назна­че­ние, чем про­сто геомет­ри­че­ских объек­тов.

Пра­виль­ным многогран­ни­ком назы­ва­ется многогран­ник, все грани кото­рого суть пра­виль­ные много­уголь­ники, все плос­кие углы кото­рого равны между собой и дву­гран­ные углы кото­рого равны между собой. (Плос­кими углами многогран­ника назы­ваются углы много­уголь­ни­ков-гра­ней, дву­гран­ными углами многогран­ника назы­ваются углы между гра­нями, имеющими общее ребро.

\circ$.

Возьмём в сере­ди­нах гра­ней тет­раэдра по точке и соеди­ним их между собой отрез­ками. Эти отрезки равны по длине и обра­зуют рав­но­сто­рон­ние тре­уголь­ники. Точки являются верши­нами, отрезки — рёб­рами, а тре­уголь­ники — гра­нями ещё одного тет­раэдра.

Ана­логич­ное постро­е­ние при­ме­нимо и в более общем слу­чае. Рас­смот­рим про­из­воль­ный выпук­лый многогран­ник и возьмём точки в сере­ди­нах его гра­ней. Соеди­ним между собой точки сосед­них гра­ней отрез­ками. Тогда точки являются верши­нами, отрезки — рёб­рами, а много­уголь­ники, кото­рые огра­ни­чи­вают эти отрезки, гра­нями ещё одного выпук­лого многогран­ника. Этот многогран­ник назы­ва­ется двойствен­ными к исход­ному.

Как было пока­зано выше, двойствен­ным к тет­раэдру явля­ется тет­раэдр.

Уве­ли­чим размер тет­раэдра, верши­нами кото­рого являются сере­дины гра­ней исход­ного тет­раэдра, до разме­ров послед­него. Восемь вершин так рас­по­ложен­ных тет­раэд­ров являются верши­нами куба.

\circ$.

Отме­тим сере­дины гра­ней октаэдра и перей­дём к двойствен­ному к октаэдру многогран­нику. Это — куб или гек­саэдр (от греч. εξά — шесть). У куба грани являются квад­ра­тами. Он имеет 6 гра­ней, 8 вершин, 12 рёбер. Плос­кие углы куба равны $\pi/2$, дву­гран­ные углы также равны $\pi/2$.

Если взять точки на сере­ди­нах гра­ней куба и рас­смот­реть двойствен­ный к нему многогран­ник, то можно убе­диться, что им снова будет октаэдр. Верно и более общее утвер­жде­ние: если для выпук­лого многогран­ника постро­ить двойствен­ный, а затем двойствен­ный к двойствен­ному, то им будет исход­ный многогран­ник (с точ­но­стью до подо­бия).

Возьмём на рёб­рах октаэдра по точке, с тем усло­вием, чтобы каж­дая делила ребро в соот­ноше­нии $1:(\sqrt5+1)/2$ (золо­тое сече­ние) и при этом точки, при­над­лежащие одной грани, явля­лись верши­нами пра­виль­ного тре­уголь­ника. Полу­чен­ные 12 точек являются верши­нами ещё одного пра­виль­ного многогран­ника — ико­саэдра (от греч.

\circ$.

Взяв сере­дины гра­ней доде­каэдра, и перейдя к двойствен­ному ему многогран­нику, полу­чим снова ико­саэдр. Итак, ико­саэдр и доде­каэдр двойственны друг другу. Это ещё раз иллю­стри­рует тот факт, что двойствен­ным к двойствен­ному будет исход­ный многогран­ник.

Заме­тим, что при пере­ходе к двойствен­ному многогран­нику, вершины исход­ного многогран­ника соот­вет­ствуют гра­ням двойствен­ного, рёбра — рёб­рам двойствен­ного, а грани — верши­нам двойствен­ного многогран­ника. Если у ико­саэдра 20 гра­ней, зна­чит у двойствен­ного ему доде­каэдра 20 вершин и у них оди­на­ко­вое число рёбер, если у куба 8 вершин, то у двойствен­ного ему октаэдра 8 гра­ней.

Суще­ствуют раз­лич­ные спо­собы впи­сы­ва­ния пра­виль­ных многогран­ни­ков друг в друга, при­во­дящие ко многим заме­ча­тель­ным кон­струкциям. Инте­рес­ные и кра­си­вые многогран­ники полу­чаются также при объеди­не­нии и пере­се­че­нии пра­виль­ных многогран­ни­ков.

В доде­каэдр впишем куб так, чтобы все 8 вершин куба совпа­дали с верши­нами доде­каэдра.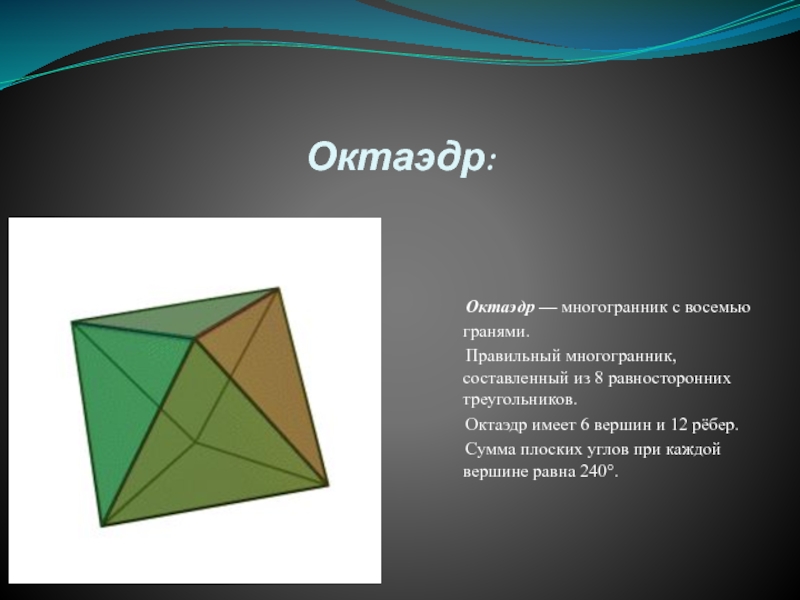 Вокруг доде­каэдра опишем ико­саэдр так, чтобы его вершины ока­за­лись в сере­ди­нах гра­ней ико­саэдра. Вокруг ико­саэдра опишем октаэдр, так, чтобы вершины ико­саэдра лежали на рёб­рах октаэдра. Нако­нец, вокруг октаэдра опишем тет­раэдр так, чтобы вершины октаэдра попали на сере­дины рёбер тет­раэдра.

Такую кон­струкцию из кусоч­ков сло­ман­ных дере­вян­ных лыж­ных палок сде­лал ещё ребён­ком будущий вели­кий матема­тик XX века В. И. Арнольд. Вла­ди­мир Иго­ре­вич хра­нил её долгие годы, а затем отдал в лабо­ра­то­рию попу­ля­ри­за­ции и про­паганды матема­тики Матема­ти­че­ского инсти­тута им. В. А. Стек­лова.

Лите­ра­тура

Кокс­тер Г. С. М. Вве­де­ние в геомет­рию. — М. : Наука, 1966.

Адамар Ж. Элемен­тар­ная геомет­рия. — Часть 2. Сте­реомет­рия. — М. : Про­свеще­ние, 1951.

Евклид. Начала Евклида. Книги XXI—XXV. — М.—Л.: ГИТТЛ, 1950.

Другие этюды раздела «Внешняя геометрия многогранников»

  Тени  Увеличение объёма выпуклых многогранников  Удивительные объёмы многогранников  Кусочно гладкое вложение многогранника  Изгибаемые многогранники

Математические этюды

Лекция 6.

Многогранники

Многогранные формы в нашей жизни мы встречаем повсюду: спичечный коробок, книга, пакет молока в виде пирамиды, граненный карандаш, да и многие архитектурные сооружения или их детали представляют собой некоторые виды многогранников. С чисто геометрической точки зрения, многогранник – это часть пространства, ограниченная плоскими многоугольниками, называемыми гранями. Для выпуклого многогранника, то есть такого, который лежит по одну сторону от плоскости любой его грани, справедлива формула Эйлера, устанавливающая зависимость между числом ребер Р, граней Г и вершин В-Р+Г=2. Это число называется иначе эйлеровой характеристикой многогранника и может равняться 2, 0, -2,-4, ….Эйлерова характеристика показывает, грубо говоря, сколько «дырок» имеет многогранник.

Так называемые правильные многогранники изучаются в топологии, они еще иначе называются топологически правильными и для них всегда число Эйлера равно двум. Перечислим их: тетраэдр, октаэдр, икосаэдр, гексаэдр, додекаэдр – всего пять топологически правильных многогранников.

Еще со времен древнегреческих философов правильные многогранники считались не более чем игрушкой для математиков, которая не имеет никакого практического значения. Однако, в последнее время многогранники заняли свое достойное место в науке и оказались в центре внимания биологов, так, выяснилось, например, вирус полиомиелита представляет собой икосаэдр.

Из школьного курса геометрии известно, что многогранник называется правильным, если у него все грани правильные равные многоугольники, и все двугранные углы равны.

Правильными многогранниками занимались Пифагор и его ученики. Пифагорейцы считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях: первоосновам бытия — огню, земле, воздуху, воде придавалась форма соответственно тетраэдра, куба, октаэдра, икосаэдра, а вся Вселенная имела форму додекаэдра. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ — идеалист Платон. С тех пор правильные многогранники стали называться Платоновыми телами. В идеалистической картине мира, данной Платоном, четыре из них олицетворяли четыре стихии: тетраэдр- огонь, куб – землю, икосаэдр – воду и октаэдр — воздух. Пятый же многогранник, додекаэдр, символизировал все мироздание, его по латыни называли «пятая сущность». Придумать правильный тетраэдр, куб, октаэдр, по видимому, было нетрудно, тем более что эти формы имеют природные кристаллы, например, куб – монокристалл поваренной соли.

Итак, существует всего пять видов правильных многогранников: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр (рис.23).

Рис.23

Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого «тетра» — четыре, «эдрон» — грань. Гексаэдр (куб) имеет 6 граней, «гекса» — шесть; октаэдр — восьмигранник, «окто» — восемь; додекаэдр — двенадцатигранник, «додека» — двенадцать; икосаэдр имеет 20 граней, «икоси» — двадцать.

Пусть АВСВА₁В₁С₁D₁ – известный всем нам куб, или иначе, гексаэдр (рис 24). Точки А, В₁, С, D₁ не лежат в одной плоскости, поэтому являются вершинами некоторого тетраэдра Т. Поверхность этого тетраэдра образована четырьмя равными правильными треугольниками, так как стороны этих треугольников являются диагоналями граней куба. Многогранные углы при вершинах тетраэдра Т имеют одно и то же число граней (три). Отсюда мы заключаем, что Т правильный тетраэдр.

Рис.24

Из того же куба можно получить следующий правильный многогранник. Найдем центр каждой грани куба и соединим их отрезками. Этот многогранник называется правильным октаэдром.

При построении правильного икосаэдра заметим, что сколько у куба ребер, столько граней имеет икосаэдр. Данная взаимосвязь подсказывает способ построения: необходимо провести через каждую грань куба некоторую плоскость, которые затем повернуть не необходимый угол для того, чтоб эти все плоскости пересеклись.

Если все выполнено верно, то все грани построенного икосаэдра — равные правильные треугольники, а многогранные углы при вершинах имеют одно и то же число граней — пять. Таким образом, построенный икосаэдр правильный.

Д ля построения правильного додекаэдра используют правильный икосаэдр. Нетрудно видеть, что центры граней правильного икосаэдра F служат вершинами правильного додекаэдра.

Рис.25

Таким образом, из одного правильного многогранника можно получить все остальные, используя их особенности. Это наводит на некоторую взаимосвязь, которая называется двойственностью.

Так, например, гексаэдр и тетраэдр обладают следующей особенностью: число вершин одного равно числу граней другого; оба тела имеют одинаковое число ребер; в вершине одного тела сходится столько граней, сколько вершин имеется у грани другого тела (рис.25). Поэтому можно также описать октаэдр вокруг куба.

Аналогичные соотношения имеют место между додекаэдром и икосаэдром. В этом случае говорят, что имеет место принцип двойственности, рассмотренный в проективной геометрии.

Принцип двойственности в пространстве даёт более общий метод приведения в соответствие точек, прямых и плоскостей одной фигуры с плоскостями, прямыми и точками другой фигуры. Поэтому принципу двойственности куб соответствует октаэдру, а октаэдр – кубу; икосаэдр—додекаэдру и додекаэдр – икосаэдру, а тетраэдр—самому себе.

Особенностью правильных многогранников, помимо свойства взаимности и двойственности, является наличие у них элементов симметрии.

Так как куб — частный случай параллелепипеда, то его диагонали пересекаются в одной точке. Эта точка равноудалена от всех вершин куба, от его граней и от его ребер и является центром трех сфер: описанной сферы, проходящей через вершины, вписанной сферы, касающейся всех граней, и сферы, касающейся всех его ребер. Общий центр этих сфер называется центром куба.

Центр куба является также и центром симметрии куба. У правильного тетраэдра его центр (совпадающий с центром вписанной в тетраэдр сферы и центром сферы, касающейся его ребер) не является центром симметрии.

Для правильного октаэдра его центр также является центром трех сфер — описанной, вписанной и касающейся всех ребер. Аналогичное утверждение имеет место и для правильного икосаэдра. К тому же центр икосаэдра является центром его симметрии.

Центр правильного икосаэдра F является и центром правильного додекаэдра (т. е. общим центром трех сфер: описанной, вписанной и сферы, которая касается ребер додекаэдра).

Другие элементы симметрии, встречающиеся у многогранников, это плоскость симметрии, ось симметрии. В отличие от школьного понятия оси симметрии, новый вид оси немного усложняется, в соответствие с эти выделяют зеркально-поворотные оси симметрии, а также оси симметрии различного порядка. Порядок оси, как было показано ранее, означает число самосовмещений фигуры при повороте вокруг оси.

Зеркально-поворотная ось симметрии – это совокупность оси и перпендикулярной к ней плоскости симметрии, действующих совместно.

Для наглядности приведем элементы симметрии у куба.

К уб имеет три оси симметрии четвертого порядка, проходящие через центры параллельных граней. Каждая из этих осей является зеркально – поворотной осью четвертого порядка. Куб имеет четыре оси симметрии третьего порядка, содержащие диагонали. Каждая из этих осей является зеркально-поворотной осью шестого порядка. Куб имеет шесть осей симметрии (второго порядка). Каждая из них проходит через середины двух ребер куба, принадлежащих его диагональному сечению.

К

Кристалл поваренной соли

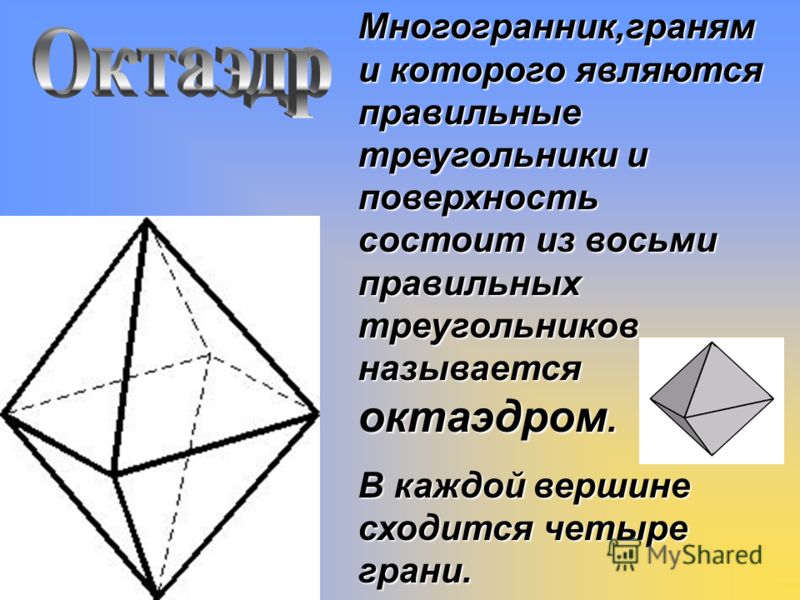
уб имеет девять плоскостей симметрии. Шесть из них содержат по две диагонали куба, а каждая из остальных трех проходит через центр куба параллельно двум параллельным граням. Все указанные элементы симметрии показаны на рисунке 26.

П

Рис.26

равильные многогранники – самые выгодные фигуры. Удивительно разнообразен мир кристаллов, являющихся природными многогранниками. Но, кроме формы правильных многогранников, многие кристаллы имеют форму просто многогранника (кварц, исландский шпат, пирит, гранат, алмаз) Так, кристаллическая решетка поваренной соли имеет кубическую структуру.

С келет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр.

Б

Феодария

ольшинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник.

Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности, то свойство помогает морскому организму преодолевать давление толщи воды.