| Распределение ПуассонаPoisson distribution Распределение Пуассона
− распределение случайной величины , принимающей целые неотрицательные значения. Оно определяет вероятность наблюдения величины n в конкретном измерении, если события происходят независимо и характеризуются средней величиной Одним из классических примеров распределения Пуассона является распределение числа распадов радиоактивного источника постоянной интенсивности. Распределение Пуассона в этом случае показывает, как распределяются результаты отдельных измерений интенсивности n вокруг среднего значения интенсивности , т.е. вероятность получить значение интенсивности n в данном отдельном измерении, если среднее значение интенсивности равно . Дисперсия D в случае распределения Пуассона равна среднему числу частиц D = . Стандартное отклонение σ = √D = √. С увеличением распределение Пуассона становится всё более симметричным относительно и переходит в распределение Гаусса.
|
Пуассон против нормального распределения: в чем разница?
Распределение Пуассона и нормальное распределение являются двумя наиболее часто используемыми распределениями вероятностей в статистике.
В этом руководстве дается краткое объяснение каждого дистрибутива, а также два основных различия между дистрибутивами.
Обзор: распределение ПуассонаРаспределение Пуассона описывает вероятность получения k успехов за заданный интервал времени.
Если случайная величина X подчиняется распределению Пуассона, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = λk * e – λ / k !
куда:
- λ: среднее количество успехов за определенный интервал
- k: количество успехов
- e: константа, равная приблизительно 2,71828.

Например, предположим, что в конкретной больнице в среднем рождается 2 человека в час. Мы можем использовать приведенную выше формулу, чтобы определить вероятность 3 рождений в данный час:
P(X=3) = 2 3 * e – 2 / 3! = 0,1805
Вероятность рождения 3 детей в час равна 0,1805 .
Обзор: нормальное распределениеНормальное распределение описывает вероятность того, что случайная величина примет значение в пределах заданного интервала.
Функция плотности вероятности нормального распределения может быть записана как:
P(X=x) = (1/σ√ 2π )e-1/2 ((x-μ)/σ) 2
куда:
- σ: стандартное отклонение распределения
- μ: среднее значение распределения
- x: значение для случайной величины
Например, предположим, что вес определенного вида выдр нормально распределен с μ = 40 фунтов и σ = 5 фунтов.
Если мы случайным образом выберем выдру из этой популяции, мы можем использовать следующую формулу, чтобы найти вероятность того, что она весит от 38 до 42 фунтов:
P(38 < X < 42) = (1/σ√ 2π )e -1/2((42-40)/5) 2 – (1/σ√ 2π )e -1/2((38-40) /5) 2 = 0,3108
Вероятность того, что случайно выбранная выдра весит от 38 до 42 фунтов, равна 0,3108 .
Отличие №1: дискретные и непрерывные данныеПервое различие между распределением Пуассона и нормальным распределением заключается в типе данных, которые моделирует каждое распределение вероятностей.
Распределение Пуассона используется, когда вы работаете с дискретными данными , которые могут принимать только целочисленные значения, равные или большие нуля. Вот некоторые примеры:
- Количество звонков, полученных в час в колл-центре
- Количество посетителей в день в ресторане
- Количество ДТП в месяц
В каждом сценарии случайная величина может принимать только значения 0, 1, 2, 3 и т. д.
д.
Нормальное распределение используется, когда вы работаете с непрерывными данными , которые могут принимать любое значение от отрицательной бесконечности до положительной бесконечности. Вот некоторые примеры:
- Вес определенного животного
- Высота определенного растения
- Время марафона женщин
- Температура в градусах Цельсия
В этих сценариях случайные величины могут принимать любое значение, например -11,3, 21,343435, 85 и т. д.
Отличие № 2: Форма дистрибутивовВторое различие между пуассоновским и нормальным распределением заключается в форме распределений.
Нормальное распределение всегда имеет форму колокола:
Однако форма распределения Пуассона будет варьироваться в зависимости от среднего значения распределения.
Например, распределение Пуассона с небольшим значением среднего значения, например μ = 3 , будет сильно искажено вправо :
Однако распределение Пуассона с большим значением среднего, например μ = 20 , будет иметь колоколообразную форму, как и нормальное распределение:
Обратите внимание, что нижняя граница распределения Пуассона всегда будет равна нулю, независимо от значения среднего, потому что распределение Пуассона можно использовать только с целочисленными значениями, которые равны или больше нуля.
В следующих руководствах представлена дополнительная информация о распределении Пуассона:
Введение в распределение Пуассона
Четыре предположения о распределении Пуассона
5 реальных примеров распределения Пуассона
В следующих руководствах представлена дополнительная информация о нормальном распределении:
Введение в нормальное распределение
6 реальных примеров нормального распределения
Генератор набора данных нормального распределения
1.7 Распределения
1.7 РаспределенияДля этого документа требуется Netscape 3.x или совместимый веб-браузер.
Биостатистика для клиницистаУрок 1. Техасский университет в Хьюстоне
Медицинский научный центрУрок 1.7
Распределения
Суммарные измерения данных 1/7–1
Биостатистика для клинициста1.7.1 Почему важно?
Зачем вам нужно знать о частотных распределениях, обычно называют просто «распределениями»? Опять же, ответ в том, что они происходят неоднократно упоминается в медицинской литературе. Понимать литературу и уметь критически оценивать исследования, чтобы вы могли применить их результаты, вам нужно знать о раздачах.Что понимается под дистрибутивом? частота распределение — это просто таблица, диаграмма или график, в которых каждое другое значение, полученное с номером или доля раз, когда это происходит. Таким образом, в любое время, когда у вас есть набор значений, каждое значение может быть построен в зависимости от количества или доли раз, когда это происходит используя график со значениями на горизонтальной оси и подсчетами или пропорции по вертикальной оси. Такой график очень удобный способ представления частотного распределения (см.
любой из рисунки ниже).
Оказывается, некоторые распределения особенно важны, потому что они часто возникают в клинических ситуациях. Несколько из Наиболее важными дистрибутивами являются Гаусс, в биномиальный и Пуассон дистрибутивы.
Урок 1. Суммарные измерения данных 1.7–2
Распределения Практика
Упражнение 1:Вам необходимо знать о дистрибутивах для: Нет ответа
Оценка медицинских исследований
Диагностировать болезнь
Вычислить статистику
Ничего из вышеперечисленного
Биостатистика для клинициста1.7.2 Гауссовский
Семейство распределений Гаусса или колоколообразных кривых (также известный как нормальное распределение), безусловно, является наиболее важным набором дистрибутивов.Когда значения получаются путем суммирования числа случайных результатов, что, как правило, имеет место со многими переменными встречаются в клинике, сумма имеет тенденцию принимать гауссово распределение. Итак, гауссовские распределения встречаются исключительно часто и оказываются основой для многих логические статистические тесты.
Распределение Гаусса дает точную математическую формулировку «закон ошибок». При проведении измерений обычно возникают ошибки. Большинство ошибок будут небольшими и близкими к фактическому значению. С другой стороны, некоторые измерения будут иметь большую погрешность. Но по мере увеличения размера погрешностей измерения количество таких ошибок уменьшается. Распределение Гаусса или Кривая Гаусса показывает точное соотношение между размером ошибка и как часто ошибка может возникать (частота ошибок). На рисунке ниже показано, что такое Распределение Гаусса имеет вид (см. рисунок).
Гауссово распределение Урок 1.
Распределения Практика
Упражнение 2:Распределения Гаусса особенно важны, потому что они: Нет ответа
Возникают часто
Представляют закон ошибок
Поддерживают логические тесты
Все вышеперечисленноеСуммарные измерения данных 1.7–3
Биостатистика для клинициста1.7.3 Биномиальный
Семейство биномиальных распределений актуально, когда происходят независимые испытания, которые можно охарактеризовать как имеющие два возможные результаты, которые можно описать как «успех» или «неудача» и известные вероятности связаны с каждым из исходов. Например, не зная правильных ответов для вопросов верно-ложно будут равные вероятности каждого ответ правильный или неправильный. Вопрос, на который должен ответить тогда биномиальное распределение может звучать так: «Что такое вероятность получить не менее 7 правильных ответов на 10 вопросов верно/неверно контрольная работа?Предположим, вы хотите узнать вероятность того, что при бросании игральной кости что за 5 бросков выпадет шестерка или две шестерки. Здесь вероятность «успеха» составляет 1/6. Вероятность «неудачи» — 5/6. бином распределение снова будет описывать вероятности, связанные с различными количество «успехов» и «неудачи» в таких ситуациях.
Наконец, в качестве другого примера предположим, что вы хотите определить вероятность возникновения генетически обусловленного дефекта в детей из семей разного размера, учитывая наличие особенность одного из родителей. Биномиальное распределение будет описывать вероятности того, что любое количество детей от ожидается, что семья унаследует дефект. Все эти ситуации описывают дихотомические (двузначные) переменные, который при графическом отображении нескольких испытаний можно ожидать биномиального распределения (см. рисунок ниже).
Биномиальные распределения
Распределения Практика
Упражнение 3:Биномиальные распределения описывают вероятности данного количество «успешных» испытаний из большего числа испытаний когда каждое испытание может иметь: Нет ответа
Один результат
Два результата
Несколько результатов
Ни один из вышеперечисленных1.
7.4 Пуассон Другим важным набором дискретных распределений является Распределение Пуассона. Полезно подумать о Пуассон распределение как частный случай биномиального распределения, где число испытаний очень велико, а вероятность очень маленький. В частности, Пуассон часто используется для модельные ситуации, когда число испытаний неопределенно велико, но вероятность того или иного события при каждом испытании приближается нуль. Количество бактерий на чашке Петри можно представить как распределение Пуассона. Крошечные области на пластине можно рассматривать как испытаний, и бактерия может появиться или не появиться в такой области. Вероятность того, что бактерия окажется в любой заданной области, равна очень мало, но таких очень много области на плите. Похожий случай будет при подсчете количества красных клеток, попадающих в квадрат на сетка гемоцитометра, глядя на распределение числа человек в Америке, убитых ударами молнии за один год, или случаев уколов иглой, связанных с ВИЧ, в больницах США каждый год.
Таким образом, пуассоновскую модель можно рассматривать как аппроксимацию биномиальное распределение. Аппроксимация хорошая достаточно, чтобы быть полезным, даже если размер выборки (N) лишь умеренно большой (скажем, N > 50), а вероятность (p) относительно мала (п
Распределения Пуассона
Распределения Практика
Упражнение 4:Можно использовать более простое распределение Пуассона. приближение к биномиальному распределению, когда: Нет ответа
Выборки большие
Изменчивость большая
Вероятность мала
Выборки большие, а вероятность мала
Заключительные инструкции Нажмите кнопку ниже для вашего счета.
- После завершения урока 1.7, включая все практические упражнения, нажмите кнопку «Отправить…» ниже для Урока 1.7 кредит участия в исследовании.
- После того, как вы нажмете «Отправить…», возможно, Netscape скажет вы не можете подключиться из-за необычно высокой системы требования. Если вы не получили сообщение об ошибке при отправке ты в порядке. Но если Netscape выдает сообщение об ошибке после нажатия кнопки «Отправить…», подождите немного и отправьте повторно или проконсультируйтесь с оператором.
- Наконец, нажмите «Оглавление…» кнопка ниже, чтобы правильно закончить Урок 1.7 и вернуться к Оглавление так что вы можете продолжить урок 2.
Конец урока 1.7
Распределения
Урок 1. Суммарные измерения данных 1.7–4
Стандартные статистические распределения (например, нормальное, пуассоновское, биномиальное) и их применение
Статистика: Распределения
Сводка
Нормальное распределение описывает непрерывные данные, которые имеют симметричное распределение с характерной колоколообразной формой.
Биномиальное распределение описывает распределение двоичных данных из конечной выборки. Таким образом, он дает вероятность получения r событий из n испытаний.
Распределение Пуассона описывает распределение двоичных данных из бесконечной выборки. Таким образом, это дает вероятность получения r событий в популяции.
Нормальное распределение
С медицинскими данными часто бывает так, что гистограмма непрерывной переменной, полученная в результате одного измерения различных субъектов, будет иметь характерное «колоколообразное» распределение, известное как нормальное распределение. Одним из таких примеров является гистограмма массы тела при рождении (в килограммах) 3226 новорожденных, показанная на рисунке 1.
Чтобы различить использование одного и того же слова в нормальном диапазоне и нормальном распределении, мы везде использовали строчные и прописные буквы.
Гистограмма выборочных данных представляет собой оценку распределения массы тела при рождении новорожденных в популяции. Это распределение популяции можно оценить по наложенной гладкой «колоколообразной» кривой или показанному «нормальному» распределению. Мы предполагаем, что если бы мы могли рассмотреть всю популяцию новорожденных, то распределение массы тела при рождении имело бы в точности Нормальную форму. Мы часто делаем вывод, исходя из выборки, гистограмма которой имеет приблизительную нормальную форму, что популяция будет иметь именно эту нормальную форму или настолько близкую, насколько это не имеет практического значения.
Нормальное распределение полностью описывается двумя параметрами μ и σ, где μ представляет среднее значение совокупности или центр распределения, а σ стандартное отклонение совокупности. Он симметрично распределен вокруг среднего. Популяции с малыми значениями стандартного отклонения σ имеют распределение, сосредоточенное вблизи центра µ; те, у которых большое стандартное отклонение, имеют широкое распределение вдоль оси измерения.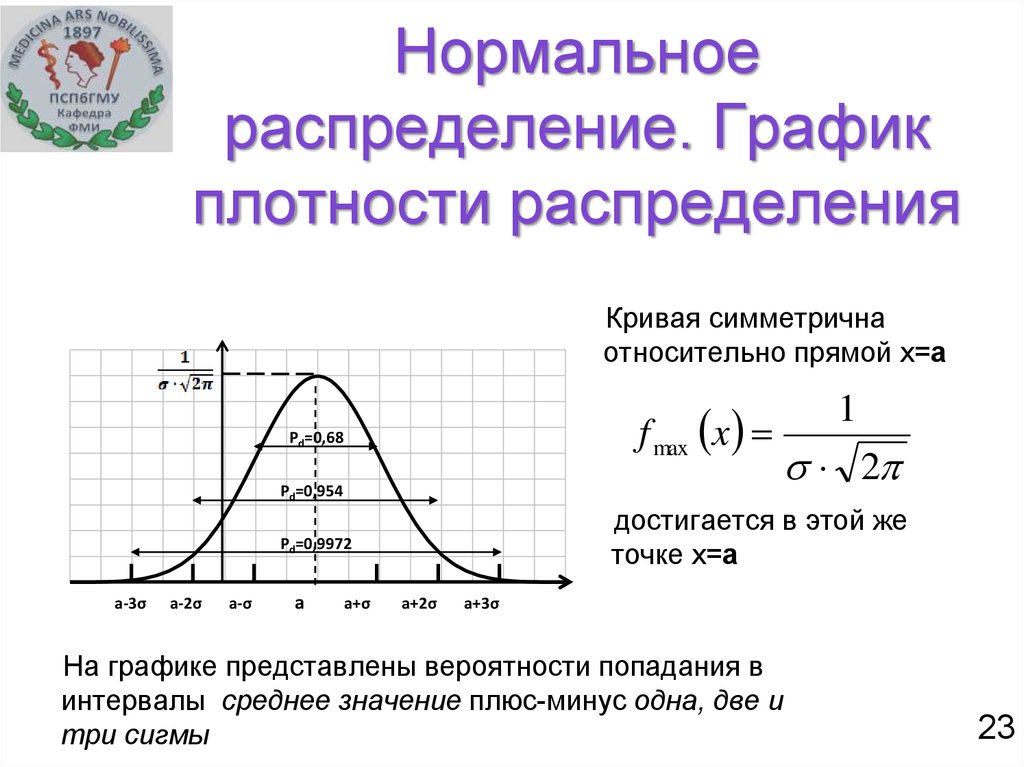 Одним из математических свойств нормального распределения является то, что ровно 95% распределения лежит между
Одним из математических свойств нормального распределения является то, что ровно 95% распределения лежит между
\(μ — (1,96 x σ) и μ + (1,96 x σ)\)
При изменении множителя 1,96 на 2,58 ровно 99% нормального распределения находится в соответствующем интервале.
На практике два параметра нормального распределения, μ и σ, должны оцениваться по данным выборки. Для этого сначала берется случайная выборка из населения. Затем вычисляются среднее значение выборки и стандартное отклонение выборки, \(SD ({\bar x}) = S\) . Если выборка берется из такого нормального распределения и при условии, что выборка не слишком мала, то примерно 95% выборки лежат в интервале:
\(\bar x\; — \left[ {1,96\; \times SD\left( {\bar x} \right)} \right]\) до \( \bar x + \left[ {1,96\; \times SD\left( {\bar x} \right)} \right]\)
Это вычисляется простой заменой параметров совокупности μ и σ выборкой оценки и 90 253 s 90 256 в предыдущем выражении.
В соответствующих обстоятельствах этот интервал может определять референтный интервал для конкретного лабораторного теста, который затем используется в диагностических целях.
Мы можем использовать тот факт, что наша выборка данных о весе при рождении имеет нормальное распределение, чтобы рассчитать эталонный диапазон. Мы уже упоминали, что около 95% наблюдений (из нормального распределения) лежат в пределах ±1,96 SD от среднего значения. Таким образом, референтный диапазон для нашей выборки младенцев с использованием значений, приведенных на гистограмме выше, составляет:
Масса тела ребенка при рождении тесно связана с риском смертности в течение первого года жизни и, в меньшей степени, с проблемами развития в детстве и риском различных заболеваний во взрослом возрасте. Если данные не распределены нормально, то мы можем основывать нормальный контрольный диапазон на наблюдаемых процентилях выборки, т.е. 95% наблюдаемых данных лежат между 2,5 и 97,5 процентилями. В этом примере референтный диапазон на основе процентиля для нашей выборки был рассчитан от 2,19 кг до 4,43 кг.
Большинство контрольных диапазонов основаны на выборках более 3500 человек. За многие годы и миллионы рождений ВОЗ установила нормальный диапазон веса при рождении для новорожденных. Эти диапазоны представляют собой результаты, которые являются приемлемыми для новорожденных, и фактически охватывают средние 80% распределения популяции, то есть от 10 до 9 лет.0-й центиль. Младенцы с низкой массой тела при рождении обычно определяются (ВОЗ) как вес менее 2500 г (10-й процентиль) независимо от гестационного возраста, а дети с большой массой тела при рождении определяются как дети с массой тела более 4000 кг (90-й центиль). Следовательно, нормальный диапазон веса при рождении составляет от 2,5 до 4 кг. Для наших выборочных данных диапазон от 10-го до 90-го центиля был аналогичным, от 2,75 до 4,03 кг.
За многие годы и миллионы рождений ВОЗ установила нормальный диапазон веса при рождении для новорожденных. Эти диапазоны представляют собой результаты, которые являются приемлемыми для новорожденных, и фактически охватывают средние 80% распределения популяции, то есть от 10 до 9 лет.0-й центиль. Младенцы с низкой массой тела при рождении обычно определяются (ВОЗ) как вес менее 2500 г (10-й процентиль) независимо от гестационного возраста, а дети с большой массой тела при рождении определяются как дети с массой тела более 4000 кг (90-й центиль). Следовательно, нормальный диапазон веса при рождении составляет от 2,5 до 4 кг. Для наших выборочных данных диапазон от 10-го до 90-го центиля был аналогичным, от 2,75 до 4,03 кг.
Биномиальное распределение
Если группе пациентов дается новое лекарство для облегчения определенного состояния, то пропорция p последовательно пролеченных пациентов можно рассматривать как показатель успешности лечения в популяции.
Пропорция выборки p аналогична выборочному среднему в том смысле, что если мы наберем 0 баллов для тех s пациентов, у которых лечение оказалось неэффективным, и 1 для тех r , которые добились успеха, то p = r/ n , где n = r + s — общее количество пролеченных больных. Таким образом, p также представляет собой среднее значение. 9{n — r}}\)
… для последовательных значений R от 0 до n. В приведенном выше n! читается как «n факториал», а r ! как «r факториал». Для r = 4, r != 4×3×2×1=24. Оба 0! и 1! принимаются равными 1. Заштрихованная область, отмеченная на рис. 2 (ниже), соответствует приведенному выше выражению для биномиального распределения, рассчитанного для каждого из r =8,9,…,20 и затем сложенного. Эта площадь составляет 0,1018. Таким образом, вероятность восьми и более ответов из 20 равна 0,1018.
Для фиксированного размера выборки n форма биномиального распределения зависит только от . Предположим, что 90 253 n 90 256 = 20 пациентов нуждаются в лечении, и известно, что в среднем четверть, или = 0,25, будет реагировать на это конкретное лечение. Количество фактически наблюдаемых ответов может принимать только целочисленные значения от 0 (нет ответов) до 20 (все ответы). Биномиальное распределение для этого случая показано на рисунке 2.
Распределение несимметрично, оно имеет максимум при пяти ответах, а высота блоков соответствует вероятности получения определенного количества ответов от 20 пациентов, которые еще не получены. лечиться. Следует отметить, что математическое ожидание для r , количество успехов, которые еще предстоит наблюдать, если мы пролечим n пациентов, равно (nx). Потенциальное изменение этого ожидания выражается соответствующим стандартным отклонением:
\({\rm{SD}}\left( r \right) = \;\sqrt {n\pi \left({1 — \pi} \right)}\)
На рисунке 2 также показано нормальное распределение с μ = n = 5 и σ = √[n(1 — )] = 1,94, наложенное на биномиальное распределение с = 0,25 и n = 20 В этом случае нормальное распределение довольно точно описывает биномиальное распределение. Однако если n мало или близко к 0 или 1, несоответствие между нормальным и биномиальным распределениями с одинаковыми средним значением и стандартным отклонением увеличивается, и нормальное распределение больше нельзя использовать для аппроксимации биномиального распределения. В таких случаях должны использоваться вероятности, генерируемые самим биномиальным распределением.
Однако если n мало или близко к 0 или 1, несоответствие между нормальным и биномиальным распределениями с одинаковыми средним значением и стандартным отклонением увеличивается, и нормальное распределение больше нельзя использовать для аппроксимации биномиального распределения. В таких случаях должны использоваться вероятности, генерируемые самим биномиальным распределением.
Кроме того, только в ситуациях, когда существует разумное соответствие между распределениями, мы будем использовать приведенное ранее выражение доверительного интервала. По техническим причинам выражение, данное для доверительного интервала для пропорции, является приблизительным. Аппроксимация обычно будет достаточно хорошей при условии, что p не слишком близко к 0 или 1, в ситуациях, когда либо почти никто, либо почти все пациенты не реагируют на лечение. Аппроксимация улучшается с увеличением размера выборки n .
Рисунок 2. Биномиальное распределение для n=20 с =0,25 и нормальное приближение размер популяции n велик, вероятность отдельного события мала, но ожидаемое количество событий n умеренное (скажем, пять или более).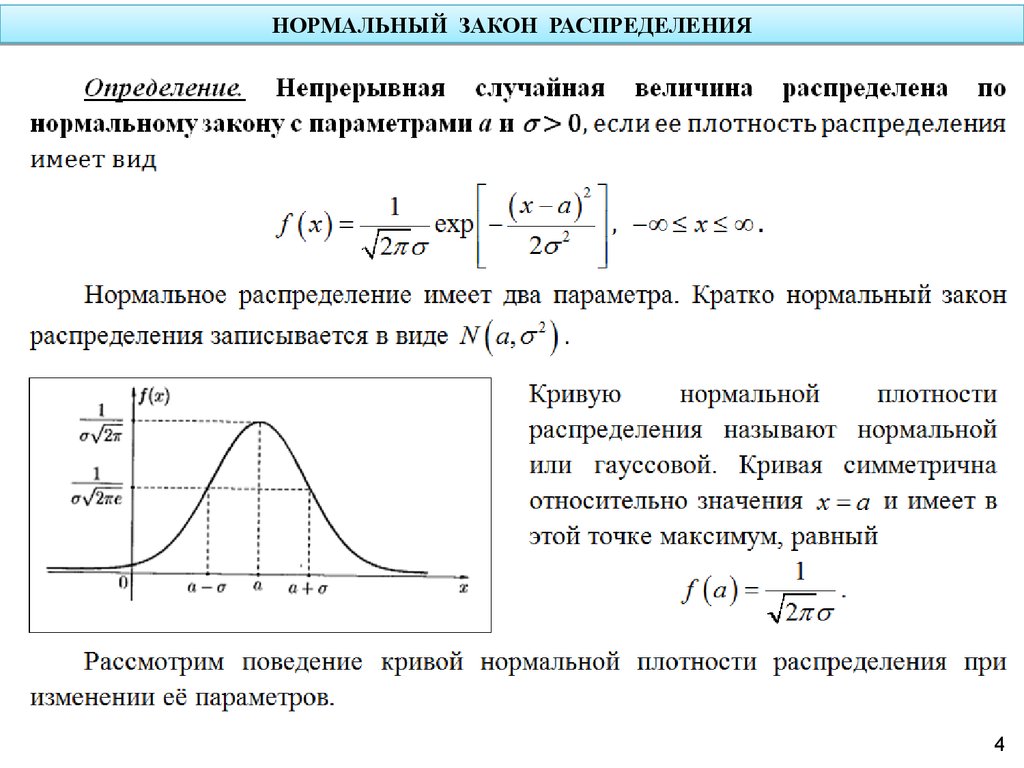 Типичными примерами являются количество смертей в городе от той или иной болезни в день или количество госпитализаций в конкретную больницу.
Типичными примерами являются количество смертей в городе от той или иной болезни в день или количество госпитализаций в конкретную больницу.
Пример
Wight et al (2004) изучили вариации числа доноров органов с работающим сердцем в Великобритании. Они обнаружили, что за два года с 1999 по 2000 год в Великобритании было 1330 доноров органов в возрасте от 15 до 69 лет. Доноры с бьющимся сердцем — это тяжелобольные пациенты, находящиеся в отделении интенсивной терапии (ОИТ) и подключенные к аппарату искусственной вентиляции легких.
Теперь видно, что распределение числа доноров принимает только целые значения, поэтому распределение в этом отношении похоже на биномиальное. Тем не менее, нет теоретического ограничения на количество доноров органов, которое может произойти в конкретный день. Здесь население — население Великобритании в возрасте 15-69 лет., в течение двух лет, что составляет более 82 миллионов человеко-лет, поэтому в этом случае можно считать, что каждый участник имеет очень небольшую вероятность того, что он действительно перенесет событие, в этом случае он будет госпитализирован в отделение интенсивной терапии и помещен на ИВЛ с угрожающее жизни состояние.
Среднее количество доноров органов в день за двухлетний период рассчитывается как:
\(r = \;\frac {{1330}}{{\left( {365 + 365} \right)}} = \;\frac{{1330}}{{730}} = 1,82\) донорских органов в день
Следует отметить, что выражение для среднего аналогично выражению для , за исключением того, что здесь часто встречаются несколько значений данных; и поэтому вместо того, чтобы записывать каждое как отдельную цифру в числителе, они сначала группируются и подсчитываются. Для данных, полученных из распределения Пуассона, стандартная ошибка, то есть стандартное отклонение r , оценивается как SE( r ) = √( r/n ), где n — общее количество дней. (или альтернативная единица времени). При условии, что уровень донорства органов не слишком низок, 95%-й доверительный интервал для базовой (истинной) нормы донорства органов λ можно рассчитать обычным способом:
\(r — \left[ {1,96\; \times {\rm{SE}}\left( r \right )} \right]\;\;{\rm{to\;\;}}r + \left[ {1,96{\rm{\;}} \times {\rm{SE}}\left( r \right )} \right]\)
В приведенном выше примере r = 1,82, SE( r ) = √ (1,82/730) = 0,05, и поэтому 95% доверительный интервал для λ составляет от 1,72 до 1,92 донорских органов в день. Точные доверительные интервалы можно рассчитать, как описано Altman et al. (2000). 9{ — \lambda }}\;\)
Точные доверительные интервалы можно рассчитать, как описано Altman et al. (2000). 9{ — \lambda }}\;\)
…для последовательных значений r от 0 до бесконечности. Здесь e — экспоненциальная константа 2,7182…, а λ — коэффициент популяции, который в приведенном выше примере оценивается как r .
Пример
Предположим, что до исследования Wight et al. (2004) ожидалось, что количество донорских органов в день будет примерно два. Тогда, предполагая λ = 2, мы ожидаем, что вероятность 0 донорских органов в данный день будет (2 0 /0!)e -2 =e — 2 = 0,135. (Помните, что 2 0 и 0! оба равны 1.) Вероятность донорства одного органа будет (2 1 /1!)e — 2 = 2(e — 2 ) = 0,271. Точно так же вероятность двух донорских органов в день равна (2 2 /2!)e -2 = 2(e -2 ) = 0,271; и так далее, чтобы дать за три пожертвования 0,180, четыре пожертвования 0,090, пять пожертвований 0,036, шесть пожертвований 0,012 и т. д. Если затем исследование будет проводиться в течение 2 лет (730 дней), каждая из этих вероятностей умножается на 730, чтобы получить ожидаемое количество дней, в течение которых произойдет 0, 1, 2, 3 и т. д. пожертвований. Эти ожидания 98,8, 197,6, 197,6, 131,7, 26,3, 8,8 сут. Затем можно провести сравнение между ожидаемым и фактически наблюдаемым.
д. Если затем исследование будет проводиться в течение 2 лет (730 дней), каждая из этих вероятностей умножается на 730, чтобы получить ожидаемое количество дней, в течение которых произойдет 0, 1, 2, 3 и т. д. пожертвований. Эти ожидания 98,8, 197,6, 197,6, 131,7, 26,3, 8,8 сут. Затем можно провести сравнение между ожидаемым и фактически наблюдаемым.
Другие дистрибутивы
Краткое описание некоторых других дистрибутивов дано для полноты картины.
t-распределение
Распределение Стьюдента t- представляет собой непрерывное распределение вероятностей с формой, аналогичной нормальному распределению, но с более широкими хвостами. 9Распределения 0253 t- используются для описания выборок, взятых из совокупности, и точная форма распределения зависит от размера выборки. Чем меньше размер выборки, тем более разбросаны хвосты, и чем больше размер выборки, тем ближе распределение t- к нормальному распределению (рис. 3). В то время как обычно нормальное распределение используется в качестве приближения при оценке средних значений выборок из популяции с нормальным распределением, когда один и тот же размер невелик (скажем, n<30), 9Предпочтительно использовать дистрибутив 0253 t-.
3). В то время как обычно нормальное распределение используется в качестве приближения при оценке средних значений выборок из популяции с нормальным распределением, когда один и тот же размер невелик (скажем, n<30), 9Предпочтительно использовать дистрибутив 0253 t-.
Рис. 3. Распределение Стьюдента для различных размеров выборки. По мере увеличения размера выборки t-распределение все больше приближается к нормальному.
Распределение хи-квадрат
Распределение хи-квадрат представляет собой непрерывное распределение вероятностей, форма которого определяется числом степеней свободы. Это распределение с наклоном вправо, но по мере увеличения числа степеней свободы оно приближается к нормальному распределению (рис. 4). Распределение хи-квадрат важно для его использования в тестах хи-квадрат. Они часто используются для проверки отклонений между наблюдаемыми и ожидаемыми частотами или для определения независимости между категориальными переменными. При проведении теста хи-квадрат значения вероятности, полученные из распределений хи-квадрат, можно найти в статистической таблице.
При проведении теста хи-квадрат значения вероятности, полученные из распределений хи-квадрат, можно найти в статистической таблице.
Рис. 4. Распределение хи-квадрат для различных степеней свободы. Распределение становится менее наклонным вправо по мере увеличения числа степеней свободы.
Ссылки
- Altman D.G., Machin D., Bryant T.N., & Gardner M.J. STATMIST. Доверительные интервалы и статистические рекомендации (2-е издание). Лондон: британский
Медицинский журнал, 2000 - Кэмпбелл М.Дж., Мачин Д. и Уолтерс С.Дж. Медицинская статистика: подход, основанный на здравом смысле, 4-е изд. Чичестер: Wiley-Blackwell 2007
- O’Cathain A., Walters S.J., Nicholl J.P., Thomas K.J., & Kirkham M. Использование брошюр, основанных на фактических данных, для содействия информированному выбору в сфере охраны материнства: рандомизированное
контролируемое исследование в повседневной практике.

 Чармоний
Чармоний


 Суммарные измерения данных 1/7–1
Суммарные измерения данных 1/7–1  любой из
рисунки ниже).
любой из
рисунки ниже). Когда значения получаются путем суммирования числа
случайных результатов, что, как правило, имеет место со многими переменными
встречаются в клинике, сумма имеет тенденцию принимать гауссово распределение.
Итак, гауссовские распределения встречаются исключительно
часто и оказываются основой для многих
логические статистические тесты.
Когда значения получаются путем суммирования числа
случайных результатов, что, как правило, имеет место со многими переменными
встречаются в клинике, сумма имеет тенденцию принимать гауссово распределение.
Итак, гауссовские распределения встречаются исключительно
часто и оказываются основой для многих
логические статистические тесты.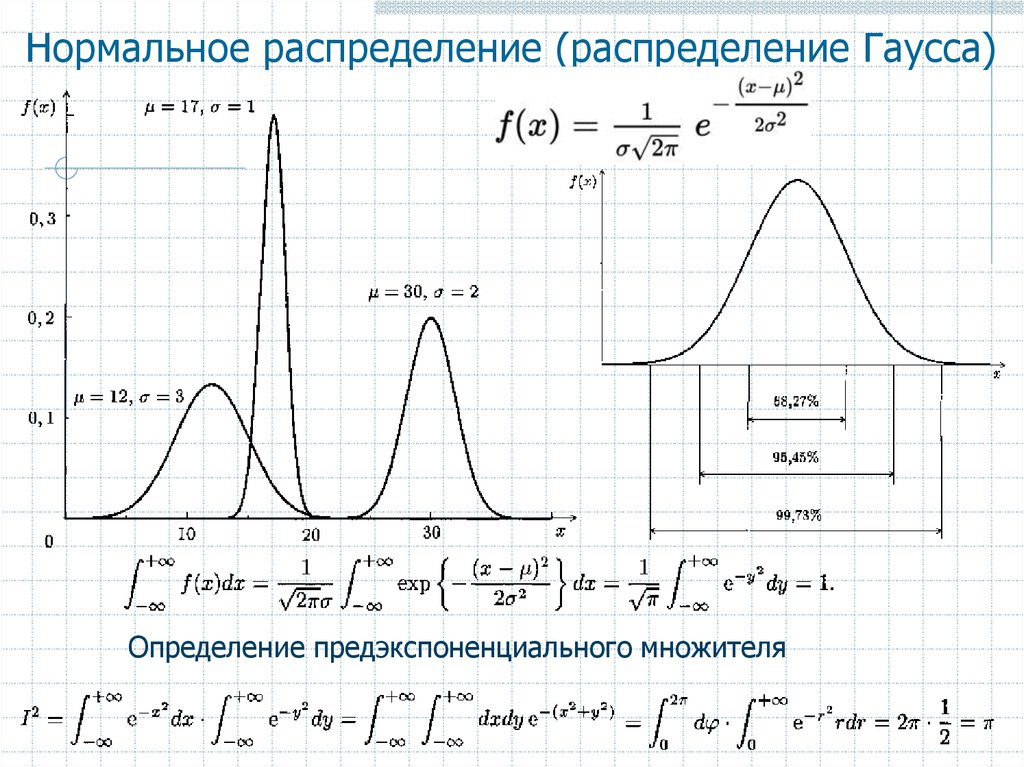 Суммарные измерения данных 1.7–3
Суммарные измерения данных 1.7–3 
 7.4 Пуассон Другим важным набором дискретных распределений является
Распределение Пуассона. Полезно подумать о Пуассон
распределение как частный случай биномиального распределения,
где число испытаний очень велико, а вероятность
очень маленький. В частности, Пуассон часто используется для
модельные ситуации, когда число испытаний неопределенно велико,
но вероятность того или иного события при каждом испытании приближается
нуль. Количество бактерий на чашке Петри можно представить как
распределение Пуассона. Крошечные области на пластине можно рассматривать как
испытаний, и бактерия может появиться или не появиться в такой области.
Вероятность того, что бактерия окажется в любой заданной области, равна
очень мало, но таких очень много
области на плите. Похожий случай будет
при подсчете количества красных клеток, попадающих в квадрат на
сетка гемоцитометра, глядя на распределение числа
человек в Америке, убитых ударами молнии за один год, или
случаев уколов иглой, связанных с ВИЧ, в больницах США каждый
год.
7.4 Пуассон Другим важным набором дискретных распределений является
Распределение Пуассона. Полезно подумать о Пуассон
распределение как частный случай биномиального распределения,
где число испытаний очень велико, а вероятность
очень маленький. В частности, Пуассон часто используется для
модельные ситуации, когда число испытаний неопределенно велико,
но вероятность того или иного события при каждом испытании приближается
нуль. Количество бактерий на чашке Петри можно представить как
распределение Пуассона. Крошечные области на пластине можно рассматривать как
испытаний, и бактерия может появиться или не появиться в такой области.
Вероятность того, что бактерия окажется в любой заданной области, равна
очень мало, но таких очень много
области на плите. Похожий случай будет
при подсчете количества красных клеток, попадающих в квадрат на
сетка гемоцитометра, глядя на распределение числа
человек в Америке, убитых ударами молнии за один год, или
случаев уколов иглой, связанных с ВИЧ, в больницах США каждый
год.
