|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 20Следующая ⇒ Если нам известны координаты точек (естественно, в заданной системе координат), то однозначно известно их положение. Поэтому можно найти любые геометрические характеристики их взаимного расположения. Получим формулы, позволяющие по известным координатам двух точек вычислить расстояние между ними. s = |x2 − x1|, (3)
где х1, х2 − координаты точек А1 и А2 соответственно. Пусть на плоскости задана система координат ХОY, в которой координаты точки А1 равны х1 и у1, а координаты точки А2, соответственно, равны х2 и у2 (рис. 8).
рис. 8
В прямоугольном треугольнике А1А2В длина стороны А2В равна |х2 − х1|, а длина стороны А1В = |у2 − у1|, поэтому расстояние между точками А1 и А2 можно найти по теореме Пифагора: s = √{(x2 − x1)2 + (y2 − y1)2}. (4) Упражнение Покажите, что расстояние между двумя точками в пространстве вычисляется по формуле s = √{(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2}. Давайте теперь попытаемся вычислить расстояние между этими же точками, но в другой системе отсчета Х/О/Y/, которая сдвинута относительно исходной системы координат ХОY. В этой системе отсчета координаты точек А1 и А2 можно найти по формулам преобразований (1) x1/ = −xo + x1; x2/ = −xo + x2
Как следует из этих формул, х2 − х1 = х2/ − х1/, что, впрочем, и должно быть: если вторая точка лежит правее первой, то это их взаимное расположение не зависит от выбора системы координат, расстояние между проекциями точек на одну и ту же ось не зависит от начала отсчета. Аналогичное соотношение можно записать и для координат у этих точек, поэтому, как следует из здравого смысла, результат вычисления по формуле (4) не зависит от выбора системы координат (конечно, при неизменной единице измерения длины). Величины, которые остаются неизменными при изменении системы координат, называются инвариантными. Вот еще одно подтверждение возможности использования систем координат − можно найти физические величины, которые не зависят от выбора системы координат. Поиск таких инвариантных физических величин очень важен, потому что, как правило, именно они проще всего поддаются измерению, именно они фактически определяют протекание того или иного физического процесса, именно они убеждают скептиков в возможностях правильного физического описания различных явлений. Полярная система координат Декартовая система координат на плоскости является, безусловно, самой простой, однако не единственно возможной.
рис. 9
Положение точки А на плоскости в этом случае описывается координатами: величинами ρ − полярное расстояние (ОА) и φ − полярный угол (АОх). Очевидно, что координата ρ неотрицательна, угол φ может принимать любые значения. Легко выразить декартовые координаты точки через полярные:
x = ρcosφ; y = ρsinφ. (1)
Обратное преобразование несколько сложнее: ρ = √{x2 + y2}; φ = arctg(y/x) ± kπ. (2)
Заметим, что полярный угол определяется неоднозначно, при добавлении к нему любого кратного 2π положение точки на плоскости не изменяется. Получим теперь формулы преобразования координат точки при повороте системы координат. Рассмотрим две декартовые системы координат ХОY и Х/ОY/, начала отсчета которых совпадают, а оси повернуты на некоторый угол φo (рис. 10).
рис. 10
Очевидно, что в обеих системах расстояния до начала отсчета одинаковы, а полярные углы связаны линейным соотношением ρ/ = ρ, φ/ = φ − φo. (3)
Эти простые формулы и выражают преобразования координат при повороте осей. Получим также и формулы преобразования поворота для декартовых координат. Запишем выражения для декартовых координат в «штрихованной» системе отсчета
x/
y/ = ρ/sinφ/ = ρsin(φ − φo).
Используем известные тригонометрические формулы для синуса и косинуса разности углов:
x/ = ρcos(φ − φo) = ρcosφcosφo + ρsinφsinφo;
y/ = ρsin(φ − φo) = ρsinφcosφo − ρcosφsinφo. Наконец, замечая, что ρcosφ = x, а ρsinφ = y, получим искомые выражения:
x/ = xcosφo + ysinφo; y/ = ycosφo − xsinφo. (4)
Заметьте, что формулы обратного преобразования получаются из системы (4) посредством очевидной замены φo на −φo, что также является следствием относительности координат. Эти преобразования, конечно, можно было получить и геометрическим способом с помощью приведенного рисунка. Упражнения 1. 2. Покажите, что расстояние между двумя точками, полярные координаты которых (ρ1, φ1) и (ρ2, φ2), определяется по формуле S = √{ρ12 + ρ22 − 2ρ1ρ2cos(φ1 − φ2)}. ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Алгоритмические операторы Matlab Конструирование и порядок расчёта дорожной одежды Исследования учёных: почему помогают молитвы? Почему терпят неудачу многие предприниматели? |
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 105; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Все правила по сольфеджио
Мы показали это для преобразования сдвига, однако очевидно, что и при повороте системы координат формула (4) должна давать один и тот же результат. Весьма интересная ситуация: все четыре координаты при изменении системы отсчета изменяются, а величина расстояния остается неизменной!
Во многих случаях предпочтительнее использовать другие криволинейные системы координат. Среди этих координат наиболее часто используется полярная система (рис. 9).
Эта неоднозначность редко приводит к недоразумениям, зато оговоренное произвольное (от минус до плюс бесконечности) изменение угла позволяет легко и красиво описывать некоторые виды механического движения тел (например, вращение).
Покажите, что формулы преобразования (4) не изменяют расстояния до начала координат.
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)3 метода как рассчитать расстояние между двумя точками по координатам и примеры
В этом уроке мы обсудим различные методы, с помощью которых пользователь может рассчитать расстояние между двумя местами на Земле. geopy – это библиотека Python, которая помогает рассчитать географическое расстояние.
Сначала нужно установить geopy с помощью следующей команды:
pip install geopy
После успешной установки мы готовы к работе с библиотекой geopy.
Ниже приведены важные методы, которые мы будем использовать, чтобы рассчитать расстояние между двумя точками с помощью GEOPY в Python:
- Метод 1: с использованием геодезического расстояния
Геодезическое расстояние – это длина кратчайшего пути между двумя точками на любой поверхности Земли.
В следующем примере мы покажем, как пользователь может вычислить геодезическое расстояние на основе данных широты и долготы.
Пример:
# First, import the geodesic module from the geopy library
from geopy.distance import geodesic as GD
# Then, load the latitude and longitude data for New York & Texas
New_York = (40.7128, 74.0060)
Texas = (31.9686, 99.9018)
# At last, print the distance between two points calculated in kilo-metre
print ("The distance between New York and Texas is: ", GD(New_York, Texas).km)
Выход:
The distance between New York and Texas is: 2507.14797665193
- Метод 2: с использованием расстояния по большому кругу
Расстояние по большому кругу – это кратчайший путь между двумя точками на сфере. В этом случае мы предположим, что Земля – это идеальная сфера. В следующем примере показано, как пользователь может рассчитать расстояние по большому кругу, используя данные долготы и широты двух точек.
Пример:
# First, import the great_circle module from the geopy library
from geopy.distance import great_circle as GC
# Then, load the latitude and longitude data for New York & Texas
New_York = (40.7128, 74.0060)
Texas = (31.9686, 99.9018)
# At last, print the distance between two points calculated in kilo-metre
print ("The distance between New York and Texas is: ", GC(New_York, Texas).km)
Выход:
The distance between New York and Texas is: 2503.045970189156
- Метод 3: с использованием формулы гаверсинуса
Ортодромическое расстояние используется для вычисления кратчайшего расстояния между двумя точками широты и долготы на поверхности земли.
Используя этот метод, пользователю необходимо иметь координаты двух точек (P и Q).
Сначала нужно преобразовать значения точек широты и долготы из десятичных градусов в радианы, а затем разделить значения широты и долготы на (180 / π).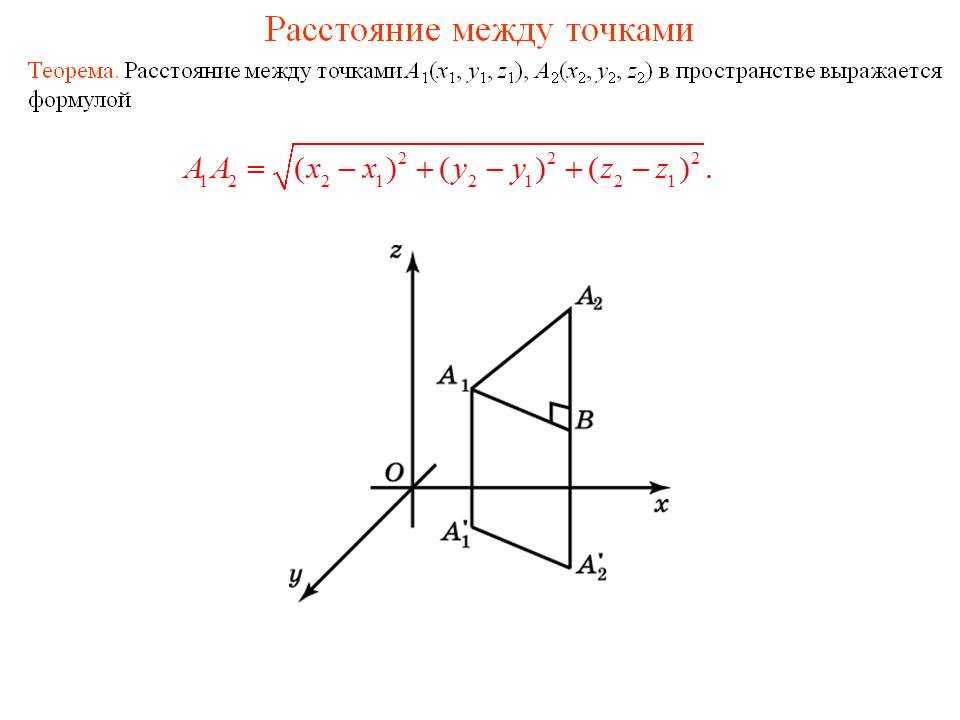
Пользователь должен использовать значение «π = 22/7». Тогда значение (180 / π) будет «57,29577». Если пользователь хочет рассчитать расстояние в милях, он может использовать значение радиуса Земли, то есть «3963», а если в километрах – использовать значение «6,378,80».
Формулы:
How to calculate the value of latitude in radians: The value of Latitude in Radian: Latitude (La1) = La1 / (180/?) OR The value of Latitude in Radian: Latitude (La1) = La1 / 57.29577 How to calculate the value of longitude in radians: The value of Longitude in Radian: Longitude (Lo1) = Lo1 / (180/?) OR The value of Longitude in Radian: Longitude (Lo1) = Lo1 / 57.29577
Пользователю нужны координаты точки P и точки Q с точки зрения долготы и широты, а затем необходимо использовать приведенную выше формулу для преобразования их в радианы.
Теперь рассчитаем расстояние между двумя точками по следующей формуле.
Формула:
Для миль:
Distance (D) = 3963.0 * arccos[(sin(La1) * sin(La2)) + cos(La1) * cos(La2) * cos(Lo2 - Lo1)]
Для километров:
Distance (D) = 3963.0 * arccos[(sin(La1) * sin(La2)) + cos(La1) * cos(La2) * cos(Lo2 - Lo1)]
Таким образом, пользователь может рассчитать кратчайшее расстояние между двумя заданными точками на Земле с помощью формулы гаверсинуса.
Пример:
from math import radians, cos, sin, asin, sqrt
# For calculating the distance in Kilometres
def distance_1(La1, La2, Lo1, Lo2):
# The math module contains the function name "radians" which is used for converting the degrees value into radians.
Lo1 = radians(Lo1)
Lo2 = radians(Lo2)
La1 = radians(La1)
La2 = radians(La2)
# Using the "Haversine formula"
D_Lo = Lo2 - Lo1
D_La = La2 - La1
P = sin(D_La / 2)**2 + cos(La1) * cos(La2) * sin(D_Lo / 2)**2
Q = 2 * asin(sqrt(P))
# The radius of earth in kilometres.
R_km = 6371
# Then, we will calculate the result
return(Q * R_km)
# driver code
La1 = 40.7128
La2 = 31.9686
Lo1 = -74.0060
Lo2 = -99.9018
print ("The distance between New York and Texas is: ", distance_1(La1, La2, Lo1, Lo2), "K.M")
# For calculating the distance in Miles
def distance_2(La1, La2, Lo1, Lo2):
# The math module contains the function name "radians" which is used for converting the degrees value into radians.
Lo1 = radians(Lo1)
Lo2 = radians(Lo2)
La1 = radians(La1)
La2 = radians(La2)
# Using the "Haversine formula"
D_Lo = Lo2 - Lo1
D_La = La2 - La1
P = sin(D_La / 2)**2 + cos(La1) * cos(La2) * sin(D_Lo / 2)**2
Q = 2 * asin(sqrt(P))
# The radius of earth in Miles.
R_Mi = 3963
# Then, we will calculate the result
return(Q * R_Mi)
print ("The distance between New York and Texas is: ", distance_2(La1, La2, Lo1, Lo2), "Miles")
R_km = 6371
# Then, we will calculate the result
return(Q * R_km)
# driver code
La1 = 40.7128
La2 = 31.9686
Lo1 = -74.0060
Lo2 = -99.9018
print ("The distance between New York and Texas is: ", distance_1(La1, La2, Lo1, Lo2), "K.M")
# For calculating the distance in Miles
def distance_2(La1, La2, Lo1, Lo2):
# The math module contains the function name "radians" which is used for converting the degrees value into radians.
Lo1 = radians(Lo1)
Lo2 = radians(Lo2)
La1 = radians(La1)
La2 = radians(La2)
# Using the "Haversine formula"
D_Lo = Lo2 - Lo1
D_La = La2 - La1
P = sin(D_La / 2)**2 + cos(La1) * cos(La2) * sin(D_Lo / 2)**2
Q = 2 * asin(sqrt(P))
# The radius of earth in Miles.
R_Mi = 3963
# Then, we will calculate the result
return(Q * R_Mi)
print ("The distance between New York and Texas is: ", distance_2(La1, La2, Lo1, Lo2), "Miles")
Выход:
The distance between New York and Texas is: 2503.
04243426357 K.M
The distance between New York and Texas is: 1556.985899699659 Miles
В этом уроке мы обсудили различные методы расчета расстояния между двумя точками на поверхности земли с помощью библиотеки geopy и показали примеры каждого метода.
Михаил Русаков
Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
Еще для изучения:
Расчет расстояния между двумя точками с помощью примеров кода
Расчет расстояния между двумя точками с помощью примеров кода
Добрый день, ребята. В этом посте мы рассмотрим, как решить программную головоломку «Вычислить расстояние между двумя точками».
по умолчанию расстояние (p1, p2):
return math.sqrt(((p1[0] - p2[0]) ** 2) + ((p1[1] - p2[1]) ** 2))
Ниже вы найдете несколько примеров различных способов решения задачи «Вычислить расстояние между двумя точками».
1.
Получить координаты обеих точек в пространстве.
1. Вычесть координаты x одной точки из другой, то же самое для компонентов y.
1. Возведите в квадрат оба результата по отдельности.
1. Суммируйте значения, полученные на предыдущем шаге.
1. Найдите квадратный корень из приведенного выше результата.
(x1-x2) в квадрате + (y1 + y2) в квадрате = расстояния в квадрате
Мы научились решать задачу «Вычислить расстояние между двумя точками», рассмотрев ряд различных случаев.
Какое расстояние между точками А и В?
Расстояния в геометрии всегда положительны, за исключением случаев, когда точки совпадают. Расстояние от A до B такое же, как расстояние от B до A. Чтобы вывести формулу для расстояния между двумя точками на плоскости, мы рассмотрим две точки A (a, b) и B (c, d) .
Как найти расстояние между двумя точками в пространстве?
Формула расстояния утверждает, что расстояние между двумя точками в пространстве xyz равно квадратному корню из суммы квадратов разностей между соответствующими координатами.
То есть, учитывая P1 = (x1,y1,z1) и P2 = (x2,y2,z2), расстояние между P1 и P2 определяется как d(P1,P2) = (x2 x1)2 + (y2 y1) 2 + (z2 z1)2.
Что такое пример формулы расстояния?
Формула расстояния в координатной геометрии используется для вычисления расстояния между двумя заданными точками. Формула расстояния для вычисления расстояния между двумя точками (x1,y1) (x1, y1) и (x2,y2) (x2, y2) задается как D=√(x2−x1)2+ (y2−y1)2 D знак равно ( Икс 2 — Икс 1 ) 2 + ( y 2 — y 1 ) 2 .
Пример расчета расстояния?
Какое расстояние между 3 точками?
Формула расстояния между 3 точками Чтобы рассчитать расстояние между 3 точками, рассчитайте расстояние между всеми 3 комбинациями точек, просуммируйте эти значения, а затем разделите на 3.27-Sept-2022
Как найти расстояние между двумя точками в прямоугольной системе координат?
Формула расстояния d=√(x2−x1)2+(y2−y1)2 выводится из теоремы Пифагора и дает нам расстояние между любыми двумя точками (x1,y1) и (x2,y2), в прямоугольной координатной плоскости.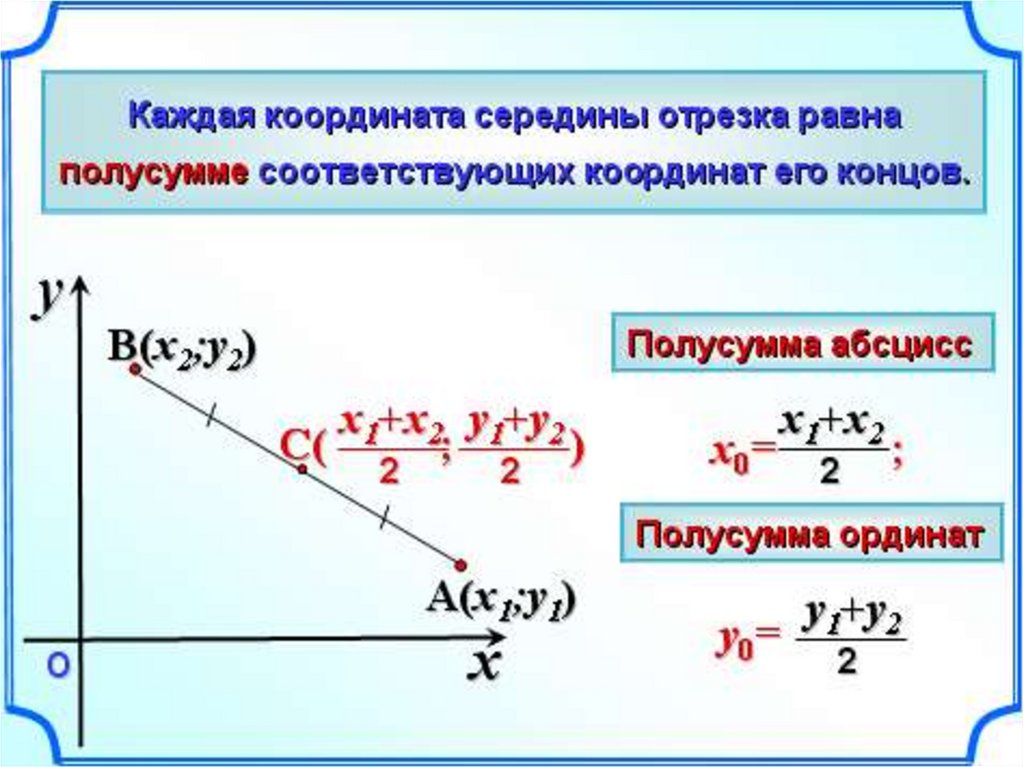
06-окт-2021
Как найти расстояние между двумя точками на графическом калькуляторе?
Какова формула для нахождения общего расстояния?
Расстояние = время * скорость. д = v * т.
Для чего используется формула расстояния?
Формула расстояния — это формула, используемая для нахождения расстояния между двумя точками. Эти точки могут быть в любом измерении. Например, вам может понадобиться найти расстояние между двумя точками на прямой (1d), двумя точками на плоскости (2d) или двумя точками в пространстве (3d).
Почему работает формула расстояния?
Расстояние между двумя точками на числовой прямой
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4715
- Ларри Грин
- Общественный колледж Лейк-Тахо
Результаты обучения
- Вычислите расстояние между двумя точками на числовой прямой, когда обе точки неотрицательны.
- Вычислите расстояние между двумя точками на числовой прямой, если хотя бы одна из них имеет отрицательное значение.
Числовая линия является основной визуальной базой в статистике, и нам часто нужно посмотреть на две точки на числовой прямой и определить расстояние между ними. Это используется для нахождения основания прямоугольника или другой фигуры, лежащей выше числовой прямой. К концу этого раздела вы сможете определить расстояние между любыми двумя точками на числовой прямой, полученной из статистического приложения.
Ключ к нахождению расстояния между двумя точками состоит в том, чтобы помнить, что геометрическое определение вычитания — это расстояние между двумя числами, пока мы вычитаем меньшее число из большего.
Пример \(\PageIndex{1}\)
Найдите расстояние между точками 2,5 и 9,8, как показано ниже на числовой прямой.
Решение
Чтобы найти расстояние, мы просто вычитаем:
\[9,8\:-\:2,5\:=\:7,3 \нечисло\]
Пример \(\PageIndex{2}\)
При нахождении вероятностей с равномерным распределением мы должны найти основание прямоугольника, лежащего на числовой прямой.
Найдите основание прямоугольника, показанного ниже, который представляет равномерное распределение от 2 до 9.
Решение
Мы просто вычитаем:
\[9\:-\:2\:=\:7 \ nonumber\]
В статистике часто встречаются точки на числовой прямой, где обе точки не положительны, и нам нужно найти расстояние между ними.
Пример \(\PageIndex{3}\)
На приведенной ниже диаграмме показан доверительный интервал для разницы между долей мужчин, планирующих работать в сфере здравоохранения, и долей женщин. Какова ширина доверительного интервала?
Решение
Всякий раз, когда мы хотим найти расстояние между двумя числами, мы всегда вычитаем. Напомним, что вычитание отрицательного числа — это сложение.
\[0,01\:-\:\влево(-0,04\вправо)\:=\:0,01\:+\:0,04\:=\:0,05 \не число\]
Следовательно, ширина доверительного интервала равна 0,05.
Пример \(\PageIndex{4}\)
Средняя стоимость счетов кредитных карт составляет -6358 долларов.
Было проведено исследование недавних выпускников колледжей, и выяснилось, что их средняя стоимость счетов кредитных карт составляет -5215 долларов. Числовая строка ниже показывает эту ситуацию. Насколько далеко друг от друга эти значения?
Решение
Мы вычтем два числа и вспомним, что когда мы вычитаем два отрицательных числа, когда смотрим на правое минус левое, мы делаем их положительными и вычитаем положительные числа.
\[-5215\:-\:\left(-6358\right)\:=\:6358\:-\:5215\:=\:1143 \nonnumber\]
Таким образом, средний остаток по кредитной карте равен 1143 доллара друг от друга.
Упражнение
В статистике нас просят найти z-показатель, который говорит нам, насколько необычным является событие. Первым шагом в нахождении z-показателя является вычисление расстояния, на котором значение находится от среднего. Числовая строка ниже показывает среднее значение 18,56 и значение 20,43. Найдите расстояние между этими двумя точками.