делители, простота, двоичный вид, куб, квадрат
Укажите число, чтобы получить всю информацию о нем:
Случайное число
| Четность: |
Число 1296 является четным. |
| Сумма цифр: | 18 |
| Произведение цифр: | 108 |
| Количество цифр: | 4 |
| Все делители числа | 1 2 3 4 6 8 9 12 16 18 24 27 36 48 54 72 81 108 144 162 216 324 432 648 1296 |
| Количество делителей | 25 |
| Сумма делителей | 3751 |
| Простое число |
Составное число |
| Квадратный корень | 36 |
| Кубический корень | 10,9027235569928 |
| Квадрат | 1679616 |
| Куб | 2176782336 |
| Обратное число | 0,000771604938271605 |
| Предыдущее число: 1295 | Следующее число: 1297 |
Натуральное число 1296
является четырехзначным.
Оно записывается 4 цифрами.
Сумма цифр, из которых состоит число 1296, равна 18, а их произведение равно 108.
Число 1296 является четным.
Всего число 1296 имеет 25 делителей:
1,
2,
3,
4,
6,
8,
9,
12,
16,
18,
24,
27,
36,
48,
54,
72,
81,
108,
144,
162,
216,
324,
432,
648,
1296,
. Сумма делителей равна 3751. Куб числа 1296 равен 1679616, а квадрат составляет 2176782336.
Квадратный корень рассматриваемого числа равен 36. Кубический корень равен 10,9027235569928.
Число, которое является обратным к числу 1296, выглядит как 0,000771604938271605.
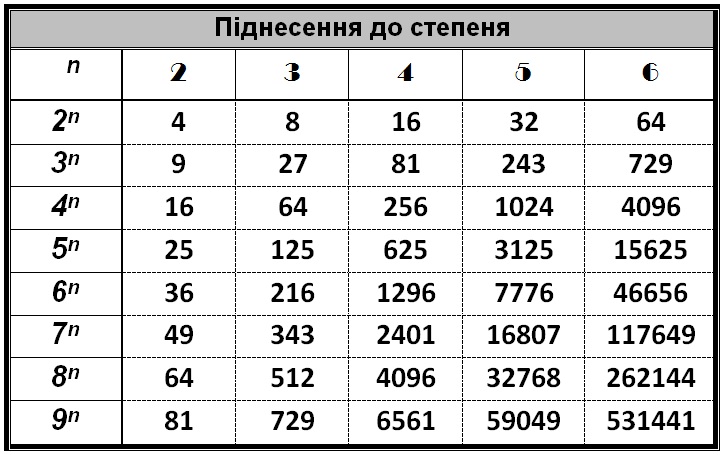
Чему равен корень четвертой степени из $1296$?
Ответить
Проверено
177.
3k+ просмотров
Подсказка: Чтобы упростить этот вопрос, нам нужно решить его шаг за шагом. Для того, чтобы решить и записать выражение в простейшем виде. . Квадратный корень связан с выяснением того, каким должно быть число, которое при умножении само на себя равно числу под символом квадратного корня $\sqrt {} $. Этот символ известен как радикал. Так как в нашем случае мы дали вопрос, в котором мы должны решить и найти четвертое значение корня из $ 1296$, мы сначала избавимся от радикала и удалим квадратный корень, так как нам нужно исходное значение 1296$.
Полное пошаговое решение:
Термин радикал или корень означает, что он является математической противоположностью экспоненты, так же как сложение противоположно вычитанию. Наименьший радикал — это квадратный корень, обозначаемый символом $\sqrt {} $. А следующий радикал — это кубический корень, корень четвертой степени и т. д., представленный символом $\sqrt[3]{{}}$, $\sqrt[4]{{}},\sqrt[n]{{} }$.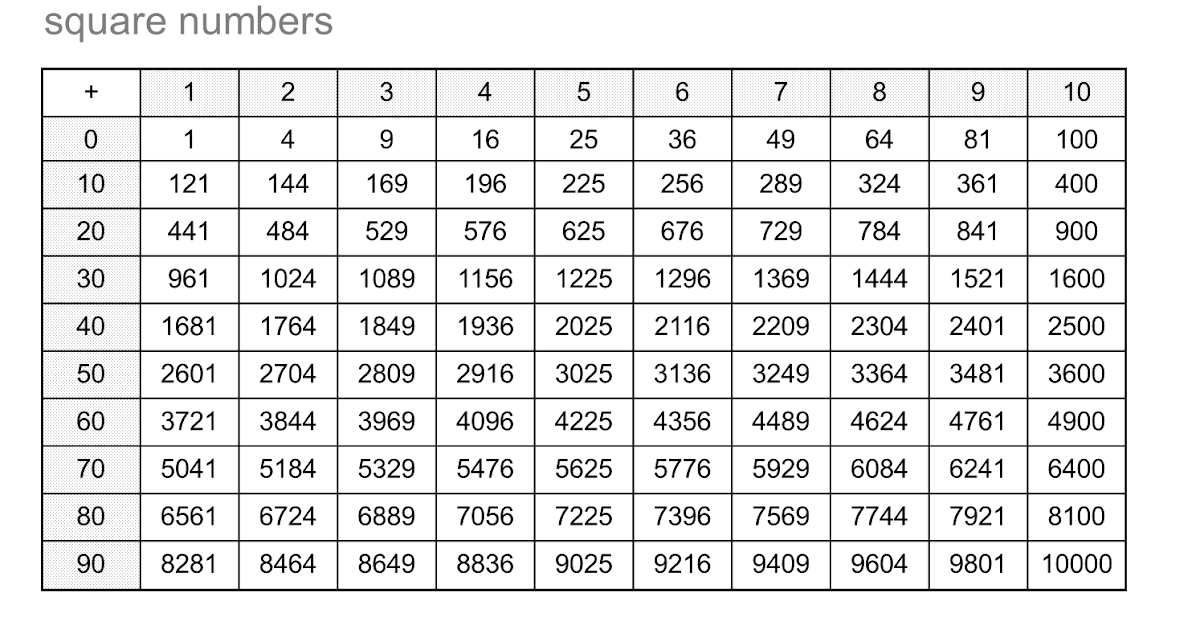
Также маленькое число перед радикалом является его порядковым номером.
Мы можем использовать простую факторизацию для числа $1296$ внутри корня и вытащить нерадикальные члены или полные квадраты внутри квадратного корня, чтобы упростить решение.
Получаем-
1296 полный квадрат числа 36 =
$
\sqrt {1296} = \sqrt {2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 \times 3} \\
= \sqrt {(2 \times 2) \times (2 \times 2) \times (3 \times 3) \times (3 \times 3)} \\
= 4 \times 9 \\
= 36 \\
$
Кубический корень из $1296$ =
\[
= \sqrt[3]{{(2 \times 2 \times 2) \times 2 \times (3 \times 3 \times 3) \times 3}} \\
= 2 \times 3 \times \sqrt[3]{6} \\
= 6 \times \sqrt[3]{6} \\
= 10,903 \\
\]
Корень четвертой степени из $1296$ =
\[
= \sqrt[4]{{(2 \times 2 \times 2 \times 2) \times (3 \times 3 \times 3 \times 3 )}} \\
= 6 \\
\]
Следовательно, требуемый ответ равен 6 .
