Расстояние от точки до плоскости калькулятор онлайн: Онлайн калькулятор. Расстояние от точки до плоскости

Расстояние от точки до плоскости онлайн

С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Для нахождения расстояния от точки M₀ до плоскости α, необходимо найти расстояние от точки M₀ до проекции точки M₀ на плоскость α:

Нахождение расстояния от точки до плоскости содержит следующие шаги:

1. построение прямой L, проходящей через точку M₀ и перпендикулярной плоскости α.
2. нахождение точки M₁ пересечения плоскости α с прямой L(Рис.1).
3. вычисление расстояния между точками M₀ и M₁.

1. Общее уравнение плоскости имеет вид:

где n(A,B,C)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M

₀(x₀, y₀, z₀) и ортогональной плоскости (1) имеет следующий вид:

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр t.

2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

A(At+x0)+B(Bt+y0)+C(At+z0)+D=0,

A2t+Ax0 +B2t+By0+C2t+Cz0+D=0,

Подставляя значение параметра t в выражения (4), находим проекцию M₁(x₁, y₁, z₁) точки M₀ на плоскость (1).

3. Найдем, наконец, расстояние от точки M₀ до плоскости (1). Очевидно, что расстояние от точки M₀ до плоскости (1) − это расстояние от точки M₀ до точки M₁. А это расстояние вычисляется так:

Учитывая значение параметра t, имеем:

 

Пример 1. Найти расстояние от точки M₀(2, -1, -9/31) до плоскости

Решение.

Нормальный вектор плоскости имеет вид:

n=(5, 1, 2),

т.е. A=5, B=1, C=2.

Координаты точки M₀: x₀=2, y₀=−1, z₀=−9/31.

Подставляя координаты точки M₀ и нормального вектора плоскости в (5), получим:

Из выражений (4) находим:

Проекцией точки M₀(2, -1, -9/31) на плоскость (7) является точка:

Вычислим расстояние между точками M₀ и M₁:

Упростим:

Ответ:

Расстояние от точки M₀(2, -1, -9/31) до плоскости (7):

Найти расстояние от точки до плоскости — онлайн калькулятор

• Справочник
• Онлайн-калькуляторы
• Тесты с ответами

Расстояние от точки до плоскости определяется как длина перпендикуляра, опущенного из точки к плоскости. Вычисления можно осуществить самостоятельно, но для этого потребуется время. Также есть вероятность ошибочного выбора алгоритма и потери данных между действиями.

Чтобы получить правильное решение и ответ, воспользуйтесь нашим сервисом. На сайте мы собрали калькуляторы, которые позволяют освоить темы из школьной и университетской программы по алгебре и геометрии.

1. Введите данные из условия задания для уравнения плоскости и координаты точки.

2. Получите подробное решение и ответ после отправки задания на вычисление кнопкой «Рассчитать».

Ответ:

Решение

Ответ:

Похожие калькуляторы:

• Длина отрезка. Расстояние между точками
• Середина отрезка
• Каноническое уравнение прямой проходящей через две точки
• Параметрическое Уравнение прямой проходящей через две точки
• Расстояние от точки до прямой на плоскости
• Уравнение плоскости (координаты трех точек)
• Уравнение плоскости (координаты вектора нормали и точки)
• Точка пересечения прямых (с угловыми коэффициентами)
• Расстояние от точки до прямой в пространстве
• Расстояние между плоскостями
• Угол между плоскостями
• Угол между прямой и плоскостью

Нахождение расстояния от точки до плоскости онлайн-калькулятором

В сервис заложен алгоритм, который находит расстояние по формуле:

Чем полезна программа:

• Отсутствием платежей. Воспользоваться любым расчетом на сайте можно бесплатно. Школьники смогут обойтись без репетиторов при подготовке домашних заданий и повторении тем к поступлению в университет.
• Круглосуточным доступом без ограничений в расчетах. Лимита на вычисления нет. Любой пользователь может отправлять необходимое количество запросов в каждом из разделов.
• Подробными действиями. Сервис выдает последовательное решение и ответ. Имея перед глазами действия легче свериться с собственными расчетами и найти ошибку.
• Комплексом расчетов внутри программы. Вам не придется самим производить никаких промежуточных вычислений. Требуется только ввести данные и получить результат.

Если у вас не получилось разобраться в теме с помощью программы, напишите консультанту. Он найдет преподавателя из нашего штата, который доходчиво и за короткое время объяснит непонятный материал. Также мы оказываем услуги по решению задач, предоставляем дистанционную помощь на контрольных, зачетах, экзаменах.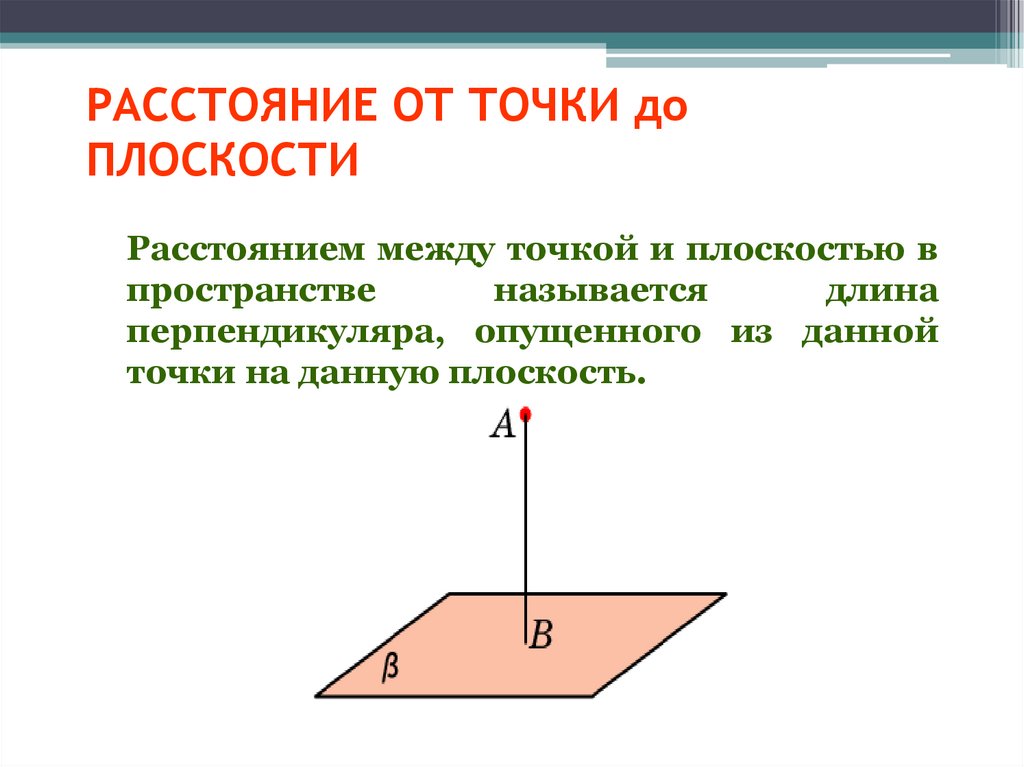

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

• Процент
• Решение матриц
• Точка, прямая, плоскость
• Конвертеры
• Объем фигур
• Калькуляторы площади фигур
• Решение уравнений
• Операции над векторами
• Периметр фигур

Поможем с любой работой

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Решение задач
• Отчеты по практике

Все наши услуги

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Калькулятор расстояния от точки до плоскости

Всякий раз, когда вам нужно рассчитать расстояние от точки до плоскости в трехмерном пространстве , Omni здесь, чтобы помочь.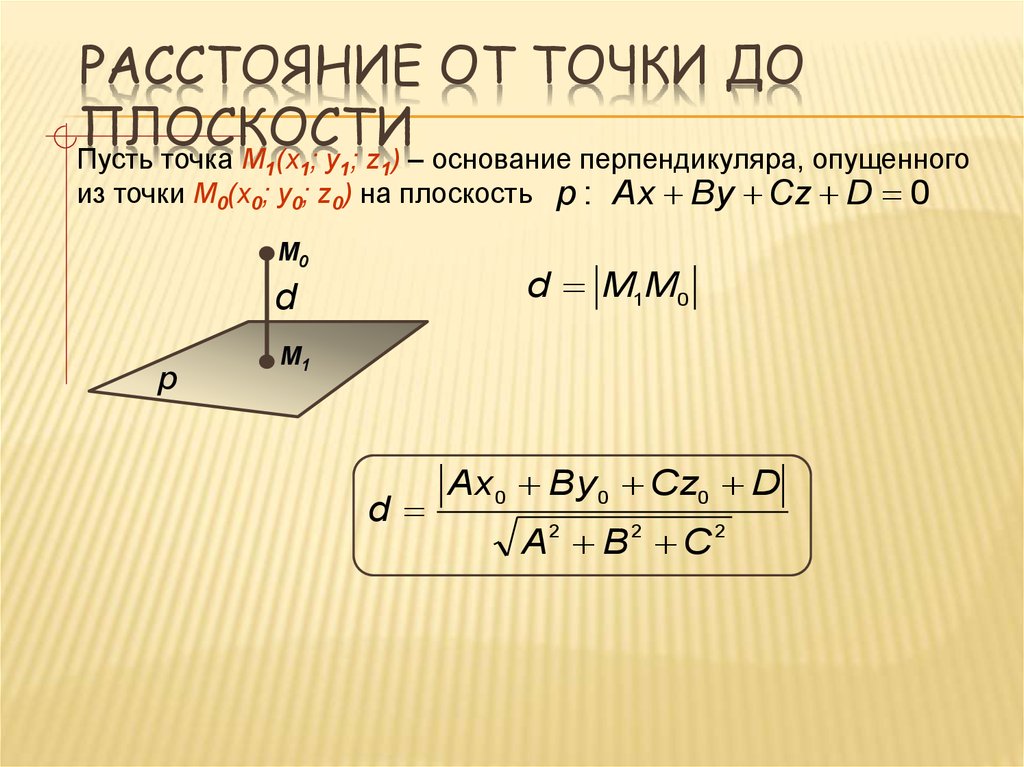 Если вы новичок в теме нахождения минимального расстояния от точки до плоскости, вы можете прочитать статью ниже, где мы обсуждаем:

• Что такое кратчайшее расстояние от точки до плоскости;
• расстояние от точки до плоскости формула ;
• Как найти расстояние от точки до плоскости вручную ; и
• Частные случаи , такие как расстояние до плоскости xy от точки или расстояние от любой плоскости до начала координат в пространстве.

🙋 Если наш калькулятор расстояния от точки до плоскости не совсем то, что вы ищете, ознакомьтесь с нашим калькулятором расстояния, который охватывает тему расстояния в гораздо более широком контексте.

Каково кратчайшее расстояние от точки до плоскости?

Когда кто-то дает нам точку и плоскость в трехмерном пространстве, Кратчайшее расстояние от одного до другого проходит по линии , перпендикулярной плоскости , опущенной из точки. Другими словами, это величина вектора нормали , которая начинается в данной точке и заканчивается на плоскости.

💡 Посетите калькулятор векторной величины Omni, если вам нужно освежить знания.

Эквивалентным объяснением, которое может представиться вашему воображению, может быть следующее: представьте себе шар с центром в точке. Мы надувать мяч до тех пор, пока его поверхность не коснется плоскости. Радиус этого шара как раз и есть расстояние от нашей точки до плоскости!

Держите этот образ в голове, и вы никогда не забудете, что такое минимальное расстояние от точки до плоскости!

Формулы расстояния от точки до плоскости

Как только мы узнаем, что означает расстояние по перпендикуляру от точки до плоскости, давайте обсудим, как вычислить его для данной точки (a,b,c) и плоскости. Мы обсудим два подхода: когда у вас есть стандартное уравнение формы вашей плоскости и когда у вас есть ее вектор нормали и одна точка на плоскости. 92}} L=A2+B2+C2

​∣A⋅a+B⋅b+C⋅c+D∣​

где:

• L — Расстояние ;
• A , B , C , и D — Коэффициенты стандартного уравнения плоскости; и
• a , b и c — Координаты вашей точки.

Что делать, если знаменатель равен нулю, интересно? Как рассчитать расстояние? Ну, вы не знаете. Напомним, что условие для Ax + By + Cz + D = 0 для описания плоскости в трехмерном пространстве заключается в том, что A , B и C не должны быть равны нулю. Это переводится как A ² + B ² + C ² > 0 . Итак, если у вас получилось ноль в знаменателе, это означает, что ваше уравнение плоскости неверно.

Вектор нормали и точка

Здесь мы предполагаем, что ваша плоскость задана вектором нормали n = [A, B, C] и точкой p = (x, y, z) принадлежащий самолету.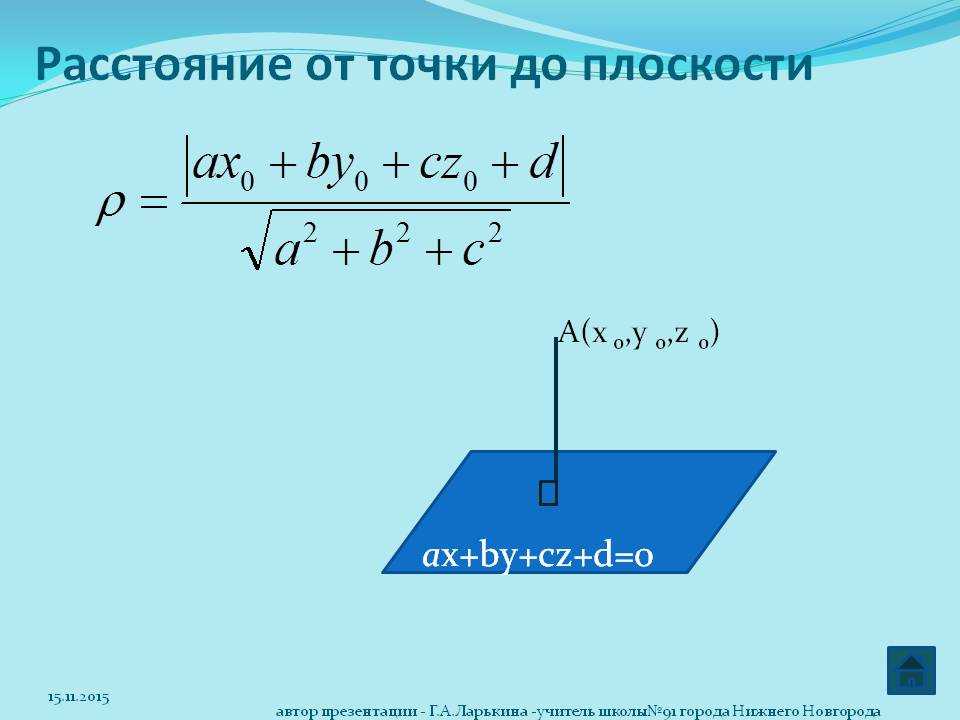 2}}Л=А2+В2+С2

​∣A(a−x)+B(b−y)+C(c−z)∣​

В этой версии:

• L — расстояние ;
• A , B , C — коэффициенты вектора нормали, n ;
• x , y , z — координаты точки p принадлежащей плоскости; и
• a , b и c — это координаты точки, от которой вы вычисляете расстояние.

Условие A ² + B ² + C ² > 0 соответствует тому, что модуль вектора нормали не может быть равен нулю.

🙋 Нужно освежить в памяти векторов ? Попробуйте наш векторный калькулятор !

Вот как мы находим расстояние от точки до плоскости. Как видите, эти формулы не очень сложные, но и не самые простые.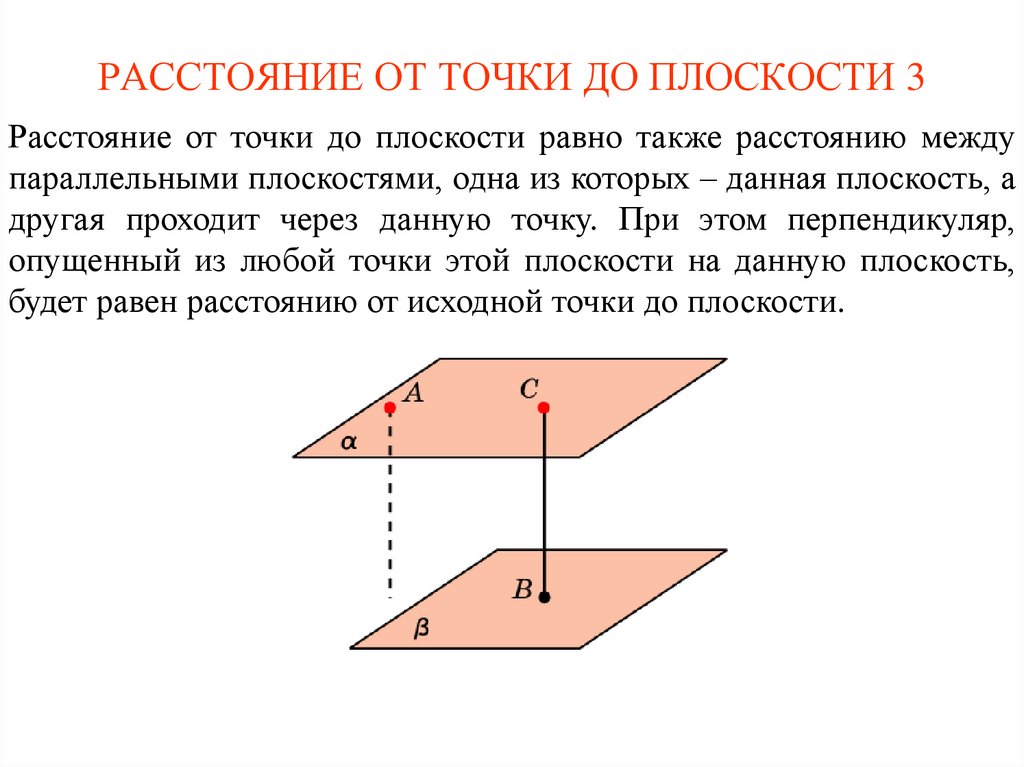 К счастью, наш калькулятор расстояния от точки до плоскости может выполнить расчеты за вас!

Как использовать калькулятор перпендикулярного расстояния от точки до плоскости?

Если вы хотите использовать наш инструмент для определения кратчайшего расстояния от точки до плоскости, вам необходимо:

1. Введите координаты точки в поля a , b и c .
2. Решите на , как вы хотите ввести плоскость . Вы можете выбрать между
   • Уравнение стандартной формы; и
   • Вектор нормали и одна точка от плоскости.
3. Что бы вы ни выбрали, введите данные в поля нашего калькулятора расстояния от точки до плоскости.
4. Наш калькулятор немедленно покажет результат .

Часто задаваемые вопросы

Как вычислить расстояние от точки до плоскости?

Для определения расстояния от точки до плоскости:

1. Запишите стандартное уравнение формы вашей плоскости. Он должен быть в виде Ax+By+Cz+D=0 .
2. Рассчитать A ² + B ² + C ² . Если он равен нулю, ваше уравнение плоскости неверно.
3. Запишите координаты точки (a, b, c) , от которой вы хотите рассчитать расстояние.
4. Вычислить |A×a + B×b + C×c + D|.
5. Разделите его на квадратный корень из значения, полученного на шаге 2. Это и есть искомое расстояние!

Как найти расстояние от точки до плоскости xy?

Расстояние от точки (a, b, c) до плоскости xy равно модулю последней координаты, т. е. |c| . Чтобы увидеть, как это следует из общей формулы расстояния от точки до плоскости, нужно подставить A = B = D = 0 и C = 1 , что дает |C×c| / √(C ² ) = |C × c| / |С| = |с| .

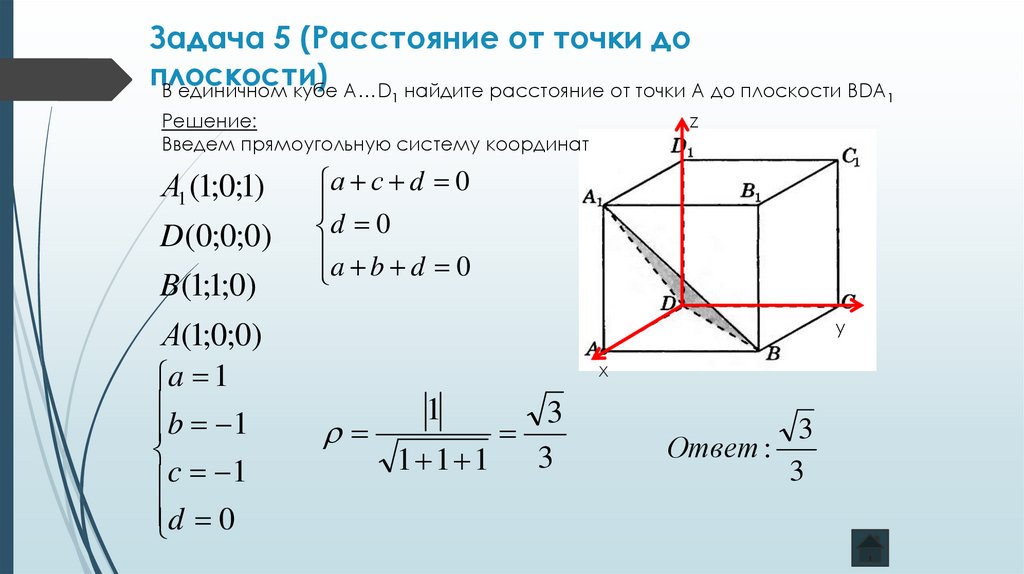
Каково расстояние от точки (1,1,1) до плоскости x+y=0?

Расстояние √2 ≈ 1,41 .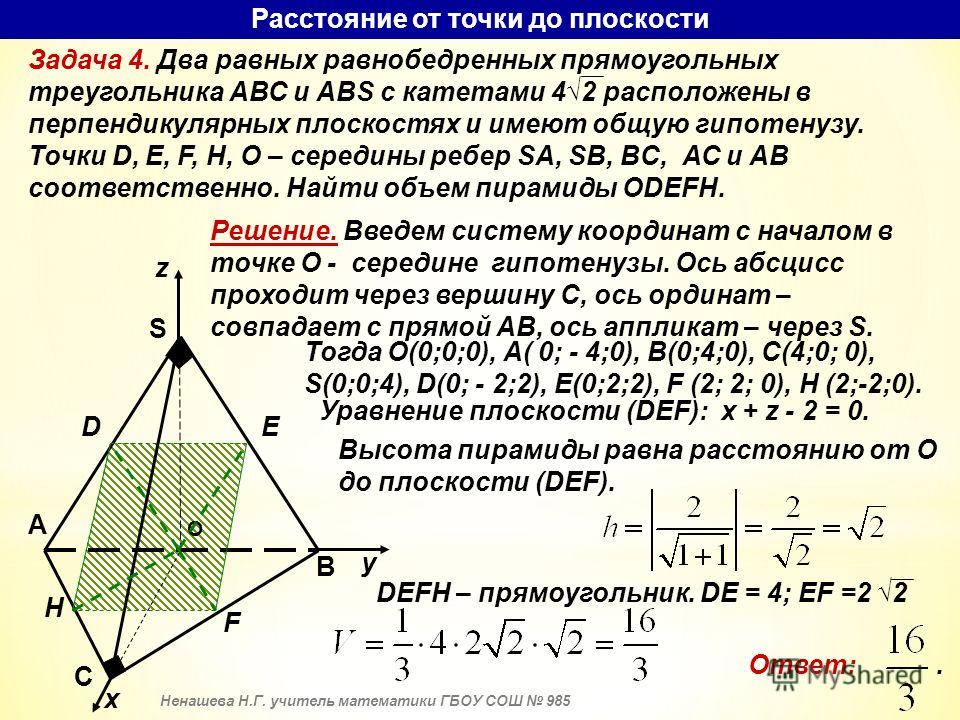 Чтобы получить этот результат, мы применяем формулу расстояние = |A×a + B×b + C×c|/√(A ² + B ² + C ² ) с A=B= 1 и C=D=0 и а = b = с = 1 . Получаем расстояния = |1×1 + 1×1 + 0×1| / √(1 ² + 1 ² ) = |2| / √2 = √2 .

Какое расстояние от плоскости до начала космического пространства?

Для вычисления расстояния от плоскости Ax + By + Cz + D = 0 до точки (0,0,0) :

1. Вычислить A ² + B ² + C ² .
2. Извлеките квадратный корень из числа из шага 1.
3. Вычислите абсолютное значение D и разделите его на число из шага 2.
4. Вот оно! Вы можете проверить свой результат с помощью онлайн-калькулятора расстояния от точки до плоскости.

Онлайн калькулятор: Трилатерация

  Исследование  Математика  Геометрия

Этот онлайн-калькулятор решает задачу трилатерации — определение координат точки по расстоянию от этой точки до трех других точек с известными координатами.

Результат решения задачи может быть одним из трех:

1. Нет точки, расстояния от которой до остальных трех соответствуют заданным
2. Существует ровно одна точка, расстояния от которой до трех других соответствуют заданным.
3. Есть две точки, расстояния которых до трех других соответствуют заданным

Расчетные формулы и иллюстрации для каждого случая приведены под калькулятором.

Трилатерация

Координаты первой известной точки (x, y, z)

Расстояние до первой точки

Координаты второй известной точки (x, y, z)

Расстояние до второй точки

Координаты третьей известной точки (x, y, z)

Расстояние до третьей точки

Результат

Растворы

ПРОТИВАЯ ПЕЗИЦИЯ

Цифры после десятичной точки: 2

ТРИЛЕРТА

МЕСТИ ОПЕРЫ, ЛЕКОВЫЕ ЛОКОВОЙ В НАСТОЯЩЕМ СТАВИТЕЛЬНОМ R 669

МЕСТО, ЛЕКА, ЛЕКОВЫЕ, ЛЕКОВЫЕ В НАСТОЯЩЕМ СТАВАНИЕ R 6669

МЕСТО, лежащие на расстоянии R 66666,

. с координатами (x, y, z) является поверхностью сферы радиусом r с центром в точке (x, y, z) . Таким образом, с точки зрения геометрии задача трилатерации состоит в том, чтобы найти координаты пересечения трех сфер. Эти координаты находятся путем решения системы уравнений, основанной на следующих рассуждениях ¹ :
Каждая пара сфер пересекается по окружности. Его центр находится на прямой линии, соединяющей центры сфер. Сама окружность лежит в плоскости, перпендикулярной этой прямой. Рассмотрим три сферы: сфера 1 с радиусом r ₁ с центром в точке O ₁ (x ₁ , y ₁ >, z ₁ ) 3 сфера с радиусом 9 ,9083 с центром в точке O ₂ (x ₂ , y ₂ , z ₂ ) и сфера 3 с радиусом R ₃ Центр O ₃ > (x ₃ , Y ₃ > (x ₃ , Y ₃ .

Уравнение плоскости, в которой лежит окружность, образованная пересечением сфер 1 и 2, выглядит следующим образом:

Уравнение плоскости, в которой лежит окружность, образованная пересечением сфер 1 и 3, выглядит следующим образом:

Уравнение плоскости треугольника, образованного центрами сфер:

Пересечение первых двух плоскостей дает линию, перпендикулярную последней плоскости. Пересечение этой линии с плоскостью треугольника есть перпендикуляр из искомой точки пересечения сфер к плоскости треугольника, образованного центрами сфер. Эта точка пересечения принадлежит всем трем плоскостям, и ее координаты являются решением приведенной выше системы трех линейных алгебраических уравнений.

Решив эту систему, получим координаты точки О (х ₀ , у ₀ , з ₀ ) .
Тогда координаты точки пересечения трех сфер определяются по следующим формулам:

Выражение для вычисления k определяет количество решений.