Рациональные числа, зачем нужны рациональные числа, в чем их особенность
Какие числа называются рациональными
Рациональные числа — это числа, которые можно записать в виде отношения mn, где m — целое число, a n — натуральное число.
Чтобы понимать. что такое рационального числа, необходимо знать, что такое натуральные числа, целые числа, дроби (правильные \(\frac{2}{3}\), неправильные \(\frac{3}{2}\), бесконечные периодические 0,(4) и смешанные \(4 \frac{2}{3}\),).
Натуральные числа представляют собой числа, которые мы используем при счете (1, 2, 3…). Является ли натуральное число рациональным? Да. Рациональные числа включают в себя все натуральные числа (1, 2, 3, 4, и так далее), так как их можно записать в виде дроби, где числитель — это само число, а знаменатель равен 1. Например, число 3 можно записать как 3/1, что является дробью и, следовательно, рациональным числом.
В свою очередь целые числа – это натуральные числа, а также противоположные им и ноль (1, 2, 0, -1, -2…).
Дробью называется число, записанное в виде отношения mn (\(\frac{2}{3}\)), где m – целое, а n – натуральное число. Понятие дроби берет свое начало еще с древних времен, когда людям в торговых делах и бытовых нуждах требовалось определить часть какого-либо целого.
История рациональных чисел
История рациональных чисел началась с возникновением финансово-кредитных отношений между людьми. Чтобы в численном виде представить задолженность человека, нужно было записывать числа, противоположные натуральным. Так появились отрицательные числа (-3, -167). А для того, чтобы записывать часть целого (например, возвращение долга частями), стали использовать дроби. Именно поэтому математикам необходимо было как-то объединить такие характерные числа, дать им общее название. Так появились рациональные числа (от латинского ratio – «отношение»).
Для усвоения материала приведем пример задания на определение рациональных чисел из ряда чисел.
Рациональные числа: пример с ответом
Задача. Даны числа: -34, 480, 0,11, \(\frac{1}{2}\), 8. Какие из них рациональные?
Даны числа: -34, 480, 0,11, \(\frac{1}{2}\), 8. Какие из них рациональные?
Решение.
Рассмотрим отдельно каждое из заданных чисел:
- Число -34 – целое число;
- Число 480 – натуральное число;
- Число 0,11 = \(\frac{11}{100} \) – десятичная дробь;
- Число \(\frac{1}{2}\) — правильная дробь;
- Число 8 – натуральное число.
Каждое из заданных чисел можно представить в виде дроби с целым и натуральным знаменателем. Значит, все 5 чисел являются рациональными числами.
Ответ: все числа являются рациональными.
Чтобы хорошо понимать специфику рациональных чисел, нужно усвоить два правила:
- Сумма рациональных чисел является рациональным числом.
Теория в математике очень важна. Умение отличать натуральные числа от целых, рациональные от иррациональных поможет Вам не запутаться и не ошибиться в практике. Удачи!
Удачи!
Часто задаваемые вопросы
Рациональные числа — что это такое (примеры)
Обновлено 20 июля 2021 Просмотров: 178 177 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы вновь поговорим о математических терминах.
И на этот раз расскажем все о РАЦИОНАЛЬНЫХ ЧИСЛАХ. Они обязательно входят в школьную программу, и дети начинают изучать их в 6 классе.
Само слово «рациональный» знакомо многим. И под ним подразумевается нечто «логичное» и «правильное». На деле так и есть.
Рациональные числа — это …
Термин имеет латинские корни, и в переводе «ratio» означает «число», «расчет», «разум», «рассуждение» и «нумерация». Но есть и другие переводы – «дробь» и «деление».
РАЦИОНАЛЬНОЕ ЧИСЛО – любое число, которое можно показать в виде дроби a/b. Здесь а – целое число, а b – натуральное.
Стоит напомнить, что:
- Целые числа – это все возможные числа, как отрицательные, так и положительные.
 И к ним же относится ноль. Главное условие – они не должны быть дробными. То есть -15, 0 и +256 можно назвать целыми числами, а 2,5 или -3,78 – нет.
И к ним же относится ноль. Главное условие – они не должны быть дробными. То есть -15, 0 и +256 можно назвать целыми числами, а 2,5 или -3,78 – нет. - Натуральные числа – это числа, которые используются при счете, то есть они имеют «натуральное происхождение». Это ряд из 1, 2, 3, 4, 5 и так далее до бесконечности. А вот ноль и отрицательные числа, как и дробные – к натуральным не относятся.
И если применить эти определения, то мы можем сказать, что:
РАЦИОНАЛЬНОЕ ЧИСЛО – это вообще все возможные числа, кроме бесконечных непериодических десятичных дробей. Среди них натуральные и целые числа, обыкновенные и конечные десятичные дроби, а также бесконечные периодические дроби.
История изучения рациональных чисел
Точно неизвестно, когда люди начали изучать дроби. Есть мнение, что много тысяч лет назад. И началось все с банального дележа. Например, кому-то нужно было разделить добычу, но на равные части это не получалось сделать. Зато получалось сколько-то целых, и сколько-то в довесок.
Скорее всего, дроби изучали и в Древнем Египте, и в Древней Греции. Тогдашние математики далеко продвинулись в науке. И трудно предположить, что эта тема осталась ими не изучена. Хотя, к сожалению, ни в одних трудах так и не было найдено конкретных указаний на рациональные числа.
А вот официально считается, что понятие десятичной дроби появилось в Европе в 1585 году. Этот математический термин в своих трудах увековечил голландский инженер и математик Симон Стевин.
До занятия наукой, он был обыкновенным купцом. И скорее всего, именно в торговых делах часто сталкивался с дробными числами. Что потом и описал в своей книге «Десятая».
В ней Стевин не только объяснял полезность десятичных дробей, но и всячески пропагандировал их использование. Например, в системе мер для точного определения величины чего-либо.
Разновидности рациональных чисел
Мы уже написали, что под понятия рациональные числа подпадают практически все возможные варианты. Теперь рассмотрим более подробно существующие варианты:
Теперь рассмотрим более подробно существующие варианты:
- Натуральные числа. Любое число с 1 и до бесконечности можно представить в виде дроби. Достаточно вспомнить простое математическое правило. Если поделить число на единицу, то получится то же самое число. Например, 5 = 5/1, 27 = 27/1, 136 = 136/1 и так далее.
- Целые числа. Точно такая же логика, как в случае с натуральными числами, действует и тут. Отрицательные числа также можно представить в виде дроби с делением на единицу. И точно также будет в отношении нуля. Например, -356 = -356/1, -3 = -3/1, 0 = 0/1 и так далее.
- Обыкновенные дроби. Это напрямую говорится в определении рациональных чисел. Например, 6/11, 2/5, -3/10 и так далее.
- Бесконечные периодические дроби. Это числа, у которых после запятой бесконечное множество знаков и их последовательность повторяется. Самые простые примеры 1/3, 5/6 и так далее.
- Конечные десятичные дроби.
 Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.
Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.
Все числа, которые входят в понятие рациональных, называются МНОЖЕСТВОМ рациональных чисел. В математике его принято обозначать латинской буквой Q.
А графически это можно изобразить вот так:
Свойства рациональных чисел
Рациональные числа подчиняются всем главным законам математики:
- А + В = В + А
- А + (В + С) = (А + В) + С
- А + 0 = А
- А + (-А) = 0
- А * В = В * А
- А * 1 = А
- А * 0 = 0
- (А + В) * С = А * С + В * С
- (А – В) * С = А * С – В * С
Ради интереса можете попробовать подставить вместо букв любые числа и убедиться, что эти законы верны.
Вместо заключения
Раз есть в математике рациональные числа, значит, должны быть и им противоположные. Так и есть – они называются иррациональными. Это числа, которые нельзя записать в виде обычной дроби.
Так и есть – они называются иррациональными. Это числа, которые нельзя записать в виде обычной дроби.
К таким числам относится математическая константа «пи». Многие знают, что она равна 3,14 и бесконечное количество знаков после запятой, причем их последовательность никогда не повторяется.
Также к иррациональным числам относится много корней. Это касается тех, у кого в результате не получается целого числа. Самый простой пример – корень из 2. Но это уже тема для другой статьи.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
- Математика
рациональных чисел — Определение | Примеры
Рациональные числа представлены в виде p/q, где p и q могут быть любыми целыми числами и q ≠ 0. Это означает, что рациональные числа включают натуральные числа, целые числа, целые числа, дроби целых чисел и десятичные дроби ( завершающие десятичные дроби и повторяющиеся десятичные дроби). Давайте узнаем больше о рациональных числах и о том, как идентифицировать рациональные числа и примеров рациональных чисел в этом уроке.
Давайте узнаем больше о рациональных числах и о том, как идентифицировать рациональные числа и примеров рациональных чисел в этом уроке.
| 1. | Что такое рациональные числа? |
| 2. | Типы рациональных чисел |
| 3. | Как определить рациональные числа? |
| 4. | Рациональные и иррациональные числа |
| 5. | Часто задаваемые вопросы о рациональных числах |
Что такое рациональные числа?
Слово «рациональный» произошло от слова «рацио». Итак, рациональные числа хорошо связаны с концепцией дробей, которые представляют отношения. Другими словами, если число может быть выражено в виде дроби, где и числитель, и знаменатель являются целыми числами, число является рациональным числом.
Определение рациональных чисел
Рациональное число — это число, имеющее форму p/q, где p и q — целые числа, а q не равно 0.
Набор рациональных чисел
Множество рациональных чисел обозначается Q. Следует отметить, что рациональные числа включают в себя натуральные числа, целые числа, целые числа и десятичные дроби.
Обратите внимание на следующий рисунок, определяющий рациональное число.
Примеры рациональных чисел
Если число может быть представлено в виде дроби, где и числитель, и знаменатель являются целыми числами, это число является рациональным числом. Ниже приведены некоторые примеры рациональных чисел.
- 56 (что можно записать как 56/1)
- 0 (другая форма 0/1)
- 1/2
- √16, что равно 4
- -3/4
- 0,3 или 3/10
- -0,7 или -7/10
- 0,141414… или 14/99
Типы рациональных чисел
Различные типа рациональных чисел даны следующим образом.
- Целые числа, такие как -2, 0, 3 и т. д., являются рациональными числами.

- Дроби, числители и знаменатели которых являются целыми числами, такими как 3/7, -6/5 и т. д., являются рациональными числами.
- Завершающие десятичные дроби, такие как 0,35, 0,7116, 0,9768 и т. д., являются рациональными числами.
- Неконечные десятичные числа с некоторыми повторяющимися шаблонами (после запятой), например 0,333…, 0,141414… и т. д., являются рациональными числами. Они широко известны как непрерывающиеся повторяющиеся десятичные дроби.
Как определить рациональные числа?
Рациональные числа легко идентифицировать с помощью следующих характеристик.
- Все целые числа, целые числа, натуральные числа и дроби с целыми числами являются рациональными числами.
- Если десятичная форма числа завершается или повторяется, как в случае 5,6 или 2,141414, мы знаем, что это рациональные числа.
- Если десятичные дроби кажутся бесконечными или неповторяющимися, то такие числа называются иррациональными.
 Как и в случае √5, равного 2,2360679.77499789696409173… иррациональное число.
Как и в случае √5, равного 2,2360679.77499789696409173… иррациональное число. - Другой способ определить рациональные числа — посмотреть, может ли число быть выражено в форме p/q, где p и q — целые числа, а q не равно 0.
Пример: Является ли 0,923076923076923076923076923076… рациональным числом?
Решение:
Возьмем другой пример.
Пример: Является ли √2 рациональным числом?
Решение: Если мы запишем десятичное значение √2, мы получим √2 = 1,414213562…, которое является непрерывающимся и неповторяющимся десятичным числом. Следовательно, это не рациональное число. Это иррациональное число.
Рациональные числа в десятичной форме
Рациональные числа также могут быть представлены в десятичной форме. Вы знаете, что 1,1 — рациональное число? Да, потому что 1,1 можно записать как 1,1 = 11/10. Теперь давайте поговорим о некончающихся десятичных дробях, таких как 0,333… Поскольку 0,333… можно записать как 1/3, значит, это рациональное число. Следовательно, неконечные десятичные числа, имеющие повторяющиеся числа после запятой, также являются рациональными числами.
Теперь давайте поговорим о некончающихся десятичных дробях, таких как 0,333… Поскольку 0,333… можно записать как 1/3, значит, это рациональное число. Следовательно, неконечные десятичные числа, имеющие повторяющиеся числа после запятой, также являются рациональными числами.
Является ли 0 рациональным числом?
Да, 0 — рациональное число, поскольку его можно записать в виде дроби целых чисел, например 0/1, 0/-2,… и т. д. Другими словами, 0/5 = 0, 0/-2 = 0 , 0/1 = 0 и так далее.
Список рациональных чисел
Из приведенной выше информации становится ясно, что существует бесконечное количество рациональных чисел. Следовательно, невозможно определить весь список рациональных чисел. Однако некоторые рациональные числа могут быть перечислены как 3, 4,57, 3/4, 0, -7 и так далее. Это показывает, что все натуральные числа, целые числа, целые числа, дроби и десятичные числа (завершающие десятичные числа и повторяющиеся десятичные числа) считаются рациональными числами.
Сложение и вычитание рациональных чисел
Для сложения и вычитания рациональных чисел мы используем те же самые правила сложения и вычитания целых чисел. Давайте разберемся в этом с помощью примера.
Пример: Решить 1/2 — (-2/3)
Решение: Решим это, используя следующие шаги:
- Шаг 1: Поскольку мы упрощаем 1/2 — (-2 /3), мы будем следовать правилу сложения и вычитания чисел, согласно которому факт вычитания может измениться на факт сложения, а знак вычитаемого изменится на противоположный. Это сделает его 1/2 + 2/3
- Шаг 2: Теперь нам нужно сложить эти дроби 1/2 + 2/3
- Шаг 3: Используя правила сложения дробей, мы преобразуем данные дроби в подобные дроби, чтобы получить общие знаменатели, чтобы их стало легче складывать. Для этого нам нужно найти НОК знаменателей 2 и 3, который равен 6. Затем мы преобразуем дроби в соответствующие им эквивалентные дроби, что сделает их 3/6 + 4/6.
 Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)
Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)
Умножение и деление рациональных чисел
Умножение и деление рациональных чисел можно выполнять так же, как дроби. Чтобы умножить любые два рациональных числа, мы умножаем их числители и знаменатели по отдельности и упрощаем полученную дробь. Давайте разберемся в этом с помощью примера.
Пример:
Решение: Решим это, выполнив следующие шаги:
- Шаг 1: Чтобы умножить 3/5 × (-2)/7, мы сначала умножим числители, а затем умножим знаменатели.
- Шаг 2: В этом случае, когда мы умножаем числители, это будет 3 × (-2) = -6.
- Шаг 3: Когда мы умножим знаменатели, получится 5 × 7 = 35. Следовательно, произведение будет -6/35.
Когда нам нужно разделить любые две дроби, мы умножаем первую дробь (которая является делимым) на величину, обратную второй дроби (которая является делителем). Давайте разберемся в этом с помощью примера.
Давайте разберемся в этом с помощью примера.
Пример: Разделить 3/5 ÷ 2/7
Решение: Решим это, используя следующие шаги:
- Шаг 1: Чтобы разделить 3/5 ÷ 2/7, мы сначала напишет обратную величину второй дроби. Это составит 3/5 × 7/2 .
- Шаг 2: Теперь мы умножим числители Это будет 3 × 7 = 21.
- Шаг 3: Затем умножим знаменатели, будет 5 × 2 = 10. Следовательно, произведение будет 21/10 или \(2\dfrac{1}{10}\)
Рациональные и иррациональные числа
Числа, которые НЕ являются рациональными числами, называются иррациональными числами. Множество иррациональных чисел представлено Q´. Разницу между рациональными и иррациональными числами можно понять из следующего рисунка и таблицы, приведенных ниже.
| Рациональные числа | Иррациональные числа |
|---|---|
Это числа, которые можно представить в виде целых чисел. Примеры: 1/2, 0,75, -31/5 и т. д. | Это числа, которые нельзя представить в виде целых чисел. Примеры: √5, π и т. д. |
| Завершающие десятичные дроби. | Они НИКОГДА не завершают десятичные дроби, которые не имеют точного значения. |
Они могут быть неконечными десятичными знаками с повторяющимися шаблонами десятичных знаков или повторяющимися десятичными знаками. Пример: 1.414, 414, 414 … содержит повторяющиеся десятичные дроби, где 414 повторяется. | Они должны быть неконечными десятичными знаками без повторяющихся шаблонов десятичных знаков. Пример: √5 = 2,236067977499789696409173…. не имеет повторяющихся десятичных знаков |
| Множество рациональных чисел содержит полностью натуральные числа, все целые числа и все целые числа. | Набор иррациональных чисел является отдельным набором и НЕ содержит никаких других наборов чисел.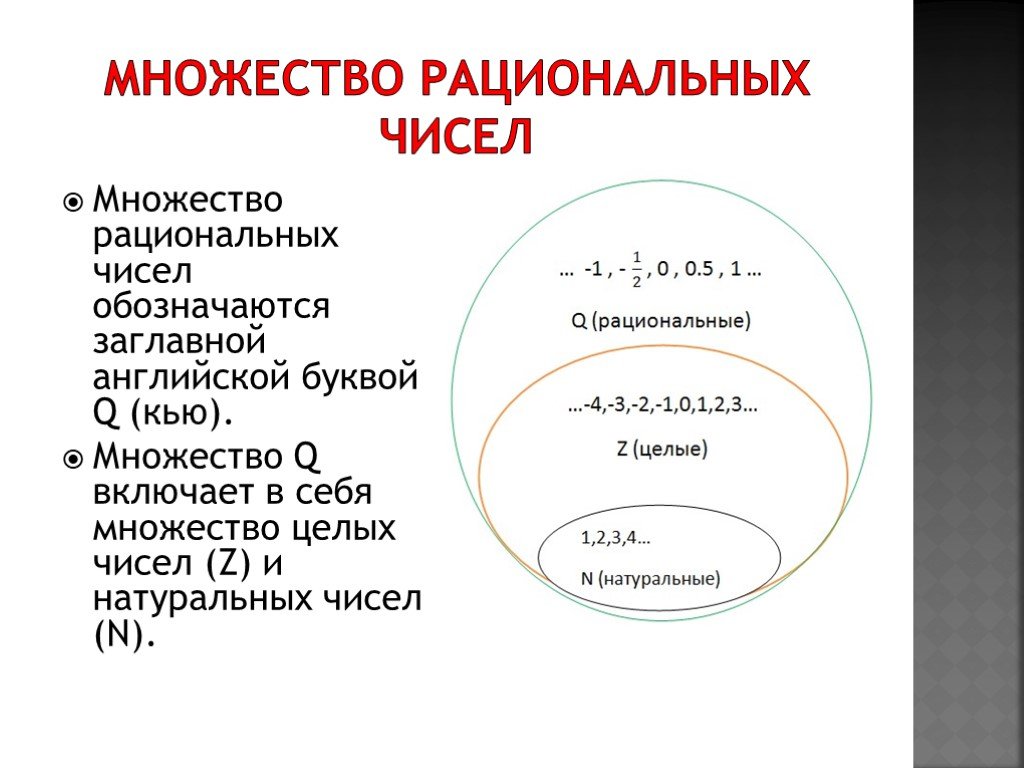 |
Советы и рекомендации по рациональным числам
- Рациональные числа включают дроби и любые числа, которые могут быть представлены дробями.
- Натуральные числа, целые числа, целые числа, дроби целых чисел и конечные десятичные дроби являются рациональными числами.
- Неконечные десятичные дроби с повторяющимися шаблонами десятичных дробей, то есть повторяющиеся десятичные дроби, также являются рациональными числами.
☛ Статьи по теме
- Простые числа
- Составные номера
- Четные числа
- Нечетные числа
- Реальные числа
- Натуральные числа
- Целые числа
- Иррациональные числа
- Подсчет чисел
- Кардинальные числа
- Четные и нечетные числа
Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12.
Примеры рациональных чисел
Пример 1: Определите рациональные числа среди следующих: √4, √3, √5/2, -4/5, π, 1,41421356237309504…..
Решение:
Рациональное число, когда упрощенный должен быть либо конечным десятичным числом, либо неконечным десятичным числом с повторяющимся шаблоном десятичных знаков. Следовательно, рациональные числа среди заданных чисел равны √4 (в результате получается 2) и -4/5.
Пример 2: Укажите истинное или ложное значение относительно рациональных чисел.
а.) Каждое целое является рациональным числом.
б.) Каждое рациональное число является целым числом.
c.) Каждое рациональное число является целым числом.

г.) Каждое действительное число является рациональным числом.
д.) Каждое целое число является рациональным числом.
Решение:
а.) Верно, каждое целое число является рациональным числом.
б.) Неверно, каждое рациональное число не является целым числом. Это может быть часть целых чисел или десятичная дробь. К рациональным числам относятся натуральные числа, целые числа, целые числа и дроби целых чисел.
c.) Ложь, каждое рациональное число не является целым числом, потому что рациональные числа включают дроби и конечные десятичные дроби, а целые числа включают только отрицательные числа, положительные числа и 0
d.) Нет, каждое действительное число не является рациональным числом, потому что действительное числа включают в себя и иррациональные числа.
д.) Верно, каждое целое число является рациональным числом.
Пример 3:
Запишите следующее рациональное число в десятичной форме: 1/2
Решение:
Рациональное число 1/2 можно преобразовать в десятичное число, разделив числитель на знаменатель.
 Нам нужно разделить 1 на 2 и мы получим 0,5
Нам нужно разделить 1 на 2 и мы получим 0,5
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Забронируйте бесплатный пробный урок
Практические вопросы по рациональным числам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о рациональных числах
Что такое рациональное число в математике?
Любое число в форме p/q, где p и q — целые числа, а q не равно 0, является рациональным числом . Примеры рациональных чисел: 1/2, -3/4, 0,3 или 3/10.
Как определить рациональное число?
Чтобы определить, является ли данное число рациональным или иррациональным, нам нужно преобразовать его в десятичную форму. Если десятичная дробь заканчивается или не заканчивается повторяющимися десятичными знаками, то число является рациональным. В противном случае это нерационально. Например, 1,414, 414, 414… имеет повторяющиеся шаблоны десятичных знаков, где повторяется 414. Значит, это рациональное число. С другой стороны, если мы возьмем пример √5 = 2,236067977499789696409173…., мы видим, что оно не завершается и не имеет повторяющихся шаблонов десятичных знаков. Значит, это иррациональное число. Другой способ определить рациональное число — проверить, является ли оно натуральным числом, целым числом, целым числом или дробью целых чисел. Если это одно из них, то это рациональное число.
В противном случае это нерационально. Например, 1,414, 414, 414… имеет повторяющиеся шаблоны десятичных знаков, где повторяется 414. Значит, это рациональное число. С другой стороны, если мы возьмем пример √5 = 2,236067977499789696409173…., мы видим, что оно не завершается и не имеет повторяющихся шаблонов десятичных знаков. Значит, это иррациональное число. Другой способ определить рациональное число — проверить, является ли оно натуральным числом, целым числом, целым числом или дробью целых чисел. Если это одно из них, то это рациональное число.
Что такое завершающие рациональные числа?
Завершающими рациональными числами являются те десятичные числа, которые заканчиваются после определенного количества знаков после запятой. Например, 1,5, 3,4, 0,25 и т. д. являются конечными числами. Все конечные числа являются рациональными числами, поскольку их легко записать в виде p/q.
В чем разница между рациональными и иррациональными числами?
Рациональное число — это число, десятичная форма которого является конечной или повторяющейся по своей природе. Например, 2,67 и 5,666 … Принимая во внимание, что иррациональные числа — это те числа, десятичная форма которых не заканчивается и не повторяется после определенного количества знаков после запятой. Например, √5 = 2,236067977499789696409173…. не имеет повторяющихся десятичных знаков и не заканчивается, поэтому это иррациональное число.
Например, 2,67 и 5,666 … Принимая во внимание, что иррациональные числа — это те числа, десятичная форма которых не заканчивается и не повторяется после определенного количества знаков после запятой. Например, √5 = 2,236067977499789696409173…. не имеет повторяющихся десятичных знаков и не заканчивается, поэтому это иррациональное число.
Что такое иррациональные числа?
Иррациональные числа — это те, которые не могут быть представлены целыми числами в форме p/q. Множество иррациональных чисел обозначается Q´. Несколько примеров иррациональных чисел: √2, √5 и так далее. Их десятичные формы не прекращаются и не повторяются.
Является ли 0 рациональным числом?
Да, 0 — рациональное число, так как мы можем записать его как 0/1, где 0 и 1 — целые числа, а знаменатель не равен 0.
Какое число нужно добавить к числу Пи, чтобы получить рациональное число?
Если мы добавим — π к π, мы получим, — π + π = 0. Эта сумма является рациональным числом. Следовательно, добавляя — π к π, мы получаем рациональное число.
Следовательно, добавляя — π к π, мы получаем рациональное число.
Как складывать рациональные числа?
Для сложения рациональных чисел используются те же правила сложения целых чисел. Давайте разберемся в этом с помощью примера. Если нам нужно добавить 4,53 + 2,31, мы начнем добавлять с правой стороны. Расставив числа в столбцах в соответствии с их разрядностью, начнем с сотого места. Итак, 3 + 1 = 4. Переходя к десятому столбцу, мы добавляем 5 + 3 = 8. Затем мы добавляем цифры в столбце единиц, то есть 4 + 2 = 6. Таким образом, мы получаем сумму как 6,84
Как делить рациональные числа?
Чтобы разделить рациональные числа, мы используем обычные правила деления целых чисел, дробей или десятичных дробей, в зависимости от обстоятельств. Например, разделим дроби 7/5 ÷ 1/5. Чтобы разделить 7/5 ÷ 1/5, сначала напишем обратную величину второй дроби. Это сделает его 7/5 × 5/1. Теперь мы умножим числители. Это будет 7 × 5 = 35. Затем мы умножим знаменатели, это будет 5 × 1 = 5. Следовательно, произведение будет 35/5, что равно 7.
Следовательно, произведение будет 35/5, что равно 7.
Как умножать рациональные числа?
Рациональные числа можно умножать, используя правила умножения. Например, давайте умножим 43 × 10, мы получим произведение как 430.
Откуда начинаются рациональные числа?
Рациональные числа не начинаются с какого-либо определенного числа. Они включают в себя все натуральные числа, целые числа и целые числа, а также конечные десятичные дроби и дроби, которые могут быть представлены в виде p/q, где q не равно 0.
В чем разница между дробями и рациональными числами?
Существует небольшая разница между дробями и рациональными числами, которая приведена ниже:
- Любое число, которое может быть представлено в виде p/q, где ‘p’ и ‘q’ — целых числа и q не должны быть равно 0. Например, 1/2, -3/4, 7/9, -100/21 и т.д.
- Дроби могут быть записаны в виде p/q, но ‘p’ и ‘q’ должны быть целыми числами .
 Например, 3/4, 1/9, и так далее. Это означает, что значения p и q не могут быть отрицательными.
Например, 3/4, 1/9, и так далее. Это означает, что значения p и q не могут быть отрицательными.
Все ли целые числа рациональны?
Да, все целые числа являются рациональными числами, поскольку рациональные числа включают в себя все натуральные числа, целые числа, целые числа, конечные десятичные дроби и дроби в форме p/q, где «p» и «q» — это целых числа , а q не должно быть равным 0.
Все ли целые числа рациональны?
Да, все целые числа являются рациональными числами, поскольку рациональные числа включают в себя все натуральные числа, целые числа, целые числа, конечные десятичные дроби и дроби в форме p/q, где ‘p’ и ‘q’ равны целые числа и q не должны быть равны 0.
Скачать БЕСПЛАТНО учебные материалы
Скачать бесплатно рабочие листы для 9 класса
Что такое рациональные числа? Определение, свойства, примеры
Основой овладения любым предметом является знание его лексики. То, как мы комбинируем буквы алфавита, чтобы составить слово, а затем упорядочиваем слова в предложениях, чтобы передать наши мысли, является для нас естественным инстинктом только потому, что мы знаем английский алфавит. Итак, каким должен быть 101 балл, чтобы сделать математику естественным инстинктом? Знание его рудиментарной единицы: чисел. Мы учим считать, используя целые числа, но одним из наиболее важных аспектов математической системы счисления являются рациональные числа, или, проще говоря, числа между числами.
Итак, каким должен быть 101 балл, чтобы сделать математику естественным инстинктом? Знание его рудиментарной единицы: чисел. Мы учим считать, используя целые числа, но одним из наиболее важных аспектов математической системы счисления являются рациональные числа, или, проще говоря, числа между числами.
Что такое рациональные числа?
Рациональные числа — это числа, которые можно записать в виде pq, где p и q — целые числа, а q≠0. Отличие рациональных чисел от дробей заключается в том, что у дробей не может быть отрицательных числителя или знаменателя. Следовательно, числитель и знаменатель дроби — целые числа (знаменатель ≠ 0), тогда как в случае рациональных чисел числитель и знаменатель — целые числа.
Родственные игры
Примеры рациональных чисел
- $\frac{4}{5}$, $\frac{-10}{15}$, $\frac{9}{-17}$, $\frac{-2}{-7}$
- Ноль является рациональным числом, поскольку его можно записать в виде $\frac{0}{10}$, $\frac{0}{2}$, $\frac{0}{-15}$, $\ frac{0}{27}$ и т.
 д.
д.
Итак, ноль можно представить в виде дроби с ненулевым знаменателем.
- Каждое натуральное число является рациональным числом.
1 = $\frac{1}{1}$, 5 = $\frac{5}{1}$, 8 = $\frac{8}{1}$
Итак, каждое натуральное число можно выразить как дробь с 1 в знаменателе.
- Каждое целое число является рациональным числом.
-7 = $\frac{-7}{1}$, -13 = $\frac{-13}{1}$
Итак, каждое целое число можно представить в виде дроби с 1 в знаменателе.
- Каждая дробь является рациональным числом.
$\frac{2}{3}$, $\frac{18}{7}$, $\frac{19}{11}$
Где числитель и знаменатель являются целыми числами, а знаменатель не равен до нуля.
- Положительные рациональные числа
Рациональное число положительно, если его числитель и знаменатель имеют одинаковые знаки (либо оба положительные, либо оба отрицательные).
$\frac{-5}{-6}$, $\frac{7}{12}$, $\frac{-19}{-12}$, $\frac{42}{85}$
- Отрицательные рациональные числа
Рациональное число отрицательно, если его числитель и знаменатель имеют противоположные знаки (один из них положительный, а другой отрицательный).
$\frac{-32}{43}$, $\frac{27}{-63}$, $\frac{-12}{14}$, $\frac{9}{-16}$
- Десятичные числа: 0,45, 0,5446, 0,01864. Поскольку десятичные дроби можно записать в виде дробей со знаменателем 10, 100, 1000… десятичные числа также считаются рациональными числами.
Связанные рабочие листы
Непримеры рационального числа
- Квадратный корень, кубический корень и т. д. натуральных чисел, если их точное значение не может быть определено.
$\sqrt{2}$, $\sqrt{3}$, $\sqrt[2]{8}$, $\sqrt[3]{81}$, $\sqrt[4]{27}$
- $\sqrt{3}$, – $\sqrt{5}$, 8 + $\sqrt{10}$, $\sqrt{2}$ + $\sqrt{3}$
Стандартная форма рациональных чисел
Говорят, что рациональное число $\frac{p}{q}$ находится в стандартной форме, если числитель и знаменатель (p и q) не имеют общего делителя (или множитель), кроме 1 и знаменатель « q » положительный.
Как преобразовать рациональное число в стандартную форму:
- Рассмотрим рациональное число $\frac{18}{–24}$;
Давайте посмотрим, как мы можем преобразовать это рациональное число в его стандартную форму.
Шаг 1: Убедитесь, что знаменатель положительный. Если нет, умножьте числитель и знаменатель на «-1», чтобы изменить знак.
Шаг 2: Найдите все общие делители числителя и знаменателя.
Здесь числа 18 и 24 имеют общие делители 1, 2, 3, 6.
Шаг 3: Разделите числитель и знаменатель на их наибольший общий делитель. Вот так:
Шаг 3 не требуется! Как видите, $\frac{–3}{4}$ – стандартное рациональное число и стандартная форма $\frac{18}{–24}$.
- Рассмотрим десятичное число 0,5
Шаг 1: Чтобы преобразовать десятичное число в стандартное рациональное число, мы сначала преобразуем его в рациональное число.
Шаг 2: Теперь выполните те же шаги для преобразования рационального числа в его стандартную форму, как определено выше, и мы получим
Операции над рациональными числами
Сложение рациональных чисел:
- числа равны:
Сложите числители и оставьте знаменатели прежними.
Например, мы можем сложить два рациональных числа 2/8 и ⅜ следующим образом:
- Когда знаменатели данных чисел не равны:
Например, чтобы сложить рациональные числа ⅖ и ¾
Шаг 1: Найдите НОК знаменателя заданных рациональных чисел. Здесь НОК 4 и 5 равен 20.
Шаг 2: Преобразуйте каждое рациональное число в эквивалентное рациональное число с НОК в качестве нового знаменателя.
Шаг 3: Для этих новых рациональных чисел сложите числители и оставьте прежними знаменатели, и это будет окончательный ответ.
Следовательно, ⅖ + ¾ = 23/20.
Вычитание рациональных чисел:
- Когда знаменатели данных чисел равны:
Вычтите числители и оставьте знаменатель прежним.
Например:
- Когда знаменатели данных чисел не равны:
Например, чтобы вычесть ⅓ из ½
Шаг 1: Найдите НОК знаменателя заданных рациональных чисел. В этом случае НОК 2 и 3 равен 6.
Шаг 2: Преобразуйте каждое рациональное число в эквивалентное рациональное число с НОК в качестве нового знаменателя.
Шаг 3: Выполните шаги вычитания рациональных чисел с одинаковыми знаменателями.
Следовательно, ½ – ⅓ = ⅙
Умножение рациональных чисел:
Это, пожалуй, самая простая операция над рациональными числами.
Чтобы умножить два рациональных числа, просто умножьте числитель и знаменатель первого рационального числа на числитель и знаменатель второго рационального числа соответственно.
Например, чтобы умножить рациональные числа ⅖ и ¾,
Решаемые примеры
Пример 1: Выразите $\frac{25}{40}$ в стандартной форме.
Решение:
Наибольший делитель 25 и 40 = 5
Пример 2. Сложите: $\frac{2}{11}+\frac{7}{11}$ .
Решение:
$\frac{2}{11}+\frac{7}{11}= \frac{2+7}{11}=\frac{9}{11}$
Пример 3. Вычтите $\frac{5}{7}$ из $\frac{9}{7}$ .
Вычтите $\frac{5}{7}$ из $\frac{9}{7}$ .
Решение:
$\frac{9}{7}–\frac{5}{7}= \frac{9–5}{7}=\frac{2}{7}$
Практические задачи
1Число 398 можно выразить рациональным числом следующим образом:398/1 0/398 1/398 398 не является рациональным числом. Правильный ответ: 398/1 Число 0,7 можно представить в виде рационального числа как:$\frac{10}{7}$ $\frac{7}{10}$ $\frac{0.7}{10}$ 0,7 не является рациональным числом Правильный ответ составляет: $\frac{7}{10}$ Стандартная форма числа $\frac{–20}{15}$:1 $\ frac{2}{5}$ $\frac{-10}{3}$ $\frac{3}{-10}$ Правильный ответ: $\frac{-10}{3} $ |

 И к ним же относится ноль. Главное условие – они не должны быть дробными. То есть -15, 0 и +256 можно назвать целыми числами, а 2,5 или -3,78 – нет.
И к ним же относится ноль. Главное условие – они не должны быть дробными. То есть -15, 0 и +256 можно назвать целыми числами, а 2,5 или -3,78 – нет. Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.
Это числа, которые можно записать двумя разными вариантами, и у которых вполне конкретное количество знаков после запятой. Самый простой пример – половина. Ее можно обозначить дробью 0,5 или дробью ½.
 Как и в случае √5, равного 2,2360679.77499789696409173… иррациональное число.
Как и в случае √5, равного 2,2360679.77499789696409173… иррациональное число. Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)
Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)

 Нам нужно разделить 1 на 2 и мы получим 0,5
Нам нужно разделить 1 на 2 и мы получим 0,5 Например, 3/4, 1/9, и так далее. Это означает, что значения p и q не могут быть отрицательными.
Например, 3/4, 1/9, и так далее. Это означает, что значения p и q не могут быть отрицательными. д.
д. 