Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
02.16
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его .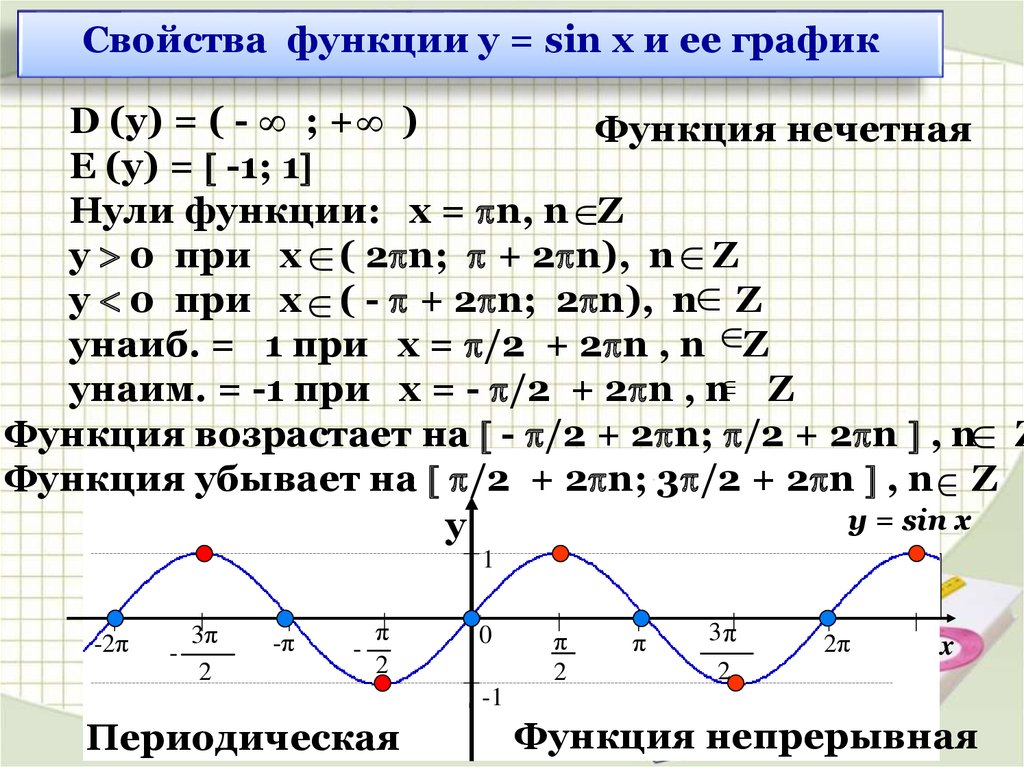
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
шмель и оса полетели с…
Решено
Из пункта А в пункт В,расположенный ниже по течению реки,отправился плот. Одновременно с ним из пункта А вышел катер.Дойдя до В,катер сразу же…
Решено
два самолёта вылетели с аэродрома…
Пользуйтесь нашим приложением
Синус и косинус. Их свойства и уравнения 9 класс онлайн-подготовка на Ростелеком Лицей
Тема урока, введение, повторение
Напоминание:
Числовой аргумент tмы откладываем на единичной окружности, которая помещена в координатную плоскость Каждому числу tсоответствует т. М на единичной окружности (рис.1).
Числовая окружность помещена в координатную плоскость, значит т.
М имеет две координаты
Первую координату назвали косинусом числа t, вторую – синусом числа t.
Свойства точек числовой окружности
Свойства:
1. Если каждому числу t соответствует только одна точка М, то точке М соответствуют все числа вида: n-количество оборотов в положительном или отрицательном направлении.
;
Соотношение (1) показывает, что период функций синус и косинус равен наименьший положительный период равен
Если задано число , мы получаем только одну точку М . Но если задана точка, ей соответствует не только одно число (длина дуги АМ), но и все числа вида , т.е. чисел, соответствующих точке числовой окружности бесчисленное множество.
2. Если длина дуги единичной окружности равна , то она численно равна ÐАОМ в радианах.
— геометрическая интерпретация.
3. – уравнение единичной окружности.
;
– основное тригонометрическое тождество.
Свойства синуса и косинуса
Свойства синуса и косинуса.
1.
Проиллюстрируем на числовой окружности.
длина дуги
длина дуги
Абсциссы точек одинаковы, т.е. , а ординаты противоположны, т.е.
2.
Проиллюстрируем на числовой окружности.
Пусть т. М соответствует числу тогда отличается от т. М на половину окружности. И абсциссы и ординаты точек противоположны, значит
3.
Это следует из определения: так как мы рассматриваем единичную окружность, то абсциссы и ординаты принадлежащих ей точек находятся в промежутке от до
Пример
Пример: Решить уравнение:
Таким образом, по заданной ординате находим все точки единичной окружности, а по точкам находим множество всех действительных чисел, им соответствующих.
Ответ:
Таким образом, мы рассмотрели свойства синуса и косинуса.
Заметили, что
Заключение
В заключение отметим, что знаки синуса и косинуса легко установить по определению:
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.
Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на ресурсы интернет
1. Открытая математика (Источник).
2. РЕШУ ЕГЭ (Источник).
3. РЕШУ ЕГЭ (Источник).
4. РЕШУ ЕГЭ (Источник).
Рекомендованное домашнее задание
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.
№№ 577; 579; 583; 584; 592; 594.
Как найти период функции
Обновлено 14 мая 2018 г.
Автор John Papiewski
Когда вы рисуете тригонометрические функции, вы обнаруживаете, что они периодические; то есть они дают результаты, которые предсказуемо повторяются.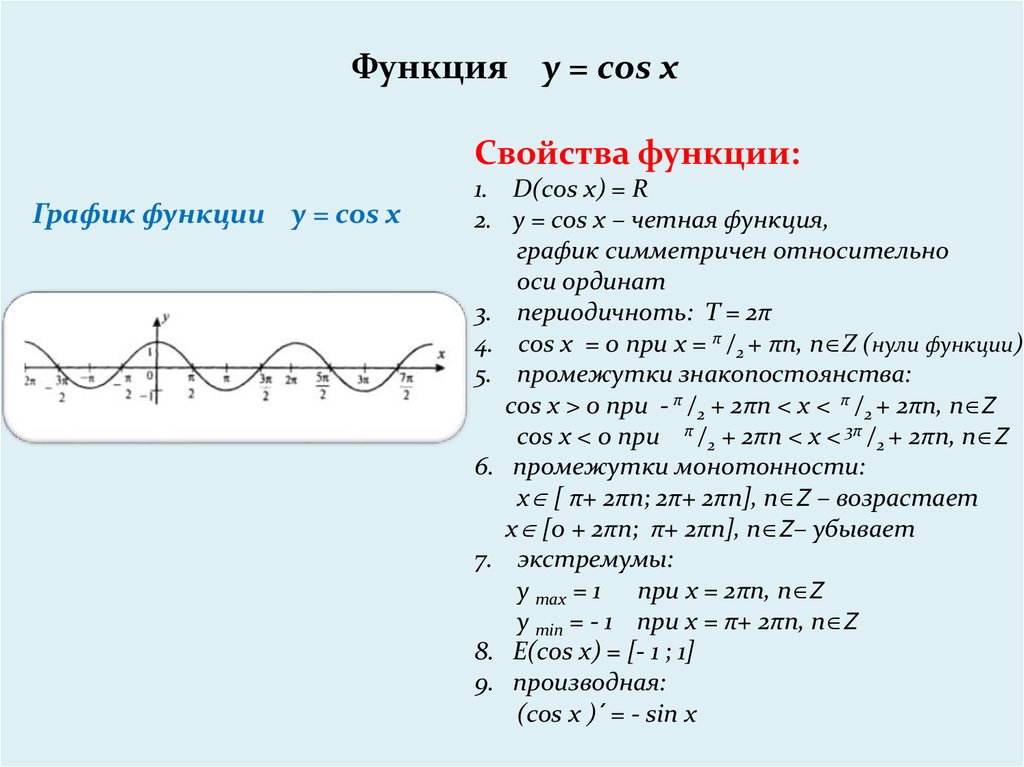
Чтобы найти период заданной функции, вам нужно знать каждую из них и то, как изменения в их использовании влияют на период. Как только вы поймете, как они работают, вы сможете без проблем разобрать триггерные функции и найти период.
TL;DR (слишком длинный; не читал)
Период функций синуса и косинуса составляет 2π (пи) радиан или 360 градусов. Для функции тангенса период составляет π радиан или 180 градусов.
Определено: период функции
Когда вы наносите их на график, тригонометрические функции создают регулярно повторяющиеся волновые формы. Как и любая волна, формы имеют узнаваемые черты, такие как пики (высокие точки) и впадины (низкие точки). Период говорит вам об угловом «расстоянии» одного полного цикла волны, обычно измеряемом между двумя соседними пиками или впадинами. По этой причине в математике вы измеряете период функции в угловых единицах. Например, начиная с нулевого угла, синусоидальная функция дает гладкую кривую, которая поднимается до максимума 1 при π/2 радианах (90 градусов), пересекает ноль при π радиан (180 градусов), уменьшается до минимума -1 при 3π / 2 радианах (270 градусов) и снова достигает нуля при 2π радиан (360 градусов).
После этой точки цикл повторяется бесконечно, создавая те же функции и значения по мере увеличения угла в положительном направлении x .
Синус и косинус
Функции синуса и косинуса имеют период 2π радиан. Функция косинуса очень похожа на синус, за исключением того, что она «опережает» синус на π/2 радиана. Функция синуса принимает значение нуля при нуле градусов, тогда как косинус равен 1 в той же точке.
Функция тангенса
Вы получаете функцию тангенса, разделив синус на косинус. Его период равен π радианам или 180 градусам. График тангенса ( x ) равен нулю при нулевом угле, изгибается вверх, достигает 1 в π / 4 радианах (45 градусов), затем снова изгибается вверх, где достигает точки деления на ноль в π / 2 радианах. Затем функция становится отрицательной бесконечностью и описывает зеркальное отражение ниже оси y , достигая −1 при 3π / 4 радианах, и пересекает y 9ось 0016 на π радиан.
Хотя она имеет значения x , при которых она становится неопределенной, функция тангенса по-прежнему имеет определяемый период.
Секанс, косеканс и котангенс
Три другие триггерные функции, косеканс, секанс и котангенс, являются обратными величинами синуса, косинуса и тангенса соответственно. Другими словами, косеканс ( x ) равен 1/sin( x ), секанс ( x ) = 1/cos( x ) и cot( x ) = 1/tan( x ). ). Хотя их графики имеют неопределенные точки, периоды для каждой из этих функций такие же, как для синуса, косинуса и тангенса.
Множитель периода и другие факторы
Умножая x в тригонометрической функции на константу, вы можете сократить или увеличить ее период. Например, для функции sin(2_x_) период составляет половину ее нормального значения, потому что аргумент x удваивается. Он достигает своего первого максимума при π/4 радианах вместо π/2 и завершает полный цикл в π радианах.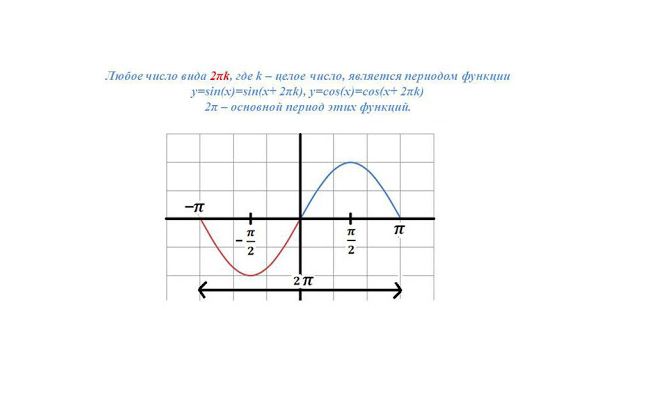
Другие факторы, которые вы обычно видите в триггерных функциях, включают изменения фазы и амплитуды, где фаза описывает изменение начальной точки на графике, а амплитуда — это максимальное или минимальное значение функции, игнорируя отрицательный знак минимума. Выражение 4 × sin(2_x_ + π), например, достигает максимума 4 из-за множителя 4 и начинает с кривой вниз, а не вверх из-за того, что к периоду добавляется константа π. Обратите внимание, что ни константы 4, ни константы π не влияют на период функции, а только на ее начальную точку, а также максимальное и минимальное значения.
Период функции
Интервал времени между двумя волнами называется периодом, тогда как функция, которая повторяет свои значения через равные интервалы или периоды, может быть определена как периодическая функция. Или мы можем сказать, что периодическая функция — это функция, которая повторяет свои значения через каждый конкретный интервал. Это определение периодической функции.
Предположим, у нас есть функция f, которая будет периодической с периодом m, поэтому, если мы можем написать
f (a + m) = f (a), для каждого значения m > 0,
Это показывает, что данная функция f(a) имеет те же значения после заданного значения интервала «m».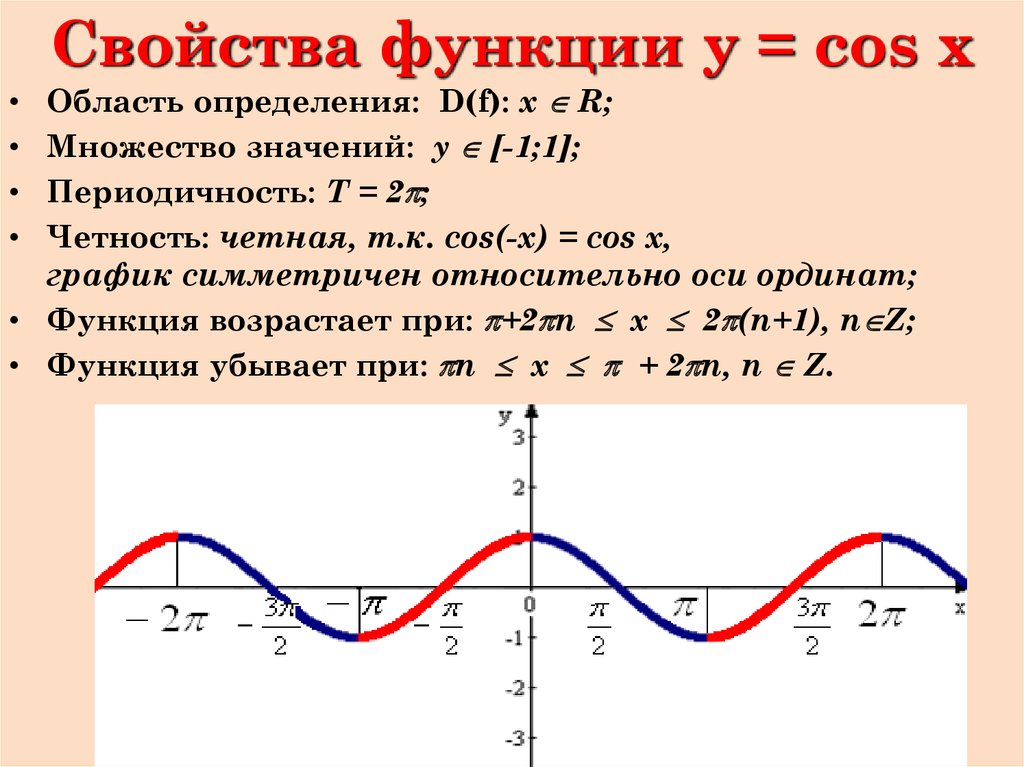
Можно также сказать, что после каждого интервала «m» данная функция f повторяет все свои значения.
Примеры периодических функций. Функция синуса sin a имеет период 2 π, потому что 2 π — это наименьшее число, для которого значение sin (a + 2π) = sin a для всех значений a.
Мы всегда можем рассчитать период, используя формулу, полученную из основных уравнений синуса и косинуса. Период для функции y = A sin (Ba – c) и y = A cos (Ba – c) равен 2πB радиан.
Обратная величина периода функции равна ее частоте.
Частота может быть определена как количество циклов, совершаемых в секунду (за период в одну секунду). Если мы обозначим период функции через P и пусть f будет ее частотой, то формула для частоты может быть записана как –f =1/P.
Основной период функции
Согласно определению периодической функции основной период функции можно определить как период функции, которые имеют вид
f(x+k)= f(x)
f(x+k)=f(x), тогда k называется периодом функции, а функция f называется периодической функцией.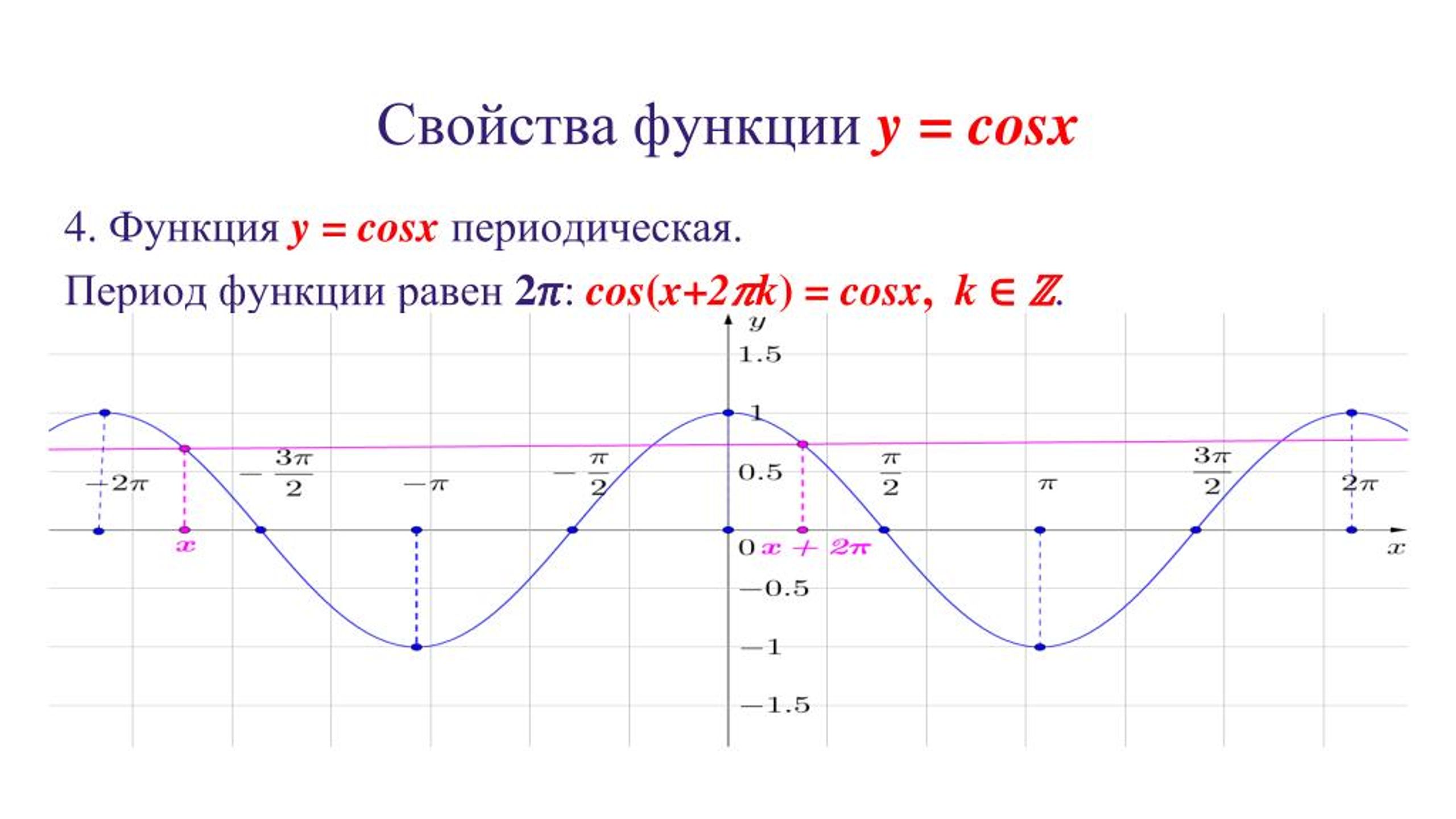
Примеры периодических функций: —
Теперь мы определим функцию h (t) на интервале [0,2] следующим образом:
Изображение будет загружено в ближайшее время
R по уравнению,
h(t+2)=h(t)
Тогда h периодично с периодом 2.
Изображение скоро будет загружено
Период тригонометрических функций —
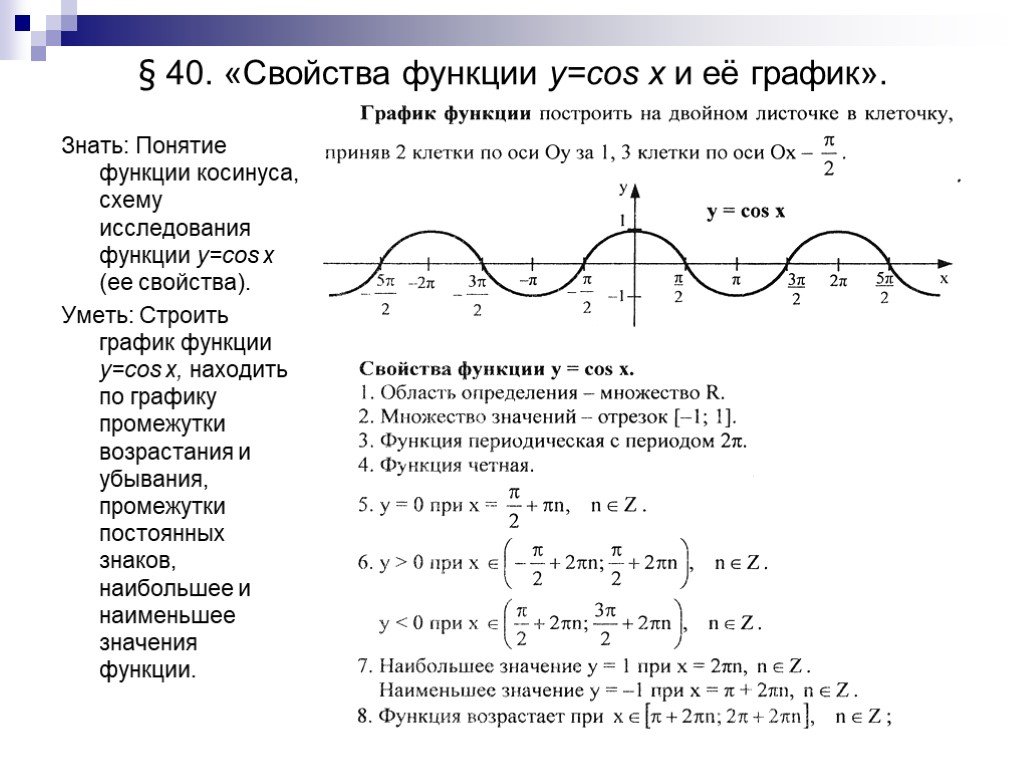
Когда вы наносите тригонометрические функции на график, тригонометрические функции создают регулярно повторяющиеся волновые формы. Как и в любой волне, формы имеют узнаваемые особенности, такие как пики (которые также известны как высокие точки) и впадины (которые также известны как низкие точки). Слово период говорит вам об угловом «расстоянии» одного полного цикла волны, которое обычно измеряется между двумя соседними пиками или впадинами. По этой причине в математике вы должны измерять период функции в угловых единицах. Это известно как период тригонометрической функции
Вот, например, предположим, что мы начинаем с нулевого угла, тригонометрическая функция дает гладкую кривую, которая поднимается до максимального значения 1 при π / 2 радианах (что равно 90 градусам), пересекает ноль при π радиан (что равно 180 градусам), уменьшается до минимума -1 при 3π / 2 радианах (что равно 270 градусам) и снова достигает нуля при 2π радианах (то есть 360 градусов).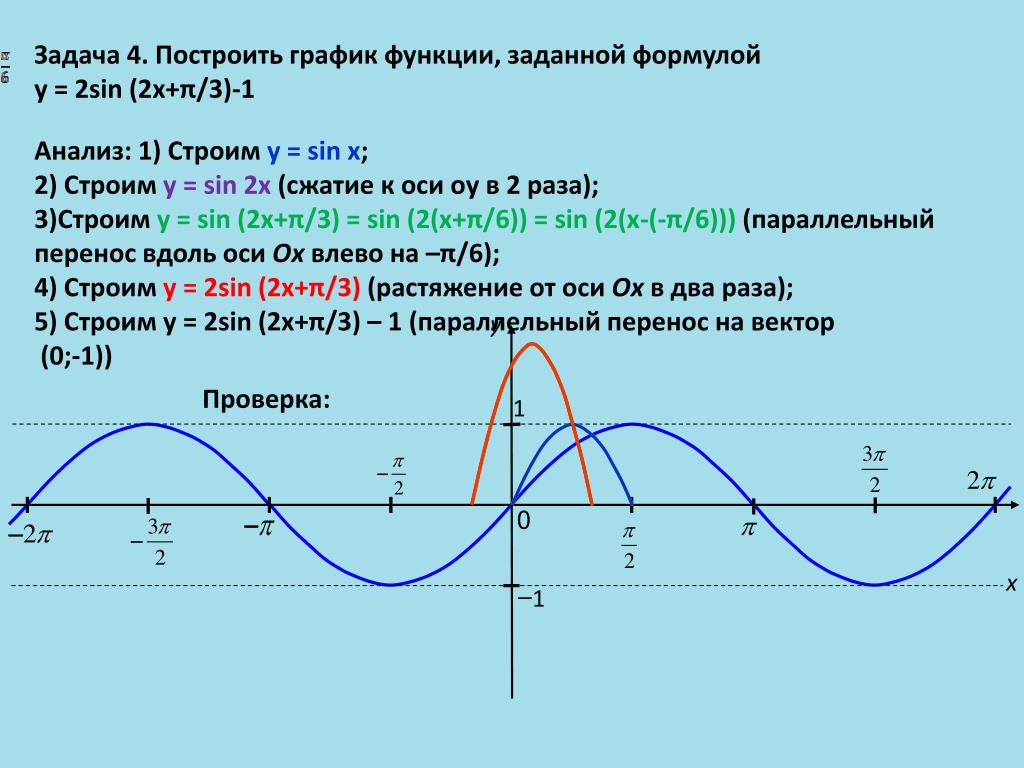
И после этой точки цикл повторяется бесконечно, производя одни и те же функции и те же значения по мере увеличения угла в положительном направлении x.
Для функций синуса и косинуса: | Функции синуса и косинуса являются тригонометрическими функциями, обе имеют период 2π радиан. Функция косинуса очень похожа на функцию синуса, за исключением того, что она «опережает» синус на величину π/2 радиан. Функция синуса принимает значение нуля при нуле градусов, где косинус равен 1 в той же точке |
Для функции тангенса: | Вы в основном получаете функцию тангенса, разделив функцию синуса на функцию косинуса. Его период составляет от π радиан или 180 градусов. График тангенса (x) равен нулю при нулевом угле, изгибается вверх и достигает 1 при π / 4 радианах (что равно 45 градусам), затем снова изгибается вверх, где функция тангенса достигает точки деления на ноль при π / 2 радиана. |
Для функций секанса, косинуса и котангенса: | Три другие тригонометрические функции, косеканс, секанс и котангенс, являются обратными функциями синуса, косинуса и тангенса соответственно. Другими словами, косеканс (x) можно записать как 1/sin(x), секанс(x) можно записать как 1/cos(x), а cot(x) можно записать как 1/tan(x). Хотя их графики имеют неопределенные точки, для каждого периода тригонометрические функции такие же, как для функций синуса, косинуса и тангенса. |
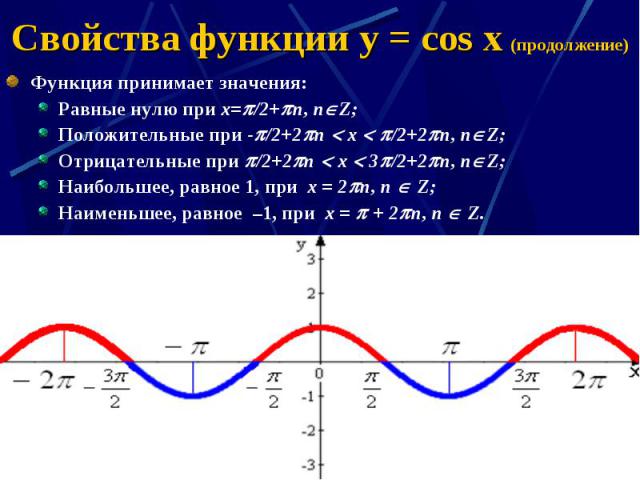Затем функция тангенса становится отрицательной бесконечностью и описывает зеркальное отражение ниже оси y, достигая -1 при 3π / 4 радианах, и пересекает ось y при π радианах, что составляет 180 градусов. Хотя у функции есть значения x, при которых она становится неопределенной, у функции тангенса есть определяемый период..
Как найти период функции?
Если функция повторяется с постоянным периодом, мы можем назвать ее периодической функцией.
